材料力学第二章-12 应力集中的概念
材料力学简答题

材料的三个弹性常数是弹性模量E,剪切弹性模量G和泊松比μ,它们的关系是G=E/2(1+μ)。
2、何谓挠度、转角?挠度:横截面形心在垂直于梁轴线方向上的线位移。
转角:横截面绕其中性轴旋转的角位移。
3、强度理论分哪两类?最大应切力理论属于哪一类强度理论?Ⅰ.研究脆性断裂力学因素的第一类强度理论,其中包括最大拉应力理论和最大伸长线应变理论;Ⅱ. 研究塑性屈服力学因素的第二类强度理论,其中包括最大切应力理论和形状改变能密度理论。
4、何谓变形固体?在材料力学中对变形固体有哪些基本假设?在外力作用下,会产生变形的固体材料称为变形固体。
变形固体有多种多样,其组成和性质是复杂的。
对于用变形固体材料做成的构件进行强度、刚度和稳定性计算时,为了使问题得到简化,常略去一些次要的性质,而保留其主要性质。
根据其主要的性质对变形固体材料作出下列假设。
1.均匀连续假设。
2.各向同性假设。
3.小变形假设。
5、为了保证机器或结构物正常地工作,每个构件都有哪些性能要求?强度要求、刚度要求和稳定性要求。
6、用叠加法求梁的位移,应具备什么条件?用叠加法计算梁的位移,其限制条件是,梁在荷载作用下产生的变形是微小的,且材料在线弹性范围内工作。
具备了这两个条件后,梁的位移与荷载成线性关系,因此梁上每个荷载引起的位移将不受其他荷载的影响。
7、列举静定梁的基本形式?简支梁、外伸梁、悬臂梁。
8、列举减小压杆柔度的措施?(1)加强杆端约束(2)减小压杆长度,如在中间增设支座(3)选择合理的截面形状,在截面面积一定时,尽可能使用那些惯性矩大的截面。
9、欧拉公式的适用范围?只适用于压杆处于弹性变形范围,且压杆的柔度应满足:λ≥λ1= 10、列举图示情况下挤压破坏的结果?一种是钢板的圆孔局部发生塑性变形,圆孔被拉长;另一种是铆钉产生局部变形,铆钉的侧面被压扁。
11、简述疲劳破坏的特征?(1)构件的最大应力在远小于静应力的强度极限时,就可能发生破坏;(2)即使是塑性材料,在没有显著的塑性变形下就可能发生突变的断裂破坏;(3)断口明显地呈现两具区域:光滑区和粗糙区。
刘鸿文版材料力学第二章

A 1
45°
图示结构,试求杆件AB、CB的 应力。已知 F=20kN;斜杆AB为直 径20mm的圆截面杆,水平杆CB为 15×15的方截面杆。
B
C
2
FN 1
FN 2 45°
y
B F
F
解:1、计算各杆件的轴力。 (设斜杆为1杆,水平杆为2杆) 用截面法取节点B为研究对象
x
∑F ∑F
x y
=0
目录
§2.4 材料拉伸时的力学性能
力学性能:在外力作用下材料在变形和破坏方 面所表现出的力学特性。 一 试 件 和 实 验 条 件
常 温 、 静 载
目录
§2.4 材料拉伸时的力学性能
目录
§2.4 材料拉伸时的力学性能
二 低 碳 钢 的 拉 伸
目录
§2.4 材料拉伸时的力学性能
σ
e
b
σb
f
2、屈服阶段bc(失去抵 抗变形的能力)
目录
FRCy
W
§2.2 轴向拉伸或压缩时横截面上的内力和应力
B d
由三角形ABC求出
0.8m
C 1.9m
α
sin α =
A
Fmax
BC 0.8 = = 0.388 AB 0.82 + 1.92 W 15 = = = 38.7kN sin α 0.388
Fmax
斜杆AB的轴力为
FN = Fmax = 38.7kN
F
a
a′ b′
c
c′ d′
F
b
d
平面假设—变形前原为平面的横截面, 变形后仍保持为平面且仍垂直于轴线。
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
《材料力学第二章》课件

弹性变形是可恢复的,而塑性变形是不可恢复的。
弹性变形能与塑性变形能
弹性变形能
01
物体在弹性变形过程中所吸收的能量,与应力和应变关系呈正
比。
塑性变形能
02
物体在塑性变形过程中所吸收的能量,与应力和应变关系呈非
线性。
弹性变形能与塑性变形能的比较
03
弹性变形能是可逆的,而塑性变形能是不可逆的。
材料力学的重要性
总结词
材料力学是工程设计和科学研究的重要基础,对于保证工程安全、优化产品设 计、降低成本等方面具有重要意义。
详细描述
在工程设计和科学研究中,材料力学提供了对材料行为的深入理解,有助于保 证工程结构的稳定性和安全性,优化产品的设计,降低生产成本,提高经济效 益。
材料力学的基本假设和单位
04
CATALOGUE
变形分析
变形的基本概念
变形
物体在外力作用下,形状 和尺寸发生变化的现象。
弹性变形
当外力去除后,物体能够 恢复原状的变形。
塑性变形
当外力去除后,物体不能 恢复原状的变形。
弹性变形与塑性变形
弹性变形特点
可逆、无残余应变、与外力大小成正比。
塑性变形特点
不可逆、有残余应变、外力达到屈服极限后发生。
建筑结构的优化设计
利用材料力学理论,对建筑结构进行优化设计,降低建筑物的重量 和成本,提高建筑物的性能和寿命。
机械工程中的应用
机械零件的强度和刚度分析
利用材料力学知识,对机械零件的强度和刚度进行分析和计算,确保零件在使用过程中不 会发生断裂或变形。
机械设备的动力学分析
通过材料力学的方法,对机械设备的动力学特性进行分析和计算,确保机械设备在使用过 程中具有良好的稳定性和可靠性。
工程力学名词解释

工程力学名词解释1.静力学中研究的两个问题:(1力系的简化;2.物体在力系作用下的平衡条件。
2.刚体:任何状态下都不变形的物体3.多余约束:如果的体系中增加一个约束,体系的独立运动参数并不减少,此类约束为多余约束4.摩擦角;当摩擦力达到最大值时,全反力与法线间的夹角5.材料的塑性:材料能产生塑性变形的性质6.中性轴:在平面弯曲和斜弯曲情况下,横截面与应力平面的交线上各点的正压力值均为零,这条交线叫中性轴7.超静定:如果所研究的问题中,未知量的数目大于对应的独立平衡方程的数目时,仅仅用平衡方程不能求出全部未知量8.低碳钢的冷作硬化;若材料曾一度受力到达强化阶段,然后卸载,则再重新加载时,比例极限和屈服点将提高,而断裂后的塑性变形将减小9.材料力学中的内力:物体内部某一部分与另一部分的相互作用的力10.应力集中:局部区域应力突然增大的现象11.自锁现象;与力的大小无关而与摩擦角有关的平衡条件称为自锁条件,物体在这种条件下的平衡现象称为自锁现象12应力:分布在单位面积上的内力。
13低碳钢的拉伸曲线四个阶段:(1)弹性阶段(2)屈服阶段(3)强化阶段(4)局部变形14.横力弯曲:剪切面上同时存在弯矩M和剪力Fs。
这种弯曲称为和横力弯曲。
Fs为零而弯矩M为常量,这种弯曲称为纯弯曲15剪切:两力间的横截面发生相对错动的形式。
16挤压应力:由于挤压力而引起的应力。
17单元体:如果以横截面和纵向截面自筒壁上取出一个微小的正六面体。
18纯剪切:在单元体上将只有切应力而无正应力的作用。
19中性轴:中性层与横截面的交线。
20提高梁抗弯强度的措施(1)选用合理的截面(2)采用变截面梁(3)适度布置载荷和支座位置21挠曲线:梁弯曲后的轴线。
22.提高梁刚度和强度的主要措施有:1.合理安排梁的支承2.合理的布置载荷3.选择梁的合理截面23.挠度:梁轴线上的一点在垂直于梁变形前轴方向的线位移24.转角:梁任一截面绕其中性轴转动的角度。
材料力学复习资料

一基本概念1.工程构件正常工作必须满足强度、刚度和稳定性的要求。
杆件的强度代表了杆件抵抗破坏的能力;杆件的刚度代表了杆件抵抗变形的能力;杆件的稳定性代表了杆件维持原有平衡形态的能力。
2.变形固体的基本假设是连续性假设、均匀性假设、各向同性假设。
连续性假设认为固体所占据的空间被物质连续地充满而毫无空隙;均匀性假设认为材料的力学性能是均匀的;各向同性假设认为材料沿各个方向具有相同的力学性质。
3.截面法的三个步骤是截取、代替和平衡。
4.杆件变形的基本形式有:拉压,扭转,剪切,弯曲。
5.截面上一点处分布内力的集度,称为该截面该点处的应力。
6.截面上的正应力方向垂直于截面,切应力的方向平行于截面。
7.在卸除荷载后能完全消失的变形称为弹性变形,不能消失而残留下来的变形称为塑性变形。
8.低碳钢受拉伸时,变形的四个阶段为弹性阶段、屈服阶段、强化阶段和局部变形阶段。
9.由杆件截面骤然变化而引起的局部应力骤增的现象称为应力集中。
10.衡量材料塑性的两个指标是伸长率和断面收缩率。
11.受扭杆件所受的外力偶矩的作用面与杆轴线垂直。
12.低碳钢圆截面试件受扭转时,沿横截面破坏;铸铁圆截面试件受扭转时,沿45度角截面破坏。
13.梁的支座按其对梁在荷载作用平面的约束情况,可以简化为三种基本形式,即固定端、固定铰支座、可(活)动铰支座。
14.工程上常用的三种基本形式的静定梁是:简支梁、悬臂梁、外伸梁。
15.平面弯曲梁的横截面上有两个内力分量,分别为剪力和弯矩。
16.拉(压)刚度、扭转刚度和弯曲刚度的表达式分别是EA、GI p和EI z。
17.当梁上有横向力作用时,梁横截面上既有剪力又有弯矩,该梁的弯曲称为横力弯曲。
梁横截面上没有剪力(剪力为0),弯矩为常数,该梁的弯曲称为纯弯曲。
18.在弯矩图发生拐折处,梁上必有集中力的作用。
19.在集中力偶作用处,剪力图将不变。
20.梁的最大正应力发生在最大弯矩所在截面上离中性轴最远的点处。
材料力学第二章

拉压杆横截面上的应力Stresses over the cross section 1.试验观察 Experimental observation
变形后横线仍为直线,仍垂直于杆件轴线,只是间距增大. Transversal line after deformation : straight; perpendicular to the axis.
E= tanα -elastic modulus 弹性模量
1.等直杆或小锥度杆Straight bar(or stepped bar) with uniform section, or with small taper ; 2.外力过轴线 The applied force P acts through the centroid of the cross section; 3.当外力均匀地加在截面上,此式对整个杆件都 适用,否则仅适用于离开外力作用处稍远的截面 The normal stress distribution in an axially loaded member is uniform, except in the near vicinity of the applied load (known as Saint-Venant's Principle) .
§4~5 Mechanical Properties of Materials
材料的力学性能 拉伸试验与应力-应变图Tensile Tests and Stress-Strain Diagram 低碳钢拉伸应力-应变曲线Tensile Stress-Strain Curve for Mild Steel 卸载与再加载路径Unloading and Reloading Path 名义屈服极限Conditional Yield Limit 脆性材料拉伸应力-应变曲线Stress-Strain Curves for Brittle Materials 复合与高分子材料的力学性能Strength Properties of Composite Materials
关于应力集中的概念及其避免措施的讨论

由于应力集中能使结构发生裂纹,甚至断裂,须采取措施,防止因应力集中而造成的 结构损坏,主要措施有:①改善结构外形,避免形状突变,尽可能开圆孔或椭圆孔;②结构 内必须开孔时,尽量避开高应力区,而在低应力区开孔;③根据孔边应力集中的分析成果进 行孔边局部加强。
2、实际工程中圆滑的角避免应力集中 在制作各种拉力工具时,拉脚的拐弯处应设圆角,这并不是为了美观,这是为了避免 应力集中。应力集中指由于受力构件由于几何形状、外形尺寸发生突变而引起的局部范围内 内应力显著增大的现象。应力集中会造成构件的断裂。圆角的大小应根据工具的外形尺寸决 定,太大影响工具的效应,太小工具容易断裂损坏。对于常用的较小拉制工具,圆角半径在 2-3 毫米为佳,较大在 5 毫米左右。对于特殊形状的工具根据实际情况确定。但或大或小必 须留圆角。 参考文献: 1、《材料力学Ⅰ》 主编:刘鸿文 出版社:高等教育出版社 出版时间:2004-01 第四版 2、《材料力学Ⅱ》 主编:刘鸿文 出版社:高等教育出版社 出版时间:2004-01 第四版 3、《工程力学》 作者:王彪 出版社:中国科学技术大学出版社 4、《设计中的应力集中系数》 作者:R.E.彼德逊 出版社 :中国工业出版社 出版时间:1965 年 05 月北京第 1 版 5、《建筑钢结构进展》 作者:澳门大学土木及环境工程系 中国澳门(郭伟明);香港理 工大学土木及结构工程系 中国香港(滕锦光;钟国辉) 出版时间:2007-03 6、王威,王社良,苏三庆,徐金兰 ;《钢铁材料结构构件 工作应力的检测方法及特点[J ]》; 《钢结构》;2004 年 05 期
过一点所方向面上应力的集合,称为这一点的应力状态

应力是指物体内部受到的力的作用,它可以通过单位面积上的力来描述。
在工程力学中,应力是非常重要的物理量,它与物体的形状、材料特性和外部力的作用密切相关。
本文将围绕应力的概念展开讨论,针对其在材料力学中的应用进行深入分析。
一、应力的定义和分类1.1 应力的概念应力是单位面积上的力,常用符号表示为σ,其计算公式为力F除以面积A,即σ=F/A。
在物体内部,由于外部力的作用,各处都会受到应力的作用,这种应力称为内应力。
而外部施加在物体表面上的力也会导致应力的产生,这种应力称为外部应力。
1.2 应力的分类根据应力的作用方向和大小,可以将应力分为正应力、剪切应力和法向应力三种类型。
正应力是垂直于物体截面的应力,常用符号表示为σn。
而沿着截面方向的应力称为剪切应力,常用符号表示为τ。
另外,法向应力是指作用在物体某一点上的应力。
二、应力状态的描述2.1 应力张量在三维空间中,一个点的应力状态可以由一个3x3的对称矩阵来描述,这个对称矩阵称为应力张量。
应力张量的分量代表了在不同方向上的应力情况,可以通过数学方法进行求解和分析。
2.2 应力状态的表示一个点处的应力状态可以通过应力张量的特征值和特征向量来表示。
特征值代表了应力状态的大小,特征向量则代表了应力作用的方向。
通过对特征值和特征向量的分析,可以判断物体处于何种应力状态,从而进行相应的力学分析和设计。
三、应力的应用3.1 工程材料的性能应力是描述物体受力情况的重要参数,它直接影响着材料的强度、刚度和韧性等性能。
在工程中,通过对材料的应力状态进行分析,可以评估材料的可靠性和安全性,为工程设计提供参考依据。
3.2 结构的稳定性对结构件的受力状态进行分析,可以判断结构在外部载荷作用下的稳定性。
通过对结构的应力分布和应力集中区域的分析,可以预测结构是否会发生破坏或失稳现象,为结构设计和改进提供重要参考。
3.3 力学设计在工程实践中,需要根据实际的力学要求来设计各种零部件和结构件。
材料力学简答题

1、(中)材料的三个弹性常数是什么它们有何关系材料的三个弹性常数是弹性模量E,剪切弹性模量G和泊松比μ,它们的关系是G=E/2(1+μ)。
2、何谓挠度、转角挠度:横截面形心在垂直于梁轴线方向上的线位移。
转角:横截面绕其中性轴旋转的角位移。
3、强度理论分哪两类最大应切力理论属于哪一类强度理论Ⅰ.研究脆性断裂力学因素的第一类强度理论,其中包括最大拉应力理论和最大伸长线应变理论;Ⅱ. 研究塑性屈服力学因素的第二类强度理论,其中包括最大切应力理论和形状改变能密度理论。
4、何谓变形固体在材料力学中对变形固体有哪些基本假设在外力作用下,会产生变形的固体材料称为变形固体。
变形固体有多种多样,其组成和性质是复杂的。
对于用变形固体材料做成的构件进行强度、刚度和稳定性计算时,为了使问题得到简化,常略去一些次要的性质,而保留其主要性质。
根据其主要的性质对变形固体材料作出下列假设。
1.均匀连续假设。
2.各向同性假设。
3.小变形假设。
5、为了保证机器或结构物正常地工作,每个构件都有哪些性能要求强度要求、刚度要求和稳定性要求。
6、用叠加法求梁的位移,应具备什么条件用叠加法计算梁的位移,其限制条件是,梁在荷载作用下产生的变形是微小的,且材料在线弹性范围内工作。
具备了这两个条件后,梁的位移与荷载成线性关系,因此梁上每个荷载引起的位移将不受其他荷载的影响。
7、列举静定梁的基本形式简支梁、外伸梁、悬臂梁。
8、列举减小压杆柔度的措施(1)加强杆端约束(2)减小压杆长度,如在中间增设支座(3)选择合理的截面形状,在截面面积一定时,尽可能使用那些惯性矩大的截面。
9、欧拉公式的适用范围=只适用于压杆处于弹性变形范围,且压杆的柔度应满足:λ≥λ110、列举图示情况下挤压破坏的结果一种是钢板的圆孔局部发生塑性变形,圆孔被拉长;另一种是铆钉产生局部变形,铆钉的侧面被压扁。
11、简述疲劳破坏的特征(1)构件的最大应力在远小于静应力的强度极限时,就可能发生破坏;(2)即使是塑性材料,在没有显着的塑性变形下就可能发生突变的断裂破坏;(3)断口明显地呈现两具区域:光滑区和粗糙区。
工程材料力学名词解释

应变(strain):为一微小材料(元素)承受应力时所产生的单位长度变形量(力学定义,无量纲)弹性变形(elastic deformation): 材料在外力作用下产生变形,当外力去除后恢复其原来形状,这种随外力消失而消失的变形。
重要特征:可逆性、胡克定律(是力学基本定律之一。
适用于一切固体材料的弹性定律,它指出:在弹性限度内,物体的形变跟引起形变的外力成正比)4)塑性变形(plastic deformation):材料在外力作用下产生的永久不可恢复的变形。
(5)断裂(fracture,rupture 破裂、crack裂纹):物体在外力作用下产生裂纹以至断开的现象。
脆性断裂(未发生较明显的塑性变形)、韧性断裂(发生较明显的塑性变形),宏观特征(1)弹性(elasticity):是指物体(材料)本身的一种特性,发生形变后可以恢复原来的状态的一种性质.(2)弹性变形(elastic deformation):材料在外力作用下产生变形,当外力去除后恢复其原来形状,这种随外力消失而消失的变形。
(3)弹性模量(elastic modulus,modulus of elasticity):是表征材料弹性的物理参数,是指材料在弹性变形范围内,应力和对应的应变的比值E=σ/ε,也是材料内部原子之间结合力强弱的直接量度。
(4)刚度(stiffness):指物体(固体)在外力作用下抵抗变形的能力,可用使产生单位形变所需的外力值来量度.刚度越高,物体表现越硬。
(5)弹性比功(elastic specific work): 表示材料吸收弹性变形功的能力,弹性比能、应变比能,决定于弹性模量和弹性极限(即材料由弹性变形过渡到弹-塑性变形时的应力)。
(6)滞弹性(anelasticity):在弹性范围内加快加载或卸载后,随时间延长产生附加弹性应变的现象。
7)循环弹性(cyclic elasticity):在交变载荷(振动)下材料吸收不可逆变形功的能力. (8)包申格效应(Bauschinger′s effect,Bauschinger effect):简单地说,就是经过预先加载产生少量塑性变形后的金属材料,再次进行同向或反向加载,会产生残余伸长应力(弹性极限或屈服极限)增加或降低的现象。
材料力学基本概念(最新整理)

材料力学基本概念一、基本概念1 材料力学的任务是:研究构件的强度、刚度、稳定性的问题,解决安全与经济的矛盾。
2 强度:构件抵抗破坏的能力。
3 刚度:构件抵抗变形的能力。
4 稳定性:构件保持初始直线平衡形式的能力。
5 连续均匀假设:构件内均匀地充满物质。
6 各项同性假设:各个方向力学性质相同。
7 内力:以某个截面为分界,构件一部分与另一部分的相互作用力。
8 截面法:计算内力的方法,共四个步骤:截、留、代、平。
9 应力:在某面积上,内力分布的集度(或单位面积的内力值)、单位Pa。
10 正应力:垂直于截面的应力(σ)11 剪应力:平行于截面的应力( )12 弹性变形:去掉外力后,能够恢复的那部分变形。
13 塑性变形:去掉外力后,不能够恢复的那部分变形。
14 四种基本变形:拉伸或压缩、剪切、扭转、弯曲。
二、拉压变形15 当外力的作用线与构件轴线重合时产生拉压变形。
16 轴力:拉压变形时产生的内力。
17 计算某个截面上轴力的方法是:某个截面上轴力的大小等于该截面的一侧各个轴向外力的代数和,其中离开该截面的外力取正。
18 画轴力图的步骤是:①画水平线,为X轴,代表各截面位置;②以外力的作用点为界,将轴线分段;③计算各段上的轴力;④在水平线上画出对应的轴力值。
(包括正负和单位)19 平面假设:变形后横截面仍保持在一个平面上。
20 拉(压)时横截面的应力是正应力,σ=N/A21 斜截面上的正应力:σα=σcos²α22 斜截面上的切应力: α=σSin2α/223 胡克定律:杆件的变形时与其轴力和长度成正比,与其截面面积成反比,计算式△L=NL/EA(适用范围σ≤σp)24 胡克定律的微观表达式是σ=Eε。
25 弹性模量(E)代表材料抵抗变形的能力(单位P a)。
26 应变:变形量与原长度的比值ε=△L/L(无单位),表示变形的程度。
27 泊松比(横向变形与轴向变形之比)μ=∣ε1/ε∣28 钢(塑)材拉伸试验的四个过程:比例阶段、屈服阶段、强化阶段、劲缩阶段。
材料力学 第2章应力集中 剪切与挤压

键的右侧的下半部分受到轴给键的作用力,合力大小F‘;
(3)、剪切面: 两组力的作用线交错的面;
A = bl
(4)、挤压面: 相互压紧的局部接触面;
Abs
=
hl 2
(5) 挤压应力
σ bs
=
F Abs
例 齿轮与轴由平键(b×h×L=20 ×12 ×100)连接,它传递的
扭矩m=2KNm,轴的直径d=70mm,键的许用剪应力为[τ]= 60M Pa ,许用挤压应力为[σbs]= 100M Pa,试校核键的强度。
h
L
AQ
b
m P
d
综上,键满足强度要求。
接头的强度计算 在铆钉钢板的接头中,有几种可能的破坏?
P P
可能造成的破坏: (1)因铆钉被剪断而使铆接被破坏;
(2)铆钉和板在钉孔之间相互挤压过大,而使铆接被 破坏;
(3)因板有钉孔,在截面被削弱处被拉断。
N1a − N3a = 0
Δl1
=
N 1l EA
Δl2
=
N2l EA
Δ与原长相比为无穷小;
Δl3
=
N3l EA
且由静力学关系得知 Δl1 = Δl3
3、协调关系 作协调图,确定各变形量之间的关系; 协调关系 Δ -⊿L2= ⊿L1
4、补充方程
Δ -⊿L2= ⊿L1 5、联立求解
Δ − N2l = N1l EA EA
A
B
由于在安装阶段,迫使杆件产生变形,
必定会在杆内 产生应力; 装配应力:
12
3
静不定结构中, 由于杆件的尺寸不准确, A
B
强行装配在一起,在未受载荷之前,杆内已产生应力。
即由于强行装配在一起而引起的应力。 装配应力的特点:
(完整版)材料力学名词解释(1)

名词解释第一章:1弹性比功:金属材料吸收弹性变形功的能力,一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。
2.滞弹性:金属材料在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象称为滞弹性,也就是应变落后于应力的现象。
3.循环韧性:金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。
4.包申格效应:金属材料经过预先加载产生少量塑性变形,卸载后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
5.解理刻面:这种大致以晶粒大小为单位的解理面称为解理刻面。
6.塑性:金属材料断裂前发生不可逆永久(塑性)变形的能力。
韧性:指金属材料断裂前吸收塑性变形功和断裂功的能力。
7.解理台阶:当解理裂纹与螺型位错相遇时,便形成一个高度为b的台阶。
8.河流花样:解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样。
是解理台阶的一种标志。
9.解理面:是金属材料在一定条件下,当外加正应力达到一定数值后,以极快速率沿一定晶体学平面产生的穿晶断裂,因与大理石断裂类似,故称此种晶体学平面为解理面。
10.穿晶断裂:穿晶断裂的裂纹穿过晶内,可以是韧性断裂,也可以是脆性断裂。
沿晶断裂:裂纹沿晶界扩展,多数是脆性断裂。
11.韧脆转变:具有一定韧性的金属材料当低于某一温度点时,冲击吸收功明显下降,断裂方式由原来的韧性断裂变为脆性断裂,这种现象称为韧脆转变12.弹性不完整性:理想的弹性体是不存在的,多数工程材料弹性变形时,可能出现加载线与卸载线不重合、应变滞后于应力变化等现象,称之为弹性不完整性。
弹性不完整性现象包括包申格效应、弹性后效、弹性滞后和循环韧性等13.弹性极限:式样加载后再卸载,以不出现残留的永久变形为标准,材料能够完全弹性恢复的最高应力。
14.静力韧度:金属材料在静拉伸时单位体积材料断裂前所吸收的功。
15.正断型断裂:断裂面取向垂直于最大正应力的断裂。
工程材料力学名词解释

应变(strain):为一微小材料(元素)承受应力时所产生的单位长度变形量(力学定义,无量纲)弹性变形(elastic deformation): 材料在外力作用下产生变形,当外力去除后恢复其原来形状,这种随外力消失而消失的变形。
重要特征:可逆性、胡克定律(是力学基本定律之一。
适用于一切固体材料的弹性定律,它指出:在弹性限度内,物体的形变跟引起形变的外力成正比)4)塑性变形(plastic deformation):材料在外力作用下产生的永久不可恢复的变形。
(5)断裂(fracture,rupture 破裂、crack裂纹):物体在外力作用下产生裂纹以至断开的现象。
脆性断裂(未发生较明显的塑性变形)、韧性断裂(发生较明显的塑性变形),宏观特征(1)弹性(elasticity):是指物体(材料)本身的一种特性,发生形变后可以恢复原来的状态的一种性质。
(2)弹性变形(elastic deformation):材料在外力作用下产生变形,当外力去除后恢复其原来形状,这种随外力消失而消失的变形。
(3)弹性模量(elastic modulus,modulus of elasticity):是表征材料弹性的物理参数,是指材料在弹性变形范围内,应力和对应的应变的比值E=σ/ε,也是材料内部原子之间结合力强弱的直接量度。
(4)刚度(stiffness):指物体(固体)在外力作用下抵抗变形的能力,可用使产生单位形变所需的外力值来量度。
刚度越高,物体表现越硬。
(5)弹性比功(elastic specific work):表示材料吸收弹性变形功的能力,弹性比能、应变比能,决定于弹性模量和弹性极限(即材料由弹性变形过渡到弹-塑性变形时的应力)。
(6)滞弹性(anelasticity):在弹性范围内加快加载或卸载后,随时间延长产生附加弹性应变的现象。
7)循环弹性(cyclic elasticity):在交变载荷(振动)下材料吸收不可逆变形功的能力。
应力集中
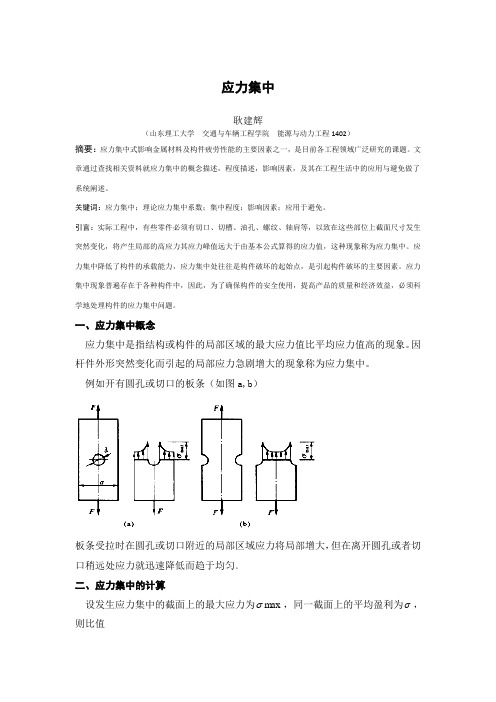
应力集中耿建辉(山东理工大学交通与车辆工程学院能源与动力工程1402)摘要:应力集中式影响金属材料及构件疲劳性能的主要因素之一,是目前各工程领域广泛研究的课题。
文章通过查找相关资料就应力集中的概念描述,程度描述,影响因素,及其在工程生活中的应用与避免做了系统阐述。
关键词:应力集中;理论应力集中系数;集中程度;影响因素;应用于避免。
引言:实际工程中,有些零件必须有切口、切槽、油孔、螺纹、轴肩等,以致在这些部位上截面尺寸发生突然变化,将产生局部的高应力其应力峰值远大于由基本公式算得的应力值,这种现象称为应力集中。
应力集中降低了构件的承载能力,应力集中处往往是构件破坏的起始点,是引起构件破坏的主要因素。
应力集中现象普遍存在于各种构件中,因此,为了确保构件的安全使用,提高产品的质量和经济效益,必须科学地处理构件的应力集中问题。
一、应力集中概念应力集中是指结构或构件的局部区域的最大应力值比平均应力值高的现象。
因杆件外形突然变化而引起的局部应力急剧增大的现象称为应力集中。
例如开有圆孔或切口的板条(如图a,b)板条受拉时在圆孔或切口附近的局部区域应力将局部增大,但在离开圆孔或者切口稍远处应力就迅速降低而趋于均匀。
灰二、应力集中的计算σ,同一截面上的平均盈利为σ,则设发生应力集中的截面上的最大应力为max比值称为理论应力集中系数,其值大于1,反映了应力集中的程度。
实验结果表明:截面尺寸改变的越急剧,角越尖,孔越小,应力集中地程度就越严重。
因此零部件上应尽可能的避免带尖角的孔和槽,在阶梯轴的轴肩处要用圆弧过渡,而且尽量使圆弧半径大一些。
(如下图)二、三三 三、产生应力的原因1. 受集中力作用。
如:梁的支撑点,齿轮轮齿之间的接触点,火车车轮与钢轨的接触点等。
2. 材料本身的不连续性。
钢材中的非金属杂质、混凝土中的气孔、木材中的树脂穴等,会使构件产生高度的应力集中。
例如,铸铁构件中的夹砂与气孔是产生应力集中的根源,于是铸铁构件常取较大 的安全系数。
材料力学概念及基础知识

材料力学概念及基础知识材料力学是一门研究构件承载能力的科学,其任务是在保证安全和经济的前提下,研究构件的强度、刚度和稳定性问题。
强度是指构件抵抗破坏的能力,刚度是指构件抵抗变形的能力,稳定性是指构件保持初始直线平衡形式的能力。
为了研究这些问题,材料力学假设构件内均匀充满物质,并且在各个方向力学性质相同。
在材料力学中,内力是指构件内由于发生变形而产生的相互作用力。
计算内力的方法是通过截面法,包括四个步骤:截、留、代、平。
应力是在某个面积上内力分布的集度,单位为Pa。
正应力是垂直于截面的应力,而剪应力是平行于截面的应力。
材料力学研究的基本变形包括拉伸或压缩、剪切、扭转和弯曲。
拉压变形发生在外力的作用线与构件轴线重合时,此时会产生轴力。
计算某个截面上轴力的大小等于该截面的一侧各个轴向外力的代数和,其中离开该截面的外力取正。
轴力图的绘制步骤是先画出水平线作为X轴,然后以外力的作用点为界将轴线分段。
最后,材料力学的研究对象包括杆件、板壳和块体等构件。
为了完成材料力学的任务,理论分析和实验研究都是必不可少的手段。
材料力学主要研究构件的强度、刚度和稳定性理论。
其中,杆件包括直杆(轴线为直线)和曲杆(轴线为曲线)。
杆件受到大小相等、方向相反且作用平面垂直于杆件轴线的力偶作用时,杆件的横截面会产生相对转动。
变形性质可以分为弹性变形和塑性变形。
研究内力的方法是截面法,而表示内力密集程度的指标是应力。
基本变形有轴向拉伸或压缩、剪切、扭转和弯曲。
轴力图可以表示轴力与横截面积的关系。
平面假设是指受轴向拉伸的杆件,在变形后横截面积仍保持不变的情况下,两平面相对位移了一段距离。
应力集中是指在某些局部位置,应力骤然增大的现象。
低碳钢的四个表现阶段是弹性阶段、屈服阶段、强化阶段和局部变形阶段。
材料强度性能的主要指标是屈服强度和抗拉强度,而塑性指标主要是伸长率和断面收缩率。
材料的脆性和塑性可以通过延伸率来区分。
连接杆主要有铆钉链接、螺栓链接、焊接、键连接和销轴链接。
材料力学应力应变部分

材料力学(应力应变部分)→规定载荷作用下,强度要求,就是指构件应有足够的抵抗破坏的能力。
刚度要求,就是指构件应有足够的抵抗变形的能力。
→变形的基本假设:连续性假设,均匀性假设,各向同性假设。
→沿不同方向力学性能不同的材料,称为各向异性材料,如木材、胶合板和某些人工合成材料。
→ 分布力 表面力集中力(火车轮对钢轨压力,滚珠轴承对轴的反作用力) 体积力是连续分布于物体内各点的力,例如物体的自重和惯性力等。
→动载荷,静载荷→应力p 应分解为正应力σ ,切应力τ 。
→应力单位pa ,1pa=1N/m 2;常用Mpa ,1Mpa=106pa 。
第二章 拉伸、压缩与剪切2.2 轴向拉伸或压缩时横截面上的内力和应力→习惯上,把拉伸的轴力规定为正,压缩时的轴力规定为负。
→用横截面上的应力来度量杆件的受力程度。
→F N =σA ;σ(x)=F N (x)/A(x)2.3 直杆轴向拉伸或压缩时斜截面上的内力和应力 α轴向拉伸(压缩)时,在杆件的横截面上,正应力为最大值;在与杆件轴线成45°的斜截面上,切应力为最大值。
最大切应力在数值上等于最大正应力的二分之一。
此外,α=90°时,σα=τα=0 ,这表示在平行于杆件轴线的纵向截面上无任何应力。
(应力,p=F/A ,45°斜截面上,力→√22,面积→√22。
) 2.7 安全因数许用应力和安全因数的数值,可以在有关部门的一些规范中查到。
目前一般机械制造中,在静载的情况下,对塑性材料可取n s =1.2~2.5。
脆性材料均匀性较差,且断裂突然发生,有更大的危险性,所以取n b =2~3.5,甚至取到3~9。
2.8 轴向拉伸或压缩时的变形→胡克定律,当应力不超过材料的比例极限时,应力与应变成正比。
σ=Eε ,弹性模量E 的值随材料而不同。
∆l l=ε=σE =F AE ;∆l =FLAE即,对长度相同,受力相等的杆件,有EA 越大则变形Δl越小,所以称EA 为杆件的抗拉/压刚度。
《材料力学》教案

《材料力学》课程授课教案课程编号:B03086课程中文名称:材料力学/ Material Mechanics课程总学时/学分: 76/4 (其中理论 60 学时,实验 16 学时)适用专业:过程控制专业、材料成型专业一、课程地位本课程是机械及土木类专业的主要技术基础课,其目的是掌握最基本的杆、杆系、刚架结构的计算原理和方法,了解各类结构的内力分布特征,为机械和土木类工程后续课程如结构力学、弹性力学、机械制造及设计类课程、混凝土结构设计、钢结构等打好力学基础,并培养结构分析与计算方面的能力,该课程须先修完高等数学、工程数学、大学物理、理论力学课程后学习。
二、教材及主要参考资料教材:刘鸿文主编《.材料力学》(I、 II).第四版高等教育出版社 2004年1月主要参考资料:1. 孙训方等编《.材料力学》(I、 II).第四版高等教育出版社2、胡增强编《材料力学学习指导》高等教育出版社3、顾志荣、吴永生编《材料力学学习方法及解题指导》同济大学出版社4、苟文选主编《材料力学导学、导教、导考(上、下册) 》西北工业大学出版社四、课时分配五、考核方式与成绩核定办法1. 考核方式:期末笔试+平时考核2. 成绩核定办法:笔试占70%,平时占30%六、授课方案第一章绪论1. 教学要求了解材料力学的任务,了解杆件变形基本形式。
掌握可变形固体的性质及其基本假设,熟练掌握应力、应变概念,2. 教学重点与难点重点:变形固体的性质及其基本假设、切应变。
难点:切应变概念。
3. 教学策略多媒体加板书讲授、课堂提问、练习,注意受力分析多采用板书讲授为好4. 参考书目:1、胡增强编《材料力学学习指导》高等教育出版社2、顾志荣、吴永生编《材料力学学习方法及解题指导》同济大学出版社3、苟文选主编《材料力学导学、导教、导考(上、下册) 》西北工业大学出版社5. 教学内容:1.1材料力学的任务为保证工程结构或机械的正常工作,构件应有足够的能力负担起应当承受的载荷。
材料力学性能名词总结

名词解释第一章1.正应变是单位长度的伸缩变化量,亦称线应变;2.切应变一般指的是两个直线段间夹角的改变量,以角度变小的变化量为正,变大为负,以弧度表示。
3.主平面:切应力等于零的平面。
把此时该面上的正应力称作主应力。
4.平面应变状态:应变发生在同一个平面内。
5.胡克定律:在材料的线弹性范围内,固体的单向拉伸变形与所受的外力成正比。
6.应力集中:应力在局部增大的现象,一般出现在物体形状急剧变化的地方,如缺口、孔洞、沟槽以及有刚性的约束处。
7.理论应力集中因数:在材料的弹性范围内,最大局部应力与名义应力的比值;Kt=σmax σ8.应力状态软性系数:三个主应力可以按“最大切应力理论”计算最大切应力,按“相当最大正应力理论”计算最大正应力,而二者的比值表示他们的相对大小.第二章1.弹性模量E、比例极限Rp、弹性极限Re、上屈服强度Reh、下屈服强度Rel、抗拉强度Rm、断后伸长率A、断面收缩率Z(各定义的点以及公式)2.规定塑性延伸强度:拉伸中当试样的塑形伸长率等于L0的某一百分率时所对应的应力值;3.应变硬化指数:。
4.形变强化:屈服后的应力-应变曲线的上升被描述为形变强化(加工硬化)。
也就是随着应变的增加,材料的变形抗力增加5.静态韧性:在静载作用下,材料断裂前所吸收的能量,称作静态韧性,静态韧性可能包含三部分能量,即弹性变形能、塑性变形能和断裂能(形成两个断裂表面的能)。
6.静态韧度:静态韧度是表征静态韧性的力学性能指标,7.断裂强度:拉伸断裂时的真应力称为断裂强度,记为σf ;也有称为断裂真应力,记为Sk8.断裂延性:拉伸断裂后的真应变称为断裂延性,记为εf ,或称断裂真应变。
9.弹性比功:材料吸收变形功而又不发生永久变形的能力,也就是在开始塑性变形前,单位体积材料所能吸收的最大弹性变形功。
第三章1.比弹性模量:弹性模量与密度的比值;2.比刚度:刚度与密度的比值;3.弹性不完善性:应变不止与应力有关,还与时间和加载速率有关。
