微波技术-第3章1矩形波导
矩形波导的模式(3篇)

第1篇一、矩形波导的模式分类矩形波导中的电磁波模式主要分为TE(横电磁波)模式和TM(纵电磁波)模式。
1. TE模式TE模式是指电场只在波导的横向(垂直于传播方向)分量存在,而磁场则在纵向(沿传播方向)分量存在。
根据电场和磁场在波导横截面上的分布,TE模式又可以分为TE10、TE20、TE01等模式。
(1)TE10模式:TE10模式是矩形波导中最基本、最常用的模式。
其电场分布呈矩形,磁场分布呈椭圆。
TE10模式的截止频率最高,适用于高频传输。
(2)TE20模式:TE20模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率低于TE10模式,适用于中频传输。
(3)TE01模式:TE01模式的电场分布呈矩形,磁场分布呈椭圆。
其截止频率最低,适用于低频传输。
2. TM模式TM模式是指磁场只在波导的横向分量存在,而电场则在纵向分量存在。
根据电场和磁场在波导横截面上的分布,TM模式又可以分为TM01、TM11、TM21等模式。
(1)TM01模式:TM01模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率最高,适用于高频传输。
(2)TM11模式:TM11模式的电场分布呈矩形,磁场分布呈椭圆。
其截止频率低于TM01模式,适用于中频传输。
(3)TM21模式:TM21模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率最低,适用于低频传输。
二、矩形波导的模式特性1. 截止频率截止频率是矩形波导中一个重要的参数,它决定了电磁波在波导中能否有效传输。
不同模式的截止频率不同,其中TE10模式的截止频率最高,适用于高频传输。
2. 相速度相速度是指电磁波在波导中传播的速度。
不同模式的相速度不同,TE模式的相速度比TM模式快。
3. 模式损耗模式损耗是指电磁波在波导中传播时,由于波导壁的吸收和辐射等原因,能量逐渐衰减的现象。
不同模式的损耗不同,TE模式的损耗比TM模式小。
4. 传输特性矩形波导中不同模式的传输特性不同,如TE模式的传输特性较好,适用于高频传输;TM模式的传输特性较差,适用于低频传输。
微波技术-第3章1矩形波导

在左侧壁上: n = x ˆ ˆ
JS
ˆ ˆ = x ? zH z x= 0
ˆ - x
ˆ - y Hz
ˆ = - H10e j ( w t - b z ) y x= 0
在右侧壁上:n = ˆ
JS
x= a
ˆ ˆ = - x? zHz
ˆ y Hz
x= a
= - H10e
j (wt - b z )
ˆ y
Ey ja
a j a x jz Hx H 10 sin e a x jz
H z H 10 cos a E x Ez H y 0 e
H 10 sin
x
e j z
分析上式可以得出:
①电场
其电场只有Ey分量,电力线是 一些平行于y轴的电力线;
y = 0, b
x = 0, a
2.导模的场结构
导模的场结构,是波导中电场和磁场的强和弱,这 里我们用电力线和磁力线的疏密来表示。 由场解可知,矩形波导中可能存在的电磁场有无限多个 解,即TEmn(Hmn)和TMmn(Emn)模式,或将此称为“波型”。 对于每一个的TEmn(Hmn)和TMmn(Emn)模而言,每一
骣 ÷ mb çl ÷ = h 1- ç ÷ çl ÷ ç c e k 桫
2
(5)TE10模矩形波导的传输功率
v v* 轾 1 v P = Re 犏ò E 捶H ds 犏 S 2 臌 a b v v* 1 ˆ = Re 蝌 E 捶H zdydx x= 0 y= 0 2 a b 1 = Re 蝌 E y H x * dydx x= 0 y= 0 2 wma 3 b 2 = H 10 b TE10 2 4p
ab E10 P= 4 ZTE10
微波专业技术与天线实验3利用HFSS仿真分析矩形波导

微波技术与天线实验报告实验名称:实验3:利用HFSS仿真分析矩形波导学生班级:学生姓名:学生学号:实验日期:2011年月日一、 实验目的学会HFSS 仿真波导的步骤,画出波导内场分布随时间变化图,理解波的传播与截止概念;计算传播常数并与理论值比较。
二、 实验原理矩形波导的结构如图1,波导内传播的电磁波可分为TE 模和TM 模。
x yz图 1矩形波导1) TE 模,0=z E 。
coscos z z mn m x n y H H e a b γππ-= 2cos sin x mn c z n m x n y E H b a bj k e γπππωμ-= 2sin cos z y mn c j m m x n y E H e k a a b γωμπππ-=-2sin cos z x mn c m m x n y H H e k a a bγλπππ-= 2cos sin z y mn c n m x n y H H e k ba b γλπππ-= 其中,c kmn H 是与激励源有关的待定常数。
2) TM 模Z H =0,由Z E 的边界条件同样可得无穷多个TM 模。
注意:对于mn TM 和mn TE 模,m, n 不能同时为零,否则全部的场分量为零。
mn TM 和mn TE 模具有相同的截止波数计算公式,即c k (mn TM )=c k (mn TE )所以,它们的截止波长c λ和截止频率c f 的计算公式也是一样的,即c λ(mn TM )=c λ(mn TE )=222⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛b n a mc f (mn TM )=c f (mn TE )对于给定的工作频率或波长,只有满足传播条件(f >c f 或λ<c λ)的模式才能在波导中传播。
由公式可以看出矩形波导的c f ,c λ不仅与波导的尺寸a, b 有关,还和模指数m, n 有关。
当a, b 一定时,随着f 的改变,矩形波导可以多模传播,也可以单模传播,甚至也可以处于截止状态。
微波技术基础课件第三章规则金属波导

第3章 规则金属波导
(2) TE01模与TE0n模的场结构TE01模只有Ex、Hy和Hz三个 场分量,其场结构与TE10模的差别只是波的极化面旋转了 90°,即场沿a边不变化,沿b边有半个驻波分布,如图3.1-2 (c)所示。
(3.1-4) (3.1-5)
E0z (x, y) 0, y 0, aTM导波 E0z (x, y) 0, y 0, b
(3.1-6)
第3章 规则金属波导
(1) TE模(TE modes) 其Ez=0,Hz(x,y,z)=H0z(x,y)e-jβz≠0。应用分离变量法,即 令
H0z(x,y)=X(x)Y(y)
(3.1-7)
代入本征值方程,得到
1 X (x)
d 2 X (x) dx2
1 Y ( y)
d 2Y ( y) dy2
k
2 c
0
(3.1-8)
第3章 规则金属波导
此式要成立,每项必须等于常数。定义分离变数为kx和ky,
则得到方程:
d
2X dx
(
2
x)
k
2 x
X
(
x)
0
(3.1-9)
d
2Y ( y) dy2
第3章 规则金属波导
(1) TE10模与TEm0模的场结构 TE10(m=1,n=0)模的场分量由式(3.1-161)求得为
Ey
ja
H10
sin
x
a
e jz
Hz
ja
标准矩形波导

标准矩形波导
标准矩形波导是一种常见的波导结构,广泛应用于微波通信、雷达系统和微波加热等领域。
它具有较宽的频带、低传输损耗和良好的抗干扰能力,因此备受青睐。
本文将对标准矩形波导的结构特点、工作原理和应用进行介绍。
结构特点。
标准矩形波导由金属矩形管和金属盖板组成,其截面呈矩形。
矩形波导的宽度和高度决定了其工作频率范围,通常采用常见的规格,如WR90、WR75等。
矩形波导内壁通常采用电镀银或金属镀层,以降低传输损耗和提高抗氧化能力。
波导的两端可以通过连接器与其他设备相连,形成封闭的传输通道。
工作原理。
当高频信号进入矩形波导时,会在波导内壁上产生电磁场,这些电磁场沿着波导传播,并在波导的另一端输出。
由于矩形波导内壁的导电性,电磁波会在波导内壁上发生多次反射,从而实现信号的传输。
矩形波导的工作原理类似于光纤,都是利用全反射来传输
信号,但波导的工作频率通常在兆赫至千兆赫的微波范围内。
应用领域。
标准矩形波导在微波通信系统中扮演着重要角色,常用于天线和收发模块之间的信号传输。
此外,矩形波导还被广泛应用于雷达系统中,用于天线阵列、相控阵和波束形成等方面。
在微波加热设备中,矩形波导也被用于传输高频能量,实现对食品和工业原料的加热处理。
总结。
标准矩形波导作为一种重要的微波传输结构,在通信、雷达和加热等领域都有着广泛的应用。
其结构特点、工作原理和应用领域都体现了其独特的优势和价值。
随着微波技术的不断发展,矩形波导将继续发挥重要作用,为各种微波应用提供可靠的传输支持。
矩形波导的设计讲解

矩形波导的设计讲解矩形波导模式和场结构分析第⼀章绪论1.1选题背景及意义矩形波导(circular waveguide)简称为矩波导,是截⾯形状为矩形的长⽅形的⾦属管。
若将同轴线的内导线抽⾛,则在⼀定条件下,由外导体所包围的矩形空间也能传输电磁能量,这就是矩形波导。
矩波导加⼯⽅便,具有损耗⼩和双极化特性,常⽤于要求双极化模的天线的馈线中,也⼴泛⽤作各种谐振腔、波长计,是⼀种较常⽤的规则⾦属波导。
矩波导有两类传输模式,即TM 模和TE 模。
其中主要有三种常⽤模式,分别是主模TE 11模、矩对称TM 01模、低损耗的TE 01模。
在不同⼯作模式下,截⽌波长、传输特性以及场分布不尽相同,同时,各种⼯作模式的⽤途也不相同。
导模的场描述了电磁波在波导中的传输状态,可以通过电⼒线的疏密来表⽰场得强与弱。
本毕业课题是分析矩形波导中存在的模式、各种模式的场结构和传播特性,着重讨论11TE 、01TE 和01TM 三个常⽤模式,并利⽤MATLAB 和三维⾼频电磁仿真软件HFSS 可视化波导中11TE 、01TE 和01TM 三种模式电场和磁场波结构。
1.2国内外研究概况及发展趋势由于电磁场是以场的形态存在的物质,具有独特的研究⽅法,采取重叠的研究⽅法是其重要的特点,即只有理论分析、测量、计算机模拟的结果相互佐证,才可以认为是获得了正确可信的结论。
时域有限差分法就是实现直接对电磁⼯程问题进⾏计算机模拟的基本⽅法。
在近年的研究电磁问题中,许多学者对时域脉冲源的传播和响应进⾏了⼤量的研究,主要是描述物体在瞬态电磁源作⽤下的理论。
另外,对于物体的电特性,理论上具有⼏乎所有的频率成分,但实际上,只有有限的频带内的频率成分在区主要作⽤。
英国物理学家汤姆逊(电⼦的发现者) 在1893 年发表了⼀本论述麦克斯韦电磁理论的书,肯定了矩⾦属壁管⼦(即矩波导) 传输电磁波的可实现性, 预⾔波长可与矩柱直径相⽐拟, 这就是微波。
他预⾔的矩波导传输, 直到1936 年才实现。
矩形波导

(二)壁电流分布
J s n Ht
JS
x 0
n H t x z H z y H z y j E0 cos a a
x e j (t z ) x 0
y j E0 e j (t z ) J y a j (t z ) J S x a n H t x z H z y H z y j a E0 cos a x e x a
2 c
• 根据TE波的边界条件 • x=0 , ( x, y ) 0 ,得:C2=0
x • x=a , ( x, y ) 0 ,得: k x x
m (m=0,1,2,┄) a
• y=0 , ( x, y ) 0 ,得:C4=0 y n ( x, y ) • y=b , (n=0,1,2,┄) 0 ,得: k y y b
TE01 TE11 TM11 TE20
TE30 TE21 TM21 TE31 TM31
TE40
lc(cm) 图3-2 BJ-100型波导不同波型截止波长的分布图
在矩形波导中实现TE10单模传输,则要求电磁 波的工作波长必须满足下列条件
lc (TE20 ) l lc (TE10 ) l lc (TE01 )
k 2 k
1 2 2 c
2 2 2 m n a b
1 2
H T I ( z ) T ( x, y )
ET U ( z ) T ( x, y ) z
z E0 sin a
矩形波导 PPT

m 场量沿x轴[0,a]出现的半周期(半个纯驻波)的数目;
n 场量沿y轴[0,b]出现的半周期的数目。
④j 相位关系 Ey-Hx、Ex-Hy
z轴有功率传输
Ez-Hx、Ez-Hy
x、y轴无功率传输
所以行波状态下,沿波导纵向(z轴)传输有功功率、横向(x、
y轴)无功功率。
2) 场结构
为了能形象和直观的了解场的分布(场结构),可以 利用电力线和磁力线来描绘它。电力线和磁力线遵循 的规律:
力线上某点的切线方向
该点处场的方向
力线的疏密程度
场的强弱
电力线 发自正电荷、止于负电荷,也可以环绕着交变磁场构 成闭合曲线,电力线之间不能相交。在波导壁的内表面(假设为 理想导体)电场的切向分量为零,只有法向分量(垂直分量), 即在波导内壁处电力线垂直边壁。
磁力线 总是闭合曲线,或者围绕载流导体,或者围绕交变电 场而闭合,磁力线之间不能相交,在波导壁的内表面上只能存在 磁场的切向分量,法向分量为零。
3)相速和群速
TMmn和TEmn波型的相速和群速表示式相同:
vp
v
1(/c)2
vg v 1-c2
4)波型阻抗
TMmn和TEmn波型阻抗为:
ZTE
1
1c2
g
ZTM
1c2
g
5)尺寸选择——矩形波导的工作波型图
基于前面的定义,根据波导横截面尺寸、工作波长、 截止波长之间关系,构成矩形波导工作波型图。根据不 同要求,可利用波型图对波导的横截面尺寸和波导波长 作出选择。
TE0n和TEm0是非简并模;其余的TEmn和TMmn都存在简并模: 若a=b, 则TEmn 、TEnm、TMmn和TMnm是简并模;若a=2b,则TE01与TE20,TE02和 TE40,TE50、TE32和TM32是简并模。
微波技术矩形波导中电磁波的通解

二、矩形波导中TM波的场方程 矩形波导中 波的场方程 TM波(E波): Hz = 0 , Ez ≠ 0 。 波 波
∂2 ∂2 2 ( 2 + 2 )Ez (x, y) + kc Ez (x, y) = 0 ∂x ∂ y 进一步对E 分离变量, 进一步对 z( x , y )分离变量,得其解 分离变量
代入(3-57)得 得 代入 d 2 X (x) 2 + k1 X (x) = 0 (3−59a) 2 dx d 2Y( y) 2 + k2Y( y) = 0 (3−59b) 2 dy 为二阶常微分方程,其通解为: 为二阶常微分方程,其通解为:
X (x) = Acos(k1x +ϕ1) Y( y) = Bcos(k2 y +ϕ2 )
∂2 ∂2 2 ( 2 + 2 )Hz (x, y) + kc Hz (x, y) = 0 (3− 54) ∂x ∂ y
− jωµ 0 ∂Hz Ex = = ±ηTE Hy 2 kc ∂y jωµ 0 ∂Hz Ey = 2 = ∓ηTE Hx
(3− 34a)
(3− 34b)
进一步对H 分离变量, 进一步对 z分离变量,令 Hz (x, y) = X (x)Y( y) (3−55) 代入(3-54),得 , 代入
Ez (x, y, z) = 0
2 c
(3− 65 f )'
2 2
m 式中 , n = 0, 1, 2,⋯, k = mπ + nπ , a b
ωµ0 ηTE = β
可见, 可取任意正整数和零, 可见,(1) m , n 可取任意正整数和零,但不得同时 为零; 取值不同,对应于不同的场分布, 为零;(2) m , n 取值不同,对应于不同的场分布,称为 不同的模式, 不同的模式,记为 TEmn 或 Hmn , m , n 称为模序数。 称为模序数。 (3-65)’乘上时间因子 e jω t 得(3-65) 后取实部,即得各 ’ 后取实部, 分量的瞬时值。 分量的瞬时值。
微波技术矩形波导1

(3-11)
一、矩形波导的一般解
E jH
i j k j ( H x i H y H z k ) j Ez
x
Ex
y
Ey
一、矩形波导的一般解
E z y E y jH x E z jH y E x x E y E x jH z y x
2
(3-2)
一、矩形波导的一般解
波导的一般解采用纵向分量法,其流图如下所示, 上式也称Helmholtz方程
出发点 无源区中 Maxwell 方程
支配方程 2 2 Ek E 0 2 2 Hk H 0
纵向分量方程 2 Ez k 2 Ez 0 2 H z k 2 H z 0
H z H 0 cos x cos(t z ) a Ey
H 0 sin x sin(t z ) a k2 a
H x 2 H 0 sin x sin(t z ) a kc a
由于其独立性,上式各项均为常数
1 2 Z (z ) 2 2 Z ( z ) z 2 t E ( x, y ) k 2 0 t E ( x, y )
(3-6)
(3-7)
一、矩形波导的一般解
其中
k k
2 t 2 2
(3-8)
称为截止波数,则式(3-7)中第一方程的解是
(3-20)
二、矩形波导的横向解
其中,
m n k k k a b
2 2 c 2 x 2 y 2
(3-21)
上面称为TEmn波 m——表示x方向变化的半周期数 (即小→大→小) n——表示y方向变化的半周期数。
微波技术-矩形波导章节习题课课件

当 f = 10GHz 时, 能传输TE10和TE20模。 7. 空气填充的矩形波导中a =7.2cm, b=3.4cm。 (1) 当工作波长( = c/f )分别为16、8、6.5cm时,此 波导可能有哪几个传输模?(2) 求 TE10 单模传输的频率 范围,并要求此频带的低端比TE10的 fc大5%,其高端 比最相近的高阶模的 fc 低5% 。
a max 2a 2b
TE10
2a
圆波导
同轴线 带状线 微带线
TE11
3.41a
2.62a 3.41a
TEM TEM
(D d ) / 2
真空 2w r , 真空 2h r 真空 2w r , 真空 2h r
或横向谐振频率
c
c
c
截止频率与介质电磁参数μ、ε有关
各种传输线主模
在波导中,一般称截止波长最大(对应截止波数或截止频 率最小)的模式为主模,也称基模或最低模式,而将其它 模式称为高次模式。各类传输线主模如表所示。
传输线类型 平行双线 矩形波导 主模
TEM
截止波长 c
单模传输条件 无截止特性
解: (1)
c fc ( m a ) 2 ( n b) 2 c 2
c
b<a<2b,主模为TE10模,次高模为TE01模。
( f c )TE10
由题义得
c , 2a
( f c )TE01
c 2b
3 109 (3 108 2a) 0.2 8 3 10 2a (3 108 ) (2b) 3 109 0.2 8 (3 10 ) (2b)
若填充介质r = 2, r = 1, 截止频率计算公式为
《微波技术与天线》傅文斌-习题答案-第3章

第3章 规则波导和空腔谐振器3.1什么是规则波导?它对实际的波导有哪些简化?答 规则波导是对实际波导的简化。
简化条件是:(1)波导壁为理想导体表面(∞=σ);从而可以利用理想导体边界条件;(2)波导被均匀填充(ε、μ为常量);从而可利用最简单的波动方程;(3)波导内无自由电荷(0=ρ)和传导电流(0=J );从而可利用最简单的齐次波动方程;(4)波导沿纵向无限长,且截面形状不变。
从而可利用纵向场法。
3.2纵向场法的主要步骤是什么?以矩形波导为例说明它对问题的分析过程有哪些简化?答 纵向场法的主要步骤是:(1)写出纵向场方程和边界条件(边值问题),(2)运用分离变量法求纵向场方程的通解,(3)利用边界条件求纵向场方程的特解,(4)导出横向场与纵向场的关系,从而写出波导的一般解,(5)讨论波导中场的特性。
运用纵向场法只需解1个标量波动方程,从而避免了解5个标量波动方程。
3.3什么是波导内的波型(模式)?它们是怎样分类和表示的?各符号代表什么物理意义? 答 运用纵向场法得到的解称为波导内的波型(模式)。
分为横电模和横磁模两大类,表示为TEmn 模和TMmn 模,其中TE 表示横电模,即0=z E ,TM 表示横磁模,即0=z H 。
m 表示场沿波导截面宽边分布的半波数;n 表示场沿波导截面窄边分布的半波数。
3.4矩形波导存在哪三种状态?其导行条件是什么?答 矩形波导存在三种状态,见表3-1-1。
导行条件是222⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛<b n a m λ3.5从方程H E ωμj -=⨯∇和E H ωεj =⨯∇出发,推导矩形波导中TE 波的横向分量与纵向分量的关系式(3-1-25)。
解 对TE 波,有0=z E 。
由H E ωμj -=⨯∇和E H ωεj =⨯∇、 βj z-=∂∂得 ()x y z E H j yH ωεβj =--∂∂ ⑴ ()y zx E x H H j ωεβj =∂∂-- ⑵0=∂∂-∂∂yH x H x y⑶()x y H E j ωμβj -=-- ⑷()y x H E j ωμβj -=- ⑸z x y H yE x E ωμj -=∂∂-∂∂ ⑹ 由式⑴、⑸y H k E zcx ∂∂-=2j ωμ⑺ 由式⑵、⑷xH k E zc y ∂∂=2j ωμ⑻ 由式⑷得xH k H zc x ∂∂-=2j β⑼ 由式⑸得y H k H zc y ∂∂-=2j β⑽ 3.6用尺寸为2mm 04.3414.72⨯的JB-32矩形波导作馈线,问:(1)当cm 6=λ时波导中能传输哪些波型?(2)写出该波导的单模工作条件。
矩形波导

(44)
带入到(42)式的3、 4式,有
cos(k x x x ) sin y 0 对任意x都成立,则必有 sin y 0 即 y 0 cos(k x x x ) sin k y b 0 对任意x都成立,则必有
sin k y b 0
m 同样有 k x a
2 2 2 k x k y kc
(51)
其中:
d 2 X ( x) 2 X ( x) A cos(k x x x ) k x X ( x) 0 dx2 则有 Y ( y ) B cos(k y y y ) d 2Y ( y ) 2 k y Y ( y) 0 2 dy E z ( x, y ) D cos(k x x x ) cos(k y y y ) (52)
考虑波导边界的形状,建立直角坐标系
则 H z H z ( x, y ) Z ( z ) 而且 Z ( z ) A e z H z ( x, y ) 满足 t2 H z ( x, y) kc2 H z ( x, y) 0
2 2 其中 2 2 x y
无耗介 质中 i 1
( x, y ) j H z j k D sin(k x ) cos(k y ) Hx x x x y y kc2 x kc2 ( x, y ) j H z j k D cos(k x ) sin(k y ) Hy y x x y y kc2 y kc2 j Ex ( x, y ) TE H y 2 TE k y D cos(k x x x ) sin(k y y y ) kc j E y ( x, y ) TE H x 2 TE k x D sin(k x x x ) cos(k y y y ) kc
第3章矩形波导

《微波技术》
Harbin Harbin Engineering Engineering University University
3-5 矩形波导
一、矩形波导中传输波型及其场分量 (一)TM波
d2 X ( x ) 2 + k X ( x) = 0 x 2 dx d 2Y ( y ) 2 k + yY ( y ) = 0 2 dy ⎫ ⎪ ⎪ ⎬ ⎪ ⎪ ⎭
Note:
k +k =k
2 x 2 y
2 c
通解为
X ( x ) = C1 cos k x x + C2 sin k x x Y ( y ) = C3 cos k y y + C4 sin k y y
Ez = − j Hz = 0 U sin x ⎟ sin ⎜ y ⎟ e β 0 ⎜ a ⎝ ⎠ ⎝b ⎠ ⎪ ⎪ ⎪ ⎪ ⎭
⎛ mπ ⎞ ⎛ mπ ⎞ ⎛ nπ ⎞ j(ω t − β z ) Ex = −U 0 ⎜ x ⎟ sin ⎜ y⎟e ⎟ cos ⎜ ⎝ a ⎠ ⎝ a ⎠ ⎝ b ⎠ ⎛ nπ ⎞ ⎛ mπ ⎞ ⎛ nπ ⎞ j(ω t − β z ) E y = −U 0 ⎜ ⎟ sin ⎜ x ⎟ cos ⎜ y⎟e ⎝ b ⎠ ⎝ a ⎠ ⎝ b ⎠
截止波数为
⎛ mπ ⎞ ⎛ nπ ⎞ kc = ⎜ ⎟ +⎜ ⎟ ⎝ a ⎠ ⎝ b ⎠
《微波技术》
2 2
Harbin Harbin Engineering Engineering University University
三、矩形波导管中电磁波的传输特性 微波技术基础 课件 PPT
2
1
m
2
n
2
a b
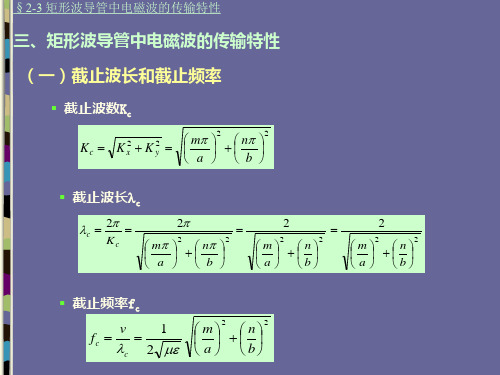
§2-3 矩形波导管中电磁波的传输特性——三、矩形波导管中电磁波的传输特性
❖ 简并现象:不同波型具有相同截止波长(或截止频率)的现象
简并波型的kc、fc、vg、vp以及g都是相同的 kc
o 一般情况下: ▪ TE0n和TEm0是非简并模(TM最低次模为TM11)
2 m 2 n 2 a b
矩形波导管管壁电流立体分布图
❖ 左右两侧壁的电流 ❖ 只有Jy分量 ❖ 大小相等,方向相同。
❖ 上下宽壁内的电流 ❖由Jz和Jx合成, ❖ 同一位置上下宽壁内的管壁电流大小 相等,方向相反。
§2-3 矩形波导管中电磁波的传输特性——四、矩形波导管的管壁电流
了解管壁电流的分布情况,对解决某些实际问题有帮助
ax
s
in
2
a
x dxdy
Em2 axb
2ZTE10
a sin 2
0
a
x dx ab
2ZTE10
Em2 ax
§2-3 矩形波导管中电磁波的传输特性——三、矩形波导管中电磁波的传输特性
▪ 功率容量Pbr:波导能够传输(承受)的最大允许功率(极限功率)
Emax Ey xa / 2 Ebr
a 0.7
b 0.4 ~ 0.5a
▪ 使用的波导已标准化:可根据需要选用
§2-3 矩形波导管中电磁波的传输特性——
四、矩形波导管的管壁电流
▪ 导行波在金属波导内壁表面上将感应出高频电流,称为管壁电流。
▪ 管壁电流如何分布?
假定内表面是理想导体, ▪ Js表示内表面上的表面电流密度矢量 ▪ H表示内表面处切线方向的磁场强度 ▪ an表示内表面法线方向的单位矢量
微波技术与天线实验3利用HFSS仿真分析矩形波导

微波技术与天线实验报告实验名称:实验3:利用HFSS仿真分析矩形波导学生班级:学生姓名:学生学号:实验日期:2011年月日一、 实验目的学会HFSS 仿真波导的步骤,画出波导内场分布随时间变化图,理解波的传播与截止概念;计算传播常数并与理论值比较。
二、 实验原理矩形波导的结构如图1,波导内传播的电磁波可分为TE 模和TM 模。
xyz图 1矩形波导1)TE 模,0=z E 。
coscos zz mn m x n y H H e a bγππ-= 2cos sin x mn c z n m x n y E H b a bj k e γπππωμ-=2sin cos z y mn c j m m x n y E H e k a a bγωμπππ-=-2sincos z x mn c m m x n y H H e k aa bγλπππ-=2cossin z y mn c n m x n y H H e k ba bγλπππ-=其中,c kmn H 是与激励源有关的待定常数。
2)TM 模Z H =0,由Z E 的边界条件同样可得无穷多个TM 模。
注意:对于mn TM 和mnTE 模,m, n 不能同时为零,否则全部的场分量为零。
mn TM 和mn TE 模具有相同的截止波数计算公式,即c k (mn TM )=c k (mn TE )所以,它们的截止波长c λ和截止频率c f 的计算公式也是一样的,即c λ(mn TM )=c λ(mn TE )=222⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛b n a mc f (mn TM )=c f (mn TE )对于给定的工作频率或波长,只有满足传播条件(f >c f 或λ<c λ)的模式才能在波导中传播。
由公式可以看出矩形波导的c f ,c λ不仅与波导的尺寸a, b 有关,还和模指数m, n 有关。
当a, b 一定时,随着f 的改变,矩形波导可以多模传播,也可以单模传播,甚至也可以处于截止状态。
微波技术矩形波导中电磁波的通解要点

j 0 H z Ex TE H y 2 kc y j 0 H z Ey TE H x 2
(3 34a)
(3 34b)
进一步对Hz分离变量,令 H z ( x, y) X ( x)Y ( y) (3 55) 代入(3-54),得
d 2 X ( x) d 2Y ( y ) 2 Y ( y) X ( x ) k c X ( x)Y ( y ) 0 2 2 dx dy 除以 X ( x)Y ( y) 得 1 d 2 X ( x) 1 d 2Y ( y ) 2 k c 2 2 X ( x) d x Y ( y) d y
Ex ( x, y, z) TE H y ( x, y) e
j z
j 0 H 0 n m n j z cos( x ) sin( y ) e kc2 b a b
(3 65d )'
E y ( x, y, z) TE H x ( x, y)e j z
思考题: 2-4, 2-7
第三节 矩形波导中电磁波的通解
矩形波导取坐标系如图。 考虑无限长均匀无介质情况, 假定波导内壁为理想导体 , 求其中导行波解的具体形式。 波导内只能传输TE波和 TM波,不能传输TEM波。
y b a z x
一、矩形波导中TE波的场方程 TE波(H波):Ez=0,Hz 0 。 已求出了沿 z 方向传输的TE波的分布函数表达 式(用纵向分量表示横向分量):
j 0 H 0 m m n j z sin( x ) cos( y ) e kc2 a a b (3 65e)'
Ez ( x, y, z) 02 cຫໍສະໝຸດ (3 65 f )'
波导内壁为理想导体 ,其边界条件是所有内壁上的 电场切向分量均为零。
矩形波导PPT幻灯片课件

g
vp f
1 ( c )2
2 2 g
1 ( c )2
其中 λ为工作波长。
第2章 规则金属波导
对均不为零的m和n, TEmn和TMmn模具有相同的截止波长 和λc截止波数Kc,Kc和λc相同但波型不同称为简并模, 虽然它们 场分布不同, 但具有相同的传输特性。
则有:
Hz
m
H0 cos( a
x) cos(n
b
y)e jz
第2章 规则金属波导
TE波的全部场分量表示式为:
Ex
j Kc2
H0
n
b
cos(m
a
x) sin(n
b
y)e jz
Ey
j
K
2 c
H0
m
a
s in( m
a
x) cos(n
b
y)e jz
Ez 0
第2章 规则金属波导
二、 矩形波导中的场
由上节分析可知, 矩形金属波导中只能存在TE波和 TM波。下面分别来讨论这两种情况下场的分布。 (一)TM
(1)场分量的表示式
此时Hz=0, Ez≠0, 且满足
Ez E0 cos(Kx x x ) cos(Ky y y )e jz
根据边界条件(波导管壁内表面电场切向分量为零)求解 上式中待定常数:
第2章 规则金属波导
TE21模场结构图
第2章 规则金属波导
三、 矩形波导的传输特性
1) 截止波数、截止波长、
由前述分析,矩形波导TEmn和TMmn模的截止波数均为
Kcmn
m 2 n 2
a b
《电磁场与微波技术教学课件》2.2 矩形波导

雷达天线
矩形波导可以作为雷达系统的天线, 利用其高方向性和低副瓣特性,提高 雷达的探测精度和距离分辨率。
毫米波雷达
在毫米波雷达中,矩形波导常被用作 发射和接收天线,其宽带宽和低损耗 特性有助于实现高分辨率和高灵敏度 的探测。
测量技术中的应用
微波测量
矩形波导在微波测量技术中常被用作标准测量器件,用于校准和检测微波设备 的性能参数。
100%
军事应用
在二战期间,矩形波导在雷达和 通信系统中得到广泛应用。
80%
技术进步
随着微波技术的不断发展,矩形 波导的性能得到不断提升和优化 。
02
矩形波导的传输特性
传输模式
01
02
03
04
TEM模
在矩形波导中,当工作频率较 低时,只有TM01模可以传输 ,随着频率的升高,会出现 TE11模,TM02模等其他模式 。在某些频率下,可能存在多 个模式同时传输的情况。
矩形波导的应用
雷达系统
矩形波导可用于雷达发射和接收天线,传输高频率 的微波信号。
卫星通信
在卫星通信系统中,矩形波导常用于传输信号,确 保信号的稳定传输。
加热与熔炼
矩形波导的高功率容量使其在工业加热和熔炼中得 到广泛应用。
矩形波导的发展历程
80%
早期研究
20世纪初,科学家开始研究矩形 波导的传输特性。
色散效应
由于色散现象的存在,矩形波导中的信号传输会受到一定的影响。例如,脉冲信号的展宽 、信号畸变等。因此,在设计微波系统时,需要考虑矩形波导的色散效应,以减小其对系 统性能的影响。
பைடு நூலகம் 03
矩形波导的尺寸选择与设计
波导尺寸的选择
01
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ey =
-
jwma p
px H10 sin a
e-
jb z
Hx =
jb a p
px H10 sin a
e-
jb z
Hz =
H10
cos
px a
e-
jb z
Ex = Ez = H y = 0
其幅度不随 y 变化(与y无关), 故沿b边电场无变化;
Ey与x轴有关,且Ey与
s
in
x
a
成正比;如图,沿宽边a电
mp a
x
e-
jb z
Hx =
jb a mp
Hm0
sin
mp a
x
e-
jb z
Hz
=
Hm0
cos
mp a
x
e-
jb z
Ex = Ez = H y = 0
其场分量不随y变化(与y无关),故沿b边场无变化; 沿宽边a电场有m个半驻波分布或m个TE10模场结构分布。 沿z轴则为正弦分布,波沿此方向传播,即整个场型沿 z轴
注:TE11与TM11是简并模,这种简并称为模式简并; 同理,TEmn与TMmn (m>0, n>0) 是简并模。
3.管壁电流
J s nˆ Htan
主模:TE10模工作下
波导底面 y = 0 ; nˆ = yˆ
JS
=
y= 0
yˆ ? [ xˆH x
zˆHz ] = xˆHz - zˆH x
=
只为是余y弦和分z的布变(量为,半E个x和驻H波y分沿布b边)为。与的正T极弦E化1分0模面布的旋,差转而异了H为9z0沿波0 b边 TE0n模的场结构是沿a边不变化,沿b边有n个半驻波分
布或n个TE01模场结构分布。
(3) TE11模 TEmn模
m和n均不为零的最简单的TE模是TE11模。其场沿 a边和b边都有半个驻波分布。
轾 犏 犏 臌H10
解各种情况下的亥姆霍兹方程的电场或磁场纵向 分量特解; 由横纵向场关系式求各横向场分量。
§3.1 矩形波导
矩形波导:截面为矩形的 金属波导管。
尺寸:
a b, a b
1.矩形波导的导模
1)TE模
对于TE模:
Ez = 0,
Hz ? 0
导体边界上电场的 切向分量为零
其边界条件为:
e- jb z
Ex ( x, y, z) = E0x ( x, y)X (z) = 0 Ey ( x, y, z) = E0 y ( x, y)Y (z) = 0
由分离变量法分解得:
E0x (x, y) = 0, E0y (x, y) = 0,
y = 0,b x = 0,a
2.导模的场结构
导模的场结构,是波导中电场和磁场的强和弱,这 里我们用电力线和磁力线的疏密来表示。
由场解可知,矩形波导中可能存在的电磁场有无限多个解,
即TEmn(Hmn)和TMmn(Emn)模式,或将此称为“波型”。
场按正弦律变化。在x=0和x=a处,电场Ey为零;在x=a/2
处,电场Ey为最大;为一个半驻波分布;波沿+z方向传播,
即整个场型沿z 轴传播。
② 磁场
磁场有Hx和Hz两个分量 v H = xˆH x + zˆHz
Ey =
-
jwma p
px H10 sin a
e-
jb z
Hx =
jb a p
H10
sin
TEmn模:其场沿a边有m个、沿b边有n个半驻波分布
或TE11模场;如图。
(4) TM11模与TMmn模
TM导模中最简单的模为TM11模,其磁力线完全 分布在横截面内,为闭合曲线(Hz=0);电力线 则是空间曲线。
其场沿a边和b边均有半个驻波的分布。
TMmn模:其场沿a边 有m个、沿b边有n个半 驻波分布或TM11模场; 如图。
(1) TE10模与TEm0模
TE10模中,m=1, n=0,代入场分量:(某时刻)
Ey
ja
x
H10 sin a
e jz
Hx
ja
H10
sin
x
a
e
jz
Hz
x
H10 cos a
e jz
Ex Ez H y 0
分析上式可以得出:
①电场
其电场只有Ey分量,电力线是 一些平行于y轴的电力线;
H10
sin
px a
sin(wt
-
b z)
Hx =
ba p
H10
sin
px a
sin(wt
-
bz+ p)
Hz =
H10
cos
px a
cos(w
t
-
b z)
Ex = Ez = H y = 0
TE10
TE10 h
TE10 e
对于TEm0波,其场分量: 与TE10模类似:
Ey
=
-
jwma mp
Hm0
sin
第三章 规则金属波导
§3.1 矩形波导 §3.2 圆形波导 §3.3 同轴线
规则金属波导管壁材料:铜、铝,有时其壁上镀金或银。
金属波导优点:导体损耗和介质损耗小、功率容量大、 没有辐射损耗、结构简单、易于制造。
形状:横截面有矩形、圆形、脊形、椭圆形、三角形等。 使用范围:3000MHz(3GHz)~300GHz 导波模式:(非TEM波)TE波,TM波,混合波。
对于每一个的TEmn(Hmn)和TMmn(Emn)模而言,每一 种场分布都是不同的,一般情况下具有不同的传播特性 (它们都单独满足矩形波导的边界条件,能够独立地在 波导中存在)。
最基本的场结构模型
TE10 TE01 TE11 TM11
相应的高次模与基本场结构模有一定的关系。
不同的模式具有相同的传输特性参量的现象称为“简并”。
传播TE0n模
其场分量为
Ex =
jwmb np
H mn
sin
np y b
e-
jb z
Hy =
jb b np
H mn
sin
np b
y
e-
jb z
Hz
=
H
mn
cos
np b
y
e-
jb z
Ey = Ez = Hx = 0
TE01模只有Ex、Hy和Hz三个场分量,它们与x无关,故 沿a边场无变化;
➢ 导波的种类
导波的种类
TE波 (M波)
TM波 (E波)
TEM波
Ez = 0 Hz ¹ 0
的导波
Hz = 0 Ez ¹ 0
的导波
Ez = 0
Hz = 0 的导波
➢导波场的求解方法
在规则导行系统中:
由麦克斯韦方程组导出横、纵向场关系式; 由麦克斯韦方程组导出电场或磁场纵向分量满足
各坐标系中的亥姆霍兹方程。 由各种情况下的边界条件(波导内壁:Et=0)求
px a
e-
jb z
Hz =
H10
cos
px a
e-
jb z
Ex = Ez = H y = 0
平行于波导宽边的xz平面内,磁力线是闭合曲线。同样, 磁场与y无关(在y方向场不变);
Hx在波导宽边上为正弦分布,而Hz在波导宽边上为余弦 分布;
Hx 和 Hx 在a 边上均有半个驻波分布。
Ey =
wma p
