九年级上册数学第一章图形与证明(二)单元试题
九年级数学上册 第一章 证明二测试A卷 试题

第一章证明二测试A卷一、填空题:〔每一小题5分,一共40分〕1、如图:点B、F、C、E在同一条直线上,点A、D在直线BE的两侧,AB∥DE,BF = CE,请添加一个适当的条件,使得AC = DF.2、等腰三角形的两边长分别是3cm 、4cm,那么这个等腰三角形的周长是 cm.3、:在Rt△ABC中,∠C = 90°,AB = 6cm ,∠A = 30°,那么AC= cm.4、到三角形三个顶点间隔相等的点是三角形的交点.5、定理“等腰三角形的两个底角相等〞的逆命题是;此命题是命题(填真或者假).6、如图:在△ABC中,∠C = 90°,∠B = 30°,AD平分∠CAB ,AD = 8cm ,那么D点到直线AB的间隔是 cm.7、如图,△ABC中,AB=AC,∠A = 30°, ED是AC的垂直平分线,那么∠BCD= .8、如图:在Rt△ABC中,∠C = 90°,BC = 6cm ,AC = 8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是 cm2.第1题第6题第7题第8题二、解答题:〔每一小题15分,一共60分〕9、:点E、F在B C上,BE = CF,∠A = ∠D,∠B = ∠C,AF与DE交于点O求证:⑴ AB = CD,⑵试判断△OEF的形状,并说明理由。
创作;朱本晓创作;朱本晓10、:△ABC 中,AD 平分∠BAC ,DE ⊥AB ,DF ⊥AC ,求证:⑴AE = AF ; ⑵AD 是EF 的垂直平分线.11、作图题:〔不写作法,但要保存作图痕迹〕:线段a .求作:△ABC ,使得AB = AC ,底边BC = 2a ,高AD = a.12、 如图,在△ABC 中,∠C = 90°,AC=BC , AD 平分∠BAC , 且交BC 于D ,DE ⊥AB 于E ,CD = 2cm ,计算AC 的长.a A EF D C B励志赠言经典语录精选句;挥动**,放飞梦想。
九年级数学第一章图形与证明(二)-练习及答案剖析

第一章图形与证明(二练习题一、选择题1.(2010,广州市在△ABC 中,D 、E 分别是边AB 、AC 的中点,若BC =5,则DE 的长是(A .2.5B .5C .10D .152.(2010,燕山已知等边△ABC 的边长为a ,则它的面积是( [来源:学#科#网Z#X#X#K] A .21a 2 B .23a 2 C .42a 2 D .43a 23.(2010,浙江省已知等腰三角形的一个内角为040,则这个等腰三角形的顶角为 (A.040B.0100C.040或0100D.070或0504.(2010,江西已知等腰三角形的两条边长分别是7和3,则下列四个数中,第三条边的长是(A .8B .7C . 4D .35.(2010,宁波市如图,在△ABC 中,AC AB =,︒=∠36A ,BD 、CE 分别是△ABC、△BCD 的角平分线,则图中的等腰三角形有(A 、5个B 、4个C 、3个D 、2个6.(2010,黄冈市如图,过边长为1的等边△ABC 的边AB 上一点P ,作PE⊥AC 于E ,Q 为BC 延长线上一点,当PA =CQ 时,连PQ 交AC 边于D ,则DE 的长为(A .13B .12C .23D .不能确定7.(2010,益阳市如图,已知△ABC ,求作一点P ,使P 到∠A 的两边的距离相等,且PA =PB .下确定P 点的方法正确的是(A.P 为∠A 、∠B 两角平分线的交点B.P 为∠A 的角平分线与AB 的垂直平分线的交点C.P 为AC 、AB 两边上的高的交点D.P 为AC 、AB 两边的垂直平分线的交点8.(2010,浙江台州市如图,矩形ABCD 中,AB >AD ,AB =a ,AN 平分∠DAB ,DM ⊥AN 于点M ,CN ⊥AN 于点N .则DM +CN 的值为(用含a 的代数式表示(aNMCDA B (第8题 AB C DE第5题第6题 ABCP第7题FE DC B A A BC DHEGOAB C D PA .aB .a54 C .a 22 D .a 239.(2010,江西如图,已知矩形纸片ABCD ,点E 是AB 的中点,点G 是BC 上的一点,∠BEG>60°,现沿直线EG 将纸片折叠,使点B 落在纸片上的点H 处,连接AH ,则与∠BEG 相等的角的个数为(A .4B .3C .2D .1第10题第11题10.(2010,山东聊城如图,点P 是矩形ABCD 的边AD 上的一个动点,矩形的两条边AB 、AC 的长分别为3和5,那么点P 到矩形的两条对角线AC 和BD 的距离之和是( A .125 B .65 C .245D .不确定 11.(2010,滨州如图,把一个长方形纸片对折两次,然后剪下一个角.为了得到一个正方形,剪刀与折痕所成的角的度数应为( A.60° B.30° C.45° D.90°12.(2010,重庆市已知:如图,在正方形ABCD 外取一点E ,连接AE 、BE 、DE .过点A 作AE的垂线交DE 于点P .若AE =AP =1,PB = 5 .下列结论:①△APD ≌△AEB ;②点B 到直线AE 的距离为 2 ;③EB ⊥ED ;④S △APD +S △APB =1+ 6 ;⑤S 正方形ABCD =4+ 6 .其中正确结论的序号是(A .①③④B .①②⑤C .③④⑤D .①③⑤第12题第13题第14题二、填空题13. (2010,滨州如图,平行四边形ABCD 中, ∠ABC=60°,E 、F 分别在CD 、BC 的延长线上,AE ∥BD,EF ⊥BC,DF=2,则EF 的长为14. (2010,福建晋江如图,请在下列四个关系中,选出两个恰当....的关系作为条件,推出四边形ABCD 是平行四边形 .(写出一种即可AB C D第9题关系:①AD ∥BC ,②CD AB =,③C A ∠=∠,④︒=∠+∠180C B .15.如图,正方形纸片ABCD 的边长为8,将其沿EF 折叠,则图中①②③④四个三角形的周长之和为_____________.16.(2010,山东德州在四边形ABCD 中,点E ,F ,G ,H 分别是边AB ,BC ,CD ,DA 的中点,如果四边形EFGH 为菱形,那么四边形ABCD 是 (只要写出一种即可.17.(2010,珠海如图,P 是菱形ABCD 对角线BD 上一点,PE ⊥AB 于点E ,PE =4cm ,则点P到BC 的距离是_____cm.18.(2010,益阳市如图,在△ABC 中,AB =AC =8,AD 是底边上的高,E 为AC 中点,则DE = .19.数学活动课上,老师在黑板上画直线平行于射线AN (如图,让同学们在直线l 和射线AN 上各找一点B 和C ,使得以A 、B 、C 为顶点的三角形是等腰直角三角形.这样的三角形最多能画个.20.(2010,青岛市把一张矩形纸片(矩形ABCD 按如图方式折叠,使顶点B 和点D 重合,折痕为EF .若AB = 3 cm ,BC = 5 cm ,则重叠部分△DEF 的面积是 cm 2.三、解答题21.(2010,青岛已知:如图,在正方形ABCD 中,点E 、F 分别在BC 和CD 上,AE = AF .(1求证:BE = DF ;(2连接AC 交EF 于点O ,延长OC 至点M ,使OM = OA ,连接EM 、FM .判断四边形AEMF是什么特殊四边形?并证明你的结论.B D CBAC ′F E ③②①④ (第15题A D BEFOCA BCFE 'A ('B D第17题ABD EC第18题• Al N (第19题第20题DC B A OE22.(2010,福建龙岩如图,平行四边形ABCD 中,E 、F 是对角线BD 上的点,且BE =DF . (1请你写出图中所有的全等三角形;(2试在上述各对全等三角形中找出一对加以证明.23.(2010,四川省眉山市如图,O 为矩形ABCD 对角线的交点,DE ∥AC ,CE∥BD .(1试判断四边形OCED 的形状,并说明理由; (2若AB =6,BC =8,求四边形OCED 的面积.24. (2010,滨州如图,四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点. (1请判断四边形EFGH 的形状?并说明为什么.(2若使四边形EFGH 为正方形,那么四边形ABCD 的对角线应具有怎样的性质?25.(2010,江苏泰州如图,四边形ABCD 是矩形,∠EDC =∠CAB ,∠DEC =90°.(1求证:AC ∥DE ;(2过点B 作BF ⊥AC 于点F ,连结EF ,试判断四边形BCEF 的形状,并说明理由.26.(2010,毕节如图,已知: 口ABCD 中,∠ABC 的平分线交边A D 于E ,A B C ∠的平分线BG 交CE 于F ,交A D 于G .求证:A E D G =.27.(2010,江苏宿迁如图,在□ABCD 中,点E 、F 是对角线AC 上两点,且AE =CF .求证:∠EBF =∠FDE .A BCDEF G CABDEF28.(2010,安徽)如图,AD∥FE,点 B、C 在 AD 上,∠1=∠2,BF=BC ⑴求证:四边形 BCEF 是菱形;⑵若 AB=BC=CD,求证:△ACF≌△BDE. 29.(2010,宁波市)如图 1,有一张菱形纸片 ABCD,,(1)请沿着 AC 剪一刀,把它分成两部分,把剪开的两部分拼成一个平行四边形,在图 2 中用实数画出你所拼成的平行四边形;若沿着 BD 剪开,请在图 3 中用实线画出拼成的平行四边形;并直接写出这两个平行四边形的周长. (2)沿着一条直线剪开,拼成与上述两种都不全等的平行四边形,请在图 4 中用实线画出拼成的平行四边形. (注:上述所画的平行四边形都不能与原菱形全等) D C D C D D C A B (图1) C A (图 2) B A (图 3) B A (图 4) B 周长为__________ 周长为__________ 6第二章图形与证明(二)练习题答案一、选择题题号答案 A 1 D 2 C 3 B 4 A5 B6 B7 C8 B9 A 10 C 11 D 12 二、填空题 13. 2 3 14.①③(或①④或③④或②④) 15.32 17.4 20. 5.1 16.正方形(或矩形或等腰梯形或对角线相等的四边形)18.4 19.3 三、解答题 21~28 题(略) 29.解:(1) D C D C D C A 周长为 26 B AB 周长为 22 A B 答案不唯一 7。
(完整)九年级数学上册第一章综合练习题及答案(2)

慧学云教育九 年 级 数 学 试 题(图形与证明二)一.选择题1、顺次连接任意四边形各边中点所得到的四边形一定是( )A 平行四边形B 菱形C 矩形D 正方形2、 国家级历史文化名城——金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB EF DC ∥∥,BC GH AD ∥∥,那么下列说法中正确的是( ) A .红花、绿花种植面积一定相等 B .绿花、黄花种植面积一定相等 C .红花、蓝花种植面积一定相等 D .蓝花、紫花种植面积一定相等3.如图,直线1l ∥2l ,若155,265∠=︒∠=︒,则3∠A 50︒B 55︒C 60︒D 65︒4、若等腰三角形的一个底角为50°,则顶角为( A .50° B .100° C .80° D .65°5、如图1,□ABCD 的周长是28㎝,△ABC 的周长是22㎝,则AC 的长为 ( )A .14㎝B .12㎝C .10㎝D .8㎝1 26、下列命题中,真命题是 ( )A.两条对角线相等的四边形是矩形 B.两条对角线互相垂直的四边形是菱形C.两条对角线互相垂直且相等的四边形是正方形 D.两条对角线互相平分的四边形是平行四边形7、已知菱形的两条对角线长分别为6和8,则菱形的周长为( ) A .20 B .30 C .40 D .108、如图2,在菱形ABCD 中,不一定成立的是( ) A .四边形ABCD 是平行四边形 B .AC ⊥BDDCB AA F C DB E3C .△ABD 是等边三角形 D .∠CAB =∠CAD9、如图3,在ABC △中,点E D F ,,分别在边AB ,BC ,CA 上,且DE CA ∥,DF BA ∥.下列四个判断中,不正确...的是 ( ) A.四边形AEDF 是平行四边形B.如果90BAC ∠=o ,那么四边形AEDF 是矩形 C.如果AD 平分BAC ∠,那么四边形AEDF 是菱形D.如果AD BC ⊥且AB AC =,那么四边形AEDF 是正方形10.如图,正方形ABCD 的边长为2,点E 在AB 边上,四边形EFGB 也为正方形, 设△AFC 的面积为S ,则 ( ) A .S=2 B .S=4 C .S=2.4 D .S 与BE 长度有关二.填空题11.已知平行四边形ABCD 中,AB =14cm,BC =16cm,则此平行四边形的周长为 _____cm.12.矩形的两条对角线的夹角为600,较短的边长为12cm,则对角线长为 cm.13.如下图(1),在平行四边形ABCD 中,CE AB ⊥,E 为垂足.如果125A =o ∠,则BCE =∠14.在四边形ABCD 中,已知AB ∥CD ,请补充一个条件: ,使得四边形ABCD 是平行四边形。
九年级数学图形与证明单元试题

第一章图形与证明(二)测试题 (时间 60分钟 满分150分)一、选择题与填空(9×5′+9×6′=99′) 1、若等腰三角形底角为72 0,则顶角为( )A 、1080B 、720C 、540D 、3602、如图,将矩形ABCD 沿AE 折叠,若∠BAD′=30°,则∠AED′ 等于( )A 、30°B 、45°C 、60°D 、75°3、 正方形具有而菱形不一定具有的性质是( )A 、对角线相等B 、对角线互相垂直平分C 、对角线平分一组对角D 、四条边相等4、用两个全等的直角三角形拼下列图形:①平行四边形(不包含菱形、矩形、正方形)②矩形 ③正方形 ④等腰三角形,一定可以拼成的图形的是( )A 、①②③B 、②③④C 、①③④D 、①②④ 5、已知菱形的边长为6cm ,一个内角为600,则菱形较短对角线长是( )ED ′DCA(第2题)A 、6cm B、、3cm D、6、将边长都为1cm 的正方形按如图所示摆放,点A 1、A 2、A 3、A 4分别是正方形的中心,则前5( )A 、14B 、12C 、1D 、27、在梯形ABCD 中,AD ∥BC ,对角线AC ⊥BD ,且AC =12,BD =9.,则梯形两腰中点的连线EF 长是( ) A 、10 B 、212C 、152 D 、128、如图,正方形ABCD 中,E 、F 是对角线AC 上两点,连接BE 、BF 、DE 、DF ,则添加下列哪一个条件可以判定四边形BEDF 是菱形( )A 、∠1=∠2B 、BE =DFC 、∠EDF =600D 、AB =AF9、如图,在梯形ABCD 中,AB ∥CD ,中位线EF 与对角线 AC 、BD交于M 、N 两点,若EF =18cm,MN=8cm,则AB 的长等于( ) A 、10cm B 、13cmFCEDBA 12(第8题图)ADCF BEMN(第9题图)D(第11题图)C、20cmD、26cm10、写出等腰梯形的两个性质,。
九年级(上)数学单元测试卷--第一章-证明(二)

九年级(上)数学单元测试卷--第一章-证明(二)本页仅作为文档页封面,使用时可以删除This document is for reference only-rar21year.March2九年级(上)数学单元测试卷 第一章 证明(二)(试卷满分为120分,考试时间为120分钟.)一、选择题(本大题共10小题,每小题3分,共30分)1.已知等腰三角形的两边长分别为5㎝、2㎝,则该等腰三角形的周长是( )A .7㎝B .9㎝C .12㎝或者9㎝D .12㎝2.如图,加条件能满足AAS 来判断⊿ACD ≌⊿ABE 的条件是( )A .∠AEB = ∠ADC ,∠C = ∠D B .∠AEB = ∠ADC , CD = BE C .AC = AB , AD = AE D .AC = AB , ∠C =∠B3.已知△ABC 的三边长分别是6cm 、8cm 、10cm ,则△ABC 的面积是 ( ) A.24cm 2B.30cm 2C.40cm 2D.48cm 24.到△ABC 的三个顶点距离相等的点是△ABC 的( )A.三边中线的交点B.三条角平分线的交点C.三边上高的交点D.三边的垂直平分线的交点5.△ABC 中,∠A ∶∠B ∶∠C=1∶2∶3,若BC=2,则AB 等于( )A.1B. 2C.4D.326、在下列条件中:①∠A+∠B=∠C ,②∠A ∶∠B ∶∠C=1∶2∶3,③∠A=90°-∠B , ④∠A=∠B=12 ∠C 中,能确定△ABC 是直角三角形的条件有( ) A 、1个 B 、2个 C 、3个 D 、4个7.如图,△ABC 中,AB=AC ,点D 在AC 边上,且BD=BC=AD ,则∠A 的度数为( )A.30°B.36°C.45°D.70°8.如图,△ABC ≌△AEF ,AB =AE ,∠B =∠E ,则对于结论①AC =AF .②∠FAB =∠EAB ,③EF =BC ,④∠EAB =∠FAC ,其中正确结论的个数是( )A.1个 B.2个 C.3个 D.4个9.如图,等边△ABC 中,BD=CE ,AD 与BE 相交于点P ,则∠APE 的度数是( )A.45°B.55°C.60°D.75° 10.已知:如图,AB=AC,∠A=36°,AB的垂直平分线交AC于D,则下列结论:①∠C=72°;②BD是∠ABC的平分线;③△ABD是等腰三角形;④△BCD是等腰三角形,其中正确的有( )A.1个 B.2个 C.3个 D.4个7题图 8题图 9题图10题图二、填空题(本大题共8小题,每小题3分,共24分)11.“等边对等角”的逆命题是______________________________.12.已知⊿ABC 中,∠A = 090,角平分线BE 、CF 交于点O ,则∠BOC = 13.在△ABC 中,∠A=40°,AB=AC ,AB 的垂直平分线交AC 与D ,则∠DBC 的度数为 .14.在△ABC 中,AB=5cm ,BC=6cm ,BC 边上的中线AD=4cm ,则∠ADC 的度数是 度.15.⊿ABC 中,∠C= 090,∠A = 030,AC=32,则AB 边上的中线CD= 。
九年级(上)第一章证明(二)单元测试卷(2)(北师大版)-.docx
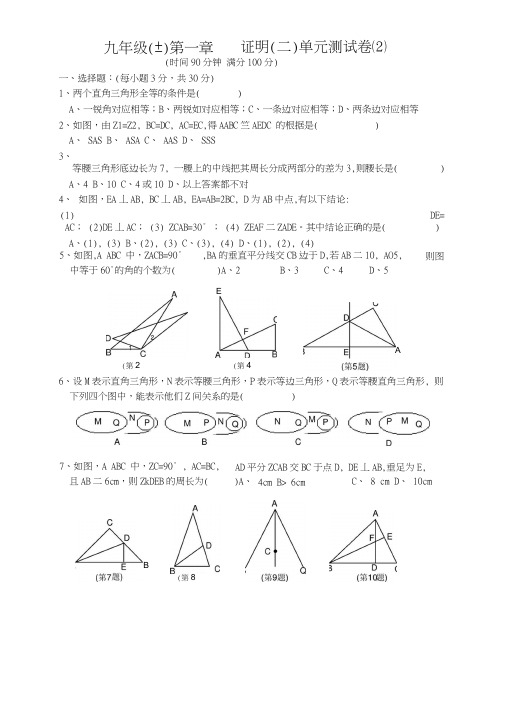
(时间90分钟 满分100分)一、选择题:(每小题3分,共30分) 1、两个直角三角形全等的条件是()A 、一锐角对应相等;B 、两锐如对应相等;C 、一条边对应相等;D 、两条边对应相等 2、如图,由Z1=Z2, BC=DC, AC=EC,得AABC 竺AEDC 的根据是( )A 、 SASB 、 ASAC 、 AASD 、 SSS3、等腰三角形底边长为7, 一腰上的中线把其周长分成两部分的差为3,则腰长是( )A 、4B 、10C 、4或10D 、以上答案都不对4、 如图,EA 丄AB, BC 丄AB, EA=AB=2BC, D 为AB 中点,有以下结论: (1)DE=AC ; (2)DE 丄AC ; (3) ZCAB=30° ; (4) ZEAF 二ZADE 。
其中结论正确的是( ) A 、(1), (3) B 、(2), (3) C 、(3), (4) D 、(1), (2), (4) 6、设M 表示直角三角形,N 表示等腰三角形,P 表示等边三角形,Q 表示等腰直角三角形, 则下列四个图中,能表示他们Z 间关系的是()九年级(±)第一章证明(二)单元测试卷⑵5、如图,A ABC 中,ZACB=90° ,BA 的垂直平分线交CB 边于D,若AB 二10, AO5, 则图中等于60°的角的个数为()A 、2B 、3C 、4D 、57、如图,A ABC 中,ZC=90° , AC=BC, 且AB 二6cm ,则ZkDEB 的周长为(AD 平分ZCAB 交BC 于点D, DE 丄AB,垂足为E, 4cm B> 6cm)A 、 C 、 8 cm D 、 10cm(第2题)E(第4题)AB(第8题)8、如图,△ ABC中,AB=AC,点D在AC边上,A、30°B、36°C、45°且BD二BOAD,则ZA的度数为( D、70°9、 如图,已知AC 平分ZPAQ,点B, B'分别在边AP, AQ 上,如果添加一个条件,即可推 出AB 二AB',那么该条件可以是()A 、BB'丄ACB 、BOB'C C 、ZACB=ZACB ,D 、ZABC=ZAB ZC10、 如图,ZiABC 中,AD 丄BC 于D, BE 丄AC 于E, AD 与BE 相交于F,若BF 二AC,贝I 」ABC 的大小是( )A 、 40°B 、 45° C、 50° D、 60°二、填空题:(每小题3分,共24分)11、 如果等腰三角形的一个底角是80° ,那么顶角是 ________ 度.12、 如图,点F 、C 在线段BE 上,且Z1二Z2, BC 二EF,若要使△ ABC^ADEF,则述须补充 一个条件 ___________ .13、 如图,点D 在AB 上,点E 在AC 上,CD 与BE 相交于点0,且AD=AE, AB 二AC 。
九年级数学上册第一章证明(二)单元测试题

九年级数学第一章 证明(二) 测试题班次 学号 姓名一 、填空题〔每题3分〕: 1.如图,修建抽水站时,沿着倾斜角为300的斜坡铺设管道,假设量得水管AB 的长度为80米,那么点B 离水平面的高度BC 的长为 米。
2、如果一个三角形的一条角平分线恰好是对边上的高,那么这个三角形是 三角形.3、如图,AC=DB ,要使△ABC ≌△DCB ,只需增加的一个条件是或 . 4、命题:“全等三角形的对应角相等〞的逆命题是___。
___________________________________ 这条逆命题是______命题〔填“真〞或“假〞〕5、如图,一个顶角为40º的等腰三角形纸片,剪去顶角后,得到一个四边形,那么=∠+∠21_________ ;6、在△ABC 中,AB =AC ,AD 是中线,∠B =70°,BC =15cm ,那么∠BAC = ,∠DAC = , BD = cm ; 7、,如图,O 是△ABC 的∠ABC 、∠ACB 的角平分线的交点,OD ∥AB 交BC 于D ,OE ∥AC 交BC 于E ,假设BC = 10,那么△ODE 的周长为 .8、如图,在Rt △ABC 中,∠B=90°,∠A=40°,AC 的垂直平分线MN 与AB 相交于D 点,那么∠BCD 的度数是 .9、△ABC 中,∠C=90°,AD 平分∠BAC ,交BC 于点D 。
假设DC=7,那么D 到AB 的距离是 .10、如图,∠AOP=∠BOP=15°,PC ∥OA ,PD ⊥OA ,假设PC=4,那么PD 的长为 .二、 选择题〔每题3分〕1、等腰三角形底边上的高与底边的比是1∶2,那么它的顶角等于〔 〕 A 、90° B 、60° C 、120° D 、150°2.以下两个三角形中,一定全等的是 〔 〕 (A ) 有一个角是40°,腰相等的两个等腰三角形 〔B 〕两个等边三角形〔C 〕有一个角是100°,底相等的两个等腰三角形〔D 〕有一条边相等,有一个内角相等的两个等腰三角形 3、到△ABC 的三个顶点距离相等的点是△ABC 的〔 〕 A.三边中线的交点 B.三条角平分线的交点 C.三边上高的交点 D.三边垂直平分线的交点第18题图 C B A 第1题 第5题4、△ABC 中,∠A ∶∠B ∶∠C=1∶2∶3,CD ⊥AB 于点D 假设BC=a ,那么AD 等于〔 〕 A.21a B.23a C.23a D.3a 5、如图,△ABC 中,AB=AC ,点D 在AC 边上,且BD=BC=AD ,那么∠A的度数为〔 〕A.30°B.36°C.45°D.70°三、解答题〔每题12分〕1、如图,AD ⊥CD ,AB=10,BC=20,∠A=∠C=30°。
九年级上册第一章图形与证明(二)单元试题(苏科版)

九年级上册第一章图形与证明(二)单元试题(苏科版)第一章图形与证明(二)检测题【本检测题满分:100分,时间:90分钟】一、选择题(每小题3分,共30分)1.如图,在△ABC中,,点D在AC边上,且,则∠A的度数为()A.30°B.36°C.45°D.70°2.如图,在△ABC中,AB的垂直平分线交AC于点D,交AB于点E,如果5cm,4cm,那么△DBC的周长是()A.6cmB.7cmC.8cmD.9cm3.使两个直角三角形全等的条件有()A.一锐角对应相等B.两锐角对应相等C.一条边对应相等D.两条边对应相等4.(2012年浙江台州中考)如图,点D,E,F分别为△ABC三边的中点,若△DEF的周长为10,则△ABC的周长为()A.5B.10C.20D.405.如图,在平行四边形中,对角线,相交于点O,若,的和为18cm,,△AOB的周长为13cm,那么BC的长是()A.6cmB.9cmC.3cmD.12cm6.(2012年长沙中考)下列四边形中,对角线一定不相等的是()A.正方形B.矩形C.等腰梯形D.直角梯形7.从菱形的钝角顶点向对角的两条边作垂线,垂足恰好是该边的中点,则菱形的内角中钝角的度数是()A.150°B.135°C.120°D.100°8.顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形中满足条件的是()①平行四边形;②菱形;③等腰梯形;④对角线互相垂直的四边形.A.①③B.②③C.③④D.②④9.已知一矩形的两边长分别为10cm和15cm,其中一个内角的平分线分长边为两部分,这两部分的长为()A.6cm和9cmB.5cm和10cmC.4cm和11cmD.7cm和8cm10.在梯形ABCD中,AD∥BC,对角线AC⊥BD,且,,则梯形两腰中点的连线EF的长是()A.10B.C.D.12二、填空题(每小题3分,共30分)11.(2012年哈尔滨中考)一个等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为_________.12.如图,已知∠120°,,AC的垂直平分线交BC于D,则∠______.13.如图,在△中,∠90°,平分∠,20cm,则点M到AB的距离是_________.14.用两个全等的直角三角形拼下列图形:①平行四边形(非菱形、矩形和正方形);②矩形;③正方形;④等腰三角形.一定可以拼成的图形是_________.(把所有符合条件的图形的序号都写上)15.(2012年宁夏中考)已知菱形的边长为6,一个内角为60°,则菱形的较短对角线的长是_________.16.如图,BD是平行四边形ABCD的对角线,点E,F在BD上,要使四边形AECF是平行四边形,还需要添加的一个条件是_________.(只需写出一个符合题意的条件即可)17.如图,在梯形中,∥,中位线与对角线,分别交于,两点,若18cm,8cm,则AB的长等于_____.18.如图,在菱形ABCD中,∠B=60°,点E,F分别从点B,D同时以同样的速度沿边BC,DC向点C运动.给出以下四个结论:①;②∠∠;③当点E,F分别为BC,DC的中点时,△AEF是等边三角形;④当点E,F分别为边BC,DC的中点时,△AEF的面积最大.上述结论正确的序号有.19.如图,四边形ABCD是正方形,延长AB到点E,使,则∠BCE的度数是20.如图,矩形的两条对角线交于点,过点作的垂线,分别交,于点,,连接,已知△的周长为24cm,则矩形的周长是cm.三、解答题(共40分)21.(5分)如图,在△ABC中,∠B=90°,M是AC上任意一点(M与A不重合),MD⊥BC,MD交∠BAC的平分线于点D,求证:.22.(5分)如图,在四边形ABCD中,,,BD平分∠ABC.求证:∠∠180°.23.(5分)用反证法证明:在一个三角形中,如果两条边不相等,那么这两条边所对的角也不相等.24.(5分)辨析纠错.已知:如图,在△ABC中,AD是∠BAC的平分线,DE∥AC,DF∥AB.求证:四边形AEDF是菱形.对于这道题,小明是这样证明的.证明:∵平分∠,∴∠1=∠2(角平分线的定义).∵∥,∴∠2=∠3(两直线平行,内错角相等).∴∠1=∠3(等量代换).∴(等角对等边).同理可证:.∴四边形是菱形(菱形定义).老师说小明的证明过程有错误,你能看出来吗?(1)请你帮小明指出他错在哪里.(2)请你帮小明做出正确的解答.25.(6分)(2012年浙江温州中考)如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.26.(7分)(2012年宁夏中考)正方形ABCD的边长为3,E,F分别是AB,BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.(1)求证:EF=FM;(2)当AE=1时,求EF的长.27.(7分)已知在等腰梯形D中,∥.(1)若,,梯形的高是4,求梯形的周长;(2)若,,梯形的高是h,梯形的周长为c,请用表示c;(3)若,,.求证:⊥.第一章图形与证明(二)检测题参考答案一、选择题1.B解析:因为,所以∠=∠.因为,所以∠∠,∠∠C.又因为∠∠∠,所以∠∠∠∠∠2∠,所以∠2∠2∠180°,所以∠36°.2.D解析:因为垂直平分AB,所以.所以△的周长=(cm).3.D解析:直角三角形的全等比一般三角形的全等更容易判断,它们本身已有一对角对应相等,只要再有两条边对应相等即可.4.C解析:根据中位线定理可得BC=2DF,AC=2DE,AB=2EF,继而结合△DEF 的周长为10,可得出△ABC的周长.∵D,E,F分别为△ABC三边的中点,∴DE,DF,EF都是△ABC的中位线,∴BC=2DF,AC=2DE,AB=2EF,故△ABC的周长=AB+BC+AC=2(FE+DF+DE)=20.故选C.5.A解析:因为,,18cm,所以9cm.因为△AOB的周长为13cm,所以(cm).又因为,,,所以cm.6.D解析:正方形、矩形、等腰梯形的对角线一定相等,直角梯形的对角线一定不相等.7.C解析:如图,在菱形ABCD中,AE⊥CD,AF⊥BC,连接AC.因为,所以AE是CD的中垂线,所以,所以三角形ADC是等边三角形,所以∠60°,从而∠120°.8.D解析:因为顺次连接任意一个四边形的各边中点,得到的是平行四边形,而要得到矩形,根据矩形的判定(有一个角是直角的平行四边形是矩形),所以该四边形的对角线应互相垂直,只有②④符合. 9.B解析:如图,在矩形ABCD中,10cm,15cm,是∠的平分线,则∠∠C.由AE∥BC得∠∠AEB,所以∠∠AEB,即,所以10cm,(cm),故选B.10.C解析:如图,作∥,则四边形为平行四边形,,.又⊥,,,所以⊥.根据勾股定理得,根据梯形中位线的定义,.二、填空题11.16或17解析:当等腰三角形的腰长为5时,其周长为5×2+6=16;当等腰三角形的腰长为6时,其周长为6×2+5=17.所以这个等腰三角形的周长为16或17.12.60°解析:由题意可知,所以∠∠.又∠∠30°,所以∠∠∠60°.13.20cm解析:根据角平分线上的点到这个角两边的距离相等可得.14.①②④解析:两全等的直角三角形对应的直角边叠合,当一个直角三角形的直角顶点对应另一个直角三角形的非直角顶点时,拼成平行四边形(非矩形、菱形、正方形);当一个直角三角形的直角顶点对应另一个直角三角形的直角顶点时,拼成等腰三角形.两全等的直角三角形对应的斜边叠合,两互余角的顶点对应时,拼成矩形.15.6解析:较短的对角线将菱形分成两个全等的等边三角形,所以较短对角线的长为6.16.答案不唯一,只要正确即可,如或∠∠.17.26cm解析:由EF是梯形ABCD的中位线,则EF∥CD∥AB,且,,则所以EM是△ADC的中位线,所以DC.同理,DC.所以所以.又MF为△ABC的中位线,所以26cm.18.①②③解析:因为四边形ABCD为菱形,所以ABADCBCD,∠B=∠D,BE=DF,所以△≌△,所以AEAF,①正确.由CB=CD,BE=DF得CE=CF,所以∠CEF=∠CFE,②正确.当E,F分别为BC,CD的中点时,BE=DF=BC=DC.连接AC,BD,知△为等边三角形,所以⊥,⊥,所以∠AEF=,由①知AEAF,故△为等边三角形,③正确.设菱形的边长为1,当点E,F分别为边BC,DC的中点时,的面积为,而当点E,F分别与点B,D重合时,=.故④错.19.22.5°解析:由四边形是正方形,得∠∠又,所以,所以∠20.48解析:由矩形可知,又⊥,所以垂直平分,所以.已知△的周长为24cm,即所以矩形ABCD的周长为三、解答题21.证明:∵⊥,且∠90°,∴∥,∴∠∠D.又∵AD为∠的平分线,∴∠∠,∴∠∠,∴.22.分析:从条件BD平分∠ABC,可联想到角平分线定理的基本图形,故要作垂线段.证明:如图,过点D作DE⊥AB交BA的延长线于点E,过点D作于点F.因为BD平分∠,所以.在Rt△和Rt△中,,所以Rt△≌Rt△(HL).所以∠∠.因为∠∠180°,所以∠∠180°.23.解:已知:如图,在△ABC中,,求证:∠∠.证明:假设∠∠C,那么根据“等角对等边”可得,但已知条件是,矛盾,因此∠∠.24.解:能.⑴小明错用了菱形的定义.⑵改正:∵∥,∥,∴四边形是平行四边形.∵平分∠,∴∠∠2.∵∥,∴∠∠2,∴∠=∠3.∴,∴平行四边形是菱形.25.分析:根据平移的性质可得CF=AD=10cm,DF=AC=10cm,就可以根据四条边都相等的四边形是菱形得到结论.证明:由平移变换的性质得CF=AD=10cm,DF=AC.∵∠B=90°,AB=6cm,BC=8cm,∴AC=10cm.∴AC=DF=AD=CF=10cm,∴四边形ACFD是菱形.26.(1)证明:∵△DAE逆时针旋转90°得到△DCM,∴∠FCM=∠FCD+∠DCM=180°,∴F,C,M三点共线,DE=DM,∠EDM=90°,∴∠EDF+∠FDM=90°.∵∠EDF=45°,∴∠FDM=∠EDF=45°.在△DEF和△DMF中,DE=DM,∠EDF=∠MDF,DF=DF,∴△DEF≌△DMF(SAS),∴EF=MF.(2)解:设EF=MF=x,∵AE=CM=1,且BC=3,∴BM=BC+CM=3+1=4,∴BF=BM-MF=BM-EF=4-x.∵EB=AB-AE=3-1=2,在Rt△EBF中,由勾股定理得EB2+BF2=EF2,即22+(4-x)2=x2,解得:x=,即EF=.27.(1)解:如图,作DE∥AB,DF⊥BC.因为AD∥BC,所以四边形ABED是平行四边形,所以AB=DE,AD=BE.因为AB=CD,所以DE=DC.又DF⊥BC,所以EF=FC.因为AD=5,BC=11,梯形的高是4,所以EC=BC-AD=6,EF=FC=3,DF=4,从而,梯形的周长为AB+BC+CD+AD=5+11+5+5=26.(2)解:若AD=a,BC=b,梯形的高是h,则DF=h,EF=FC=(b-a),. 所以梯形的周长c=AB+BC+CD+AD=.(3)证明:如图,过点D作AC的平行线,交BC的延长线于点E. 由等腰梯形的性质得AC=BD.因为AD∥BC,ED∥AC,所以四边形ACED是平行四边形,所以AD=CE,AC=DE,从而BD=DE=.又BE=BC+CE=BC+AD=10,所以,所以DE⊥BD,即AC⊥BD.。
(数学试卷九年级)第一章 证明二练习题及答案全套

一、填空题1、 如图1,若⊿ABE ⊿ADC ,则AD = AB ,DC= ;∠D = ∠ ;∠BAE = ∠ ;2、如图2,在△ABC 中,AD =DE ,AB =BE ,∠A =80°则∠DEC = .3、等腰三角形的两边分别是7 cm 和3 cm ,则周长为_________;4、在等腰三角形中顶角为40°时底角等于_________,一个底角为50°,则顶角等于_________;5、如图,∠AOB 是一钢架,且∠AOB=10°,为了使钢架更加牢固,需在其内部添加一些钢管EF 、FG 、GH ……添加的钢管长度都与OE 相等,则最多能添加这样的钢管 根。
二、选择题6、给出下列命题,正确的( ) ①等腰三角形的角平分线、中线和高重合; ②等腰三角形两腰上的高相等; ③等腰三角形最小边是底边;④等边三角形的高、中线、角平分线都相等;⑤等腰三角形都是锐角三角形( ) (A )1个 (B )2个 (C )3个 (D )4个7、满足下列条件的两个三角形一定全等的( )A 、腰相等的两个等腰三角形B 、一个角对应相等的两个等腰三角形C 、斜边对应相等的两个直角三角形D 、底相等的两个等腰直角三角形§1.1.1证明(二)8、已知如图3,在△ABC中,AB=AC,BC=BD,AD=DE=EB,则∠A的度数是()(A)30°(B) 36°(C)45°(D)54°9、如图4,在△ABC中,AB=AC ,∠A=36,BD、CE分别为∠ABC与∠ACB的角平分线,且交于点F,则图中的等腰三角形有()(A)6个(B)7个(C)8个(D)9个10、如图5,等边△ABC中,BD=CE,AD 与BE相交于点P,则∠APE的度数是()(A)45°(B)55°(C)60°( D)75°三、解答题11、阅读下题及其证明过程:已知:如图,D是△ABC中BC边上一点,EB=EC,∠ABE=∠ACE,求证:∠BAE=∠CAE.证明:在△AEB和△AEC中,⎪⎩⎪⎨⎧=∠=∠=AEAEACEABEECEB∴△AEB≌△AEC(第一步)∴∠BAE=∠CAE(第二步)问:上面证明过程是否正确?若正确,请写出每一步推理根据;若不正确,请指出错在哪一步?并写出你认为正确的推理过程;12、已知:线段a、h(如图)求作:△ABC,使AB=AC,且BC=a,高AD=h.请你用尺规作图,并补全作法作法:(1)作线段BC= .(2)作.(3) .(4)连结 .则△ABC 为所求等腰三角形.一、填空题1、等腰三角形底边上的__________,底边上的__________,顶角__________,均把它分成两个全等三角形 2、已知△ABC ,如下左图所示,其中∠B=∠C ,则_______=________..3、如上中图,在△ABC 中,AB=AC ,∠A=120°,D 是BC 的中点,DE⊥AC,则∠C=__________°;CE ∶EA=__________.4、如上右图,已知AD 是△ABC 的外角平分线,且AD ∥BC ,则∠1__________∠B ,∠2__________∠C ,△ABC 是__________三角形.5、在△ABC 中,∠A=∠B=21∠C ,则△ABC 是__________三角形. 二、选择题6、如果一个三角形的一个外角是130°,且它恰好等于一个不相邻的内角的2倍,那么这个三角形是( ) A.钝角三角形 B.直角三角形 C.等腰三角形D.等边三角形7、如下左图,在△ABC 中,AB=AC ,∠C=2∠A ,BD 是∠ABC 的平分线,则图中共有等腰三角形( )A.1个B.2个C.3个D.4个§1.1.2证明(二)ECAD CBA 21E ADCBDCBAC8、如上右,△BDC′是将矩形ABCD,沿对角线BD折起得到的,图中(包括实线、虚线图形),共有全等三角形()A.2对 B、3 对 C.4对D.5对9、如下左图,在△ABC中,∠B=∠C=40°,D,E是BC上两点,且∠ADE=∠AED=80°,则图中共有等腰三角形()A.6个B.5个C.4个D.3个10、如上右图,已知△ABC中,CD平分∠ACB交AB于D,又DE∥BC,交AC于E,若DE=4 cm,AE=5 cm,则AC等于()A.5 cmB.4 cmC.9 cmD.1 cm三、解答题11、已知,如左下图,△ABC中,AD是∠BAC的平分线,DE∥AC交AB于E,DF ∥AB交AC于F,AE=6,求四边形AFDE 的周长. 12、如图,DE∥BC,CG=GB,∠1=∠2,求证:△DGE是等腰三角形.13、.如右图所示,△ABC中,∠ACB=90°,CD⊥AB,垂足是D,∠A=60°.求证:BD=3AD.一、填空题1、已知,等腰△ABC,AB=AC:(1)若AB=BC,则△ABC为_________三角形;(2)若∠A=60°,则△ABC为_______三角形;(3)若∠B=60°,则△ABC为_______三角形.2、在线段、直角、等腰三角形、直角三角形中,成轴对称图形的是__________.3、底与腰不等的等腰三角形有__________条对称轴,等边三角形有__________条对称轴.请你在图(1)中作出等腰△ABC,等边△DEF的对称轴.4、如图上右图,已知△ABC是等边三角形,AD∥BC,CD⊥AD,垂足为D,E为AC的中点,AD=DE=6cm则∠ACD=_____°,AC=______cm,∠DAC=_______°,△ADE是______三角形.5、如左下图,△ABC是等边三角形,AD ⊥BC,DE⊥AB,垂足分别为D,E,如果AB=8 cm,则BD=_______cm,∠BDE=_____°,BE=______cm.6、如右上图,Rt△ABC中,∠A=30°,AB+BC=12 cm,则AB=__________cm.二、选择题7、下列说法不正确的是§1.1.3证明(二)A.等边三角形有三条对称轴B.线段AB只有一条对称轴C.等腰三角形的对称轴是底边上的中线D.等腰三角形的对称轴是底边上的高所在的直线8、下列命题不正确的是A.等腰三角形的底角不能是钝角B.等腰三角形不能是直角三角形C.若一个三角形有三条对称轴,那么它一定是等边三角形D.两个全等的且有一个锐角为30°的直角三角形可以拼成一个等边三角形9、在Rt△ABC中,如右图所示,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离DE=3.8 cm,则BC等于A.3.8 cmB.7.6 cmC.11.4 cmD.11.2 cm三、解答与证明10、如下图,在△ABC中,∠A=20°,D 在AB上,AD=DC,∠ACD∶∠BCD=2∶3,求:∠ABC的度数.11、如下图,在△ABC中,∠B=90°,M是AC上任意一点(M与A不重合)MD⊥BC,交∠BAC的平分线于点D,求证:MD=MA.12、如右图,已知△ABC和△BDE都是等边三角形,求证:AE=CD.一、判断题1.如果一个命题正确,那么它的逆命题也正确2.定理不一定有逆定理3.在直角三角形中,任意给出两条边的长可以求第三边的长二、填空题4、Rt△ABC中,∠C=90°,如图下左图,若b=5,c=13,则a=__________;若a=8,b=6,则c=__________.5、等边△ABC,AD为它的高线,下中图所示,若它的边长为2,则它的周长为__________,AD=__________,BD∶AD∶AB=__________∶__________∶__________.5、上右图所示,正方形ABCD,AC为它的一条对角线,若AB=2,则AC=__________;若AC=2,则AB=__________;AC∶AB=__________∶__________.6、如右图,△ABC中,∠A+∠C=2∠B,∠A=30°,则∠C=__________;若AB=6,则BC=__________.7、若直角三角形的三条边长分别是6,8,a则(1)当6,8均为直角边时,a=__________;(2)当8为斜边,6为直角边时,§1.2.1证明(二)a=__________.三、选择题8、如右图,等腰直角△ABC,AB=2,则S△ABC等于( )A.2B.1C.4D.29、若三角形的三边分别为a,b,c,则下面四种情况中,构成直角三角形的是( )A.a=2,b=3,c=4B.a=12,b=5,c=13C.a=4,b=5,c=6D.a=7,b=18,c=1710、如左下图,在△ABC中,AD⊥BC于D,BD=5,DC=1,AC=5,那么AB的长度是A.27B.27C.10D.2511、如右上图,AB⊥BC,DC⊥BC,E是BC上一点,∠BAE=∠DEC=60°,AB=3,CE=4,则AD等于( )A.4 8B.24C.10D.12四、解答题12、已知,如下图,等边三角形ABC,AD为BC边上的高线,若AB=2,求△ABC 的面积.13、已知:如下图,△ABC中,CD⊥AB于D,AC=4,BC=3,DB=59.(1)求DC的长;(2)求AD的长;(3)求AB的长;(4)求证:△ABC是直角三角形.14、如右图,为修铁路需凿通隧道AC,测得∠A=50°,∠B=40°,AB=5 km,BC=4km,若每天凿隧道0.3km,问几天才能把隧道凿通?一、填空题1、如图,Rt△ABC和Rt△DEF,∠C=∠F=90(1)若∠A=∠D,BC=EF,则Rt△ABC≌Rt△DEF的依据是__________. (2)若∠A=∠D,AC=DF,则Rt△ABC≌Rt△DEF的依据是__________.(3)若∠A=∠D,AB=DE,则Rt△ABC ≌Rt△DEF的依据是__________. (4)若AC=DF,AB=DE,则Rt△ABC≌Rt△DEF的依据是__________.(5)若AC=DF,CB=FE,则Rt△ABC≌Rt△DEF的依据是__________.2、如右图,在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△__________≌△__________,其判定依据是__________,还有△__________≌△__________,其判定依据是__________.3、已知:如图下左图,AE⊥BC,DF⊥BC,垂足分别为E,F,AE=DF,AB=DC,则△__________≌△__________(HL).§1.2.2证明(二)4、已知:如上中图,BE,CF为△ABC 的高,且BE=CF,BE,CF交于点H,若BC=10,FC=8,则EC=__________.5、已知:如上右图,AB=CD,DE⊥AC于E,BF⊥AC于F,且DE=BF,∠D=60°,则∠A=______°.二、选择题6、如下左图,O是∠BAC内一点,且点O到AB,AC的距离OE=OF,则△AEO≌△AFO的依据是( ) A.HLB.AASC.SSSD.ASA7、在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,如上右图,那么下列各条件中,不能使Rt△ABC≌Rt△A′B′C′的是( )A.AB=A′B′=5,BC=B′C′=3B.AB=B′C′=5,∠A=∠B′=40°C.AC=A′C′=5,BC=B′C′=3D.AC=A′C′=5,∠A=∠A′=40°8、下列条件不可以判定两个直角三角形全等的是( ) A.两条直角边对应相等面B.有两条边对应相等C.一条边和一锐角对应相等D.一条边和一个角对应相等三、证明题9、如下图,CD⊥AD,CB⊥AB,AB=AD,求证:CD=CB.10、已知:如下图,CD、C′D′分别是Rt△ABC,Rt△A′B′C′斜边上的高,且CB=C′B′,CD=C′D′.求证:△ABC≌△A′B′C′.11、如下图,已知∠ABC=∠ADC=90°,E 是AC上一点,AB=AD,求证:EB=ED. 一、填空题1、如下左图,已知直线MN是线段AB 的垂直平分线,垂足为D,点P是MN上一点,若AB=10 cm,则BD=__________cm;若PA=10 cm,则PB=__________cm;此时,PD=__________cm.2、如下中图,在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABD的周长是12 cm,AC=5cm,则AB+BD+AD=________cm;AB+BD+DC=__________cm;△ABC的周长是__________cm.3、如上右图,在Rt△ABC中,∠C=90°,∠B=15°,DE是AB的中垂线,垂足为D,交BC于E,BE=5,则AE=_________,∠AEC=_________,AC=__________ .4、已知线段AB及一点P,PA=PB=3cm ,§1.3.1证明(二)则点P在__________上.5、如果P是线段AB的垂直平分线上一点,且PB=6cm,则PA=__________cm.6、如图下左图,P是线段AB垂直平分线上一点,M为线段AB上异于A,B的点,则PA,PB,PM的大小关系是PA________PB________PM.7、如图下中图,在△ABC中,∠C=90°,∠A=30°,BD平分∠ABC交BC于D,则点D在__________上.8、如图上右图,BC是等腰△ABC和等腰△DBC的公共底,则直线AD必是__________的垂直平分线.二、选择题9、下列各图形中,是轴对称图形的有多少个①等腰三角形②等边三角形③点④角⑤两个全等三角形A.1个B.2个C.3个D.4个10、如下左图,AC=AD,BC=BD,则A.CD垂直平分ADB.AB垂直平分CDC.CD平分∠ACBD.以上结论均不对11、如上右图,△ABC中,AB的垂直平分线交AC于D,如果AC=5 cm,BC=4cm,那么△DBC的周长是A.6 cmB.7 cmC.8 cmD.9 cm12、如果三角形三条边的中垂线的交点在三角形的外部,那么,这个三角形是A.直角三角形B.锐角三角形C.钝角三角形D.等边三角形三、解答题13、如右图,P是∠AOB的平分线OM 上任意一点,PE⊥CA于E,PF⊥OB于F,连结EF.求证:OP垂直平分EF.一、判断题1、三角形三条边的垂直平分线必交于一点2、以三角形两边的垂直平分线的交点为圆心,以该点到三角形三个顶点中的任意一点的距离为半径作圆,必经过另外两个顶点3、平面上只存在一点到已知三角形三个顶点距离相等4、三角形关于任一边上的垂直平分线成轴对称二、填空题5、如左下图,点P为△ABC三边中垂线交点,则PA__________PB__________PC.6、如右上图,在锐角三角形ABC中,∠A=50°,AC、BC的垂直平分线交于点O,则∠1_______∠2,∠3______∠4,∠5______∠6,∠2+∠3=________度,∠§1.3.2证明(二)1+∠4=______度,∠5+∠6=_______度,∠BOC=_______度.7、如左下图,D为BC边上一点,且BC=BD+AD,则AD__________DC,点D在__________的垂直平分线上.8、如右上图,在△ABC中,DE、FG分别是边AB、AC的垂直平分线,则∠B__________∠1,∠C__________∠2;若∠BAC=126°,则∠EAG=__________度.9、如左下图,AD是△ABC中BC边上的高,E是AD上异于A,D的点,若BE=CE,则△__________≌△__________(HL);从而BD=DC,则△________≌△_________(SAS);△ABC是__________三角形. 10、如右上图,∠BAC=120°,AB=AC,AC的垂直平分线交BC于D,则∠ADB=_________度.三、作图题11、(1)分别作出点P,使得PA=PB=PC(2)观察各图中的点P与△ABC的位置关系,并总结规律:当△ABC为锐角三角形时,点P在△ABC的__________;当△ABC为直角三角形时,点P在△ABC的__________;当△ABC为钝角三角形时,点P在△ABC的__________;反之也成立,且在平面内到三角形各顶点距离相等的点只有一个.四、类比联想12、既然任意一个三角形的三边的垂直平分线交于一点,那三角形的三边上的中线是否也交于一点;三个角的平分线是否也交于一点;试通过折纸或用直尺、圆规画图验证这种猜想. 一、判断题1、角的平分线上的点到角的两边的距离相等2、到角的两边距离相等的点在角的平分线上3、角的平分线是到角两边距离相等的点的集合4、角平分线是角的对称轴二、填空题5、如图下左图,AD平分∠BAC,点P在AD上,若PE⊥AB,PF⊥AC,则PE__________PF.6、如图下中图,PD⊥AB,PE⊥AC,且PD=PE,连接AP,则∠BAP__________∠CAP.§1.4.1证明(二)7、如图上右图,∠BAC=60°,AP平分∠BAC,PD⊥AB,PE⊥AC,若AD=3,则PE=______.8、已知,如图(4),∠AOB=60°,CD⊥OA于D,CE⊥OB于E,若CD=CE,则∠COD+∠AOB=__________度.9、如图(5),已知MP⊥OP于P,MQ⊥OQ于Q,S△DOM=6 cm2,OP=3 cm,则MQ=__________cm.三、选择题10、下列各语句中,不是真命题的是( )A.直角都相等B.等角的补角相等C.点P在角的平分线上D.对顶角相等11、下列命题中是真命题的是( )A.有两角及其中一角的平分线对应相等的两个三角形全等B.相等的角是对顶角C.余角相等的角互余D.两直线被第三条直线所截,截得的同位角相等12、如左下图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3 cm,那么AE+DE等于A.2 cmB.3 cmC.4 cmD.5 cm13、如右上图,已知AB=AC,AE=AF,BE 与CF交于点D,则①△ABE≌△ACF②△BDF≌△CDE ③D在∠BAC的平分线上,以上结论中,正确的是A.只有①B.只有②C.只有①和②D.①,②与③四、解答题14、试用对称的观点分析说明线段的垂直平分线和角平分线的联系与区别.15、如右图,已知BE⊥AC于E,CF⊥AB 于F,BE、CF相交于点D,若BD=CD.求证:AD平分∠BAC. 一、判断题1、在同一平面内,到三角形三边距离相等的点只有一个2、在同一平面内,到三角形三边所在直线距离相等的点只有一个3、三角形三条角平分线交于一点4、等腰三角形底边中点到两腰的距离相等5、三角形是以它的角平分线为对称轴的轴对称图形二、填空题6、如图(1),点P为△ABC三条角平分线交点,PD⊥AB,PE⊥BC,PF⊥AC,则PD__________PE__________PF.7、如图(2),P是∠AOB平分线上任意一点,且PD=2cm,若使PE=2cm,则PE 与OB的关系是__________.8、如图(3),CD为Rt△ABC 斜边上的§1.4.2证明(二)高,∠BAC的平分线分别交CD、CB于点E、F,FG⊥AB,垂足为G,则CF__________FG,∠1+∠3=__________度,∠2+∠4=__________度,∠3__________∠4,CE__________CF.9、如右图,E、D分别是AB、AC上的一点,∠EBC、∠BCD的角平分线交于点M,∠BED、∠EDC的角平分线交于N.求证:A、M、N在一条直线上.证明:过点N作NF⊥AB,NH⊥ED,NK⊥AC过点M作MJ⊥BC,MP⊥AB,MQ⊥AC∵EN平分∠BED,DN平分∠EDC ∴NF__________NH,NH__________NK ∴NF__________NK∴N在∠A的平分线上又∵BM平分∠ABC,CM平分∠ACB∴__________=__________,__________=__________∴__________=__________∴M在∠A的__________上∴M、N都在∠A的__________上∴A、M、N在一条直线上三、作图题10、利用角平分线的性质,找到△ABC内部距三边距离相等的点.11、在下图△ABC所在平面中,找到距三边所在直线..距离相等的点.12、如下图,一个工厂在公路西侧,在河的南岸,工厂到公路的距离与到河岸的距离相等,且与河上公路桥南首(点A)的距离为300米.请用量角器和刻度尺在图中标出工厂的位置.四、解答题13、已知:如下图在△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若BC=32,且BD∶CD=9∶7,求:D到AB边的距离. 班级:_______姓名:________得分:__________一、填空题1.一个等腰三角形有一角是70°,则其余两角分别为_________.2.一个等腰三角形的两边长为5和8,则此三角形的周长为_________.3.如下左图,△ABC中,∠C=90°,AM 平分∠CAB,CM=20 cm,则点M到AB的距离是_________.4.如上右图,等边△ABC中,F是AB中点,EF⊥AC于E,若△ABC的边长为10,则AE=_________,AE∶EC=_________.5.如下左图,△ABC中,DE垂直平分BC,垂足为E,交AB于D,若AB=10 cm,AC=6 单元测试证明(二)cm,则△ACD的周长为_________.6.如上右图,∠C=90°,∠ABC=75°,∠CDB=30°,若BC=3 cm,则AD=_________ cm.7.如下左图,B在AC上,D在CE上,AD=BD=BC,∠ACE=25°,∠ADE=_________.8.等腰直角三角形一条边长是1 cm,那么它斜边上的高是_________ cm.9.如上右图,在∠AOB的两边OA、OB 上分别取OQ=OP,OT=OS,PT和QS相交于点C,则图中共有_________对全等三角形.10.等腰三角形两腰上的高相等,这个命题的逆命题是________________,这个逆命题是_________命题.11.三角形三边分别为a、b、c,且a2-bc=a(b-c),则这个三角形(按边分类)一定是_________三角形.二、选择题12.等边三角形的高为23,则它的边长为()面A.4 B.3C.2D.513.等腰三角形的顶角是n°,那么它的一腰上的高与底边的夹角等于()A.290οοn-B.90-2οnC.2οnD.90°-n°14.下列由线段a、b、c组成的三角形,不是直角三角形的是()A.a=3,b=4,c=5B.a=1,b=34,c=35C.a=9,b=12,c=15D.a=3,b=2,c=515.直角三角形的三边长为连续自然数,则它的面积为()A.6B.7.5C.10D.12 16.△ABC 中,∠A ∶∠B ∶∠C=1∶2∶3,最小边BC=4 cm ,最长边AB 的长是( )A.5 cmB.6 cmC.5 cmD.8 cm 17.如右图,△ABC 中,AB=AC ,BC=BD , AD=DE=EB ,则∠A 的度数为( )A.55°B.45°C.36°D.30°18.等腰△ABC 中,AC=2BC ,周长为60,则BC 的长为( )A.15B.12C.15或12D.以上都不正确19.直角三角形两直角边分别是 5 cm 、12 cm ,其斜边上的高是( ) A.13 cm B.1330cm C.1360 cm D.9cm20.直角三角形中,以直角边为边长的两个正方形的面积分别为30和20,则以斜边为边长的正方形的面积为( ) A.25 B.50C.100D.6021.等腰三角形的底边为a ,顶角是底角的4倍,则腰上的高是( ) A.23a B.33 a C.63a D. 21a 22.若一个三角形的三条高线交点恰好是此三角形的一个顶点,则此三角形一定是( ) A.等腰三角形B.等边三角形C.等腰直角三角形D.直角三角形 23.等腰三角形ABC 中,∠A=120°,BC 中点为D ,过D 作DE ⊥AB 于E ,AE=4 cm ,则AD 等于( )A.8 cmB.7 cmC.6 cmD.4 cm 24.下列说法中,正确的是( ) A.两边及一对角对应相等的两个三角形全等B.有一边对应相等的两个等腰三角形全等C.两边及其中一边上的中线对应相等的两个三角形全等D.两边及其中一边上的高对应相等的两个三角形全等25.如右图,AB⊥CD,△ABD、△BCE都是等腰三角形,如果CD=8,BE=3,那么AC长为()A.8B.5C.3D.3426.将两个全等的有一个角为30°的直角三角形拼成下右图,其中两条长直角边在同一直线上,则图中等腰三角形的个数是()A.4B.3C.2D.127.下列定理中逆定理不存在的是()A.角平分线上的点到这个角的两边距离相等B.在一个三角形中,如果两边相等,那么它们所对的角也相等C.同位角相等,两直线平行D.全等三角形的对应角相等*28.已知一个直角三角形的周长是4+26,斜边上中线长为2,则这个三角形的面积为()A.5B.2C.45D.1三、解答题29.已知:如图,AB=AC,DE∥AC,求证:△DBE是等腰三角形.30.已知:如图,在Rt △ABC 中,∠C=90°,∠BAD=21∠BAC ,过点D 作DE ⊥AB ,DE 恰好是∠ADB 的平分线,求证:CD=21DB.31.已知三角形的三边分别是n 2+n ,n+21和n 2+n+21(n >0),求证:这个三角形是直角三角形.32.如图,△ABC 中,AB=AC ,∠1=∠2,求证:AD 平分∠BAC.33.如图,以等腰直角三角形ABC的斜边AB与边面内作等边△ABD,连结DC,以DC当边作等边△DCE,B、E在C、D的同侧,若AB=2,求BE的长. *34.①在△ABC中,AB=AC,AB的垂直平分线交AC于N,交BC的延长线于M,∠A=30°,求∠NMB的大小.②如果将①中的∠A的度数改为70°,其余条件不变,再求∠NMB 的大小.③你感到存在什么样的规律性?试证明.(请同学们自己画图)④将①中的∠A改为钝角,对这个问题规律性的认识是否需要加以修改?参考答案1.1.1全等与等腰三角形一、1、BE B DAC 2、100 3、17㎝4、70 805、8二、6、B 7、D 8、C 9、C 10、C 三11、略12略1.1.2等腰三角形性质一、1.锐角2.AB AC3.高线中线平分线4.30 3∶15.= = 等腰6.等腰直角二、1.C 2.C 3.C 4.C 5.C三、1.解:∵AD平分∠BAC,∴∠EAD=∠FAD,且DF∥AE∴∠EAD=∠ADF,∴∠FAD=∠ADF∴AF=FD.同理,可得AE=ED,∠EAD=∠EDA∴在△ADE和△ADF中,⎪⎩⎪⎨⎧∠=∠=∠=∠FDAEDAADADFADEAD∴△ADE≌△ADF(ASA)∴AE=AF,DE=DF综上,AE=ED=DF=AF=6∴四边形AFDE的周长为4AE=4×6=24.2.证明:∵∠1=∠2,∴AD=AE又∵DE∥BC,∴∠1=∠B,∠2=∠C且∠B=∠C∴AB=AC ,∴AB -AD=AC -AE 即DB=EC∴在△DBG 和△ECG 中,⎪⎩⎪⎨⎧=∠=∠=CG BG C B EC DB ∴△DBG ≌△ECG (SAS ) ∴DG=GE ,∴△DGE 是等腰三角形 3.证明:∵CD ⊥AB ,∴∠ADC=90°, 又∵∠A=60°,∴∠ACD=30° ∴在Rt △ACD 中,AD=21AC , 又∵∠ACB=90°,在Rt △ACB 中,∴∠B=30°,∴AC=21AB ∴AD=4AB ,则AD=31BD ,即BD=3AD.1.1.3等腰三角形判别一、1.(1)等边 (2)等边 (3)等边2.线段、直角、等腰三角形3.一三4.30 12 60 等边5.4 30 26.8二、1.C 2.B 3.C三、1.解:∵AD=DC ,且∠A=20°,∴∠A=∠ACD=20°, 又∵∠ACD ∶∠BCD=2∶3 ∴∠BCD=30°,∴∠ACB=50° ∴∠ABC=180°-∠A -∠ACB=180°-20°-50°=110°2.证明:∵MD ⊥BC ,且∠B=90°, ∴AB ∥MD ,∴∠BAD=∠D 又∵AD 为∠BAC 的平分线 ∴∠BAD=∠MAD ,∴∠D=∠MAD ,∴MA=MD3.证明:∵△ABC 是等边三角形,∴AB=BC ,∠ABE=60°又∵△BDE 是等边三角形,∴BE=BD ,∠DBE=60°, ∴∠ABE=∠DBE∴在△ABE和△CBD 中,⎪⎩⎪⎨⎧=∠=∠=BD BE DBE ABE BC AB ∴△ABE ≌△CBD (SAS ),∴AE=CD 1.2.1勾股定理 一、1.× 2.√ 3.√二、1.12 10 2.6 3 1 3 2 3.22 2 2 1 4.90° 35.(1)10 (2)27. 三、1.B 2.B 3.C 4.C四、1.解:∵△ABC 为等边三角形,且AD ⊥BC ,∴AD 平分∠BAC ,即∠BAD=∠CAD=30°.∴BD=21AB=1,而BD 2+AD 2=AB 2 ∴AD 2=AB 2-BD 2=3 ∴AD=3 ∴S △ABC =21AD ·BC=21×3×2=3 ∴△ABC 的面积为3.2.(1)解:在Rt △DCB 中,DC 2+DB 2=BC 2∴DC 2=9-251442581= ∴DC=512(2)解:在Rt △ACD 中,AD 2+CD 2=AC 2∴AD 2=16-2525625144=∴AD=516(3)解:AB=AD+DB=516+59=5 (4)证明:∵AC 2+BC 2=16+9=25,AB 2=25∴AC 2+BC 2=AB 2 ∴∠ACB=90°, ∴△ABC 是直角三角形.3.解:∵∠A=50°,∠B=40°,∴∠C=90°,∴AC 2=AB 2-BC 2=(3 km )2 ∴AC=3 km ∵3.03=10天 ∴10天才能将隧道凿通.1.2.2直角三角形全等的判定一、1.(1)AAS (2)ASA (3)AAS(4)HL (5)SAS 2.ABC DCB HL ABO DCO AAS 3.ABE DCF 4.6 5.30二、1.A 2.B 3.D三、1.证明:连结AC ,CD ⊥AD ,CB ⊥AB∴在Rt △ADC 和Rt △ABC 中⎩⎨⎧==AC AC ABAD ∴Rt △ADC ≌△Rt △ABC(HL)∴CD=CB.(本题也可用勾股定理直接证明) 2.证明:∵CD ⊥AB ,C ′D ′⊥A ′B ′ ∴在Rt △CDB 和Rt △C ′D ′B ′中,⎩⎨⎧''=''=CB BCD C CD ∴Rt △CDB ≌Rt △C ′D ′B ′(HL) ∴∠B=∠B ′∴在△ABC 和△A ′B ′C ′中,⎪⎩⎪⎨⎧'∠=∠''='''∠=∠B B C B BC B C A ACB ∴△ABC ≌△A ′B ′C ′(ASA). 3.证明:在Rt △ADC 和Rt △ABC 中,⎩⎨⎧==AC AC ADAB ∴Rt △ABC ≌Rt △ADC(HL) ∴∠DCE=∠BCE ∴在△DCE和△BCE中,⎪⎩⎪⎨⎧=∠=∠=CE CE BCE DCE BC DC ∴△DCE ≌△BCE (SAS ),∴EB=ED 1.3.1线段的垂直平分线 一、1.× 2. × 3.× 4.√二、1.5 10 53 2.12 12 17 3.5 30° 215 4.线段AB 的垂直平分线 5.66.= >7.线段AB 的垂直平分线8.线段BC三、1.D 2.B 3.D 4.C四、证明:∵PE ⊥OA 于E ,DF ⊥OB 于F∴∠PEO=90°=∠PFO∴在△PEO 和△PFO 中,⎪⎩⎪⎨⎧=∠=∠∠=∠OP OP FOP EOP PFO PEO ∴△PEO ≌△PFO ,∴PE=PF ,EO=FO∴O 、P 在EF 的中垂线上, ∴OP 垂直平分EF.1.3.2三角形三条中垂线交于一点 一、1.√2.√3.√4.×二、1.= = 2.= = = 50 50 80 1003.= AC4.= = 72°5.BED CED BAD CAD 等腰6.60°三、1.略 (2)内部 斜边的中点 外部四、类比联想:略 1.4.1角的平分线一、1.√ 2.√ 3.√ 4.× 二、1.= 2.= 3.1 4.90 5.4 三、1.C 2.A 3.B 4.D四、1.提示:联系:说出线段的垂直平分线和角的平分线所在直线都是相应图形的对称轴即可.区别:说出线段垂直平分线的性质与角平分线的性质即可.2.证明:在△BDF 和△CDE 中⎪⎩⎪⎨⎧=∠=∠︒=∠=∠CD BD CDEBDF CED BFD 90 ∴△BDF ≌△CDE ,∴DF=DE ∴D 在∠A 的平分线上,∴AD 平分∠BAC.1.4.2三角形三角的平分线交于一点一、1.√ 2.× 3.√ 4.√ 5. ×二、1.= = 2.垂直 3.= 90 90 ==4.= = = MP MJ MQ MJ MPMQ 平分线 平分线三、提示:1.三个内角平分线交点2.一个内角平分线与另外两个角外角平分线的交点3.略四、解:过点D 作DE ⊥AB ,则DE 是点D 到AB 的距离∵BD ∶CD=9∶7, ∴CD=BC ·16732167⨯==14 而AD 平分∠CAB ,∴DE=CD=14第一章单元测试卷一、1.55°,55°或70°,40° 2.18或21 3.20 cm 4.251∶3 5.16 cm 6.6 7.75° 8.22或219.4 10.如果一个三角形两边上的高相等,那么这个三角形是等腰三角形 真 11.等腰二、12.A 13.C 14.D 15.A 16.D17.B 18.B 19.C 20.B 21.D 22.D23.A 24.C 25.D 26.B 27.D 28.B三、29.略 30.略 31.略 32.略33.134.①15°②35°③AB的垂直平分线与底边BC所夹的锐角等于∠A的一半④不需要修改。
九年级数学上册-第一单元证明二全单元练习-北师大版

北师九上 第一单元证明(二)全单元练习1.1你能证明它们吗目标:1、了解作为证明基础的几条公理的内容,掌握证明的基本步骤和书写格式.2、经历“探索-发现-猜想-证明"的过程。
能用综合法证明等腰和等边三角形的相关性质定理和判定定理。
3、结合实例体会反证法的含义与应用。
重点:了解作为证明基础的几条公理的内容,掌握证明的基本步骤和书写格式。
难点:能够用综合法证明等腰和等边三角形的关性质定理和判定定理(特别是证明时辅助线做法),并解决实际问题。
章节训练导航:1。
等腰、等边、直角三角形的性质 2。
反证法一、填空题1.在等腰三角形中顶角为40°时底角等于_________,一个底角为50°,则顶角等于_________。
2。
由在同一三角形中“等角对等边"“等边对等角”两个定理我们可以联想到大边对_________,大角对_________.3。
等腰三角形的两边分别是7 cm 和3 cm ,则周长为_________。
4.一个等边三角形的角平分线、高、中线的总条数为_________.5。
等腰三角形的一边长为23,周长为43+7,则此等腰三角形的腰长为_________.6。
等边三角形两条中线相交所成的锐角的度数为_________。
7。
如图1,D 在AC 上,且AB =BD =DC ,∠C =40°,则∠A =_________,∠ABD =_________。
图1 图28。
如图2,Rt △ABC 中,∠ACB =90°,点D 在AB 上,且AD =AC ,若∠A =40°,则∠ACD =_______,∠DCB =_______,若∠A =α,则∠BCD =_________,由此我们可得出∠BCD 与∠A 的关系是∠BCD =_________。
9.△ABC 中,若∠A =∠B =21∠C ,则此三角形为_________三角形。
10.Rt △ABC 中,∠C =90°,∠CAB =60°,AD 平分∠CAB ,点D 到AB 的距离是3.8 cm ,则BC =_______ cm.11。
九年级上册数学第一章图形与证明(二)单元试题

九年级上册数学第一章图形与证明( 二) 单元试题以下是为您介绍的九年级上册数学第一章图形与证明( 二 ) 单元试题,希望本篇文章对您学习有所帮助。
九年级上册数学第一章图形与证明(二)单元试题时间: 100 分钟满分:150分一、选择题 (3 分 8=24 分 )1.已知等腰三角形的一个内角为 40,则这个等腰三角形的顶角为【】A.40B.100C. 40或100D. 70或502. 使两个直角三角形全等的条件【】A. 一锐角对应相等B. 两锐角对应相等C. 一条边对应相等D. 两条边对应相等3. 下面判断四边形是平行四边形的方法中,错误的选项是【】A. 一组对边平行,另一组对边也平行B. 一组对角相等,另一组对角也相等C. 一组对边平行,一组对角相等D. 一组对边平行,另一组对边相等4.已知四边形 ABCD是平行四边形,以下结论中不正确的选项是【】A. 当 AB=BC时,它是菱形B. 当 ACBD时,它是菱形C. 当 ABC=90时,它是矩形D. 当 AC=BD时,它是正方形5.如图,等腰△ ABC 的周长为 21,底边 BC=5, AB的垂直均分线 DE交 AB于点 D,交 AC于点 E,则△ BEC的周长为【】6.按次连接四边形四条边的中点,所得的四边形是菱形,则原四边形必然是【】A. 平行四边形 .B. 对角线相等的四边形.C. 矩形 .D. 对角线互相垂直的四边形.7.如图,在□ ABCD中, E 是 BC的中点,且 AEC=DCE,则以下结论不正确的选项是A. B. DF=2BFC. 四边形 AECD是等腰梯形D.△ABE 是等腰三角形8.将矩形纸片 ABCD按以下列图的方式折叠,获取菱形 AECF. 若 AB=3,则 BC的长为二、填空题 (3 分 8=24 分 )9. 如图,在△ ABC中,C=90,AD均分 CAB,BC=8cm,BD=5cm,,那么 D 点到直线 AB的距离是 cm.10.等腰梯形ABCD中,AD//BC,AD=3cm,BC=5cm,C=60,则梯形的腰长是 cm.11.如图,矩形 ABCD的对角线 AC, BD订交于点 O, AB=2,BOC=120,则 AC的长是 __________.12.如图,菱形 ABCD中, AE垂直均分 BC,垂足为 E, AB=4. 则菱形 ABCD的面积是,对角线BD的长是.13.在梯形 ABCD中, AD//BC,对角线 ACBD,且 AC=5cm,BD=12cm,则梯形中位线的长等于 ______cm.14.如图,菱形 ABCD的两条对角线分别长 6 和 8,点 P 是对角线 AC上的一个动点,点M、N 分别是边 AB、 BC的中点,则PM+PN的最小值是_____________.15.如图,若将边长为 1 的正方形 ABCD绕点 A 逆时针旋转 30 到正方形ABCD,则图中阴影部分的面积为.16.如图,有一张面积为 1 的正方形纸片 ABCD, M, N 分别是AD, BC边的中点,将 C 点折叠至MN上,落在 P 点的地址,折痕为 BQ,连接 PQ,则 PQ= .三、解答题 ( 共 102 分 )17.( 本题 8 分 ) 在等腰△ ABC 中, AB=AC=8, BAC=100, AD是BAC的均分线,交 BC于 D,点 E 是 AB的中点,连接 DE. 求:(1) 求 BAD的度数 ;(2) 求 B 的度数 ;(3) 求线段 DE的长 . 18.( 本题8 分 ) 如图,已知 ACBC, BDAD,AC 与 BD 交于 O,AC =BD.求证: (1)BC=AD; (2) △OAB 是等腰三角形 .19.( 本题 8 分 ) 我们把依次连接任意一个四边形各边中点得到的四边形叫做中点四边形. 如图,在四边形 ABCD中,E,F,G, H 分别是 AB,BC, CD,DA的中点,依次连接各边中点得到中点四边形EFGH.(1)这其中点四边形 EFGH的形状是 _________;(2)请证明你的结论 .20.( 本题 10 分 ) 如图 , 已知菱形 ABCD的对角线订交于点 O,延长 AB至点 E, 使 BE=AB,连接 CE.(1)求证 :BD=EC;(2)若 E=50 , 求 BAO的大小 .21.( 本题 10 分 ) 有公路 l1 同侧、 l2 异侧的两个城镇A, B,以以下列图 . 电信部门要修建一座信号发射塔,依照设计要求,发射塔到两个城镇A,B 的距离必定相等,到两条公路l1 ,l2 的距离也必定相等,发射塔 C 应修建在什么地址?请用尺规作图找出所有吻合条件的点,注明点 C 的地址 .( 保留作图印迹,不要求写出画法)22.( 本题 10 分 ) 如图,在梯形 ABCD中, AB∥DC, DB 均分ADC,过点 A 作 AE∥BD,交 CD的延长线于点 E,且 C=2E.(1)求证:梯形 ABCD是等腰梯形 ;(2)若 BDC=30, AD=5,求 CD的长 .23.( 本题 10 分 ) 如图,在△ ABC 中, D 是 BC边上的一点, E 是 AD的中点,过点 A 作 BC的平行线交 BE的延长线于 F,且AF=DC,连接 CF.(1)求证: D 是 BC的中点 ;(2)若是 AB=AC,试猜想四边形 ADCF的形状,并证明你的结论 .24.( 本题 12 分 ) 如图,等腰梯形 ABCD中, AD∥BC,点 E 是线段 AD上的一个动点 (E 与 A、 D 不重合 ) , G、 F、H 分别是BE、 BC、CE的中点 .(1)试试究四边形 EGFH的形状,并说明原由 ;(2)当点 E 运动到什么地址时,四边形 EGFH是菱形 ?并加以证明 ;(3)若 (2) 中的菱形 EGFH是正方形,请研究线段 EF 与线段 BC 的关系,并证明你的结论.25.( 本题 12 分 ) 我们给出以下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形. 请解答以下问题:(1)写出你所学过的特别四边形中是等对角线四边形的两种图形的名称 ;(2)研究:当等对角线四边形中两条对角线所夹锐角为 60 时,这对 60 角所对的两边之和与其中一条对角线的大小关系,并说明你的结论 .26.( 本题 14 分 ) 如图,在边长为 4 的正方形 ABCD中,点 P 在 AB上从 A 向 B 运动,连接DP交 AC于点 Q.(1)试证明:无论点 P 运动到 AB上哪处时,都有△ADQ≌△ ABQ ;(2)当点 P 在 AB上运动到什么地址时,△ ADQ 的面积是正方5 / 6(3)若点 P 从点 A 运动到点 B,再连续在 BC上运动到点 C,在整个运动过程中,当点P 运动到什么地址时,△ADQ 恰为等腰三角形 .。
【九年级】九年级上册第一章证明(二)单元试题(北师大附答案)

【九年级】九年级上册第一章证明(二)单元试题(北师大附答案)第一章证明(二)检测题(本试卷满分:120分,时间:120分钟)一、(每小题3分后,共30分后)1.下列命题:①等腰三角形的角平分线、中线和高重合;②等腰三角形两腰上的高相等;③等腰三角形的最轻边就是底边;④等边三角形的高、中线、角平分线都成正比;⑤等腰三角形都就是锐角三角形.其中恰当的存有()a.1个b.2个c.3个d.4个2.如图所示,△abc就是等腰三角形,点d就是底边bc上异于bc中点的一个点,∠ade=∠dac,de=ac.运用这个图(不嵌入辅助线)可以表明以下哪一个命题就是骗人命题?()a.一组对边平行,另一组对边相等的四边形是平行四边形b.存有一组对边平行的四边形就是梯形c.一组对边相等,一组对角相等的四边形是平行四边形d.对角线成正比的四边形就是矩形3.如图,在△abc中,,点d在ac边上,且,则∠a的度数为()a.30°b.36°c.45°d.70°4.以下命题,其中真命题存有()①4的平方根是2;②存有两边和一角成正比的两个三角形全系列等;③连接任意四边形各边中点的四边形是平行四边形.a.0个b.3个c.2个d.1个5.已知等边三角形的高为2,则它的边长为()a.4b.3c.2d.56.在△abc中,∠a∶∠b∶∠c=1∶2∶3,最短边c,则最长边ab的长是()a.5cb.6cc.cd.8c7.等腰三角形的底边长为a,顶角是底角的4倍,则腰上的高是()a.ab.ac.ad.a8.以下观点中,恰当的就是()a.两边及一对角对应相等的两个三角形全等b.存有一边对应成正比的两个等腰三角形全系列等c.两边及其中一边上的中线对应相等的两个三角形全等d.两边及其中一边上的高对应成正比的两个三角形全系列等9.已知一个直角三角形的周长是2,斜边上的中线长为2,则这个三角形的面积为()a.5b.2c.d.110.如图,在△abc中,ab的垂直平分线交ac于点d,交ab于点e,如果c,c,那么△的周长是()a.6cb.7cc.8cd.9c二、题(每小题3分后,共24分后)11.如图所示,在等腰△abc中,ab=ac,∠bac=50°,∠bac的平分线与ab的中垂线处设点o,点c沿ef折叠后与点o重合,则∠oec的度数是.12.若一个三角形的三条高线交点恰好就是此三角形的一个顶点,则此三角形是______三角形.13.在△abc和△adc中,以下论点:①;②;③,把其中两个论点做为条件,另一个论点做为结论,写下一个真命题:____________.14.如图,在△abc中,,a平分∠,c,则点到ab的距离就是_________.15.如图,在等边△abc中,f是ab的中点,ef⊥ac于e,若△abc的边长为10,则_________,_________.16.一个等腰三角形的两边长分别为5或6,则这个等腰三角形的周长是.17.例如图,未知的垂直平分线处设点,则.18.一副三角板叠在一起如图所示放置,最小锐角的顶点d恰好放在等腰直角三角板的斜边ab上,bc与de交于点,如果∠adf=100°,那么∠bd为度.三、答疑题(共66分后)19.(8分)如图,在△abc中,,是上任意一点(与a不重合),d⊥bc,且交∠的平分线于点d,澄清:.20.(8分)联想三角形外心的概念,我们可引入如下概念.定义:至三角形的两个顶点距离成正比的点,叫作此三角形的科东俄外心.举例:如图(1),若pa=pb,则点p为△abc的准外心.应用:如图(2),cd为等边三角形abc的高.科东俄外心p在低cd上,且pd=ab,谋∠apb的度数.探究:未知△abc为直角三角形,斜边bc=5,ab=3,科东俄外心p在ac边上,先行探究pa的长.21.(8分后)例如图,在四边形中,,平分∠.澄清:.22.(8分)如图,以等腰直角三角形abc的斜边ab为边作等边△abd,连接dc,以dc为边作等边△dce,b、e在c、d的同侧,若,求be的长.23.(8分后))例如图,在rt△abc中,,点d是ac的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与a、d重合,连接be、ec.先行悖论线段be和ec的数量及边线关系,并证明你的悖论.24.(8分)求证:在一个三角形中,如果两条边不相等,那么这两条边所对的角也不成正比.25.(8分)已知:如图,,是上一点,于点,的延长线交的延长线于点.澄清:△就是等腰三角形.26.(10分)在△中,,ab的垂直平分线交ac于点n,交bc的延长线于点,.(1)求的大小.(2)如果将(1)中的∠a的度数改成70°,其余条件维持不变,Ploudalm∠的大小.(3)你认为存在什么样的规律?试用一句话说明.(请同学们自己画图)(4)将(1)中的∠a改成钝角,对这个问题规律的重新认识与否须要予以修正?第一章证明(二)检测题参考答案一、1.b解析:只有②④正确.2.c解析:∵△abc就是等腰三角形,∴ab=ac,∠b=∠c.∵de=ac,ad=ad,∠ade=∠dac,即为,∴△ade≌△dac,∴∠e=∠c,∴∠b=∠e,ab=de.但是四边形abde不是平行四边形,故一组对边成正比,一组对角成正比的四边形不是平行四边形,故挑选c.3.b解析:因为,所以.因为,所以,.又因为,所以,所以所以4.d解析:4的平方根就是±2,存有两边和一角成正比的两个三角形不一定全系列等.故命题①②都就是骗人命题,只有命题③就是真命题,故挑选d.5.a解析:设等边三角形的边长为a,则6.d解析:因为∠a∶∠b∶∠c=1∶2∶3,所以△abc为直角三角形,且∠c为直角.又因为最短边c,则最久边c.7.d解析:因为等腰三角形的顶角是底角的4倍,所以顶角就是120°,底角就是30°.例如图,在△中,则8.c解析:a.两边及夹角对应成正比的两个三角形全系列等,故a项错误;b.有一腰及顶角对应相等的两个等腰三角形全等,故b项错误;c.两边及其中一边上的中线对应成正比的两个三角形全系列等,恰当;d.两边及其中一边上的高对应相等的两个三角形不一定全等,d项错误.9.b解析:设此直角三角形为△abc,其中因为直角三角形斜边的长等同于其中线长的2倍,所以又因为其周长就是,所以.两边平方得,.由勾股定理言,所以.10.d解析:因为垂直平分,所以.所以△的周短(c).二、题11.100°解析:如图所示,由ab=ac,ao平分∠bac得ao所在直线是线段bc的垂直平分线,连接ob,则ob=oa=oc,所以∠oab=∠oba=×50°=25°,得∠boa=∠coa=所以∠obc=∠ocb==40°.由于eo=ec,故∠oec=180°-2×40°=100°.12.直角解析:直角三角形的三条高线交点恰好就是此三角形的一个顶点;锐角三角形的三条高线交点在此三角形的内部;钝角三角形的三条高线交点在三角形的外部.13.在△abc和△adc中,如果那么14.20c解析:根据角平分线的性质:角平分线上的的边角两边的距离成正比可以得答案.15.1∶3解析:因为,f是ab的中点,所以.在rt△中,因为,所以.又,所.16.16或17解析:当等腰三角形的腰长为5时,其周长为5×2+6=16;当等腰三角形的腰长为6时,其周长为6×2+5=17.∴这个等腰三角形的周长为16或17.17.解析:∵∠bac=120,ab=ac,∴∠b=∠c=∵ac的垂直平分线交bc于点d,∴ad=cd.∴∴18.85解析:∵∠bd=180°-100°-30°=50°,∴∠bd=180°-50°-45°=85°.三、解答题19.证明:∵,,∴∥,∴.又∵为∠的平分线,∴,∴,∴.20.分析:应用:分pb=pc,pa=pc,pa=pb三种情况讨论.探究:同上分后三种情况探讨.解:应用:若pb=pc,连接pb,则∠pcb=∠pbc.∵cd为等边三角形的高,∴ad=bd,∠pcb=30°,∴∠pbd=∠pbc=30°,∴pd=db=ab,与未知pd=ab矛盾,∴pb≠pc.若pa=pc,连接pa,同理,可得pa≠pc.若pa=pb,由pd=ab,得pd=bd,∴∠bpd=45°,所以∠apb=90°.探究:若pb=pc,设pa=x,则x2+32=(4-x)2,∴x=,即pa=.若pa=pc,则pa=2.若pa=pb,由图(2)知,在rt△pab中,不可能.故pa=2或.指点:分类探讨问题必须努力做到不轻、拣.21.分析:从条件bd平分∠abc,可联想到角平分线定理的基本图形,故要作垂线段.证明:例如图,过点d作de⊥ab交ba的延长线于点e,过d作于点f.因为bd平分∠abc,所以.在rt△ead和rt△fcd中,,所以rt△ead≌rt△fcd(hl).所以∠=∠.因为∠∠80°,所以∠∠.22.求解:因为△abd和△cde就是等边三角形,所以,∠∠60°.所以∠∠∠∠,即为∠∠.在△和△中,因为所以△≌△,所以.又,所以.在等腰直角△中,,故.23.求解:,be⊥ec.证明:∵,点d是ac的中点,∴.∵∠∠45°,∴∠∠135°.∵,∴△eab≌△edc.∴∠∠,.∴∠∠90°.∴,⊥.24.求解:未知:例如图,在△中,,澄清:∠∠.证明:假设∠∠,那么根据“等角对等边”可得,但已知条件就是二者矛盾,因此∠∠.25.证明:∵,∴∠∠.∵于,∴∠∠.∴∠∠∠∠.∴∠∠.∵∠∠,∴∠∠.∴△是等腰三角形.26.求解:图画出来图形如图所示.(1)因为,所以.所以.因为d是ab的垂直平分线,所以,所以.(2)同(1),同理可得.(3)ab的垂直平分线与底边bc的延长线所夹的锐角等于∠a的一半.(4)将(1)中的改成钝角,这个规律的重新认识无须修正,仍存有全等三角形一腰的垂直平分线与底边或底边的延长线相交,所成的锐角等于顶角的一半.。
北师大版九年级数学上册第一章——证明(二)单元测试卷(有答案)

第一章 证明(二)单元评估卷(1)一、选择题1.等腰三角形周长为cm 13,其中一边长为cm 3,则该等腰三角形的底边长为( B ) (A )cm 7 (B )cm 3 (C )cm 7或cm 3 (D )cm 5 2.如图1,P 在AB 上,AD =AC ,BD =BC ,则图中全等三角形的对数有( C )(A )1 (B )2 (C )3 (D )4 3.下列命题的逆命题是真命题的是( D )(A ) 对顶角相等 (B )若a =b ,则|a |=|b |(C ) 末位是零的整数能被5整除 (D )直角三角形的两个锐角互余4.如图2,△ABC 中,∠ACB =90°,CD 是AB 边上的高,∠BAC 的平分线AF 交CD 于点E ,则△CEF 必为( A ) (A )等腰三角形 (B )等边三角形 (C )直角三角形 (D )等腰直角三角形5.等腰三角形一腰上的高等于这腰的一半,则这个等腰三角形的顶角等于( C )(A )30° (B )60° (C )30°或150° (D )60°或120°6.若三角形的一边等于另一边的一半,那么这边所对的角度为( D ) (A )30 (B )45° (C )60° (D )无法确定7.如图3,∠A O P =∠B O P =15°,PC ∥O A ,PD ⊥O A 若PC =4,则PD 的长为( B ) A .4 B .2 C .1 D .38.一个三角形的两边长为4和5,要使三角形为直角三角形,则第三边的长为( D )(A )3 (B )41 (C )3或31 (D )3或41 9.如图4,在△ABC 中,∠C =90°,∠B =30°,AB 的垂直平分线DE 交BC 于点D ,点E 为垂足,若BD =cm 10,则DC 等于( B )(A )cm 4 (B )cm 5 (C )cm 6 (D )cm 7 图2P D CBA 图1 图4图5图310.如图5所示由4个全等的有一个角等于300的直角三角形拼成的大正方形 的边长为2,则中间小正方形的边长为( D ) A .8 B .4 C .232- D .13-11.等腰三角形底边长为7,一腰上的中线把其周长分成两部分的差为3,则腰长是( C ) A 、4 B 、10 C 、4或10 D 、以上答案都不对二、填空题11.等腰三角形的一个底角是50°,则其顶角为 80° . 12.在△ABC 中,已知∠A =80°,则∠B 、∠C 的角平分线相交所成的钝角为 130° .13.用反证法证明“三角形的三个内角中至少有一个角不小于60度” 第一步应假设三角形的每个内角都小于60度.14.如图6,点M 是AOB ∠平分线上一点,MP OA MQ OB ⊥⊥,,垂足分别为P Q ,,26cm S POM =∆,cm OP 3=,则MQ = 4 cm .15.如图7,ABC △中,106BAC ∠=︒,EF MN ,分别是AB AC ,的垂直平分线,点E 、M 在BC 上,则EAM ∠等于 32 度.图6 BM APO QED CBA第一章 证明(二)单元评估卷(2)三、解答题16.如图8,在△ABC 中,AB =AC ,点M、N分别在BC 所在直线上,且AM =AN . 求证:BM =CN证明:∵在△ABC 中,AB =AC ,∴∠ABC =∠ACB ∴∠ABM =∠ACN 又∵ AM =AN ∴ ∠AMN =∠ANM在∆AMB 和ANC ∆中∠AMB =∠ANC ∠ABM =∠ACN AB =AC ∴ ∆AMB ≌ANC ∆(AA S ) ∴ BM =CN17.先作图,再证明.(1)在所给的图形(图9)中完成下列作图 (保留作图痕迹).①作∠ACB 的平分线CD ,交AB 于点D ; ②延长BC 到E ,使CE =CA ,连接AE .(2)求证:CD ∥AE .【答案】(1)如右图所示(2)∵∠ACB 是直角,CD 是∠ACB 的平分线 ∴∠BCD =45°又∵在Rt ∆ACE 中,CE =CA ∴ ∠E =45° ∴ CD ∥AE .18.如图10,在△AFD 和△CEB 中,点A 、E 、F 、C 在同一条直线上,有下面四个结断:①AD =CB ;②AE =CF ;③∠B =∠D ;④AD ∥BC .请用其中三个作为条件,余下的一个作为结论编一道数学题,并证明结论成立.答案:已知:在△AFD 和△CEB 中,点A 、E 、F 、C 在同一条直线上, AD =CB ;AD ∥BC ;AE =CF ,求证:∠B =∠D证明:∵ AE =CF∴ AF =CE∵ AD ∥BC∴ ∠A =∠C在△AFD 和△CEB 中AD =CB ∠A =∠C AF =CE∴ △AFD ≌△CEB (S A S )∴∠B =∠D (答案不唯一)图9 FE D B A 图10AC MNA图8A B CM N19.如图11,已知BE AC CF AB ⊥⊥,,垂足分别为E F ,,BE CF ,相交于点D ,若BD CD =.求证:AD 平分BAC ∠.答案:证明:∵ BE AC CF AB ⊥⊥,∴∠DFB =∠DEC =90°在△DFB 和△DEC 中∠DFB =∠DEC ∠FDB =∠EDC BD CD =∴ △DFB ≌△DEC (AA S ) ∴ DF DE =即点D 在BAC ∠的平分线上 ∴AD 平分BAC ∠20.如图12,ABC △中,22.5B ∠=,60C ∠=,AB 的垂直平分线交BC 于D ,交AB 于F,BD =AE BC ⊥于E ,求答案:解:连接AD .DF ∵是AB 的垂直平分线,AD BD =∴=122.5B ∠=∠=∴ 21B ∠=∠+∠∴又AE BC ∵⊥,3902904545∠=-∠=-=∴,23∠=∠∴ AE DE ∴=222DE AE AD +=∵222AE =∴,6AE =∴.在R t ACE △中,60C ∠=430∠=∴2AC CE =∴(30所对的直角边等于斜边的一半)222AC EC AE -=∵(勾股定理)222(2)CE CE AE -=∴,223CE AE =∴,212CE =∴,CE =∴.图11ABCD E F。
九年级第一章证明(二)单元测试卷2

九年级(上)数学单元测试卷第一章证明(二)班级 _________ 姓名 __________ 成绩__________一、选择题(每小题3分,共30分)1已知△ ABC 的三边长分别是 3cm 、4cm 、5cm ,则△ ABC 的面积是( )2 2 2 2A.6cm B.7.5cm C.10cm D.12cm 2、下列判断正确的是()A.有两边和其中一边的对角对应相等的两个三角形全等B. 有两边对应相等,且有一角为 30°的两个等腰三角形全等C. 有一角和一边对应相等的两个直角三角形全等D. 有两角和一边对应相等的两个三角形全等 3、具有下列条件的两个等腰三角形,不能判断它们全等的是( )A.顶角、一腰对应相等B.底边、一腰对应相等C.两腰对应相等D. 一底角、底边对应相等4、 在平面直角坐标系 xoy 中,已知A (2,- 2),在y 轴上确定点卩,使厶AOP 为等到腰三 角形,则符合条件的点 P 共有( )A.2个B.3个C. 4个D.5个5、到厶ABC 的三个顶点距离相等的点是△ ABC 的( )A.三边中线的交点B.三条角平分线的交点C.三边上高的交点6、角平分线的尺规作图,其根据是构造两个全等三角形,由作图可知:判断所构造的两个 三角形全等的依据是( ) A.SSS B.ASA C.SAS D.AAS7、一架长2.5m 的梯子,斜立在一竖直的墙上,这时梯子底端距墙底端 0.7m ,如果梯子的顶端沿墙下滑0.4m ,那么梯子底端将滑动()二、填空题(每小题3分,共30分) 11、 如图,已知 AC=DB ,要使△ ABCDCB ,只需增加的一个条件是 _________ 或 _______D.三边中垂线的交点 A.0.9m 8、A ABC C.0.5m B :/ C=1 : D.0.8m2 : 3, CD 丄AB 于点D 若BC=a ,贝U AD 等于( 1 A. 一 a29、如图, A.30 °B.1.5m ;中,/ A :/ 3B. a2△ ABC 中,AB=AC ,点D 在AC 边上,且BD=BC=AD ,则/ A 的度数为( B.363 C. 一a2D. 3 aR(第9题图)10、如图,等边△ A.45 ° B.55(第12题图)ABC 中,BD=CE , AD 与BE 相交于点P ,则/ APE 的度数是( C.60° D.75 OC12、如图,△ ABC中,/ ACB=90。
九年级数学 第一章图形与证明二单元测试题

第一章?图形与证明〔二〕?单元测试题班级_____学号____姓名_______得分______一.选择题(3分×8=24分)1.平行四边形ABCD 的一边长为10,那么对角线AC 、BD 的长可取以下数组为:〔 〕 A.4,8B.6,8C.8,10D.11,13 2.如图,矩形ABCD 沿着AE 折叠,使D 点落在BC 边上的F 点处,假如∠BAF =600,那么∠DAE 等于〔 〕 A.150B.300 C.450 D.6003.以下说法:〔1〕平行四边形的对角线互相平分。
〔2〕菱形的对角线互相垂直平分。
〔3〕矩形的对角线相等,并且互相平分。
〔4〕正方形的对角线相等,并且互相垂直平分。
其中正确的选项是〔 〕 A ①②B ①②③C ②③④D ①②③④4.假如等边三角形的边长为3,那么连结各边中点所成的三角形的周长为〔〕A9B6C3D295.等腰梯形的一个角为120°,两底分别为10和30,那么它的腰长为:〔 〕ABCD EFA 、10B 、20C 、103D 、2036.假设一个梯形的中位线长为15,一条对角线把中位线分成两条线段, 这两条线段的比是3:2,那么梯形的上、下底长分别是()A.3,4.5B.6,9C.12,18D.2,37.小许拿了一张正方形的纸片如图甲,沿虚线对折一次得图乙.•再对折一次得丙.然后用剪刀沿图丙中的虚线〔虚线与底边平行〕剪去一个角.翻开后的形状是〔• 〕.8.将边长都为1cm 的正方形按如下图摆放,点A 1.A 2.A 3.A 4分别是正方形的中心,那么前5个这样的正方形重叠局部的面积和为〔 〕 A.14B.12C.1D.2〔3分×10=30分〕9.假设矩形的一个内角平分线把矩形的一条边分成3cm 和5cm 的两段,那么〔第18A 1A 2A 3 A 4〔第8题图〕该矩形的周长_____10.平行四边形的周长是25cm,对边的间隔分别是2cm、3cm,那么这个平行四边形的面积为___11.等腰三角形的一个角50°,它的另外两个角的度数分别为12.等腰三角形的底角为15º,腰长为10㎝,那么它的面积是13.矩形ABCD中,AD=1,AB=3,那么此矩形的两条对角线所成的锐角是_______°14.平行四边形ABCD中,AB=14cm,BC=16cm,那么此平行四边形的周长为_____cm.15.菱形的两条对角线长为12cm和6cm,那么这个菱形的面积为________cm2.16.矩形ABCD的周长是14cm,对角线相交于O,ΔAOD与ΔAOB的周长的差是1cm,那么这个矩形的面积是______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级上册数学第一章图形与证明(二)单元试
题
以下是为您推荐的九年级上册数学第一章图形与证明(二)单元试题,希望本篇文章对您学习有所帮助。
九年级上册数学第一章图形与证明(二)单元试题
时间:100分钟满分:150分
一、选择题(3分8=24分)
1.已知等腰三角形的一个内角为40,则这个等腰三角形的顶角为【】
A.40
B.100
C. 40或100
D. 70或50
2.使两个直角三角形全等的条件【】
A.一锐角对应相等
B.两锐角对应相等
C.一条边对应相等
D.两条边对应相等
3.下面判定四边形是平行四边形的方法中,错误的是【】
A.一组对边平行,另一组对边也平行
B.一组对角相等,另一组对角也相等
C.一组对边平行,一组对角相等
D.一组对边平行,另一组对边相等
4.已知四边形ABCD是平行四边形,下列结论中不正确的是【】
A.当AB=BC时,它是菱形
B.当ACBD时,它是菱形
C.当ABC=90时,它是矩形
D.当AC=BD时,它是正方形
5.如图,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC
于点E,则△BEC的周长为【】
6.顺次连结四边形四条边的中点,所得的四边形是菱形,则原四边形一定是【】
A.平行四边形.
B.对角线相等的四边形.
C.矩形.
D.对角线互相垂直的四边形.
7.如图,在□ABCD中,E是BC的中点,且AEC=DCE,则下列结论不正确的是
A. B. DF=2BF
C.四边形AECD是等腰梯形
D.△ABE是等腰三角形
8.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为
二、填空题(3分8=24分)
9.如图,在△ABC中,C=90,AD平分CAB,BC=8cm,BD=5cm,,那么D点到直线AB的距离是 cm.
10.等腰梯形ABCD中,AD//BC,AD=3cm,BC=5cm,C=60,则梯形的腰长是 cm.
11.如图,矩形ABCD的对角线AC,BD相交于点O,AB=2,BOC=120,则AC的长是__________.
12.如图,菱形ABCD中,AE垂直平分BC,垂足为E,AB=4.则菱形ABCD的面积是,对角线BD的长是 .
13.在梯形ABCD中,AD//BC,对角线ACBD,且AC=5cm,
BD=12cm,则梯形中位线的长等于______cm.
14.如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、
N分别是边AB、BC的中点,则PM+PN的最小值是
_____________.
15.如图,若将边长为1的正方形ABCD绕点A逆时针旋转30到正方形ABCD,则图中阴影部分的面积为 .
16.如图,有一张面积为1的正方形纸片ABCD,M,N分别是AD,BC边的中点,将C点折叠至MN上,落在P点的位置,折痕为BQ,连结PQ,则PQ= .
三、解答题(共102分)
17.(本题8分)在等腰△ABC中,AB=AC=8,BAC=100,AD是BAC的平分线,交BC于D,点E是AB的中点,连接DE. 求:(1)求BAD的度数;(2)求B的度数;(3)求线段DE的长.
18.(本题8分)如图,已知ACBC,BDAD,AC 与BD 交于O,AC =BD.
求证:(1)BC=AD; (2)△OAB是等腰三角形.
19.(本题8分)我们把依次连接任意一个四边形各边中点得到的四边形叫做中点四边形.如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,依次连接各边中点得到中点四边形EFGH.
(1)这个中点四边形EFGH的形状是_________;
(2)请证明你的结论.
20.(本题10分)如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若E=50 ,求BAO的大小.
21.(本题10分)有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)
22.(本题10分)如图,在梯形ABCD中,AB∥DC, DB平分ADC,过点A作AE∥BD,交CD的延长线于点E,且C=2E.
(1)求证:梯形ABCD是等腰梯形;
(2)若BDC=30,AD=5,求CD的长.
23.(本题10分)如图,在△ABC中,D是BC边上的一点,E 是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DC,连接CF.
(1)求证:D是BC的中点;
(2)如果AB=AC,试猜测四边形ADCF的形状,并证明你的结论.
24.(本题12分)如图,等腰梯形ABCD中,AD∥BC,点E是线段AD上的一个动点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.
(1)试探索四边形EGFH的形状,并说明理由;
(2)当点E运动到什么位置时,四边形EGFH是菱形?并加以证明;
(3)若(2)中的菱形EGFH是正方形,请探索线段EF与线段BC 的关系,并证明你的结论.
25.(本题12分)我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:
(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;
(2)探究:当等对角线四边形中两条对角线所夹锐角为60时,这对60角所对的两边之和与其中一条对角线的大小关系,并说明你的结论.
26.(本题14分) 如图,在边长为4的正方形ABCD中,点P 在AB上从A向B运动,连接DP交AC于点Q.
(1)试证明:无论点P运动到AB上何处时,都有
△ADQ≌△ABQ ;
(2)当点P在AB上运动到什么位置时,△ADQ的面积是正方形ABCD面积的 ;
(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形.。
