最新浙教版九年级数学下册1.1锐角三角函数公开课优质PPT课件(12)
合集下载
浙教版九年级下册 1.1 锐角三角函数 课件(共27张PPT)

AB A. sinA B. sinB C. tanA D. tanB 2.如图,已知在 Rt△ABC 中,∠C=90°,AC=4,tanA=1,则 BC 的长是( )
2 A. 2 B. 8 C. 2 5 D. 4 5
3.在△ABC 中,∠C=90°,AB=2,AC=1,则 sinB 的值是( )
A. 1 2
B. 2 2
C. 3 2
D. 2
4.如图,在△ABC 中,∠C=90°,BC∶AC=1∶2,则 sinA=___.
5.如图,在Rt△ABC中,∠C=90°,b=20,c=20, 则∠B的度数为________.
6.如图,在△ABC 中,∠ABC=90°,BD⊥AC 于点 D,∠CBD=α,AB=3,BC=4, 求 sinα,cosα,tanα的值.
B
B1 (1)直角三角形AB1C1和直角三角形ABC 有什么关系?
(2) BC 和 B1C1 , AC 和 AC1 ,
AB AB1 AB AB1
BC 和 B1C1有什么关系?
AC AC1
(3)如果改变B在AB1上的位置呢?
A
C
想一想
B
B1 (1)直角三角形AB1C1和直角三角形ABC 有什么关系?
1.1 锐角三角函数(1)
复习回顾
勾股定理
?当直角三角形的锐角不是
直 角
特殊角度时,三边之间是否
三
也有类似的定值数量关系呢?
角
形
想一想
B
A
C
B1 (1)直角三角形AB1C1和直角三角形ABC 有什么关系? (2) BC 和 B1C1 , AC 和 AC1 ,
AB AB1 AB AB1
BC 和 B1C1有什么关系?
2 A. 2 B. 8 C. 2 5 D. 4 5
3.在△ABC 中,∠C=90°,AB=2,AC=1,则 sinB 的值是( )
A. 1 2
B. 2 2
C. 3 2
D. 2
4.如图,在△ABC 中,∠C=90°,BC∶AC=1∶2,则 sinA=___.
5.如图,在Rt△ABC中,∠C=90°,b=20,c=20, 则∠B的度数为________.
6.如图,在△ABC 中,∠ABC=90°,BD⊥AC 于点 D,∠CBD=α,AB=3,BC=4, 求 sinα,cosα,tanα的值.
B
B1 (1)直角三角形AB1C1和直角三角形ABC 有什么关系?
(2) BC 和 B1C1 , AC 和 AC1 ,
AB AB1 AB AB1
BC 和 B1C1有什么关系?
AC AC1
(3)如果改变B在AB1上的位置呢?
A
C
想一想
B
B1 (1)直角三角形AB1C1和直角三角形ABC 有什么关系?
1.1 锐角三角函数(1)
复习回顾
勾股定理
?当直角三角形的锐角不是
直 角
特殊角度时,三边之间是否
三
也有类似的定值数量关系呢?
角
形
想一想
B
A
C
B1 (1)直角三角形AB1C1和直角三角形ABC 有什么关系? (2) BC 和 B1C1 , AC 和 AC1 ,
AB AB1 AB AB1
BC 和 B1C1有什么关系?
浙教版九下 1.1锐角三角函数 课件

铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
梯子越陡——倾斜角_越__大__
倾斜角越大——铅直高度与梯子的比_越__大__ 倾斜角越大——水平宽度与梯子的比_越__小__
倾斜角越大——铅直高度与水平宽度
的比_越__大__
铅 直 高
度
水平宽度
想一想
B
A
C
B1
(1)直角三角形AB1C1和直角三 角 形ABC有什么关系?
(2)
B C 和 B 1C 1
A B AB1
, A C 和 A C 1,
AB
AB1
BC AC
和 B 1 C 1 有什么关系?
AC 1
(3)如果改变B在梯子上的位置
呢?
C1
想一想
B
B1
C
取宝物比赛
10m
10m
(1)
1m
5m
(2)
谈谈今天的收获
B
∠A的对边
sinA
斜边
斜边
∠A的对边 cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
作业
1.书本作业题第6题 2.同步练习
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
梯子越陡——倾斜角_越__大__
倾斜角越大——铅直高度与梯子的比_越__大__ 倾斜角越大——水平宽度与梯子的比_越__小__
倾斜角越大——铅直高度与水平宽度
的比_越__大__
铅 直 高
度
水平宽度
想一想
B
A
C
B1
(1)直角三角形AB1C1和直角三 角 形ABC有什么关系?
(2)
B C 和 B 1C 1
A B AB1
, A C 和 A C 1,
AB
AB1
BC AC
和 B 1 C 1 有什么关系?
AC 1
(3)如果改变B在梯子上的位置
呢?
C1
想一想
B
B1
C
取宝物比赛
10m
10m
(1)
1m
5m
(2)
谈谈今天的收获
B
∠A的对边
sinA
斜边
斜边
∠A的对边 cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
作业
1.书本作业题第6题 2.同步练习
浙教版九年级下册数学《锐角三角函数和解直角三角形》PPT课件

回味无穷
▪ 定义中应该注意的几个问题:
1.sinA,cosA,tanA, 是在直角三角形中定义的, ∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA, 是一个完整的符号,表示∠A 的正切,习惯省去“∠”号; 3.sinA,cosA,tanA, 是一个比值.注意比的顺序, 且sinA,cosA,tanA, 均﹥0,无单位. 4.sinA,cosA,tanA, 的大小只与∠A的大小有关, 而与直角三角形的边长无关. 5.角相等,则其三角函数值相等;两锐角的三角函
(2) BC和 B1C1 , AC 和 AC1, BC
AB AB1 AB AB1 AC
和 B1C1有什么关系?
AC1
BC B1C1
=
AB AB1
AC AC1
=
AB AB1
BC B1C1
=
AC AC1
C1
想一想
B
ß
A
C
(1)直角三角形AB1C1和直角三 角 形ABC有什么关相系似?
B1 (2) BC 和 B1C1 , AC 和 AC1, BC
1、sinA 不是一个角 2、sinA不是 sin与A的乘积 3、 sinA 是一个比值 4、sinA 没有单位
▪ 求出图19.3.3所示的Rt△ABC中∠A的三个三 角函数值.
8
15
图 19.3.1
例2 如图:在Rt△ABC中 ,∠B=900,AC=200,sinA=0.6.求:BC的长.
C 200
值变了吗?
对于锐角A的每一个确定的值,其对 边与斜边、邻边与斜边、邻边与对边 的比值也是惟一确定的
这几个比值都是锐角∠A的函数,记
作sin A、cos A、tan A,即
新浙教版九年级数学下册第一章《锐角三角函数的计算》精品课件.ppt

w2 一辆汽车沿着一山坡行驶了100m,
34
2
5
其铅直高度上升了50m.求山坡与水平
6
面所成的锐角的大小.
7
w3. 图中的螺旋形由一系列直角三角形组
成.每个三角形都不得是以点O为一顶点.
w(1)求∠A0OA1,∠A1OA2,∠A2OA3,的大小. w(2)已知∠An-1OAn,是一个小于200的角,求 n的值.tanA7O8A 180.353, 6∴∠A7OA8=19.470.∴n=8.
sinABC101. AC 40 4
w那么A是多少 度呢? w要解决这问题,我们可以借助科学计算器.
w请与同伴交流你是怎么做的?
做一做 3
知识在于积累
w已知三角函数值求角度,要用到三个键, sin cos tan 和第二功能键Sin-1 cos-1 tan-1 和2ndf .
w例如,
SinA=0.9816 CosA=0.8607 tanA=0.1890
∴V型角的大小约550.
学化
呀!
随堂练习 7
真知在00m,其铅直高度 上升了50m.求山坡与水平面所成的锐角的大小.
咋办
?
w老师期望: w你具有成功的把握.
例题欣赏 5
行家看“门道”
w例2 如图,一名患者体内某重要器官后面有一肿瘤.
在接受放射性治疗时,为了最大限度地保证疗效,并且
tanA=56.78
按键的顺序 2ndf Sin-1 0 . 9 8 1 6 = 2ndf cos-1 0 . 8 6 0 7 = 2ndf tan-1 0 . 1 8 9 0 = 2ndf tan-1 5 6 . 7 8 =
显示结果
Sin-1=0.9816 =78.99184039 coS-1=0.8607 =30.60473007 tan-1=0.1890 =10.70265749
浙教版数学九下1.1锐角三角函数课件

AC 5 5
sin B AC 5 ,cosB BC 2,tan B AC 5 .
AB 3
AB 3
BC 2
延伸:由上面的计算,你能猜想∠A,∠B的正弦、余弦值 有什么规律吗?
结论:一个锐角的正弦等于它余角的余弦,或一个锐角的 余弦等于它余角的正弦.
请同学们拿出
自己的学习工具— 1
2
—一副三角尺,思
AB 5
BC 3
2、 如图,在Rt△ABC中,∠C=90°,BC=2,
AB=3,求∠A,∠B的正弦、余弦、正切值. B
解:在RtABC中,
3
2
AC AB2 BC2 32 22 5,
A
C
sin A BC 2,cos A AC 5 ,tan A BC 2 2 5 .
AB 3
AB 3
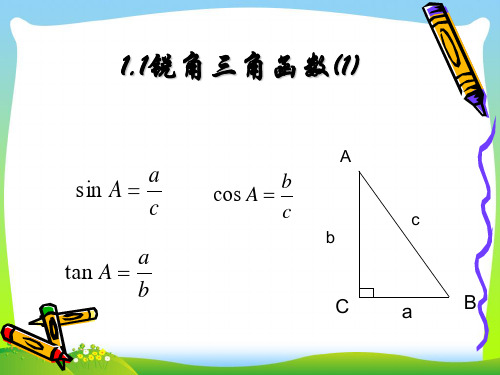
c 斜边
B
a 对边
A
bC
例如,当∠A=30°时,我们有
sin A sin 30 1 2
当∠A=45°时,我们有
sin A sin 45 2 2
在图中 ∠A的对边记作a ∠B的对边记作b ∠C的对边记作c
注意
▪ sinA是一个完整的符号,它表示∠A的正弦, 记号里习惯省去角的符号“∠”;
▪ sinA没有单位,它表示一个比值,即直角 三角形中∠A的对边与斜边的比;
,
则sin∠A=___.
b3
5、如图,在△ABC中, AB=CB=5, sinA= ,求△ABC 的面积.
4 5
B
5
5
A
C
如图,在Rt△ABC中,∠C=90°,
我们把锐角A的邻边与斜边的比叫做∠A的
余弦(cosine),记作cosA, 即
新浙教版九年级数学下册第一章《锐角三角函数1》课件

n 比值 AB
n 比值
AC 叫做∠α的余弦,记做cosα
AB
BC 叫做∠α的正切 ,记做tanα
AC
B
α
AC
sin BC cos AC tan BC
AB
AB
AC
锐角α的正弦、余弦、正切 统称为∠α的三角函数
•sin如图 B,ACB在Rts⊿inAABC中A,斜的边 ∠对C边=Rt∠ A
cos AC
3 3 ,13
13
13
2 2 13
13
13 ,
3
y P (2,3)
α
O
x
M
2
w1.如图,在Rt△ABC中,锐角A的对边和邻边同时
扩大100倍,tanA的值( )
B
wA.扩大100倍 B.缩小100倍
wC.不变
D.不能确定
w2.已知∠A,∠B为锐角
A
┌ C
w(1)若∠A=∠B,则tanA tanB;
sinA= 3
B
5
D
C
A
2、如图,在△ABC中,D若AB=5,BC=3,则下列 结论正确的是( )
A.sinA=
4
5
3
B.sinA=
5
3
C.sinA=
D.以上结论都不正确
4
3、如图,在Rt△ABC中,∠ACB=90°,作CD⊥AB于D,
若BD=2,BC=3.则sinA=
.
2
3
A
5 A
B 3 C
C 3 B
体验到一种学习方法:猜想 证明 归纳 应用
∠α的正弦 ∠α的余弦 ∠α的正切
书面作业: 教科书P6中的作业题。(必做题)
新浙教版九年级数学下册第一章《锐角三角函数(1)》精品课件1.ppt
• 10、人的志向通常和他们的能力成正比例。2021/1/142021/1/142021/1/141/14/2021 6:41:13 PM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2021/1/142021/1/142021/1/14Jan-2114-Jan-21 • 12、越是无能的人,越喜欢挑剔别人的错儿。2021/1/142021/1/142021/1/14Thursday, January 14, 2021 • 13、志不立,天下无可成之事。2021/1/142021/1/142021/1/142021/1/141/14/2021
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
边之比 定义 表示 公式
B
∠A的对边a 正弦函数
斜边c
∠A的
对边 ∠A的邻边b
a
斜边c
余弦函数
sinA cosA
sssiiinnn
AAA
===
aaa ccc
cccooosss
AAA
===
bbb ccc
A
∠ A的邻边b
C
∠A的对边a ∠A的邻边b
正切函数
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
边之比 定义 表示 公式
B
∠A的对边a 正弦函数
斜边c
∠A的
对边 ∠A的邻边b
a
斜边c
余弦函数
sinA cosA
sssiiinnn
AAA
===
aaa ccc
cccooosss
AAA
===
bbb ccc
A
∠ A的邻边b
C
∠A的对边a ∠A的邻边b
正切函数
新浙教版九年级数学下册第一章《锐角三角函数2》优质公开课课件

w 看图说话: w 直角三角形三边的关系. w 直角三角形两锐角的关系. w 直角三角形边与角之间的关系. w 特殊角300,450,600角的三角函数
值.
w 互余两角之间的三角函数关系. w 同角之间的三角函数关系
B
c
a
┌
A
b
C
300 450
450 ┌ 600 ┌
习题
w1.计算;(1)tan450-sin300; w(2)cos600+sin450-tan300;
2
w例2 如图:一个小孩荡秋千,秋千链子的长度
为2.5m,当秋千向两边摆动时,摆角恰好为600, 且两边摆动的角度相同,求它摆至最高位置时与 其摆至最低位置时的高度之差(结果精确到 0.01m).
O
w老师提示: 将实际问 题数学化.
●
2.5
B ┌C D A
例3。一位同学的手臂长65cm,当他高 举双臂时,指尖高出头顶35cm。问当他 的手臂与水平成角60度时,指尖高出头 顶多少cm(精确到0。1cm)?
1.1锐角三角函数(2)
n 300,450,600角的三角函数值
脑中有“图”,心中有
锐角三角函数“定式”义
w直角三角形中边与角的关系:锐角三角函数.
w在直角三角形中,若一个锐角确定,那么这个角的对边,
邻边和斜边之间的比值也随之确定.
sin A a , cos A b ,
c
c
B
sin B b , c
3 6 ta 2 3 0 n 0 3 s6 i0 n 0 2 c4 o 0 .5 s
w2.如图,河岸AD,BC互相平行,桥AB 垂直于两岸.桥长12m,在C处看桥两端 A,B,夹角∠BCA=600. w求B,C间的距离(结果精确到1m).
浙教版数学九年级下册 1.1 锐角三角函数 课件(共18张PPT)

? 求BE的长.
B(山顶)
H
当锐角为30°时,
30°
西坡
其所对的直角边与
斜边之比始终
30°
A
D
B(山顶)
为 1.
C
2
E
东坡
当锐角为45°时,
其所对的直角边
30°
CF
D
B(山顶)
与 斜边之比始 终为 2 .
2
当锐角为50°时,
G 南坡
这个比值是一个确 定的值.
C
HD
任意作一个锐角∠A,在角的边上任意取两点B
与B1分别作BC⊥AC于点C ,B1C1⊥A1C1于点C1.
判断 BC 与 B1C1 是否相等,并说明理由. B1
AB
AB1
B
A
C C1
对于每一个确定的锐角α,在角的边上任意取
一点B作BC⊥AC于点C,比值 BC 是一个确
定的值.
AB
B
A
C
直角三角形中锐角ɑ与其对边与斜边比值关系
ɑ
BC (对边与斜边比值)
1.1锐角三角函数(1)
我关心的是本质 其它都是细节(爱因斯坦)
一 情境创小设红、小强、小颖约好去爬山,他们沿不同倾 斜度的三条道路上山,若山顶与山下的铅垂距离为100 米,你能分别求出他们到达山顶要走的路程吗?
南坡
50°
小颖出发地
西坡
东坡
30°
小红出发地
45°
小强出发地
转化成的数学问题 B(山顶)
2.sinα是一个完整的符号,单独的“sin”没有意义.
练一练
1. 如图△ABC中,∠C=90°,BC=5,AC=12B.
5
计算:(1)sinA= 13.
B(山顶)
H
当锐角为30°时,
30°
西坡
其所对的直角边与
斜边之比始终
30°
A
D
B(山顶)
为 1.
C
2
E
东坡
当锐角为45°时,
其所对的直角边
30°
CF
D
B(山顶)
与 斜边之比始 终为 2 .
2
当锐角为50°时,
G 南坡
这个比值是一个确 定的值.
C
HD
任意作一个锐角∠A,在角的边上任意取两点B
与B1分别作BC⊥AC于点C ,B1C1⊥A1C1于点C1.
判断 BC 与 B1C1 是否相等,并说明理由. B1
AB
AB1
B
A
C C1
对于每一个确定的锐角α,在角的边上任意取
一点B作BC⊥AC于点C,比值 BC 是一个确
定的值.
AB
B
A
C
直角三角形中锐角ɑ与其对边与斜边比值关系
ɑ
BC (对边与斜边比值)
1.1锐角三角函数(1)
我关心的是本质 其它都是细节(爱因斯坦)
一 情境创小设红、小强、小颖约好去爬山,他们沿不同倾 斜度的三条道路上山,若山顶与山下的铅垂距离为100 米,你能分别求出他们到达山顶要走的路程吗?
南坡
50°
小颖出发地
西坡
东坡
30°
小红出发地
45°
小强出发地
转化成的数学问题 B(山顶)
2.sinα是一个完整的符号,单独的“sin”没有意义.
练一练
1. 如图△ABC中,∠C=90°,BC=5,AC=12B.
5
计算:(1)sinA= 13.
优秀课件浙教版九年级数学下册1.1《锐角三角函数(1)》教学课件 (共16张PPT)

观察归纳
1、了解三角函数的概念; 2、会用符号表示一个锐角的三种三角函数; 3、掌握在直角三角形中,锐角三角函数与边之比的关系;
4、会根据锐角三角函数的定义求锐角三角函数。
sin读音 cos读音 tan读音源自结 论这里邻边指的都是直角边.
探究1
探究2
探究3
在RtΔABC中,如果各边长度都扩大为原来
1.1 锐角三角函数
——第1课时
自学指导
结合思考题自学P(4)--(5)课内练习前内容,并完
成课内练习
显示练习(点我)
思考下面问题: 1、sinα、cos、tanα 分别代表什么意义,这个α有什么要求? 2、sinα、cos、tanα 的范围分别是什么? 3、sinα、cos、tanα 是不是函数,为什么?
的2倍,则锐角A的正切值( D )
(A)扩大2倍 (B)缩小2倍
(C)扩大4倍
(D)没有变化
返回(点我)
浙教版数学九年级下册 1.1 锐角三角函数 课件(共25张PPT)

观察以上计算结果,你发现了什么?
sinA=cosB ,cosA=sinB (∠A+∠B=90)
tanA·tanB=1
(∠A+∠B=90)
B
c
a
┌
A
b
C
sin A a cos A b tan A a
c
c
b
sin B b cos B a
c
c
tan B b a
如图,在△ABC中,若AB=5,BC=3,则下列结论正确
锐角A,A′的余弦值的关系为( ) A
A.cosA=cosA′ B.cosA=3cosA′ C.3cosA=cosA′ D.不能确定 2.如图,已知P是射线OB上的任意一点,PM⊥OA于M,
且PM:OM=3:4,则cosα的值等于( C)
3 A.4
4 B.3
C.4 5
3
D.
5
3.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,
是关于锐角α的三角函数。
AB AB AC
B
A
C
锐角α的正弦,余弦和正切统称∠α的三角函数.
比值 BC 叫做∠α的正弦(sine),记做sinα.
AB
BC
比值 AC
即sinα= AB
叫做∠α的余弦(cosine) ,记做cosα.
AB
即cosα= AC
AB 比值 叫做∠α的正切(tangent) ,记做tanα.
b,c,则下列各项中正确的是( ) B
A.a=c·sinB B.a=c·cosB C.a=c·tanB D.以上均不正确
4.在Rt△ABC中,∠C=90°,cosA= 2 ,则tanB等于( )
C
新浙教版九年级数学下册第一章《锐角三角函数1》公开课课件

想一想
B
B1
(1)直角三角形AB1C1和直角三 角 形ABC有什么关系?
BC
B 1C 1 A C
AC1 BC
(2) A B 和 A B 1 , A B 和A B 1 , A C
和B
A
1C C
1 1
有什么关系?
A
(3)如果改变B在梯子上的位置
呢?
C C1
动手实践,寻找规律 • 由推理可得:角度不变,比值不变 • 由动态演示:动手实践,寻找规律 • 由推理可得:角度不变,比值不变 • 由动态演示:角度改变,比值改变
5.如图, ∠C=90°CD⊥AB.
()()()
sin B .
()()()
A
C
┌ DB
6.在上图中,若BD=6,CD=12.求cosA的值.
w7.如图,分别根据图(1) 和图(2)求∠A的三个三角 函数值.
w8.在Rt△ABC中,∠C=90°, (1)AC=3,AB=6,求sinA和cosB (2)BC=3,sinA= 5 ,求AC和AB.
5 sinB= 4
5 B
4 cosA= 5 cosB= 3
5
3 tanA=
4 tanB= 4
3
观察以上计算结果,你发现了什么?
若AC=5,BC=3呢? C
变变
• 在Rt⊿ABC中,∠C=Rt∠, 求锐角∠A的余弦
sinA= 3 5
B
A
C
变变变
在Rt⊿ABC中,∠C=Rt∠, sinA CD⊥AB,求锐角∠DCB的余弦
=
3 5
B D
C
A
例2 如图:在Rt△ABC中,∠B=900,AC=200,sinA=0.6.
1.1 锐角三角函数(第1课时)(课件)九年级数学下册(浙教版)

当堂检测
7.在Rt△ABC中,∠C=90°, AB=15,tanA=3,求AC和BC.
4
∴设BC=3k,AC=4k.
15
A
4k
B
3k
┌ C
课堂小结
【正切的定义】 如图,在Rt△ABC中,∠C=90°, 我们把∠A的对边a与邻边b的比,叫做∠A的正切,
记作tanA,tanA
=
∠A的对边 ∠A的邻边
正切。 3.坡度越大,坡面越陡。
讲授新课
知识归纳
【坡度的定义】 通常把坡面的垂直高度h与水平方向的距离l的比叫做坡度(或叫做坡比), 坡度越大,坡越陡
讲授新课
典例精析
【例2】如图,某人从山脚下的点A走了200m后到达山顶的点B.已知山顶B 到山脚下的垂直距离是55m,求山坡的坡度(结果精确到0.001m).
AC2
AC1
B2C2 , AC2
B1 B2 B3
C3 C2
C1
(3)如果改变B2在梯子上的位置(如B3)呢? 比值不变
(4)由此你能得出什么结论? 直角三角形中,锐角大小确定后,对 应的对边和邻边的比值也就确定了
讲授新课
归纳:
由此可得,在有一个锐角相等的所有直角三角形中,这个锐角的对边
与邻边的比值是一个常数,与直角三角形的大小无关.
数学(浙教版)
九年级 下册
第1章 解直角三角形
1.1 锐角三角函数 第1课时 正切
学习目标
1. 理解正切的意义和与现实生活的联系; 2.能够用表示直角三角形中两直角边的比,表示生活中物体的倾 斜程度、坡度(坡比)等; 3.能够根据直角三角形的边角关系,用正切进行简单的计算;
温故知新
对直角三角形的边角关系,已经研究了什么?还可以研究 什么?
新浙教版九年级数学下册第一章《锐角三角函数的计算(1)》公开课课件.ppt

及其三角函数 求另一边
求另一边
sin A a , c
acsin A. c a . sin A
B
ca ┌
A bC
cos A b , c
bccoA.s c b . cos A
A
tan A a , b
abtaA n. b a . tan A
α β┌
w 2模型: A D ta9n00 ata9n00 . B a C
Bα
β
C
A
w9 如图,根据图中
已知数据,求AD.
α β┌ Ba C D
探索下列关系式是否成立(00〈α〈900)?
(1) sinα+cos α≤1 (2) sin2α= 2sinα
P16 习题1.4 1,2题
w1.用计算器求下列各式的值: w(1)tan320;(2)sin24.530; w(3)sin62011′;(4)tan39039′39 ″w2..如图,物华大厦离小伟家60m,小伟 从自家的窗中眺望大厦,并测得大厦顶 部仰角是450,而大厦底部的俯角是370, 求该大厦的的高度 (结果精确到0.1m).
• 10、人的志向通常和他们的能力成正比例。2020/12/192020/12/192020/12/1912/19/2020 11:30:37 AM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2020/12/192020/12/192020/12/19Dec-2019-Dec-20 • 12、越是无能的人,越喜欢挑剔别人的错儿。2020/12/192020/12/192020/12/19Saturday, December 19, 2020 • 13、志不立,天下无可成之事。2020/12/192020/12/192020/12/192020/12/1912/19/2020
