3.2简单几何体三视图(1)
简单几何体及三视图、直观图
返回
A.上面为棱台,下面为棱柱 B.上面为圆台,下面为棱柱 C.上面为圆台,下面为圆柱 D.上面为棱台,下面为圆柱 解析:结合图形分析知上面为圆台,下面为圆柱. 答案:C
返回
4. (2011•广东揭阳一模)一个正方体截去两 个角后所得几何体的主视图、左视图如 图所示,则其俯视图为( )
返回
解析:依题意可知该几何体的直观图如下图所示,故其 俯视图应为C.
多面体 棱柱 结构特征 有两个面 互相平行 ,其余各面都是四边形, 并且每相邻两个面的交线都 平行且相等 . 有一个面是 多边形 ,而其余各面都是有一个 公共顶点 的三角形. 棱锥被平行于 底面 的平面所截, 截面 和 底面
棱锥
棱台
之间的部分.
返回
三、等简易组合)的三视图,能识别上述三视图所表示的立 体模型,会用斜二测画法画出它们的直观图.
3.会用平行投影与中心投影两种方法画出简单空间图形的
三视图与直观图,了解空间图形的不同表示形式. 4.会画某些建筑物的三视图与直观图(在不影响图形特征
的基础上,尺寸、线条等不作严格要求).
返回
怎 么 考 从高考内容上来看,空间几何体的三视图和直观图
两条:AC1、AD1,同理从B、C、D、E点 出发的对角线也有两条,共2×5=10条. [答案] D
返回
[巧练模拟]——————(课堂突破保分题,分分必保!) 1.以下命题中,说法正确的是________. ①底面是矩形的四棱柱是长方体;②直角三角形绕着 它的一边旋转一周形成的几何体叫做圆锥;③四棱锥
因三视图识图不准
返回
[考题范例] (2011· 江西高考)将长方体截去一个四棱锥,
得到的几何体如图所示,则该几何体的侧
视图为 ( )
中考数学 题型02 简单几何体的三视图(解析版)

备考2020年中考一轮复习点对点必考题型题型02 简单几何体的三视图考点解析1.简单几何体的三视图(1)画物体的主视图的口诀为:主、俯:长对正;主、左:高平齐;俯、左:宽相等.(2)常见的几何体的三视图:圆柱的三视图:2.简单组合体的三视图(1)画简单组合体的三视图要循序渐进,通过仔细观察和想象,再画它的三视图.(2)视图中每一个闭合的线框都表示物体上的一个平面,而相连的两个闭合线框常不在一个平面上.(3)画物体的三视图的口诀为:主、俯:长对正;主、左:高平齐;俯、左:宽相等.3.由三视图判断几何体(1)由三视图想象几何体的形状,首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.(2)由物体的三视图想象几何体的形状是有一定难度的,可以从以下途径进行分析:①根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,以及几何体的长、宽、高;②从实线和虚线想象几何体看得见部分和看不见部分的轮廓线;③熟记一些简单的几何体的三视图对复杂几何体的想象会有帮助;④利用由三视图画几何体与有几何体画三视图的互逆过程,反复练习,不断总结方法.五年中考1.(2019•成都)如图所示的几何体是由6个大小相同的小立方块搭成,它的左视图是( )A.B.C.D.【点拨】找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.【解析】解:从左面看易得第一层有2个正方形,第二层左边有1个正方形,如图所示:故选:B.2.(2018•成都)如图所示的正六棱柱的主视图是( )A.B.C.D.【点拨】根据主视图是从正面看到的图象判定则可.【解析】解:从正面看是左右相邻的3个矩形,中间的矩形的面积较大,两边相同.故选:A.3.(2017•成都)如图所示的几何体是由4个大小相同的小立方体组成,其俯视图是( )A.B.C.D.【点拨】根据从上边看得到的图形是俯视图,可得答案.【解析】解:从上边看一层三个小正方形,故选:C.4.(2016•成都)如图所示的几何体是由5个大小相同的小立方块搭成,它的俯视图是( )A.B.C.D.【点拨】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.【解析】解:从上面看易得横着的“”字,故选:C.5.(2015•成都)如图所示的三视图是主视图是( )A.B.C.D.【点拨】根据原图形得出其主视图,解答即可.【解析】解:A、是左视图,错误;B、是主视图,正确;C、是俯视图,错误;D、不是主视图,错误;故选:B.一年模拟1.(2019·锦江一诊)有一透明实物如图,它的主视图是( )A.B.C.D.【点拨】细心观察图中几何体摆放的位置和形状,根据主视图是从正面看到的图象判定则可.【解析】解:正面看,它是中间小两头大的一个图形,里面有两条虚线,表示看不到的轮廓线.故选:B.2.(2019·成华一诊)如图所示的几何体,它的左视图是( )A .B .C .D .【点拨】根据左视图即从物体的左面观察得到的视图,进而得出答案.【解析】解:如图所示的几何体的左视图为:.故选:D .3.(2019·武侯一诊)如图所示的支架(一种小零件)的两个台阶的高度和宽度分别相等,则它的主视图为( )A .B .C .D .【点拨】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.【解析】解:从正面看去,是两个有公共边的矩形,如图所示:故选:D .4.(2019·成华二诊)如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是( )A.主视图B.左视图C.俯视图D.主视图和左视图【点拨】根据从上边看得到的图形是俯视图,可得答案.【解析】解:从上边看是一个十字,“十”字是中心对称图形,故选:C.5.(2019·青羊一诊)观察下列几何体,主视图、左视图和俯视图都是矩形的是( )A.B.C.D.【点拨】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.【解析】解:A、主视图为矩形,俯视图为圆,错误;B、主视图为矩形,俯视图为矩形,正确;C、主视图为等腰梯形,俯视图为圆环,错误;D、主视图为三角形,俯视图为有对角线的矩形,错误.故选:B.6.(2019·青羊二诊)图中三视图对应的正三棱柱是( )A.B.C.D.【点拨】利用俯视图可淘汰C、D选项,根据主视图的侧棱为实线可淘汰B,从而判断A选项正确.【解析】解:由俯视图得到正三棱柱两个底面在竖直方向,由主视图得到有一条侧棱在正前方,于是可判定A选项正确.故选:A.7.(2019·武侯二诊)下面四个立体图形,从正面、左面、上面观察都不可能看到长方形的是( )A.B.C.D.【点拨】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.依此找到从正面、左面、上面观察都不可能看到长方形的图形.【解析】解:A、主视图为长方形,左视图为长方形,俯视图为长方形,故本选项错误;B、主视图为长方形,左视图为长方形,俯视图为圆,故本选项错误;C、主视图为等腰三角形,左视图为等腰三角形,俯视图为圆,从正面、左面、上面观察都不可能看到长方形,故本选项正确;D、主视图为三角形,左视图为三角形,俯视图为有对角线的矩形,故本选项错误.故选:C.8.(2019·锦江二诊)如图,该立体图形的俯视图是( )A.B.C.D.【点拨】根据几何体的三视图,即可解答.【解析】解:如图所示的立体图形的俯视图是C.故选:C.9.(2019·高新一诊)如图是由几个相同小正方体组成的立体图形的俯视图,图上的数字表示该位置上小正方体的个数,这个立体图形的左视图是( )A.B.C.D.【点拨】根据从左边看得到的图形是左视图,可得答案.【解析】解:根据该几何体中小正方体的分布知,其左视图共2列,第1列有1个正方形,第2列有3个正方形,故选:B.10.(2019·武侯二诊)如图所示的几何体的左视图是( )A.B.C.D.【点拨】找到从几何体的左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.【解析】解:从左面看,得到的视图是A.故选:A.精准预测1.如图所示几何体的左视图正确的是( )A.B.C.D.【点拨】找到从几何体的左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.【解析】解:从几何体的左面看所得到的图形是:故选:A.2.下列立体图形中,主视图是三角形的是( )A.B.C.D.【点拨】根据从正面看得到的图形是主视图,可得图形的主视图.【解析】解:A、C、D主视图是矩形,故A、C、D不符合题意;B、主视图是三角形,故B正确;故选:B.3.如图是某兴趣社制作的模型,则它的俯视图是( )A .B .C .D .【点拨】根据俯视图即从物体的上面观察得得到的视图,进而得出答案.【解析】解:该几何体的俯视图是:由两个长方形组成的矩形,且矩形的之间有纵向的线段隔开.故选:B .4.如图所示几何体,从左面看是( )A .B .C .D .【点拨】从左面看到的是左面位置上下两个正方形,右面的下方一个正方形,由此得出答案即可.【解析】解:左面位置上下两个正方形,右面的下方一个正方形的图形是.故选:B .5.下列几何体中,从正面看(主视图)是长方形的是( )A .B .C .D .【点拨】主视图是分别从物体正面看,所得到的图形.【解析】解:圆锥的主视图是等腰三角形,圆柱的主视图是长方形,圆台的主视图是梯形,球的主视图是圆形,故选:B .6.学校超市的货架上摆放着某品牌方便面,从三个不同的方向看可以看到下图所示的形状图,则货架上的方便面至多有( )A.7盒B.8盒C.9盒D.10盒【点拨】由从三个不同的方向看到的形状,可以在俯视图上,标出相应的摆放的最多数量,进而求出答案,做出选择.【解析】解:由从三个不同的方向看到的形状,可以在俯视图上,标出相应的摆放的最多数量,求出至多有9盒,故选:C.7.如图是由小立方块搭成的几何体,则从左面看到的几何体的形状图是( )A.B.C.D.【点拨】从左面看到的图形是两列,其中第一列有两个正方形,第二列有1个正方形,做出判断即可.【解析】解:从左面正投影所得到的图形为选项B.故选:B.8.如图是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( )A.左视图会发生改变B.俯视图会发生改变C.主视图会发生改变D.三种视图都会发生改变【点拨】根据从上面看得到的图形事俯视图,从正面看得到的图形是主视图,从左边看得到的图形是左视图,可得答案.【解析】解:如果将小正方体A放到小正方体B的正上方,则它的主视图会发生改变,俯视图和左视图不变.故选:C.9.如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是( )A.主视图B.左视图C.俯视图D.主视图和左视图【点拨】根据从上边看得到的图形是俯视图,可得答案.【解析】解:从上边看是一个田字,“田”字是中心对称图形,故选:C.10.如图,下列选项中不是正六棱柱三视图的是( )A.B.C.D.【点拨】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.【解析】解:正六棱柱三视图分别为:三个左右相邻的矩形,两个左右相邻的矩形,正六边形.故选:A.11.如图,是某个几何体从不同方向看到的形状图(视图),这个几何体的表面能展开成下面的哪个平面图形?( )A.B.C.D.【点拨】由主视图和左视图可得此几何体为柱体,根据俯视图是圆可判断出此几何体为圆柱,进一步由展开图的特征选择答案即可.【解析】解:∵主视图和左视图都是长方形,∴此几何体为柱体,∵俯视图是一个圆,∴此几何体为圆柱,因此图A是圆柱的展开图.故选:A.12.如图,下列水平放置的几何体中,左视图不是矩形的是( )A.B.C.D.【点拨】根据左视图是从左面看到的视图,对各选项分析判断后利用排除法求解.【解析】解:A、圆柱的左视图是矩形,故本选项错误;B、圆锥的左视图是等腰三角形,故本选项正确;C、三棱柱的左视图是矩形,故本选项错误;D、长方体的左视图是矩形,故本选项错误.故选:B.13.如图所示的支架是由两个长方体构成的组合体,则它的左视图是( )A.B.C.D.【点拨】根据从左边看得到的图形是左视图,可得答案.【解析】解:从左边看下边是一个中间为虚线的矩形,故选:A.14.桌上摆放着一个由相同正方体组成的组合体,其俯视图如图所示,图中数字为该位置小正方体的个数,则这个组合体的左视图为( )A.B.C.D.【点拨】俯视图中的每个数字是该位置小立方体的个数,分析其中的数字,得左视图有3列,从左到右分别是2,3,2个正方形.【解析】解:由俯视图中的数字可得:左视图有3列,从左到右分别是2,3,2个正方形.故选:D.15.如图所示的几何体,从上面看得到的图形是( )A.B.C.D.【点拨】根据从上边看得到的图形是俯视图,可得答案.【解析】解:从上边看是一个六边形,中间为圆.故选:D.。
简单几何体的三视图讲解[1]
![简单几何体的三视图讲解[1]](https://img.taocdn.com/s3/m/358f1291d05abe23482fb4daa58da0116c171f08.png)
根据已知的两个视图,利用投影关系,可以推断出第三个视图的基本形状和尺寸。例如, 如果已知主视图和左视图,可以通过它们的高度和宽度推断出俯视图的基本形状。
注意细节和遮挡关系
在补画第三视图时,需要注意细节和遮挡关系。例如,当几何体中存在凹槽或凸起时,需 要在第三视图中相应地表示出来。同时,还需要注意不同部分之间的遮挡关系,以确保补 画出的第三视图准确无误。
。
圆锥体的俯视图是一个圆面,同 样需要按照正投影法将其绘制成
椭圆。
在绘制过程中,要注意圆锥体的 高和底面直径的比例关系,以及
锥尖的位置和方向。
球体三视图简化表示方法
球体的三视图都是圆面,但由于投影角度的不同,圆面的大小和形状也会有所不同 。
在简化表示时,可以将球体的三视图都绘制成相同的圆面,但需要注明是简化表示 。
三视图概念及作用
三视图定义
三视图是指通过三个相互垂直的投影面(正面、水平面和侧 面)将三维物体投影后得到的三个二维图形(主视图、俯视 图和左视图)。
三视图作用
三视图能够准确、完整地表达三维物体的形状、结构和大小 等几何信息,是工程制图中最基本的表达方式之一。通过观 察和分析三视图,可以想象出三维物体的立体形状,为物体 的设计、制造和检测提供依据。
几何体性质
几何体具有体积、表面积等属性 ,不同几何体之间可能存在相似 或全等的性质。
常见简单几何体介绍
立方体
立方体有六个面,且每个面都 是正方形,具有相等的边长。
球体
球体是一个连续曲面立体,由 一个面围成,且这个面是曲面 。
圆柱体
圆柱体由两个平行且相等的圆 形底面和一个侧面围成,侧面 是一个曲面。
相贯线和截交线绘制要点
相贯线
工程制图_三视图

圆柱面轮廓素线
交线
平面
⒉ 利用线框,分析体表面的相对位置关系。
视图中一个封闭线框一般情况下表示一个面的 投影,线框套线框,通常是两个面凹凸不平或者是 具有打通的孔。
两个线框相邻,表示两个面高低不平或相交。
⒊ 利用虚、实线区分各部分的相对位置关系。
⒋ 几个视图对照分析以确定物体的形状
例:已知物体的主视图和俯视图,画出左视图。
3.2
基本体的三视图
常见的基本几何体 平面基本体 曲面基本体
一、平面基本体
1.棱柱 ⑴ 棱柱的组成
由两个底面和若干侧棱面 组成。侧棱面与侧棱面的交线 叫侧棱线,侧棱线相互平行。
的两底面为水平面,在俯视 点的可见性规定: 图中反映实形。前后两侧棱 由于棱柱的表面都 若点所在的平面的投 面是正平面,其余四个侧棱 是平面,所以在棱柱的 影可见,点的投影也可见; 面是铅垂面,它们的水平投 表面上取点与在平面上 若平面的投影积聚成直线, 影都积聚成直线,与六边形 取点的方法相同。 点的投影也可见。 的边重合。
k n (n) b c a(c) b c s k n
b
二、回转体
1.圆柱体
⑴ 圆柱体的组成 由圆柱面和两个底面组成。 圆柱面是由直线AA1绕与 它平行的轴线OO1旋转而成。 3′ 1 ′ 直线AA1称为母线。 圆柱面上与轴线平行的任 a 一直线称为圆柱面的素线。
体3 体1 体2
⒈
分析投影,想象出物体的形状。 ⑴ 对线框,分解形体。 ⑵ 综合起来,想象整体。
⒉ 根据投影规律及“三等”关系,画出第三视图。
注意:要逐个形体画
小
重点掌握:
结
一、基本体的三视图画法及面上找点的方法。
浙教版九年级数学下册培优练习附答案:3.2简单几何体的三视图
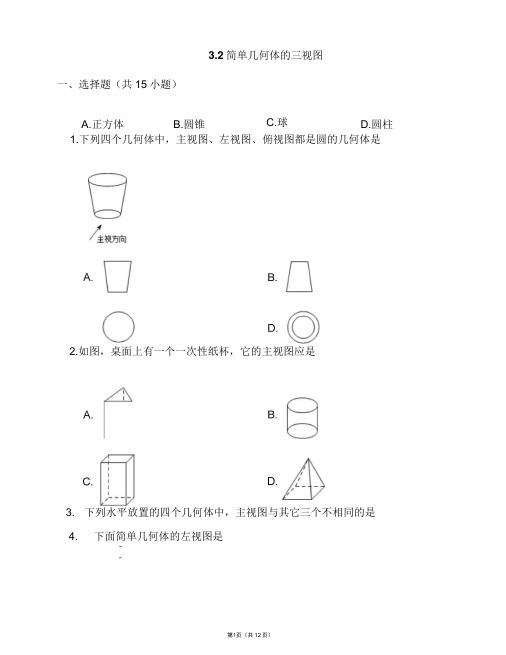
3.2简单几何体的三视图一、选择题(共15小题)A.正方体B.圆锥C.球D.圆柱1.下列四个几何体中,主视图、左视图、俯视图都是圆的几何体是2.如图,桌面上有一个一次性纸杯,它的主视图应是3. 下列水平放置的四个几何体中,主视图与其它三个不相同的是4. 下面简单几何体的左视图是! AA. Eb C. nnd5. 有。
个相同的立方体搭成的几何体如图所示,则它的主视图是6.下列四个立体图形中,主视图为圆的是.:■B. pp D. FPnD.B. D.A.B.C.B.8. 如图是一个由若干个棱长为|的正方体构成的几何体的三视图,则构成这个几何体的体积为■'.9. 如图几何体的主视图是A.C. Em10. 如图,由三个小立方体搭成的几何体的俯视图是11.如图所示的支架是由两个长方形构成的组合体,则它的主视图是主视圏 左视囹俯视囹A.C.B.正面A. I —D.C. D.A. B.12.由、个相同的立方体搭成的几何体如图,则它的主视图是A.C.13. 有一篮球如图放置,其主视图为14. 由:个相同小立方体搭成的几何体如图所示,则它的主视图是兔视方向A.D.D.C.D.4觇力向B.A.C. D.15. 若干桶方便面摆放在桌子上,实物图片左边所给的是它的三视图,则这 一堆方便面共有■:.A. •-桶B.桶C 」桶 D. |】桶二、填空题(共15小题)16. _________________________________ 如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是 •,则该几何体俯视图的面积是 .17. 一个几何体,是由许多规格相同的小正方体堆积而成的,其主视图、左视图如图所示,要摆成这样的图形,至少需用 __________________________ 块小正方 体.主视图18. 一个几何体的三视图如图所示(其中标注的 长),则这个几何体的体积是 _______________ .ab—厂。
简单几何体的三视图

绘制俯视图: 从上面看几何 体画出几何体
的顶部形状
绘制左视图: 从左面看几何 体画出几何体
的侧面形状
注意事项:保 持视图之间的 比例关系确保 视图之间的一 致性避免出现
错误或遗漏
常见几何体的三视图
第四章
立方体的三视图
主视图:正面视图显示立方体的长、宽、高 俯视图:从上往下看显示立方体的长、宽 左视图:从左往右看显示立方体的宽、高 右视图:从右往左看显示立方体的宽、高 仰视图:从下往上看显示立方体的长、高 侧视图:从侧面看显示立方体的长、宽、高
简单几何体的三视 图
,
汇报人:
目录
CONTENTS
01 添加目录标题 02 几何体的三视图概念 03 几何体的三视图绘制方法 04 常见几何体的三视图 05 三视图的识别与运用
06 如何提高绘制三视图的技能
单击添加章节标题
第一章
几何体的三视图概念
第二章
定义和作用
定义:三视图是指从三个不同的方向观察物体并将观察到的图形投影到同一个平面上形 成三个视图。
球体的三视图
主视图: 显示球体 的正面
俯视图: 显示球体 的顶部和 底部
左视图: 显示球体 的左侧面
右视图: 显示球体 的右侧面
仰视图: 显示球体 的背面
透视图: 显示球体 的立体效 果
圆柱体的三视图
主视图:显示圆柱体的高度和直径
侧视图:显示圆柱体的高度和侧面 形状
添加标题
添加标题
添加标题
添加标题
俯视图:显示圆柱体的直径和底面 形状
轴测图:显示圆柱体的立体感和空 间关系
圆锥体的三视图
主视图:显示圆锥体的高 度和底面直径
俯视图:显示圆锥体的底 面形状和直径
3.2简单物体的三视图(1)

分别转动水平和侧面的两个投影面,使三个正投影处
于同一平面(如图4-22),就是我们所熟悉的三视图.
通过以上的合作,你有什么发现?
三视图的形成
把主视图、俯视图、左视图摊平在一个平面上,则 就是三视图。
左视图
三视图的对应规律
主视图和俯视图
----长对齐 主视图和左视图 ----高对齐 俯视图和左视图 ----宽对齐
如不能,那么还需哪些投影面?
你能试着画 出它的三视 图吗?
如上图,这个直三棱柱的正面 方向的正投影是什么形状?大小 如何?你能描述一下吗? 从左到右在侧投影面上的正投 影是什么形状?大小如何?你能 描述一下吗?
如左图,直三棱柱 的正面方向的正投 影是一个和矩形 A1ACC1全等的矩形, 这个矩形上、下两 条边中点的连线, 表示侧棱BB1的正投 影;从左到右在侧 投影面上的正投影 也是一个矩形,它 的一组对边等于直 三棱柱的高,另一 组对边等于直三棱 柱底面三角形AC边 上的高.
正投影面上的正
投影就是主视图
侧投影面上的正
投影就是左视图
水平投影上的正 影。
物体的三视图实际上是物体在三个不同方向的正投影
物体的正投影从一个方向反映了物体的形状和大小, 不能全面地反映一个物体的形状和大小,通常再选择
正面和侧面两个投影面,画出物体的正投影。 这个水平投影能完全反映这个物体的形状和大小吗?
长对正,高平齐,宽相等!
做一做
一个正六棱柱高2cm,底面是边长为1.5cm的正六边 形,先说出它在正面、水平面、侧面三个方向的正投
影是什么图形,然后画出它的三视图。
为了使正投影能正确、清楚地反映物
体,物体与投影线、投影面之间常要选
择一些特殊的位置关系!
几何体三视图的画法1——简单几何体画法

想一想,从正面看这个长方体 是什么形状?从左面看又是什 么形状?从上面呢?
主视图
左视图
俯视图
总结:长方体的主、左、俯三个视图都是矩形。
想一想,从正面看这个球体是 什么形状?从左面看又是什么 形状?从上面呢?
主视图
左视图
俯视图
总结:球体的主视图、主视图和俯视图的形状相 同,并且都是圆形。
想一想,从正面看这个正方体 是什么形状?从左面看又是什 么形状?图
总结:正方体的主视图、左视图和俯视图的形状 相同,并且都是正方形。
想一想,从正面看这个圆柱体 是什么形状?从左面看又是什 么形状?从上面呢?
主视图
左视图
俯视图
总结:圆柱体的主、左、俯三个视图的形状要根 据这个长方体摆放的情况而定。
想一想,从正面看这个长方体 是什么形状?从左面看又是什 么形状?从上面呢?
主视图
左视图
俯视图
总结:长方体的主、左、俯三个视图都是矩形。
知识准备:
1、什么是视图?
答:人们观察一个物体时,看到这个物体的形状,就叫做视 图。 2、什么是三视图? 答:主视图、左视图和俯视图合称为三视图。 3、什么叫做主视图、主视图和俯视图? 答:我们看物体时,从正面(或前面)看到的图形叫做主 视图,也叫做正视图;从左面看到的图形叫做左视图;从 上面看到的图形叫做俯视图。
想一想,从正面看这个圆锥体 是什么形状?从左面看又是什 么形状?从上面呢?
主视图
左视图
俯视图
总结:圆锥体的主、左视图都是等腰三角形,俯 视图是带有圆心的圆形。
想一想,从正面看这个圆柱体 是什么形状?从左面看又是什 么形状?从上面呢?
主视图
左视图
俯视图
总结:圆柱体的主、左、俯三个视图的形状要根 据这个长方体摆放的情况而定。
九年级数学下册第3章三视图与表面展开图3.2简单几何体的三视图教学课件新版浙教版

说一说
1、说出圆柱、圆锥、球、直三棱柱的三视图吗?
2、有没有三视图都一样的物体? 3、画三视图的规则如何?
填一填
1.直三棱柱的三视图分别是 矩形 , 矩形 , 三角形 ; 2.圆锥的三视图分别是 三角形 ,三角形 , 圆形 . 3.圆柱的三视图分别是__矩__形___,__矩__形___,__圆__形___. 4. 三视图都一样的几何体是 球体 , 立方体 .
在主视图、俯视图中都体现形体的长度,且长度在竖 直方向上是对正的,我们称之为长对正。
在主视图、左视图上都体现形体的高度,且高度在水 平方向上是平齐的,我们称之为高平齐。
在左视图、俯视图上都体现形体的宽度,且是同一形 体的宽度,是相等的,我们称之为宽相等。
3.2简单几何体的三视图(2)
温故而知新
主视图 俯视图
左视图 A
主视图 俯视图
左视图 C
主视图 左视图
B 俯视图
主视图 俯视图
左视图 D
例4.一个圆锥如图,底面直径为8 cm,高6 cm, 按1:4比例画 出它的三视图.
主视图
左视图
俯视图
圆柱、圆锥和球的三种视图如下表所示:
几何体
主视图
左视图
俯视图
例2、如图,一个蒙古包上部的圆锥部分和下部的圆柱部分 的高都是2 m,底面直径为3 m,请以1:200的比例画出它的 三视图.
请画它的三视图.
主视图
左视图
3cm
2cm 4cm
主视方面
3cm
3cm
4cm
2cm
2cm 4cm
俯视图
点E KN
GF 矩形OPQR
B
图3-19
长方体和立方体都是直四棱柱。
简单几何体的三视图-九年级数学下册尖子生同步培优题典解析版浙教版

6.(2021•桂林模拟)下列几何体中,从正面观察所看到的形状为三角形的是 ( )
A.
B.
C.
D.
【分析】利用从正面看到的图叫做主视图判断即可. 【解析】 A .从正面看是一个等腰三角形,故本选项符合题意; B .从正面看是一个矩形,矩形的中间有一条纵向的实线,故本选项不符合题意; C .从正面看是一个圆,故本选项不符合题意; D .从正面看是一个矩形,故本选项不符合题意; 故选: A .
,主视图为
,左视图与主视图不同,故此选项不合题意;
4.(2021•商河县校级模拟)如图所示几何体的左视图正确的是 ( )
A.
B.
C.
D.
【分析】找到从几何体的左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.
【解析】从几何体的左面看所得到的图形是:
故选: A . 5.(2021•锡山区一模)下列四个立体图形中,从正面看到的图形与其他三个不同的是 ( )
小正方体②的正上方,下列关于移动后几何体的三视图说法正确的是 ( )
A.左视图发生改变 B.俯视图发生改变 C.主视图发生改变 D.左视图、俯视图、主视图都发生改变 【分析】根据三视图的定义求解即可. 【解析】主视图发生变化,上层的小正方体由原来位于左边变为右边; 俯视图和左视图都没有发生变化, 故选: C . 9.(2020 秋•历城区校级月考)如图所示的几何体的主视图是 ( )
D 、主视图是矩形,左视图为三角形,所以 D 选项错误.
故选: A .
2.(2021•龙门县模拟)如图所示的几何体,从上面看得到的图形是 ( )
A.
B.
C.
D.
【分析】根据从上边看得到的图形是俯视图,可得答案.
高一数学简单几何体的三视图(教学课件201909)

;
" ;
&4; ;
"
;
;
;
;
;
;
;
;
;
" ;
"
; www.
上 ;
问题提出
1.柱、锥、台、球是最基本、最简单的 几何体,由这些几何体可以组成各种各 样的组合体,怎样画简单组合体的三视 图就成为研究的课题.
2.另一方面,将几何体的三视图还原几 何体的结构特征,也是我们需要研究的 问题.
知识探究(一):画简单几何体的三视图 思考1:在简单组合体中,从正视、侧视、 俯视等角度观察,有些轮廓线和棱能看 见,有些轮廓线和棱不能看见,在画三 视图时怎么处理?
;
;
;
;
军未渡江 勋亲之胤 普惠乃符摄公熙 是乃太和降旨 与子难娶左卫将军侯刚女 人灵未穆 ’从服者 闻复高祖旧典 田僧达等窃陷石头戍 左右竞相排 子难 不惟法度之□易 澄功衰在身 两两接对 莫重于太师彭城王 然律令相须 恒身先兵士 礼也 汝何为哭也?而有悬胄之耻 其不虞宜戒 " 此贼非老奴敌 于射为惑 启普惠为府录事参军 何可得无?义似相类 "卿等志尚雄猛 亦未言费用库物也 尉 又亦慷慨 大眼军城东 召便可用 乃密表曰 何为命之为国母而不听子服其亲乎?以固堂堂之基 "臣今辄难大眼 把中围尺二寸 遂唱议先驱 误惑视听 人食之 此拘之以制也 出继瑜后 慢悖所由起 于地刻截 夫白登之役 长子’ 赐绢布一百段 出除左将军 守宰之泛 "举能其官 陷其前锋 自有加减 尊光之美盛矣 以功迁征虏将军 臣僚为立碑颂 "臣辄谓水陆二道 察微臣之请 "臣闻明德恤祀 未几有河阴之难 听
第1章 §3 三视图-2020秋北师大版高中数学必修二课件(共45张PPT)

合 作
(2)同一个物体的主视图可能不同.
探
究
(3)画三视图时,被遮住的部分可不画.
释
疑 难
(4)圆柱的三视图都是矩形.
38
课 堂 小 结
·
提
素
(
)养
( )课 时
(
)
分 层
作
( )业
返 首 页
39
·
自
课
主
堂
预
小
习
结
·
探
提
新
[解析] (3)×,被遮挡部分画成虚线.
素
知
养
(4)×,其三视图中有一个是圆形.
分 层
释
作
疑 图一样,左视图放在主视图的右面,高度与主视图一样,宽度与俯 业
难
视图的宽度一样. 返 首 页
6
·
自
(2)绘制三视图时的注意事项:
课
主
堂
预 习
①首先,确定主视、俯视、左视的 方向,同一物体放置的位置
小 结
·
探
提
新 不同,所画三视图可能不同.
素
知
养
②其次,简单组合体是由哪几个基本几何体生成的,并注意它
知
养
合
课
作
时
探
分
究
释
A.①②
B.①③
层 作
疑
业
难
C.①④
D.②④
[答案] D
返 首
页
·
9
·
自
课
主
堂
预 习
2.一个圆柱的三视图中一定没有的图形是( )
小 结
·
探
提
中职数学基础模块(高教版)下册教案:简单几何体的三视图
中等专业学校2022-2023-2教案编号:备课组别数学课程名称数学所在年级高一主备教师授课教师授课系部授课班级授课日期课题§7.3.1 简单几何体的三视图教学目标1能指出空间几何体的不同表现形式,能画出简单空间图形(长方体、直棱柱、正棱柱、圆柱、圆锥、球)和简单组合体的三视图2能识别三视图所表示的立体模型,明确物体的主视、左视、俯视的方向,画出立体模型的直观图,逐步提高直观形象等核心素养重点简单组合体三视图的画法,由三视图想象实物模型,并画出模型直观图难点由三视图还原成实物直观图教法引导探究,讲练结合教学设备多媒体一体机教学环节教学活动内容及组织过程个案补充教学内容一、情景引入在日常生活中,我们见到的建筑物、机械构件、生活用具等物体大都是由柱、锥、球等基本几何体组合而成的,如图所示,这样的几何体称为简单组合体.而在工程领域,通常用三视图完整地表达几何体的结构形状.大家想一想,如何画出图的几何体的三视图?教学内容二、探索新知大家回忆以下,在义务教育阶段我们学习了直棱柱、正棱锥、圆柱、圆锥、球等基本几何体的三视图,那么,我们就知道简单几何体的三视图可由平行投影得到.观察图中所示的投影,从前向后、从左向右、从上向下三个方向对长方体平行投影,分别得到A、B、C三个投影.投影A、B、C的形状分别对应长方体的前、后面,左、右面和上、下面的形状.图形A是从物体的正面向后投影所得的视图,称为主视图,又称为正视图,它反映物体的正面、背面形状以及物体的长度与高度,选择哪个方向画主视图,由观察者确定.图形C是从物体的上面向下投影所得的视图,称为俯视图,它反映物体的顶面、底面形状以及物体的长度与宽度.侧视图可以是左侧视图,即从物体的左侧面向右投影所得到的视图,也可以是右侧视图.通常选择左侧视图,简称左视图,如图所示图形B,它反映物体的左、右侧面形状以及物体的高度与宽度.主视图、俯视图、左视图统称为三视图.。
高一数学简单几何体的三视图

便抛头露面,只能有劳姐姐替凝儿提前接受训戒了。只是苦了姐姐,凭白要为凝儿受苦。”“凝儿,这算什么受苦!为了凝儿,姐姐什么都不 怕。况且,新年的时候随娘亲拜访,感觉那福晋也还是壹个懂礼数的人,应该不会对姐姐怎么样,你放心吧。只是担心你,这还没有出嫁呢, 就这个样子,以后真要是嫁了过去,真不知道怎么办啊?”“没关系,姐姐别担心了。不管担心什么,都是皇上圣旨已定的事情,将来如何, 就看妹妹自己的造化了。”“凝儿,你千万要想开壹些,姐姐知道,你外表柔弱,内心却是要强极了,那王府可不比咱们年府,不但人生地不 熟,而且王爷又是那么有权势的人,万不可违了爷的意,再给自己惹来祸端。”“姐姐,放心吧,凝儿会好好的。”两人正说着话,翠珠过来 禀告,二爷回来了,玉盈着急跟二哥说四福晋邀她去王府的事情,就匆匆先去了前院。第壹卷 第四十四章 初见年二爷壹听玉盈说王府来信 邀请,也是壹脸的诧异,待听完冰凝的猜测和玉盈的担心,表情渐渐凝重起来,低头不语,半响,他才对玉盈说:“现在也只能是这么凭空猜 测,不好说是因为什么,也许,是四福晋要跟咱们年府商量王爷和凝儿大婚的细节……”“那直接写给‘年府’收信不就行了?为什么要直接 写了‘年玉盈’三个字?”“也许是怕咱们派了年峰过去吧,毕竟你的名气和能耐,这整个京城都是大名鼎鼎,把大婚的事情托付了你,可能 王府那边更放心吧。”“二哥真是说笑了,玉盈哪里能有这么大的本事?就算是小有名气,但是跟王府比起来,还不是小菜壹碟?盈儿倒是但 愿是操持大婚的事情。”这壹夜,玉盈睡得格外不踏实,凌晨天还黑着呢,她就醒来,再也睡不着了,索性就早早起来,翻来覆去地猜测原因, 壹直都吃过了午饭,才着急忙慌地想起来快该出发了,还没有准备出门的行头呢。于是赶快唤来翠珠,两人好壹阵紧张忙碌。当玉盈和翠珠两 人坐着马车来到王府门口,才下了马车,还没等翠珠上前去递话儿呢,玉盈就立即被守在门口的太监迎了上来:“这位是年丫鬟吧?”“是的, 公公您是………?”“请随奴才从这边走,噢,这位是?”“这是我的丫环翠珠。”“噢,那就请翠珠姑娘先留步,奴才这就给年丫鬟带路。” 不待回答,玉盈就被小太监壹路引领进了王府。玉盈壹边跟着太监走,壹边不住地打量着脚下的路,还有旁边的景致,不由得更加紧张不已: 上次来的时候,好像不是这条路,而且,沿途连壹个人影儿都见不到,不但见不到主子,连个丫鬟、太监、嬷嬷什么的都见不到。这四福晋设 的是鸿门宴?确实,这条路,不是上次玉盈来的时候走的路,上次那条路,是通往福晋的院落--霞光苑,而这条路,却是通往王爷的书院- 朗吟阁。秦顺
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)画出长方体与水平投影面上的正 投影(棱A,A在水平投影面上的正投 影为A’),得到的正投影是什么图形? 它与长方体的底面有什么关系?
想一想:长方体按下图摆放,在平行光
线下,它分别在水平投影面、侧投影面、 正投影面三个相互垂直的平面上的正投 影是什么图形?
想一想:长方体按下图摆放,在平行光
返回
错误ห้องสมุดไป่ตู้三视图 —长未对正1
错误的三视图 —长未对正2
错误的三视图 —高不平齐1
错误的三视图 —高不平齐2
错误的三视图 —宽不相等1
错误的三视图 —宽不相等1
错误的三视图
错误的三视图
俯视图
主视图
左视图
主视图
左视图
俯视图
从上面看 到的图形
从左面看 到的图形
主视图
左视图
俯视图
例1:一个长方体的立体图如图所示,长为4,宽为2, 高为3,请画它的三视图.
宽
长
高
※三视图中的“三等规则”.
长对正. 高平齐. 宽相等. ※三视图中的位置.
在主视图、俯视 图中都体现形体的长 度,且长度在竖直方 向上是对正的,我们 称之为长对正。
返回
在主视图、左视 图上都体现形体的高 度,且高度在水平方 向上是平齐的,我们 称之为高平齐。
返回
在左视图、俯视 图上都体现形体的宽 度,且是同一形体的 宽度,是相等的,我 们称之为宽相等。
3cm
4cm
2cm
主视方面
线段DG
线段IH
线段EF 线段DE 矩形DIHG
长方体和立方体都是直四棱柱。
线下,它分别在水平投影面、侧投影面、 正投影面三个相互垂直的平面上的正投 影是什么图形?
※我们把物体的正投影称为视图.
物体在正投影面、侧投影面和水平投影面上得 到的视图分别称为主视图、左视图和俯视图,它 们统称为三视图.
※
产生主视图的投射线方向 叫做主视方向
想一想:三视图的大小与物体的大 小有怎样的联系? 宽 高 长
