九年级数学画角平分线
人教版初中数学《角的平分线的性质》_完美课件

交OA于点M,交OB于点N
尺规法画角平分线
A M
C
O
NB
分别以点M,N为圆心,大于½MN的长度为半径画
弧,两弧在∠AOB的内部交于点C
尺规法画角平分线
A M
C
O
NB
画射线OC,即为∠AOB的角平分线
思考和交流
• 在你刚才画好的角平分线OC 上任意取一点P,过点P画出 OA和OB的垂线段,分别记 垂足为D,E。PD和PE的长 度有什么关系?
• 在OC上再取几个点试一下, 并和你的伙伴交流结论,你 们发现角平分线有什么性质?
思考和交流
• 经过测量,PD=PE总成立。 • 经过讨论,我们猜想: • 角分线上的点到角两边的距
离相等。
你能用全等三角 形证明吗?
怎样证明几何命题?
• 证明几何命题,先明确已知和求证。
– 已知:一个点在一个角的平分线上。 – 求证:这个点到这个角两边的距离相等。
角分线上的点到角两边的距离相等
A D
∵OC平分∠AOB,
O
P C PD⊥OA,PE⊥OB
∴PD=PE
EB
动脑想一想
• 如图,要在S区建一个 集贸中心,使它到铁路、 公路的距离相等,并且 离公路与铁路的交叉处 500m,这个集贸中心应 建在哪里?
动脑想一想
• 角分线上的点到角两边的距离相等。 • 到角的两边的距离相等的点是否也在角的
DC=BC(已知) ∴ △ADC≌△ABC (SSS) ∴∠DAC=∠BAC(对应角相等) 即 AE平分∠BAD
动脑想一想
• 通过刚才的启发,你能想到怎样画出下面 的角的平分线吗?
A
仅用尺规作图,
已知∠AOB,
求作∠AOB的
初中数学 如何画出一个角的平分线

初中数学如何画出一个角的平分线
要画出一个角的平分线,我们可以采用以下步骤:
步骤1:准备工作
在纸上用直尺绘制一个角。
我们可以使用直尺的一条边作为角的一条边,然后用另一条边延长出来作为另一条边。
确保角的两边相交于一个顶点。
步骤2:确定角的平分线的起点
在角的顶点处,使用直尺绘制一条线段,作为平分线的起点。
这个起点可以是任意长度,只需确保它足够长以后续步骤的绘制。
步骤3:以顶点为中心,绘制一个圆弧
以角的顶点为中心,使用指定的半径,在角的两个边上各绘制一个圆弧。
这两个圆弧应该相交于一个点,这个点将成为平分线与角的顶点相交处。
步骤4:以圆弧相交点为半径,作两个圆弧
以圆弧相交点为圆心,以相同的半径作两个圆弧。
这两个圆弧应该分别与角的两个边相交,分别在两个边的延长线上。
步骤5:连接起点和两个相交点
使用直尺连接平分线的起点与两个圆弧相交点,分别得到与角的两个边相交的点。
这两个点将成为平分线与角的两个边相交处。
步骤6:连接起点和角的顶点
使用直尺连接平分线的起点与角的顶点,得到平分线的终点。
至此,我们成功地画出了角的平分线。
需要注意的是,如果角的两边相交于一个直角或钝角的顶点,那么平分线的绘制将稍有不同。
在这种情况下,我们需要将角的两边延长,使其相交于一个锐角的顶点,然后按照上述步骤进行绘制。
总结起来,画出一个角的平分线的步骤包括准备工作、确定平分线的起点、绘制圆弧、连接起点和圆弧相交点、连接起点和角的顶点。
通过这些步骤,我们可以准确地画出角的平分线。
专题08 三角形中的重要模型-平分平行(平分射影)构等腰、角平分线第二定理模型

三角形中的重要模型-平分平行(平分射影)构等腰、角平分线第二定理模型角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各大模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,,本专题就角平分线的非全等类模型作相应的总结,需学生反复掌握。
平分平行(射影)构等腰模型、角平行线第二定理模型(内角平分线定理和外角平分线定理模型) 模型1、平分平行(射影)构等腰1)角平分线加平行线必出等腰三角形.模型分析:由平行线得到内错角相等,由角平分线得到相等的角,等量代换进行解题.平行线、角平分线及等腰,任意由其中两个条件都可以得出第三个。
(简称:“知二求一”,在以后还会遇到很多类似总结)。
平行四边形中的翻折问题就常出现该类模型。
图1 图2图3 条件:如图1,OO ’平分∠MON ,过OO ’的一点P 作PQ//ON. 结论:△OPQ 是等腰三角形。
条件:如图2,△ABC 中,BD 是 ∠ ABC 的角平分线,DE ∥ BC 。
结论:△BDE 是等腰三角形。
条件:如图3,在中,平分,平分,过点O 作的平行线与,分别相交于点M ,N .结论:△BOM 、△CON 都是等腰三角形。
2)角平分线加射影模型必出等腰三角形.→图4条件:如图4,BE 平分∠CBA ,∠ACB =∠CDA =90°. 结论:三角形CEF 是等腰三角形。
ABC !BO ABC ÐCO ACB ÐBC AB AC FCDE××○○×线交于点.若,则的度数为( )A .B .C .D .例2.(2023.湖南长沙八年级期中)如图,点O 为△ABC 的∠ABC 和∠ACB 的平分线的交点,OD // AB 交BC 于点D , OE // AC 交BC 于点E .若AB =5 cm ,BC =10 cm ,AC =9 cm ,则△ODE 的周长为( )A .10 cmB .9 cmC .8 cmD .5 cm例3.(2023·广东·八年级期末)如图,▱ABCD 中,AB =3cm ,BC =5cm ,BE 平分∠ABC 交AD 于E 点,CF 平分∠BCD 交AD 于F 点,则EF 的长为 cm .例4.(2023.成都市青羊区八年级期中)如图,在中,,于点D ,的平分线BE 交AD 于F ,交AC 于E ,若,,则_____________.例5.(2023.山东八年级期末)如图①,△ABC 中,AB =AC ,∠B 、∠C 的平分线交于O 点,过O 点作EF ∥BC 交AB 、AC 于E 、F .(1)图①中有几个等腰三角形?猜想:EF 与BE 、CF 之间有怎样的关系.(2)如图②,若AB ≠AC ,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF 与BE 、CF 间的关系还存在吗?(3)如图③,若△ABC 中∠B 的平分线BO 与三角形外角平分线CO 交于O ,过O 点作OE ∥BC 交AB 于E ,交AC 于F .这时图中还有等腰三角形吗?EF 与BE 、CF 关系又如何?说明你的理由.AF 1l B 130BCA Ð=°1Ð20°25°30°50°ABC △90BAC Ð=°AD BC ^ABC Ð3AE =2DF =AD =ABF EDC模型2、角平行线第二定理(内角平分线定理和外角平分线定理)模型图1 图2图3例5.(2022秋·北京·八年级北京八十中校考期中)在中,D 是边上的点(不与点B 、C 重合),连接.(1)如图1,当点D 是边的中点时,_____;(2)如图2,当平分时,若,,求的值(用含m 、n 的式子表示);(3)如图3,平分,延长到E .使得,连接,若,求的值.ABC !BC AD BC :ABD ACD S S =△△AD BAC ÐAB m =AC n =:ABD ACD S S △△AD BAC ÐAD AD DE =BE 3,5,10BDE AC AB S ===△ABC S !课后专项训练1.(2023春·山东淄博·九年级校考期中)如图,中,,点I 为各内角平分线的交点,ABC !90ABC Ð=°ABC !11.(2023秋·安徽滁州·八年级统考期末)12.(2023.广东九年级期中)如图所示,在△ABC 中,BC =6,E 、F 分别是AB 、AC 的中点,动点P 在射线EF 上,BP 交CE 于D ,∠CBP 的平分线交CE 于Q ,当CQ =CE 时,EP +BP =________.13.(2023春·山东淄博·七年级统考期末)如图,在中,,是斜边上的高,的平分线交于点,交于点.(1)求证:是等腰三角形.(2)若,.求的长度.14.(2023秋·江苏·八年级专题练习)如图,在中,,是边上的高,是的角平分线,与交于点,求证:是等腰三角形.15.(2023广东江门八年级月考)(1)如图1,已知,在中,,平分,平分,过点作,分别交、于、两点,则图中共有________个等腰三角形:与、之间的数量关系是________,的周长是________.(2)如图2,若将(1)中“中,”改为“若为不等边三角形,,”其余条件不变,则图中共有________个等腰三角形;与、之间的数量关系是什么?证明你的结论,并求出的周长.13ABC !90ACB Ð=°CE AB ABC ÐBD CE M AC D CDM V 10AB =8AC =ME ABC !90ACB Ð=°CD AB AE BAC ÐAE CD F CEF △ABC !10AB AC ==BD ABC ÐCD ACB ÐD EF BC AB AC E F EF BE CF AEF △ABC !10AB AC ==ABC !8AB =10AC =EF BE CF AEF △(3)已知:如图3,在外,,且平分,平分的外角,过点作,分别交、于、两点,则与、之间又有何数量关系呢?写出结论并证明.16.(2022秋·福建厦门·八年级厦门市湖里中学校考期中)如图,为的角平分线.(1)如图1,若于点,交于点,,.则________; (2)如图2,若,,的面积是10,求的面积;(3)如图3,若,,,请直接写出的长(用含,的式子表示)D ABC !AB AC >BD ABC ÐCD ABC !ACG ÐD DE BC AB AC EF EF BE CF AD ABC D CE AD ^F AB E 7AB =5AC =BE =7AB =5AC =ACD D ABC D 2C B Ð=ÐAB m =AC n =BD m n。
【数学课件】角平分线的性质(1)

A
E D
B
C
练一练
2. 在△ABC中,AC⊥BC,AD为∠BAC的 平分线,DE⊥AB,AB=7㎝,AC=3㎝,求 BE的长。
A
E
C
B
D
在∠AOB的平分线 OC上任取一点P,然后, 作点P到∠AOB两边的 垂线段PD、PE,画一 画,量一量,从中你有 什么新发现?你能说明 其中的道理吗?
几何语言:
∵OC是∠AOB的平分线,
A
D C
PD⊥OA,PE⊥OB
∴PD=PE
B
P
·
E
O
一起来证明这个性质:
已知: ∠AOC= ∠BOC,点P 在OC上, PD ⊥OA,PE ⊥OB, 求证: PD=PE
证明:
C
A D
证明一个几何命题的步骤: 1. 2. 3.
(课本21页)
P
·
E
O
B
1. 在Rt△ABC中, ∠C 为直角,BD平分 ∠ABC,DE⊥AB于E,则:
好好学习,天天向上。
角平分线上的点到角两边 的距离相等。
从这节课中你 有哪些收获?
课堂小测
• 堂堂清
作 业
• 1.课本22页第2题。(作业本) • 2.练习册 • 3.预习教材21页。自学例题并思考点P在角 A的平分线上吗? • 能力提升题:
课本23页第5题。(作业本)
1、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之毁灭。——卢梭 2、教育人就是要形成人的性格。——欧文 3、自我教育需要有非常重要而强有力的促进因素——自尊心、自我尊重感、上进心。——苏霍姆林斯基 4、追求理想是一个人进行自我教育的最初的动力,而没有自我教育就不能想象会有完美的精神生活。我认为,教会学生自己教育自己,这是一种 最高级的技巧和艺术。——苏霍姆林斯基 5、没有时间教育儿子——就意味着没有时间做人。——(前苏联)苏霍姆林斯基 6、教育不是注满一桶水,而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基 8、教育的根是苦的,但其果实是甜的。——亚里士多德 9、教育的目的,是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——(前苏联)苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美,人的关系的美而看到的精神的高尚、善良和诚实,并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知,而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品,就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心,这种道德上的自勉。要是儿童自己不求上进,不知自勉,任何教育者就都不能在他的身 上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方,儿童才会产生上进心。——苏霍姆林斯基 17、教育能开拓人的智力。——贺拉斯 18、作为一个父亲,最大的乐趣就在于:在其有生之年,能够根据自己走过的路来启发教育子女。——蒙田 19、教育上的水是什么就是情,就是爱。教育没有了情爱,就成了无水的池,任你四方形也罢、圆形也罢,总逃不出一个空虚。班主任广博的爱 心就是流淌在班级之池中的水,时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么,但它能启发儿童创造力以从事于创造工作。——陶行知
初中数学角平分线问题的六种方法

初中数学角平分线问题的六种方法
角平分线是指将一个角分成两个相等的角的线。
在初中数学中,有六种常见的方法可以求解角平分线问题。
方法一:作弧上的等分线法
以角的顶点为圆心,画一个圆,并将圆分成需要的等分数。
然后将等分点和角的两个端点相连,这些线段就是所求的角平分线。
方法二:作垂线法
以角的一边为直径作一个圆,然后将另一边的端点与圆上的点连成线段。
连接角的两个顶点与圆心,这两条线段就是所求的角平分线。
方法三:作过顶点的角平分线法
以角的顶点为圆心,任意作一个大于角的两边的弧,将弧上的两个点与角的两个端点连成线段。
连接圆心与弧的两个端点,这两条线段就是所求的角平分线。
方法四:作等距离线段法
以角的一边为直径作一个圆,在圆上选择等距离原点的多个点,然后将这些点与角的两个端点连成线段。
与角度相等的线段即为所求的角平分线。
方法五:作锐角三等分线法
将角分成三个相等的锐角,然后以这三个锐角的顶点为圆心,分别作三个圆。
连接圆心与圆上的点,这些线段即为所求的角平分线。
方法六:利用角度性质法
利用角的度数关系来求解角平分线。
如果角的两边垂直,则角平分线就是两边的垂线;如果角的两边相等,则角平分线就是两边的中垂线;如果角的两边呈比例关系,则角平分线是两边之比的垂线。
以上六种方法是初中数学中常见的角平分线求解方法。
每种方法都有其独特的应用场景,根据题目给出的条件,选择合适的方法来求解即可。
同时,理解角平分线的定义和性质,掌握角的几何构造技巧,也能在解决问题中起到很好的帮助作用。
画角平分线PPT教学课件

方法: 搜集一些关于鸟的歌曲,并学唱。如歌曲《飞吧,鸽子》。
4、鸟与科学
方法: 阅读《古鸟化石》、《飞机与鸟》、《鹰眼的启示》等文章,也可再搜集些类似 的资料,谈谈鸟给人类科学研究带来的启发。
5、鸟文化博览会
方法: 用一节课的时间来展示学生的探究成果。如:诗歌朗诵、歌曲、 绘画、文学短评 集、话题讨论“人与鸟”等。
爱护大自然
的每一个生命, 也是给我们多留 一份生存的空间。
活动过程
1、鸟与美学——欣赏鸟的体形美、色彩 美、鸣声美、飞翔的姿态美以及鸟所具 有的人性美
方法:①亲自饲养鸟儿,进行零距离观察;
②欣赏图片、录像。(推荐新纪录片《鸟 的迁徙》)
③谈谈自己最欣赏鸟的什么美,为什么。
2、鸟与文学
方法: 1、搜集写鸟的精彩片段或古诗句进行积累并诵读。 2、欣赏配乐散文《鸟的故事》、《珍珠鸟》,写文学短评。 3、阅读《鸽子》和《空山鸟语》,完成书上的习题。
顶角∠BAC=∠α, ∠BAC的平 分线为m。
m
• 已知△ABC中,∠A=900,
• 求作⊙P,使圆心P在AC上,且 与AB、BC的两边都相切。
C
A
B
• 说说本节你的收获、体会、疑 惑
鸟
自
然
专 题
精
探 究
灵
方
案
活动目的
1、对鸟的种类、形态特征、生活 习性、生存状态能有一些了解。 2、能从观鸟的过程中获得美感。 3、能继续训练想象能力。 4、能正确认识鸟与人的关系。
尺规作图画角平分线
九年级数学组
复习
• 看图填空。 • (1)在
上截取
•
=
=
;
(2)以
九年级数学画角平分线

O
B
D
求作一个角等于已知角POQ,
• 作法:(1)作
O1P1;
• (2)以O为圆心,以
交
;交
作弧, ;
• (3)以为圆心,以
交
;
作弧,
• (4)以 径作弧,交
为圆心,以
半
ቤተ መጻሕፍቲ ባይዱ
;
• (5)经过
作
即为所求的角。
。则
A C
O
B
D
; 优游新闻网
;
其中插着一只箭。父亲郑重对儿子说:“这是家袭宝箭,配带身边,力量无穷,但千万不可抽出来。” 那是一个极其精美的箭囊,厚牛皮打制,镶着幽幽泛光的铜边儿,再看露出的箭尾。一眼便能认定用上等的孔雀羽毛制作。儿子喜上眉梢,贪婪地推想箭杆、箭头的模样,耳旁仿 佛嗖嗖地箭声掠过,敌方的主帅应声折马而毙. 果然,配带宝箭的儿子英勇非凡,所向披靡。当鸣金收兵的号角吹响时,儿子再也禁不住得胜的豪气,完全背弃了父亲的叮嘱,强烈的欲望驱赶着他呼一声就拔出宝箭,试图看个究竟。骤然间他惊呆了。 一只断箭,箭囊里装着一 只折断的箭。 我一直刳着只断箭打仗呢!儿子吓出了一身冷汗,仿佛顷刻间失去支柱的房子,轰然意志坍塌了。 结果不言自明,儿子惨死于乱军之中。 拂开蒙蒙的硝烟,父亲拣起那柄断箭,沉重地啐一口道:“不相信自己的意志,永远也做不成将军。” 62、尚未凝 固的水泥路面 1899年爱因斯坦在瑞士苏黎世联邦工业大学就读时,他的导师是数学家明可夫斯基。 有一次,爱因斯坦问明可夫斯基:“一个人,比如我吧,究竟怎样才能在科学领域、在人生道路上,留下自己的闪光足迹、做出自己的杰出贡献呢?”这是一个“尖端”的问题, 明可夫斯基表示要好好想一想日后予以解答。三天后,明可夫斯基告诉爱因斯坦答案来了!他拉起爱因斯坦就朝一处建筑工地走去,而且径直踏上了建筑工人们刚刚铺平的水泥地面。在建筑工人们的呵斥声中,爱因斯坦被弄得一头雾水,不解地问明可夫斯基:“老师,您这不是领我误入 ‘歧途’吗?”“对、对,正是这样!”明可夫斯基说:“看到了吧?只有尚未凝固的水泥路面,才能留下深深的脚印。那些凝固很久的老路面,那些被无数人、无数脚步走过的地方,你别想再踩出脚印来……”听到这里,爱因斯坦沉思良久,意味深长地点了点头。 从此,一种非 常强烈的创新和开拓意识,开始主导着爱因斯坦的思维和行动。用他自己的话说就是,“我从来不记忆和思考词典、手册里的东西,我的脑袋只用来记忆和思考那些还没载入书本的东西。”于是,就在爱因斯坦走出校园,初涉世事的几年里,他作为伯尔尼专利局里默默无闻的小职员,利 用业余时间进行科学研究,为人类做出了卓越的贡献,在科学史册上留下了深深的闪光的足迹。 63、闲话图书馆 中国一向只有藏书楼。不管是官家的还是私家的,重点都在“藏”,看,是其次的。天一阁大大有名,不要说外人,就是范家的人,要上楼也不容易。据说一位女子 因歆羡其藏书,嫁到了范家,结果也未能登楼入室、一饱眼福,终于饮恨而终。这样把书藏起来,与无书何异? 大概受了藏书楼式管理的影响,中国有了公共图书馆之后,在管理方法上也大体是主藏。“馆藏”若干,“善本”若干,是炫耀的资本。至于借阅,手续之繁复,条件之 苛刻,几乎是一贯的。更有甚者,把公共的资源当成了单位牟利的手段。 那年去旧金山,因为逗留时间稍长,办了一张市图书馆的阅览。办极简单,拿着护照,到借阅处一登记,那里输入电脑,随即就递过了借阅。这可以在旧金山市的十几个社区图书馆通用,每次可以借阅一二十 本书,借阅时间也很宽裕,从容看完,无人催索。图书完全开架,任你自选。还书更为方便,每家图书馆门外都有一个大方桶,略似邮筒而体积更大,投口也大。不论在哪家借的书,还的时候只要投入你最为方便的一个还书筒中即可,无需再办什么手续。图书馆每天有车收罗还书,分送 各馆。残疾人和年老行动不便的老人,需要借阅盲文或音像资料,打一个电话就有人送上门来。还的时候只需丢在邮筒里自会有邮递员送回。 我很少听到美国人说什么几条便民利民措施之类的话,但他们的各种公共事业似乎都明白一个道理:他们是为公众服务的,无论定什么制度, 立什么规矩,都是为了公众方便,而不是为了自己方便。比如图书馆,就要便利于读者借书和看书,而不是相反。令我诧异的是,为什么几乎天天把公众利益挂在嘴上的国人,一到办事的时候,似乎首先想到的是自己和小团体的利益与方便。公众呢?让他们麻烦去吧——这就不独图书馆 了。 64、一生 当你1岁的时候,她喂你并给你洗澡,而作为报答,你整晚哭着。 当你3岁的时候,她怜爱地为你做菜,而作为报答,你把一盘她做的菜扔在地上。 当你4岁的时候,她给你买下彩色笔,而作为报答,你涂了满墙的抽象画。 当你9岁的时候,她付了 很多钱给你辅导钢琴,而作为报答,你常常旷课并且从不练习。 当你14岁的时候,她付了你一个月的野营费,而你没有给她打一个电话。 当你18岁的时候,她为你高中毕业感动得流下眼泪,而你跟朋友聚会到明天。 当你19岁的时候,她付了你的大学学费又送你到学校, 你要求她在离校门口比较远的地方下车,怕被朋友看见会丢脸。 当你20岁的时候,她问你:“你整天去哪里?”而你回答:“我不想像你一样。” 当你23岁的时候,她给你买家具让你布置你的新家,而你对朋友说她买的家具真是糟糕。 当你30岁的时候,她对怎样照顾婴 儿提出劝告,而你对她说:“妈,现在的时代已不同了。” 当你40岁的时候,她给你打个电话告诉你有亲戚过生日,而你答她:“妈,我很忙,没时间。” 当你50岁的时候,她常患病,需要你的看护,你反而在读一本关于父母在孩子家寄身的书。 终有一天,她去世了。 突然你想起了所有从来没做过的事,它们像榔头痛击着你的心。 65、拒绝遗忘 面对上个世纪五六十年代中国所经历的许多充满暴力的政治运动,人们就“回忆还是忘却”的问题一直有着两种不同的观点。一种观点认为,悲惨痛苦的历史是不能遗忘的,因为只有通过时常的回忆 才能使人清醒,才能让人吸取教训。而另一种观点则认为,只有忘记不堪回首的历史,才有可能彻底放下包袱,然后再轻松地重新起步。而持后一种观点的大有人在。 在新著《关于我父母的一生》中,南帆以拒绝遗忘的态度将书写的对象指向了自己熟悉的父母:“父亲”放弃少爷 的舒适生活,积极投身于改天换代的革命,可是他却永远改变不了血缘的历史,于是革命的曙光到来之后,所遭受的便是怀疑、排挤、关押、批斗、下放农村……“母亲”因此跟着受牵连,整天担惊受怕;“我仨兄妹”随之受连累。而等到噩梦结束时,返城的父母因长年的惊吓而改变了 性格,变得沉默寡言、小心翼翼和谨慎处事,仿佛是自己亏欠了时代或别人什么东西。 历史不可能有假如,只存在如此。问题是我们对人为不正常的“如此一段历史”,常常缺少足够的反思精神和批判意识,甚至还有意无意地将其轻松地演义为一个个“激情燃烧的岁月”故事。只 要我们保持记忆和回忆,历史就不可能重演。但若是存在大面积的群体性失语和社会性遗忘,那就无法保历史不会重演。故而,面对沉默的大多数,我们当然需要巴金的《随想录》,需要韦君宜的《思痛录》,需要南帆的《关于我父母的一切》…… 66、乘奇而入 45年前,联邦 德国的福斯汽车公司准备入主美国汽车大市场,此前曾派出大批人马做了一番细致入微的市场调查研究。在调研中了解到:美国人最大的天性之一就是争强好胜,喜欢标新立异。 于是,他们特意设计生产出了一种造型奇特,犹如“金甲虫”状的微型小卧车,当年就畅销40余万辆, 打开了美国汽车营销大市场,增加了人们对福斯汽车的认可度。 6 7、乘高而入 日本东京滨松町一家新开张的咖啡屋,开张当日就在当地传媒打出了通栏广告:每杯咖啡售价5000日元,闻者无不大吃一惊,吃惊过后就登门看个究竟,一时间主顾如云。其实,5000日元一杯的高 价咖啡里有说道: 盛装咖啡的杯子是世界精品,每只售价都高达4000日元以上。喝完之后,杯子即归主顾。店家既能从饮料上取利,又能从杯子营销商那里提成,可谓慧眼独到。 68、乘热而入 一位叫帕特的美国推销员,经过很长时间的推销动作,终于就一套可供一座高 层办公大楼使用的空调系统,与买方达成了买卖意向书,面临的最后一关需要买方董事会的同意。帕特一出场,几位董事就提出了一连串尖端的问题。 帕特急中生智,说:“今天天气酷热,请允许我脱掉外衣。”董事们仿佛也受到感召似地纷纷脱去外衣,有的董事甚至抱怨:“这 里怎么没空调,闷死人了!”恰逢此时,帕特才开始介绍他的空调系统,生意立马拍板成交。 69、乘静而入 菲律宾有家餐馆生意一直很清淡,这家餐馆老板特意到周围的餐馆光顾一番后发现:这些餐馆清一色的现代装饰,使气氛格外火爆,食客出不少。于是这位老板就反其道 而行之,决定突出本餐馆与众不同的古朴、幽静的独家特色: 室内是白色房柱,座席被绿色植物簇拥,用印度的古战车送菜,莎士比亚时代的酒桶盛酒……此举一出,餐馆生意立马击败所有对手,迅速走红。 70、乘虚而入 日本国最大的森永与明治两家制糖公司,以前生 产的朱古力糖均以少儿为主流消费群体。后来森永公司根据成人特点,独家推出了“高王冠”朱古力糖,售价70日元。 而明治公司则采用乘虚而入的谋略作回应:推出了不同质量与价格的朱古力,每块40日元的面向十二三岁的中小学生,每块60日元的面向十七八岁的高中生,每块 100日元的面向中老年人……此举,使“明治”很快击败了“森永”。71、换只手 摩根是美国的大富豪,在他年轻携妻闯美国时,还是一个穷光蛋,为了生计,开了一家小杂货铺卖鸡蛋。摩根卖鸡蛋时发现顾客常常抱怨他的鸡蛋小。经过一段时间的观察总结,于是他让妻子来卖鸡蛋, 结果顾客不仅不嫌鸡蛋小,反而对摩根的态度和印象也大大改观了。 原因是摩根的手又粗又大,使鸡蛋相形见小。同是一个鸡蛋,放在一个女人的纤细手里和放在一个男人粗壮的手上,在购买者的视觉上,鸡蛋就不是同一个鸡蛋了。能够把鸡蛋放在纤细女人手上卖,“粗”与“细” 一颠倒,便顾客盈门,财源滚滚。 72、生命的立起 一只很小的虫子,能在没有水分的茫茫大漠一代代生存繁衍,我纳闷它们靠什么活着?看了电视上的一个自然类节目,让我再一次惦记起这些小生命,并对它们生出几分崇敬来。 清晨,小虫们早早起床,打开房门,一只 接一只地从沙丘底部它们的家爬上沙丘,
2025年九年级中考数学一轮考点复习课件:微专题四角平分线的常见辅助线作法

∴△CDE≌△CDF(SAS),
∴CE=CF,∴BC=BF+CF=AB+CE.
类型四
作平行线,构造等腰三角形
情形1:
条件
如图,点P是∠AOB的平分线上一点
示例
结论
PQ=OQ, △POQ是等腰三角形
情形2:
条件
如图,OC是∠AOB的平分线,点D是OA上的一点
示例
结论
OE=OD,△EOD是等腰三角形
长BD至点E,使ED=AD,连接CE.求证:BC=AB+CE.
证明:如图所示,在BC上取一点F使得BF=AB,连接DF.
∵∠A=100°,∠ABC=40°,
∴∠ACB=∠ABC=40°.
∵BD平分∠ABC,
∴∠ABD=∠FBD=20°.
= ,
在△ABD和△FBD中, Байду номын сангаас = ∠,
+ = .
类型二
遇角平分线的垂线,联想“三线合一”
条件 如图,点P是∠MON的平分线上一点,AP⊥OP于点P
示例
结论 Rt△BOP≌Rt△AOP,△AOB是等腰三角形,OP垂直平分AB
对点训练
3.如图,△ABC的面积为6,AP垂直∠ABC的平分线BP于点P,求△PBC的面
积.
解:如图,延长AP交BC于点E.
∵AC平分∠BAD,
∴∠BAC=∠EAC.
又∵AC=AC,
∴△BAC≌△EAC(SAS),
∴∠B=∠AEC,BC=EC.
∵∠D= ∠B,
∴∠D= ∠AEC,∴∠D=∠ECD,
∴CE=DE,∴BC=DE,
∴AD=AE+DE=AB+BC=4+2=6.
九年级数学角平分线

到一个角的两边的距 离相等的点,在这个 角的平分线上。
常见误区及纠正方法
01
误区一
认为角平分线就是角的对称轴。实际上,角平分线所在的直线是这个角
的对称轴,但角平分线本身不是对称轴。
02 03
误区二
认为角平分线将角所在的平面分成面积相等的两部分。实际上,这个结 论只在一些特殊情况下成立,例如当角是直角或角所在的三角形是等腰 三角形测量建筑物的角 度,利用角平分线的性质可以简化测量过 程并提高精度。
在地理定位中,可以利用角平分线判断两 个地点之间的相对方向,从而确定目标位 置。
军事领域中阵地布局
物理学中光线传播路径分析
在军事领域中,角平分线可用于阵地布局 和火力分配,提高作战效率。
在物理学中,光线传播遵循直线传播和反 射定律,利用角平分线可以分析光线在不 同介质中的传播路径。
PART 05
角平分线在实际问题中应 用
REPORTING
WENKU DESIGN
角度测量问题解决方法
利用角平分线性质定理
角平分线将相邻两边按比例分割,根据已知角度和边长,可求解 未知角度。
构造全等三角形
通过角平分线构造两个全等三角形,利用全等三角形的性质求解角 度。
应用三角函数
在直角三角形中,利用角平分线与对边所形成的角,结合三角函数 求解角度。
答案及详细解析提供
练习题2答案及解析
解:过点D作DE⊥AB于点E。由于AD平分∠BAC,∠C=90°,所以CD=DE。在Rt△BDE和Rt△ACD中,由 于∠BDE=∠ADC=90°,∠B=∠CAD,所以Rt△BDE∽Rt△ACD。因此,BD:AD=DE:CD。设CD=7x,则 BD=9x。由于BC=32,所以7x+9x=32,解得x=2。因此,CD=14,DE=CD=14。所以点D到AB的距离 为14。
【数学(人教版)】角的平分线的性质(第二课时)

回顾 利用尺规作角的平分线: 已知:∠AOB(如图). 求作:∠AOB的平分线.
A
O
B
回顾 角的平分线的性质
角的平分线上的点到角的两边的距离相等.
符号语言:
A
∵∠AOP = ∠BOP (OP平分∠AOB), PD⊥OA于D,
D C
P
PE⊥OB于E,
O
EB
∴PD = PE.
课后作业
1.(教材51页 习题12.3第1题)用三角尺可按下面方 法画角平分线,在已知的∠AOB的两边上,分别取 OM = ON,再分别过点M、N作OA,OB的垂线, 交点为P,画射线OP,则OP平分∠AOB,为什么?
2 .如图所示,在△ABC中:
(1)下列操作中,作∠ABC的平分线的正确顺序
是
(3)若AB = 18,BC = 12,S△ABC = 120,过点D作 DE⊥AB于点E,求DE的长.
例 如图,△ABC中,AD 是它的角平分线,且BD = CD, DE⊥AB,DF⊥AC,垂足分别为E,F. 求证:EB = FC.
A
E
F
B
D
C
证明: ∵AD平分∠BAC,DE⊥AB,DF⊥AC, ∴DE = DF(角的平分线的性质).
B H
CP
作法:作∠ABC的平分线, 交AC于点P.则点P为所求. 证明:作PH⊥AB于H. A ∵∠C = 90°,∴PC⊥AC. ∴PC = PH.
.(将序号按正确顺序写在横线上)
①分别以点M,N为圆心,大于 MN的长为半径作弧,
在∠ABC内,两弧交于点P;
②以点B为圆心,适当长为半径
作弧,交AB于点M,交BC于N点;
③画射线BP,交AC于点D.
角平分线的八种画法

角平分线的八种画法角平分线是数学中非常重要的一个概念,在几何、代数、微积分等各个分支学科中,角平分线具有重要的作用。
今天就让我们重新认识角平分线,探讨一下它的绘制方法。
角平分线的定义是:对它的定义,从图形上可以看出,是将角分成两个相等的部分。
在几何学中,一个角可以用角度来表示,用符号ABC来表示角ABC,其中A为角的起点,B、C为角的顶点,BC为角的终点。
角平分线就是将这个角ABC分成两个相等的角,即∠ABD =CDB,其中D为角平分线的点。
对于角平分线的画法,一共有八种方法,它们分别是:1.知边、角和角平分线,求其余边:这类问题属于角平分线的最常见的应用方式。
根据所给的信息,通过三角函数的运用可以确定其余两边的值,从而画出该角平分线所在的三角形。
2.知两边和它们间夹角,求角平分线:这类问题也属于角平分线常见的应用情况之一。
根据所给的两边及夹角,通过正弦定理可以求出其相交的夹角,从而再经过三角函数的运算即可找到角平分线的点。
3.知一边、角和相邻边,求角平分线:这类角平分线问题也属于常见的计算情形。
根据所给的信息,通过角平分线的定义,很轻松地可以求得该点在三角形ABC中的位置。
4.知三角形的两边和非邻角,求角平分线:这类问题也属于角平分线的特殊情形。
由于一个正数的平方根只有一个,因此,可以根据此性质,计算出的平方根值是唯一的,可以求得角平分线点的位置。
5. 从角ABC的端点构造角平分线:这是构造角平分线最简单的方法,也是最直观的方法之一。
从角ABC的两个端点出发,向内部夹角的中心点D画一条线段,即为角平分线点D。
6.角平分线的两顶点连线,构成的新的角平分线:这是一种比较新颖的画法,可以将角平分线构筑成一个褶缝状,角ABC的两个顶点如果连线,就可以构成一条新的角平分线,此新角平分线达到同样的效果。
7.两边的中点把它们连线,构成的新的角平分线:这是一种比较新颖的画法,它可以使两边的中点ABC、BD和D连线,形成一条新的角平分线。
北师大版初中九年级上册数学课件 《角平分线》证明PPT课件
1
2
B
E' D C
得解;(2)有线
E
''
段的和差关系时, 常用截长补短法作
1
2
3
辅助线化和差关系 为相等关系。
角的平分线
线段的垂直平分线
A
D
C
P
M P
O
E
B
A
B
N
定理1:在角的平分线上的点到这个角 定理:线段垂直平分线上的点和这条线段两
的两边的距离相等。
个端点的距离相等。
定理2:到一个角的两边的距离相等的 逆定理:和一条线段两个端点距离相等的
点,在这个角的平分线上。
点,在这条线段的垂直平分线上。
线段的垂直平分线可以看作是和线段两上端 角的平分线是到角的两边距离相等的所点距离相等的所有点的集合 有点的集合
点的集合是一条射线
点的集合是一条直线
作业(必做题):课本:习题,配套练习
问题探讨: 1、如图,如图所示∆ABC中, AD⊥BC于D,∠B=2∠C。求 证:AB+BD=CD。 若在ΔABC中,AD⊥BC于D, AB+BD=DC试问:∠B与∠C是 什2、么在关V型系公?路(∠AOB)内部,
认知结构中去.
问题引入
如图,浑南新区一个工厂,在公路西侧,到公 路的距离与到河岸的距离相等,并且与河上公 路桥较近桥头的距离为300米。你能尝试确定工 厂的位置吗?并说明理由。
北
比例尺1:20000
例1、如图,某开发区有一个工厂在公路西侧, 到公路的距离与到河岸的距离相等,并且与河 上公路桥较近桥头的距离为300米。你能尝试确 定工厂的位置吗?并说明理由。
DA
分析:要证明PD=PE,
九年级数学画角平分线

初中数学画角平分线教案

初中数学画角平分线教案教学目标:1. 知识与技能:了解角的平分线的概念,学会用尺规作图的方法画出一个角的平分线。
2. 过程与方法:通过实际操作,培养学生的观察能力、操作能力和解决问题的能力。
3. 情感态度与价值观:激发学生对数学的兴趣,培养学生的合作意识和创新精神。
教学重点:1. 角的平分线的概念。
2. 尺规作图的方法画角的平分线。
教学难点:1. 理解角的平分线的性质。
2. 熟练运用尺规作图的方法画角的平分线。
教学准备:1. 尺子、圆规、直尺、橡皮擦等作图工具。
2. 教学PPT或黑板。
教学过程:一、导入新课1. 引导学生回顾之前学过的知识,如角的概念、角的分类等。
2. 提问:同学们,你们知道如何画一个角的平分线吗?二、探究新知1. 讲解角的平分线的概念:角的平分线是将一个角平分成两个相等角的直线。
2. 演示如何用尺规作图的方法画角的平分线:a. 以角的顶点O为圆心,任意长为半径画一个圆弧,交角的两边AB和AC于点M和N。
b. 以点M和N为圆心,大于MN长为半径画两个圆弧,分别交角的两边于点P和Q。
c. 连接点P和Q,线段PQ即为所求的角的平分线。
3. 让学生分组合作,尝试自己画出几个角的平分线,并观察平分线与角的两边的关系。
三、巩固新知1. 提问:同学们,你们能总结出角的平分线的性质吗?2. 引导学生归纳角的平分线的性质:a. 角的平分线将角平分成两个相等角。
b. 角的平分线与角的两边垂直。
c. 角的平分线上的点到角的两边的距离相等。
3. 举例说明角的平分线的性质在实际问题中的应用。
四、课堂练习1. 让学生独立完成练习题,巩固画角的平分线的方法。
2. 引导学生相互讨论,解决练习题中的问题。
五、总结1. 回顾本节课所学的内容,让学生再次确认角的平分线的概念和画法。
2. 强调角的平分线在实际问题中的应用价值。
教学反思:本节课通过引导学生回顾旧知识,引入新概念,让学生通过实际操作,掌握画角的平分线的方法。
数学:第一章-4.角平分线-第1课时-角平分线的性质与判定--课件(北师大版九年级上)

线段垂直平分线与角平分线的区别与联系: (1)都有“平分、距离相等”的特点. (2)线段的垂直平分线是一条直线;角平分线是一条射线. (3)三角形三边的垂直平分线的交点到三角形三个顶点的距 离相等,三角形角平分线的交点到三边的距离相等.
角平分线性质定理的逆定理(难点) 3 .如图 4 ,CD ⊥OA ,CE ⊥OB ,若 CD =CE ,则 C 在 ∠__A__O_B__的__角__平__分__线_.
图4 4.如图 5,已知 AB=CD,△PAB 的面积与△PCD 的面积 相等.求证:OP 平分∠AOD.
图5 答案:略
用尺规作角的平分线 5.如图 6,在直线 MN 上求作一点 P,使点 P 到∠AOB 的 两边的距离相等(写出作法).
图2
角平分线的性质定理(重点) 1.如图 3,P 是∠AOB 平分线上的一点,PC⊥OA,PD⊥ OB,垂足分别为 C、D,图中的两组相等的线段是P__C_=__P_D__,__O_C_=__O__D.
图3 2.两条小河相交成一个三角建一个小房子,并使房子到两条 小河的距离相等,但它不知该如何选址,你能帮帮它吗? 答案:略
4.角平分线
第 1 课时 角平分线的性质与判定
1.角平分线的性质定理 探究: 如图 1,条件:①OP 平分∠AOB;②HM⊥OA,HN⊥OB. 结论:__H_M___=__H__N__. 归纳:角平分线上的点到这个角的两边的距离__相__等__.
图1
2.角平分线性质定理的逆定理 在一个角的内部,且到角的两边距离相等的点,在这个角
的_平__分__线__形_上.
3.用尺规作角的平分线 已知:∠AOB(如图 2).求作:射线 OC,使∠AOC=∠BOC. 作法: ①在 OA 和 OB 上,分别截取 OD、OE,使 OD=OE; ②分别以点 D、E 为圆心,大于___12_D_E___的长为半径作弧, 在∠AOB 内,两弧交于点 C; ③作射线____O_C___,则 OC 就是所求的射线.
(完整版)中考数学尺规作图专题复习(含答案)
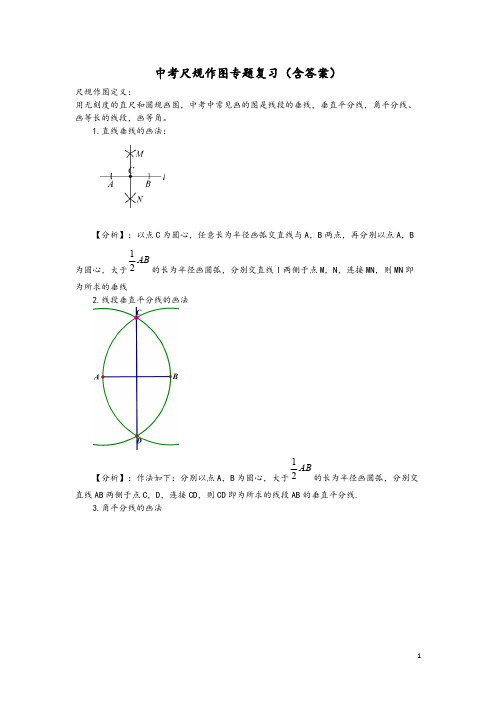
中考尺规作图专题复习(含答案)尺规作图定义:用无刻度的直尺和圆规画图,中考中常见画的图是线段的垂线,垂直平分线,角平分线、画等长的线段,画等角。
1.直线垂线的画法:【分析】:以点C 为圆心,任意长为半径画弧交直线与A ,B 两点,再分别以点A ,B为圆心,大于的长为半径画圆弧,分别交直线l 两侧于点M ,N ,连接MN ,则MN 即12AB为所求的垂线2.线段垂直平分线的画法【分析】:作法如下:分别以点A ,B 为圆心,大于的长为半径画圆弧,分别交12AB 直线AB 两侧于点C ,D ,连接CD ,则CD 即为所求的线段AB 的垂直平分线.3.角平分线的画法l l【分析】1.选角顶点O 为圆心,任意长为半径画圆,分别交角两边A ,B 点,再分别以A ,B 为圆心,大于的长为半径画圆弧,交H 点,连接OH ,并延长,则射线OH 即为12AB 所求的角平分线.4.等长的线段的画法直接用圆规量取即可。
5.等角的画法【分析】以O 为圆心,任意长为半径画圆,交原角的两边为A,B 两点,连接AB ;画一条射线l ,以上面的那个半径为半径,l 的顶点K 为圆心画圆,交l 与L ,以L 为圆心,AB 为半径画圆,交以K 为圆心,KL 为半径的圆与M 点,连接KM ,则角LKM 即为所求.备注:1.尺规作图时,直尺主要用作画直线,射线,圆规主要用作截取相等线段和画弧;2.求作一个三角形,其实质是依据三角形全等的基本事实或判定定理来进行的;3.当作图要满足多个要求时,应逐个满足,取公共部分.例题讲解AB=BC=AC=a.例题1.已知线段a,求作△ABC,使解:作法如下:①作线段BC=a;(先作射线BD,BD截取BC=a).②分别以B、C为圆心,以a半径画弧,两弧交于点A;③连接AB、AC.则△ABC要求作三角形.,∠A=∠α.例2.已知线段a和∠α,求作△ABC,使AB=AC=a解:作法如下:①作∠MAN=∠α;②以点A为圆心,a为半径画弧,分别交射线AM,AN于点B,C.③连接B,C.△ABC即为所求作三角形.例3.(深圳中考)如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项中,正确的是(D)【解析】由题意知,做出AB的垂直平分线和BC的交点即可。
中考数学常见几何模型角平分线的基本模型(二)非全等类

专题08 角平分线的重要模型(二)非全等类角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各大模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,,本专题就角平分线的非全等类模型作相应的总结,需学生反复掌握。
模型1.双角平分线模型(导角模型) 【模型解读】双角平分线模型(导角模型)指的是当三角形的内角(外角)的平分线相交时,可以导出平分线的夹角的度数。
【模型图示】条件:BD ,CD 是角平分线.结论:1902BDC A∠=︒+∠1902BDC A ∠=︒-∠12BDC A ∠=∠ 1.(2022·广东·九年级专题练习)BP 是∠ABC 的平分线,CP 是∠ACB 的邻补角的平分线,∠ABP =20°,∠ACP =50°,则∠P =( )4231AFCB4321DAA.30°B.40°C.50°D.60°【答案】A【分析】据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和,可求出∠P 的度数.【详解】∠BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∠∠ABP=∠CBP=20°,∠ACP=∠MCP=50°,∠∠PCM是△BCP的外角,∠∠P=∠PCM−∠CBP=50°−20°=30°,故选:A.【点睛】本题考查三角形外角性质以及角平分线的定义,解题时注意:一个三角形的外角等于与它不相邻的两个内角的和.2.(2022·山东·济南中考模拟)如图1,在△ABC中,∠BAC的平分线AD与∠BCA的平分线CE交于点O.∠ABC;(1)求证:∠AOC=90°+12(2)当∠ABC=90°时,且AO=3OD(如图2),判断线段AE,CD,AC之间的数量关系,并加以证明.∠MK=ML,角与第三个内角的数量关系”进行了探究.(1)如图1,在△ABC中,∠ABC与∠ACB的平分线交于点P,∠A=64°,则∠BPC=;(2)如图2,△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E.其中∠A=α,求∠BEC.(用α表示∠BEC);(3)如图3,∠CBM、∠BCN为△ABC的外角,∠CBM、∠BCN的平分线交于点Q,请你写出∠BQC 与∠A的数量关系,并说明理由.(4)如图4,△ABC外角∠CBM、∠BCN的平分线交于点Q,∠A=64°,∠CBQ,∠BCQ的平分线交于点P,则∠BPC=°,延长BC至点E,∠ECQ的平分线与BP的延长线相交于点R,则∠R=°.【分析】(1)根据三角形的内角和角平分线的定义;(2)根据三角形的一个外角等于与它不相邻的两个内角的和,用∠A与∠1表示出∠2,再利用∠E与∠1表示出∠2,于是得到结论;(3)根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠EBC与∠ECB,然后再根据三角形的内角和定理列式整理即可得解;(4)结合(1)(2)(3)的解析即可求得.【解答】解:(1)∵PB、PC分别平分∠ABC和∠ACB,∴∠PBC=12∠ABC,∠PCB=12∠ACB(角平分线的性质),∴∠BPC+∠PBC+∠PCB=180°(三角形内角和定理),∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣(12∠ABC+12∠ACB)=180°−12(∠ABC+∠ACB)=180°−12(180°﹣∠A)=180°﹣90°+12∠A=90°+12∠A=90°+12×64°=122°.故答案为:122°;(2)∵BE是∠ABD的平分线,CE是∠ACB的平分线,∴∠ECB=12∠ACB,∠ECD=12∠ABD.∵∠ABD是△ABC的外角,∠EBD是△BCE的外角,∴∠ABD=∠A+∠ACB,∠EBD=∠ECB+∠BEC,∴∠EBD=12∠ABD=12(∠A+∠ACB)=∠BEC+∠ECB,即12∠A+∠ECB=∠ECB+∠BEC,∴∠BEC=12∠A=12α;(3)结论∠BQC=90°−12∠A.∵∠CBM与∠BCN是△ABC的外角,∴∠CBM=∠A+∠ACB,∠BCN=∠A+∠ABC,∵BQ,CQ分别是∠ABC与∠ACB外角的平分线,∴∠QBC=12(∠A+∠ACB),∠QCB=12(∠A+∠ABC).∵∠QBC+∠QCB+∠BQC=180°,∴∠BQC=180°﹣∠QBC﹣∠EQB=180°−12(∠A+∠ACB)−12(∠A+∠ABC),=180°−12∠A−12(∠A+∠ABC+∠ACB)=180°−12∠A﹣90°=90°−12∠A;(4)由(3)可知,∠BQC=90°−12∠A=90°−12×64°=58°,由(1)可知∠BPC=90°+12∠BQC=90°+12×58°=119°;由(2)可知,∠R=12∠BQC=29°故答案为119,29.【点评】本题考查了三角形的外角性质与内角和定理,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.4.(2022·辽宁沈阳·九年级期中)阅读下面的材料,并解决问题(1)已知在∠ABC中,∠A=60°,图1-3的∠ABC的内角平分线或外角平分线交于点O,请直接写出下列角度的度数,如图1,∠O=;如图2,∠O=;如图3,∠O=;∠A(2)如图4,点O是∠ABC的两条内角平分线的交点,求证:∠O=90°+12(3)如图5,在∠ABC中,∠ABC的三等分线分别与∠ACB的平分线交于点O1O2,若∠1=115°,∠2=135°,求∠A的度数.模型2.角平分线加平行线等腰现(角平分线+平行线)【模型解读】1)过角平分线上一点作角的一边的平行线,构造等腰三角形;2)有角平分线时,过角一边上的点作角平分线的平行线,交角的另一边的直线于一点,也可构造等腰三角形。
九年级数学角平分线知识点

九年级数学角平分线知识点角平分线,作为数学中的一个重要概念,是九年级数学教学内容中的一部分。
它在几何学中扮演着重要的角色,不仅是解决几何问题的关键,也是应用于实际生活中的数学原理之一。
本文将详细介绍角平分线的定义、性质和应用。
1. 定义角平分线是指一个线段将一个角分成两个相等的角。
具体来说,对于一个给定角ABC,在其中选择一个点D,并且连接AD,使其刚好平分角ABC,那么线段AD就是角ABC的平分线。
同样的,角的平分线也可以延长,即延长线段AD,则其也仍然保持平分角ABC。
2. 性质(1)角平分线上的任意一点都在该角的内部。
(2)一个角的内角平分线可以与该角的外角平分线相交。
(3)如果一个点在一个角的内角平分线上,那么该点到角两边的距离相等。
(4)如果一个角的两边被一条角平分线分为两个相等的线段,那么该角是一个直角。
(5)如果一个角的两边被一条角平分线分为两个不相等的线段,那么该角不是一个直角。
3. 应用角平分线的性质和定义在解决几何问题时发挥着重要的作用。
它被广泛应用于测量和校准领域。
例如,在地理测量中,我们可以利用角平分线的概念来确保准确测量两个点之间的距离。
在建筑设计中,使用角平分线可以保证建筑物的结构和比例的准确性。
此外,角平分线的性质还可以应用于证明问题。
证明某个角是直角或者某条线段是角平分线,都可以利用角平分线的性质进行推导。
通过使用角平分线的定义和性质,我们可以解决许多几何问题,并推广到更复杂的应用中。
总结起来,九年级数学中的角平分线知识点是十分重要的。
了解角平分线的定义、性质和应用,可以帮助我们更好地应用数学知识解决实际问题。
而且,角平分线的概念也为我们理解和学习更高级的几何概念打下了基础。
因此,在学习数学过程中,我们应该仔细研究角平分线的知识点,并在实践中加以运用。
通过不断练习和掌握,我们可以更好地应用角平分线解决实际问题,并提高数学解决问题的能力。
总的来说,角平分线是一个十分有用的数学概念,在解决几何问题和实际应用中起到了关键的作用。
角平分线的画法的依据

角平分线的画法的依据角平分线是一个重要的几何概念,它指的是将一个角分成两个相等的角的直线。
在数学中,角平分线被广泛应用于各种几何问题的解决中,因此了解和掌握角平分线的画法是非常重要的。
本文将介绍角平分线的画法的依据,并详细解释如何准确地画出角平分线。
首先,我们需要了解角平分线的定义。
角平分线是从某个角的顶点开始,将该角分成两个相等角的直线。
在画角平分线之前,需要先画出待分角。
给定一个角ABC,其中A为顶点,角度为θ。
为了构造角ABC的角平分线,我们需要遵循以下步骤:1. 使用直尺绘制一条从角的顶点A开始的射线AC。
这条射线将成为角的一条边,并且应该足够长以确保角平分线与角的另一条边相交。
2. 使用直尺绘制一条从角的另一条边AB上的任意一点B开始的射线BD。
这条射线应该与射线AC相交,并且尽可能接近垂直于射线AC。
3. 通过使用指南针工具,设置一个合适的半径,将B作为圆心在射线AC上绘制一个弧段,与射线BD两次相交。
这两个相交点分别标记为E和F。
4. 使用直尺绘制一条连接顶点A和弧段上的任意一个交点E的直线AE。
同样,使用直尺绘制一条连接顶点A和弧段上的另一个交点F 的直线AF。
5. 直线AE和直线AF分别是角ABC的两条平分线,因为它们将角ABC分成两个相等角。
根据以上步骤,我们可以成功地绘制出角ABC的角平分线。
这个方法的依据主要是基于几何学中的一些公设和定理。
首先,我们应用了平行公设和定理。
在步骤1中,我们绘制了从顶点A开始的射线AC,这条射线与角的一条边AB平行。
在步骤2中,我们绘制了从角的另一条边AB上的点B开始的射线BD,该射线应该足够接近垂直于射线AC。
通过这样的构造,我们可以得到一条平行于射线AC的射线BD,并且这两条射线相交于角ABC的顶点A。
其次,我们应用了圆的性质。
在步骤3中,我们使用圆心B和半径BE(或BF)在射线AC上绘制了一个弧段。
根据圆的性质,弧段上的任意两个点与圆心B的距离相等。
角平分线的画法及原理

角平分线的画法及原理宝子,今天咱们来唠唠角平分线这个超有趣的东西呀。
先来说说角平分线的画法吧。
咱有一种特别简单又好玩的方法哦。
拿个圆规来,把圆规的针尖放在角的顶点上,然后随便画个弧,这个弧呢就和角的两条边都相交啦。
这就像是给角的两边都戴了个小帽子一样,是不是很可爱呢?接着呢,不要动圆规的半径哦,分别以刚才和角两边相交的那两个点为圆心,再画两个小弧,这两个小弧呀就会在角的内部相交啦。
最后呢,用直尺把角的顶点和这个相交点连起来,哇塞,这条线就是角平分线啦。
就好像是找到了角这个小世界里最公平的那条分割线一样呢。
那为啥这么画就能得到角平分线呢?这就涉及到一些超酷的原理啦。
咱先看那第一步画的弧,它和角的两边相交得到的那两个点到角的顶点的距离是相等的呀,因为是用同一个半径画的弧嘛。
然后呢,后面又分别以这两个点为圆心画弧,这两个小弧相交的那个点到这两个点的距离也是相等的。
这就像是在角的内部找到了一个到角两边距离都相等的神秘点呢。
从数学的角度来说,角平分线的定义就是把一个角平均分成两个相等的角的线。
我们这么画出来的线,它具有一个超厉害的性质,就是角平分线上的点到角两边的距离相等。
想象一下哦,如果我们在角平分线上随便取一个点,然后向角的两边作垂线,这两条垂线的长度是一样的呢。
这就好像是这个点在角的两边之间找到了一种完美的平衡。
咱再换个角度想,就像分蛋糕一样,如果要把一个角这个“蛋糕”分成相等的两部分,我们通过这样画弧、找交点、连线的方式,就精准地找到了那条分界线。
而且呀,这个方法是经过很多很多聪明的数学家验证过的,超级靠谱呢。
其实角平分线在生活中也有很多应用呢。
比如说在建筑设计里,如果要设计一个对称的建筑,可能就会用到角平分线的知识来确定一些对称轴之类的。
还有在一些艺术创作里,要是想把一个图案按照某个角平均分开,也能用到这个方法哦。
宝子,你看这角平分线是不是既好玩又超级有用呢?它就像是数学这个大宝藏里的一颗亮晶晶的小宝石,虽然看起来小小的,但是蕴含着很多很多的智慧呢。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
