有限元作业1
有限元 1-2-杆单元

第2章杆系单元和杆系结构整体分析2.1杆系单元2.2杆系结构整体分析第2章杆系单元和杆系结构整体分析2.1杆系单元2.2杆系结构整体分析对象、任务对象任务对象:研究有限大小的个体(element)对象研究有限大小的个体任务:1. 建立应变与结点位移分量之间的关系;2. 建立应力与结点位移分量之间的关系;33. 建立结点力与结点位移分量之间的关系;4. 把作用在单元内的外载转化成结点荷载,即单元等效节点力。
一、分离单元1 结构离散取杆件与杆件交点、集中力作用点、杆件与支承的交点为节点。
相邻两节点间的杆件段是单元。
节点编号时力求单元两端点号差最小。
YX2 坐标系有限元中的标系有体标系和局部标系有限元中的坐标系有整体坐标系和局部坐标系。
对于一个结构,整体坐标系一般只有一个;而局部坐标系有很多个,一个单元就有一个局部坐标。
并标系有很多个个单元就有个局部标并且局部坐标系每一个单元的规定都是相同的,这样,同类型单元刚度矩阵相同。
YX杆系结构单元主要有铰接杆单元和梁单元两种类型。
它们都只有2个节点i 、j 。
¾约定:单元坐标系的原点置于节点i ;节点i 到j 的杆轴(形心轴)方向为单元坐标系中x 轴的正向。
y 轴、z 轴都与x 轴垂直,并符合右手螺旋法则。
¾对于梁单元,y 轴和z 轴分别为横截面上的两个惯性主轴惯性主轴。
·x yj·z i土木工程学院有限单元法二、杆单元单元分析维杆单元下图示出了一维铰接杆单元,横截面积为A ,长1、一维杆单元度为l ,弹性模量为E ,轴向分布载荷为p x 。
单元有2,单元坐标为一维坐标轴个结点i ,j ,单元坐标为维坐标轴x 。
··i j x p x u ju i l LINK土木工程学院有限单元法P-8··i x p x j l u ju i LINK⎫⎧=i e u ⎧单元结点位移向量{}⎭⎬⎩⎨j u δ单元结点力向量:⎬⎫⎨=j i e F F F }{⎭⎩(1)位移模式和形函数①位移模式因为只有2个结点,每个结点位移只有1个自由度,因此单元的位移模式可设为:12u a a x =+(3)式中a 1、a 2为待定常数,可由结点位移条件时x =x i 时,u =u ix =x j 时,u =u j确定。
(完整版)有限元考试试题——第一组

有限元考试试题一、简答题(5道,共计25分)。
1.有限单元位移法求解弹性力学问题的基本步骤有哪些?(5分)2. 在划分网格数相同的情况下,为什么八节点四边形等参数单元精度大于四边形矩形单元?(5分)3.轴对称单元与平面单元有哪些区别?(5分)4.有限元空间问题有哪些特征?(5分)5.简述四节点四边形等参数单元的平面问题分析过程。
(5)分)二、论述题(3道,共计30分)。
1. 简述四节点四边形等参数单元的平面问题分析过程。
(10分)2.轴对称问题的简单三角形单元是否是常应力,常应变?为什么?(10分)3.在薄板弯曲理论中做了哪些假设?薄板单元和厚板单元的基本假设有什么不同?(10分)三、计算题(3道,共计45分)。
ν=;1.如图所示等腰直角三角形单元,其厚度为t,弹性模量为E,泊松比0单元的边长及结点编号见图中所示。
求(1)形函数矩阵N(2)应变矩阵B和应力矩阵S(3)单元刚度矩阵e K(12分)2.如图所示的四结点矩形单元,求出节点3的位移。
设厚度t=1m,μ=0,E 为常量。
(13分)注:对于四节点矩形单元有:()()()()()()()()()⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫+-=++=-+=--=ηξηξηξηξ1141114111411141.14321N N N N →)4,3,2,1()1)(1(41=++=i N i i i ηηξξ()[][][][]eT Aek k k k k k k k k k k k k k k k y x t B D B k ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==⎰⎰44434241343332312423222114131211d d .2,[][][][][][][]()()()()())4,3,2,1,( 3111311a 212123111311218d d d d 21111=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-+-+⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-===⎰⎰⎰⎰--j i b a b b a a b Et B D B abt y x t B D B k j i j i j i j i j i j i j i j i j i j i j i j i jTijTAiijηηξξμξξηηηξμξμηηξμξμηξξηημηηξξμηξ3.有一如图3(a)所示的剪力墙,墙顶作用竖向荷载P 。
弹性力学:平板弯曲问题的有限元分析(1)

平板弯曲问题的有限元分析(1) Kirchhoff弹性薄板理论
参考文献: “弹性力学(下册)”第13章。徐芝纶
x
2w
2 (z2
2
2
)dz 4
E 3 12(1 2 )
x
2w
(c)
同样,在y为常量的截面上,每单位宽度内的 y , yx , yz
也分别合成如下的弯矩,扭矩,和横向剪力:
M y
2 2
z
y dz
E
12(1
3
2
)
(
2w y2
2w x2
)
(d)
M yx
2
2
z yxdz
E 3 12(1 2 )
(9-6)
( z )z q
(f)
2
将(9-6)式代入薄板上板面的边界条件:
得:
E
12(1
3
2
)
4
w
q
(9-7)
或 D4w q, (9-8)
其中
D
E
12(1
3
2
)
(9-9)
薄板的弹性曲面微分方程
为薄板的弯曲刚度
§9-3 薄板横截面上的内力
► 薄板横截面上的内力,称为薄板内力,是指薄板横截面的单 位宽度上,由应力合成的主矢量和主矩。
对z积分,得到: z
2(1 2 )
2
( 4
z
z2 )4w 3
F3 (x,
有限元分析报告(1)

有限元分析报告(1)有限元仿真分析实验⼀、实验⽬的通过刚性球与薄板的碰撞仿真实验,学习有限元⽅法的基本思想与建模仿真的实现过程,并以此实践相关有限元软件的使⽤⽅法。
本实验使⽤HyperMesh 软件进⾏建模、⽹格划分和建⽴约束及载荷条件,然后使⽤LS-DYNA软件进⾏求解计算和结果后处理,计算出钢球与⾦属板相撞时的运动和受⼒情况,并对结果进⾏可视化。
⼆、实验软件HyperMesh、LS-DYNA三、实验基本原理本实验模拟刚性球撞击薄板的运动和受⼒情况。
仿真分析主要可分为数据前处理、求解计算和结果后处理三个过程。
前处理阶段任务包括:建⽴分析结构的⼏何模型,划分⽹格、建⽴计算模型,确定并施加边界条件。
四、实验步骤1、按照点-线-⾯的顺序创建球和板的⼏何模型(1)建⽴球的模型:在坐标(0,0,0)建⽴临时节点,以临时节点为圆⼼,画半径为5mm的球体。
(2)建⽴板的模型:在tool-translate⾯板下node选择临时节点,选择Y-axis,magnitude输⼊,然后点击translate+,return;再在2D-planes-square ⾯板上选择Y-axis,B选择上⼀步移下来的那个节点,surface only ,size=30。
2、画⽹格(1)画球的⽹格:以球模型为当前part,在2D-atuomesh⾯板下,surfs 选择前⾯建好的球⾯,element size设为,mesh type选择quads,选择elems to current comp,first order,interactive。
(2)画板的⽹格:做法和设置同上。
3、对球和板赋材料和截⾯属性(1)给球赋材料属性:在materials⾯板内选择20号刚体,设置Rho为,E为200000,NU为。
(2)给球赋截⾯属性:属性选择SectShll,thickness设置为,QR设为0。
(3)给板赋材料属性:材料选择MATL1,其他参数:Rho为,E为100000,Nu 为,选择Do Not Export。
第2章_弹性力学基础及有限元法的基本原理1

W U
当外力的形式是多样的时,外力的虚功等于:
W f Pc f Pv dV f Ps dS
T T T v s
• 1.4 平面问题定义
严格地讲,任何结构都是空间的。对于某些特殊情 况,空间问题可以转化为平面问题。
(1)平面应力问题 满足条件: 1)几何条件 厚度尺寸远远小于截面尺寸; 2)载荷条件 载荷平行于板平面且沿厚度方向均匀 分布,而板平面不受任何外力作用。
1)位移函数 分片插值→ 假设一种函数来表示单元位移分布 一般选取多项式(简单而且易求导)
可用于离散的单元: • 三角形单元; • 矩形单元; • 不规则四边形单元。 DOF 节点的自由度:节点所具有的位移分量的数量。 一个单元所有节点的自由度总和称为单元自由度。 (1)单元参数只能通过节点传递到相邻单元 (2)单元和节点必须统一编号
2.2 单元分析(位移、应力、应变) 任务:形成单元刚度矩阵,建立单元特性方程 因此必须建立坐标系,如下图:
1D问题的弹性模量
E杨氏弹性模量
泊松比是指材料在单向受拉或受压时,横向正应变与轴向 正应变的绝对值的比值,也叫横向变形系数,它是反映材 料横向变形的弹性常数。 若在弹性范围内加载,横向应变εx与纵向应变εy之间存 在下列关系: εx=- νεy 式中ν为材料的一个弹性常数,称为泊松比。泊松比是 量纲为一的量。 可以这样记忆:空气的泊松比为0,45#钢0.3,水的泊松 比为0.5,中间的可以推出。
• 未知数 应力 6个+应变 6个+位移 3个=15个 • 方程个数 平衡方程 3个+几何方程6个+物理方程6个=15个 原则上可以根据15个方程求出15个未知物理量 但实际求解时先求出一部分再通过方程求解剩下的。 目前有限元法主要采用的是位移法,以三个位移 分量为基本未知量。位移-应变-应力,应力和外力平衡
国科大有限元作业1
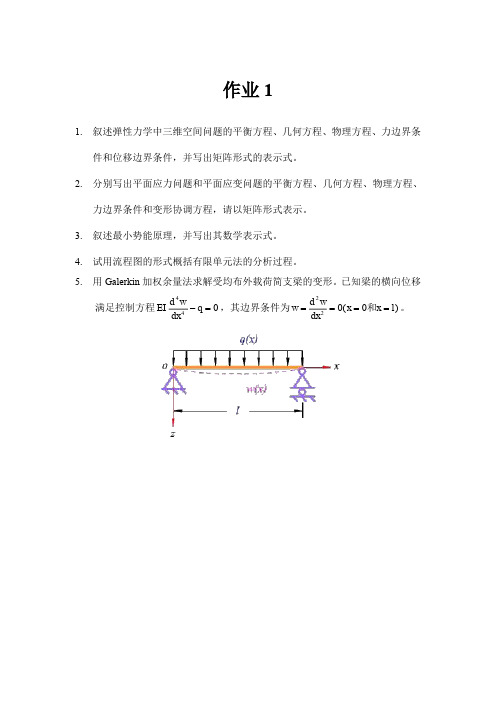
作业1
1.叙述弹性力学中三维空间问题的平衡方程、几何方程、物理方程、力边界条
件和位移边界条件,并写出矩阵形式的表示式。
2.分别写出平面应力问题和平面应变问题的平衡方程、几何方程、物理方程、
力边界条件和变形协调方程,请以矩阵形式表示。
3.叙述最小势能原理,并写出其数学表示式。
4.试用流程图的形式概括有限单元法的分析过程。
5.用Galerkin加权余量法求解受均布外载荷简支梁的变形。
已知梁的横向位移
满足控制方程
4
4
w
d
EI q
dx
-=,其边界条件为
2
2
0(0)
d w
w x x l
dx
====
和。
第五章 有限元法-1-泛函与变分

设待求变分问题(5-4)的解答(极值函数)为 y=y(x) (5-7)
因y是x的函数,但讨论的是y的变化
设想函数y从极值解(5-7)稍稍变动到y+dy,并把变分dy改记为:eh(x),
e是一个任意给定的微量实参数(实变量);
h(x)是定义于区间[x1,x2],且满足齐次边界条件的任意选定的可微函数,即有: h(x1)=h(x2)=0。
15
与多元函数的极值问题相对应,在几何、力学上的求解泛 函极值的问题。 最速降线问题。
研究当质点从定点A自由下滑到定点B时,为使滑行时间最短,试 求质点应沿着怎样形状的光滑轨道y=y(x)下滑。 取A点为坐标原点,y轴竖直向下(图5-1)。
则沿曲线y=y(x)滑行线段ds所需的时间为
16
18
在最速下降问题,在端点x1和x2给定的无数个函数之中, y ( x) 仅有一个函数 能使式( 5-2a)中的定积分达到极小 y ( x) 值函数,这一函数 被称为极值函数。 所谓变分问题就在于寻求使泛函达到极值的该极值函数, 即分析研究泛函的极值问题。 物理学各分支都存在有相应的变分问题(变分原理),例 如
因此
式中
26
故可得
简写为
将上式与式(5-6)相比较,只相差一个数值因子e。
27
故(5-8)等价于变分方程
也即
(线性主部)
利用分部积分,根据变分与微分顺序可以互换的原理,即 dy’=(dy)’,得
28
在变分问题中,变分dy在端点保持为零
于是,必要条件(5-12)成为
有限元分析第4章 平面问题有限单元法1

6
P
3
4 5
4
2
位移协调条件:各单元共享节点的位移相等 节点平衡条件:各节点单元内力与节点外力构成平衡力系
最终数学模型: K Q
基本概念
单元(element) 节点 (node)
回顾
单元节点位移 (node displacement)
单元节点内力 (node force)
单元刚度矩阵 (element stiffness matrix)
e
bx u by v
d
S
e p
px u py v dS
代入
u v
N
e
{} [B]{ }e
{ } [S]{ }e
得
内力虚功=
e x x y y xy xy d
T d
cj
y)v j
(am
bmx
cm y)vm ]
二、平面问题三角形单元分析
三角形单元形函数
形函数
u x,
y
1 2A
[(ai
bi x
ci
y)ui
(a j
bj x
cj
y)u j
(am
bm x
cm
y)um ]
v x,
y
1 2A
[(ai
bi x
ci
y)vi
(a j
插值系数的确定:待定系数法
ui a1 a2 xi a3 yi u j a1 a2 x j a3 y j um a1 a2 xm a3 ym
第5章 有限元法-1

(5-2)
称为单元的节点力列阵;若 {F} 为外载荷,则称为载荷列阵。
显然,梁的节点力和节点位移是有联系的。在弹性小变形范围 内,这种关系是线性的,可用下式表示
Fxi
Fyi
k11 k21
k12 k22
k13 k23
k14 k15 k24 k25
k16 k26
ui
vi
M zi
Fxj
EA , l
根据静力平衡条件
Fyi 0,
M zi 0
EA Fxj Fxi l ,
Fyj Fyi 0,
M zj 0
由式(5-3a)解得
k11
Fxi
EA , l
k41
Fxj
EA , l
k21 Fyi 0, k51 Fyj 0,
k31 M zi 0 k61 M zj 0
(2) 同理,设vi=1,其余位移分量均为零,即ui=iz=uj=vj=zj= 0,
图5-4所示是xoy平面中的一简支梁简图,现以它为例,来说明 用直接刚度法建立单元刚度矩阵的思想和过程。
图5-4 平面简支梁元及其计算模型
由上图可见:
梁在横向外载荷(可以是集中力或分布力或力矩等)作用下产 生弯曲变形,在水平载荷作用下产生线位移。
对于该平面简支梁问题: 梁上任一点受有三个力的作用: 水平力Fx,
位移法优点是比较简单,规律性强,易于编写计算机程序。所以 得到广泛应用,其缺点是精度稍低。
(2)力法
该法是以节点力作为基本未知量,在节点处建立位移连续方 程,求解出节点力后,再求解节点位移和单元应力。
力法的特点是计算精度高。
(3)混合法
此法是取一部分节点位移和一部分节点力作为基本未知量,建 立平衡方程进行求解。
第六章 有限元法基础1

第六章 有限元法概述第一节 单元分析简例1、单元分析的主要任务:求出单元节点位移和节点力之间的转换关系。
在推导此关系时规定:力和位移的方向若和坐标轴正方向一致者为正。
先举一个简单例子,图1示一拉压弹簧,弹簧系数为常量c ,其轴线和x 坐标轴重合,令此弹簧为一个单元,则弹簧的两端点i , j 是此单元的两个节点。
设在节点i , j 上分别有轴向力j i U U ,和轴向位移jiu u ,。
则当节点对单元有jiU U ,的作用力时,单元对节点有大小相等、方向相反的反作用力,节点力:这节点和单元之间的作用力和反作用力都称为节点力,对单元来讲节点力是作用于单元之力。
2、节点力和节点位移的关系 。
图1可分解为两步1)设节点j 被固定,节点i 产生正位移i u ,则此时节点i 作用在单元上的力是i i cu U ='而节点j 作用在单元上的力是i i cu U -='2)是设节点i 被固定,节点j 产生正位移1u ,此节点j 对单元的作用力是i i cu U =''i U iu iyj u jU jx节点i 对单元的作用力是iicu U -=''将两式合并,就得到⎪⎩⎪⎨⎧+-=''+'=-=''+'=ji j j i ji i i i cu cu U U U cu cu U U U 由式可以看出一个节点上的节点力不仅决定于本节点的位移,而且也决定于本单元其他节点的位移。
设以{}eF 表示单元节点力向量:{}⎭⎬⎫⎩⎨⎧=j i eU U F 以{}eδ表示节点位移向量:{}⎭⎬⎫⎩⎨⎧=j i eu u δ 则式(1.1)可改写成:{}{}eek F δ][=式中⎥⎦⎤⎢⎣⎡---=c c c c k ][式中(1.2)就是单元节点位移{}eδ和节点力{}eF 之间的转换关系。
][k 是转换矩阵,称为单元刚度矩阵。
有限元题1

1.有限元法是近似求解(连续)场问题的数值方法。
2.有限元法将连续的求解域(离散化),得到有限个单元,单元和单元之间用(节点)相连。
3.从选择未知量的角度来看,有限可分为三类(位移法)(力法)(混合法)。
4.以(节点位移)为基本未知量的求解方法称为位移法。
5.以(节点力)为基本未知量求解方法为力法。
6.一部分以(节点位移),另一部分以(节点力)为基本未知量的求解方法为综合法。
7.直梁在外力作用下,横截面上的内力有(剪力Q)和(弯矩M)两个。
8.平面钢架结构在外力作用下,横截面上内力有(轴力T)(剪力Q)(弯矩M)。
9.进行质量的有限元分析,梁单位上每个节点的节点位移为(挠度)和(转角)10.进行平面钢架结构的有限元分析。
平面钢架单元上每个节点的节点位移为(轴向位移)(横向桡度)和(截面转角)10.平面钢架结构中,已知单元e的坐标变换矩阵[Te]及局部坐标系x’O’y’下的单元刚度矩阵【k’】e,则单元在整体坐标系xOy下的单元刚度矩阵为(【K】e=【T e】【K’】e【T e】)11.平面钢架结构中,已知单元e的坐标变换矩阵【Te】及整体坐标系xOy下的单元??12.在弹性范围和小变形的前提下,节点力和节点位移之间是(线性)关系13.弹性力学问题的方程个数有(15)个,未知量个数有(15)个14.弹性力学平面问题的方程个数有(8)个,未知量个数有(8)个15.几何方程是研究(正应变)和(位移)之间关系的方程16.物理方程是描述(应力)和(应变)关系的方向17.平衡方程反应了(应力)和(体力)之间关系的18.把经过物体内任意一点各个(截面)上的应力状况叫做(一点)的应力状态19.形函数在单元节点上的值,具有本点为(一),它点为零的性质,并且在三角形单元的任一节点上,三个形函数之和为(一)20.形函数是(三角形)单元内部坐标的(线性位移)函数,它反应了单元的(位移)状态21.位移模式已知时,形函数由(面积)确定22.在进行节点编号时,要尽量使用同一单元的相邻节点的(狭长的带状)尽可能小,以便最大限度的缩小刚度矩阵带宽,节省存储,提高计算效率23.三角形单元的位移模式为(线性位移模式)24.矩形单元的位移模式为(双线性位移模式)25.在选择多项式位移模式的阶次时,要求(所选的位移模式)与局部坐标系的方位无关的性质成为(几何)各向同性26.单元刚度矩阵描述了(节点力)和(节点位移)之间的关系27.整体刚度矩阵描述了(节点载荷)和(节点位移)之间的关系28.在选择多项式作为单元的位移模式时,多项式阶次的确定,要考虑解答收敛性,即要满足单元的(完备性)和(协调性)要求29.三节点三角形单元内的应力和应变是(常数),四节点矩阵单元内的应力和应变是(线性)变化的30.在矩形单元的边界上,位移是(线性)变化的31.整体刚度矩阵是一个呈(狭长的带状)分布的稀疏矩阵32.整体刚度矩阵[k]是一个奇异阵,在排除(刚体位移)后,它是正义阵。
有限元期末考试试题及答案—湖南大学

(7 分)
a 0 0 0 -a 0 1 1 1 B1 2 0 -a , B2 2 0 a , B3 2 0 0 ; B B1 a a a -a a a 0 0 -a
B2
B3
a
y
2N / m 1N / m 2
O
x
2N / m 2m 2m
(a ) 2、解: (1) 对称性及计算模型正确 (2) 正确标出每个单元的合理局部编号 (3) 求单元刚度矩阵 K e () (4 分) (3 分)
(5) 应用适当的位移约束之后,给出可供求解的整体平衡方程(不需要求解) 。 (5 分)
1、有限元分析的基本思路(3 分)
首先,将物体或求解域离散为有限个互不重叠仅通过节点互相连接的子域(即单元),原始边界条件也被转化为节点上的边界条件, 此过程称为离散化。其次,在单元内,选择简单近似函数来分片逼近未知的求解函数,即分片近似。具体做法是在单元上选择一些合适的 节点作为求解函数的插值点,将微分方程中的变量改写成由各变量或其导数的节点值与所选用的插值函数组成的线性表达式,这是有限元 法的创意和精华所在。而整体区域上的解函数就是这些单元上的简单近似函数的组合。最后,基于与原问题数学模型(基本方程和边界条 件)等效的变分原理或加权残值法,建立有限元方程(即刚度方程),从而将微分方程转化为一组变量或其导数的节点值为未知量的代数 方程组。从而借助矩阵表示和计算机求解代数方程组得到原问题的近似解。
(1)位移模式必须包含单元刚体位移;(2)位移模式必须包含单元的常应变;(3)位移模式在单元内要连续,且唯一在相邻单元 之间要协调。
4、写出弹性力学的基本方程、基本假设和基本变量(3 分)
平衡方程 几何方程 物理方程 具体方程见笔记
西北工业大学网络教育学院 有限元及程序设计 章节测试1-11含答案

A、 正确 B、 错误 标准答案:A 8. ( 单选题 ) 极坐标系下的基本未知量只有径向正应力σr,环向正应力σθ,剪应力τrθ( )。
A、 正确 B、 错误 标准答案:A 7. ( 单选题 ) 薄板的边界不包括( )。(本题 13 分)
第3页共6页
西北工业大学网络教育学院 有限元及程序设计 章节测试 1-11
A、 简支边界 B、 固定边界 C、 自由边界和荷载边界 D、 非固定边界 标准答案:D 8. ( 单选题 ) 通过挠曲微分方程求出位移后即可确定所有物理量,是按坐标求解法( )。 A、 正确 B、 错误 标准答案:B
应力函数φ=cθ求得圆盘的应力为
, 的值为(
A、 1 B、 0 C、 -1 D、 2 标准答案:B 2. ( 多选题 ) 轴对称情况下,应力分量可简化为( )。(本题 12 分)
)。
A、
B、
C、
D、
1 标准答案:ABC
3. ( 单选题 ) 轴对称问题应力分量只是坐标 r 的函数,不随θ而变,同时剪应力为零,应
A、 线性项 B、 非线性项 C、 边界项 D、 体力项 标准答案:A 8. ( 单选题 ) 按应力求解具体可分为逆解法和 半逆解法 两种( )。(本题 13 分)
A、 正确 B、 错误 标准答案:A
1. ( 单选题 ) 已知圆环在 r=a 的内边界被固定,在 r=b 的外边界作用着均布剪力τ0,用
西北工业大学网络教育学院 有限元及程序设计 章节测试 1-11
1. ( 多选题 ) 弹性力学的基本假设有( )。(本题 13 分) A、 假设物体是连续的 B、 假设物体是均匀的和各向同性的 C、 假设物体是完全弹性
有限元思考题(1)

有限元思考题(1)思考题第⼀章V u1-1. ⽤加权余量法求解微分⽅程,其权函数和场函数的选择没有任何限制。
(×)答:权函数V的选取必须保证残值的加权积分为零,强迫近似解所产⽣的残值在某种平均意义上等于零;场函数u必须保证任何⼀点都满⾜积分⽅程式(不⼀定连续),在边界每⼀点上都满⾜边界条件。
1-2. 加权余量法仅适合为传热学问题建⽴基本的有限元⽅程,⽽基于最⼩势能原理的虚功原理仅适合为弹性⼒学问题建⽴基本的有限元⽅程。
(×)分析:加权余量法只要能形成场的微分⽅程都能⽤,不局限于温度场。
尤其适合于具有连续场的⾮⼒学问题(如声、电、磁、热)的有限元⽅程的建⽴。
虚功原理(或虚位移原理)不仅可以应⽤于弹性性⼒学问题,还可以应⽤于⾮线性弹性以及弹塑性等⾮线性问题。
最⼩势能原理仅适⽤于弹性⼒学问题。
加权残值法尤其适⽤于具有连续场的⾮⼒学问题的有限元⽅程的建⽴。
1-3. 现代⼯程分析中的数值分析⽅法主要有有限差分法、有限元法和边界元法。
这些⽅法本质上是将求解区域进⾏⽹格离散化,然后求解⽅程获得数值结果。
是否可以将求解区域离散成结点群,但是没有⽹格进⾏求解?答:可以⽤⽆⽹格⽅法求解。
有限元法是基于⽹格的数值⽅法,它通⽤、灵活并被作为⼀种⼯业标准⼴泛遵循,但其在分析涉及特⼤变形(如:加⼯成型、⾼速碰撞、流固耦合)、奇异性或裂纹动态扩展等问题时遇到了许多困难。
近年来,⽆⽹格法得到了迅速发展,它不需要划分⽹格,克服了有限元法对⽹格的依赖,在涉及⽹格畸变、⽹格移动等问题时显⽰出明显的优势,同时⽆⽹格法的前处理过程也⽐有限元更为简单。
⽬前⽆⽹格法主要还是处在研究阶段,解决的⼯程实际问题相对较简单,与有限元的发展还有较⼤距离。
(⽆⽹格⽅法数值求解的基本思想:在每个节点上构建待求物理量近似值的插值函数,并⽤加权残量法和该近似函数对微分⽅程进⾏离散,形成与待求物理量相关的各节点近似值的离散⽅程,并求解之。
)第⼆章2-1. ANSYS软件有哪些功能模块?在GUI⽅式下的六个窗⼝有何功能和特点。
CATIA有限元分析计算实例1

有限元分析计算实例11.1例题1 受扭矩作用的圆筒11.1-1划分四面体网格的计算(1)进入【零部件设计】工作台启动软件。
单击【开始】→【机械设计】→【零部件设计】选项,如图11-1所示,进入【零部件设计】工作台。
图11-1 单击【开始】→【机械设计】→【零部件设计】选项单击后弹出【新建零部件】对话框,如图11-2所示。
在对话框内输入新的零件名称,在本例题中,使用默认的零件名称【1】。
点击对话框内的【确定】按钮,关闭对话框,进入【零部件设计】工作台。
(2)进入【草图绘制器】工作台在左边的模型树中单击选中【平面】, 如图11-3所示。
单击【草图编辑器】工具栏内的【草图】按钮,如图11-4所示。
这时进入【草图绘制器】工作台。
图11-2 【新建零部件】对话框图11-3 单击选中【平面】(3)绘制两个同心圆草图点击【轮廓】工具栏内的【圆】按钮,如图11-5所示。
在原点点击一点,作为圆草图的圆心位置,然后移动鼠标,绘制一个圆。
用同样分方法再绘制一个同心圆,如图11-6所示。
图11-4 【草图编辑器】工具栏图11-5【轮廓】工具栏下面标注圆的尺寸。
点击【约束】工具栏内的【约束】按钮,如图11-7所示。
点击选择圆,就标注出圆的直径尺寸。
用同样分方法标注另外一个圆的直径,如图11-8所示。
图11-6 两个同心圆草图图11-7 【约束】工具栏双击一个尺寸线,弹出【约束定义】对话框,如图11-9所示。
在【直径】数值栏内输入100,点击对话框内的【确定】按钮,关闭对话框,同时圆的直径尺寸被修改为100。
用同样的方法修改第二个圆的直径尺寸为50。
修改尺寸后的圆如图11-10所示。
图11-8 标注直径尺寸的圆草图图11-9 【约束定义】对话框(4)离开【草图绘制器】工作台点击【工作台】工具栏内的【退出工作台】按钮,如图11-11所示。
退出【草图绘制器】工作台,进入【零部件设计】工作台。
图11-10 修改直径尺寸后的圆图11-11【工作台】工具栏(5)拉伸创建圆筒点击【基于草图的特征】工具栏内的【凸台】按钮,如图11-12所示。
有限元分析作业报告英文版1

有限元分析与应用上机实验报告学院:机电工程学院专业:机械工程班级:硕士1606班*名:***学号: *********指导教师:***日期: 2016.12.021.QuestionFig.1. Schematic diagram of herringbone roof truss.Question: The geometric dimensions of the chevron roof is shown in Fig.1,you should analyze it by statics,as a result you should give the displacement and axial force and axial force diagram of the deformation diagram.Conditions: The ends of the roof truss were fixed, the sectional area of the truss is 0.01m2, elastic modulus is2.0×1011 N/m2, poisson's ratio is 0.3.2.The software usedANSYS Finite element software (APDL 15.0)3.Solving processPoint 1 was choosed as the Coordinate point, horizontal to the right was the X axis,the upright direction is choosed as the Y axis to create a coordinate system. The nodes was numbered as shown in Figure 1,node 1 and node 5 was fixed,and the force on node 6,7,8 was is 1k N,the direction is opposite to the Y-axis3.1 The preparatory work before analysis(1)Specify the new file name. Select Utility>Menu> File>Change Jobname, then pop-up the dialog box Change Jobname, input the the working file name ‘2D-sp’ in the Enter New Jobname, click OK to finish the difinition, as shown in Fig.2.Fig.2. The difinition of working file name.(2)Specify a new title. Select Utility>Menu>File>Change Title,then pop-up the dialog box Change Title, input the the file name ‘2D-sp pro’ in the Enter New Title, click OK to finish the difinition, as shown in Fig.3.Fig.3. The difinition of file name.(3)Re-refresh the graphics window.Select Utility>Menu>Plot>Replot, the defined information was displayed in the graphics window.(4)Define the structural analysis. Run the main menu Main Menu>Preferences,then choose the Structural, click OK to complete the definition of the analysis type , as shown in Fig.4.Fig.4. The definition of the structural analysis.3.2 Define the element typeRun the main menu Main Menu>Preprocessor>Element Type>Add, then pop-up the dialog box Element Types, click the button Add to build a new element type, then pop-up the dialog box Library of Element Types, choose Link first, and then select 3D finit stn 180(Link1),click the button OK to finish the definition of the element type, click the button Close to finish the settings, as shown in Fig.5.Fig.5. The definition of the element type.3.3 Define the real constantsRun the main menu Main Menu>Preprocessor>Real Constants Add, then pop-up the dialog box of real constants, click the button Add to come into the constant input dialog box, as shown in Fig.6. Input the sectional area of the truss (0.01m2) in AREA, click the button OK to finish the input of the real constants, as shown in Fig.7.Fig.6. Get into the instance constant dialog box.Fig.7. The definition of the real constants.3.4 Define the material propertiesRun the main menu Main Menu>Preprocessor>Material Props>Material Models,then pop-up the dialog box of material properties, and select Structure、Linear、Elastic、Isotropic, as shown in Fig.8.When the selection was completed, appeared the MaterialProperties input dialog box appears,then input elastic modulus 2e11 and the poisson's ratio 0.3, as shown in Fig.9, click OK to finish the input of the material properties.Fig.8. Get into the setting of material properties.Fig.9. The difinition of the material properties.3.5 Establish the analytical model(1)Create the nodes. The coordinates of the 1—8 nodes as shown in Table.1. Run the main menu Main Menu>Preprocessor> Modeling>Create>Nodes>In Active CS. The create node entry dialog box appears as shown in Fig.10. I nput the first node 1 and its’ x, y, z coordinate, then click Apply to finish the creating of the node. Similarly, create the nodes 2—8, click OK to finish the creating of the nodes, as shown in Fig.10.Table.1.The coordinates of geometry model nodes.Fig.10. The dialog box of nodes input.Fig.11. The creation of the nodes.The created nodes as shown below:(2)Created the bar unitRun the main menu MainMenu>Preprocessor>Modeling>Create >Elements>Auto Numbered>Thru Nodes, then pop-up the dialog box Element from Nodes, pick the nodes 1 and 2, click Apply to complete the first lever unit . Similarly, pick both ends of the rod in turn, click Apply to complete the lever unit, lastly click OK, as shown in Fig.12.Fig.12. Model establishment of the herringbone truss.3.6 Apply constraints and loads(1)Impose constraintsRun the main menu Main Menu>Solution>Define Loads>Apply>Structural> Displacement>On Nodes, the pick menu appears, select nodes 1 and 5 in turn, then click OK, the constraint definition dialog box appears,as shown in Fig.13. Choose All DOF to constrain all degrees of freedom,other items by default,then click the button OK to complete the constraint definition.Fig.13. Impose the constraints.(2)Apply the loadRun the main menu Main Menu>Solution>Define Loads>Apply>Structural> Force/Moment>On Nodes, the pick menu appears, select nodes 6, 7 and 8 in turn, click OK , then the load definitions dialog box appears,as shown in Fig.14. The load type is concentrated force FY. The value is -1000 , Then clickthe OK button to complete the application of the load.Fig.14. The application of the load.Figure after load application as shown below:3.7 SolutionRun the main menu Main Menu>Solution>Solve>Current LS, then pop-up the dialog box Solve Current Load Step, click STAT Command, then click STAT Command>File>Close toclose the STAT Command window, then click OK to finish the steps.Then the computer started the solution. The promption of "Solution is done" indicated that the solution was completed, click the button Close to finish the solution, as shown in Fig.15.Fig.15. The process of the solution.3.8 View the analysis results(1)Define the cell table. In ANSYS, some data can not be directly accessed, so we need to complete the definition of cell to access the results.Run the main menu Main Menu>General Postproc>Element Table>Define Table, then pop-up the dialog box, click the button Add. The unit table definition dialog box appeared, as shown in Fig.16.Fig.16a. The definition of the cell table.Fig.16b. The definition of the cell table.(2)Display the axial force (axial stress) diagram. Run the main menu Main Menu>General Postproc>Plot Results> Contour Plot>Elem Table. Then pop-up the cell table result selection dialog box , as shown in Fig.17. Choose A-STR and click OK to view the axial force (axial stress) diagram , as shown in Fig.18.Fig.17. Contor plot of Element Table Data.(3)Display the result. The result as shown in Fig.18.Fig.18. The final result.。
哈工大有限元大作业1-16S108346殷琪

有限元大作业1
一、题目
两对边简支、另两对边固支的矩形薄板(如图1),其上承受均布压力q的作用,已知:a = 1000mm, b = 500mm,板厚 h = 20mm, q=-1N/mm2,E=2.1×105N,μ = 0 .3 求对称截面上的挠度w及弯矩 Mx、My的分布曲线。
图1.矩形薄板
二、求解过程
1.进入ANSYS 2.设置计算类型 3.选择单元类型 4.定义材料参数5.确定薄板的厚度 6.生成几何模型 7.网格划分
8.模型施加约:
a 分别给两长边施加固支约束、给两短边施加简支约束
b 给薄板施加均布载荷
9.分析计算
11.弯矩Mx云图显示(如下图)
13.定义与YOZ平面和长边平行的对称面Mx上的路径14.显示对称截面Mx上的挠度(Mx)曲线(如下图)
16.定义与XOZ平面和长边平行的对称截面Mx上的路径17.显示对称截面My上的挠度(My)曲线(如下图)
三、计算结果及感受
在本次分析报告中,平面Mx为与YOZ平面平行的对称截面,平面My为与XOZ 平面平行的对称截面。
我根据《ANYSYS基础进阶》一书中所提供的步骤来做的分析,得到的结果如上面的图中所示,根据薄板Z方向的挠度云图可知,薄板的挠度为-1.08559mm。
通过这次作业感受到了陈老师所说的ANSYS等有限元分析软件只是一个工具,而真正的奥妙在有限元理论中,以前只是单纯的用智能划分网格(smart),现在知道了去想如何划分才能得到较合理分析。
