多元统计分析论文
多元统计聚类分析论文_多元统计分析论文

多元统计聚类分析论文_多元统计分析论文多元统计分析论文篇1多元统计分析课程教学探讨摘要:多元统计分析是统计学的一个重要分支,它在自然科学、社会科学、教育卫生以及经济金融等领域具有广泛的应用。
利用多元统计分析方法分析和处理实际数据、解决实际问题是统计学专业学生必备的基本能力,因此,如何进行多元统计分析课程的教学具有相当重要的意义。
本文从教学实践出发,对多元统计分析课程的教学进行了探索和实践,提出了一些教学方法。
关键词:以人为本;案例教学;软件编程;考试改革;创新教学多元统计分析是统计学中内容极其丰富、应用极其广泛的一个重要分支。
随着计算机和统计学的发展,它在自然科学、社会科学、教育卫生以及经济金融等领域中的应用越来越广泛,它已成为进行多元数据分析与处理的非常重要的工具之一。
随着社会的发展,我们常需要处理较为复杂的多维数据以及高维或超高维数据,特别地,对于统计学专业的学生,利用多元统计分析方法分析和处理日常生活中的多维数据是他们应该具备的基本能力。
因此,如何让学生很好地掌握一些基本的多元分析方法并能在实践中加以应用是我们统计学专业的教师应该思考的重要问题。
通过多年的实践教学,我们对多元统计分析课程的教学进行了探索和实践,主要在以下几个方面进行了探索和尝试。
一、转变教育观念,树立“以人为本”的教学理念教育的对象是大学生,教育的目的是以学生的终身发展为基础的。
在教学过程中,我们教师首先应转变教育观念,处处体现以学生为本的人文关怀与教育。
关注学生的思想、学生的需要以及在当今时代下学生所面临的挑战与机遇,争取成为学生的良师益友,建立良好的师生关系;通过案例教学、启发式教学等等多种教学方法,鼓励和促使学生积极参与课堂教学,变被动学习为主动学习,使学生成为课堂的主体;正视学生之间的个体差异,不歧视差生也不偏爱优等生,实施因材施教,使每个学生都得到不同程度的提高与进步。
二、注重案例教学,培养“学以致用”的学习意识三、结合软件教学,提高学生编程和数据处理能力多元分析方法分析和处理的数据是多维数据,通常维数较多,而且观测数据也较多,计算量都比较大,通常需要计算机才能实现。
多元统计分析 课程论文.doc

HUNAN UNIVERSITY 课程论文论文题目:有关我国居民消费因素的分析指导老师:学生名字:学生学号:专业班级:经济统计学院名称: xxx学院目录概述 (1)一、引言 (2)二、数据概述系 (2)三、分析方法 (3)四、数据分析 (3)(一)相关分析 (3)(二)因子分析 (10)(三)聚类分析 (15)五、分析与建议 (18)六、心得体会 (19)参考文献 (20)有关我国居民消费因素的分析概述生活离不开消费,随着社会发展,生活水平提高,消费也在逐渐变化,并且随着经济发展,各个地区的发展水平的差异,消费也产生了不同的变化,此篇论文主要目的是利用多元统计的方法,借助spss软件,对我国31个地区的居民消费情况进行分析。
了解我国31个地区的居民消费情况与统计指标食品烟酒、衣着、居住等8个指标之间的一些联系。
并且通过因子得分,计算并排列出消费因素的综合得分,最后通过聚类分析,对我国31个地区的居民消费情况做一个大致分类,进而对各个地区分类后的情况做一个分析和总结并结合文献以及资料提出一些意见和看法。
一.引言消费在宏观经济学中,指某时期一人或一国用于消费品的总支出。
与经济活动有着密不可分的关系,消费作为社会再生产的最终阶段,是生产者生产产品的目的和导向。
如果没有了消费,生产的存在也会变得毫无意义,消费促进了生产,给生产带来了源动力。
消费者的消费需求,也推动了生产的发展。
并且消费促进了货币流通,提供了就业岗位,降低失业率,拉动了经济增长,最终有助于提高人民的生活水平。
消费是国民经济保持增长的动力,只有拉动消费需求的增长,才能促进投资,促进产业结构的调整、宏观经济的增长,满足人民的物质生活的需求,实现生活水平的提高。
故消费和生活水平有着密切的关系,从而,通过对我国居民消费水平的分析,不但可以直观了解到我国总的消费趋向,各地区不同的消费主导因素,还能客观反映我国总的生活水平也就是经济发展的大致情况。
统计年鉴中的八项指标:食品烟酒、衣着、居住、生活用及服务、交通通信、教育文化娱乐、医疗保健、其他用品及服务。
多元统计分析论文
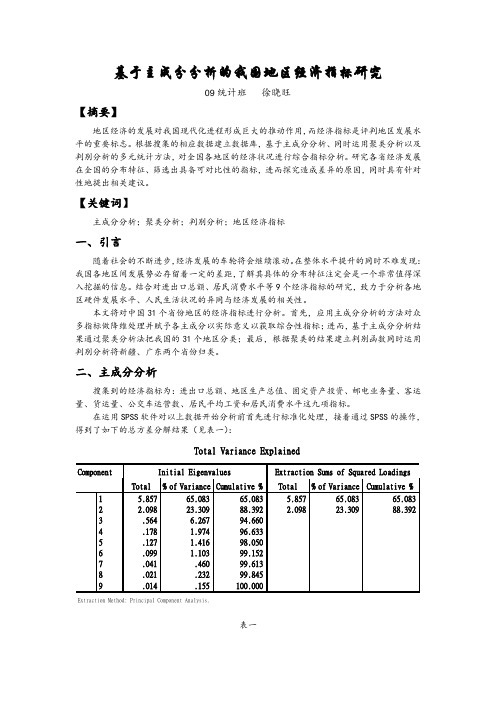
基于主成分分析的我国地区经济指标研究09统计班徐晓旺【摘要】地区经济的发展对我国现代化进程形成巨大的推动作用,而经济指标是评判地区发展水平的重要标志。
根据搜集的相应数据建立数据库,基于主成分分析、同时运用聚类分析以及判别分析的多元统计方法,对全国各地区的经济状况进行综合指标分析。
研究各省经济发展在全国的分布特征、筛选出具备可对比性的指标,进而探究造成差异的原因,同时具有针对性地提出相关建议。
【关键词】主成分分析;聚类分析;判别分析;地区经济指标一、引言随着社会的不断进步,经济发展的车轮将会继续滚动。
在整体水平提升的同时不难发现:我国各地区间发展势必存留着一定的差距,了解其具体的分布特征注定会是一个非常值得深入挖掘的信息。
结合对进出口总额、居民消费水平等9个经济指标的研究,致力于分析各地区硬件发展水平、人民生活状况的异同与经济发展的相关性。
本文将对中国31个省份地区的经济指标进行分析。
首先,应用主成分分析的方法对众多指标做降维处理并赋予各主成分以实际意义以获取综合性指标;进而,基于主成分分析结果通过聚类分析法把我国的31个地区分类;最后,根据聚类的结果建立判别函数同时运用判别分析将新疆、广东两个省份归类。
二、主成分分析搜集到的经济指标为:进出口总额、地区生产总值、固定资产投资、邮电业务量、客运量、货运量、公交车运营数、居民平均工资和居民消费水平这九项指标。
在运用SPSS软件对以上数据开始分析前首先进行标准化处理,接着通过SPSS的操作,得到了如下的总方差分解结果(见表一):表一由表一中结果可以看到保留2个主成分为宜,这2个主成分集中了原始9个变量信息的88.392%,可见效果比较好,这样原来的9个指标就可以通过这2个综合指标来反映。
此时,这2个主成分就起到了降维的作用。
通过SPSS进一步的操作还可以得到如下的主成分系数矩阵(见表二):表二由表二可以得出前2个主成分的线性组合为:Y1 = 0.852 X1 + 0.979 X2 + 0.821 X3 + 0.957 X4 + 0.885 X5 + 0.742 X6 + 0.967 X7 +0.226 X8 + 0.513 X9Y2 = 0.393 X1 - 0.113 X2 - 0.419 X3 - 0.032 X4 - 0.233 X5 - 0.483 X6 + 0.109 X7 +0.915 X8 + 0.786 X9通过对上述线性组合的观察,我们可以得出:在主成分1中进出口总额、地区生产总值、固定资产投资、邮电业务量、客运量、货运量和公交车运营数这几项指标的系数明显比主成分2的系数大,可以将Y1归类为地区经济发展中的硬件基础指标;在主成分2中平均工资和消费水平指标的系数最大,可以将Y2归类为地区经济发展中的居民生活指标。
多元统计分析期末论文

吉林财经大学2012-2013学年第一学期多元统计分析期末论文学院:工商管理专业:人力资源管理年级:1012学号:0802101218姓名:齐婧妍我国地区经济发展浅析摘要:本文主要运用聚类分析法,主成分分析法,因子分析法三种多元统计分析方法对2011年我国31个省、市、自治区的地区经济发展状况以及影响地区经济发展的主要因素(指标)相结合进行剖析。
根据不同分类方法得出不同的分析结果,从而从不同角度分析我国各地区经济发展存在的主要差异以及导致这些差异出现的原因,并最终就三种统计分析方法的结果对我国目前地区经济发展状况进行客观的综合概述。
关键字:地区发展水平聚类分析法主成分分析法因子分析法一、引言在日常生活过程中,我们常常遇到一些计算量大,分析工作复杂度高的数据分析工作,为了能够更加简便地进行数据分析,在此给大家介绍几种多元统计分析的方法。
本文主要运用了聚类分析法,主成分分析法和因子分析法对2011年我国31个省市自治区地区经济发展水平以及影响地区经济发展的几项重要指标进行了统计分析。
二、聚类分析聚类分析是研究“物以类聚”的一种方法。
聚类分析是应用最广泛的一种分类技术,它把性质相近的个体归为一类,使得同一类中的个体具有高度的同质性,不同类之间的个体具有高度的异质性。
聚类分析的职能是建立一种分类方法,它是将一批样品或变量,按照它们在性质上的相似程度进行分类。
通常我们用距离来度量样品之间的相似程度,用相似系数来度量变量之间的相似程度。
1.参与聚类的样本总量表通过观察上表,我们可以看出,在整个聚类过程中,描述我国所有省、市、自治区经济发展状况的31个样品都参与了聚类分析过程,没有遗失或未参与的样品。
这充分说明此次聚类分析已经对全部31个样品的各项指标进行了相似聚类,不需要再利用判别分析再进行二度聚类。
2.样品聚为3类时的样品归类表3.所有样品的聚类树形图(1)结合以上样品归类情况表和聚类树形图,分别给出了将2011年我国31个省、市、自治区经济发展状况作为样品聚类分为三类时的各样品所属类别。
多元统计分析课程论文

HUNAN UNIVERSITY 课程论文论文题目:有关我国居民消费因素的分析指导老师:学生名字:学生学号:专业班级:经济统计学院名称:xxx学院目录12...2.. .3. .. (3).. 310.15.18....19....20....有关我国居民消费因素的分析概述生活离不开消费,随着社会发展,生活水平提高,消费也在逐渐变化,并且随着经济发展,各个地区的发展水平的差异,消费也产生了不同的变化,此篇论文主要目的是利用多元统计的方法,借助spss软件,对我国31 个地区的居民消费情况进行分析。
了解我国31 个地区的居民消费情况与统计指标食品烟酒、衣着、居住等 8 个指标之间的一些联系。
并且通过因子得分,计算并排列出消费因素的综合得分,最后通过聚类分析,对我国31 个地区的居民消费情况做一个大致分类,进而对各个地区分类后的情况做一个分析和总结并结合文献以及资料提出一些意见和看法。
一 .引言消费在宏观经济学中,指某时期一人或一国用于消费品的总支出。
与经济活动有着密不可分的关系,消费作为社会再生产的最终阶段,是生产者生产产品的目的和导向。
如果没有了消费,生产的存在也会变得毫无意义,消费促进了生产,给生产带来了源动力。
消费者的消费需求,也推动了生产的发展。
并且消费促进了货币流通,提供了就业岗位,降低失业率,拉动了经济增长,最终有助于提高人民的生活水平。
消费是国民经济保持增长的动力,只有拉动消费需求的增长,才能促进投资,促进产业结构的调整、宏观经济的增长,满足人民的物质生活的需求,实现生活水平的提高。
故消费和生活水平有着密切的关系,从而,通过对我国居民消费水平的分析,不但可以直观了解到我国总的消费趋向,各地区不同的消费主导因素,还能客观反映我国总的生活水平也就是经济发展的大致情况。
统计年鉴中的八项指标:食品烟酒、衣着、居住、生活用及服务、交通通信、教育文化娱乐、医疗保健、其他用品及服务。
囊括了居民消费的全部项目,居民日常消费可以清楚地从数据中了解到。
多元统计分析论文范文精选3篇(全文)

多元统计分析论文范文精选3篇多元统计分析法是证券投资中非常重要的分析方法,它的理论内容包含了多个方面的理论方法,每个理论分析方法对证券投资有着不同的分析作用,应该对每个分析方法进行认真研究得出相关的结论,再应用到实际经济生活中。
1聚类分析在证券投资中的应用(1)定义:聚类分析是依据研究对象的特征对其进行分类、减少研究对象的数目,也叫分类分析和数值分析,是一种统计分析技术。
(2)在证券投资中应用聚类分析,是基于证券投资的各种基本特点而决定的。
证券投资中包含着非常多的动态的变化因素,要认真分析证券投资中各种因素的动态变化情况,找出合适的方法对这种动态情况进行把握规范处理,使投资分析更加的准确、精确。
1)弥补影响股票价格波动因素的不确定性证券市场受到非常多方面的影响,具有很大的波动性和不稳定性,这种波动性也造成了证券市场极不稳定的进展状态,这些状态的好坏对证券市场投资者和小股民有着非常重要的影响。
聚类分析的方法是建立在基础分析之上的,立足基础进展长远,并对股票的基本层面的因素进行量化分析,并认真分析掌握结果再应用于证券投资实践中,从股票的基本特征出发,从深层次挖掘股票的内在价值,并将这些价值发挥到最大的效用。
影响证券投资市场波动的因素非常多,通过聚类分析得出的数据更加的全面科学,对于投资者来说这些数据是进行理性投资必不可少的参考依据。
2)聚类分析深层次分析了与证券市场相关的行业和公司的成长性聚类分析是一种非常专业的投资分析方法,它善于利用证券投资过程中出现的各种数据来对证券所涉及的各种行业和公司进行具体的行业分析,这些数据所产生额模型是证券投资者进行证券投资必不可少的依据。
而所谓成长性是一种是一个行业和一个公司进展的变化趋势,聚类分析通过各种数据总结归纳出某个行业的进展历史和未来进展趋势,并不断的进行自我检测和自我更新。
并且,要在实际生活中更好的利用这种分析方法进行分析研究总结,就要有各种准确的数据来和不同成长阶段的不同参数,但是,猎取这种参数比较困难,需要在证券市场实际交易和对行业和公司的不断调查研究中才能得出正确的数据。
浅谈多元统计相关论文

浅谈多元统计相关论文摘要:我国中药发展已有悠久历史,中药大多采用复方制剂,以其复方疗效显著而越来越受到重视,在其成分分析中,多元统计分析方法的运用,本质上是一种多变量协同考量的思路。
本文通过对以往多元统计分析方法在中药成分分析数据中的应用作整理总结,对今后相关研究提供理论依据。
关键词:多元统计分析中药成分分析中药物质基础的阐明和科学质量控制方法的建立是中药现代化和国际化的关键,在化学计量学中,多元统计分析方法得到了很好的应用,通过优化了化学量测过程,提高分析效果,应用统计分析方法及其他数学方法和计算机软件的应用对其数据进行整理,已较好的阐明了中药物质成分,结构与其性能之间的复杂关系。
一、应用现状1.1方法在中药成分分析中,多元统计分析方法如多元回归,多元相关分析,逐步回归分析,最大似然法,判别分析,聚类分析和主成分分析,利用电子计算机能迅速而大量地处理实验数据,还广泛采用了蒙特卡洛Monte Carlo统计模拟法,都能在某一特定方面很好的说明其成分,但尚未有统一理论支撑整个体系,也是国内着力于建立中成药数据库的缘由之一。
要进一步定性定量的确定中药成分,并很好的分析中药成分还需不断努力。
在应用中,应用最多的为多元线性回归和Logistic回归方法,其次是通径分析,因子分析和聚类分析的运用较少,比如风险模型,典型相关,MCA分析和Probit分析。
1.1.1成分提取在对中药复方有效成分的整体提取方法,指纹图谱条件优化及定量评价指标,以及基于药理活性的组方条件优化的基础上,化学模式识别方法引入中药分析体系,模式识别,指通过相关软件等用数学方法来实现模式的自动处理和判别,模式识别可大致分为用监督模式识别判别分析方法,是实现规定分类的标准和种类的数模,并且通过大批已知样本的信息处理找出规律,再预报未知样本的类型,如贝叶斯法Bayes逐步判别分析方法,人工神经网络判别法等,无监督模式识别聚类分析方法,是对一组尚无明确分类的样本,根据它们所变现的变量特征,按相似程度的大小加以归类,最终通过信息处理找出合适的分类方法并实现样本的分类,如系统聚类分析,模糊聚类分析等以及基于特征投影的降维显示方法,另外还有一类基于特征投影的降维显示方法,如主成分分析方法,基于偏最小二乘法的降维方法等,中药的化学模式识别方法可以从复杂的化学测量数据出发,进一步揭示复杂化合物之间的隐藏规律,为中药整体研究提供十分有用的信息。
多元统计分析论文

多元统计分析论文多元统计分析是一种统计方法,用于分析多个自变量与一个或多个因变量之间的关系。
该方法可以帮助研究者探索自变量之间的相互作用,并确定它们与因变量之间的关系。
本文将通过一个案例研究来说明多元统计分析的应用。
假设我们想研究工资水平与教育程度、工作经验和性别之间的关系。
我们收集了200个参与者的数据,其中包括他们的工资水平(因变量),教育程度、工作经验和性别(自变量)。
我们将使用多元线性回归分析来检验这些自变量对工资水平的影响。
我们首先进行数据的描述性统计分析,以了解各个变量的分布和关系。
我们发现工资水平的平均值为5000美元,标准差为1000美元。
教育程度的平均值为12年,标准差为3年。
工作经验的平均值为5年,标准差为2年。
性别中,男性占60%,女性占40%。
接下来,我们进行多元线性回归分析。
我们将工资水平作为因变量,教育程度、工作经验和性别作为自变量。
我们的回归模型如下所示:工资水平=β0+β1*教育程度+β2*工作经验+β3*性别+ε在这个模型中,β0是截距,β1、β2和β3是回归系数,ε是误差项。
回归系数表示自变量对因变量的影响,正值表示正相关,负值表示负相关。
通过进行多元线性回归分析,我们得到了以下结果:教育程度对工资水平有显著影响(β1=1000,p<0.001),工作经验对工资水平也有显著影响(β2=500,p<0.01),性别对工资水平的影响不显著(β3=200,p>0.05)。
由此可见,教育程度和工作经验对工资水平具有显著影响,教育程度每增加1年,工资水平平均增加1000美元;工作经验每增加1年,工资水平平均增加500美元。
而性别对工资水平的影响不显著,即性别不是工资水平的显著预测因素。
在多元统计分析中,我们还可以使用其他方法,如多元方差分析、聚类分析、主成分分析等。
这些方法可以根据研究问题和数据类型的不同,来解读和分析自变量与因变量之间的关系。
总结而言,多元统计分析是一种强大的方法,可以帮助研究者探索多个自变量与因变量之间的关系。
应用多元统计分析论文

河北省十一城市综合实力统计分析摘要:本文根据中国城市经济发展研究中心提出的城市综合经济实力和区域的概念,并利用2009年各城市社会经济发展状况的截面数据,就山东省11市的经济数据进行分析。
首先建立了评价的指标体系,其次,分别采用主成分分析法和聚类分析法对山东省根据行政区域划分的11个市的综合经济实力进行了全面的评价和比较,并在此基础上提出了促进山东各市经济协调发展、共同进步的相关措施。
关键词:城市经济主成分分析聚类分析一、引言在区域经济发展中,城市处于核心和龙头的地位,提高城镇化水平、加快城市化进程是解决当前和未来一系列问题的关键。
山东经济发展显示出不平衡的态势,鲁东的少数几个城市GDP几乎占据全省三分之二[1]。
很显然,山东省各市的城市化水平也存在显著差异, 青岛、济南等的城市化水平始终走在全省乃至全国前列,泰安和滨州则相对落后。
随着黄河三角洲经济一体化进程的加快,山东作为沿海省份必须清楚的看到发展差异并找出差异形成的原因,通过核心城市的优先发展带动区域经济和社会的快速发展,是现实提出的急需解决的问题。
为此,本文在参阅相关文献的基础上,根据中国城市经济发展研究中心提出的城市综合经济实力以及区域的概念,根据区域的行政划分,从山东省11个市出发,利用2009年各城市社会经济发展状况的截面数据,首先建立了评价指标体系,其次,分别采用主成分分析法和聚类分析法对山东省11个市的综合经济实力进行了综合的评价和排位,并在此基础上提出了促进山东省各市经济协调发展、共同进步的相关措施。
面对区域差距带来的影响,山东省应该继续加大固定资产投资的力度,在制定区域发展策略时应该加强区域间的交流和合作,促进各地区优势互补,共同发展。
同时,也要积极鼓励引进外资和开拓国际市场,加快与国际经济的接轨和融合。
另外,还要继续扩大中心城市的规模,在积极建设环渤海产业带的同时,不断加强鲁西和鲁中产业带的建设,提高中心城市的综合竞争力,扩大其对周围地区的辐射和带动作用,最终逐步缩小区域差距,促进各地区和谐发展、共同繁荣。
应用多元统计分析论文

应用多元统计分析论文本篇论文介绍了应用多元统计分析的相关内容。
在引言部分,我们将简要介绍本篇论文的主题和目的,解释多元统计分析在研究中的重要性,并概述论文的结构。
多元统计分析是一种统计方法,用于分析多个变量之间的关系和相互影响。
在研究领域中,多元统计分析被广泛应用,可以帮助研究者理解和解释复杂的数据结构和关系。
它能够帮助研究者发现变量之间的模式、趋势和相关性,从而得出更准确的结论。
本论文旨在探讨如何应用多元统计分析方法来分析特定数据集,并得出相关结论。
我们将介绍所采用的多元统计分析方法和技术,并具体说明它们对于研究结果的解释和解读的意义。
接下来的章节将依次介绍多元统计分析的相关概念、数据集的描述和预处理、统计模型的建立和分析方法的应用。
最后,我们将总结研究结果,并讨论其对研究领域的意义和可能的应用价值。
通过本篇论文的详细介绍和分析,读者将能够了解多元统计分析的基本原理和应用方法,以及如何运用这些方法来解读和分析特定领域的研究数据。
本论文的目的是为学术研究者和相关领域的专业人士提供一个有益的参考,帮助他们在研究中更好地使用多元统计分析方法,并取得可靠的研究成果。
请继续阅读下面的章节,以了解更多关于应用多元统计分析的内容。
研究背景多元统计分析是一个广泛应用于各个学科领域的研究方法。
选择进行多元统计分析研究的原因可以有很多,首先,通过多元统计分析,我们可以从多个变量的角度来探索和解释问题。
这能够使我们更全面地了解现象背后的本质,并且提供更深入的洞察。
在相关的研究领域和现有的研究成果方面,多元统计分析已经被广泛应用于社会科学、医学、教育、经济学等等领域。
许多研究已经表明,多元统计分析是一种有效的研究方法,可以帮助研究者发现变量之间的关系和相互影响。
然而,尽管多元统计分析已经被广泛应用,仍然存在一些研究空白需要填补。
例如,某些特定领域可能缺乏基于多元统计分析的研究,或者现有研究可能只关注了特定方面而忽略了其他重要变量。
多元统计分析课程论文

《应用多元统计分析》期末论文农村居民生活消费分析——2014年我国农村居民消费分析目录摘要 .......................................................................... 错误!未定义书签。
一、引言 (2)二、因子分析法 (2)2.1统计思想 (2)2.2因子的确定 (3)2.3分析过程 (4).................................................................................. 错误!未定义书签。
.................................................................................. 错误!未定义书签。
.................................................................................. 错误!未定义书签。
三、聚类分析法 (8)3.1系统聚类法的思想 (9)3.2系统聚类 (9)四、影响农村居民消费因素 (9)4.1收入影响 (10)4.2消费环境影响 (10)4.3消费观念影响 (10)五、参考文献 (11)六、附录: (11)农村居民生活消费分析——2014年我国农村居民消费分析摘要:本文综合了因子分析与聚类分析,先进行因子分析, 再用因子分析的结果进行聚类分析。
在2014 年农村居民消费结构的数据基础上, 本文较多运用了31个省份的因子得分,计算出单因子情况下31个省份的得分和31个省份在八项消费产生的3个因子上的综合得分, 再把该得分作为31个省份的属性, 采用离差平方和(ward)方法进行聚类, 最后将城市分为三层,对整体进行综合评价和说明。
关键词:因子分析;聚类分析;综合评价2014年我国农村居民消费分析一、引言由于我国国土辽阔,自然条件差异很大,经济发展极不平衡,一些地区、一些乡村、一些居民群体的生活目前与小康指标仍有差距,有的甚至还没有解决温饱问题。
多元统计期末论文

多元统计分析期末论文论文题目:分析影响蔬菜价格波动的因素作者:学号:完成日期:2013年月评语:论文成绩:背景与问题蔬菜市场瞬息万变,蔬菜价格影响到每个人的日常生活。
蔬菜价格与市场供应量密切相关,如何利用现有的信息来预测未来蔬菜市场价格的走势,合理的引导农贸市场蔬菜的供应意义重大。
现有的信息量巨大,这些信息涉及到天气,一定周期内该蔬菜的价格以及其他有竞争关系的蔬菜的价格的影响。
本文的问题和任务是以冬瓜为例,从现有信息中挑选出对冬瓜价格走势(未来24小时)有影响的因素,以及确定这些影响因素与价格走势之间的模型关系。
摘要在探究影响蔬菜价格的因素中,本文主要通过系统距离法和主成分分析法来筛选出影响因素,又运用主成分回归模拟出具体各影响因素和价格波动的具体关系。
本文的数据是2012年11月1日到12月11日,四十天的天气(气温,天气,风力)数据记录,和几乎所有日常生活中常见的蔬菜在此期间的价格,共32种。
数据量庞大,且混杂有无关因素。
有效的筛选出有利信息,去除干扰数据,不仅有利于提高最终结论的准确性,还能使结果避免过于复杂。
本文主要通过主成分分析来达到上述目的。
由系统聚类法得到的变量个数仍然较多,且相互之间具有一定的关联度,比如都受天气状况的影响较大。
因而,反映的信息在一定程度上有重叠,且变量个数太多,使后续确定各因素与价格走势的数学关系式过于复杂,因此,此处用主分量分析法获得较少的综合变量,使他们既能充分反映样本信息,又有利于后续模型的建立。
符号说明t时刻各种蔬菜的价格 p(t);t时刻气温T(t);t时刻天气量化值W(t);t时刻风力F(t);准备工作1对各项指标进行量化天气状况的量化本文涉及的样本中天气状况共有:晴、晴转多云、多云转晴、多云、多云转阴、阴、阴转小雨、小雨、阴转雾、雨夹雪,这几种天气状况。
为了数据处理的未来24小时蔬菜价格的走势(价格的变化率,本文定义为价格的变化率=预测的未来24的价格-当前价格)和天气状况的影响,并且相关的有竞争关系的蔬菜的价格走势密切相关。
多元统计分析论文

因子分析和聚类分析在全国省会城市经济实力分析中的应用摘要:本文利用SPSS中的因子分析和聚类分析功能对全国26个省会城市经济实力进行分析。
先用因子分析,再对因子分析的结果进行聚类分析。
本文选取2012年上半年26个省会城市的9个经济指标,通过因子分析提取两个因子计算出26个省会城市的综合得分函数,再根据因子分析得出的得分函数对这些城市进行聚类分析,分类结果为:然后再对分类后的城市进行分析说明,最后针对分类的结果进而得出经济综合实力的结论。
关键词:因子分析聚类分析 SPSS 经济实力一、引言城市的发展是经济发展和社会进步的重要标志。
目前,我国正处于加快推进现代化的历史阶段。
现代城市既要有发达的经济,也要有发达的文明。
文明城市是指在全面建设小康社会、推进社会主义现代化建设新的发展阶段,物质文明、政治文明与精神文明协调发展,经济和社会事业全面进步,精神文明建设取得显著成就,市民整体素质和城市文明程度较高的城市。
文明城市,是反映一个地区现代文明程度、城市综合竞争实力的重要标志。
创建文明城市对经济社会发展所产生的现实意义和深远影响,已经远远超出了原来一般意义上的群众性精神文明建设活动。
我们要从战略高度来看待创建文明城市的重要意义,提高对创建文明城市重要性的认识。
随着改革开放的脚步,全国各地经济都有着飞速的发展,人们越来越关注各个省会城市经济实力。
经济是衡量一个地区综合实力的重要指标,而依照经济实力对城市进行分类可以看出一个地区综合实力以及发展潜力,利用经济分类,我们也可以得出该地区的发展状况,以及在哪些方面做得不够,哪些方面可以得到改进。
基于以上原因,本文运用SPSS 对全国26个省会城市,合肥, 武汉, 长沙, 郑州, 南昌, 太原, 西安, 福州, 石家庄, 沈阳, 哈尔滨, 长春, 南京, 杭州, 济南, 南宁, 成都, 贵阳, 昆明, 兰州, 西宁, 银川, 海口, 广州, 乌鲁木齐, 呼和浩特2012年上半年的9类经济指标进行因子分析,聚类分析。
多元统计分析聚类分析多元统计聚类分析论文

多元统计分析聚类分析多元统计聚类分析论文多元统计分析论文—论科研经费与效益的关系[摘要]研究多元统计分析的理论,利用主成分分析和聚类分析的方法对区域经济指标体系进行分析和综合,找出实质体的数量特征和内在统计规律性。
通过实际的历史数据进行演算,证实与当时的客观实际情况相吻合,为决策部门衡量本地区的经济发展,制定科学决策提供了有利的支持。
[关键词]多元统计分析;主成分分析;聚类分析;因子分析;Study on the theory of multivariate statistical analysis, using the methods of principal component analysis and cluster analysis on the index system of regional economyFor analysis and synthesis, to find out the essence of the number of features and the internal statistical regularity. Through the historical data of calculus, that is consistent with the actual circumstances, to measure the local area for the decision-making department of economic development, and provide beneficial support to make scientific decision.1.引言在日常生活中,我们常常遇到一些计算量大,分析工作复杂度高的数据分析工作,为了能够更加简便的进行数据分析,在此给大家介绍几种多元统计分析的方法。
本文主要运用了聚类分析法,因子分析法,主成分分析法对科研经费与效益的关系进行统计分析。
多元统计分析论文.

关于各地区住宿业企业基本情况和经营情况的统计分析班级:统计一班姓名:学号:************指导教师:***摘要:关键词:住宿业营业额频数分析因子分析聚类分析判别分析正文:序言:正文:第一步、录入数据:图-1图-2第二步、进行频数分析:表-1统计量法人企业(个) 年末从业人数(人)营业额(亿元)客房收入餐费收入N 有效31 31 31 31 31 缺失0 0 0 0 0 均值506.87 68005.77 90.253 42.250 36.899 中值423.00 56088.00 54.669 25.676 24.175 标准差370.251 59799.092 93.3595 43.5005 37.8579 方差137086.116 3.576E9 8715.988 1892.295 1433.219 偏度 1.296 2.272 1.892 1.895 1.886 偏度的标准误.421 .421 .421 .421 .421 峰度 1.624 7.040 3.405 3.219 3.578 峰度的标准误.821 .821 .821 .821 .821 百分位数25 234.00 26098.00 30.930 15.178 12.91650 423.00 56088.00 54.669 25.676 24.17575 654.00 87962.00 98.731 47.758 44.373 表-1为统计量表,从上表中可以看出各个变量的均值、中值、标准差、方差、偏度、峰度、以及它们的标准误差,法人企业的营业额基本上是由客房收入和餐费收入平摊,但相对来说还是客房收入占得比例较大些。
图-3图-3为带有正态曲线的直方图,描述的是法人企业个数的方面的问题,从图中可以看到各个城市的平均法人个数为506.87,标准误差为370.251,总共有31个城市,而且在这些城市中,法人企业个数在250个的城市居多,大约占到九个。
多元统计分析论文

多元统计分析论文本文主要介绍多元统计分析论文的背景和重要性,并概述了该大纲的目的和结构。
多元统计分析是一种重要的统计方法,用于研究多个变量之间的关系和影响。
在许多领域,如社会科学、经济学、医学等,多元统计分析被广泛应用于数据分析和决策支持。
该大纲旨在帮助读者了解多元统计分析论文的基本要素和结构。
它将包括以下几个部分:引言:介绍多元统计分析论文的背景和重要性,概述该大纲的目的和结构。
文献综述:回顾相关领域的研究成果和知识,介绍已有的多元统计分析方法和应用案例。
研究问题和假设:明确研究中要解决的问题和所提出的假设。
数据收集和变量选择:描述数据收集的方法和过程,并讨论变量的选择和测量。
多元统计分析方法:介绍常用的多元统计分析方法,如多元方差分析、线性回归、因子分析等。
结果分析与讨论:展示并解释多元统计分析的结果,讨论研究发现的实际意义。
结论和建议:总结研究的主要发现,提出对进一步研究的建议。
参考文献:列出引用的文献和资料。
通过阅读该大纲,读者将能够了解如何撰写一篇结构合理、内容详实的多元统计分析论文,并能够应用多元统计分析方法进行数据分析和解释研究结果。
确定该论文研究的核心问题,包括研究对象和相关变量。
本章将详细介绍多元统计分析的相关方法,包括因子分析、聚类分析和回归分析等。
对每种方法的原理、步骤和适用场景进行全面介绍。
因子分析因子分析是一种常用的多元统计分析方法,用于探索变量之间的内在关系。
它可以揭示出变量背后的共性因素,并将多个变量综合为少数几个主成分。
原理因子分析基于统计模型,通过对观测数据进行因子提取和旋转,找出能够解释数据方差的主成分。
这些主成分代表了原始变量的共同变异。
步骤因子分析一般包括以下步骤:数据准备:收集所需的原始数据,并进行预处理,如缺失值处理和标准化等。
因子提取:使用合适的因子提取方法,如主成分分析或主因子分析,将原始变量转化为主成分或因子。
因子旋转:通过旋转因子矩阵,使得因子之间更易解释和理解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北联合大学多元统计课程论文论文题目:对中国各地区综合实力测评学院:理学院专业:统计学班级:统计1班姓名:侯雅琴学号:指导教师:高艳目录摘要、关键字、引言 (1)1 数据说明 (2)2 因子分析 (2)3 聚类分析 (7)4 判别分析 (9)5 结果分析 (12)6 参考文献 (13)附表 (14)对中国各地区综合实力测评【摘要】本文对中国各地区综合实力进行测评,以31个地区2010年的10项指标数据为样本,采用因子分析对描述各地区的实力的各项指标变量进行分析,以聚类分析和判别分析相结合对地区发展类型进行分析,再利用各指标变量间的相关性进行分析,得出相关结论以分析各地区的发展情况。
【关键词】各地区综合实力测评因子分析聚类分析判别分析引言:在这样一个信息时代,只有全面的可持续的发展才是衡量一个地区综合实力的指标,仅仅是经济发展情况不再能全面具体的体现一个地区的综合实力,经济发展水平、科技发展水平、能源储量和利用率、基础设施建设、文化发展水平等等,这些综合的因素才是体现一个地区真正的面貌,单纯的GDP指标并不能完全反映一个地区的经济发展水平,为了克服单纯GDP指标的缺陷,我们在GDP指标的基础上,综合考虑其他各方面的发展指数,本文就外商投资进出口总额、地区生产总值、地区运输路线总长度、医疗卫生室数量、创新产品项目数、创新经费、高校数目、等10个指标变量对31地区的综合实力进行测评,通过因子分析、聚类分析、等多元统计方法对各指标变量以及各地区进行统筹分析,以总结促进各地区和谐可持续发展的原因。
一、数据说明对各地区进行综合测评的各指标变量:原始数据来源:《中国统计年鉴——2010》原始数据见附录表-1二、因子分析:1.考察原有指标变量是否适合因子分析(原有变量之间是否存在一定的线性关系):借助变量的相关系数矩阵,KMO和巴特利特球度检验,进行分析。
表—2由相关矩阵可以看出外商投资进出口总额与地区生产总值、创新产品项目数、创新经费、社会服务设施数的相关系数较高(相关系数值均大于0.5),五个变量间呈现较强的线性关系,农业用地面积和林地面积高度相关,医疗卫生室数量和运输路线长度也具有较高的相关性,都可从中提取公共因子,进行因子分析。
表—3KMO 和 Bartlett 的检验取样足够度的 Kaiser-Meyer-Olkin 度量。
.748Bartlett 的球形度检验近似卡方391.067df 45Sig. .000根据KMO检验,KMO值(小于1)越大表示数据适合做因子分析,由表可知,KMO 值为0.748,根据KMO度量标准可知原始变量适合进行因子分析,同时Bartlett泅渡检验统计的观测值为391.067,相应的p值为0,表明变量间存在较强的相关性,适合做因子分析。
2.提取因子:根据原有变量的相关矩阵,采用主成分分析法提取因子,并选取特征值大于1的特征根。
表—4由上表各因子的累积方差贡献率一列可以看出,前三个因子已经可以解释90.739%的信息量。
因此提取三个主成分已经可以抓住指标变量所表达的内容表—5旋转成份矩阵a成份1 2 3外商投资进出口总额.924-.142 -.063地区生产总值.901.386 -.104运输路线长度.184 .870.334医疗卫生室数量.076 .938-.043创新产品项目数.966.161 -.156创新经费.963.126 -.175高校数目.626 .647-.240社会服务设施数.821.317 -.117林地面积-.150 .175 .922农业用地面积-.179 -.067 .938提取方法 :主成分分析法。
旋转法 :具有 Kaiser 标准化的正交旋转法。
a. 旋转在 5 次迭代后收敛。
从上表可知:对因子进行旋转后每个变量仅在一个公共因子上有较大的载荷,效果更佳,所以有因子旋转的必要,从旋转成分矩阵可得,外商投资进出口总额、地区生产总值、创新产品项目数、创新经费、社会服务设施数在第一公共因子上有较大的载荷,可以归为一类:科技增长型经济指标;运输路线总长度和医疗卫生室数量以及高校数目在第二公共因子上有较大的载荷,可以归为一类:社会基础设施指标;同理,林地面积和农业用地面积归为:土地资源指标。
图—1图—1:旋转后的因子(成分)载荷图,分别以第一主成分和第二主成分第三主成分为轴坐标,按表中数据作图得到主成分图。
从图中可以看出旋转后各成分的变量更集中了。
从图中也可以更具象的看出各指标变量间的关系。
表—7为因子得分系数矩阵。
根据因子得分系数和原始变量的标准化值,可以计算每个观测量的各因子的得分数,并可以据此对观测量进行进一步的分析。
旋转后的因子表达式可以写成:FACT:10 987654321100.0 064.0170.0036.0236.0234.0147.0047.0183.0288.01X XXXXXXXXX FACT++++++--+=10 987654321120.0020.0034.0253.0084.0068.0478.0385.0054.0288.02X XXXXXXXXX FACT-+++--+++-=10 987654321525.0 495.0022.0113.0030.0038.0112.0130.0035.0177.03X XXXXXXXXX FACT+++-++-++=三、聚类分析表—8部分相似矩阵(这是一个不相似矩阵)分析:此表是欧氏不相似性系数矩阵,在行列交叉点上是两个地区的10个变量的欧氏距离,体现的是不相似性,即数值越大,两个地区越不相似,由表可知:广东、浙江、江苏、山东与其他各地区的不相似度较高,说明这四个地区的发展类型相似而与其他地区的发展差异性较大,说明这四个地区的可能属于同一类型。
图—2Rescaled Distance Cluster CombineC A S E 0 5 10 15 20 25Label Num +---------+---------+---------+---------+---------+ 海南 21 -+-+宁夏 30 -+ +-----+北京 1 -+ | |天津 2 -+-+ |上海 9 -+ +-+黑龙江 8 -+-+ | |云南 25 -+ | | |贵州 24 -+ +-----+ |甘肃 28 -+-+ |吉林 7 -+ | |重庆 22 -+ | |辽宁 6 -+ | |安徽 12 -+ | +---------+江西 14 -+-+ | |陕西 27 -+ | |山西 4 -+ | |福建 13 -+ | |广西 20 -+ | +---------------------------+西藏 26 -+ | | |青海 29 -+---+ | | |新疆 31 -+ +-----+ | |内蒙古 5 -----+ | |湖北 17 -+-+ | |湖南 18 -+ +-----------------+ |河北 3 -+ | |河南 16 -+-+ |四川 23 -+ |江苏 10 -+---+ |广东 19 -+ +-------------------------------------------+浙江 11 ---+-+山东 15 ---+图—3从树状图和冰柱图可以看出分为4类时,类间距离比较大,分类层次清晰,说明各类的特点比较突出,分类结果如下:第一类:西、北京、天津、福建、吉林、黑龙江、辽宁、上海、第二类:湖北、湖南、河南、河北、四川第三类:西藏、内蒙古、青海、新疆第四类:江苏广东浙江山东四、判别分析表—10外商投资进出口总额、地区生产总值、创新产品项目数、创新经费相关性较强,地区生产总值与高校数目相关性也很强,说明了科技创新对经济的强大推动力,运输路线总长度和医疗卫生室数量相关性较强,体现了社会基础设施建设各项目之间的关系,林地面积和农业用地面积相关性较强,高校数目和创新经费相关性很强,体现了高校对提升创新水平的作用,从中也可以看出经济建设和社会基础建设与农林地面积呈现一定的负相关,说明了地区的建设对农林地有一定的破坏性,总体上从此表大致了解到各指标标量之间发展促进和制约的关系。
此表给出未标准化的典则判别函数的系数,从表中可以得出判别函数分别是:368..2024.071-=X y 根据典则判别式函数的系数可以计算出判别分数判别函数如下:250.6002.0002.0131.010812.210062.110978.810637.710938.1109766453625171-+-+⨯-⨯-⨯+⨯+⨯=-----X X X X X X X X F 582.23003.0006.0002.0009.010129.4001.010856.2001.010609.110987665352172-+-++⨯-+⨯++⨯=---X X X X X X X X X F 726.64027.0034.0002.0028.010983.5003.010854.4002.010073.110987665352163-+-++⨯--⨯-+⨯=---X X X X X X X X X F 191.129003.0004.0008.0879.010348.1005.010974.6003.010842.110987665352164-+-+-⨯++⨯++⨯-=---X X X X X X X X X F 现在选择具有代表性的地区:西藏、江苏 ,利用判别函数判别其分类,以验证聚类分析的结果的正确性西藏: 3F >2F >1F >4F 所以西藏属于第三类 江苏: 4F >1F >2F >3F 所以江苏属于第四类 验证了聚类分析结果的正确性五、结果分析由因子分析结果我们可以知道科技创新指标变量和经济指标变量归为一类:科技增长型经济指标,从新经济增长理论的视角将经济增长、科技创新整合为一个理论分析框架进行实证研究,结果表明:区域经济非均衡增长在很大程度上依赖于科技进步、科技知识生产等情况。
凡是科技创新能力较强的省区,大多都是经济实力较强的省区,多是东部省区,如: 浙江省、广东省,与聚类分析结果的第四类结果相同;而科技创新能力较弱的省区,同时也是经济实力比较弱的省区,多属于西部省区。
因此,聚类结果中的第三类西藏实施西部大开发战略,其中一个重要方面就是实施西部科技创新战略,提高西部科技创新能力。
所以聚类分析结果与实际情况和相关政策很符合。
找到发展制约因素所在,我们就要对症下药,特别在科技发展日新月异、经济增长方式由粗放型向集约型转变的情况下,科技进步更成为经济增长的主要推动力和决定性制约因素。
所以更要加强中西部地区的科技创新能力,让科学技术成为第一生产力。
