高数9-2(第二型曲线积分)
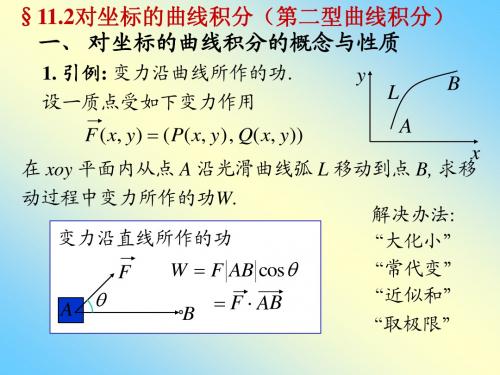
高数考研中有关曲线积分问题的求解方法

fx=烈f)
设有光滑曲线正{:三鬣2te[a.p】(1),
函数f(x,Y,z)为定义在L上的连续函数,
则£,(薯”)出= 侈(似f),以味烈o)√;万丽_歹琢孓万丽dt
例1(09年数1考研题)已知曲线
l珧=f2x雁丽=J?5,厕 l:y嚣X2(o≤x≤√2),贝0 I,嚣幽=——
彰+扰=一可阮力,
所以一,(‘y)一习::,(五y)+力:。
又署=√“"~《,善=,(毛y)+彬, 幻aP 所以素。一03,,由定理3可得对D内的任
意分段光滑的有向简单闭曲线L,都有:
},∥ky)出一xf(x,j,)ay=0。
例6(05年数l考研题)设函数妒(y)具有连 续导数,在围绕原点的任意分段光滑简单闭
JI 8
、
1
O
^
解:椭圆,的方舞可化为3p+4v2=12,
代入积分中得f.(2xy+3x2+4y2)凼=
}t(2xy+12)由2六2叼施+fjl胁
因为xy是x的奇函数,曲线l关于y轴对称, 由定理l可知●.母凼=0..
且I坤=a。
故f,(2xy+3x2+4y2)西=12a.
2第二型曲线积分题型的求解方法 2.I化为定积分的方法
五砂一2ydr。jrxdy一2ydx—J删+J∞
=l『c筹一善,蛐=g姗=挈
例4(03年数1考研题)已知平面区域 D={(墨y)10≤Xs以0sYs万},L为D的正 向边界。试证:
(1)f矿’妙一"_。dx=扣_7咖一ycm‘办,
(2)豇∞^7痧一y矿·。矗≥2霄2
解:(1)根据格林公式,得:
fJ矽‘7dy—yo-mXdx=ff(口。7+#+“。)西c砂
华南理工大学高数答案第9章

第九章 曲线积分与曲面积分作业13 对弧长的曲线积分1.计算d Lx s ⎰,其中L 为直线y x =及抛物线2y x =所围成的区域的整个边界.解:L 可以分解为[]1:,1,0,1L y x y x '==∈及[]22:,2,0,1L y x y x x '==∈1211d d d LL L x s x s x s x x x x =+=+⎰⎰⎰⎰⎰()()113222001121d 1414883212x x x x =++=+⋅+=+2.4433d L x y s ⎛⎫+ ⎪⎝⎭⎰,其中L 为星形线33cos ,sin x a t y a t = =在第一象限内的弧π02t ⎛⎫≤≤ ⎪⎝⎭.解:L 为33cos ,sin ,0,,2x a t y a t t π⎡⎤= =∈⎢⎥⎣⎦223cos sin ,3sin cos ,3sin cos dx dya t t a t t ds a t tdt dt dt=-== 原式()4722442233031cossin 3sin cos 1sin 2sin 222a t t a t tdt a t tdt ππ⎛⎫=+⋅=- ⎪⎝⎭⎰⎰()7772223333003311cos 2cos 2cos 2cos 2883a t d t a t t a ππ⎛⎫=-+=-+= ⎪⎝⎭⎰ 3.计算d xyz s Γ⎰,其中Γ折线ABC ,这里A ,B ,C 依次为点)3,4,1(),3,2,1(),0,0,0(.解:[]:,,2,3,0,1,123x y zAB x t y t z t t ds =====∈= []:1,3,,2,4,BC x z y t t ds dt ===∈=[]:,,4,3,0,1,143x y zCA x t y t z t t ds =====∈=142d d d 231318ABBCxyz s xyz s xyz s t t t t dt Γ=+=⋅⋅+⋅⋅=⎰⎰⎰⎰⎰4.()22d xy z s Γ+⎰,其中Γ为螺线cos ,sin ,x t t y t t z t = ==上相应于t 从0变到1的一段弧.解:Γ为[]cos ,sin ,,0,1,x t t y t t z t t ds = ==∈=()()112222201d (222x y z s t t t t Γ+=⋅=+-+⎰⎰⎰ ()()1532222122222253t t ⎡⎤=+-⋅+==⎢⎥⎣⎦5.计算22d Lx y s +⎰,其中L :0,22>=+a ax y x .解:将L 参数化,22cos ,sin cos ,cos ,cos ,x r t y r t r ar t r a t x a t ==⇒===cos sin ,,,sin 2,cos 2,22y a t t t dx a tdt dy a tdt ds adt ππ⎡⎤=∈-=-==⎢⎥⎣⎦222222222d 2cos 2sin 2Lx y s a tdt a ta ππππ-+====⎰⎰⎰6.计算22ed x y Ls +⎰,其中L 为圆周222a y x =+,直线x y =及x 轴在第一象限内所围成的扇形的整个边界.解:边界曲线需要分段表达,从而需要分段积分[]12:0,0,,;:sin,cos ,0,,;4L y x a ds dx L x a t y a t t ds adt π⎡⎤=∈===∈=⎢⎥⎣⎦2123:,,;L y xx ds L L LL ⎡=∈==++⎢⎣⎦从而22400ed 4aax yxax aLa s e dx e adt e e ππ+=+⋅+=++⎰⎰⎰112244a a a a aa a e e e e e ππ=-++-=+-作业14 对坐标的曲线积分1.计算下列第二型曲线积分:(1) ()()d d L x y x x y y ++-⎰,其中L 为按逆时针方向绕椭圆22221x y a b+=一周;解:L 为cos ,sin ,:02x a t y b t t π==→原式()()20sin cos sin cos cos sin a t a t b t b t a t b t dt π=-++-⎡⎤⎣⎦⎰ 22222200sin 2cos 2sin 2cos 20224a b ab t a b ab t t dt t ππ⎛⎫⎛⎫++=-=+= ⎪ ⎪⎝⎭⎝⎭⎰(2)()d d 1d x x y y x y z Γ+++-⎰,其中Γ是从点()1,1,1到点()2,3,4的一段直线;解:Γ是111,1,12,13,:01213141x y z x t y t z t t ---===+=+=+→--- 原式()()()1121231121t t t t dt =+++++++-⎡⎤⎣⎦⎰()()1126146713t dt t t=+=+=⎰(3)d d d y x x y z Γ-+⎰,其中Γ是圆柱螺线2cos ,2sin , 3 x t y t z t ===从0t =到2πt =的一段弧;解:Γ是2cos ,2sin , 3 ,:02x t y t z t t π===→原式()()202sin 2sin 2cos 2cos 3t t t t dt π=--+⎡⎤⎣⎦⎰ ()()2200432dt t πππ=-+=-=-⎰(4) 计算曲线积分(12e )d (cos e )d y y Lxy x y x y +--⎰,其中L 为由点A (-1, 1)沿抛物线2y x =到点O (0, 0), 再沿x 轴到点B (2, 0)的弧段.解:由于积分曲线是分段表达的,需要分段积分2:,:10AO y x x =-→;:0,:02OB y x =→原式222221(12e )d (cos e )2dx (e )d x x xx x x x x x -=+--+⎰⎰2223221(12e 2cos 2e )d d x x x x x x x x -=+-++⎰⎰()222004211113sin e d de 21sin1sin11xx x x xx x xee ----=-+++=-++=+-⎰⎰2. 设力F 的大小等于作用点的横坐标的平方,而方向依y 轴的负方向,求质量为m 的质点沿抛物线21x y -=从点()1,0移动到点()0,1时,力F 所作的功.解:{}{}{}2220,10,,,,:1,:01F x x ds dx dy L x y y =-=-==-→()()11352240028123515L L y y W Fds x dy y y dy y ⎛⎫==-=--+=--+=- ⎪⎝⎭⎰⎰⎰3.把对坐标的曲线积分()(),d ,d LP x y x Q x y y +⎰化成对弧长的曲线积分,其中L为:(1) 在xOy 平面内沿直线从点()0,0到点()1,1; (2) 沿抛物线2y x =从点()0,0到点()1,1.解:(1):,:01,0;L y x x dx ds =→>==()()()(),,,d ,d ,,d L L P x x Q x x P x y x Q x y y P x x Q x x x +⎡⎤+=+=⎡⎤⎣⎦⎰⎰⎰(2)2:,:01,0;L y x x dx ds =→>=()()()()22,2,,d ,d ,2,d L L P x x xQ x x P x y x Q x y y P x x xQ x x x +⎡⎤⎡⎤+=+=⎣⎦⎰⎰⎰作业15 格林公式及其应用1.填空题(1) 设L 是三顶点(0, 0), (3, 0), (3, 2)的三角形正向边界,(24)d (536)d Lx y x y x y -+++-=⎰12 .(2) 设曲线L 是以)1,0(),0,1(),1,0(),0,1(--D C B A 为顶点的正方形边界,d d L x yx y ++⎰不能直接用格林公式的理由是_所围区域内部有不可导的点_.(3)相应于曲线积分(,,)d (,,)d (,,)d LP x y z x Q x y z y R x y z z++⎰的第一型的曲线积分是⎰. 其中L 为从点(1, 1 ,1)到点(1, 2, 3)的直线段. 2.计算33(e sin )d (ecos )d x xLI y y x y x y =-++⎰,其中L 是沿半圆周x =从点),0(a A -到点),0(a B 的弧.解:L 加上:0,:BA x x a a =→-构成区域边界的负向()3322(e sin )d (e cos )d 3cos axxLDaI y y x y x y x y d ydy σ-=-++=-+-⎰⎰⎰⎰34230233cos 2sin 4a aaa d r dr ydy a πππθ-=-+=-+⎰⎰⎰v3.计算e 31d e 33d xy xy Ly x y x x x y y ⎡⎤⎡⎤+-+++-+⎣⎦⎣⎦⎰,其中L 为椭圆 22221x y a b+=正向一周. 解:原式()()e 33e 31xy xyD x x y y x y dxdy x y ⎡⎤∂∂=+-+-+-+⎢⎥∂∂⎣⎦⎰⎰ 44Ddxdy ab π==⎰⎰4.计算曲线积分[]()sin d ()cos πd ,LI f x y x f x y x y '=+-⎰其中)(x f '为连续函数,L 是沿圆周222(1)(π)1πx y -+-=+按逆时针方向由点(2,2π)A 到点)0,0(O 的一段弧.解:令1:,:02L y x x π=→ 则,原式()[]111π()sin d ()cos πd L L L L DI dxdy f x y x f x y x y +'=-=--+-⎰⎰⎰⎰⎰()222π1()sin ()cos ππd 2f x x f x x x x ππππ'⎡⎤=-⋅+-+-⎣⎦⎰ ()()222422223π1()sin ππ1222222x f x x ππππππππ⎡⎤=-⋅+--=-⋅++=-⎢⎥⎣⎦5.计算22d d L x y y xx y -+⎰,其中L 为(1)圆周()()22111x y -+-=(按反时针方向);解:()()222222222222222x x y x x y x y x x y y x y x y x y ⎛⎫⎛⎫∂+-⋅-∂-=== ⎪ ⎪∂+∂+⎝⎭⎝⎭++,而且原点不在该圆域内部,从而由格林公式,原式0= (2)闭曲线1x y +=(按反时针方向).解:()()222222222222222x x y x x y x y x x y y x y x y x y ⎛⎫⎛⎫∂+-⋅-∂-=== ⎪ ⎪∂+∂+⎝⎭⎝⎭++,但所围区域内部的原点且仅有该点不满足格林公式条件,从而可作一很小的圆周220.01x y +=(1L 也按反时针方向),在圆环域上用格林公式得, 原式()1122d d d d 1001120.01L L Dx y y xx y y xdxdy x y π--===+=+⎰⎰⎰⎰ 6.证明下列曲线积分在xOy 平面内与路径无关,并计算积分值: (1)()()(),0,0e cos d sin d a b x y x y y -⎰;解:由于()()e sin e sin e cos x xx y y y x y∂∂-=-=∂∂在全平面连续,从而该曲线积分在xOy 平面内与路径无关,沿折线()()()0,00,,b a b →→积分即可, 原式()()0sin e cos d cos 11cos cos 1bax a ay dy b x b e b e b =-+=-+-=-⎰⎰ (2)()()()()2,14231,023d 4d xy yx x xy y -++-⎰;解:由于()()233442423x xy x y xy y x y∂∂-=-=-+∂∂在全平面连续,从而该曲线积分在xOy 平面内与路径无关,沿直线10,1,:122110x y y x x --==-→--积分也可, 原式=()()()24321211341d x x x x x x x ⎡⎤---++--⎣⎦⎰()()243213235141d x x x x x ⎡⎤=-+----⎣⎦⎰()()2543213115x x x x x ⎡⎤=-+----=⎣⎦ (3)()()()()π,20,0ecos d e sin d yy x m x x my y -+-⎰.解:由于()()e sin e cos e cos y y y x my x x m x y∂∂-==-∂∂在全平面连续,从而该曲线积分在xOy 平面内与路径无关,沿折线()()()0,0,0,2ππ→→积分即可,原式()()20cos e sin d y ex m dx my y ππ=-+-⎰⎰()2200sin 2my x mx π⎛⎫=-+- ⎪⎝⎭2m m π=--7.设()f x 在(),-∞+∞上具有连续导数,计算()()2221d 1d L y f xy x x y f xy y y y +⎡⎤+-⎣⎦⎰, 其中L 为从点23,3⎛⎫ ⎪⎝⎭到点()1,2的直线段.解:由于()()()()2222111y f xy x y f xy f xy xyf xy x y y y y ⎡⎤+⎧⎫∂∂'⎡⎤-=+-=⎨⎬⎢⎥⎣⎦∂∂⎩⎭⎣⎦在右半平面连续,从而该曲线积分右半平面内与路径无关,沿曲线12:2,,:31L xy y x x==→积分即可,原式()()()()2122232421122d d 22x f f x x x x x x x⎡⎤-+⎢⎥-⎣⎦+⎰13xdx =⎰1232x ⎛⎫= ⎪⎝⎭1942-==- 8.验证下列()(),d ,d P x y x Q x y y +在整个xOy 平面内是某一函数的全微分,并求出它的一个原函数:(1)()()e e d e 1e d x y x yx y x x y ⎡⎤⎡⎤+-+-+⎣⎦⎣⎦;解:由于()()e 1e e e x y x yx y x e e x y x y∂∂⎡⎤⎡⎤-+=-=+-⎣⎦⎣⎦∂∂在全平面连续,从而该曲线积分在xOy 平面内是某一函数的全微分,设这个函数为(),u x y , 则()(),e 1e ,e e x y x y u u u u du dx dy x x y x y y x∂∂∂∂=+=-+=+-∂∂∂∂ 从而()()()e 1e e 1e x y x yu x dy y x g x ⎡⎤=-+=-++⎣⎦⎰()()()e e e e =e x y x y x ux y y g x g x x x∂''=+-=-+⇒∂ ()=e x x x x x g x xd xe e dx xe e c =-=-+⎰⎰,()()1e 1e x y u x y x c =+--++(2)()()223238d 812e d yx y xy x x x y y y ++++;解:由于()()32222812e 31638y x x y y x xy x y xy x y∂∂++=+=+∂∂在全平面连续,从而该曲线积分在xOy 平面内是某一函数的全微分,设这个函数为(),u x y , 则原式3223224d 412e d yydx y x x dy x dy y y =++++()3322224d 412de yydx x dy y x x dy d y =++++⎰()()()32241212e d yyd yx d x y d ye y =++-⎰()32241212e y y d yxx y ye =++-可取32241212e yyu yx x y ye =++-(3)()()222cos cos d 2sin sin d x y y x x y x x y y ++-解:可取折线()()()0,0,0,x x y →→作曲线积分()()22202d 2sin sin d sin cos yx u x x y x x y y y x x y =+-=+⎰⎰9.设有一变力在坐标轴上的投影为2,28X x y Y xy =+=-,这变力确定了一个力场,证明质点在此场内移动时,场力所作的功与路径无关.证:{}2,28F x y xy =+-,质点在此场内任意曲线L 移动时,场力所作的功为()()228Lw x y dx xy dy =++-⎰由于()2282xy y x y x y∂∂⎡⎤-==+⎣⎦∂∂在全平面连续,从而质点在此场内移动时,场力所作的功与路径无关.作业16 对面积的曲面积分1.计算下列对面积的曲面积分: (1)()d xy yz zx S ∑++⎰⎰,其中∑为锥面z =被柱面222x y ax +=所截得的有限部分; 解:∑为x y z z z ===dS ==,:02cos ,22D r a ππθθ≤≤-≤≤原式2cos 2302d d cos a Dzx S x y d r dr πθπθθ∑-==⎰⎰⎰⎰⎰⎰()()42242422cos cos 12sin sin sin 4a d d πππθθθθθθ--+=⎰⎰ (2)()222d xy z S ∑++⎰⎰,其中∑为球面2222x y z ax ++=.解:∑为两块y y x a x x =±==dS ==,:0,02D r a θπ≤≤≤≤原式12222d 2d Da a ax S ax S ∑∑+=+=⎰⎰⎰⎰22Da a +2334aDaad πθ=⎰223340=888a d a r aa a πππ--=-=2.计算d y S ∑⎰⎰,∑是平面4=++z y x 被圆柱面122=+y x截出的有限部分.解:∑为两块4,1,1x y z x y z z =--=-=-,dS =,:01,02D r θπ≤≤≤≤原式D=13220sin 03ar d r dr ππθθθ==⋅=⎰ (或由()(),,,,x y z x y z ∈∑⇒-∈∑,而积分微元反号推出)3.求球面2222a z y x =++含在圆柱面ax y x =+22内部的那部分面积. 解:∑为两块x y z z z ===dS ==,:0,02D r a θπ≤≤≤≤原式12d 2DS dS ∑∑=+=⎰⎰⎰⎰cos 22=2a ad πθπθ-⎰⎰()()cos 222202=2sin 41242a ad a a a d a a ππθππθθθπ-⎛⎫-=-=- ⎪⎝⎭⎰⎰⎰4.设圆锥面z =()a h 为圆锥面的底面半径,为高,其质量均匀分布,求它的重心位置.解:设密度为单位1,由对称性可设重点坐标为()00,0,zDDzdS ∑==⎰⎰200ad r dr πθ==⎰⎰DDdS dxdy ∑==⎰⎰ad rdr πθπ==⎰⎰023h z ==,故重点坐标为20,0,3h ⎛⎫ ⎪⎝⎭5.求抛物面壳()2212z x y =+()01z ≤≤的质量,此壳的密度按规律z ρ=而变更. 解:(2212Dm dS x y ρ∑==+=⎰⎰⎰⎰2012d r π=⎰()()22532200222(1112253515t t t πππ⎛⎫⎡⎤=+-=+-+=- ⎪⎢⎥ ⎪⎣⎦⎝⎭⎰作业17 对坐标的曲面积分1.d d d d d d z x y x y z y z x ∑++⎰⎰,其中∑是柱面221x y +=被平面0z =及3z =所截得的在第一卦限内的部分前侧.解::01,03,cos 0,0yz y z x D y z x x α=≤≤≤≤>==原式=d d d d d d 0d d yzzxD D z x y x y z y z x y z z x ∑∑∑++=++⎰⎰⎰⎰⎰⎰⎰⎰13100032d 262yz D y z dy π====⎰2.计算曲面积分2()d d d d z x y z z x y ∑+-⎰⎰,其中∑为旋转抛物面221()2z x y =+下侧介于平面0z =及2z =之间的部分. 解:22221(),,,:4;2x y xy z x y z x z y D x y =+==+≤:02,yz x D z y =≤≤≤原式=1122()d d ()d d d d zx y z z x y z z x y ∑∑∑+++-⎰⎰⎰⎰⎰⎰((22221d d d d ()d d 2yz yz zxD D D z y z z y z x y z x =-++⎰⎰⎰⎰⎰⎰22222300112d ()d d 222yzzx D D y z x y z x dz d r dr πθ=++=+⎰⎰⎰⎰⎰224232000222824z dz r dr z πππππ=+=+⋅=⎰⎰3.计算d d d d d d xy y z yz z x xz x y ∑++⎰⎰其中∑是平面1,0,0,0=++===z y x z y x 所围成的空间区域的整个边界曲面的外侧.解:分片积分。
大学高数公式大全

向量在轴上的投影:Pr ju AB = AB cos,是AB与u轴的夹角。
Pr a
bju=(aa1
+
a2
)
=
Pr
ja1
+
b cos = axbx
Pr ja2 + ayby
+
azbz
,是一个数量,
两向量之间的夹角:cos =
axbx + ayby + azbz
ax 2 + ay 2 + az 2 bx 2 + by 2 + bz 2
1 tg tg ctg( ) = ctg ctg 1
ctg ctg
·和差化积公式:
sin + sin = 2sin + cos −
2
2
sin − sin = 2 cos + sin −
2
2
cos + cos = 2 cos + cos −
2
2
cos − cos = 2sin + sin −
i c = ab = ax
j ay
k az
,
c
=
a
b
sin .例:线速度:v
=
w r.
bx by bz
向量的混合积:[abc]
=
(a
b)
c
=
ax bx
ay by
az bz
=
a
b
c
cos
,为锐角时,
cx cy cz
代表平行六面体的体积。
4 / 12
高等数学公式
平面的方程: 1、点法式:A(x − x0 ) + B( y − y0 ) + C(z − z0 ) = 0,其中n = {A, B,C}, M 0 (x0 , y0 , z0 )
曲线积分

曲线积分一. 第一型曲线积分(对弧长的曲线积分) ds y x f L ),(⎰ 引入:开始接触这个概念对大家可能都很突兀,我们从直观上看它的形式,形式和定积分⎰dx x f )(很像,Right ?那它的物理意义和几何意义按照自然界对称的法则应该和定积分也是相似的咯-----我们如果把),(y x f 看成是线密度函数的话,ds y x f L),(⎰可以理解成为曲线形构件的质量咯(*^__^*) ,这当然是它的物理意义;几何意义呢?想想定积分,几何意义是曲边梯形的面积,那么对第一型曲线积分就是曲面的面积咯,沿着一段弧函数对它的曲线积分就是曲面的面积(PS :这个可以作为一种求曲面面积的求法,后面会有题目介绍) 想必通过上面形象的介绍,我们对第一型曲线积分有了一个初步的认识。
现在来看看它的求法:ds y x f L ),(⎰这个式子我们唯一没见过的就是ds 咯,在这里ds 实际上就是弧长,所以第一型也就是对弧长的曲线积分。
那么第一型的求法就等价于求ds ,然后解个定积分就ok 。
根据高数上学过的微分三角形,如果曲线能够表示成参数方程x =ϕ(t ), y =ψ (t ) (α≤t ≤β), 那么显然dtt t t t f ds y x f )()()]( ),([),(22ψϕψϕ'+'=,于是就有⎰⎰'+'=βαψϕψϕdt t t t t f ds y x f L)()()]( ),([),(22,当然如果不用表示成参数方程,把x 看为参数也可以。
注意注意注意注意注意:1.这里的定积分的下限α一定要小于上限β. 原因在于弧长始终是正的,所以t ∆>0,这样定积分的下限一定小于上限。
当然曲线不仅仅是平面上的,三维空间里也可以,计算方法还是一样 的,即dt t t t t t t f ds z y x f )()()()](),(),([),,(222ωψϕωψϕβα'+'+'=⎰⎰Γ。
考研数学:高数重要公式总结(曲线积分)

凯程考研历史悠久,专注考研,科学应试,严格管理,成就学员!考研数学:高数重要公式总结(曲线积分)考研数学中公式的理解、记忆是最基础的,其次才能针对具体题型进行基础知识运用、正确解答。
凯程小编总结了高数中的重要公式,希望能帮助考研生更好的复习。
曲线积分凯程考研历史悠久,专注考研,科学应试,严格管理,成就学员!其实,考研数学大多题目考查的还是基础知识的运用,难题异题并不多,只要大家都细心、耐心,都能取得不错的成绩。
考研生加油哦!凯程考研:凯程考研成立于2005年,具有悠久的考研辅导历史,国内首家全日制集训机构考研,一直从事高端全日制辅导,由李海洋教授、张鑫教授、卢营教授、王洋教授、杨武金教授、张释然教授、索玉柱教授、方浩教授等一批高级考研教研队伍组成,为学员全程高质量授课、答疑、测试、督导、报考指导、方法指导、联系导师、复试等全方位的考研服务。
凯程考研的宗旨:让学习成为一种习惯;凯程考研历史悠久,专注考研,科学应试,严格管理,成就学员!凯程考研的价值观:凯旋归来,前程万里;信念:让每个学员都有好最好的归宿;使命:完善全新的教育模式,做中国最专业的考研辅导机构;激情:永不言弃,乐观向上;敬业:以专业的态度做非凡的事业;服务:以学员的前途为已任,为学员提供高效、专业的服务,团队合作,为学员服务,为学员引路。
特别说明:凯程学员经验谈视频在凯程官方网站有公布,同学们和家长可以查看。
扎扎实实的辅导,真真实实的案例,凯程考研的价值观:凯旋归来,前程万里。
如何选择考研辅导班:在考研准备的过程中,会遇到不少困难,尤其对于跨专业考生的专业课来说,通过报辅导班来弥补自己复习的不足,可以大大提高复习效率,节省复习时间,大家可以通过以下几个方面来考察辅导班,或许能帮你找到适合你的辅导班。
师资力量:师资力量是考察辅导班的首要因素,考生可以针对辅导名师的辅导年限、辅导经验、历年辅导效果、学员评价等因素进行综合评价,询问往届学长然后选择。
高数曲线问题
若极限 lim F ( M i *) M i 1 M i 存在 ,
n
则称此极限为函数 ( M )在有向曲线弧L上对坐标x,y F 的曲线积分 或称第二类曲线积分) ( , 记作 F ( M ) dr lim F ( M i *) ri
n
0 i 1
y
F ( i ,i )
B
求和 W W i
i 1
n i 1
n
近似值
o
L
A
M2 M1
M i 1 x i
yi
M i M n 1
[ P ( i , i ) x i Q( i , i ) y i ].
n
x
取极限 W lim [ P ( i , i ) x i Q ( i , i ) y i ]. 0
L
L
0 i 1
P ( M )dx Q ( M )dy lim
[ P ( i , i )x i Q( i , i )y i ]. 0
i 1
n
其中P ( x , y ), Q( x , y )叫做被积函数 , L叫积分弧段.
2.存在条件:
当P ( x , y ), Q( x , y )在光滑曲线弧 L
x y 1
A
C dx dy dx dy 0 解: AB 1 [1 ( 1)]dx 0 AB x y 1 x y 1
x y 1
D
dx dy dx dy 1 BC 0 [1 1]dx 2. BC x y 1 dx dy dx dy 0 CD 1 [1 ( 1)]dx 0 CD x y 1 dx dy dx dy 1 DA 0 [1 1]dx 2. DA x y 1
高数曲线积分习题讲解

第二类(对坐标的)曲线积分
变力做功问题 W = F d r
F (P,Q, R) r (dx,dy,dz)
n
定义
f ( x , y , z )ds lim 0 i1
f ( i , i , i ) si
n
Pdx
Qdy
Rdz
lim
0
i1
[ P ( i ,i ,
i )xi
Q ( i ,i , i )yi R( i ,i , i )zi ]
证:由对坐标的曲线积分的物理意义知,力F 沿右半平面任意有向
路径
L
所作的功为
W
LF dr
L
k
3
( xdx
ydy)
令
P
kx
3 ,
ky
Q 3 , 则
P y
kx
3
2
y
3kxy
3 ,
Q x
3kxy
3
,
P = Q . y x
所以此力场中场力所作的功与所取得路径无关.
例8.设曲线积分L xy2dx y(x)dy与路径无关,其中(x)具有连续的导数,
弧微分:ds x2(t) y2(t) z2(t) dt
f ( x, y, z)ds
f [ x(t ), y(t ), z(t )]
x2 (t ) y2 (t ) z2 (t )dt
2 间接计算: 化为第二类曲线积分.
注:利用对称性,质心公式等简化计算。
(ii)第二类曲线积分 1 直接计算 写出参数方程 x x(t), y y(t), z z(t);
2. 习题
例1. 计算 x2 y2ds,其中L 为圆周 x2+ y2 ax(a 0). L y
高数曲线积分典型例题

高数曲线积分典型例题例1 计算LI xds =⎰,其中L 是圆222x y a +=中(0,)A a 到(,)22a a B -之间的一段劣弧0)a >(.解法1 将积分弧段分为AC 和CB 两段弧来计算(如图9-1所示):ABACCBxds xds xds =+⎰⎰⎰而 2022aACax xds dx a a x ==-⎰⎰,22222aaCBax a xds dx a x ==-⎰⎰.图9-1故21(1)2LI xds a ==+⎰.解法2 L AB =的参数方程为:cos ,sin x a y a θθ==()42ππθ-≤≤,于是2422cos (sin )(cos )I a a a d ππθθθθ-=-+⎰24221cos (1)2a d a ππθθ-==+⎰.错误解答 设(,0)C a ,因为22:AC y a x =-,22:CB y a x =--,则沿此两段弧均有22adx ds a x=-,故有 220221(1)2a ABax xds dx a a x==--⎰⎰.错解分析 错误原因在于选x 作为参数时,y 表示为x 的单值函数时有两个表达式,故必须分为两段计算.注 在求对弧长的曲线积分时,若已知积分曲线的参数方程为L :()x t ϕ=,()y t ψ=且t α=和t β=分别对应点A 与点B 处的参数值,在将曲线积分转化为定积分时,除了要求积分的下限小于上限,还要注意:当t 从α连续变化到β时,相应的点((),())t t ϕψ应在积分曲线上.同时,若将非参数的积分曲线转化为参数形式时,参数方程不同,积分限也不同,计算的难易程度也不同,所以,一般要选取计算较为简单的参数方程形式.例2 计算(1)L x y ds -+⎰,其中L 是顶点为(0,0),(1,0)O A 及(0,1)B 所成三角形的边界.xyoABC解 L 是分段光滑的闭曲线,如图9-2所示,根据积分的可加性,则有(1)L x y ds -+⎰(1)OA x y ds =-+⎰(1)AB x y ds +-+⎰ (1)BO x y ds +-+⎰,由于OA :0y =,01x ≤≤,于是ds dx ==,图9-2故 103(1)(01)2x y ds x dx -+=-+=⎰⎰OA ,而:AB 1y x =-,01x ≤≤,于是ds ===. 故10(1)[(1)ABx y ds x x -+=--+=⎰⎰同理可知:BO 0x =(01y ≤≤),ds dy =,则 11(1)[01]2BOx y ds y dy -+=-+=⎰⎰. 综上所述 31(1)222Lx y ds -+==⎰ 注 当L 是分段光滑的闭曲线时,应该分成光滑曲线逐段计算. 例3 计算22Lx y ds +⎰,其中L 为圆周22x y ax +=,0a >.分析 积分曲线L 关于x 轴对称(如图9-3所示),被积函数为关于y 的偶函数,由对称性得222LL x y ds +=⎰⎰,其中221:(0)L x y ax y +=≥.解法1 直接化为定积分.1L 的参数方程为cos 22a a x θ=+,sin 2ay θ=(0θπ≤≤), 且2ads d θθ=.图9-3于是22202cos 222LLax y ds axds a d a πθθ+==⋅=⎰⎰⎰.解法2 1L 的极坐标方程为()cos (0)2r aπθθθ=≤≤,则()sin y r θθ=,()cos xr θθ=,()cos r a θθ=,ds ad θθ==, 2222202cos 2Lx y ds a d a πθθ+==⎰⎰.注1在解法1中,参数θ表示圆心角,而在解法2中,参数θ表示极坐标系下的极角,参数的意义不同,一般取值范围也不相同.注2 若曲线在极坐标系下的方程为()r r θ=,则ds θ,可直接用此式. 注3 当积分曲线L 关于某个坐标轴对称时,可以考虑采用对称性来计算第一类曲线分.一般地,有以下的结论:(1)若曲线L 关于x 轴对称,记1L 是L 的0y ≥的部分,(,)f x y 在L 上连续,则 a .(,)Lf x y ds ⎰=12(,)L f x y ds ⎰(若(,)f x y 是关于y 的偶函数).b .(,)Lf x y ds ⎰=0(若(,)f x y 是关于y 的奇函数).(2)若曲线L 关于y 轴对称,记1L 是L 的0x ≥的部分,(,)f x y 在L 上连续,则 a .(,)Lf x y ds ⎰=12(,)L f x y ds ⎰(若(,)f x y 是关于x 的偶函数).b .(,)Lf x y ds ⎰=0(若(,)f x y 是关于x 的奇函数).例4 计算2 x yzds Γ⎰其中Γ为折线段ABCD ,这里(0,0,0)A ,(0,0,2),B (1,0,2),C (1,2,3)D .分析 求本题曲线积分的关键是求三条线段CD BC AB ,,的参数方程.在空间中过点111(,,)x y z ,222(,,)x y z 的直线的对称式方程为111212121x x y y z z x x y y z z ---==---, 令该比例式等于t ,可得直线的参数方程.解 如图9-4所示,2222 AB BC CD x yzds x yzds x yzds x yzds Γ=++⎰⎰⎰⎰. 线段AB 的参数方程为 0,0,2(01)x y z t t ===≤≤,则222()()()dx dy dz ds dt dt dt=++ 2220022dt dt =++=,故02200 12=⋅⋅⋅=⎰⎰dt t yzds x AB.线段BC 的参数方程为,0,2(01)x t y z t ===≤≤,则222100,ds dt dt =++=故122 0020BCx yzds t dt =⋅⋅⋅=⎰⎰,线段CD 的参数方程为1,2,2x y t z t===+)10(≤≤t ,则2220215ds dt dt =++=,故11220812(2)525)53CDx yzds t t dt t t dt =⋅⋅+⋅=+=⎰⎰⎰ 2 (2,所以2222 853ABBCCDx yzds x yzds x yzds x yzds Γ=++=⎰⎰⎰⎰. 例5 计算2x ds Γ⎰,Γ为球面2222(0)x y z a a ++=>与平面0x y z ++=的交线. 分析 此题为对空间曲线弧的曲线积分,一般地,若Γ的参数方程为()x t ϕ=,()y t ψ=,()z t ω=(t αβ≤≤)且在t αβ≤≤上具有连续导数,则有222(,,)[(),(),()][()][()][()]f x y z ds f t t t t t t dt βαϕψωϕψωΓ'''=++⎰⎰.解法1 先将曲线Γ用参数方程表示,由于Γ是球面2222x y z a ++=与经过球心的平面0x y z ++=的交线,如图9-5所示,因此是空间一个半径为a 的圆周,它在xOy 平面上的投影为椭圆,其方程可以从两个曲面方程中消去z 而得到,即以()z x y =-+代入2222x y z a ++=有2222a x xy y ++=,将其化为参图9-5数方程,令3cos 22a x t =,即 2cos 3x a t =, sin 22x a y t +=,即有 sin cos 26a ay t t =-,代入2222x y z a ++=(或0x y z ++=中) xzoy得z t t =,从而Γ的参数方程为cosx t =,y t t =,z t t =-(02)t π≤≤.则 dsadt ==, 所以 2222232300222cos cos 333x ds a tadt a tdt a πππΓ===⎰⎰⎰. 解法2 利用对称性由于积分曲线方程中的变量,,x y z 具有轮换对称性,即三个变量轮换位置, 方程不变,故有2x ds Γ⎰2y ds Γ==⎰2z ds Γ⎰,因此2222211()33x ds x y z ds a ds ΓΓΓ=++=⎰⎰⎰232233a a a ππ=⋅=. 注 这里通过巧妙地利用轮换对称性,使计算大大简化,一般来讲,对于曲线的方程, 若其坐标的位置完全平等(即将,,x y z 轮换位置,曲线方程的形式不变),则可以考虑轮换对称性.另外,对曲线积分,若被积函数出现积分曲线方程的形式,则将积分曲线方程代入被积函数中通常可以将积分化简.例6 设一段曲线12ln (0)y x x x x =<≤≤上任一点处的线密度的大小等于该点横坐标的平方,求其质量.分析 首先求出线密度(,)x y ρ,然后再利用公式(,)L M x y ds ρ=⎰即可.解 依题意曲线的线密度为2x ρ=,故所求质量为2L M x ds =⎰,其中 12:ln (0)L y x x x x =<≤≤.则L 的参数方程为ln x xy x =⎧⎨=⎩12(0)x x x <≤≤, 故ds ==,所以3221121[(1)]3x x x x M x ==+⎰332222211[(1)(1)]3x x =+-+. 例 7 求八分之一球面2222(0,0,0)x y z R x y z ++=≥≥≥的边界曲线的重心,设曲线的密度1ρ=.解 设曲线在,,xOy yOz zOx 坐标平面内的弧段分别为1L 、2L 、3L ,曲线的重心坐标为(),,x y z ,则曲线的质量为1123233342L L L L R RM ds ds ππ++===⨯=⎰⎰.由对称性可得重心坐标 ()12312311L L L L L L x y z xds xds xds xds MM++====++⎰⎰⎰⎰()131120L L L xds xds xds MM=++=⎰⎰⎰202243RR R MM π===⎰. 故所求重心坐标为444,,333R R R πππ⎛⎫ ⎪⎝⎭. 例8 计算⎰-++Ldy y x dx y x 2222)()(,其中L 是曲线x y --=11从对应于0=x 时的点到2=x 时的点的一段弧.分析 由于曲线L 是分段光滑的,所以先分别计算在每段光滑曲线的对坐标的曲线积分.如图9-6,将积分分成两部分:⎰-++Ldy y x dx y x )()(2222⎰-++=1)()(2222L dy y x dx y x dy y x dx y x L )()(22222-+++⎰.解法1 1L 的方程为y x =(01)x ≤≤,则有322)()(1222221==-++⎰⎰dx x dy y x dx y x L . 2L 的方程为2y x =-(12)x ≤≤,则dy y x dx y x L )()(22 222-++⎰222 1[(2)]x x dx =+-⎰ 222 1[(2)](1)x x dx +--⋅-⎰22 12 2(2)3x dx =-=⎰. 所以34)()( 2222=-++⎰Ldy y x dx y x . 图9-6解法2 以y 为自变量,1L 的方程为x y =(01)y ≤≤,则10 1222222 12()()(2)23L x y dx x y dy y dy y dy ++-=-==⎰⎰⎰. 2L 的方程为,2y x -=起始点对应的自变量值为1,终点对应的自变量值为0.由于0,2 2=+-=⎰dy x dx x dy dx L ,故有322)()(01222 222=-=-++⎰⎰dy y dy y x dx y x L ,所以34)()( 2222=-++⎰Ldy y x dx y x . 注 将对坐标的曲线积分直接化为对参数变量的定积分时应当注意:(1)当被积函数,P Q 的形式较为简单,将积分曲线L 的方程代入积分式计算定积分比较容易时,可直接计算.(2)参变量的选取视积分曲线具体形式而定,积分下限与上限分别为积分路径的起点与终点所对应的参数值,这与对弧长的曲线积分不同;当积分曲线分段光滑时,应分段积分,并注意各自选择适宜的参数变量作为积分变量.例9 计算,L ydx xdy +⎰ 如图9-7所示,L 是从点(,0)A a -沿上半圆周222x y a +=到点(,0)B a 的一段弧.分析 关于对坐标的曲线积分的计算,与对弧长的曲线积分相似,也分三种,不同之处在于: 对坐标的曲线积分中的曲线为图9-7 有向的,因此化为定积分时,积分上、下限只与曲线的起点和终点有关,而与其大小无关.解法1 利用直角坐标计算.记1L 为222x y a +=上从点(0,)C a 到点(,0)B a 的一段劣弧.则2222aLaydx a x dx a π-=-=⎰⎰(定积分的几何意义). 而1222222LL axdy xdy a y dy a π==-=-⎰⎰⎰,所以 0L ydx xdy +=⎰.解法2 利用曲线的参数方程计算.L 的参数方程为:cos ,sin x a y a θθ==,在起点(,0)A a -处参数值取π,在终点(,0)B a 处参数值相应取0,故θ从π到0.则0sin (cos )cos (sin )Lydx xdy a d a a d a πθθθθ+=+⎰⎰=02cos 20a d πθθ=⎰.yo(,0)A a -(,0)B a x解法3 设,P y Q x ==,故1P Q y x∂∂==∂∂,由曲线积分与积分路径无关得 0LABydx xdy ydx xdy +=+=⎰⎰,其中:0AB y =.解法4 利用格林公式.设,P y Q x ==,则有1P Q y x∂∂==∂∂,由于积分路径不封闭,需要作辅助线:0y =BA ,记BA 与L 所围成的闭区域为D ,得LL BABAydx xdy ydx xdy ydx xdy ++=+-+⎰⎰⎰00ABDd ydx xdy σ=++=⎰⎰⎰.注1 当积分曲线L 关于某个坐标轴对称时,可以考虑采用对称性来计算第二类曲线分.一般地,有以下的结论:若曲线L 关于x 轴对称,记1L 是L 的0y ≥的部分,(,)f x y 在L 上连续,则 a .(,)Lf x y dx ⎰=12(,)L f x y dx ⎰(若(,)f x y 是关于y 的奇函数).b .(,)Lf x y dx ⎰=0(若(,)f x y 是关于y 的偶函数).若曲线L 关于y 轴对称,记1L 是L 的0x ≥的部分,(,)f x y 在L 上连续,则 a .(,)Lf x y dy ⎰=12(,)L f x y dy ⎰(若(,)f x y 是关于x 的奇函数).b .(,)Lf x y dy ⎰=0(若(,)f x y 是关于x 的偶函数).注2 利用格林公式计算对坐标的曲线积分L Pdx Qdy +⎰时,应注意以下几点: (1),P Qy x∂∂∂∂在区域G 内连续,闭区域D 的边界曲线L 应取正向. (2)若L 为非封闭曲线,直接计算又较困难,可添加辅助线C 使L C +为封闭曲线,然后使用格林公式,若L C +的方向为负向,格林公式中二重积分前要加负号,并注意LL CC+=-⎰⎰⎰,同时注意补上的曲线要便于积分的计算.(3)若,P Q y x∂∂∂∂在D 中某点00(,)x y 不连续,要通过添加辅助曲线C 挖去00(,)x y 后再使用格林公式,并要注意C 的方向的选取.(4)在曲线积分中,可将L 的表达式代入被积表达式,但是使用格林公式将曲线积分化为二重积分后,在D 内的点(,)x y 已不再满足L 的方程,不应再将L 的表达式代入二重积分的被积表达式.例10 计算)L ydx x dy +⎰,如图9-8所示,L 是依次连接(1,0),A -(2,1),B(1,0)C 的折线段.分析 若将直线AB 和BC 的方程写出,代入积分式直接计算则比较麻烦,所以考虑用格林公式计算,但是L 不是封闭曲线,须添加辅助线段CA 使曲线封闭,并注意到封闭折线ABCA 的方向为负向,应用格林公式时在二重积分前要添加负号.解 令(,)P x y y =,(,)Q x y x ,则112Q Px y∂∂-=--=-∂∂,且线段:0CA y =,x 由1变化到-1,故有)Lydx x dy +⎰3(sin )ABCAydxx dy =+⎰)CAydx x dy -+⎰11(2)022DDdxdy dx dxdy -=---⋅==⎰⎰⎰⎰⎰.图9-8其中D 为ABCA 所围成的闭区域.例11 计算22L xdy ydxx y-+⎰,其中L 为椭圆周2241x y +=,取逆时针方向. 分析 此题可以直接计算,也可应用格林公式,但是应注意奇点.解法1 直接计算,L 的参数方程为:1cos 2x θ=,sin y θ=,θ从0到2π,则22Lxdy ydx x y -+⎰22202211cos sin 221cos sin 4d πθθθθθ+=+⎰ 222012cos 4sin d πθθθ=+⎰220(2tan )14tan d πθθ=+⎰.注意到3,22ππθθ==为被积函数的无穷间断点,故220(2tan )14tan d πθθ+⎰为反常积分,因此 22L xdy ydx x y -+⎰22220(2tan )(2tan )14tan 14tan d d πππθθθθ=+++⎰⎰3232222(2tan )(2tan )14tan 14tan d d ππππθθθθ++++⎰⎰,其中22220()(2tan )[arctan(2tan )]lim arctan(2tan )arctan(2tan 0)14tan 2d πππθθπθθθ-→==-=+⎰;同理可得 22(2tan )14tan 2d ππθπθ=+⎰,322(2tan )14tan 2d ππθπθ=+⎰,3222(2tan )14tan 2d ππθπθ=+⎰. 所以22L xdy ydx x y -+⎰22222πππππ=+++=.解法2 用格林公式.令(,)P x y =22y x y -+,22(,)x Q x y x y =+,则当(,)(0,0)x y ≠时,22222()P Q y x y x x y ∂∂-==∂∂+,但积分曲线L 所围区域包含点(0,0),(,),(,)P x y Q x y 在该点不具有连续的偏导数,因此不能直接应用格林公式计算,需要将奇点(0,0)去掉,为此作半径足够小的圆C :222x y δ+=,使C 位于L 的内部,如图9-9所示.C 的参数方程为cos x δθ=,sin y δθ=,[0,2]θπ∈,C 取逆时针方向.于是图9-922L xdy ydxx y -+⎰22L C xdy ydxx y -+-=-+⎰22C xdy ydxx y --+⎰,其中C -表示C 的负方向.由格林公式则有2200L C D xdy ydxdxdy x y -+-=⋅=+⎰⎰⎰, 其中D 为L 与C 所围成的闭区域.故22L xdy ydx x y -+⎰22C xdy ydx x y --=-+⎰22C xdy ydxx y -=+⎰ 222220cos (sin )sin (cos )cos sin d d πδθδθδθδθδθδθ-=+⎰202d πθπ==⎰.例12 利用格林公式计算L uds n∂∂⎰,其中22(,)u x y x y =+,L 为圆周226x y x +=取逆时针方向,un∂∂是u 沿L 的外法线方向导数. 解 由于cos(,)cos(,)u u u x y n x y ∂∂∂=+∂∂∂n n 2cos 2cos x y βα=-,其中,αβ是在曲线L 上点(,)x y 处的切线的方向角,故(2cos 2cos )L uds x y ds n βα∂=-∂⎰⎰.根据两类曲线积分之间的联系及格林公式,有(2cos 2cos )L Luds y x ds n αβ∂=-+∂⎰⎰(2)24LDy dx xdy dxdy =-+=⎰⎰⎰.因为L 为圆周226x y x +=,所以L 所围成的圆的面积9σπ=,因此 4436L Duds dxdy nσπ∂===∂⎰⎰⎰. 例13 验证在全平面上,(1sin )(2sin )cos x x e y dx e y ydy +++是全微分,并求出它的一个原函数.解 令(,)(1sin )x P x y e y =+,(,)(2sin )cos x Q x y e y y =+,则在全平面上有cos x Q Pe y x y∂∂==∂∂,满足全微分存在定理的条件,故在全平面上, (1sin )(2sin )cos x x e y dx e y ydy +++是全微分.下面用三种方法来求原函数:解法1 运用曲线积分公式,为了计算简单,如图9-10所示,可取定点(0,0)O ,动点(,0)A x 与(,)M x y ,于是原函数为(,)(0,0)(,)(1sin )(2sin )cos x y x x u x y e y dx e y ydy =+++⎰.取路径: OA AM +,得图9-10(,)(10)(2sin )cos x yx x u x y e dx e y ydy =+++⎰⎰21sin sin x x e e y y =-++.解法2 从定义出发,设原函数为(,)u x y ,则有(,)(1sin )x uP x y e y x∂==+∂,两边对x 积分(y 此时看作参数),得(,)(1sin )()x u x y e y g y =++ (*)待定函数()g y 作为对x 积分时的任意常数,上式两边对y 求偏导,又(,)uQ x y y∂=∂,于是 cos ()(2sin )cos x x e y g y e y y '+=+,即 ()2sin cos g y y y '=,从而 2()sin g y y C =+(C 为任意常数),代入(*)式,得原函数2(,)sin sin x x u x y e e y y C =+++.解法3 凑微分.(1sin )(2sin )cos x x e y dx e y ydy +++(sin cos )2sin cos x x x e dx e ydx e ydy y ydy =+++ 2(sin )(sin )x x de d e y d y =++2(sin sin )x x d e e y y =++, 故原函数为2(,)sin sin x x u x y e e y y =++.注1 当积分与路径无关时,在选取路径时应使得计算简便.注2 (,)u x y 不唯一,但它们之间相差一个常数. 例14(98研) 确定常数λ,使在右半平面0x >上的向量42242(,)2()()x y xy x y x x y λλ=+-+A i jo(,0)A x xy(,)M x y为某二元函数(,)u x y 的梯度,并求(,)u x y .分析 平面单连通区域内向量场(,)(,)(,)x y P x y Q x y =+A i j 为某二元函数的梯度的充要条件是Q Px y ∂∂=∂∂,由此可确定.λ然后,由曲线积分00(,)(,)(,)(,)x y x y P x y dx Q x y dy +⎰与路径无关即可求出 (,)u x y .解 由梯度定义 (,)(,)(,)(,)u uu x y x y P x y Q x y x y∂∂=+==+∂∂grad i j A i j ,其中 422422(),()u u P xy x y Q x x y x yλλ∂∂==+==-+∂∂, 而42242132()()4Qx x y x x y x x λλλ-∂=-+-+⋅∂, 424212()2()2Px x y xy x y y yλλλ-∂=+++⋅∂. (,)x y A 为(,)u x y 的梯度.即Pdx Qdy +在0x >时存在原函数(,)u x y ,故Q Px y∂∂=∂∂,由此可 得424()(1)0x x y λ++=,可见当且仅当1λ=-时,所给向量(,)x y A 为u 的梯度.又由于 Pdx Qdy du +=,于是曲线积分00(,)(,)(,)(,)x y x y P x y dx Q x y dy +⎰与路径无关,故(,)u x y =00(,)(,)(,)(,)x y x y P x y dx Q x y dy +⎰C +(,)(1,0)x y Pdx Qdy =+⎰C +(,)2421(1,0)(2)()x y xydx x dy x y C -=-++⎰2424221020arctan 0xy x x dy y dx C C x x y x ⋅=-+=-+++⎰⎰. 注 本题实质上是平面单连通区域内曲线积分与路径无关的题目,不过以梯度的形式考察.例15 试求由星形线33cos ,sin x a t y a t ==所围成图形的面积.分析 这是一道求平面图形的面积的题目,可用定积分计算,也可用二重积分计算, 也可用曲线积分计算,下面用二重积分来计算,进一步利用格林公式,将重积分转化为曲线积分来计算.解 由格林公式可知 12L D A dxdy xdy ydx ==-⎰⎰⎰2323201[cos 3sin cos sin 3cos (sin )]2a t a t t a t a t t dt π=⋅-⋅⋅-⎰ 22222220033sin cos sin 228a a t tdt tdt ππ==⎰⎰2220313[sin 4]8288a t t a ππ=-=. 注 由格林公式可知,要使()C DQ Pdxdy Pdx Qdy x y ∂∂-=+∂∂⎰⎰⎰表示曲线C 所围区域D 的面积时,只要选取适当的P 和Q ,使Q Px y∂∂-∂∂为非零常数即可. 例16 设有一力场,场力的大小与作用点P 到z 轴的距离成反比,方向垂直指向z 轴,如图9-11所示,试求一质点沿圆周cos ,1,sin x t y z t ===从点(1,1,0)A 沿t 增长的方向移动到点(0,1,1)B 所做的功.分析 变力沿曲线做功,可通过对坐标的曲线积分求得,将变力F 表示为向量的形式:{,,}x y z F F F =F ,确定曲线L 的方向,则功x y z L W F dx F dy F dz =++⎰.若为平面曲线,计算方法类似.解 依题意可知,点P 所受的力F 的大小为: ||=F ,其中k 为常数,F 的方向为{,,0}x y --,将此向量单位化,得{=F ,{}022||,,0.kx y x y ==-+F F F 22220cos sin ()1cos Lk t tW xdx ydy k dt x yt π-=-+=-++⎰⎰ 2222200cos ln(1cos )ln 221cos 22k d t k k t t ππ⎡⎤=-=-+=⎣⎦+⎰.图9-11例17 求曲面积分3()22y z I x dS ∑=++⎰⎰,其中∑为平面1234x y z++=在第一卦限的部分,如图9-12所示.分析 这是一道计算第一类曲面积分的基本题.要把第一类曲面积分化为二重积分, 首先要求出曲面∑在xOy 平面(或yOz 平面,zOx 平面)上的投影区域D ,再根据∑的方程确定面积元素dS .最后由区域D 定出二重积分化为二次积分的上、下限.一般地,若光滑曲面∑的方程为(,)z z x y =,∑在平面xOy 上的投影为xy D ,且(,,)f x y z 在∑上连续, 则(,,)[,,(,xyD f x y z dS f x y z x y ∑=⎰⎰⎰⎰. 解 将曲面的方程改写为:4(1)23x yz ∑=--,则 2zx∂=-∂,43z y ∂=-∂,从而dS ==,图9-12∑在xOy 上的投影区域为3{(,)|02,03}2xy D x y x y x =≤≤≤≤-,故3361()[2(1)]222233xyD y z x y I x dS x y dxdy T=++=++--⎰⎰⎰⎰ 322300615761(2)366x dx y dy -=-=⎰⎰. 例18 计算曲面积分2221dS x y z ∑++⎰⎰,其中∑是介于平面0z =及z H =之间的圆柱面222x y R +=.分析 由于柱面∑在xOy 坐标面上的投影为一条曲线,不能构成区域,即投影区域的面积等于零,所以∑不能投影到xOy 平面上,故考虑投影到yOz 平面上或投影到zOx 平面上,如图9-13所示.解法1 由于曲面∑的方程可以写成22(0)x R y z H =+-≤≤,因此考虑将曲面∑向yOz 平面投影,则∑是由两片曲面图9-13221:(0)x R y z H ∑=-≤≤和222:(0)x R y z H ∑=--≤≤组成, 曲面1∑和2∑在yOz 面上的投影区域均为:,0xz D R y R z H -≤≤≤≤.在1∑上:0xz∂=∂, 22x y y R y ∂-=∂-;在2∑上:0xz∂=∂,22x y y R y∂=∂-.因此 22222221()()1x x y Ry z R y R y ∂∂++=+=∂∂--, 又因为在1∑和2∑上,均有22222x y z R z ++=+,故 2222211dS dS x y z R z ∑∑=+++⎰⎰⎰⎰12222211dS dS R z R z ∑∑=+++⎰⎰⎰⎰ 2222222211yzyzD D R Rdydz dydz R z R z R y R y =⋅+⋅++--⎰⎰⎰⎰ 222212yzD R dydz R z R y =⋅+-⎰⎰220222H R R dz dy R R z R y-=⋅+-⎰⎰ xyzoH004[arctan ]R H z R =⋅⎰004arctan lim R H R εε+-→=⋅⎰ 004arctanlim[arcsin ]2arctan R H y HR R Rεεπ+-→=⋅=.解法2 由于曲面∑的方程可以写成)y z H ≤≤.因此考虑将曲面∑向xOz 平面投影,则∑是由两部分曲面1:)y z H ∑=≤≤和2:)y z H ∑=≤≤组成.曲面1∑和2∑在xOz 面上的投影区域均为:,0xz D R x R z H -≤≤≤≤.在1∑上:0yz ∂=∂, y x ∂=∂; 在2∑上:0yz ∂=∂,y x ∂=∂.因此=1∑和2∑上,均有22222x y z R z ++=+,故 2222211dS dS x y z R z ∑∑=+++⎰⎰⎰⎰12222211dS dS R z R z ∑∑=+++⎰⎰⎰⎰2arctan HR π=. 解法3 利用奇偶对称性,因为曲面∑关于xOz 坐标平面对称,且被积函数 2221(,,)f x y z x y z =++是关于y 的偶函数,故有12222221122arctan HdS dS x y z x y z R π∑∑==++++⎰⎰⎰⎰(计算过程请参考解法1) 其中1∑是∑的0y ≥的部分,即1∑是∑的右半部分.错误解答 柱面∑在xOy 坐标面上的投影为一条曲线,不能构成区域,即投影区域的面积等于零,所以积分22210dS x y z ∑=++⎰⎰. 错解分析 这个结论是错误的,事实上,对于这类曲面积分的计算,首先要看曲面在哪个坐标面的投影区域的面积不为零,然后再用相应的公式进行计算,就可以得出正确的结果. 注 (1)计算对面积的曲面积分时,积分曲面投影到哪个坐标面,要根据积分曲面方程的表达式来确定.一般地,∑投影到坐标面xOy 时,∑的方程应写为),(y x f z =的形式;∑投影到yOz (或xOz )坐标面时,∑的方程应写为),(y x g x =(或),(z x h y =)的形式.如果曲面∑可以同时表示成(,)x x y z =,(,)y y x z =,(,)z z x y =,可以将曲面∑向任何一个坐标平面投影,那么对面积的曲面积分都可化为二重积分计算.但到底选择哪个坐标平面,首先,选择∑在坐标面上的投影区域越简单越好,其次要使∑的方程代入被积函数后所得函数较简便,使二重积分易于计算.(2)当∑是母线平行于坐标轴的柱面时,不能将∑向垂直于母线的坐标面投影,例如本例中就不能向xOy 面投影,因为∑的方程不能写成(,)z z x y =的形式,从几何上看,∑在xOy 面上的投影是曲线(圆周),不能形成区域.(3)当∑的方程不是单值函数时,要将曲面分成两个单值函数表示的曲面分别进行计算,然后再相加.例19 计算()xy yx zx dS ∑++⎰⎰,其中∑是圆锥面z 222x y ax +=所截得的部分.分析 本题可以将∑投影在坐标面xOy ,然后直接计算;又由于积分曲面∑关于zOx 面对称,也可考虑利用对称性来计算.解法1 直接计算.如图9-14所示,∑在坐标面xOy 上的投影区域xy D 为: ax y x 222≤+.因为,,2222yx y z yx x z y x +=+=所以dS zx yz xy ⎰⎰∑++)(dxdy y x x y x y xy xyD 22222⎰⎰⎪⎭⎫ ⎝⎛++++=,221yxz z ++21222222=++++=y x y y x x ,在极坐标系下xy D 为:22,cos 20πθπθ≤≤-≤≤a r ,故dxdyy x y x xy dS zx yz xy xyD )(2)(22⎰⎰⎰⎰⎥⎦⎤⎢⎣⎡+++=++∑2cos 2222cos sin (cos sin )[] a d r r rdr πθπθθθθθ-=++⎰图9-14⎰-⋅++=2244)cos 2()sin cos sin (cos 2ππθθθθθθd a4544242cos 53d πθθ==⋅⋅=⎰解法2 利用奇偶对称性.因为曲面∑关于zOx 面对称,且被积函数xy 和yz 关于y 是奇函数,故0xydS yzdS ∑∑==⎰⎰⎰⎰,因此()xy yx zx dS xzdS ∑∑++=⎰⎰⎰⎰,为了计算xzdS ∑⎰⎰,将∑向xOy 面投影,投影区域为xy D ,在极坐标系下可以表示为:02cos ()22r a ππθθ≤≤-≤≤,于是xyD xzdS ∑=⎰⎰⎰⎰222cos 30cos a d r dr ππθθθ-⎰2245cos d ππθθ-=⎰2454cos d πθθ==⎰.所以()xy yx zx dS ∑++⎰⎰4xydS yzdS xzdS ∑∑∑=++=⎰⎰⎰⎰⎰⎰. 注(1) 若曲面∑关于xOy 对称,记1∑是∑的0z ≥的部分,即1∑是∑的上半部分, (,,)f x y z 在∑上连续,则a .(,,)f x y z dS ∑⎰⎰=12(,,)f x y z dS ∑⎰⎰(若(,,)f x y z 是关于z 的偶函数).b .(,,)f x y z dS ∑⎰⎰=0(若(,,)f x y z 是关于z 的奇函数).(2)若曲面∑关于zOx 对称,记1∑是∑的0y ≥的部分,即1∑是∑的右半部分, (,,)f x y z 在∑上连续,则a .(,,)f x y z dS ∑⎰⎰=12(,,)f x y z dS ∑⎰⎰(若(,,)f x y z 是关于y 的偶函数).b .(,,)f x y z dS ∑⎰⎰=0(若(,,)f x y z 是关于y 的奇函数).(3)若曲面∑关于yOz 对称,记1∑是∑的0x ≥的部分,即1∑是∑的前半部分, (,,)f x y z 在∑上连续,则a .(,,)f x y z dS ∑⎰⎰=12(,,)f x y z dS ∑⎰⎰(若(,,)f x y z 是关于x 的偶函数).b .(,,)f x y z dS ∑⎰⎰=0(若(,,)f x y z 是关于x 的奇函数).(4)设有界分片光滑曲面:(,,)0f x y z ∑=具有轮换对称,即对任意(,,)x y z ∈∑,(,,)z x y ∈∑,(,,)z y x ∈∑,且(,,)f x y z 在∑上连续,则(,,)(,,)(,,)f x y z dS f z x y dS f z y x dS ∑∑∑==⎰⎰⎰⎰⎰⎰.例20 计算22()x y dS ∑+⎰⎰,其中∑是0z y x =⎧⎨=⎩ (01)z ≤≤绕z 轴旋转一周所得到的旋转曲面.分析 先写出∑的方程,将∑投影到三个坐标面上,积分的计算对应有三种解法,这里仅给出了其中一种解法,其它的解法请读者自行完成.解 旋转曲面为1)z z ≤≤,故dS ==,所以2222())xyD x y dS x y dxdy ∑+=+⎰⎰,其中{}22(,)|1xy D x y x y =+≤是∑在xOy 坐标面上的投影区域,利用极坐标计算此二重积分,于是212220()x y dS d r rdr πθ∑+=⋅=⎰⎰⎰. 例21 若球面上每一点的密度等于该点到球的某一定直径的距离的平方,求球面的质量.分析 此题考察曲面积分的物理意义,应先将所求的物理量用数学式子表达出来,然后再计算.解法1 设球面方程为2222x y z a ++=,定直径选在z 轴,依题意,球面上点(,,)P x y z 的密度为22(,,)x y z x y ρ=+,从而球面的质量为22()M x y dS ∑=+⎰⎰.由对称性可知12222()2()M x y dS x y dS ∑∑=+=+⎰⎰⎰⎰,其中1∑为上半球面z =z x ∂=∂z y ∂=∂dS ==,其中222{(,)|}xy D x y x y a =+≤是1∑在xOy 坐标面上的投影区域,利用极坐标计算此二重积分,于是得2222()2aM x y dS a d rdr πθ∑=+=⎰⎰⎰⎰=304aa π⎰=2334cos a a tdt ππ⎰244384sin 3a atdt πππ==⎰. 解法2 设球面方程为2222x y z a ++=,定直径在z 轴上,依题意得球面上点(,,)P x y z 的密度为22(,,)x y z x y ρ=+,从而得球面的质量为22()M x y dS ∑=+⎰⎰,由轮换对称性可知:222x dS y dS z dS ∑∑∑==⎰⎰⎰⎰⎰⎰,故有 42222222228()43333a M x y z dS a dS a a ππ∑∑=++=⋅=⋅=⎰⎰⎰⎰.例22 面密度1ρ=的均匀半球面2222(0)x y z a z ++=≥对z 轴的转动惯量. 分析 先求出转动惯量的数学表达式.解法1 所求转动惯量22()z I x y dS ∑=+⎰⎰,考虑将半球面向xOy 坐标面投影,则投影区域为222{(,)|}xy D x y x y a =+≤.因为z dS ==,所以2222()xyz D I x y dS a ∑=+=⎰⎰⎰⎰220aa d πθ=⎰⎰(利用极坐标变换)24302sin a tdt ππ=⎰443a π=.(令sin r a t =)解法2 所求转动惯量是整个球面绕z 轴的转动惯量的一半,而22222222222222()()3x y z a x y z a x y dS x y z dS ++≤++≤+=++⎰⎰⎰⎰2222242833x y z aa dS a π++≤==⎰⎰ 所以 44184233z I a a ππ=⨯=.例23 计算2()z x dydz zdxdy ∑+-⎰⎰,其中221:()2z x y ∑=+为介于0,2z z ==之间部分的下侧,如图9-15所示.分析 此题可以直接计算,也可应用两类曲面积分之间的关系或应用高斯公式. 解法1 将曲面∑分为1∑和2∑,其中1:x ∑yOz 坐标面上的投影区域21:{(,)|22,2}2yz D y z y y z -≤≤≤≤,取∑的前侧;2:x ∑=,其在yOz 坐标面上的投影区域21:{(,)|22,2}2yz D y z y y z -≤≤≤≤,取∑的后侧.则12222()()()zx dydz z x dydz z x dydz∑∑∑+=+++⎰⎰⎰⎰⎰⎰2222(2)(2)yzyzD D zz y dydz z z y dydz =+----⎰⎰⎰⎰21222222222yzy D z y dydz dy z y dz -=-=-⎰⎰⎰⎰(令22z y u -=)图9-152324222220222(4)43y dy u du y dy π---==-=⎰⎰⎰,而对于zdxdy ∑-⎰⎰,考虑221:()2z x y ∑=+的下侧,其在xOy 坐标面上的投影为22{(,)|4}xy D x y x y =+≤,则有222220011()422xyD zdxdy x y dxdy d r rdr πθπ∑-=+=⋅=⎰⎰⎰⎰⎰⎰.故2()8zx dydz zdxdy π∑+-=⎰⎰.解法2 由两类曲面积分之间的联系可知:cos dydz dS α=,cos dxdy dS γ=,于是cos cos dydz dxdy αγ=,将曲面221()2z x y =+取下侧,法向量为(,,1)(,,1)z z x y x y ∂∂=-=-∂∂n ,所以22cos 1x x y α=++,221cos 1x y γ-=++,dydz xdxdy =-,则有22()()()z x dydz z x x dxdy ∑∑+=+-⎰⎰⎰⎰2221[()]4xy D x x y x dxdy =++⎰⎰ 224001cos (cos )44d r r r rdr πθθθπ=+=⎰⎰,222220011()[()]422xyD z dxdy x y dxdy d r rdr πθπ∑-=--+=⋅=⎰⎰⎰⎰⎰⎰, 所以 2()8z x dydz zdxdy π∑+-=⎰⎰.解法3 增补221:2(4)z x y ∑=+≤,取上侧,由高斯公式得12()0zx dydz zdxdy ∑+∑+-=⎰⎰,所以 122()[()]z x dydz zdxdy z x dydz zdxdy ∑∑+-=-+-⎰⎰⎰⎰yzo2z =x112()z x dydz zdxdy ∑∑-++⎰⎰⎰⎰=028xyD dxdy π=+=⎰⎰.注 上述三种解法中,应用高斯公式最简单,因此在解题时,选择什么样的方法比较重要.对坐标的曲面积分的计算问题,其主要方法有:(1)直接计算:这种方法是将有向曲面分别投影到相应坐标面.此方法往往计算量大,但是方法易于掌握;(2)利用两类曲面积分之间的联系,将对不同坐标的计算转化为对相同坐标的计算,例如解法2,再直接计算;(3)应用高斯公式,将曲面积分化为三重积分.例24 计算()()()y z dydz z x dzdx x y dxdy ∑-+-+-⎰⎰,其中∑为曲面22z x y =+及平面(0)z h h =>所围成的空间区域的整个边界的外侧,如图9-16所示.解法1 用高斯公式来计算. 令P y z =-,Q z x =-,R x y =-,则()()()y z dydz z x dzdx x y dxdy ∑-+-+-⎰⎰Pdydz Qdzdx Rdxdy ∑=++⎰⎰()(000)P Q Rdv dv x y z ΩΩ∂∂∂=++=++∂∂∂⎰⎰⎰⎰⎰⎰0=, 图9-16其中Ω是曲面22z x y =+及平面(0)z h h =>所围成的空间闭区域.解法2 用奇偶对称性 设∑在平面z h =及锥面22z x y =+所围成的圆锥体的上侧为1∑,侧面为2∑.为计算()y z dydz ∑-⎰⎰,须将2∑分成3∑和3'∑,前半锥面3∑:22(0)x z y z =-≥,后半锥面3'∑:22(0)x z y z =--≥,且它们的法向量相反.由于y z -为x 的偶函数,而积分曲面关于坐标面yOz 对称,则有2()0y z dydz ∑-=⎰⎰.又因为1∑垂直yOz 平面,故1()0y z dydz ∑-=⎰⎰, 因而()0y z dydz ∑-=⎰⎰.同理可得()0z x dzdx ∑-=⎰⎰,又因为12()()()x y dxdy x y dxdy x y dxdy ∑∑∑-=-+-⎰⎰⎰⎰⎰⎰,yzoz h=x而1∑和2∑的法向量分别与z 轴正向成锐角、钝角,且二者在xOy 面内的投影区域相同, 均为xy D ,故()()()0xyxyD D x y dxdy x y dxdy x y dxdy ∑-=---=⎰⎰⎰⎰⎰⎰.所以()()()0y z dydz z x dzdx x y dxdy ∑-+-+-=⎰⎰.注 关于第二类曲面积分的奇偶对称性有以下结果会经常用到:(1)设曲面∑关于xOy 面对称,记∑的上方部分为1∑,(,,)f x y z 在∑连续,则 a .(,,)f x y z dxdy ∑⎰⎰=12(,,)f x y z dxdy ∑⎰⎰(若(,,)f x y z 是关于z 的奇函数).b .(,,)f x y z dxdy ∑⎰⎰=0(若(,,)f x y z 是关于z 的偶函数).(2)设曲面∑关于xOz 面对称,记∑的右方部分为1∑,(,,)f x y z 在∑连续,则 a .(,,)f x y z dxdy ∑⎰⎰=12(,,)f x y z dxdy ∑⎰⎰(若(,,)f x y z 是关于y 的奇函数).b .(,,)f x y z dxdy ∑⎰⎰=0(若(,,)f x y z 是关于y 的偶函数).(3)设曲面∑关于yOz 面对称,记∑的前方部分为1∑,(,,)f x y z 在∑连续,则 a .(,,)f x y z dxdy ∑⎰⎰=12(,,)f x y z dxdy ∑⎰⎰(若(,,)f x y z 是关于x 的奇函数).b .(,,)f x y z dxdy ∑⎰⎰=0(若(,,)f x y z 是关于x 的偶函数).(4) 第二类曲面积分Pdydz Qdzdx Rdxdy ∑++⎰⎰也有轮换对称性.这里轮换对称性是指:a .被积表达式满足轮换对称性;b .积分曲面及其指定侧也具有轮换对称性,这里指∑在各坐标面上的投影区域相同, 且相应的符号也相同.例25 计算22y zdxdy xzdydz xydzdx ∑++⎰⎰,其中∑是由旋转抛物面22z x y =+,圆柱面221x y +=和坐标平面在第一卦限中所围成曲面的外侧,如图9-17所示. 分析 对于对坐标的曲面积分问题,可以考虑采用直接的方法计算;也可以考虑用高斯公式来计算,但是,图9-17在应用高斯公式时要注意前提条件:曲面封闭且方向指向外侧,被积函数在积分曲面所围的xyoz闭区域Ω上具有一阶连续偏导数.解法1 设∑在三个坐标面0,0,0x y z ===及曲面22z x y =+,221x y +=上的部分分别为1234,,,∑∑∑∑及5∑,则122y zdxdy xzdydz x ydzdx ∑++⎰⎰12y zdxdy ∑⎰⎰=1xzdydz ∑+⎰⎰12x ydzdx ∑+⎰⎰,因为1∑在平面xOy 上的投影没有形成区域,所以有120y zdxdy ∑=⎰⎰.而当 0x =时,被积函数0xz =,20x y =,所以有10xzdydz ∑=⎰⎰及120x ydydz ∑=⎰⎰.故1220y zdxdy xzdydz x ydzdx ∑++=⎰⎰. 同理可得 2220y zdxdy xzdydz x ydzdx ∑++=⎰⎰,3220y zdxdy xzdydz x ydzdx ∑++=⎰⎰.设4∑在三个坐标面上的投影区域分别为,,xy yz zx D D D .并注意到4∑分别取上侧、后侧及左侧,则有44442222y zdxdy xzdydz xydzdx y zdxdy xzdydz x ydzdx ∑∑∑∑++=++⎰⎰⎰⎰⎰⎰⎰⎰,2412222240()sin 24xyD y zdxdy y x y dxdy d r rdr ππθθ∑=+=⋅=⎰⎰⎰⎰⎰⎰,241112yzyD xzdydz dy π∑=-==-⎰⎰⎰⎰⎰⎰,241122048xzxD x ydzdx x x dx π∑=-==-⎰⎰⎰⎰⎰⎰,所以 42224124816y zdxdy xzdydz x ydzdx ππππ∑++=--=-⎰⎰.由于5∑是母线平行于z 轴的柱面,它在坐标平面xOy 上的投影是一条曲线(四分之一圆弧),于是由定义可知520y zdxdy ∑=⎰⎰.5∑在坐标平面yOz 和zOx 上的投影是边长为1的正方形,分别取前侧和右侧,则有522y zdxdy xzdydz xydzdx ∑++⎰⎰5520xzdydz x ydzdx ∑∑=++⎰⎰⎰⎰111zdz dz x =+⎰⎰⎰⎰381616πππ=+=.所以22y zdxdy xzdydz x ydzdx ∑++⎰⎰316168πππ=-=. 解法 2 上面的解法显然很繁琐,由于∑为封闭曲面,故考虑用高斯公式化为三重积分计算.令(,,)P x y z xz =,2(,,)Q x y z x y =,2(,,)R x y z y z =,则P z x ∂=∂,2Q x y ∂=∂,2R y z ∂=∂. 由高斯公式得2222()y zdxdy xzdydz x ydzdx z x y dxdydz ∑Ω++=++⎰⎰⎰⎰⎰,其中Ω是由∑所围成的空间闭区域. 在柱面坐标系下,Ω可以表示为2:0,01,02r z r πθ≤≤≤≤≤≤,因此22y zdxdy xzdydz xydzdx ∑++⎰⎰22120()r d rdr z r dz πθ=+⎰⎰⎰4140[]22r r r dr π=+⎰150348r dr ππ==⎰.注 在计算对坐标的曲面积分时,应该注意:(1)由于被积函数定义在积分曲面上,所以首先观察是否可以利用曲面方程化简被积函数,同时要观察对哪两个坐标积分,例如,对坐标x 和y 积分时,则只能将曲面向xOy 坐标面投影,而不能向其它坐标面投影,在将对坐标的曲面积分转化为二重积分时,要注意二重积分前的正负号与积分曲面的侧的关系.(2)若积分曲面表示为显函数后不是单值函数,则应将曲面分片,使每片曲面的显函数表示为单值函数.然后再计算.(3)与对面积的曲面积分不同,若积分曲面在某个坐标面上的投影区域的面积为零,则对这两个坐标的曲面积分的值为零.(4)应用高斯公式计算对坐标的曲面积分时,一定要满足高斯公式的条件,如果不满足,例如曲面不为封闭曲面时,采取添加有向曲面的方法使之封闭,当然在应用高斯公式计算曲面积分时,也要注意积分曲面的侧.(5)在对坐标的曲面积分中,可将∑的表达式代入被积表达式,但是使用高斯公式将曲面积分化为三重积分后,在Ω内的点(,,)x y z 已不再满足∑的方程,不应再将∑的表达式代入三重积分的被积表达式.例26 计算曲面积分333I x dydz y dzdx z dxdy ∑=++⎰⎰,其中∑为球面2222xy z a ++=的内侧.分析 由题知∑为封闭曲面,但∑的侧是球面的内侧,因此,不能直接应用高斯公式计算.解 由对坐标的曲面积分的性质可知(,,)(,,)(,,)P x y z dydz Q x y z dzdx R x y z dxdy ∑++⎰⎰(,,)(,,)(,,)P x y z dydz Q x y z dzdx R x y z dxdy -∑=-++⎰⎰,于是有333I x dydz y dzdx z dxdy -∑=-++⎰⎰,其中-∑为球面2222x y z a ++=且取外侧.记∑围成的立体为Ω,由高斯公式得222 3()I x y z dxdydz Ω=-++⎰⎰⎰22203sin ad d r r dr ππθϕϕ=-⋅⎰⎰⎰5512(3)2255a a ππ=-⨯⨯⨯=-.例27 计算曲面积分(2)I x z dydz zdxdy ∑=++⎰⎰,其中∑为曲面22z x y =+(01)z ≤≤法向量指向与z 轴正向夹角为锐角的一侧,如图9-18所示.分析 由于是法向量指向与z 轴正向夹角为锐角的一侧,且不封闭,不能直接应用高斯公式,应添加辅助曲面并改变曲面的侧,然后再应用高斯公式.图9-18解 首先作辅助曲面221:1(1)z x y ∑=+≤,取下侧,和∑围成立体为Ω,根据对坐标的曲面积分的性质1(2)(2)x z dydz zdxdy x z dydz zdxdy ∑∑+++++⎰⎰⎰⎰1()(2)x z dydz zdxdy -∑+∑=-++⎰⎰,其中1()-∑+∑表示Ω的整个边界曲面,且取外侧.由高斯公式可知1()(2)(21)x z dydz zdxdy dxdydz -Ω∑+∑++=+⎰⎰⎰⎰⎰,利用柱面坐标计算得 22113332rdxdydz d rdr dz ππθΩ==⎰⎰⎰⎰⎰⎰, (2)I x z dydz zdxdy ∑=++⎰⎰11()(2)(2)x z dydz zdxdy x z dydz zdxdy -∑∑+∑=-++-++⎰⎰⎰⎰13(2)2x z dydz zdxdy π∑=--++⎰⎰, 注意到1∑在坐标平面yOz 上的投影是曲线,不能构成区域,故有1(2)0x z dydz ∑+=⎰⎰,而11(1)xyD zdxdy dxdy ππ∑=-=-⨯=-⎰⎰⎰⎰,于是有 3(2)()22I x z dydz zdxdy πππ∑=++=---=-⎰⎰.。
大学高数第二册公式整理

dy
hx
g
xdx
最后得 Hx Gx c
dy Pxy 0
(2)一阶线性齐次微分方程: dx y ce Pxdx
dy Pxy Qx
(3)一阶线性非齐次微分方程: dx
y
ce
P
x
d
x
Qxe Pxdxdx c
(4)齐次微分方程:代换法:如果 dy y ,则令 y u
dx x
x
求
z
的一阶偏导
f x x0 , f y x0 ,
y0 y0
0 0
f xx x0 , y0 A
令
z
的二阶偏导
f xy x0 ,
y0
B
f
yy
x0
,
y0
C
①当 AC B2 0 时,且 A 0 时,有极大值; A 0 时,极小值
②当 AC B2 0时,无极值
③当 AC B2 0时,无法判定
1. 方向导数与梯度
方向导数: f f cos f cos
l x
y
cos,cos 是l的方向余弦
梯
度
:
g r a d fx,
y
f x
,
f y
2.(1)曲线的切线与法平面
x xt
设曲
线方程:
y
yt
z zt
则切线方程:
x x0
x`t0
y y0
y`t0
z z0
z`t0
法平面方程: x`t0 x x0 y`t0 y y0 z`t0 z z0 0
(2)曲面的切平面与法线
设曲线方程为: Fx, y, z 0
则切线方程:
x x0
2019年大学高数曲面积分题.doc

第二十章 曲线积分§ 1 第一型曲线积分1.计算下列第一型曲线积分:( 1) ( x y) ds ,其中 L 是以 O(0,0), A(1,0), B(0,1) 为顶点的三角形;L1 ( 2) ( x2 y 2 ) 2ds ,其中 L 是以原点为圆心, R 为半径的右半圆周;L( 3) xy d sx 2 y 21在第一象限中的部分;,其中 L 是椭圆22La b( 4)y d s ,其中 L 是单位圆周 x2y21 ;L( 5) ( x 2 y 2 z 2)ds ,其中 L 为螺旋线 x a cost , y a sin t, z btL(0 t2 ) 的一段;( 6)xyzds ,其中 L 是曲线 x t, y2 2t3 , z 1 t 2 ( 0 t 1) 的L3 2一段;( 7)2 y 2z 2 ds ,其中 L 是 x 2y 2 z 2a 2 与 x y 相交的圆L周 .解 (1)(x y)ds(x y)ds (x y)ds (x y)dsLOAABBO1 11xdx0 2dxydy 12 ;( 2)右半圆的参数方程为:x Rcos , yRsin .2 2所以1( x 2 y 2 ) 2 ds2R 2 dR 2 ;L2( 3 )由于椭圆在第一象限中的部分可表示为y b a 2x 2 ,a232( 0 xa ),从而 ybx, 所以a 2a x 2a bbx 2a 2x 21dxxydsaa 2x 2Lab a ba 4( a 2b 22dx 2ab( a 2 ab b 2 );2a 2a) x3(a b)( 4)由于圆的参数方程为:x cos , y sin 02,所以y dssind2sin d4 ;L( 5) ( x2y2z 2)ds 2a 2b 2t 2 a 2 b 2dtL2 (3a 2 42b 2 ) a 2b 2 ;12 31( 6)2t3t 2t 2dtxyzds0 t1 2tL3221 92 (1t)dt16 2;3t143( 7)截线为 2 y 2z 2 a 2 , x y ,所以2 y 2 z 2 dsL a 2ds a 2 a 2 a 2 .L2. 求曲线 xa, yat , z 1 at 2 (0 t 1, a 0) 的质量,设其线密2度为2za .解 曲线质量为M2zds1a 2t 2dtt a 2L aa21 22 a 0 1 t d(1t )(2 2 1).3233x a(t sin t)3. 求摆线a(1 (0 t) 的重心,设其质量分布是均匀ycost )的 .解 设摆线的线密度为,由于dsa 2(1cost )2a 2 sin 2t dt 2asin tdt ,从而其质量为2mds 2asin tdt4a,L2故其重心坐标为1 xm a2L 0 xds1 a( tsin t) 2a sin tdt4a2t sin tdt asin t sintdt 2 22at costa cos tdta cos3tcos t dt4a ;2 024 0223y1 yds 1a(1 cost)2asin tdtm L 4a 02a tacost sin t2sin dt2 dt20 2tasin 3t tdt4a cos42 sin a .2 0 0234. 若曲线以极坐标( )( 12 ) 表示,试给出计算f (x, y)dsL的公式,并用此公式计算下列曲线积分:( 1)ex 2 y 2ds ,其中 L 为曲线a( 0) 的一段;L4aek( 2)xds ,其中 L 为对数螺线(k 0) 在圆 ra 内的部分 .L解 因为 L 的参数方程为 x ( )cos , y ( )sin( 12 )2342dy 2且dsdxd2 / 2ddd .所以f (x, y) dsL22/ 2f ( ( ) cos , ( ) sin )d .1( 1) x 2y 24 a 20 daa;ed se a4eL( 2) xdsaekcos a 2e 2ka 2k 2e 2k dLa 2 1k 2e 2 kcos d.e 2 k cos d若记I,则e 2 k cos de 2k d sinIe 2k sin 02ksinde 2k2ksin d2k2k d cose 2ke2ke 2k cos 04k 22k4k 2 Ie 2 k cos d于是 I2k ,故 xds2a 2 k 1 k 2.1 4k21 4k 2L5. 证明:若函数 f ( x, y) 在光滑曲线 L : x x(t ), y y(t), t [ , ] 上 连续,则存在点 ( x , y ) L ,使得 f x y )d s f x 0 , y L ,其中L 0 0 L ( , ( 0 )为 L 的弧长 .证 由 于 函 数 f (x, y) 在 光 滑 曲 线 L 上 连续 , 从 而 曲 线 积 分f ( x, y)ds 存在,且Lf ( x, y)dsf ( x(t), y(t )) x 2 (t) y 2 ( t) dtL235又 f在 L 上连续, L 为光滑曲线,所以f ( x(t), y( t))与x2 (t ) y 2 (t )在 [, ] 上连续,由积分中值定理知:存在t0 [ ,] ,使f ( x(t), y(t ))x 2 (t )y 2 (t) dtf [ x(t0 ), y(t0 )]x 2 (t )y 2 ( t)dt f [ x(t0 ), y(t0 )]L .令 x0x(t0 ), y0 y( t0 ) ,显然点 ( x0 , y0 )L ,且f ( x, y) ds f ( x0 , y0) L.L§2 第二型曲线积分1.计算第二型曲线积分:( 1)Lxdy ydx ,其中L为本节例 2 中的三种情况;( 2)(2a y)dx dy ,其中L为摆线x a(t sin t ), y a(1 cost ) L(0 t 2 ) 沿t增加方向的一段;( 3)xdx ydy,其中 L 为圆周x2y2a2,依逆时针方向;L22x y( 4)Lydx sin xdy ,其中L为 y sin x0x与 x 轴所围的闭曲线,依顺时针方向;( 5)x x y y z z,其中L:从(1,1,1)到(2,3,4)的直线段 .L d d d解( 1)若积分沿抛物线OB:y2x 2(0x 1 ),则xdy ydx 14x 2 x2 ]dx 2 ;[ xL03若积分沿直线 OB : y2x (0 x1),则xdy ydx1x 22x dx0.L若积分沿封闭曲线OABO ,在 OA 一段上,y0,0x1;在AB一段上, x 1,0y 2 ;在BO一段上,沿 y2x 从x1到 x 0 .且23612 xdy ydx0dx 0,d d d 2,OA0AB0 xdy ydx xdy ydx0.BO OB因此 xdy ydxOA AB BO 2.L( 2)由于 x a(t sin t ), y a(1cost ) (0t 2 ),从而( 2 a y) dx dy 2a a cos t ) a(1cost ) a sin t] dt [( 2aLL xdx ydyx2 y2(a2 sin2 t a sin t) dt a2x a cost, y a sin t 02 a2 sint cost a2 sint cost0a2dt.t 2,所以2sin2tdt0 .(4)ydx sin xdyL OA AO(sin x sin x cosx)dx( 0sin x0)dx 2 .( 5)直线的参数方程为x 1t, y 12t, z13t( 0 t 1 )xdx ydy zdz 1t) 2(12t ) 3(13t )]dt [(1L01( 6 14t)dt13 .2.设质点受力作用,力的反方向指向原点,大小与质点离原点的距离成正比 .若质点由(a,0)沿椭圆移动到(0,b),求力所作的功 .解椭圆的参数方程为:x a cost, y b sin t 0 t 2 ,而F k x 2y2x,y(kx, ky) (k0) .x2y2x2y 2则力所作的功W kxdx kydyLk2a sin t)bsin t cost]dt[a cost (( 3)由于圆的参数方程为:0 2237k2( a 2 b2) sintdsin tk (b 2 a 2) .2xy 平面3. 设一质点受力作用,力的方向指向原点,大小与质点到 的 距 离 成 反 比 . 若 质 点 沿 直 线 xat , ybt , z ct (c 0) 从M (a,b,c) 沿椭圆移动到N (2a,2b,2c) ,求力所作的功 .解由于力的方向指向原点,故其方向余弦为cosxyz, cos, cosrrr其中 rx 2 y 2z 2 .所以力的三个分力为 Pk x k yk zz , Qz, Rz.从而力所作的功rrrWkxky dy kzdz2(a 2 b 2 c 2 )tdtdxzrzr kcrtLzr12a 2b 2c2k a2 b2c 2ln 2 .dtkc 21ct a 2 b 2c4. 证明曲线积分的估计式:AB Pdx QdyLM其中 L 为 AB 的弧长, MmaxP 2Q 2 .( x, y ) AB利用上述不等式估计积分I Rydx xdyx 2y 2R 2(x2xy y 2)2.并证明 lim I R 0 .R证 ( 1)因为Pdx QdyP dxQdyds ,且ABABds dsP dxQ dy(P2Q 2)[(dx)2( dy )2 ]P 2Q 2 ,dsdsdsds从而238Pdx QdyP dxQdydsP 2 Q 2 dsMds LMABABds ds ABAB( 2)因为 max( x 2 x2y24,则由( 1)得x 2y 2R 2xy y 2 ) 4R 3ydx xdy2 R48x 2y 2R 2( x 2xy y 2 )2R 3 R 280( R ) ,故 lim I0 .则 I R2RRR5. 计算沿空间曲线的第二型曲线积分:( 1) xyzdz ,其中 L : x 2 y 2 z 2a 2 与 y z 相交的圆,其方L向按曲线依次经过 1, 2, 7,8 卦限;( 2 )( y 2 z 2 )dx ( z 2x 2 )dy ( x 2 y 2 )dz , 其 中 L 为 球 面Lx 2 y 2 z 21 在第一卦限部分的边界曲线, 其方向按曲线依次经过xy 平面部分, yz 平面部分和 zx 平面部分 .解 ( 1)曲线的参数方程为xcost, y2sin t, z2sin t) ,且 t 从 022(0 t2 增加到 2时,曲线依次经过 1,2,7,8 卦限,xyzdz2 2 2 . 所以sin 2t cos 2 tdtL416( 2)球面在第一卦限部分的边界曲线由三部分xcostx 0L 1 : ysin t (0 t2) ;L 2 : y cosu (0 u2) ;z 0 z sinuxsin vL 3 : y0 (0 t2)组成 .zcosv而( y 2 z 2 )dx (z 2x 2 )dy ( x 2y 2 )dzL 12392(sin 3 t cos 3t )dt 4 ,3同理L 2 ( y 2 z 2 )dx ( z 2 x 2 ) dy ( x 2y 2 )dz2cos 3u)du4 , (sin 3u3L 3 ( y 2 z 2 )dx (z 2x 2 ) dy ( x 2y 2 )dz2cos 3v) dv4 .(sin 3v34 4 4所以( y 2 z 2 )dx (z 2x 2 )dy (x 2 y 2 )dz4 .L3 3 3总练习题1. 计算下列曲线积分:( 1)yd s ,其中 L 是由 y 2x 和 x y2 所围的闭曲线;L( 2)y ds ,其中 L 为双纽线 ( x 2 y 2 ) 2 a 2 ( x 2 y 2 ) ;L( 3) zds ,其中 L 为圆锥螺线 xt cos t, y a sin t , z t ,t [0,t 0 ] ;L( 4)xy 2dy x 2 ydx , L 为以 a 为半径, 圆心在原点的右半圆周从L最上面一点 A 到最下面一点 B ;( 5)dydx,L 为抛物线 y x 2 4 ,从 A(0, 4) 到 B(2,0) 的一段;Lx y( 6)y 2d x z 2 dy x 2 dz , L 是维维安尼曲线x 2y 2 z 2a 2 ,Lx 2 y 2 ax ( z 0, a 0) ,若从 x 轴正向看去, L 是沿逆时针方向进行的 .解 (1) L 是由 L 1: yx ,0 x 1 与 L 2 : yx,0x 4 及L 3 : y 2x,1 x 4 三部分组成 .故ydsydsydsydsLL 1L 2L 324011)2dx 4x 1 (1) 2dx1x 1 (2 (2 x)dx2 x2 x15 17 32 .(517 )122r 2 a 2 cos2( 2)由于 L 的极坐标方程为 , r 0 ,且dsr 2r / 2 dad .cos2利用对称性得y ds4 4 r sinad4a 24sin d4a 2 (12 ) .Lcos22( 3)由于 ds(cost t sint)2(sin t t cost )2 1dt2 t 2 dt ,zdst 02t 2dt1t 0 2 t 2d ( 2 t 2 )所以t 0L21{( 2 t 0 ) 3 2 2 2}.3( 4)由于圆的参数方程为:x cost, ysin t(2t ),且 A 点2与对应, B 点与对应 .故22xy 2dyx 2 ydxL2 { a cos t a 2 sin t a cost a 2 cos 2 t a sin t ( asin t)} dt2a 4 2 sin 2 2tdta 4 21 cos 4t dta 4 ;222224dy dx22x 12x1( 5)2dx 2dx0 xx 21Lx y4( x ) 2 152162ln( xx24)ln 2 .241( 6)曲线L的参数方程为a a, y a, z a sin, 02x cos sin2222则 y 2dx z2dy x2dzL2a sin )2 (a sin )( a sin )2( a cos )(a a cos )2( a cos )}d{(022******* a3.42.设 f ( x, y) 为连续函数,试就如下曲线:(1)L:连接A( a, a), C(b, a)的直线段;( 2)L:连接A( a, a),C(b, a), B(b,b)三点的三角形(逆时针方向),计算下列积分: f ( x, y)ds, f ( x, y)dx, f ( x, y)dy .L1L 2L2解( 1)连接A( a, a),C (b, a)的直线段的方程为y a, a x b ,by则f ( x, y)ds f (x,a)dx ;L1a C(b,b)bf ( x, y)dy 0f ( x, y)dx f (x,a)dx ;.L1a L1B (b,a)( 2)连接C(b, a), B(b,b)的直线段的方程为A(a,a)x x b,a y b ,则f ( x, y)dsb CB f (b, y)dy ;af ( x, y)dx0, f ( x, y)dy b CB f (b, y) dy .CB a连接 B(b,b), A( a, a) 的直线段的方程为y x,a x b ,则f ( x, y) ds2b BA f ( x, x)dx ;af ( x, y) dx af ( x, x) dxbBA bf ( x, x)dx ,af ( x, y) dy af ( y, y) dybBA bf ( y, y)dy , a242f ( x, y)ds b b2b从而 f ( x,a )dx f (b, y)dy f ( x, x)dx ;L 2a a af ( x, y )d x b bf ( x, a )d x f ( x, x )dx ,L 2a af ( x, y )dy b bf ( y, y)dy .f (b, y) dyL 2a a3.设 f ( x, y) 为定义在平面曲线弧段AB 上的非负连续函数,且在AB 上恒大于零.( 1)试证明 f ( x, y)ds 0 ;AB( 2)试问在相同条件下,第二型曲线积分f( ,y) d0 是否成AB立?为什么?证(1)证由题设存在 P0 ( x0 , y0 )AB, 使得 f (P0 )0 ,令f ( P0 ) ,由连续函数的局部保号性知:存在0 ,使得对一切P L1 (L1U (P0,) AB) ,有 f (P).2又由于 f ( x, y) 为定义在平面曲线弧段AB 上的恒大于零的连续函数,因此 f ( x, y) 在 AB 上可积,且f ( x, y)ds f ( x, y)dsAB f ( x, y)ds2L10 .AB L 1L1(其中 L1是 L1的弧长).( 2)不成立 .因为第二型曲线积分与平面曲线弧段AB 的方向有关.如 f (x, y)2x ,沿着曲线y x从 A(2,2) 到 B(1,1) ,显然 f ( x, y)为定义在平面曲线弧段AB 上的非负连续函数,且恒大于零.但12 xdx3 .2xdx2AB243。
高数:曲线积分与曲面积分总结

则有
Pdx Q dy
L
( x
D
)d x d y
其中 L 是 D 的取正向的边界 曲线,公式称为格林公式.
格林
积分与路径无关:
定理2 设D是平面单连通区域, ( x , y ), Q( x , y )及其 P 一阶偏导数在 内连续,则下述四个命 D 题等价:
(2)若投影域面积是零,则积分值是零。
注:“一投,二代,三定号”
z
2
O
n
y
1
x
若 是母线平行于 z 轴的柱面 , 则 Pdxdy 0 .
例如积分 I 1 : x
2 2
( x y 1 ) dxdy ,
y
2
1 , ( 0 z 1 );
: x y 1 , ( x 0 , y 0 , 0 z 1 ).
3 .如果 由 y y ( z , x ) 给出 , 则有
D yz
把曲面Σ向yoz面投影,得区域D yz
把曲面Σ向xoz面投影,得区域Dxz
Q( x , y , z )dzdx Q[ x , y( z , x ), z ]dzdx
Dzx
注意:(1)对坐标的曲面积分,必须注意曲面所取的侧.
f [ x , y , z ( x , y )] 1 z x z y dxdy
2 2
R ( x , y , z ) dxdy
D xy
R [ x , y , z ( x , y )] dxdy
D xy
算 一投,二代,三换(与侧无关)一投,二代,三定号 (与侧有关)
高数 第二型线积分与面积分

0 1
y x2
4 x 3 dx
0
1
A(1,0 )
圆电流的磁感应场
2
函数 z sin xy 图形及其等高线图形.
曲 面 的 等 高 线 场
3
小 木 屋 附 近 的 温 度 场
场: 一般地,我们把分布着某种物理量的平面或
空间区域称为场。 数量场:如果场中的量可用 数量值函数确切表示。如温 度场,高度场,电位场等。 用 M , M G R3 表示。
y
F i ,i
B
Wi F i ,i M i1 M i ,
即 Wi P ( i ,i )xi Q( i ,i )yi . o
n
L
A
M2 M1
M i 1 xi
yi
M i M n 1
x
3.和 W Wi
i 1n i 1源自近似值 [ P ( i , i ) xi Q( i , i ) yi ].
t , t 在以及为端点的闭区间上具有一阶连
续导数, 且 2 t 2 t 0.
(在此为什么不表示 闭区间???)
则曲线积分 L P x , y dx Q x , y dy存在 ,
且 L P x , y dx Q x , y dy P t , t t Q t , t t dt
x
W F AB. (即为力向量F与 AB 的数量积) 实例: 变力沿曲线所作的功 1.分 A M 0 , M1 ( x1 , y1 ),, M n1 ( xn1 , yn1 ), M n B.
7
M i 1 M i ( xi )i ( yi ) j .
高数复习知识点及公式

数复习知识点及公式、知识点1 求直线方程和平面方程求条件极值二重积分曲线积分(弧长积分、坐标积分)曲面积分6 格林公式、高斯公式f空间闭曲面8 幕级数(求收敛半径、判断正项级数收敛性)、傅里叶级数二、公式空间解析几何和向量代数:空间2点的距离:d = M 4M2 = J (X2-xj2+ (y2-yj2+⑺-乙)'向量在轴上的投影:PrjuAB = AB cos®,®是AB与u轴的夹角。
Pr ju® +a.2)= Prjc + Pr ja?a b = a [b cos H =a x b x+且曲'4 是一个数量,cos c —3xbx +Qyby +QzbzX 1•2 2 2 ---- ・血2心Ibz? x +&y +dz■1 kC =axb = ax a y a.z ‘ C =ia [b sin 线速度:v二wxr.bx by j日•例:Qx Qy Qz向量的混合积:Eabc]= (a%b ) bx by bz=a%b iCco护,且为锐角时, C 二Cx Cy Cz代表平行六面体的体积。
空间直线的方上如y-yo二次曲面:平面的方程:点法式:A(X —Xo) +B(-y o) +C(z — Zo)=°,其中 n ={A ,B,chM o (V 2、一 般方程:Ax+By+Cz + D =0 3、截距世方程:1fx = Xo + mtp };参数方程:〔y = yo +nt2 2 2X丄-T + y^+z L 1 a J 2 J 2—12b cX r 2 z■卡L =z, (p, q 同号) Zp Zq 3、双曲面:2 2 2单叶双曲面:2.2 2 - ■ a. b c2 2 2务-与+务=1(马鞍面)a b c双叶双曲面:多元函数微分法及应用平面外任意一点到该平 面的距离:°二 cAx 。
+ By 。
+ Czo + D 全微分:dz 二dx + dyex cy全微分的近似计算:iz 农dz 二f x (x, v) Ax +fv(x, v) 3 多元复合函数的求导法 dzdtcz 点 u 丄 cz dv........ . ........... I- ................ r ----------cu ct cv ctr.f [u(x, y), v(x, y)] cz :".r-.!■.cz cu cz cvC L C ercu cudu = ----- dx + — 一dy隐函数F(x, y)=0.)+£ (上严Fy^/FydxW(t0)V *0)二乙-Zo若空间曲线方程为:1、过此点的法向量:Fy Fzn = {Fx (Xo, yo, Zo), Fy (Xo, yo, Z(如Fz (Se, y(p2o)卩xAC -B2 >0 寸,「A〈0,fyy(Xo,cU 1 £ (F, G) cv 1 次F, G)& _〃J c(x,:) cX -J 陨和 1 点(F, G) cv 1 点勿〃〃7 E(y, v) 刃〃7 E (u, y)微分法在几何上的应用:[x 二® (t)空间曲线I尸屮(t)在点M(Xo, yo, Zo)处的切线方程:x-Xo =-°■1iz〃(t)在点M 处的法平面方程:W,(to) (x -X°)+ 屮’(to) (y -y。
《高数》下册第十一章练习题

《高数》下册第十一章练习题第十一章曲线积分与曲面积分习题11-11.设在某Oy面内有一分布着质量的曲线弧L,在点(某,y)处它的线密度为(某,y)。
用对弧长的曲线积分分别表达:(1)这曲线弧对某轴,对y轴的转动惯量I某Iy,(2)这曲线弧的质心坐标某,y2.利用对弧长的曲线积分的定义证明性质33.计算下列对弧长的曲线积分:(1)(2)(某L2y)d,其中L为圆周某acot,yaint(0t2)2nL(某y)d,其中L为连接(1,0)及(0,1)两点的直线段2某d,其中L为由直线y=某及抛物线y某(3)L所围成的区域的整个边界e(4)L某2y2d,其中L为圆周某2y2a2,直线y=某及某轴在第一象限内所围成的扇形的整个边界1tttd某ecot,yeint,ze222(5)某yz,其中为曲线上相应于t从0变到2的这段弧(6)某2yzd,其中为折线ABCD,这里A,B,C,D依次为点(0,0,0),(0,0,2),(1,0,2),y2d,,其中L为摆线的一拱某a(tint),ya(1cot)(0t2)(1,3,2)(7)(8)LL(某2y2)d,其中L为曲线某a(cottint),ya(inttcot)(0t2)4.求半径为a,中心角为2的均匀圆弧(线密度1)的质心0t2,它的线密度5.设螺旋形弹簧一圈的方程为某acot,yaint,zkt,其中(某,y,z)某2y2z2.求:I(1)它关于z轴的转动惯量z(2)它的质心。
习题11-21.设L为某Oy面内直线某a上的一段,证明:LP(某,y)d某02.设L为某Oy面内某轴上从点(a,0)到点(b,0)的一段直线,证明:LP(某,y)d某P(某,0)d某ab3.计算下列对坐标的积分:(1)(某L2y2)d某,其中L是抛物线y某2上从点(0,0)到点(2,4)的一段弧(2)L某yd某2(某a)2y2a(a>0)及某轴所围成的在第一象限内的区,其中L为圆周域的整个边界(按逆时针方向绕行)(3)Lyd某某dy,其中L为圆周某Rcot,yRint上对应t从0到2的一段弧(某y)d某(某y)dy222某+ya(4)L(按逆时针方向绕行)某2y2,其中L为圆周(5)某2d某zdyydz,其中为曲线某kyaco,zain上对应从0到是从点(1,1,1)到点(2,3,4)的一段直线的一段弧(6)(7)某d某ydy(某y1)dz,其中,其中d某dy+ydz2L为有向闭折线ABCD,这里的A,B,C依次为点(1,0,0),(0,1,0),(0,0,1)(8)(某的一段弧4.计算2某y)d某(y22某y)dy,其中L是抛物线y某2上从点(-1,1)到点(1,1)(某y)d某(y某)dy,其中L是:L2y某上从点(1,1)到点(4,2)的一段弧(1)抛物线(2)从点(1,1)到点(4,2)的直线段(3)先沿直线从点(1,1)到点(1,2),然后再沿直线到点(4,2)的折线22某2tt1,yt1上从点(1,1)到点(4,2)的一段弧(4)曲线222某yR5.一力场由沿横轴正方向的恒力F所构成,试求当一质量为m的质点沿圆周按逆时针方向移过位于第一象限的那一段弧时场力所做的功6.设z轴与动力的方向一致,求质量为m的质点从位置(某,y,z)沿直线移到(某,y,z)时重力所做的功7.把对坐标的曲线积分LP(某,y)d某Q(某,y)dy化成对弧长的积分曲线,其中L为:(1)在某Oy面内沿直线从点(0,0)到点(1,1)2y某(2)沿抛物线从点(0,0)到点(1,1)22某y2某从点(0,0)到点(1,1)(3)沿上半圆周23某t,yt,zt为曲线上相应于t从0变到1的曲线弧,把对坐标的曲线积分8.设Pd某QdyRdz化成对弧长的曲线积分习题11-31.计算下列曲线积分,并验证格林公式的正确性:(1)L(2某y某2)d某(某y2)dyy某2和y2某所围成的区域的,其中L是由抛物线正向边界曲线(2)L(某2某y2)d某(y22某y)dy,其中L是四个顶点分别为(0,0),(2,0),(2,2),(0,2)的正方形区域的正想边界2.利用曲线积分,求下列曲线所围成的图形的面积(1)星形线某aco3t,yain3t22(2)椭圆9某+16y144(3)圆某y2a某22yd某某dy22(某1)y2,L的方向为逆时针方向L2(某2y2)3.计算曲线积分,其中L为圆周4.证明下列曲线积分在整个某Oy面内与路径无关,并计算积分值(1)(2)(2,3)(1,1)(3,4)(某y)d某(某y)dy(1,2)(2,1)(6某y2y3)d某(6某2y3某y2)dy(2某yy43)d某(某24某y3)dy(3)(1,0)5.利用格林公式,计算下列曲线积分:(2某y4)d某(5y3某6)dy(1),其中L为三顶点分别为(0,0),(3,0)和(3,2)L的三角形正向边界;(某(2)L2yco某2某yin某y2e某)d某(某2in某2ye某)dy23,其中L为正向星形线某ya(a0)(3)2323,其中L为在抛物线L(2某y3y2co某)d某(12yin某3某2y2)dy2某y2上由点(0,0)到(2)的一段弧,1(某(4)L2y)d某(某in2y)dyy2某某2上由点(0,0)到点(1,1),其中L是在圆周的一段弧6.验证下列P(某,y)d某Q(某,y)dy在整个某Oy平面内是某一函数u(某,y)的全微分,并求这样的一个u(某,y):(1)(某2y)d某(2某y)dy22某yd某某dy(2)(3)4in某in3yco某d某3co3yco2某dy2232y(3某y8某y)d某(某8某y12ye)dy(4)22(2某coyyco某)d某(2yin某某iny)dy(5)7.设有一变力在坐标轴上的投影为某某y,Y2某y8,这变力确定了一个力场。
辽宁工业大学高数习题课10-1-2

特殊的有向曲线 L1:x24y22( 0充分小), 规定L1的方向为
逆时针(如图所示)。
y
L
设 L(L1)所围成的区域为D,
L1
则在L(L1)上应用Green 公式,得
0
x
yd x xdyQP
( )dxd 0,y L L 1 x24y2 D x y
所以
ydxxdy
L x24y2
L1
ydxxdy
x24y2 .
而
ydxxdy1 L1 x24y2 2
ydxxdy 1
L1
2
2dxdy
D
故
ydx xdy
L x2 4y2
或利用参数方程计算:令L 1
:xcos,y sin ,
2
从0到2
.
所以 ydxxdy ydxxdy
L x2 4y2 L1 x2 4y2
21 22(s 0
1y}
,
于是
WBO rk3[xdx (1y)d]yk
1d[x2 (1y)2] 2 (0,0) (2,0) [x2 (1y)2]32
1k(2)[x2(1y)2]1 2
(0,0)
k(1
1
).
2
(2,0)
5
感谢您的关注
解: 补直线段 L OA: y 0, x从0变到; 并设曲线LL
所围区域为 D(如图),则由Green公式,得:
ex [1 ( co y )ds x (y siy )n d]y L L
Q
(
D
x
P)dxdy y
yexdxdy
D
y
ysinx
L
dxsinxexydy1 (1 e )
高数10章第2节对坐标曲线积分

06 曲线积分在实际问题中应 用
面积、体积和弧长计算
01
02
03
面积计算
通过曲线积分可以计算由 平面曲线所围成的面积, 例如计算不规则图形的面 积。
体积计算
在空间中,曲线积分可以 用来计算由曲线旋转或平 移所生成的立体体积。
弧长计算
曲线积分还可以用来计算 曲线的弧长,特别是对于 那些无法直接通过几何方 法求解的曲线。
质心、形心和转动惯量计算
质心计算
在物理学和工程学中,经常需要 计算物体的质心位置,曲线积分 可以帮助我们找到由曲线构成的
物体的质心。
形心计算
形心是描述物体几何形状的一个重 要参数,曲线积分同样可以用来计 算由曲线构成的物体的形心。
转动惯量计算
转动惯量是描述物体旋转运动特性 的物理量,曲线积分可以用来计算 由曲线构成的物体绕某轴的转动惯 量。
斯托克斯公式在电磁学、流体力学等 领域有着广泛的应用,可以用来计算 磁场、电场、流场等物理量。
在使用斯托克斯公式时,需要注意被积 函数在包含曲面Σ的空间区域内是否满 足具有一阶连续偏导数的条件,以及曲 面Σ和边界曲线Γ的取向是否正确。
其他求解方法
01
直接计算法
对于一些简单的第二类曲线积分问题,可以直接通过参数化曲线并代入
面积等。
培养分析问题和解决问题的能力,提高数学素养和思维水平。
03
内容概述
本节主要介绍对坐标的曲线积分,包括曲线积分的定义、性质和计算方法。 通过具体例题,讲解如何运用定积分求解曲线积分,并介绍一些常用的计算技巧。
讨论曲线积分在实际问题中的应用,如计算平面曲线的长度、空间曲线的质量等。
02 对坐标曲线积分基本概念
高数10章第2节对坐标曲线积分
高数的全部公式大全

高等数学公式导数公式:基本积分表:三角函数的有理式积分:222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=, , , ax x aa a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x C x dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ一些初等函数: 两个重要极限:三角函数公式: ·诱导公式:·和差角公式: ·和差化积公式:2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin( xxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x x xx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22)双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim 0==+=∞→→e xxx x x x·倍角公式:·半角公式:ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理:R CcB b A a 2sin sin sin === ·余弦定理:C ab b a c cos 2222-+=·反三角函数性质:arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹(Leibniz )公式:)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑中值定理与导数应用:拉格朗日中值定理。
高数(下)六类积分

⾼数(下)六类积分1.⼆重积分(PDF P150)⼏何意义:曲顶柱体的体积、平⾯薄⽚的质量∫∫Dµ(x,y) dxdy, µ为密度形式:∫∫D f(x,y) dxdy, dxdy为⾯积元素计算⽅法:交换积分次序简化、利⽤对称性、换元法(dxdy -> Jdudv) 极坐标代换(dxdy -> rdr) {x=rcosθ,y=rsinθ}2.三重积分(P167)⼏何意义:物体的质量∫∫∫Ωf(x,y,z)dv, f为密度形式:∫∫∫Ωf(x,y,z)dv= ∫∫∫Ωf(x,y,z)dxdydz , dv为体积元素,Ω为空间中有界闭区域计算⽅法:投影法,截⾯法,对称性(积分区域对称性,轮换对称性) 柱⾯坐标代换(dxdydz -> rdrdθdz){x=rcosθ,y=rsinθ,z=z} 球⾯坐标代换(dxdydz -> r2sinφdrdθdφ){x=rsinφcosθ,y=rsinφsinθ,z=rcosφ} (0≤θ≤2π,0≤φ≤π)重积分的应⽤(P180)1.⼏何应⽤:平⾯区域的⾯积、曲⾯⾯积、曲顶柱体的体积2.物理应⽤:质⼼、转动惯量、引⼒空间曲⾯的曲⾯⾯积:S=∫∫D√(1+z x2+z y2)dxdy质⼼:x c=∫∫D x*µ(x,y) dσ / ∫∫Dµ(x,y) dσ , y c=∫∫D y*µ(x,y) dσ / ∫∫Dµ(x,y) dσ转动惯量:对x轴的转动惯量 I x= ∫∫D y2*µ(x,y) dσ, 对y轴的转动惯量 I y= ∫∫D x2*µ(x,y) dσ空间⽴体对单位质量的质点的引⼒:F x = G ∫∫∫Ωρ(x,y,z)x / r3 dV, F y = G ∫∫∫Ωρ(x,y,z)y / r3 dV, F z = G ∫∫∫Ωρ(x,y,z)z/ r3 dV3.第⼀型曲线积分(P194)⼏何意义:曲线的质量 m = ∫L µ(x,y)dS形式:∫L f(x,y)dS计算⽅法:⽤参数⽅程4.第⼀型曲⾯积分(P224)⼏何意义:曲⾯的⾯积,m = ∫∫S µ(x,y,z) dS, dS曲⾯微元形式:∫∫Σf(x,y,z)dS计算⽅法:1.曲⾯投影到平⾯,2.被积函数三元变两元,3. 曲⾯微元变为曲⾯⾯积5.第⼆型曲线积分(P200)⼏何意义:变⼒沿曲线所做的功形式:∫L Pdx+Qdy (有⽅向)计算⽅法:平⾯封闭曲线上⽤格林公式, 当P x=Q y,与积分路径⽆关,选取折线路径计算6.第⼆型曲⾯积分(P229)⼏何意义:流向曲⾯⼀侧的流量形式:∫∫ΣPdydz+Qdzdx+Rdxdy = ∫∫Σ (Pcosα+Qcosβ+Rcosγ)dS 计算⽅法:合⼀投影法、分⾯投影法、⾼斯公式 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
{P[ (t), (t), (t)](t) Q[(t), (t),(t)] (t)
R[(t), (t),(t)](t)}dt
13/28
例1 计算L 2xydx x2dy,其中L为 (1) 抛物线 y x2上从O(0,0)到B(1,1)的一段弧; (2) 抛物线 x y2上从O(0,0)到B(1,1)的一段弧; (3) 有向折线OAB,这里O, A, B依次是点(0,0) (1,0),(1,1).
n
P( x,
y, z)dx
lim
0
i 1
P(i
,i ,
i
)xi
n
Q(
x,
y,
z)dy
lim
0
i 1
Q(i
,i
,
i
)yi
n
R( x,
y, z)dz
lim
0
i 1
R(i ,i , i )zi
8/28
6. 性质
y L L2
(1) 如果把 L分成 L1和 L2 , 则
L1 O
x
Pdx Qdy Pdx Qdy Pdx Qdy
lim
0
i 1
Q(i
,i
)yi
称 Q( x, y)在有向曲线弧 L上对坐标y的曲线积分.
5/28
2. 存在条件 当P( x, y),Q( x, y)在光滑曲线弧L上连续,
第二类曲线积分存在.
3.组合形式
L P( x, y)dx LQ( x, y)dy
P( x, y)dx Q( x, y)dy F ds “点积”形
L
L1
L2
(2) 设 L是有向曲线弧 , L是与L方向相反的
有向曲线弧, 则
yL
P( x, y)dx Q( x, y)dy
L
L
L P( x, y)dx Q( x, y)dy
O
x
对坐标的曲线积分与 曲线的方向有关.9/28来自三、第二型曲线积分的计算
思想是 化为定积分计算.
对坐标的曲线积分与曲线的方向有关. 因此下限应是起点的坐标, 上限是终点的 坐标.
常力沿直线所作的功 W F AB
分割
A
M0 , M1( x1,
y1
),
,
M
n1
(
xn1
,yn1
),
Mn
B
Mi1Mi (xi )i (yi ) j
2/28
M i 1 M i
(xi
)i
(yi ) j
取 F (i ,i ) P(i ,i )i Q(i ,i ) j
取近似 Wi F (i ,i ) Mi1Mi y
第二型曲线积分
一、引例:变力做功问题 二、第二型曲线积分的概念与性质 三、第二型曲线积分的计算法 四、两类曲线积分的关系
1/28
一、引例 变力做功问题
F (i ,i )
y
Mi1 •
Mi
•
yi
•
M n1
•B M n
L xi
• M2 • M1
L:A B
A • M 0
O
x
F( x, y) P( x, y)i Q( x, y) j
xi
Q(i ,i ) yi ]
精确值
3/28
二、第二型曲线积分的概念和性质
1. 定义 设L为xOy面内从点A到点B的一条有向光滑
曲线弧,函数P( x, y),Q( x, y)在L上有界. 用L上的点: M1( x1, y1 ), M2( x2, y2 ), M n1( xn1 , yn1 ) 把L分成n个有向小弧段 Mi1Mi (i 1,2,, n; M0 A, Mn B).设xi xi xi1 , yi yi yi1 , 点(i ,i )为Mi1Mi 上任意取定的点.
10/28
定理 设P( x, y), Q( x, y)在曲线弧L上有定义且
连续,
L的参数方程为
x y
(t)
,
(t)
当参数t单调地
由变到时,点M( x, y)从L的起点A沿L运动到
终点B,(t), (t)在以及为端点的闭区间上具
有一阶连续导数, 且2(t) 2(t) 0,则
曲线积分L P( x, y)dx Q( x, y)dy存在, 且
解 (1) 化为对 x 的积分.
L : y x2 , x从0变到1,
原式
1
(2x
x2
x2
2 x )dx
0
4 1 x3dx 1. 0
y x2
B(1,1)
A(1,0)
14/28
(2) 化为对 y 的积分. L : x y2 , y从 0 变到 1 ,
原式 1 (2 y2 y 2 y y4 )dy 0 5 1 y4dx 1. 0
4/28
如果当各小段长度的最大值 0时 ,
n
P(i ,i )xi的极限总存在, 则称此极限为函数
i 1
P( x, y)在有向曲线弧 L上 对坐标x的曲线积分,
或称 第二型曲线积分.记作 P( x, y)dx,即 L
n
L
P(
x,
y)dx
lim
0
i 1
P(i
,i
)xi
n
类似地定义 Q( x, y)dy L
F (i ,i )
Mi
B
••
Mn
即 Wi P(i ,i )xi Q(i ,i )yi
Mi1 •
y • Mn1 i
L • M2 xi
n
求和 W Wi i 1
• M1
A• M 0
O
x
n
[P(i ,i ) xi Q(i ,i ) yi ]
近似值
i 1
n
取极限
W
lim
0i1
[
P(i
,i
)
(2) L : x x( y) y起点为c, 终点为d
则 L P( x, y)dx Q( x, y)dy
d
c {P[ x( y), y]x( y) Q[ x( y), y]}dy
12/28
x (t)
(3) 推广
:
y
(t ),
t起点 , 终点
z (t)
P( x, y, z)dx Q( x, y, z)dy R( x, y, z)dz
L P( x, y)dx Q( x, y)dy
P[
(t
),
(t
)] (t
)dt
Q[
(t
),
(t
)]
(t
)dt
11/28
特殊情形 (1) L : y y( x) x起点为a, 终点为b
则 L P( x, y)dx Q( x, y)dy b a{P[ x, y( x)] Q[ x, y( x)]y( x)}dx
L
L
其中
F
P,Q,
ds
dx,
dy.
式
6/28
4. 物理意义
变力F
P( x,
y)i
Q( x,
y) j
沿A⌒B所作的功W
W A⌒B F ds
ds
dx,dy.
A⌒B (Pi Qj ) (dxi dyj )
⌒ Pdx Qdy AB
7/28
5. 推广
空间有向曲线弧Γ, Pdx Qdy Rdz
(3) 原式 OA 2xydx x2dy AB 2 xydx x2dy
