三重积分在柱面坐标下的计算习题解析
微积分:利用柱坐标计算三重积分

a Dxy
r
,
cos
x
o
y
z x2 y2
I
4
a
2 4 cos
d d r 2 sin2 r 2 sin dr
x r sin cos
y
r
sin
sin
z r cos
00 0
dv r2 sin drdd
I ( x2 y2 )dxdydz
2
a
d 4 d cos r 2 sin2 r 2 sin dr
2
2
dz d
ze z2 rdr
1
0 0r
2 2 ez2 zdz (e4 e). 1
z
z2
z x2 y2
z1
O
y
x
y Dz
x
x2 y2 z2
计算(x y z)2dv,
其中是抛物面 z
x2
y2和 球 面x2
y2
z
z2
2
所围成的空间闭区域.
解 ( x y z)2 x2 y2 z2 2( xy yz zx)
且 当( x, y) Dxy时, x2 y2 z 2 x2 y2 ,
Dxy : x2 y2 1,
y Dxy
x
x2 y2 z 2 x2 y2,
x2 y2 1
2 x2 y2
V 1 dv dxdy
1 dz
x2 y2
Dxy
(2 2 x 2 2 y 2 )dxdy
Dxy
2
2
d
1 (1 r 2 )rdr
0
0
0
0
t (0, )
0 r t
所以,F (t)在(0, )内 单调增加.
利用柱面坐标求三重积分例题

利用柱面坐标求三重积分例题在数学中,求解三重积分是一种常见的计算方法,而柱面坐标系是一种常用的坐标系,特别适用于具有旋转对称性的问题。
本文将介绍如何利用柱面坐标系来求解一个三重积分的例题。
问题描述考虑以下三重积分:$$ \\iiint\\limits_{D}z\\,dx\\,dy\\,dz $$其中区域D由 $0\\leq z\\leq 1$, $x^2+y^2\\leq z^2$, $z\\geq 0$ 所确定。
解题思路首先,我们要将积分区域D在柱面坐标系下进行描述。
在柱面坐标系下,位置(x,y,z)可以表示为 $(r\\cos\\theta, r\\sin\\theta, z)$,其中r为极径,$\\theta$ 为极角。
根据 $0\\leq z\\leq 1$ 和 $z\\geq 0$,可得 $0\\leq z\\leq 1$。
而$x^2+y^2\\leq z^2$ 可以使用极坐标的形式表示为 $r^2\\leq z^2$,进而可以得到$0\\leq r\\leq z$。
另外,由于积分中包含z,我们可以先对z进行积分,再对r和 $\\theta$ 进行积分。
计算过程首先,对z进行积分:$$ \\begin{aligned} \\int_0^1 z\\,dz &= \\frac{1}{2}z^2\\Big|_0^1 \\\\ &=\\frac{1}{2} \\end{aligned} $$接下来,对r和 $\\theta$ 进行积分:$$ \\begin{aligned} \\int_0^{\\frac{\\pi}{2}}\\int_0^z\\int_0^1 z\\cdotr\\,dr\\,d\\theta\\,dz &= \\int_0^{\\frac{\\pi}{2}}\\int_0^z\\frac{1}{2}z^2\\,d\\theta\\,dz \\\\ &=\\int_0^{\\frac{\\pi}{2}}\\frac{1}{2}z^2\\theta\\Big|_0^z\\,dz \\\\ &=\\int_0^{\\frac{\\pi}{2}}\\frac{1}{2}z^3\\,dz \\\\ &= \\frac{1}{8}z^4\\Big|_0^1 = \\frac{1}{8} \\end{aligned} $$因此,最终的三重积分结果为 $\\frac{1}{8}$。
第三节、(3)三重积分在柱坐标系下的计算

1
下底: z = r
1
z
1 I = ∫∫ rdrdθ ∫ 2 dz 2 r r + z D
=∫
2π 0
r dθ ∫ dr ∫ 2 dz 0 r r + z2
1 1
= π (ln 2 − 2 +
Байду номын сангаас
π
2
D
0
1
y
)
. .
x
例3利用柱面坐标计算三重积分 ∫∫∫ zdxdydz , 其中
Ω
0 0
2π
1
2− ρ 2
2
ρ
ρ ( 2 ρ cos θ + z )dz
2 2 2
π = (90 2 − 89). 60
例.6 计算三重积分I = ∫∫∫ ( x + y )dv,
2 2 (V )
z
其中(V )由z = x 2 + y 2 , z = h所围.
解 (V )在xoy面投影域(σ )为圆 : 0 ≤ ρ ≤ h , xy
I = ( ∫∫∫ − ∫∫∫ )( x + y )dxdydz
2 2 Ω1 Ω2
= ∫∫ ρdρdθ ∫ρ 2 f ( ρ ,θ )dz
D1 2
8
− ∫∫ ρdρdθ ∫ρ 2 f ( ρ ,θ )dz
D2 2
2
= ∫ dθ ∫ dρ ∫ρ 2 ρ ⋅ ρ dz
2 0 0
2
2π
4
8
− ∫ dθ ∫ dρ ∫ρ 2 ρ ⋅ ρ dz
Ω是由曲面z = x 2 + y 2与平面z = 4所围成的区域.
0 ≤ θ ≤ 2 π. 0 ≤ ρ ≤ 2,
柱面球面下三重积分

这就化为一个定积分和 一个二重积分的运算
0
.
y
D
x
三 重 积 分的换元法
教学目的与要求: (1) 掌握重积分的柱面和球面变换 (2) 了解n重积分的变量变换 教学重点,难点: 重点:重积分的柱面变换 难点:重积分的球面变换
三重积分换元法
x = x ( u, v , w ) 设变换T : y = y( u, v , w ), 把 uvw 空间中的区域 z = z ( u, v , w )
=
z=g
Ω
∫∫ dxdy , z )dz
M
z=e
∫
b
a
dx ∫ dy ∫ f ( x , y , z )dz
e
.
0
.
c
d
y
a
x
b
D
P
计算三重积分
I = ∫∫∫ f ( x , y , z )dxdydz
Ω
积分区域是曲顶柱体
z
N
z2(x,y)
Ω为图示曲顶柱体
I =∫∫ dxdy∫z ( x , y ) f ( x , y , z )dz
∂x ∂v ∂y ∂v ∂z ∂v
∂x ∂w ∂y ≠ 0, ( u, v , w ) ∈ V ′ ∂w ∂z ∂w
则∫∫∫ f ( x , y , z ) dxdydz
V
= ∫∫∫ f ( x ( u, v , w ), y( u, v , w ), z ( u, v , w )) | J | dudvdw
2π
2 h
∫
h
x
y
=
4
[(1 + 4h) ln(1 + 4 h) − 4 h]
利用柱面坐标计算三重积分x^2+y^2dv

利用柱面坐标计算三重积分 x^2 + y^2 dv在数学中,三重积分是一种计算多变量函数在三维空间内某个区域上的积分的方法。
本文将探讨如何利用柱面坐标系统来计算三重积分x2+y2。
首先,让我们回顾一下柱面坐标。
在三维空间中,柱面坐标由极径r、极角$\\theta$ 和高度z来描述一个点的位置。
其中,$x = r\\cos(\\theta)$,$y =r\\sin(\\theta)$,z保持不变。
假设我们需要计算的三重积分为:$$ \\iiint_D x^2 + y^2 \\, dV $$其中D为一个柱面和平面z=0所围成的区域。
我们可以通过柱面坐标来简化这个积分。
首先,将x和y换成柱面坐标表示:$x = r\\cos(\\theta)$,$y = r\\sin(\\theta)$。
然后,计算体积元素dV。
在柱面坐标下,体积元素dV可表示为:$dV = r\\, dr\\, d\\theta\\, dz$。
将x和y用柱面坐标表示,将dV替换为 $r\\, dr\\, d\\theta\\, dz$,我们可以将原积分转换为柱面坐标下的积分形式:$$ \\iiint_D (r^2\\cos^2(\\theta) + r^2\\sin^2(\\theta)) \\, r\\, dr\\,d\\theta\\, dz $$即$$ \\iiint_D r^3\\, dr\\, d\\theta\\, dz $$接下来,我们可以按照柱面坐标系下的积分计算方法进行计算:$$ \\int_0^{2\\pi} \\int_0^R \\int_0^H r^3\\, dr\\, dz\\, d\\theta $$,其中R代表柱面的半径,H代表柱面的高度。
继续计算得到$$ \\int_0^{2\\pi} \\int_0^R \\left. \\frac{1}{4}r^4 \\right|_0^H dz\\,d\\theta \\\\ = \\int_0^{2\\pi} \\int_0^R \\frac{1}{4}H^4 dz\\, d\\theta \\\\ =\\int_0^{2\\pi} \\frac{1}{4}H^4R d\\theta \\\\ = \\frac{1}{4}H^4R\\int_0^{2\\pi} d\\theta \\\\ = 2\\pi \\cdot \\frac{1}{4}H^4R \\\\ =\\frac{1}{2}\\pi H^4R $$因此,利用柱面坐标计算三重积分 $\\iiint_D x^2 + y^2 \\, dV$ 的结果为$\\frac{1}{2}\\pi H^4R$。
极坐标与球面坐标计算三重积分-极系下的三重积分
例11 利用柱面坐标计算三重积分 zdxdydz,其中是由曲
面 zx2y2 与平面 z4 所围成的闭区域.
z
解 闭区域可表示为:
4
r 2z4,0r2,0q2.
于是
zdxdydz zrdrdqdz
zx2y2 或 zr2
2
2
4
dq rdr zdz
0
0
r2
1
2
dq
2 r(16 r 4 )dr
例2 求半径为a 的球面与半顶角a为的内接锥面所围成的立
体的体积.
z 2a
a
O
y
x
例2 求半径为a 的球面与半顶角a为的内接锥面所围成的立
体的体积.
解 该立体所占区域可表示为:
0r2a cos j ,0ja ,0q2.
z
于是所求立体的体积为
2a
V dxdydz r2 sinj drdjdq
r4 sin 3 jdrdjdq
2
dq
sin 3 j dj
a r4dr 2 a2M ,
0
0
0
5
其中 M 4 a3 为球体的质量.
3
2
dq
a
dj
2a cosj r 2 sin jdr
0
0
0
2
a
s in jdj
2a cosj r 2 dr
0
0
jr a
16a3 a cos3 j sinjdj
30
O
y
4a3 (1 cos4 a) .
x
3
例3 求均匀半球体的重心.
z
解 取半球体的对称轴为 z 轴,
原点取在球心上,又设球半径为a.
二利用柱面坐标计算三重积分

一 柱面坐标系 二 利用柱面坐标计算三重积分 三 球面坐标系 四 利用球面坐标计算三重积分 五 小结与思考判断题
2019/5/28
1
一 柱面坐标系
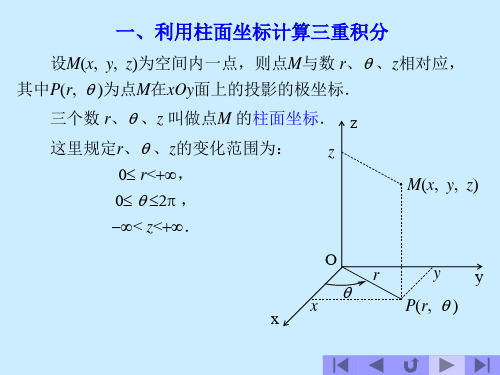
设 M ( x, y, z) 为空间内一点,并设点M 在
xoy 面上的投影 P 的极坐标为r,,则这样的三
个数 r, , z 就叫点 M 的柱面坐标.
2019/5/28
9
规定: 0 r , 0 , 0 2.
如图,三坐标面分别为
r 为常数
为常数 为常数
球 面; 圆锥面; 半平面.
2019/5/28
10
如图,
z
设点 M 在 xoy 面上的投影为P,
r M(x, y,z)
点 P 在 x 轴上的投影为 A,
dv r2 sindrdd ,
r
rd
d
o
y
f ( x, y, z)dxdydz
d
x
f (r sin cos ,r sin sin ,r cos )r2 sindrdd .
2019/5/28
12
例 3 计算 I ( x2 y2 )dxdydz,其中 是锥面
由 x 2 y2 z 2 2a 2
r 2a,
z x2 y2 ,
4 : 0 r 2a, 0 ,
4
0 2,
2019/5/28
15
由三重积分的性质知 V dxdydz,
V
2
d
4 d
2a r 2 sin dr
0
0
高等数学三重积分例题

高等数学三重积分例题一、计算三重积分∭_varOmega z dV,其中varOmega是由锥面z = √(x^2)+y^{2}与平面z = 1所围成的闭区域。
1. 利用柱坐标计算在柱坐标下x = rcosθ,y = rsinθ,z = z,dV = rdzdrdθ。
锥面z=√(x^2)+y^{2}在柱坐标下就是z = r。
由锥面z = r与平面z = 1所围成的闭区域varOmega,其在柱坐标下的范围为:0≤slantθ≤slant2π,0≤slant r≤slant1,r≤slant z≤slant1。
2. 计算积分则∭_varOmegaz dV=∫_0^2πdθ∫_0^1rdr∫_r^1zdz。
先计算关于z的积分:∫_r^1zdz=(1)/(2)(1 r^2)。
再计算关于r的积分:∫_0^1r×(1)/(2)(1 r^2)dr=(1)/(2)∫_0^1(rr^3)dr=(1)/(2)((1)/(2)-(1)/(4))=(1)/(8)。
最后计算关于θ的积分:∫_0^2πdθ = 2π。
所以∭_varOmegaz dV=(1)/(8)×2π=(π)/(4)。
二、计算三重积分∭_varOmega(x + y+z)dV,其中varOmega是由平面x = 0,y = 0,z = 0及x + y+z = 1所围成的四面体。
1. 利用直角坐标计算对于由平面x = 0,y = 0,z = 0及x + y + z=1所围成的四面体varOmega,其范围为0≤slant x≤slant1,0≤slant y≤slant1 x,0≤slant z≤slant1 x y。
则∭_varOmega(x + y + z)dV=∫_0^1dx∫_0^1 xdy∫_0^1 x y(x + y + z)dz。
2. 计算积分先计算关于z的积分:∫_0^1 x y(x + y+z)dz=(x + y)z+(1)/(2)z^2big|_0^1 x y=(x + y)(1 x y)+(1)/(2)(1 x y)^2展开得x + y-(x^2+2xy + y^2)+(1)/(2)(1 2x 2y+x^2+2xy + y^2)进一步化简为x + y x^2-2xy y^2+(1)/(2)-x y+(1)/(2)x^2+xy+(1)/(2)y^2即(1)/(2)-x^2-xy (1)/(2)y^2。
§7.3[2]利用柱面坐标和球坐标计算三重积分
![§7.3[2]利用柱面坐标和球坐标计算三重积分](https://img.taocdn.com/s3/m/ab56616c1eb91a37f1115c11.png)
o
x
y
V = ∫∫∫ dv = ∫∫∫ r 2 sindrddθ
= ∫0 dθ ∫0 d ∫0
4
2π
π
2a 2
r sindr
x = r sin cosθ , y = r sin sinθ , z = r cos.
4 = π ( 2 1)a3. 3
dv = r 2 sindrddθ
�
: x2 + y2 + z2 ≤ 1.
o
y
x
0 ≤ θ ≤ 2π , : 0 ≤ ≤ π , 0 ≤ r ≤ 1.
z
∫∫∫
z2dv =
r 2 cos2 r 2 sin dr d dθ ∫∫∫
o
y
= ∫0 dθ ∫
= ∫0 dθ ∫
2π
2π
x 1 4 2 d 0 r cos sin dr 0 5 1 r π 2 cos sin d 0 5 0
一,利用柱面坐标计算三重积分
xoy 面上的极坐标 + z 坐标
0 ≤ r < +∞,
z
0 ≤ θ ≤ 2π ,
∞ < z < +∞.
M( x, y, z)
y
o r θ
x
P(r,θ )
如图, 如图,三坐标面分别为
z
r 为常数
圆柱面; 圆柱面; 半平面; 半平面; 平 面.
x
z
θ 为常数
z 为常数
z
x
r
为常数
θ 为常数
o
θ
y
球面坐标与直角坐标的关系为
z
x = r sin cosθ , y = r sin sinθ , z = r cos.
二利用柱面坐标计算三重积分-

V2d 4d2ar2si n dr 0 00
2 4si n( 2a)3d
0
3
4( 21)a3. 3
2019/11/4
16
五 小结与思考判断题
三重积分计算
柱面坐标
球面坐标
(1) 柱面坐标的体积元素
dxd rydd d rzd z
(2) 球面坐标的体积元素
2019/11/4
9
规定: 0r , 0, 0 2 .
如图,三坐标面分别为
r 为常数
为常数 为常数
球 面; 圆锥面; 半平面.
2019/11/4
10
如图,
z
设点M在xoy面上的投P影 ,为 rM(x,y,z)
点P在x轴上的投A影 ,为
z
o 则 O x A ,A y P ,P M z . Ax y
第三节 三重积分(2)
一 柱面坐标系 二 利用柱面坐标计算三重积分 三 球面坐标系 四 利用球面坐标计算三重积分 五 小结与思考判断题
2019/11/4
1
一 柱面坐标系
设M(x, y,z)为空间内一点,M并 在设点
xoy面上的投 P的 影极坐标 r,为 ,则这样的三
个数r,,z就叫点 M的柱面坐标.
解 由 锥 面 和 球 面 围 成 , 采 用 球 面 坐 标 ,
由 x 2 y 2 z2 2 a 2
r 2a,
z x2y2 , 4
:0 r 2 a , 0 , 0 2 , 4
2019/11/4
15
由 三 重 积 分 的 性 质 知 V d x , dy
2d 4dcaosr4si3 ndr
高等数学随堂讲解三重积分在柱坐标与球坐标系下计算

一、三重积分在柱坐标系下的计算
(一)柱坐标系 (二)柱坐标系的适用条件 (三)三重积分计算公式 (四)化为累次积分的方法
➢柱坐标系 平面极坐标系添加oz轴得到的空间坐标系
➢柱坐标 设 M (x, y, z) R3,
➢直角坐标与柱坐标的关系
x cos
点M的柱坐标
z
y sin
zz
z M (x, y, z)
规定
在柱坐标系下
常数 常数
圆柱面 半平面
o
y
x (x, y,0)
z 常数
平面
一、三重积分在柱坐标系下的计算
(一)柱坐标系 (二)柱坐标系的适用条件 (三)三重积分计算公式 (四)化为累次积分的方法
一、三重积分在柱坐标系下的计算
(一)柱坐标系 (二)柱坐标系的适用条件 (三)三重积分计算公式 (四)化为累次积分的方法
➢球坐标系下三重积分计算公式
f (x, y, z)dv f (r sin cos , r sin sin , r cos )r 2 sin drdd
二、三重积分在球坐标系下的计算
(一)球坐标系 (二)球坐标系的适用条件 (三)三重积分计算公式 (四)化为累次积分的方法
二、三重积分在球坐标系下的计算
三重积分在柱坐标和球坐标系下的计算
一、三重积分在柱坐标系下的计算 二、三重积分在球坐标系下的计算
三重积分在柱坐标和球坐标系下的计算
一、三重积分在柱坐标系下的计算 二、三重积分在球坐标系下的计算
一、三重积分在柱坐标系下的计算
(一)柱坐标系 (二)柱坐标系的适用条件 (三)三重积分计算公式 (四)化为累次积分的方法
(一)球坐标系 (二)球坐标系的适用条件 (三)三重积分计算公式 (四)化为累次积分的方法
利用柱面坐标计算三重积分

Ω 2
解
∵ ( x + y + z)
2 2 2
2
= x + y + z + 2( xy + yz + zx )
其中 xy + yz 是关于 y 的奇函数 ,
且 Ω 关于 zox 面对称, ∴
2008年5月12日10时3 分
∫∫∫ ( xy + yz )dv = 0 ,
Ω
21
利用柱面坐标和球面坐标计算三重 积分(33)
一般地, 当积分区域 Ω 关于 xoy 平面对称, 且被 积函数 f ( x , y , z ) 是关于 z 的奇函数,则三重积分为 则三重 零, 若被积函数 f ( x , y , z ) 是关于 z 的偶函数, 积分为 Ω 在 xoy 平面上方的半个闭区域的三重积分 的两倍.
2008年5月12日10时3 分 利用柱面坐标和球面坐标计算三重 积分(33) 19
a ∵ z=a ⇒r= , cosϕ
π x + y =z ⇒ϕ= , 4
2 2 2
a π ∴Ω : 0 ≤ r ≤ , 0 ≤ ϕ ≤ , 0 ≤ θ ≤ 2π , cos ϕ 4
2008年5月12日10时3 分 利用柱面坐标和球面坐标计算三重 积分(33) 14
I = ∫∫∫ ( x 2 + y 2 )dxdydz
2 2 2
8
2π
I1 = ∫∫ rdrdθ ∫r 2 fdz = ∫
D1 2
0
210 π, dθ ∫ dr ∫r 2 r ⋅ r 2dz = 0 3 2
4 8
Ω2
I 2 = ∫∫ rdrdθ ∫r 2 fdz = ∫
D2 2
利用柱坐标计算三重积分

f (x, y, z) d v
ab DZ f (x, y, z) d x d ydz
记作
bd
a
z
DZ
f (x, y, z)dxd y
z
d
z Dz
c
y
x
面密度≈
f (x, y, z) d z
2. 利用柱坐标计算三重积分
设 M (x, y, z) R3,将x, y用极坐标 , 代替, 则(, , z)
一、利用空间区域的对称性或被积函数的奇偶性计算三重积
分
(1)若空间闭区域关于平面 对称xo, y即
(x, y, z) V , (x, y, z) V , 则当 f (x, y, z) f (x, y, z)
即被积函数关于z 为奇函数时,
f (x, y, z)dxdydz 0
V
当 f (x, y, z) f (x, y, z) 即被积函数关于z为偶函数时,
由 z 1 (x2 y2 ), z 1, z 4围成. 2
解: I x2 d x d y d z 5 xy2 sin x2 y2 d x d y d z
利用对称性
关于 为x 奇函数
z
1 2
( x2
y2
)d xd
yd
z
1
4
dz
( x2 y2 )d xd y
21
Dz
1
4
区域D上的二重积分,完成”后二“这一步。
f (x, y, z)dv
d xd y z2 (x,y) f (x, y, z) d z
D
z1 ( x, y )
方法2. 截面法 (“先二后一”)
:
(x, y
c
3.5利用柱面坐标和球面坐标计算三重积分

z dxdydz z r dr d dz
0 d 0 dr r 2 r z dz
0 d 0
2 2
2
2
4
z r 2 2 dr r
2 4
2 2 1 0 d 0 (16r r 5 )dr 2
2 2 1 1 0 8r r 6 d 2 6 0 2
0 2 , : 0 , 4 0 R.
],
z
R
即
o
x
y
( x 2 y 2 z 2 ) dv
2 2 sin dd d
x sin cos , y sin sin , z cos .
0 0 0
1
d
0
2
0
cos sin d dv 2 sin ddd 5 0
5 2
1
x sin cos , y sin sin , z cos .
2 1 0 d 0 cos2 sin d 5 2 1 0 d 0 cos2 d (cos ) 5
2 r r dr d dz.
2 2 ( x y ) dv
0 d 0 dr
2 H 3
2
H
H 3 r r
dz
0 d 0 r z
H
x r cos , y r sin , z z. dv r dr d dz ,
规定:
z
0 , 0 ,
0 2 .
高数讲义第三节三重积分(二)

Dxy : 0 2 , 0 a
x2 y2 z2 z ,
4
o
y
: 0 2 , 0 a, z a, x
Dxy
I ( x2 y2 )dxdydz 02 d 0ad a 2dz
2 0a 3(a )d
a5. 10
解 由锥面和球面围成, 采用球面坐标,
: 0 2 , 0 2, 2 z 4,
例 5 计算 I zdxdydz,其中 是抛物面
z x2 y2及平面 z = 4 所围的立体. z
解
Dxy {(x, y) | x2 y2 4}
{(, ) | 0 2 , 0 1}
z1 x2 y2 2, z2 4,
3
z2 2
4 2
d
2
3
二、利用球面坐标计算三重积分
球面坐标:设 M ( x, y, z) 为空间内一点, 点 M 到原点的距离记为 r ,
有向线段 OM 与 z 轴正向的夹角记为 ,
点 M 在xoy 面上的投影 为P ( x, y)
自x 轴按逆时针方向旋转到有向线段 z
OP 的角度记为
则三元有序数组( r, , )
例 5 计算I zdxdydz,其中 是抛物面.
z x2 y2及平面 z = 4 所围的立体. z
解
由
z
x2
y2 ,
z 4
知曲面与平面的交线为
x2
y2
4,
z4
o
y
x
Dxy {(x, y) | x2 y2 4} {(, ) | 0 2 , 0 2}
z1 x2 y2 2, z2 4,
y
sin
,
z z.
o
• P(, )
利用柱面坐标计算三重积分_图文

课堂练习题一、填空题: 1、Ω 由曲面 z 2 = 3( x 2 + y 2 和球面 x 2 + y 2 + z 2 = 16 若所围(含 z 轴部分),则三重积分∫∫∫ f ( x , y , z dv 表Ω 示成直角坐标下的三次积分是______________; 在柱面坐标下的三次积分是________________; 在球面坐标下的三次积分是________________. 2、若Ω 为二曲面 x 2 + y 2 = az 及z = 2a − x 2 + y 2 所围( a > 0 ),则其体积可表为三重积分______; 或二重积分________________;或柱面坐标下的三次积分__________________. 2008年5月12日10时3 分利用柱面坐标和球面坐标计算三重积分(33 26二、计算下列三重积分: 1、∫∫∫ ( x 2 + y 2 dv ,其中Ω 由不等式Ω 1≤ x 2 + y 2 + z 2 ≤ 2, z ≥ 0 所确定. x2 y2 z2 2、∫∫∫ ( 2 + 2 + 2 dxdydz , 其中a b c Ω ⎧⎫ x2 y2 z2 Ω = ⎨( x , y , z 2 + 2 + 2 ≤ 1⎬ . a b c ⎩⎭ *三、曲面 x 2 + y 2 + az = 4a 2 将球体 x 2 + y 2 + z 2 ≤ 4az 分成两部分( a > 0 ),试求两部分的体积比. 2008年5月12日10时3 分利用柱面坐标和球面坐标计算三重积分(33 27课堂练习题答案一、1、∫ dx ∫ 2 −2 4− x 2 − 4− x 2 dy ∫ 16 − x 2 − y 2 3( x 2 + y 2 f ( x , y , z dz 3( x 2 + y 2 2 2 + 2π ∫ 2 −2 dx ∫ 2 4− x 2 2 − 4− x dy ∫ − − 16 − x − y f( x , y , z dz , ∫0 d θ ∫0 rdr ∫ 3r 2π 2 − 3r + ∫ d θ ∫ rdr ∫ 0 0 − 16 − r 16 − r 2 f ( r cos θ , r sin θ , z dz f ( r cos θ , r sin θ , z dz , 2 ∫0 2π d θ ∫ d ϕ∫ f ( r sin ϕcos θ , 0 π 6 0 4 r sin ϕsin θ , r cos ϕ r 2 sin ϕdr 4 0 + ∫0 2π d θ ∫5 π d ϕ∫ f ( r sin ϕcos θ , π r sin ϕsin θ , r cos ϕ r 2 sin ϕ dr ; 2008年5月12日10时3 分利用柱面坐标和球面坐标计算三重积分(33 28 6x2 + y2 2、∫∫∫ dv , ∫∫ ( 2a − x 2 + y 2 − dxdy , a Ω D ∫0 2π dθ ∫ rdr ∫r 2 0 a a 2a− rdz . 4 124 二、1、 2、πabc . π;5 15 37 3 πa 37 V1 6 *三、= = . V2 27 πa 3 27 6 2008年5月12日10时3 分利用柱面坐标和球面坐标计算三重积分(33 29。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一卦限内的三重积分,再乘以 4,即
2
( 5 4 4
5 )
2
2 0
2 (516 32 ) 8 . 42
I
(x2 y2 )dxdydz
4
2 d
0
2
d
0
5 5
2dz
.
2
(4) I x ydxdydz ,Ω 是由柱面 x2 y2 1及平面 z=1,z=0,x=0,y=0 所围成的
f (x, y, z)dxdydz dx dy
f (x, y, z)dz .
1
1x2
x2 y2
D
在柱面坐标系中(xOy 面换成极坐标系,z 轴保持不变),
{(,, z) | 0 2,0 1, z 1},
图3 此时,原三重积分可化为三次定积分: 注意不要漏掉
2
1
1
f (x, y, z)dxdydz 0 d 0 d f ( cos, sin, z)dz .
0
0
凑微分
( 1 cos 2 4
2 0
)
(
4 4
1 0
)
(
z
1 0
)
图 10
[( 1) (11)] (1 0) (1 0) 1 1 1 1 .
4
4
24 8
(5) I sin zdxdydz ,Ω 是由曲面 z x2 y2 及平面 z=π 所围成的闭区域.
解析: 先求出曲面 z x2 y2 及平面 z=π 的交线在 xOy 面的投影曲线.
(其中,积分区域 Ω 在 xOy 面的投影区域为
D {(x, y) | x2 y2 1}见图 2,图 3).
D
图1
在空间直角坐标系中,
D
{(x, y, z) | 1 x 1, 1 x2 y 1 x2 , x2 y2 z 1},
此时,原三重积分可化为三次定积分:
图2
1
1 x 中消去
z,
z 5
得 25(x2 y2 ) 4 25 ,即 x2 y2 4 .
由 yOz 面上的两条直线 z 5 y 2
绕 z 轴旋转一周而成的旋转曲面
于是,投影曲线为
x2
y2
4
,
z0
这是 xOy 面上的圆. 因此,积分区域 Ω(图 7)在 xOy 面
上的投影区域为 D {(x, y) | x2 y2 4}(图 8).
D {(x, y) | 0 x 1, 0 y 1 x2 },
化为极坐标形式 D {(, ) | 0 , 0 1} . 2
因此,本题中的积分区域
{(, , z) | 0 , 0 1, 0 z 1 2 } . 2
I x yzdxdydz
1
1 2
2 d d
先在方程组
z
x2 y2 中消去 z,
z
得 x2 y2 2 ,即 .
由 yOz 面上的两条直线 z y 绕 z 轴旋转一周而成的旋转曲面
的上半部分
于是,投影曲线为
x2
y2
2
,
z0
这是 xOy 面上的圆. 因此,积分区域 Ω(图 11)在 xOy 面
上的投影区域为 D {(x, y) | x2 y2 2}(图 12).
考查以下知识点—— (以下各题解析仅供参考,大家还可想想其他方法.)
1、把三重积分 f (x, y, z)dxdydz 化为三次定积分,其中积分区域 Ω 是由曲面
z x2 y2 及平面 z=1 所围成的闭区域.
解析: 本题的积分区域 Ω 见图 1,可写为:
{(x, y, z) | x2 y2 1, x2 y2 z 1}
4 2 0
d 0
d 2
zdz .
2
1
43 2
I zdxdydz 0
d d
0
2
zdz
下方曲面 z x2 y2
上方曲面 z 4 3(x2 y2)
2
d
0
1 (z2
0
2
43 2 2
) d
2
d
0
1
4 3 2 (
4
) d
0
22
2
d
1
(2
3 3
5
) d
0
0
22
可以看作两次定积分的乘积
图 11
上方平面 z = π
2
I sin z dxdydz 0 d 0 d sin zdz
2
d
0
0
( cos
z
)d
下方曲面 z x2 y2
2
d (1 cos )d
0
0
可以看作两次
定积分的乘积
图 12
2 0 ( cos )d
2 0 d 2 0 cos d
0
0
0
( cos ) ( sin ) zdz
下方为 xOy 面
图 13 上方为球面 z 1 x2 y2
2 (cos sin )d
1 3 d
1 2
zdz
0
0
0
图 14
2
sin 2
d
02
1 3 ( z2
0
2
1 2 0
)d
2
sin 2
d(2 )
1 3 (1 2
0)d
04
0
图7
I
(x2 y2 )dxdydz
2
d
0
2
d
0
5 5
2dz
2
上方平面 z =5
2
d
0
2 3(z
0
5 5
)d
2
下方曲面 4z2 25(x2 y2 )
2
d
2 3 (5 5 )d
0
0
2
可以看作两次 定积分的乘积
图8
2 2 (53 5 4 )d
0
2
说明:大家也可以自己试着利用对称性,只算
y cos
不妨取
z
sin
此时,被积函数 f (x, y, z) y2 z2 可化为 f (, , x) 2 .
原三重积分可化为三次定积分:
( y2 z2 )dxdydz
2
d
10
d
5 2
2dx
0
0
2
2
d
0
10 3 d
0
5
2 dx
2
d
0
10 0
3(x
5 2
I x y dxdydz
1
1
2 0
d
0
d
0
(
cos
sin
)dz
2 (cos sin )d
1 3 d
1
dz
0
0
0
可以看作三次
定积分的乘积
(1
2 sin 2d ) (
1 3 d) (
1
dz)
20
0
0
图9
[1 1
2 sin 2d(2 )] (
1 3 d) (
1
dz)
2 20
2 ( 2 2
0
)
2
d(sin )
0
分部积分法
2 2 2 (sin 2
0
sin d)
0
3
2
(0 cos
0
)
3
2
(2) 3
4
.
(6)设 Ω 为第一卦限内的球面 x2 y2 z2 1及三张坐标面所围成的闭区域,求
I x yzdxdydz .
解析: 本题中的积分区域 Ω 如图 13 所示,Ω 在 xOy 面的投影区域 D 如图 14 所示,
第一卦限内的闭区域;
解析: 已知条件中的平面 x=0 就 是 yOz 面,平面 y=0 就 是 xOz 面,平面 z=0 就 是 xOy 面,而平面 z=1 是 平 行 于 xOy 面的平面.
由柱面 x2 y2 1及平面 z=1,z=0,x=0,y=0 所围成的第一卦限内的闭区域 Ω 如
图 9 所示,Ω 在 xOy 面上的投影区域为 D {(x, y) | x2 y2 1, x 0, y 0}如图 10 所示 .
解析: 先求出曲面 z 4 3(x2 y2 ) 及 z x2 y2 的交线在 xOy 面的投影曲线.
根据课本第 35 页公式,先在方程组
z
4 3(x2 z x2 y2
y2)
中消去 z,得
4 3(x2 y2 ) (x2 y2 )2 ,记 x2 y2 2 ,
有 4 3 2 4 ,即 4 32 4 (2 4)(2 1) 0 , 求得 2 1 ,也即 x2 y2 1.
)d
2
2
2
d
10 3 (5 2 )d
2
d
10 (53 5 )d
0
0
2
0
0
2
2 5 4 (
04
6 ) 12
10 0
d
2 (125 250)d
0
3
2 (125 250)d 125 2 d 125 2 250 .
0
3
30
3
3
(2) I zdxdydz ,Ω 是由曲面 z 4 3(x2 y2 ) 及 z x2 y2 所围成的闭区域;
2
( 1 cos 2 4
2 0
)
1 2
1(3 5 )d
0
1
1 4
( ) (11) (
4
24
1 0
6 6
1 0
)
1 1 (1 1) 1 . 4 4 6 48
(本题还可用球面坐标计算,有兴趣的同学可以自主学习课本第 102~104 页.)
