利用柱面坐标和球面坐标计算三重积分汇总
合集下载
三重积分在柱面及球坐标系下的计算
= ∫ dθ ∫
0
2π
R
0
1 2 1 4 2 ( R − ρ ) ρdρ = πR . 2 4
思考： 思考：是否可考虑用切片法来求解？
例2 计算三重积分I = ∫∫∫ ( x + y )dv,
2 2 (V )
z
其中(V )由z = x 2 + y 2 , z = h所围.
解 (V )在xoy面投影域(σ )为圆 : 0 ≤ ρ ≤ h , xy
π
4
θ
y
,0 ≤ ρ ≤ R.
x
∴ I = ∫ dθ
0
2π
∫
π /4
0
dϕ
∫
R
0
ρ 2 ⋅ ρ 2sinϕ dρ
2− 2 5 = πR . 5
练习 试用三种坐标系分别计算三重积分
z
2
σz
I = ∫∫∫ zdv, 其中(V ) : x 2 + y 2 + z 2 ≤ 2 z.
(V )
解法1 解法 直角坐标系(切片法)
1
= 2π ∫ ρ ⋅ 2 1 − ρ 2 dρ
1
4π = . 3
0
解法3 解法 球面坐标系计算
∫∫∫ zdv
(V )
z
2
x2 + y2 + z2 = 2z
球面为 : ρ = 2 cos ϕ , 其中
0 ≤ θ ≤ 2π ,0 ≤ ϕ ≤
ϕ
o
π
2
,0 ≤ ρ ≤ 2 cos ϕ .
θ
ρ cos ϕ ⋅ ρ 2 sin ϕdρ
z
• •
其中(V )由z = R 2 − x 2 − y 2 与 z = 0所围.
柱面坐标系和球面坐标系求三重积分
z x2 y2所围 .
分析 (V )为由半球面与锥面所围,
故可用球面坐标,
y
此 ,0 时 2 ,0 ,0R . x
4
2
I d
/4
d
R22sind
0
0
0
2 2 R5.
5
练习 试用三种坐标系算 分三 别重 计积分
I zdv,其中(V): x2 y2 z2 2z. (V)
解法1 直角坐标(切 系片法 )
x
则 (V )f(c o,s si,n z)d d dz ,
]d d
[ z2(,)f(co ,ssin,z)dz
( ) z1(,)
例1 计算三重积I分 (Vz)dv,
其中(V)由z R2 x2 y2与 z 0所围.
解 (V )向 xo 面 y 投 (x)y 为 影 :0 圆 R , 02 x
I d d
zdz
0
0 1 1 2
x
2012 12d
4 . 3
•1
xy
解法3 球面坐标系计算zdv (V) x2y2z22z
z
2
球面 : 为 2co,s其中
02 ,0,02co .s
2
o
y
I 2d /2d 2coscos2sxind
0
0
0
2/24co5ssind 4 .
0
3
z
h•
此,时 2zh.
I [ h 2dz ]dd ( xy ) 2
•
o•
x
y
( xy )
2d h(3h5)d
0
0
1 h3.
6
思考：本题是否也可考虑用切片法来求解？
4-2-2 球面坐标系下三重积分的计算
高等数学利用柱面坐标和球面坐标计算三重积分教案
时间---------月---------日 星期----------------- 课 题§10.3 三重积分2教学目的 学习和掌握利用柱面坐标和球面坐标计算三重积分。
教学重点 掌握利用柱面坐标计算三重积分。
教学难点 掌握利用球面坐标计算三重积分。
课 型 专业基础课 教学媒体教法选择讲 授教 学 过 程教法运用及板书要点一、利用柱面坐标计算三重积分设M x y z (,,)为空间内一点,该点在xoy 面上的投影为P ,P 点的极坐标为,r θ,则,,r z θ三个数称作点M 的柱面坐标。
规定,,r z θ的取值范围是：0r ≤<+∞，02≤≤θπ，-∞<<+∞z 。
柱面坐标系的三组坐标面分别为：(r a =常数),表示以z 轴为轴，半径为a 的圆柱面；(b θ=常数),即过z 轴，极角为b 的半平面；(z c =常数),即与xoy 面平行且相距为c 的平面。
点M 的直角坐标与柱面坐标之间有关系式为：cos x r θ=；sin y r θ=；z z =。
用三组坐标面(r a =常数),(b θ=常数),(z c =常数),将Ω分割成许多小区域,除了含Ω的边界点的一些不规则小区域外,这种小闭区域都是柱体。
考察由,,r z θ各取得微小增量,,dr d dz θ所成的柱体,该柱体是底面积为此表2学时填写一份，“教学过程”不足时可续页与平面所围成的闭区域。
解: πθρρ20,20,4:2≤≤≤≤≤≤Ωz ，πρρθρπ364420202==⎰⎰⎰⎰⎰⎰Ωzdz d d dxdydz z 2、利用球面坐标计算三重积分(,,)M x y z 为空间内一点，M 则点可用三个有次序的数r ϕθ，，来确定，其中r O M 为原点与点间的距离，ϕ为有向线段OM z 与轴正向之间的夹角，θ为z x 从正轴来看自轴按逆时针方向转到有向线段OP 的角度，这里点P 为点M 在xoy 面上的投影。
柱坐标、球坐标下的三重积分
解：由图知：直角系：
D
y
x
2
4 x2
6x2 y2
I dx
dy
f (x, y, z)dz
2
4x2
x2 y2
柱标系： I
2
d
2
rdr
6r 2
f (r cos , r sin , z)dz
0
0
r
杂例
在三种坐标系下化三重积分 f (x, y, z)dv为三次积分，
z
其中：z 6 x2 y2, z x2 y2 z 6 x2 y2 6
四、柱坐标、球坐标下的三重积分
1. 柱坐标：(θ,r,z)
zz
变换为：x r cos , y r sin , z z
即：(x, y, z) (r cos , r sin , z),其中：
0 r ,0 2 ,| J || (x, y, z) | r ( , r, z)
x
注：柱坐标— 极坐标平面竖起一根Z轴。x
上顶： z 1 x2 y2
下底： z = 0
z
Dxy: x 2 y 2 1
x y
I dxdy
zdz
Dxy
用哪种坐标？ 柱面坐标 .
.
2π
1
1r 2
I = 0 dθ 0 rdr0 zdz
Dxy 0
1
4
x
z0
1y
注：用柱坐标求 fdv分成两个步骤：
第一步：先一后二，对z积分后将二重积分化为极坐 标下的二重积分；
元素区域由六个坐标面围成：
半平面及+d ;
半径为r及 r+dr的园柱面；
平面 z及 z+dz；
dz
柱面坐标和球面坐标计算定积分
一、利用柱面坐标计算三重积分
设 M ( x, y, z) 为空间内一点，并设点M 在
xoy 面上的投影 P 的极坐标为r,，则这样的三 个数 r, , z 就叫点 M 的柱面坐标．
z
规定： 0 r ,
0 2,
z .
• M(x, y,z)
or
•
y
P(r, )
x
如图，三坐标面分别为
r 为常数
三个有次序的数r，， 来确定，其中r 为原 点 O 与点 M 间的距离， 为有向线段 OM与 z 轴正向所夹的角， 为从正 z 轴来看自 x 轴按
逆时针方向转到有向线段 OP 的角，这里 P 为
点 M 在 xoy 面上的投影，这样的三个数 r，， 就叫做点 M 的球面坐标．
规定： 0 r , 0 , 0 2.
y
r
sin
sin
,
z r cos .
如图，
z
球面坐标系中的体积元素为
dv r2 sindrdd ,
f ( x, y, z)dxdydz
dr
d r sin
r
o
d
x
r sind rd
d
y
f (r sin cos ,r sin sin ,r cos )r2 sindrdd .
例 3 计算 I ( x2 y2 )dxdydz，其中 是锥面
1 8
I1 rdrd r2 fdz
D1
2
2
d
0
2
4
dr
0
8
r2
r
r
2dz
2
45 3
,
2
I2 rdrd r2 fdz
D2
2
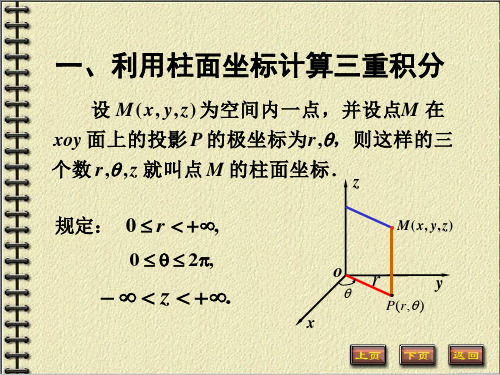
设 M ( x, y, z) 为空间内一点，并设点M 在
xoy 面上的投影 P 的极坐标为r,，则这样的三 个数 r, , z 就叫点 M 的柱面坐标．
z
规定： 0 r ,
0 2,
z .
• M(x, y,z)
or
•
y
P(r, )
x
如图，三坐标面分别为
r 为常数
三个有次序的数r，， 来确定，其中r 为原 点 O 与点 M 间的距离， 为有向线段 OM与 z 轴正向所夹的角， 为从正 z 轴来看自 x 轴按
逆时针方向转到有向线段 OP 的角，这里 P 为
点 M 在 xoy 面上的投影，这样的三个数 r，， 就叫做点 M 的球面坐标．
规定： 0 r , 0 , 0 2.
y
r
sin
sin
,
z r cos .
如图，
z
球面坐标系中的体积元素为
dv r2 sindrdd ,
f ( x, y, z)dxdydz
dr
d r sin
r
o
d
x
r sind rd
d
y
f (r sin cos ,r sin sin ,r cos )r2 sindrdd .
例 3 计算 I ( x2 y2 )dxdydz，其中 是锥面
1 8
I1 rdrd r2 fdz
D1
2
2
d
0
2
4
dr
0
8
r2
r
r
2dz
2
45 3
,
2
I2 rdrd r2 fdz
D2
2
3.5 利用柱面坐标和球面坐标的计算三重积分
三重积分的计算关键在于选取适当的坐标系, 确定单积 分的积分上下限. 通常是球形域或球与圆锥面围成时用球坐标, 是圆柱形或投影域为圆时用柱坐标.
ex6.设f ( u)具有连续的导数, 且f (0) 0, 求 1 lim 4 t 0 t
x2 y2 z2 t 2
f (
r2 则 {( r , , z ) | z 4 r 2 , 0 r 3,0 2 } 3 z I zrdrddz z 4 r2
0 d 0 dr r 2
3
2
3
4 r 2
r zdz
13 . 4
r2 z 3 x
y
2
x
02 d 0
2 cos
8 2 a2 8 3 2 r dr 0 zdz 02 cos d a . 9 2 3
a
二. 在球面坐标下计算三重积分
1. 球面坐标及坐标面
设 M ( x , y, z ) 为空间内一点，则点M 可用 三个有次序的数 ，， 来确定，其中 为原 点 O 与点 M 间的距离， 为有向线段 OM与 z 轴正向所夹的角， 为从正 z 轴来看自 x 轴按 逆时针方向转到有向线 OP 的角，这里 P 为 段 点 M 在 xoy 面上的投影，这样的三 个数 ，，
x sin cos y sin sin z cos
z
x
M ( x, y, z )
z
o
A
y
y
x
P
3. 球面坐标下的三次积分
球面坐标系中的体积元素为
d
z
d
sin
ex6.设f ( u)具有连续的导数, 且f (0) 0, 求 1 lim 4 t 0 t
x2 y2 z2 t 2
f (
r2 则 {( r , , z ) | z 4 r 2 , 0 r 3,0 2 } 3 z I zrdrddz z 4 r2
0 d 0 dr r 2
3
2
3
4 r 2
r zdz
13 . 4
r2 z 3 x
y
2
x
02 d 0
2 cos
8 2 a2 8 3 2 r dr 0 zdz 02 cos d a . 9 2 3
a
二. 在球面坐标下计算三重积分
1. 球面坐标及坐标面
设 M ( x , y, z ) 为空间内一点，则点M 可用 三个有次序的数 ，， 来确定，其中 为原 点 O 与点 M 间的距离， 为有向线段 OM与 z 轴正向所夹的角， 为从正 z 轴来看自 x 轴按 逆时针方向转到有向线 OP 的角，这里 P 为 段 点 M 在 xoy 面上的投影，这样的三 个数 ，，
x sin cos y sin sin z cos
z
x
M ( x, y, z )
z
o
A
y
y
x
P
3. 球面坐标下的三次积分
球面坐标系中的体积元素为
d
z
d
sin
利用柱面坐标计算三重积分
`z
z
j r
zdv
dvΒιβλιοθήκη zdvO
dv
a 2 0 2
．
q
x
a y
dv 2 dj dq
2
0
0
2a 3 , r sin jdr 3
a
1 a4 , zdv 2 dj dq r cos j r 2 sin jdr 2 0 0 0 2 4 3a 3a 因此`z ．重心为(0，0， )． 8 8
§9．5 利用柱面坐标和球面坐标计算三重积分
一、利用柱面坐标计算三重积分
柱面坐标、 柱面坐标系的坐标面 直角坐标与柱面坐标的关系、柱面坐标系中的体积元素
柱面坐标系中的三重积分
二、利用球面坐标计算三重积分
球面坐标、球面坐标系的坐标面 直角坐标与球面坐标的关系、球面坐标系中的体积元素 球面坐标系中的三重积分
，r sin q ，z) rdrdqdz．
例1 例1 利用柱面坐标计算三重积分 zdxdydz，其中是由曲
面 zx2y2 与平面 z4 所围成的闭区域．
z 4 zx2y2 或 zr2
解 闭区域可表示为：
r 2z4，0r2，0q2． 于是
zdxdydz zrdrdqdz
2 r sin jdrdjdq dq sin j dj r 4 dr a 2 M , 0 0 0 5
4 3
2
3
a
4 3 其中 M a 为球体的质量． 3
一、利用柱面坐标计算三重积分
设M(x, y, z)为空间内一点，则点M与数 r、q 、z相对应， 其中P(r, q )为点M在xOy面上的投影的极坐标． 三个数 r、q 、z 叫做点M 的柱面坐标． z 这里规定r、q 、z的变化范围为： 0 r<， 0 q 2 ， < z<． O x r y P(r, q ) y z
z
j r
zdv
dvΒιβλιοθήκη zdvO
dv
a 2 0 2
．
q
x
a y
dv 2 dj dq
2
0
0
2a 3 , r sin jdr 3
a
1 a4 , zdv 2 dj dq r cos j r 2 sin jdr 2 0 0 0 2 4 3a 3a 因此`z ．重心为(0，0， )． 8 8
§9．5 利用柱面坐标和球面坐标计算三重积分
一、利用柱面坐标计算三重积分
柱面坐标、 柱面坐标系的坐标面 直角坐标与柱面坐标的关系、柱面坐标系中的体积元素
柱面坐标系中的三重积分
二、利用球面坐标计算三重积分
球面坐标、球面坐标系的坐标面 直角坐标与球面坐标的关系、球面坐标系中的体积元素 球面坐标系中的三重积分
，r sin q ，z) rdrdqdz．
例1 例1 利用柱面坐标计算三重积分 zdxdydz，其中是由曲
面 zx2y2 与平面 z4 所围成的闭区域．
z 4 zx2y2 或 zr2
解 闭区域可表示为：
r 2z4，0r2，0q2． 于是
zdxdydz zrdrdqdz
2 r sin jdrdjdq dq sin j dj r 4 dr a 2 M , 0 0 0 5
4 3
2
3
a
4 3 其中 M a 为球体的质量． 3
一、利用柱面坐标计算三重积分
设M(x, y, z)为空间内一点，则点M与数 r、q 、z相对应， 其中P(r, q )为点M在xOy面上的投影的极坐标． 三个数 r、q 、z 叫做点M 的柱面坐标． z 这里规定r、q 、z的变化范围为： 0 r<， 0 q 2 ， < z<． O x r y P(r, q ) y z
极坐标与球面坐标计算三重积分-极系下的三重积分
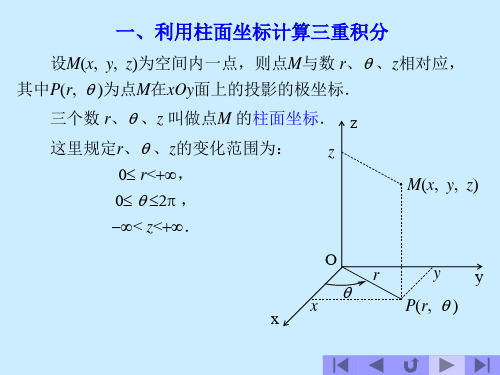
例11 利用柱面坐标计算三重积分 zdxdydz，其中是由曲
面 zx2y2 与平面 z4 所围成的闭区域．
z
解 闭区域可表示为：
4
r 2z4，0r2，0q2．
于是
zdxdydz zrdrdqdz
zx2y2 或 zr2
2
2
4
dq rdr zdz
0
0
r2
1
2
dq
2 r(16 r 4 )dr
例2 求半径为a 的球面与半顶角a为的内接锥面所围成的立
体的体积．
z 2a
a
O
y
x
例2 求半径为a 的球面与半顶角a为的内接锥面所围成的立
体的体积．
解 该立体所占区域可表示为：
0r2a cos j ，0ja ，0q2．
z
于是所求立体的体积为
2a
V dxdydz r2 sinj drdjdq
r4 sin 3 jdrdjdq
2
dq
sin 3 j dj
a r4dr 2 a2M ,
0
0
0
5
其中 M 4 a3 为球体的质量．
3
2
dq
a
dj
2a cosj r 2 sin jdr
0
0
0
2
a
s in jdj
2a cosj r 2 dr
0
0
jr a
16a3 a cos3 j sinjdj
30
O
y
4a3 (1 cos4 a) ．
x
3
例3 求均匀半球体的重心．
z
解 取半球体的对称轴为 z 轴，
原点取在球心上，又设球半径为a．
最新95利用柱面坐标和球面坐标计算三重积分汇总
95利用柱面坐标和球面坐标计算三重积分§9.5 利用柱面坐标和球面坐标计算三重积分对于某些三重积分,由于积分区域和被积函数的特点,往往要利用柱面坐标和球面坐标来计算。
一、利用柱面坐标计算三重积分1、柱面坐标设«Skip Record If...»为空间的一点,该点在«Skip Record If...»面上的投影为«Skip Record If...»,«Skip Record If...»点的极坐标为«Skip Record If...»,则«Skip Record If...»三个数称作点«Skip Record If...»的柱面坐标。
规定«Skip Record If...»的取值范围是«Skip Record If...»，«Skip Record If...»，«Skip Record If...»柱面坐标系的三组坐标面分别为«Skip Record If...»,即以«Skip Record If...»轴为轴的圆柱面；«Skip Record If...»,即过«Skip Record If...»轴的半平面；«Skip Record If...»,即与«Skip Record If...»面平行的平面。
点«Skip Record If...»的直角坐标与柱面坐标之间有关系式«Skip Record If...»(1)2、三重积分«Skip Record If...»在柱面坐标系中的计算公式«Skip Record If...»用三组坐标面«Skip Record If...»,«Skip Record If...»,«Skip Record If...»,将«Skip Record If...»分割成许多小区域,除了含«Skip Record If...»的边界点的一些不规则小区域外,这种小闭区域都是柱体。
讲 柱坐标和球坐标系三重积分的计算
z dv
z r d
dv
dz
r
d
dr
r d
y
x r d dr r dr d
d
y
r sin
x
平面极坐标下的面积元素 ds
r sin d
28
在柱面坐标系下: dv r dr d dz,
f (x, y, z)d x d y dz
f (r cos , r sin , z) r dr d dz
在球面坐标系下: dv r 2 sin drd d ,
x2 y2 z2， 与平面z a (a 0)所围的立体.
解 1 采用球面坐标
za r a , cos
x2 y2 z2 ,
4
: 0 r a , 0 , 0 2,
cos
4
16
皮肌炎图片——皮肌炎的症状表现
• 皮肌炎是一种引起皮肤、肌肉、 心、肺、肾等多脏器严重损害的， 全身性疾病，而且不少患者同时 伴有恶性肿瘤。它的1症状表现如 下：
2r4
0
d
r
64 5
1
2 2
31
3. 计算
由 z 1 (x2 y2 ), z 1, z 4围成. 2
解:
利用对称性
1 2
(
x2
y2
)d
xd
yd
z
1
4
dz
( x2 y2 )d xd y
21
Dz
1
4
dz
2
d
2z r3 d r 21
21 0
0
其中
z 4
1
Dz
oy x
32
o
y
d
x
f ( cos , sin , z) dddz.
§7.3[2]利用柱面坐标和球坐标计算三重积分
![§7.3[2]利用柱面坐标和球坐标计算三重积分](https://img.taocdn.com/s3/m/ab56616c1eb91a37f1115c11.png)
o
x
y
V = ∫∫∫ dv = ∫∫∫ r 2 sindrddθ
= ∫0 dθ ∫0 d ∫0
4
2π
π
2a 2
r sindr
x = r sin cosθ , y = r sin sinθ , z = r cos.
4 = π ( 2 1)a3. 3
dv = r 2 sindrddθ
�
: x2 + y2 + z2 ≤ 1.
o
y
x
0 ≤ θ ≤ 2π , : 0 ≤ ≤ π , 0 ≤ r ≤ 1.
z
∫∫∫
z2dv =
r 2 cos2 r 2 sin dr d dθ ∫∫∫
o
y
= ∫0 dθ ∫
= ∫0 dθ ∫
2π
2π
x 1 4 2 d 0 r cos sin dr 0 5 1 r π 2 cos sin d 0 5 0
一,利用柱面坐标计算三重积分
xoy 面上的极坐标 + z 坐标
0 ≤ r < +∞,
z
0 ≤ θ ≤ 2π ,
∞ < z < +∞.
M( x, y, z)
y
o r θ
x
P(r,θ )
如图, 如图,三坐标面分别为
z
r 为常数
圆柱面; 圆柱面; 半平面; 半平面; 平 面.
x
z
θ 为常数
z 为常数
z
x
r
为常数
θ 为常数
o
θ
y
球面坐标与直角坐标的关系为
z
x = r sin cosθ , y = r sin sinθ , z = r cos.
柱面坐标系和球面坐标系求三重积分
(V )
z
其中(V )由z R 2 x 2 y 2 与 z 0所围.
xoy面所围, 分析 (V )为由半球面与 故可用球面坐标 ,
此时,0 2 ,0
y
x
2
R
,0 R.
I d
0
2
/2
0
d cos 2sin d
y
( xy )
x
此时 0 z R 2 2 .
I
2 0
( xy )
[
R
R2 2
0
zdz ]dd
d
0
1 2 1 4 2 ( R ) d R . 2 4
思考：是否可考虑用切片法来求解？
例2 计算三重积分 I ( x y )dv,
4
y
,0 R.
x
I d
0
2
/4
0
d
R
0
2 2sin d
2 2 5 R . 5
练习 试用三种坐标系分别计 算三重积分
z
2
z
I zdv, 其中(V ) : x 2 y 2 z 2 2 z.
(V )
解法1 直角坐标系 (切片法)
0
4 . 4 cos sin d 3
2 cos
0
cos 2 sin d
x
3、化为累次积分
z 2 ,
1 ,
(1)用x sin cos , y sin sin , z cos
z
其中(V )由z R 2 x 2 y 2 与 z 0所围.
xoy面所围, 分析 (V )为由半球面与 故可用球面坐标 ,
此时,0 2 ,0
y
x
2
R
,0 R.
I d
0
2
/2
0
d cos 2sin d
y
( xy )
x
此时 0 z R 2 2 .
I
2 0
( xy )
[
R
R2 2
0
zdz ]dd
d
0
1 2 1 4 2 ( R ) d R . 2 4
思考：是否可考虑用切片法来求解？
例2 计算三重积分 I ( x y )dv,
4
y
,0 R.
x
I d
0
2
/4
0
d
R
0
2 2sin d
2 2 5 R . 5
练习 试用三种坐标系分别计 算三重积分
z
2
z
I zdv, 其中(V ) : x 2 y 2 z 2 2 z.
(V )
解法1 直角坐标系 (切片法)
0
4 . 4 cos sin d 3
2 cos
0
cos 2 sin d
x
3、化为累次积分
z 2 ,
1 ,
(1)用x sin cos , y sin sin , z cos
利用柱面坐标与球面坐标计算三重积分
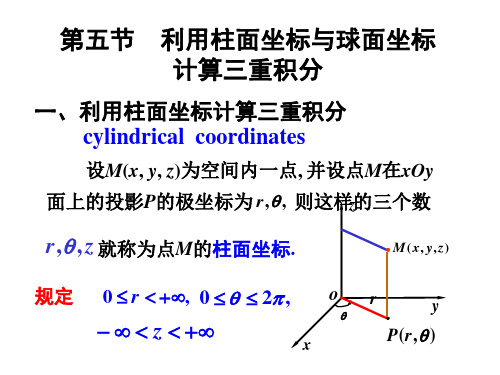
f ( r cos , r sin , z )rdrddz.
rdrd
Dr
z2 ( r , ) z1 ( r , )
f ( r cos , r sin , z )dz .
通常化为先对 z、再对 r、后对θ 的三次积分.
先将Ω在xOy面上的投影域用极坐标不等式表示
设M(x, y, z)为空间内一点,记向量OM来自长为r , OM与z轴z
r
M ( x, y, z )
z
正方向间的夹角为 , 再将OM
A x
x
O
y
y
P
向xOy平面投影, 记投影向量与x轴正方向的 夹角为 , 称 ( r , , ) 为点M的球面坐标. 规定 0 r , 0 , 0 2 .
=常数: 半平面P
0
y
x
直角坐标与柱面坐标的关系为
x r cos , y r sin , z z.
在柱面坐标下 1. 若被积函数形如
x y r . 因此
2 2 2
f (x y ) ;
2 2
2. 积分区域Ω是由柱面、锥面、旋转抛物面、平 面或球面所围成.
y
球面坐标下的体积元素
z
元素区域由六个坐标面围成：
圆锥面
球面r+d r
半平面 及+d ； 圆锥面及+d
rsind
半径为r及r+dr的球面；
r
圆锥面+d
1
1
2 1dr 2 0 1 r
1
1 r
Dxy
0
1
y
9-3(2)三重积分
3、在球面坐标系下将三重积分化为三次单积分
主要有两种情况：
1° 的边界曲面是一个包围原点在内的闭曲面。
曲面坐标为r r ( , )
则 I d d
0 0 2
r ( , )
0
F ( r , , )r 2 sindr
其中 : F ( r , , ) f ( r sin cos , r sin sin , r cos )
rsind
半径为r及r+dr的球面；
dV
r
圆锥面及+d
dv r sindrdd ,
2
f ( x, y, z )dxdydz
0
d
y
2 f ( r sin cos , r sin sin , r cos ) r sindrdd .
dz
dV
平面 z及 z+dz；
dV = rdrddz
f ( x , y , z )dxdydz
.
z
0
d
r
y
f ( r cos , r sin , z ) r drddz
x
底面积 ：r drd
3、在柱面坐标系下将三重积分化为三次单积分
次序通常选择为z ，r ，
0
r dr z dz
2 0
a
2 d
0
2 cos
0
2 2 cos z a 2 2 r dr 2 d r dr 0 0 2 2 0
2 8 a 8a 2 3 d cos d 9 6 0
2 a
a 2
2
r 2 0 3 0
利用柱面坐标和球面坐标计算三重积分
解
由x
2
由锥面和球面围成， 采用球面坐标， Ω 由锥面和球面围成， 采用球面坐标，
+ y + z = 2a
2 2
2
⇒ r = 2a ,
z=
π x + y ⇒ ϕ= , 4
2 2
Ω : 0 ≤ r ≤ 2a ,
π 0≤ϕ≤ , 4
0 ≤ θ ≤ 2π ,
由三重积分的性质知 V =
∫∫∫ dxdydz ,
例 3 计算 I = ∫∫∫ ( x 2 + y 2 )dxdydz ，其中Ω 是锥面
x 2 + y 2 = z 2 ， 与平面 z = a
解: 采用球面坐标
a ∵ z=a ⇒r = , cos ϕ
π x + y = z ⇒ϕ= , 4
2 2 2
Ω
( a > 0) 所围的立体.
a π , 0 ≤ ϕ ≤ , 0 ≤ θ ≤ 2π , ∴Ω : 0 ≤ r ≤ cos ϕ 4
z ln( x 2 + y 2 + z 2 + 1) ∫∫∫ x 2 + y 2 + z 2 + 1 dxdydz = 0. Ω
三、小结
柱面坐标 三重积分换元法 球面坐标
（1） 柱面坐标的体积元素 ）
dxdydz = rdrdθdz
（2） 球面坐标的体积元素 ） dxdydz = r 2 sin ϕdrdθdϕ （3） 对称性简化运算 ）
r2 Ω: ≤ z ≤ 4 − r 2， 3 0 ≤ r ≤ 3, 0 ≤ θ ≤ 2 π.
I = ∫ dθ ∫ dr ∫r 2
0 0
3
2π
3
最新95利用柱面坐标和球面坐标计算三重积分汇总
最新95利⽤柱⾯坐标和球⾯坐标计算三重积分汇总95利⽤柱⾯坐标和球⾯坐标计算三重积分§9.5 利⽤柱⾯坐标和球⾯坐标计算三重积分对于某些三重积分,由于积分区域和被积函数的特点,往往要利⽤柱⾯坐标和球⾯坐标来计算。
⼀、利⽤柱⾯坐标计算三重积分1、柱⾯坐标设?Skip Record If...?为空间的⼀点,该点在?Skip Record If...?⾯上的投影为?Skip Record If...?,?Skip Record If...?点的极坐标为?Skip Record If...?,则?Skip Record If...?三个数称作点?Skip Record If...?的柱⾯坐标。
规定?Skip Record If...?的取值范围是Skip Record If...，?Skip Record If...?，?Skip Record If...?柱⾯坐标系的三组坐标⾯分别为Skip Record If...,即以?Skip Record If...?轴为轴的圆柱⾯；Skip Record If...,即过?Skip Record If...?轴的半平⾯；Skip Record If...,即与?Skip Record If...?⾯平⾏的平⾯。
点?Skip Record If...?的直⾓坐标与柱⾯坐标之间有关系式Skip Record If...(1)2、三重积分?Skip Record If...?在柱⾯坐标系中的计算公式Skip Record If...⽤三组坐标⾯?Skip Record If...?,?Skip Record If...?,?Skip Record If...?,将?Skip Record If...?分割成许多⼩区域,除了含?Skip Record If...?的边界点的⼀些不规则⼩区域外,这种⼩闭区域都是柱体。
考察由?Skip Record If...?各取得微⼩增量?Skip Record If...?所成的柱体,该柱体是底⾯积为?Skip Record If...?,⾼为?Skip Record If...?的柱体,其体积为Skip Record If...这便是柱⾯坐标系下的体积元素, 并注意到(1)式有Skip Record If (2)(2)式就是三重积分由直⾓坐标变量变换成柱⾯坐标变量的计算公式。
《高等数学》第九章 3.2 利用柱面坐标和球面坐标计算三重积分
z.
z
z
or
y
x
z
M(x, y, z)
o
x
r
y
P(r, )
如图，柱面坐标系中的 体积元素为
dv rdrd dz,
z
rd
dr
r
dz
于是，
f ( x, y, z)dxdydz
o
y
x d
f (r cos , r sin , z) r drd dz.
再根据 中 z，r， 的关系，化为三次积分。
02
d
02dr
4
r 2
r
z
dz
2
0
d
2
0
r
z2 2
4 r2
dr
1 2
2
0
d
2
0
(16r
r5 )dr
1 2
2
0
8r 2
1 6
r
6
2
d
0
1 2
2
8r 2
1 6
r
6
2 0
64 3
.
例 2 求I zdxdydz，其中 是球面 x2 y2 z2 4
r 3
o
A
或
D:
0 2 ,
0 r 3 .
过 (r, )∈D 做平行于 z 轴
的直线，得
r2 z 4 r2 .
x
3
0 2 ,
即 : 0 r 3 , r 2 3 z 4 r 2 .
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
z
rd
dr
dv rdrddz,
f ( x , y, z )dxdydz
r
dz
o
x
d
y
f ( r cos , r sin , z )rdrddz.
例1 计算 I
2 2 2
zdxdydz ，其中
2 2
是球面
x y z 4 与抛物面 x y 3 z
0 2 ,
2 a a
I ( x y )dxdydz d rdr r 2dz
0
0
r
5 a a 2 r (a r )dr 2[a ] a . 0 4 5 10
a 3
4 5
例 4 求曲面 x y z 2a 与 z 所围 成的立体体积.
r
3 cos a 4 2 d 2 sin d r2 d r 0 0 0 2 3 2 1 a sin cos d a 3 0 3 3
x
y
dv r 2 sin dr d d
三、小结
柱面坐标 三重积分换元法 球面坐标
x
f ( sin cos , sin sin , cos ) 2 sin d d d .
是锥面 例 3 计算 I ( x 2 y 2 )dxdydz ，其中
x 2 y 2 z 2 ， 与平面z a
解1 采用球面坐标
（1） 柱面坐标的体积元素
dxdydz rdrd dz
（2） 球面坐标的体积元素 dxdydz r 2 sindrdd （3） 对称性简化运算
思考题
若为R 3中关于xy面对称的有界闭区域， f ( x , y , z )为 上的连续函数, 则
当f ( x , y, z )关于 ____为奇函数时, f ( x , y, z )dv 0;
D2 2
2
2
0
5 2 d dr r 2 r r 2dz , 0 2 6
2 2
45 25 原式 I 336 . 3 6
例3. 计算三重积分
柱面 x 2
其中为由
y
2
2 x 及平面
z 0, z a (a 0), y 0 所围
成半圆柱体.
3
0
2 cos 3
8 3 d a 9
例4. 计算三重积分
其中由抛物面
x y 4z
2
2
与平面 z
h (h 0) 所围成 .
z
h
解: 在柱面坐标系下
x 2 d d z 原式 = d 2 0 0 1 4 d v d d d z 2 2 h 2 (h ) d 2 0 4 1
0 0
2
4
2a
0
r 2 sin dr
2
4 0
4 ( 2a )3 3 sin d ( 2 1)a . 3 3
例5. 计算三重积分
与球面
其中 所围立体.
解: 在球面坐标系下
0rR : 0 4 0 2
z
rR
2 0
0 2 cos 解: 在柱面坐标系下 : 0 2 0 za
原式 z d d d z
2
z a
o
y
zd z
0
a
0
2 d
0
2 cos
2 d
2 2 cos x
dv d d d z
2 4a
0 a x 2 y 2 z 2 A, z 0 所确定. x2 y2 z2 3、 ( 2 2 2 )dxdydz , a b c 2 2 2 x y z 其中 ( x , y , z ) 2 2 2 1 . a b c 2 2 2 2 z 5 x y 三、求曲面 及 x y 4 z 所围成的立 体的体积. 2 2 2 2 2 2 四、曲面 x y az 4a 将球体 x y z 4az 分 成两部分,试求两部分的体积之比. 五、求由曲面 z x 2 y 2 , x y a , x 0, y 0, z 0 所围成立体的重心(设密度 1 ).
(a 0) 所围的立体.
za r
2 2 2
a , cos
x y z , 4
a : 0 r , 0 , 0 2 , cos 4
I ( x 2 y 2 )dxdydz
d d
0
2
4 0
2
2 2
3
解: 由曲面方程可知, 立体位于xoy面上部, 且关于 xoz
yoz面对称, 并与xoy面相切, 故在球坐标系下所围立体为
: 0 r a 3 cos , 0 2 , 0 2
利用对称性, 所求立体体积为
V d v
z r a 3 cos a
2
2 h
h
o
y
二、利用球面坐标计算三重积分
设点 M 在 xoy 面上的投影为 P， z 点 P 在 x 轴上的投影为 A，
则 OA x , AP y, PM z .
A
x
M ( x, y, z )
z
o
y
球面坐标与直角坐标的关系为
x
y
P
x sin cos , y sin sin , z cos .
2 2 2 2
x2 y2
解
由x
2
由锥面和球面围成， 采用球面坐标，
y z 2a
2 2
2
r 2a,
z
x y , 4
2 2
: 0 r 2a ,
0 , 4
0 2 ,
由三重积分的性质知 V
dxdydz ,
V d d
dx
2
4 x 2
dy
3( x 2 y 2 )
16 x 2 y 2
0 d0 rdr 3r 2 2 3r d rdr 0 0 16 r
一、利用柱面坐标计算三重积分
设 M ( x , y , z ) 为空间内一点，并设点M 在 xoy 面上的投影 P 的极坐标为 r ,，则这样的三 个数 r , , z 就叫点 M 的柱面坐标．
规定： 0 r ,
0 2,
z
M ( x, y, z )
z .
z 当f ( x , y , z )关于 ____ z 为偶函数时,
1
2 f ( x, y, z )dv f ( x, y, z )dv ___
其中1为在xy面上方的部分 .
练习题
一、填空题: 1 、若 由曲面 z 2 3( x 2 y 2 )和 x 2 y 2 z 2 16 所 围, 则三重积分 f ( x , y , z )dv 表示成直角坐标下
I I1 I 2 ( x y )dxdydz ( x y )dxdydz,
2 2 2 2 1
5 4 d dr r 2 r r 2dz , 0 3 2
4 8
I1 rdrd r 2 fdz
D1 2
8
2
2
0
I 2 rdrd r 2 fdz
规定：
0 r , 0 ,
如图，三坐标面分别为
r 为常数
球 面；
0 2.
为常数
为常数
圆锥面；
半平面．
如图，
z
球面坐标系中的体积元素为 d
dv 2 sin drd d ,
d
sin
o
sin d
d
d
y
d
f ( x, y, z )dxdydz
其值为_______.
3、若空间区域 为二曲面x 2 y 2 az 及 z 2a x 2 y 2 所围, 则其体积可表为三重积分 _______________; 或 二 重 积 分 ______________; 或柱面坐标下的三次积分___________________. 4 、 若 由 不 等 式 x 2 y 2 (z a)2 a 2 , x 2 y 2 z 2 所确定, 将 zdv 表为球面坐标下的三次积分为
( x 2 y 2 z 2 )d xd yd z
0 4 sin d
4
d
R 4 r dr 0
x
o
y
1 R 5 (2 2) 5
dv r 2 sin dr d d
例6.求曲面 ( x
2
y z ) a z (a 0) 所围立体体积.
所围的立体.
x r cos 解 由 y r sin , zz
r 2 z 2 4 2 r 3z
知交线为
z 1, r 3,
把闭区域 投影到 xoy 面上，如图，
r2 : z 4 r 2， 3 0 r 3, 0 2.
绕 oz 轴旋转得，
2 2
旋转面方程为 x y 2z ,