数学建模优化模型与Lingo Lindo软件
合集下载
lindo 与Lingo入门
优化建模
在LINGO中使用LINDO模型
LINGO的界面
• LINGO软件的主窗口（用 户界面），所有其他窗口 都在这个窗口之内。
• 当前光标 的位置 • 模型窗口（Model Window），用于输入 LINGO优化模型（即 LINGO程序）。
• 状态行（最左边显 示“Ready”，表示 “准备就绪”）
即证券A,C,E分别投资2.182百万元，7.364 百万元,0.454百万元，最大税后收益为0.298 百万元. (2)由(1)的结果中影子价格可知,若资金增加 100万元,收益可增加0.0298百万元.大于 2.75%的利率借到100万元资金的利息,所以 应借贷.投资方案需将上面模型第2个约束右 端改为11,求解得到:证券A,C,E分别投资2.40 百万元,8.10百万元,0.50百万元,最大税后收 益为0.3007百万元.
除“LG4”文件外， 另外几种格式的文件 都是普通的文本文件， 可以用任何文本编辑 器打开和编辑。
•.MPS：示MPS（数学规划系统）格式的模型文件。
优化建模
在LINGO中使用LINDO模型
在LINGO中可以直接使用LINDO语法编写的优化模型（即优化程序）。 作为一个最简单的例子，在名为EXAM0201.LTX的模型文件中保存了一个 LINDO模型，我们现在看看如何用LINGO把它打开。
选择菜单命令 “File|Open(F3)”， 可以看到 “打开文 件”对话框。 （如 图）
①
优化建模
在LINGO中使用LINDO模型
②
打开“EXAM0201.LTX”文件 （如下图）
选择“LINGO|Solve （Ctrl+S）”来运行这 个程序（运行状态窗口 如右图）
优化模型与LINDOLINGO优化软件
前面是两个循环语句的用法，函数以 “@”开头，里面是循环变量以及界定循环 变量的变化范围，后面是循环体。还有另 外的两个循环函数：@min和@max，其用 法相类似。
从一维数组派生二维数组在数学上是常 用的，比如运输问题，由顶点集可以派生 边，大家可以使用本方法产生标准的运输 问题的Lingo程序。可以参考例子。
• Preprocess：预处理(生成割平面)； • Preferred Branch：优先的分枝方式：
“Default”（缺省方式）、 “Up”（向上取整优先）、 “Down”（向下取整优先）；
• IP Optimality Tol：IP最优值允许的误 差上限（一个百分数，如5%即0.05）； • IP Objective Hurdle：IP目标函数的篱 笆值，即只寻找比这个值更优最优解
2，Lingo程序的结构和语法
一个规划问题，包括下面的一些内容：变量、常量、目标、约束。还是以 前面的例子，说明最基本的程序构成。 model: linear programming sets:
cargo/1..n/:c,x; rhs/1..m/:b; mat(rhs,cargo):a; endsets data c=2,3; b=2,1/2; A=1,1,1,-2; enddata max=@sum(cargo(i):c(i)*x(i)); @for(rhs(j):@sum(cargo(i):a(j,i)*x(i))<b(j));
1 )现 有 2料 场 ， 位 于 A (5 ,1 ),B (2 ,7 ), 记 (x j,y j),j= 1 ,2 , 日 储 量 e j各 有 2 0吨 。
目标：制定每天的供应计划，即从 A, B 两料场分别向
各工地运送多少吨水泥，使总的吨公里数最小。
优化建模与LINGO第02章2
输出格式（Output）中所包括的4个选项： Status Window（状态窗口）选项： 用于控制求解模型时是否显示状态窗口（缺省设置为显示）。 Terse Output（以简明的形式显示结果）选项： 用于控制是否以简明的形式报告结果（缺省设置为以详细 （Verbose）的形式报告结果）。 Page Length Limit（页长限制）： 用于控制输出时每页最多显示多少行（可以设置为任意正整数； 缺省设置是“None”，表示无限制）。 Terminal Width（终端宽度）： 每行的最大宽度（每行多少字符），可以设为40-132之间的整 数（缺省设置为80）。
保存时可以有三种文件格式可供选择：*.PUN (以MPS（数 学规划系统）的"Punch" 格式保存)； *.FBS(以LINDO格式 保存)；*. SDBC (以数据库格式按列（变量）保存)。具体请 参考2.6节中对应的行命令。
优化建模
File|Title 显示当前模型的名称（如果该模型被命名过，即模型的程序 中出现过Title语句）。
File|Save （F5） 保存文件
Edit|Paste
(Ctrl+V) 粘贴
Edit | Paste Symbol （Ctrl+P） 粘贴符号
Report | Solution （Alt+0） 显示解答
Window|Tile (Alt+T) 平铺窗口
File|View （F4） 浏览文件
Edit|Copy （Ctrl+C ） 复制
EDIT|OPTIONS 该命令打开一个对话框（见下一页），用于设置LINDO系统 运行的内部参数，这对于比较专业的用户是有帮助的。
优化建模
从对话框可以看出，可修改的参数分成两大类： 左边一类是关于优化程序的（Optimizer这里是指优化程序， 也就是LINDO求解器，而不是最优解的意思）, 右边一类是关于输出格式的（Output）。
保存时可以有三种文件格式可供选择：*.PUN (以MPS（数 学规划系统）的"Punch" 格式保存)； *.FBS(以LINDO格式 保存)；*. SDBC (以数据库格式按列（变量）保存)。具体请 参考2.6节中对应的行命令。
优化建模
File|Title 显示当前模型的名称（如果该模型被命名过，即模型的程序 中出现过Title语句）。
File|Save （F5） 保存文件
Edit|Paste
(Ctrl+V) 粘贴
Edit | Paste Symbol （Ctrl+P） 粘贴符号
Report | Solution （Alt+0） 显示解答
Window|Tile (Alt+T) 平铺窗口
File|View （F4） 浏览文件
Edit|Copy （Ctrl+C ） 复制
EDIT|OPTIONS 该命令打开一个对话框（见下一页），用于设置LINDO系统 运行的内部参数，这对于比较专业的用户是有帮助的。
优化建模
从对话框可以看出，可修改的参数分成两大类： 左边一类是关于优化程序的（Optimizer这里是指优化程序， 也就是LINDO求解器，而不是最优解的意思）, 右边一类是关于输出格式的（Output）。
数学建模——LINDO_LINGO的实用与优化模型
目标：制定每天的供应计划，即从 A, B 两料场分别
向各工地运送多少吨水泥，使总的吨公里数最小。
决策变量：ci j (料场j到工地i的
运量）~12维
26
mi n
cij [(x j ai )2 ( y j bi )2 ]1/ 2
j 1 i1
2
s.t.
cij di , i 1,..., 6
X1
20.000000
0.000000
X2
30.000000
0.000000
end
ROW SLACK OR SURPLUS DUAL PRICES
三
原料无剩余 2)
0.000000
48.000000
种
时间无剩余 3)
0.000000
2.000000
资 源
加工能力剩余40
4)
40.000000
0.000000
不变！
结果解释
影子价格有意义
RANGES IN WHICH THE BASIS IS UNCHANGED: 时约束右端的允
OBJ COEFFICIENT RANGES
许变化范围
VARIABLE CURRENT ALLOWABLE ALLOWABLE COEF INCREASE DECREASE
(目标函数不变)
例如： “sub x1 10”的作用等价于“x1<=10”
但用“SUB”和“SLB”表示的上下界约束不计入模 型的约束，也不能给出其松紧判断和敏感性分析。
14. “END”后对0-1变量说明：INT n 或 INT name
15. “END”后对整数变量说明：GIN n 或 GIN name
LINGO求解举例 — 例：选址问题
向各工地运送多少吨水泥，使总的吨公里数最小。
决策变量：ci j (料场j到工地i的
运量）~12维
26
mi n
cij [(x j ai )2 ( y j bi )2 ]1/ 2
j 1 i1
2
s.t.
cij di , i 1,..., 6
X1
20.000000
0.000000
X2
30.000000
0.000000
end
ROW SLACK OR SURPLUS DUAL PRICES
三
原料无剩余 2)
0.000000
48.000000
种
时间无剩余 3)
0.000000
2.000000
资 源
加工能力剩余40
4)
40.000000
0.000000
不变！
结果解释
影子价格有意义
RANGES IN WHICH THE BASIS IS UNCHANGED: 时约束右端的允
OBJ COEFFICIENT RANGES
许变化范围
VARIABLE CURRENT ALLOWABLE ALLOWABLE COEF INCREASE DECREASE
(目标函数不变)
例如： “sub x1 10”的作用等价于“x1<=10”
但用“SUB”和“SLB”表示的上下界约束不计入模 型的约束，也不能给出其松紧判断和敏感性分析。
14. “END”后对0-1变量说明：INT n 或 INT name
15. “END”后对整数变量说明：GIN n 或 GIN name
LINGO求解举例 — 例：选址问题
数学建模讲座优化建模与LINGO优化软件
x1 x2 50
12x1 8x2 480
约束条件
劳动时间 加工能力 非负约束
3x1 100 x1 , x2 0
线性 规划 模型 (LP)
模型求解
OBJECTIVE FUNCTION VALUE
max =72*x1+64*x2; x1+x2<50;
REDUCED COST 0.000000
Lingo
基 础
计算结果为
Objective value:89.88349
模型的集部分
LINGO 有 两 种 类 型 的 集 ： 原 始 集 ( primitive set) 和 派 生 集 ( derived set)。 一个原始集是由一些最基本的对象组成 的。 一个派生集是用一个或多个其它集来定 义的，也就是说，它的成员来自于其它 已存在的集。
如果在Lingo文件example3_4.lg4 加上以下内容 其他不变 data:
@ole("d:\ 数 学 建 \EXAMPLE3_4.XLS","result")=c; @ole("d:\ 数 学 \EXAMPLE3_4.XLS","x")=x; 建 模 模
@ole("d:\ 数 学 \EXAMPLE3_4.XLS","y")=y;
@OLE 的使用例子 Lingo文件example3_4.lg4 的内容 data: a,b,d,e=@OLE("d:\数学建模 \EXAMPLE3_4.XLS"); enddata init: x,y=@Ole("d:\数学建模 \Example3_4.xls"); endinit
(外校培训课件)优化模型与LINGO软件求解——LINGO学习集全资料文档
NLP: 非线性规划
(2)最优状态 全局全优
(3)最优目标值: 10
约束条件情况最优解： (1)约束总个数X4=100,按方法4 (2)非线性个数X6=50, 按方法6
25
[例1] 下料(截割问题)及求解
❖ [模型-2]的求解结果：
最优目标函 数值：90
x1=40, 按方法1截割 x2=20, 按方法2截割 x6=30. 按方法6截割
26
[例1] 下料(截割问题)及求解
❖ 求解结果分析：
在追求“余料最少”目标时，“≥”约 束把条件放宽了。
修正方法：改为“=”约束
模型(1)的求解结果： 最优目标(余料)=10m
(x4,x6)=(100,50) 耗用原料 = 150根
是否符 合原问 题要求?
不符合。 (1)问题出在哪里? (2)如何修正?
2
一、竞赛题中的优化模型总结
❖ 2.优化类竞赛题小结 ❖ 在全国数模竞赛中，优化问题是出现频率最
高的一类竞赛题。 ❖ 从1992-20××年全国大学生数模竞赛试题
的解题方法统计结果来看，优化模型共出现 了17次以上，占到了50%。 ❖ 即每两道竞赛题中就有一道涉及到利用优化 理论来建模和求解。
3
一、竞赛题中的优化模型总结
题
13
(三) 典型数学规划问题及求解
❖ 例1 下料(截割)问题及求解 ❖ 例2 运输问题及求解 ❖ 例3 非线性规划问题及求解 ❖ 例4 分派(选址)问题及求解 ❖ 例5 动态规划问题及求解
14
[例1] 下料(截割)问题及求解
1. 问题提出 2. 建立数学模型 3. 编写LINGO求解程序 4. 执行程序 5. 获得计算结果并分析 6. 修正模型，重新求解 7.课后作业 8.编程小结
优化建模与LINGO
1 2 3 4
：
•LINGO总是根据“MAX=”或“MIN=”寻找目标函数， 而除注释语句和TITLE语句外的其他语句都是约束条 件，因此语句的顺序并不重要 。 •限定变量取整数值的语句为“@GIN(X1)”和 “@GIN(X2)”，不可以写成“@GIN(2)”，否则 LINGO将把这个模型看成没有整数变量。
• 运行状态窗口
优化建模 当前模型的类型 :LP，QP，ILP，IQP，PILP， PIQP，NLP，INLP，PINLP （以I开头表示 IP，以PI开头表示PIP） 当前解的状态 : "Global Optimum", "Local Optimum", "Feasible", "Infeasible“(不可行), "Unbounded“(无界), "Interrupted“(中断), "Undetermined“(未确定) 当前约束不满足的总量(不是不 满足的约束的个数):实数（即使 该值=0，当前解也可能不可行， 因为这个量中没有考虑用上下界 命令形式给出的约束）
•LINGO中函数一律需要以“@”开头，其中整型变量 函数（@BIN、@GIN）和上下界限定函数（@FREE、 @SUB、@SLB）与LINDO中的命令类似。而且0/1变 量函数是@BIN函数。
优化建模
输出结果： 运行菜单命令“LINGO|Solve”
最大利润=11077.5
最优整数解 X=(35，65)
优化建模
1. LINGO入门 2.在LINGO中使用集合
3. 运算符和函数
2.在LINGO中使用集合 4. LINGO的主要菜单命令 5. LINGO命令窗口 6.习题
优化建模
LINGO软件在优化模型中的应用
羊羽lingo是linearinteractivegeneraloptimizer的缩写即交互式的线性和通用优化求解器由美国lindo系统公司推出的可以用于求解非线性规划也可以用于一些线性和非线性方程组的求解等功能十分强大是求解优化模型的最佳选择
LINGO软件 ——在优化模型中的应用
腾讯微博：羊羽
LINGO软件在优化模型中的应用
LINGO软件在优化模型中的应用
解：设每天用x1 桶牛奶在甲车间生产，用x2 桶牛 奶在乙车间生产，可获利z 元。
则该问题的数学模型为： max z=72x1+64x2 s.t x1+x2≤50 12x1+8x2≤480 3x1≤100 x1,x2≥0
LINGO软件在优化模型中的应用
结果：
这个线性规划的最优解为x1=20，x2=30，最优值 为z=3360，即用20 桶牛奶在甲车间生产，30 桶 牛奶在乙车间生产，可获最大利润3360 元。
优点
3）强大的求解器 LINGO拥有一整套快速的，内建的求 解器用来求解线性、非线性、二次约束和 整数优化问题。
LINGO软件在优化模型中的应用
优点
4）交互式模型 在LINGO内可以直接创建和求解模型， 也可以从自己编写的应用程序中直接调用 LINGO。对于开发交互式模型，LINGO提 供了一整套建模环境，用来求解和分析构 建的模型。
从该问题的求解我们可以看到用LINGO 软件求 解线性规划是非常方便、快捷的，比单纯形法人 工计算效率高很多。
LINGO软ห้องสมุดไป่ตู้在优化模型中的应用
附加问题：
1） 若用35元可以买到1桶牛奶，应否作这项投资？ 若投资，每天最多购买多少桶牛奶？ 2） 若可以聘用临时工人以增加劳动时间，付给临 时工人的工资最多是每小时几元？ 3） 由于市场需求变化，甲车间奶制品的获利增加 到30元，应否改变生产计划？
LINGO软件 ——在优化模型中的应用
腾讯微博：羊羽
LINGO软件在优化模型中的应用
LINGO软件在优化模型中的应用
解：设每天用x1 桶牛奶在甲车间生产，用x2 桶牛 奶在乙车间生产，可获利z 元。
则该问题的数学模型为： max z=72x1+64x2 s.t x1+x2≤50 12x1+8x2≤480 3x1≤100 x1,x2≥0
LINGO软件在优化模型中的应用
结果：
这个线性规划的最优解为x1=20，x2=30，最优值 为z=3360，即用20 桶牛奶在甲车间生产，30 桶 牛奶在乙车间生产，可获最大利润3360 元。
优点
3）强大的求解器 LINGO拥有一整套快速的，内建的求 解器用来求解线性、非线性、二次约束和 整数优化问题。
LINGO软件在优化模型中的应用
优点
4）交互式模型 在LINGO内可以直接创建和求解模型， 也可以从自己编写的应用程序中直接调用 LINGO。对于开发交互式模型，LINGO提 供了一整套建模环境，用来求解和分析构 建的模型。
从该问题的求解我们可以看到用LINGO 软件求 解线性规划是非常方便、快捷的，比单纯形法人 工计算效率高很多。
LINGO软ห้องสมุดไป่ตู้在优化模型中的应用
附加问题：
1） 若用35元可以买到1桶牛奶，应否作这项投资？ 若投资，每天最多购买多少桶牛奶？ 2） 若可以聘用临时工人以增加劳动时间，付给临 时工人的工资最多是每小时几元？ 3） 由于市场需求变化，甲车间奶制品的获利增加 到30元，应否改变生产计划？
优化建模与lingo优化软件
Teaching Plan on Optimization in Lingo
• 1992年: (Ａ)作物生长的施肥效果问 题 (B)化学试验室的实验数据分解问题 • 1993年: (Ａ)通讯中非线性交调的频率设计问题 (Ｂ)足球甲级联赛排名问题
（1）1992-2008全国大学生数学建 模竞赛题目如下：
4、合理设定变量上下界，尽可能给出变量初始值
5、模型中使用的参数数量级要适当 (如小于103)
Teaching Plan on Optimization in Lingo
优化问题1：
min z ( x1 1) 2 ( x1 x 2) 2 ( x 2 x3) 2 ( x3 x 4) 2 ( x 4 x5) 2
Teaching Plan on Optimization in Lingo
• 2009 (A)制动器试验台的控制方法分析 (B)眼科病床的合理安排 (C)卫星和飞船的跟踪测控 (D)会议筹备
Teaching Plan on Optimization in Lingo
(最)优化理论是运筹学的基本内容
3 x1 x2 2 x3 3 2 x2 x3 x4 2 s.t x1 x5 2 5 x 5 i
i 1,2,5
Teaching Plan on Optimization in Lingo
需要掌握的几个重要方面
LINGO：
掌握集合(SETS)的应用；
非 线 性 规 划
整 数 规 划
组 合 优 化
不 确 定 规 划
多 目 标 规 划
目 标 规 划
网 络 优 化
动 态 规 划
Teaching Plan on Optimization in Lingo
数学建模软件LinDoLinGo的简介(修改)
X——表示变量X可取任意实数值。 GIN X——表示变量X只取非负整数值。 INT X——表示变量X只能取0或1。 SLB X value——表示变量X以value为下界。 SUB X value——表示变量X以value为上界。 FREE m——表示问题的前m个变量为自由变量 GIN m——表示问题前m个变量为非负整数值 INT m——表示问题前m个变量为0－1变量。
LINGO 示例
查看简单例子
LINHGO程序
Lindo模型到Lingo模型的转换
“ST”在Lingo模型中不再需要，所以删除了； 在每个系数与变量之间增加了运算符“*”；
将目标函数的表示方式从“MAX”变成“MAX=”；
每行（目标、约束和说明语句）后面均增加了一
个分号“;”； 约束的名字被放ngo中模型以“Model:”开始，以“END”结束。 对简单模型，这两个语句也可以省略。
LINDO/LINGO软件 使用简介
LinDo/LinGo简介
LINDO（Linear Interactive and Discrete Optimizer），即“交互式的线性和离散优化求解 器”，可以用来求解线性规划（LP）和二次规划 （QP）； LINGO（Linear Interactive and General Optimizer），即“交互式的线性和通用优化求解 器”，除了用来求解线性规划（LP）、二次规划 （QP）和非线性规划，还可用于线性和非线性方程 组的求解。 最大的特色：允许决策变量是整数（即整数规划，包 括0-1规划）。
Lindo求解整数规划
Lindo求解整数规划程序
LP OPTIMUM FOUND AT STEP 2 OBJECTIVE VALUE = 998.811951
优化建模与LINDO,LINGO优化软件
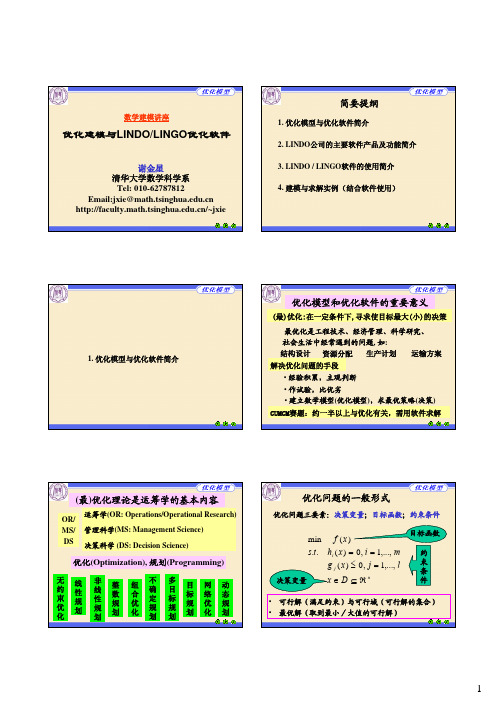
ROW SLACK OR SURPLUS DUAL PRICES
三
原料无剩余
2)
0.000000
种
时间无剩余
3)
0.000000
资 源
加工能力剩余40
4)
40.000000
48.000000 2.000000 0.000000
“资源” 剩余为零的约束为紧约束（有效约束）
结果解释
OBJECTIVE FUNCTION VALUE
1. 优化模型与优化软件简介
优化模型和优化软件的重要意义
(最)优化:在一定条件下,寻求使目标最大(小)的决策
最优化是工程技术、经济管理、科学研究、 社会生活中经常遇到的问题, 如: 结构设计 资源分配 生产计划 运输方案 解决优化问题的手段 • 经验积累，主观判断 • 作试验，比优劣 • 建立数学模型(优化模型)，求最优策略(决策) CUMCM赛题：约一半以上与优化有关，需用软件求解
2)
0.000000
48.000000
3)
0.000000
2.000000
4) 40.000000
0.000000
NO. ITERATIONS= 2
reduced cost值表 示当该非基变量 增加一个单位时 （其他非基变量 保持不变）目标 函数减少的量(对 max型问题)
也可理解为：
为了使该非基变 量变成基变量， 目标函数中对应 系数应增加的量
2
50.000000 10.000000
6.666667 90，在允许范
3 480.000000 53.333332
80.000000 围内
4 100.000000 INFINITY 40.000000
优化模型与Lingo Lindo软件
Lingo/Lindo软件介绍
---Lingo
对前面的线性规划模型，编写Lingo程序如下：
点击图标
运行，屏幕上显示运行状态窗口如下：
对于Lingo运行状态窗口， 我们给于以下解释：
变量数目：变量总数 （Total）、非线型变量 数（Nonlinear）、整数 变量数（Integer） 约束变量：约束总数 （ Total ）、非线性约束 个数（Nonlinear） 非线性系数数量：总数 （ Total ）、非线性项的 系数个数（Nonlinear） 内存使用量：单位为千字节
① 除具备Lindo的全部功能外，还可以用于求解非线性规划问题；
② Lingo包含了内置的建模语言，允许以简练、直观的方式描述较大规 模的优化问题，模型中所需的数据可以以一定的格式保存在独立的 文件中。
事实上，Lindo公司目前已经将Lindo软件从其产品目 录中删除，而将Lindo软件的所有功能都在Lingo中得到了 支持，所以在不久的将来总有一天人们会废弃Lindo软件不 再使用，但Lingo的生命力应该还是很顽强的！
Infeasibility 约束不满足的量；0表示这个解是可行的 Objective 显示当前解的目标函数值 Best IP 显示整数规划当前解的最佳标函数值：N/A 表示无答案或无意义 显示分支定界算法已经计算的分支数： N/A 表示无答案或无意义
IP Bound 显示整数规划的界 Branches
Lingo/Lindo软件介绍
这套软件包由美国芝加哥大学的Linus Scharge教
授于1980年前后开发，专门用于求解最优化问题，后 经不断完善和扩充，并成立LINDO公司进行商业化运 作，取得了巨大的成功。全球《财富》杂志500强的企 业中，一半以上使用该公司产品，其中前25强企业中 有23家使用该产品。 该软件包功能强大，版本也很多，而我们 使用的只 是演示版（试用版），演示版与正式版功能基本上是 类似的，只是能够求解问题的规模受到限制，总变量数 不超过30个，这在我们目前的使用过程中，基本上是 足够。
lindo和lingo简介
LINDO和LINGO是美国LINDO系统公司开发的一套专门用于求解最优化问题的软件包。
LINDO 用于求解线性规划和二次规划，LINGO除了具有LINDO的全部功能外，还可以用于求解非线性规划，也可以用于一些线性和非线性方程组的求解以及代数方程求根等。
LINDO和LINGO软件的最大特色在于可以允许优化模型中的决策变量是整数（即整数规划），而且执行速度很快。
LINGO实际上还是最优化问题的一种建模语言，包括许多常用的函数可供使用者建立优化模型时调用，并提供与其它数据文件（如文本文件、EXCEL电子表格文件、数据库文件等）的接口，易于方便地输入、求解和分析大规模最优化问题。
由于这些特点，LINDO和LINGO软件在教学、科研和工业、商业、服务等领域得到广泛应用。
１）目标函数及各约束条件之间一定要有“Subject to (ST) ”分开。
２）变量名不能超过８个字符。
３）变量与其系数间可以有空格，单不能有任何运算符号（如乘号“＊”等）。
４）要输入<=或>=约束，相应以<或>代替即可。
５）一般LINDO中不能接受括号“（）“和逗号“，“，例：400(X1+X2) 需写成400X1+400X2；10,000需写成10000。
６）表达式应当已经过简化。
不能出现 2 X1+3 X2-4 X1，而应写成-２X1+3 X2。
用LINDO求解施工中的线性规划（LP）问题1 引言线性规划是现代化管理的常用工具与方法，在施工过程中，很多实际问题，如配（下）料，运输（土石方调配），施工机具车辆调度，施工场地的合理设点，成品、半成品、原材料的合适库存量规划问题等等，都需要运用线性规划方法求得最优方案。
线性规划一般需要先确定要求的未知变量和目标函数，然后找出所有的约束条件，表示为线性方程或不等式，建立问题的数学模型，对于变量数目和约束条件较少的情况可用手工计算，较多的情况则需运用计算机来求解。
2 LINDO介绍LINDO是Linear INteractive and Discrete Optimizer字首的缩写形式，是由Linus Schrage 于1986年开发的优化计算软件包。
数学模型与lingo软件
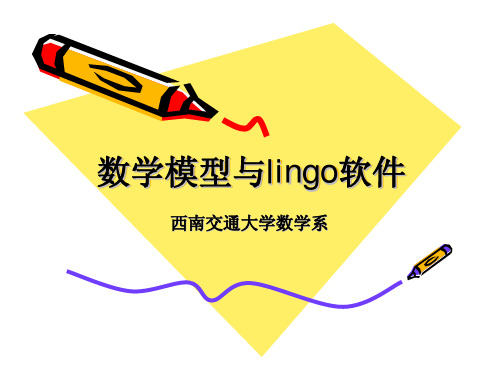
LINGO 主菜单 Generate: 以线性形式显示目标函数和约 束（只有非零项会显示）。如果有非线性 变量项，对应的非线性变量前的系数将以 问号（“？”）显示.按照是否在屏幕上显 示结果的要求， “Display”和“Don’t display”两个子菜单供选择。在屏幕上 不显示时，运行该命令的目的可能仅仅是 为了以后选择适当的求解程序使用。
模型的数据部分 数据部分提供了模型相对静止部分和数据分离的可能性。显 然，这对模型的维护和维数的缩放非常便利。 数据部分以关键字“data:”开始，以关键字“enddata”结束。在这 里，可以指定集成员、集的属性。其语法如下：
object_list = value_list;
对象列（object_list）包含要指定值的属性名、 要设置集成员的集名，用逗号或空格隔开。一 个对象列中至多有一个集名，而属性名可以有 任意多。如果对象列中有多个属性名，那么它 们的类型必须一致。如果对象列中有一个集 名，那么对象列中所有的属性的类型就是这个 集。
除“LG4”文件外，这里的另外几 种格式的文件其实都是普通的 文本文件，可以用任何文本编 辑器打开和编辑
状态窗口的参数解释 变量数量（其中包括变量总数、 非线性变量数、整数变量数）
约束数量 （约性项的个数）
内存使用量、求 解花费的时间
状态窗口的参数解释(2) 求解器状态框
数值列（value_list）包含要分配给对象列中的对象的 值，用逗号或空格隔开。注意属性值的个数必须等于 集成员的个数。 sets: set1/A,B,C/: X,Y; endsets data: X=1,2,3; Y=4,5,6; enddata
数据部分的未知数值 有时只想为一个集的部分成员的某个属性指定值，而 让其余成员的该属性保持未知，以便让LINGO去求出 它们的最优值。在数据声明中输入两个相连的逗号表 示该位置对应的集成员的属性值未知。两个逗号间可 以有空格 sets: years/1..5/: capacity; endsets data: capacity = ,34,20,,; enddata 属性capacity的第2 个和第3个值分别 为34和20，其余的 未知
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
型
表二 ：5名队员4中泳姿百米平均成绩
队员
甲
乙
丙
丁
戊
蝶泳 66.8 57.2
78
70
67.4
仰泳 75.6
66
67.8
74.2
71
蛙泳
87
66.4 84.6
69.6
83.8
自由泳 58.6
53
59.4
57.2
62.4
线 性 规
·划
模 型
决策变量：引入0-1变量xij 若选择队员 i 参加泳姿 j
例-1 某服务部门一周中每天需要不同数目的
雇员：周一到周四每天至少需要50人，周五
需要80人，周六和周日需要90人。现规定应
聘者需连续工作5天，试确定聘用方案，即周
线
一到周日每天聘用多少人，是5在满足需要的 前况下聘用总人数最少？
性
优化模型
规
决策变量：记周一到周日每天聘用的人数分别为X1，
划
X2，X3，X4，X5，X6 ，X7，这就是问题的决策变量。
的比赛，记 xij=1，否则记 xij=0.这就是问题的决策变量， 共20个。
目标函数：当队员队员 i 入选泳姿 j 的比赛时，
cij xij表示他的成绩，否则cij xij=0。于是接力队的成绩
可以表示为：
45
f
cij xij
j1 i1
约束条件：根据组成接力队的要求， xij 应该满足下面
方案。显然这不是解决问题的最好方法，随着问题
线
规模的变大，穷举法的计算量是无法接受的。
性
可以用0-1变量表示一个队员是否入选接力队， 从而建立这个问题的0-1规划模型.
规
记甲、乙、丙、丁、戊分别为队员 i=1，2，3，4，5；
划
记蝶泳、仰泳、蛙泳、自由泳分别为泳姿 j=1，2，3，
模
4；记队员 i 的第 j 种泳姿的百米成绩为 cij（s），则表 一可以表示成为：
3.此外，为了解决实际问题的需要，还可以分为： 单目标规划，多目标规划，动态规划，多层规划等。
（1）线性规划（LP）的一般形式
常
目标函数和所有的约束条件都是变量的线性 函数。
用
n
的 min f x ci xi , i 1,2,...,n
优
i 1
化 模 型
n
s.t. i1
ai xi
bi , bi
蛙泳 1’27” 1’06”4 1’24”6 1’09”6 1’23”8
自由泳 58”6
53”
59”4
57”2 1’02”4
问题分析：问题要求从5名队员中选出4人组成接
力队，每人一种泳姿，且四人的泳姿各不相同，使
接力队成绩最好。容易想到穷举法，组成接力队的
方案有5！=120中，逐一计算并做比较即可找出最优
（1）
s. t. h( x ) 0 i 1,2, ,m
（2）
g( x ) 0 j 1,2, ,n （3）
这里opt 最优化的意思，可以是min（求极大， 即minamize的缩写）或max （求极小，即minamize 的缩写）的两者之一；s.t. （即subject to）“受约 束于”之意。
优化模型基本类型
1.决策变量x的所有分量xi均为连续数值
a）f ,hi ,gi都是线性函数，则为线性规划（LP） b）f ,hi ,gi至少有一个是非线性，则为非线性规划（NLP）
c） f 是二次函数,hi ,gi 都是线性，则为二次规划（QP）
2.决策变量x的的一个或多个分量xi取离散值
a） x的至少一个分量只取整数数值，则为整数规划（IP） b） x的分量限定只取整数0或1，则为0-1规划（ZOP）
优化模型：Lingo Lindo软件
优化模型
优化模型的三要素
（1）决策变量，通常是某一问题需要求解的未知量，
用n维向量x= x1 ,x2 , xn T 表示，当对x赋值后它通常
称为该问题的一个解；
（2）目标函数，通常是某一问题需要优化（最大或 最小）的那个目标的数学表达式，它是决策变量x的 函数，可以 抽象的记作f ( x )；
两个约束条件：
① 每人最多只能入选4种泳姿之一，即对于员 i=1，2，3，
4，应该有：
4
xij 1
j 1
② 每种泳姿有且只能有1人入选，即对于员 j=1，2，3，4，
5，应该有：
5
xij 1
i 1
综上所述，这个问题的优化模型可以写作：
45
min
cij xij ;
x1 x2 x3 x6 x7 50
线 性 规
x1 x2 x3 x4 x7 50 x1 x2 x3 x4 x5 80 x2 x3 x4 x5 x6 90
划
x3 x4 x5 x6 x7 90
模
显然，人数应该是正整数，所以
型
xi 0 i 1, 2, 7
问题归结为在以上约束条件下求解min z的 整数规划模型。由于目标函数和约束条件关于 决策变量都是线性函数，所以这是一个整数向 行规划模型。
模
目标函数：目标函数即是聘用总人数，即
型
z x1 x2 x3 x4 x5 x6 x7
约束条件：由每天需要的人数确定。由于每人连续
工作五天，所以一周的雇员应该是周四到周一聘用的， 按照需要至少50人，于是
x1 x4 x5 x6 x7 50
类似的，有
x1 x2 x5 x6 x7 50
（3）约束条件，由该问题对决策变量的现实条件给 出，即x允许的取值范围为x ，称为可行域，常
用一组关于x的等式hi( x ) 0i 1,2, m和（或）不 等式g j( x ) 0 j 1,2, n来界定，分别称为等式约
束和不等式约束。
于是，优化模型从数学上可以表述为
opt z f ( x )
, bi ,
形 式
xi 0,i 1,2,...,n
（2）二次规划问题
常
目标函数为二次函数，约束条件为线性约束。
用 的
n
1n
min f
x
i 1
ci xi
2
i,
bij
j 1
xi
x
Hale Waihona Puke j优 化 模 型 形 式
n
ai xi bi , bi
, bi .
s
.t
.
i 1
xi
0.
i, j 1,2,...,n.
例-2 某班准备从5名游泳队员中选择4人组成
接力队，参加学校的4*100混合泳接力比赛。
5名队员4中泳姿的百米平均成绩如下表所示，
线
问应该如何选拔队员组成接力队？
性
规
表一 ：5名队员4中泳姿百米平均成绩
划
队员
甲
乙
丙
丁
戊
模
蝶泳 1’06”8 57”2 1’18” 1’10” 1’07”4
型
仰泳 1’15”6 1’06” 1’07”8 1’14”2 1’11”