北航理论力学王琪
北航理论力学王琪

2009-10-9
23
理论力学
木桁架节点
§3-2 桁架
榫接
2009-10-9
24
理论力学
钢桁架节点
§3-2 桁架
铆接
2009-10-9
焊接
25
理论力学
钢筋混凝土桁架节点
§3-2 桁架
刚接
2009-10-9 26
理论力学
桁架模型简化的基本假设
§3-2 桁架
假设1:各杆件都用光滑铰链相连接
2009-10-9 27
2009-10-9 10
F
理论力学
三、刚体系的平衡问题
§3-1 刚体系的平衡
刚体系平衡 ⇔ 系统中每个刚体平衡 例:已知 F,M ,AB = BC = L ,F 作用在BC杆的中点, 求:A、C 处的约束力。 A
M
B
F
600
C
2009-10-9
11
理论力学
A
M
§3-1 刚体系的平衡
B
F
60
0
C
求:A、C 处的约束力。
理论力学
§3-2 桁架
假设2:各杆件轴线都是直线,并通过铰链中心
2009-10-9
28
理论力学
§3-2 桁架
假设3:所有外力(荷载及支座约束力)都作用在节点上
2009-10-9
29
理论力学
桁架模型简化的基本假设:
§3-2 桁架
假设1:各杆件都用光滑铰链相连接 假设2:各杆件轴线都是直线,并通过铰链中心 假设3:所有外力(荷载及支座约束力)都作用在节点上
例:已知 F,求 AG 杆上的约束力。
B 2a E a O a
A H
北京航空航天大学理论力学课件-王琪-ch5A

O
vx = x &⎫ ⎪ vy = y &⎬ ⎪ vz = z &⎭
2015-10-28
x
加速度
x & & = a x = 0(m/s 2 )
y & & = a y = −10(m/s 2 )
曲率半径 v2 v2 20 ρ= = = m 0 an a cos 30 3
20
ax = & x& ⎫ ⎪ ay = & y &⎬ ⎪ az = & z& ⎭
2、P 点的速度和加速度
2015-10-28 8
理论力学
3、P点的运动轨迹
§5-1 点的运动学
y A P O
θቤተ መጻሕፍቲ ባይዱ
B
ϕ
x
l 2 ⎫ xp = R cosθ + L − R2 sin2 θ ⎪ L ⎬ R ⎪ y p = (L − l ) sinθ ⎭ L
消去上述方程中 参数θ可得 P 点 的轨迹方程。
z
&⎫ 解: v x = x ⎪ vy = y &⎬ ⎪ vz = z &⎭
u
v= x &2 + y &2 + z & = R2ω2 + u2 = const &2 = s
2 a= & x y z &2 + & &2 + & &2 = Rω
ωR
ax = & x& ⎫ ⎪ ay = & y &⎬ ⎪ az = & z& ⎭
T’
•曲率(curvature)
北航 王琪教授讲义

• 在实践的基础上创新
– 在解决问题的过程中“有问题可思考”,“有方法可推敲”, 善于提出自己的观点与方法,培养创新意识。
4
汇报的主要内容
• 目标与理念 • 内容与实践 • 体会与设想
5
内容与实践
1. 探究型课堂教学模式 2. 探究型实践教学平台 3. 科研与教学有机融合
6
1、探究型课堂教学模式 原有的课堂教学模式:
• 实验装置的来源:
– 购置和自制结合
27
数值仿真实验
• 实验目的:
– 应用数值仿真揭示力学现象 – 解决数值仿真中遇到的力学和数学问题 – 定性分析与定量分析的结合
• 实验内容:
– 习题中的数值仿真算例 – 实际工程问题的数值仿真算例
28
数值仿真实验
非光滑质点动力学仿真: 数值 方法给出质点位置、速度和切 向加速度随时间的变化规律
θ 0 = 0 rad , θ 0 = 0 rad/s, f = 0 .1
O
θ
r
mg
θ (t ) θ (t ) θ (t )
t(s)
29
数值仿真实验
掌握应用定性分析 方法判断数值仿真 结果的正确性。
30
数值仿真实验 倒摆数值 仿真实验
A
1 2 1 mLθ + cθ + kθ − mgLsinθ = kbcost 3 2
实现4个结合
• 定性分析与定量分析结合 • 解析分析与数值分析结合 • 理论研究与实际应用结合 • 传授知识与能力培养结合
10
1、探究型课堂教学模式
定性分析与定量分析结合 解析分析与数值分析结合
11
1、探究型课堂教学模式
理论研究与实际应用结合
理论力学课后答案-谢传峰、王琪-动力学第九章、第十章

1 2
2l m dx(
x sin )2 0 2l
2 ml 2
2 sin2 3
O C
系统的动能 T T1 T2 。 取 900 为势能零点,则系统的势能为:
V mgl cos
则拉格朗日函数:
L T V 2 ml2 (2
2 sin2 ) mgl cos 3
x
楔块 B 的速度 vB ,以及 B 相对于 A 的相对速度
满足如下的矢量关系(方向如图所示):
vB vA vBr
系统的动能为:
vBr vA
T
1 2
m
Av
A
2
1 2
mBvB 2
P1 2g
x 2
P2 2g
[(x
s cos)2
(ssin)2 ]
1 2g
(P1
P2 )x 2
度
转动。物体的质心 G 在垂直于 O1O2 的直线上,O3G l 。设 O1O2 和 O3G 是物体过 O3
点的惯量主轴,转动惯量为 J1 和 J 2 ,物体对另一过 O3 点的惯量主轴的转动惯量为 J 3 ,试
求物体的动能表达式并建立物体的运动微分方程。 解:
以该物体为研究对象,有一个自由度,取 O3G 和 OC 的夹角 为广义坐标。若以框架 O1O2OC 为动系,则物体的相对运动是以角速度 绕轴 O1O2 的定轴转动,牵连运动是以角 速度
垂直于 O1O2 的平面
z’
O3
θ G
y’
坐标系 O3 x y z 的三个坐标轴为过 O3 点的三个惯量主轴,则系统的动能为:
T
北航理论力学王琪

理论力学
笔记本电脑
问题的引出
硬盘自动保护装置
2010-5-15
4
理论力学
计算机硬盘结构示意图
问题的引出
定点运动刚体动力学问题:研究力与运动间的关系。 问题:用什么方法建立力与运动的关系?
2010-5-15 5
理论力学
§6-2 欧拉动力学方程
z
一、刚体定点运动的动量矩
Ox’y’z’为随体参考系 Oxyz 为惯性参考系 刚体对O点的动量矩:
2010-5-15
x
o
y
y'
整个刚体对O 点的动量矩:
LO = ∑ LOi
7
理论力学
§6-2 欧拉动力学方程
LOi = mi [( y 'i2 + z 'i2 )ω x ' − x'i y 'i ω y ' − x'i z 'i ω z ' ]i ' + mi [− x'i y 'i ω x ' + ( x'i2 + z 'i2 )ω y ' − y 'i z 'i ω z ' ] j ' + mi [− x'i z 'i ω x ' − y 'i z 'i ω y ' + ( x'i2 + y 'i2 )ω z ' ]k '
+ ∑ mi [− x'i z 'i ω x ' − y 'i z 'i ω y ' + ( x'i2 + y 'i2 )ω z ' ]k '
习题课A(10月28日PPT)北航理论力学王琪

习题课I
2009-10-28 1
BUAA
对于刚体: •主矢 •主矩
平衡条件
基本原理与定理
{F1 , F2 , L , Fn } = {FR , M O }
FR = ∑Fi = ∑Fi '
i =1 n n
M O = ∑ M i = ∑ ri × Fi
n
i =1
n
FR = 0, M O = 0
1
2
C
D
设:杆1的长度为L
2009-10-28
dL < 0
28
BUAA
C D
E
C D 设:CD杆的长度为L dL > 0
2009-10-28 29
BUAA
思考题:系统如图所示。若人重W < > 板重P且人有足够大的 力量。下列两种情况中,哪个系统能在图示位置维持平衡?
(a)
(b)
A:图(a)
2009-10-28
z
F1
o
FR
F2
y
⎧ ∑ M l1 = 0 ⎪ ⎨ ∑ M l2 = 0 ⎪ ⎩ ∑ M l3 = 0
确定三根轴的位置
4
x
2009-10-28
Fn
BUAA
题8:给出空间平行力系平衡方程的三矩式
z
FR
Fi
y
o
x
MO
⎧∑ M x = 0 ⎪ ⎨∑ M y = 0 ⎪ ⎩∑ M L = 0
如何确定L轴?
2009-10-28
F1
D:力螺旋
F2
3
BUAA
题5:空间汇交力系的平衡方程独立的充分必要条件:
⎧ ∑ Fx = 0 ⎪ ⎨∑ Fy = 0 ⎪ ⎩ ∑ Fz = 0
北航理论力学王琪

理论力学
上次课的主要内容
§3-1 刚体平面运动的运动学
研究刚体平面运动速度问题的几种方法: 1、基 点 法: v B = v A + v BA
y
ω
y'
vBA
B
vB β B vA vA
2、速度投影法: [v B ]AB = [v A ]AB
v M = v MP = ω × rPM 3、速度瞬心法:
A r0
上式在铅垂轴上投影: aBA cosθ = aB =
t n
上式在水平轴上投影:
t aBA sin
θ
t = aB
u L u
2
A
B
θ
α AB =
t aBA
u = 2 AB L cosθ
2
α BC
t aB u2 = = 2 tan θ BC L
u2 aB = α AB L = L cosθ
8
2009-12-11
α
ω
vr O ar
a
vr ω= R
u
v &r − ar α =ω &= = R R
v rB = v rO + v rBO v aB = v eB + v rB v aB = v e + v rO + v rBO
12
2、求圆盘最高点B的速度
A
vaB = u − vr − ωR = u − 2vr
2009-12-11
16
理论力学
§3-1 刚体平面运动的运动学
例:图示机构中,AB杆的A端以速度 u 匀速运动,求图示瞬时
DE杆的角速度。已知该瞬时,AB杆与水平线的夹角为450,套
筒D 位于AB杆的中点,DE杆水平。
习题课II北航理论力学王琪

A: 速度的模增加;
2009-11-18
B: 速度的模减小
10
理论力学
讲解过
A
演示过
o
过
θ
u
x
2009-11-18
11
理论力学
试题:已知图示瞬时圆盘中心O的速度和加速度,求此瞬时 AB 杆的角速度和角加速度。
动点:圆盘中心O A 动系:AB杆 速度分析
aa
vr a n e o ve t a e v B Ra a
2009-11-18 2
理论力学
•元功(elementary work):
虚位移原理
δW = F • vd t = F • d r
等效力系作功定理: 若作用于刚体上的力系等效 即:{F1 , F2 , L , Fn } = { P1 , L , Pm } = {FR , M O } 则
n m
∑W (F ) = ∑W ( P ) = W (F ) + W ( M
• 点的复合运动
– 绝对运动、相对运动、牵连运动 – 绝对速度、相对速度、牵连速度 – 绝对加速度、相对加速度、牵连加速度、科氏加速度
• 基本定理与方程
– 速度合成定理、加速度合成定理 – 质点动力学方程(惯性参考系和非惯性参考系)
2009-11-18 6
理论力学
基本公式
&⎫ vx = x ⎪ &⎬ vy = y ⎪ &⎭ vz = z
反映速度方向的变化
mar = ∑ F + Fe + FC
7
理论力学
• •
解决问题的方法与基本步骤
受力分析-根据约束条件和已知量,,确定力的方向、分析哪些是未知量 运动分析-利用几何性质和约束条件,建立运动学(包括几何、速度和 加速度)关系,确定系统的自由度和未知量数目。
理论力学高等教育出版社谢传峰王琪第十一章课件

[注]①减小绳子拉力途径:减小跑车速度或者增加绳子长度。 ②拉力Tmax由两部分组成, 一部分等于物体重量,称为静拉力 一部分由加速度引起,称为附加动拉力。全部拉力称为动拉力。
10
2.第二类:已知作用在质点上的力,求质点的运动(积分问题) 已知的作用力可能是常力, 也可能是变力。变力可能是时间、 位置、速度或者同时是上述几种变量的函数。 解题步骤如下: ①正确选择研究对象。 ②正确进行受力分析,画出受力图。判断力是什么性质的力 (应放在一般位置上进行分析,对变力建立力的表达式)。 ③正确进行运动分析。 (除应分析质点的运动特征外,还要确定 出其运动初始条件)。
1.第一类:已知质点的运动,求作用在质点上的力(微分问题)
解题步骤和要点:
①正确选择研究对象(一般选择联系已知量和待求量的质点)。
②正确进行受力分析,画出受力图(应在一般位置上进行分析)。
③正确进行运动分析(分析质点运动的特征量)。
④选择并列出适当形式的质点运动微分方程(建立坐标系)。 ⑤求解未知量。
11
④选择并列出适当的质点运动微分方程。
⑤求解未知量。应根据力的函数形式决定如何积分,并利用运
动的初始条件,求出质点的运动。 如力是常量或是时间及速度函数时, dv 可直接分离变量 dt 积分 。 如力是位置的函数,需进行变量置换
dv dv v , 再分离变量积分。 dt ds
12
[例2] 煤矿用填充机进行填充, 为保证充 填材料抛到距离为S=5米,H=1.5米的顶 板A处。求 (1)充填材料需有多大的初速 度v0 ? (2)初速 v0 与水平的夹角a0? 解:属于已知力为常量的第二类问题。 选择填充材料M为研究对象,受力如图所示,M作斜抛运动。
北京航空航天大学理论力学课件-王琪-ch1B

非自由体实例
非自由体的运动受到了限制
2015-9-16 5
理论力学
一、约束与约束力
•约
§1-3 平衡问题的解法
束(constraint):限制物体运动的条件。
•约束体(constraint body):约束非自由体运动的物体。 • 列车是非自由体 ? ? • 铁轨是约束体 • 铁轨作用在车轮 上的力为约束力
北京南站顶棚拱架支座
2015-9-16
13
理论力学
2、连接铰链
§1-3 平衡问题的解法
B A FBy C
FBx
B
' FBy
C
注意:作用力与反作用力的关系
A
B
' FBx
思考题:试画出作用在AB杆B端的约束力(不计销钉质量)
2015-9-16 14
理论力学
§1-3 平衡问题的解法
2015-9-16
15
理论力学
作业要求:
作业:1-3、1-4、1-8
画出研究对象的受力图、速度图和加速度图 一个研究对象画一个受力图 计算题要画相应的图,列写方程,给出计算结果 作业不符合要求的,无作业成绩
每周一 交 前一周的作业
平时成绩占总成绩的20%左右 作业由课代表收齐后,作业放到讲台上的资料袋内
2015-9-16 1
• 基本方法
– 共点力系的合成及其平衡条件(矢量法、解析法) – 受力分析:根据约束的类型和特点画受力图
2015-9-16 27
3、Α.Π.马尔契夫著,李俊峰(清华大学)译《理论力学》高 教育出版社
俄罗斯高校教材(理论深入,内容丰富;是一本很好的力学专业的 教材,例题较少,无习题)
2015-9-16 2
北航《理论力学(第二学期)》考题整理

,
aC
=
;
8、质量为 m,边长为 L 的正方形均质板静止放在光滑的水平
A
B
地面上。若在板上作用一水平冲量 I,使板获得最大的动能, 该冲量将如何作用在板上,则板获得的最大动能
5
D
图 10
C
北京航空航天大学交通科学与工程学院《理论力学(第二学期) 》复习资料
T=
。
2 (将冲量 I 的作用点和作用线画在图上,已知板对质心的转动惯量为 mL )
3
系中的运动微分方程为:
。
mg cx ; A: mx
3
B: mx
D: mx
3 ; mg cx
3 ; mg cx
M mg
x
mg cx ; C: mx
3
E: A、B、C、D 中没有给出正确答案。
图1
o
2、圆盘 A 放在光滑的水平地面上运动,杆 AB 通过圆柱铰链与圆盘中心 A 连 接,系统在图示铅垂面内运动,如图 2 所示。若圆盘和杆为非匀质刚体,则 有: A:系统的机械能守恒; B:系统的动量在水平方向的投影守恒; C:圆盘对铰链 A 的动量矩守恒; D:AB 杆对铰链 A 的动量矩守恒。
O
A
图 11
B
10、质量为 m0 的物块放在水平面上,其上有一半径为 R 的半圆槽,质量为 m 的小 球 B 可在槽内运动,忽略所有摩擦,如图 12 所示。 (1)若取 , 作为系统的广义坐标,用广义速度和广义坐标给出系统在任意位 置时动能和势能的表达式(取坐标原点为势能零点,即 x0 (2)若初始时,小球在 A 处,系统从无初速 开始运动。给出系统拉格朗日方程的首次 积分。 系统的动能 T= 系统的势能 V= 广义动量积分: 广义能量积分:
北航-951力学基础

951力学基础考试大纲(2010版)注意:理论力学部分占40%,材料力学部分占60%理论力学部分基本内容和要求静力学1、几何静力学(第1-3章)●基本内容:静力学的基本公理,受力分析,力系简化的基本方法和有关力学量的基本计算,平衡方程的建立与求解,摩擦(滑动摩擦和滚动摩擦)问题,桁架内力的计算,平衡结构的静定性问题。
●基本要求:深入理解静力学中有关的公理,熟练掌握刚体(刚体系)的受力分析,力系简化的基本方法和有关基本概念和基本量的计算,能够确定给定力系作用下独立平衡方程的数目,能够用定性和定量的方法研究刚体(刚体系)的平衡问题。
能够分析研究考虑摩擦时刚体或刚体系的平衡问题以及平面桁架的内力计算问题。
2、分析静力学(第4章)●基本内容:各种力(重力、弹性力、有势力、摩擦力、合力、等效力系)的功,约束及其分类、广义坐标和自由度、虚位移与虚功、理想约束、虚位移原理及其应用、有势力作用下质点系平衡位置的稳定性。
●基本要求:熟练计算各种力的功,能够确定系统的约束类型,确定系统的自由度和广义坐标,理解虚位移的基本概念,会判断约束是否是理想约束;能够熟练应用虚位移原理求解质点系平衡问题;会判断有势力作用下质点系平衡位置的稳定性。
动力学1、质点动力学(第一章)●基本内容:质点的运动方程、速度、加速度的各种表示方法(矢量法、直角坐标法、自然坐标法)以及有关基本量的计算,质点运动微分方程,点的复合运动(三种运动分析、速度合成定理和加速度合成定理),质点相对运动动力学基本方程。
●基本要求:熟练掌握质点运动方程、速度和加速度的各种表示方法和有关基本量的计算,能够熟练建立质点运动微分方程,对于简单的运动微分方程能够求解。
熟练应用点的复合运动的基本理论与方法研究点的复合运动(速度和加速度)问题,能够在非惯性参考系下建立质点相对运动动力学基本方程,具有对质点的运动学和动力学问题进行定性和定量分析的初步能力。
2、质点系动力学(第二章)●基本内容:质点系的动量定理、变质量质点动力学方程、动量矩定理(包括对固定点、动点和质心的动量矩定理)、动能定理及其有关基本量的计算。
理论力学课后答案-谢传峰、王琪-动力学部分
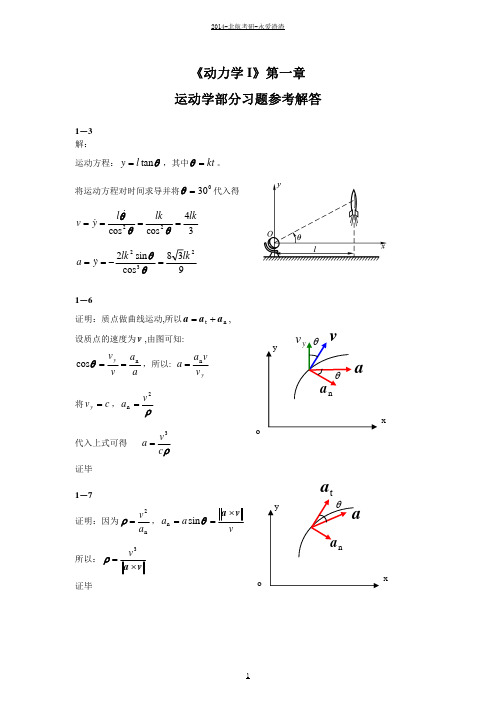
n a
根据矢量形式的质点运动微分方程有:
m(aat aan ) F FO mg
将该式分别在 x 轴上投影:
m(aat sin aan cos ) FO cos
ve
va
r
M vr
O
r aan
ar
aat
M
根据速度合成定理有 由此可求出: va
va ve v r
ve v 。再根据加速度合成定理有: aa ae ar cos cos
由于绝对运动是圆周运动,牵连运动是匀速直线平移,所以 ae 0 ,并且上式可写成:
aat aan ar
由于动点 M 的绝对速度与动系的选取无关,即 va2 va1 ,由上两式可得:
ve1 v r1 ve2 vr2
(a)
4
2014-北航考研-永爱渣渣
将(a)式在向在 x 轴投影,可得:
ve1 sin 300 ve2 sin 300 vr2 cos 300
由此解得:
vr2 tan 300 (ve2 ve1 ) OM tan 300 ( 2 1 )
vB v A cos
因为
(a)
cos
x2 R2 x
(b)
将上式代入(a)式得到 A 点速度的大小为:
v A R
2
x x R2
2
2
(c)
, x R Rx ,将该式两边平方可得: 由于 v A x (c)式可写成: x
2 (x2 R2 ) 2 R2 x2 x
3理论力学__课后答案_(范钦珊_刘燕_王琪_著)_清华大学出版社
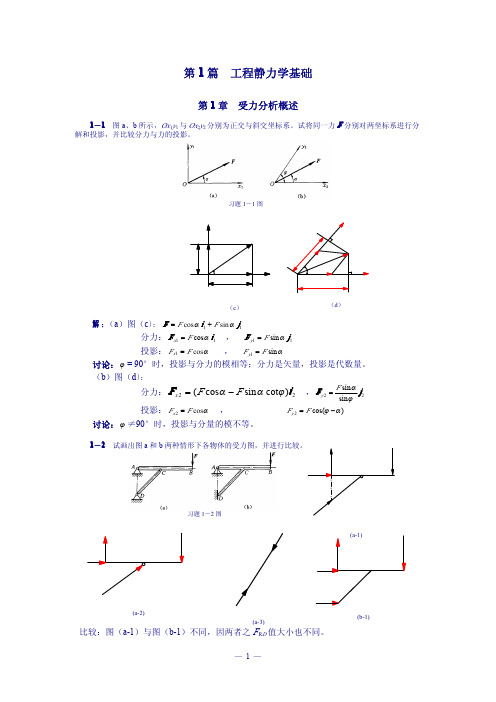
解:杆 3 为二力杆 图(a) : ΣMi = 0
F3 ⋅ d − M = 0
F3 =
M d
F = F3(压) 图(b): ΣFx = 0 F2 = 0 ΣFy = 0
F1 = F = M (拉) d
(a)
习题 3-10 图
F1
(b)
3–11 图示空间构架由三根不计自重的有杆组成,在 D 端用球铰链连接,A、B 和 C 端则用球铰链固 定在水平地板上,若拴在 D 端的重物 P = 10 kN,试求铰链 A、B、C 的反力。
A FR D FBy
FR E
′ FBx
F2 B
′ FBy
D
B FBx
E C FR E
FCy
FCx
1-7f
D A E F
FR D
F Ay FEy
D
′ FCy
A
G
′ FEx
FAx
C
G
C
FCy
FCx
FBy
FEx
′ FCx
C
E
F
′ FBx
E
′ FEy
B
B
FBx
B
′ FBy
1-7g
FAy D E C H FBy
F ED
习题 3-2 图 (a)
A
(b)
A
解: ∑ Fy = 0 , FED sin α = F
∑ Fx = 0 , FED cos α = FDB
F FED = sin α F FDB = = 10 F tan α
F2
45
�
由图(a)计算结果,可推出图(b)中:FAB = 10FDB = 100F = 80 kN。
北京航空航天大学理论力学课件-王琪-习题课I15

B
A
M1 > M 2
2015-10-12 10
BUAA
题14:确定各杆端点约束力的方向 (不计构件自重和所有摩擦)
A
M
M
O
B
2015-10-12
11
BUAA
题15:确定铰链 A、B 处 约束力的方向,不计构件 自重和所有摩擦。
先研究AD杆 再研究整体
A
D
F
B
L L L
2015-10-12
C
12
BUAA
0
AC tan(450 − ϕ m ) = BC tan(450 + ϕ m )
1− tanϕm 1+ tanϕm AC = BC 1+ tanϕm 1− tanϕm
2015-10-12
1− tanϕm BC =± 1+ tanϕm AC
0 < ϕm < 450
tan ϕm1 ≈ 0.224
22
三力汇交有:
O
(AB、BCD、DE)构成的系统相对 OC轴具有几何对称性,且刚体BCD上 作用有一力偶M,不计构件自重。
B
O M
D
B
O M
D
C A
2015-10-12
C E A 瞬态机构不能平衡 G 静定结构 E
28
G
题26: 试确定下图结构中铰链A、B约束力的方向。 注:该结构是25题图1所示系统中增加了一个T字形刚体而构成
BUAA
题22:作业习题分析:已知P,M,D,求平衡时的摩擦系数 方法一 M P
FN 1 FS 1 FN 2
平衡条件
FS 2
无滑动临界条件
∑ ∑ ∑
理论力学习题答案 谢传峰、王琪 高等教育出版社
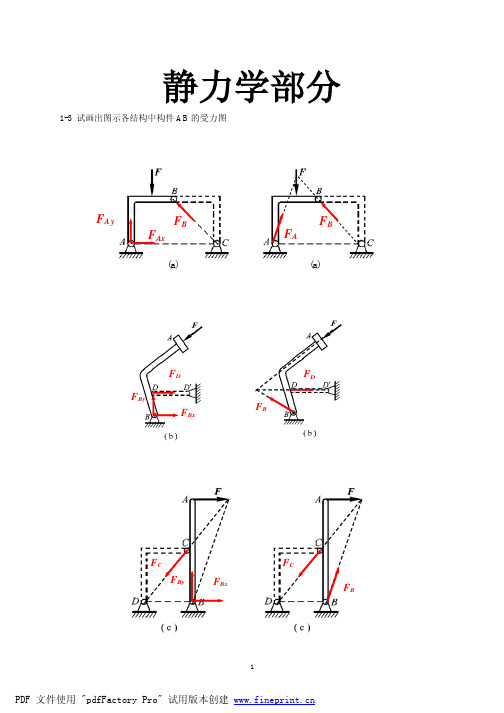
M A = P (1 + cosα )l (逆时针方向)
法2 FA y 解: 设滑轮半径为 R。选择梁和滑轮为研究对象,受力如图,列平衡方程:
FAx
∑Fx = 0
∑Fy = 0 ∑M = 0
A
FAx + P sin α = 0 FAy − P − P cos α = 0 M A − P (l − R) − P cos α (l − R) − P sin α
fs 。
∑ Fx = 0 ∑ Fy = 0 M =0 ∑ O
补充方程:
0 F1 + p cos 45 − N 2 = 0 0 F2 − p sin 45 + N 1 = 0 D ( F1 + F2 ) ⋅ − M = 0 2
F1 = f s N1 F2 = f s N 2
解: 当 α = 45 时,取杆 AB 为研究对象,受力如图所示。 列平衡方程:
0
∑ Fx = 0 ∑ Fy = 0 M =0 ∑ A
方向如左图所示。由于 FR ⊥ M A ,可进一步简化为一个不过 A 点的力(绿色的),主矢不变,其作 用线距 A 点的距离 d = 2-6b 同理如右图所示,可将该力系简化为一个不过 A 点的力(绿色的) ,主矢为: FR = −2 Fi 其作用线距 A 点的距离 d =
3 a ,位置如左图所示。 4
3
FB PDF 文件使用 "pdfFactory Pro" 试用版本创建
杆 AB 受到主动力偶 M 的作用,A 点和 B 点处的约束力必须构成一个力偶才能使曲杆 AB 保持平衡。 AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正) :
北京航空航天大学4系推荐课表
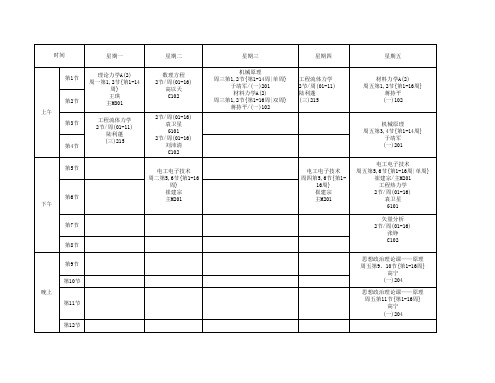
第5节
第6节 下午
电工电子技术 周四第5,6节{第116周} 崔建宗 主M201
第7节 第8节 第9节 第10节 晚上 第11节
第12节
数学建模 周六第2节{第1-16 周} 数学建模 周六第3,4节{第1-16 周} 刘来福 主219
第4节
机械原理 周五第3,4节{第1-14周} 于靖军 (一)201 电工电子技术 周五第5,6节{第1-16周|单周} 崔建宗/主M201 工程热力学 2节/周(01-16) 袁卫星 G101 矢量分析 2节/周(01-16) 张铮 C102 思想政治理论课——原理 周五第9、10节{第1-16周} 高宁 (一)204 思想政治理论课——原理 周五第11节{第1-16周} 高宁 (一)204
星期三 机械原理 周三第1,2节{第1-14周|单周} 于靖军/(一)201 材料力学A(2) 周三第1,2节{第1-16周|双周} 蒋持平/(一)102
星期四
星期五
星期六Leabharlann 第1节第2节 上午 第3节
工程流体力学 2节/周(01-11) 陆利蓬 (三)215
材料力学A(2) 周五第1,2节{第1-16周} 蒋持平 (一)102
时间
星期一 理论力学A(2) 周一第1,2节{第1-14 周} 王琪 主M301 工程流体力学 2节/周(01-11) 陆利蓬 (三)215
星期二 数理方程 2节/周(01-16) 高以天 C102 工程热力学 2节/周(01-16) 袁卫星 G101 2节/周(01-16) 刘沛清 C102 电工电子技术 周二第5,6节{第1-16 周} 崔建宗 主M201
北京航空航天大学理论力学第一学期总复习.ppt

M
vM
CV
13
BUAA
4、平面图形上各点的加速度
aB
aA
aBnA
a
t BA
aBt A AB aBnA AB 2
y
y' aBt A
B
A
aBnA x'
o
aA x
•加速度瞬心:在某瞬时,平面图形上加速度为零的点。 当平面图形的角速度与角加速度不同时为零时,必存
处的静/动摩擦因数均为f。现欲以水平力F 拉动此物体。若F
较小未拉动物体时,根据已知条件 b 能分别求出A,B
两处的静摩擦力。若物体被拉动,则在其运动过程中A,B 两
处的摩擦力 b
相等。
FA
FI
FB
a:一定;
2019/11/16
b:一定不; c:不一定
26
BUAA
基本概念:惯性积、惯量主轴、
中心惯量主轴、动平衡、静平衡
在唯一的一点,在该瞬时其加速度为零。
要求:能熟练求解刚体平面运动和点的复合运动的综合 性问题。
2019/11/16
14
BUAA
思考题:半径为 R 的圆盘做平面运动,已知某瞬时圆盘边缘 上两点A、B的加速度a (大小、方向如图所示),试判 断下列结论哪些是正确的:
A:这种运动不存在; B:能求出圆盘的角速度(大小和方向) C:能求出圆盘上任一点的加速度; D:能求出圆盘的角加速度(大小和方向)
dp
dt
Fi(e) maC
miaCi
Fi ( e )
m dvC dt
Fi ( e )
dm dt
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
I 20
ar a N aR r ( r rAB ) r rAB 2 2 r 0 vr a r 4 r 20 N r 0r 0 .5 r 0 .5 r 2 vr 2 a r 4 R r 0r r r 40 0 .5 r 2 2 aa ( ae a R a K ) 2 a N 2 50 r
理论力学
习题课
第六章动力学(II)
2014-1-15 1
理论力学
刚体一般运动习题
例题:已知细杆AB的A端沿z轴运动,B端沿x’轴运动,图示
瞬时A点的速度为vA,求B端的速度和AB连线的角速度。 z A vA O x L B L
vB v B v A rAB
rAB L(i j k )
3 3 vB i ( i j k ) v A k ( i j k ) 3 3
vB
x’
v B v A rAB
2014-1-15
vB v A
3
理论力学
刚体一般运动习题
思考题:若A点沿z 轴运动,B点在Oxy平面内运动。 已知 v A u, ,求图示瞬时B点的速度。 z A vA
理论力学
vr ro
刚体一般运动习题
I
习题6-7:已知 vr 和 ω O ,求该瞬时B 点的绝对加速度。
ωa 解:取ABC圆锥为研究对象
rOA
r 运动分析:
ABC圆锥作刚体一般运动
aB a A ωa (ωa rAB ) αa rAB a A o (o rOA )
a1
2 a1 4r0
aB a A ωa (ωa rAB ) αa rAB
a 0
a B a A a (a rAB ) a A o (o rOA )
2 2 a A rOA0 2r0
a2
2 a2 4r0
2 2 aB (a1 a A ) 2 a2 2 50 r
2014-1-15 9
24-1-15
8
理论力学
vr ro
刚体定点运动与点的复合运动的应用
aR aK
解:取B点为动点,圆盘I为动系
rOA
ae
I a N
r
aa ae a K a r
2 ae 0 (0 rOA ) ae 2r0
aK 2e v Br
e I
vBr 2vr
vB II rOB sin 60 0 r rOB sin 60 0 (II r )rOB sin 60 0 L 0 ( II r ) sin 60 cos 30 0
6
va ve v r
ve II rOB vr r rOB
2014-1-15
I 20
a 0
7
理论力学
a1
rOA
刚体一般运动习题
I a 2
aA
vr r0
r e 20
r
a e r
a ( a rAB ) ( e r ) [( e r ) rAB ]
(e r ) [ r rAB ] e [ r rAB ] r [ r rAB ]
习题6-6:已知 vr 和 ω II ,求该瞬时B 点的绝对速度,OA=L
rOB
a e r II r
v Ar r rOA v B a rOB
vr L sin 30 0 ( II r ) rOB
II
r
r
方法二:
II rOB r rOB
a e r I r
r 0 vr r 20 0 .5 r 0 .5 r
2014-1-15
a a e r e r
vr r i 402 i e 0 0.5r 2 ωe ωr er i 40 i r ω
va ve v r
在动系上看杆AB作平面运动
O
x
vr
L ve C
vr
B
vA u AC 2L u vr L 2
ve 2L
vBa 0.5u 2 (2 L2 2 )
5
2014-1-15
理论力学
刚体定点运动习题
方法一: v B a rOB
已知量: rAB
j k 2 2 vBx i vBy j uk 2 2 L L L
4
用方程(1)有: i
理论力学
z A vA L y B L
A va
刚体一般运动习题
方法二:应用点的复合运动求解 动点:杆上的B点, 动系:透明版
2014-1-15
x’
2 2 i j k 解: 2 2 j i 2 2 v B i v A k y 2 2 L L L 2 i : vB L L 2 2 j: 0 L L 2 2 L 2L k : 0 v A 2 2
O x L
u vBy L 2 u u vBx L , 2 2L 2014-1-15
方法一: 应用刚体一般运动速度基点法 v B v A rAB (1)
L y
B L
i 2 j k 2 2 2
L(i j k ), v A , 未知量: v B vBx i vBy j ,
k L
vB v A 2 vA 2L v A 2L
2
理论力学
刚体一般运动习题
思考题:若上题中只求B端的速度,用什么方法最简单?
z A vA O x L B L L
解: 应用速度投影定理
l AB
y
3 (i j k ) 3
v B l AB v A l AB v B vB i , v A v A ( k )
