解线性方程组的矩阵三角分解法 共16页PPT资料
合集下载
数值分析课程课件 直接三角分解方法
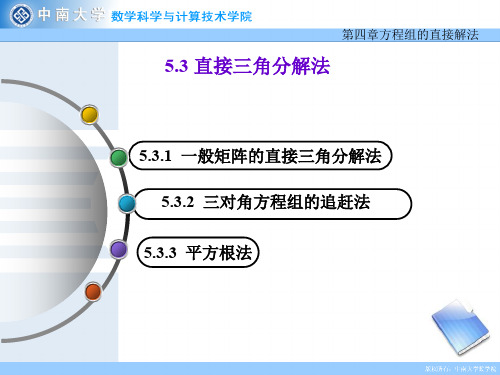
u22
u11
u2n
l n1 l n2
1
unn
即
a11 a12 a 21 a22
a1n
a2n
u11 l21u11
u12 l21u12 u22
u1n
l21u1n
u2n
a n1 a n2
ann
ln1u 11
由（5.3.1）- （5.3.4）求得L和U后，解方程组Ax=b 化为求解LUx=b，若记Ux=y，则有Ly=b。于是可分两部解 方程组LUx=b，只要逐次向前代入的方法即可求得y。第
二步求解Ux=y，只要逐次用向后回代的方法即可求得x。 设 x=（x1 ，x2， ···xn) T, y=（y1, y2, ···yn) T,
n
i1
lniuin
unn
第四章方程组的直接解法
由A的第1行和第1列可计算出U的第1行和L的第1列，即
u1 j a1 j , j 1, 2, , n,
（5.3.1）
lk1
ak1 u11
,k
2, 3,
, n.
（5.3.2）
如果U的第1至k-1列和L的第1至k-1列已经算出，则由
解 设 A=LU，即
l11 a11 1, l21 a21 2, l31 a31 0
u12
a12 l11
2, u13
a13 l11
1,
l22 a22 l21u12 3, l32 a32 l31u12 1
3.2矩阵三角分解,平方根
2014-12-29
北京信息科技大学
4
2 3 1 0 2 3 1 0 2 3 例如A= 4 1 2 1 0 5 2 3 0 5 / 3
这里有A的两种不同的三角分解，类似可举出很多，一般， 若A=LU是一个三角分解，任取与A同阶的非奇异对角矩阵D， 则
xn yn / unn xi ( yi i n 1,
k i 1
u
n
ik
xk ) / uii
, 2,1
2014-12-29
北京信息科技大学
23
例 用杜利特尔分解法求解方程组
2 x1 2 x2 3 x3 3 4 x1 7 x2 7 x3 1 2 x 4 x 5 x 7 1 2 3
， 则矩 , n 1 ）
U 为上三角阵。 其中 L 为单位下三角阵，
其中
A LU
1 l21 1 L l31 l32 l n1 ln 2
1 ln ,n 1
u11 u12 u22 ，U 1
u1n u2 n unn
矩阵三角分解法
矩阵直接三角分解法是高斯消去法的变形方法。 高斯消去法 有多种变形，有的是高斯消去法的改进，有的是用于某种特殊系 数矩阵的化简。 分解原理 1．概述 高斯消去法解线性方程组先消元，然后再回代。当用矩阵描 述时，是对系数矩阵分解为一个上三角阵和一个下三角阵的乘 积，即 LU 分解。因此，高斯消去法与矩阵的 LU 分解是一致的。
2014-12-29 北京信息科技大学 15
紧凑格式
2 2 3 A 4 7 7 5 2 4 (2) 2 (4) 2 (-2) -1 (2) 2 (7) 3 (4) 2 (3) 3 (7) 1 (5) 6
用直接三角分解法解线性方程组
三角阵。等式左边是单位下三角阵，右边是上三角阵，要使等式
成则立L ， L只1 ,能U等于U单1，位即矩此阵三I。角于分是解L唯1一L1。
UU
1 1
I,
1 2 1
1 2 1
例7 解：
设 A 3 7
1
，试将A进行三角分解。
1 1 3
由高斯消去法得到
m21
3 1
3，m31
1 1
1
m 32
L1
1 1
0 0 1 2
例：
求
0 1 2
0 1 0
3 0 1
103的PLU分 解 。
解：用1，2， ，n的排列表示n阶置换阵P，其中排列的第i个元素
j，表示P的i行非零元素位于j列。则分解过程如下：
1 0 0 1 2
3 1 1 0 1
3 1 1 0
2 0
43
1 2
0 1 0
3 0 1
0 1 3
Ux j y j
Ly
j
bj
n1
k
n(n 1)
n2
n 次乘法
k 1
2
22
Ux j y j n k n(n 1) n2 n 次乘除法
k 1
2
22
即共需n 2 次乘除法运算。
n 2 次 乘 除 法
三角分解法的存放元素的方法：
以A (a ij )33 为例，
a11 A a21
1 mk1,k 1
k，
Lk1
1 mk1,k 1
k
mnk
1
mn,k
1
A ( L11 L21
L1 n1
)U
LU，1
a (1) 11
线性代数方程组的解法
2 3 2 n O( n ) 3
mult a(i , j ) a( j, j ); for k j 1 : n a(i , k ) a(i , k ) mult * a( j , k ); end b(i ) b(i ) mult * b( j ); end
end
LU分解
求A的LU分解（L是下三角矩阵，U是上三角矩阵）
1 1 1 1 3 4 3 4
LU分解
性质1 设向量
, xn ) 且 xk 0 T 则存在唯一的下三角阵 Lk I lk ek ,满足 x ( x1 , x2 ,
T
Lk x ( x1 ,
第三章 线性方程组的直接解法
/*Direct Method for Solving Linear Systems*/
求解 A x b, A R
Cramer法则:
nn
det( A) 0
Di xi D
i 1, 2,
,n
所需乘除法的运算量大约为(n+1)!+n
n=20时，每秒1亿次运算速度的计算机要算30多万年！
Gauss消去法的消元过程算法
for for
j 1: n 1
i j 1: n
2 3 2 n O( n ) 3
mult a(i , j ) a( j, j ); for k j 1 : n a(i , k ) a(i , k ) mult * a( j , k ); end b(i ) b(i ) mult * b( j ); end
方程组可化为下面两个易求解的三角方程组
Ly b Ux y
二、 高斯消去法
5.3 矩阵的三角分解法
8
解： (1)分解A LU，令 2 5 6 1 4 13 19 l 21 6 3 6 l31 0 1 l32 0 u11 0 1 u12 u22 u13 u23 u33
24
由A L( DLT ) 1 l 21 l31 ... l n1 1 l32 ... ln 2 1 ... ... lnn 1 1 d1 ... d1l21 d2 ... d1l31 d 2 l32 d3 ... ... ... ... d1 l n1 d 2 ln2 d 3 ln 3 dn
25
由 i j时aij = l ik d k l jk l ij d j , 知
k =1
j -1
L, D元素计算公式
lij =
aij lik d k l jk
k =1
j -1
dj
j -1
( j 1, 2, ,i 1)
2 d i =aii l ik d k ( i 1, 2, , n) k =1
y1 b1 i -1 y y b l i ij i j j 1
i 2, 3, , n
( i n 1, , 1)
7
或 用 Doolittle 分解法
例:用矩阵的直接三角分解法解方程组
5 6 x1 10 2 4 13 19 x 19 2 6 3 6 30 x3
27
d1 a11
改进平方根法解方程组
1. 分解计算A=LDLT ,
d1 a11 对于i 2, 3, ..., n j 1 c a cik l jk ij ij k 1 cij ( j 1, 2, ..., i 1) lij dj i 1 d i aii cik l ik k 1
解线性方程组的三角分解法
⎛1 0 ⎛1 3 2 1 ⎞ ⎜3 1 ⎜ ⎟ ⎜ 3 13 12 9 ⎜ ⎟ = ⎜2 3 ⎜ 2 12 29 15 ⎟ ⎜ 2 ⎜ ⎟ ⎜ 1 9 15 34 3 ⎝ ⎠ ⎜1 ⎜ 2 ⎝ ⎛1 ⎜ ⎜3 =⎜ ⎜2 ⎜ ⎜ ⎜1 ⎝ 0 1 3 2 3 2 0⎞ ⎟ 0⎟⎛1 ⎜ ⎟⎜0 1 0⎟⎜ 0 ⎟⎜ 1 ⎟ 0 1⎟⎝ 4 ⎠ 0 0
⎛1⎞ 0 0 0 ⎞ ⎛ y1 ⎞ ⎛ 1 ⎞ ⎛ y1 ⎞ ⎜ 5 ⎟ ⎜ ⎟ ⎜ ⎟ ⎟⎜ ⎟ ⎜ ⎟ y 4 0 0 ⎟ ⎜ y2 ⎟ ⎜ 10 ⎟ 2 ⎟。 = ，得到 ⎜ 2 ⎟ = ⎜ ⎜ ⎜ ⎟ ⎜ ⎟ ⎟ ⎜ ⎟ y3 0 16 0 y3 24 3⎟ ⎜ ⎟ ⎜ ⎟ ⎟⎜ ⎟ ⎜ ⎟ 0 0 25 ⎠ ⎝ y4 ⎠ ⎝ 50 ⎠ ⎝ y4 ⎠ ⎜ 2 ⎟ ⎜2⎟ ⎝ ⎠
⎛ 1 0 0 0⎞ ⎜ ⎟ 6 ⎞ ⎜ 2 1 0 0⎟⎛3 ⎟ห้องสมุดไป่ตู้⎟⎜0 6 ⎟ ⎜3 ⎜ ⎟⎜ = 1 8⎟ ⎜ 0 1 0⎟⎜0 ⎟ ⎜3 ⎟⎜ 12 ⎠ ⎜ ⎟⎝0 4 1 0 1 ⎜ ⎟ ⎝3 ⎠
6 3 6⎞ ⎟ 1 0 2⎟ 0 2 6⎟ ⎟ 0 0 2⎠
解方程组
⎛ 1 0 0 0⎞ ⎜ ⎟ ⎜ 2 1 0 0 ⎟ ⎛ y1 ⎞ ⎛ 9 ⎞ ⎜3 ⎟⎜ y ⎟ ⎜ 7 ⎟ ⎜1 ⎟⎜ 2 ⎟ = ⎜ ⎟ 0 1 0 ⎟ ⎜ y3 ⎟ ⎜ 1 ⎟ ⎜ ⎜3 ⎟⎜ ⎟ ⎜ ⎟ ⎜4 ⎟ ⎝ y4 ⎠ ⎝13 ⎠ 1 0 1⎟ ⎜ ⎝3 ⎠
⎛3 ⎜ ⎜2 ⎜1 ⎜ ⎝4
6 3 5 2 2 3
6 6 8
1 0 0 0 1 0 0 0 1
9 4 12 0 0 0
2 3 1 0 2 6 − 3 4 1 0 4 − 3 1 0 2 −
三角分解法解线性方程组
三角分解法解线性方程组线性方程组是数学中一类重要的方程组，它包含了一系列线性方程。
在实际问题中，线性方程组有时需要通过三角分解法进行求解。
三角分解法是一种常用的线性方程组求解方法，它通过将方程组转化为上、下三角形矩阵进行分解，从而求解出未知数的值。
本文将详细介绍三角分解法的步骤及实际案例。
首先，我们来介绍三角矩阵的概念。
上三角矩阵是指除了主对角线上方的元素均为0的矩阵，下三角矩阵则是指除了主对角线下方的元素均为0的矩阵。
我们的目标是将线性方程组转化为上、下三角形矩阵进行求解。
步骤1：将线性方程组表示为矩阵形式，即AX=B，其中A为系数矩阵，X为未知数向量，B为常数向量。
步骤2：进行三角分解，将系数矩阵A分解为一个上三角矩阵U和一个下三角矩阵L，即A=LU。
其中L为下三角矩阵，U为上三角矩阵。
步骤3：将方程组AX=B进行变量代换，令Y=UX。
此时，方程组变为LY=B。
步骤4：解得矩阵Y，再通过回代法求解出未知数向量X。
下面我们通过一个实际案例来详细说明三角分解法的应用。
案例：有三个变量x,y,z的线性方程组：2x+y+z=4x+3y+2z=133x+2y+3z=15首先将该方程组表示为矩阵形式：⎛211⎛⎛x⎛⎛4⎛⎛132⎛⎛y⎛=⎛13⎛⎛323⎛⎛z⎛⎛15⎛然后进行三角分解，将系数矩阵A分解为上三角矩阵U和下三角矩阵L：A=⎛211⎛=⎛100⎛⎛211⎛⎛132⎛⎛110⎛⎛021⎛⎛323⎛⎛321⎛⎛001⎛接下来，将方程组AX=B进行变量代换，令Y=UX，即LY=B：⎛100⎛⎛Y₁⎞⎛4⎛⎛110⎛⎛Y₂⎟=⎛13⎛⎛021⎛⎛Y₃⎠⎝15⎛我们可以通过高斯消元法求解上述方程组，得到Y的解：Y₁=4Y₂=9Y₃=-2最后，通过回代法求解未知数向量X：X₃=Y₃=-2X₂=Y₂-2X₃=9-2(-2)=13X₁=Y₁-X₂=4-13=-9因此，该线性方程组的解为：x=-9，y=13，z=-2三角分解法是一种常用且有效的线性方程组求解方法。
三角分解解线性方程组的公式47页
1
8/30/2019
6
平方根法（Cholesky分解）
续1
AT ALT D R T D R T L T R T ( D T ) L ( D ) R
由Doolittle分解的唯一性有
R T L DLT DR
（D可逆）
L R
9
平方根法（Cholesky分解）
k1
aikk1lim lk m
l11 l21 ln1
l22
ln1
lnn
lnn
第一步 ： a11l121l11 a11
ai1 l11li1li1 ai1/l11
i2,3 n
设L前k-1列元素已求出，则 第k步
n
k1
ak k lk m lk m lk2mlk2k
续2
L LD
这时 L 为一般的下三角矩阵，故 ALLT，若 L 的对角 元全为正时，由Doolittle分解的唯一性及上述分解 的推理过程，可以得到Cholesky分解的唯一性。
8/30/2019
8
平方根法（Cholesky分解）： 分解公式
l11
Al21 l22
8/30/2019
5
平方根法（Cholesky分解） 定理证明
证明：因为 A对称正定，故其顺序主式 k0 k 1 ,2 , n，
1
u11 u1n
Al21
ln1 1
m1
m1
k1
lkk akk lk2m m1
i k n
a ik lim l km m 1
8/30/2019
6
平方根法（Cholesky分解）
续1
AT ALT D R T D R T L T R T ( D T ) L ( D ) R
由Doolittle分解的唯一性有
R T L DLT DR
（D可逆）
L R
9
平方根法（Cholesky分解）
k1
aikk1lim lk m
l11 l21 ln1
l22
ln1
lnn
lnn
第一步 ： a11l121l11 a11
ai1 l11li1li1 ai1/l11
i2,3 n
设L前k-1列元素已求出，则 第k步
n
k1
ak k lk m lk m lk2mlk2k
续2
L LD
这时 L 为一般的下三角矩阵，故 ALLT，若 L 的对角 元全为正时，由Doolittle分解的唯一性及上述分解 的推理过程，可以得到Cholesky分解的唯一性。
8/30/2019
8
平方根法（Cholesky分解）： 分解公式
l11
Al21 l22
8/30/2019
5
平方根法（Cholesky分解） 定理证明
证明：因为 A对称正定，故其顺序主式 k0 k 1 ,2 , n，
1
u11 u1n
Al21
ln1 1
m1
m1
k1
lkk akk lk2m m1
i k n
a ik lim l km m 1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3
计算 LU 分解
利用矩阵乘法直接计算 LU 分解
1 l21 ln1
u11 u121 源自u22 ln,n1 1
u1n a11 a12 u2na21 a22
unn an1 an2
a1n a2n
ann
LU =A
比较等式两边的第一行得：u1j = a1j ( j = 1,…, n )U 的第一行
1 AL D L T l21 1
d1
d2
ln 1
ln,n1 1
1l21 1 dn
ln 1 ln2
1
计算公式
n
j1
aij likdkljk likdkljklijdjljj
k1
k1
aij likdkljk likdkljklijdjljj
n
j1
aij likljk likljkljjlij
k1
k1
a1n a2n
ann
9
Cholesky 分解算法
算法 ：(Cholesky 分解 )
for j = 1 to n
1
l jj
ajj
j1
l
2 jk
2
,
k1
j1
lij aij likljk ljj ,
8
计算 Cholesky 分解
Cholesky 分解的计算
直接比较等式两边的元素
l11 l21 ln1
l11 l21
l22
l22
ln,n1 lnn
计算公式
ln1 a11 a12 ln2a21 a22
lnn an1 an2
比较等式两边的第一列得：li1 ai1 u11 ( i = 2,…,Ln的) 第一列
比较等式两边的第二行得：u2j a2j l21u1j ( j =U2,…的,第n二) 行
比较等式两边的第二列得：li2ai2li1u 12 u 22 ( iL=的3,第…二, n列)
4
计算 LU 分解
j1
aikkm ka i x naik , Ip (k)ik
akj aik j , j = 1, 2, …, n
aik aik akk, i = k+1, …, n
k1
akj akj akiaij , j = k+1, …, n
i1
end
Matlab程序：上机练习 7
Cholesky 分解
第 k 步：此时 U 的前 k-1 行和 L 的前 k-1 列已经求出
比较等式两边的第 k 行得：
k 1
u k j a k jlk 1 u 1 j lk ,k 1 u k 1 ,j a k jlk iu ij
i 1
比较等式两边的第 k 列得：
( j = k, …, n )
i 1
lika ik li1 u 1 k li,k 1 u k 1 ,k u k k a ikliju jk u k k j 1
( i = k+1, …, n )
直到第 n 步，便可求出矩阵 L 和 U 的所有元素。
5
LU 分解算法
算法 ：(LU 分解 )
12
改进的 Cholesky 分解
算法 ：(改进的 Cholesky 分解 )
for j = 1 to n
j1
dj ajj
l
d 2
jk k
,
k1
j1
lij aij likdkljk dj ,
k1
end
i = j +1, …, n
优点：避免开方运算
n
j1
k1
end
i = j +1, …, n
n
j1
aij likljk likljkljjlij
k1
k1
10
平方根法
Ax b A 对称正定
算法 ：(解对称正定线性方程组的平方根法 )
计算 A 的 Cholesky 分解 解方程：Ly = b 和 LTx = y
i1
对称正定矩阵的三角分解－－Cholesky 分解
定理：设 A 是对称矩阵，若 A 的所有顺序主子式 都不为 0，则 A 可唯一分解为
A = LDLT
其中 L 为单位下三角阵，D 为对角矩阵
定理：（Cholesky分解）若 A 对称正定，则 A 可唯 一分解为
A = LLT
其中 L 为下三角实矩阵，且对角元素都大于 0
6
k -1
PLU 分解
ukj a kj lki uij i1
矩阵的 PLU 分解
k 1
lik aik liju jk ukk
j1
PALU
for k = 1 to n k-1
aik aik aijajk , i = k, k+1, …, n
y1b1 l11, yi bi likyk lii , i = 2, 3, …, n k1
xnynlnn, xi yin lkixk lii i = n-1, …, 2, 1
ki1
11
改进的 Cholesky 分解
改进的 Cholesky 分解
计算方法
第五章 解线性方程组的直接方法
—— 矩阵三角分解法
1
本讲内容
一般线性方程组 LU 分解与 PLU 分解
对称正定线性方程组 平方根法－－Cholesky 分解
对角占优三对角线性方程组 追赶法
2
LU 分解
矩阵的三角分解
将一个矩阵分解成结构简单的三角形矩阵的乘积
矩阵的 LU(Doolittle) 分解 ALU 矩阵的 LDR 分解 ALDR 克洛脱 (Crout) 分解 A LU
for k = 1 to n
k-1
a kj
ukj akj lkiuij ,
i1
乘除法运算量：(n3 - n)/3
j = k, …, n
a ik
k1
lik aik lijujk ukk , i = k+1, …, n
j1
end
Matlab程序参见：ex51.m
为了节省存储空间，通常用 A 的绝对下三角部分来存放 L (对角线元素无需存储)，用 A 的上三角部分来存放 U
计算 LU 分解
利用矩阵乘法直接计算 LU 分解
1 l21 ln1
u11 u121 源自u22 ln,n1 1
u1n a11 a12 u2na21 a22
unn an1 an2
a1n a2n
ann
LU =A
比较等式两边的第一行得：u1j = a1j ( j = 1,…, n )U 的第一行
1 AL D L T l21 1
d1
d2
ln 1
ln,n1 1
1l21 1 dn
ln 1 ln2
1
计算公式
n
j1
aij likdkljk likdkljklijdjljj
k1
k1
aij likdkljk likdkljklijdjljj
n
j1
aij likljk likljkljjlij
k1
k1
a1n a2n
ann
9
Cholesky 分解算法
算法 ：(Cholesky 分解 )
for j = 1 to n
1
l jj
ajj
j1
l
2 jk
2
,
k1
j1
lij aij likljk ljj ,
8
计算 Cholesky 分解
Cholesky 分解的计算
直接比较等式两边的元素
l11 l21 ln1
l11 l21
l22
l22
ln,n1 lnn
计算公式
ln1 a11 a12 ln2a21 a22
lnn an1 an2
比较等式两边的第一列得：li1 ai1 u11 ( i = 2,…,Ln的) 第一列
比较等式两边的第二行得：u2j a2j l21u1j ( j =U2,…的,第n二) 行
比较等式两边的第二列得：li2ai2li1u 12 u 22 ( iL=的3,第…二, n列)
4
计算 LU 分解
j1
aikkm ka i x naik , Ip (k)ik
akj aik j , j = 1, 2, …, n
aik aik akk, i = k+1, …, n
k1
akj akj akiaij , j = k+1, …, n
i1
end
Matlab程序：上机练习 7
Cholesky 分解
第 k 步：此时 U 的前 k-1 行和 L 的前 k-1 列已经求出
比较等式两边的第 k 行得：
k 1
u k j a k jlk 1 u 1 j lk ,k 1 u k 1 ,j a k jlk iu ij
i 1
比较等式两边的第 k 列得：
( j = k, …, n )
i 1
lika ik li1 u 1 k li,k 1 u k 1 ,k u k k a ikliju jk u k k j 1
( i = k+1, …, n )
直到第 n 步，便可求出矩阵 L 和 U 的所有元素。
5
LU 分解算法
算法 ：(LU 分解 )
12
改进的 Cholesky 分解
算法 ：(改进的 Cholesky 分解 )
for j = 1 to n
j1
dj ajj
l
d 2
jk k
,
k1
j1
lij aij likdkljk dj ,
k1
end
i = j +1, …, n
优点：避免开方运算
n
j1
k1
end
i = j +1, …, n
n
j1
aij likljk likljkljjlij
k1
k1
10
平方根法
Ax b A 对称正定
算法 ：(解对称正定线性方程组的平方根法 )
计算 A 的 Cholesky 分解 解方程：Ly = b 和 LTx = y
i1
对称正定矩阵的三角分解－－Cholesky 分解
定理：设 A 是对称矩阵，若 A 的所有顺序主子式 都不为 0，则 A 可唯一分解为
A = LDLT
其中 L 为单位下三角阵，D 为对角矩阵
定理：（Cholesky分解）若 A 对称正定，则 A 可唯 一分解为
A = LLT
其中 L 为下三角实矩阵，且对角元素都大于 0
6
k -1
PLU 分解
ukj a kj lki uij i1
矩阵的 PLU 分解
k 1
lik aik liju jk ukk
j1
PALU
for k = 1 to n k-1
aik aik aijajk , i = k, k+1, …, n
y1b1 l11, yi bi likyk lii , i = 2, 3, …, n k1
xnynlnn, xi yin lkixk lii i = n-1, …, 2, 1
ki1
11
改进的 Cholesky 分解
改进的 Cholesky 分解
计算方法
第五章 解线性方程组的直接方法
—— 矩阵三角分解法
1
本讲内容
一般线性方程组 LU 分解与 PLU 分解
对称正定线性方程组 平方根法－－Cholesky 分解
对角占优三对角线性方程组 追赶法
2
LU 分解
矩阵的三角分解
将一个矩阵分解成结构简单的三角形矩阵的乘积
矩阵的 LU(Doolittle) 分解 ALU 矩阵的 LDR 分解 ALDR 克洛脱 (Crout) 分解 A LU
for k = 1 to n
k-1
a kj
ukj akj lkiuij ,
i1
乘除法运算量：(n3 - n)/3
j = k, …, n
a ik
k1
lik aik lijujk ukk , i = k+1, …, n
j1
end
Matlab程序参见：ex51.m
为了节省存储空间，通常用 A 的绝对下三角部分来存放 L (对角线元素无需存储)，用 A 的上三角部分来存放 U