05 第三章 空间数据模型 第3节 矢量数据模型
合集下载
空间数据模型 ppt课件

3、数据类型
几何数据(空 间数据、图形 数据)
关系数据—实 体间的邻接、 关联包含等相 互关系
属性数据—各 种属性特征和 时间
元数据
4、数据结构
矢量、栅格 、TIN(专用 于地表或特 殊造型)
RDBMS属性表 ----采用MIS 较成熟
空间元数据
• 几何数据
– 根据空间实体的几何特征,空间对象可分为点 对象、线对象、面对象和体对象。
空间实体类型 :线实体
• 有长度,但无宽度和高度 • 用来描述线状实体,通常在网络分析中使用较多 •有一定范围的点元素集合,表示相同专题点的连 续轨迹
香港城市道路网分布
空间实体类型 :面实体
• 具有长和宽的目标 •表示平面区域大范围连续分布的特征 •有些面状目标有确切的边界,有些面状目标 在实地上没有明显的边界
– 关联:不同类图形之间的拓扑关系 – 邻接:同类图形元素之间的拓扑关系 – 连通:由节点和弧段构成的有向图网络图形中,节点之间是否存
在通达的路径,即是否具有连接性,是一种隐含于网络中的关系 – 包含:多边形内是否包含了其他弧段或多边形
• 拓扑关系涉及的术语有:
– 邻接、相交、相离、包含、重合等
点—点 点—线 点—面 线—线 线—面 面—面
第三章 空间数据模型
徐敬海 南京工业大学
本章内容
• 现实世界的抽象 • 空间实体 • 空间数据 • 空间数据结构 • 面向对象的空间数据模型 • 时空数据模型
2.1 现实世界的抽象
空间Байду номын сангаас据模型是现实世界的一个抽象,它通过使用一个
数据对象集合来支持对空间信息的显示、查询、编辑和分析
。
编码
测量
地理信息系统GIS—第3章矢量数据

空间关系及其表达
绝对空间关系:坐标、角度、方位、距离等 相对空间关系:相邻、包含、关联(连接)
等
相对空间关系的类型
拓扑空间关系:描述空间对象的相邻、包含、关联 关系等。
顺序空间关系:描述空间对象在空间上的排列次序 ,如前后、左右、东、西、南、北等。
地图、遥感影像上的空间关系是通过图形识别的, 在GIS中的空间关系则必须显式的进行定义和表达
地理信息系统
第三章 矢量数据模型
第二章内容回顾
1、什么叫坐标系? 2、为什么要建立坐标系? 3、为什么要建立地球的坐标系? 4、如何建立地球的坐标系统? 5、坐标系统与地图绘制有什么关系?
第二章内容回顾
1. 什么是地图投影? 2. 地图投影主要有几种分类方法? 3. 中国、美国的地图投影主要有哪几种? 4. 在地图投影过程中需要设置哪两部分内容?需要设
3.2 拓扑
Topology一词来自希腊文,它的原意是“形状 的研究”。拓扑学属于数学中几何学的内容, 最早由德国数学家莱布尼茨1679年提出。历 史上著名的哥尼斯堡七桥问题、多面体的欧 拉定理、四色问题等都是拓扑学发展史的重 要问题。
3.2 拓扑-哥尼斯堡七桥问题
问:能不能每座桥都 只走一遍,最后又回 到原来的位置?
空间数据结构
数据结构的概念:
数据结构即指数据组织的形式,是适于计算机存 储、管理和处理的数据逻辑结构。
对空间数据而言,数据结构则是地理实体的空间 排列方式和相互关系的抽象描述。
在地理系统中描述地理要素和地理现象的空间数 据主要包括:空间位置、拓扑关系和属性三个方 面的内容。
常用的空间数据结构
ArcGIS中的矢量数据模型
Coverage Shapefile
06 第三章 空间数据模型 4- 7节 TIN模型及模型比较

4
B C D E F
G K P
12
H
10
J M
9
11
G H I J ...
N
13 14
O
Q
S
15
Node Attribute Table
Node 1 2 3 X x1 x2 x3 Y y1 y2 y3 Z z1 z2 z3
...
...
...
...
三、TIN的生成
1. 如何选择点(How to pick points)?
一、模型的比较
1. 理解和感知的差异 2. 模型特性的差异
理解和感知的差异
现实世界
完全定义或可定义 的实体(如地籍)
概念模型
连续但可定义的对象 (如高程表面)
平滑和连续的空间变化 (如温度)
数据模型 及其表达
边界轮廓 (点、线、多边形)
矢量
表面 (三角形表面) TIN
镶嵌 (正方形, 像元)
栅格
3 3 3 3 3 3 2 3 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 2 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 2 3 3 3 3 3 3 1 7 3 3 3 3 3 3 3 2 3 3 3 3 3 1 7 7 3 3 3 3 3 3 3 2 3 3 3 3 3 1 7 7 3 3 3 3 3 3 3 2 3 3 3 3 1 7 7 7 3 3 3 3 3 3 3 3 2 3 3 1 7 7 7 7 3 3 3 3 3 3 3 3 2 3 3 1 7 7 7 7 3 3 3 3 3 3 3 3 2 3 1 7 7 7 7 7 3 3 3 3 3 3 3 3 2 1 7 7 7 7 7 7 3 3 3 3 3 3 3 3 2 1 7 7 7 7 7 7 3 3 3 1 1 1 1 1 1 1 1 4 6 6 6 6 2 7 7 7 7 7 7 7 4 4 4 4 6 6 6 6 6 2 7 7 7 7 7 7 4 4 4 4 4 6 6 6 6 2 7 7 7 7 7 7 4 4 4 4 4 6 6 6 6 2 7 7 7 7 7 7 4 4 4 4 4 6 6 6 6 2 7 7 7 7 7 7 4 4 4 4 4 6 6 6 6 6 2 7 7 7 7 7 4 4 4 4 4 6 6 6 6 6 2 7 7 7 7 7 4 4 4 4 4 6 6 6 6 6 2 7 7 7 7 7 4 4 4 4 4 6 6 6 6 6 2 7 7 7 7 7 4 4 4 4 4 6 6 6 6 6 6 2 7 7 7 7 4 4 4 4 4 6 6 6 6 6 6 2 7 7 7 7
第3章 空间数据模型

*通过描述小面块的几何形态、相邻关系及面块内属性 特征的变化来建立空间数据的逻辑模型;
*小面块之间不重叠且能完整铺满整个地理空间; *根据面块的形状,镶嵌数据模型可分为 规则镶嵌数据模型 不规则镶嵌数据模型
规则镶嵌数据模型
不规则镶嵌数据模型
TIN和Voronoi多边形数据模型
Voronoi 图又称为Dirichlet ( tessellation) ,其概念由 Dirichlet 于1850 年首先提出; 1907 后俄国数学家 Voronoi 对此作了进一步阐述,并提出高次方程化简; 1911 年荷兰气候学Thiessen为提高大面积气象预报 的准确度,应用Voronoi 图对气象观测站进行了有效 区域划分。因此在二维空间中,Voronoi 图也称为泰 森多边形。
2 作为两个面域之间的一个边界。
3 作为一个面域特征,精确表达河流的堤岸、辫 状河道以及河流上的运河。
4 作为一条曲线以构成表面模型上的沟槽。根据 地表上河流的路径,可以算出其横截面、落差度、 排水流域以及在预测降雨下的洪水爆发可能性。
针对真实的世界,每一个人都在创建他 自己的主观模型。GIS的观点是为真实世 界建立一个通用的模型。
泰森(Thiessen)多边形的特点: 1 组成多边形的边总是与两相邻样点的连线垂直; 2 多边形内的任意位置总是离该多边形内样点的距 离最近,离相邻多边形内样点距离远; 3 每个多边形内包含且仅包含一个样点。
(五)面向对象数据模型
为了有效地描述复杂的事物或现象,需要 在更高层次上综合利用和管理多种数据结构 和数据模型,并用面向对象的方法进行统一 的抽象。
空间逻辑数据模型作为概念模型向 物理模型转换的桥梁,是根据概念模型 确定的空间信息内容,以计算机能理解 和处理的形式,具体地表达空间实体及 其关系。
第三章 空间数据的表达方法

(一)特点: 1.用离散的点或线描述地理现象及特征 2.用拓扑关系描述矢量数据之间关系
3.面向目标的操作
4.数据结构复杂且难以同遥感数据结合
5.难于处理位置关系
空间对象(实体)的地图表达
点:位置:(x,y) 属性:符号 线:位置:(x1,y1),(x2,y2),…,(xn,yn) 1 1 2 2),„,(xn n 属性:符号—形状、颜色、尺寸
7 7 7 7ຫໍສະໝຸດ 7 7 7 77 7 7 7
7 7 7 7
7 7 7 7
7 7 7 7
空间单元人为划定成 大小相等的正方形网 格,有着统一的定位 参照系。每个空间 单元只记录其属性值, 而不记录它的坐标值。
2
2
2 2 1 4 4 4 4 4 4 4
2
2 2 1 4 4 4 4 4 4 4
2
2 2 1 4 4 4 4 4 4 4
2
2 2 1 4 4 4 4 4 4 4
2
2 1 4 4 4 4 4 4 4 4
2
1 4 4 4 4 4 4 4 4 4
1
1 4 4 4 4 4 4 4 4 4
1
7 1 4 4 4 4 4 4 4 4
7
7 7 1 4 4 4 4 4 4 4
7
7 7 7 1 4 4 4 4 4 4
7
7 7 7 7 1 4 4 4 4 4
地理信息系统为什么要研究数据模型
现实世界真实模型
空间数据处理
空间数据查询
空间数据分析
空间数据模型 空间数据复原 空间数据结构
数据库:空间数据物 理结构
空间信息 3.2 空间数据模型 3.3 空间数据结构 3.4 地貌的表达——数字化地形模型
第三章 矢量数据模型
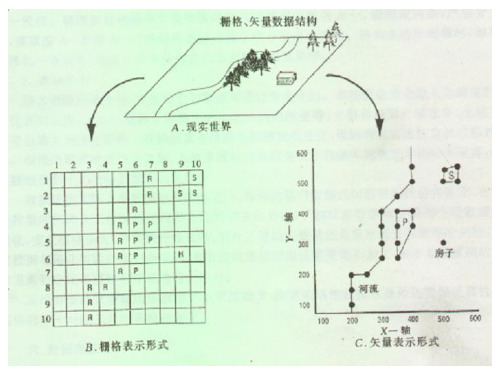
3.3.2 拓扑矢量数据
• 拓扑数据模型定义:不仅表达几何位置和属 性,还表示空间拓扑关系的矢量数据模型。 • 拓扑关系具体可由4个关系表来表示:
– (1)结点—弧段关系 – (2)弧段—结点关系 – (3)弧段—多边形关系 – (4)多边形—弧段关系
结点-弧
1
A b a 3 2
c
B e D 6 C 5 7
线:位置: (x1,y1),(x2,y2),„,(xn,yn) 属性:符号—形状、颜色、尺寸
面:位置: (x1,y1),(x2,y2),„,(xi,yi),„,(xn,yn) 属性:符号变化 等值线
点
抽象的点, 有位置,无宽度和长度;
美国佛罗里达洲地震监测站2002年9月该洲可 能的500个地震位置
1)关联性
• 关联性: 不同 类要素之间关 系
– 结点与弧段 如V9与L5,L6,L3 – 多边形与弧段 如P2与L3,L5,L2
2)邻接性
• 邻接性:同类元素 之间关系
– 多边形之间、结 点之间。 – 邻接矩阵 : 重叠:-- 邻接:1 不邻接:0
P1 P2 P3 P4 P -1 1 1 P2 1 -1 0 P3 1 1 -0 P4 1 0 0 --
5 6
表中数字前负号为相反方向
7
B
—
空间拓扑关系表达:面与弧
1
A b a 3 2 c B
多边形-弧拓扑
e
D 7
面号
6
弧号 -1,-2,3 2,-7,5,0,-6 -3,-5,4 6
A B
C
5
4
d
a: 结点号 1: 弧段号
A: 多边形号 弧段数字化方向
C D
表中数字前负号为相反方向
GIS第三章空间数据模型

图元素独 立存储
点坐标文件 线坐标文件
通过FID连接
点属性表文件 线属性表文件
面坐标文件
面属性表文件
不包含拓扑数据
101 202
203
301
201 302
102
(b)拓扑模型
图元素非 独立存储
点坐标文件 线坐标文件
通过FID连接
点属性表文件 线属性表文件
几类?
3.要素模型
2)离散欧氏平面上的空间对象
离散一维对象 B 样条曲线
多边线 线段
3.要素模型
3)要素模型和场模型的比较
要素模型
现实世界
场模型
选择要素
选择一个位置
它在哪里
那里怎么样
数据
3.要素模型
• 2. 矢量数据模型
空间图形
空间数据
属性数据
101 202
203
301
201 302
102
(a)Spaghetti模型
• 常用的嵌入式空间类型: – 欧式空间(距离、方位) – 量度空间(距离) – 拓扑空间(拓扑关系) – 面向集合的空间(只采用一般的基于集合的关系)
3.要素模型
1)欧氏平面上的空间对象类型
空间对象
零维对象点
延伸对象
一维对象
二维对象
弧
环
面对象
简单弧
简单环
面域对象
域单位对象
要素(对象) 的类型有哪
– 欧氏平面:把空间特性转换成实数的元组特性,而形成 的二维模型即欧氏平面
– 地理实体:分布于地球表面的人文和自然现象的总称 实体必须符合三个条件:
• 可被识别 • 重要(与问题有关) • 可被描述(有特征)
p03第三章 空间数据模型-第六-八节1

第六节、 ArcGIS介绍
1. 厂家:ARCGIS是美国环境系统研究所(Environmental System Research Institute, Co.,简称ESRI)于20世纪80年 代初推出的一个通用GIS软件 。
2. 运行平台:uninx-NT(96年)(2000)-pc
Ar析
2、ArcCatalog
• 空间数据管理:
– ESRI coverage、 shape file
– CADData – 遥感图像 – 栅格 – TINS – Geodatabase – 属性表格
• 察看空间数据、源 数据等
3、ArcToolbox
• 超过140个工具,用 于进行geoprocessing 处理;
六、ARCGIS的开发环境
在Windows环境下以可编程控件(OCX)的形式为用户提 供在其应用中增加制图和GIS功能的可能性(MapObjects);
在ArcView和MapObjects中提供Internet网上的GIS和制图 功能;
ArcObject和ArcEngineer面向组件的开发技术。 Arcsever开发工具
三、ArcGIS Workstation 的功能模块(1)
1. ARC是ARCGIS Workstartion的其他功能模块的运行环境;
① ARC主要完成对工作空间和数据单元的操作和管理; ② 进行空间数据操作; ③ 建立拓扑关系,进行数据格式和投影转换; ④ 进行某些基于矢量的空间分析。
2. INFO是一个完整的关系型数据库管理系统,用于完成对属 性数据库的管理和维护;
第三章 空间数据模型
空间数据模型是GIS的基础;
空间数据模型:指利用特定的数据结构来表达空间对 象的空间位置、空间关系和属性信息;是对空间对象 的数据描述。
空间数据模型基于对象的矢量数据模型与栅格数据模型讲课文档

多边形内编号 1 2 3 4 5 6 7
弧数 4 3 4 4 3 1 1
各弧的内编号 1,3,4,6 5,2,1 6,7,9,5 2,9,8,3 8,7,4 10 11
现在二十三页,总共七十九页。
4 拓扑具体编辑过程——确定左右多边形 如果在组成一个多边形时,一条弧是从
首结点到尾结点,则定义为该多边形是 在这条弧的右边;
(a)多边形、弧段、结点(自上到下)
多边形 弧段
P1 a4 a5 a6
P2 a1 a8 a5 P3 a3 a6 a7 P4 a2 a7 a8
弧段 结点
a1 N1 N2
a2 N2 N4
a3 N4 N5 a4 N1 N5
a5 N1 N3
a6 N3 N5
a7 N3 N4 a8 N2 N3
(b)结点、弧段、多边形
处理嵌套多边形比较麻烦
现在八页,总共七十九页。
5 Arcgis软件Shape文件数据模型
Shape文件将空间要素的图形及属性信息以 非拓扑的形式存储在数据集中。要素的几何 形状数据存储成为具有矢量坐标的图形。
Shape文件数据模型是非拓扑的数据库模型。 因此,在数据显示速度上比较快,数据的编 辑也比较容易实现。通过编程的方式很容易 实现对Shape文件的存取操作。这一特性是 其优点,也是缺点。
一、栅格数据模型要素
格网方向
像元大小
西南角格网坐标 (XWS,YWS)
Y:行
X:列
现在二十九页,总共七十九页。
2 混合像元大小处理
方案一
B
.O C A
重要性 法
方案二:缩小栅格单元的面积
现在三十页,总共七十九页。
面积占优法
长度占优法
第三章 空间概念和数据模型

3.1 空间信息模型 三、空间对象操作
面向方位的操作:
绝对的:以全球作为参照系,如东、西、南、 北、东北等 相对的:以给定目标为参照,如左、右、前、 后、上、下等
面向度量的操作:
度量空间:集合X满足下列条件就称为一个度量 空间:如果对X中的任意一点对x、y,都存在与之 相关联的实数d(x,y),称x到y的距离(也称为一种 度量),且对于任意x、y、z满足如下性质:
3.1 空间信息模型 六、空间对象模型小结
OGIS 标准预定义了一系列空间数据类型和操作 空间对象模型和面向对象的软件有很多相似之处 可以方便地和多种语言集成,采用类似Java, C++, Visual basic等编程实现建模(如2.1.6节中JAVA程序实 现) 和后关系数据库(Post-relational databases, e.g. OODBMS, ORDBMS)集成。
3.1 空间信息模型 二、对象模型
对象模型: 对象:空间信息中可以抽象成明确的、可识别的和 相关的事物或实体。 对象具有相应的属性和方法 以道路图为例: 对象:道路, 里程碑, ... 道路对象属性: 空间属性:位置, 如道路的多边形边界 非空间属性:道路名, 道路类型 (国道、省道等),车 道数, 限速等 道路对象的方法: 确定道路中心线,确定道路长度, 确 定道路交叉口等
Dimension
Point
Curve Surface
City
River Country
0
1 2
OGIS数据模型中的空间对象 UML表示
3.1 空间信息模型 三、空间对象操作
面向集合的:面向集合的空间操作。在所有内
嵌空间中,最简单且最通用的类型是面向集合的 内嵌空间。这种集合可以利用一些常见的关系, 即在基于集合的关系中常见的并、交、包含和属 于关系。层次关系(如森林包含林分,州立公园 包含森林,州包含州立公园)就适于用集合理论 来建模 。如两个多边形的相交操作产生一个新的 多边形。
第3章 空间数据模型

第三节 要素模型
1、欧氏平面上的空间对象类型
图3-8表示了在连续的二维欧氏平面上的一种可能的对象继承等级图。
空间对象
零维对象点
延伸对象
一维对象
二维对象
弧
环
面对象
简单弧
简单环
面域对象
域单位对象
图3-8:连续空间对象类型的继承等级
第三节 要素模型
图3-8:连续空间对象类型的继承等级
第三节 要素模型
第二节 场模型
二、场的特征
1、空间分辨率和属性域 2、连续和分段连续
3、各向同性和各向异性:各种性质是否随方向的变化而变化是空间场的一
个重要特征。如果一个场中的所有性质都与方向无关,则称为各向同性场 (Isotropic Field)。反之与方位有关的场称为各向异性场(Anisotropic Field)。 4、空间自相关:空间自相关是空间场中的数值聚集程度的一种量度,距离近 的事物之间的联系性强于距离远的事物之间的联系性。一个空间场中类似的 数值有聚集的倾向,则空间场表现出很强的正空间自相关;如类似属性值在
第三节 要素模型
第三节 要素模型
第三节 要素模型
第三节 要素模型
第三节 要素模型
第三节 要素模型
“空间对象”具有最高抽象层次,它派生为零维的点对象和延伸对象,延伸
对象又可以派生一维和二维对象类。一维对象的两个子类:弧和环(Loop),如
果没有相交,则称为简单弧(Simple Arc)和简单环(Simple Loop)。二维空 间对象类中连通的面对象称为面域对象,没有“洞”的简单面域对象称为域单位 对象。 2、离散欧氏平面上的空间对象 欧氏空间的平面因连续而不可计算,必须离散化才适合于计算。图3-8中所 有连续类型的离散形式都存在。图3-9表示了部分离散一维对象继承等级关系。
空间数据模型

Equals(anotherGeometry)
Disjoint(anotherGeometry ) Intersects(anotherGeometry ) Touches(anotherGeometry ) 空间 Crosses(anotherGeometry) 关系 Within(anotherGeometry) 运算
3.2.2 网状数据模型
在网状数据模型中,虽然每个结点可以有多个 父结点,但是每个双亲记录和子女记录之间的 联系只能是1:N的联系,对于M:N的联系, 必须人为地增加记录类型, 把M:N的联系分 解为M个1:N的二元联系。
学生/选课/课程的网状模型
3.2.2 网状数据模型
网状模型在具体实现时,把整个模型划
OGC的SFS中定义的空间操作算子包括基本操作、 空间关系运算和空间分析操作。
操作 方法名称
类别 Dimension ( ) GeometryType ( ) SRID ( )
基本 Envelope( ) AsText( )
操作 AsBinary( ) IsEmpty( ) IsSimple( ) Boundary( )
3.3 面向对象模型
类(class):是属性集和方法集相同的所有 对象的组合。
类允许嵌套结构。
可以在现在类的基础上通过继承来构造新的 类。现在的类称为超类,新子类是从现有类 中派生出来的,称派生类。子类继承超类上 定义的全部属性和方法,实现了软件的可重 用性。同时,子类还可以包含其他的属性和 方法。
通过继承构造类,采用多态性为每个类指定 其表现行为。
3.3 面向对象模型
面向对象模型是采用面向对象的观点来描述现实世
界中实体及其联系的模型,现实世界中的实体都被
第3章 空间数据模型

– 现实世界许多地理事物和现象可以构成网络,如公路、 铁路、通讯线路、管道、自然界中的物质流、物量流 和信息流等
空间数据概念模型
• 网络是由一系列节点和环链组成的,与对象模型 没有本质的区别 • 网络模型可以看成对象模型的一个特例,它是由 点对象和线对象之间的拓扑空间关系构成的 • 空间数据概念模型归结为对象模型(或称要素模 型)和场模型(或称域模型)两类
空间数据概念模型
• 不规则多边形区。将平面区域划分为简单连通的多边形区 域,每个多边形区域的边界由一组点所定义;每个多边形 区域对应一个属性常量值,而忽略区域内部属性的细节变 化 • 不规则三角形区。将平面区域划分为简单连通三角形区域, 三角形的顶点由样点定义,且每个顶点对应一个属性值; 三角形区域内部任意位置的属性值通过线性内插函数得到 • 等值线。用一组等值线C1,C2,…,Cn,将平面区域划 分成若干个区域。每条等值线对应一个属性值,两条等值 线中间区域任意位置的属性是这两条等值线的连续插值
(a) 规则分布的点
( b ) 不规则分布的 点
(c)规则矩形区
(d) 不规则多边形区
(e) 不规则三角形区
(f) 等值线
空间数据概念模型
• 网络模型
– 网络模型与对象模型类似,都是描述不连续的地理现 象,不同之处在于它需要考虑通过路径相互连接多个 地理现象之间的连通情况 – 网络是由欧式空间R2中的若干点及它们之间相互连接 的线(段)构成
地理空间与空间实体
• 属性特征
– 也称为非空间特征或专题特征,是与空间实体相联系 的、表征空间实体本身性质的数据或数量,如实体的 类型语义定义、量值等 – 类型
• 定性属性,如名称、类型、特性等 • 定量属性,如数量、等级等
空间数据概念模型
• 网络是由一系列节点和环链组成的,与对象模型 没有本质的区别 • 网络模型可以看成对象模型的一个特例,它是由 点对象和线对象之间的拓扑空间关系构成的 • 空间数据概念模型归结为对象模型(或称要素模 型)和场模型(或称域模型)两类
空间数据概念模型
• 不规则多边形区。将平面区域划分为简单连通的多边形区 域,每个多边形区域的边界由一组点所定义;每个多边形 区域对应一个属性常量值,而忽略区域内部属性的细节变 化 • 不规则三角形区。将平面区域划分为简单连通三角形区域, 三角形的顶点由样点定义,且每个顶点对应一个属性值; 三角形区域内部任意位置的属性值通过线性内插函数得到 • 等值线。用一组等值线C1,C2,…,Cn,将平面区域划 分成若干个区域。每条等值线对应一个属性值,两条等值 线中间区域任意位置的属性是这两条等值线的连续插值
(a) 规则分布的点
( b ) 不规则分布的 点
(c)规则矩形区
(d) 不规则多边形区
(e) 不规则三角形区
(f) 等值线
空间数据概念模型
• 网络模型
– 网络模型与对象模型类似,都是描述不连续的地理现 象,不同之处在于它需要考虑通过路径相互连接多个 地理现象之间的连通情况 – 网络是由欧式空间R2中的若干点及它们之间相互连接 的线(段)构成
地理空间与空间实体
• 属性特征
– 也称为非空间特征或专题特征,是与空间实体相联系 的、表征空间实体本身性质的数据或数量,如实体的 类型语义定义、量值等 – 类型
• 定性属性,如名称、类型、特性等 • 定量属性,如数量、等级等
第三空间数据模型【实用资料】

• 一个点在一个区域的边界上 方向关系又称为方位关系、延伸关系,它定义了地物对象之间的方位,如“河北省在河南省北部”就描述了方向关系。
栅格数据模型是基于连续铺盖的,它是将连续空间离散化,即用二维铺盖或划分覆盖整个连续空间;
• 一个点在一个区域的内部 一个点的位置可以二维或者三维中的坐标的单一集合来描述
2.2栅格数据模型
• 栅格数据模型是基于连续铺盖的,它是将
连续空间离散化,即用二维铺盖或划分覆 盖整个连续空间;铺盖可以分为规则的和 不规则的
• 基于栅格的空间模型把空间看作像元(
Pixel)的划分(Tessellation),每个像元 都与分类或者标识所包含的现象的一个记 录有关
3.要素模型 3.1要素模型的基本概念
3.2矢量数据ห้องสมุดไป่ตู้型
• 矢量方法强调了离散现象的存在,由边界
线(点、线、面)来确定边界,因此可以 看成是基于要素的。
• 矢量数据模型将现象看作原形实体的集合
,且组成空间实体。在二维模型内,原型 实体是点、线和面;而在三维中,原型也 包括表面和体
• 矢量模型的表达源于原型空间实体本身,
通常以坐标来定义。一个点的位置可以二 维或者三维中的坐标的单一集合来描述
4.1.2拓扑空间关系描述——9交 模型
• 设有现实世界中的两个简单实体A、B,
B(A)、B(B)表示A、B的边界,I(A)、I(B)表 示A、B的内部,E(A)、E(B)表示A、B余。 Egenhofer[1993]构造出一个由边界、内部 、余的点集组成的9-交空间关系模型(9Intersection Model,9-IM)如下:
• 一个面的连续性(给定面上任意两点,从一点可以 重要(与问题相关);
拓扑一词来自于希腊文,意思是“形状的研究”。
栅格数据模型是基于连续铺盖的,它是将连续空间离散化,即用二维铺盖或划分覆盖整个连续空间;
• 一个点在一个区域的内部 一个点的位置可以二维或者三维中的坐标的单一集合来描述
2.2栅格数据模型
• 栅格数据模型是基于连续铺盖的,它是将
连续空间离散化,即用二维铺盖或划分覆 盖整个连续空间;铺盖可以分为规则的和 不规则的
• 基于栅格的空间模型把空间看作像元(
Pixel)的划分(Tessellation),每个像元 都与分类或者标识所包含的现象的一个记 录有关
3.要素模型 3.1要素模型的基本概念
3.2矢量数据ห้องสมุดไป่ตู้型
• 矢量方法强调了离散现象的存在,由边界
线(点、线、面)来确定边界,因此可以 看成是基于要素的。
• 矢量数据模型将现象看作原形实体的集合
,且组成空间实体。在二维模型内,原型 实体是点、线和面;而在三维中,原型也 包括表面和体
• 矢量模型的表达源于原型空间实体本身,
通常以坐标来定义。一个点的位置可以二 维或者三维中的坐标的单一集合来描述
4.1.2拓扑空间关系描述——9交 模型
• 设有现实世界中的两个简单实体A、B,
B(A)、B(B)表示A、B的边界,I(A)、I(B)表 示A、B的内部,E(A)、E(B)表示A、B余。 Egenhofer[1993]构造出一个由边界、内部 、余的点集组成的9-交空间关系模型(9Intersection Model,9-IM)如下:
• 一个面的连续性(给定面上任意两点,从一点可以 重要(与问题相关);
拓扑一词来自于希腊文,意思是“形状的研究”。
05矢量数据结构

基于对象数据模型(Object-based data model ) – ArcGIS: geodatabase
15
§ 2 实体数据结构
实体数据结构 – 以基本的空间实体(点、线、多边形)为单位进行 组织 – 只记录空间对象的位置坐标和属性信息 – 不记录拓扑关系的矢量数据模型。(又称面条结 构)。
线:位置: (x1,y1),(x2,y2),…,(xn,yn) 属性:符号—形状、颜色、尺
寸
面:位置: (x1,y1),(x2,y2),…,(xi,yi),…,(xn,yn)
属性:符号变化 等值线
5
2.几何对象 点:空间的一个坐标点; 线:多个点组成的弧段; 面:多个弧段组成的封闭多边形;
B
t124
1,6,7,4,5,1
6
B 5
点号
坐标
1
1,2
2
3,4
4
3
5,6
4
7,8
5
…
35
§4 点位字典数据结构
36
索引式结构
37
§5空间实体间关系
1.关系类型 2.识别与描述 3.拓扑关系 4.GIS中引入拓扑关系的优缺点 5.拓扑结构采用原则
38
§4空间实体间关系
1 关系类型 – 拓扑空间关系:描述空间对象的相邻、包含等 – 顺序空间关系:描述空间对象在空间上的排列次序, 如前后、左右、东、西、南、北等。 – 度量空间关系:描述空间对象之间的距离等。
2 识别与描述 – 地图、遥感影象上的空间关系是通过图形识别的。 – 在GIS中的空间关系则必须显式的进行定义和表达。 – 空间关系的描述多种多样。不同的GIS可能采用不同 的方法进行描述。
15
§ 2 实体数据结构
实体数据结构 – 以基本的空间实体(点、线、多边形)为单位进行 组织 – 只记录空间对象的位置坐标和属性信息 – 不记录拓扑关系的矢量数据模型。(又称面条结 构)。
线:位置: (x1,y1),(x2,y2),…,(xn,yn) 属性:符号—形状、颜色、尺
寸
面:位置: (x1,y1),(x2,y2),…,(xi,yi),…,(xn,yn)
属性:符号变化 等值线
5
2.几何对象 点:空间的一个坐标点; 线:多个点组成的弧段; 面:多个弧段组成的封闭多边形;
B
t124
1,6,7,4,5,1
6
B 5
点号
坐标
1
1,2
2
3,4
4
3
5,6
4
7,8
5
…
35
§4 点位字典数据结构
36
索引式结构
37
§5空间实体间关系
1.关系类型 2.识别与描述 3.拓扑关系 4.GIS中引入拓扑关系的优缺点 5.拓扑结构采用原则
38
§4空间实体间关系
1 关系类型 – 拓扑空间关系:描述空间对象的相邻、包含等 – 顺序空间关系:描述空间对象在空间上的排列次序, 如前后、左右、东、西、南、北等。 – 度量空间关系:描述空间对象之间的距离等。
2 识别与描述 – 地图、遥感影象上的空间关系是通过图形识别的。 – 在GIS中的空间关系则必须显式的进行定义和表达。 – 空间关系的描述多种多样。不同的GIS可能采用不同 的方法进行描述。
第三章-空间数据模型

多 边 形 与 弧 段 : P2 与 L3,L5,L2
2)邻接性: (同类元素之 间)
多边形之间、结点之间。
邻接矩阵
重叠:-- 邻接:1 不邻接: 0
P1 P2 P3 P4 P1 -- 1 1 1 P2 1 -- 1 0 P3 1 1 -- 0 P4 1 0 0 --
3)连通性:与邻接性相类似,指对弧段连接的判别,如用于网络 分析中确定路径、街道是否相通。
连通矩阵: 重叠:-- 连通:1 不连通:0
V1 V2 V3 …
V1 -- 1 0 V2 1 -- 1 V3 0 1 --
4)拓扑包含:指面状实体包含了哪些线、点或面状实体。
主要的拓扑关系:拓扑邻接、拓扑关联、拓扑包含。
P2
P1
P2
P3 P2
P1 P1
P2
拓扑关系的表达 拓扑关系具体可由4个关系表来表示: (1) 面--链关系: 面 构成面的弧段 (2) 链--结点关系: 链 链两端的结点 (3) 结点--链关系: 结点 通过该结点的链 (4) 链—面关系: 链 左面 右面
2 杨树 x1, y1;x2, y2;…; 林 xn, yn; x1, y1
3 松树 x1, y1;x2, y2;…; 林 xn, yn; x1, y1
空间对象的矢量数据模型
3.4 空间逻辑数据模型
二、栅格数据模型
在栅格数据模型中,点实体是一 个栅格单元(cell)或像元,线实体 由一串彼此相连的像元构成,面实 体则由一系列相邻的像元构成,像 元的大小是一致的。
象)
分类
子类/超类 等效
空间关系 非空间关系 时间关系
地理空间 空间要素
几何坐标
子部分 超部分
非空间属性
2)邻接性: (同类元素之 间)
多边形之间、结点之间。
邻接矩阵
重叠:-- 邻接:1 不邻接: 0
P1 P2 P3 P4 P1 -- 1 1 1 P2 1 -- 1 0 P3 1 1 -- 0 P4 1 0 0 --
3)连通性:与邻接性相类似,指对弧段连接的判别,如用于网络 分析中确定路径、街道是否相通。
连通矩阵: 重叠:-- 连通:1 不连通:0
V1 V2 V3 …
V1 -- 1 0 V2 1 -- 1 V3 0 1 --
4)拓扑包含:指面状实体包含了哪些线、点或面状实体。
主要的拓扑关系:拓扑邻接、拓扑关联、拓扑包含。
P2
P1
P2
P3 P2
P1 P1
P2
拓扑关系的表达 拓扑关系具体可由4个关系表来表示: (1) 面--链关系: 面 构成面的弧段 (2) 链--结点关系: 链 链两端的结点 (3) 结点--链关系: 结点 通过该结点的链 (4) 链—面关系: 链 左面 右面
2 杨树 x1, y1;x2, y2;…; 林 xn, yn; x1, y1
3 松树 x1, y1;x2, y2;…; 林 xn, yn; x1, y1
空间对象的矢量数据模型
3.4 空间逻辑数据模型
二、栅格数据模型
在栅格数据模型中,点实体是一 个栅格单元(cell)或像元,线实体 由一串彼此相连的像元构成,面实 体则由一系列相邻的像元构成,像 元的大小是一致的。
象)
分类
子类/超类 等效
空间关系 非空间关系 时间关系
地理空间 空间要素
几何坐标
子部分 超部分
非空间属性
空间数据模型

坐标表和属性表之间共享同一识别码
通过坐标表和属性表之间共享同一识别码来使属性信息和位置信 息相结合
4、多类信息的表示 、
空间数据的分类,是指根据系统功能及国家规范和标准,将具有不同属性 或特征的要素区别开来的过程,以便从逻辑上将空间数据组织为不同的信 息层(见下图);
用于表示地理实体的数据模型
①面积; ②周长; ③内岛 ④形状(锯齿状、凸凹性等); ⑤重叠性与非重叠性。 ⑥独立性或与其它的地物相邻,如中国 及其周边国家;
4、立体状实体 、
Volume:立体状实体用于描述三维空间中 的现象与物体,它具有长度、宽度及高度 等属性。 ① 体积:如工程开掘和填充的土方量; ② 每个二维平面的面积; ③ 每个二维平面的周长; ④ 断面图与剖面图。 ⑤ 内岛或锯齿状外形; ⑥ 含有孤立块或相邻块;
三种最主要的拓扑关系
空间数据的拓扑关系是空间对象空间关系的一种,但却是最 重要的空间关系,在GIS中最主要的拓扑关系包括。 相邻性(Adjacency) (Adjacency): 表示两个多边形是否相邻( ① 相邻性 (Adjacency) : 表示两个多边形是否相邻 ( 同 类元素间的相邻关系) 类元素间的相邻关系); 包含性(Containment) (Containment): ② 包含性 (Containment) : 表示一个图元要素是否包含于 某个多边形中。 同类不同级别对象之间的包含关系) 某个多边形中。(同类不同级别对象之间的包含关系) 连通性(Connectivity) 表示两条线段是否相连。 (Connectivity): ③ 连通性(Connectivity):表示两条线段是否相连。
GIS的数据模型分为两大类:矢量数据模型和栅格数据模型。
空间数据模型
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
– 字符型 (Character) – 整型( Integer) – 实型 (Real) – 日期型 (Date)
• 字段宽度: Field width (size): • ArcView示例
3、关系表的基本操作
• 搜索 (Search)
– 穷尽搜索 Exhaustive Search (学生姓名列表未排序) – 二进制搜索 Binary Search (学生姓名列表未排序)
一、基本概念
• • • • • 现实世界和矢量表达 位置和边界被清楚地记录 对象可以被识别 属性值与对象相联系 空间关系可以清晰表达
二、关系数据模型和关系表
1. 2. 3. 4. 定义 数据结构 关系表的基本操作 GIS 中关系表的应用
1、定义
• 在关系数据模型中,数据是以简单的记录形 式集中表达的, • 每一条记录代表一个事实(永久相关的值) • 记录的集合组成一个二维表
– 行(row )被称为记录(record),代表一个对象及其 相关的属性值 – 列(column)也称为字段(field)或项(item)代表一 个属性
• 例子:学生信息表
2、数据结构
• 多少字段,应该是什么 • 字段名: Field Name (Item Name): • 字段类型: Field Type (Item Type):
四、矢量数据模型-拓扑数据模型
1. 2. 3. 4. 术语 拓扑三角形 完全拓扑数据模型 GBF/DIME 数据模型 (US Census Bureau)
可以理解为矢量数据的压缩方式
1、术语(Terminology)
• • • • • • • • 顶点(Vertex ): 线性要素改变方向的点 线段(Line segment): 连接两个顶点的直线 多边形线(Polyline): 由一个以上的线段组成 线(Line): 通用术语,指线段或多边形线 Line : 结点(Node): 两个或多个线的交点 弧(Arc): 有方向的线 多边形(Polygon): 由一系列弧围成的面 标识点(Label point): 地图上用于放置标识的点
三、矢量数据模型( Spaghetti Model)
1) 实体与实体模型 (Spaghetti Model)
(a)定义
点、线、面要素的表达
(b)解释
(1) 简单列表表达(Simple lists) (2) 点目录(Point directory)
(c) Spaghetti models的比较 (d) 总结(Summary):
40
60
X
Polygon Topology
Poly A B C D Arcs a1, a2 a2, a4, 0, a3 a3 NILL Nodes n1, n4 n1, n4, 0, n2 n2 NILL Node n1 n2 n3 n4
Node Topology
Arcs a1, a2, a4 a3 NILL a1, a2, a4 Polygon A, B B, C 0, B A, B X, Y 80, 60 70, 25 25, 20 10, 25
Arc Topology
Arc a1 a2 a3 a4 Start Node n4 n1 n2 n1 End Node n1 n4 n2 n4 Left Poly. D B C D Right Poly. A A B B Shape Points s8 s2,s1 s4,s5,s3 s6,s7
Shape Point Table
A K H B G C I J
(xn, yn) (x1, y1)
(a)
(xn, yn)
F (b)
E (c)
D
一维矢量具有方向、长度
方向:即有起始结点和终止结点 长度:可以用以下方式表达:
引入欧氏空间的距离概 念: 长度 = ∑ [( xi − xi −1 ) 2 + ( y i − y i −1 ) 2 ]1 / 2
矢量模型(vector model)
一维矢量线
• 一维矢量可以闭合,但不能与自身相交 • 闭合时,首位相接, (x1,y1)=(xn,yn) 或(x1,y1,z1)=(xn,yn,zn) • 如果相交,则应以交点为界,将其分成几个一维矢量
(a)
(b)
(c)
(d)
一维矢量自身的可能空间关系
(x1, y1)
A
P1 P2 P5 P6 P7 P8 P1
B
P2 P3 P4 P6 P5 P2
P1: x1, y1 P2: x2, y2 P3: x3, y3 P4: x4, y4 P5: x5, y5 P6: x6, y6 P7: x7, y7 P8: x8, y8
思考题
1. 什么是关系数据模型(表)?关系数据模型的关键数据结 构要素有哪些? 2.什么是二进制搜索binary search?与穷尽搜索 (exhaustive search)对搜索表的需求方面有何不同? 3. 条件是如何用于选择被表达记录的? 4. 关系数据模型中进行表的连接(join)和相关(relate)操 作有何区别? 5.矢量数据模型是如何表达空间数据的?点、线、面特征是 如何被表达的? 6. 矢量数据模型的优缺点有哪些? 7. 简单列表数据模型和点目录数据模型的主要区别是什么? 这两种模型为什么不被认为是拓扑数据模型?
i=2 n
平面投影距离为地图学 研究广泛采用。
二维矢量-面
• 表示空间的一个面状要素 • 由一组闭合弧段所包围的空间区域 • 又称多边形
描述二维矢量的特征参数
• 面积:
– 二维面积: – 三维面积:表面积(计算复杂)和投影面积 (常用)
• 凹凸性:形态描述 • 单调性: • 走向、倾角和倾向:地形、地层描述中常 用的概念,是三维空间中曲面法向矢量的 另外一种描述方法
spaghetti models的比较
P2 (x2, y2) P1 (x1, y1) P3 (x3, y3)
B A
P5 (x5, y5)
P8 (x8, y8) P7 (x7, y7) P6 (x6, y6)
P4 (x4, y4)
Simple List Method
Polygon Representation
DLG (USGS)
思考题
1. 什么是弧(arc)和结点(node)?任何点都能 是结点吗?弧(arc)和多边形线( polyline,由 许多直线线段组成的线)的区别是什么? 2. 拓扑数据模型中的三个基本几何要素是如何用来 获取空间拓扑的? 3. 什么是拓扑数据模型?什么是拓扑三角形? 4. 拓扑数据模型的优缺点有哪些? 5. 用给定的拓扑三角形中的拓扑关系,试用拓扑数 据模型对一个简单地图进行编码。
i=2 n
在三维空间中一维矢量 的距离有两种概念一为 沿路程距离,表示为 长度 = ∑ [( xi − xi −1 ) 2 + ( y i − y i −1 ) 2 + z i − z i −1 ) 2 ]1 / 2 (
i=2 n
另一种为平面投影距离 ,二维平面的定义相同 : 长度 = ∑ [( xi − xi −1 ) 2 + ( y i − y i −1 ) 2 ]1 / 2
(1) 地理要素被当成单个对象对待
空间边界可以被清晰的编码
(2)对象之间没有关系
要素间的空间拓扑不被记录
矢量表达法
• 不同的空间特征具有不同的矢量维数
– 0维矢量-点:即空间中的一个点,没有大小、 方向,二维和三维欧氏空间中为:(x,y),(x,y,z) – 一维矢量-线:空间中的线划要素或空间对象间 的边界,也称为弧段、链 – 二维欧氏空间(x1,y1),(x2,y2),…(xn,yn) – 三维欧氏空间(x1,y1,z1),(x2,y2 , z2),…(xn,yn , zn) – 起点和终点称为结点(node),其它点称拐点 (vertex)
Point Directory Method
Polygon Representation Point Directory
B
P2 P3 P4 P6 P5 P2
P1: x1, y1 P2: x2, y2 P3: x3, y3 P4: x4, y4 P5: x5, y5 P6: x6, y6 P7: x7, y7 P8: x8, y8
2、拓扑三角形
Arc
Is part of
Node
Consists of
Polygon
3、完全拓扑数据模型
60 50 40 30 20 10 0
Y
s8 a1 n4 a4 s7 0 10 s1 n3 a4 20 30
a1
D
s2 B s3 a3 n
n1 a4 s6 80
A
a2 s5 50
D
C
2
s4 70
B
x2, y2 x3, y3 x4, y4 x6, y6 x5, y5 x2, y2
P2 (x2, y2) P1 (x1, y1)
P3 (x3, y3)
点 目 录 方 法
A
P1 P2 P5 P6 P7 P8 P1
P8 (x8, y8)
B A
P5 (x5, y5)
P4 (x4, y4) P7 (x7, y7) P6 (x6, y6)
Shape Point s1 s2 s3 s4 X, Y 20,25 60,35 55,25 70,15 Shape Point s5 s6 s7 s8 X, Y 48,15 80,10 10,10 10,60
空间实体示意图
空间实体拓扑结构的关系表
4、GBF/DIME 数据模型 (US Census Bureau)
空间曲面
• 矢量实现方法多样 • 常用等值线法、剖面法
三维矢量-体
• • • • • 指三维空间中的实体 由一组或多组闭合曲面所包围的空间对象 2维 面 2.5维 表面(surface) 2.5 surface 3维 体
• 字段宽度: Field width (size): • ArcView示例
3、关系表的基本操作
• 搜索 (Search)
– 穷尽搜索 Exhaustive Search (学生姓名列表未排序) – 二进制搜索 Binary Search (学生姓名列表未排序)
一、基本概念
• • • • • 现实世界和矢量表达 位置和边界被清楚地记录 对象可以被识别 属性值与对象相联系 空间关系可以清晰表达
二、关系数据模型和关系表
1. 2. 3. 4. 定义 数据结构 关系表的基本操作 GIS 中关系表的应用
1、定义
• 在关系数据模型中,数据是以简单的记录形 式集中表达的, • 每一条记录代表一个事实(永久相关的值) • 记录的集合组成一个二维表
– 行(row )被称为记录(record),代表一个对象及其 相关的属性值 – 列(column)也称为字段(field)或项(item)代表一 个属性
• 例子:学生信息表
2、数据结构
• 多少字段,应该是什么 • 字段名: Field Name (Item Name): • 字段类型: Field Type (Item Type):
四、矢量数据模型-拓扑数据模型
1. 2. 3. 4. 术语 拓扑三角形 完全拓扑数据模型 GBF/DIME 数据模型 (US Census Bureau)
可以理解为矢量数据的压缩方式
1、术语(Terminology)
• • • • • • • • 顶点(Vertex ): 线性要素改变方向的点 线段(Line segment): 连接两个顶点的直线 多边形线(Polyline): 由一个以上的线段组成 线(Line): 通用术语,指线段或多边形线 Line : 结点(Node): 两个或多个线的交点 弧(Arc): 有方向的线 多边形(Polygon): 由一系列弧围成的面 标识点(Label point): 地图上用于放置标识的点
三、矢量数据模型( Spaghetti Model)
1) 实体与实体模型 (Spaghetti Model)
(a)定义
点、线、面要素的表达
(b)解释
(1) 简单列表表达(Simple lists) (2) 点目录(Point directory)
(c) Spaghetti models的比较 (d) 总结(Summary):
40
60
X
Polygon Topology
Poly A B C D Arcs a1, a2 a2, a4, 0, a3 a3 NILL Nodes n1, n4 n1, n4, 0, n2 n2 NILL Node n1 n2 n3 n4
Node Topology
Arcs a1, a2, a4 a3 NILL a1, a2, a4 Polygon A, B B, C 0, B A, B X, Y 80, 60 70, 25 25, 20 10, 25
Arc Topology
Arc a1 a2 a3 a4 Start Node n4 n1 n2 n1 End Node n1 n4 n2 n4 Left Poly. D B C D Right Poly. A A B B Shape Points s8 s2,s1 s4,s5,s3 s6,s7
Shape Point Table
A K H B G C I J
(xn, yn) (x1, y1)
(a)
(xn, yn)
F (b)
E (c)
D
一维矢量具有方向、长度
方向:即有起始结点和终止结点 长度:可以用以下方式表达:
引入欧氏空间的距离概 念: 长度 = ∑ [( xi − xi −1 ) 2 + ( y i − y i −1 ) 2 ]1 / 2
矢量模型(vector model)
一维矢量线
• 一维矢量可以闭合,但不能与自身相交 • 闭合时,首位相接, (x1,y1)=(xn,yn) 或(x1,y1,z1)=(xn,yn,zn) • 如果相交,则应以交点为界,将其分成几个一维矢量
(a)
(b)
(c)
(d)
一维矢量自身的可能空间关系
(x1, y1)
A
P1 P2 P5 P6 P7 P8 P1
B
P2 P3 P4 P6 P5 P2
P1: x1, y1 P2: x2, y2 P3: x3, y3 P4: x4, y4 P5: x5, y5 P6: x6, y6 P7: x7, y7 P8: x8, y8
思考题
1. 什么是关系数据模型(表)?关系数据模型的关键数据结 构要素有哪些? 2.什么是二进制搜索binary search?与穷尽搜索 (exhaustive search)对搜索表的需求方面有何不同? 3. 条件是如何用于选择被表达记录的? 4. 关系数据模型中进行表的连接(join)和相关(relate)操 作有何区别? 5.矢量数据模型是如何表达空间数据的?点、线、面特征是 如何被表达的? 6. 矢量数据模型的优缺点有哪些? 7. 简单列表数据模型和点目录数据模型的主要区别是什么? 这两种模型为什么不被认为是拓扑数据模型?
i=2 n
平面投影距离为地图学 研究广泛采用。
二维矢量-面
• 表示空间的一个面状要素 • 由一组闭合弧段所包围的空间区域 • 又称多边形
描述二维矢量的特征参数
• 面积:
– 二维面积: – 三维面积:表面积(计算复杂)和投影面积 (常用)
• 凹凸性:形态描述 • 单调性: • 走向、倾角和倾向:地形、地层描述中常 用的概念,是三维空间中曲面法向矢量的 另外一种描述方法
spaghetti models的比较
P2 (x2, y2) P1 (x1, y1) P3 (x3, y3)
B A
P5 (x5, y5)
P8 (x8, y8) P7 (x7, y7) P6 (x6, y6)
P4 (x4, y4)
Simple List Method
Polygon Representation
DLG (USGS)
思考题
1. 什么是弧(arc)和结点(node)?任何点都能 是结点吗?弧(arc)和多边形线( polyline,由 许多直线线段组成的线)的区别是什么? 2. 拓扑数据模型中的三个基本几何要素是如何用来 获取空间拓扑的? 3. 什么是拓扑数据模型?什么是拓扑三角形? 4. 拓扑数据模型的优缺点有哪些? 5. 用给定的拓扑三角形中的拓扑关系,试用拓扑数 据模型对一个简单地图进行编码。
i=2 n
在三维空间中一维矢量 的距离有两种概念一为 沿路程距离,表示为 长度 = ∑ [( xi − xi −1 ) 2 + ( y i − y i −1 ) 2 + z i − z i −1 ) 2 ]1 / 2 (
i=2 n
另一种为平面投影距离 ,二维平面的定义相同 : 长度 = ∑ [( xi − xi −1 ) 2 + ( y i − y i −1 ) 2 ]1 / 2
(1) 地理要素被当成单个对象对待
空间边界可以被清晰的编码
(2)对象之间没有关系
要素间的空间拓扑不被记录
矢量表达法
• 不同的空间特征具有不同的矢量维数
– 0维矢量-点:即空间中的一个点,没有大小、 方向,二维和三维欧氏空间中为:(x,y),(x,y,z) – 一维矢量-线:空间中的线划要素或空间对象间 的边界,也称为弧段、链 – 二维欧氏空间(x1,y1),(x2,y2),…(xn,yn) – 三维欧氏空间(x1,y1,z1),(x2,y2 , z2),…(xn,yn , zn) – 起点和终点称为结点(node),其它点称拐点 (vertex)
Point Directory Method
Polygon Representation Point Directory
B
P2 P3 P4 P6 P5 P2
P1: x1, y1 P2: x2, y2 P3: x3, y3 P4: x4, y4 P5: x5, y5 P6: x6, y6 P7: x7, y7 P8: x8, y8
2、拓扑三角形
Arc
Is part of
Node
Consists of
Polygon
3、完全拓扑数据模型
60 50 40 30 20 10 0
Y
s8 a1 n4 a4 s7 0 10 s1 n3 a4 20 30
a1
D
s2 B s3 a3 n
n1 a4 s6 80
A
a2 s5 50
D
C
2
s4 70
B
x2, y2 x3, y3 x4, y4 x6, y6 x5, y5 x2, y2
P2 (x2, y2) P1 (x1, y1)
P3 (x3, y3)
点 目 录 方 法
A
P1 P2 P5 P6 P7 P8 P1
P8 (x8, y8)
B A
P5 (x5, y5)
P4 (x4, y4) P7 (x7, y7) P6 (x6, y6)
Shape Point s1 s2 s3 s4 X, Y 20,25 60,35 55,25 70,15 Shape Point s5 s6 s7 s8 X, Y 48,15 80,10 10,10 10,60
空间实体示意图
空间实体拓扑结构的关系表
4、GBF/DIME 数据模型 (US Census Bureau)
空间曲面
• 矢量实现方法多样 • 常用等值线法、剖面法
三维矢量-体
• • • • • 指三维空间中的实体 由一组或多组闭合曲面所包围的空间对象 2维 面 2.5维 表面(surface) 2.5 surface 3维 体
