3.2回归分析
DOE详细讲解(两篇)

引言概述:本文将对设计实验(DesignofExperiments,简称DOE)进行详细讲解,旨在帮助读者深入了解和掌握这一方法。
DOE是一种系统的试验设计方法,通过合理地安排试验方案,可以帮助我们充分挖掘数据中的信息,从而更准确地预测和控制我们感兴趣的因变量。
本文将从DOE的基本原理、试验设计、数据分析和实际应用等方面进行阐述,希望能为读者提供一份全面的DOE参考文献。
正文内容:一、DOE的基本原理1.1DOE的定义和作用1.2影响因素与响应变量关系的建立1.3统计分析在DOE中的作用1.4DOE的优势与局限性1.5DOE的基本原理总结二、试验设计的基本原则2.1因素与水平的选择2.2试验设计的类型2.3试验次数的确定2.4试验方案的随机化与均衡2.5试验设计的基本原则总结三、DOE的数据分析3.1假设检验与方差分析3.1.1单因素方差分析3.1.2多因素方差分析3.1.3方差分析的解释和应用3.2回归分析与响应曲面法3.2.1简单线性回归分析3.2.2多元回归分析3.2.3响应曲面法的建模和优化3.3数据分析中常见问题的处理3.3.1离群值处理3.3.2缺失值处理3.3.3交互作用和噪声因素的分析3.4DOX的数据分析总结四、DOE在实际应用中的案例分析4.1工程设计中的DOE案例4.1.1确定最佳参数设置4.1.2优化产品设计4.1.3降低产品成本4.2制造过程优化中的DOE案例4.2.1优化工艺参数4.2.2提高产品质量4.2.3提高生产效率4.3医学研究中的DOE案例4.3.1药物剂量优化4.3.2疾病诊断与治疗4.3.3临床试验设计4.4DOX在实际应用中的总结五、DOE的发展与未来展望5.1DOE的发展历程5.2目前的研究热点与前沿5.3DOE在大数据时代的应用前景5.4DOE在新兴行业中的应用展望5.5DOX的发展与未来展望总结总结:DOE作为一种系统的试验设计方法,能够帮助我们更加准确地预测和控制感兴趣的因变量。
3.2回归分析

例题2 下表是随机抽取的8对母女的身高数据, 试根据这些数据探讨y与x之间的关系.
母亲身高x/cm 154 157 158 159 160 161 162 163 女儿身高y/cm 155 156 159 162 161 164 165 166
问题2:对于线性相关的两个变量用什么方法 来刻划之间的关系呢? 2、最小二乘估计 最小二乘估计下的线性回归方程:
ˆ a ˆ bx ˆ y
ˆ b
( x X )( y
i 1 i
n
i
Y )
(X
i 1
n
i
X)
ˆ ˆ Y bX a
例如: 对一作直线运动的质点的运动过程作了8次观 测,得到下表,试估计x=9s时的位置y的值。
例1.下表给出我国从1949至1999年人口数 据资料,试根据表中数据估计我国2004年 的人口数。
年份 49 人口 542 数/ 百万 54 603 59 672 64 705 69 807 74 909 79 975 84 89 94 1177 99 1246 1035 1107
对题中的数据进行检验
即建立的线性回归 模型是否合理?
需要对x,y 的线性相关 性进行检验
如何对一组数据之 间的线性相关程 度作出定量分析?
散点图只是形象地描述点的分布情况,它的“线性”是否 明显只能通过观察,要想把握其特征,必须进行定量的研究
建构数学
• 1.计算公式
相关系数
r=
(x
i=1 n i=1
n
i
- x)(yi - y)
例1.下表给出我国从1949至1999年人口数 据资料,试根据表中数据估计我国2004年 的人口数。
新大计量地理学实验指导03回归分析

本试验主要是引导学生掌握利用 SPSS 软件进行回归分析的基本方法,包括一元线性回归分析,多元线性回归分析,包含虚拟变量的线性回归分析,曲线参数估计法,二值多元Logistic 回归分析。
特别是,学生应掌握在 SPSS 软件中进行多元线性回归方法和曲线参数的估计方法。
线性回归分析(Linear 过程)回归分析(Regression) 是研究一个自变量或多个自变量与一个因变量(Dependent)之间是不存在某种线性关系或非线性关系的一种统计学分析方法。
而线性回归分析(Linear Regression) 是研究一个或多个自变量(independent)与一个因变量之间是否存在某种线性关系的统计学方法。
在菜单中选择Analyze==>Regression==>liner,系统弹出线性回归对话框如下:【Dependent 框】用于选入回归分析的应变量。
【Block 按钮组】由Previous 和Next 两个按钮组成,用于将下面Independent 框中选入的自变量分组。
由于多元回归分析中自变量的选入方式有前进、后退、逐步等方法,如果对不同的自变量选入的方法不同,则用该按钮组将自变量分组选入即可。
【Independent 框】用于选入回归分析的自变量。
【Method 下拉列表】用于选择对自变量的选入方法,有Enter (强行进入法)、Stepwise (逐步法)、Remove (强制剔除法)、Backward (向后法)、Forward (向前法) 五种。
该选项对当前Independent 框中的所有变量均有效。
【Selection Variable 框】选入一个筛选变量,并利用右侧的Rules 钮建立一个选择条件,这样,只有满足该条件的记录才会进入回归分析。
【Case Labels 框】选择一个变量,他的取值将作为每条记录的标签。
最典型的情况是使用记录ID 号的变量。
【WLS>>钮】可利用该按钮进行权重最小二乘法的回归分析。
多元回归分析讲解和分析预测法

2021/3/10
34
消除多重共线性的常用方法:
(一)删除不重要的自变量 自变量之间存在共线性,说明自变量所提供的信息是重叠的,可以 删除不重要的自变量减少重复信息。 (二)追加样本信息 由于资料收集及调查的困难,追加样本信息在实践中并不容易。 (三)利用非样本先验信息 非样本先验信息主要来自经济理论分析和经验认识。 (四)改变解释变量的形式 改变解释变量的形式是解决多重共线性的一种简易方法,例如对于 横截面数据采用相对数变量,对于时间序列数据采用增量型变量。 (五)逐步回归法
2021/3/10
51
参考流程图
Hale Waihona Puke 2021/3/1052
2021/3/10
53
传统机械按键结构层图:
按
PCBA
键
开关 键
传统机械按键设计要点: 1.合理的选择按键的类型, 尽量选择平头类的按键,以 防按键下陷。 2.开关按键和塑胶按键设计 间隙建议留0.05~0.1mm,以 防按键死键。 3.要考虑成型工艺,合理计 算累积公差,以防按键手感 不良。
2021/3/10
28
3.模型检验
2021/3/10
31
2021/3/10
32
t检验的基本步骤: 首先,通过公式计算t统计量
最后,进行判断
2021/3/10
33
4.多重共性分析
在预测分析中,若两个解释变量之间存在者较强的相关,则 认为回归分析中存在多重共线性。
多重共线性可能引起以下后果: (1)参数估计的精度较低; (2)回归参数的估计值对样本容量非常敏感,不稳定; (3)不能正确判断各解释变量对y的影响是否显著。 通过计算自变量之间的相关系数矩阵和经验直觉,来判断分 析自变量之间是否存在多重共线性。
3.2 回归分析-王后雄学案

张喜林制3.2 回归分析教材知识检索考点知识清单1.对于一组具有线性相关关系的数据,),,(),,(2211 y x y x),,(n n y x我们知道其回归方程的截距和斜率的最小二乘估计公式分别为:(1)(2)其中,1,111i ni i n i y n y x n x ∑∑==== 称为样本点的中心,回归直线必然过样本点的中心,,2e a bx y ++=⋅这里a 和b 为模型的未知参数,e 是y 与+=bx yˆ a之间的误差,通常e 为随机变量,称为随机误差,它的均值,0)(=e E方差.0)(2>=σe D这样线性回归模型的完整表达式为:=i eˆ.3 i eˆ 称为相应于点),(i i y x的残差.类比样本方差估计总体方差的思想,可以用 作为2σ的估计量,其中b h aˆ*ˆ 由相应公式给出,)ˆ,ˆ(b aQ 称为残差平方和( residual sum of squares).可以用2ˆσ衡量回归方程的预报精度,通常2ˆ,σ越小,预报精度越高.4.在研究两个变量间的关系时,首先要根据 来粗略判断它们是否线性相关,是否可以用线性回归模型来拟合数据,然后,可以通过残差 来判断模型拟合的效果,判断原始数据中是否存在可疑数据,这方面的分析工作称为残差分析,要点核心解读1.变量间的相关关系及线性回归方程(1)变量间的相关关系:①变量与变量间的两种关系:a .函数关系:这是一种确定性的关系,即一个变量能被另一个变量按照某种对应法则唯一确定.例如圆的面积S 与半径r 之间的关系2r s π=为函数关系.b .相关关系:这是一种非确定性关系.即当自变量取值一定时,因变量的取值有一定的随机性,它还受一些其他因素的影响,例如人的身高不能确定体重,但一般来说“身高者,体重也重”,我们说身高与体重这两个变量具有相关关系.相关关系又包括两种:a .在两个变量中,一个变量是可控制变量,另一个变量是随机变量,如施肥量与水稻产量.b .两个变量均为随机变量,如某学生的语文成绩与化学成绩.本书主要涉及上述相关关系的前一种情况.②散点图:将两个变量的各对数据在直角坐标系中描点而得到的图形叫做散点图,它直观地描述了两个变量之间有没有相关关系.这是我们判断的一种依据,③正相关与负相关:根据变量相关性的不同,线性相关关系可分为正相关与负相关.正相关是指两个变量之间的变化趋势方向一致,即一个变量随另一个变量的增长而呈增长趋势;负相关是指两个变量变化趋势方向相反,如产品单位成本降低,利润随之增加就是负相关.(2)线性回归方程:①线性回归模型:一组数据对应点在一条直线附近,但并不在同一条直线上,也就是说,两者之间不能用线性关系准确地表示出来,为此我们将两者之间的关系表示为,⊕++=εbx a y其中a+ bx 称为确定性函数,£称为随机误差,它产生的原因主要有:a .所用的确定性函数不恰当引起的误差.b .忽略了某些因素的影响;c .观测误差.我们将方程④称为线性回归模型( linearregression model).②回归直线:一般地,设x 与y 是具有相关关系的两个变量,且对应于几组观测值的几个点),,2,1)(,(n i y x i i =大致分布在一条直线附近,我们就称这两个变量之间具有线性相关关系.显然,这样的直线可以画出许多条,其中“最贴近”这些数据点的一条叫做回归直线,③线性回归方程:根据线性回归模型,对于每一个,i x对应的随机误差),(i i i bx a y +-=ε利用最小二乘法可求出线性回归方程( equation of linear regression)为.ˆˆˆxb a y += 其中的aˆ 称为回归截距,bˆ 称为回归系数,yˆ称为回归值.求b aˆˆ- 的具体计算公式为⎪⎪⎪⎩⎪⎪⎪⎨⎧-=-=--=∑∑∑∑∑=====.ˆˆ,)()()(ˆ22112111x b y aS y x xy x x n y x y x n b x n i i n i i n i i n i i n i i i 其中x与x S分别表示数据),,2,1(n i x i =的均值和标准差,γ⋅表示数据=⋅i y i (),,2,1n的均值,xy表示数据),,2,1(n i y x i i =的均值.b aˆˆ 的意义是:以aˆ 为基数,x 每增加一个单位,y 相应地平均变化⋅bˆ卜单位.从单调性 的角度看,回归系数0ˆ0ˆ<>b b h时,回归方程表示的函数分别是增函数、减函数.2.相关性检验x 与y 之间可以用一个直线方程x b a yˆˆˆ+= 来反映其关系,而对x 与y 的具体变化规律应对x 与y 作线性相关性检验,简称相关性检验.对于变量x 与y 随机抽取到的n 对数据,(1x),,(,),,(),221n n y x y x y检验统计量是样本相关系数=r,)()())((21211y y x xy y x xi n i i n i i i n i ----∑∑∑--= 即))((212221y n y x n x y x n y x r n i i nt i i i in i ---=∑∑∑--= 这种方法是用参数r 检验线性相关的程度,这个r 称为y 与x 的样本相关系数,简称相关系统( correlation coefficient).其中.11≤≤-r若r >0,则称x 与y 正相关,即x 增加,y 随之相应地增加;若x 减少,y 随之相应地减少.若r <0,则称x 与y 负相关,即x 增加,y 随之相应地减少;若x 减少,y 随之相应地增加,若r =0,则称x 与y 不相关,即x 与y 无线性相关关系,|x |越接近于1,y 与x 的线性相关程度越高,若r=l 或-1,则x 与y 为完全线性相关.|r |越接近于0,则x 与y 线性相关程度越弱.上面公式计算相关系数r ,通常计算量较大,通过变形可将上面公式化为⋅-=yx s s y x xy r 其中y x s s ,分别表示数据=i y x i i (,),,2,1n的标准差,检验的步骤如下:(1)提出统计假设x 与y 不具有线性相关关系;(2)根据小概率0.05与n-2在附表中查出 r 的一个临界值,05.0r(3)根据样本相关系数计算公式算出r 的值;(4)作出统计推断:如果05||αr r >表明有95%的把握认为x与y 之间具有线性相关关系,如果,||05αr r ≤我们没有理由拒绝原来的假设,这时寻求回归直线方程是毫无意义的.3.回归分析对于回归分析问题,在解题时应首先利用散点图或相关性检验判断x 与y 是否具有线性相关关系,如果线性相关,才能求解后面的问题.否则求线性回归方程没有实际意义,它不能反映变量x 与y 之间的变化规律.只有在x 与y 之间具有相关关系时,求线性回归方程才有实际意义.相关性检验的依据:主要利用检验统计量yx i n i i n i i in i s s y x xy y y x xyx n y x r -=---=∑∑∑--=21211)(.)( (其中化简式容易记也好用)求出检验统计量的样本相关系数,再利用r 的性质确定x 和y 是否具有线性相关关系,r 具有的性质为:1||≤r且|r |越接近于1,线性相关程度越强;|r |越接近于0,线性相关程度越弱.4.非线性回归分析问题(1)对于非线性回归分析问题,如果给出了经验公式可直接利用换元,使新元与y 具有线性相关关系,进一步求出y 对新元的线性回归方程,换回x 即可得y 对x 的回归曲线方程.(2)非线性回归问题有时并不给出经验公式,这时按以下步骤求回归方程:①画出已知数据的散点图,看是否是线性回归分析问题,如果不是,把它与必修数学中学过的函数(幂函数、指数函数、对数函数等)图像作比较,挑选一种跟这些散点拟合得最好的函数,采用适当的变量置换,把非线性回归分析问题化为线性回归分析问题.②作相关性检验,即判断寻找线性回归方程是否有意义,③当寻找线性回归方程有意义时,计算系数,ˆ,ˆb a得到线性回归方程.④代回x 得y 对x 的回归曲线方程.5.求线性回归方程的三种方法在求具有线性相关关系的两个变量之间的回归方程时,由于所给两个变量的数据较多并且量大,致使运算量大且繁杂,常常使我们望而生“畏”,望而生“烦”,下面给出求线性回归方程的几种方法,以供参考.(1)用最小二乘法求线性回归方程:对于两个变量,在确定具有线性相关关系后,可以利用“最小二乘法”来求回归方程.用“最小二乘法”求线性回归方程的关键在于正确地利用回归方程中系数公式=--=∑∑==a xn x y x n y x b i ni i in i ˆ,ˆ2211 .ˆx by - 求出系数,ˆ,ˆb a这样回归方程也就建立起来了.为了使计算更加有条理,我们通过制作表格来先计算出212111i n i thn i ih n i i n i y x y x ∑∑∑∑====、和,1ii ni y x ∑= 再计算出,1,111i ni i n i x n x y n y ∑∑==== 然后利用公式yy n i i xx L x n x L ,212-=∑=-=-=∑∑==ni i i xy n i iy x L y n y 1212, ,y x n计算,ˆˆ,ˆx b y a r x xxL L -== 最后写出线性回归方程..ˆˆˆa x b y+= (2)用函数型计算器求线性回归方程:在求线性回归方程时,所给的数据一般较多,运算量大,我们可以借助函数型计算器来代替人工完成这种复杂的数字计算,以提高运算速度.(3)用Excel 软件作散点图并求线性回归方程.在直角坐标系中描出数据的散点图,直观判断散点图是否在一条直线附近;用线性回归方程拟合二者的关系,这一过程还可以用Excel 软件来帮助我们完成,实现上机操作, 典例分 类剖析考点1 相关关系命题规律当一个变量变化时,另一个变量的取值有一定的相关性,这种关系是相关关系.相关关系可以利用散点图和相关系数进行判定.[例1] 在某种产品表面进行腐蚀刻线试验,得到腐蚀深度y 与腐蚀时间x 的一组数据如下表所示.(1)画出散点图.(2)根据散点图,你能得出什么结论?[解析] 利用散点图,直观地归结出相关关系的两个变量所具备的特点,【解] (1)如图3-2 -1所示散点图.(2)结论:设戈与y 是具有相关关系的两个变量,且相应于n 组观测值的n 个点大致分布在一条直线附近,其中整体上与这n 个点最接近的一条直线最能代表x 与y 之间的关系.[点拨]散点图能帮助我们发现变量之间的线性关系,直观地反映了数据的变化规律.母题迁移 1.如图3 -2-2所示的5组数据中,去掉占剩下的4组数据的线____点, 性相关系数最大.考点2求线性回归方程命题规律利用公式yx S S y x xy r -= 计算相关系数,与对应r 的一个临界值进行比较,确定x 、y 之间是否相关;运用相应公式求出线性回归方程中的函数.ˆ,ˆb a[例2]近几年来,随着我国经济的发展,汽车已进入普通百姓家中.根据某汽车协会资料统计,国产某种型号家庭轿车的使用年限x (年)和所支出的维修费用y (千元),如下表:(1)求出相关系数r ,并根据所求的r 判断两个变量之间的线性相关关系的强弱;(2)试求出回归直线方程,若某家庭购得此型号的汽车,请你为他们估计一下使用年限为10年时,维修费用是多少?、 [解析] 通过求出相关系数r ,从而判断出是否具有相关关系;再求回归方程,从而进行回归预测.[解] (1)根据公式,求得r≈0.9792 >0.878,故两个变量之间有较强的线性相关关系. ?(2)设所求的回归方程为,ˆˆˆa x b y+= 则,08.0ˆˆ,23.155ˆ225151=-==--=∑∑==x b y a xx y x y x b i i i ii 即所求的回归直线方程为.08.023.1ˆ+=x y当x=10时,代入回归直线方程得,38.12ˆ=y所以估计使用年限为10年时,维修费用是1.238万元.[点拨] 求x 与y 的回归直线方程,应首先判断x 与y 是否具有线性相关关系,如果直接求x 与y 的回归直线方程,它就没有任何实际价值,也就不能准确反映变量x 与y 之间的变化规律.母题迁移2.测得某种物质在温度x (单位:℃)下吸附另一种物质的重量y(单位:mg)的对应数据如下:(1)对变量y 与x 进行相关性检验;(2)若x 与y 具有线性相关关系,求y 对x 的回归直线方程[例3] 已知某地每单位面积菜地年平均使用氮肥量x( kg)与每单位面积蔬菜年平均产量y(t)之间的关系有如下数据:(1)求x 与y 之间的相关系数,并检验是否线性相关;(2)若线性相关,求蔬菜产量y 与使用氮肥量x 之间的回归直线方程,并估计每单位面积施肥150 kg 时,每单位面积蔬菜的年平均产量.[解析] (1)使用样本相关系数计算公式来完成.(2)先作统计假设,由小概率0.05与n-2在附表中查得相关系数临界值,05L r若05.0r r则线性相关,否则不线性相关.[解] 列出下表,并用科学计算器进行相关计算:)15)(15(15)1(215121215121151---=--⋅-=∑∑∑y y x x y x y x r i i i ii )11.101555.1628)(10115161125(11.10101158.16076⨯-⨯-⨯⨯-= 45.87915.760~ .864.0~由小概率0.05与n-2 =13在附表中查得,514.0.0=ωrx r r ∴>,||05α与y 线性相关.221511511515ˆ)2(x xyx y x b ii i ii -⋅-=∑∑== 21011516112511.10101158.16076⨯-⨯⨯-= ,37.0~ω.6463.010137.011.10ˆˆ=⨯-=-=ωx b y a.‘.回归直线方程为.6463.00937.0ˆ+=x y...当每单位面积施肥150 kg 时,每单位面积蔬菜的年平均产量为⋅=+⨯)(7.14~~7013.146463.015037.0t ω[点拨] 求解两个变量的相关系数及它们的回归直线方程的计算量较大时,需要细心、谨慎地计算.母题迁移 3:-个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,测得的数据如下:(l)y 与x 是否具有线性相关关系?(2)如果y 与x 具有线性相关关系,求回归直线方程.(3)根据求出的回归直线方程,预测加工150个零件所用的时间为多少?考点3 线性回归方程的三种解法[例4】测得某地10对父子身高(单位:英寸)如下:父亲身高(x )606264656667687067 68 707274儿子身高(y)63.665.26665.566.967.165. 5 66. 9 67. 167.468: 370.17070如果x 与y 之间具有线性相关关系,求线性回归方程,如果父亲的身高为78英寸,试估计儿子的身高.[解] 解法一:先将两个变量的有关数据在表中计算出来,如下表所示:由表中数据可计算,====101.6,8.6610668r y x=∑=1101,01.67y x i i,44794,4.448422111=∑=x i,101293.44941∑==⋅i y i代入公式=⨯-⨯⨯-28.66104479401.678.66104.44842 ≈6.17172.79 .646.04所以4646.001.67ˆˆ-=-=x b y a.975.358.66≈⨯因而所求得线性回归方程为:.975.354646.0ˆ+=x y当78=x时,=yˆ 975.35784646.0+⨯.2.722138.72≈=所以当父亲的身高为78英寸时,估计儿子的身高约为72.2英寸.解法二:用计算器求这个线性回归方程:(计算参数)a得35.977,(计算参数)ˆb得0.4646.所以所求线性回归方程为:.977.354646.0ˆ+=x y当78=x时,⨯=4646.0ˆy.2.722158.72977.3578≈=+所以当父亲的身高为78英寸时,估计儿子的身高约为72.2英寸,解法三:运用计算机中的Excel 软件:(1)输入数据x ,y:x6062646566672.665.6368707274y9.566.66654.167.67)2.(170.370.68选择数据,生成散点图:在菜单中选定“插入”中的“图表”,选择“xy 散点图”,连续点击“下一步”,可得到如图3 -2 -3所示的散点图.(3)建立回归直线:选中“图表”中的“添加趋势线”,点击“类型”标签,选定“趋势预测/回归分析类型”中的“线性”选项,单击“确定”,得到回归直线.(4)求得回归直线方程:双击回归直线,弹出“趋势线格式”,单击“选项”,选定“显示公式”,最后单击“确定”就得到回归直线方程,如图3 -2 -4所示.所求回归直线方程为:;977.354646.0ˆ+=x y当x=78时,977.35784646.0ˆ+⨯=y,2.722158.72≈=所以当父亲的身高为78英寸时,估计儿子的身高约为72.2英寸.[点拨] (1)“最小二乘法”是求线性回归方程常用的方法,在线性回归方程b a lr a x b yˆ,ˆ,ˆˆˆ+= 是线性回归方程中的系数,其中bˆ 是线性回归的斜率,表示自变量变化1个单位时因变量的平均变化值,在数值计算的过程中可以用计算器来帮助完成复杂的计算.(2)用函数型计算器求线性回归方程,避免了繁琐的计算,节省了时闽,因而大大地提高了解题的速度.(3)在运用计算机中的Excel 软件求线性回归方程时,只要严格按照运算程序一步步进行下去,最终总能求出回归直线方程并且得到如上图的图像,总之,求线性回归方程的方法是较多的,既有最常用的“最小二乘法”,又有简便易行的计算器法,还有用计算机软件来完成的方法,这些方法在以后的学习中同学们要逐步体会,考点4非线性回归的转化命题规律借助指数、幂、对数函数,将变量间的变换转化为回归问题.[例5] 在一化学反应过程中某化学物质的反应速度yg /min 与一种催化剂的量xg 有关,现收集了8组数据列于表中,试建立y 与x 之间的回归方程.[解析] 两个变量不一定是线性关系,不能直接利用线性回归方程建立两个变量的关系,可以通过变换的方法将非线性关系转化为线性回归模型.[解】根据收集的数据作散点图:图3 -2 -5根据样本点分布情况,可选用两种曲线模型来拟合.(1)可认为样本点集中在某二次曲线221c x c y +=的附近,令,2x t =则变换后样本,点 应该分布在直线==+=a c b a bt y ,(1)2c的周围,由题意得变换后的t 与y 的样本数据表如下:作y 与 t 的散点图,由y 与t 的散点图可观察到样本数据点并不分布在一条直线的周围,因此不宜用线性回归方程a tb yˆˆˆ+=来拟合,即不宜用二次曲线221c x c y +=来拟合y 与x 之间的关系.(2)根据x 与 y 的散点图也可以认为样本点集中在某一条指数型函数曲线.1c e c y =的周围,今,ln y z =则,ln 12c x c z +=即变换后样本点应该分布在直线),ln (21c b c a a bx z ==+=的周围,由y 与x 数据表可得z 与x 的数据表作出z 与x 的散点图.由散点图可观察到大致在一条直线上,所以可用线性回归方程来拟合它,由z 与x 的数据表,得到线性回归方程,,8485.01812.0ˆ-=x z所以非线性回归方程为,ˆ8485.01812.0-=x e y因此,该化学物质反应速度关于催化剂的量的非线性回归方程为8485.01812.0ˆ-=x e y[点拨] 非线性回归问题有时并不给出经验公式,这时我们可以画出已知数据的散点图,把它与学过的各种函数图像作比较,挑选一种跟这些散点拟舍得最好的函数,然后像本例这样,采用适当的变量置换,把问题化为线性回归分析问题,使之得到解决,母题迁移4.某种图书每册的成本费y(元)与印刷册数x(千册)有关,经统计得到数据如下:检测每册书的成本费y与印刷册数的倒数1x之间是否具有线性相关关系?如有,求出y对x的回归方程.优化分层测训学业水平测试1.下列变量之间的关系是函数关系的是( ).A .已知二次函数,2c bx ax y ++=其中a ,c 是已知常数,取b为自变量,因变量是这个函数的判别式ac b 42-=∆B .光照时间和果树亩产量C .降雪量和交通事故发生的数量D .每亩施用肥料量和粮食产量2.对于线性相关系数r ,下列叙述正确的是( ).||),,0(||.r r A +∞∈越大,相关程度越大,反之,相关程度越小r r B ),,(||.+∞-∞∈越大,相关程度越大,反之,相关程度越小,1||.≤r C且lrl 越接近于1,相关程度越大;|r |越接近于0,相关程度越小D .以上说法都不对3.工人月工资y (元)按劳动生产率x (千元)变化的回归方程为,8050ˆx y+= 下列判断正确的是( ).①劳动生产率为1000元时,则月工资为130元;②劳动生产率提高1000元时,则月工资提高80元;③劳动生产率提高1000元时,则月工资提高130元;④当月工资为210元时,劳动生产率为2000元.A .① B.② C.③. D .④4.为了考查两个变量x 和y 之间的线性关系,甲、乙两位同学各自独立做了10次和15次试验,并利用线性回归方法,求得回回归直线分别为,21l l N已知两人获得的试验数据中,变量x 和y的数据的平均值都相等,且分别都是s 、t ,那么下列说法正确的是( ).A .直线21*nl l一定有公共点(s ,t)B .直线21*l l ∏相交,但交点不一定是(s ,t)C .直线21*nl l可能没有交点21.kJl l D必定重合5.在一次实验中,测得(x ,y)的四组值分别是A(l ,2),B(2,3),),5,4(),4,3(D C则y 与x 之间的回归直线方程为( ).1ˆ.+=x yA 2ˆ+=⋅x yB 12ˆ+=⋅x yC 1ˆ.-=x yD 6.弹簧长度),( cm)随所挂物体质量x(g)不同而变化的情况如下:(1)画出散点图;(2)求y 对x 的回归直线方程;(3)预测所挂物体的质量为27 g 时的弹簧长度(精确到0.01 cm).7.随着人们经济收入的不断增长,购买家庭轿车已不再是一种时尚.车的使用费用,尤其是随着使用年限的增加,所支出的费用到底会增长多少,一直是购车一族非常关心的问题.某汽车销售公司为此进行了一次抽样调查,并统计得出某款车的使用年限x 与所支出的总费用y (万元)有如下的数据资料:若由资料知,y 对x 呈线性相关关系,试求:(1)线性回归方程a xb yˆˆˆ+= 的回归系数,ˆˆb a、 (2)估计使用年限为10年时,车的使用总费用是多少?嵩考能力测试(测试时间:90分钟测试满分:120分)一、选择题(本大题共7小题,每小题5分.共35分)1.下面两个变量间的关系不是函数关系的是( ).A .正方形的棱长与体积B .角的度数与它的正弦值C .单产为常数时,土地面积与粮食总产量D .日照 时间与水稻亩产量2.(2011年江西高考题)变量x 与y 相对应的一组数据为,10();5,13(),4,5.12(),3,8.11(),2,3.11(),1变量u 与v 相对应的一组数据为),2,5.12(),3,8.11(),4,3.11(),5,10(1),1,13(r表示变量y 与x 之间的线性相关系数,2r表示变量v 与u 之间的线性相关系数,则().0.12<<r r A120.r r B <<120.r r C <<12.r r D =3.为了表示n 个点与相应直线在整体上的接近程度,我们常用( ).)ˆ(.1i i ni y y A -∑=表示)ˆ(.1i i ni y y B -∑=表示21)ˆ(.i i ni y y C -∑=表示21)(.y y D i ni -∑=表示4.设一个回归方程为,53ˆx y -=变量x 增加一个单位时( ).A .y 平均增加3个单位 B.y 平均减少5个单位C.y 平均增加5个单位 D.y 平均减少3个单位5.线性回归方程a xb yˆˆˆ+= 必过( ).)0,0.(A)0,.(x B),0(y C ⋅),.(y x D6.已知两个变量x 和y 之间具有线性相关关系,5次试验的观测数据如下:经计算得回归方程a bx y+=ˆ 的系数,575.0=b则a=9.14.-A9.13.-B9.12.-C9.14.D7.判断图3 -2 -8中的两个变量,具有相关关系的是( ).二、填空题(本大题共3小题,每小题5分,共15分)8.(2011年广东高考题)某数学老师身高176 cm ,他爷爷、父亲和儿子的身高分别是173 cm ,170 cm 和182 cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为____ cm.9.-唱片公司欲知出歌费用x (十万元)与唱片销售量y (千张)之间的关系,从其所发行的唱片中随机抽选了10张,得到如下的资料:,4.303,282101101==∑∑≡=i i ti x x γ ,5.598,75211011101==∑∑≈y yx i i ,237101=∑≈i ti y x则y 与x 的相关系数r 的绝对值为10.某五星级大饭店的入住率x(%)与每天每间客房的成本,,(元)如下:则y 关于x 的回归直线方程是____三、解答题(70分)11.(10分)设有资料如下表所示:两位评酒员对10种品牌白酒的主观排序及白酒种类试问两位评酒员的评审顺序是否具有一定的线性相关关系?(按5%的显著水平检验)12.(12分)用镁合金X 光探伤时,要考虑透视电压U 与透视厚度l 的关系,做了5次独立试验结果如下:(1)画出散点图;(2)进行相关性检验;(3)求U 关于l 的线性回归方程,并预测当透视厚度l 为40 mm 时,透视电压U 是多少千伏.13.(12分)下表提供了某厂节能降耗技术改造后生产甲产品过’程中记录的产量x(t)与相应的生产能耗y (吨标准煤)的几组数据:(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出Y 关于x 的线性回归方程;ˆˆˆa x b y+= (3)已知该厂技改前100t 甲产品的生产能耗为90t 标准煤.试根据(2)求出的线性回归方程,预测生产100t 甲产品的生产能耗比技改前降低多少吨标准煤?(参考数值:3×2.5+4 x3 +5 x4+6 x4.5 =66.5)14.(12分)每立方米混凝土的水泥用量x (单位:kg )与28天后混凝土的抗压强度(单位:)/2cm kg之间的关系有如下数据:(1)对变量y 与x 进行相关性检验;(2)如果y 与x 之间具有线性相关关系,求回归直线方程.15.(12分)下表为收集到的一组数据:(1)作出x 与y 的散点图,并猜测x 与y 之间的关系;(2)建立x 与y 的关系,预报回归模型并计算残差;(3)利用所得模型,预报x=40时y 的值.16.(12分)已知10只狗的血球体积及红血球数的测量值如下表:(1)画出上表的散点图;(2)求出回归直线方程.单元知识整合2.本章注意问题在本章的学习中我们必须注意以下几个问题:(1)函数关系是一种确定关系,而相关关系是一种非确定关系,函数关系有具体的函数关系式,而相关关系没有一个确定的关系式,用回归直线来估计相应的量的关系,但这种关系也不是确切的,存在着一定的误差.(2)利用散点图来确定两个变量之间是否具有线性相关关系时,作图要规范,如果样本点呈条形分布,我们就认为具有线性相关关系,如果有个别的样本点出现异常,而绝大多数的样本点在这个条形区域内,我们可以不考虑这个别的点,或认为这几个出现异常的点对我们的结论影响不大.但如果出现异常的点过多就认为不具有线性相关关系.(3)样本相关系数的计算公式为,)()())((21211y y x xy y x x r i n i i n i i i n i ----=∑∑∑=-= 可以用来衡量两个变量之间的线性相关关系,当r >0时,表示两个变量正相关;当r<0时,表示两个变量负相关.在实际判断中用…进行衡量,如果|r |越接近于1,表明两个变量之间的线性相关性越强,|r |越接近于0,表明两个变量之间几乎不存在线性相关关系;通常当|r |大于0.75时,就认为两个变量之间有很强的线性相关关系,就可以求回归直线方程,并且在r >0时,回归系数bˆ 为正,在r<0时,bˆ 为负.(4)回归直线方程a xb yˆˆˆ+= 过样本点中心).,(y x(5)在线性回归模型中,随机误差用y ∧预报真实值_y 的误差.它是一个不可预测的变量,但可以通过这个随机变量的数字特征来刻画它的一些总体特征,均值是反映随机变量取值平均水平的数字特征,方差是反映随机变量集中于均值程度的数字特征,而随机误差的均值为O ,因此可以用方差来衡量随机误差的大小.(6)在研究两个变量之间的关系时,可以先根据散点图来粗略地判断它们是否存在线性相关关系,是否可以用线性回归模型来拟合两个变量的关系,如果可以用线性回归模型来拟合时,再求出面归直线方程,.最后再作残差分析来判断拟合的效果,并判断原始数据中是否存在可疑数据.(7)在判断两个分类变量的可信程度时要特别注意计算的准确度,准确代数,准确计算,准确比较,准确下结论.(8)在实际问题中,经常会面临需要推断的问题,在对问题进行推断时,我们不能仅凭主观意愿作出结论,还需要通过收集数据,并根据独立性检验的基本原理作出合理的推断.(9)统计方法是可能犯错误的,不管是回归分析还是独立性检验,得到的结论都可能犯错误,好的统计方法就是要尽量降低犯错误的概率,比如在推断吸烟与患肺癌是否有关时,通过收集数据、整理分析数据得到“吸烟与患肺癌有关”的结论,而且这个结论出错的概率在0.01以下,实际上这是统计思维与确定性思维差异的反应.结合本章的学习,谈谈你对统计思维和确定性思维差异的理解.3.热点透视(1)独立性检验思想在日常生活中的应用.(2)了解线性回归思想,会求线性回归方程及进行相关性检验,掌握回归分析在生活中的应用.4.思想方法总结类型1 独立性检验思想在生活中的应用 ‘由题意列出事件A 与B 的2×2列联表,据公式计算出,2x若,706.22>x则有90%的把握认为事件A 与B 有关,若>2x,635.6则有99%的把握认为事件A 与B 有关;若,828.102>x则有99.9%的把握认为事件A 与B 有关,若,706.22≤x。
回归分析知识点总结框架

回归分析知识点总结框架一、引言1.1 背景介绍1.2 研究目的1.3 研究意义1.4 文章结构二、回归分析的基本概念2.1 回归分析的定义2.2 回归分析的基本原理2.3 简单线性回归与多元线性回归的区别2.4 回归分析的应用领域三、回归分析的基本假设3.1 线性关系假设3.2 多重共线性假设3.3 随机误差项的假设3.4 检验回归模型的假设条件四、简单线性回归4.1 简单线性回归的模型4.2 参数估计4.3 拟合优度的度量4.4 假设检验4.5 模型诊断4.6 模型应用与解释五、多元线性回归5.1 多元线性回归的模型5.2 参数估计5.3 拟合优度的度量5.4 假设检验5.5 多重共线性的诊断和处理 5.6 异方差的诊断和处理5.7 模型的解释与应用六、回归模型的诊断6.1 残差分析6.2 异方差性检验6.3 多重共线性检验6.4 模型的适用性检验6.5 模型的稳健性检验七、回归分析的应用案例7.1 教育经济学中的回归分析 7.2 医学研究中的回归分析7.3 金融领域中的回归分析7.4 市场营销中的回归分析7.5 社会科学研究中的回归分析八、高级回归模型8.1 非线性回归模型8.2 广义线性模型8.3 自变量选择与建模8.4 时间序列回归分析8.5 多层次回归分析九、回归分析软件的应用9.1 SPSS中的回归分析9.2 SAS中的回归分析9.3 R语言中的回归分析9.4 Python中的回归分析9.5 MATLAB中的回归分析十、结论与展望10.1 研究总结10.2 研究不足10.3 未来研究方向十一、参考文献十二、附录以上是回归分析知识点总结的框枋,每个部分可以进一步细化,写入详细的内容来进行阐述。
3.2 双变量线性回归模型的参数估计

i
i
i
ˆ
X Y X
2 i
i i
样本回归线的性质
通过Y和X的样本均值点 估计的Yi的均值等于实际观测的Yi的 均值 残差的均值为0 残差与解释变量Xi不相关 残差与估计的Yi值不相关
高斯定理
结论:在古典假定条件下 ,OLS 估计式是最佳线 性无偏估计式(BLUE)
三、最大似然估计法(ML)
2
评价要素(高斯定理前奏)
1.无偏性,方法、样本一定,抽样不同 2.最小方差性,样本一定,方法不同 3.渐进性,大样本时,具有最小渐近方差 (渐近有效)
二、参数的普通最小二乘估计(OLS)
给定一组样本观测值(Xi, Yi)(i=1,2,…n)要 求样本回归函数尽可能好地拟合这组值。
普通最小二乘法(Ordinary least squares, OLS)给出的判断标准是:残差的平方和最小。
基本原理: 对于最大似然法,当从模型总体随机抽 取n组样本观测值后,最合理的参数估计量 应该使得从总体中抽取该n组样本观测值的 概率最大。
双变量线性回归模型: Yi 1 2 X i ui
在满足11条基本假定的条件下
Yi ~ i.i.n.(1 2 X i , )
2
Yi的概率密度函数为 (i=1,2,…n)
将该似然函数极大化,即可求得到模型参 数的最大似然估计量。
对lnLF求极大值:
解得模型的参数估计量为:
2
~ ( X X )(Y Y ) x y x (X X )
i i i 2 i 2 i i
1 Y 2 X
~
~
2 ~2 u ˆ i n
可见,在满足一系列基本假设的情况下, 模型结构参数的最大似然估计量与普通最小 二乘估计量是相同的。
数据统计分析方法

数据统计分析方法标题:数据统计分析方法引言概述:数据统计分析是一种通过收集、整理、处理和解释数据来揭示数据背后规律和趋势的方法。
它在各个领域中都有广泛的应用,包括市场调研、金融分析、医学研究等。
本文将介绍数据统计分析的五个主要方法。
一、描述性统计分析1.1 数据的中心趋势测量:通过计算平均值、中位数和众数等指标来描述数据的中心位置。
1.2 数据的离散程度测量:通过计算标准差、方差和四分位差等指标来描述数据的离散程度。
1.3 数据的分布特征分析:通过绘制直方图、箱线图和概率图等图表来分析数据的分布特征。
二、推断统计分析2.1 参数估计:通过样本数据来估计总体参数,如均值、比例和方差等。
2.2 假设检验:通过收集样本数据并进行统计推断,来验证关于总体参数的假设。
2.3 方差分析:用于比较两个或多个总体均值是否存在显著差异的统计方法。
三、回归分析3.1 线性回归分析:通过建立线性模型来研究自变量与因变量之间的关系,并进行参数估计和显著性检验。
3.2 多元回归分析:在线性回归的基础上,引入多个自变量来解释因变量的变异。
3.3 非线性回归分析:适用于自变量与因变量之间存在非线性关系的情况,可以通过拟合曲线来进行分析。
四、时间序列分析4.1 趋势分析:通过绘制时间序列图和计算趋势指标,来分析数据的长期趋势。
4.2 季节性分析:通过分解时间序列数据,研究数据中的季节性变动。
4.3 预测分析:利用历史数据来预测未来的趋势和变动。
五、因子分析5.1 主成分分析:通过降维技术,将多个相关变量转化为少数几个无关变量,以便更好地理解数据。
5.2 因子提取:通过因子分析方法,提取出能够解释原始变量方差的共同因子。
5.3 因子旋转:通过旋转因子载荷矩阵,使得因子具有更好的解释性和解释力。
结论:数据统计分析方法是一种重要的工具,可以帮助我们理解数据背后的规律和趋势。
在实际应用中,根据具体情况选择合适的统计方法非常重要。
同时,数据的质量和样本的大小也会对统计分析的结果产生影响,因此在进行数据统计分析时,需要注意数据的收集和处理过程。
数学苏教选修课后训练: 回归分析 含解析

3.2 回归分析练习1.对某种机器购置后运营年限次序x(1,2,3,…),与当年增加利润y的统计分析知具备线性相关关系,回归方程为:y=10.47-1.3x,估计该台机器使用__________年最合算.2若由此资料知y与.3由资料表明y对__________万元.4)的几组统计数据:__________.5.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:试预测加工106.某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发=+;求出y关于x的线性回归方程y bx a(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?7如果y与x(1)作出这些数据的散点图;(2)求这些数据的线性回归方程;(3)预测当广告费支出为9百万元时的销售额.8.有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得(2)从散点图中发现气温与热饮销售杯数之间关系的一般规律;(3)求回归方程;(4)如果某天的气温是2 ℃,预测这天卖出的热饮杯数.9.某个服装店经营某种服装,在某周内获纯利y(元),与该周每天销售这种服装件数x已知721280iix==∑,2145309iiy==∑,13487i iix y==∑.(1)求x,y;(2)判断纯利y与每天销售件数x之间是否线性相关,如果线性相关,求出回归方程.10.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次(2)据此估计加工200个零件所用的时间是多少?参考答案1. 答案:8解析:令y ≥0,即10.47-1.3x ≥0,∴x ≤8,∴估计该台机器使用8年较为合算. 2. 答案:y =0.08+1.23x解析:代入5152215=1.235i ii ii x y x yb xx ==-=-∑∑,y a bx =+,∴a =0.08.∴线性回归方程是y =0.08+1.23x . 3. 答案:64.5解析:∵x =95,y =50代入公式求得b =0.58,a =-5.1, ∴线性回归方程为y =0.58x -5.1.将x =120代入线性回归方程得y =64.5(万元).∴估计购买120平方米的房屋时,购买房屋费用是64.5万元. 4. 答案:y =1.23x +0.08 解析:∵521ii x=∑=4+9+16+25+36=90,且x =4,y =5,n =5,∴112.354512.31.239051610b -⨯⨯===-⨯,a =5-1.23×4=0.08,∴回归直线为y =1.23x +0.08. 5. 解:2+3+4+5=3.54x =, 2.5+3+4+4.5 3.54y ==,41i ii x y =∑=2×2.5+3×3+4×4+5×4.5=52.5,421ii x=∑=4+9+16+25=54,∴252.54 3.5 3.50.7544 3.5b -⨯⨯==-⨯, a =3.5-0.7×3.5=1.05.∴回归直线方程为y =0.7x +1.05, 当x =10时,y =0.7×10+1.05=8.05, ∴预测加工10个零件需要8.05小时. 6. 解:(1)由数据,求得x =13(11+13+12)=12, y =13(25+30+26)=27,3x y =972.31i ii x y =∑=11×25+13×30+12×26=977,321ii x=∑=112+132+122=434,23432x =.由公式,求得122197797254344322ni ii ni i x y nx yb x nx==--===--∑∑,a y bx =-=27-52×12=-3.所以y 关于x 的线性回归方程为y =52x -3. (2)当x =10时,y =52×10-3=22,|22-23|<2. 同样,当x =8时,y =52×8-3=17,|17-16|<2.所以,该研究所得到的线性回归方程是可靠的.7. 解:(1)(2)x =5,y =50,511390i ii x y==∑,521145i i x ==∑,515221572i ii ii x y x yb xx ==-==-∑∑,a =y -b x =15,∴线性回归方程为y =7x +15.(3)当x =9时,y =78.即当广告费支出为9百万元时,销售额为78百万元. 8. 解:(1)散点图如下图所示:(2)从上图看到,各点散布在从左上角到右下角的区域里,因此,气温与热饮销售杯数之间呈负相关,即气温越高,卖出去的热饮杯数越少.(3)从散点图可以看出,这些点大致分布在一条直线的附近,因此,可用公式求出回归方程的系数.x ≈15.364,y ≈111.636,11214335i i x ==∑,11114778i i i x y ==∑.∴11111222111 2.3521111i ii ii x y x yb xx x ==-=≈---∑∑.a y bx =-≈147.767.∴回归方程为:y =-2.352x +147.767. (4)当x =2时,y ≈143.因此,某天的气温为2 ℃时,这天大约可以卖出143杯热饮. 9. 解:(1)3+4+5+6+7+8+967x ==,66+69+73+81+89+90+9179.867y =≈;(2)画出散点图可知,y 与x 有线性相关关系, 设回归直线方程:y bx a =+,5593487761337 4.7528073628b -⨯⨯===-⨯,a =79.86-6×4.75=51.36,∴回归直线方程y =4.75x +51.36.10. 解:(1)列出下表,并用科学计算器进行计算.设所求的回归直线方程为bx a =+.同时,利用上表可得1011022211055950105591.70.66838500105510i ii ii x y x yb xx ==--⨯⨯==≈-⨯-∑∑, a y bx =-=91.7-0.668×55=54.96,即所求的回归直线方程为y =0.668x +54.96.(2)这个回归直线方程的意义是当x 增大1时,y 的值约增加0.668,而54.96是y 不随x增大而变化的部分.因此当x=200时,y的估计值为y=54.96+0.668×200=188.56≈189.故加工200个零件时所用的时间约为189分.。
何晓群:《应用回归分析》第四版-第三章多元线性回归

由 y X 及正态假定 ~ N (0, 2In ) , 有
y ~ N ( X , 2 In )
于是, 似然函数为
L
(2
)n/ 2 (
2
)n / 2
exp{
1
2
2
(
y
X
)'(
y
X
)}
对数似然函数为
ln
L
n 2
ln(2
)
n 2
ln(
2
)
1
2
2
(
y
北京 天津 河北 山西 内蒙古 辽宁 吉林 黑龙江 上海 江苏 浙江 安徽 福建 江西 山东 河南 湖北 湖南 广东 广西 海南
x1 1.94 0.33 6.16 5.35 3.78 11.2 2.84 8.64 3.64 30.9 6.26 4.13 5.85
6.7 10.8 4.16 4.64 7.08 16.3 4.01
(3.23)
为 yi 的残差. 称 e (e1,e2 ,,en )' y yˆ 为回归残差向量. 有
e y Hy (I H ) y
e y Hy (I H ) y 记
cov(e, e) (cov(ei , e j ))nn 为残差向量 e 的协方差阵, 或称为方差阵. 记为D(e).
yn 0 1 xn1 2 xn2 p xnp n
(3.4)
y1 0 1 x11 2 x12 p x1 p 1 y2 0 1 x21 2 x22 p x2 p 2
yn 0 1 xn1 2 xn2 p xnp n
高中数学苏教版选修2-3同步课件:3.2 回归分析

xi- x · yi- y 2
i=1
课前探究学习
课堂讲练互动
i=1
xiyi-n x y
.
n
n
=
2 2 x2 y2 i -n x · i -n y i=1 i=1 n
因为两式的分子相同,而分母都大于0,所以b与r的符号相同.
^
课前探究学习
课堂讲练互动
平均值.
课前探究学习
课堂讲练互动
题型一 线性相关的判断 【例1】 某校高三(1)班的学生每周用于数学学习的时间x(单位:h) 与数学平均成绩y(单位:分)之间有表格所示的数据. x 24 15 23 19 16 11 20 16 17 13 y 92 79 97 89 64 47 83 68 71 59
课前探究学习
课堂讲练互动
试一试 确定相关系数r与回归系数b 的符号关系.
^
提示 因为b=
^
i=1
xi- x yi- y xiyi-n x y
i=1 n
n
n
=
i=1
,
i=1 2 x2 i -n x
xi- x
n
2
i=1
xi- x yi- y
n 2 n
n
而r=
课堂讲练互动
(2)由已知数据求得 x =17.4, y =74.9, x2 i =3 i=1
10
182, yi2=58 i=1
10
375, xiyi=13 578,
i=1
10
所以相关系数
i=1
xiyi-10 x y
≈0.920.
10
r=
10 2 2 xi -10 x yi2-10 y 2 i=1 i=1
3.2 回归分析
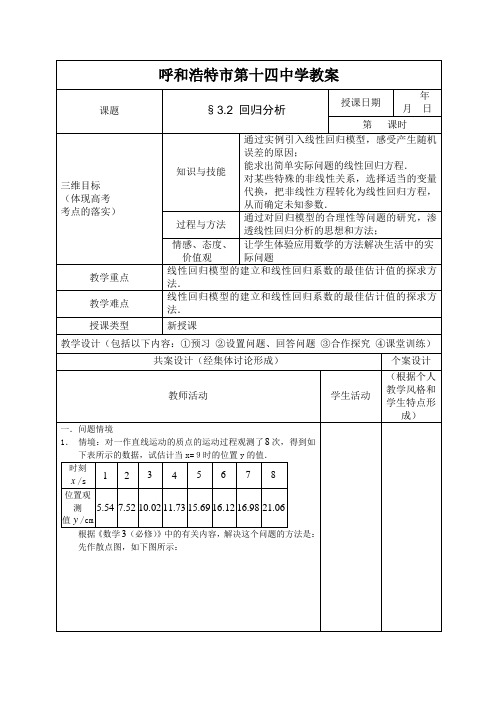
2.问题:在时刻 时,质点的运动位置一定是 吗?
三.建构数学
1.线性回归模型的定义:
我们将用于估计 值的线性函数 作为确定性函数;
的实际值与估计值之间的误差记为 ,称之为随机误差;
将 称为线性回归模型.
说明:(1)②忽略了某些因素的影响;
③存在观测误差.
(2)对于线性回归模型,我们应该考虑下面两个问题:
①模型是否合理(这个问题在下一节课解决);
②在模型合理的情况下,如何估计 , ?
2.探求线性回归系数的最佳估计值:
对于问题②,设有 对观测数据 ,根据线性回归模型,对于每一个 ,对应的随机误差项 ,我们希望总误差越小越好,即要使 越小越好.所以,只要求出使 取得最小值时的 , 值作为 , 的估计值,记为 , .
二.学生活动
学生讨论后,教师提出课题:
这就是上节课提到的问题①,即模型的合理性问题.为了回答这个问题,我们需要对变量 与 的线性相关性进行检验(简称相关性检验).
三.建构数学
1.相关系数的计算公式:
对于 , 随机取到的 对数据 ,样本相关系数 的计算公式为
2.相关系数 的性质:
(1) ;
(2) 越接近与1, , 的线性相关程度越强;
情感、态度、
价值观
让学生体验应用数学的方法解决生活中的实际问题
教学重点
线性回归模型的建立和线性回归系数的最佳估计值的探求方法.
教学难点
线性回归模型的建立和线性回归系数的最佳估计值的探求方法.
授课类型
新授课
教学设计(包括以下内容:①预习②设置问题、回答问题③合作探究④课堂训练)
共案设计(经集体讨论形成)
计量地理学第三章——2 回归分析

例1
一元线性回归方法的基本公式为:
y a bx
式中:a,b为待定参数,其表达式如下:
b Lxy Lxx
n i 1
xi yi
1 n
n
(
i 1
xi )(
n i 1
n i 1
xi2
1 n
n
(
i 1
xi )2
yi )
a y bx
变差 来源 回归
误差
总和
平方和
自由度
n
SSR (Yˆi Y )2
地区编号 1 2 3 4 5 6 7 8
月平均销售收 入(万元)y
31
40
30
34
25
20
35
40
月平均广告支 出(万元)x
5 10 5
7
4
3
7
9
要求:对于不同的月平均广告支出预测月平均销售收入
解:由计算结果可知,回归方程为
SST=338.875 SSR=314.532 SSE=24.343
Y 14.669 2.753X
因此,对于不同的月平均广告支出,其月平均销售收入的预测 结果如下:单位:万元
月平均广告支出 平均收入的点预测 平均收入的区间预测
6
31.187
(25.956,36.418)
8
36.693
(31.296,42.090)
12
47.705
(40.872,54.538)
直线回归、相关分析的注意事 项:
1)相关分析只是以相关系数来描述两个变量间线性相关 的程度和方向,并不阐明事物间存在联系的本质,也不是两事 物间存在联系的证据。要阐明两事物间的本质联系,必须凭专 业知识从理论上加以论证。因此,把两个毫无关系的事物放在 一起作相关分析是毫无意义的。同样,回归分析也要有实际意 义。
-回归分析(生猪决策).精选优秀PPT

称f〔x〕为Y对X的回归函数,ε为Y与f〔x〕的偏差,
它是一个随机变量,并假定E〔ε〕=0。
“回归〞一词始于英国统计学家盖尔登〔Galton〕和 皮 尔逊〔Pearson〕,他们研究儿子的身高Y与其父母的平均 身高X之间的关系,通常双亲的平均身高较矮时,其子的身 高也较矮;双亲的平均身高较高时,其子的身高也较高, 但是他们发现,如果双亲属于高个类〔高于1000多对夫妇 的平均身高〕时,其子比他父亲更高的概率会较小;相反 地,如果双亲属于低个类时,其子比他父亲更矮的概率也 较小,所以,平均身高偏高或偏矮的双亲,其子的身高都 有一种“向中心回归〞的现象,基于这个事实,盖尔登把 求 描述儿子与双亲身高关系的直线称为回归直线。
为是多元线性回归;假设回归函数f〔x1,x2,…,xm〕是非 线
性函数,那么称为是非线性回归。对非线性回归,经常采用线
性化的方法来处理。所以,目前研究最多的是线性回归,且
假定X1,X2,…,Xm和Y均服从正态分布。回归分析的任务就
多元回归模型的应用是相当广泛的,例如,某种商品的 销售量可能受收入水平、风俗习惯、产品质量、价格、宣传 广告等多种因素的影响;某种产品的质量可能受生产该产品 时的温度、湿度、压力、原材料的质量和有害成份的含量等 影响;工人的劳动生产率可能受学历、智力水平、情绪的稳 定性和才能等因素的影响;某城市的用水量可能与该城市的 人口数及工业总产值有关。诸如此类的关系,可以通过多元 回归分析模型进行研究。
3.2 多元线性回归分析
某种水泥在凝固时放出的热量y〔卡/克〕与水泥中以下 4种化学成份有关。
x1:3CaO·Al2O3的成份〔%〕 x2:3CaO·SiO2的成份〔%〕 x3:4CaO·Al2O3·Fe3O3的成份〔%〕 x4:2CaO·SiO2的成份〔%〕 现记录了13组数据,列在表3—4中,根据表中的数据, 试研究y与x1,x2,x3,x4四种成份的关系。
回归分析教学设计

3.2回归分析教学设计引言:新一轮课程改革要求我们在教育教学的过程当中要着力落实“以生为本”的教学理念。
所谓“以生为本”就是以学生的发展为本,关注学生的思维能力的发展,动手能力的发展及应用意识的发展。
为此,讲授本节课之前,我做了如下的准备:一、教学内容分析及学情分析:(一)教学内容分析:《回归分析》是高中数学人教B版选修2—3第三章《统计案例》的第二节内容,本节是中学阶段统计学的完结篇。
其内容与第一节《独立性检验》及必修3中的统计知识均有着密切的联系。
它是必修3中回归直线方程知识的加深和升华,也是对第一节《独立性检验》中统计方法的补充。
其实,统计学发展到今天已经有许多较成熟的统计方法,独立性检验和回归分析只是其中的两种方法。
教材把一个个的案例直接呈现在学生面前,通过探究案例,解决问题,使学生们了解这两种统计方法的基本思想、解题步骤及其初步应用。
在统计案例的教学中,应培养学生对数据的直观感觉,认识统计方法的特点(如估计结果的随机性、统计推断可能犯错误等),体会统计方法应用的广泛性,理解其方法中蕴涵的思想。
避免学生单纯记忆和机械套用公式进行计算。
教学中应鼓励学生使用计算机及统计软件等现代技术手段来处理数据,解决实际问题。
应尽量给学生提供充分的实践活动机会,要求学生在实践中体会统计思想。
学习本节课后高中阶段的统计学知识全部学完,学生应该能够独立地分析简单的统计数据,能够独立完成简单的统计分析问题。
这种能力既是到高校继续深造的需要,更是作为新时代合格公民的必备素质。
(二)学情分析1、在学习本节课之前,学生已经在初中及高中数学人教B版必修3第二章中初步掌握了统计学的相关知识,特别是已经掌握了线性相关的回归直线方程的求法,能够通过对散点图的观察发现较直观的线性相关关系并求出其回归直线方程。
2、高二学生的自主学习能力和探究能力都很强,特别在学习了本章《统计案例》第一节的独立性检验的统计思想之后,初步掌握了统计分析的思想方法,这都为本节课教学奠定了坚实的基础。
统计学中的回归分析与相关性

统计学中的回归分析与相关性回归分析与相关性是统计学中重要的概念和方法,用于研究变量之间的关系和预测。
本文将介绍回归分析和相关性分析的基本原理、应用领域以及实际案例。
一、回归分析回归分析是研究两个或多个变量之间关系的一种统计方法。
它的基本思想是通过对一个或多个自变量与一个因变量之间的关系进行建模,来预测因变量的取值。
1.1 简单线性回归简单线性回归是回归分析中最基本的形式,用于研究一个自变量和一个因变量之间的关系。
其数学模型可以表示为:Y = β0 + β1X + ε,其中Y是因变量,X是自变量,β0和β1是回归系数,ε是误差项。
1.2 多元回归多元回归是回归分析的扩展形式,用于研究多个自变量对一个因变量的影响。
其数学模型可以表示为:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε。
1.3 回归诊断回归分析需要对建立的模型进行诊断,以确保模型的有效性和合理性。
常见的回归诊断方法包括检验残差的正态性、检验变量之间的线性关系、检验残差的独立性和方差齐性等。
二、相关性分析相关性分析是统计学中用来研究两个变量之间线性关系强弱的方法。
通过计算两个变量的相关系数,可以判断它们之间的相关性。
2.1 皮尔逊相关系数皮尔逊相关系数是最常用的衡量两个连续变量之间线性相关强度的指标,取值范围在-1到1之间。
当相关系数接近1时,表示两个变量呈正相关;当相关系数接近-1时,表示两个变量呈负相关;当相关系数接近0时,表示两个变量之间没有线性关系。
2.2 斯皮尔曼相关系数斯皮尔曼相关系数是一种非参数统计量,用于衡量两个变量之间的等级相关性。
与皮尔逊相关系数不同,斯皮尔曼相关系数不要求变量呈线性关系。
三、回归分析与相关性的应用回归分析和相关性分析在各个领域都有广泛的应用。
下面以两个实际案例来说明其应用:3.1 股票市场分析在股票市场分析中,可以使用回归分析来研究某只股票的收益率与市场整体指数之间的关系。
第3章 3.2 回归分析 学业分层测评

第3章 3.2 回归分析学业分层测评学业分层测评(建议用时:45分钟)[学业达标]一、填空题1.如图3-2-2所示,对变量x,y有观测数据(x i,y i)(i=1,2,…,10),得散点图(1);对变量u,v有观测数据(u i,v i)(i=1,2,…,10),得散点图(2).由这两个散点图可以判断________.图3-2-2①变量x与y正相关,u与v正相关;②变量x与y正相关,u与v负相关;③变量x与y负相关,u与v正相关;④变量x与y负相关,u与v负相关.【解析】由图(1)知,x与y是负相关,由图(2)知,u与v是正相关,故③正确.【答案】③2.已知对一组观测值(x i,y i)(i=1,2,…,n)作出散点图后,确定具有线性^=a^+b^x,求得b^=0.51,x=61.75,y=38.14,则线性回相关关系,若对于y归方程为________.^=y-b^x=38.14-0.51×61.75=6.647 5≈6.65.【解析】∵a^=0.51x+6.65.∴y^=0.51x+6.65【答案】y3.某产品的广告费用x与销售额y的统计数据如下表:广告费用x(万元)423 5销售额y(万元)49263954根据上表可得回归方程y=b x+a中的b为9.4,据此模型,预报广告费用为6万元时销售额为______万元.^=y--b^x-=42-9.4×3.5=9.1,所【解析】样本中心点是(3.5,42),则a7.对具有线性相关关系的变量x ,y 有观测数据(x i ,y i )(i =1,2,…,10),它们之间的线性回归方程是y =3x +20,若∑i =110x i =18,则∑i =110y i =________.【解析】 由于∑i =110x i =18,则x -=1.8,∵(x -,y -)在回归方程上, ∴y -=3×1.8+20=25.4, ∴∑i =110y i =10y -=254.【答案】 2548.已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程是________.【解析】 由斜率的估计值为1.23,且回归直线一定经过样本点的中心(4,5),可得y ^-5=1.23(x -4),即y ^=1.23x +0.08.【答案】 y ^=1.23x +0.08 二、解答题 9.对于数据组:x 1 2 3 4 y1.94.16.17.9(1)(2)求线性回归方程.【解】 (1)作图略.x ,y 具有很好的线性相关性. (2)设y ^=a ^+b ^x ,因为x -=2.5,y -=5,∑4i =1x i y i=60, ∑4i =1x 2i=30, 故b ^=60-4×2.5×530-4×2.52=2,a ^=y --b ^x -=5-2×2.5=0, 故所求的回归直线方程为y ^=2x .10.下表为某地近几年机动车辆数与交通事故的统计资料,求出y 关于x 的线性回归方程.机动车辆数 x /千台 95 110 112 120 129 135 150 180交通事故数 y /千件6.27.57.7 8.58.7 9.810.2 13【解】 ∑i =1x i =1 031,∑i =1y i =71.6,∑i =1x 2i=137 835,∑i =1x i y i =9 611.7,x -=128.875,y -=8.95,将它们代入⎩⎨⎧b ^=∑ni =1x i y i -n x - y -∑ni =1x 2i -n (x -)2,a ^=y --b ^x -,计算得b ^≈0.077 4.a ^=-1.025,所以,所求线性回归方程为y ^=0.077 4x -1.025.[能力提升]1.对具有线性相关关系的变量x ,y 有观测数据(x i ,y i )(i =1,2,…,10),它们之间的线性回归方程是y ^=3x +20,若∑10i =1x i =18,则∑10i =1y i=________. 【解析】 由∑10i =1x i=18,得x =1.8. 因为点(x ,y )在直线y ^=3x +20上,则y =25.4. 所以∑10i =1y i =25.4×10=254. 【答案】 2542.已知对一组观测值(x i ,y i )(i =1,2,…,n )作出散点图后,确定具有线性相关关系,若对于y ^=a ^+b ^x ,求得b ^=0.51,x -=61.75,y -=38.14,则线性回归方程为________.【解析】 ∵a ^=y --b ^x -=38.14-0.51×61.75=6.647 5≈6.65.∴y ^=0.51x +6.65. 【答案】 y =0.51x +6.653.若线性回归方程中的回归系数b ^=0,则相关系数r =________.【解析】 b ^=∑i =1n(x i -x -)(y i -y -)∑i =1n(x i -x -)2,r =∑i =1n(x i -x -)(y i -y -)∑i =1n(x i -x -)2∑i =1n(y i -y -)2.由计算公式知,若b =0,则r =0. 【答案】 04.某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100棵种子中的发芽数,得到如下资料:日期 12月 1日 12月 2日 12月 3日 12月 4日 12月 5日 温差x (℃) 10 11 13 12 8 发芽y (颗)2325302616方程,剩下的2组数据用于回归方程检验.(1)若选取的是12月1日与12月5日的2组数据,请根据12月2日至12月4日的数据,求出y 关于x 的线性回归方程y ^=b ^x +a ^;(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?(3)请预测温差为14 ℃的发芽数.【解】 (1)由数据求得,x =12,y =27, 由公式求得,b ^=52,a ^=y -b ^x =-3.所以y 关于x 的线性回归方程为y ^=52x -3.(2)当x =10时,y ^=52×10-3=22,|22-23|<2;当x =8时,y ^=52×8-3=17,|17-16|<2.所以该研究所得到的线性回归方程是可靠的. (3)当x =14时,有y ^=52×14-3=35-3=32,所以当温差为14 ℃时的发芽数约为32颗.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ˆ 34.92 0.78161 160.5. y
这就是说当母亲身高为161cm时女儿的身高大致也接近161cm
(三)非线性回归问题的解法 例3.在彩色显影中,经经验知,形成染料光学 密度Y与析出银的光学密度x有公式
y Ae (b<0)表示,现测得试验数据如下:
xi 0.05 0.06 0.25 0.31 0.07 0.10 0.38 0.43 0.14 0.20 0.47
一个临界值r0.05;
(3)根据样本相关系数计算公式求出r的值;
(xi x )(yi y )
2
n n
r
(xi x ) (yi y)2
i 1 i 1
i 1 n
n 2
xi yi n x y
n
i 1
( xi n x )( yi n y )
2
例2
为了了解某地区母亲身高x与女儿身高Y的相关关系, 随机测得10对母女的身高如下表所示:
159 160 160 163 159 154 159 158 159 157
母亲身高(x/cm) 女儿身高(x/cm)
158 159 160 161 161 155 162 157 162 156
试对x与Y进行一元线性回归分析, 并预测当母亲身高为161cm时女儿的身高为多少? 序号 x y x2 y2 xy
y x
1 … 合计
例2
为了了解某地区母亲身高x与女儿身高Y的相关关系, 随机测得10对母女的身高如下表所示:
159 160 160 163 159 154 159 158 159 157
母亲身高(x/cm) 女儿身高(x/cm)
158 159 160 161 161 155 162 157 162 156
回归系数
^
37.2 b 0.78, 47.6
^
a 159.1 0.782158.8 34.92,
所以Y对x的回归直线方程是
^
ˆ 34.92 0.78x. y
回归系数 b 0.78 的意思是,反映出当母亲身高每增加1cm时女儿 ^ 身高平均增加0.78cm, 可以理解为女儿身高不受母亲身高 a 34 . 92 影响的部分。 把x=161代人,易得
2
n
2
i 1
i 1
(4)作统计推断,如果|r|>r0.05,表明有 95%的把握认为x与Y之间具有线性相关关系。 如果|r|≤r0.05,我们没有理由拒绝原 来的假设。这时寻找回归直线方程是毫无意 义的。
例4.以下是收集到的新房屋的销售价格y和 房屋的大小x的数据:
(1)画出数据的散点图; (2)用最小二乘估计求回归直线方程, 并在散点图上加上回归直线; (3)此回归直线有意义吗?
试对x与Y进行一元线性回归分析, 并预测当母亲身高为161cm时女儿的身高为多少?
检验的步骤如下: (1)作统计假设:x与Y不具有线性相关关系。 (2)根据小概率0.05与n-2在附表中查出r的一个临界值r0.05. (3)根据样本相关系数计算公式算出r的值。 (4)作统计推断。如果︱r︱>r0.05,, 表明有95%的把握认为x与Y之间具有线性相关关系。 如果∣r∣≤r0.05,我们没有理由拒绝原来的假设。 这时寻找回归直线方程是毫无意义的。
( x1 , y1 ), ( x2 , y2 ),, ( xn , yn ),
检验统计量是样本相关系数
(xi x )(yi y )
2 n n
r
(xi x ) (yi y)2
i 1 i 1
i 1 n
n 2
x y n i i xy
n
i 1
( xi n x )( yi n y )
再见
1、:根据下表,(1)画出散点图(2)求回归方程.
1、列表
2、代入公式计算
3、写出回归直线方程
例 1 研究某灌溉渠道水的流速Y与水深x之间的关系,测得一组数据如下:
水深x/m 流速Y/(m· s-1) 1.40 1.50 1.60 1.70 1.80 1.90 2.00 2.10 1.70 1.79 1.88 1.95 2.03 2.10 2.16 2.21
解:根据以上的分析,由题目给出的经验公式
b y Ae 两边取自然对数,便得 ln y ln A x , 1 与线性回归直线方程相对照,只要取u= , x
b x
v=lny, a=lnA,就有v=a+bu。这是v对u的线性回 归直线方程,对此我们已掌握了一套相关性检 验、求a与回归系数b的方法。
第三章 统计案例
3.2 回归分析
复习提问:
1.什么叫相关关系?相关关系分哪几类?
当自变量取值一定时因变量的取值带有一定的随机性的 两个变量之间的关系叫做相关关系。相关关系分为正相 关和负相关两大类。
2.什么是散点图?
为了得到变量X和Y 之间的关系,在直角坐标系中标出 每一组观测值(X,Y),得到表示具有相关关系的两个变 量之间的关系的图形,称为散点图。
,v ln y ,可
ˆ e y
0.146 0.548 x
e
0.548
e
0.146 x
1.73 e
0.146 x
这就是Y对于x的回归方程,试验点及回归曲 线的图形如图所示。
课堂小结:
两个变量线性相关检验的步骤如下: (1)作统计假设:x与Y不具有线性相关关系; (2)根据小概率0.05与n-2在附表中查出r的
ˆx a ˆ ˆ b y ˆ b ( xi x ) ( yi y )
i1 n n
i1
x iy i n x y
i1 n
n
( xi x )2
i1
xi 2 n x
2
ˆx ˆ yb a
(2)请根据上表提供的数据,用最小二乘法求出 y 关于 x 的回归直 线方程y =b x+a ;
解:(1) 数据的散点图见右图
1 5 (2)x 5 xi =109, i 1 1 5 y yi 23.2 5 i 1
lxx ( xi x )2 1570
i 1
5
lxy ( xi x )( yi y ) 308
i 1
n
5
b
^
( x x)( y
3.如何判断两个变量之间是否具有相关关系?
若散点图杂乱无章,则两个变量之间不具有相关关系; 若比较整齐,有一定的规律,则具有相关关系。
4.什么是回归直线?什么是回归直线方程?
一般地,设X与Y是具有相关关系的两个变量,且相应 于n 组观测值的n个点大致 分布在一条直线附近,这样 的直线叫做回归直线,直线的方程叫做回归直线方程。
b x
yi
0.10 0.14 1.00 1.12 0.23 0.37 1.19 1.25 0.59 0.79 1.29
试求Y对于x的回归方程。
分析:本例与前面例子不同,是非线性回归分 析问题。由于题目已给出了所要求的曲线类型, 只要通过已知的11对样本数据,把A与b确定下 来,就找到了描述x与Y相关关系的一条函数曲 线。 在此我们特别指出,确定性关系(如公式、函 数关系等)和相关关系之间并没有一条不可逾 越的鸿沟。由于有试验误差、测量误差等存在, 变量之间的确定性关系往往通过研究相关关系 表现出来。反过来,在有些问题中,可以通过 研究相关关系来深入了解变量变化的内在规律, 从而找到它们的确定性关系。
ui vi 20.00 0 -2.30 16.66 7 -1.96 4.000 0 3.226 0.113 14.28 6 -1.47 10.00 0 -0.99 2.632 0.174 2.326 0.223 7.143 -0.53 5.000 -0.236 2.128 0.255
(1)作统计假设:u对V不具有线性相关关系; (2)由小概率0.05与n-2=9在附表中查得 r0.05=0.602; (3)进行计算得|r|=0.998.
r
( x x )( y y )
i 1 i i 2 2 ( x x ) ( y y ) i i i 1 i 1 5 5
5
0.9597
查表,n-2=3时,临界值r0.05=0.878, 由 r>r0.05知,变量 y与 x之间具有线性相 关关系,回归直线是有意义的.
得到了下面的数据:
年份
2007 24.4 19
2008 29.6 6
2009 32.9 1
2010 28.7 10
2011 30.3 1
2012 28.9 8
x(℃) y(日)
(1)对变量x、y进行相关性检验;
解答
2、如何由r的取值判断两个变量之间是否具有
线性相关关系? 检验的步骤如下:
(1)作统计假设:x与Y不具有线性相关关系。 (2)根据样本相关系数计算公式算出r的值。 根据小概率0.05与n-2在附表中查出r的一个 ( 3) 临界值r0.05.(教材97页) (4)作统计推断。如果︱r︱>r0.05, 表明有95%的把握认为x与Y之间具有 线性相关关系。 如果∣r∣≤r0.05,我们没有理由拒绝原 来的假设。这时寻找回归直线方程是毫无 意义的。
i 1 i n i 1
i
y)
l xy l xx
2 ( x x ) i
308 0.1962 1570
308 a y b x 23.2 109 1.8166 1570
^
ˆ =1.8166+0.1962x. ∴ 回归直线方程为 y
(3) y与x的相关系数
^ ^ ^
解答
(3) 试根据求出的回归直线方程,预测记忆力为 9 的同学的判 断力.
