二次函数与根的判别式
北师大版数学九年级下册《二次函数与根的判别式的关系》教案2

北师大版数学九年级下册《二次函数与根的判别式的关系》教案2一. 教材分析《二次函数与根的判别式的关系》这一节的内容,主要让学生了解二次函数的根与判别式之间的关系,掌握判别式的计算方法,并能运用判别式判断二次方程的根的情况。
内容安排合理,由浅入深,既注重了知识的形成过程,又培养了学生的动手操作能力、归纳推理能力、数学语言表达能力。
二. 学情分析九年级的学生已经学习了二次函数的相关知识,对二次函数的图象和性质有一定的了解。
但根与判别式的关系这一概念较为抽象,学生可能难以理解。
因此,在教学过程中,我将以学生已有的知识为基础,引导学生通过观察、操作、归纳等方法,理解并掌握根与判别式之间的关系。
三. 教学目标1.知识与技能目标:让学生掌握二次方程的根与判别式之间的关系,能运用判别式判断二次方程的根的情况。
2.过程与方法目标:通过观察、操作、归纳等方法,让学生体会数学知识的形成过程,培养学生的动手操作能力和归纳推理能力。
3.情感态度与价值观目标:让学生在解决实际问题的过程中,感受数学与生活的紧密联系,增强学生对数学的兴趣和信心。
四. 教学重难点1.重点:二次函数的根与判别式之间的关系。
2.难点:理解判别式的计算方法和运用判别式判断二次方程的根的情况。
五. 教学方法1.情境教学法:通过生活实例引入课题,激发学生的学习兴趣。
2.引导发现法:引导学生观察、操作、归纳,发现二次函数的根与判别式之间的关系。
3.讲解法:在学生理解的基础上,进行讲解,使学生掌握知识。
4.练习法:通过适量练习,巩固所学知识。
六. 教学准备1.教学课件:制作课件,展示二次函数的图象和性质。
2.练习题:准备一些有关二次函数与根的判别式的练习题。
七. 教学过程导入(5分钟)1.利用生活实例引入二次函数的概念,让学生回顾二次函数的图象和性质。
2.提出问题:二次函数的根与判别式之间有什么关系?呈现(10分钟)1.利用课件展示二次函数的图象,引导学生观察二次函数的根与判别式之间的关系。
二次函数的根与判别式

二次函数的根与判别式二次函数是数学中常见的一类函数,其一般形式为f(x) = ax^2 + bx + c,其中a、b、c为实数且a不等于0。
二次函数的根是指函数f(x) = 0的解,即使得f(x)等于零的x值。
而判别式则是用来判断二次函数的根的性质和个数的重要工具。
本文将详细介绍二次函数的根与判别式的概念、计算方法以及相关性质。
一、二次函数的根二次函数的根即是使得f(x) = 0的x值。
为了求解二次函数的根,我们可以使用求根公式。
求根公式有两种形式,分别适用于一般形式和标准形式的二次函数。
1. 一般形式的二次函数对于一般形式的二次函数f(x) = ax^2 + bx + c,我们可以使用以下求根公式来求解其根:x = (-b ± √(b^2 - 4ac)) / (2a)其中,“±”表示两个解,即一个解为加号,另一个解为减号。
求根公式中的判别式b^2 - 4ac在后文中将详细介绍。
2. 标准形式的二次函数对于标准形式的二次函数f(x) = a(x - h)^2 + k,其中(h, k)为顶点坐标,我们可以通过移项和开平方的方式求解其根。
具体步骤如下:1) 将二次函数转化为一般形式:展开平方并化简得到f(x) = ax^2 + bx + c的形式;2) 根据一般形式的求根公式求解二次函数的根。
二、二次函数的判别式二次函数的判别式是用来判断二次函数的根的性质和个数的重要工具。
判别式的值可以分为三种情况:1. 判别式大于0(Δ > 0)当判别式大于0时,二次函数有两个不相等的实根。
也就是说,方程f(x) = 0有两个不同的实数解。
2. 判别式等于0(Δ = 0)当判别式等于0时,二次函数有两个相等的实根。
也就是说,方程f(x) = 0有且仅有一个实数解。
3. 判别式小于0(Δ < 0)当判别式小于0时,二次函数没有实根。
也就是说,方程f(x) = 0没有实数解。
三、二次函数根与判别式的关系二次函数的根与判别式之间存在着紧密的关系。
分析二次函数的根与判别式

分析二次函数的根与判别式二次函数是代数学中常见的一种函数形式,其一般表达式为:f(x) = ax^2 + bx + c其中,a、b、c为常数,且a ≠ 0。
根据二次函数的一般表达式,我们可以推导出二次函数的判别式:Δ = b^2 - 4ac其中,Δ代表判别式。
在讨论二次函数的根的情况时,判别式起到了关键作用。
接下来,我们将分析二次函数的根与判别式之间的关系。
1. 当Δ > 0时,二次函数有两个不相等的实根。
在这种情况下,判别式Δ大于0,意味着二次函数的图像与x轴有两个交点,即函数方程f(x) = 0有两个不相等的实根。
这意味着二次函数的抛物线与x轴相交于两个不同的点,图像呈现出凹向上的形状。
2. 当Δ = 0时,二次函数有两个相等的实根。
当判别式Δ等于0时,二次函数的图像与x轴有且仅有一个交点,这意味着函数方程f(x) = 0有两个相等的实根。
此时,二次函数的抛物线在x轴上切于一个点,图像呈现出一种特殊的情况,即对称轴与x轴重合。
3. 当Δ < 0时,二次函数没有实根。
如果判别式Δ小于0,那么二次函数的图像与x轴没有交点,函数方程f(x) = 0没有实根。
这种情况下,二次函数的抛物线完全位于x轴的上方或下方,图像呈现出凹向上或凹向下的形状。
通过分析二次函数的根与判别式,我们可以更好地理解二次函数的图像特征和解析特点。
判别式Δ的正负性决定了二次函数的根的情况,进而影响了函数的图像形状。
在应用中,我们可以利用二次函数的根与判别式来解决实际问题,如求解方程、优化问题等。
总之,判别式Δ在二次函数中的作用是决定了函数的根的情况,从而影响了函数的图像以及解析特征。
通过分析判别式Δ的正负性,我们可以准确地得知二次函数的根的情况,为进一步的数学研究和实际应用提供了便利。
二次函数的解析式和根的判别式

二次函数的解析式和根的判别式二次函数是一种常见的数学函数形式,具有解析式和根的判别式。
在本文中,我们将探讨二次函数的解析式以及根的判别式,并通过例子来说明它们的应用。
一、二次函数的解析式二次函数的一般形式为:y = ax² + bx + c,其中a、b、c为常数,且a ≠ 0。
这里的x和y分别代表函数的自变量和因变量。
解析式是二次函数的数学表示方式,它们可以帮助我们准确地描绘二次函数的图像。
解析式中的系数a、b、c决定了二次函数的特征,如开口方向、顶点坐标等。
通过解析式,我们可以推导出二次函数的重要参数:1. 开口方向:若a > 0,则二次函数开口向上;若a < 0,则二次函数开口向下。
2. 顶点坐标:对于开口向上的二次函数,顶点坐标为(-b/2a, -Δ/4a),其中Δ为判别式;对于开口向下的二次函数,顶点坐标为(-b/2a, Δ/4a)。
3. 对称轴:二次函数的对称轴为x = -b/2a。
4. y轴截距:二次函数与y轴交点的纵坐标为常数项c。
5. x轴截距:二次函数与x轴交点的横坐标可通过令y = 0解方程获得。
通过解析式,我们可以更好地理解和分析二次函数的性质。
二、二次函数的根的判别式根的判别式是用来判断二次函数的根的性质和情况的一种公式,它由解析式中的系数a、b、c推导得出。
根的判别式Δ的计算公式为:Δ = b² - 4ac。
根的判别式Δ可以有以下三种情况:1. 当Δ > 0时,二次函数有两个不相等的实根。
这意味着二次函数与x轴有两个交点,此时二次函数图像与x轴相交于两处。
2. 当Δ = 0时,二次函数有两个相等的实根,也称为重根。
这意味着二次函数与x轴有一个交点,此时二次函数图像与x轴相切于一处。
3. 当Δ < 0时,二次函数没有实根,而是有两个共轭的虚根。
这意味着二次函数图像与x轴没有交点,完全位于x轴的上方或下方。
通过根的判别式,我们可以判断二次函数的根的情况,进而推断二次函数的图像特征。
二次函数的根与判别式

二次函数的根与判别式二次函数在数学中占据着重要的地位,在各种实际问题中都有广泛的应用。
而要了解二次函数的性质和解法,首先需要了解二次函数的根以及与之相关的判别式。
本文将详细介绍二次函数的根与判别式的概念、计算方法以及应用。
一、二次函数的根二次函数是一种形如f(x) = ax² + bx + c的函数,其中a、b、c为常数,且a ≠ 0。
我们知道,二次函数的图像一般呈现出抛物线的形状,而二次函数的根即为使得函数值等于零的x值。
对于二次函数f(x) = ax² + bx + c,它的根可以通过求解方程f(x) = 0来得到。
根据一元二次方程的求解公式可知,二次函数的根的计算公式为:x = (-b ± √(b² - 4ac)) / (2a)其中,±表示两个根的取值可能性,√表示开平方根。
根据这个公式,我们可以计算出二次函数的根,进而对二次函数在坐标轴上的位置和特性进行进一步的分析。
二、二次函数的判别式为了更好地了解二次函数的性质,我们引入判别式的概念。
二次函数的判别式是一个用来判断二次函数根的性质的参数,通过判别式的值可以判断二次函数的根的情况。
对于二次函数f(x) = ax² + bx + c,它的判别式D的计算公式为:D = b² - 4ac根据判别式的值可以得到以下结论:1. 当D > 0时,二次函数有两个不相等的实根;2. 当D = 0时,二次函数有两个相等的实根;3. 当D < 0时,二次函数没有实根,但可能有复数根。
通过判别式,我们可以进一步了解和分析二次函数的根的情况,从而更好地解决实际问题。
三、二次函数根与判别式的应用二次函数的根与判别式在应用中具有重要的作用。
以下是一些相关的应用场景:1. 求解方程:通过计算二次函数的根,可以解决各种与二次函数相关的方程问题。
2. 几何性质:通过分析二次函数的根和判别式,可以得到二次函数在坐标轴上的位置和形态。
二次函数与根的判别式的关系6
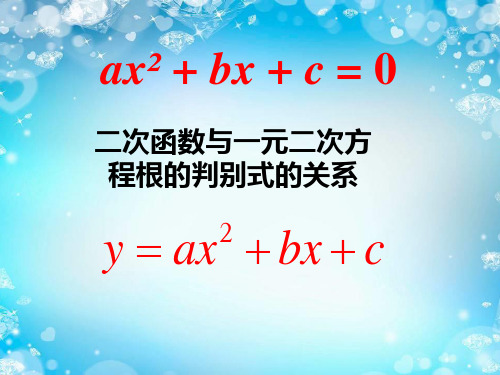
4.一元二次方程 3 x2+x-10=0的两个根是x1=-2 ,
x2=
5,那么二次函数
3
y=
3
x2+x-10与x轴的交点坐标
是_(-_2,_0_) _( __,_0. )
5.不与x轴相交的抛物线是( D )
A. y = 2x2 – 3 B. y=-2 x2 + 3
C. y= -x2 – 3x D. y=-2x2 - 4x - 5
6、如图,铅球运动员掷铅球的高度y(m)与水平 距离x(m)之间的函数关系式y=- 1 x2+ 2 x+ 5 ,则
12 3 3
该运动员此次掷铅球的成绩是___1_0_____。
总结提高
通过本节课的学习,你有哪些收获? 还有什么疑惑?说给老师或同学听听. ①二次函数与一元二次方程的关系. ②二次函数与一元二次方程根的情况之间的 关系. ③事物是普遍联系的,运用方程知识可以解
写成点的坐标.
y=x2+2x与x轴交点 (-2,0)和(0,0)
y=x2-2x+1与X轴 的交点 (1,0)
y=x2-2x+2与x 轴无交点
y=x2+2x
y=x2-2x+1
y=x2-2x+2
议一 议、取长补短
观察下列二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2x²+ bx + c = 0
二次函数与一元二次方 程根的判别式的关系
y ax2 bx c
一、温故知新
(1)一次函数y=x+2的图象与x轴的交点为 (-2,0 )
一元一次方程x+2=0的根为__X_=_-_2___ (2) 一次函数y=-3x+6的图象与x轴的交点为
北师大版九年级下册数学:二次函数与根的判别式的关系 (共15张PPT)

独立 作业
知识的升华
P35 1---9题.
祝你成功!
驶向胜利 的彼岸
下课了!
结束寄语
•只有不断的思考,才会 有新的发现;只有量的 变化,才会有质的进步.
读书当将破万卷;求知不叫一疑存。读书之法,在循序而渐进,熟读而精思,喜欢读书,就等于把生活中寂寞的辰光换成巨大享受的时刻。自得读书乐,不邀为善名。有时 间读书,有时间又有书读,这是幸福;没有时间读书,有时间又没书读,这是苦恼。不读书的人,思想就会停止。读书时要深思多问。只读而不想,就可能人云亦云,沦为 书本的奴隶;或者走马看花,所获甚微。为乐趣而读书。立身以立学为先,立学以读书为本读书而不能运用,则所读的书等于废纸。读书可以培养一个完人,谈话可以训练 一个敏捷的人,而写作则可造就一个准确的人。读书是在别人思想的帮助下,建立起自己的思想。养心莫若寡欲;至乐无如读书。身边永远要着铅笔和笔记本,读书和谈话 时碰到的一切美妙的地方和话语都把它记下来。凿壁偷光,聚萤作囊;在读书上,数量并不列于首要,重要的是书的品质与所引起的思索的程度。劳于读书,逸于作文。、 没有比读书更廉价的娱乐,更持久的满足了。从来没有人为了读书而读书,只有在书中读自己,在书中发现自己,或检查自己。不怕读得少,只怕记不牢。莫等闲,白了少 年头,空悲切!书籍是培育我们的良师,无需鞭答和根打,不用言语和训斥,不收学费,也不拘形式,对图书倾注的爱,就是对才智的爱。熟读唐诗三百首,不会作诗也会 吟。书到精绝潜心读;文穷情理放声吟读万卷书,行万里路。书犹药也,善读之可以医愚。如果把生活比喻为创作的意境,那么阅读就像阳光。书籍是少年的食物,它使老 年人快乐,也是繁荣的装饰和危难的避难所,慰人心灵。在家庭成为快乐的种子,在外也不致成为障碍物,但在旅行之际,却是夜间的伴侣。读书是在别人思想的帮助下, 建立起自己的思想。饭可以一日不吃,觉可以一日不睡,书不可以一日不读。、读过一本好书,像交了一个益友。读书有三到,谓心到,眼到,口到立身以立学为先,立学 以读书为本。读书而不思考,等于吃饭而不消化。为中华之崛起而读书。来书籍是在时代的波涛中航行的思想之船,它小心翼翼地把珍贵的货物运送给一代又一代。书籍是 最好的朋友。当生活中遇到任何困难的时候,你都可以向它求助,它永远不会背弃你。1、抱最大的希望,为最大的努力,做最坏的打算。有些事情本身我们无法控制,只 好控制自己。挫折时,要像大树一样,被砍了,还能再长;也要像杂草一样,虽让人践踏,但还能勇敢地活下去。人的活动如果没有理想的鼓舞,就会变得空虚而渺小。莫 向不幸屈服,应该更大胆、更积极地向不幸挑战!一个人炫耀什么,说明内心缺少什么。志在山顶的人,不会贪念山腰的风景。当一个人先从自己的内心开始奋斗,他就是 个有价值的人。旁观者的姓名永远爬不到比赛的计分板上。强者向人们揭示的是确认人生的价值,弱者向人们揭示的却是对人生的怀疑。不要对挫折叹气,姑且把这一切看 成是在你成大事之前,必须经受的准备工作。成功源于不懈的努力。积极思考造成积极人生,消极思考造成消极人生。对的,坚持;错的,放弃!理想的路总是为有信心的 人预备着。这社会你改变不了就得适应,适应不了就得被淘汰!这叫适者生存!宁愿跑起来被拌倒无数次,也不愿规规矩矩走一辈子,就算跌倒也要豪迈的笑。没有伞的孩 子必须努力奔跑。你不勇敢,没人替你坚强。态度决定一切,实力捍卫尊严!人要经得起诱惑耐得住寂寞!虽然你的思维相对于宇宙智慧来说只不过是汪洋中的一滴水,但 这滴水却凝聚着海洋的全部财富;是质量上的一而非数量上的一;你的思维拥有一切宇宙智慧。成功者绝不放弃,放弃者绝不会成功。人生不售来回票,一旦动身,绝不能 复返。自己要先看得起自己,别人才会看得起你。即使爬到最高的山上,一次也只能脚踏实地地迈一步。1、人生的光荣,不在于永不言败,而在于能够屡扑屡起。——拿 破仑游手好闲的人最没有空闲不经风雨,长不成大树;不受百炼,难以成钢过去属于死神,未来属于你自己。人的一生,是很短的,短暂的岁月要求我好好领会生活的进 程……攀登顶峰,这种奋斗的本身就足以充实人的心。人们必须相信,垒山不止就是幸福。老骥伏枥,志在千里;烈士暮年,壮心不已。大鹏一日同风起,扶摇直上九万里。 不会宽容人的人,是不配受到别人的宽容的。不经过本身的努力,就永远达不到自己的目的,任何外来的帮助也不能代替本身的努力。子女中那种得不到遗产继承权的幼子, 常常会通过自身奋斗获得好的发展。而坐享其成者,却很少能成大业。明日复明日,明日何其多!日日待明日,万事成蹉跎。世人皆被明日累,明日无穷老将至。晨昏滚滚 水东流。今古悠悠日西坠。百年明日能几何?请君听我《明日歌》我希望你照自己的意思去理解自己,不要小看自己,被别人的意见引入歧途。百金买骏马,千金买美人; 万金买高爵,何处买青春除非一个人有大量的工作要做,否则他不可能从懒散空闲中得到乐趣。如果我们以为只有野心和爱情这类强烈的激情才能抑制其他情感,那就错了。 懒惰尽管柔弱似水,却常常把我们征服:它渗透进生活中一切目标和行为,时钟随着指针的移动滴答在响:“秒”是雄赳赳气昂昂列队行进的兵士,“分”是士官,“小时”是带 队冲锋陷阵的骁勇的军官。,所以当你百无聊赖,胡思乱想的时候,请记住你掌上有千军万马;你是他们的统帅。检阅他们时,你不妨问问自己——他们是否在战斗中发挥 了最大的作用。沧海可填山可移,男儿志气当如斯。从来便没有什么救世主,也不靠神仙皇帝,要创造人类的幸福,全靠我们自己。任何人都应该有自尊心自信心独立性, 不然就是奴才。但自尊不是轻人,自信不是自满,独立不是弧立。三更灯火五更鸡,正是男儿发愤时。黑发不知勤学早,白首方悔读书迟。醉斩长鲸倚天剑,笑凌骇浪济川 舟。富贵不淫贫贱乐,男儿到此是豪雄。滴自己的汗,吃自己的饭。自己的事情自己干,靠人靠天靠祖上,不算是好汉。你要做一个勇敢的少年人,不可为一些芝麻小事在 那儿大惊小怪。你知道,弱者在这世界上是不好过日子的。真正的敏捷是一件很有价值的事。因为时间是衡量事业的标准,如金钱是衡量货物的标准时间是一位可爱的恋人, 对你是多么的爱慕倾心,每分每秒都在叮嘱;劳动创造别虚度了一生。与善人居,如入兰芷之室,久而不闻其香;与恶人居。如入鲍鱼之肆,久而不闻其。光勤劳是不够的, 蚂蚁也非常勤劳。你在勤劳些什么呢?有两种过错是基本的,其他一切过错都由此而生:急躁和懒惰。时间会刺破青春的华丽精致,会把平行线刻上美人的额角,会吃掉稀 世珍宝,天生丽质,什么都逃不过他横扫的镰刀。人,只要有一种信念,有所追求,什么艰苦都能忍受,什么环境也都能适应。我年轻时注意到,我每做十件事有九件不成 功,于是我就十倍地去努力干下去。滴自己的汗,吃自己的饭。自己的事情自己干,靠人靠天靠祖上,不算是好汉。”天行健,君子以自强不息;地势坤,君子以厚德载物。 古今中外,凡成就事业,对人类有所作为的人,无一不是脚踏实地艰苦登攀的结
二次函数的根与判别式

二次函数的根与判别式二次函数是数学中常见的一类函数形式,可以表示为$y=ax^2+bx+c$,其中 $a$、$b$、$c$ 是常数,且 $a\neq0$。
在解析几何和代数学中,研究二次函数的根和判别式是非常重要的内容。
本文将系统地介绍二次函数的根的概念、求根公式以及判别式的含义和应用。
一、二次函数的根的概念在解析几何中,我们说 $x_0$ 是二次函数 $y=ax^2+bx+c$ 的根,是指当 $x=x_0$ 时,函数的值 $y=ax_0^2+bx_0+c$ 等于零。
换句话说,$x_0$ 是函数图像与 $x$ 轴的交点的横坐标。
二次函数的根可以分为以下三种情况:1. 当判别式 $D=b^2-4ac>0$ 时,方程 $ax^2+bx+c=0$ 有两个不相等的实根;2. 当判别式 $D=b^2-4ac=0$ 时,方程 $ax^2+bx+c=0$ 有两个相等的实根;3. 当判别式 $D=b^2-4ac<0$ 时,方程 $ax^2+bx+c=0$ 没有实根,但有两个虚根。
二、求根公式求解二次函数根的常用方法是利用求根公式。
二次函数的求根公式为:\[x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]其中,$\pm$ 表示可以选择取正号或者负号,这取决于具体的方程和问题。
三、判别式的含义与应用判别式 $D=b^2-4ac$ 是判断二次函数根的重要指标。
它可以用来确定方程的根的性质,并在实际应用中起到重要的作用。
1. 当判别式 $D>0$ 时,方程有两个不相等的实根。
这意味着二次函数的图像与 $x$ 轴有两个交点,函数在这两个交点处取零值。
在实际中,我们可以利用这两个实根来求解问题,例如求解物体运动的时间、距离等。
2. 当判别式 $D=0$ 时,方程有两个相等的实根。
这意味着二次函数的图像与 $x$ 轴有一个交点,函数在该点处取零值。
在实际中,这种情况常常出现在对称性问题中,例如求解抛物线的对称轴。
二次函数的根与判别式知识点总结详细

二次函数的根与判别式知识点总结详细介绍二次函数是高中数学中的重要概念,了解二次函数的根和判别式是解决与二次函数相关问题的基础。
本文档将详细介绍二次函数的根和判别式的相关知识点。
二次函数的一般形式二次函数的一般形式可以表示为:$f(x) = ax^2 + bx + c$,其中$a$、$b$、$c$ 是实数,且 $a \neq 0$。
二次函数的根二次函数的根是函数 $f(x)$ 与 $x$ 轴的交点,即函数取值为0的$x$值。
根据二次函数的一般形式,我们可以通过求解二次方程$ax^2 + bx + c = 0$ 来求得二次函数的根。
二次函数根的判别式二次函数根的判别式可以用来判断二次函数的根的情况。
判别式的计算公式为 $D = b^2 - 4ac$。
判别式 $D$ 的值可以分为三种情况:1. 当 $D > 0$ 时,二次方程有两个不相等的实根;2. 当 $D = 0$ 时,二次方程有两个相等的实根;3. 当 $D < 0$ 时,二次方程没有实根,根为虚根。
根的求解公式根据二次函数根的判别式,可以得到根的求解公式:1. 当 $D > 0$ 时,设 $x_1$、$x_2$ 分别为方程的两个实根,则有:- $x_1 = \frac{-b + \sqrt{D}}{2a}$- $x_2 = \frac{-b - \sqrt{D}}{2a}$2. 当 $D = 0$ 时,方程有相等的实根,即 $x_1 = x_2 = \frac{-b}{2a}$3. 当 $D < 0$ 时,方程没有实根,根为虚根。
总结二次函数的根和判别式是解决与二次函数相关问题的基础。
根据根的判别式的值,我们可以判断二次方程的根的情况,进而使用根的求解公式求得根的具体值。
希望本文档对你了解和掌握二次函数的根和判别式有所帮助!。
二次函数的根与判别式

二次函数的根与判别式二次函数是一种重要的代数函数形式,可表示为y = ax^2 + bx + c的形式,其中a、b、c为实数且a不等于零。
在解析几何和数学建模中,二次函数经常被用来描述抛物线、物体的运动轨迹、经济增长模型等等。
对于二次函数而言,其根和判别式是非常重要的概念。
一、二次函数的根一元二次方程的解,又被称为方程的根。
对于二次函数y = ax^2 +bx + c来说,我们可以通过求解方程ax^2 + bx + c = 0来确定其根。
根的个数与二次方程的判别式有关,判别式的计算公式为Δ = b^2 -4ac。
根据判别式的三种情况可以推导出二次函数的根的情况:1. 当Δ > 0时,方程有两个不相等的实根。
此时,抛物线与x轴相交于两点,分别称为根。
2. 当Δ = 0时,方程有且仅有一个实根。
此时,抛物线与x轴相切于一个点,即有一个重根。
3. 当Δ < 0时,方程无实根。
此时,抛物线与x轴没有交点。
在求解根的过程中,可以应用二次方程的求根公式。
根据求根公式,当Δ > 0时,方程的两个根分别为x1 = (-b + √Δ)/(2a)和x2 = (-b -√Δ)/(2a);当Δ = 0时,方程的根为x = -b/(2a);当Δ < 0时,方程无实根。
二、二次函数判别式的意义判别式Δ在解析几何和数学建模中有重要的实际意义。
首先,根的个数与判别式的正负有关,因此可以通过判别式的值来判断方程的解的情况。
其次,在几何意义上,判别式Δ反映了二次函数与x轴的交点情况。
具体而言:1. 当Δ > 0时,判别式大于零,方程有两个不相等的实根。
此时,抛物线与x轴相交于两点。
2. 当Δ = 0时,判别式等于零,方程有一个实根。
此时,抛物线与x轴相切于一个点。
3. 当Δ < 0时,判别式小于零,方程无实根。
此时,抛物线与x轴没有交点。
通过判别式的值,我们可以快速了解二次函数的性质,比如抛物线开口的方向、与x轴的交点情况等。
二次函数的根与判别式

二次函数的根与判别式在学习二次函数的过程中,我们常常需要确定二次函数的根,也就是解二次方程的根。
而判别式则是用来判断二次方程的根的性质。
在本文中,我们将探讨二次函数的根与判别式的相关概念及应用。
1. 二次函数的定义与一般形式二次函数是指具有形式为f(x) = ax^2 + bx + c的函数,其中a、b、c为实数且a不等于零。
该函数在坐标平面上呈现出抛物线的形状,开口方向与a的正负有关。
2. 二次方程与二次函数的关系二次方程与二次函数密切相关,二次方程的一般形式为ax^2 + bx +c = 0,在解二次方程时,我们需要求解方程的根,也就是函数的零点。
因此,二次方程的根即是二次函数的横坐标对应的函数值为零的点。
3. 二次函数的根的求解方法为了求解二次函数的根,我们可以使用求根公式或者配方法来进行计算。
(1) 求根公式:二次函数的根可以通过求根公式 x = (-b ± √(b^2 - 4ac)) / (2a) 来计算。
其中,±表示两个相反的解,√表示平方根。
(2) 配方法:使用配方法可以将一般形式的二次函数转化为一个完全平方形式的二次函数。
具体步骤为首先将二次函数中的二次项与线性项配成一个完全平方,然后将其他项移至等式的另一边,最后完成平方运算并求解根。
4. 判别式的定义与求解判别式是用来判断二次方程的根的性质的一个重要指标,可以通过判别式的正负和零来分析二次方程的根的情况。
判别式的一般形式为Δ = b^2 - 4ac,其中Δ为判别式,a、b、c分别为二次方程的系数。
(1) 若Δ > 0,则二次方程有两个不相等的实根;(2) 若Δ = 0,则二次方程有两个相等的实根,也称为重根;(3) 若Δ < 0,则二次方程没有实根,但有一对共轭复根。
通过计算判别式的值,我们可以直观地了解二次方程的根的性质,并在解题过程中依据判别式的结果选择适当的解法。
5. 二次函数根与判别式的应用二次函数的根和判别式的应用非常广泛,包括但不限于以下几个方面:(1) 求二次方程的根:通过求根公式或配方法计算二次函数的根,可以帮助我们求解实际问题中的未知数。
二次函数的根与判别式

二次函数的根与判别式二次函数是高中数学中的重要概念之一,它的根与判别式是求解二次方程的重要工具。
在这篇文章中,我将详细介绍二次函数的根与判别式的概念、计算方法以及应用。
通过阅读本文,读者将能够更好地理解和运用二次函数的相关知识。
一、二次函数的概念二次函数是形如f(x) = ax^2 + bx + c的函数,其中a、b、c分别是常数,且 a ≠ 0。
它是一个二次方程对应的函数关系,图像是一个抛物线。
二次函数有很多重要性质,其中之一是它的根。
二、二次函数的根二次函数的根是使得函数值为0的x值,即满足f(x) = 0的x值。
由于二次方程是一个二次函数的解析表达式,所以求解二次方程的根和求解二次函数的根是等价的。
根的个数可以通过判别式来确定。
三、二次函数的判别式二次函数的判别式是Δ = b^2 - 4ac,它是判断二次方程有几个不同实根的重要指标。
根据判别式的值,可以分为以下几种情况:1. 当Δ > 0时,二次方程有两个不同实根。
2. 当Δ = 0时,二次方程有两个相等的实根。
3. 当Δ < 0时,二次方程没有实根,但有复数根。
四、计算二次函数的根和判别式求解二次函数的根需要先计算判别式的值,然后根据判别式的值来确定根的情况。
具体的计算步骤如下:1. 计算判别式Δ = b^2 - 4ac。
2. 根据Δ的值判断根的情况:a. 当Δ > 0时,根据求根公式x = (-b ± √Δ) / 2a,计算两个不同实根。
b. 当Δ = 0时,根据求根公式x = -b / 2a,计算两个相等的实根。
c. 当Δ < 0时,无实根,但可以使用复数形式表示。
五、二次函数根的应用二次函数的根在数学和实际应用中有着广泛的应用。
以下是一些常见的应用场景:1. 解决二次方程:利用根的概念和判别式的求解方法,可以解决各种形式的二次方程,从而求得未知数的值。
2. 求解最值问题:通过求解二次函数的根,可以判断该函数的开口方向,从而确定函数的极值点。
二次函数与根的关系掌握二次函数与根的关系解决相关问题

二次函数与根的关系掌握二次函数与根的关系解决相关问题二次函数是高中数学学习中的重要内容之一,它与根(解)的关系密切相关。
在解决相关问题时,我们需要正确理解和掌握二次函数与根之间的关系,才能应用正确的方法解答问题。
本文将从二次函数与根的定义、计算和应用等方面进行详细讨论,帮助读者全面掌握二次函数与根的关系并解决相关问题。
1. 二次函数与根的定义二次函数是形如 f(x) = ax^2 + bx + c 的函数,其中 a、b、c 是实数且a ≠ 0。
该函数的图像在坐标平面上呈现出抛物线的形状。
根(解)是指二次函数的值等于零的输入变量值,即 f(x) = 0 的解。
二次函数的根可以是一个实数或复数,取决于 b^2 - 4ac 的值。
2. 二次函数的根的计算为了计算二次函数的根,我们可以使用求根公式或配方法。
求根公式是二次方程 ax^2 + bx + c = 0 解的通用公式,即:x = (-b ± √(b^2 - 4ac)) / 2a其中±表示两个解,分别对应加号和减号。
通过代入 a、b、c 的值即可计算出二次函数的根。
配方法是利用二次函数的性质,将其转化为完全平方的形式来求解。
具体步骤为:1) 将二次函数写作 a(x + m)^2 + n,其中 m 和 n 是待定值。
2) 展开得到 a(x^2 + 2mx + m^2) + n。
3) 将展开后的式子与原式进行比较,得到 2am = b 和 am^2 + n = c 两个方程。
4) 解方程组,求出 m 和 n 的值。
5) 将 m 和 n 的值代入 a(x + m)^2 + n,得到二次函数的标准形式。
6) 根据标准形式求根。
3. 二次函数与根的关系二次函数与根之间存在着紧密的联系。
当二次函数的根为实数时,我们可以通过判别式 b^2 - 4ac 的正负性来判断二次函数的图像与 x 轴的交点情况。
1) 当判别式大于零时,即 b^2 - 4ac > 0,二次函数有两个不相等的实数根。
二次函数的判别式

二次函数的判别式
二次函数的判别式是指二次函数的一个重要特征,它可以用来判断二次函数的性质。
一般来说,二次函数的判别式可以表示为:D=b^2-4ac,其中a、b、c分别为二次函数的系数,即
f(x)=ax^2+bx+c。
根据判别式的定义,可以得出以下结论:
1. 如果D>0,则二次函数有两个不同的实根;
2. 如果D=0,则二次函数有两个相同的实根;
3. 如果D<0,则二次函数没有实根,只有两个虚根。
因此,二次函数的判别式可以用来判断二次函数的性质,从而帮助我们更好地理解二次函数的特性。
二次函数与根与系数关系综合运用

二次函数与根与系数关系综合运用二次函数是数学中一种重要的函数类型,其表达式可以写成:$y=ax^2+bx+c$,其中$a, b, c$为常数,且$a\neq0$。
二次函数的图像是一个抛物线,其根的数量取决于判别式$S=b^2-4ac$的正负性。
一、根与系数的关系根据二次函数的定义,我们可以推导出根与系数之间的关系。
1.虚根的情况若判别式$S=b^2-4ac$小于零,则二次函数的图像与$x$轴没有交点,即方程$ax^2+bx+c=0$无实根。
此时,方程的根为复数。
2.重根的情况若判别式$S=b^2-4ac$等于零,则二次函数的图像与$x$轴有一个交点,即方程$ax^2+bx+c=0$有一个实根。
此时,方程的根为重根。
3.两个不同实根的情况若判别式$S=b^2-4ac$大于零,则二次函数的图像与$x$轴有两个交点,即方程$ax^2+bx+c=0$有两个不同实根。
此时,方程的根为实数。
二、根与系数的综合应用根与系数的关系在实际问题中有着广泛的应用,下面我们来看几个例子:例1:已知二次函数$y=ax^2+bx+c$的图像上有两个交点$(1,3)$和$(-2,7)$,求该二次函数的表达式及其判别式。
解:由已知条件可得两个方程:\[a+b+c=3 \quad...(1)\]\[4a-2b+c=7 \quad...(2)\]将(1)式左右两边乘以2,再与(2)式相减可以解得:\[-4b+3a=1 \quad...(3)\]解得$a=\frac{5}{3}, b=-\frac{7}{6}$。
将$a, b$的值代入(1)式或(2)式中,可以解得$c=\frac{7}{3}$。
所以该二次函数的表达式为:\[y=\frac{5}{3}x^2-\frac{7}{6}x+\frac{7}{3}\]判别式$S=(-\frac{7}{6})^2-4(\frac{5}{3})(\frac{7}{3})=\frac{49}{36}-\frac{140}{27}=-\frac{23}{108}<0$。
二次函数的根与判别式

二次函数的根与判别式二次函数是一种常见的数学函数形式,具有一般形式为y = ax² + bx + c的特点。
其中,a、b、c是常数,且a ≠ 0。
二次函数的图像通常为一个开口朝上或朝下的抛物线。
在二次函数中,根是指使函数等于0的x值。
判别式是用来确定二次函数的根的性质的一种方法。
1. 根的定义和计算根是指使二次函数等于0的x值,也是函数图像与x轴的交点。
为了计算二次函数的根,可以使用求根公式:x = (-b ± √(b² - 4ac)) / (2a)其中,b² - 4ac被称为判别式。
2. 判别式的性质判别式的值可以判断二次函数的根的情况:- 当判别式大于0时,即b² - 4ac > 0,二次函数有两个不相等的实根。
- 当判别式等于0时,即b²- 4ac = 0,二次函数有两个相等的实根。
- 当判别式小于0时,即b² - 4ac < 0,二次函数没有实根,但可能有复数根。
3. 根的解释和图像解释根表示二次函数与x轴的交点,因此根的数量和位置对应着二次函数的图像形状。
- 当二次函数有两个不相等的实根时,抛物线与x轴有两个交点,图像开口朝上或朝下。
- 当二次函数有两个相等的实根时,抛物线与x轴有一个交点,图像开口朝上或朝下,且顶点在x轴上。
- 当二次函数没有实根但有复数根时,抛物线与x轴没有交点,图像完全位于x轴的上方或下方。
4. 根与二次函数参数的关系二次函数的参数a、b、c对于根的性质有着重要的影响。
- 当a > 0时,二次函数开口朝上,根的情况由判别式决定。
- 当a < 0时,二次函数开口朝下,根的情况由判别式决定。
- 当判别式为零时,二次函数有两个相等的实根,顶点在x轴上。
5. 案例分析假设有一个二次函数y = x² - 4x + 4,我们可以分析其根和判别式。
- 将a、b、c的值代入判别式公式中:b² - 4ac = (-4)² - 4(1)(4) = 0 - 根据判别式等于0,可以推断二次函数有两个相等的实根。
二次函数根

二次函数根
二次函数的根(也称零点、解、交点)是指二次函数与x 轴相交的点,即函数图像与x 轴的交点。
对于一般形式的二次函数y = ax2 + bx + c,它的根可以用以下公式求出:x = (-b ±sqrt(b2 - 4ac)) / 2a 其中,sqrt 表示平方根符号,±表示两个解,即正负两个方向的交点。
这个公式叫做求根公式。
如果判别式D=b2-4ac 的值为正数,则二次函数与x 轴有两个不相等的交点,也就是有两个根;如果 D 等于零,则二次函数与x 轴有一个交点,也就是有一个根;如果D 小于零,则二次函数与x 轴没有交点,也就是没有实数根(但有复数根)。
需要注意的是,二次函数的根取决于函数的系数a、b、c 的值,因此每个二次函数的根数和位置都可能不同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 知识结构:
2. 重点、难点分析
(1)本节的重点是会用判别式判定根的情况.一元二次方程的根的判别式是比较重要的,用它可以判断一元二次方程根的情况,有助于我们顺利地解一元二次方程,也可以利用它进一步学习函数的有关内容,所以,它是本节课的重点.
(2)本节的难点是一元二次方程根的三种情况的推导.教科书首先将一元二次方程用配方法变形为.因为,所以方程右边的符号就由来确定,而方程左边的不可能是一个
负数,因此,把分三种情况来讨论方程根的情况.推导过程中利用了分
类的思想方法,对于分类讨论学生感觉到较难,老师应该讲明分类的基本思想。
3. 教法建议:
(1)引入要自然、合理
新课引入前,作一个铺垫:前面我们讲了一元二次方程的解法,我们掌握了开平方法、公式法和因式分解法后,就可以解任何一个一元二次方程,但是,存在这样一个问题,并不是所有的一元二次方程都有解,我们可以通过把解求出来,来解方程,也可以通过判定方程无解,来解方程,这样我们就面临着一个问题,什么时候方程有解?什么时候方程无解?我们不解方程能不能判定根的情况?
那就是我们本节所要研究的问题.让学生首先感觉到所要学习的知识并不突然,也显露了本节课的重点.
(2)利用多媒体进行教学
本节是根的判别式结论的推导,比较抽象,为了便于学生理解,使用所提供的动画,有助于学生对所讲内容的理解,调动学生主动思维的积极性,活跃课堂气氛,提高学习效率.
(3)本节在推导根的判别式的结论时,利用了分类的思想,对于学生这是一个难点,一定给学生讲清楚分类的依据,分类的基本思想,使学生对所得结论深信不疑.
一、教学目标
1. 理解一元二次方程的根的判别式,并能用判别式判定根的情况;
2. 通过根的判别式的学习,培养学生从具体到抽象的观察、分析、归纳的能力;
3.通过根的情况的研究过程,让学生深刻体会转化和分类的思想方法.
二、重点·难点及解决办法
1.教学重点:会用判别式判定根的情况。
2.教学难点:一元二次方程根的三种情况的推导.
3.解决办法:(1)求判别式时,应先将方程化为一般形式,确定a、b、c。
(2)利用判别式可以判定一元二次方程的存在性情况(共四种);方程有两个实数根,方程有两个不相等的实数根,方程有两个相等的实数根,方程没有实数根。
三、教学步骤
(一)教学过程
1.复习提问
(1)平方根的性质是什么?
(2)解下列方程:①;②;③。
问题(1)为本节课结论的得出起到了一个很好的铺垫作用。
问题(2)通过自己亲身感受的根的情况,对本节课的结论的得出起到了一个推波助澜的作用。
2.任何一个一元二次方程用配方法将其变形为
,因此对于被开方数来说,
只需研究为如下几种情况的方程的根。
(1)当时,方程有两个不相等的实数根。
即
(2)当时,方程有两个相等的实数根,即。
(3)当时,方程没有实数根。
教师通过引导之后,提问:究竟谁决定了一元二次方程根的情况?
答:。
3.①定义:把叫做一元二次方程的根的判别式,通常用符号“”表示。
②一元二次方程。
当时,有两个不相等的实数根;
当时,有两个相等的实数根;
当时,没有实数根。
反之亦然。
注意以下几个问题:
(1)这一重要条件在这里起了“承上启下”的作
用,即对上式开平方,随后有下面三种情况。
正确得出三种情况的结论,需对平方根的概念有一个深刻的、正确的理解,所以,在课前进行了铺垫。
在这里应向学生渗透转化和分类的思想方法。
(2)当,说“方程没有实数根”比较
好。
有时,也说“方程无解”。
这里的前提是“在实数范围内无解”,也就是方程无实数根的意思。
4.例题讲解
例1 不解方程,判别下列方程的根的情况:
(1);(2);(3)。
解:(1)
∴原方程有两个不相等的实数根。
(2)原方程可变形为。
,
∴原方程有两个相等的实数根。
(3)原方程可变形为。
∴原方程没有实数根。
学生口答,教师板书,引导学生总结步骤,(1)化方程为一般形式,确定a、b、c的(2)计算的值;(3)判别根的情况。
强调两点:(1)只要能判别值的符号就行,具体数值不必计算出。
(2)判别根据的情况,不必求出方程的根。
练习:不解方程,判别下列方程的情况:
(1);(2);
(3);(4);
(5);(6)
学生板演、笔答、评价。
(4)题可去括号,化一般式进行判别,也可设,判别方程根的情况,由此判别原方程根的情况。
例2 不解方程,判别方程的根的情况。
解:。
又∵不论k取何实数,,
∴原方程有两个实数根。
教师板书,引导学生回答。
此题是含有字母系数的一元二次方程。
注意字母的取值范围,从而确定的取值。
练习:不解方程,判别下列方程根的情况。
(1);
(2);
(3)。
学生板演、笔答、评价。
教师渗透、点拨。
(3)解:
∵不论m取何值,,即。
∴方程无实数解。
由数字系数,过渡到字母系数,使学生体会到由具体到抽象,并且注意字母的取值。
(二)总结、扩展
1.判别式的意义及一元二次方程根的情况。
(1)定义:把叫做一元二次方程的根的判别
式,通常用符号“”表示。
(2)一元二次方程。
当时,有两个不相等的实数根;
当时,有两个相等的实数根;
当时,没有实数根。
反之亦然。
2.通过根的情况的研究过程,深刻体会转化的思想方法及分类的思想方法。
四、布置作业
教材P27A1~4。
5.不解方程,判断下x的方程的根的情况
(1)
(2)
五、板书设计。
