2019-2020学年北京市燕山区八年级上学期期末数学真题试卷 (学生版+解析版)
2019-2020北京燕山八年级上数学期末试卷答案(图片版)

燕山地区2019—2020学年度第一学期期末考试八年级数学试卷参考答案及评分标准 2020.01一、选择题(本题共16分,每小题2分)二、填空题(本题共16分,每小题2分)9. -2 10.2)(a x +答案不唯一 11.x 12.6 13.答案不唯一,∠D =∠B 14.12, -12 15.20202 16.41°三、解答题(本题共68分,第17-21题,每小题5分;第22题4分;第23题7分;第24-27题,每小题5分,第28,29题,每小题6分)17. 解:原式= 12a 3÷3a +6a 2÷3a -3a ÷3a ………………………………3分= 4a 2 +2a -1 ………………………………5分18. 解:(1))1)(1()1(23-+=-=-x x x x x x x = ………………………………2分(2)222)1(3)12(3363-=+-=+-x y x x y y xy y x ………… ………………5分19. 解:去分母得,x-1=2(x-2)+1, ………………………………1分去括号x-1=2x-4+1, ………………………………2分 移项合并同类项得,2x- x =4-1-1, ………………………………3分 系数化1得, x =-2, ………………………………4分 检验:x =-2是原方程的解. ………………………………5分20. 证明:∵AB =AB , ………………………………1分又∵∠α=∠β, ∠C =∠D 在△AB C 和△ABD 中,⎪⎩⎪⎨⎧=∠=∠∠=∠AB AB D C βα∴△AB C ≌△ABD ……………4分 ∴AC =AD …………………5分21.证明:∵等边三角形ABC∴AB =BC=AC , ………………………………1分 ∠ABC =∠ACB,∴∠DB C =∠ACE ………………………………2分在△AB C 和△ABD 中,⎪⎩⎪⎨⎧=∠=∠=CE BD ACE DBC ACBC∴△DB C ≌△ECA ……………………4分 ∴∠BCD =∠C AE . …………………5分22.图略,每个图2分共计4分。
北京市各区2019-2020学年上学期八年级期末数学试卷精选汇编:化解求值专题(含答案)

222244244=(2)2(2)(2)4(2)22422221x x x y x x x x x x x x x x x x x x x x x -=⋅++-⋅+++-+=⋅+++-=++++=+=北京市各区2019-2020学年上学期八年级期末数学试卷精选汇编:化解求值专题(含答案)海淀区21.已知2220a ab b -+=,求代数式()()()422a a b a b a b --+-的值.21. 解: ∵2220a ab b -+=,∴2()0a b -=. ………………………1分∴a b =.…………………3分…………………4分∴原式=()0b b a -= . …………………5分 23.已知+2x a b =-,222+y ab a b -=.(1)用x 表示y ;(2)求代数式44()2x x x y x -⋅++的值. 23.解:(1)∵+2x a b =-,222+y ab a b -=,∴+2a b x =+,2222+()y a ab b a b =+=+. ………………………1分∴2(2)y x =+. ………………………2分(2)由题意可知:原式 ………………………3分………………………4分………………………5分 ………………………6分()()()2222422(4)(4)a a b a b a b a ab a b b ab--+-=---=-东城区25. 先化简,再求值:22214()2442a a a a a a a a ----÷++++,其中a 是满足|3|3a a -=-的最大整数. 22222221225.[](2)(2)44(1)2[](2)(2)442(2124)4231a a a a a a a a a a a a a a a a a a a a a a a--+=-⋅++---+=-⋅++--+=⋅+-⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯=+解:原式分分分分 ∵a 是满足|3|3a a -=-的最大整数,∴30a -≥.∴3a ≤.∴=3a . ……………………5分∴1=15原式.……………………6分 丰台区22.先化简,再求值:219123()÷x x x -++-,其中32x =-. 22. 解:原式=3分 =. 4分 ∴当时,原式=.6分密云区20. 已知3a b =+2222322()a b a a b a b a b+-÷--+的值. 20.解:2222322()a b a a b a b a b+-÷--+ =22222232()2[]a b a a b a b a b a b++-÷--+ ………………1分=222232()2a b a a b a b a b+-+÷-+ ………………2分 =222222a b ab a b a b+-÷-+ ………………3分 =2().()()2a b a b a b a b -++- =2a b - ………………4分Q a b =+∴ 原式 ………………5分 门头沟区22. 如果230x x +-=,求代数式321121x x x x x x -⎛⎫-÷ ⎪--+⎝⎭的值. 22.化简求值(本小题满分6分) 321121x x x x x x -⎛⎫-÷ ⎪--+⎝⎭ =21(1)(1)1(1)x x x x x x x -++-⎛⎫÷ ⎪--⎝⎭……………………………………………………………2分 =1(1)1(1)x x x x -⎛⎫⋅ ⎪-+⎝⎭ =1(1)x x + ……………………………………………………………………4分 当230x x +-=,即23x x +=时,……………………………………………………5分原式=13……………………………………………………………………………………6分 顺义区24.求()2122x x -++的值,其中 1x =.24.(5分)解:()2122x x -++= 22122x x x -+++.. ........ ........ ........ ........….... .... .... .... .... .... .... .... .... .... ............1分 23x =+.. ........ ........ ........ ........…......... .... .... .... .... .... .... .... .... .... .... .... .... .... .... .......2分∵1x =∴原式23x =+)213=+.. ........ ... .... .... .... .... .... .... .... ......... ........ ........…............3分313=-+ . . ........ ........ .... .... .... .... .... .... .... .... .... .... ........ ........…............4分7=-. .. .............. ........…. .... .... .... .... .... .... .... .... .... .... .... .... .... ...............5分 昌平区24.先化简222221412x x x x xx x x ⎛⎫-+-+÷ ⎪-+⎝⎭,再从﹣2、﹣1、0、1、2中选择一个合适的数 代入求值.24. 解:原式2(1)(2)(2)1(1)(2)x x x x x x x x ⎡⎤-+-=+÷⎢⎥-+⎣⎦……………………………………………… 2分 121+x x x x x--⎛⎫=÷ ⎪⎝⎭ ……………………………………………………… 3分 121x x x x-+-=÷ 23x x x -=⋅ ……………………………………………………… 4分 23x =- . ……………………………………………………… 5分 当x =2时,原式=2×2-3=1. ……………………………………………………… 6分 (或当x =-1时,原式=2×(-1)-3=-5.)平谷区24.已知012=--a a ,求代数式321a (1)121a a a -÷+++的值. 24.解:原式12)1111(23++÷+-++=a a a a a a …………………………………………1 1211123++÷+-+=a a a a a12123++÷+=a a a a a ……………………………………………2 32)1(1a a a a +⋅+= (3)21a a +=……………………………………………4 10122+=∴=--a a a a Θ ∴原式111=++=a a ……………………………………………5 燕山地区26.先化简,再求值:11112122+⋅-+÷+--t t t t t t t ,其中t =2019. 26. 解:11112122+⋅-+÷+--t t t t t t t =1111112+⋅+-⨯--+t t t t t t t )())((=1+t t ……………………………3分 当t =2019时,原式= =+12019201920202019 ……………………………5分 延庆区21.(5分)先化简,再求值22221()(2)m n m mn n m mn m++-+-g ,其中1m n -=. 21. 解: ()()()()()()22233m n m n m n m m n m m n m m n m m n m n ⎛⎫+-=+- ⎪ ⎪--⎝⎭=--=-g g 原式 ∵1m n -=∴原式=3. --------------------------------------------5分 房山区23. 解: 原式=222()2m n mn m n m m+--÷ ………….………..……….1分 =22m n m m m n-⋅-() ………….………..……….3分 =2m n - ………….………..……….4分 -------------------------------- 2分 -------------------------------- 3分 -------------------------------- 4分∵23m n -= 所以原式=2m n -=232=3. ………….………..……….5分 西城区石景山区通州区。
北京市燕山地区2018-2019学年八年级上期末数学试题及答案

燕山地区2019—2019学年度第一学期八年级期末考试数 学 试 卷 2019月1月一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个....是符合题意的,请将正确答案前的字母填入下面的答题表中.题号 1 2 3 4 5 6 7 8 9 10 选项1.下列四个图形中,不是..轴对称图形的是A .B .C .D .2.英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯,获得了诺贝尔物理学奖.石墨烯是目前世界上最薄却最坚硬的纳米材料,同时也是导电性最好的材料,其理论厚度仅0.000 000 34毫米,将0.000 000 34用科学记数法表示应为A .60.3410-⨯B .73.410-⨯C .83.410-⨯D .83410-⨯ 3.若分式221x x -+的值为0,则x 的值为 A .2 B .-2 C .12D .-124.点M (-2,1)关于x轴的对称点N 的坐标是A .(2,1)B .(-2,1)C .(-2,-1)D .(2,-1) 5.已知一次函数1+=kx y ,y 随x 的增大而减小,则该函数的图象一定经过A .第一、二、三象限B .第一、二、四象限C .第一、三、四象限D .第二、三、四象限6.如图,在△A B C 中,A B 的垂直平分线交A C 于点P ,已知P A =5,则线段P B 的 长度为A .8B .7C .6D .5 7.已知一个等腰三角形的两边长分别为3和7,则它的周长为A .13B .17C .13或17D .6或14AB CP8.2019年9月,北京到大连的高铁开通运营,高铁列车的运行时间比原动车组的运行时间还要快2小时,已知北京到大连的铁路长约为910千米,原动车组列车的平均速度为x 千米/时,高铁列车的平均速度比原动车组列车增加了52千米/时.依题意,下面所列方程正确的是 A .910910252x x -=+ B .910910252x x -=- C .910910252x x-=+ D .22(52)910x x ++= 9.如图,已知正方形ABCD ,沿直线BE 将∠A 折起,使点A 落在对角线BD 上的A′处,连结A′C ,则∠BA′C =A .45°B .60°C .67.5°D .75° 10.如右图,正方形ABCD 的边长为4,点P 为正方形边上一动点,若点P 从点A 出发沿A →D →C →B →A 匀速运动一周.设点P 走过的路程为x ,△ADP 的面积为y ,则下列图象能大致反映y 与x 的函数关系 的是二、填空题(本题共18分,每小题3分) 11.函数y =15x +的自变量x 的取值范围是 . 12.将直线l :y =2x 向上平移3个单位后得到的函数解析式是 . 13.如图,已知AC =AD ,要证明△ABC ≌△ABD ,还需添加的一个条件是 .(只添一个条件即可)14.如图,∠A O B =30°,O P 平分∠A O B ,P D ⊥O B 于D ,P C ∥O B 交O A 于C .若PC =10,则OC = ,PD = .A'EABDCPA BD C15.小王开车从甲地到相距320千米的乙地,如果油箱剩余油量y (升)与行驶里程x (千米)满足一次函数关系,其图象如右图所示,则y 与x 的函数解析式为 ,到达乙地时油箱剩余油量是 升.16.对于实数a 、b ,定义一种运算“⊗”为:2(1)a ab ab a-⊗=-. 有下列命题:① 1(3)3⊗-=; ② a b b a ⊗=⊗; ③ 方程1()102x -⊗=的解为12x =; ④ 若函数(2)y x =-⊗的图象经过A (-1,m ),B (3,n )两点,则n m <. 其中正确命题的序号是 .(把所有..正确命题的序号都填上) 三、解答题(本题共23分.第17题3分;第18题~21题,每题各5分) 17.计算:21a -2()3b a-. 18.解方程:32x - =22xx -- .19.如图,在△ABC 和△DEF 中,点B ,E ,C ,F 在同一条直线上,AB ∥DE ,且AB =DE ,BE =CF .求证:△ABC ≌△DEF .ABDCFEx (千米)y (升)253205020020.已知一次函数y =kx +b 的图象平行于直线y =-2x +4,且经过点A (2,-2). (1)求此一次函数解析式;(2)在给出的直角坐标系中画出该一次函数的图象;(3)根据该一次函数的图象,当0>y 时,x 的取值范围是 .21.先化简,再求值:22222a b ab b a a a ab ⎛⎫-+÷+ ⎪-⎝⎭,其中2a =,1b =-.四、解答题(本题共15分,每题各5分) 22.列方程解应用题:为满足居民住房需求,某市政府计划购买180套小户型二手住房,重新装修后作为廉租住房提供给住房困难的家庭.现有甲、乙两家公司都具备装修能力,政府派出相关人员分别到这两家公司了解情况,获得如下信息:信息一:甲公司单独完成这批装修任务比乙公司单独完成这批装修任务多15天; 信息二:乙公司平均每天装修的数量是甲公司平均每天装修数量的1.5倍. 根据以上信息,求甲、乙两家公司单独完成这批装修任务分别需要多少天?43214321Oxy23.在平面直角坐标系中,有点A (2,0),B (0,3),C (0,2),点D 在第二象限,且△AOB ≌△OCD .(1) 请在图中画出△OCD ,并直接写出点D 的坐标: D ( , ) ; (2) 点P 在直线AC 上,且△PCD 是等腰直角三角形,求点P 的坐标.24.如图,等边△ABC 中,D 为BC 边中点,CP 是BC 的延长线.按下列要求作图并回答问题:(要求:尺规作图,不写作法,保留作图痕迹) (1) 作∠ACP 的平分线CF ;(2) 作∠ADE =60°,且DE 交CF 于点E ;(3) 在(1),(2)的条件下,可判断AD 与DE 的数量关系是 ; 请说明理由.ADCPByxOC 1B A1五、解答题(本题共14分,每题各7分)25.在△ABC 中,AB =AC ,D 是直线BC 上一点,以AD 为一边在AD 的右侧作△ADE ,使AE =AD ,∠DAE =∠BAC ,连接CE .设∠BAC =α,∠DCE =β.(1)如图⑴,点D 在线段BC 上移动时,角α与β之间的数量关系是 ;证明你的结论;(2)如图⑵,点D 在线段BC 的延长线上移动时,角α与β之间的数量关系是 ,请说明理由;(3)当点D 在线段BC 的反向延长线上移动时,请在图⑶中画出完整图形并猜想角α与β之间的数量关系是 .图⑴图⑵图⑶AD C EBBCAAD C EB图⑴图⑵26.规定:把一次函数y =kx +b 的一次项系数和常数项互换得y =bx +k ,我们称y =kx +b 和y=bx +k (其中0≠⋅b k ,且b k ≠)为互助一次函数,例如232+-=x y 和322-=x y 就是互助一次函数.如图,一次函数y =kx +b 和它的互助一次函数的图象1l ,2l 交于P 点,1l ,2l 与x 轴,y 轴分别交于A ,B 点和C ,D 点.(1) 如图⑴,当k =-1,b =3时,① 直接写出P 点坐标: P ( , ) ;② Q 是射线..CP 上一点(与C 点不重合),其横坐标为m ,求四边形OCQB 的面积S 与m 之间的函数关系式,并求当△BCQ 与△ACP 面积相等时m 的值;(2) 如图⑵,已知点M (-1,2),N (-2,0).试探究随着k ,b 值的变化,MP +NP 的值是否发生变化?若不变,求出MP +NP 的值;若变化,求出使MP +NP 取最小值时的P 点坐标.以 下 为 草 稿 纸C Dl 2l 1ABP O xy1N Ml 2l 11POxy燕山地区2019—2019学年度第一学期八年级期末考试数学试卷参考答案与评分标准 2019年1月一、选择题(本题共30分,每小题3分)C .B .A .C .B .D .B .A .C .D . 二、填空题(本题共18分,每小题3分)11.5-≠x ; 12. 32+=x y ; 13.BC =BD (或∠CAB =∠DAB ); 14.10,5; 15. )3200(5081≤≤+-=x x y ,10; 16. ①④ 三、解答题(本题共23分.第17题3分;第18题~21题,每题各5分)17.原式=21a-229a b ………………1分=299a -229ab ………………2分=2299ab - ………………3分 18.解:去分母得,)2(23---=x x , ………………1分去括号得,423+--=x x , ……………2分 移项合并同类项得,13=x , ……………3分 系数化1得,31=x , ……………4分 检验:31=x 是原方程的解. ………………5分 19.证明:∵AB ∥DE ,∴∠B =∠DEF . ………………1分∵BE =CF ,∴BE +EC =FC +EC ,即BC =EF . ………………2分在△ABC 和△DEF 中, ⎪⎩⎪⎨⎧=∠=∠=,,,EF BC DEF B DE AB∴ △ABC ≌△DEF . ……………5分 20.(1) 由b kx y +=的图象平行于直线y =-2x +4,得2-=k . ………………1分由点A (2,-2)在直线b x y +-=2上,得b +⨯-=-222,2=b . ………………2分∴ 此一次函数解析式为y =-2x +2. ………………3分 (2) 直线y =-2x +2与x 轴,y 轴分别交于B (1,0),C (0,2)两点,图象如下图. ………………4分(3) 1<x . ………………5分21.原式=abab a b a a b a b a 222)())((++÷--+=2)()())((b a ab a a b a b a +⋅--+ =ba +1. ……………4分 当2=a ,1-=b 时,原式=121-=1. ……………5分 四、解答题(本题共15分,每题各5分)22.解法一:设甲公司单独完成这批装修任务需要x 天,则乙公司单独完成任务需要 (x -15)天, ……………1分 根据题意,得xx 1805.115180⨯=-, ……………2分 解这个方程,得 x =45. ………………3分 经检验:x =45是所列方程的解,且符合题意. ………………4分15-x =45-15=30(天).答:甲公司单独完成任务需要45天,乙公司单独完成任务需要30天.……………5分 解法二:设甲公司平均每天装修数量为x 套,则乙公司平均每天装修的数量为x 5.1套, ………………1分根据题意,得155.1180180=-xx , ……………2分 解这个方程,得 x =4. ……………3分 经检验:x =4是所列方程的解,且符合题意. ……………4分454180=(天),45-15=30(天). 答:甲公司单独完成任务需要45天,乙公司单独完成任务需要30天. …………5分23.(1) 正确画出△COD , …………1分D (-3,2). ………………2分(2) 由OC =OA =2,∠AOC =90°, ∴∠OAC =45°. ① 当CD 为直角边时,A C B43214321Oxy E P 2P 1D 1AB 1C Oxy如图,过点D 作P 1D ⊥CD ,交AC 于P 1, 由DC ∥OA ,易得△P 1DC 为等腰直角三角形, ∵CD =DP 1=3,∴P 1(-3,5). ……………………4分 ② 当CD 为斜边时,如图,过点D 作DP 2⊥AC 于P 2,易得△CP 2D 为等腰直角三角形,作P 2E ⊥CD 于E ,易得CE =P 2E =21CD =1.5, ∴P 2(-1.5,3.5). ……………………5分 综上,在直线AC 上,使△PCD 是等腰直角三角形的点P 坐标为:P 1(-3,5),P 2(-1.5,3.5). 24.(1) 尺规作图,如图; …………………1分 (2) 尺规作图,如图; ……………………2分 (3) AD =DE . ……………………3分 理由如下:解法一:如图,连接AE , ∵等边△ABC 中,D 为BC 边中点, ∴BD =DC ,∠ADB =∠ADC =90°, ∵∠B =∠ADE =60°, ∴∠BAD =∠EDC =30°,∵∠ACP =120°,CE 为∠ACP 的平分线, ∴∠ACE =∠ECP =60°, ∴∠DEC =∠ECP -∠EDC =30°, ∴∠DEC =∠EDC =30°,∴CE =CD =BD . ……………………4分 在△ABD 和△ACE 中,∵AB =AC ,∠B =∠ACE =60°,BD =CE , ∴△ABD ≌△ACE (SAS ), ∴AD =AE . 又∵∠ADE =60°, ∴△ADE 是等边三角形,∴AD =DE . ……………………5分 解法二:如图,过点D 作DM ∥AC 交AB 于点P , ∵△ABC 是等边三角形,∴△BDM 为等边三角形,BM =BD ,∠BMD =∠BDM =60°.FADCPEBMBEPCDA F∵AB =BC ,∴AB -BM =BC -BD ,即AM =CD . ∵∠ADC 为△ABD 的外角, ∴∠ADC =∠BAD +∠B , 而∠ADC =∠EDC +∠ADE , ∠B =∠ADE =60°,∴∠BAD =∠EDC . ……………………4分 ∵∠ACP =120°,CE 为∠ACP 的平分线, ∴∠ACE =60°,∴∠DCE =∠ACD +∠ACE =120°, ∴∠AMD =∠DCE =120°. 在△ADM 和△DEC 中,∵∠DAM =∠EDC ,AM =DC ,∠AMD =∠DCE , ∴△ADM ≌△DEC (ASA ),∴AD =DE . ……………………5分 五、解答题(本题共14分,每题各7分)25.(1)α+β=180°; ……………………1分证明:∵∠DAE =∠BAC , ∴∠DAE -∠DAC =∠BAC -∠DAC , ∴∠CAE =∠BAD . ∵在△ABD 和△ACE 中,AB =AC ,∠BAD =∠CAE ,AD =AE ,∴△ABD ≌△ACE (SAS ), ……………………2分 ∴∠ABD =∠ACE ,∵∠BAC +∠ABD +∠ACB =180°, ∴∠BAC +∠ACE +∠ACB =180°,∴∠BAC +∠BCE =180°,即α+β=180°. ………………3分 (2)α=β; ………………4分 理由如下:∵∠DAE =∠BAC , ∴∠DAE +∠CAD =∠BAC +∠CAD , ∴∠BAD =∠CAE . 在△BAD 和△CAE 中,∵AB =AC ,∠BAD =∠CAE ,AD =AE ,∴△ABD ≌△ACE (SAS ), ……………………5分BECDA∴∠ABD =∠ACE ,∵∠ACD =∠ABD +∠BAC =∠ACE +∠DCE ,∴∠BAC =∠DCE ,即α=β. ……………………6分 (3)如图,α=β. …………7分26.(1) ① P (1,2); ……………………1分 ② 如图,连接OQ ,∵y =-x +3与y =3x -1的图象1l ,2l 与x 轴,y 轴分别交于A ,B 点和C ,D 点. ∴A (3,0),B (0,3),C (31,0),D (0,-1). …………………2分 ∵Q (m ,3m -1) (31>m ), ∴S =S △OBQ +S △OCQ =)13(3121321-⨯⨯+⨯⨯m m =)31(612>-m m . ……………………3分 ∴S △BCQ =S -S △BOC =31321612⨯⨯--m =322-m ,而S △ACP =2)313(21⨯-⨯=38,由S △BCQ =S △ACP ,得 322-m =38, 解得m =35. ………………4分 (2) 由⎩⎨⎧+=+=k bx y b kx y ,, 解得 ⎩⎨⎧+==bk y x ,1,即P (1,k +b ),∴随着k ,b 值的变化,点P 在直线x =1上运动,MP +NP 的值随之发生变化.…………5分如图,作点N (-2,0)关于直线x =1的对称点N '(4,0),连接MN '交直线x =1于点P ,则此时MP +NP 取得最小值.设直线MN '的解析式为d cx y +=,依题意⎩⎨⎧=+=+-04,2d c d c , 解得 ⎪⎪⎩⎪⎪⎨⎧=-=58,52y c ,QC Dl 2l 1ABP O xyN'1NMx =1l 2l 11POxy∴直线MN '的解析式为5852+-=x y . ……………………6分 令x =1,则56=y ,∴P (1,56), 即 使MP +NP 取最小值时的P 点坐标为(1,56). ……………………7分说明:各解答题的其他正确解法请参照以上标准按分步给分的原则酌情评分.。
北京市各区2019-2020学年上学期八年级期末数学试卷精选汇编:几何综合专题(含答案)
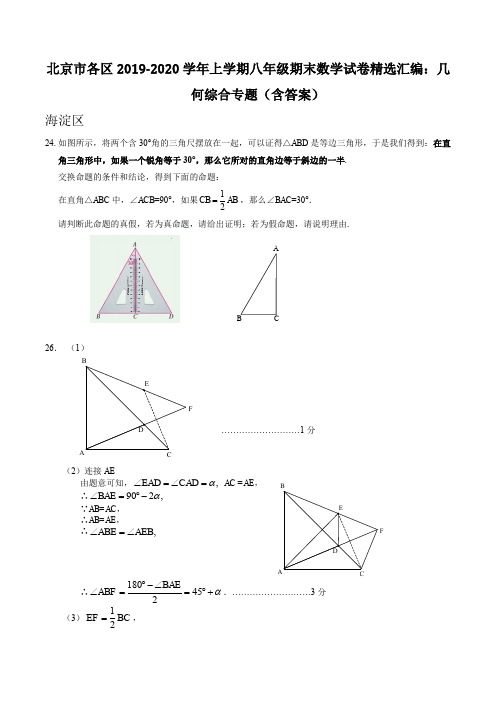
FFA北京市各区2019-2020学年上学期八年级期末数学试卷精选汇编:几何综合专题(含答案)海淀区24.如图所示,将两个含30°角的三角尺摆放在一起,可以证得△ABD 是等边三角形,于是我们得到:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半. 交换命题的条件和结论,得到下面的命题: 在直角△ABC 中,∠ACB =90°,如果12CB AB =,那么∠BAC =30°. 请判断此命题的真假,若为真命题,请给出证明;若为假命题,请说明理由.26. (1)………………………1分(2)连接AE由题意可知,,EAD CAD α∠=∠= AC =AE , ∴902,BAE α∠=︒- ∵AB=AC ,∴AB=AE , ∴,ABE AEB ∠=∠∴180452BAEABF α︒-∠∠==︒+.………………………3分(3)12EF BC =, CA证明:由(2)可知45,AEB ABE α∠=∠=︒+ ∴.CBF α∠= ………………………4分 ∵点C 关于直线AD 的对称点为点E , ∴135,ACF AEF α∠=∠=︒- ∴90,BCF α∠=︒-∵90,CBF BCF ∠+∠=︒ ………………………5分 ∴△BCF 是直角三角形.∵△ACE 是等边三角形, ∴30.α=︒∴30CBF ∠=︒ ∴1.2EF CF BC ==………………………6分东城区23.在三角形纸片ABC 中,∠B =90°,∠A =30°,AC =4,点E 在AC 上,AE =3.将三角形纸片按图1方式折叠,使点A 的对应点A '落在AB 的延长线上,折痕为ED ,A E '交BC 于点F. (1)求∠CFE 的度数;(2)如图2,,继续将纸片沿BF 折叠,点A '的对应点为A '',A F ''交DE 于点G .求线段DG 的长.图1图224. 如图,△ABC .(1)尺规作图:过点C 作AB 的垂线交AB 于点O .不写作法,保留作图痕迹; (2)分别以直线AB ,OC 为x 轴,y 轴建立平面直角坐标系,使点B ,C 均在正半轴上.若AB=7.5,OC =4.5,∠A =45°,写出点B 关于y 轴的对称点D 的坐标; (3)在(2)的条件下,求△ACD 的面积.23.解:(1)∵∠A =30°,∴∠A '=30°. ……………………1分∵∠A BF '=90°,∴∠A FB '=60°. ……………………2分 ∵∠CFE =∠A FB ', ∴∠CFE =60°. ……………………3分(2)∵点A 与点A '关于直线DE 对称, ∴DE ⊥AA '. ∵∠A =30°,AE =3, ∴1322DE AE == . ……………………4分 由(1)知,∠CFE =60°,∠C =60°,∴△CFE 是等边三角形.∴EF =CE =AC -AE =1. ……………………5分 同理,△EFG 也是等边三角形,∴12DG DE EG =-=DG =DE -EG =.……………………6分24.解:(1)……………………………………………………………………………………2分(2)D (-3,0); ……………………4分 (3)13927==2228ACD S ⨯⨯△.……………………6分 密云区25.已知如图,点A 、点B 在直线l 异侧,以点A 为圆心,AB 长为半径作弧交直线l 于C 、D 两点.分别以C 、D 为圆心,AB 长为半径作弧,两弧在l 下方交于点E,连结AE. (1)根据题意,利用直尺和圆规补全图形; (2)证明:l 垂直平分AE.lAB25.(1)图2A………………2分(2)证明:AC=AD=AB,CE=ED=AB,∴AC=CE,AD=DE又CD=CD∴△ACD ≌△ECD………………4分∴∠ACD=∠ECD∵AC=CE ∴l 垂直平分AE.………………6分门头沟区24.如图,在△ABC 中,AC 的垂直平分线交AC 于点D , 交BC 延长线交于点E ,连接AE ,如果∠B =50°,∠BAC =21°,求∠CAE 的度数.24.解答题(本小题满分5分) ∵AC 的垂直平分线交AC 于点D ∴EA =EC ……………………………………… 1分 ∴∠E AC =∠ECA ………………………… 2分∵∠B =50°,∠BAC =21°∴∠ECA=∠B+∠BAC=71°………………… 4分∴∠E AC =71° ………………… 5分27. 如图,在△ABC 中,AB=AC ,点M 在△ABC 内,AM 平分∠BAC .点D 与点M 在AC 所在直线的两侧,AD ⊥AB ,AD= BC ,点E 在AC 边上,CE=AM ,连接MD 、BE . (1) 补全图形;(2) 请判断MD 与BE 的数量关系,并进行证明;(3) 点M 在何处时,BM+BE 会有最小值,画出图形确定点M 的位置;如果AB =5,BC = 6,求出BM+BE的最小值.BBB27.解答题(本小题满分7分) 解:(1)补全图形正确 ………………………………………………………1分 (2)MD =BE ………………………………………………………2分证明:延长AM 交BC 于点F (如图2). ∵ AM 平分∠BAC , ∴ ∠BAM =∠CAM .∵ AD ⊥AB , ∴ ∠MAD +∠BAM =90°. ∴ ∠MAD +∠CAM =90°∵ AB=AC ,AM 平分∠BAC ,∴ AF ⊥BC .∴ ∠C +∠CAM =90°.∴ ∠MAD =∠C . ………………………………3分 又∵ AM= CE ,AD= BC ,∴ △AMD ≌△CEB . …………………………………………… 4分 ∴ MD =BE . …………………………………………… 5分(3) 点M 的位置如图 …………………………………………… 6分∵ AB=5,BC = 6, ∴ AD = BC=6,.∴BD ==∴ BM+BE……………… 7分朝阳区26.如图,△ABC 是等边三角形,△ADC 与△ABC 关于直线AC 对称,AE 与CD 垂直交BC 的延长线于点E ,∠EAF=45º,且AF 与AB 在AE 的两侧,EF ⊥AF . (1)依题意补全图形.(2)①在AE 上找一点P ,使点P 到点B ,点C 的距离和最短;②求证:点D 到AF ,EF 的距离相等.26.(1)补全图形,如图………………………..2分(2与AE 的交点.B B…………..4分②证明:连接DE ,DF .∵△ABC ,△ADC 是等边三角形,∴AC =AD ,∠ACB =∠CAD =60°. ∵AE ⊥CD , ∴∠CAE =21∠CAD =30°. ∴∠CEA =∠ACB -∠CAE =30°. ∴∠CAE =∠CEA. ∴CA =CE . ∴CD 垂直平分AE . ∴DA =DE .∵EF ⊥AF ,∠EAF =45°, ∴∠FEA =45°. ∴∠FEA =∠EAF . ∴F A =FE .∴△F AD ≌△FED .∴∠AFD =∠EFD .点D 到AF ,EF 的距离相等. ……………..7分顺义区27.在平面内,给定∠AOB =60°,及OB 边上一点C ,如图所示.到射线OA ,OB 距离相等的所有点组成图形G ,线段OC 的垂直平分线交图形G 于点D ,连接CD .(1)依题意补全图形;直接写出∠DCO 的度数;(2)过点D 作OD 的垂线,交OA 于点E ,OB 于点F .求证:CF =DE .O27.(5分)F EDCBA(1)画图………………………………… 2分30°………………………………… 3分(2) 证明:∵OD 是∠AOB 的平分线,∠AOB =60°, ∴∠1 =∠2=30°,又∵点D 在OC 的垂直平分线上, ∴CD =OD ,∴∠3 =∠2=30°, ∵EF ⊥OD ,∴∠EDO =∠FDO =90°, ∴∠DFO =60°,∴∠4 =30°,∠4 =∠3, ∴CF =DF ,又∵△OED ≌△OFD ,……………………………………4分 ∴DE =DF ,∴CF =DE .…………………………………………………5分昌平区27.如图,将△ABC 分别沿 AB ,AC 翻折得到△ABD 和△AEC ,线段 BD 与AE交于点 F ,连接BE .(1)如果∠ABC =16º,∠ACB =30°,求∠DAE 的度数; (2)如果BD ⊥CE ,求∠CAB 的度数.27. 解:(1)∵△ABC 沿AC 、AB 翻折得到△AEC 和△ABD , ∴△AEC ≌△ABC ,△ABD ≌△ABC.∴∠2=∠1=30°, ∠4=∠3=16°. …………1分 ∠EAC =∠BAD =∠BAC =180°-30°--16°=134°. ……2分∵∠DAC =360°-∠BAD -∠BAC ,O54321F EDCBA∴∠DAC=360°-134°-134°=92°. ………………3分∴∠DAE=∠EAC -∠DAC=134°-92°=42°. …………4分(2)∵BD ⊥CE ,∴∠5=90°. . …………………………………………………………………… 5分∴∠DBC+∠ECB=90°.∵∠1=∠2,∠3=∠4,∴∠DBC+∠ECB=2∠3+2∠1=90°.∴∠3+∠1=45°. . …………………………………………… 6分 在△ABC 中,∠CAB =180°-(∠3+∠1)=180°-45°=135°. …… 7分平谷区27. 已知:在△ABC 中,∠ABC =45°,BD ⊥AC 于点D ,过点C 作CE ⊥AB 于点E ,交BD 于点F .(1)依题意补全图形; (2)求证:∠ABD =∠ACE (3)求证:EF =AE27. (1) 依题意补全图形………………………………………………… 1 (2)证明:∵CE ⊥AB ,BD ⊥AC∴∠BEC=∠BDC=90°………………………2 ∴∠ABD+∠EFB=90°∠ACE+∠CFD=90° ∵∠EFB=∠CFD∴∠ABD=∠ACE (3)(3)∵∠BEC=90°,∠ABC=45° ∴ BE=EC (4)在△BEF 和△AEC 中 ⎪⎩⎪⎨⎧∠∠=∠=∠ACE =ABD ECBE AEC BEC∴BEF ∆≌AEC ∆)(ASA (5)∴EF =AE燕山地区27.阅读下面材料:学习了三角形全等的判定方法(即“SAS ”“ASA ”“AAS ”“SSS ”)和直角三角形全等的判定方法(即“HL ”)后,明明继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行探究明明将命题用符号语言表示为:在△ABC 和△DEF 中,AC=DF ,BC=EF ,∠B =∠E . 明明的探究方法是把∠B 分为“直角、钝角、锐角”三种情况进行探究.(1) 当∠B 是直角时,如图甲,△ABC 和△DEF 中,AC=DF ,BC=EF ,∠B =∠E =90°, 根据“HL ”定理,可以知道Rt △ABC ≌ Rt △DEF.(2)当∠B 是锐角时,如图乙,BC=EF ,∠B =∠E ﹤90°,在射线EM 上有点D,使DF=AC,画出符合条件的点D ,则△ABC 和△DEF 的关系是 ;A. 全等B. 不全等C.不一定全等(3)当∠B 是钝角时,如图丙,在△ABC 和△DEF 中,AC=DF ,BC=EF ,∠B =∠E ﹥90°.过点C 作AB 边的垂线交AB 延长线于点M;同理过点F 作DE 边的垂线交DE 延长线于N ,根据“ASA ”,可以知道△CBM ≌△FEN,请补全图丙,进而证出△ABC ≌△DEF.A27.(2)画出点D 正确,选C ………………… 2分 (3)补全图 ………………… 3分证明:由△CBM ≌△FEN得,CM=FN,BD=EN 又在Rt △CMA 和Rt △FND 中⎩⎨⎧==FN CM DF AC ∴△CMA ≌△FND ∴AM=DN∴AB=DE ……………… 4分 又在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧===DE AB EF BC DFAC ∴△ABC ≌△DEF ……………… 5分房山区26.(1)证明:∵AB AD =,=60A ∠︒,∴△ABD 是等边三角形.∴60ADB ∠=︒. …….………..……….1分∵CE ∥AB ,∴60CED A ∠=∠=︒. …….………..……….2分 ∴CED ADB ∠=∠. (2)解:连接AC 交BD 于点O ,∵AB AD =,BC DC =, ∴AC 垂直平分BD . ∴30BAO DAO ∠=∠=︒. ∵△ABD 是等边三角形,8AB = ∴8AD BD AB ===,∴4BO OD ==. ………….………..……….3分 ∵CE ∥AB , ∴ACE BAO ∠=∠.∴6AE CE ==, 2DE AD AE =-=.O F EDBA∵60CED ADB ∠=∠=︒.∴60EFD ∠=︒.∴△EDF 是等边三角形.∴2EF DF DE ===,∴4CF CE EF =-=,2OF OD DF =-=.在Rt △COF 中,∴OC ==. …….………..……….4分 在Rt △BOC 中,∴BC ===. …….………..……….5分 大兴区26. 解:∵AD 是△ABC 的高∴90ADB ADC ∠=∠= ………………………… 1分∵45ABC ∠=∴45DBA ABC ∠=∠=o∴BD =AD ………………………… 2分∵BE 是△ABC 的高∴90BEC ∠=∴90EBC C ∠+∠=∵90ADC ∠=∴90DAC C ∠+∠=∴EBC DAC ∠=∠ ………………………… 3分在△BDF 和△ADC 中,EBC DAC BD ADBDF ADC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BDF ≌△ADC . ………………………… 4分∴DF =CD . ………………………… 5分∵CD =4∴DF =4 ………………………… 6分27.解:(1)EBA ………………………… 2分(2)∵将线段CD 绕点C 逆时针旋转90°得到线段CE ,∴90DCE ∠=,CD =CE∵ ∠ACB =90°∴ACD BCE ∠=∠ ………………………… 3分在△ACD 和△BCE 中,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩∴△ACD ≌△BCE ………………………… 5分∴CBE A ∠=∠ ………………………………………… 6分 ∵90,ACB AC BC ∠==o∴45A ∠=o∴45CBE ∠=o∵90DCE ∠=,CD =CE∴45CED ∠=……………………………………………………… 7分 在△BCE 中, BCE ACD α∠=∠=.∴90DEB ∠=-α…………………………………………………… 8分 石景山区通州区。
2020-1北京市燕山地区初二年级第一学期期末-数学试题及答案

北京燕山地区2019-2020学年八年级(上)期末数学试卷一.选择题(共8小题)1.下面是同学们设计的一些美丽有趣的图案,其中是轴对称图形的是()A.B.C.D.2.为庆祝首个“中国农民丰收节”,十渡镇西河村举办“西河稻作文化节”活动.西河水稻种植历史悠久,因“色白粒粗,味极香美,七煮不烂”而享誉京城.已知每粒稻谷重约0.000035千克,将0.000035用科学记数法表示应为()A.35×10﹣6B.3.5×10﹣6C.3.5×10﹣5D.0.35×10﹣43.如果在实数范围内有意义,则x的取值范围是()A.x≠7 B.x<7 C.x>7 D.x≥74.下列运算正确的是()A.=±2 B.()2=4 C.=﹣4 D.(﹣)2=﹣4 5.如图,Rt△ABC≌Rt△DEF,∠E=55°,则∠A的度数为()A.25°B.35°C.45°D.55°6.如图,△ABC中,∠C=90°,AD平分∠CAB,交BC于点D,DE⊥AB于点E,若CD=,则DE的长为()A.2 B.3 C.D.27.如图,△ABC中,AB=AC,AD⊥BC,垂足为D,DE∥AB,交AC于点E,则下列结论不正确的是()A.∠CAD=∠BAD B.BD=CD C.AE=ED D.DE=DB8.如图,有三种规格的卡片共9张,其中边长为a的正方形卡片4张,边长为b的正方形卡片1张,长,宽分别为a,b的长方形卡片4张.现使用这9张卡片拼成一个大的正方形,则这个大正方形的边长为()A.2a+b B.4a+b C.a+2b D.a+3b二.填空题(共8小题)9.若分式的值为0,则x的值是.10.计算的结果是.11.计算(+2)(﹣2)的结果是.12.在△ABC中,AB=AC,BC=5,∠B=60°,则△ABC的周长是.13.如图,线段AB与CD相交于点O,且OA=OD,连接AC,BD,要说明△AOC≌△DOB,还需添加的一个条件是.(只需填一个条件即可)14.写出一个能用平方差公式分解因式的多项式:.15.已知x2+2x=3,则代数式(x+1)2﹣(x+2)(x﹣2)+x2的值为.16.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中记载了一个“折竹抵地”问题:“今有竹高二丈,末折抵地,去本六尺,问折者高几何?”译文:“有一根竹子,原高二丈(1丈=10尺),现被风折断,竹梢触地面处与竹根的距离为6尺,问折断处离地面的高度为多少尺?”如图,我们用点A,B,C分别表示竹梢,竹根和折断处,设折断处离地面的高度BC=x 尺,则可列方程为.三.解答题(共3小题)17.计算:(×﹣)÷.18.分解因式:4ma2﹣mb2.19.解方程:=1﹣.20.如图,AB=AC,点D,E分别是线段AB,AC的中点,连接BE,CD.求证:∠B=∠C.21.下面是小芸设计的“作三角形一边上的高”的尺规作图过程.已知:△ABC.求作:△ABC的边BC上的高AD.作法:①以点A为圆心,适当长为半径画弧,交直线BC于点M,N;②分别以点M,N为圆心,以大于MN的长为半径画弧,两弧相交于点P;③作直线AP交BC于点D,则线段AD即为所求△ABC的边BC上的高.根据小芸设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明:证明:∵AM=,MP=,∴AP是线段MN的垂直平分线.()(填推理的依据)∴AD⊥BC于D,即线段AD为△ABC的边BC上的高..22.如图,四边形ABCD中,∠B=90°,∠ACB=30°,AB=2,CD=3,AD=5.(1)求证:AC⊥CD;(2)求四边形ABCD的面积.23.如图,在平面直角坐标系xOy中,点O(0,0),A(﹣1,2),B(2,1).(1)在图中画出△AOB关于y轴对称的△A1OB1,并直接写出点A1和点B1的坐标;(不写画法,保留画图痕迹)(2)在x轴上存在点P,使得PA+PB的值最小,则点P的坐标为,PA+PB的最小值为.24.先化简,再求值:(1﹣),其中m=2019.25.下面是两位同学的一段对话:聪聪:周末我们去国家博物馆参观“伟大的变革﹣﹣庆祝改革开放40周年大型展览”吧.明明:好啊,我家离国家博物馆约30km,我坐地铁先走,地铁的平均行驶速度是公交车的1.5倍呢.聪聪:嗯,我周末住奶奶家,离国家博物馆只有5km,坐公交车,你出发40分钟后我再出发就能和你同时到达.根据对话内容,请你求出公交车和地铁的平均行驶速度.26.阅读下列材料:在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”.下面是小涵同学用换元法对多项式(x2﹣4x+1)(x2﹣4x+7)+9进行因式分解的过程.解:设x2﹣4x=y原式=(y+1)(y+7)+9(第一步)=y2+8y+16(第二步)=(y+4)2(第三步)=(x2﹣4x+4)2(第四步)请根据上述材料回答下列问题:(1)小涵同学的解法中,第二步到第三步运用了因式分解的;A.提取公因式法B.平方差公式法C.完全平方公式法(2)老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果:;(3)请你用换元法对多项式(x2+2x)(x2+2x+2)+1进行因式分解.27.已知BC=5,AB=1,AB⊥BC,射线CM⊥BC,动点P在线段BC上(不与点B,C重合),过点P作DP⊥AP交射线CM于点D,连接AD.(1)如图1,若BP=4,判断△ADP的形状,并加以证明.(2)如图2,若BP=1,作点C关于直线DP的对称点C′,连接AC′.①依题意补全图2;②请直接写出线段AC′的长度.28.一般情况下,=+1不成立,但有些数可以使得它成立,例如:a=1,b=2.我们称使得=+1成立的一对数a,b为“相伴数对”,记为(a,b).(1)判断数对(﹣2,1),(3,3)是否是“相伴数对”;(2)若(k,﹣1)是“相伴数对”,求k的值;(3)若(4,m)是“相伴数对”,求代数式的值.参考答案与试题解析一.选择题(共8小题)1.下面是同学们设计的一些美丽有趣的图案,其中是轴对称图形的是()A.B.C.D.【分析】根据轴对称的定义,结合所给图形进行判断即可.【解答】解:A、是轴对称图形;B、不是轴对称图形;C、不是轴对称图形;D、不是轴对称图形;故选:A.2.为庆祝首个“中国农民丰收节”,十渡镇西河村举办“西河稻作文化节”活动.西河水稻种植历史悠久,因“色白粒粗,味极香美,七煮不烂”而享誉京城.已知每粒稻谷重约0.000035千克,将0.000035用科学记数法表示应为()A.35×10﹣6B.3.5×10﹣6C.3.5×10﹣5D.0.35×10﹣4【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:0.000035=3.5×10﹣5,故选:C.3.如果在实数范围内有意义,则x的取值范围是()A.x≠7 B.x<7 C.x>7 D.x≥7【分析】直接利用二次根式有意义的条件分析得出答案.【解答】解:∵在实数范围内有意义,∴x﹣7≥0,解得:x≥7.故选:D.4.下列运算正确的是()A.=±2 B.()2=4 C.=﹣4 D.(﹣)2=﹣4 【分析】根据算式平方根的定义和二次根式的性质逐一化简可得.【解答】解:A.=2,此选项错误;B.()2=4,此选项正确;C.=4,此选项错误;D.(﹣)2=4,此选项错误;故选:B.5.如图,Rt△ABC≌Rt△DEF,∠E=55°,则∠A的度数为()A.25°B.35°C.45°D.55°【分析】根据三角形内角和定理求出∠EDF,根据全等三角形的性质解答.【解答】解:∵∠EFD=90°,∠E=55°,∴∠EDF=90°﹣55°=35°,∵Rt△ABC≌Rt△DEF,∠A=∠EDF=35°,故选:B.6.如图,△ABC中,∠C=90°,AD平分∠CAB,交BC于点D,DE⊥AB于点E,若CD=,则DE的长为()A.2 B.3 C.D.2【分析】根据角平分线的性质即可求出答案.【解答】解:∵AD平分∠CAB,DE⊥AB,∠C=90°,∴CD=DE=,故选:C.7.如图,△ABC中,AB=AC,AD⊥BC,垂足为D,DE∥AB,交AC于点E,则下列结论不正确的是()A.∠CAD=∠BAD B.BD=CD C.AE=ED D.DE=DB【分析】根据等腰三角形的性质,直角三角形的性质解答.【解答】解:∵AB=AC,AD⊥BC,∴∠CAD=∠BAD,A正确,不符合题意;BD=CD,B正确,不符合题意;∵DE∥AB,∴∠EDA=∠BAD,∵∠EAD=∠BAD,∴∠EAD=∠EDA,∴AE=ED,C正确,不符合题意;DE与DB的关系不确定,D错误,符合题意;故选:D.8.如图,有三种规格的卡片共9张,其中边长为a的正方形卡片4张,边长为b的正方形卡片1张,长,宽分别为a,b的长方形卡片4张.现使用这9张卡片拼成一个大的正方形,则这个大正方形的边长为()A.2a+b B.4a+b C.a+2b D.a+3b【分析】先计算出这9张卡片的总面积,其和为一完全平方式,因式分解即可求得大正方形的边长.【解答】解:由题可知,9张卡片总面积为4a2+4ab+b2,∵4a2+4ab+b2=(2a+b)2,∴大正方形边长为2a+b.故选:A.二.填空题(共8小题)9.若分式的值为0,则x的值是 4 .【分析】根据分式的值为零的条件即可求出答案.【解答】解:由题意可知:解得:x=4,故答案为:410.计算的结果是 2 .【分析】根据分式的运算法则即可求出答案.【解答】解:原式==2,故答案为:211.计算(+2)(﹣2)的结果是﹣1 .【分析】利用平方差公式计算,再根据二次根式的性质计算可得.【解答】解:原式=()2﹣22=3﹣4=﹣1,故答案为:﹣1.12.在△ABC中,AB=AC,BC=5,∠B=60°,则△ABC的周长是15 .【分析】根据等边三角形的判定和性质即可解决问题.【解答】解:∵AB=AC,∠B=60°,∴△ABC是等边三角形,∴△ABC的周长为15,故答案为15.13.如图,线段AB与CD相交于点O,且OA=OD,连接AC,BD,要说明△AOC≌△DOB,还需添加的一个条件是OC=OB或AB=CD或∠A=∠D或∠B=∠C.(只需填一个条件即可)【分析】已知条件中OA=OD,且∠AOC=∠DOB为对顶角相等,则还需添加这一对角的另一对对应边相等或另一组对应角相等即可.【解答】解:∵OA=OD,且∠AOC=∠DOB,∴添加OC=OB或AB=CD时,依据SAS即可判定△AOC≌△DOB;添加∠A=∠D或∠B=∠C,依据ASA或AAS即可判定△AOC≌△DOB;故答案为:OC=OB或AB=CD或∠A=∠D或∠B=∠C.(答案不唯一)14.写出一个能用平方差公式分解因式的多项式:a2﹣4 .【分析】这是一道自由发挥问题,根据能用平方差公式因式分解的多项式的特点,只要是两个平方项,且符号相反即可.【解答】解:∵(a+2)(a﹣2),=a2﹣2a+2a﹣4,=a2﹣4,∴满足条件的多项式是:a2﹣4.故答案可以是:a2﹣4.15.已知x2+2x=3,则代数式(x+1)2﹣(x+2)(x﹣2)+x2的值为8 .【分析】根据完全平方公式、平方差公式可以化简题目中的式子,然后根据x2+2x=3整体代入即可解答本题.【解答】解:(x+1)2﹣(x+2)(x﹣2)+x2,=x2+2x+1﹣(x2﹣4)+x2,=x2+2x+5,∴原式=3+5=8.故答案为:8.16.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中记载了一个“折竹抵地”问题:“今有竹高二丈,末折抵地,去本六尺,问折者高几何?”译文:“有一根竹子,原高二丈(1丈=10尺),现被风折断,竹梢触地面处与竹根的距离为6尺,问折断处离地面的高度为多少尺?”如图,我们用点A,B,C分别表示竹梢,竹根和折断处,设折断处离地面的高度BC=x 尺,则可列方程为x2+62=(20﹣x)2.【分析】竹子折断后刚好构成一直角三角形,设竹子折断处离地面x尺,则斜边为(20﹣x)尺,利用勾股定理解题即可.【解答】解:设竹子折断处离地面x尺,则斜边为(20﹣x)尺,根据勾股定理得:x2+62=(20﹣x)2.故答案为x2+62=(20﹣x)2.三.解答题(共3小题)17.计算:(×﹣)÷.【分析】根据二次根式的混合运算顺序和运算法则计算可得.【解答】解:原式=(﹣)÷=÷﹣÷=﹣=2﹣.18.分解因式:4ma2﹣mb2.【分析】应先提取公因式4m,再对余下的多项式利用平方差公式继续分解.【解答】解:4ma2﹣mb2,=m(4a2﹣b2),=m(2a+b)(2a﹣b).19.解方程:=1﹣.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得,3x=3x+3﹣2x,移项合并同类项得,2x=3,系数化1得,x=,检验:x=是原方程的解.20.如图,AB=AC,点D,E分别是线段AB,AC的中点,连接BE,CD.求证:∠B=∠C.【考点】KD:全等三角形的判定与性质.【专题】14:证明题.【分析】证明△ABE≌△ACD(SAS),即可求解.【解答】证明:∵点D,E分别是线段AB,AC的中点,∴AD=AB,AE=AC,∵AB=AC,∴AD=AE,在△ABE和△ACD中,AB=AC,∠A=∠A,AD=AE,∴△ABE≌△ACD(SAS),∴∠B=∠C.21.下面是小芸设计的“作三角形一边上的高”的尺规作图过程.已知:△ABC.求作:△ABC的边BC上的高AD.作法:①以点A为圆心,适当长为半径画弧,交直线BC于点M,N;②分别以点M,N为圆心,以大于MN的长为半径画弧,两弧相交于点P;③作直线AP交BC于点D,则线段AD即为所求△ABC的边BC上的高.根据小芸设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明:证明:∵AM=AN,MP=NP,∴AP是线段MN的垂直平分线.(到一条线段两个端点距离相等的点在这条线段的垂直平分线上)(填推理的依据)∴AD⊥BC于D,即线段AD为△ABC的边BC上的高.【考点】KG:线段垂直平分线的性质;N3:作图—复杂作图.【专题】13:作图题.【分析】(1)利用几何语言画出对应的几何图形;(2)通过作图得到AM=AN,MP=NP,则根据线段垂直平分线的性质定理的逆定理可判断AP是线段MN的垂直平分线,从而得到AD⊥BC.【解答】解:(1)补全的图形如图所示;(2)证明:∵AM=AN,MP=NP,∴AP是线段MN的垂直平分线(到一条线段两个端点距离相等的点在这条线段的垂直平分线上)∴AD⊥BC于D,即线段AD为△ABC的边BC上的高.故答案为AN,NP,到一条线段两个端点距离相等的点在这条线段的垂直平分线上.22.如图,四边形ABCD中,∠B=90°,∠ACB=30°,AB=2,CD=3,AD=5.(1)求证:AC⊥CD;(2)求四边形ABCD的面积.【考点】KQ:勾股定理;KS:勾股定理的逆定理.【专题】554:等腰三角形与直角三角形.【分析】(1)根据直角三角形的性质得到AC=2AB=4,根据跟勾股定理的逆定理即可得到结论;(2)根据勾股定理得到BC==2,根据三角形的面积公式即可得到结论.【解答】(1)证明:在Rt△ABC中,∠B=90°,∠ACB=30°,AB=2,∴AC=2AB=4,在△ACD中,AC=4,CD=3,AD=5,∵42+32=52,即AC2+CD2=AD2,∴∠ACD=90°,∴AC⊥CD;(2)解:在Rt△ABC中,∠B=90°,AB=2,AC=4,∴BC==2,∴Rt△ABC的面积为AB•BC=×2×2=2,又∵Rt△ACD的面积为AC•CD=×4×3=6,∴四边形ABCD的面积为:2+6.23.如图,在平面直角坐标系xOy中,点O(0,0),A(﹣1,2),B(2,1).(1)在图中画出△AOB关于y轴对称的△A1OB1,并直接写出点A1和点B1的坐标;(不写画法,保留画图痕迹)(2)在x轴上存在点P,使得PA+PB的值最小,则点P的坐标为(1,0),PA+PB 的最小值为3.【考点】P7:作图﹣轴对称变换;PA:轴对称﹣最短路线问题.【专题】13:作图题;24:网格型;558:平移、旋转与对称.【分析】(1)分别作出点A和点B关于y轴的对称点,再与点O首尾顺次连接即可得;(2)作点B关于x轴的对称点B′,连接AB′,与x轴的交点即为所求点P,AB′的长即为PA+PB的最小值,利用勾股定理计算可得答案.【解答】解:(1)如图所示,△A1OB1即为所求;由图知A1(1,2),B1(﹣2,1);(2)由图知,点P即为所求,点P的坐标P(1,0),PA+PB的最小值为=3,故答案为:(1,0),3.24.先化简,再求值:(1﹣),其中m=2019.【考点】6D:分式的化简求值.【专题】11:计算题;513:分式.【分析】先根据分式的混合运算顺序和运算法则化简原式,再将m的值代入计算可得.【解答】解:原式=(﹣)•=•=,当m=2019时,原式==.25.下面是两位同学的一段对话:聪聪:周末我们去国家博物馆参观“伟大的变革﹣﹣庆祝改革开放40周年大型展览”吧.明明:好啊,我家离国家博物馆约30km,我坐地铁先走,地铁的平均行驶速度是公交车的1.5倍呢.聪聪:嗯,我周末住奶奶家,离国家博物馆只有5km,坐公交车,你出发40分钟后我再出发就能和你同时到达.根据对话内容,请你求出公交车和地铁的平均行驶速度.【考点】B7:分式方程的应用.【专题】522:分式方程及应用.【分析】根据题意列出分式方程,解方程得到答案.【解答】解:设公交车平均行驶速度为xkm/h,则地铁的平均行驶速度为1.5xkm/h,根据题意,得﹣=,解得,x=22.5,经检验:x=22.5是所列方程的解,且符合题意,5x=1.5×22.5=33.75km/h.答:公交车和地铁的平均行驶速度分别为22.5 km/h和33.75km/h.26.阅读下列材料:在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”.下面是小涵同学用换元法对多项式(x2﹣4x+1)(x2﹣4x+7)+9进行因式分解的过程.解:设x2﹣4x=y原式=(y+1)(y+7)+9(第一步)=y2+8y+16(第二步)=(y+4)2(第三步)=(x2﹣4x+4)2(第四步)请根据上述材料回答下列问题:(1)小涵同学的解法中,第二步到第三步运用了因式分解的C;A.提取公因式法B.平方差公式法C.完全平方公式法(2)老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果:(x ﹣2)4;(3)请你用换元法对多项式(x2+2x)(x2+2x+2)+1进行因式分解.【考点】54:因式分解﹣运用公式法.【专题】23:新定义;512:整式.【分析】(1)根据完全平方公式进行分解因式;(2)最后再利用完全平方公式将结果分解到不能分解为止;(3)根据材料,用换元法进行分解因式.【解答】解:(1)故选:C;(2)(x2﹣4x+1)(x2﹣4x+7)+9,设x2﹣4x=y,原式=(y+1)(y+7)+9,=y2+8y+16,=(y+4)2,=(x2﹣4x+4)2,=(x﹣2)4;故答案为:(x﹣2)4;(3)设x2+2x=y,原式=y(y+2)+1,=y2+2y+1,=(y+1)2,=(x2+2x+1)2,=(x+1)4.27.已知BC=5,AB=1,AB⊥BC,射线CM⊥BC,动点P在线段BC上(不与点B,C重合),过点P作DP⊥AP交射线CM于点D,连接AD.(1)如图1,若BP=4,判断△ADP的形状,并加以证明.(2)如图2,若BP=1,作点C关于直线DP的对称点C′,连接AC′.①依题意补全图2;②请直接写出线段AC′的长度.【考点】KY:三角形综合题.【专题】15:综合题.【分析】(1)先判断出PC=AB,再用同角的余角相等判断出∠APB=∠PDC,得出△ABP ≌△PCD(AAS),即可得出结论;(2)①利用对称的性质画出图形;②先求出CP=4,AB=AP,∠CPD=45°,进而得出C'P=CP=4,∠C'PD=∠CPD=45°,再判断出四边形BQC'P是矩形,进而求出AQ=BQ﹣AB=3,最后用勾股定理即可得出结论.【解答】(1)△ADP是等腰直角三角形.证明:∵BC=5,BP=4,∴PC=1,∵AB=1,∴PC=AB.∵AB⊥BC,CM⊥BC,DP⊥AP,∴∠B=∠C=90°,∠APB+∠DPC=90°,∠PDC+∠DPC=90°,∴∠APB=∠PDC,在△ABP和△PCD中,∴△ABP≌△PCD(AAS)∴AP=PD,∵∠APD=90°,∴△ADP是等腰直角三角形.(2)①依题意补全图2;②∵BP=1,AB=1,BC=5,∴CP=4,AB=AP,∵∠ABP=90°,∴∠APB=45°,∵∠APD=90°,∴∠CPD=45°,连接C'P,∵点C与C'关于DP对称,∴C'P=CP=4,∠C'PD=∠CPD=45°,∴∠CPC'=90°,∴∠BPC'=90°,过点C'作C'Q⊥BA交BA的延长线于Q,∴∠Q=90°=∠ABP=∠BPC',∴四边形BQC'P是矩形,∴C'Q=BP=1,BQ=C'P=4,∴AQ=BQ﹣AB=3,在Rt△AC'Q中,AC′=28.一般情况下,=+1不成立,但有些数可以使得它成立,例如:a=1,b=2.我们称使得=+1成立的一对数a,b为“相伴数对”,记为(a,b).(1)判断数对(﹣2,1),(3,3)是否是“相伴数对”;(2)若(k,﹣1)是“相伴数对”,求k的值;(3)若(4,m)是“相伴数对”,求代数式的值.【考点】45:整式的加减—化简求值.【专题】512:整式.【分析】(1)利用“相伴数对”的定义化简,计算即可求出b的值;(2)根据“相伴数对”的定义解答即可;(3)利用“相伴数对”定义得到m2﹣4m=﹣1,原式去括号整理后代入计算即可求出值.【解答】解:(1)∵+≠+1,∴(﹣2,1)不是“相伴数对”;∵+=+1,∴(3,3)是“相伴数对”;(2)∵(k,﹣1)是“相伴数对”,∴+=+1,解得k=1;(3)∵(4,m)是“相伴数对”,∴+=+1,∴m2﹣4m=﹣1,∴=====﹣.。
2020-2021学年北京市燕山区八年级(上)期末数学复习题及答案解析

2020-2021学年北京市燕山区八年级(上)期末数学复习题一、选择题(本大题共8小题,共16.0分)1. 下面是同学们设计的一些美丽有趣的图案,其中是轴对称图形的是( ) A. B. C. D.2. 目前,世界上能制造出的最小晶体管的长度只有0.00 000 004米,将0.00 000 004用科学记数法表示为( ).A. 4×108B. 4×10−8C. 0.4×108D. −4×1083. 若√x −6在实数范围内有意义,则x 的取值范围是( )A. x >0B. x >6C. x ≥6D. x ≤64. 下列计算中,正确的是( )A. √121=11B. √(−1)2=−1C. √(136)2=16D. √1625=±455. 已知△ABC≌△DEF ,∠A =70°,∠E =50°,则∠F 的度数为( )A. 50°B. 60°C. 70°D. 80°6. 如图,在Rt △ABC 中,∠C =90°,∠CAB 的平分线AD 交BC 于点D ,DE ⊥AB 于点E ,若CD =4,则DE 的长为( )A. 2B. 3C. 4D. 57. 如图,△ABC 中,AB =AC ,AD ⊥BC ,垂足为D ,DE//AB ,交AC 于点E ,则下列结论不正确的是( )A. ∠CAD=∠BADB. BD=CDC. AE=EDD. DE=DB8.如图,有三种卡片,分别是边长为a的正方形卡片1张,边长为b的正方形卡片4张和长宽为a、b的长方形卡片4张,现使用这9张卡片拼成一个大的正方形,则这个大的正方形边长为()A. a+3bB. 2a+bC. a+2bD. 4ab二、填空题(本大题共8小题,共16.0分)9.若分式2x−13x+5的值为0,则x的值为______.10.已知3x −2y=3,则4x−xy−6y5xy+9y−6x=______ .11.计算:(√7+2)(√7−2)=______.12.△ABC中,∠B=60°,AB=AC,BC=3,则△ABC的周长为______.13.如图,线段AB,CD相交于点O,AO=BO,添加一个条件,能使△AOC≌△BOD,所添加的条件可以是______14.分解因式:16−x2=______.15.如果x+y=−4,x−y=8,那么代数式x2−y2的值是________.16.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根四尺,问折者高几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远.问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程______.三、计算题(本大题共4小题,共22.0分)17. (−2)2×√12−4√3(4−√3)+2−318. 解方程:2−5x−2=x+32−x .19. 先化简,再求值:(1−1a+1)÷2a a 2−1,其中a =−3.20. 把下列各式因式分解:(1)2x 2−4x ;(2)x 2(a −b)+4(b −a);(3)2x 3−8x 2+8x ;(4)简算:20082−4016×2007+20072.四、解答题(本大题共8小题,共46.0分)21.分解因式(1)4a2−16(2)x2(x−2)+4(2−x)22.如图,CA=CB,AD=BD,E,F分别是AC,BC的中点.求证:DE=DF.23.如图,在△ABC中,∠C=90°.(1)尺规作图:作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);(2)在(1)的条件下,连接BD,当BC=5cm,AB=13cm时,求△BCD的周长.24.如图,在四边形ABCD中,∠D=90°,AD=2√3,CD=2,BC=3,AB=5,求四边形ABCD的面积.25.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(−1,1),B(3,1),C(2,3)(1)作出△ABC关于x轴对称的图形△A1B1C1;(2)在x轴上找一点E,使AE+BE最小;并直接写出点E的坐标.26.华联商场预测某品牌衬衫能畅销市场,先用了8万元购入这种衬衫,面市后果然供不应求,于是商场又用了17.6万元购入第二批这种衬衫,所购数量是第一批购入量的2倍,但单价贵了4元.商场销售这种衬衫时每件定价都是58元,最后剩下的150件按定价的八折销售,很快售完.试求:(1)第一次购买这种衬衫的单价是多少?(2)在这两笔生意中,华联商场共赢利多少元?27.如图,AB⊥BC,射线CM⊥BC,且AB=7cm,BC=22cm,点P是线段BC(不与点B、C重合)上的动点,过点P作DP⊥AP交射线CM于点D,连结AD.(1)如图1,当BP=______时,△ADP是等腰直角三角形.(2)如图2,若P是BC的中点,求证:DP平分∠ADC.(3)若△PDC是等腰三角形,作点B关于AP的对称点B′,连结B′D,则B′D=______cm.28.一般情况下a2+b3=a+b2+3不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得a2+b3=a+b2+3成立的一对数a,b为“相伴数对”,记为(a,b).(1)若(1,b)是“相伴数对”,求b的值;(2)写出一个“相伴数对”(a,b),其中a≠0,且a≠1;(3)若(m,n)是“相伴数对”,求代数式m−223n−[4m−2(3n−1)]的值.-------- 答案与解析 --------1.答案:A解析:解:A、是轴对称图形;B、不是轴对称图形;C、不是轴对称图形;D、不是轴对称图形;故选:A.根据轴对称的定义,结合所给图形进行判断即可.本题考查了轴对称图形的知识,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.2.答案:B解析:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a的值以及n的值.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.解:0.00000004=4×10−8,故选B.3.答案:C解析:解:√x−6在实数范围内有意义,则x−6≥0,故x的取值范围是:x≥6.故选:C.直接利用二次根式的定义分析得出答案.此题主要考查了二次根式有意义的条件,正确把握二次根式的定义是解题关键.4.答案:A解析:解:A 、√121=11,正确; B 、√(−1)2=1,故此选项错误;C 、√(136)2=136,故此选项错误;D 、√1625=45,故此选项错误; 故选:A .直接利用二次根式的性质化简得出答案.此题主要考查了二次根式的性质,正确掌握二次根式的性质是解题关键.5.答案:B解析:解:∵△ABC≌△DEF ,∴∠D =∠A =70°,∵∠E =50°,∴∠F =180°−50°−70°=60°,故选:B .根据全等三角形的性质可得∠D =∠A =70°,再根据三角形内角和定理可得答案.此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应角相等.6.答案:C解析:解:∵AD 是∠CAB 的平分线,∠C =90°,DE ⊥AB ,∴DE =DC =4.故选:C .根据角平分线的性质定理解答即可.本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键. 7.答案:D解析:本题考查的是等腰三角形的性质,平行线的性质.根据等腰三角形的性质进行角相等和边相等的转化,以及直角三角形的性质解答.解:∵AB =AC ,AD ⊥BC ,∴∠CAD =∠BAD ,A 正确,不符合题意;BD =CD ,B 正确,不符合题意;∵DE//AB ,∴∠EDA =∠BAD ,∵∠EAD =∠BAD ,∴∠EAD =∠EDA ,∴AE =ED ,C 正确,不符合题意;DE 与DB 的关系不确定,D 错误,符合题意;故选D .8.答案:C解析:本题考查了完全平方公式几何意义的理解,利用完全平方公式分解因式后即可得出大正方形的边长.可分别计算出这9张卡片的总面积,其和为一完全平方公式,可求得大正方形的边长. 解:设拼成后大正方形的边长为x ,则a 2+4ab +4b 2=x 2,则(a +2b)2=x 2,∴x =a +2b ,故选C .9.答案:12解析:解:由题意可知:{2x −1=03x +5≠0, 解得:x =12,故答案为:12根据分式的值为零的条件即可求出答案.本题考查分式的值为零的条件,解题的关键是熟练运用分式的值为零的条件,本题属于基础题型. 10.答案:−12解析:解:∵3x−2y=3,∴3y−2x=3xy,∴原式=2(2x−3y)−xy5xy+3(3y−2x)=−6xy−xy 5xy+9xy=−12.故答案为:−12.由已知,可得3y−2x=3xy,根据对分式的分子分母变形,化成2x−3y或3y−2x的形式,等量代换,进而可求出答案.本题考查分式的化简求值,解题的关键是变形得到3y−2x=3xy,本题属于中档题.11.答案:3解析:解:原式=(√7)2−22=7−4=3,故答案为:3.根据平方差公式展开,再依次计算乘方和减法即可得.本题主要考查二次根式的混合运算,解题的关键是掌握二次根式的混合运算顺序和运算法则以及平方差公式.12.答案:9解析:解:∵AB=AC,∴△ABC是等腰三角形,又∵∠B=60°,∴△ABC是等边三角形,∴AB=BC=CA=3,∴△ABC的周长为:9.故答案为:9.依据有一个角是60°的等腰三角形是等边三角形即可判定三角形是等边三角形,然后根据周长求法求得.本题考查了等边三角形的判定.13.答案:OC=OD或∠A=∠B或∠C=∠D解析:解:∵∠AOC=∠BOC,AO=BO,∴当OC=OD时,△AOC≌△BOD;当∠A=∠B时,△AOC≌△BOD;当∠C=∠D时,△AOC≌△BOD.故答案为OC=OD或∠A=∠B或∠C=∠D.利用对顶角相等得到∠AOC=∠BOC,加上AO=BO,当OC=OD时,根据“SAS“可判断△AOC≌△BOD;当∠A=∠B时,可根据“ASA”判断△AOC≌△BOD;当∠C=∠D时,根据“AAS”可判断△AOC≌△BOD.本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.14.答案:(4+x)(4−x)解析:本题考查利用平方差公式分解因式,熟记公式结构是解题的关键.16和x2都可写成平方形式,且它们符号相反,符合平方差公式特点,利用平方差公式进行因式分解即可.解:16−x2=(4+x)(4−x).故答案为:(4+x)(4−x).15.答案:−32解析:本题主要考查的是代数式的值,平方差公式,运用了整体代入法的有关知识,先将给出的代数式进行变形,然后整体代入求值即可.解:原式=(x−y)(x+y),把x+y=−4,x−y=8代入原式,原式=−4×8=−32.故答案为−32.16.答案:x2+42=(10−x)2解析:解:设竹子折断处离地面x尺,则斜边为(10−x)尺,根据勾股定理得:x2+42=(10−x)2.故答案为x2+42=(10−x)2.竹子折断后刚好构成一直角三角形,设竹子折断处离地面x尺,则斜边为(10−x)尺,利用勾股定理解题即可.此题考查了勾股定理的应用,解题的关键是利用题目信息构造直角三角形,从而运用勾股定理解题.17.答案:解:原式=4×2√3−16√3+12+8(2+√3)=8√3−16√3+12+16+8√3=28.解析:本题考查二次根式的混合运算,根据运算法则和运算顺序仔细运算即可.18.答案:解:去分母得:2(x−2)−5=−(x+3),移项合并得:3x=6,解得:x=2,经检验,x=2是原方程的增根,所以,原方程无解.解析:此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.19.答案:解:原式=(a+1a+1−1a+1)÷2a(a+1)(a−1)=aa+1⋅(a+1)(a−1)2a=a−12,当a=−3时,=−2.原式=−3−12解析:原式利用分式混合运算顺序和运算法则化简,再将a的值代入计算可得.本题主要考查分式的化简求值,解题的关键是熟练掌握分式混合运算顺序和运算法则.20.答案:解:(1)2x2−4x=2x(x−2).(2)x2(a−b)+4(b−a)=(a−b)(x2−4)=(a−b)(x+2)(x−2);(3)2x3−8x2+8x=2x(x2−4x+4)=2x(x−2)2;(4)20082−4016×2007+20072=20082−2×2008×2007+20072=(2008−2007)2=12=1.解析:此题主要考查了公式法以及提取公因式法分解因式,熟练利用公式法分解因式是解题关键.(1)首先提取公因式2x分解因式即可;(2)首先提取公因式(a−b),再利用平方差公式分解因式即可;(3)首先提取公因式2x,再利用完全平方公式分解因式即可;(4)直接利用完全平方公式分解因式即可.21.答案:解:(1)4a2−16=4(a2−4)=4(a+2)(a−2);(2)x2(x−2)+4(2−x)=x2(x−2)−4(x−2)=(x−2)(x2−4)=(x−2)2(x+2).解析:(1)先提取公因式4a,再对余下的多项式利用平方差公式继续分解;(2)先提取公因式(x−2),再对余下的多项式利用平方差公式继续分解.本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,理解因式分解与整式的乘法是互逆运算是解题的关键.22.答案:证明:连接CD.在△CAD和△CBD中,{CA=CB AD=BD CD=CD,∴△CAD≌△CBD(SSS),∴∠A=∠B,又∵AC=CB,E,F分别为AC,BC的中点,∴AE=12AC,BF=12BC,即AE=BF,在△ADE和△BDF中,{AE=BF ∠A=∠B AD=BD,∴△ADE≌△BDF(SAS),∴DE=DF.解析:本题考查了全等三角形的性质和全等三角形的判定,分别利用SSS和SAS定理证出三角形全等,再利用全等三角形的性质即可证明此题.23.答案:解:(1)如图所示;(2)在Rt△ABC中,∵AB=13cm,BC=5cm,∴AC=√AB2−BC2=12cm,∵DE为AB的中垂线,∴DA=DB,∴△BCD的周长=BC+BD+CD=BC+AD+CD=BC+AC=5+12=17cm.解析:本题考查了作图−复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了线段垂直平分线的性质.(1)作线段AB的垂直平分线即可;(2)先根据勾股定理计算出AC=12cm,再利用线段垂直平分线的性质得到DA=DB,则可把△BCD 的周长转为AC与BC的和,从而达到解决问题的目的.24.答案:解:∵连接AC,如图所示:∵∠D=90°,AD=√12,CD=2,∴AC=√AD2+CD2=4.∵BC=3,AB=5,32+42=52,∴△ABC是直角三角形,∠ACB=90°,∴S四边形ABCD =S△ACD+S△ABC=12×√12×2+12×4×3=2√3+6.解析:先根据勾股定理求出AC的长,再由勾股定理的逆定理判断出△ABC的形状,根据三角形的面积公式即可得出结论.本题考查的是勾股定理和勾股定理的逆定理以及三角形面积的计算.25.答案:解:(1)如图所示,△A1B1C1即为所求.(2)如图所示,点E即为所求,其坐标为(1,0).(1,0)解析:(1)分别作出点A,B,C关于x轴的对称点,再首尾顺次连接即可得;(2)连接A1B,与x轴的交点即为所求作的点E.本题主要考查作图−轴对称变换,熟练掌握轴对称变换的定义和性质,并据此得出变换后的对应点是解题的关键.26.答案:解:第一批第二批单价x x+4总价 80000 176000数量80000x 176000 x+4(1)设第一批购入的衬衫单价为x元/件,则有:80000x ×2=176000x+4.解得:x=40,经检验x=40是方程的解,此即为第一批购入衬衫的单价.(2)由(1)知,第一批购入了80000÷40=2000件.在这两笔生意中,华联商场共赢利为:2000×(58−40)+(2000×2−150)×(58−44)+150×(58×0.8−44)=90260元.答:第一批购入这种衬衫的单价为40元,两笔生意中华联商场共赢利90260元.解析:(1)两次进货的总成本已知,两次的价格差距为4,而量上是2倍关系,根据成本除以单价=数量,可列方程.(2)在(1)的基础上可求出两次进货的数量以及单价,又每件定价两次都是58元,最后剩下的150件按定价的八折销售,则可利用每件利润×件数=总利润来解答.本题考查分式方程的应用,关键是找等量关系列出方程,注意分式方程必须检验,属于中考常考题型.27.答案:15cm17解析:解:(1)当BP=15cm时,△ADP是等腰直角三角形,∵∠APD=90°,∴∠APB+∠DPC=90°,∵∠ABP=90°,∴∠APB+∠BAP=90°,∴∠BAP=∠CPD,∵BP=15,∴PC=BC−BP=7,∴AB=PC,在△ABP和△PCD中,{∠ABP=∠PCD AB=CP∠BAP=∠CPD,∴△ABP≌△PCD(ASA),∴PA=PD,又DP⊥AP,∴△ADP是等腰直角三角形,故答案为:15cm;(2)延长线段AP、DC交于点E,在△ABP和△ECP中,{∠ABP=∠ECP PA=PE∠APB=∠EPC,∴△DPA≌△DPE(ASA),∴PA=PE,又DP⊥AP,∴DA=DE,∴∠ADP=∠EDP,即DP平分∠ADC;(3)连接B′A,B′P,延长AB′交CD于H,∵△PDC是等腰三角形,∴∠DPC=45°,∴∠APB=45°,∴BP=AB=7,∴CP=CD=15,∵△ABP为等腰直角三角形,B关于AP的对称点B′,∴四边形ABPB′为矩形,∴B′P=AB=7,AH⊥CD,∴四边形B′PCH为矩形,∴B′H=PC=15,DH=DC−CH=8,在Rt△DB′H中,√B′H2+DH2=17(cm),故答案为:17.(1)证明△ABP≌△PCD,根据全等三角形的性质得到PA=PD,根据等腰直角三角形的概念证明;(2)延长线段AP、DC交于点E,证明△DPA≌△DPE,得到PA=PE,根据等腰三角形的性质证明;(3)连接B′A,B′P,延长AB′交CD于H,证明四边形ABPB′为矩形,得到B′P=AB=7,AH⊥CD,根据勾股定理计算.本题考查的是全等三角形的判定和性质,等腰直角三角形的概念,轴对称,掌握全等三角形的判定定理和性质定理是解题的关键.28.答案:解:(1)∵(1,b)是“相伴数对”,∴12+b3=1+b2+3,解得:b=−94;(2)(2,−92)(答案不唯一);(3)由(m,n)是“相伴数对”可得:m2+n3=m+n2+3,即3m+2n6=m+n5,即9m+4n=0,则原式=m−223n−4m+6n−2=−43n−3m−2=−9m+4n3−2=−2.解析:(1)利用“相伴数对”的定义化简,计算即可求出b的值;(2)写出一个“相伴数对”即可;(3)利用“相伴数对”定义得到9m+4n=0,原式去括号整理后代入计算即可求出值.此题考查了整式的加减,以及代数式求值,弄清题中的新定义是解本题的关键.。
2020-2021学年北京市燕山区八年级(上)期末数学试卷

2020-2021学年北京市燕山区八年级(上)期末数学试卷一、选择题(本题共24分,每小题3分)第1-8题均有四个选项,符合题意的选项只有一个.1.(3分)下面图形中,是轴对称图形的是()A.B.C.D.2.(3分)芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一,它作为食品和药物,得到广泛的使用.经测算,一粒芝麻的质量约为0.00000201kg,将100粒芝麻的质量用科学记数法表示约为()A.20.1×10﹣3kg B.2.01×10﹣4kgC.0.201×10﹣5kg D.2.01×10﹣6kg3.(3分)下列运算正确的是()A.x5÷x3=x2B.(y5)2=y7C.D.4.(3分)正十边形的外角和为()A.180°B.360°C.720°D.1440°5.(3分)下列式子为最简二次根式的是()A.B.C.D.6.(3分)如图,△ABC中,∠A=40°,AB的垂直平分线分别交AB,AC于点D,E,连接BE,则∠BEC的大小为()A.40°B.50°C.80°D.100°7.(3分)下列因式分解正确的是()A.n2﹣5n+6=n(n﹣5)+6B.4x2+1=(2x+1)2C.y2+4y﹣4=(y+2)2D.4t2﹣1=(2t﹣1)(2t+1)8.(3分)如图甲,直角三角形ABC的三边a,b,c,满足a2+b2=c2的关系.利用这个关系,探究下面的问题:如图乙,△OAB是腰长为1的等腰直角三角形,∠OAB=90°,延长OA至B1,使AB1=OA,以OB1为底,在△OAB外侧作等腰直角三角形OA1B1,再延长OA1至B2,使A1B2=OA1,以OB2为底,在△OA1B1外侧作等腰直角三角形OA2B2,…,按此规律作等腰直角三角形OA n B n(n≥1,n为正整数),则A2B2的长及△OA2021B2021的面积分别是()A.2,22020B.4,22021C.2,22020D.2,22019二、填空题(本题共24分,每小题3分)9.(3分)若分式的值等于0,则a的值为.10.(3分)如图,已知△ABC,通过测量、计算得△ABC的面积约为cm2.(结果保留一位小数)11.(3分)如图,点B,F,C,E在一条直线上,已知AB=DE,AB∥DE,请你添加一个适当的条件使得△ABC≌△DEF.12.(3分)依据如图流程图计算﹣,需要经历的路径是(只填写序号),输出的运算结果是.13.(3分)装裱在我国具有悠久的历史和鲜明的民族特色,是我国特有的一种保护和美化书画以及碑帖的技术.如图,整个画框的长(3m+n)分米,宽为(2m+n)分米,中间部分是长方形的画心,长和宽均是(m+n)分米,则画心外阴影部分面积是平方分米,并求当m=2,n=1时的阴影部分面积是平方米.14.(3分)有两块总面积相等的场地,左边场地为正方形,由四部分构成,各部分的面积数据如图所示,右边场地为长方形,长为(a+b),则宽为.15.(3分)我国古代数学中的“杨辉三角”是重要的成就,它的发现比欧洲早五百年左右,(如图),这个三角形给出了(a+b)n(n=1,2,3,4,5,6)的展开式(按a的次数由大到小顺序排列)的系数规律.例如,第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中各项的系数;第五行的五个数1,4,6,4,1,恰好对应着(a+b)4=a4+4a3b+6a2b2+4ab3+b4展开式中各项的系数.则(a+b)5展开式中各项系数的和为.16.(3分)已知等边三角形ABC.如图,(1)分别以点A,B为圆心,大于AB的长为半径作弧,两弧相交于M,N两点;(2)作直线MN交AB于点D;(3)分别以点A,C为圆心,大于AB的长为半径作弧,两弧相交于H,L两点;(4)作直线HL交AC于点E;(5)直线MN与直线HL相交于点O;(6)连接OA,OB,OC.根据以上作图过程及所作图形,下列结论:①OC=2OD;②AB=2OA;③OA=OB=OC;④∠DOE=120°.正确的是.三、解答题(本题共52分,第17题6分,第18-22题,每小题6分,第23-25题,每小题6分)解答应写出文字说明、演算步骤或证明过程。
2019-2020学年北京北京八年级上数学期末试卷

2019-2020学年北京北京八年级上数学期末试卷一、解答题 1. 若分式−2x+9x−1值为正整数,则x 的值为________.2. 已知c a+b =a b+c =13,则bc+a =________ .3. 若x ,y 为变量,m ,n 为参数,则关于y 的一元一次方程(n −1)x m−2+(m −2)y m+n−5=8的解为________.4. 若x 2−3x +1=0,则3x 2−233x +8+4x 2+1=________ .5. 若关于x 的方程4x+3x−5−mx+35−x=1无解,则m 的值为________.6. 如果关于x ,y 的方程组{ax −5y =62x +3y =b 有无穷多组解,请比较a 和b 的大小关系:________(填写a >b,a =b,a <b 中的一个)7. 若关于x 的一元一次不等式组{2(x −3)≥3(x −1)mx ≥x +1的解为x ≤−5,则m 的值为________.8. 有两个行向量(行矩阵):A =(1−k ,+2k)和B =(x −y ,x +y),无论k 取何值,总能保证A ×B T =2成立,则x 的值为________.9. 已知关于x ,y 的方程组{2ax −y =2a +5x +y =2a +4的解为正整数(解得x ,y 均为正整数),且a 为整数,则a =________ .10. 若x 满足2+2x 2+1x≥0,则x 的取值范围是________.11. 已知ba +ab =3,则a 4+a 2b 2+b 4a 4+a 3b+ab 3+b 4的值为________.12. 求(20112−2017)(20112+4019)2008×2010×2014=________.13. 已知行列式满足以下关系:|a 2−21|≤|34b 2|≤|1−33a |,则a +4b 的绝对值的最大值是________.14. 若x 满足|x −3|−|x +1|<2,则x 的取值范围是________.15. 若将关于x 的分式2x 2+3x+1x 4−x,化成部分分式为A x +B x−1+Cx+Dx 2+x+1,则A +B +C +D =________.16. 已知a ,b ,c 均不为0,且3a−2b 2a−b =b−5c b−2c =−c+3a c−a,则ab =________.17. 已知x ,y 满足(3−213)×(x y )=(3k −13k +1)和(2 1)×(x y )=3,则k 的值为________.18. 已知a ,b 满足a ≠−2, b ≠−2,设M =aa+2+bb+2,N =1a+2+1b+2,则下面叙述正确的有________ . ①ab =1时,M <2N ;②ab =2时,M =2N ;③a +b =0时,M ⋅N ≤0;④ab =2且a +b >0时,MN >1.19. 已知关于x 的不等式{5(x −1)≤3x +7x +7<2x +3k 只有3个整数解,则k 的取值范围是________.20. 对于数x ,符号[x ] 表示不超过x 的最大整数,暨[x ]≤x <[x ]+1.若关于x 的方程[x+2|a|5]=4有正整数解,则a 的取值范围是________.21. 解方程或不等式(1)解关于x 的方程:|x −|2x +1||=3.(2)解关于x 的方程:x+3x+1+x 2+3x−2x 2+4x+3−2x+7x+3=0.(3)请用克莱姆法则求解方程:{2x +3y =73x +2y =9.(4)解关于x ,y 的方程组:{2x −y =bx −2ay =2b +2.(5)解关于x,y,z 的方程组:{ 1x −2y +2z =31x +1y +1z =51x +3y +1z =7(6)将行列式|a −1a(a −1)ab −1b(b −1)b c −1c (c −1)c|因式分解.(7)解关于x 的不等式组:{|2x +4|≤2ax −a ≤x +2.22. 在通信系统中,传输的过程一般需要进行加密.一种加密方法是发送方将原有的信息X 左乘一个加密矩阵A ,作为加密后的信息S 发送出去,暨S =AX .接收方在接收到信息S 后只需要再左乘一个解密矩阵B ,便可得到X ,暨BS =X .(1)现已知X 和S 都是3×1的列向量(列矩阵),加密矩阵A 如下所示,请尝试去解密矩阵B . A =(132313231)(2)在发射端可以对X 进行多重加密,暨在X 左边乘上多个矩阵作为加密后的信息S .例如:三重加密时S =ABCX ,其中,A ,B ,C 均为可逆的加密方阵.为了对多重加密进行解密,也可以采取相同的方式,在解密端对S 左乘一个矩阵D ,使得DS =X ,根据矩阵逆的定义和性质,D 应该为ABC 的逆矩阵,暨D =(ABC )−1,求证:(ABC )−1=C −1B −1A −1.23. 并行计算是计算机科学中最漂亮的工具之一.它的基本原理是:将一个复杂的问题,分成若干个简单的子问题,将这些子问题放在多台计算机上同时进行运算.相比于在一台计算机上完成所有运算,并行运算的运算时间会被大大缩减(多台计算机并行运算的总时间为最后一台计算机完成计算的时间).并行计算被广泛运用到当今时代的“云计算”场景中.下面举例说明云计算中是如何进行两个n ×n 的矩阵A 和B 的乘法运算的,A 和B 如下所示: A =(a 11⋅a 1n ⋮⋱⋮a n1⋯a nn ),B =(b 11⋅b 1n⋮⋱⋮b n1⋯b nn) 如果使用一台计算机直接计算A ×B ,需要进行很多次的乘法运算和很多次的加法运算.但如果把矩阵A 和B都拆成更小的矩阵放在多台计算机上进行运算则能节省很多时间,例如,将矩阵A 拆成一个个行向量(行矩阵),矩阵B 拆成一个个列向量(列矩阵),则可以把矩阵的乘法A ×B 看成n ×n 次独立的行向量乘以列向量的运算.把这些行向量乘以列向量的运算平均分配到k 台计算机中运算,则每台计算机最多只用进行[n×n k]+1次行向量乘以列向量的运算,其中[n×n k]表示取n×n k的整数部分.假如一台计算机计算一次加法运算所需要的时间t 1=1×10−9秒,计算一次乘法运算需要的时间是t 1=3×10−9秒.如果n =104 ,则(1)完成一次行向量乘以列向量所耗费的时间是多少秒?(2)如果是用一台计算机,完成A ×B 运算耗费的总时间是多少秒?(3)如果要求A ×B 在1秒之内完成运算,则至少需要几台计算机?24. 卷积神经网络(Convolutionai Neural Networks ,CNN)是一类包含卷积计算且具有深度结构的前馈神经网络,是深度学习(Deep Learning )的代表算法之一,也是人工智能时代开启的标志性算法,已经被广泛应用于图像处理(Image Processing )和行为认知(Acting Recognition )等场景中.图(a)是一个在图像处理中的卷积神经网络使用案例.图像在计算机中一般用矩阵进行储存,矩阵中的每一个元素值暨代表图像中对应点颜色的深浅.将图像反复经过卷积神经网络中的两种运算:卷积(Convolution)和池化(Pooling),便可得到最后的输出结果,用来判断图像中的物体是否属于哪一类.如图30(a)中,经过卷积神经网络,计算机可以自动判断图像是一条狗.本题是关于池化过程的应用题.池化是卷积神经网络的一个重要过程,其核心思想是用一个数值(记为s )来代替矩阵.例如:对于如下所示的一个3×3的矩阵A ,在池化过程中可以使用a 11来代替矩阵A .池化用矩阵的乘法就可以实现,如下所示: A =[a 11a 12a 13a 21a 22a 23a 31a 32a 33] a 11=[100][a 11a 12a 13a 21a 22a 23a 31a 32a 33][100] 若B 是一个行向量(行矩阵):(b 11,b 12,b 13),请尝试只用矩阵的乘法求B 中所有元素的平均值.进一步的,希望用A 中所有元素的平均值,来进行池化过程,请只使用矩阵的乘法实现求A 中所有元素的平均值的池化过程.(可以引入新的矩阵,但是不能使用加法、求逆等乘法之外的其他运算)25. 本题是关于卷积过程的应用题.为了能够更好地引入卷积,我们首先引入矩阵的内积运算(记作⊙),用来表示两个矩阵所有对应项的乘积的和.对于两个n ×n 的矩阵A 和B ,如下所示:内积运算定义如下:A ⊙B =a 11b 11+a 12b 12+⋯a 1n b 1n +a 21b 21+⋯+a nn b nn =∑∑a ij nj=1n i=1b ij 图(b )是一个更为简单的两个2×2的矩阵内积运算过程如下:(1)对于任意两个3×3 的矩阵A 和B ,若A 是单位阵(只有对角线元素为1,其他元素均为0),B 的主对角线上所有元素均为1,其他元素均不为0.求A ⊙B .(2)求证:对于任意三个3×3 内矩阵A 、B 、C ,均有(A +B )⊙C =A ⊙C +B ⊙C .卷积运算可以在内积运算基础上进行定义.对于一个m ×m 的矩阵A 和一个n ×n 的矩阵B (m ≤n );A 与B 的卷积运算记作A ∗B .定义如下:图(c )是一个更为直观的2×2矩阵与一个4×4矩阵进行卷积的例子:(3)已知两个矩阵A =(1001),B =(123242136763426731),求A ∗B .参考答案与试题解析2019-2020学年北京北京八年级上数学期末试卷一、解答题1.【答案】此题暂无答案【考点】分使的凝【解析】此题暂无解析【解答】此题暂无解答2.【答案】此题暂无答案【考点】列代明式织值【解析】此题暂无解析【解答】此题暂无解答3.【答案】此题暂无答案【考点】一元一表方磁的定义【解析】此题暂无解析【解答】此题暂无解答4.【答案】此题暂无答案【考点】分式因化简优值列较洗式源值情法的优势【解析】此题暂无解析【解答】此题暂无解答5.【答案】此题暂无答案【考点】分式明程稀解【解析】此题暂无解析【解答】此题暂无解答6.【答案】此题暂无答案【考点】二元一都接程组的解【解析】此题暂无解析【解答】此题暂无解答7.【答案】此题暂无答案【考点】解一元表次镜等式组【解析】此题暂无解析【解答】此题暂无解答8.【答案】此题暂无答案【考点】整式较混合轻算【解析】此题暂无解析【解答】此题暂无解答9.【答案】此题暂无答案【考点】二元一都接程组的解【解析】此题暂无解析【解答】此题暂无解答10.【答案】此题暂无答案【考点】解一元因次不丙式【解析】此题暂无解析【解答】此题暂无解答11.【答案】此题暂无答案【考点】列代明式织值【解析】此题暂无解析【解答】此题暂无解答12.【答案】此题暂无答案【考点】列较洗式源值情法的优势【解析】此题暂无解析【解答】此题暂无解答13.【答案】此题暂无答案【考点】绝对值【解析】此题暂无解析【解答】此题暂无解答14.【答案】此题暂无答案【考点】绝对值【解析】此题暂无解析【解答】此题暂无解答15.【答案】此题暂无答案【考点】分式因混合似算【解析】此题暂无解析【解答】此题暂无解答16.【答案】此题暂无答案【考点】列较洗式源值情法的优势【解析】此题暂无解析【解答】此题暂无解答17.【答案】此题暂无答案【考点】二元一因方程似应用【解析】此题暂无解析【解答】此题暂无解答18.【答案】此题暂无答案【考点】有理数三混合运臂列较洗式源值情法的优势【解析】此题暂无解析【解答】此题暂无解答19.【答案】此题暂无答案【考点】一元三次实等另组每整数解【解析】此题暂无解析【解答】此题暂无解答20.【答案】此题暂无答案【考点】方射的加【解析】此题暂无解析【解答】此题暂无解答21.【答案】此题暂无答案【考点】解一使以次方程解于姆方程二元一都接程组的解二元一都接程组的解解三元体次序程组因水都解解一元表次镜等式组【解析】此题暂无解析【解答】此题暂无解答22.【答案】此题暂无答案【考点】规律型:因字斯变化类有理数三混合运臂【解析】此题暂无解析【解答】此题暂无解答23.【答案】此题暂无答案【考点】列使数种有理数三混合运臂一元体次拉程的言亿——其他问题【解析】此题暂无解析【解答】此题暂无解答24.【答案】此题暂无答案【考点】有理数三混合运臂【解析】此题暂无解析【解答】此题暂无解答25.【答案】此题暂无答案【考点】定射新从号代明综约【解析】此题暂无解析【解答】此题暂无解答。
北京市燕山地区2018-2019学年八年级上期末数学试题含答案

燕山地区2019—2019学年度第一学期初三年级期末考试数 学 试 卷 2019年1月一、选择题(本题共30分,每小题3分)(下面各题均有四个选项,其中只有一个是.....符合题意的) 1. 剪纸是我国传统的民间艺术,下列剪纸作品中,是轴对称图形的为A . B. C. D.2. 下列运算正确的是A.3a+2b=5abB.5a ﹣2a=3aC. b 2•b 3=b 6D .(x+y )2=x 2+y 23.已知一个等腰三角形两边长分别为3,7,那么它的周长是A . 17B . 13C . 13或17D .10或13 4.如图,AB ∥CD ,BC ∥AD ,AB =CD ,BE =DF,图中全等的三角形的对数是 A .3B .4C .5 D.6 5. 下列式子为最简二次根式的是B.C.D.6.若分式392--x x 的值为0,则x 的值等于A .0B .±3C .3D .-37. 如图,DE 是△ABC 中AC 边的垂直平分线,若BC =8,AB =10,则△EBC 的周长是 A .13 B .16 C .18 D .20ABC DEFABDCE8.②8a 2b 2·⎪⎭⎫ ⎝⎛-243b a =-6a 3;③111222-=+÷-a aa a a a; ④a ÷b ·b 1=a ;A.1个B.2个C.3个D.4个9.根据计算正方形ABCD 的面积,可以说明下列哪个等式成立( )A. 2222)(b ab a b a ++=+B. 2222)(b ab a b a +-=-C. 22))((b a b a b a -=-+D.ab a b a a -=-2)( 10.如图,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 最小,则这个最小值为( )A .B .C D .二、填空题(本大题共6小题,每小题2分,共12分)11. 计算:=2)3( .12. 如果式子1+x 在实数范围内有意义,那么的取值范围是 .13.如图,BC EF =,1F ∠=∠.请你添加一个适当的条件, 使得△ABC ≌△DEF (只需填一个答案即可). 14. △ABC 在平面直角坐标系中的位置如图所示,现另有一点D,满足以A,B,D 为顶点的三角形与△ABC 全等,则 D 点坐标为aaaabbbCE15.2002年国际数学家大会在中国北京举行,这是21世纪全世界数学家的第一次大聚会。
北京市燕山区2018-2019学年第一学期期末八年级数学试题(含答案)

燕山区2018—2019学年度第一学期八年级期末数学试卷 2019年1月一、选择题(本题共16分,每小题2分)1.下面是同学们设计的一些美丽有趣的图案,其中是轴对称图形的是()2.为庆祝首个“中国农民丰收节”,十渡镇西河村举办“西河稻作文化节”活动.西河水稻种植历史悠久,因“色白粒粗,味极香美,七煮不烂”而享誉京城.已知每粒稻谷重约0.000 035千克,将0.000 035用科学记数法表示应为( )A .63510-⨯B .63.510-⨯C .53.510-⨯D .40.3510-⨯ 3.如果7x -在实数范围内有意义,则x 的取值范围是( )A .7x ≠B .7x <C .7x >D .7x ≥ 4.下列运算正确的是( )A .42±=B .244()=C .2(4)4-=-D .244(-)=-5.如图,Rt △ABC ≌Rt △DEF ,∠E =55°,则∠A 的度数为( )FAC DBEA .25°B .35°C .45°D .55° 6.如图,△A B C 中,∠C =90°,A D 平分∠C A B ,交B C 于点D ,DE ⊥A B 于点E ,若CD =3,则DE 的长为( )A .2B .3C .3D .237.如图,△ABC 中,AB =AC ,AD ⊥BC ,垂足为D ,DE ∥AB ,交AC 于点E ,则下列结论不正确...的是( )A .∠CAD =∠BADB .BD =CDC .AE =ED D .DE =DB8.如图,有三种规格的卡片共9张,其中边长为a 的正方形卡片4张,边长为b 的正方形卡片1张,长,宽分别为a ,b 的长方形卡片4张.现使用这9张卡片拼成一个大的正方形,则这个大正方形的边长为( )A .2a +bB .4a +bC .a +2bD .a +3b 二、填空题(本题共16分,每小题2分)9.若分式4x x -的值为0,则x 的值是 . 10.计算2211a a a ---的结果是 . 11.计算(32)(32)+-的结果是 .12.在△ABC 中,AB =AC ,BC =5,∠B =60°,则△ABC 的周长是 .13.如图,线段AB 与CD 相交于点O ,且OA =OD ,连接AC ,BD ,要说明△AOC ≌△DOB ,还需添加的一个条件是 .(只需填一个条件即可)OACDB14.写出一个能用平方差公式分解因式的多项式: .15.已知2+23x x =,则代数式()()()22122x x x x +-+-+的值为 .16.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中记载了一个“折竹抵地”问题:“今有竹高二丈,末折抵地,去本六尺,问折者高几何?”译文:“有一根竹子,原高二丈(1丈=10尺),现被风折断,竹梢触地面处与竹根的距离为6尺,问折断处离地面的高度为多少尺?”如图,我们用点A ,B ,C 分别表示竹梢,竹根和折断处,设折断处离地面的高度BC =x 尺,则可列方程为 .B AC三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27,28题,每小题7分) 解答应写出文字说明,演算步骤或证明过程. 17.计算:(8312)6⨯-÷.18.分解因式:224ma mb -.19.解方程:2113(1)x x x x =-++.20.如图,AB =AC ,点D ,E 分别是线段AB ,AC 的中点,连接BE ,CD .求证:∠B =∠C .ABDCE21.下面是小芸设计的“作三角形一边上的高”的尺规作图过程.已知:△ABC .求作:△ABC 的边BC 上的高AD .AB C作法:① 以点A 为圆心,适当长为半径画弧,交直线BC 于点M ,N ;② 分别以点M ,N 为圆心,以大于12MN 的长为半径画弧,两弧相交于点P ; ③ 作直线AP 交BC 于点D ,则线段AD 即为所求△ABC 的边BC 上的高. 根据小芸设计的尺规作图过程,(1) 使用直尺和圆规,补全图形;(保留作图痕迹) (2) 完成下面的证明:证明:∵AM = ,MP = ,∴AP 是线段MN 的垂直平分线.( . )(填推理的依据) ∴AD ⊥BC 于D ,即线段AD 为△ABC 的边BC 上的高.22.如图,四边形ABCD 中,∠B =90°,∠ACB =30°,AB =2,CD =3,AD =5.(1) 求证:AC ⊥CD ;(2) 求四边形ABCD 的面积.AB CD23.如图,在平面直角坐标系xOy 中,点O (0,0),A (-1,2),B (2,1).(1) 在图中画出△AOB 关于y 轴对称的△A 1OB 1,并直接写出点A 1和点B 1的坐标; (不写画法,保留画图痕迹) (2) 在x 轴上存在点P ,使得PA +PB 的值最小,则点P 的坐标为 ,PA +PB 的最小值为 .21331y Ox2-3-2-1-1-2-3B A24.先化简,再求值:22216(1)22m m m m--÷--,其中m =2019.25.下面是两位同学的一段对话:聪聪:周末我们去国家博物馆参观“伟大的变革——庆祝改革开放40周年大型展览”吧.明明:好啊,我家离国家博物馆约30km ,我坐地铁先走,地铁的平均行驶速度是公交车的1.5倍呢. 聪聪:嗯,我周末住奶奶家,离国家博物馆只有5km ,坐公交车,你出发40分钟后我再出发就能和你同时到达.根据对话内容,请你求出公交车和地铁的平均行驶速度.26.阅读下列材料:在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”.下面是小涵同学用换元法对多项式22(41)(47)9x x x x -+-++进行因式分解的过程.请根据上述材料回答下列问题:(1) 小涵同学的解法中,第二步到第三步运用了因式分解的 ;A .提取公因式法B .平方差公式法C .完全平方公式法(2) 老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果: ; (3) 请你用换元法对多项式22(2)(22)1x x x x ++++进行因式分解.27.已知BC =5,AB =1,AB ⊥BC ,射线CM ⊥BC ,动点P 在线段BC 上(不与点B ,C 重合),过点P 作DP ⊥AP 交射线CM 于点D ,连接AD .(1) 如图1,若BP =4,判断△ADP 的形状,并加以证明.(2) 如图2,若BP =1,作点C 关于直线DP 的对称点C ′,连接AC ′.① 依题意补全图2;② 请直接写出线段AC ′的长度.28.一般情况下,131ba b ab+=+不成立,但有些数可以使得它成立,例如:a=1,b=2.我们称使得131ba b ab+=+成立的一对数a,b为“相伴数对”,记为(a,b).(1) 判断数对(-2,1),(3,3)是否是“相伴数对”;(2) 若(k,-1)是“相伴数对”,求k的值;(3) 若(4,m)是“相伴数对”,求代数式2432(41)3(4)m m mm m⎡⎤---⎣⎦-的值.燕山地区2018—2019学年度第一学期期末考试八年级数学试卷参考答案及评分标准 2019.01 一、选择题(本题共16分,每小题2分)题号 1 2 3 4 5 6 7 8 选项 ACDBBCDA二、填空题(本题共16分,每小题2分)9.4 10.2 11.-1 12.15 13.答案不唯一,如:OC =OB ,AB =CD ,∠A =∠D ,∠B =∠C14.答案不唯一,如:21x - 15.8 16.2226(20)x x +=-三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27,28题,每小题7分)17.解:原式=(2412)6-÷ ………………………………1分=246126÷-÷ ………………………………3分 =42-=22-. ………………………………5分 18.解:224mamb -=22(4)m a b - ………………………………3分=(2)(2)m a b a b -+. ………………………………5分19.解:去分母得,33(1)2x x x =+-, ………………………………1分去括号得,3332x x x =+-, ………………………………2分 移项合并同类项得,23x =, ………………………………3分 系数化1得,32x =, ………………………………4分 检验:32x =是原方程的解. ………………………………5分 20.证明:∵点D ,E 分别是线段AB ,AC 的中点,∴AD =12AB ,AE =12AC , ∵AB =AC ,∴AD =AE . ………………………………1分在△ABE 和△ACD 中,AB AC A A AD AE =⎧⎪∠=∠⎨⎪⎩,,=,∴△ABE ≌△ACD , ………………………………4分 ∴∠B =∠C . ………………………………5分21.解:(1) 补全的图形如图所示; ………………………………2分(2) AN ,NP ,与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.………………………………5分22.(1) 证明:在Rt △ABC 中,∠B =90°,∠ACB =30°,AB =2,∴AC =2AB =4. ………………………………1分 在△ACD 中,AC =4,CD =3,AD =5, ∵222435+=,即222AC CD AD +=, ∴∠ACD =90°,∴AC ⊥CD ; ………………………………2分(2) 解:在Rt △ABC 中,∠B =90°,AB =2,AC =4,∴BC =2242-=23, ………………………………3分∴Rt △ABC 的面积为12AB ·BC =12×2×23=23, 又∵Rt △ACD 的面积为12AC ·CD =12×4×3=6,∴四边形ABCD 的面积为:23+6. ………………………………5分23.解:(1) 画出△A 1OB 1如图所示; ………………………………2分A 1(1,2),点B 1(-2,1); ………………………………4分 (2) 点P 的坐标P (1,0),PA +PB 的最小值为32. ………………………………6分24.解:原式=22(4)(4)()22(2)m m m m m m m --+-÷--- ………………………………3分 N PMD CB AAB C DB 1A 121331y Ox2-3-2-1-1-2-3B A=4(2)2(4)(4)m m m m m m ----+g=4mm +. ………………………………5分 当m =2019时,原式=201920194+=20192023. ………………………………6分25.解:设公交车平均行驶速度为x km/h ,则地铁的平均行驶速度为1.5x km/h ,………………………………1分 根据题意,得305401.560x x -=, ………………………………2分 解这个方程,得 x =22.5. ………………………………3分 经检验:x =24是所列方程的解,且符合题意. ………………………………4分 1.5x =1.5×22.5=33.75km/h . ………………………………5分 答:公交车和地铁的平均行驶速度分别为22.5 km/h 和33.75km/h . ………………6分 26.解:(1) C ; ………………………………1分 (2) 4(2)x -; ………………………………3分 (3) 设22x x y += ………………………………4分原式=(2)1y y ++=221y y ++=2(1)y + ………………………………5分 =22(21)x x ++=4(1)x +. ………………………………6分27.(1) △ADP 是等腰直角三角形. ………………………………1分证明:∵BC =5,BP =4,∴PC =1, ∵AB =1,∴PC =AB . ………………………………2分∵AB ⊥BC ,CM ⊥BC ,DP ⊥AP , ∴∠B =∠C =90°,∠APB +∠DPC =90°,∠PDC +∠DPC =90°,∴∠APB =∠PDC , ………………………………3分在△ABP 和△PCD 中,B C APB PDC AB PC ∠=∠⎧⎪∠=∠⎨⎪=⎩,,,∴△ABP ≌△PCD , ………………………………4分 ∴AP =PD , P M D C B A∴△ADP 是等腰直角三角形. ………………………………5分 (2) ①依题意补全图2; ………………………………6分 ② AC ′=10. ………………………………7分 28.解:(1) ∵11312121+≠+--⨯,∴(-2,1)不是“相伴数对”; ∵31313333+=+⨯,∴(3,3)是“相伴数对”. ………………………………2分 (2) ∵ (k ,-1)是“相伴数对”, ∴11311k k-+=+--, ………………………………3分 解得k =1. ………………………………4分 (3) ∵(4,m )是“相伴数对”, ∴13144m m m+=+, ∴241m m -=-, ………………………………5分 ∴2432(41)3(4)m m m m m ⎡⎤---⎣⎦-=224(382)3(4)m m m m m --+-=2231223(4)m m m m -+-- =223(4)23(4)m m m m ---- ………………………………6分 =3(1)23(1)-⨯--⨯-=-13. ………………………………7分说明:各解答题的其他正确解法请参照以上标准按分步给分的原则酌情评分.。
2019-2020学年北京市燕山区八年级(上)期末数学试卷解析版

2019-2020学年北京市燕山区八年级(上)期末数学试卷一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个.1.(2分)在以下绿色食品、节能、节水、回收四个标志中,是轴对称图形的是()A.B.C.D.2.(2分)下列计算正确的是()A.3x﹣x=2B.a3÷a4=1aC.(x﹣1)2=x2﹣x﹣1D.(﹣2a2)3=﹣8a63.(2分)能用平方差公式分解因式的多项式是()A.x2﹣2x+1B.x2+9C.ax﹣ay D.﹣x2+44.(2分)太阳光照射到地球上需要的时间约是5×102s,光的速度约是3×105km/s,那么太阳到地球的距离用科学记数法表示约为()A.15×107B.1.5×107C.1.5×108D.15×10105.(2分)已知,△ABC≌△DEF,且△ABC的周长为20,AB=8,BC=3,则DF等于()A.3B.5C.9D.116.(2分)已知EF是△EBC的角平分线,FD⊥EB于D,且FD=3cm,则点F到EC的距离是()A.2cm B.3cm C.4cm D.6cm7.(2分)如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为()A.(2a2+5a)cm2B.(6a+15)cm2C.(6a+9)cm2D.(3a+15)cm28.(2分)豆豆老师到学校距离是8千米,她开车上班的平均速度是乘公交车平均速度的2.5倍,已知豆豆老师自己开车上班比乘公交车上班所需的时间少用小时,若设乘公交车平均每小时走x千米,根据题意可列方程为()A.=B.=15+C.D.二、填空题(本题共16分,每小题2分)9.(2分)若分式的值为0,则x的值为.10.(2分)如图,根据图形,写出一个正方形ABCD的面积的表达式.(一个即可)11.(2分)化简+的结果为.12.(2分)有一个正多边形的外角是60°,那么该正多边形是正边形.13.(2分)如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,需添加一个条件是.(只需添加一个条件即可)14.(2分)若4x2+kxy+9y2是一个完全平方式,则k的值为.15.(2分)下面一组按规律排列的数,2,4,8,16,32,……则第2020个数是.16.(2分)如图,在△ABC中,按以下步骤作图:①以B为圆心,任意长为半径作弧,交AB于D,交BC于E;②分别以D,E为圆心,以大于DE的同样长为半径作弧,两弧交于点M;③作射线BM交AC于N.如果BN=NC,∠A=57°,那么∠ABN的度数为.三、解答题(本题共68分,第17-21题,每小题5分;第22题4分;第23题7分;第24-27题,每小题5分,第28,29题,每小题5分)解答应写出文字说明,演算步骤或证明过程.17.(5分)计算:(12a3+6a2﹣3a)÷3a.18.(5分)分解因式:(1)x3﹣x;(2)3x2y﹣6xy+3y.19.(5分)解方程:.20.(5分)已知:如图,∠1=∠2,∠C=∠D.求证:AC=AD.21.(5分)如图:在等边三角形ABC中,点D、E分别是AB、BC延长线上的点,且BD=CE.求证:∠BCD =∠CAE.22.(4分)如图1为L形的一种三格骨牌,它是由三个全等的正方形连接而成.请以L形的三格骨牌为基本图形,在图2,图3中各设计一个轴对称图形,要求如下:(1)每个图形由两个L形三格骨牌组成,骨牌的顶点都在小正方形的顶点上.(2)设计的图形用斜线涂出,若形状相同,则视为一种.23.(7分)阅读下列材料分解因式:4x﹣16x3小云的做法:原式=16x3﹣4x①=4x(4x2﹣1)②=4x(2x﹣1)(2x+1)③小朵的做法:原式=4x(1﹣4x2)①=4x(1﹣4x)(1+4x)②小天的做法:原式=x(4﹣16x2)①=x[22﹣(4x)2]②=x(2﹣4x)(2+4x)③请根据上述材料回答下列问题:(1)小云的解题过程从步出现错误的,错误的原因是:.小朵的解题过程从步出现错误的,错误的原因是:.小天的解题过程从步出现错误的,错误的原因是:.(2)若都不正确,请你写出正确的解题过程.24.(5分)已知∠AOB=30°,点P在∠AOB的内部,点C和点P关于OA对称,点P关于OB的对称点是D,连接CD交OA于M,交OB于N,CD=15.(1)补全图,并且保留作图痕迹.(2)写出∠COD=°.△PMN的周长为.25.(5分)通过整式乘法的学习,我们进一步了解了利用图形面积来说明法则、公式等的正确性的方法,例如利用图甲可以对平方差公式(a+b)(a﹣b)=a2﹣b2给予解释.图乙中的△ABC是一个直角三角形,∠C=90°,人们很早就发现直角三角形的三边a,b,c满足a2+b2=c2的关系.图丙是2002年国际数学家大会的会徽,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,弦图是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,求出(a+b)2的值.26.(5分)先化简,再求值:,其中t=2019.27.(5分)阅读下面材料:学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究小聪将命题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E.小聪的探究方法是对∠B分为“直角、钝角、锐角”三种情况进行探究.第一种情况:当∠B是直角时,如图1,△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据“HL”定理,可以知道Rt△ABC≌Rt△DEF.第二种情况:当∠B是锐角时,如图2,BC=EF,∠B=∠E<90°,在射线EM上有点D,使DF=AC,画出符合条件的点D,则△ABC和△DEF的关系是;A.全等B.不全等C.不一定全等第三种情况:当∠B是钝角时,如图3,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E>90°.过点C作AB边的垂线交AB延长线于点M;同理过点F作DE边的垂线交DE延长线于N,根据“ASA”,可以知道△CBM≌△FEN,请补全图形,进而证出△ABC≌△DEF.28.(6分)如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这个分式为“和谐分式”.(1)下列分式中,是和谐分式(填写序号即可);①;②;③;④(2)若a为整数,且为和谐分式,请写出a的值;(3)在化简﹣÷时,小冬和小奥分别进行了如下三步变形:小冬:原式=﹣=﹣=小奥:原式=﹣=﹣=显然,小奥利用了其中的和谐分式,第三步所得结果比小冬的结果简单,原因是:,请你接着小奥的方法完成化简.29.(6分)在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,且DM=DN.(1)如图甲,若∠C=90°,∠BAC=60°,AC=9,∠MDN=120°,ND∥AB.①写出∠MDA=°,AB的长是.②求四边形AMDN的周长.(2)如图乙,过D作DF⊥AC于F,先补全图乙再证明AM+AN=2AF.2019-2020学年北京市燕山区八年级(上)期末数学试卷参考答案与试题解析一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个.1.【解答】解:A、是轴对称图形,故本选项正确;B、不是轴对称图形,故本选项错误;C、不是轴对称图形,故本选项错误;D、不是轴对称图形,故本选项错误.故选:A.2.【解答】解:A.3x﹣x=2x,故本选项不合题意;B.a3÷a4=,故本选项不合题意;C.(x﹣1)2=x2﹣2x﹣1,故本选项不合题意;D.(﹣2a2)3=﹣8a6,正确,故本选项符合题意.故选:D.3.【解答】解:A、原式=(x﹣1)2,不符合题意;B、原式不能分解,不符合题意;C、原式=a(x﹣y),不符合题意;D、原式=(﹣x+2)(x+2),符合题意,故选:D.4.【解答】解:3×105×5×102=1.5×108.故选:C.5.【解答】解:∵△ABC的周长为20,AB=8,BC=3,∴AC=20﹣3﹣8=9,∵△ABC≌△DEF,∴DF=AC=9,故选:C.6.【解答】解:∵FD⊥EB于D,且FD=3cm,∴点F到EB的距离为3cm,∵EF是△EBC的角平分线,∴点F到EB和EC的距离相等,∴点F到EC的距离是3cm.故选:B.7.【解答】解:矩形的面积是:(a+4)2﹣(a+1)2=(a+4+a+1)(a+4﹣a﹣1)=3(2a+5)=6a+15(cm2).故选:B.8.【解答】解:设乘公交车平均每小时走x千米,根据题意可列方程为:,故选:D.二、填空题(本题共16分,每小题2分)9.【解答】解:依题意得:x+2=0且x﹣3≠0,解得x=﹣2.故答案是:﹣2.10.【解答】解:由题意可知:(x+a)(x+a)=(x+a)2,故答案为:(x+a)211.【解答】解:原式=﹣==x.故答案为:x.12.【解答】解:这个正多边形的边数:360°÷60°=6.故答案为:六.13.【解答】解:当∠D=∠B时,在△ADF和△CBE中∵,∴△ADF≌△CBE(SAS),故答案为:∠D=∠B.(答案不唯一)14.【解答】解:∵4x2+kxy+9y2是一个完全平方式,∴k=±12,故答案为:±1215.【解答】解:∵一列数为:2,4,8,16,32,……,∴这列数的第n个数为2n,∴第2020个数是22020,故答案为:22020.16.【解答】解:根据作图方法可得BN是∠ABC的角平分线,∴∠ABN=∠CBN,∵BN=NC,∴∠C=∠NBC,设∠ABN=x°,则∠CBN=∠C=x°,x+x+x+57=180,解得:x=41,故答案为:41°.三、解答题(本题共68分,第17-21题,每小题5分;第22题4分;第23题7分;第24-27题,每小题5分,第28,29题,每小题5分)解答应写出文字说明,演算步骤或证明过程.17.【解答】解:原式=12a3÷3a+6a2÷3a﹣3a÷3a=4a2+2a﹣118.【解答】解:(1)原式=x(x2﹣1)=x(x+1)(x﹣1);(2)原式=3y(x2﹣2x+1)=3y(x﹣1)2.19.【解答】解:去分母得,x﹣1=2(x﹣2)+1,去括号x﹣1=2x﹣4+1,移项合并同类项得,2x﹣x=4﹣1﹣1,系数化1得,x=2,经检验:x=2是增根,分式方程无解.20.【解答】证明:∵在△ACB与△ADB中,,∴△ACB≌△ADB(AAS),∴AC=AD.21.【解答】证明:∵等边三角形ABC∴AB=BC=AC,∠ABC=∠ACB,∴∠DBC=∠ACE,在△ABC和△ABD中,,∴△DBC≌△ECA(SAS),∴∠BCD=∠CAE.22.【解答】解:如图所示:.23.【解答】解:(1)小云的解题过程从①步出现错误的,错误的原因是:提取负号后,负号丢失,没弄清方程还是多项式;小朵的解题过程从②步出现错误的,错误的原因是平方差公式用错;小天的解题过程从③步出现错误的,错误的原因是:分解因式不完整还可以继续分解;(2)若都不正确,请你写出正确的解题过程.原式=4x(1﹣4x2)=4x(1﹣2x)(1+2x).故答案为:(1)①,提取负号后,负号丢失,没弄清方程还是多项式;②,错误的原因是平方差公式用错;③,分解因式不完整还可以继续分解;24.【解答】解:(1)如图所示:(2)如图,连接OC,OD,OP,∵点C和点P关于OA对称,点P关于OB的对称点是D,∴∠AOC=∠AOP,∠BOD=∠BOP,∴∠COD=2∠AOB,又∵∠AOB=30°,∴∠COD=60°;∵AO垂直平分CP,BO垂直平分PD,∴PM=CM,PN=DN,∴△PMN的周长=PM+MN+PN=CM+MN+DN=CD=15.故答案为:60;15.25.【解答】解:根据勾股定理可得a2+b2=13,四个直角三角形的面积是:ab×4=13﹣1=12,即2ab=12,则(a+b)2=a2+2ab+b2=13+12=25.故(a+b)2的值为25.26.【解答】解:原式=•,=,当t=2019时,原式==.27.【解答】解:第二种情况选C.理由:由题意满足条件的点D有两个,故△ABC和△DEF不一定全等(如图所示)故选C.第三种情况补全图.证明:由△CBM≌△FEN得,CM=FN,BD=EN又在Rt△CMA和Rt△FND中,∴△CMA≌△FND,∴AM=DN,∴AB=DE,又在△ABC和△DEF中,∴△ABC≌△DEF.28.【解答】解:(1)下列分式中,④是和谐分式(填写序号即可);(2)由是和谐分式,可得y2+ay+4能分解因式,∴a的值是4或﹣4;(3)原因是:小奥利用和谐公式找的是最简公分母,所以通分后比小冬的简单,接着小奥的方法完成化简,如下:原式=﹣×=﹣===.29.【解答】解:(1)①∵AD平分∠BAC,∴∠BAD=∠CAD=∠BAC=30°,∵ND∥AB,∴∠NDA=∠BAD=30°,∴∠MDA=∠MDN﹣∠NDA=120°﹣30°=90°,∵∠C=90°,∠BAC=60°,∴∠ABC=30°,∴AC=AB,∴AB=2AC=18,故答案为:90,18;②∵∠ABC=30°,ND∥AB,∴∠NDC=30°,又∵∠MDN=120°,∴∠MDB=30°,∴∠MAD=∠NAD=∠ADN=∠MBD=30°,∴BM=MD,DN=AN,∵DM=DN,∴BM=MD=DN=AN,在Rt△ADM中,设MD=x,则AM=2x,BM=MD=DN=AN=x,∵AB=18,∴3x=18,∴x=6,∴AM=12,MD=DN=AN=6,∴四边形AMDN的周长=AM+MD+DN+AN=12+6+6+6=30;(2)补全图如图乙所示:证明:过点D作DE⊥AB于E,如图丙所示:∵DE⊥AB,DF⊥AC,AD平分∠BAC,∴∠DEM=∠DFN=90°,DE=DF,在Rt△DEA和Rt△DF A中,,∴Rt△DEA≌Rt△DF A(HL),∴AE=AF,在Rt△DEM和Rt△DFN中,,∴Rt△DEM≌Rt△DFN(HL),∴EM=FN,∴AM+AN=AE+EM+AF﹣NF=2AF.。
北京市各区2019-2020学年上学期八年级期末数学试卷精选汇编:代数综合专题(含答案)

北京市各区2019-2020学年上学期八年级期末数学试卷精选汇编:代数综合专题(含答案)海淀区25.对于代数式,不同的表达形式能表现出它的不同性质.例如代数式245A x x =-+,若将其写成()221A x =-+的形式,就能看出不论字母x 取何值,它都表示正数;若将它写成()2=12(1)2A x x ---+的形式,就能与代数式B=222x x -+建立联系.下面我们改变x 的值,研究一下A ,B 两个代数式取值的规律:(1)完成上表; (2)观察表格可以发现:若x =m 时,222=B x x n =-+,则x =m +1时,245A x x n =-+=.我们把这种现象称为代数式A 参照代数式B 取值延后,此时延后值为1.①若代数式D 参照代数式B 取值延后,相应的延后值为2,求代数式D ;②已知代数式210ax x b -+参照代数式234x x c -+取值延后,请直接写出b -c 的值:_____________.25.解(1)2;2,1,2. ………………………2分(2)①∵代数式D 参照代数式B 取值延后,相应的延后值为2,∴22(2)2(2)2610D x x x x =---+=-+. …………………4分 ② 7 ………………………6分东城区26. 列方程,解应用题:第二届中国国际进口博览会于2019年11月5日至10日在上海国家会展中心举行.与首届相比,第二届进博会的展览面积更大,企业展设置科技生活、汽车、装备等七个展区,展览面积由的270 000平方米增加到330 000平方米.参展企业比首届多了约300家,参展企业平均展览面积增加了12.8%,求首届进博会企业平均展览面积.(1) 在解应用题时,我们常借助表格、线段图等分析题目中的数量关系. 设首届进博会企业平均展览面积为x 平方米,把下表补充完整:(2)270 000330000+300=(1+12.8%)x x.……………………6分 丰台区24.已知a ,b ,m 都是实数,若a +b =2,则称a 与b 是关于1的“平衡数”.(1)4与 是关于1的“平衡数”,3与 是关于1的“平衡数”;(2)若=2(-m +,判断m +与2-是否是关于1的“平衡数”,并说明理由.24. 解:(1);. 2分(2)不是.∵, ∴.∴. ∴.∴==3. 4分∴与不是关于 1的“平衡数”. 6分密云区26.数学课堂上,老师提出问题:可以通过通分将两个分式的和表示成一个分式的形式,是否也可以将一个分式31(1)(1)x x x ++-表示成两个分式和的形式?其中这两个分式的分母分别为x+1和x -1.小明通过观察、思考,发现可以用待定系数法解决上面问题.具体过程如下: 设31(1)(1)x x x ++-11A Bx x =++- 则有31(1)(1)x x x ++-(1)(1)()(1)(1)(1)(1)(1)(1)A xB x A B x B Ax x x x x x -+++-=+=+-+-+-故此31A B B A +=⎧⎨-=⎩ 解得12A B =⎧⎨=⎩所以31(1)(1)x x x ++-=1211x x ++- 问题解决: (1)设1(1)1x A Bx x x x -=+++,求A 、B.(2)直接写出方程111(1)(1)(2)2x x x x x x x --+=++++ 的解.26. (1)∵(1)=1(1)(1)A B A x Bx x x x x x x ++++++ ………………1分()1(1)(1)A B x A xx x x x ++-==++………………2分 ∴1,1A B A +=-= ………………3分 ∴2B =-………………4分(2)23x =………………6分门头沟区26.信息1:我们已经学完了解分式方程,它的一般步骤为:确定最简公分母、化为整式方程、求出整式方程的解、进行检验(第一,代入最简公分母验证是否为零,第二代入分式方程的左右两边检验是否相等)、确定分式方程的解。
北京市燕山区2019-2020学年初二期末数学试题及答案

2019-2020学年八年级(上)期末数学试卷一.选择题(共8小题)1.下面是同学们设计的一些美丽有趣的图案,其中是轴对称图形的是()A.B.C.D.2.为庆祝首个“中国农民丰收节”,十渡镇西河村举办“西河稻作文化节”活动.西河水稻种植历史悠久,因“色白粒粗,味极香美,七煮不烂”而享誉京城.已知每粒稻谷重约0.000035千克,将0.000035用科学记数法表示应为()A.35×10﹣6B.3.5×10﹣6C.3.5×10﹣5D.0.35×10﹣43.如果在实数范围内有意义,则x的取值范围是()A.x≠7 B.x<7 C.x>7 D.x≥74.下列运算正确的是()A.=±2 B.()2=4 C.=﹣4 D.(﹣)2=﹣4 5.如图,Rt△ABC≌Rt△DEF,∠E=55°,则∠A的度数为()A.25°B.35°C.45°D.55°6.如图,△ABC中,∠C=90°,AD平分∠CAB,交BC于点D,DE⊥AB于点E,若CD=,则DE的长为()A.2 B.3 C.D.27.如图,△ABC中,AB=AC,AD⊥BC,垂足为D,DE∥AB,交AC于点E,则下列结论不正确的是()A.∠CAD=∠BAD B.BD=CD C.AE=ED D.DE=DB8.如图,有三种规格的卡片共9张,其中边长为a的正方形卡片4张,边长为b的正方形卡片1张,长,宽分别为a,b的长方形卡片4张.现使用这9张卡片拼成一个大的正方形,则这个大正方形的边长为()A.2a+b B.4a+b C.a+2b D.a+3b二.填空题(共8小题)9.若分式的值为0,则x的值是.10.计算的结果是.11.计算(+2)(﹣2)的结果是.12.在△ABC中,AB=AC,BC=5,∠B=60°,则△ABC的周长是.13.如图,线段AB与CD相交于点O,且OA=OD,连接AC,BD,要说明△AOC≌△DOB,还需添加的一个条件是.(只需填一个条件即可)14.写出一个能用平方差公式分解因式的多项式:.15.已知x2+2x=3,则代数式(x+1)2﹣(x+2)(x﹣2)+x2的值为.16.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中记载了一个“折竹抵地”问题:“今有竹高二丈,末折抵地,去本六尺,问折者高几何?”译文:“有一根竹子,原高二丈(1丈=10尺),现被风折断,竹梢触地面处与竹根的距离为6尺,问折断处离地面的高度为多少尺?”如图,我们用点A,B,C分别表示竹梢,竹根和折断处,设折断处离地面的高度BC=x 尺,则可列方程为.三.解答题(共3小题)17.计算:(×﹣)÷.18.分解因式:4ma2﹣mb2.19.解方程:=1﹣.20.如图,AB=AC,点D,E分别是线段AB,AC的中点,连接BE,CD.求证:∠B=∠C.21.下面是小芸设计的“作三角形一边上的高”的尺规作图过程.已知:△ABC.求作:△ABC的边BC上的高AD.作法:①以点A为圆心,适当长为半径画弧,交直线BC于点M,N;②分别以点M,N为圆心,以大于MN的长为半径画弧,两弧相交于点P;③作直线AP交BC于点D,则线段AD即为所求△ABC的边BC上的高.根据小芸设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明:证明:∵AM=,MP=,∴AP是线段MN的垂直平分线.()(填推理的依据)∴AD⊥BC于D,即线段AD为△ABC的边BC上的高..22.如图,四边形ABCD中,∠B=90°,∠ACB=30°,AB=2,CD=3,AD=5.(1)求证:AC⊥CD;(2)求四边形ABCD的面积.23.如图,在平面直角坐标系xOy中,点O(0,0),A(﹣1,2),B(2,1).(1)在图中画出△AOB关于y轴对称的△A1OB1,并直接写出点A1和点B1的坐标;(不写画法,保留画图痕迹)(2)在x轴上存在点P,使得PA+PB的值最小,则点P的坐标为,PA+PB的最小值为.24.先化简,再求值:(1﹣),其中m=2019.25.下面是两位同学的一段对话:聪聪:周末我们去国家博物馆参观“伟大的变革﹣﹣庆祝改革开放40周年大型展览”吧.明明:好啊,我家离国家博物馆约30km,我坐地铁先走,地铁的平均行驶速度是公交车的1.5倍呢.聪聪:嗯,我周末住奶奶家,离国家博物馆只有5km,坐公交车,你出发40分钟后我再出发就能和你同时到达.根据对话内容,请你求出公交车和地铁的平均行驶速度.26.阅读下列材料:在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”.下面是小涵同学用换元法对多项式(x2﹣4x+1)(x2﹣4x+7)+9进行因式分解的过程.解:设x2﹣4x=y原式=(y+1)(y+7)+9(第一步)=y2+8y+16(第二步)=(y+4)2(第三步)=(x2﹣4x+4)2(第四步)请根据上述材料回答下列问题:(1)小涵同学的解法中,第二步到第三步运用了因式分解的;A.提取公因式法B.平方差公式法C.完全平方公式法(2)老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果:;(3)请你用换元法对多项式(x2+2x)(x2+2x+2)+1进行因式分解.27.已知BC=5,AB=1,AB⊥BC,射线CM⊥BC,动点P在线段BC上(不与点B,C重合),过点P作DP⊥AP交射线CM于点D,连接AD.(1)如图1,若BP=4,判断△ADP的形状,并加以证明.(2)如图2,若BP=1,作点C关于直线DP的对称点C′,连接AC′.①依题意补全图2;②请直接写出线段AC′的长度.28.一般情况下,=+1不成立,但有些数可以使得它成立,例如:a=1,b=2.我们称使得=+1成立的一对数a,b为“相伴数对”,记为(a,b).(1)判断数对(﹣2,1),(3,3)是否是“相伴数对”;(2)若(k,﹣1)是“相伴数对”,求k的值;(3)若(4,m)是“相伴数对”,求代数式的值.参考答案与试题解析一.选择题(共8小题)1.下面是同学们设计的一些美丽有趣的图案,其中是轴对称图形的是()A.B.C.D.【分析】根据轴对称的定义,结合所给图形进行判断即可.【解答】解:A、是轴对称图形;B、不是轴对称图形;C、不是轴对称图形;D、不是轴对称图形;故选:A.2.为庆祝首个“中国农民丰收节”,十渡镇西河村举办“西河稻作文化节”活动.西河水稻种植历史悠久,因“色白粒粗,味极香美,七煮不烂”而享誉京城.已知每粒稻谷重约0.000035千克,将0.000035用科学记数法表示应为()A.35×10﹣6B.3.5×10﹣6C.3.5×10﹣5D.0.35×10﹣4【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:0.000035=3.5×10﹣5,故选:C.3.如果在实数范围内有意义,则x的取值范围是()A.x≠7 B.x<7 C.x>7 D.x≥7【分析】直接利用二次根式有意义的条件分析得出答案.【解答】解:∵在实数范围内有意义,∴x﹣7≥0,解得:x≥7.故选:D.4.下列运算正确的是()A.=±2 B.()2=4 C.=﹣4 D.(﹣)2=﹣4 【分析】根据算式平方根的定义和二次根式的性质逐一化简可得.【解答】解:A.=2,此选项错误;B.()2=4,此选项正确;C.=4,此选项错误;D.(﹣)2=4,此选项错误;故选:B.5.如图,Rt△ABC≌Rt△DEF,∠E=55°,则∠A的度数为()A.25°B.35°C.45°D.55°【分析】根据三角形内角和定理求出∠EDF,根据全等三角形的性质解答.【解答】解:∵∠EFD=90°,∠E=55°,∴∠EDF=90°﹣55°=35°,∵Rt△ABC≌Rt△DEF,∠A=∠EDF=35°,故选:B.6.如图,△ABC中,∠C=90°,AD平分∠CAB,交BC于点D,DE⊥AB于点E,若CD=,则DE的长为()A.2 B.3 C.D.2【分析】根据角平分线的性质即可求出答案.【解答】解:∵AD平分∠CAB,DE⊥AB,∠C=90°,∴CD=DE=,故选:C.7.如图,△ABC中,AB=AC,AD⊥BC,垂足为D,DE∥AB,交AC于点E,则下列结论不正确的是()A.∠CAD=∠BAD B.BD=CD C.AE=ED D.DE=DB【分析】根据等腰三角形的性质,直角三角形的性质解答.【解答】解:∵AB=AC,AD⊥BC,∴∠CAD=∠BAD,A正确,不符合题意;BD=CD,B正确,不符合题意;∵DE∥AB,∴∠EDA=∠BAD,∵∠EAD=∠BAD,∴∠EAD=∠EDA,∴AE=ED,C正确,不符合题意;DE与DB的关系不确定,D错误,符合题意;故选:D.8.如图,有三种规格的卡片共9张,其中边长为a的正方形卡片4张,边长为b的正方形卡片1张,长,宽分别为a,b的长方形卡片4张.现使用这9张卡片拼成一个大的正方形,则这个大正方形的边长为()A.2a+b B.4a+b C.a+2b D.a+3b【分析】先计算出这9张卡片的总面积,其和为一完全平方式,因式分解即可求得大正方形的边长.【解答】解:由题可知,9张卡片总面积为4a2+4ab+b2,∵4a2+4ab+b2=(2a+b)2,∴大正方形边长为2a+b.故选:A.二.填空题(共8小题)9.若分式的值为0,则x的值是 4 .【分析】根据分式的值为零的条件即可求出答案.【解答】解:由题意可知:解得:x=4,故答案为:410.计算的结果是 2 .【分析】根据分式的运算法则即可求出答案.【解答】解:原式==2,故答案为:211.计算(+2)(﹣2)的结果是﹣1 .【分析】利用平方差公式计算,再根据二次根式的性质计算可得.【解答】解:原式=()2﹣22=3﹣4=﹣1,故答案为:﹣1.12.在△ABC中,AB=AC,BC=5,∠B=60°,则△ABC的周长是15 .【分析】根据等边三角形的判定和性质即可解决问题.【解答】解:∵AB=AC,∠B=60°,∴△ABC是等边三角形,∴△ABC的周长为15,故答案为15.13.如图,线段AB与CD相交于点O,且OA=OD,连接AC,BD,要说明△AOC≌△DOB,还需添加的一个条件是OC=OB或AB=CD或∠A=∠D或∠B=∠C.(只需填一个条件即可)【分析】已知条件中OA=OD,且∠AOC=∠DOB为对顶角相等,则还需添加这一对角的另一对对应边相等或另一组对应角相等即可.【解答】解:∵OA=OD,且∠AOC=∠DOB,∴添加OC=OB或AB=CD时,依据SAS即可判定△AOC≌△DOB;添加∠A=∠D或∠B=∠C,依据ASA或AAS即可判定△AOC≌△DOB;故答案为:OC=OB或AB=CD或∠A=∠D或∠B=∠C.(答案不唯一)14.写出一个能用平方差公式分解因式的多项式:a2﹣4 .【分析】这是一道自由发挥问题,根据能用平方差公式因式分解的多项式的特点,只要是两个平方项,且符号相反即可.【解答】解:∵(a+2)(a﹣2),=a2﹣2a+2a﹣4,=a2﹣4,∴满足条件的多项式是:a2﹣4.故答案可以是:a2﹣4.15.已知x2+2x=3,则代数式(x+1)2﹣(x+2)(x﹣2)+x2的值为8 .【分析】根据完全平方公式、平方差公式可以化简题目中的式子,然后根据x2+2x=3整体代入即可解答本题.【解答】解:(x+1)2﹣(x+2)(x﹣2)+x2,=x2+2x+1﹣(x2﹣4)+x2,=x2+2x+5,∴原式=3+5=8.故答案为:8.16.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中记载了一个“折竹抵地”问题:“今有竹高二丈,末折抵地,去本六尺,问折者高几何?”译文:“有一根竹子,原高二丈(1丈=10尺),现被风折断,竹梢触地面处与竹根的距离为6尺,问折断处离地面的高度为多少尺?”如图,我们用点A,B,C分别表示竹梢,竹根和折断处,设折断处离地面的高度BC=x 尺,则可列方程为x2+62=(20﹣x)2.【分析】竹子折断后刚好构成一直角三角形,设竹子折断处离地面x尺,则斜边为(20﹣x)尺,利用勾股定理解题即可.【解答】解:设竹子折断处离地面x尺,则斜边为(20﹣x)尺,根据勾股定理得:x2+62=(20﹣x)2.故答案为x2+62=(20﹣x)2.三.解答题(共3小题)17.计算:(×﹣)÷.【分析】根据二次根式的混合运算顺序和运算法则计算可得.【解答】解:原式=(﹣)÷=÷﹣÷=﹣=2﹣.18.分解因式:4ma2﹣mb2.【分析】应先提取公因式4m,再对余下的多项式利用平方差公式继续分解.【解答】解:4ma2﹣mb2,=m(4a2﹣b2),=m(2a+b)(2a﹣b).19.解方程:=1﹣.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得,3x=3x+3﹣2x,移项合并同类项得,2x=3,系数化1得,x=,检验:x=是原方程的解.20.如图,AB=AC,点D,E分别是线段AB,AC的中点,连接BE,CD.求证:∠B=∠C.【考点】KD:全等三角形的判定与性质.【专题】14:证明题.【分析】证明△ABE≌△ACD(SAS),即可求解.【解答】证明:∵点D,E分别是线段AB,AC的中点,∴AD=AB,AE=AC,∵AB=AC,∴AD=AE,在△ABE和△ACD中,AB=AC,∠A=∠A,AD=AE,∴△ABE≌△ACD(SAS),∴∠B=∠C.21.下面是小芸设计的“作三角形一边上的高”的尺规作图过程.已知:△ABC.求作:△ABC的边BC上的高AD.作法:①以点A为圆心,适当长为半径画弧,交直线BC于点M,N;②分别以点M,N为圆心,以大于MN的长为半径画弧,两弧相交于点P;③作直线AP交BC于点D,则线段AD即为所求△ABC的边BC上的高.根据小芸设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明:证明:∵AM=AN,MP=NP,∴AP是线段MN的垂直平分线.(到一条线段两个端点距离相等的点在这条线段的垂直平分线上)(填推理的依据)∴AD⊥BC于D,即线段AD为△ABC的边BC上的高.【考点】KG:线段垂直平分线的性质;N3:作图—复杂作图.【专题】13:作图题.【分析】(1)利用几何语言画出对应的几何图形;(2)通过作图得到AM=AN,MP=NP,则根据线段垂直平分线的性质定理的逆定理可判断AP是线段MN的垂直平分线,从而得到AD⊥BC.【解答】解:(1)补全的图形如图所示;(2)证明:∵AM=AN,MP=NP,∴AP是线段MN的垂直平分线(到一条线段两个端点距离相等的点在这条线段的垂直平分线上)∴AD⊥BC于D,即线段AD为△ABC的边BC上的高.故答案为AN,NP,到一条线段两个端点距离相等的点在这条线段的垂直平分线上.22.如图,四边形ABCD中,∠B=90°,∠ACB=30°,AB=2,CD=3,AD=5.(1)求证:AC⊥CD;(2)求四边形ABCD的面积.【考点】KQ:勾股定理;KS:勾股定理的逆定理.【专题】554:等腰三角形与直角三角形.【分析】(1)根据直角三角形的性质得到AC=2AB=4,根据跟勾股定理的逆定理即可得到结论;(2)根据勾股定理得到BC==2,根据三角形的面积公式即可得到结论.【解答】(1)证明:在Rt△ABC中,∠B=90°,∠ACB=30°,AB=2,∴AC=2AB=4,在△ACD中,AC=4,CD=3,AD=5,∵42+32=52,即AC2+CD2=AD2,∴∠ACD=90°,∴AC⊥CD;(2)解:在Rt△ABC中,∠B=90°,AB=2,AC=4,∴BC==2,∴Rt△ABC的面积为AB•BC=×2×2=2,又∵Rt△ACD的面积为AC•CD=×4×3=6,∴四边形ABCD的面积为:2+6.23.如图,在平面直角坐标系xOy中,点O(0,0),A(﹣1,2),B(2,1).(1)在图中画出△AOB关于y轴对称的△A1OB1,并直接写出点A1和点B1的坐标;(不写画法,保留画图痕迹)(2)在x轴上存在点P,使得PA+PB的值最小,则点P的坐标为(1,0),PA+PB 的最小值为3.【考点】P7:作图﹣轴对称变换;PA:轴对称﹣最短路线问题.【专题】13:作图题;24:网格型;558:平移、旋转与对称.【分析】(1)分别作出点A和点B关于y轴的对称点,再与点O首尾顺次连接即可得;(2)作点B关于x轴的对称点B′,连接AB′,与x轴的交点即为所求点P,AB′的长即为PA+PB的最小值,利用勾股定理计算可得答案.【解答】解:(1)如图所示,△A1OB1即为所求;由图知A1(1,2),B1(﹣2,1);(2)由图知,点P即为所求,点P的坐标P(1,0),PA+PB的最小值为=3,故答案为:(1,0),3.24.先化简,再求值:(1﹣),其中m=2019.【考点】6D:分式的化简求值.【专题】11:计算题;513:分式.【分析】先根据分式的混合运算顺序和运算法则化简原式,再将m的值代入计算可得.【解答】解:原式=(﹣)•=•=,当m=2019时,原式==.25.下面是两位同学的一段对话:聪聪:周末我们去国家博物馆参观“伟大的变革﹣﹣庆祝改革开放40周年大型展览”吧.明明:好啊,我家离国家博物馆约30km,我坐地铁先走,地铁的平均行驶速度是公交车的1.5倍呢.聪聪:嗯,我周末住奶奶家,离国家博物馆只有5km,坐公交车,你出发40分钟后我再出发就能和你同时到达.根据对话内容,请你求出公交车和地铁的平均行驶速度.【考点】B7:分式方程的应用.【专题】522:分式方程及应用.【分析】根据题意列出分式方程,解方程得到答案.【解答】解:设公交车平均行驶速度为xkm/h,则地铁的平均行驶速度为1.5xkm/h,根据题意,得﹣=,解得,x=22.5,经检验:x=22.5是所列方程的解,且符合题意,5x=1.5×22.5=33.75km/h.答:公交车和地铁的平均行驶速度分别为22.5 km/h和33.75km/h.26.阅读下列材料:在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”.下面是小涵同学用换元法对多项式(x2﹣4x+1)(x2﹣4x+7)+9进行因式分解的过程.解:设x2﹣4x=y原式=(y+1)(y+7)+9(第一步)=y2+8y+16(第二步)=(y+4)2(第三步)=(x2﹣4x+4)2(第四步)请根据上述材料回答下列问题:(1)小涵同学的解法中,第二步到第三步运用了因式分解的C;A.提取公因式法B.平方差公式法C.完全平方公式法(2)老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果:(x ﹣2)4;(3)请你用换元法对多项式(x2+2x)(x2+2x+2)+1进行因式分解.【考点】54:因式分解﹣运用公式法.【专题】23:新定义;512:整式.【分析】(1)根据完全平方公式进行分解因式;(2)最后再利用完全平方公式将结果分解到不能分解为止;(3)根据材料,用换元法进行分解因式.【解答】解:(1)故选:C;(2)(x2﹣4x+1)(x2﹣4x+7)+9,设x2﹣4x=y,原式=(y+1)(y+7)+9,=y2+8y+16,=(y+4)2,=(x2﹣4x+4)2,=(x﹣2)4;故答案为:(x﹣2)4;(3)设x2+2x=y,原式=y(y+2)+1,=y2+2y+1,=(y+1)2,=(x2+2x+1)2,=(x+1)4.27.已知BC=5,AB=1,AB⊥BC,射线CM⊥BC,动点P在线段BC上(不与点B,C重合),过点P作DP⊥AP交射线CM于点D,连接AD.(1)如图1,若BP=4,判断△ADP的形状,并加以证明.(2)如图2,若BP=1,作点C关于直线DP的对称点C′,连接AC′.①依题意补全图2;②请直接写出线段AC′的长度.【考点】KY:三角形综合题.【专题】15:综合题.【分析】(1)先判断出PC=AB,再用同角的余角相等判断出∠APB=∠PDC,得出△ABP ≌△PCD(AAS),即可得出结论;(2)①利用对称的性质画出图形;②先求出CP=4,AB=AP,∠CPD=45°,进而得出C'P=CP=4,∠C'PD=∠CPD=45°,再判断出四边形BQC'P是矩形,进而求出AQ=BQ﹣AB=3,最后用勾股定理即可得出结论.【解答】(1)△ADP是等腰直角三角形.证明:∵BC=5,BP=4,∴PC=1,∵AB=1,∴PC=AB.∵AB⊥BC,CM⊥BC,DP⊥AP,∴∠B=∠C=90°,∠APB+∠DPC=90°,∠PDC+∠DPC=90°,∴∠APB=∠PDC,在△ABP和△PCD中,∴△ABP≌△PCD(AAS)∴AP=PD,∵∠APD=90°,∴△ADP是等腰直角三角形.(2)①依题意补全图2;②∵BP=1,AB=1,BC=5,∴CP=4,AB=AP,∵∠ABP=90°,∴∠APB=45°,∵∠APD=90°,∴∠CPD=45°,连接C'P,∵点C与C'关于DP对称,∴C'P=CP=4,∠C'PD=∠CPD=45°,∴∠CPC'=90°,∴∠BPC'=90°,过点C'作C'Q⊥BA交BA的延长线于Q,∴∠Q=90°=∠ABP=∠BPC',∴四边形BQC'P是矩形,∴C'Q=BP=1,BQ=C'P=4,∴AQ=BQ﹣AB=3,在Rt△AC'Q中,AC′=28.一般情况下,=+1不成立,但有些数可以使得它成立,例如:a=1,b=2.我们称使得=+1成立的一对数a,b为“相伴数对”,记为(a,b).(1)判断数对(﹣2,1),(3,3)是否是“相伴数对”;(2)若(k,﹣1)是“相伴数对”,求k的值;(3)若(4,m)是“相伴数对”,求代数式的值.【考点】45:整式的加减—化简求值.【专题】512:整式.【分析】(1)利用“相伴数对”的定义化简,计算即可求出b的值;(2)根据“相伴数对”的定义解答即可;(3)利用“相伴数对”定义得到m2﹣4m=﹣1,原式去括号整理后代入计算即可求出值.【解答】解:(1)∵+≠+1,∴(﹣2,1)不是“相伴数对”;∵+=+1,∴(3,3)是“相伴数对”;(2)∵(k,﹣1)是“相伴数对”,∴+=+1,解得k=1;(3)∵(4,m)是“相伴数对”,∴+=+1,∴m2﹣4m=﹣1,∴=====﹣.。
2022-2023学年北京燕山地区八年级数学第一学期期末质量监测卷附答案解析

2022-2023学年北京燕山地区八年级数学第一学期期末质量监测卷2022年12月满分100分。
考试时间100分钟一、选择题(共30分,每题3分)第1—10题均有四个选项,符合题意的选项只有一个..... 1.在数学活动课中,同学们利用几何画板绘制出了下列曲线,其中不是..轴对称图形的是等角螺旋线 心形线 四叶玫瑰线 蝴蝶曲线A .B .C .D .2.随着人类基因组(测序)计划的逐步实施以及分子生物学相关学科的迅猛发展,越来越多的动植物、微生物基因组序列得以测定.已知某种基因芯片每个探针单元的面积为0.0000064cm 2,将0.0000064用科学记数法表示应为A .50.6410-⨯B .56.410-⨯C .66.410-⨯D .76410-⨯ 3.下列各组线段能组成三角形的是A .1cm ,2cm ,3cmB .3cm ,4cm ,5cmC .3cm ,3cm ,6cmD .3cm ,4cm ,9cm 4.已知一个多边形的内角和是540°,则这个多边形的边数是A .4B .5C .6D .7 5.下列等式中,从左到右的变形是因式分解的是A .2(3)(3)9x x x +-=-B .22(2)44+=++x x xC .2(3)(5)215-+=+-x x x xD .2224129(23)-+=-x xy y x y 6.下列各式中,运算结果为6a 的是A .42+a aB .23a aC .23()aD .122÷a a7.某方舱医院采购A ,B 两种型号的机器人进行院内物资配送.已知A 型机器人比B 型机器人每小时多配送200件物资,且A 型机器人配送1000件物资所用的时间与B 型机器人配送750件物资所用的时间相同.若设B 型机器人每小时配送x 件物资,根据题意可列方程为A .1000750200=-x x B .1000750200=+x x C .1000750200=-x x D .1000750200=+x x8.如图,△ABC 中,AB =AC ,AD 为BC 边的中线,∠BAD =28°,则∠C =A .31°B .56°C .62°D .76°9.如图,△ABC 中,BD 是AC 边的高线,CE 平分∠ACB ,DE =1cm ,BC =4cm ,则△BEC 的面积是A .1cm 2B .2cm 2C .3cm 2D .4cm 210.某学校要举行科技文化艺术节活动,现计划在教学楼之间的广场上搭建舞台.已知广场中心有一座边长为b 的正方形的花坛,学生会提出两个方案(舞台平面图与具体数据如图所示): 方案一:如图1,绕花坛搭建外围是正方形的“回”字形舞台(阴影部分),面积为1S ;方案二:如图2,在花坛的四周用四个相同的长方形搭建“十”字形舞台(阴影部分),面积为2S . 则1S 与2S 的大小关系是A .1S >2SB .1S =2SC .1S <2SD .无法确定 二、填空题(共16分,每题2分) 11.若分式4+x x的值为0,则x 的值为 . 12.分解因式:2327-a = . 13.化简111+--x x x的结果是 . 14.已知24510=+-m m ,则代数式2(21)(3)(3)+++-m m m 的值为 . 15.已知Rt △ABC 中,∠C =90°,∠A =60°,AB =8,则AC = .16.数学课上老师布置了“测量锥形瓶内部底面的内径”的探究任务,小聪想到老师讲过“利用全等三角形对应边相等,可以把不能直接测量的物体‘移’到可以直接测量的位置测量”.于是他设计了如下方案:如图,用螺丝钉将两根小棒AC ,BD 的中点O 固定,只要测得C ,D 之间的距离,就可知道内径AB 的长度.此方案中,判定△AOB ≌△COD 的依据是 .17.如图,正方形网格中,点A ,B ,C 都在格点上,则∠CAB +∠ACB = °.(第10题) 图1 b a a b a 3b 2--2bb3b a 图2(第8题) A BC D (第9题) D E A B C (第16题) OA B C D A BC D E F (第18题)(第17题) C B18.如图,等腰△ABC 中,AB =AC ,∠BAC =120°,AD ⊥BC 于点D ,点E 在BA 的延长线上,点F在线段AD 上,且EF =FC .有下面四个结论: ①AB =2AD ; ②△AEF ≌△ACF ; ③△EFC 是等边三角形; ④F A +AE =EC . 其中所有正确结论的序号是 .三、解答题(共54分,第19题-第23题,每题5分;第24题-第25题,每题6分;第26题5分;第27题-第28题,每题6分)19.计算:()02π202324-+-+-||.20.解方程:132=-x x.21.如图,点D ,E 分别在线段AB ,AC 上,AB =AC .现给出下列条件:①∠B =∠C ;②BE =CD ;③AE =AD ,请你选择一个合适的条件,添加到已知条件中,使得△ABE ≌△ACD ,并证明.22.下面是小青设计的“过直线外一点作这条直线的平行线”的尺规作图过程.已知:直线l 及直线l 外一点P . 求作:直线PQ ,使得PQ ∥l . 作法:如图,①在直线l 上取点A ,连接P A ;②作线段P A 的垂直平分线MN ,分别交直线l , 直线P A 于点B ,O ;③以点O 为圆心,OB 长为半径画弧, 交直线MN 于另一点Q ;④作直线PQ .所以直线PQ 就是所求作的直线. 根据小青设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹) (2)完成下面的证明. 证明:连接PQ ,∵线段P A 的垂直平分线交P A 于点O , ∴OA =OP ,( ) (填推理的依据)又∵∠AOB =∠POQ ,OB = , ∴△AOB ≌△POQ ,( ) (填推理的依据)∴∠PQO =∠ABO , ∴PQ ∥l .EA BD C l23.如图,在平面直角坐标系xOy 中,已知点A (‒2,4),B (4,2),△AOB 与△A 1OB 1关于x 轴对称.(1)画出△A 1OB 1;(2)直接写出点A 1,B 1的坐标;(3)在x 轴找一点P ,使得△P A 1B 1的周长最短,请在图中画出点P 的位置. (不写画法,保留作图痕迹)24.求代数式222211211-⎛⎫+÷ ⎪-+--⎝⎭a a a a a a的值,其中1-=a .25.列方程解应用题:为落实节约用水的政策,某单位进行设施改造,将手拧水龙头全部更换成感应水龙头.已知该单位在设施改造后,平均每天用水量比原来减少了40%,30吨水可以比原来多用4天,该单位在设施改造后平均每天用水多少吨?26.阅读下列材料:我们知道,假分数可以写成带分数的形式,在这个计算过程中,先计算分子中含有几个分母,求出整数部分,再把剩余部分写成一个真分数.例如:91224414=+=. 对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,称之为“真分式”.类似地,我们可以把一个“假分式”写成整式和一个“真分式”的和的形式.例如:232(1)12(1)12111111----==-=------x x x x x x x x ; 2299(3)(3)9933333-++-+===-+++++x x x x x x x x x . 请根据上述材料解决下列问题: (1)请写出一个假分式: ;(2)请将分式2323+++x xx化为整式与真分式的和的形式;(3)设M=341++xx,则当02<<x时,M的取值范围是.27.如图,△ABC中,AB<AC,点D为BC边中点,∠BAD=α.作点B关于直线AD的对称点B',连接BB'交AD于点E,过点C作CF∥AB交直线AB'于点F.(1)依题意补全图形,并直接写出∠AB'E和∠AFC的度数(用含α的式子表示);(2)用等式表示线段AB,AF,CF之间的数量关系,并证明.燕山地区2022—2023学年第一学期八年级期末质量监测 数学试卷参考答案及评分标准 2022.12一、选择题(共30分,每题3分)二、填空题(共16分,每题2分)11.-4; 12.3(3)(3)-+a a ; 13.1; 14.-7; 15.4; 16.SAS ; 17.45; 18.①③.三、解答题(共54分,第19题-第23题,每题5分;第24题-第25题,每题6分;第26题5分;第27题-第28题,每题6分) 19.解:原式=1144++ =154. …………………………………5分 20.解:去分母得,x =3(x -2), …………………………………1分去括号得,x =3x -6, …………………………………2分 移项合并同类项得,2x =6, …………………………………3分 系数化1得,x =3. …………………………………4分 检验:当x =3时,x (x -2)≠0,原方程的解为x =3. …………………………………5分21.方法一:选择条件①∠B =∠C . …………………………………1分证明:在△ABE 和△ACD 中,∠∠⎧⎪⎨⎪∠∠⎩=,=,=,A A AB AC B C ∴△ABC ≌△BDE . …………………………………5分 方法二:选择条件③AE =AD . …………………………………1分 证明:在△ABE 和△ACD 中,⎧⎪∠∠⎨⎪⎩=,=,=,AE AD A A AB AC ∴△ABC ≌△BDE , …………………………………5分22.解:(1) 补全的图形如图所示; …………………………………2分(2)线段垂直平分线上的点到线段两端点的距离相等;OQ ;SAS . …………………………………5分23.解:(1)画出△A 1OB 1如图所示; …………………………………2分(2)A 1(-2,-4),B 1(4,-2); …………………………………4分 (3)画出点P 的位置如图所示. …………………………………5分 24.解:原式=22(1)11[](1)1(1)-+÷---a a a a a …………………………………3分=21()(1)11+---a a a a =3(1)1--a a a =3a . …………………………………5分当1-=a 时,原式=-3. …………………………………6分25.解:设该单位在设施改造前平均每天用水x 吨,则在设施改造后平均每天用水量为(1-40%)x 吨,…………………………………1分根据题意,得30304(140%)-=-x x, …………………………………2分解这个方程,得 x =5. …………………………………3分 经检验:x =5是所列方程的解,且符合题意. …………………………………4分 (1-40%)x =0.6×5=3吨. …………………………………5分 答:该单位在设施改造后平均每天用水3吨. …………………………………6分26.解:(1)答案不唯一,如21+x x. …………………………………1分(2)232(3)22333++++==++++x x x x x x x x . …………………………………3分(3)1043<<M . …………………………………5分27.解:(1) 依题意补全图形,如图; …………………………………1分∠A B'E =(90-α)°; …………………………………2分 ∠AFC =(180-2α)°. …………………………………3分(2) AF =AB +CF . ………………………………4分 证法一:如图,延长AD ,FC 交于点G . ∵点D 为BC 中点, ∴BD =DC . ∵CF ∥AB , ∴∠BAD =∠G . 又∵∠ADB =∠GDC , ∴△ABD ≌△GCD , ∴AB =GC .∵点B ,B'关于直线AD 对称,∴∠BAD =∠B'AD , ∴∠G =∠B'AD , ∴A F =F G .∵F G =GC +CF =AB +CF ,∴A F =AB +CF . ………………………………6分 证法二:如图,连接D B',C B'. ∵点B ,B'关于直线AD 对称,∴∠BAD =∠B'AD ,AB =A B',DB =D B',AD ⊥BB', ∴∠1=∠2,∠BAB'=2α°. ∵点D 为BC 中点, ∴BD =DC , ∴DB'=DC , ∴∠3=∠4,∴∠2+∠3=∠1+∠4. ∵∠1+∠2+∠3+∠4=180°,EFB'DCBAGEFB'DCBA4321F EB'DCBA∴∠BB'C =∠2+∠3=90°, 即BB'⊥B'C , ∴AD ∥B'C ,∴∠CB'F =∠DAB'=α°. ∵CF ∥AB ,∴∠BAB'+∠F =180°,∴∠F =180°-∠BAB'=180°-2α°. 又∵∠FCB'+∠FB'C +∠F =180°, ∴∠FCB'+α°+180°-2α°=180°, ∴∠FCB'=α°, ∴∠FCB'=∠FB'C , ∴B'F =CF ,∴A F =AB'+B'F =AB +CF . ………………………………6分 28.解:(1)①d AB =4; ………………………………1分②d CD =1. ………………………………2分(2)①∵点E (‒1,m ),F (2,m +2),∴E ,F 关于直线的对称点为G (‒1,4‒m ),H (2,2‒m ).∵d GH =3,且4‒m>2‒m ,∴4‒m =3(如图1),或m‒2=3(如图2).∴m =1,或m =5. ………………………………4分 ②m 的取值范围是m ≤‒1,或m ≥3. ………………………………6分2=y 图2-575y =256-2-1-3-4-3-1-243124312Oxy -4HG FE 图1-575y =256-2-1-3-4-3-1-243124312Oxy -4HG F E。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020学年北京市燕山区八年级(上)期末数学试卷一、选择题(共8个小题).1.在以下绿色食品、节能、节水、回收四个标志中,是轴对称图形的是( )A .B .C .D .2.下列计算正确的是( ) A .32x x -= B .341a a a ÷= C .22(1)1x x x -=--D .236(2)8a a -=-3.能用平方差公式分解因式的多项式是( ) A .221x x -+B .29x +C .ax ay -D .24x -+4.太阳光照射到地球上需要的时间约是2510s ⨯,光的速度约是5310/km s ⨯,那么太阳到地球的距离用科学记数法表示约为( ) A .71510⨯B .71.510⨯C .81.510⨯D .101510⨯5.已知,ABC DEF ∆≅∆,且ABC ∆的周长为20,8AB =,3BC =,则DF 等于( ) A .3B .5C .9D .116.已知EF 是EBC ∆的角平分线,FD EB ⊥于D ,且3FD cm =,则点F 到EC 的距离是( )A .2cmB .3cmC .4cmD .6cm7.如图,从边长为(4)a cm +的正方形纸片中剪去一个边长为(1)a cm +的正方形(0)a >,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为( )A .22(25)a a cm +B .2(615)a cm +C .2(69)a cm +D .2(315)a cm +8.豆豆老师到学校距离是8千米,她开车上班的平均速度是乘公交车平均速度的2.5倍,已知豆豆老师自己开车上班比乘公交车上班所需的时间少用14小时,若设乘公交车平均每小时走x 千米,根据题意可列方程为( ) A .8815 2.5x x+=B .8815 2.5x x=+C .8184 2.5x x+=D .8812.54x x =+ 二、填空题(本题共16分,每小题2分) 9.若分式23x x +-的值为0,则x 的值为 . 10.如图,根据图形,写出一个正方形ABCD 的面积的表达式 .(一个即可)11.化简211x xx x+--的结果为 . 12.有一个正多边形的外角是60︒,那么该正多边形是正 边形.13.如图,点E ,F 在AC 上,AD BC =,DF BE =,要使ADF CBE ∆≅∆,需添加一个条件是 .(只需添加一个条件即可)14.若2249x kxy y ++是一个完全平方式,则k 的值为 .15.下面一组按规律排列的数,2,4,8,16,32,⋯⋯则第2020个数是 . 16.如图,在ABC ∆中,按以下步骤作图:①以B 为圆心,任意长为半径作弧,交AB 于D ,交BC 于E ;②分别以D ,E 为圆心,以大于12DE 的同样长为半径作弧,两弧交于点M ;③作射线BM 交AC 于N .如果BN NC =,57A ∠=︒,那么ABN ∠的度数为 .三、解答题(本题共68分,第17-21题,每小题5分;第22题4分;第23题7分;第24-27题,每小题5分,第28,29题,每小题5分)解答应写出文字说明,演算步骤或证明过程. 17.计算:32(1263)3a a a a +-÷. 18.分解因式: (1)3x x -; (2)2363x y xy y -+. 19.解方程:11222x x x-=---. 20.已知:如图,12∠=∠,C D ∠=∠.求证:AC AD =.21.如图:在等边三角形ABC 中,点D 、E 分别是AB 、BC 延长线上的点,且BD CE =.求证:BCD CAE ∠=∠.22.如图1为L 形的一种三格骨牌,它是由三个全等的正方形连接而成.请以L 形的三格骨牌为基本图形,在图2,图3中各设计一个轴对称图形,要求如下:(1)每个图形由两个L 形三格骨牌组成,骨牌的顶点都在小正方形的顶点上. (2)设计的图形用斜线涂出,若形状相同,则视为一种.23.阅读下列材料 分解因式:3416x x - 小云的做法: 原式3164x x =-①24(41)x x =-②4(21)(21)x x x =-+③小朵的做法: 原式4x = 2(14)x -① 4(14)x x =- (14)x +②小天的做法: 原式x = 2(416)x -①22[2(4)]x x =-②(24)x x =- (24)x +③请根据上述材料回答下列问题:(1)小云的解题过程从 步出现错误的,错误的原因是: .小朵的解题过程从 步出现错误的,错误的原因是: .小天的解题过程从 步出现错误的,错误的原因是: .(2)若都不正确,请你写出正确的解题过程.24.已知30AOB ∠=︒,点P 在AOB ∠的内部,点C 和点P 关于OA 对称,点P 关于OB 的对称点是D ,连接CD 交OA 于M ,交OB 于N ,15CD =. (1)补全图,并且保留作图痕迹.(2)写出COD ∠= ︒.PMN ∆的周长为 .25.通过整式乘法的学习,我们进一步了解了利用图形面积来说明法则、公式等的正确性的方法,例如利用图甲可以对平方差公式22()()a b a b a b +-=-给予解释.图乙中的ABC ∆是一个直角三角形,90C ∠=︒,人们很早就发现直角三角形的三边a ,b ,c 满足222a b c +=的关系.图丙是2002年国际数学家大会的会徽,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,弦图是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为a ,较长直角边长为b ,求出2()a b +的值.26.先化简,再求值:22112111t t tt t t t -+÷-+-+g ,其中2019t =.27.阅读下面材料:学习了三角形全等的判定方法(即“SAS ”“ ASA ”“ AAS ”“ SSS ” )和直角三角形全等的判定方法(即“HL ” )后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究小聪将命题用符号语言表示为:在ABC ∆和DEF ∆中,AC DF =,BC EF =,B E ∠=∠. 小聪的探究方法是对B ∠分为“直角、钝角、锐角”三种情况进行探究.第一种情况:当B ∠ 是直角时,如图1,ABC ∆和DEF ∆中,AC DF =,BC EF =,90B E ∠=∠=︒,根据“HL ”定理,可以知道Rt ABC Rt DEF ∆≅∆.第二种情况:当B ∠ 是锐角时,如图2,BC EF =,90B E ∠=∠<︒,在射线EM 上有点D ,使DF AC =,画出符合条件的点D ,则ABC ∆和DEF ∆的关系是 ; A .全等 B .不全等 C .不一定全等第三种情况:当B ∠是钝角时,如图3,在ABC ∆和DEF ∆中,AC DF =,BC EF =,90B E ∠=∠>︒.过点C 作AB 边的垂线交AB 延长线于点M ;同理过点F 作DE 边的垂线交DE 延长线于N ,根据“ASA ”,可以知道CBM FEN ∆≅∆,请补全图形,进而证出ABC DEF ∆≅∆.28.如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这个分式为“和谐分式”.(1)下列分式中, 是和谐分式(填写序号即可);①222()a b a b ++; ②2224t b t b --;③22x y x y +-;④2211m m -+(2)若a 为整数,且214y y ay -++为和谐分式,请写出a 的值;(3)在化简22344m m nmn n n -÷-时, 小冬和小奥分别进行了如下三步变形:小冬:原式22222323232232444444()()m m m m m n m mn n mn n n n mn n n mn n n --=-⨯=-=--- 小奥:原式22223222444444()()()m m m m m m m n mn n n n n m n n n m n --=-⨯=-=--- 显然,小奥利用了其中的和谐分式,第三步所得结果比小冬的结果简单,原因是: ,请你接着小奥的方法完成化简.29.在ABC ∆中,AD 平分BAC ∠交BC 于D ,MDN ∠的两边分别与AB ,AC 相交于M ,N 两点,且DM DN =.(1)如图甲,若90C ∠=︒,60BAC ∠=︒,9AC =,120MDN ∠=︒,//ND AB . ①写出MDA ∠= ︒,AB 的长是 .②求四边形AMDN的周长.(2)如图乙,过D作DF AC+=.⊥于F,先补全图乙再证明2AM AN AF参考答案一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个.1.在以下绿色食品、节能、节水、回收四个标志中,是轴对称图形的是( )A .B .C .D .解:A 、是轴对称图形,故本选项正确; B 、不是轴对称图形,故本选项错误; C 、不是轴对称图形,故本选项错误;D 、不是轴对称图形,故本选项错误.故选:A .2.下列计算正确的是( ) A .32x x -= B .341a a a ÷= C .22(1)1x x x -=--D .236(2)8a a -=-解:.32A x x x -=,故本选项不合题意; B .341a a a÷=,故本选项不合题意; C .22(1)21x x x -=--,故本选项不合题意;D .236(2)8a a -=-,正确,故本选项符合题意.故选:D .3.能用平方差公式分解因式的多项式是( ) A .221x x -+B .29x +C .ax ay -D .24x -+解:A 、原式2(1)x =-,不符合题意; B 、原式不能分解,不符合题意; C 、原式()a x y =-,不符合题意;D 、原式(2)(2)x x =-++,符合题意,故选:D .4.太阳光照射到地球上需要的时间约是2510s ⨯,光的速度约是5310/km s ⨯,那么太阳到地球的距离用科学记数法表示约为( ) A .71510⨯B .71.510⨯C .81.510⨯D .101510⨯解:528310510 1.510⨯⨯⨯=⨯. 故选:C .5.已知,ABC DEF ∆≅∆,且ABC ∆的周长为20,8AB =,3BC =,则DF 等于( ) A .3B .5C .9D .11解:ABC ∆Q 的周长为20,8AB =,3BC =, 20389AC ∴=--=, ABC DEF ∆≅∆Q , 9DF AC ∴==,故选:C .6.已知EF 是EBC ∆的角平分线,FD EB ⊥于D ,且3FD cm =,则点F 到EC 的距离是( )A .2cmB .3cmC .4cmD .6cm解:FD EB ⊥Q 于D ,且3FD cm =, ∴点F 到EB 的距离为3cm ,EF Q 是EBC ∆的角平分线, ∴点F 到EB 和EC 的距离相等, ∴点F 到EC 的距离是3cm .故选:B .7.如图,从边长为(4)a cm +的正方形纸片中剪去一个边长为(1)a cm +的正方形(0)a >,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为( )A .22(25)a a cm +B .2(615)a cm +C .2(69)a cm +D .2(315)a cm +解:矩形的面积是:22(4)(1)a a +-+ (41)(41)a a a a =++++-- 3(25)a =+2615()a cm =+.故选:B .8.豆豆老师到学校距离是8千米,她开车上班的平均速度是乘公交车平均速度的2.5倍,已知豆豆老师自己开车上班比乘公交车上班所需的时间少用14小时,若设乘公交车平均每小时走x 千米,根据题意可列方程为( ) A .8815 2.5x x+=B .8815 2.5x x=+C .8184 2.5x x+=D .8812.54x x =+ 解:设乘公交车平均每小时走x 千米,根据题意可列方程为:8812.54x x =+, 故选:D .二、填空题(本题共16分,每小题2分) 9.若分式23x x +-的值为0,则x 的值为 2- . 解:依题意得:20x +=且30x -≠, 解得2x =-. 故答案是:2-.10.如图,根据图形,写出一个正方形ABCD 的面积的表达式 2()x a + .(一个即可)解:由题意可知:2()()()x a x a x a ++=+, 故答案为:2()x a +11.化简211x xx x +--的结果为 x . 解:原式211x xx x =---(1)1xx x -=- x =.故答案为:x .12.有一个正多边形的外角是60︒,那么该正多边形是正 六 边形.解:这个正多边形的边数:360606︒÷︒=.故答案为:六.13.如图,点E ,F 在AC 上,AD BC =,DF BE =,要使ADF CBE ∆≅∆,需添加一个条件是 D B ∠=∠ .(只需添加一个条件即可)解:当D B ∠=∠时,在ADF ∆和CBE ∆中Q AD BC D B DF BE =⎧⎪∠=∠⎨⎪=⎩,()ADF CBE SAS ∴∆≅∆, 故答案为:D B ∠=∠.(答案不唯一)14.若2249x kxy y ++是一个完全平方式,则k 的值为 12± .解:2249x kxy y ++Q 是一个完全平方式,12k ∴=±,故答案为:12±15.下面一组按规律排列的数,2,4,8,16,32,⋯⋯则第2020个数是 20202 . 解:Q 一列数为:2,4,8,16,32,⋯⋯,∴这列数的第n 个数为2n ,∴第2020个数是20202,故答案为:20202.16.如图,在ABC ∆中,按以下步骤作图:①以B 为圆心,任意长为半径作弧,交AB 于D ,交BC 于E ;②分别以D ,E 为圆心,以大于12DE 的同样长为半径作弧,两弧交于点M ; ③作射线BM 交AC 于N .如果BN NC =,57A ∠=︒,那么ABN ∠的度数为 41︒ .解:根据作图方法可得BN 是ABC ∠的角平分线,ABN CBN ∴∠=∠,BN NC =Q ,C NBC ∴∠=∠,设ABN x ∠=︒,则CBN C x ∠=∠=︒,57180x x x +++=,解得:41x =,故答案为:41︒.三、解答题(本题共68分,第17-21题,每小题5分;第22题4分;第23题7分;第24-27题,每小题5分,第28,29题,每小题5分)解答应写出文字说明,演算步骤或证明过程.17.计算:32(1263)3a a a a +-÷.解:原式321236333a a a a a a =÷+÷-÷2421a a =+-18.分解因式:(1)3x x -;(2)2363x y xy y -+.解:(1)原式2(1)(1)(1)x x x x x =-=+-;(2)原式223(21)3(1)y x x y x =-+=-.19.解方程:11222x x x-=---.解:去分母得,12(2)1x x -=-+,去括号1241x x -=-+,移项合并同类项得,2411x x -=--,系数化1得,2x =,经检验:2x =是增根,分式方程无解.20.已知:如图,12∠=∠,C D ∠=∠.求证:AC AD =.【解答】证明:Q 在ACB ∆与ADB ∆中,12C D AB AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ACB ADB AAS ∴∆≅∆,AC AD ∴=.21.如图:在等边三角形ABC 中,点D 、E 分别是AB 、BC 延长线上的点,且BD CE =.求证:BCD CAE ∠=∠.【解答】证明:Q 等边三角形ABCAB BC AC ∴==,ABC ACB ∠=∠,DBC ACE ∴∠=∠,在ABC ∆和ABD ∆中,BC AC DBC ACE BD CE =⎧⎪∠=∠⎨⎪=⎩,DBC ECA ∴∆≅∆ ()SAS ,BCD CAE ∴∠=∠.22.如图1为L 形的一种三格骨牌,它是由三个全等的正方形连接而成.请以L 形的三格骨牌为基本图形,在图2,图3中各设计一个轴对称图形,要求如下:(1)每个图形由两个L 形三格骨牌组成,骨牌的顶点都在小正方形的顶点上.(2)设计的图形用斜线涂出,若形状相同,则视为一种.解:如图所示:.23.阅读下列材料分解因式:3416x x -小云的做法:原式3164x x =-①24(41)x x =-②4(21)(21)x x x =-+③小朵的做法:原式4x = 2(14)x -①4(14)x x =- (14)x +②小天的做法:原式x = 2(416)x -①22[2(4)]x x =-②(24)x x =- (24)x +③请根据上述材料回答下列问题:(1)小云的解题过程从 ① 步出现错误的,错误的原因是: .小朵的解题过程从 步出现错误的,错误的原因是: .小天的解题过程从 步出现错误的,错误的原因是: .(2)若都不正确,请你写出正确的解题过程.解:(1)小云的解题过程从①步出现错误的,错误的原因是:提取负号后,负号丢失,没弄清方程还是多项式;小朵的解题过程从②步出现错误的,错误的原因是平方差公式用错;小天的解题过程从③步出现错误的,错误的原因是:分解因式不完整还可以继续分解;(2)若都不正确,请你写出正确的解题过程.原式24(14)4(12)(12)x x x x x =-=-+.故答案为:(1)①,提取负号后,负号丢失,没弄清方程还是多项式;②,错误的原因是平方差公式用错;③,分解因式不完整还可以继续分解;24.已知30AOB ∠=︒,点P 在AOB ∠的内部,点C 和点P 关于OA 对称,点P 关于OB 的对称点是D ,连接CD 交OA 于M ,交OB 于N ,15CD =.(1)补全图,并且保留作图痕迹.(2)写出COD ∠= 60 ︒.PMN ∆的周长为 .解:(1)如图所示:(2)如图,连接OC ,OD ,OP ,Q 点C 和点P 关于OA 对称,点P 关于OB 的对称点是D ,AOC AOP ∴∠=∠,BOD BOP ∠=∠,2COD AOB ∴∠=∠,又30AOB ∠=︒Q ,60COD ∴∠=︒;AO Q 垂直平分CP ,BO 垂直平分PD ,PM CM ∴=,PN DN =,PMN ∴∆的周长15PM MN PN CM MN DN CD =++=++==.故答案为:60;15.25.通过整式乘法的学习,我们进一步了解了利用图形面积来说明法则、公式等的正确性的方法,例如利用图甲可以对平方差公式22()()a b a b a b +-=-给予解释.图乙中的ABC ∆是一个直角三角形,90C ∠=︒,人们很早就发现直角三角形的三边a ,b ,c 满足222a b c +=的关系.图丙是2002年国际数学家大会的会徽,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,弦图是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为a ,较长直角边长为b ,求出2()a b +的值.解:根据勾股定理可得2213a b +=,四个直角三角形的面积是:14131122ab ⨯=-=,即212ab =, 则222()2131225a b a ab b +=++=+=.故2()a b +的值为25.26.先化简,再求值:22112111t t t t t t t -+÷-+-+g ,其中2019t =. 解:原式2(1)(1)1(1)11t t t t t t t -+-=-++g g , 1t t =+, 当2019t =时,原式20192019201912020==+. 27.阅读下面材料:学习了三角形全等的判定方法(即“SAS ”“ ASA ”“ AAS ”“ SSS ” )和直角三角形全等的判定方法(即“HL ” )后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究小聪将命题用符号语言表示为:在ABC ∆和DEF ∆中,AC DF =,BC EF =,B E ∠=∠. 小聪的探究方法是对B ∠分为“直角、钝角、锐角”三种情况进行探究.第一种情况:当B ∠ 是直角时,如图1,ABC ∆和DEF ∆中,AC DF =,BC EF =,90B E ∠=∠=︒,根据“HL ”定理,可以知道Rt ABC Rt DEF ∆≅∆.第二种情况:当B ∠ 是锐角时,如图2,BC EF =,90B E ∠=∠<︒,在射线EM 上有点D ,使DF AC =,画出符合条件的点D ,则ABC ∆和DEF ∆的关系是 C ;A .全等B .不全等C .不一定全等第三种情况:当B ∠是钝角时,如图3,在ABC ∆和DEF ∆中,AC DF =,BC EF =,90B E ∠=∠>︒.过点C 作AB 边的垂线交AB 延长线于点M ;同理过点F 作DE 边的垂线交DE 延长线于N ,根据“ASA ”,可以知道CBM FEN ∆≅∆,请补全图形,进而证出ABC DEF ∆≅∆.解:第二种情况选C .理由:由题意满足条件的点D 有两个,故ABC ∆和DEF ∆不一定全等(如图所示)故选C .第三种情况补全图.证明:由CBM FEN ∆≅∆得,CM FN =,BD EN =又在Rt CMA ∆和Rt FND ∆中AC DF CM FN =⎧⎨=⎩, CMA FND ∴∆≅∆,AM DN ∴=,AB DE ∴=,又在ABC ∆和DEF ∆中AC DF BC EF AB DE =⎧⎪=⎨⎪=⎩,ABC DEF ∴∆≅∆.28.如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这个分式为“和谐分式”.(1)下列分式中, ④ 是和谐分式(填写序号即可); ①222()a b a b ++; ②2224t b t b--;③22x y x y +-;④2211m m -+ (2)若a 为整数,且214y y ay -++为和谐分式,请写出a 的值; (3)在化简22344m m n mn n n -÷-时, 小冬和小奥分别进行了如下三步变形: 小冬:原式22222323232232444444()()m m m m m n m mn n mn n n n mn n n mn n n --=-⨯=-=--- 小奥:原式22223222444444()()()m m m m m m m n mn n n n n m n n n m n --=-⨯=-=--- 显然,小奥利用了其中的和谐分式,第三步所得结果比小冬的结果简单,原因是: ,请你接着小奥的方法完成化简.解:(1)下列分式中,④是和谐分式(填写序号即可);(2)由214y y ay -++是和谐分式,可得24y ay ++能分解因式, a ∴的值是4或4-或5;(3)原因是:小奥利用和谐公式找的是最简公分母,所以通分后比小冬的简单, 接着小奥的方法完成化简,如下: 原式222232222444444()44()()()()m m m m m m m n mn m mn n n n n m n n n m n n m n n m n --=-⨯=-===-----. 29.在ABC ∆中,AD 平分BAC ∠交BC 于D ,MDN ∠的两边分别与AB ,AC 相交于M ,N 两点,且DM DN =.(1)如图甲,若90C ∠=︒,60BAC ∠=︒,9AC =,120MDN ∠=︒,//ND AB . ①写出MDA ∠= 90 ︒,AB 的长是 .②求四边形AMDN 的周长.(2)如图乙,过D 作DF AC ⊥于F ,先补全图乙再证明2AM AN AF +=.解:(1)①AD Q 平分BAC ∠,1302BAD CAD BAC ∴∠=∠=∠=︒, //ND AB Q ,30NDA BAD ∴∠=∠=︒,1203090MDA MDN NDA ∴∠=∠-∠=︒-︒=︒, 90C ∠=︒Q ,60BAC ∠=︒,30ABC ∴∠=︒, 12AC AB ∴=, 218AB AC ∴==,故答案为:90,18;②30ABC ∠=︒Q ,//ND AB ,30NDC ∴∠=︒,又120MDN ∠=︒Q ,30MDB ∴∠=︒,30MAD NAD ADN MBD ∴∠=∠=∠=∠=︒, BM MD ∴=,DN AN =,DM DN =Q ,BM MD DN AN ∴===,在Rt ADM ∆中,设MD x =,则2AM x =, BM MD DN AN x ====,18AB =Q ,318x ∴=,6x ∴=,12AM ∴=,6MD DN AN ===,∴四边形AMDN 的周长1266630AM MD DN AN =+++=+++=;(2)补全图如图乙所示:证明:过点D 作DE AB ⊥于E ,如图丙所示: DE AB ⊥Q ,DF AC ⊥,AD 平分BAC ∠, 90DEM DFN ∴∠=∠=︒,DE DF =,在Rt DEA ∆和Rt DFA ∆中,DE DF AD AD =⎧⎨=⎩, Rt DEA Rt DFA(HL)∴∆≅∆,AE AF ∴=,在Rt DEM ∆和Rt DFN ∆中,DE DF DM DN =⎧⎨=⎩, Rt DEM Rt DFN(HL)∴∆≅∆, EM FN ∴=,2AM AN AE EM AF NF AF ∴+=++-=.。
