四边形之间的关系 精品课件
四边形,梯形,平行四边形之间的关系

四边形,梯形,平行四边形之间的关系四边形,梯形,平行四边形之间的关系一、四边形的定义•四边形是由四条线段构成的几何图形。
•四边形的四个顶点可以是任意位置,并且四条边可以是任意长度。
•四边形的内部可以是凹四边形或凸四边形。
二、梯形的定义•梯形是一种特殊的四边形。
•梯形有两对平行边,其中一对边被称为底,另一对边被称为腰。
•梯形的底边上的两个角分别被称为底角,非底边上的两个角分别被称为顶角。
三、平行四边形的定义•平行四边形是一种特殊的四边形。
•平行四边形的对边是平行的。
•平行四边形的对边长度相等。
四、四边形、梯形和平行四边形之间的关系•梯形是四边形的一种特殊情况,即梯形也是四边形的一种。
•平行四边形也是四边形的一种特殊情况,即平行四边形也是四边形的一种。
•但是,不是所有的四边形都是梯形或平行四边形。
五、总结•四边形是一个普遍的几何图形,具有多种形状和性质。
•梯形是具有特殊性质的四边形,它有两对平行边。
•平行四边形也是具有特殊性质的四边形,它的对边是平行的且长度相等。
•了解四边形、梯形和平行四边形之间的关系,有助于我们理解和应用几何学中的基本概念和性质。
六、四边形、梯形和平行四边形的性质比较四边形梯形平行四边形定义由四条线段构成的几何图形有两对平行边的四边形对边平行且长度相等的四边形形状可以是任意形状可以是任意形状,但有两对平行边平行四边形的边与角分布均匀、对称特殊性质可以是凹四边形或凸四边形有两对平行边,但不一定具有其他特殊性质对边平行且长度相等,对角度相等子集关系所有梯形都是四边形平行四边形是一种梯形,但不是所有梯形都无四边形梯形平行四边形是平行四边形应用举例房屋、车辆、物体等的外形都可以是四边形斜坡、天平等的形状可以是梯形网格、棋盘、标志等常见的平行四边形形状总结:四边形是一个普遍的几何图形,可包括梯形和平行四边形。
梯形具有两对平行边的特殊性质,而平行四边形具有相等且平行的对边。
通过了解它们之间的关系和性质,我们可以更好地理解和应用几何学中的概念。
四边形之间的关系
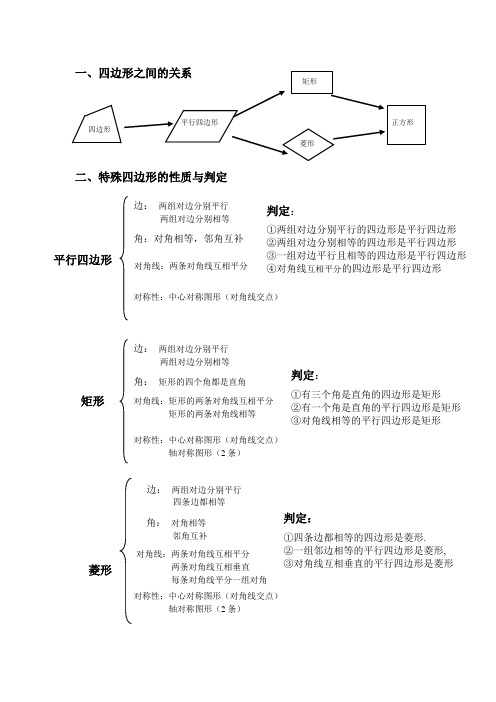
二、特殊四边形的性质与判定四边形正方形边: 两组对边分别平行 两组对边分别相等 角: 矩形的四个角都是直角对角线:矩形的两条对角线互相平分 矩形的两条对角线相等 对称性:中心对称图形(对角线交点) 轴对称图形(2条) 矩形 菱形 边: 两组对边分别平行四条边都相等角: 对角相等邻角互补 对角线:两条对角线互相平分 两条对角线互相垂直 每条对角线平分一组对角 对称性:中心对称图形(对角线交点) 轴对称图形(2条) 判定: ①有三个角是直角的四边形是矩形②有一个角是直角的平行四边形是矩形③对角线相等的平行四边形是矩形判定: ①四条边都相等的四边形是菱形. ②一组邻边相等的平行四边形是菱形, ③对角线互相垂直的平行四边形是菱形 边: 两组对边分别平行 两组对边分别相等 角:对角相等,邻角互补对角线:两条对角线互相平分 对称性:中心对称图形(对角线交点) 平行四边形 判定: ①两组对边分别平行的四边形是平行四边形 ②两组对边分别相等的四边形是平行四边形 ③一组对边平行且相等的四边形是平行四边形 ④对角线互相平分的四边形是平行四边形三.中点四边形:对角线 的四边形的中点四边形是平行四边形 对角线 的四边形的中点四边形是菱形 对角线 的四边形的中点四边形是矩形 对角线 的四边形的中点四边形是正方形 (1) 顺次连接四边形各边中点所得的四边形是 . (2) 顺次连接平行四边形各边中点所得的四边形是 . (3) 顺次连接矩形各边中点所得的四边形是 . (4) 顺次连接菱形各边中点所得的四边形是 . (5) 顺次连接正方形各边中点所得的四边形是中点四边形的面积和原来的四边形的面积有什么关系?中点四边形的周长和原来的四边形的什么量有直接关系?正方形边: 两组对边分别平行四条边都相等 角: 四个角都是直角对角线:两条对角线互相平分 两条对角线相等两条对角线互相垂直 每条对角线平分一组对角对称性:中心对称图形(对角线交点) 轴对称图形(4条) 判定:有一组邻边相等的矩形是正方形. 有一个角是直角的菱形是正方形. ①对角线相等的菱形是正方形②对角线互相垂直的矩形是正方形.③对角线互相垂直,平分,相等的四边形是正方形第4~5章特殊四边形的知识点复习表1各四边形的性质表2各四边形的判定方法3.画出四边形,平行四边形,矩形,菱形,正方形之间的关联图.。
《平行四边形和梯形》课件(共18张PPT)四年级上册数学人教版

视察与思考
下面的图形哪些是平行四边形,哪些是梯形?
平行四边形( ① ② ⑥ ⑧ ) 梯形( ④ ⑤ )
视察与思考
四边形之间的关系:
平行四边形 长方形 正方形
梯形 四边形
我们可以用左面的图 来表示四边形之间的
关系
长方形和正方形是特殊的平行四边形。
视察与思考
做一做,想一想。
我发现平行四边形容易变 形,具有不稳定性。
智力大比拼
做一做: 1. 说一说日常生活中应用平行四边形容易变形这一特性的例子. 2. 画出下面两个图形的高.
智力大比拼
做一做: 1. 说一说日常生活中应用平行四边形容易变形这一特性的例子. 2. 画出下面两个图形的高.
智力大比拼
判断:对的做“√”,错的做“×” :
× 1. 两组对边分别平行的图形是平行四边形。
视察与思考
做一做,想一想。
高 底
从平行四边形一条边上的一点 到对边引一条垂线,这点和垂 足之间的线段叫做平行四边形 的高,垂足所在的边叫做平行
四边形的底。
视察与思考
做一做,想一想。
上底
腰
高
来给梯形的各部分起 个名字吧!
腰
下底
两腰相等的梯形叫做等腰梯形。
智力大比拼
做一做: 1. 说一说日常生活中应用平行四边形容易变形这一特性的例子. 2. 画出下面两个图形的高.
平行四边形和梯形
2. 有一组对边平行的四边形是梯形。
×
3. 平行四边形的两组对边分别平行并且相等。√
4. 长方形、正方形都是特殊的平行四边形。 √
智力大比拼
从右面图形中找出平行四 边形和梯形,并画出它们 的高.
梯形
平行四边形
人教版四年级数学上册《认识梯形、四边形间的关系》优秀课件

认识梯形
谢谢观看!
认识梯形
认识梯形、四边形间的关系
复习导入
探究新知
课堂练习
课堂小结
课后作业
认识梯形
复习导入
例3
你见过下面这样 的图形吗?
它们有什么 共同点?
认识梯形
探究新知
认识梯形
认识梯形
认识梯形
通过观察图形,你有什么发现?
只有一组对边平行的四边形叫做梯形。
认识梯形
梯形各部分名称叫什么?
上底
腰高
腰
下底
认识梯形
平行四边形 长方形 正方形
梯形 四边形
认识梯形
课堂练习
1.下面哪些图形是梯形?画出每个梯形的高,分 别指出它们的上底、下底和腰。
梯形 梯形
梯形
认识梯形
2.请将这张平行四边形的纸剪成两个一样的梯形。
认识梯形
课堂小结
这节课你们都学会了哪些知识? . 只有一组对边平行的四边形叫做梯形。
认识梯形
课后作业
有哪些特殊的梯形?
等腰梯形 两腰相等的梯形叫做等腰梯形。
认识梯形
有哪些特殊的梯形?
直角梯形 有一个角是直角的梯形叫做直角梯形。
认识梯形
例题4
我们认识了哪些四边形?
我们认识了长 方形、正方形、 平行四边形和 梯形。
长方形和正 方形可以看 成特殊的平 行四边形吗? 为什么?
认识梯形
我们可以用下面的图来表示四边形 之间的关系。
四边形之间的关系

示例
多个动作连动
公司角色与定位
全面 产品与服务与提供者
技术与产品供应商 应用集成商
信息服务运营商
课程内容
创建演示文稿 修饰幻灯片 幻灯片连接
放映设置和打印
幻灯片的连接
• 串连(要制作完整的PowerPoint演示文
稿 ,要将单张幻灯片连接起来,似“串珍 ★珠思”路)。: 散串性:单张幻灯片的内容可以是独立 的,需要通过线索把这些“珍珠”串起 来。
➢ 12字真言:“能用图,不用表;能用表,不
不断循环渐进的过程
目标
示例
评估与检查
宗旨
计划时间表
共同计划
计划要素分解
部门间协作互动
以项目为部门间线索驱动的横向沟通配合
示例
打破部门之间[筒仓]结构 强调部门间协作互动关系
项目1 项目2
项目3
......
项目N
部门A
部门B
部门C
…...
回顾
我想知道…
• 文本(字体、字间距、横、竖、项目符号)
基本图形运用
插入图片
• 图形制作
图表运用(看差距用柱状图、看百分比用饼状图) 对象(声音或影视文件)
示例
三维效果
• 单击〔样式〕按钮,选择“三维设置”命令,即 可打开“三维设置”工具栏,栏上的每个按钮都 有特定的功能 。
图表运用
2007年销售分布
7%
2%
★插入动画﹑超链接 、连动效果、先后顺
序
★绘图:形象化图形:
•基本图形 •图片 •图表 •对象...
修饰:
•二维/三维 •阴影 •边框 •色彩
绘图: •组合 •叠放次序 •旋转
2023年人教版数学四年级上册第6课时 四边形之间的关系课件优选课件

►为你理想的人,否则,爱的只是你在他身上找到的你的影子。 ►有时候,我们愿意原谅一个人,并不是我们真的愿意原谅他,而是我们 不愿意失去他。不想失去他,惟有假装原谅他。不管你爱过多少人,不管 你爱得多么痛苦或快乐。最后,你不是学会了怎样恋爱,而是学会了,怎 样去爱自己。
►A man is not old as long as he is seeking something. A man is not old until regrets take the place of dreams. 只要一个人还有追求,他就没有老。直到后悔取代了梦想,一个人才 算老。 ►Bad times make a good man. 艰难困苦出能人。 ►Life is a path winding in the mountain, bumpy and zigzagging. 生活是蜿蜒在山中的小径,坎坷不平。
发现:这些图形的四个角的度数和都是360°。
4. 用长方形纸剪出一个平行四边形。
四边形之间的关系:
►如果我们不曾相遇,你的梦里就不会有我的出现,我们都在不断地 和陌生人擦肩;如果人生不曾相遇,我的生命里就不会有你的片段, 我们都在细数着自己的日子。 ►当离别的脚步声越来越清晰,我们注定分散两地,继续彼此未完的 人生,如果我说放不下,短短一个月的光景,你是否愿意相信,我的 真诚,我的执着,只源于内心深处那一份沉沉的不舍。
5 平行四边形和梯形
第6课时 四边形之间的关系
优 翼
我们认识了哪些四边形?
我们认识了长方形、正方形、 平行四边形和梯形。
长方形和正方形可以看成特殊的 平行四边形吗?为什么?
我们可以用下面这样的图来表示四边形之 间的关系。
平行四边形 长方形 正方形
平行四边形性质及定理PPT课件

的平衡和美感。
图案设计
02
平行四边形在图案设计中也有广泛应用,如纺织品、壁纸、地
毯等的设计。
舞台布景和道具设计
03
在舞台布景和道具设计中,平行四边形也常被用于创造视觉效
果和空间感。
THANKS FOR WATCHING
感谢您的观看
一组对边平行
总结词
如果一个四边形中有一组对边平 行,则该四边形是平行四边形。
详细描述
这是平行四边形的一个基本判定 定理。如果一个四边形的对边平 行,则这个四边形必然是平行四 边形。
一组对边相等
总结词
如果一个四边形中有一组对边相等, 则该四边形是平行四边形。
详细描述
这也是平行四边形的一个基本判定定 理。如果一个四边形的对边相等,则 这个四边形必然是平行四边形。
窗户和门的形状设计
平行四边形因其独特的对边平行和相 对边相等的特性,常被用于创造空间 感和视觉效果。
窗户和门的形状设计经常采用平行四 边形,以实现采光和通风的最佳效果。
建筑结构的稳定性
平行四边形的对角线互相平分,这使 得它在建筑结构设计中具有稳定性, 如桥梁、房屋的支撑结构等。
机械设计中的应用
机械零件的形状设计
平行四边形性质及定理ppt课件
contents
目录
• 平行四边形的基本性质 • 平行四边形的判定定理 • 特殊平行四边形 • 平行四边形在实际生活中的应用
01 平行四边形的基本性质
对边平行
总结词
平行四边形的对边是平行的。
详细描述
这是平行四边形的基本性质之一,即相对的两条边是平行的,不会相交于一点。
直角三角形斜边中线定 理,矩形的对角线相等
且互相平分。
四年级上册数学课件认识梯形四边形间的关系人教版

2.请将这张平行四边形的纸剪成两个一样的梯形。
四年级上册数学课件58认识梯形、四 边形间 的关系 人教版1 5
返回
认识梯形、四边形间的关系
课堂小结
这节课你们都学会了哪些知识? . 只有一组对边平行的四边形叫做梯形。
返回
认识梯形、四边形间的关系
课后作业 1.从教材课后习题中选取; 2.从课时练中选取。
有哪些特殊的梯形?
直角梯形 有一个角是直角的梯形叫做直角梯形。
四年级上册数学课件58认识梯形、四 边形间 的关系 人教版1 5
返回
四年级上册数学课件58认识梯形、四 边形间 的关系 人教版1 5
认识梯形、四边形间的关系
例题4 我们认识了哪些四边形?
我们认识了长 方形、正方形、 平行四边形和 梯形。
人教版 数学 四年级 上册
5 平行四边形和梯形
认识梯形、四边形间的关系
情境导入
探究新知
课堂练习
课堂小结
课后作业
认识梯形、四边形间的关系
情境导入
例题3
你见过下面这样 的图形吗?
它们有什么 共同点?
返回
认识梯形、四边形间的关系
探究新知
返回
认识梯形、四边形间的关系
返回
认识梯形、四边形间的关系
返回
四年级上册数学课件58认识梯形、四 边形间 的关系 人教版1 5
平行四边形 长方形 正方形
梯形 四边形
返回
四年级上册数学课件58认识梯形、四 边形间 的关系 人教版1 5
认识梯形、四边形间的关系
课堂练习
1.下面哪些图形是梯形?画出每个梯形的高,分 别指出它们的上底、下底和腰。
四年级上册数学课件58认识梯形、四 边形间 的关系 人教版1 5
人教版四年级上册数学《四边形间的关系》(课件)

创设情境 探究新知 巩固练习 课堂小结 布置作业
你有什么收获?
四边形间的关系:
(平行四边形) ( 长方形)
(正方形)
(梯形)
四边形
创设情境 探究新知 巩固练习 课堂小结 布置作业
教材P68第8、9题。
再见
(2)梯形是特殊的四边形 。
(√ )
(3)两个完全相同的梯形一定能拼成一个长方形。(×)
创设情境 探究新知 巩固练习 课堂小结 布置作业
2.选一选。
(A) ( D ) 平行四边形
(C )
长方形
正方形
四边形
( B ) 梯形
A.四个角都是直角 C.四条边的长度都相等
B.只有一组对边平行 D.两组对边分别平行
正方形
平行四边形
梯形
创设情境 探究新知 巩固练习 课堂小结 布置作业
巩固特征
在下表中的适当空格内填上“√”,再说一说 几种图形之间的联系和区别。
√
√
√
√
√
√
√
√
√
√
创设情境 探究新知 巩固练习 课堂小结 布置作业
自主探索
如果用下图表示四边形之间的关系,那么四边形、 长方形、正方形、平行四边形和梯形,分别在哪个圈里?
四边形间的关系
第五单元 平行四边形和梯形
四
学习目标
边
形
✓ 通过分类、比较、归纳等多种方法,理解平行四边 形、梯形、正方形、长方形之间的关系。
间
✓ 培养分类思考、推理能力,发展空间观念。
的
关
准备好了吗?一起去探索吧!
系
创设情境 探究新知 巩固练习 课堂小结 布置作业
我们已经认识了哪些四边形?
第6课时 四边形之间的关系

第5单元平行四边形和梯形第6课时四边形之间的关系【教学内容】:教材第66页例4。
【教学目标】:巩固平行四边形和梯形的概念及特征,探讨学过的几种四边形之间的关系,并会用集合图表示。
【重点难点】:理解和掌握平行四边形、长方形、正方形之间的关系。
【教学过程】:一、创设情境1.我们认识了哪些四边形?2.这些图形各有什么特点?指名回答后,继续提问。
3.长方形和正方形可以看成是特殊的平行四边形吗?这些图形之间有什么样的关系呢?这就是我们要探讨的问题。
(板书课题:四边形之间的关系)二、自主探究1.出示例4。
根据学生前面的回答,出示几个不同的四边形。
2.探讨图形之间的关系。
师:同学们,每一个图形都有自己的特点,请你仔细观察一下,这几个图形之间又有什么联系呢?学生回答长方形、正方形和平行四边形的共同之处。
教师演示:一个平行四边形框,手拿它的两个对角拉动它,边拉边问是什么图形,继续拉到四个角变为直角的位置。
问学生:现在是什么形状?师:有同学说是长方形,有同学说是平行四边形,那我们一起来看:平行四边形两组对边分别互相平行,现在这个图形的两组对边分别互相平行吗?师:它符合平行四边形的特点,它就是平行四边形,只不过它比起刚才的平行四边形特殊了一点,你知道它特殊在哪儿吗?学生回答出角的特点,四个角都是直角。
师:这种特殊的平行四边形叫做长方形,现在你知道长方形和平行四边形的关系吗?长方形是特殊的平行四边形。
(用同样的方法让学生发现正方形和长方形之间的关系)师:同学们通过观察、思考,理解了正方形、长方形、平行四边形、梯形之间的关系,我们能不能用一种形式清楚地表示出来呢?请大家想一想。
学生用各种形式表示:语言叙述、画图表示……师:大家一起来看(点击课件),我们就可以把四边形看成是一个大家庭,但其中不仅仅包括这四种图形,还有任意四边形。
教师用集合图的形式表示这些图形之间的相互关系,你有什么问题吗?用语言叙述他们之间的关系。
课件出示:3.巩固练习:教材“练习十一”第8题。
四边形ppt课件

02 四边形的周长和面积
周长的计算
总结词
周长是指一个封闭图形的边的总长度 。
详细描述
对于四边形,周长的计算公式是四条 边的长度之和。假设四边形的四条边 分别为a、b、c和d,则周长 P=a+b+c+d。
面积的计算
总结词
面积是指一个封闭图形所占的二维空间大小。
详细描述
对于四边形,其面积的计算方法有多种,其中一种是使用海伦公式。假设四边形的四个顶点坐标分别 为(x1, y1)、(x2, y2)、(x3, y3)和(x4, y4),则面积A=s(s-a)(s-b)(s-c),其中s=(a+b+c)/2,a、b、c 分别为三条边的长度。
四边形的面积和周长的计算公式在几何学中非常重要,是解决各种 几何问题的关键。
对称性和稳定性研究
四边形具有多种对称性,其稳定性在建筑和结构设计中有重要应用 。
在日常生活中的应用
建筑结构
四边形的稳定性使其成为 建筑设计和施工中的重要 元素,如墙角、窗户和门 框等。
家具设计
许多家具的框架和结构都 采用四边形,如桌子、椅 子、床等。
03
对角线互相平分
四边形中的对角线互相平 分,将四边形分成两个相 等的三角形。
对角线互相垂直
在菱形和正方形中,对角 线互相垂直,且长度相等 。
对角线相等
在矩形和正方形中,对角 线长度相等。
对角线的长度计算
使用勾股定理
对于直角三角形,可以使用勾股定理计 算对角线的长度。
VS
计算三角形的面积
先计算与对角线相关的三角形面积,再乘 以2,再开方得到对角线长度。
03 四边形的内角和外角
内角和的定义及计算
四边形之间的关系ppt课件
判断:对的打 “√”,错的打 “×”。 1、两组对边分别平行的图形是平行四边形。( ) 反例 :
怎样改?
2、有一组对边平行的四边形是梯形。( ) 怎样改? 只有一组。
火灾袭来 时要迅 速疏散 逃生, 不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
自学指导(二)
1、请把这些四边形分分类。说说你为什么这样分? 2、小组内交流你的分类方法。 A:①②⑥⑧ B:④⑤ C:③⑦
火灾袭来 时要迅 速疏散 逃生, 不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
自学指导(三)
自学书66页例4,对照集合图说一说: 1、长方形、正方形、平行四边形之间的关系。 2、长方形、正方形、平行四边形、梯形、四边形之
学习目标
1、进一步掌握平行四边形和梯形的特征。 2、认识各种四边形之间的关系。
Hale Waihona Puke 火灾袭来 时要迅 速疏散 逃生, 不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
自学指导(一)
1、说说平行四边形的特征。 两组对边分别平行且相等,两对角分别相等。
3、平行四边形的两组对边分别平行并且相等。( ) 4、长方形、正方形都是特殊的平行四边形。( ) 5、两个完全一样的梯形可以拼成一个平行四边形( )
火灾袭来 时要迅 速疏散 逃生, 不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
课堂小结
2、说说梯形的特征。 只有一组对边平行的四边形
3 、说说长方形的特征。 两组对边平行且相等,四个角都是直角。
四边形边长之间的关系

四边形边长之间的关系
稿子一:
嘿,亲爱的小伙伴们!今天咱们来聊聊四边形边长的那些事儿。
你看啊,四边形就像一个大家庭,四条边就像是家里的兄弟姐妹。
它们之间的关系可有趣啦!
先说平行四边形吧,它的对边那叫一个友好,长度相等,就像双胞胎一样整整齐齐的。
这对边啊,不管四边形怎么变形,它们的长度都不会变,可忠诚啦!
再看看矩形,不仅对边相等,而且四个角都是直角,这就好像家里有严格的规矩一样,边长都得规规矩矩的。
菱形呢,它的四条边都相等,就像四胞胎一样,谁也不比谁特殊,简直太公平啦!
还有梯形,它的两条底边长度可不一定一样哦,一长一短,就像家里有个大哥哥和小弟弟。
四边形的边长关系多种多样,每个四边形都有自己的特点,就像我们每个人都有自己的个性一样。
是不是很有意思呀?
稿子二:
嗨呀,朋友们!咱们来唠唠四边形边长的关系。
你想啊,四边形就像一个神秘的小世界。
比如说正方形,那四条边简直就是一模一样的四胞胎,长度完全相同,而且每个角都是 90 度,规规矩矩的超可爱。
长方形呢,对边长度相等,就像是两个双人组合,两两相同,特别和谐。
普通的四边形就比较调皮啦,四条边想多长就多长,没有什么固定的规律,完全看它自己的心情。
而等腰梯形呢,两条腰长度相等,就像两个小伙伴手拉手,不离不弃。
还有一些不规则的四边形,边长那叫一个随心所欲,有的长有的短,凑在一起组成了一个独特的小团体。
所以说呀,四边形边长的关系真是丰富多彩,每一种四边形都有自己的小秘密和独特之处,等着我们去发现呢!怎么样,是不是觉得很有趣?。
平行四边形和梯形四边形间的关系-完整版课件

√ √
四、将两张长方形纸,或长方形和三角形纸随意交叉摆放,重叠部分是什么 图形?
五、将下面的图形改成平行四边形。
372-98= 274 23×20= 460 20×7+50= 190
634+101= 735 40×3+8= 128 84÷4+84= 105
21×9= 189 7+3×60= 187
金榜行动 上册
5 平行四边形和梯形
第7课时 四边形间的关系
一、我会选。
1.三角形具有( A ),平行四边形( B )。
A.稳定性
B.容易变形
C.对边平行
2.平行四边形有( B )对边分别平行。
A.1 组
B.2 组
C.3 组
3.一个梯形的上底与下底间的距离( A )。
A.相等
B.不相等
C.不一定相等
4.一个四边形,只有一组对边平行,两个底角相等,它是( C )。
A.长方形
B.平行四边形
C.等腰梯形
二、我会填。 1.
2.画出下面两个图形指定底边上的高,并填空。 平行四边形一条底边上的高有( 无数 )条,这些高的长度( 相等 )。 梯形的高有( 无数 )条,这些高的长度( 相等 )。
三、找出对称的四边形,在( )里打“√”。
第6课时 四边形之间的关系

第5单元平行四边形和梯形第6课时四边形之间的关系【教学内容】:教材第66页例4【教学目标】:巩固平行四边形和梯形的概念及特征,探讨学过的几种四边形之间的【重点难点】:【教学过程】:1.2.3.长方形和正方形可以看成是特殊的平行四边形吗?这些图形之间(板书课题1.出示例42.师:同学们,每一个图形都有自己的特点,请你仔细观察一下,这几教师演示:一个平行四边形框,手拿它的两个对角拉动它,边拉边问是什么图形,继续拉到四个角变为直角的位置。
问学生:现在是什么师:有同学说是长方形,有同学说是平行四边形,那我们一起来看:平行四边形两组对边分别互相平行,现在这个图形的两组对边分别互师:它符合平行四边形的特点,它就是平行四边形,只不过它比起刚师:这种特殊的平行四边形叫做长方形,现在你知道长方形和平行四师:同学们通过观察、思考,理解了正方形、长方形、平行四边形、梯形之间的关系,我们能不能用一种形式清楚地表示出来呢?请大家学生用各种形式表示:语言叙述、画图表示师:大家一起来看(点击课件),我们就可以把四边形看成是一个大家庭,但其中不仅仅包括这四种图形,还有任意四边形。
教师用集合图的形式表示这些图形之间的相互关系,你有什么问题吗?用语言叙3.巩固练习:教材“练习十一”第81.教材“练习十一”第9学生动手摆一摆,小组内互相说一说,重叠的部分是什么图形?有没有不同的意见?2.教材“练习十一”第10先说说各是什么图形,再量出各图形中每个角的度数,并填表,你发学生动手测量,小组内合作完成,检查交流测量结果,再议一议:发四边形四个角的度数和是3603.教材“练习十一”第14*图中有哪些我们学过的图形?每种图形有几个?看谁最细心,数得又4.教材“练习十一”第11、12、13这节课你有什么收获?。
【精品课件教案PPT】 四边形之间的关系22页PPT

【精品课件教案PPT】 四边形之间的 关系
16、人民应该为法律而战斗,就像为 了城墙 而战斗 一样。 ——赫 拉克利 特 17、人类对于不公正的行为加以指责 ,并非 因为他 们愿意 做出这 种行为 ,而是 惟恐自 己会成 为这种 行为的 牺牲者 。—— 柏拉图 18、制定法律法令,就是为了不让强 者做什 么事都 横行霸 道。— —奥维 德 19、法律是社会的习惯和思想的结晶 。—— 托·伍·威尔逊 20、人们嘴上挂着的法律,其真实含 义是财 富。— —爱献 生
46、我们若已接受最坏的,就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会,使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首,不会作诗也会吟。——孙洙 50、谁和我一样用功,谁就会和我一样成功。——莫扎特
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
义务教育人教版四年级上册
5 平行四边形和梯形
四边形之间的关系
优 翼
探究新知 (教材第66页例4) 知识点:四边形之间的关系
4 我们认识了哪些四边形?
我们认识了长方形、正方 形、平行四边形和梯形。
长方形和正方形可以看成特 殊的平行四边形吗?为什么?
探究新知
我们可以用下面这样的图来表示四边形之间的 关系。
1 2 3 4.
321
1234
(答案不唯一,合理即可。)
实践应用 (教材“练习十一”第13题) 6. 用七巧板拼一拼。 (1)用其中的两块拼一个梯形。 (2)用其中的三块拼一个平行四边形。 (3)用其中的四块拼一个等腰梯形。
(答案不唯一, 合理即可。)
课堂小结
只有一组对边平行的四边形叫做梯形。
拓展练习
平行四边形
长方形 正方形
梯形 四边形
巩固练习 (教材“练习十一”第8题)
1. 下面的说法对吗?对的在( )里画“√”。
长方形也是两组对边分别平行的四边形
(1)长方形也是平行四边形。
(√ )
平行四边形是两组对边分别平行的四边形
(2)平行四边形是特殊的梯形。
(×)
梯形是一组对边分别平行的四边形
(3)两个完全相同的梯形可以拼成一个长方形。( × )
直角
实践应用 (教材“练习十一”第9题)
2. 将两张长方形纸随意交叉摆放,或将长方形纸 和三角形纸随意交叉摆放,重叠的部分是什么图形?
两组对边分别平行的 四边形是平行四边形。
两组对边分别平行的 四边形是平行四边形。
实践应用 (教材“练习十一”第9题)
2. 将两张长方形纸随意交叉摆放,或将长方形纸 和三角形纸随意交叉摆放,重叠的部分是什么图形?
数一数,下面的图形中有哪些互相平行 的线段?有哪些互相垂直且相交的线段?
互相平行:AB∥CE AE∥BD AC∥ED AE∥BC AE∥CD 互相垂直:AB⊥BC BC⊥EC CE⊥EA EA⊥AB AC⊥BE BE⊥ED AB⊥BD CE⊥CD CE⊥BD
课后作业
1.从课后习题中选取; 2.完成练习册本课时的习题。
一组对边平行的 四边形是梯形。
一组对边平行的 四边形是梯形。
实 践 应 用 (教材“练习十一”第10题)
3. 量出下面各图形中每个角的度数,再填写下表。
90º
①
90º
90º
120º
60º
②
90º 60º
120º
70º
70º
③
110º 110º
90º 90º
④
90º 90º
84º
39º
⑤
87º15Leabharlann º图形各个角的度数
四个角的 和360º
① 90º 90º 90º 90º
360º
② 60º 120º 60º 120º
360º
③ 110º 110º 70º 70º
360º
④ 90º 90º 90º 90º
360º
你⑤发现了8什7么º ?1再50任º意8画4一º个四39边º形试一试,你会
得到同样的结论吗? 四边形的内角和是360º。
实践应用 (教材“练习十一”第11题) 4. 用长方形纸剪出一个平行四边形。
.
. 将长方形纸对折,找到长的中点。 两中点分别与左右对角的端点连接,剪下即可。
答案不唯一,合理即可。
实践应用 (教材“练习十一”第12题)
5. 下面的图形是平行四边形吗?怎样改才能成为平行 四边形? 不是。
.3 2 1
