复合函数单调性
复合函数及抽象函数的单调性

复合函数的单调性复合函数的定义:设y=f(u)定义域A ,u=g(x)值域为B ,若A B ,则y 关于x 函数的y=f[g(x)]叫做函数f 与g 的复合函数,u 叫中间量复合函数的单调性复合函数的单调性由两个函数共同决定;引理1:已知函数y=f[g(x)],若u=g(x)在区间(a,b)上是增函数,其值域为(c,d),又函数y=f(u)在区间(c,d)上是增函数,那么,原复合函数y=f[g(x)]在区间(a,b)上是增函数。
引理2:已知函数y=f[g(x)],若u=g(x)在区间(a,b)上是减函数,其值域为(c,d),又函数y=f(u)在区间(c,d)上是减函数,那么,原复合函数y=f[g(x)]在区间(a,b)上是增函数。
若u=g(x)y=f(u)则y=f[g(x)]规律:当两个函数的单调性相同时,其复合函数是增函数;当两个函数的单调性不相同时,其复合函数是减函数。
“同增异减”例2. 已知f ( x )=-x2 + 2x + 8,g ( x ) = f ( 2-x 2 ),求g ( x )的单调增区间.的单调区间。
:求函数例29121)(1x x f --=抽象函数例1:设f(x)是定义在实数集R 上的奇函数,且在区间(-∞,0)上是增函数,又f(2a2+a+1)<f(3a2-2a+1),试求a 的取值范围。
问:设f(x)是定义在实数集R 上的奇函数,且在区间(-∞,0)上是增函数,问在 区间(0,+∞)上f(x)是 增函数还是减函数?例2:设f(x)是定义在实数集R 上的偶函数,且在区间(-∞,0]上是增函数,又f(2a2+a+1)<f(3a2-2a+1),试求a 的取值范围。
.2)3()()4()()()3()()()()2(1)2()1()(2的取值范围求时,满足:上的函数:定义在例x x f x f y f x f y x y f x f xy f f x f R ≤-+<>+==+.)().()()(,,1)(0)(3上的增函数是求证:有、且对于任意时,上,当定义在:函数例R x f b f a f b a f R b a x f x R x f =+∈>>例4:.]1,2[)(,2)1(,0)(),()()(,)(上的值域在区间求时,且当均有、对于任意实数已知函数--=->>+=+xffxfxyfxfyxfyxxf.,9)1()3(.),0()()2.()()1().1,0()(1,9)27(,1)1()()()()(53的取值范围求且若上的单调性,并证明在判断的奇偶性判断时当且都有、对任意实数:已知函数例aafaxfxfxfxffyfxfxyfyxxf≤+≥+∞∈<<==-=复合函数的单调性小结复合函数y=f[g(x)]的单调性可按下列步骤判断:(1) 将复合函数分解成两个简单函数:y=f(u)与u=g(x)。
复合函数的单调性

练习.求函数y 3x2x6的单调递减区间。
解:函数f (x)的定义域是 R。
令u
x2
x
6
x
1
2
13
, 则y
3u
2 2
y 3u 在定义域内是增函数。
又u
x
1 2
2
13 2
在
,
1 2
上是减函数,在
1 2
,上是增函数。
y
3x2
x6
在
,
1 2
上是减函数,在
1 2
,
上是增函数。
y
3x2
复合函数y=f[g(x)]单调性
3、对于复合函数y f [g(x)]的单调性,必须考虑y f (u)与 u g(x)的单调性,从而得出y f [g(x)]的单调性。
y f (u)
增函数
u g(x)
增函数
y f [g(x)] 法
增函数
则
增函数
减函数
减函数
同
减函数
增函数
减函数
增
减函数
减函数
又u x 22 1在2,3上是减函数。
y x2 4x 3在2,3上是减函数。
故函数y x2 4x 3的单调递减区间为2,3。
(问:函数y x2 4x 3的单调递增区间是什么?)
例4.求f (x) log x2 4x 3 的单调区间。 0.4 解: x2 4x 3 0 1 x 3,即定义域为1,3 令u x2 4x 3 x 22 1,
增函数
异
规律:当两个函数的单调性相同时,其复合函数是增函数; 减
当两个函数的单调性不相同时,其复合函数是减函数。
例1、求函数y x2 2x-3的单调区间。
复合函数单调性

复习:
减函数:若对于定义域内某个区间上的任意两个自变量
的值x1,x2,当x1<x2时,都有f( x1 )>f ( x2 ),则就说f(x)在这个区间上是减函 数。
单调性与单调区间:
如果函数y=f(x)在某个区间上是增函数或者减函数, 则说函数y=f(x)在这一区间上具有严格的单调性, 这一个区间叫做函数y=f(x)的单调区间
学习目的:
进一步掌握函数单调性的判定和证明 了解复合函数单调性的判断和证明 复合函数单调性的判断方法
重点难点: 重点: 证明函数单调性的方法和步骤 难点: 复合函数单调性的判断方法
若对于定义域内某个区间上的任意两个自变量 增函数:的值x1,x2,当x1< x2时,都有f( x1 )<f ( x2 ),则就说f(x)在这个区间上是增函 数。
例1: 已知函数f(x)在R上是增函数, g(x)在[a,b]上是减函数, 求证:f[g(x)]在[a,b]上是减函数.
证明:设x1,x2∈[a,b],且x1<x2,
∵g(x)在[a,b]上单调递减, ∴g(x1) >g(x2), 又f(x)在R上递增, 而g(x1)∈R,g(x2)∈R, ∴f[g(x1)]>f[g(x2)], ∴f[g(x)]在[a,b]上是减函数.
规律如下:
y=f(u) 增↑ u=g(x) 增↑ 减↓ y=f[g(x)] 增↑ 减 ↓
减↓ 增↑ 减↓ 减↓ 增↑
注:
1、复合函数y=f[g(x)]的单调区 间必须是其定义域的子集 2、对于复合函数y=f[g(x)]的单 调性是由函数y=f(u)及u=g(x)的 单调性确定的且规律是“同增, 异减”
复习:
判断函数在某个区间上的单调性的 步骤:
(完整版)复合函数单调性的判定方法

复合函数单调性的判定方法定理设y=f(u),u∈(m,n),u=g(x),x∈(a,b).(1)若y=f(u)是(m,n)上的减函数,则y=f[g(x)]的增减性与g(x)的增减性相反;(2)若y=f(u)是(m,n)上的增函数,则y=f[g(x)]的增减性与g(x)的增减性相同.证明:(1)若g(x)在(a,b)上是增函数,任取a<x1<x2<b,则有m<g(x1)<g(x2)<n,由f(u)在(m,n)上是减函数得f[g(x1)]>f[g(x2)],故f[g(x)]在(a,b)上是减函数.若g(x)在(a,b)上是减函数,同理可证f[g(x)]在(a,b)上是增函数.(2)若g(x)在(a,b)上是增函数,任取a<x1<x2<b,则有m<g(x1)<g(x2)<n,由f(u)在(m,n)上是增函数,得f[g(x1)]<f[g(x2)],所以f[g(x)]在(a,b)上是增函数.若g(x)在(a,b)上是减函数,同理可证f[g(x)]在(a,b)上是减函数.由此定理可知,复合函数单调性的判定是以简单函数的单调性为基础,而中学数学中的简单函数均是初等函数,因此熟悉各种初等函数的单调性是判定复合函数单调性的基础.若能对各种初等函数的图象了如指掌,则对复合函数的单调性的判定将大有裨益.我们就可借助初等函数的图象确定它的单调性,判定它的单调区间和函数值域,再利用上述定理就很容易判定复合函数的单调性.例1讨论函数f(x)=log0.5(x2+4x+4)的单调性.解 f(x)的定义域为(-∞,-2)∪(-2,+∞).f(x)可视为y=log0.5u与u=x2+4x+4复合而成.u的图象是以x=-2为对称轴,开口向上的抛物线,在(-∞,-2)上为减函数,在(-2,+∞)上为增函数.又y=log0.5u在其定义域上是减函数,故f(x)在(-∞,-2)上是增函数,在(-2,+∞)上是减函数.例2试求函数f(x)=2x2的单调区间.解函数f(x)=2x2可视为f(u)=2u与u=x2复合而成.函数u =x2在(-∞,0]上为减函数,在[0,+∞)上为增函数,且u≥0.函数f(u)=2u在u≥0时为增函数.所以,f(x)在(-∞,0]上为减函数.在[0,+∞)上为增函数.推论由有限个简单函数复合而成的多重复合函数,若在所讨论的区间内每个简单函数均有意义,且均为严格单调函数.当其中减函数的个数是偶数时,则复合函数是增函数;当减函数的个数是奇数时,则复合函数是减函数.(1)若0<a<1.当x<-1时,在构成复合函数的三个函数中,u和v=x2-x-2是减函数,则f(x)是增函数.当x>2时,y=logau是减函数,则f(x)在构成复合函数的三个函数中,只有y=loga是减函数.(2)若a>1,当x<-1时,构成复合函数的三个函数中只有一个函数y=logu是减函数,则f(x)是减函数.当x>2时,构成a复合函数的三个函数都是增函数,则f(x)是增函数.。
复合函数单调性课件

复合函数单调性与极值的关系
总结词
复合函数的单调性与极值之间存在密切关系。
详细描述
当一个复合函数在某区间内单调递增或递减时,该函数在该区间内可能存在极值点。极值点是函数值发生变化的点, 它们对于确定函数的整体性质具有重要意义。
举例
设 $f(x) = x^3$,这是一个关于 $x$ 的单调递增的复合函数。在 $x = 0$ 处,该函数取得极小值点;而 在 $x < 0$ 或 $x > 0$ 的区间内,该函数是单调递增的。
复合函数的表示方法
设$y = f(u)$,$u = g(x)$,则复合 函数为$y = f(g(x))$。
复合函数的性质
连续性
复合函数在定义域内连续,即若 $f(u)$和$g(x)$在各自的定义域
内连续,则复合函数$y = f(g(x))$在定义域内也连续。
可导性
若$f(u)$和$g(x)$在各自的定义域 内可导,则复合函数$y = f(g(x))$ 在定义域内也可导。
导数的几何意义
表示曲线在某点的切线斜率。
03
导数的应用
判断函数的单调性、求极值、求拐点等。
02
单调性的概念与性质
单调性的定义
定义
如果对于任意$x_{1} < x_{2}$,都有$f(x_{1}) leq f(x_{2})$(或$f(x_{1}) geq f(x_{2})$),则称函数$f(x)$在区间$I$上单调递增(或单调递减)。
举例
设 $f(x) = x^2$,$g(x) = frac{1}{x}$,$h(x) = log_2(x)$ ,考虑复合函数 $f(g(h(x))) = (log_2x)^2$。在 $x > 1$ 的区 间内,该复合函数是单调递增的 ,而在 $0 < x < 1$ 的区间内, 该复合函数是单调递减的。
复合函数单调性

复合函数单调性一般地,设函数)(x g =ω在区间M 上有意义,函数)(ωf y =在区间N 上有意义,且当M x ∈时,N ∈ω有以下四种情况:(1)若)(x g =ω在M 上是增函数,)(ωf y =在N 上是增函数,则)]([x g f y =在M 上也是增函数;(2)若)(x g =ω在M 上是增函数,)(ωf y =在N 上是减函数,则)]([x g f y =在M 上也是减函数;(3)若)(x g =ω在M 上是减函数,)(ωf y =在N 上是增函数,则)]([x g f y =在M 上也是减函数;(4)若)(x g =ω在M 上是减函数,)(ωf y =在N 上是减函数,则)]([x g f y =在M 上也是增函数。
注意:内层函数)(x g =ω的值域是外层函数)(ωf y =的定义域的子集。
规律:当两个函数的单调性相同时,其复合函数是增函数;当两个函数的单调性不同时,其复合函数为减函数。
即我们所说的“同增异减”规律。
求y=122)21(--x x 的单调区间.解 : 设y=u)21(.由u ∈R,u=x 2-2x -1,解得原复合函数的定义域为x ∈R.因为y=u)21(在定义域R 内为减函数,二次函数u=x 2-2x -1的单调性与复合函数的单调性相反.易知,u=x 2-2x -1=(x -1)2-2在x ≤1时单调减,由x ∈R, (复合函数定义域)x ≤1, (u 减)解得x ≤1.所以(-∞,1]是复合函数的单调增区间.同理[1,+∞)是复合函数的单调减区间. y=x17.0;((-∞,0),(0,+∞)均为单调增区间.)y=232x -;(-∞,0)为单调增区间,(0,+∞)为单调减区间) y=3)31(+x ,((-∞,+∞)为单调减区间.)y=227x x -;((-∞,1)为单调增区间,(1,+∞)为单调减区间.)指数运算和指数函数1.根式的性质(1)当n 为奇数时,有a a n n = (2)当n 为偶数时,有⎩⎨⎧<-≥==)0(,)0(,a a a a a a n n (3)负数没有偶次方根 (4)零的任何正次方根都是零2.幂的有关概念(1)正整数指数幂:)(.............*∈⋅⋅=N n a a a a a n n(2)零指数幂)0(10≠=a a (3)负整数指数幂 ).0(1*∈≠=-N p a a ap p (4)正分数指数幂 )1,,,0(>*∈>=n N n m a a a n m n m且(5)负分数指数幂 n mn ma a 1=-)1,,,0(>*∈>n N n m a 且(6)0的正分数指数幂等于0,0的负分数指数幂无意义3.有理指数幂的运算性质(1)),,0(,Q s r a a a a s r s r ∈>=⋅+ (2)),,0(,)(Q s r a a a rs s r ∈>=(3)),0,0(,)(Q r b a a a ab s r r ∈>>⋅=4.指数函数定义:函数)10(≠>=a a a y x且叫做指数函数。
复合函数的单调性与奇偶性

复合函数的性质与构成它的函数的性质密切相关,其规律可列表如下:
1.若函数 的定义域都是关于原点对称的,那么由 的奇偶性得到 的奇偶性的规律是:
函数
奇偶性
奇函数
奇函数
偶函数
偶函数
奇函数
偶函数
奇函数
偶函数
奇函数
偶函数
偶函数
偶函数
即当且仅当 和 都是奇函数时,复合函数 是奇函数.
2.若函数 在区间 上是单调函数,函数 在 或 上也是单调函数,那么复合函数 在区间 上是单调函数,其单调性规律是:
函数
单调性
增函数
增函数
减函数
减函数
增函数
减函数
增函数
减函数
增函数
减函数
减函数
增函数
即 , 增减性相同时, 为增函数,增减性相反时, 为减函数.
复合函数单调性的判断方法

【解】 (1)定义域: 0,
(4)外函数 y 2u 2 2u 1在
(2)此函数是由下列函数复合所得
y 2u 2 2u 1,( u x) log 1 x
2
(3)内函数 ( u x) log 1 x 在
2
1 1 u , 单调递减, u , 单调递增 2 2 2 1 , (5)原函数在 u , x 2 2
增减相异复合减
贰
判断
HI
贰
举例
【例 1】求函数 y log 1 x 2 4 x 3 的单调区间
2
贰
举例
【例 1】求函数 y log 1 x 2 4 x 3 的单调区间
2
【解】 (1)定义域: , 1 3,
(2)还原复合函数的复合过程:
x 2, 单调递增
(4) y log 1 u 在 u 0, 上单调递减
2
此函数是由下列函数复合所得
y log 1 u,( u x) x 4x 3
2 2
(5) y log 1 x 2 4 x 3 在
2
u x) x 4x 3 在 (3)内函数 (
2
1 单调递增, 3, 单调递减 ,
复合函数 单调性的判断方法
复合函数单调性的判断方法
1
1
2
定义
2
判断
一
定义
HI
设 y f (u ) 定义域为A, u g ( x) 的值域为B 若B A 则 y 关于 x 的函数 y f [ g ( x)] 叫做 函数 f 与 g 的复合函数, u 叫中间变量
图说复合函数的单调性

图谈复合函数的单调性1.复合函数的概念如果y 是u 的函数,u 又是x 的函数,即)(u f y =,)(x g u =,那么y 关于x 的函数)]([x g f y =叫做函数)(u f y =和)(x g u =的复合函数,其中u 是中间变量,自变量为x ,函数值为y 。
)(x g u =叫内层函数,)(u f y =叫外层函数。
例如:函数x x y 22)31(-=是由x x u 22-=, u y )31(=复合而成立。
函数)43lg(2x x y -+=是由243x x t -+=,t y lg =复合而成立。
2.复合函数单调性的判断方法定理:设函数)(x g u =在区间M 上有意义,函数)(u f y =在区间N 上有意义,且当M x ∈时,N u ∈,有以下四种情况:(1)若)(x g u =在M 上是增函数,)(u f y =在N 上是增函数,则)]([x g f y =在M 上也是增函数; 例如:x y 212=是由x u 21=与u y 2=复合而成的函数,这两个函数都是增函数,而x x y )2(221==显然是增函数;(2)若)(x g u =在M 上是减函数,)(u f y =在N 上是减函数,则)]([x g f y =在M 上也是增函数。
例如:x y -=)21(是由u=-x 与u y )21(=复合而成的函数,这两个函数都是减函数,而xx y 2)21(==-显然是增函数;(3)若)(x g u =在M 上是增函数,)(u f y =在N 上是减函数,则)]([x g f y =在M 上也是减函数; 例如:x y -=2是由u=-x 与u y 2=复合而成的函数,u=-x 是减函数,uy 2=是增函数,而x x y )21(2==-显然是减函数; (4)若)(x g u =在M 上是减函数,)(u f y =在N 上是增函数,则)]([x g f y =在M 上也是减函数;例如:x y 21)21(=是由x u 21=与u y )21(=复合而成的函数,x u 21=是增函数,u y )21(=是减函数,而x x y )21()21(21==显然是减函数; 判断口诀:同增异减3.例题学习例1. 求函数222)(-+=x x x f 的单调区间.解:函数的定义域是R ,设22-+=x x t 则t y 2=,内层函数是22-+=x x t ,外层函数是ty 2=如左图,内层函数22-+=x x t 的单调增区间:),21[+∞-,单调减区间:]21,(--∞ 由于外层函数t y 2=为增函数,所以复合函数的增区间为:),21[+∞-,复合函数的减区间为: ]21,(--∞,从右图也可以看到上述单调性及单调区间。
复合函数的单调性与赋值法证明函数的单调性

一、复合函数 y f 的单调性 g x 将复合函数分解成 y f u , u g x
u g x
增 增 减 减
y f u 增 减 增 减
y f g x
增 减 减 增
复合函数单调性归纳为“同增异减”
(1)求 f
1
(2)证明: f x 在定义域内是增函数
练习2.函数f x 对任意实数a,b都 有 f a b f a f b 明: f x 是R上的增函数
例.求函数 y x 2 x 1 的单调 区间
2
练习:求 y x 2 x 8 的 单调区间
2
二、抽象函数单调性
例1.已知 y f x 在定义域 1,1 2 上是减函数,且f 1 a f a 1 求a的取值范围
练习:已知 y f x 在定义 域 0, 是增函数,且 2 f a f 2a 3 ,求a的取值 范围
例2: 已知定义在R上的函数 f ( x) 满足:对任 意 a, b R,都有 f (a b) f (a) f (b),且当 x 0 时,f ( x) 0 ,试确定函数的单调性.
练习1:已知函数 f x 的定义域是 0, , 当x>1时, f x 0,且 f xy f x f y
专题3复合函数的单调性

二、复合函数y=f[g(x)]单调性
对于复合函数y f [g(x)]的单调性,必须考虑y f (u)与 u g(x)的单调性,从而得出y f [g(x)]的单调性.
y f (u)
u g(x)
y f [g(x)] 法
增函数
增函数
增函数
则
增函数
减函数
减函数
同
减函数
增函数
减函数
增
减函数
减函数
例3.求函数y
1 2
x2 4x3
的单调递减
小结
判断函数的单调性有哪些方法 1、定义法
2、图象法
3、利用已知函数的单调性,通过 一些简单结论、性质作出判断.
4、利用复合函数单调性的规则进行 判断.
一、复合函数y=f(x)+g(x) 与y=f(x)-g(x)单调性:
结论1:若f(x)与g(x)在R上是增函数, 则 函数y=f(x)+g(x)也是增函数.
结论2:若f(x)与g(x)在R上是减函数,则 函数y=f(x)+g(x)也是减函数.
结论3:若f(x) 在R上是增函数, g(x)在R上是减 函数,则函数y=f(x) -g(x)也是增函数.
增函数
异
规律:当两个函数的单调性相同时,其复合函数是增函数; 减
当两个函数的单调性不相同时,其复合函数是减函数.
题型1.求单调区间
例2.求函数y x2 2x 3的单调区间.
小结:考虑指数函数的单调性要先考虑函数的定 义域,在定义域范围内求函数的单调性.
练习1.求函数y x2 4x 3的单调递减区间。
专题3.复合函数单调性
一、复习: 1.对于函数的定义域I内某个区间上的任意两个自 变量x1,x2的值,
复合函数的单调性及简单的恒成立问题

u=g(x)
y=单调递减) ↓
↑ ↓ ↓ ↑
↑ ↓ ↑ ↓
1 2 x 2 x 3的单调区间. 例1:求函数y 2
y 1 2 x 2 x 3 的定义域为 (,3] [1,). 2 1 u , u x 2 2 x 3, 设 y 2
变式:已知函数 f ( x) 8 2x x , g ( x) f (2 x ), 试求 g ( x) 的单调区间.
2 2
↓
恒成立问题:
例2:已知x ax 2 0 在 x [2,3] 恒 成立,求实数a的取值范围。
2
变式1:已知x ax 2 0 在 a [2,3] 恒 成立,求实数x的取值范围。
拓展题: 已知f ( x)是定义在区间 [-1,1]上的函数,且f (1) 1, 若 f ( m) f ( n ) m、n [1,1], m n 0时,有 0, 对任意 mn x [1,1], f ( x) f ( x)都成立. 1 ( 1)解不等式f ( x ) f (1 x); 2 2 (2)若f ( x) t 2ax 1对所有x [1,1]恒成立,求实 数t的取值范围 .
复合函数的单调性及简单的 恒成立问题
复合函数的单调性判断:
1.求复合函数y=f[g(x)]单调区间的步骤(定义域优先原则): (1)确定定义域(公共定义域); (2)将复合函数分解成基本初等函数:y=f(u),u=g(x); (3)分别确定这两个函数的单调区间; (4)若这两个函数同增或同减,则y=f[g(x)]为增函数,若 这两个函数一增一减,则y=f[g(x)]为减函数。 2.复合函数单调性的判断方法可以从下表中得到(同增异减):
当 x 1 时,u是x的增函数,y是u的减函数, 故y是x的减函数。
复合函数的单调性 ppt课件

(5) 若两个函数在对应的区间上的单调性相异(即一个是 增函数,而另一个是减函数),则复合后的函数y=f[g(x)]为 减函数。
2020/12/2
5
•复合函数的单调性
若u=g(x) 增函数 减函数 增函数 减函数
y=f(u) 增函数 减函数 减函数 增函数 则y=f[g(x)] 增函数 增函数 减函数 减函数
规律:当两个函数的单调性相同时,其复合函数是增
函数;当两个函数的单调性不相同时,其复合函数是
减函数。 “同增异减”
2020/12/2
以(-∞,1)是复合函数的单调减区间.
u=x2-4x+3=(x-2)2-1,
x>3或x<1,(复合函数定义域)
x>2 (u增)
解得x>3.所以(3,+∞)是复合函数的单调增区间.
2020/12/2
8
例2 求下列复合函数的单调区间: y=log(2x-x2)
解: 设 y=logu,u=2x-x2.由u>0,u=2x-x2
因为u=g(x)在区间(a,b)上是减函数,所以g(x1)>g(x2), 记u1=g(x1),u2=g(x2),即u1>u2,且u1,u2 (c,d).因为 函数y=f(u)在区间(c,d)上是减函数,所以f(u1)<f(u2), 即y=f[g(x1)]< y=f[g(x2)],故函数y=f[g(x)]在区间(a,b) 上是增函数。
4
•复合函数的单调性
引理2:已知函数y=f[g(x)],若u=g(x)在区间(a,b) 上是减函数,其值域为(c,d),又函数y=f(u)在区间 (c,d)上是减函数,那么,原复合函数y=f[g(x)]在 区间(a,b)上是增函数。
证明:在区间(a,b)内任取两个数x1,x2,使a<x1<x2<b,
复合函数的单调性

复合函数的单调性
复合函数的单调性
复合函数是指y关于x的函数y f[g(x)],其中u是中间变量,自变量为x,函数值y。
例如,函数y x23可以拆分为函数y f(u)和函数u x22x3的复合函数。
对于函数y f(u)和函数u g(x),若在区间(a,b)上具有单调性,当x(a,b)时,u(m,n),且y f(u)在区间(m,n)上具有单调性,则复合函数y f[g(x)]在区间(a,b)上的单调性规律如下:
y f(u)。
u g(x)
增。
增
增。
减
减。
增
减。
减
证明:设x1和x2是区间(a,b)上的任意两个值,且x1<x2.因为u g(x)在区间(a,b)上是增函数,所以g(x1)<g(x2),且
g(x1),g(x2)(m,n)。
又因为y f(u)在(m,n)上是增函数,所以
f[g(x1)]f[g(x2)],所以函数y f[g(x)]在区间(a,b)上是增函数。
其它三种情况同理。
因此,复合函数y f[g(x)]的单调性规律可以概括为四个
字“同增异减”。
复合函数的单调性例题和知识点总结

复合函数的单调性例题和知识点总结在数学的学习中,函数是一个非常重要的概念,而复合函数的单调性更是函数知识中的重点和难点。
理解并掌握复合函数的单调性,对于解决函数相关的问题有着至关重要的作用。
下面,我们将通过一些例题来深入探讨复合函数的单调性,并对相关知识点进行总结。
首先,我们来明确一下复合函数的概念。
如果函数$y=f(u)$的定义域为$D_1$,函数$u=g(x)$的值域为$D_2$,且$D_2\subseteq D_1$,那么对于定义域内的某个区间上的任意一个$x$,经过中间变量$u$,有唯一确定的$y$值与之对应,则变量$y$是变量$x$的复合函数,记为$y=fg(x)$。
接下来,我们探讨复合函数单调性的判断方法——同增异减。
也就是说,当内层函数与外层函数的单调性相同时,复合函数为增函数;当内层函数与外层函数的单调性不同时,复合函数为减函数。
下面通过几个例题来加深对复合函数单调性的理解。
例题 1:求函数$f(x)=\log_2(x^2 2x + 3)$的单调性。
首先,令$u = x^2 2x + 3$,则$f(u) =\log_2 u$。
对于$u = x^2 2x + 3$,其图象开口向上,对称轴为$x = 1$。
所以$u$在$(\infty, 1)$上单调递减,在$(1, +\infty)$上单调递增。
而$f(u) =\log_2 u$在定义域$(0, +\infty)$上单调递增。
因为内层函数$u$在$(1, +\infty)$上单调递增,外层函数$f(u)$也单调递增,根据同增异减,所以复合函数$f(x)$在$(1, +\infty)$上单调递增。
又因为内层函数$u$在$(\infty, 1)$上单调递减,外层函数$f(u)$单调递增,所以复合函数$f(x)$在$(\infty, 1)$上单调递减。
例题 2:求函数$f(x) = 2^{x^2 + 2x 3}$的单调性。
令$u = x^2 + 2x 3$,则$f(u) = 2^u$。
复合函数的概念及复合函数的单调性

复合函数的概念及复合函数的单调性1.复合函数的概念如果y 是ω的函数,ω又是x 的函数,即)(ωf y =,)(x g =ω,那么y 关于x 的函数)]([x g f y =叫做函数)(ωf y =和)(x g =ω的复合函数,其中ω是中间变量,自变量为x ,函数值y 。
例如:函数x x y 22)31(-=是由μ)31(=y ,x x 22-=μ复合而成立。
函数)43lg(2x x y -+=是由ωlg =y ,243x x -+=ω复合而成立,μ、ω是中间变量。
2.复合函数单调性一般地,定理:设函数)(x g =ω在区间M 上有意义,函数)(ωf y =在区间N 上有意义,且当M x ∈时,N ∈ω 有以下四种情况:(1)若)(x g =ω在M 上是增函数,)(ωf y =在N 上是增函数,则)]([x g f y =在M 上也是增函数;(2)若)(x g =ω在M 上是增函数,)(ωf y =在N 上是减函数,则)]([x g f y =在M 上也是减函数;(3)若)(x g =ω在M 上是减函数,)(ωf y =在N 上是增函数,则)]([x g f y =在M 上也是减函数;(4)若)(x g =ω在M 上是减函数,)(ωf y =在N 上是减函数,则)]([x g f y =在M 上也是增函数。
即:同增异减注意:内层函数)(x g =ω的值域是外层函数)(ωf y =的定义域的子集。
例1、讨论下列函数的单调性(注意:要求定义域)(1)x x y 22)31(-= (2))43lg(2x x y -+= 解:练习1:1.求下列函数的单调区间。
(1)2522+-=x x y (2))32(log 221-+=x x y(3)12--=x x y (4)212)3(--=x x y例2、已知)(x f y =,且)3lg(3lg lg lg x x y -+=。
(1)求)(x f y =的表达式及定义域;(2)讨论)(x f y =的单调性。
复合函数的单调性

2
故单调递增区间为1,2 , 单调递减区间为 2,3
0 0.4 1
f ( x) log
0.4
y log0.4 t是减区间。
x
2
4 x 3的单调递增区间为 2,3 ,
2 x 4 x 3的单调性。
[u(a),u(b)]
减函数
[u(b),u(a)]
增函数
[u(b),u(a)]
减函数
y f (u ) 增函数
y f [ g ( x)] 增函数
减函数
减函数
增函数
这就是传说中的“同增异减”法则
复合函数的单调性
复合函数: 令 则 u=g(x) y=f(u)
y=f[g(x)]
内函数 外函数 原函数 以x为自变量 以u为自变量 以x为自变量
(3) 令t 2 x,
2
t 0, x (, 2]
2
y t , t [0, )
(4)令t x 4 x, x R t ( x 2) 4 4 1 t y ( ) , t 4 3 2 (5)令u x 2 x 3
y=f[g(x)]
内函数 外函数 原函数 以x为自变量 以u为自变量 以x为自变量
y=f[g(x)]
例1.将下列复合函数分解成基本初等函数 2 (1) y 1 ; x 4 (2) y 2 ; x 2x 3 1 x2 4 x (3) y 2 x ; (4) y ( ) ; 3 (5) y log 3 (3 2 x x 2 ).
y=f[g(x)]
复合函数单调性定理:
①当内外函数在各自定义域内同增同减时,原函数增 ②当内外函数在各自定义域内一增一减时,原函数减
复合函数的单调性、定义域与值域
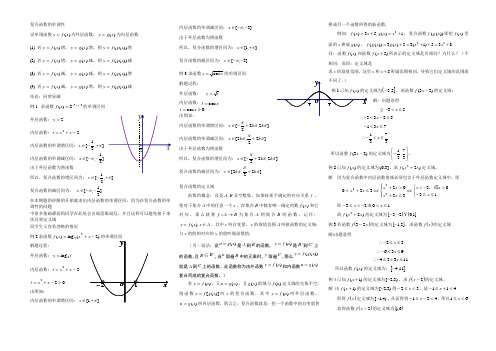
复合函数的单调性设单调函数)(xfy=为外层函数,)(xgy=为内层函数(1) 若)(xfy=增,)(xgy=增,则))((xgfy=增.(2) 若)(xfy=增,)(xgy=减,则))((xgfy=减.(3) 若)(xfy=减,)(xgy=减,则))((xgfy=增.(4) 若)(xfy=减,)(xgy=增,则))((xgfy=减.结论:同曾异减例1. 求函数222)(-+=xxxf的单调区间.外层函数:ty2=内层函数:22-+=xxt内层函数的单调增区间:],21[+∞-∈x内层函数的单调减区间:]21,[--∞∈x由于外层函数为增函数所以,复合函数的增区间为:],21[+∞-∈x复合函数的减区间为:]21,[--∞∈x在本例题的讲解的开始就求出内层函数的单调区间,因为在复合函数的单调性的问题中很多基础薄弱的同学在此处会出现思维混乱,并且这样可以避免接下来涉及到定义域而学生又容易忽略的情况.例2.求函数)2(log)(22-+=xxxf的单调区间.解题过程:外层函数:ty2log=内层函数:22-+=xxt22>-+=xxt由图知:内层函数的单调增区间:[∈x内层函数的单调减区间:]2,[--∞∈x由于外层函数为增函数所以,复合函数的增区间为:],1[+∞∈x复合函数的减区间为:]2,[--∞∈x例3.求函数xy cos=的单调区间解题过程:外层函数:ty=内层函数:xt cos=cos≥=xt由图知:内层函数的单调增区间:]2,22[πππkkx+-∈内层函数的单调减区间:]22,2[πππkkx+∈由于外层函数为增函数所以,复合函数的增区间为:]2,22[πππkkx+-∈复合函数的减区间为:]22,2[πππkkx+∈复合函数的定义域函数的概念:设是,A B非空数集,如果按某个确定的对应关系f,使对于集合A中的任意一个x,在集合B中都有唯一确定的数()f x和它对应,那么就称:f A B→为集合A到集合B的函数,记作:(),y f x x A=∈。
复合函数单调性

因此令 u 2 x
1 得 x 1 (外函数的单调增区间无法放大,但内函数的相应值域可以变小啊) 2
∴函数 y 4 x 2 x 1 的单调增区间是 (1, ) 【例 2】函数 y (log 2 x) 2 2 log 2 x 3 的单调增区间是_________ 解析:函数的定义域为 (0, ) ,设 u log 2 x ,则 y u 2 2u 3 内函数 u log 2 x 在 (0, ) 上单调增,相应值域为 R 外函数 y u 2 2u 3 在 (1, ) 上单调增(和例题 1 出现同样问题了) 令 u log 2 x 1 得 x 2 ∴函数 y (log 2 x) 2 2 log x 3 的单调增区间是 (2, )
【例 6】设 a 0 且 a 1 ,函数 f ( x) log a
1 x 在 (1, ) 上单调递减,则 f ( x) ( 1 x A.在 ( , 1) 上单调递减,在 (1, 1) 上单调递增 B.在 ( , 1) 上单调递增,在 (1, 1) 上单调递减 C.在 ( , 1) 上单调递增,在 (1, 1) 上单调递增 D.在 ( , 1) 上单调递减,在 (1, 1) 上单调递减
外函数 y 2 sin u 在 [2k
, 2 k
【例 4】已知函数 y log a (2 ax ) 在区间 [0, 1] 上是减函数,则实数 a 的取值范围( A. (0, 1) B. (1, 2) C. (0, 2) D. [2, )
)
解析:设 u 2 ax ,则 y log a u ,由复合函数的单调性知 a 1 内函数 u 2 ax 在 [0, 1] 上单调减,且相应值域为 [2 a, 2] 外函数 y log a u 在 u (0, ) 时单调增 (接下来要干吗呢?是不是要保证内函数在 [0, 1] 上的值域 [2 a, 2] 在外函数单调区间 (0, ) 内呢?) ∴ 2 a 0 , a 2 ,故实数 a 的取值范围是 (1, 2) ,选 B 【例 5】已知函数 f ( x) log 1 ( x 2 2ax 3) ,若 f ( x) 在 ( , 1] 上单调增,则 a 的取值范围是_____;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
u
u ( x 1) 1 在 0,1 递减,在 1,3 递增
2
故函数递增区间为 0,1 ,递减区间为 1,3
思:函数值域呢?
• 例2 已知函数 y a 2a 1(0 a 1)
2x x
在区间
1,1
上的最大值是14,试求a值。
• 解:设 u a x (0 a 1) ,内层函数 u a x
复合函数单调性
• 函数单调性等价定义:定义在区间D上的函 数 y f ( x) 对于任意 x1, x2 D ,当
x1 x2 时都有 ( x1 x2 )( y1 y2 ) 0 ,则函
数 y f ( x) 在D上是增函数。
思:若都有
呢? 减函数
• 复合函数 y f (x) 由外层函数 y f (u )
1 1 a 1 a 解得 a1 , 2 (不合,舍),故 5 3 3
2
1
需要注意的是内外层区间的对应不能弄错。
2
0
故复合函数单调递增
( 减)
。 注:以上只考虑内外层都单调情形,若有u1=u2,则区间要 细分。
• 结论:复合函数单调性----同增异减
• 例1:求函数 调区间。
1 x2 2 x 2 y( ) (0≤x≤3)的单 2
ቤተ መጻሕፍቲ ባይዱ
1 • 解:外层函数 y 在R上递减,内层函数 2
在R上递减,外层函数 y u2 2u 1 (u 1)2 2 当 1
1 au x 1 时, a
,而区间
1 a, a
在外
层函数对称轴的右边,则外层函数递增。
• 所以复合函数在 1,1上单调递减,函数在
左端点取得最大值14,则 a 2a 1 14,
和内层函数 u ( x) 复合而成。设
ui ( xi ), yi f (ui )(i 1, 2) ( x1 x2 )
若内外层函数单调性相同(异) , 则 ( x1 x2 )(u1 u2 ) 和 (u1 u2 )( y1 y2 ) 同 (异) 号,且都不为0,所以 又 (u1 u2 ) 则 ,
