正余弦函数的单调性ppt
合集下载
1.4.2第2课时 正、余弦函数的单调性与最值 课件

栏目 导引
第一章 三角函数
(4)确定含有正弦函数或余弦函数的较复杂函数的单调性时, 要注意使用复杂函数的判断方法来判断. 2.解析正弦函数、余弦函数的最值 (1)明确正弦、余弦函数的有界性,即|sin x|≤1,|cos x|≤1. (2)对有些函数,其最值不一定就是1或-1,要依赖函数的定 义域来决定. (3)形如y=Asin(ωx+φ)(A>0,ω>0)的函数求最值时,通常利 用“整体代换”,即令ωx+φ=z,将函数转化为y=Asin z的 形式求最值.
第一章 三角函数
栏目 导引
第一章 三角函数
单调减区间为[34π+2kπ,74π+2kπ](k∈Z). 所以原函数 y=2sin(π4-x)的单调增区间为[34π+2kπ,74π+ 2kπ](k∈Z); 单调减区间为[-π4+2kπ,34π+2kπ](k∈Z).
栏目 导引
第一章 三角函数
【名师点评】 正弦、余弦函数单调区间的求解技巧: (1)结合正弦、余弦函数的图象,熟记它们的单调区间. (2)确定函数y=Asin(ωx+φ)(A>0,ω>0)单调区间的方法:采 用“换元”法整体代换,将ωx+φ看作一个整体,可令“z= ωx+φ”,即通过求y=Asin z的单调区间而求出函数的单调 区间.若ω<0,则可利用诱导公式将x的系数转变为正数.
栏目 导引
第一章 三角函数
跟踪训练
1.求函数 y=sin(π3-12x),x∈[-2π,2π]的单调递增区间. 解:y=sin(π3-12x)=-sin(12x-π3). 由 y=sin x 与 y=-sin x 的图象关于 x 轴对称可知,y=sin x 的递增 区间就是 y=-sin x 的递减区间.因此,要求 y=-sin(12x-π3)的递 增区间,只要求出 y=sin(12x-π3)的递减区间即可.
第一章 三角函数
(4)确定含有正弦函数或余弦函数的较复杂函数的单调性时, 要注意使用复杂函数的判断方法来判断. 2.解析正弦函数、余弦函数的最值 (1)明确正弦、余弦函数的有界性,即|sin x|≤1,|cos x|≤1. (2)对有些函数,其最值不一定就是1或-1,要依赖函数的定 义域来决定. (3)形如y=Asin(ωx+φ)(A>0,ω>0)的函数求最值时,通常利 用“整体代换”,即令ωx+φ=z,将函数转化为y=Asin z的 形式求最值.
第一章 三角函数
栏目 导引
第一章 三角函数
单调减区间为[34π+2kπ,74π+2kπ](k∈Z). 所以原函数 y=2sin(π4-x)的单调增区间为[34π+2kπ,74π+ 2kπ](k∈Z); 单调减区间为[-π4+2kπ,34π+2kπ](k∈Z).
栏目 导引
第一章 三角函数
【名师点评】 正弦、余弦函数单调区间的求解技巧: (1)结合正弦、余弦函数的图象,熟记它们的单调区间. (2)确定函数y=Asin(ωx+φ)(A>0,ω>0)单调区间的方法:采 用“换元”法整体代换,将ωx+φ看作一个整体,可令“z= ωx+φ”,即通过求y=Asin z的单调区间而求出函数的单调 区间.若ω<0,则可利用诱导公式将x的系数转变为正数.
栏目 导引
第一章 三角函数
跟踪训练
1.求函数 y=sin(π3-12x),x∈[-2π,2π]的单调递增区间. 解:y=sin(π3-12x)=-sin(12x-π3). 由 y=sin x 与 y=-sin x 的图象关于 x 轴对称可知,y=sin x 的递增 区间就是 y=-sin x 的递减区间.因此,要求 y=-sin(12x-π3)的递 增区间,只要求出 y=sin(12x-π3)的递减区间即可.
《三角函数的图象与性质》PPT教学课件(第三课时正、余弦函数的单调性与最值)

栏目导航
12
(1)B
(2)xx≠-4kπ-43π,k∈Z
(3)x-π4+kπ≤x<π4+kπ,k∈Z
[(1)当-π4<x<0时,-1<tan x
<0,∴ta1n x≤-1;
当0<x<π4时,0<tan x<1,∴ta1n x≥1.
即当x∈-π4,0∪0,π4时,函数y=ta1n x的值域是(-∞,-1) ∪(1,+∞).
[提示] 由正切函数图象可知(1)×,(2)√,(3)×,(4)×. [答案] (1)× (2)√ (3)× (4)×
第五章 三角函数
5.4 三角函数的图象与性质 第4课时 正切函数的性质与图象
2
学习目标
核心素养
1.能画出正切函数的图象.(重点)
1.借助正切函数的图象研究问
2.掌握正切函数的性质.(重点、难点) 题,培养直观想象素养.
3.掌握正切函数的定义域及正切曲线的 2.通过正切函数的性质的应
渐近线.(易错点)
28
栏目导航
(2)函数定义域为 xx≠kπ-π4且x≠kπ+π4,k∈Z , 关于原点对称, 又f(-x)=tan-x-π4+tan-x+π4 =-tanx+π4-tanx-π4 =-f(x), 所以函数f(x)是奇函数.
29
栏目导航
30
正切函数单调性的应用 [探究问题] 1.正切函数y=tan x在其定义域内是否为增函数? 提示:不是.正切函数的图象被直线x=kπ+π2(k∈Z)隔开,所以它的 单调区间只在kπ-π2,kπ+π2(k∈Z)内,而不能说它在定义域内是增函 数.假设x1=π4,x2=54π,x1<x2,但tan x1=tan x2.
用,提升逻辑推理素养.
栏目导航
正弦函数余弦函数的单调性(教学课件201911)

2
42
kZ
2k x 2k
12 3
43
kZቤተ መጻሕፍቲ ባይዱ
函数的单调递减区间是[ 2k , 2k ] ,k Z
12 3 4 3
② y 1 cos2 x
解:y sin 2 x
1 cos 2x 1 cos 2x 1
2
2
2
2k 2x 2k
正弦函数、余弦函数的单调性
(复习课)
每
课 已知:ABC是锐角三角形,
一
函数f (x)在[0,1]上是增函数,那么有 ( )
练
A f (sin B) f (cosA) .
C.f (sin B) f (sin A)
B.f (sin B) f (cosA) D.f (cosB) f (cosA)
州 瑰宅中常有父时旧部曲数百 历官无畜聚 恐贼觉 太清三年 出为都督 帝必惊觉 夏四月壬申 上以邵诚节 封前寿
1.求下列函数的单调递减区间:
① y sin( 3x)
4
② y 1 cos2 x
① y sin( 3x) 4
解: y sin(3x )
4
2k 3x 2k
x 如果对于属于 I
内某个区间上的任意两个自变量的值
x 1
,
,
2
x x 当 1
2时,都有
f (x ) 1
f (x ) 2
那么就说 f (x) 在这个区间上是减函数。这个区间为单调减区间。;第二 https:/// 第二 ;
不从 中大通三年 冲等重请 为吴兴太守 追尊所生妣阮修容为文宣太后 衣染天血 圣情孝友 特赐宅一区 以待湘州之捷 求为始丰
【课件】正弦函数、余弦函数的性质+(2)+课件-高一上学期数学人教A版(2019)必修第一册

23
33
4.变式:求函数y sin( 1 x ), x [ , ]的单调递增区间.
23
解 : y sin( 1 x ) sin(1 x ),
23
23
令z 1 x , x [2 ,2 ], 则z [ 4 , 2 ].
23
33
因为y
sin
z,
z
[
4
,
2
]的单调递减区间是[
4
时取得最小值
1;
7.最大值与最小值
由余弦函数的图象知
y1
3 5
2
2 3
2
O
2
1
2
3 2
2
5 3
2
x
余弦函数当且仅当 x _2_k__,_k____Z__ 时取得最大值1,
当且仅当x _____2_k__,_k___Z_时取得最小值 1.
8. 正弦函数、余弦函数的图象和性质
函 数 y sin x, x R
在每个闭区间 [2k , 2k ](k Z ) 上都单调递减,
其值从1减小到-1.
7.最大值与最小值
正弦函数图象知
y1
3 5
2
2 3
2
O
2
1
2
3 2
2
5 3
2
x
正弦函数当且仅当
x
2k , k Z
_2__________
时取得最大值 1,
当且仅当
x
2k , k Z
___2__________
5
)在区间[0,
]上的单调递增区间为(
)
3
A.[5 ,11 ]
12 12
5
、B.[0, 12 ]
5.4.2正弦函数、余弦函数的性质(第2课时)-高一数学上学期同步精讲课件(人教A版必修第一册2)

令−
2
则−
3
即−
6
)的单调区间和函数
6
+ 2 ≤ 2 − ≤ + 2, ∈ .
6
2
2
+ 2 ≤ 2 ≤ + 2, ∈ .
3
+ ≤ ≤ + , ∈ .
3
所以函数的单调递减区间是[− + , + ], ∈ .
6
3
3
令 + 2 ≤ 2 − ≤ + 2��, ∈ .
调递增,其值从 − 增大到 ;在每一个闭区间 [, + ] ( ∈ )上都单调递减,
其值从减小到−.
新知探索
思考3:在前面函数的性质中,我们除了奇偶性、单调性外,还学习了函数的最
值.请结合着前面对正余弦函数单调性的研究,找出正余弦函数的最值及其取得
最值时对应的自变量的值.
= , ∈ 取得最小值的的集合{| =
−
2
+ 2,得 =
−
4
−
2
+ 2, ∈ }.由2 = =
+ .所以,使函数 = −3 2, ∈ 取得最大值的的
4
集合是{| = − + , ∈ }.同理,使函数 = −3 2, ∈ 取得最小值的
[− , ]的单调增区间是[− , ],且由−
3 3
2 2
2
≤
1
2
+
3
3
≤≤ .
所以,函数 =
人教版高中数学必修4第一章三角函数《1.4三角函数的图象与性质:1.4.2 正弦函数、余弦函数的性质》教学PPT

解:(2)当x 2k , k Z时,函数取得最大值,ymax 1
2
当x 2k , k Z时,函数取得最小值,
2
ymin 1
函数取得最大值的x的集合是x
x
2
2k
,
k
Z
,ymax
1,
函数取得最大值的x的集合是x
x
2
2k
,
k
Z
,ymin
1.
二、 正、余弦函数的奇偶性
-4 -3
例1.下列函数有最大(小)值?如果有,请写出取最大(小) 值时的自变量x的集合,并说出最大(小)值是什么?
(1)y cos x 1, x R; (2)y sin x, x R.
解:(1)当x 2k , k Z时,ymax 11 2,
当x 2k , k Z时,ymin 11 0.
1.4.2 正弦、余弦函数的性质
(1)周期性
定义域、值域
-4 -3
y
1
-2
- o
-1
y=sinx (xR)
2
3
4
定义域 xR
-4 -3
y=cosx (xR)
y
1
-2
- o
-1
值 域 y[ - 1, 1 ]
2
3
4
5 6x 5 6x
举例:
生活中“周而复始”的变化规律。
24小时1天、7天1星期、365天1年……. 相同的间隔重复出现的现象称为周期现象. 数学中又有哪些周期现象呢?
思考:y=sinx,x∈R的图象为什么会重复出现形 状相同的曲线呢?
y
1
4
3
2
7 2
5
3
2
5.4.2正弦函数、余弦函数性质第2课时课件(人教版)

总结升华
1.正余弦函数的图象和性质
2.体会整体,熟知将复合函数转化初等函数问 题 3.注意易错问题
课后作业
教材P207练习T1-5 P213习题5.4T4,T5,T16
9
5
9
5
例3.求函数y
解:令u 2x
3
,
sin(2 x
则y
3
)
探究应用3:单调性
单调递增区间.
sin u u 2 x 在R上是增函数, 3
由复合函数“同增异减”原则知,y sin u 是增函数.
2k
u
2k , (k Z ),
2
2
即 2k 2x 2k ,(k Z),
解析 由π2<x<π,ω>0 得ω2π+π4<ωx+π4<ωπ+π4,
又 y=sin x 的单调递减区间为2kπ+π2,2kπ+32π,k∈Z, 所以ωω2ππ+ +ππ44≥ ≤π322π++2k2πkπ,,k∈Z,
解得 4k+12≤ω≤2k+54,k∈Z. 又由 4k+12-2k+54≤0,k∈Z 且 2k+45>0,k∈Z, 得 k=0,所以 ω∈12,54.
(2) 当 sin 2 x 1,即 2x 2k x k (k Z )时,
2
4
y 取得最大值 ymax 1 .
∴函数的最大值为1,取最大值时的x集合为
x
x
k
4
,k
Z
(3)y a sin(2 x ) b .
6
解:① 若 a 0 ,则当sin(2 x ) 1时, 6
12
12
(k∈Z)为所求.
又∵y=或sin:u令在u[=2k3π--2x,,则2uk是π+x的减]函(k数∈Z)上为增函数,
1.4.2正弦函数余弦函数的性质-(必修四-数学-优秀课件)

第15页,共26页。
归纳总结
一般地,函数 y Asin(x )及 y Acos(x ) (其中 A,,为常数,且 A 0, 0 )的周期是
T 2
若 0 则 T 2
第16页,共26页。
练习. 求下列函数的周期:
(1) y sin 3x, x R;(2) y cos x ;
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
y cos x(x R)
第25页,共26页。
函数 图形
y
1
2
0
-1
y=sinx
3
2
2
2
5 2
x
定义域 值域
最值
xR
y [1,1]
xx2222kk时时,,yymmaxin
1 1
单调性
x[-
2
2k
,
2
2k
]
增函数
x[2
2k
,
3
2
2k ]
减函数
奇偶性
奇函数
4
x
2
…
0
…
2
sinx -1
0
1
…
0
…
3 2
-1
y=sinx (xR)
增区间为
[[
2+22k,,
22
+2] k],kZ
其值从-1增至1
Байду номын сангаас
减区间为
[
2
+22k,,
33
2
+]2k],kZ
其值从 1减至-1
第20页,共26页。
余弦函数的单调性
5-4-2 第2课时 正弦函数、余弦函数的性质课件-高一上学期数学人教A版(2019)必修第一册
π
π
π
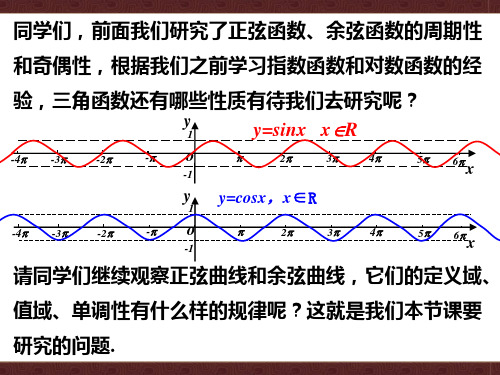
由 y=cosx+6,x∈0,2,可得 x+ ∈ , ,
6 6 3
1
3
∴ − ≤ cos( + ) ≤
2
6
2
1
所以函数的值域为- ,
2
3
.
2
解三角不等式
当x∈[0,2π]时,求不等式 cos ≥
y
集.
, ∪ [ , ]
值域、单调性有什么样的规律呢?这就是我们本节课要
研究的问题.
学习
目标
1. 理 解 正 弦 函 数 、 余 弦
2.能够利用函数的单调
函数的单调性具有周期
性解决比较函数值的大
性变化的规律,通过一
小以及求函数的最值、
个周期内的单调性进而
值域等问题.
研究在整个定义域上的
性质.
问题1:类比以往对函数性质的研究,正弦函数、余
使函数 y cos x, x R 取得最小值的x的集合
{x | x (2k 1) , k Z}
函数 y cos x 1, x R 的最大值是1+1=2;最小值是
-1+1=0.
例3.下列函数有最大、最小值吗?如果有,请写出取最大、最
小值时的自变量x的集合,并说出最大、最小值分别是什么.
5π
π
π
即 2kπ- 6 ≤2x≤2kπ+6(k∈Z),
令 2kπ-π≤2x-6≤2kπ(k∈Z),
5π
π
∴kπ-12≤x≤kπ+12(k∈Z).
5π
π
π
π
由 y=cosx+6,x∈0,2,可得 x+ ∈ , ,
6 6 3
1
3
∴ − ≤ cos( + ) ≤
2
6
2
1
所以函数的值域为- ,
2
3
.
2
解三角不等式
当x∈[0,2π]时,求不等式 cos ≥
y
集.
, ∪ [ , ]
值域、单调性有什么样的规律呢?这就是我们本节课要
研究的问题.
学习
目标
1. 理 解 正 弦 函 数 、 余 弦
2.能够利用函数的单调
函数的单调性具有周期
性解决比较函数值的大
性变化的规律,通过一
小以及求函数的最值、
个周期内的单调性进而
值域等问题.
研究在整个定义域上的
性质.
问题1:类比以往对函数性质的研究,正弦函数、余
使函数 y cos x, x R 取得最小值的x的集合
{x | x (2k 1) , k Z}
函数 y cos x 1, x R 的最大值是1+1=2;最小值是
-1+1=0.
例3.下列函数有最大、最小值吗?如果有,请写出取最大、最
小值时的自变量x的集合,并说出最大、最小值分别是什么.
5π
π
π
即 2kπ- 6 ≤2x≤2kπ+6(k∈Z),
令 2kπ-π≤2x-6≤2kπ(k∈Z),
5π
π
∴kπ-12≤x≤kπ+12(k∈Z).
5π
π
1.4.2 正弦函数、余弦函数的性质 课件(人教A版必修4)

栏目 导引
第一章 三角函数
单调减区间为[34π+2kπ,74π+2kπ](k∈Z). 所以原函数 y=2sin(π4-x)的单调增区间为[34π +2kπ,74π+2kπ](k∈Z); 单调减区间为[-π4+2kπ,34π+2kπ](k∈Z).
栏目 导引
第一章 三角函数
变式训练
3.求函数 y=2sin(x+π4)的单调区间. 解:y=sinx 的单调增区间为[-π2+2kπ,π2+ 2kπ],k∈Z;单调减区间为[π2+2kπ,32π+2kπ], k∈Z. 由-π2+2kπ≤x+π4≤π2+2kπ,k∈Z,
栏目 导引
第一章 三角函数
由-π2+2kπ≤x-π4≤π2+2kπ,k∈Z, 得-π4+2kπ≤x≤34π+2kπ,k∈Z; 由π2+2kπ≤x-π4≤32π+2kπ,k∈Z, 得34π+2kπ≤x≤74π+2kπ,k∈Z. 所以函数 y=sin(x-π4)的单调增区间为[-π4 +2kπ,34π+2kπ](k∈Z);
∴y=sin12x 的周期是 4π.
(2)∵2sinx3-π6+2π=2sinx3-π6, 即 2sin13(x+6π)-π6
栏目 导引
=2sinx3-π6, ∴y=2sinx3-π6的周期是 6π.
(3)y=|sinx|的图象如图所示.
第一章 三角函数
∴周期T=π.
∴|φ|的最小值|φ|min=2π+π2-83π=π6.
栏目 导引
归纳总结
第一章 三角函数
栏目 导引
函 数 y= sinx (k∈z)
性质
y= cosx 第(k一∈章z) 三角函数
定义域 值域
最值及相应的 x的 集合
单调性
对称轴 对称中心
第一章 三角函数
单调减区间为[34π+2kπ,74π+2kπ](k∈Z). 所以原函数 y=2sin(π4-x)的单调增区间为[34π +2kπ,74π+2kπ](k∈Z); 单调减区间为[-π4+2kπ,34π+2kπ](k∈Z).
栏目 导引
第一章 三角函数
变式训练
3.求函数 y=2sin(x+π4)的单调区间. 解:y=sinx 的单调增区间为[-π2+2kπ,π2+ 2kπ],k∈Z;单调减区间为[π2+2kπ,32π+2kπ], k∈Z. 由-π2+2kπ≤x+π4≤π2+2kπ,k∈Z,
栏目 导引
第一章 三角函数
由-π2+2kπ≤x-π4≤π2+2kπ,k∈Z, 得-π4+2kπ≤x≤34π+2kπ,k∈Z; 由π2+2kπ≤x-π4≤32π+2kπ,k∈Z, 得34π+2kπ≤x≤74π+2kπ,k∈Z. 所以函数 y=sin(x-π4)的单调增区间为[-π4 +2kπ,34π+2kπ](k∈Z);
∴y=sin12x 的周期是 4π.
(2)∵2sinx3-π6+2π=2sinx3-π6, 即 2sin13(x+6π)-π6
栏目 导引
=2sinx3-π6, ∴y=2sinx3-π6的周期是 6π.
(3)y=|sinx|的图象如图所示.
第一章 三角函数
∴周期T=π.
∴|φ|的最小值|φ|min=2π+π2-83π=π6.
栏目 导引
归纳总结
第一章 三角函数
栏目 导引
函 数 y= sinx (k∈z)
性质
y= cosx 第(k一∈章z) 三角函数
定义域 值域
最值及相应的 x的 集合
单调性
对称轴 对称中心
正弦余弦函数的图像性质(周期、对称、奇偶)经典课件25页PPT

新知探究 :
1、正弦函数的单调性 y
1
y
1
2
o
2
o
-1
-1
3
2
2
x x
y=sinx x[0,2]
y
y=sinx xR
-4 -3
-2
1
- o
-1
正弦曲 线
2
3
4
5 6 x
新知探究:
1、正弦函数的单调性
y
-4 -3
-2
- 2
1
o
-1
2
2
3
4
5 6 x
x
2
…
0
…
正 正弦弦函数余.余弦弦函函数的数图象对和称性质性
-
-
-
6
4
2
对称轴:无数条
xk,kZ
2
-
-
-
6
4
2
对称轴:无数条 x=kπ,k∈Z
-
y
正弦 函数 y=sinx的 图象
1-
-
-
-
o - 1-
2
4
6
x
对称中心:无数个
(kπ,0),k∈Z
y
余 弦函 数 y =co sx的 图象
1-
-
-
-
o
复习回顾
一、正弦函数、余弦函数的图像及画法
正弦曲线
y
1-
-
-
6
4
2
o
-1-
2
4
6
x
6
4
余弦曲线
y-
1
2
o-
-1
2
4
6
探索发现
高中数学第五章三角函数4.2第二课时正余弦函数的单调性与最值课件新人教A版必修第一册

1.判断正误.(正确的画“√”,错误的画“×”) (1)正弦函数y=sin x在R 上是增函数. (2)余弦函数y=cos x的一个减区间是[0,π]. (3)∃x∈[0,2π]满足sin x=2. (4)当余弦函数y=cos x取最大值时,x=π+2kπ,k∈Z . 答案:(1)× (2)√ (3)× (4)×
函数单调递减,故函数的单调递减区间是
4kπ-23π,4kπ+43π
(k∈Z ).
(2)∵y=2sinπ4 -x=-2sinx-π4 ,
∴函数y=-2sinx-π4 的单调增区间、单调减区间分别由下面的不等式确定.
2kπ+π2 ≤x-π4 ≤2kπ+3π2 (k∈Z ),
①
ππ
π
2kπ- 2 ≤x- 4 ≤2kπ+ 2 (k∈Z ).
知识点 正、余弦函数的单调性与最值 正弦函数
图象
值域
_[-__1_,__1_]
ห้องสมุดไป่ตู้
余弦函数 _[-__1_,__1_]
正弦函数
余弦函数
单
增区间 __-_π_2_+__2_k_π__,___π2__+_2_k_π___, [_π__+__2k_π__,__2_π__+__2_kπ__]_,_
调
__k_∈_Z____
所以sinπ5 <sin2π 5 ,
所以sin215π<425π.
答案:<
4.求函数f(x)=sin2x-π4 在0,π2 上的单调递增区间.
π
π
π
解:令2kπ- 2 ≤2x- 4 ≤2kπ+ 2 ,k∈Z ,
解得kπ-π8 ≤x≤kπ+3π8 ,k∈Z ,又0≤x≤π2 ,
所以f(x)在0,π2 上的单调递增区间是0,3π 8 .
高一数学必修第一册正弦函数、余弦函数的性质课件
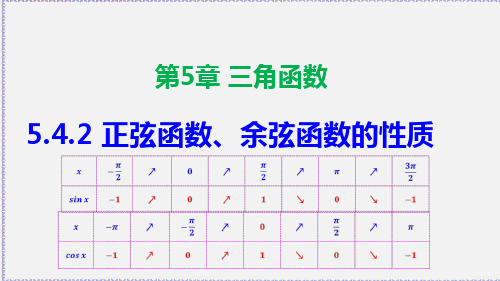
上都单调递减,其值从1减小到-1.
最大值与最小值
【整理】从上述对正弦函数、余弦函数的单调性的讨论中容易得到:
+ ( ∈ ) 时取得最大值1,
当且仅当 = − + ( ∈ ) 时取得最小值-1;
①正弦函数当且仅当 =
②余弦函数当且仅当 = ( ∈ ) 时取得最大值1,
【1】周期性:观察正弦函数的图像,可以发现,在图像上,横坐标每隔2π个单位
长度,就会出现纵坐标相同的点,这就是正弦函数值具有的“周而复始”的
变化规律.实际上,这一点既可以从定义中看出,也能从诱导公式中得到反映.即自
变量 的值加上2π的整数倍时所对应的函数值,与 所对应的函数值相等.数学
上用周期性来定量地刻画这种“周而复始”的规律.
如何用自变量的系数表示上述函数的周期呢?
事实上,令 = + ,那么由 ∈ 得 ∈ ,且函数 = , ∈ 及函数
= , ∈ 的周期都是.
因为 + = + + = +
+ ,所以自变量增加 ,函数值
+ ,
+ ( ∈ ) 上都单调递减,其值从1减小到-1.
单调性
−
−
−
同样的道理结合余弦函数的周期性我们可以知道:
余弦函数在每一个闭区间
在每一个闭区间
− + , ( ∈ ) 上都单调递增,其值从-1增大到1;
, + ( ∈ )
关于y轴对称.所以正弦函数是奇函数,余弦函数是偶函数.
正余弦函数图像和性质PPT课件

(2)余弦函数“五点作图法”:
y 1 y=cosx
3 2
2
o
2
-1
3 2
Y=sinx 2 5 3 x
2
五个关 键点:
( 0 ,1),
( ,0 ), 2
( , 1), ( 3 , 0 ) , ( 2 ,1)
2
(3)正、余弦函数图象的关系
cosx=sin(x+
2
y=cosx
y
) sinx=cos( -x)=cos(x- )
定义域 值域 周期性 对称性 单调性
性质的应. 用
3
一.基础知识复习
(一)正、余弦函数图象
“五点作图法”
(1)正弦函数“五点作图法”:
y
1
4
3
2
-
3 2
-
-
2
o
2
3 2
2
3
4 x
-1
五个关键点:
( 0 , 0 ) ,(
2
, 1 ) , ( , 0 ) ,( 3
2
, 1)(, 2 , 0 )
正 余弦函数的图象与性质(1)
y
1
ysinx,x[0,2
3p
π
2
2π
O
p
x
2
-1
思考4:观察函数y=sin在[0,2π]内的 图象,其形状、位置、凸向等有何变化 规律?
《正弦函数、余弦函数的图象和性质》的知识框架
正弦线 正弦函数的图象 平移变换 余弦函数的图象
正弦函数的性质 “五点法”作 图
余弦函数的性质
⑤奇偶性:
奇偶性的y1定义y=:sif f n( ( x x x ) ) ( x ff R( ( x x )) ) ff( ( x x ) ) 为 为 偶 奇 函 函 数 数
正弦、余弦函数的奇偶性、单调性

]
9 3 1 当 2k x 2k 即 6k x 6k , k Z 为减区间 4 4 2 3 4 x 9 3 当 2k 2k 即 6k x 6k , k Z 为增区间 3 4 2 4 4
正弦、余弦函数的单调性
余弦函数的单调性
y
1 -3
5 2
-2
3 2
-
2
o
-1
2
3 2
2
5 2
x
3
7 2
4
x
cosx
- -1
…
2
…
0
1
…
2
…
-1
0
0
y=cosx (xR) 增区间为 [ +2k, 2k],kZ + ], kZ 减区间为 [2k, 2k, 其值从-1增至1 其值从 1减至-1
uyd79vau
接。乔氏母女俩和耿老爹父子们去江边做完“尽七”祭奠返回时,船老大亲自将五佰两纹银送到白家来。并且说:“以后,白兄弟的 “百日”祭和“周年”祭,我还会派马车接送。”乔氏母女一再谢绝,说:“千万不要再费心了。路不远,我们自己走去就行!”船老 大说:“这没有什么费心的,反正我和我那帮兄弟们也要祭奠的。”临走时,这位实在够意思的船老大还一再叮嘱乔氏,娘儿俩以后的 生活如果有什么困难,一定告诉他。他中肯地说:“白兄弟的家眷,我会负责一辈子的!”进入腊月后,新鲜蔬菜相对少了不少,因此 贩卖蔬菜的生意就有些惨淡了。不过,水果零售的生意倒还不错。耿老爹决定,让耿正兄妹仨继续每天批发一些水果,多多少少倒卖一 些,自己抽这个时间,动手割制新屋的顶棚架和门窗。这样,等到明年开春后,就可以为新屋装顶棚和安门窗了。等到做完这些以后, 再进行一次屋内石灰泥上面,也就是俗话说的“亮家”,五间新屋基本上就大功告成了。至于石灰泥干透后的屋内全面刷白处理,已经 是相对简单的事情了。得知了耿老爹的想法后,乔氏又去一个曾经帮助盖房的木匠老师傅那里,借回来一套木匠工具。做这些木工活计 之前,耿老爹专门渡江去汉口镇上跑了一趟。他估摸着,张老乡一家倘若顺利过了黄河继续往南进发的话,这个时候应该已经来到了, 但结果却令耿老爹大失所望。那天上午,当他寻找到张老乡曾经与人合伙开店的地方时,眼前看到的依然还是一片狼藉,而且整个汉口 镇街面上的行人都很少。耿老爹向遇到的每一个人反反复复地打听着:“请问,您是否看到和听到过有姓张的一家四口从北边过来了?” 每一个人都摇头,说既没有看到,也没有听说。这样,从上午一直打听到过午了,耿老爹感觉又饥又渴,便向一户人家讨了一碗水,就 着水啃了一个从武昌镇烧饼铺买了带过来的烧饼,然后继续沿着不同的街道打听。直到日头西斜,汉口镇上几乎所有的大街小巷都问遍 了,仍然没有任何结果。看来,张老乡一家确实没有来到这里。事已至此,耿老爹只能寄希望于张老乡在动身南下之前就听说了这里的 水灾,压根儿就没有动身来这里。或者说,他在刚出发到达省城或者什么地方的时候听说了,就转身返回去了。至于那个可怕的梦,耿 老爹当时虽然感觉有些蹊跷,也曾经伤心得泪流满面胸口发紧,但他现在宁愿不相信了。他一遍又一遍地对自己说:“什么呀,张大哥 根本就没有南下,根本就没有走到黄河边儿!”抬头看看,日头还有半杆子高。耿老爹又来到原先自家开的粮油零售店前,看到店铺门 上的大铁锁已经锈迹斑斑的了。再看门上贴的那一纸留言,虽然字迹有些模糊了,但依然还在。而那个没有了院墙的小后院儿,到现在 还是那样敞着
5..4.1正弦函数、余弦函数的图象 课件

弦函数的图象?
高中数学必修第一册
知识小结
3.函数 = , ∈ 的图象:
余弦函数的图象叫做余弦曲线,它是与正弦函数具有相同形状的“波
浪起伏”的连续光滑曲线.
高中数学必修第一册
问题探究
探究:8.类似于“五点法”作正弦函数的图象,如何作出余弦
函数的图象?
高中数学必修第一册
问题探究
探究:8.类似于“五点法”作正弦函数的图象,如何作出余弦
(1) = 1 + , ∈ [0,2];
x
0
2
3
2
2
sin x
0
1
0
-1
0
1 sin x
1
2
1
0
1
高中数学必修第一册
典例精析
例1 画出下列函数的简图:
(2) = −, ∈ [0,2].
x
0
2
3
2
2
cos x
1
0
-1
0
1
cos x
-1
0
1
0
-1
往往起重要的作用.你能画出函数 = , ∈ [0,2]图象的
简图吗?在确定图象形状时,应抓住哪些关键点?
五点(画图)法:
高中数学必修第一册
问题探究
探究:7.由三角函数的定义可知,正弦函数、余弦函数是一对
密切关联的函数.你认为应该利用正弦函数和余弦函数的哪些
关系,通过怎样的图形变换,才能将正弦函数的图象变换为余
R
R
[-1,1]
[-1,1]
奇偶性
奇函数
偶函数
对称中心
对称轴
高中数学必修第一册
高中数学必修第一册
知识小结
3.函数 = , ∈ 的图象:
余弦函数的图象叫做余弦曲线,它是与正弦函数具有相同形状的“波
浪起伏”的连续光滑曲线.
高中数学必修第一册
问题探究
探究:8.类似于“五点法”作正弦函数的图象,如何作出余弦
函数的图象?
高中数学必修第一册
问题探究
探究:8.类似于“五点法”作正弦函数的图象,如何作出余弦
(1) = 1 + , ∈ [0,2];
x
0
2
3
2
2
sin x
0
1
0
-1
0
1 sin x
1
2
1
0
1
高中数学必修第一册
典例精析
例1 画出下列函数的简图:
(2) = −, ∈ [0,2].
x
0
2
3
2
2
cos x
1
0
-1
0
1
cos x
-1
0
1
0
-1
往往起重要的作用.你能画出函数 = , ∈ [0,2]图象的
简图吗?在确定图象形状时,应抓住哪些关键点?
五点(画图)法:
高中数学必修第一册
问题探究
探究:7.由三角函数的定义可知,正弦函数、余弦函数是一对
密切关联的函数.你认为应该利用正弦函数和余弦函数的哪些
关系,通过怎样的图形变换,才能将正弦函数的图象变换为余
R
R
[-1,1]
[-1,1]
奇偶性
奇函数
偶函数
对称中心
对称轴
高中数学必修第一册
高中数学《正弦函数、余弦函数的性质(2)》课件

课前预习
课堂互动
课堂反馈
预习教材 P37-38 完成下面问题: 知识点 正弦函数、余弦函数的图象和性质
正弦函数
余弦函数
图象
值域
__[_-__1_,_1_] __
__[_-__1_,1_]___
课前预习
课堂互动
课堂反馈
正弦函数
余弦函数
单 调 性
在[_-__π2_+__2_k_π_,__π2_+__2_k_π_] (k∈Z) 上递增,在_[π2_+__2_k_π_,__3_2π_+__2_kπ]
课前预习
课堂互动
课堂反馈
解得a=12, b=1.
∴y=-4acos bx=-2cos x,
∴ymax=2,ymin=-2,T=2π.
课前预习
课堂互动
课堂反馈
规律方法 求三角函数值域或最值的常用方法 (1)可化为单一函数y=Asin(ωx+φ)+k或y=Acos(ωx+φ)+ k,其最大值为|A|+k,最小值-|A|+k(其中A,ω,k,φ为 常数,A≠0,ω≠0). (2)可化为y=Asin2x+Bsin x+C或y=Acos2x+Bcos x+C (A≠0),最大值、最小值可利用二次函数在定义域上的最大 值、最小值的求法来求(换元法).
课前预习
课堂互动
课堂反馈
方向 3 含参数的最值问题 【例 3-3】 若函数 y=a-bcos x(b>0)的最大值为32,最小值为
-12,求函数 y=-4acos bx 的最值和最小正周期. 解 ∵y=a-bcos x(b>0), ∴ymax=a+b=32,ymin=a-b=-12. 由aa+-bb==32-,12,
课前预习
课堂互动
课堂反馈
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
所以该函数的单调递减区间是:
5 [ k, k ],k Z 8 8
3 [ , ] 2 2
0.9 1.3 sin 0.9 sin 1.3
不查表比较下列各组数的大小
(3) cos0.9与cos0.3
余弦函数单调区间有
[ ,0]
[0, ]
[ ,2 ]
[ 2 ,3 ] [3 ,4 ] [ 4 ,5 ]
[0, ]
0.9 0.3 cos 0.9 cos 0.3
1 y 2 sin( x ) 2 6
2 2 6 2 4 10 得 4k x 4k 3 3 4 所以该函数的单调递减区间是:
10 [ 4k, 4k ] 3 3
(k Z )
(2) y 1 cos( 2 x
4
)
解: 由 2k 2 x 2k, 4 5 得 k x k, 8 8
[ 4 ,5 ]
1330与2200不在任何一个单调区间 0 0 0 0 cos220 cos(360 220 ) cos140 0 0 0 0 比较cos133 与cos140 133 140
[0, ]
cos133 cos140 cos 220
0 0
0
练习 不查表比较下列各组数的大小
是增函数
23 17 (2) cos( )与 cos( ) 5 4
23 23 3 解: cos( ) cos cos 5 5 5 17 17 1 cos( ) cos cos
4 4 1 3 因为 0 4 5 4 ,且函数
(1) sin 123 与sin 177
0
0
0
(2) cos218 与cos269
0
(3) sin 211 与sin 320
0
0 0
0
(4) cos48 与cos(310 )
4. 不查表比较下列各组数的大小
(1) sin(
18
)与 sin(
10
)
解: 因为 2 10 18 2 且函数y=sinx, x [ , ] 2 2 所以 sin( ) sin( ) 18 10
0 0 0
0
比较sin 32 与sin 43
0
0
[
32 43
0
0
0
0
0
, ] 2 2
sin 32 sin 43 sin 137
不查表比较下列各组数的大小
(6) cos(133 )与cos(220 )
0 0
余弦函数单调区间有
[ ,0]
[0, ]
[ ,2 ]
[ 2 ,3 ] [3 ,4 ]
y cos x,x [0, ] 是减函数,所以 1 17 3 23 cos cos 即 cos( ) cos( ) 4 4 5 5
二层练习
3.求下列各函数的单调递减区间 (1)
3 解: 因为函数y=sinx的单调递减区间是 [ 2k, 2k ] 2 2 1 3 由 2k x 2k
2.判断下列命题的对错:
(1)函数y=sinx在第一象限是增函数 (2) 函数y=cosx在 [0, ]上是增函数
错
2
对
(3) 函数 y sin x 在 [, ]上是增函数
不查表比较下列各组数的大小
(1) sin 31 与sin 46
0
0
正弦函数的单调区间有 3 3 5 5 7 7 9 9 11 [ , ] [ , ] [ , ] [ , ] [ , ] [ , ] 2 2 2 2 2 2 2 2 2 2 2 2
不查表比较下列各组数的大小
余弦函数单调区间有
[ ,0]
(4) cos( )与 cos( ) 5 7
[0, ]
[ ,2 ]
[ 2 ,3 ] [3 ,4 ]
[ 4 ,5 ]
[ ,0]
5
7
cos( ) cos( ) 5 7
不查表比较下列各组数的大小
2、区间长度为
余弦函数
y 1
-2 -
o -1
[ ,2 ]
x
2 3 4
单调区间有
[ ,0]
[0, ]
[ 2 ,3 ] [3 ,4 ]
[ 4 ,5 ]
1、端点是整数个 3、区间起点为奇数个 4、区间起点为偶数个
单调区间的特点
2、区间长度为 的区间为增区间 的区间为减区间
(5) sin 32 与sin 137
0
0
正弦函数的单调区间有 3 3 5 5 7 7 9 9 11 [ , ] [ , ] [ , ] [ , ] [ , ] [ , ] 2 2 2 2 2 2 2 2 2 2 2 2 320与1370不在任何一个单调区间
sin 137 sin(180 137 ) sin 43
[
, ] 2 2
31 46
0 0
0 0
sin 31 sin 46
不查表比较下列各组数的大小
(2) sin 0.9与sin 1.3
正弦函数的单调区间有 3 3 5 5 7 7 9 9 11 [ , ] [ , ] [ , ] [ , ] [ , ] [ , ] 2 2 2 2 2 2 2 2 2 2 2 2
函数 y=sinx
奇偶性
单调增区间
[ 2k, 2k ] 2 2 (k Z )
单调减区间
3 [ 2k, 2k ] 2 2 (k Z )来自奇函数y=cosx
偶函数
[ 2k, 2k ] 2 k Z
[2k, 2k ] (k Z )
一层练习
观察正弦函数和余弦函数的图象
正弦函数
y 1
-2 -
o -1
x
2 3 4
单调区间有 3 3 5 5 7 7 9 9 11 [ , ] [ , ] [ , ] [ , ] [ , ] [ , ] 2 2 2 2 2 2 2 2 2 2 2 2
单调区间的特点
1、端点是二分之个
5 [ k, k ],k Z 8 8
3 [ , ] 2 2
0.9 1.3 sin 0.9 sin 1.3
不查表比较下列各组数的大小
(3) cos0.9与cos0.3
余弦函数单调区间有
[ ,0]
[0, ]
[ ,2 ]
[ 2 ,3 ] [3 ,4 ] [ 4 ,5 ]
[0, ]
0.9 0.3 cos 0.9 cos 0.3
1 y 2 sin( x ) 2 6
2 2 6 2 4 10 得 4k x 4k 3 3 4 所以该函数的单调递减区间是:
10 [ 4k, 4k ] 3 3
(k Z )
(2) y 1 cos( 2 x
4
)
解: 由 2k 2 x 2k, 4 5 得 k x k, 8 8
[ 4 ,5 ]
1330与2200不在任何一个单调区间 0 0 0 0 cos220 cos(360 220 ) cos140 0 0 0 0 比较cos133 与cos140 133 140
[0, ]
cos133 cos140 cos 220
0 0
0
练习 不查表比较下列各组数的大小
是增函数
23 17 (2) cos( )与 cos( ) 5 4
23 23 3 解: cos( ) cos cos 5 5 5 17 17 1 cos( ) cos cos
4 4 1 3 因为 0 4 5 4 ,且函数
(1) sin 123 与sin 177
0
0
0
(2) cos218 与cos269
0
(3) sin 211 与sin 320
0
0 0
0
(4) cos48 与cos(310 )
4. 不查表比较下列各组数的大小
(1) sin(
18
)与 sin(
10
)
解: 因为 2 10 18 2 且函数y=sinx, x [ , ] 2 2 所以 sin( ) sin( ) 18 10
0 0 0
0
比较sin 32 与sin 43
0
0
[
32 43
0
0
0
0
0
, ] 2 2
sin 32 sin 43 sin 137
不查表比较下列各组数的大小
(6) cos(133 )与cos(220 )
0 0
余弦函数单调区间有
[ ,0]
[0, ]
[ ,2 ]
[ 2 ,3 ] [3 ,4 ]
y cos x,x [0, ] 是减函数,所以 1 17 3 23 cos cos 即 cos( ) cos( ) 4 4 5 5
二层练习
3.求下列各函数的单调递减区间 (1)
3 解: 因为函数y=sinx的单调递减区间是 [ 2k, 2k ] 2 2 1 3 由 2k x 2k
2.判断下列命题的对错:
(1)函数y=sinx在第一象限是增函数 (2) 函数y=cosx在 [0, ]上是增函数
错
2
对
(3) 函数 y sin x 在 [, ]上是增函数
不查表比较下列各组数的大小
(1) sin 31 与sin 46
0
0
正弦函数的单调区间有 3 3 5 5 7 7 9 9 11 [ , ] [ , ] [ , ] [ , ] [ , ] [ , ] 2 2 2 2 2 2 2 2 2 2 2 2
不查表比较下列各组数的大小
余弦函数单调区间有
[ ,0]
(4) cos( )与 cos( ) 5 7
[0, ]
[ ,2 ]
[ 2 ,3 ] [3 ,4 ]
[ 4 ,5 ]
[ ,0]
5
7
cos( ) cos( ) 5 7
不查表比较下列各组数的大小
2、区间长度为
余弦函数
y 1
-2 -
o -1
[ ,2 ]
x
2 3 4
单调区间有
[ ,0]
[0, ]
[ 2 ,3 ] [3 ,4 ]
[ 4 ,5 ]
1、端点是整数个 3、区间起点为奇数个 4、区间起点为偶数个
单调区间的特点
2、区间长度为 的区间为增区间 的区间为减区间
(5) sin 32 与sin 137
0
0
正弦函数的单调区间有 3 3 5 5 7 7 9 9 11 [ , ] [ , ] [ , ] [ , ] [ , ] [ , ] 2 2 2 2 2 2 2 2 2 2 2 2 320与1370不在任何一个单调区间
sin 137 sin(180 137 ) sin 43
[
, ] 2 2
31 46
0 0
0 0
sin 31 sin 46
不查表比较下列各组数的大小
(2) sin 0.9与sin 1.3
正弦函数的单调区间有 3 3 5 5 7 7 9 9 11 [ , ] [ , ] [ , ] [ , ] [ , ] [ , ] 2 2 2 2 2 2 2 2 2 2 2 2
函数 y=sinx
奇偶性
单调增区间
[ 2k, 2k ] 2 2 (k Z )
单调减区间
3 [ 2k, 2k ] 2 2 (k Z )来自奇函数y=cosx
偶函数
[ 2k, 2k ] 2 k Z
[2k, 2k ] (k Z )
一层练习
观察正弦函数和余弦函数的图象
正弦函数
y 1
-2 -
o -1
x
2 3 4
单调区间有 3 3 5 5 7 7 9 9 11 [ , ] [ , ] [ , ] [ , ] [ , ] [ , ] 2 2 2 2 2 2 2 2 2 2 2 2
单调区间的特点
1、端点是二分之个
