三角函数单调性及最值_刘老师
三角函数的单调性与周期知识点

三角函数的单调性与周期知识点三角函数是数学中一类重要的函数,包括正弦函数、余弦函数、正切函数等。
研究三角函数的单调性与周期是深入理解和应用三角函数的基础。
在本文中,我们将重点讨论三角函数的单调性与周期的相关知识点。
一、正弦函数的单调性与周期正弦函数是最常见的三角函数之一,可以表示周期性的波动现象。
正弦函数的标准形式为:f(x) = A*sin(Bx + C) + D,其中A、B、C和D 为常数。
1. 单调性:正弦函数的单调性与其幅值A有关。
当A>0时,正弦函数在每个周期内先上升后下降,即先递增后递减,如图1所示。
当A<0时,正弦函数在每个周期内先下降后上升,即先递减后递增,如图2所示。
插入图1和图22. 周期:正弦函数的周期与参数B有关。
正弦函数的周期为2π/B,其中B 为正数。
当B增大时,正弦函数的周期变短,波动速度加快;当B减小时,正弦函数的周期变长,波动速度减慢。
二、余弦函数的单调性与周期余弦函数也是常用的三角函数之一,可以表示周期性的波动现象。
余弦函数的标准形式为:f(x) = A*cos(Bx + C) + D,其中A、B、C和D为常数。
1. 单调性:余弦函数的单调性与其幅值A有关。
当A>0时,余弦函数在每个周期内先下降后上升,即先递减后递增,如图3所示。
当A<0时,余弦函数在每个周期内先上升后下降,即先递增后递减,如图4所示。
插入图3和图42. 周期:余弦函数的周期与参数B有关。
余弦函数的周期为2π/B,其中B 为正数。
当B增大时,余弦函数的周期变短,波动速度加快;当B减小时,余弦函数的周期变长,波动速度减慢。
三、正切函数的单调性与周期正切函数是三角函数中的一种特殊函数,可以表示角度的对称性关系。
正切函数的标准形式为:f(x) = A*tan(Bx + C) + D,其中A、B、C 和D为常数。
1. 单调性:正切函数在每个周期内都存在间断点,因此不存在严格的单调性。
三角函数的单调性、奇偶性、周期性、最值、对称性

考点56 三角函数的单调性、奇偶性、周期性、最值、对称性1.(13大纲T12)已知函数()=cos sin 2f x x x ,下列结论中错误的是 ( )A.()y f x =的图象关于()π,0中心对称B.()y f x =的图象关于直线π2x =对称C.()f x ()f x 既奇函数,又是周期函数 【测量目标】三角函数的周期性、最值,对称性. 【难易程度】中等 【参考答案】C 【试题解析】A项,因为(2π)cos(2π)sin(4π2)cos()sin(2)cos sin 2()f x x x x x x x f x -=--=--=-=- ()f x 的图象关于点(,0)π中心对称,故正确.(步骤1)B 项,因为(π)cos(π)sin(2π2)cos sin 2(),f x x x x x f x -=--==所以()y f x =的图象关于直线2x π=对称,故正确,(步骤2)C 项,由题意知()()22=2cos sin 21sin sin f x x x x x =-.令sin t x =,[]1,1t ∈-,则()()232122g t t t t t =-=-.(步骤3)令()2260g t t '=-=,得=t ±.当1t =±时,函数值为0;当t =时,函数值为t =.∴()max g t =()f x 故选C.(步骤4)D 项,由()cos()sin(2)cos sin 2()f x x x x x f x -=--=-=-知其为奇函数, 综合选项A 、B 知()f x 为周期函数,故正确.(步骤5)2.(13T17)设向量)()π,sin ,cos ,sin ,0,.2x x x x x ⎡⎤==∈⎢⎥⎣⎦a b(I )若=a b 求x 的值; (Ⅱ)设函数()f x =a b ,求()f x 的最大值.【测量目标】平面向量的基本概念、向量的数量积运算、两角和与差的正弦和三角函数的最值.【难易程度】容易【试题解析】(Ⅰ)2222222)sin 4sin ,cos sin 1,x x x x x =+==+=a b ,=a b∴24sin 1.x = (步骤1)又x ∈π0,2⎡⎤⎢⎥⎣⎦,∴1sin ,2x =∴π6x =. (步骤2)(Ⅱ)()3sin f x x ==a b 211π1cos sin 2cos 2sin(2),2262x x x x x +=-+=-+ ∴当π3x =∈π0,2⎡⎤⎢⎥⎣⎦时,πsin(2)6x -取最大值1. (步骤3) ∴()f x 的最大值为32. (步骤4)3.(13T15)已知函数2π()26sin cos 2co ,s 41f x x x x x x ⎛⎫=++- ⎪⎝⎭+∈R .(Ⅰ) 求f (x )的最小正周期;(Ⅱ) 求f (x )在区间π0,2⎡⎤⎢⎥⎣⎦上的最大值和最小值.【测量目标】三角函数的周期性和最值. 【难易程度】容易【试题解析】(I)()ππ2cos2sin 3sin 2cos 244f x x x x x =+- π2sin 22cos 224x x x ⎛⎫=-=- ⎪⎝⎭,故()f x 的最小正周期2ππ2T ==;(步骤1) (II)因为()f x 在区间3π0,8⎡⎤⎢⎥⎣⎦上单调递增,在区间3ππ,82⎡⎤⎢⎥⎣⎦上单调递减,并且()02f =-,3π8f ⎛⎫=⎪⎝⎭,π22f ⎛⎫= ⎪⎝⎭,故()f x 在π0,2⎡⎤⎢⎥⎣⎦上的最大值为2-.(步骤2)4.(13T21)已知函数()2sin()f x x ω=,其中常数0ω>;(1)若()y f x =在π2π[,]43-上单调递增,求ω的取值围; (2)令2ω=,将函数()y f x =的图像向左平移π6个单位,再向上平移1个单位,得到函数()y g x =的图像,区间[,]a b (,a b ∈R 且a b <)满足:()y g x =在[,]a b 上至少含有30个零点,在所有满足上述条件的[,]a b 中,求b a -的最小值. 【测量目标】三角函数的单调性,周期,图像及其变化. 【难易程度】中等【试题解析】(1)因为0ω>,根据题意有ππ34202ππ432ωωω⎧--⎪⎪⇒<⎨⎪⎪⎩(步骤1) (2) ()2sin(2)f x x =,ππ()2sin(2())12sin(2)163g x x x =++=++ π1π()0sin(2)π324g x x x k =⇒+=-⇒=-或5π+π,12x k k =∈Z ,即()g x 的零点相离间隔依次为π3和2π3,(步骤2)故若()y g x =在[,]a b 上至少含有30个零点, 则b a -的最小值2ππ43π1415333⨯+⨯=.(步骤3) 5.(13新课标Ⅰ T15)设当x =θ时,函数f (x )=sin x -2cos x 取得最大值,则cos θ=__________.【测量目标】三角恒等变换,利用三角函数求最值. 【难易程度】较难【参考答案】【试题解析】f (x )=sin x -2cos xx x ⎫⎪⎭,(步骤1) 令cos αsin α=-f (x )α+x ),(步骤2) 当x =2k π+π2-α(k ∈Z )时,sin(α+x )有最大值1,f (x )(步骤3)即θ=2k π+π2-α(k ∈Z ),所以cos θ=πcos 2π+2k α⎛⎫- ⎪⎝⎭=πcos 2α⎛⎫- ⎪⎝⎭=sin α=5=-(步骤4) 6.(13T11)函数2sin 2yx x =+的最小正周期为T 为 . 【测量目标】三角函数的周期.【难易程度】容易 【参考答案】π【试题解析】2πsin 2sin 222sin(2)3y x x x x x =+==-+,故最小正周期为2ππ2T ==. 7.(13T1)函数π3sin(2)4y x =-的最小正周期为.【测量目标】三角函数的周期性. 【难易程度】容易 【参考答案】π【试题解析】函数π3sin(2)4y x =-的最小正周期2ππ2T ==. 8.(13T16)已知函数f (x )=4cos ωx πsin 4x ω⎛⎫+⎪⎝⎭(ω>0)的最小正周期为π. (1)求ω的值;(2)讨论f (x )在区间π0,2⎡⎤⎢⎥⎣⎦上的单调性.【测量目标】二倍角,两角和的正弦,函数sin()y A x ωϕ=+的图象与性质,三角函数的单调性、周期性. 【难易程度】中等【试题解析】(1)f (x )=4cos ωx sin π4x ω⎛⎫+⎪⎝⎭=ωx cos ωx +2ωxωx +cos 2ωx )π2sin 24x ω⎛⎫=++ ⎪⎝⎭步骤1)因为f (x )的最小正周期为π,且ω>0,从而有2π=π2ω,故ω=1.(步骤2)(2)由(1)知,f (x )=π2sin 24x ⎛⎫+ ⎪⎝⎭若0x π2,则ππ5π2444x +.(步骤3)当πππ2442x +,即π08x 时,f (x )单调递增; 当ππ5π2244x +,即ππ82x 时,f (x )单调递减.(步骤4) 综上可知,f (x )在区间π0,8⎡⎫⎪⎢⎣⎭上单调递增,在区间ππ,82⎡⎤⎢⎥⎣⎦上单调递减.(步骤5)9.(13T16)已知向量1cos ,2x ⎛⎫=- ⎪⎝⎭a ,=b ),cos 2,x x x ∈R ,设函数()=f x a b .(1)求()f x 的最小正周期;(2)求()f x 在π0,2⎡⎤⎢⎥⎣⎦上的最大值和最小值. 【测量目标】平面向量的数量积运算,三角函数的周期、最值. 【难易程度】容易 【试题解析】()1()cos,3sin ,cos 22f x x x ⎛⎫=- ⎪⎝⎭1sin cos 22x x x =-12cos 222x x =-ππcos sin 2sin cos 266x x =-πsin 26x ⎛⎫=- ⎪⎝⎭.(步骤1)(1)()f x 最小正周期为2πT ω=2ππ2==,即函数()f x 的最小正周期为π.(步骤2)(2)π0,2x ∴ππ5π2.666x --(步骤3) 由正弦函数图象的性质得,当ππ262x -=,即π3x =时,()f x 取得最大值1.(步骤4)当ππ266x -=-,即0x =时,(0)f =12-.(步骤5)当π5π266x -=,即π2x =时,π1()22f =,(步骤6)()f x ∴的最小值为12-.因此,()f x 在π(0,)2上的最大值是1,最小值是12-.(步骤7)10.(13T4)已知函数()cos()(0,0,)f x A x A ωϕωϕ=+>>∈R , 则“)(x f 是奇函数”是π2ϕ=的( ) A .充分不必要条件B. 必要不充分条件 C. 充分必要条件D.既不充分也不必要条件【测量目标】三角函数的性质,三角函数的诱导公式和三角函数的奇偶性. 【难易程度】中等 【参考答案】B【试题解析】若φ=π2,则f (x )=A cos(ωx +π2)⇒f (x )=-A sin(ωx )(A >0,ω>0,x ∈R )是奇函数;若f (x )是奇函数⇒f (0)=0,∴f (0)=A cos(ω×0+φ)=A cos φ=0.∴φ=k π+π2,k ∈Z ,不一定有φ=π2,“f (x )是奇函数”是“φ=π2”必要不充分条件.故选B.11.(12T17)已知向量(cos sin sin )x x x ωωω=-,a ,(cos sin )x x x ωωω=--b ,设函数()()f x x λ=+∈R a b 的图象关于直线πx =对称,其中ω,λ为常数,且1(,1)2ω∈.(Ⅰ)求函数()f x 的最小正周期; (Ⅱ)若()y f x =的图象经过点π,04⎛⎫⎪⎝⎭,求函数()f x 在区间3π0,5⎡⎤⎢⎥⎣⎦上的取值围. 【测量目标】平面向量的数量积运算,三角函数的变换及化简. 【难易程度】容易 【试题解析】(I )因为22()sin cos cos f x x x x ωωωλ=-+cos22.x x ωωλ=-+π2sin(2)6x ωλ=-+(步骤1).由直线πx =是()y f x =图象的一条对称轴,可πsin(2π)16ω-=±,所以ππ2ππ+()62k k ω-=∈Z ,即1().23k k ω=+∈Z 又1(,1)2k ω∈∈Z ,,所以k =1,故56ω=,所以()f x 的最小正周期为6π5.(步骤2)(II )由()y f x =的图象过点π(,0)4,得π()04f =,(步骤3)即5πππ2sin()2sin 6264λ=-⨯-=-=即λ=故5π()2sin()36f x x =--(步骤4)由3π0,5x 有π5π5π,6366x --所以15πsin()1236x --,得5π12sin()222,36x ----故函数()f x 在3π0,5⎡⎤⎢⎥⎣⎦上的取值围为12⎡---⎣.(步骤5) 12.(12T16)设函数2π())sin 4f x x x =++. (I )求函数()f x 的最小正周期;(II )设函数()g x 对任意x ∈R ,有π()()2g x g x +=,且当π[0,]2x ∈时, 1()()2g x f x =-,求函数()g x 在[π,0]-上的解析式. 【测量目标】两角和与差的三角函数公式,二倍角公式,三角函数的性质,求分段函数解析式.【难易程度】中等【试题解析】2π111()cos(2)sin cos 2sin 2(1cos 2)24222f x x x x x x =++=-+- 11sin 222x =-.(步骤1) (1)函数()f x 的最小正周期2ππ2T ==.(步骤2) (2)当π[0,]2x ∈时,11()()sin 222g x f x x =-=,(步骤3)当π[,0]2x ∈-时,ππ()[0,]22x +∈π1π1()()sin 2()sin 22222g x g x x x =+=+=-,当π[π,)2x ∈--时,π(π)[0,)2x +∈11()(π)sin 2(π)sin 222g x g x x x =+=+=.(步骤4)得:函数()g x 在[π,0]-上的解析式为1πsin 2(0),22()1πsin 2(π).22x x g x x x ⎧--⎪⎪=⎨⎪-<-⎪⎩(步骤5)13.(12T15) 已知函数(sin cos )sin 2()sin x x x f x x-=.(1)求()f x 的定义域及最小正周期; (2)求()f x 的单调递增区间.【测量目标】三角函数的定义域、周期、单调性. 【难易程度】容易 【试题解析】(sin cos )sin 2()sin x x x f x x -==(sin cos )2sin cos sin xx x xx-=2(sin cos )cos x x x-sin 21cos 2x x =--=π)14x --,{|π}x x k k ≠∈Z ,(步骤1)(1) 原函数的定义域为{|π,}x x k k ≠∈Z ,最小正周期为π;(步骤2) (2) 由πππ2π22π+,242k x k k --∈Z .解得π3πππ,,88k x k k -+∈Z 又{|π,}x x k k ≠∈Z ,原函数的单调递增区间为π[π,π)8k k k -+∈Z ,3π(π,π]8k k k +∈Z . (步骤3)14.(12T15)已知函数2ππ()sin(2)sin(2)2cos 1,33f x x x x x =++-+-∈R . (Ⅰ)求函数()f x 的最小正周期;(Ⅱ)求函数()f x 在区间ππ,44⎡⎤-⎢⎥⎣⎦上的最大值和最小值. 【测量目标】三角函数的周期性、最值. 【难易程度】中等【试题解析】(Ⅰ)2ππ()sin(2)sin(2)2cos 133f x x x x =++-+-ππ2sin 2coscos 2)34x x x =+=+ (步骤1) 函数()f x 的最小正周期为2ππ2T ==(步骤2) (Ⅱ)ππππ3π2π2sin(2)11()24444424x x x f x -⇒-+⇒-+⇔-(步骤3)当πππ2()428x x +==时,max ()f x πππ2()444x x +=-=-时,min ()1f x =-(步骤4)15.(12新课标T9)已知ω >0,函数()πsin()4f x x ω=+在π,π2⎛⎫⎪⎝⎭单调递减,则ω的取值围是( )15A.,24⎡⎤⎢⎥⎣⎦13B.,24⎡⎤⎢⎥⎣⎦1C.0,2⎛⎤⎥⎝⎦D (].0,2 【测量目标】三角函数的单调性. 【难易程度】中等 【参考答案】A【试题解析】由题意得,函数()πsin()4f x x ω=+的单调递减区间为ππ3π242x ω+, 则π5π44xω,(步骤1)所以π5π44xωω,则ππ5ππ424ωω且,解得1524ω.(步骤2) 故选A.16.(11T9)对于函数()sin f x a x bx c =++(其中,,a b ∈R ,c ∈Z ),选取,,a b c 的一组值计算()1f 和()1f -,所得出的正确结果一定不可能.....是( ) A .4和6 B .3和1 C .2和4 D .1和2 【测量目标】三角函数的奇偶性. 【难易程度】中等【参考答案】D【试题解析】()()()11sin1sin 12f f a b c a b c c +-=+++--+=,因为c ∈Z ,则()()11f f +-为偶数,四个选项中,只有D ,123+=不是偶数. 17.(11T8)函数ππsin()cos()26y x x =+-的最大值为 【测量目标】三角函数的最值.【难易程度】容易【试题解析】ππsin()cos()26y x x =+-=πcos cos()6x x -=1ππcos cos(2)266x ⎡⎤+-⎢⎥⎣⎦=1π23cos(2)2644x +-+. 18.(11T9)已知函数()sin(2)f x x ϕ=+,其中ϕ为实数,若π()()6f x f 对x ∈R 恒成立,且π()(π)2f f >,则()f x 的单调递增区间是( )A.ππ[π,π]()36k k k -+∈Z B.π[π,π]()2k k k +∈Z C.π2π[π,π]()63k k k ++∈Z D.π[π,π]()2k k k -∈Z 【测量目标】三角函数的单调性、最值.【难易程度】较难 【参考答案】C【试题解析】对x ∈R 时,π()()6f x f 恒成立,所以ππ()sin()163f ϕ=+=±,可得π5π2π2π66k k ϕϕ=+=-或,(步骤1) 因为π()sin(π)sin (π)sin(2π)sin 2f f ϕϕϕϕ=+=->=+=,故sin 0ϕ<, 所以5π2π6k ϕ=-,所以5π()sin 26f x x ⎛⎫=- ⎪⎝⎭,(步骤2) 函数单调递增区间为π5ππ2π22π262k x k -+-+,所以π2π[π,π]()63x k k k ∈++∈Z ,答案为C. (步骤3) 19.(11T15) 已知函数π()4cos sin()16f x x x =+-.(Ⅰ)求()f x 的最小正周期:(Ⅱ)求()f x 在区间ππ,64⎡⎤-⎢⎥⎣⎦上的最大值和最小值. 【测量目标】函数sin()y A x ωϕ=+的图像及其变换,两角和的正弦. 【难易程度】中等【试题解析】(Ⅰ)因为π()4cos sin()16f x x x =+-1)cos 21sin 23(cos 4-+=x x x (步骤1) 1cos 22sin 32-+=x x x x 2cos 2sin 3+=π2sin(2)6x =+(步骤2)所以)(x f 的最小正周期为π(步骤3)(Ⅱ)因为ππππ2π,2.64663x x --+所以 于是,当πππ2,626x x +==即时,)(x f 取得最大值2;(步骤4)当πππ2,,()666x x f x +=-=-即时取得最小值1-.(步骤5)20.(11全国T5)设函数()cos (0)f x x ωω=>,将()y f x =的图象向右平移π3个单位长度后,所得的图象与原图象重合,则ω的最小值等于 ( ) A.13B.3C.6D.9 【测量目标】三角函数的周期性,三角函数图象的平移变换. 【参考答案】C【试题解析】由题意得2ππ()3k k ω⨯=∈Z ,解得6k ω=,又0ω>,令1k =,得min 6ω=.21.(11T6)若函数()sin (0)f x x ωω=>在区间π[0,]3上单调递增,在区间ππ[,]32上单调递减,则ω= ( )A.3B. 2C. 32D. 23【测量目标】三角函数的单调性. 【难易程度】容易 【参考答案】C【试题解析】函数()sin (0)f x x ωω=>在区间π[0,]2ω上单调递增,在区间π3π[,]22ωω上单调递减,则ππ23ω=,即32ω=,答案应选C. 另解1:令ππ[2π,2π]()22x k k k ω∈-+∈Z 得函数()f x 在2ππ2ππ[,]22k k x ωωωω∈-+为增函数,同理可得函数()f x 在2ππ2π3π[,]22k k x ωωωω∈++为减函数,则当ππ0,23k ω==时符合题意,即32ω=,答案应选C.另解2:由题意可知当π3x =时,函数()sin (0)f x x ωω=>取得极大值,则π()03f '=,即πcos 03ωω=,即πππ()32k k ω=+∈Z ,结合选择项即可得答案应选C.另解3:由题意可知当π3x =时,函数()sin (0)f x x ωω=>取得最大值,则ππ2π()32k k ω=+∈Z ,36()2k k ω=+∈Z ,结合选择项即可得答案应选C.22.(11T17) 已知函数73()sin(π)cos(π),44f x x x x =++-∈R .( 1 )求()f x 的最小正周期和最小值; (2)已知44πcos(),cos(),(0)552a ββααβ-=+=-<<,求证:2[()]20f β-= 【测量目标】两角和差的正余弦,三角函数的周期性、最值. 【难易程度】中等. 【试题解析】(1)7π7π3π3π()sin cos cos sin cos cos sin sin 4444f x x x x x =+++x x = π2sin()4x =-max 2π,()2T f x ∴==(步骤1)(2)4cos()cos cos sin sin 5βααβαβ-=+=4cos()cos cos sin sin 5βααβαβ+=-=-cos cos 0αβ= ππ0cos 022αβββ<<⇒=⇒=2()(())20f f ββ∴=⇒-=(步骤2)23.(11新课标T11)设函数π()sin()cos()(0,)2f x x x ωϕωϕωϕ=+++><的最小正周期为π,且()()f x f x -=,则 ( )A.()f x 在π0,2⎛⎫ ⎪⎝⎭单调递减B.()f x 在π3π,44⎛⎫⎪⎝⎭单调递减C.()f x 在π0,2⎛⎫⎪⎝⎭单调递增D.()f x 在π3π,44⎛⎫⎪⎝⎭单调递增【测量目标】三角函数的周期性、奇偶性、单调性. 【难易程度】中等 【参考答案】A【试题解析】π())4f x x ωϕ=++,所以2ω=,(步骤1)又()f x 为偶函数,πππππ,424k k k ϕϕ∴+=+⇒=+∈Z ,π())22f x x x ∴=+=,选A (步骤2)24.(11新课标T16)在ABC 中,60,B AC ==2AB BC +的最大值为.【测量目标】正弦定理、三角函数的最值. 【难易程度】中等【参考答案】【试题解析】120120A C C A +=⇒=-,(0,120)A ∈,22sin sin sin BC ACBC A A B==⇒=(步骤1)22sin 2sin(120)sin sin AB ACAB C A C B==⇒==-sin A A =+;(步骤2)25sin sin())AB BC A A A A ϕϕ∴+=+=+=+,故最大值是(步骤3)25.(11T16)设()2πcos (sin cos )cos ()2f x x a x x x α∈=-+-R ,满足π()(0)3f f -=,求函数f(x)在π11π[,]424上的最大值和最小值. 【测量目标】由()sin y A x ωϕ=+的部分图象求解析式,利用函数的单调性求最值,二倍角. 【难易程度】中等【试题解析】()2πcos (sin cos )cos ()2f x x a x x x =-+- =22sin cos cos sin a x x x x -+=sin 2cos 22ax x -(步骤1)由π()(0)3f f -=得31122a +=-解得a = 所以()π2sin(2)6f x x =-,(步骤2) 所以ππ[,]43x ∈时πππ2[,]632x -∈,()f x 是增函数,(步骤3)所以π11π[,]324x ∈ 时ππ3π2[,]624x -∈,()f x 是减函数,(步骤4) 函数()f x 在π11π[,]424上的最大值是:π()23f =;(步骤5)又π()4f =11π()24f =;(步骤6)所以函数f(x)在π11π[,]424上的最小值为:11π()24f =(步骤7) 26.(10T16) 已知函数ππ()cos cos 33f x x x ⎛⎫⎛⎫=+-⎪ ⎪⎝⎭⎝⎭,()11sin 224g x x =-.(I )求函数()f x 的最小正周期;(II )求函数()()()h x f x g x =-的最大值,并求使()h x 取得最大值的x 的集合. 【测量目标】同角三角函数的基本关系,三角函数的周期性、最值.【难易程度】容易【试题解析】(I )ππ11()cos()cos()(cos )(cos )3322f x x x x x x =+-=+ =22131cos 233cos 211cos sin cos 2,448824x x x x x +--=-=- ()f x 的最小正周期为2ππ2=.(步骤1)(II )11π()()()cos 2sin 2),224h x f x g x x x x =-=-=+当π22π()4x k k +=∈Z 时,()h x 取得最大值22.(步骤2) ()h x 取得最大值时,对应的x 的集合为ππ,8x x k k ⎧⎫=-∈⎨⎬⎩⎭Z .(步骤3)27.(10T3)对于函数()2sin cos f x x x =,下列选项中正确的是 ( ) A.()f x 在(π4,π2)上是递增的 B.()f x 的图象关于原点对称 C.()f x 的最小正周期为2π D.()f x 的最大值为2 【测量目标】三角函数的单调性、对称性、周期性、最值. 【难易程度】容易 【参考答案】B【试题解析】∵()x x f 2sin =,∴易知()x f 在ππ,42⎛⎫⎪⎝⎭上是递减的,∴选项A 错误. ∵()x x f 2sin =,∴易知()x f 为奇函数,∴()x f 的图象关于原点对称,∴选项B 正确. ∵()x x f 2sin =,∴2π=π2T =,∴选项C 错误. ∵()x x f 2sin =,∴()x f 的最大值为1,∴选项D 错误. 故综上知,本题应选B .28.(10T16)已知函数2()3sin 22sin f x x x =-. (Ⅰ)求函数()f x 的最大值; (II )求函数()f x 的零点的集合.【测量目标】诱导公式,三角函数的最值,函数的零点. 【难易程度】中等【试题解析】(Ⅰ)因为π()32(1cos 2)2sin(2)1,6f x x x x =--=+-(步骤1) 所以,当ππ22π,62x k +=+即ππ()6x k k =+∈Z 时, 函数()f x 取得最大值1.(步骤2) (II )解法1 由(Ⅰ)及()0f x =得π1sin(2)62x +=(步骤3),所以 ππ22π,66x k +=+或π5π22π,66x k +=+即π,x k =或ππ.3x k =+(步骤4) 故函数()f x 的零点的集合为π|π,π.3x x k x k k ⎧⎫==+∈⎨⎬⎩⎭Z 或,(步骤5)解法2 由()0f x =得2cos 2sin ,x x x =,(步骤3)于是sin 0,x =sin ,x x =即tan x =(步骤4)由sin 0x =可知πx k =;由tan x =ππ.3x k =+(步骤5) 故函数()f x 的零点的集合为π|π,π.3x x k x k k ⎧⎫==+∈⎨⎬⎩⎭Z 或,(步骤6) 29.(10T16)已知函数()sin(3)(0,(,),0πf x A x A x =+>∈-∞+∞<<ϕϕ在π12x =时取得最大值为4. (1)求()f x 的最小正周期; (2)求()f x 的解析式;(3)若2π123125f ⎛⎫+=⎪⎝⎭α,求sinα.【测量目标】函数()sin y A x =+ωϕ的性质,三角函数的周期性. 【难易程度】中等 【试题解析】(1)min 2π2π3T ==ω.(步骤1) (2)由()f x 最大值为4,4A =,max ππ()()4sin 341212f x f ⎛⎫==⨯+= ⎪⎝⎭ϕ,即πsin 14⎛⎫+= ⎪⎝⎭ϕ,(步骤2)0π,<<ϕππ5π444∴<+<ϕπππ424⇒+=⇒=ϕϕ. π()4sin 34f x x ⎛⎫∴=+ ⎪⎝⎭.(步骤4)(3)2π2ππ124sin 3()31231245f ⎛⎫⎡⎤+=++=⎪⎢⎥⎝⎭⎣⎦αα,即2ππ3sin 3()31245⎡⎤++=⎢⎥⎣⎦α,π3sin 2,25⎛⎫+= ⎪⎝⎭α3cos 25⇒=α,(步骤5)223112sin sin 55-=⇒=αα,sin ∴=α.(步骤6) 30.(10T22)若实数x 、y 、m 满足x m y m -->,则称x 比y 远离m . (1)若21x -比1远离0,求x 的取值围;(2)对任意两个不相等的正数a 、b ,证明:33a b +比22a b ab +远离2;(3)已知函数()f x 的定义域k ππ,,24D x x k x ⎧⎫=≠+∈∈⎨⎬⎩⎭Z R .任取x D ∈,()f x 等于sin x 和cos x 中远离0的那个值.写出函数()f x 的解析式,并指出它的基本性质(结论不要求证明).【测量目标】解绝对值不等式,基本不等式证明不等式. 【难易程度】较难 【试题解析】(1)211x ->,211x ∴->或211x -<-(舍去)(步骤1)((),2,x ∴∈-∞+∞;(步骤2)(2)对任意两个不相等的正数a 、b ,有332a b +>222a b ab +>, (步骤3)()()23322220a b a b ab ab a b +--+-=+->,332222a b a b ab ∴+->+-,即33a b +比22a b ab +远离2;(步骤4)(3)π3πsin ,k π,π44()ππcos ,π,π44x x k f x x x k k ⎧⎛⎫∈++ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪∈-+ ⎪⎪⎝⎭⎩,(步骤5)性质:1︒()f x 是偶函数,图象关于y 轴对称;2︒()f x 是周期函数,最小正周期π2T =;3︒函数()f x 在区间ππππ,2422k k ⎡⎤++⎢⎥⎣⎦(k ∈Z )单调递增,在区间ππππ,2424k k ⎡⎤-+⎢⎥⎣⎦(k ∈Z )单调递减;4︒函数()f x 的值域为2⎤⎥⎣⎦.(步骤6) 31.(10T17)已知函数2()cos 2cos 1()f x x x x x =+-∈R(Ⅰ)求函数()f x 的最小正周期及在区间π0,2⎡⎤⎢⎥⎣⎦上的最大值和最小值;(Ⅱ)若006ππ(),,542f x x ⎡⎤=∈⎢⎥⎣⎦,求0cos 2x 的值. 【测量目标】三角函数、二倍角公式和三角函数的周期、最值. 【难易程度】中等【试题解析】 (1)由2()cos 2cos 1f x x x x =+-,得2π()cos )(2cos 1)2cos 22sin(2)6f x x x x x x x =+-=+=+所以函数()f x 的最小正周期为π(步骤1) 因为π()2sin 26f x x ⎛⎫=+⎪⎝⎭在区间π0,6⎡⎤⎢⎥⎣⎦上为增函数,在区间ππ,62⎡⎤⎢⎥⎣⎦上为减函数,又 ππ(0)1,2,162f f f ⎛⎫⎛⎫===- ⎪ ⎪⎝⎭⎝⎭,所以函数()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上的最大值为2,最小值为1-(步骤2)(Ⅱ)由(1)可知00π()2sin 26f x x ⎛⎫=+⎪⎝⎭又因为06()5f x =,所以0π3sin 265x ⎛⎫+= ⎪⎝⎭ 由0ππ,42x ⎡⎤∈⎢⎥⎣⎦,得0π2π7π2,636x ⎡⎤+∈⎢⎥⎣⎦从而200ππ4cos 21sin 2665x x ⎛⎫⎛⎫+=--+=- ⎪ ⎪⎝⎭⎝⎭ 所以0000ππππππ343cos 2cos 2cos 2cos sin 2sin 66666610x x x x ⎡⎤-⎛⎫⎛⎫⎛⎫=+-=+++=⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦(步骤3)32.(10T11)函数2π()sin(2)22sin 4f x x x =--的最小正周期是_________ . 【测量目标】二倍角,两角和与差的正弦,三角函数的周期性. 【难易程度】中等 【参考答案】π【试题解析】2π()sin(2)22sin 4f x x x =--=2πsin(2)2(12sin )24x x -+--(步骤1)=πsin(2)2cos 224x x -+-=πsin(2)24x +-(步骤2) 2ω=,故最小正周期为πT =,故答案为:π.33. (10T9)动点),(y x A 在圆122=+y x 上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知定时0t =时,点A 的坐标是)23,21(,则当012t 时,动点A 的纵坐标y 关于t (单位:秒)的函数的单调递增区间是 ( )A. [0,1]B. [1,7]C. [7,12]D. [0,1]和[7,12]【测量目标】平面解析几何. 【难易程度】中等 【参考答案】D【试题解析】由于12秒旋转一周,则每秒转过2π12=π6,而0t =时,y =23=sin π3,那么动点A 的纵坐标关于t 的函数关系式为y =sin (π6t +π3)(t ∈ [0,12]),(步骤1) 则对应的单调递增区间为π6t +π3∈[2πk -π2,2πk +π2],k ∈Z ,(步骤2)则有t ∈ [12k -5,12k +1],k ∈Z ,由于t ∈ [0,12],则当0k =时,t ∈ [0,1],当1k =时,t ∈ [7,12];(步骤3)34.(09T11)若π(0,)2x ∈则2tan x +tan(π2-x )的最小值为. 【测量目标】诱导公式,基本不等式求最值.【难易程度】容易 【参考答案】22 【试题解析】π12tan tan()2tan 2tan x x x x+-=+ ∵π(0,),tan 02x x ∈∴>,(步骤1)112tan 22tan 22tan tan x xxx∴+=(当且仅当2tan 2x =时,等号成立.)(步骤2)故答案为:22. 35.(09全国Ⅰ T16) 若ππ42x <<,则函数3tan 2tan y x x =的最大值为. 【测量目标】三角函数的最值. 【难易程度】中等 【参考答案】8- 【试题解析】令tan ,x t =ππ142x t <<∴>, 4432224222tan 2222tan 2tan 81111111tan 1()244x t y x x x t t t t ∴======------- 36.(09T8)已知函数()3sin cos (0)f x x x ωωω=+>,()y f x =的图象与直线2y =的两个相邻交点的距离等于π,则()f x 的单调递增区间是 ( )A.π5π[π,π],1212k k k -+∈Z B.5π11π[π,π],1212k k k ++∈ZC.ππ[π,π],36k k k -+∈ZD.π2π[π,π],63k k k ++∈Z【测量目标】两角和的余弦,三角函数的单调性,函数sin()y A x ωα=+的图象、性质及其变换.【难易程度】容易 【参考答案】C【试题解析】π()2sin(),6f x x ω=+(步骤1) 由题设()f x 的周期为πT =,2;ω∴=(步骤2)由πππ2π22π262k x k -++得,ππππ,36k xk k -+∈Z ,故选C.(步骤3)37.(09T17)设函数()2πcos(2)sin 3f x x x =++.(1) 求函数()f x 的最大值和最小正周期. (2) 设A ,B ,C 为ABC △的三个角,若1cos 3B =,1()34C f =-,且C 为锐角,求sin A . 【测量目标】三角函数的最值、周期性,同角三角函数的基本关系,两角和与差的余弦,二倍角.【难易程度】容易 【试题解析】(1)()2ππ1cos 21cos 2cos sin πcos(2)si 2sin n 2332223x x x f x x x x --+=-=++=∴函数()f x 的最大值为12,最小正周期π.(步骤1)(2)1213234C C f ⎛⎫==- ⎪⎝⎭,2sin3C ∴=,(步骤2) C 为锐角,2π33C ∴=,π2C ∴=,(步骤3) 1sin cos 3A B ∴==.(步骤4)38.(09T4)若函数()π()1cos ,(0)2f x x x x=,则()f x 的最大值为 ( )12【测量目标】同角三角函数的基本关系,三角函数的最值. 【难易程度】容易 【参考答案】B【试题解析】()()1cos cos f x x x x x =+=π2cos 3x ⎛⎫=- ⎪⎝⎭π(0)2x.(步骤1) 当π3x =时,ππ()2cos 2cos0233f x ⎛⎫=-== ⎪⎝⎭. 故选B.(步骤2) 39.(09T6)函数y =2cos 2x +sin2x 的最小值是_________. 【测量目标】三角函数的最值.【难易程度】中等 【参考答案】1-2 【试题解析】22cos sin 21cos2sin 21y x x x x =+=++=+222(cos 2sin 2)22x x +=1+π2sin(2)4x +(步骤1)当π24x +=2k ππ2-,k ∈Z ,y 有最小值1-2,故答案为1-2.(步骤2)40.(09T12)已知函数f (x )=sin x +tan x ,项数为27的等差数列{a n }满足a n ∈(-π2,π2),且公差d ≠0,若f (a 1)+f (a 2)+…+f (a 27)=0,则当k =________时,f (a k )=0.【测量目标】三角函数的奇偶性.【难易程度】中等【参考答案】14【试题解析】因为函数f (x )=sin x +tan x 是奇函数,所以图像关于原点对称,图像过原点.(步骤1)而等差数列{a n }有27项,a n ∈(-π2,π2).若f (a 1)+f (a 2)+f (a 3)+…+f (a 27)=0,则必有f (a 14)=0,所以k =14.故答案为:14.(步骤2)41.(09T16)设函数2πππ()sin()2cos 1468x x f x =--+. (Ⅰ)求()f x 的最小正周期.(Ⅱ)若函数()y g x =与()y f x =的图象关于直线1x =对称,求当4[0,]3x ∈时()y g x =的最大值.【测量目标】三角函数的周期性、最值和两角和与差的正弦.【难易程度】容易.【试题解析】(Ⅰ)()f x =πππππsin cos cos sin cos 46464x x x -- =3π3πcos 2424x x - ππ3sin()43x -.(步骤1)故()f x 的最小正周期为2ππ4T = =8.(步骤2) (Ⅱ)解法一:在()y g x =的图象上任取一点(,())x g x ,它关于1x =的对称点(2,())x g x -. 由题设条件,点(2,())x g x -在()y f x =的图象上,从而ππ()(2)sin[(2)]43g x f x x =-=--πππsin[]243x =--ππcos()43x =+.(步骤3) 当403x 时,πππ2π3433x +,因此()y g x =在区间4[0,]3上的最大值为max π32g ==.(步骤4) 解法二:因区间4[0,]3关于1x =的对称区间为2[,2]3,且()y g x =与()y f x =的图象关于1x =对称,故()y g x =在4[0,]3上的最大值为()y f x =在2[,2]3上的最大值.(步骤1)由(Ⅰ)知()f x ππsin()43x -, 当223x 时,ππππ6436x --, 因此()y g x =在4[0,]3上的最大值为max π6g ==(步骤2)。
高二数学三角函数的单调性与极值

高二数学三角函数的单调性与极值高二数学三角函数的单调性与极值三角函数是数学中一个非常重要且常见的概念,在数学课程中,我们常常会遇到讨论三角函数的单调性和极值的问题。
本文将针对高二数学课程中三角函数的单调性与极值进行详细的论述和解析。
一、三角函数的定义与基本性质在开始讨论三角函数的单调性与极值之前,我们首先需要了解三角函数的定义和基本性质。
三角函数包括正弦函数、余弦函数和正切函数等。
1. 正弦函数:由一个单位圆周上的某一点P(x, y)引出的线段OP,其中O为圆心,P在单位圆的半径为1的圆上。
正弦函数的定义为sinθ = y。
2. 余弦函数:同样由单位圆上的某一点引出的线段OP,余弦函数的定义为cosθ = x。
3. 正切函数:正切函数的定义为tanθ = sinθ / cosθ。
二、三角函数单调性的判定方法为了讨论三角函数的单调性,我们需要先了解如何判定函数的单调性。
对于区间[a, b]上的函数f(x),我们可以通过其导数的正负来判断函数的单调性。
1. 如果函数f'(x) > 0,那么函数f(x)在[a, b]上单调递增。
2. 如果函数f'(x) < 0,那么函数f(x)在[a, b]上单调递减。
3. 如果函数f'(x) = 0,那么函数f(x)在[a, b]上可能存在极值点。
三、正弦函数的单调性与极值正弦函数的图像为周期性的波浪线,在区间[0, 2π]上,正弦函数的单调性和极值如下:1. 单调递增:在区间[0, π/2]和[3π/2, 2π]上,正弦函数单调递增。
2. 单调递减:在区间[π/2, 3π/2]上,正弦函数单调递减。
3. 极值点:在区间[0, π]和[π, 2π]上,正弦函数存在极值点。
极小值点为π/2的整数倍,极大值点为π的整数倍。
四、余弦函数的单调性与极值余弦函数的图像也是周期性的波浪线,在区间[0, 2π]上,余弦函数的单调性和极值如下:1. 单调递增:在区间[3π/2, 2π]和[0, π/2]上,余弦函数单调递增。
《单调性、最大值与最小值》三角函数PPT

课前篇
自主预习
一
二
三
2.填空
(1)
曲 线
正弦曲线
对称轴方程
x=kπ+ 2 ( ∈ )
余弦曲线
x=kπ(k∈Z)
对称中心坐标
(kπ,0)(k∈Z)
π
π + 2 ,0 (k∈Z)
(2)正弦曲线(余弦曲线)的对称轴都经过正弦曲线(余弦曲线)的
最高点或最低点,即函数y=sin x(y=cos x)的最值点;正弦曲线(余弦
三角函数
第2课时 单调性、最大值与最小值
- .
-1-
首页
课标阐释
1.理解正弦函数与余弦函数的
单调性,会求函数的单调区间.
2.能够利用三角函数单调性比
较三角函数值的大小.
3.能够结合三角函数的单调性
求函数的最值和值域.
思维脉络
课前篇
自主预习
一
二
三
一、正弦函数与余弦函数的单调性
1.观察正弦曲线,正弦函数在哪些区间上是增函数?在哪些区间上
法整体代换,将ωx+φ看作一个整体,可令“z=ωx+φ”,即通过求y=Asin
z的单调区间求出原函数的单调区间.若ω<0,则可利用诱导公式将x
的系数转变为正数.
课堂篇
探究学习
探究一
探究二
探究三
探究四
变式训练 1 求函数 y=2cos
π
π
-
4
思维辨析
随堂演练
的单调递增区间.
π
解:y=2cos 4 - =2cos - 4 .
π
3π
x=2kπ+2(k∈Z)时取最大值 1,当且仅当 x=2kπ+ 2 (k∈Z)时取最小值
三角函数的单调性

三角函数的单调性三角函数是数学中的一种重要函数。
它们在数学、物理、工程等许多领域都有广泛的应用。
而了解三角函数的单调性则对解决问题、求解方程等有着很大的帮助。
本文将介绍三角函数的单调性,包括单调递增和单调递减。
要了解三角函数的单调性,我们首先需要了解什么是单调递增和单调递减。
一个函数在定义域内,如果对于任意两个不同的自变量x1和x2(x1 < x2),有f(x1) < f(x2),则称该函数在该区间上是单调递增的。
同理,如果对于任意两个不同的自变量x1和x2(x1 < x2),有f(x1) > f(x2),则称该函数在该区间上是单调递减的。
首先,我们来看正弦函数sin(x)的单调性。
正弦函数的定义域为实数集R,值域为[-1, 1]。
在定义域内,正弦函数的单调性不是严格递增也不是严格递减,而是周期性的。
也就是说,对于任意两个不同的自变量x1和x2,有sin(x1) = sin(x2 + 2kπ),k为整数。
因此,正弦函数在每个周期内既有单调递增的区间,也有单调递减的区间。
接下来,我们来看余弦函数cos(x)的单调性。
余弦函数的定义域为实数集R,值域为[-1, 1]。
与正弦函数类似,余弦函数在定义域内的单调性也是周期性的。
对于任意两个不同的自变量x1和x2,有cos(x1) = cos(x2 + 2kπ),k为整数。
因此,余弦函数在每个周期内既有单调递增的区间,也有单调递减的区间。
接下来,我们来看正切函数tan(x)的单调性。
正切函数的定义域为R - {(2k + 1)π/2},其中k为整数。
正切函数在定义域内既有单调递增的区间,也有单调递减的区间。
对于任意两个不同的自变量x1和x2(x1 < x2),我们可以推导出tan(x1) < tan(x2)。
这是因为tan(x) =sin(x)/cos(x),当x变化时,sin(x)是单调递增的,而cos(x)是单调递减的。
高二数学三角函数的递增递减区间与极值点

高二数学三角函数的递增递减区间与极值点三角函数是高中数学中重要的内容之一,它们在数学和物理等学科中都有广泛的应用。
在学习三角函数的过程中,理解三角函数的递增递减区间以及求解极值点是非常重要的。
本文将探讨高二数学中三角函数的递增递减区间与极值点。
一、三角函数的性质回顾在讨论三角函数的递增递减区间与极值点之前,我们首先回顾一下三角函数的性质。
常见的三角函数有正弦函数、余弦函数和正切函数,它们的定义域都是实数集。
1. 正弦函数:f(x) = sin(x)正弦函数是一个周期函数,周期为2π。
它的图像在一个周期内呈现上升和下降的特点。
在[0,2π]区间内,正弦函数的值从0递增至1,然后再从1递减至0。
2. 余弦函数:f(x) = cos(x)余弦函数也是一个周期函数,周期也是2π。
它的图像在一个周期内呈现上升和下降的特点。
在[0,2π]区间内,余弦函数的值从1递减至-1,然后再从-1递增至1。
3. 正切函数:f(x) = tan(x)正切函数的定义域限制为(-π/2, π/2)。
它的图像在这个定义域内呈现递增和递减的特点。
在(-π/2, π/2)区间内,正切函数的值从负无穷递增至正无穷。
二、三角函数的递增递减区间要确定一个三角函数的递增递减区间,我们需要找到它的导数,并判断导数的正负性。
1. 正弦函数的递增递减区间正弦函数的导数为f'(x) = cos(x)。
根据导数的正负性可以确定正弦函数的递增递减区间。
当cos(x)>0时,即在[0,π/2)和(3π/2,2π]区间内,正弦函数递增;当cos(x)<0时,即在(π/2,3π/2)区间内,正弦函数递减。
2. 余弦函数的递增递减区间余弦函数的导数为f'(x) = -sin(x)。
根据导数的正负性可以确定余弦函数的递增递减区间。
当-sin(x)>0时,即在(0,π)区间内,余弦函数递增;当-sin(x)<0时,即在(π,2π)区间内,余弦函数递减。
高考数学最后一课刘老师

3、思维严密,杜绝笔误
应 试 策 略
一、准备阶段
1. 集中精神,适度紧张 2. 通览全卷, 稳步启动
二、答题阶段
1. 先易后难,先熟后生,先简后繁 2.审题要慢,答题要快 3.确保中下题目,力求一次成功 4.确保“准确”,力求“快速”
5.讲求规范书写,力求既对又全
6.分秒不让,每分必争
模板 2 立体几何中的空间角问题 例 2 正三棱柱 ABC-A1B1C1 的所有棱长都为 2,D 为 CC1 的中点,求二面角 A-A1D-B 的余弦值. 思维启迪
求二面的大小, 可考虑建立空间直角坐标系 →求二面角两个面的法向量→求向量夹角.
规范解答示例 解 如图,取 BC 的中点 O,连结 AO. ∵△ABC 为正三角形,∴AO⊥BC. ∵ 在 正 三 棱 柱 ABC - A1B1C1 中 , 平 面 ABC⊥ 平 面 BCC1B1,∴AO⊥平面 BCC1B1. 取 B 1C 1 的中点 O 1,以 O 为原点, , OO1, OA 的方向为 x、 OB y、z 轴的正方向建立空间直角坐标系, 则 B(1,0,0),D(-1,1,0),A1(0,2, 3), A(0,0, 3),B1(1,2,0), 设平面 A1AD 的法向量为 n=(x,y,z).
1 π 1 (2)h(x)=f(x)+g(x)= [1+cos(2x+ )]+1+ sin 2x 2 6 2 1 π 3 1 3 1 3 = [cos(2x+ )+sin 2x]+ = ( cos 2x+ sin 2x)+ 2 6 2 2 2 2 2 1 π 3 = sin(2x+ )+ . 2 3 2 π π π 5π 当 2kπ- ≤2x+ ≤2kπ+ (k∈Z),即 kπ- ≤x≤kπ+ 2 3 2 12 π (k∈Z)时, 12 1 π 3 函数 h(x)= sin(2x+ )+ 是增函数. 2 3 2 5π π 故函数 h(x)的单调递增区间是[kπ- ,kπ+ ](k∈Z). 12 12
高中数学《三角函数的单调性与最值》教学课件

1.思考辨析(正确的画“√”,错误的画“×”)
(1)正弦函数、余弦函数在 R 上都是单调函数. ( )
(2)存在 x∈R 满足 cos x=1.2.( )
(3)函数 y=-12sin x,x∈0,π2的最大值为 0.(
)
[答案] (1)× (2)× (3)√
第2课时 单调性与最值
1
2
3
4
情境导学·探新知 合作探究·释疑难 当堂达标·夯基础 课后素养落实
第2课时 单调性与最值
1
2
3
4
情境导学·探新知 合作探究·释疑难 当堂达标·夯基础 课后素养落实
由 z∈2kπ-π2,2kπ+π2(k∈Z),
得 x-π3∈2kπ-π2,2kπ+π2(k∈Z),
即 x∈2kπ-π6,2kπ+56π(k∈Z),
故函数 y=2sinx-π3的单调递增区间为2kπ-π6,2kπ+56π(k∈Z). 同 理 可 求 函 数 y = 2sin x-π3 的 单 调 递 减 区 间 为
cos-147π=cos147π=cos4π+π4=cosπ4. ∵0<π4<35π<π,且 y=cos x 在[0,π]上是单调递减的,
∴cos35π<cosπ4,
即 cos-253π<cos-147π.
第2课时 单调性与最值
1
2
3
4
情境导学·探新知 合作探究·释疑难 当堂达标·夯基础 课后素养落实
提醒:复合函数的单调性遵循“同增异减”的规律.
第2课时 单调性与最值
1
2
3
4
情境导学·探新知 合作探究·释疑难 当堂达标·夯基础 课后素养落实
[跟进训练] 1.(1)函数 y=sin3x+π6,x∈-π3,π3的单调递减区间为________. (2)已知函数 y=cos3π-2x,则它的单调递减区间为________.
专题52 高中数学正、余弦函数的单调性与最值专题(解析版)
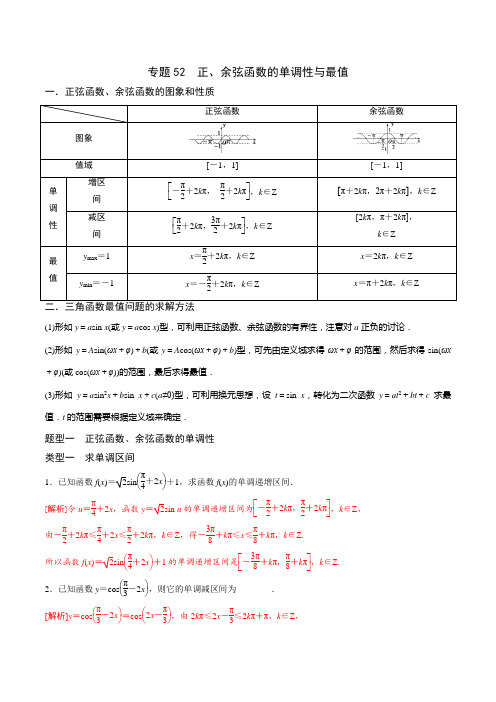
专题52 正、余弦函数的单调性与最值一.正弦函数、余弦函数的图象和性质[-1,1][-1,1](1)形如y =a sin x (或y =a cos x )型,可利用正弦函数、余弦函数的有界性,注意对a 正负的讨论.(2)形如y =A sin(ωx +φ)+b (或y =A cos(ωx +φ)+b )型,可先由定义域求得ωx +φ的范围,然后求得sin(ωx +φ)(或cos(ωx +φ))的范围,最后求得最值.(3)形如y =a sin 2x +b sin x +c (a ≠0)型,可利用换元思想,设t =sin x ,转化为二次函数y =at 2+bt +c 求最值.t 的范围需要根据定义域来确定.题型一 正弦函数、余弦函数的单调性 类型一 求单调区间1.已知函数f (x )=2sin ⎝⎛⎭⎫π4+2x +1,求函数f (x )的单调递增区间. [解析]令u =π4+2x ,函数y =2sin u 的单调递增区间为⎣⎡⎦⎤-π2+2k π,π2+2k π,k ∈Z , 由-π2+2k π≤π4+2x ≤π2+2k π,k ∈Z ,得-3π8+k π≤x ≤π8+k π,k ∈Z.所以函数f (x )=2sin ⎝⎛⎭⎫π4+2x +1的单调递增区间是⎣⎡⎦⎤-3π8+k π,π8+k π,k ∈Z. 2.已知函数y =cos ⎝⎛⎭⎫π3-2x ,则它的单调减区间为________. [解析]y =cos ⎝⎛⎭⎫π3-2x =cos ⎝⎛⎭⎫2x -π3,由2k π≤2x -π3≤2k π+π,k ∈Z ,得k π+π6≤x ≤k π+2π3,k ∈Z ,∴单调递减区间是⎣⎡⎦⎤k π+π6,k π+2π3(k ∈Z). 3.函数y =1-sin 2x 的单调递增区间.[解析]求函数y =1-sin 2x 的单调递增区间,转化为求函数y =sin 2x 的单调递减区间, 由π2+2k π≤2x ≤3π2+2k π,k ∈Z ,得π4+k π≤x ≤3π4+k π,k ∈Z , 即函数的单调递增区间是⎣⎡⎦⎤π4+k π,3π4+k π(k ∈Z). 4.求函数y =3sin ⎝⎛⎭⎫π3-2x 的单调递减区间. [解析]∵y =3sin ⎝⎛⎭⎫π3-2x =-3sin ⎝⎛⎭⎫2x -π3,∴y =3sin ⎝⎛⎭⎫2x -π3是增函数时,y =3sin ⎝⎛⎭⎫π3-2x 是减函数. ∵函数y =sin x 在⎣⎡⎦⎤-π2+2k π,π2+2k π(k ∈Z)上是增函数,∴-π2+2k π≤2x -π3≤π2+2k π, 即-π12+k π≤x ≤5π12+k π(k ∈Z).∴函数y =3sin ⎝⎛⎭⎫π3-2x 的单调递减区间为⎣⎡⎦⎤-π12+k π,5π12+k π(k ∈Z). 5.求下列函数的单调区间.(1)y =cos2x ;(2)y =2sin ⎝⎛⎭⎫π4-x ;(3) y =cos ⎝⎛⎭⎫x 2+π3 [解析] (1)函数y =cos2x 的单调递增区间、单调递减区间分别由下面的不等式确定: 2k π-π≤2x ≤2k π,k ∈Z,2k π≤2x ≤2k π+π,k ∈Z. ∴k π-π2≤x ≤k π,k ∈Z ,k π≤x ≤k π+π2,k ∈Z.∴函数y =cos2x 的单调递增区间为⎣⎡⎦⎤k π-π2,k π,k ∈Z ,单调递减区间为⎣⎡⎦⎤k π,k π+π2,k ∈Z. (2)y =2sin ⎝⎛⎭⎫π4-x =-2sin ⎝⎛⎭⎫x -π4, 函数y =-2sin ⎝⎛⎭⎫x -π4的单调递增、递减区间分别是函数y =2sin ⎝⎛⎭⎫x -π4的单调递减、递增区间. 令2k π+π2≤x -π4≤2k π+3π2,k ∈Z.即2k π+3π4≤x ≤2k π+7π4,k ∈Z ,即函数y =2sin ⎝⎛⎭⎫π4-x 的单调递增区间为⎣⎡⎦⎤2k π+3π4,2k π+7π4,k ∈Z. 令2k π-π2≤x -π4≤2k π+π2,k ∈Z.即2k π-π4≤x ≤2k π+3π4,k ∈Z.即函数y =2sin ⎝⎛⎭⎫π4-x 的单调递减区间为⎣⎡⎦⎤2k π-π4,2k π+3π4,k ∈Z. (3) 当2k π-π≤x 2+π3≤2k π,k ∈Z 时,函数单调递增,故函数的单调递增区间是⎣⎡⎦⎤4k π-8π3,4k π-2π3,k ∈Z. 当2k π≤x 2+π3≤2k π+π,k ∈Z 时,函数单调递减,故函数的单调递减区间是⎣⎡⎦⎤4k π-2π3,4k π+4π3,k ∈Z. 6.函数y =sin ⎝⎛⎭⎫3x +π6,x ∈⎣⎡⎦⎤-π3,π3的单调递减区间为________. [解析]由π2+2k π≤3x +π6≤3π2+2k π(k ∈Z),得π9+2k π3≤x ≤4π9+2k π3(k ∈Z).又x ∈⎣⎡⎦⎤-π3,π3,所以函数y =sin ⎝⎛⎭⎫3x +π6, x ∈⎣⎡⎦⎤-π3,π3的单调递减区间为⎣⎡⎦⎤-π3,-2π9,⎣⎡⎦⎤π9,π3 7.函数y =2sin ⎝⎛⎭⎫x -π3(x ∈[-π,0])的单调递增区间是( ) A.⎣⎡⎦⎤-π,-5π6 B.⎣⎡⎦⎤-5π6,-π6 C.⎣⎡⎦⎤-π3,0 D.⎣⎡⎦⎤-π6,0 [解析]解法一:y =2sin ⎝⎛⎭⎫x -π3,其单调递增区间为-π2+2k π≤x -π3≤π2+2k π,k ∈Z , 则-π6+2k π≤x ≤5π6+2k π,k ∈Z.由于x ∈[-π,0],所以其单调递增区间为⎣⎡⎦⎤-π6,0. 解法二:函数在5π6取得最大值,且其最小正周期为2π,则其单调递增区间为⎣⎡⎦⎤5π6-π,5π6, 即⎣⎡⎦⎤-π6,5π6,又因为x ∈[-π,0],所以其单调递增区间为⎣⎡⎦⎤-π6,0. 8.求函数y =⎪⎪⎪⎪sin ⎝⎛⎭⎫x +π4的单调增区间. [解析]设x +π4=u ,y =|sin u |的大致图象如图所示,函数的周期是π.当u ∈⎣⎡⎦⎤k π,k π+π2(k ∈Z)时,函数y =|sin u |递增. 函数y =⎪⎪⎪⎪sin ⎝⎛⎭⎫x +π4的单调递增区间是⎣⎡⎦⎤k π-π4,k π+π4(k ∈Z).9.函数f (x )=sin ⎝⎛⎭⎫x +π6的一个递减区间是( )A.⎣⎡⎦⎤-π2,π2 B .[-π,0] C.⎣⎡⎦⎤-2π3,2π3 D.⎣⎡⎦⎤π2,2π3[解析]∵2k π+π2≤x +π6≤2k π+3π2,k ∈Z ,∴2k π+π3≤x ≤2k π+4π3,k ∈Z.令k =0得π3≤x ≤4π3.又∵⎣⎡⎦⎤π2,2π3⊆⎣⎡⎦⎤π3,4π3 ∴函数f (x )=sin ⎝⎛⎭⎫x +π6的一个递减区间为⎣⎡⎦⎤π2,2π3.故选D. 10.函数y =sin ⎝⎛⎭⎫2x +π3在区间[0,π]的一个单调递减区间是( ) A.⎣⎡⎦⎤0,5π12 B.⎣⎡⎦⎤π12,7π12 C.⎣⎡⎦⎤5π12,11π12D.⎣⎡⎦⎤π6,π2[解析]由2k π+π2≤2x +π3≤2k π+3π2(k ∈Z)得k π+π12≤x ≤k π+7π12(k ∈Z),取k =0,则一个单调递减区间为⎣⎡⎦⎤π12,7π12. 11.求下列函数的单调递增区间.(1)y =13sin ⎝⎛⎭⎫π6-x ,x ∈[0,π];(2)y =log 12sin x . [解析] (1)由y =-13sin ⎝⎛⎭⎫x -π6的单调性,得π2+2k π≤x -π6≤3π2+2k π,k ∈Z , 即2π3+2k π≤x ≤5π3+2k π,k ∈Z.又x ∈[0,π],故2π3≤x ≤π.即单调递增区间为⎣⎡⎦⎤2π3,π.(2)由sin x >0,得2k π<x <2k π+π,k ∈Z ,∴函数的定义域为(2k π,2k π+π)(k ∈Z).设u =sin x ,则0<u ≤1,又y =log 12u 是减函数,∴函数的值域为(0,+∞).∵12<1,∴函数y =log 12sin x 的递增区间即为u =sin x (sin x >0)的递减区间,故函数y =log 12sin x 的递增区间为2k π+π2,2k π+π(k ∈Z).12.函数y =log 2⎣⎡⎦⎤sin ⎝⎛⎭⎫x +π3的单调递增区间是________. [解析]由题意,得sin ⎝⎛⎭⎫x +π3>0,所以2k π<x +π3<π+2k π,k ∈Z ,解得-π3+2k π<x <2π3+2k π,k ∈Z. 令-π2+2k π≤x +π3≤π2+2k π,k ∈Z 可得y =sin ⎝⎛⎭⎫x +π3的单调递增区间为⎣⎡⎦⎤-56π+2k π,π6+2k π,k ∈Z ,所以函数y =log 2⎣⎡⎦⎤sin ⎝⎛⎭⎫x +π3的单调递增区间为⎝⎛⎦⎤-π3+2k π,π6+2k π,k ∈Z. 13.求下列函数的单调递增区间(3)y =log 12sin ⎝⎛⎭⎫2x +π4; [解析]由对数函数的定义域和复合函数的单调性,可知⎩⎨⎧sin ⎝⎛⎭⎫2x +π4>0,2k π+π2≤2x +π4≤2k π+3π2(k ∈Z ),解得2k π+π2≤2x +π4<2k π+π(k ∈Z),即k π+π8≤x <k π+3π8(k ∈Z),故所求单调递增区间为⎣⎡⎭⎫k π+π8,k π+3π8(k ∈Z). 14.函数f (x )=⎝⎛⎭⎫13|cos x |在[-π,π]上的单调递减区间为( )A.⎣⎡⎦⎤-π2,0 B.⎣⎡⎦⎤π2,πC.⎣⎡⎦⎤-π2,0及⎣⎡⎦⎤π2,π D.⎣⎡⎦⎤-π2,0∪⎣⎡⎦⎤π2,π [解析]在[-π,π]上,依据函数图象的对称性可知y =|cos x |的单调递增区间是⎣⎡⎦⎤-π2,0及⎣⎡⎦⎤π2,π, 而f (x )依|cos x |取值的递增而递减,故⎣⎡⎦⎤-π2,0及⎣⎡⎦⎤π2,π为f (x )的单调递减区间. 15.求函数y =1+sin ⎝⎛⎭⎫-12x +π4,x ∈[-4π,4π]的单调减区间. [解析] y =1+sin ⎝⎛⎭⎫-12x +π4=-sin ⎝⎛⎭⎫12x -π4+1. 由2k π-π2≤12x -π4≤2k π+π2(k ∈Z).解得4k π-π2≤x ≤4k π+32π(k ∈Z).∴k =0时 ,x ∈⎣⎡⎦⎤-π2,3π2,k =1时,x ∈⎣⎡⎦⎤7π2,11π2,k =-1时,x ∈⎣⎡⎦⎤-9π2,-5π2. 又∵x ∈[-4π,4π],∴函数y =1+sin ⎝⎛⎭⎫-12x +π4的单调减区间为⎣⎡⎦⎤-4π,-5π2,⎣⎡⎦⎤-π2,3π2,⎣⎡⎦⎤7π2,4π. 16.下列函数中,周期为π,且在⎣⎡⎦⎤π4,π2上为减函数的是( )A .y =sin ⎝⎛⎭⎫2x +π2 B .y =cos ⎝⎛⎭⎫2x +π2 C .y =sin ⎝⎛⎭⎫x +π2 D .y =cos ⎝⎛⎭⎫x +π2 [解析]对于选项A ,注意到y =sin ⎝⎛⎭⎫2x +π2=cos 2x 的周期为π,且在⎣⎡⎦⎤π4,π2上是减函数. 17.下列函数中,以π2为周期且在区间⎝⎛⎭⎫π4,π2单调递增的是( ) A .f (x )=|cos2x |B .f (x )=|sin2x |C .f (x )=cos|x |D .f (x )=sin|x |[解析] 作出y =sin|x |的图象如图1,知其不是周期函数,排除D ;因为y =cos|x |=cos x ,周期为2π,排除C ;作出y =|cos2x |的图象如图2,由图象知,其周期为π2,在区间⎝⎛⎭⎫π4,π2单调递增,A 正确;作出y =|sin2x |的图象如图3,由图象知,其周期为π2,在区间⎝⎛⎭⎫π4,π2单调递减,排除B ,故选A.图1图2图318.下列函数中,既为偶函数又在(0,π)上单调递增的是( )A .y =cos|x |B .y =cos|-x |C .y =sin ⎝⎛⎭⎫x -π2 D .y =-sin x2[解析] y =cos|x |在⎝⎛⎭⎫0,π2上是减函数,排除A ; y =cos|-x |=cos|x |,排除B ;y =sin ⎝⎛⎭⎫x -π2=-sin ⎝⎛⎭⎫π2-x =-cos x 是偶函数,且在(0,π)上单调递增,符合题意; y =-sin x2在(0,π)上是单调递减的.[答案] C19.下列函数在⎣⎡⎦⎤π2,π上是增函数的是( )A .y =sin xB .y =cos xC .y =sin2xD .y =cos2x [解析] 因为y =sin x 与y =cos x 在⎣⎡⎦⎤π2,π上都是减函数,所以排除A 、B.因为π2≤x ≤π, 所以π≤2x ≤2π.因为y =sin2x 在2x ∈[π,2π]内不具有单调性,所以排除C.故选D.20.设函数f (x )=2sin ⎝⎛⎭⎫ωx +φ+π4(ω>0,|φ|<π2)的最小正周期为π,且是偶函数,则( ) A .f (x )在⎝⎛⎭⎫0,π2单调递减 B .f (x )在⎝⎛⎭⎫π4,3π4单调递减 C .f (x )在⎝⎛⎭⎫0,π2单调递增 D .f (x )在⎝⎛⎭⎫π4,3π4单调递增 [解析]由条件知ω=2.∵f (x )是偶函数且|φ|<π2,∴φ=π4,这时f (x )=2sin ⎝⎛⎭⎫2x +π2=2cos 2x .∵x ∈⎝⎛⎭⎫0,π2时,2x ∈(0,π),∴f (x )在⎝⎛⎭⎫0,π2上单调递减. 21.函数y =2sin ⎝⎛⎭⎫ωx +π4(ω>0)的周期为π,则其单调递增区间为( ) A.⎣⎡⎦⎤k π-3π4,k π+π4(k ∈Z) B.⎣⎡⎦⎤2k π-3π4,2k π+π4(k ∈Z) C.⎣⎡⎦⎤k π-3π8,k π+π8(k ∈Z) D.⎣⎡⎦⎤2k π-3π8,2k π+π8(k ∈Z) [解析]周期T =π,∴2πω=π,∴ω=2,∴y =2sin ⎝⎛⎭⎫2x +π4.由-π2+2k π≤2x +π4≤2k π+π2,k ∈Z ,得k π-38π≤x ≤k π+π8,k ∈Z.[答案] C 22.已知函数f (x )=sin(2x +φ),其中φ为实数,且|φ|<π.若f (x )≤⎪⎪⎪⎪f ⎝⎛⎭⎫π6对x ∈R 恒成立,且f ⎝⎛⎭⎫π2>f (π),求f (x )的单调递增区间.[解析]由f (x )≤⎪⎪⎪⎪f ⎝⎛⎭⎫π6对x ∈R 恒成立知,2·π6+φ=2k π±π2(k ∈Z).∴φ=2k π+π6或φ=2k π-5π6(k ∈Z). ∵|φ|<π,得φ=π6或φ=-5π6,又∵f ⎝⎛⎭⎫π2>f (π),∴φ=-5π6, 由2k π-π2≤2x -5π6≤2k π+π2(k ∈Z),得f (x )的单调递增区间是⎣⎡⎦⎤k π+π6,k π+2π3(k ∈Z). 类型二 利用单调性求参1.函数y =cos x 在区间[-π,a ]上为增函数,则a 的取值范围是________.[解析]因为y =cos x 在[-π,0]上是增函数,在[0,π]上是减函数,所以只有-π<a ≤0时满足条件, 故a ∈(-π,0].2.若函数f (x )=sin ωx (0<ω<2)在区间⎣⎡⎦⎤0,π3上单调递增,在区间⎣⎡⎦⎤π3,π2上单调递减,则ω等于___. [解析]根据题意知f (x )在x =π3处取得最大值1,∴sin ωπ3=1,∴ωπ3=2k π+π2,k ∈Z ,即ω=6k +32,k ∈Z.又0<ω<2,∴ω=32.3.已知ω>0,函数f (x )=sin ⎝⎛⎭⎫ωx +π3在⎝⎛⎭⎫π2,π上单调递减,则ω的取值范围是________.[解析]依题意得T 2≥π2⇒T ≥π,又ω>0,所以2πω≥π⇒0<ω≤2.由π2<x <π得ωπ2+π3<ωx +π3<ωπ+π3,由f (x )在⎝⎛⎭⎫π2,π上单调递减得⎩⎨⎧ωπ2+π3≥π2,ωπ+π3≤3π2⇒13≤ω≤76.答案:⎣⎡⎦⎤13,76 4.已知函数f (x )=sin ⎝⎛⎭⎫2x -π6. (1)求函数f (x )图象的对称轴方程;(2)解不等式:f ⎝⎛⎭⎫x +π12≥32. [解析] (1)由2x -π6=k π+π2(k ∈Z),得x =k π2+π3(k ∈Z).所以函数图象的对称轴方程为x =k π2+π3(k ∈Z).(2)由f ⎝⎛⎭⎫x +π12=sin 2x ≥32,得2k π+π3≤2x ≤2k π+2π3,k ∈Z ,解得k π+π6≤x ≤k π+π3,k ∈Z , 故不等式的解集是{|x⎭⎬⎫k π+π6≤x ≤k π+π3,k ∈Z .5.若函数f (x )=2sin ⎝⎛⎭⎫ωx +π3(ω>0),且f (α)=-2,f (β)=0,|α-β|的最小值是π2,则f (x )的单调递增区间是() A.⎣⎡⎦⎤2k π-5π6,2k π+π6(k ∈Z ) B.⎣⎡⎦⎤k π-π3,k π+π6(k ∈Z ) C.⎣⎡⎦⎤2k π-2π3,2k π+π3(k ∈Z ) D.⎣⎡⎦⎤k π-5π12,k π+π12(k ∈Z ) [解析]由题意可知14T =π2,所以T =2π,所以ω=1,所以f (x )=2sin ⎝⎛⎭⎫x +π3. 由2k π-π2≤x +π3≤2k π+π2(k ∈Z ),得2k π-5π6≤x ≤2k π+π6(k ∈Z ),所以f (x )的单调递增区间为⎣⎡⎦⎤2k π-5π6,2k π+π6(k ∈Z ).故选A. 6.已知函数f (x )=sin(ωx +φ)(ω>0,0≤φ≤π)为R 上的偶函数,其图象关于点M (34π,0)对称,且在区间[0,π2]上是单调函数,求φ和ω的值.[解析]由f (x )是偶函数,得sin φ=±1,所以φ=k π+π2,k ∈Z.因为0≤φ≤π,所以φ=π2.由f (x )的图象关于点M (3π4,0)对称,得f (3π4)=0.因为f (3π4)=sin(3ωπ4+π2)=cos 3ωπ4,所以cos 3ωπ4=0.又因为ω>0,所以3ωπ4=π2+k π,k ∈N ,即ω=23+43k ,k ∈N.当k =0时,ω=23,此时f (x )=sin(23x +π2)在[0,π2]上是减函数;当k =1时,ω=2,此时f (x )=sin(2x +π2)在[0,π2]上是减函数;当k ≥2时,ω≥103,此时f (x )=sin(ωx +π2)在[0,π2]上不是单调函数.综上,ω=23或ω=2.题型二 利用三角函数的单调性比较大小1.sin250°与sin260°;(2)cos 15π8与cos 14π9.[解析] (1)∵函数y =sin x 在[90°,270°]上单调递减,且90°<250°<260°<270°,∴sin250°>sin260°. (2)cos 15π8=cos ⎝⎛⎭⎫2π-π8=cos π8,cos 14π9=cos ⎝⎛⎭⎫2π-4π9=cos 4π9. ∵函数y =cos x 在[0,π]上单调递减,且0<π8<4π9<π,∴cos π8>cos 4π9,∴cos 15π8>cos 14π9.2.比较下列各组数的大小.(1)cos ⎝⎛⎭⎫-π8与cos 13π7;(2)sin194°与cos160°;(3) cos ⎝⎛⎭⎫-7π8与cos 6π7 [解析] (1)∵cos ⎝⎛⎭⎫-π8=cos π8,cos 13π7=cos ⎝⎛⎭⎫2π-π7=cos π7,而0<π8<π7<π2, 且y =cos x 在⎣⎡⎦⎤0,π2上单调递减,∴cos π8>cos π7.即cos ⎝⎛⎭⎫-π8>cos 13π7. (2)∵sin194°=sin(90°+104°)=cos104°,而0°<104°<160°<180°, 且y =cos x 在[0,π]上单调递减.∴cos104°>cos160°.即sin194°>cos160°. (3)cos ⎝⎛⎭⎫-7π8=cos 7π8,因为0<6π7<7π8<π,y =cos x 在(0,π)上是减函数, 所以cos7π8<cos 6π7.所以cos ⎝⎛⎭⎫-7π8<cos 6π7. 3.利用三角函数的单调性,比较下列各组数的大小.(1)sin ⎝⎛⎭⎫-π18与sin ⎝⎛⎭⎫-π10;(2)sin 196°与cos 156°;(3)cos ⎝⎛⎭⎫-235π与cos ⎝⎛⎭⎫-174π. [解析] (1)∵-π2<-π10<-π18<π2,∴sin ⎝⎛⎭⎫-π18>sin ⎝⎛⎭⎫-π10. (2)sin 196°=sin(180°+16°)=-sin 16°,cos 156°=cos(180°-24°)=-cos 24°=-sin 66°,∵0°<16°<66°<90°,∴sin 16°<sin 66°,从而-sin 16°>-sin 66°,即sin 196°>cos 156°. (3)cos ⎝⎛⎭⎫-235π=cos 235π=cos ⎝⎛⎭⎫4π+35π=cos 35π, cos ⎝⎛⎭⎫-174π=cos 174π=cos ⎝⎛⎭⎫4π+π4=cos π4.∵0<π4<35π<π,且y =cos x 在[0,π]上是减函数,∴cos 35π<cos π4,即cos ⎝⎛⎭⎫-235π<cos ⎝⎛⎭⎫-174π. 4.比较下列各组数的大小:①cos 15π8,cos 14π9;②cos 1,sin 1.[解析]①cos 15π8=cos π8,cos 14π9=cos 4π9,因为0<π8<4π9<π,而y =cos x 在[0,π]上单调递减,所以cos π8>cos 4π9,即cos 15π8>cos 14π9.②因为cos 1=sin ⎝⎛⎭⎫π2-1,而0<π2-1<1<π2且y =sin x 在⎣⎡⎦⎤0,π2上单调递增,所以sin ⎝⎛⎭⎫π2-1<sin 1, 即cos 1<sin 1.5.比较下列各组数的大小.(1)sin ⎝⎛⎭⎫-376π与sin ⎝⎛⎭⎫493π;(2)cos 870°与sin 980°. [解析] (1)sin ⎝⎛⎭⎫-376π=sin ⎝⎛⎭⎫-6π-π6=sin ⎝⎛⎭⎫-π6,sin ⎝⎛⎭⎫493π=sin ⎝⎛⎭⎫16π+π3=sin π3, 因为y =sin x 在⎣⎡⎦⎤-π2,π2上是增函数,所以sin ⎝⎛⎭⎫-π6<sin π3,即sin ⎝⎛⎭⎫-376π<sin 493π. (2)cos 870°=cos(720°+150°)=cos 150°,sin 980°=sin(720°+260°)=sin 260°=sin(90°+170°)=cos 170°, 因为0°<150°<170°<180°,且y =cos x 在[0°,180°]上是减函数, 所以cos 150°>cos 170°,即cos 870°>sin 980°. 6.sin 2π7________sin ⎝⎛⎭⎫-15π8(填“>”或“<”). [解析]sin ⎝⎛⎭⎫-15π8=sin ⎝⎛⎭⎫-2π+π8=sin π8, 因为0<π8<2π7<π2,y =sin x 在⎝⎛⎭⎫0,π2上是增函数,所以sin π8<sin 2π7,即sin 2π7>sin ⎝⎛⎭⎫-15π8. 7.下列关系式中正确的是( )A .sin 11°<cos 10°<sin 168°B .sin 168°<sin 11°<cos 10°C .sin 11°<sin 168°<cos 10°D .sin 168°<cos 10°<sin 11°[解析]由诱导公式,得cos 10°=s i n 80°,s i n 168°=s i n (180°-12°)=s i n 12°,由正弦函数y =s i n x 在[0°,90°]上是单调递增的,所以sin 11°<sin 12°<sin 80°,即sin 11°<sin 168°<cos 10°.故选C. 8.sin1,sin2,sin3按从小到大排列的顺序为__________. [解析]∵1<π2<2<3<π,sin(π-2)=sin2,sin(π-3)=sin3.y =sin x 在⎝⎛⎭⎫0,π2上递增,且0<π-3<1<π-2<π2,∴sin(π-3)<sin1<sin(π-2),即sin3<sin1<sin2. 9.将cos 150°,sin 470°,cos 760°按从小到大排列为_________.[解析]cos 150°<0,s i n 470°=s i n 110°=cos 20°>0,cos 760°=cos 40°>0且cos 20°>cos 40°, 所以cos 150°<cos 760°<s i n 470°. 10.下列不等式中成立的是( )A .sin ⎝⎛⎭⎫-π8>sin ⎝⎛⎭⎫-π10 B .sin 3>sin 2 C .sin 75π>sin ⎝⎛⎭⎫-25π D .sin 2>cos 1[解析]因为sin 2=cos ⎝⎛⎭⎫π2-2=cos ⎝⎛⎭⎫2-π2,且0<2-π2<1<π,所以cos ⎝⎛⎭⎫2-π2>cos 1,即sin 2>cos 1.故选D. 11.(1)已知α,β为锐角三角形的两个内角,则以下结论正确的是( )A .sin α<sin βB .cos α<sin βC .cos α<cos βD .cos α >cos β[解析]α,β为锐角三角形的两个内角,α+β>π2,α>π2-β,α∈⎝⎛⎭⎫0,π2,π2-β∈⎝⎛⎭⎫0,π2, 所以cos α<cos ⎝⎛⎭⎫π2-β=sin β.12.定义在R 上的偶函数f (x )满足f (x +1)=-f (x ),且在[-4,-3]上是增函数,α,β是锐角三角形的两个内角,则f (sin α)与f (cos β)的大小关系是________. [解析]由f (x +1)=-f (x ),得f (x +2)=-f (x +1)=f (x ),所以函数f (x )是周期函数,且2是它的一个周期.因为函数f (x )是偶函数且在[-4,-3]上是增函数, 所以函数f (x )在[0,1]上是增函数.又α,β是锐角三角形的两个内角,则有α+β>π2,即π2>α>π2-β>0,因为y =sin x 在⎣⎡⎦⎤0,π2上为增函数,所以sin α>sin ⎝⎛⎭⎫π2-β=cos β, 且sin α∈[0,1],cos β∈[0,1],所以f (sin α)>f (cos β).题型三 正弦函数、余弦函数的最值问题1.函数y =1-2cos π2x 的最小值,最大值分别是( )A .-1,3B .-1,1C .0,3D .0,1[解析]∵x ∈R ,∴π2x ∈R ,∴y =cos π2x 的值域[-1,1].∴y =1-2cos π2x 的最大值为3,最小值-1.2.函数y =2-sin x 的最大值及取最大值时x 的值分别为( )A .y max =3,x =π2B .y max =1,x =π2+2k π(k ∈Z)C .y max =3,x =-π2+2k π(k ∈Z)D .y max =3,x =π2+2k π(k ∈Z)[解析]∵y =2-sin x ,∴当sin x =-1时,y max =3,此时x =-π2+2k π(k ∈Z).[答案] C3.y =2cos x 2的值域是( )A .[-2,2]B .[0,2]C .[-2,0]D .R[解析]因为x ∈R ,所以x 2≥0,所以y =2cos x 2∈[-2,2]. 4.y =a cos x +1的最大值为5,则a =________. [解析]∵|a |+1=5,∴|a |=4,∴a =±4.5.设函数f (x )=A +B sin x ,当B <0时,f (x )的最大值是32,最小值是-12,则A =________,B =________.[解析]根据题意,得⎩⎨⎧A -B =32A +B =-12.解得A =12,B =-1.6.函数f (x )=sin(π6+x )+cos(π3-x )的最大值为( )A .1 B.32C. 3 D .2[解析]由π6+x 与π3-x 互余得f (x )=2sin(x +π6).故f (x )的最大值为2,故选D.7.函数f (x )=15sin ⎝⎛⎭⎫x +π3+cos ⎝⎛⎭⎫x -π6的最大值为( ) A.65 B .1 C.35 D.15[解析]∵⎝⎛⎭⎫x +π3+⎝⎛⎭⎫π6-x =π2, ∴f (x )=15sin ⎝⎛⎭⎫x +π3+cos ⎝⎛⎭⎫x -π6=15sin ⎝⎛⎭⎫x +π3+cos ⎝⎛⎭⎫π6-x =15sin ⎝⎛⎭⎫x +π3+sin ⎝⎛⎭⎫x +π3=65sin ⎝⎛⎭⎫x +π3≤65. ∴f (x )max =65.故选A.8.函数y =2sin ⎝⎛⎭⎫π3-x -cos ⎝⎛⎭⎫π6+x (x ∈R)的最小值等于( ) A .-3 B .-2 C .-1 D .- 5[解析] ∵⎝⎛⎭⎫π3-x +⎝⎛⎭⎫π6+x =π2,∴y =2sin ⎣⎡⎦⎤π2-⎝⎛⎭⎫π6+x -cos ⎝⎛⎭⎫x +π6=2cos ⎝⎛⎭⎫x +π6-cos ⎝⎛⎭⎫x +π6=cos ⎝⎛⎭⎫x +π6,∴y min =-1. 9.函数y =cos ⎝⎛⎭⎫x +π6,x ∈⎣⎡⎦⎤0,π2的值域是( )A.⎣⎡⎦⎤-32,12 B.⎣⎡⎦⎤-12,32 C.⎣⎡⎦⎤32,1D.⎣⎡⎦⎤12,1[解析]因为x ∈⎣⎡⎦⎤0,π2,所以x +π6∈⎣⎡⎦⎤π6,2π3,所以y =cos ⎝⎛⎭⎫x +π6∈⎣⎡⎦⎤-12,32. 10.求函数y =3-4cos ⎝⎛⎭⎫2x +π3,x ∈⎣⎡⎦⎤-π3,π6的最大值、最小值及相应的x 值. [解析]因为x ∈⎣⎡⎦⎤-π3,π6,所以2x +π3∈⎣⎡⎦⎤-π3,2π3,从而-12≤cos ⎝⎛⎭⎫2x +π3≤1. 所以当cos ⎝⎛⎭⎫2x +π3=1,即2x +π3=0,x =-π6时,y min =3-4=-1. 当cos ⎝⎛⎭⎫2x +π3=-12,即2x +π3=2π3,x =π6时,y max =3-4×⎝⎛⎭⎫-12=5. 综上所述,当x =-π6时,y min =-1;当x =π6时,y max =5.11.求下列函数的最大值和最小值. f (x )=sin ⎝⎛⎭⎫2x -π6,x ∈⎣⎡⎦⎤0,π2 [解析]当x ∈⎣⎡⎦⎤0,π2时,2x -π6∈⎣⎡⎦⎤-π6,5π6,由函数图象(略)知,-12≤sin ⎝⎛⎭⎫2x -π6≤1, 所以,f (x )在⎣⎡⎦⎤0,π2上的最大值和最小值分别为1,-12. 12.求下列函数的值域:y =sin ⎝⎛⎭⎫2x -π3,x ∈⎣⎡⎦⎤0,π2; [解析] 因为0≤x ≤π2,所以0≤2x ≤π,所以-π3≤2x -π3≤2π3.令2x -π3=t ,则原式转化为y =sin t ,t ∈⎣⎡⎦⎤-π3,2π3,由y =sin t 的图象知-32≤y ≤1, 所以所求函数的值域为⎣⎡⎦⎤-32,1. 13.求函数y =3+2cos ⎝⎛⎭⎫2x +π3的最值. [解析]因为-1≤cos ⎝⎛⎭⎫2x +π3≤1,所以当cos ⎝⎛⎭⎫2x +π3=1时,y max =5;当cos ⎝⎛⎭⎫2x +π3=-1时,y min =1. 14.已知函数y =a -b cos ⎝⎛⎭⎫2x +π6(b >0)的最大值为32,最小值为-12. (1)求a ,b 的值;(2)求函数g (x )=-4a sin ⎝⎛⎭⎫bx -π3的最小值并求出对应x 的集合. [解析] (1)cos ⎝⎛⎭⎫2x +π6∈[-1,1],因为b >0,所以-b <0,⎩⎨⎧ymax =b +a =32,ymin=-b +a =-12,所以a =12,b =1.(2)由(1)知:g (x )=-2sin ⎝⎛⎭⎫x -π3,因为sin ⎝⎛⎭⎫x -π3∈[-1,1],所以g (x )∈[-2,2], 所以g (x )的最小值为-2,对应x 的集合为⎩⎨⎧⎭⎬⎫x ⎪⎪x =2k π+56π,k ∈Z . 15.已知函数f (x )=a sin ⎝⎛⎭⎫2x -π3+b (a >0).当x ∈⎣⎡⎦⎤0,π2时,f (x )的最大值为3,最小值是-2,求a 和b 的值.[解析]∵0≤x ≤π2,∴-π3≤2x -π3≤2π3,∴-32≤sin ⎝⎛⎭⎫2x -π3≤1,∴f (x )max =a +b =3, f (x )min =-32a +b =-2.由⎩⎪⎨⎪⎧a +b =3,-32a +b =-2,得⎩⎨⎧a =2,b =-2+ 3.16.求下列函数的最值y =-sin 2x +3sin x +54.[解析]y =-sin 2x +3sin x +54=-(sin x -32)2+2.因为-1≤sin x ≤1,所以当sin x =32时,函数取得最大值,y max =2; 当sin x =-1时,函数取得最小值,y min =14- 3.17.函数y =cos 2x +2sin x -2,x ∈R 的值域为________. [解析] y =cos 2x +2sin x -2=-sin 2x +2sin x -1=-(sin x -1)2. 因为-1≤sin x ≤1,所以-4≤y ≤0,所以函数y =cos 2x +2sin x -2,x ∈R 的值域为[-4,0].18.求下列函数的最大值和最小值. y =-2cos 2x +2sin x +3,x ∈⎣⎡⎦⎤π6,5π6. [解析]y =-2(1-sin 2x )+2sin x +3=2sin 2x +2sin x +1=2⎝⎛⎭⎫sin x +122+12. ∵x ∈⎣⎡⎦⎤π6,5π6,∴12≤sin x ≤1.当sin x =1时,y max =5;当sin x =12时,y min =52. 19.求函数y =cos 2x -sin x 在x ∈⎣⎡⎦⎤-π4,π4上的最大值和最小值. [解析]y =cos 2x -sin x =1-sin 2x -sin x =-⎝⎛⎭⎫sin x +122+54.因为-π4≤x ≤π4,-22≤sin x ≤22, 所以当x =-π6,即sin x =-12时,函数取得最大值,y max =54;当x =π4,即sin x =22时,函数取得最小值,y min =12-22.20.求函数y =2sin 2x +2sin x -12,x ∈⎣⎡⎦⎤π6,5π6的值域. [解析]令t =sin x ,因为x ∈⎣⎡⎦⎤π6,5π6,所以12≤sin x ≤1,即12≤t ≤1.所以y =2t 2+2t -12=2⎝⎛⎭⎫t +122-1, ∵以t 为自变量的二次函数在⎣⎡⎦⎤12,1上单调递增,∴1≤y ≤72,所以原函数的值域为⎣⎡⎦⎤1,72. 21.求下列函数的值域:y =cos 2x -4cos x +5.[解析]令t =cos x ,则-1≤t ≤1.∴y =t 2-4t +5=(t -2)2+1, ∴t =-1时,y 取得最大值10,t =1时,y 取得最小值2. 所以y =cos 2x -4cos x +5的值域为[2,10].22.求函数y =cos 2x +4sin x 的最值及取到最大值和最小值时的x 的集合. [解析]y =cos 2x +4sin x =1-sin 2x +4sin x =-sin 2x +4sin x +1=-(sin x -2)2+5.所以当sin x =1,即x =2k π+π2,k ∈Z 时,y max =4;当sin x =-1,即x =2k π-π2,k ∈Z 时,y min =-4.所以y max =4,此时x 的取值集合是⎩⎨⎧⎭⎬⎫x |x =2k π+π2,k ∈Z ;y min =-4,此时x 的取值集合是⎩⎨⎧⎭⎬⎫x |x =2k π-π2,k ∈Z .23.若f (x )=2sin ωx (0<ω<1)在区间⎣⎡⎦⎤0,π3上的最大值是2,则ω=________. [解析] ∵x ∈⎣⎡⎦⎤0,π3,即0≤x ≤π3,且0<ω<1,∴0≤ωx ≤ωπ3<π3.∵f (x )max =2sin ωπ3=2, ∴sinωπ3=22,ωπ3=π4,即ω=34. 24.设函数f (x )=2sin ⎝⎛⎭⎫π2x +π5.若对任意x ∈R ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值为( )A .4B .2C .1D .12[解析]依题意得f (x 1)是f (x )的最小值,f (x 2)是f (x )的最大值.因此|x 1-x 2|=⎝⎛⎭⎫k +12T (k ∈Z ). ∴当k =0时,|x 1-x 2|min =12T =12×2ππ2=2.故选B.25.已知函数y =sin πx3在区间[0,t ]上至少取得2次最大值,则正整数t 的最小值是________.[解析]因为T =2ππ3=6.所以在[0,+∞)第一次出现最大值x =64=32,第二次出现最大值x =152,所以t ≥152.又因为t ∈Z ,所以t 的最小值为8.26.函数y =sin x 的定义域为[a ,b ],值域为⎣⎡⎦⎤-1,12,则b -a 的最大值是________. [解析]因为函数y =s i n x ,x ∈[a ,b ]的最小值和最大值分别为-1和12.不妨在一个区间[0,2π]内研究,可知sin π6=sin 5π6=12,sin 3π2=-1,结合图象(略)可知(b -a )min =3π2-5π6=2π3,(b -a )max =13π6-5π6=4π3. 27.已知函数f (x )=2a sin ⎝⎛⎭⎫2x +π6+a +b 的定义域是⎣⎡⎦⎤0,π2,值域是[-5,1],求a ,b 的值. [解析] 因为0≤x ≤π2,所以π6≤2x +π6≤7π6,所以-12≤sin ⎝⎛⎭⎫2x +π6≤1. 所以a >0时,⎩⎪⎨⎪⎧ b =-53a +b =1,解得⎩⎪⎨⎪⎧a =2b =-5.a <0时,⎩⎪⎨⎪⎧b =13a +b =-5,解得⎩⎪⎨⎪⎧a =-2b =1.因此a =2,b =-5或a =-2,b =1.。
三角函数的单调性

三角函数的单调性三角函数是数学中重要的一类函数,研究它们的单调性对于解决许多实际问题具有重要意义。
本文将讨论正弦函数、余弦函数和正切函数在其定义域内的单调性,并给出相应的证明。
一、正弦函数的单调性正弦函数是三角函数中最基本的函数之一,它在数学和物理等领域有广泛的应用。
正弦函数的定义域为整个实数集,记作f(x) = sin(x)。
现证明其在定义域内的单调性。
首先,我们知道在一个周期内,即在区间[-π, π]内,正弦函数是周期为2π的周期函数。
在该区间内,正弦函数的值是在[0,1]之间变化的,并且在x∈[-π/2, π/2]时,正弦函数是严格单调递增的;在x∈[-π, -π/2)∪(π/2, π]时,正弦函数是严格单调递减的。
其次,由于正弦函数具有周期性,我们可以将证明范围扩展到整个实数集上。
即对于任意两个实数x1和x2,若满足x1 < x2,则有:f(x1) = sin(x1) < sin(x2) = f(x2)。
因此,正弦函数在整个定义域上都是单调递增的。
二、余弦函数的单调性余弦函数是与正弦函数密切相关的三角函数,它也在数学和物理等领域有广泛的应用。
余弦函数的定义域为整个实数集,记作g(x) =cos(x)。
现证明其在定义域内的单调性。
与正弦函数类似,余弦函数也是一个以2π为周期的周期函数。
在一个周期内,即在区间[-π, π]内,余弦函数的值是在[-1,1]之间变化的,并且在x∈[0, π]时,余弦函数是严格单调递减的;在x∈[-π, 0)时,余弦函数是严格单调递增的。
同样地,由于余弦函数具有周期性,我们可以将证明范围扩展到整个实数集上。
即对于任意两个实数x1和x2,若满足x1 < x2,则有:g(x1) = cos(x1) > cos(x2) = g(x2)。
因此,余弦函数在整个定义域上都是单调递减的。
三、正切函数的单调性正切函数是三角函数中另一个重要的函数,它也在数学和物理等领域有广泛的应用。
三角函数的图象与性质(正弦函数、余弦函数的单调性与最值)高一数学课件(人教A版2019必修第一册)

分析如图所示的正弦曲线和余弦曲线及其对称轴,回答下列问题:
情境设置
合作探究·提素养
问题1:.观察正弦曲线,研究正弦函数的单调性,我们是否需要其在全体实数集上的图象?
[答案] 不需要,选择一个周期的图象就能较好地将单调性完整地呈现出来.
问题2:.如图,观察正弦函数图象(一个周期内),描述你看到的图象.
(1)异名函数化为同名函数;
(2)利用诱导公式把角转化到同一单调区间上;
(3)利用函数的单调性比较大小.
1.求下列函数的单调递增区间.
(1) ;
(2) , .
[解析] (1)由 ,得 , 所以函数 的单调递增区间为 .(2)因为 , 所以函数 的单调递增区间就是函数 的单调递减区间, 由 , ,得 , . 因为 ,所以所求函数的单调递增区间为 .
[答案] 正弦、余弦函数存在最大值和最小值,最大值和最小值分别是1和 .
情境设置
问题2:.当自变量 分别取何值时,正弦函数 取得最大值1和最小值 ?
[答案] 对于正弦函数 , ,当且仅当 , 时,函数取得最大值 ;当且仅当 , 时,函数取得最小值 .
新知生成
正弦函数、余弦函数的最值
3.下列关系式中正确的是( ).A. B. C. D.
C
[解析] , ,∴由正弦函数的单调性得, ,即 .
4.函数 在 _________________时, 取最大值.
[解析] 当函数取最大值时, ,得 .
方法总结 三角函数最值问题的求解方法:(1)形如 (或 )型,可利用正弦函数、余弦函数的有界性,注意对 正负的讨论.(2)形如 (或 )型,可先由定义域求得 的范围,然后求得 (或 )的范围,最后求得最值.(3)形如 型,可利用换元思想,设 ,转化为二次函数 求最值, 的范围需要根据定义域来确定.
高考数学复习三角函数的单调性与最值

第4讲 三角函数的图象与性质最新考纲考向预测1.能画出y =sin x ,y =cos x ,y =tan x 的图象,了解三角函数的周期性.2.理解正弦函数、余弦函数在区间[0,2π]上的性质(如单调性、最大值和最小值以及与x 轴的交点等),理解正切函数在区间⎝ ⎛⎭⎪⎫-π2,π2内的单调性. 命题趋势以考查三角函数的性质为主,题目涉及单调性、周期性、最值、零点.考查三角函数性质时,常与三角恒等变换结合,加强数形结合思想、函数与方程思想的应用意识.题型既有选择题和填空题,又有解答题,中档难度. 核心素养 直观想象、逻辑推理1.用五点法作正弦函数和余弦函数的简图(1)正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),⎝ ⎛⎭⎪⎫π2,1,(π,0),⎝ ⎛⎭⎪⎫32π,-1,(2π,0).(2)余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),⎝ ⎛⎭⎪⎫π2,0,(π,-1),⎝ ⎛⎭⎪⎫3π2,0,(2π,1).2.正弦、余弦、正切函数的图象与性质 函数y =sin xy =cos xy =tan x图象定义 域 R R {x |x ≠k π+π2,k ∈Z } 值域[-1,1][-1,1]R周期性2π2ππ奇偶性奇函数偶函数奇函数单调递增区间[-π2+2kπ,π2+2kπ],k∈Z[-π+2kπ,2kπ],k∈Z(-π2+kπ,π2+kπ),k∈Z续表函数y=sin x y=cos x y=tan x单调递减区间[π2+2kπ,3π2+2kπ],k∈Z[2kπ,π+2kπ],k∈Z无对称性对称中心(kπ,0),k∈Z⎝⎛⎭⎪⎫kπ+π2,0,k∈Z⎝⎛⎭⎪⎫kπ2,0,k∈Z 对称轴x=kπ+π2,k∈Zx=kπ,k∈Z无对称轴零点kπ,k∈Z kπ+π2,k∈Zkπ,k∈Z常用结论1.对称与周期的关系正弦曲线、余弦曲线相邻的两个对称中心、相邻的两条对称轴之间的距离是半个周期,相邻的对称中心与对称轴之间的距离是四分之一个周期;正切曲线相邻两个对称中心之间的距离是半个周期.2.与三角函数的奇偶性相关的结论(1)若y=A sin(ωx+φ)为偶函数,则有φ=kπ+π2(k∈Z);若为奇函数,则有φ=kπ(k∈Z).(2)若y=A cos(ωx+φ)为偶函数,则有φ=kπ(k∈Z);若为奇函数,则有φ=kπ+π2(k ∈Z ).(3)若y =A tan(ωx +φ)为奇函数,则有φ=k π(k ∈Z ). 常见误区1.对于y =tan x 不能认为其在定义域上为增函数,而是在每个开区间⎝ ⎛⎭⎪⎫k π-π2,k π+π2(k ∈Z )内为增函数. 2.求函数y =A sin(ωx +φ)的单调区间时要注意A 和ω的符号,尽量化成ω>0的形式,避免出现增减区间的混淆.1.判断正误(正确的打“√”,错误的打“×”) (1)y =cos x 在第一、二象限内是减函数.( ) (2)若y =k sin x +1,x ∈R ,则y 的最大值是k +1.( )(3)若非零实数T 是函数f (x )的周期,则kT (k 是非零整数)也是函数f (x )的周期.( )(4)函数y =sin x 图象的对称轴方程为x =2k π+π2(k ∈Z ).( ) (5)函数y =tan x 在整个定义域上是增函数.( ) 答案:(1)× (2)× (3)√ (4)× (5)× 2.(易错点)函数y =tan 2x 的定义域是( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠kx +π4,k ∈ZB.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠k π2+π8,k ∈Z C.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠k π+π8,k ∈Z D.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠k π2+π4,k ∈Z 解析:选D.由2x ≠k π+π2,k ∈Z ,得x ≠k π2+π4,k ∈Z ,所以y =tan 2x 的定义域为⎩⎨⎧⎭⎬⎫x |x ≠k π2+π4,k ∈Z . 3.(多选)下列函数中,最小正周期为π的偶函数有( ) A .y =tan xB .y =|sin x |C .y =2cos xD .y =sin ⎝ ⎛⎭⎪⎫π2-2x解析:选BD.对于A 选项,函数y =tan x 为奇函数,不符合题意;对于B 选项,函数y =|sin x |是最小正周期为π的偶函数,符合题意;对于C 选项,函数y =2cos x 的最小正周期为2π,不符合题意;对于D 选项,函数y =sin ⎝ ⎛⎭⎪⎫π2-2x =cos 2x ,是最小正周期为π的偶函数,符合题意.故选BD.4.函数y =cos ⎝ ⎛⎭⎪⎫2x -π4的单调递减区间为________.解析:由y =cos ⎝ ⎛⎭⎪⎫2x -π4, 得2k π≤2x -π4≤2k π+π(k ∈Z ), 解得k π+π8≤x ≤k π+5π8(k ∈Z ).所以函数的单调递减区间为⎣⎢⎡⎦⎥⎤k π+π8,k π+5π8(k ∈Z ). 答案:⎣⎢⎡⎦⎥⎤k π+π8,k π+5π8(k ∈Z )5.已知函数f (x )=2sin ⎝ ⎛⎭⎪⎫x +π4+φ是奇函数,当φ∈⎣⎢⎡⎦⎥⎤-π2,π2时,φ的值为________.解析:由已知得π4+φ=k π(k ∈Z ),所以φ=k π-π4(k ∈Z ).又因为φ∈⎣⎢⎡⎦⎥⎤-π2,π2,所以当k =0时,φ=-π4符合条件.答案:-π4第1课时 三角函数的单调性与最值求三角函数的单调区间(1)函数f (x )=sin ⎝ ⎛⎭⎪⎫-2x +π3的单调递减区间为________.(2)函数f (x )=tan(2x +π3)的单调递增区间是________.【解析】 (1)f (x )=sin ⎝ ⎛⎭⎪⎫-2x +π3=sin ⎣⎢⎡⎦⎥⎤-⎝ ⎛⎭⎪⎫2x -π3=-sin ⎝ ⎛⎭⎪⎫2x -π3,由2k π-π2≤2x -π3≤2k π+π2,k ∈Z ,得k π-π12≤x ≤k π+5π12,k ∈Z .故所求函数的单调递减区间为⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12(k ∈Z ). (2)由k π-π2<2x +π3<k π+π2(k ∈Z ),得k π2-5π12<x <k π2+π12(k ∈Z ),所以函数f (x )=tan ⎝ ⎛⎭⎪⎫2x +π3的单调递增区间为⎝ ⎛⎭⎪⎫k π2-5π12,k π2+π12(k ∈Z ).【答案】 (1)⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12(k ∈Z ) (2)⎝ ⎛⎭⎪⎫k π2-5π12,k π2+π12(k ∈Z ) 【引申探究】1.(变条件、变问法)若本例(1)f (x )变为:f (x )=-cos ⎝ ⎛⎭⎪⎫-2x +π3,求f (x )的单调递增区间.解:f (x )=-cos ⎝ ⎛⎭⎪⎫-2x +π3=-cos ⎝ ⎛⎭⎪⎫2x -π3,欲求函数f (x )的单调递增区间, 只需求y =cos ⎝ ⎛⎭⎪⎫2x -π3的单调递减区间.由2k π≤2x -π3≤2k π+π,k ∈Z , 得k π+π6≤x ≤k π+2π3,k ∈Z .故函数f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π+π6,k π+2π3(k ∈Z ).2.(变条件、变问法)本例(1)f (x )变为:f (x )=sin ⎝ ⎛⎭⎪⎫2x -π3,试讨论f (x )在区间⎣⎢⎡⎦⎥⎤-π4,π4上的单调性.解:令z =2x -π3,易知函数y =sin z 的单调递增区间是⎣⎢⎡⎦⎥⎤-π2+2k π,π2+2k π,k ∈Z .由-π2+2k π≤2x -π3≤π2+2k π, 得-π12+k π≤x ≤5π12+k π,k ∈Z .设A =⎣⎢⎡⎦⎥⎤-π4,π4,B =⎩⎨⎧⎭⎬⎫x |-π12+k π≤x ≤5π12+k π,k ∈Z ,易知A ∩B =⎣⎢⎡⎦⎥⎤-π12,π4. 所以,当x ∈⎣⎢⎡⎦⎥⎤-π4,π4时,f (x )在区间⎣⎢⎡⎦⎥⎤-π12,π4上单调递增,又因为π4-⎝ ⎛⎭⎪⎫-π4=π2<T ,所以f (x )在区间⎣⎢⎡⎦⎥⎤-π4,-π12上单调递减.求三角函数单调区间的两种方法(1)代换法:就是将比较复杂的三角函数含自变量的代数式整体当作一个角u (或t ),利用复合函数的单调性列不等式求解.(2)图象法:画出三角函数的图象,结合图象求它的单调区间.[提醒] 要注意求函数y =A sin(ωx +φ)的单调区间时ω的符号,若ω<0,那么一定要先借助诱导公式将ω化为正数.同时切莫漏掉考虑函数自身的定义域.1.函数y =|cos x |的一个单调递增区间是( ) A .[-π2,π2] B .[0,π] C .[π,3π2]D .[3π2,2π]解析:选D.将y =cos x 的图象位于x 轴下方的图象关于x 轴对称翻折到x 轴上方,x 轴上方(或x 轴上)的图象不变,即得y =|cos x |的图象(如图).故选D.2.设函数f (x )=sin ⎝ ⎛⎭⎪⎫2x -π3,x ∈⎣⎢⎡⎦⎥⎤-π2,π,则以下结论正确的是( )A .函数f (x )在⎣⎢⎡⎦⎥⎤-π2,0上单调递减B .函数f (x )在⎣⎢⎡⎦⎥⎤0,π2上单调递增 C .函数f (x )在⎣⎢⎡⎦⎥⎤π2,5π6上单调递减D .函数f (x )在⎣⎢⎡⎦⎥⎤5π6,π上单调递增解析:选C.由x ∈⎣⎢⎡⎦⎥⎤-π2,0得2x -π3∈⎣⎢⎡⎦⎥⎤-4π3,-π3,所以f (x )先减后增;由x ∈⎣⎢⎡⎦⎥⎤0,π2得2x -π3∈⎣⎢⎡⎦⎥⎤-π3,2π3,所以f (x )先增后减;由x ∈⎣⎢⎡⎦⎥⎤π2,5π6得2x -π3∈⎣⎢⎡⎦⎥⎤2π3,4π3,所以f (x )单调递减;由x ∈⎣⎢⎡⎦⎥⎤5π6,π得2x -π3∈⎣⎢⎡⎦⎥⎤4π3,5π3,所以f (x )先减后增.三角函数单调性的应用 角度一 利用三角函数的单调性比较大小已知函数f (x )=2sin ⎝ ⎛⎭⎪⎫x +π3,设a =f ⎝ ⎛⎭⎪⎫π7,b =f ⎝ ⎛⎭⎪⎫π6,c =f ⎝ ⎛⎭⎪⎫π3,则a ,b ,c的大小关系是( )A .a <c <bB .c <a <bC .b <a <cD .b <c <a【解析】 a =f ⎝ ⎛⎭⎪⎫π7=2sin 10π21,b =f ⎝ ⎛⎭⎪⎫π6=2sin π2=2,c =f ⎝ ⎛⎭⎪⎫π3=2sin 2π3=2sinπ3,因为y =sin x 在⎣⎢⎡⎦⎥⎤0,π2上单调递增,且π3<10π21<π2,所以c <a <b .【答案】 B利用函数的单调性比较大小(1)比较同名三角函数的大小,首先把三角函数转化为同一单调区间上的三角函数,利用单调性,由自变量的大小确定函数值的大小;(2)比较不同名三角函数的大小,应先化成同名三角函数,再进行比较.角度二 利用三角函数的单调性求值域(最值)(1)函数f (x )=3sin ⎝ ⎛⎭⎪⎫2x -π6在区间⎣⎢⎡⎦⎥⎤0,π2上的值域为( ) A.⎣⎢⎡⎦⎥⎤-32,32 B.⎣⎢⎡⎦⎥⎤-32,3 C.⎣⎢⎡⎦⎥⎤-332,332 D.⎣⎢⎡⎦⎥⎤-332,3 (2)函数y =sin x -cos x +sin x cos x的值域为_________________________________.【解析】 (1)当x ∈⎣⎢⎡⎦⎥⎤0,π2时,2x -π6∈⎣⎢⎡⎦⎥⎤-π6,5π6,sin ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-12,1, 故3sin ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-32,3,即此时函数f (x )的值域是⎣⎢⎡⎦⎥⎤-32,3.(2)设t =sin x -cos x ,则-2≤t ≤2,t 2=sin 2x +cos 2x -2sin x cos x ,则sin x cos x =1-t 22,所以y =-t 22+t +12=-12(t -1)2+1.当t =1时,y max =1;当t =-2时,y min =-12- 2. 所以函数y 的值域为[-12-2,1]. 【答案】 (1)B (2)[-12-2,1] 【引申探究】1.(变条件)若本例(1)中函数f (x )的解析式变为:f (x )=3cos ⎝ ⎛⎭⎪⎫2x -π6,则f (x )在区间⎣⎢⎡⎦⎥⎤0,π2上的值域为________.解析:当x ∈⎣⎢⎡⎦⎥⎤0,π2时,2x -π6∈⎣⎢⎡⎦⎥⎤-π6,5π6,cos ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-32,1, 故f (x )=3cos ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-332,3. 答案:⎣⎢⎡⎦⎥⎤-332,3 2.(变条件)若本例(2)中x ∈[0,π],则函数f (x )的值域为________. 解析:设t =sin x -cos x ,则t =2sin ⎝ ⎛⎭⎪⎫x -π4,又x ∈[0,π],所以t ∈[-1,2]. t 2=sin 2x +cos 2x -2sin x cos x , 即sin x cos x =1-t 22,所以y =-t 22+t +12=-12(t -1)2+1.当t =1时,y max =1;当t =-1时,y min =-1. 所以函数y 的值域为[-1,1]. 答案:[-1,1]三角函数值域的求法(1)利用y =sin x 和y =cos x 的值域直接求.(2)把所给的三角函数式变换成y =A sin(ωx +φ)+b (或y =A cos(ωx +φ)+b )的形式求值域.(3)把sin x 或cos x 看作一个整体,将原函数转换成二次函数求值域. (4)利用sin x ±cos x 和sin x cos x 的关系将原函数转换成二次函数求值域.1.下列关系式中正确的是( ) A .sin 11°<cos 10°<sin 168° B .sin 168°<sin 11°<cos 10° C .sin 11°<sin 168°<cos 10° D .sin 168°<cos 10°<sin 11°解析:选C.因为sin 168°=sin(180°-12°)=sin 12°,cos 10°=sin(90°-10°)=sin 80°,由正弦函数y =sin x 在0°≤x ≤90°上是增函数,得sin 11°<sin 12°<sin 80°,所以sin 11°<sin 168°<cos 10°,故选C.2.已知函数f (x )=-10sin 2x -10sin x -12,x ∈⎣⎢⎡⎦⎥⎤-π2,m 的值域为⎣⎢⎡⎦⎥⎤-12,2,则实数m 的取值范围是( )A.⎣⎢⎡⎦⎥⎤-π3,0 B.⎣⎢⎡⎦⎥⎤-π6,0 C.⎣⎢⎡⎦⎥⎤-π3,π6 D.⎣⎢⎡⎦⎥⎤-π6,π3 解析:选B.记t =sin x ,x ∈⎣⎢⎡⎦⎥⎤-π2,m ,则函数f (x )可转化为g (t )=-10t 2-10t-12=-10⎝ ⎛⎭⎪⎫t +122+2.因为函数的最大值为2,显然此时t =-12. 令g (t )=-12,得t =-1或t =0,由题意知x ∈⎣⎢⎡⎦⎥⎤-π2,m ,当x =-π2时,t =-1,g (-1)=-12,结合g (t )的图象及函数的值域为⎣⎢⎡⎦⎥⎤-12,2,可得-12≤sin m ≤0,解得-π6≤m ≤0.故选B.根据三角函数的单调性确定参数(一题多解)若函数f (x )=23sin ωx cos ωx +2sin 2ωx +cos 2ωx 在区间⎣⎢⎡⎦⎥⎤-3π2,3π2上单调递增,则正数ω的最大值为( ) A.18 B.16 C.14D.13【解析】 方法一:因为f (x )=23sin ωx cos ωx +2sin 2ωx +cos 2ωx =3sin 2ωx +1在区间⎣⎢⎡⎦⎥⎤-3π2,3π2上单调递增,所以⎩⎪⎨⎪⎧-3ωπ≥-π2,3ωπ≤π2.解得ω≤16,所以正数ω的最大值是16.故选B.方法二:易知f (x )=3sin 2ωx +1,可得f (x )的最小正周期T =πω,所以⎩⎪⎨⎪⎧-π4ω≤-3π2,π4ω≥3π2,解得ω≤16.所以正数ω的最大值是16.故选B. 【答案】 B已知函数单调性求参数—— 明确一个不同,掌握两种方法(1)明确一个不同.“函数f (x )在区间M 上单调”与“函数f (x )的单调区间为N ”两者的含义不同,显然M 是N 的子集.(2)掌握两种方法.已知函数在区间M 上单调求解参数问题,主要有两种方法:一是利用已知区间与单调区间的子集关系建立参数所满足的关系式求解;二是利用导数,转化为导函数在区间M 上的保号性,由此列不等式求解.1.若f (x )=cos x -sin x 在[-a ,a ]上是减函数,则a 的最大值是( ) A .π4 B .π2 C .3π4D .π解析:选A.f (x )=cos x -sin x =-2sin ⎝ ⎛⎭⎪⎫x -π4,当x ∈⎣⎢⎡⎦⎥⎤-π4,3π4,即x -π4∈⎣⎢⎡⎦⎥⎤-π2,π2时, y =sin ⎝ ⎛⎭⎪⎫x -π4单调递增,则f (x )=-2sin ⎝ ⎛⎭⎪⎫x -π4单调递减.因为函数f (x )在[-a ,a ]上是减函数, 所以[-a ,a ]⊆⎣⎢⎡⎦⎥⎤-π4,3π4,所以0<a ≤π4,所以a 的最大值为π4.2.若函数f (x )=sin ωx (ω>0)在区间⎣⎢⎡⎦⎥⎤0,π3上单调递增,在区间⎣⎢⎡⎦⎥⎤π3,π2上单调递减,则ω=________.解析:因为f (x )=sin ωx (ω>0)过原点, 所以当0≤ωx ≤π2,即0≤x ≤π2ω时, y =sin ωx 是增函数;当π2≤ωx ≤3π2,即π2ω≤x ≤3π2ω时,y =sin ωx 是减函数. 由已知得π2ω=π3,解得ω=32. 答案:32[A 级 基础练]1.当x ∈[0,2π],则y =tan x +-cos x 的定义域为( ) A.⎣⎢⎡⎭⎪⎫0,π2 B.⎝ ⎛⎦⎥⎤π2,π C.⎣⎢⎡⎭⎪⎫π,3π2 D.⎝ ⎛⎦⎥⎤3π2,2π 解析:选C.方法一:由题意得⎩⎪⎨⎪⎧tan x ≥0,-cos x ≥0,x ∈[0,2π],x ≠k π+π2,k ∈Z ,所以函数y 的定义域为⎣⎢⎡⎭⎪⎫π,3π2.故选C. 方法二:当x =π时,函数有意义,排除A ,D ;当x =5π4时,函数有意义,排除B.故选C.2.下列关于函数y =4sin x ,x ∈[-π,π]的单调性的叙述,正确的是( ) A .在[-π,0]上是增函数,在[0,π]上是减函数B .在⎣⎢⎡⎦⎥⎤-π2,π2上是增函数,在⎣⎢⎡⎦⎥⎤-π,-π2及⎣⎢⎡⎦⎥⎤π2,π上是减函数C .在[0,π]上是增函数,在[-π,0]上是减函数D .在⎣⎢⎡⎦⎥⎤π2,π及⎣⎢⎡⎦⎥⎤-π,-π2上是增函数,在⎣⎢⎡⎦⎥⎤-π2,π2上是减函数解析:选B.函数y =4sin x 在⎣⎢⎡⎦⎥⎤-π,-π2和⎣⎢⎡⎦⎥⎤π2,π上单调递减,在⎣⎢⎡⎦⎥⎤-π2,π2上单调递增.故选B.3.(2020·武汉市学习质量检测)已知函数f (x )=sin 2x +sin 2⎝ ⎛⎭⎪⎫x +π3,则f (x )的最小值为( )A.12 B.14 C.34D.22解析:选 A.f (x )=sin 2x +sin 2⎝ ⎛⎭⎪⎫x +π3=sin 2x +⎝ ⎛⎭⎪⎫12sin x +32cos x 2=54sin 2x +34cos 2x +32sin x cos x =34+1-cos 2x 4+34sin 2x =1+12⎝ ⎛⎭⎪⎫32sin 2x -12cos 2x =1+12sin ⎝ ⎛⎭⎪⎫2x -π6≥1-12=12,故选A. 4.(2020·贵阳市第一学期监测考试)已知函数f (x )=sin(2x +φ),其中φ∈(0,2π),若f (x )≤f ⎝ ⎛⎭⎪⎫π6对于一切x ∈R 恒成立,则f (x )的单调递增区间是( )A.⎣⎢⎡⎦⎥⎤k π,k π+π2(k ∈Z )B.⎣⎢⎡⎦⎥⎤k π-π3,k π+π6(k ∈Z ) C.⎣⎢⎡⎦⎥⎤k π+π6,k π+2π3(k ∈Z ) D.⎣⎢⎡⎦⎥⎤k π-π2,k π(k ∈Z ) 解析:选B.因为f (x )≤f ⎝ ⎛⎭⎪⎫π6对x ∈R 恒成立,则f ⎝ ⎛⎭⎪⎫π6为函数f (x )的最大值,即2×π6+φ=2k π+π2(k ∈Z ),则φ=2k π+π6(k ∈Z ),又φ∈(0,2π),所以φ=π6,所以f (x )=sin ⎝ ⎛⎭⎪⎫2x +π6.令2x +π6∈⎣⎢⎡⎦⎥⎤2k π-π2,2k π+π2(k ∈Z ),则x ∈⎣⎢⎡⎦⎥⎤k π-π3,k π+π6(k ∈Z ).故选B.5.(2020·昆明市三诊一模)已知函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx -π4(ω>0),x ∈⎣⎢⎡⎦⎥⎤0,π2的值域是⎣⎢⎡⎦⎥⎤-22,1,则ω的取值范围是( )A.⎝ ⎛⎦⎥⎤0,32 B.⎣⎢⎡⎦⎥⎤32,3 C.⎣⎢⎡⎦⎥⎤3,72 D.⎣⎢⎡⎦⎥⎤52,72 解析:选B.通解:因为x ∈⎣⎢⎡⎦⎥⎤0,π2,ω>0,所以ωx -π4∈⎣⎢⎡⎦⎥⎤-π4,ωπ2-π4.又当x ∈⎣⎢⎡⎦⎥⎤0,π2时,f (x )∈⎣⎢⎡⎦⎥⎤-22,1,所以π2≤ωπ2-π4≤5π4,解得32≤ω≤3,故选B. 优解:当ω=2时,f (x )=sin ⎝ ⎛⎭⎪⎫2x -π4.因为x ∈⎣⎢⎡⎦⎥⎤0,π2,所以2x -π4∈⎣⎢⎡⎦⎥⎤-π4,3π4,所以sin ⎝ ⎛⎭⎪⎫2x -π4∈⎣⎢⎡⎦⎥⎤-22,1,满足题意,故排除A ,C ,D ,选B.6.比较大小:sin ⎝ ⎛⎭⎪⎫-π18________sin ⎝ ⎛⎭⎪⎫-π10.解析:因为y =sin x 在⎣⎢⎡⎦⎥⎤-π2,0上为增函数且-π18>-π10>-π2,故sin ⎝ ⎛⎭⎪⎫-π18>sin ⎝ ⎛⎭⎪⎫-π10.答案:>7.已知函数f (x )=4sin ⎝ ⎛⎭⎪⎫2x -π3,x ∈[-π,0],则f (x )的单调递增区间是________.解析:由-π2+2k π≤2x -π3≤π2+2k π(k ∈Z ), 得-π12+k π≤x ≤5π12+k π(k ∈Z ), 又因为x ∈[-π,0],所以f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤-π,-7π12和⎣⎢⎡⎦⎥⎤-π12,0.答案:⎣⎢⎡⎦⎥⎤-π,-7π12和⎣⎢⎡⎦⎥⎤-π12,08.若函数f (x )=2sin ωx (0<ω<1)在区间⎣⎢⎡⎦⎥⎤0,π3上的最大值为1,则ω=________.解析:因为0<ω<1,0≤x ≤π3,所以0≤ωx <π3,所以f (x )在区间⎣⎢⎡⎦⎥⎤0,π3上单调递增,则f (x )max =f ⎝ ⎛⎭⎪⎫π3=2sin ωπ3=1,即sin ωπ3=12.又因为0≤ωx <π3,所以ωπ3=π6,解得ω=12.答案:129.已知函数f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π4.(1)求f (x )的单调递增区间;(2)当x ∈⎣⎢⎡⎦⎥⎤π4,3π4时,求函数f (x )的最大值和最小值.解:(1)令2k π-π2≤2x +π4≤2k π+π2,k ∈Z , 则k π-3π8≤x ≤k π+π8,k ∈Z .故f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π-3π8,k π+π8,k ∈Z .(2)当x ∈⎣⎢⎡⎦⎥⎤π4,3π4时,3π4≤2x +π4≤7π4,所以-1≤sin ⎝ ⎛⎭⎪⎫2x +π4≤22,所以-2≤f (x )≤1,所以当x ∈⎣⎢⎡⎦⎥⎤π4,3π4时,函数f (x )的最大值为1,最小值为- 2.10.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫2x -π6.讨论函数f (x )在区间⎣⎢⎡⎦⎥⎤-π12,π2上的单调性并求出其值域.解:令-π2≤2x -π6≤π2,则-π6≤x ≤π3. 令π2≤2x -π6≤32π,则π3≤x ≤5π6. 因为-π12≤x ≤π2,所以函数f (x )=sin ⎝ ⎛⎭⎪⎫2x -π6在区间⎣⎢⎡⎦⎥⎤-π12,π3上单调递增,在区间⎣⎢⎡⎦⎥⎤π3,π2上单调递减.当x =π3时,f (x )取得最大值为1.因为f ⎝ ⎛⎭⎪⎫-π12=-32<f ⎝ ⎛⎭⎪⎫π2=12, 所以当x =-π12时,f (x )min =-32. 所以f (x )的值域为⎣⎢⎡⎦⎥⎤-32,1.[B 级 综合练]11.(2020·湖北八校第一次联考)若函数f (x )=sin x +3cos x 在区间[a ,b ]上是减函数,且f (a )=2,f (b )=-2,则函数g (x )=cos x -3sin x 在区间[a ,b ]上( )A .是增函数B .是减函数C .可以取得最大值2D .可以取得最小值-2解析:选 D.f (x )=sin x +3cos x =2sin ⎝ ⎛⎭⎪⎫x +π3,g (x )=cos x -3sin x =2cos ⎝ ⎛⎭⎪⎫x +π3=2sin ⎝ ⎛⎭⎪⎫x +π2+π3.f (x )在区间[a ,b ]上是减函数,且f (a )=2,f (b )=-2,不妨令a +π3=π2,b +π3=3π2,则a +π2+π3=π,b +π2+π3=2π,故g (x )在[a ,b ]上既不是增函数,也不是减函数,g (x )在[a ,b ]上可以取得最小值-2,故选D.12.(多选)关于函数f (x )=sin|x |-|cos x |,下列结论正确的是( ) A .f (x )是偶函数B .f (x )在区间⎝ ⎛⎭⎪⎫π2,π上单调递减C .f (x )的最大值为 2D .当x ∈⎝ ⎛⎭⎪⎫-π4,π4时,f (x )<0恒成立解析:选ABD.因为f (-x )=sin|-x |-|cos(-x )|=sin|x |-|cos x |=f (x ),所以f (x )为偶函数,故A 正确;当x ∈⎝ ⎛⎭⎪⎫π2,π时,f (x )=sin|x |-|cos x |=sin x +cos x =2sin ⎝ ⎛⎭⎪⎫x +π4,又x ∈⎝ ⎛⎭⎪⎫π2,π,所以令t =x +π4,则t ∈⎝ ⎛⎭⎪⎫3π4,5π4,y =2sin t 单调递减,所以B 正确;因为f (x )为偶函数,所以求函数f (x )的最大值可只考虑当x ≥0时的情况,又易知当x ≥0时,2π是其一个周期,所以只需研究x ∈[0,2π]时的情况,则f (x )=sin x -|cos x |=⎩⎪⎨⎪⎧sin x -cos x ,x ∈⎣⎢⎡⎦⎥⎤0,π2∪⎝ ⎛⎦⎥⎤3π2,2πsin x +cos x ,x ∈⎝ ⎛⎦⎥⎤π2,3π2=⎩⎪⎨⎪⎧2sin ⎝ ⎛⎭⎪⎫x -π4,x ∈⎣⎢⎡⎦⎥⎤0,π2∪⎝ ⎛⎦⎥⎤3π2,2π2sin ⎝ ⎛⎭⎪⎫x +π4,x ∈⎝ ⎛⎦⎥⎤π2,3π2,则函数f (x )的值域为[-2,1],因此C 错误;当x ∈⎣⎢⎡⎭⎪⎫0,π4时,f (x )=sin x -cos x =2sin ⎝ ⎛⎭⎪⎫x -π4,则x -π4∈⎣⎢⎡⎭⎪⎫-π4,0,所以sin ⎝ ⎛⎭⎪⎫x -π4<0,即f (x )<0在x ∈⎣⎢⎡⎭⎪⎫0,π4上恒成立,因为f (x )为偶函数,所以x ∈⎝ ⎛⎭⎪⎫-π4,π4时,f (x )<0恒成立,故D 正确.综上可知,正确结论是ABD. 13.已知函数f (x )=3cos ⎝ ⎛⎭⎪⎫2x -π3-2sin x cos x .(1)求f (x )的最小正周期;(2)求证:当x ∈⎣⎢⎡⎦⎥⎤-π4,π4时,f (x )≥-12.解:(1)f (x )=3cos ⎝ ⎛⎭⎪⎫2x -π3-2sin x cos x=32cos 2x +32sin 2x -sin 2x =12sin 2x +32cos 2x =sin ⎝ ⎛⎭⎪⎫2x +π3,所以T =2π2=π.(2)证明:令t =2x +π3,因为-π4≤x ≤π4, 所以-π6≤2x +π3≤5π6,因为y =sin t 在⎣⎢⎡⎦⎥⎤-π6,π2上单调递增,在⎣⎢⎡⎦⎥⎤π2,5π6上单调递减,且sin ⎝ ⎛⎭⎪⎫-π6<sin 5π6, 所以f (x )≥sin ⎝ ⎛⎭⎪⎫-π6=-12,得证.14.已知f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π6+a +1.(1)求f (x )的单调递增区间;(2)当x ∈⎣⎢⎡⎦⎥⎤0,π2时,f (x )的最大值为4,求a 的值;(3)在(2)的条件下,求满足f (x )=1且x ∈[-π,π]的x 的取值集合. 解:(1)f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π6+a +1, 由2k π-π2≤2x +π6≤2k π+π2,k ∈Z , 可得k π-π3≤x ≤k π+π6,k ∈Z ,所以f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π-π3,k π+π6,k ∈Z . (2)当x =π6时,f (x )取得最大值4,即f ⎝ ⎛⎭⎪⎫π6=2sin π2+a +1=a +3=4,所以a =1.(3)由f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π6+2=1,可得sin ⎝ ⎛⎭⎪⎫2x +π6=-12,则2x +π6=7π6+2k π,k ∈Z 或2x +π6=116π+2k π,k ∈Z ,即x =π2+k π,k ∈Z 或x =5π6+k π,k ∈Z ,又x ∈[-π,π],解得x =-π2,-π6,π2,5π6, 所以x的取值集合为⎩⎨⎧⎭⎬⎫-π2,-π6,π2,5π6. [C 级 创新练]15.(2020·贵阳市适应性考试)已知函数f (x )=2sin ⎝ ⎛⎭⎪⎫ωx +π4(ω>0)的图象在区间[0,1]上恰有3个最高点,则ω的取值范围为( )A .⎣⎢⎡⎭⎪⎫19π4,27π4B .⎣⎢⎡⎭⎪⎫9π2,13π2C .⎣⎢⎡⎭⎪⎫17π4,25π4D .[4π,6π)解析:选C.因为x ∈[0,1],ω>0,所以ωx +π4∈⎣⎢⎡⎦⎥⎤π4,ω+π4. 因为f (x )的图象在区间[0,1]上恰有3个最高点,所以4π+π2≤ω+π4<6π+π2,解得17π4≤ω<25π4.16.如图,角α的始边与x 轴的非负半轴重合,终边与单位圆交于点A (x 1,y 1),角β=α+2π3的终边与单位圆交于点B (x 2,y 2),记f (α)=y 1-y 2.若角α为锐角,则f (α)的取值范围是________.解析:由题意可知y 1=sin α,y 2=sin β=sin ⎝ ⎛⎭⎪⎫α+2π3,所以f (α)=y 1-y 2=sin α-sin ⎝ ⎛⎭⎪⎫α+2π3=sin α+12sin α-32cos α=32sin α-32cos α=3sin ⎝ ⎛⎭⎪⎫α-π6.又因为α为锐角,即0<α<π2,所以-π6<α-π6<π3,所以-12<sin ⎝ ⎛⎭⎪⎫α-π6<32,则-32<f (α)<32,即f (α)的取值范围是⎝ ⎛⎭⎪⎫-32,32.答案:⎝ ⎛⎭⎪⎫-32,32第4讲 三角函数的图象与性质最新考纲考向预测1.能画出y =sin x ,y =cos x ,y =tan x 的图象,了解三角函数的周期性.2.理解正弦函数、余弦函数在区间[0,2π]上的性质(如单调性、最大值和最小值以及与x 轴的交点等),理解正切函数在区间⎝ ⎛⎭⎪⎫-π2,π2内的单调性. 命题趋势以考查三角函数的性质为主,题目涉及单调性、周期性、最值、零点.考查三角函数性质时,常与三角恒等变换结合,加强数形结合思想、函数与方程思想的应用意识.题型既有选择题和填空题,又有解答题,中档难度. 核心素养 直观想象、逻辑推理1.用五点法作正弦函数和余弦函数的简图(1)正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),⎝ ⎛⎭⎪⎫π2,1,(π,0),⎝ ⎛⎭⎪⎫32π,-1,(2π,0).(2)余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),⎝ ⎛⎭⎪⎫π2,0,(π,-1),⎝ ⎛⎭⎪⎫3π2,0,(2π,1).2.正弦、余弦、正切函数的图象与性质 函数y =sin xy =cos xy =tan x图象定义 域 R R {x |x ≠k π+π2,k ∈Z } 值域[-1,1][-1,1]R周期性2π2ππ奇偶性奇函数偶函数奇函数单调递增区间[-π2+2kπ,π2+2kπ],k∈Z[-π+2kπ,2kπ],k∈Z(-π2+kπ,π2+kπ),k∈Z续表函数y=sin x y=cos x y=tan x单调递减区间[π2+2kπ,3π2+2kπ],k∈Z[2kπ,π+2kπ],k∈Z无对称性对称中心(kπ,0),k∈Z⎝⎛⎭⎪⎫kπ+π2,0,k∈Z⎝⎛⎭⎪⎫kπ2,0,k∈Z 对称轴x=kπ+π2,k∈Zx=kπ,k∈Z无对称轴零点kπ,k∈Z kπ+π2,k∈Zkπ,k∈Z常用结论1.对称与周期的关系正弦曲线、余弦曲线相邻的两个对称中心、相邻的两条对称轴之间的距离是半个周期,相邻的对称中心与对称轴之间的距离是四分之一个周期;正切曲线相邻两个对称中心之间的距离是半个周期.2.与三角函数的奇偶性相关的结论(1)若y=A sin(ωx+φ)为偶函数,则有φ=kπ+π2(k∈Z);若为奇函数,则有φ=kπ(k∈Z).(2)若y=A cos(ωx+φ)为偶函数,则有φ=kπ(k∈Z);若为奇函数,则有φ=kπ+π2(k ∈Z ).(3)若y =A tan(ωx +φ)为奇函数,则有φ=k π(k ∈Z ). 常见误区1.对于y =tan x 不能认为其在定义域上为增函数,而是在每个开区间⎝ ⎛⎭⎪⎫k π-π2,k π+π2(k ∈Z )内为增函数. 2.求函数y =A sin(ωx +φ)的单调区间时要注意A 和ω的符号,尽量化成ω>0的形式,避免出现增减区间的混淆.1.判断正误(正确的打“√”,错误的打“×”) (1)y =cos x 在第一、二象限内是减函数.( ) (2)若y =k sin x +1,x ∈R ,则y 的最大值是k +1.( )(3)若非零实数T 是函数f (x )的周期,则kT (k 是非零整数)也是函数f (x )的周期.( )(4)函数y =sin x 图象的对称轴方程为x =2k π+π2(k ∈Z ).( ) (5)函数y =tan x 在整个定义域上是增函数.( ) 答案:(1)× (2)× (3)√ (4)× (5)× 2.(易错点)函数y =tan 2x 的定义域是( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠kx +π4,k ∈ZB.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠k π2+π8,k ∈Z C.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠k π+π8,k ∈Z D.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠k π2+π4,k ∈Z 解析:选D.由2x ≠k π+π2,k ∈Z ,得x ≠k π2+π4,k ∈Z ,所以y =tan 2x 的定义域为⎩⎨⎧⎭⎬⎫x |x ≠k π2+π4,k ∈Z . 3.(多选)下列函数中,最小正周期为π的偶函数有( ) A .y =tan xB .y =|sin x |C .y =2cos xD .y =sin ⎝ ⎛⎭⎪⎫π2-2x解析:选BD.对于A 选项,函数y =tan x 为奇函数,不符合题意;对于B 选项,函数y =|sin x |是最小正周期为π的偶函数,符合题意;对于C 选项,函数y =2cos x 的最小正周期为2π,不符合题意;对于D 选项,函数y =sin ⎝ ⎛⎭⎪⎫π2-2x =cos 2x ,是最小正周期为π的偶函数,符合题意.故选BD.4.函数y =cos ⎝ ⎛⎭⎪⎫2x -π4的单调递减区间为________.解析:由y =cos ⎝ ⎛⎭⎪⎫2x -π4, 得2k π≤2x -π4≤2k π+π(k ∈Z ), 解得k π+π8≤x ≤k π+5π8(k ∈Z ).所以函数的单调递减区间为⎣⎢⎡⎦⎥⎤k π+π8,k π+5π8(k ∈Z ). 答案:⎣⎢⎡⎦⎥⎤k π+π8,k π+5π8(k ∈Z )5.已知函数f (x )=2sin ⎝ ⎛⎭⎪⎫x +π4+φ是奇函数,当φ∈⎣⎢⎡⎦⎥⎤-π2,π2时,φ的值为________.解析:由已知得π4+φ=k π(k ∈Z ),所以φ=k π-π4(k ∈Z ).又因为φ∈⎣⎢⎡⎦⎥⎤-π2,π2,所以当k =0时,φ=-π4符合条件.答案:-π4第1课时 三角函数的单调性与最值求三角函数的单调区间(1)函数f (x )=sin ⎝ ⎛⎭⎪⎫-2x +π3的单调递减区间为________.(2)函数f (x )=tan(2x +π3)的单调递增区间是________.【解析】 (1)f (x )=sin ⎝ ⎛⎭⎪⎫-2x +π3=sin ⎣⎢⎡⎦⎥⎤-⎝ ⎛⎭⎪⎫2x -π3=-sin ⎝ ⎛⎭⎪⎫2x -π3,由2k π-π2≤2x -π3≤2k π+π2,k ∈Z ,得k π-π12≤x ≤k π+5π12,k ∈Z .故所求函数的单调递减区间为⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12(k ∈Z ). (2)由k π-π2<2x +π3<k π+π2(k ∈Z ),得k π2-5π12<x <k π2+π12(k ∈Z ),所以函数f (x )=tan ⎝ ⎛⎭⎪⎫2x +π3的单调递增区间为⎝ ⎛⎭⎪⎫k π2-5π12,k π2+π12(k ∈Z ).【答案】 (1)⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12(k ∈Z ) (2)⎝ ⎛⎭⎪⎫k π2-5π12,k π2+π12(k ∈Z ) 【引申探究】1.(变条件、变问法)若本例(1)f (x )变为:f (x )=-cos ⎝ ⎛⎭⎪⎫-2x +π3,求f (x )的单调递增区间.解:f (x )=-cos ⎝ ⎛⎭⎪⎫-2x +π3=-cos ⎝ ⎛⎭⎪⎫2x -π3,欲求函数f (x )的单调递增区间, 只需求y =cos ⎝ ⎛⎭⎪⎫2x -π3的单调递减区间.由2k π≤2x -π3≤2k π+π,k ∈Z , 得k π+π6≤x ≤k π+2π3,k ∈Z .故函数f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π+π6,k π+2π3(k ∈Z ).2.(变条件、变问法)本例(1)f (x )变为:f (x )=sin ⎝ ⎛⎭⎪⎫2x -π3,试讨论f (x )在区间⎣⎢⎡⎦⎥⎤-π4,π4上的单调性.解:令z =2x -π3,易知函数y =sin z 的单调递增区间是⎣⎢⎡⎦⎥⎤-π2+2k π,π2+2k π,k ∈Z .由-π2+2k π≤2x -π3≤π2+2k π, 得-π12+k π≤x ≤5π12+k π,k ∈Z .设A =⎣⎢⎡⎦⎥⎤-π4,π4,B =⎩⎨⎧⎭⎬⎫x |-π12+k π≤x ≤5π12+k π,k ∈Z ,易知A ∩B =⎣⎢⎡⎦⎥⎤-π12,π4. 所以,当x ∈⎣⎢⎡⎦⎥⎤-π4,π4时,f (x )在区间⎣⎢⎡⎦⎥⎤-π12,π4上单调递增,又因为π4-⎝ ⎛⎭⎪⎫-π4=π2<T ,所以f (x )在区间⎣⎢⎡⎦⎥⎤-π4,-π12上单调递减.求三角函数单调区间的两种方法(1)代换法:就是将比较复杂的三角函数含自变量的代数式整体当作一个角u (或t ),利用复合函数的单调性列不等式求解.(2)图象法:画出三角函数的图象,结合图象求它的单调区间.[提醒] 要注意求函数y =A sin(ωx +φ)的单调区间时ω的符号,若ω<0,那么一定要先借助诱导公式将ω化为正数.同时切莫漏掉考虑函数自身的定义域.1.函数y =|cos x |的一个单调递增区间是( ) A .[-π2,π2] B .[0,π] C .[π,3π2]D .[3π2,2π]解析:选D.将y =cos x 的图象位于x 轴下方的图象关于x 轴对称翻折到x 轴上方,x 轴上方(或x 轴上)的图象不变,即得y =|cos x |的图象(如图).故选D.2.设函数f (x )=sin ⎝ ⎛⎭⎪⎫2x -π3,x ∈⎣⎢⎡⎦⎥⎤-π2,π,则以下结论正确的是( )A .函数f (x )在⎣⎢⎡⎦⎥⎤-π2,0上单调递减B .函数f (x )在⎣⎢⎡⎦⎥⎤0,π2上单调递增 C .函数f (x )在⎣⎢⎡⎦⎥⎤π2,5π6上单调递减D .函数f (x )在⎣⎢⎡⎦⎥⎤5π6,π上单调递增解析:选C.由x ∈⎣⎢⎡⎦⎥⎤-π2,0得2x -π3∈⎣⎢⎡⎦⎥⎤-4π3,-π3,所以f (x )先减后增;由x ∈⎣⎢⎡⎦⎥⎤0,π2得2x -π3∈⎣⎢⎡⎦⎥⎤-π3,2π3,所以f (x )先增后减;由x ∈⎣⎢⎡⎦⎥⎤π2,5π6得2x -π3∈⎣⎢⎡⎦⎥⎤2π3,4π3,所以f (x )单调递减;由x ∈⎣⎢⎡⎦⎥⎤5π6,π得2x -π3∈⎣⎢⎡⎦⎥⎤4π3,5π3,所以f (x )先减后增.三角函数单调性的应用 角度一 利用三角函数的单调性比较大小已知函数f (x )=2sin ⎝ ⎛⎭⎪⎫x +π3,设a =f ⎝ ⎛⎭⎪⎫π7,b =f ⎝ ⎛⎭⎪⎫π6,c =f ⎝ ⎛⎭⎪⎫π3,则a ,b ,c的大小关系是( )A .a <c <bB .c <a <bC .b <a <cD .b <c <a【解析】 a =f ⎝ ⎛⎭⎪⎫π7=2sin 10π21,b =f ⎝ ⎛⎭⎪⎫π6=2sin π2=2,c =f ⎝ ⎛⎭⎪⎫π3=2sin 2π3=2sinπ3,因为y =sin x 在⎣⎢⎡⎦⎥⎤0,π2上单调递增,且π3<10π21<π2,所以c <a <b .【答案】 B利用函数的单调性比较大小(1)比较同名三角函数的大小,首先把三角函数转化为同一单调区间上的三角函数,利用单调性,由自变量的大小确定函数值的大小;(2)比较不同名三角函数的大小,应先化成同名三角函数,再进行比较.角度二 利用三角函数的单调性求值域(最值)(1)函数f (x )=3sin ⎝ ⎛⎭⎪⎫2x -π6在区间⎣⎢⎡⎦⎥⎤0,π2上的值域为( ) A.⎣⎢⎡⎦⎥⎤-32,32 B.⎣⎢⎡⎦⎥⎤-32,3 C.⎣⎢⎡⎦⎥⎤-332,332 D.⎣⎢⎡⎦⎥⎤-332,3 (2)函数y =sin x -cos x +sin x cos x的值域为_________________________________.【解析】 (1)当x ∈⎣⎢⎡⎦⎥⎤0,π2时,2x -π6∈⎣⎢⎡⎦⎥⎤-π6,5π6,sin ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-12,1, 故3sin ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-32,3,即此时函数f (x )的值域是⎣⎢⎡⎦⎥⎤-32,3.(2)设t =sin x -cos x ,则-2≤t ≤2,t 2=sin 2x +cos 2x -2sin x cos x ,则sin x cos x =1-t 22,所以y =-t 22+t +12=-12(t -1)2+1.当t =1时,y max =1;当t =-2时,y min =-12- 2. 所以函数y 的值域为[-12-2,1]. 【答案】 (1)B (2)[-12-2,1] 【引申探究】1.(变条件)若本例(1)中函数f (x )的解析式变为:f (x )=3cos ⎝ ⎛⎭⎪⎫2x -π6,则f (x )在区间⎣⎢⎡⎦⎥⎤0,π2上的值域为________.解析:当x ∈⎣⎢⎡⎦⎥⎤0,π2时,2x -π6∈⎣⎢⎡⎦⎥⎤-π6,5π6,cos ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-32,1, 故f (x )=3cos ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-332,3. 答案:⎣⎢⎡⎦⎥⎤-332,3 2.(变条件)若本例(2)中x ∈[0,π],则函数f (x )的值域为________. 解析:设t =sin x -cos x ,则t =2sin ⎝ ⎛⎭⎪⎫x -π4,又x ∈[0,π],所以t ∈[-1,2]. t 2=sin 2x +cos 2x -2sin x cos x , 即sin x cos x =1-t 22,所以y =-t 22+t +12=-12(t -1)2+1.当t =1时,y max =1;当t =-1时,y min =-1. 所以函数y 的值域为[-1,1]. 答案:[-1,1]三角函数值域的求法(1)利用y =sin x 和y =cos x 的值域直接求.(2)把所给的三角函数式变换成y =A sin(ωx +φ)+b (或y =A cos(ωx +φ)+b )的形式求值域.(3)把sin x 或cos x 看作一个整体,将原函数转换成二次函数求值域. (4)利用sin x ±cos x 和sin x cos x 的关系将原函数转换成二次函数求值域.1.下列关系式中正确的是( ) A .sin 11°<cos 10°<sin 168° B .sin 168°<sin 11°<cos 10° C .sin 11°<sin 168°<cos 10° D .sin 168°<cos 10°<sin 11°解析:选C.因为sin 168°=sin(180°-12°)=sin 12°,cos 10°=sin(90°-10°)=sin 80°,由正弦函数y =sin x 在0°≤x ≤90°上是增函数,得sin 11°<sin 12°<sin 80°,所以sin 11°<sin 168°<cos 10°,故选C.2.已知函数f (x )=-10sin 2x -10sin x -12,x ∈⎣⎢⎡⎦⎥⎤-π2,m 的值域为⎣⎢⎡⎦⎥⎤-12,2,则实数m 的取值范围是( )A.⎣⎢⎡⎦⎥⎤-π3,0 B.⎣⎢⎡⎦⎥⎤-π6,0 C.⎣⎢⎡⎦⎥⎤-π3,π6 D.⎣⎢⎡⎦⎥⎤-π6,π3 解析:选B.记t =sin x ,x ∈⎣⎢⎡⎦⎥⎤-π2,m ,则函数f (x )可转化为g (t )=-10t 2-10t-12=-10⎝ ⎛⎭⎪⎫t +122+2.因为函数的最大值为2,显然此时t =-12. 令g (t )=-12,得t =-1或t =0,由题意知x ∈⎣⎢⎡⎦⎥⎤-π2,m ,当x =-π2时,t =-1,g (-1)=-12,结合g (t )的图象及函数的值域为⎣⎢⎡⎦⎥⎤-12,2,可得-12≤sin m ≤0,解得-π6≤m ≤0.故选B.根据三角函数的单调性确定参数(一题多解)若函数f (x )=23sin ωx cos ωx +2sin 2ωx +cos 2ωx 在区间⎣⎢⎡⎦⎥⎤-3π2,3π2上单调递增,则正数ω的最大值为( ) A.18 B.16 C.14D.13【解析】 方法一:因为f (x )=23sin ωx cos ωx +2sin 2ωx +cos 2ωx =3sin 2ωx +1在区间⎣⎢⎡⎦⎥⎤-3π2,3π2上单调递增,所以⎩⎪⎨⎪⎧-3ωπ≥-π2,3ωπ≤π2.解得ω≤16,所以正数ω的最大值是16.故选B.方法二:易知f (x )=3sin 2ωx +1,可得f (x )的最小正周期T =πω,所以⎩⎪⎨⎪⎧-π4ω≤-3π2,π4ω≥3π2,解得ω≤16.所以正数ω的最大值是16.故选B. 【答案】 B已知函数单调性求参数—— 明确一个不同,掌握两种方法(1)明确一个不同.“函数f (x )在区间M 上单调”与“函数f (x )的单调区间为N ”两者的含义不同,显然M 是N 的子集.(2)掌握两种方法.已知函数在区间M 上单调求解参数问题,主要有两种方法:一是利用已知区间与单调区间的子集关系建立参数所满足的关系式求解;二是利用导数,转化为导函数在区间M 上的保号性,由此列不等式求解.1.若f (x )=cos x -sin x 在[-a ,a ]上是减函数,则a 的最大值是( ) A .π4 B .π2 C .3π4D .π解析:选A.f (x )=cos x -sin x =-2sin ⎝ ⎛⎭⎪⎫x -π4,当x ∈⎣⎢⎡⎦⎥⎤-π4,3π4,即x -π4∈⎣⎢⎡⎦⎥⎤-π2,π2时, y =sin ⎝ ⎛⎭⎪⎫x -π4单调递增,则f (x )=-2sin ⎝ ⎛⎭⎪⎫x -π4单调递减.因为函数f (x )在[-a ,a ]上是减函数, 所以[-a ,a ]⊆⎣⎢⎡⎦⎥⎤-π4,3π4,所以0<a ≤π4,所以a 的最大值为π4.2.若函数f (x )=sin ωx (ω>0)在区间⎣⎢⎡⎦⎥⎤0,π3上单调递增,在区间⎣⎢⎡⎦⎥⎤π3,π2上单调递减,则ω=________.解析:因为f (x )=sin ωx (ω>0)过原点, 所以当0≤ωx ≤π2,即0≤x ≤π2ω时, y =sin ωx 是增函数;当π2≤ωx ≤3π2,即π2ω≤x ≤3π2ω时,y =sin ωx 是减函数. 由已知得π2ω=π3,解得ω=32. 答案:32[A 级 基础练]1.当x ∈[0,2π],则y =tan x +-cos x 的定义域为( ) A.⎣⎢⎡⎭⎪⎫0,π2 B.⎝ ⎛⎦⎥⎤π2,π C.⎣⎢⎡⎭⎪⎫π,3π2 D.⎝ ⎛⎦⎥⎤3π2,2π 解析:选C.方法一:由题意得⎩⎪⎨⎪⎧tan x ≥0,-cos x ≥0,x ∈[0,2π],x ≠k π+π2,k ∈Z ,所以函数y 的定义域为⎣⎢⎡⎭⎪⎫π,3π2.故选C. 方法二:当x =π时,函数有意义,排除A ,D ;当x =5π4时,函数有意义,排除B.故选C.2.下列关于函数y =4sin x ,x ∈[-π,π]的单调性的叙述,正确的是( ) A .在[-π,0]上是增函数,在[0,π]上是减函数B .在⎣⎢⎡⎦⎥⎤-π2,π2上是增函数,在⎣⎢⎡⎦⎥⎤-π,-π2及⎣⎢⎡⎦⎥⎤π2,π上是减函数C .在[0,π]上是增函数,在[-π,0]上是减函数D .在⎣⎢⎡⎦⎥⎤π2,π及⎣⎢⎡⎦⎥⎤-π,-π2上是增函数,在⎣⎢⎡⎦⎥⎤-π2,π2上是减函数解析:选B.函数y =4sin x 在⎣⎢⎡⎦⎥⎤-π,-π2和⎣⎢⎡⎦⎥⎤π2,π上单调递减,在⎣⎢⎡⎦⎥⎤-π2,π2上单调递增.故选B.3.(2020·武汉市学习质量检测)已知函数f (x )=sin 2x +sin 2⎝ ⎛⎭⎪⎫x +π3,则f (x )的最小值为( )A.12 B.14 C.34D.22解析:选 A.f (x )=sin 2x +sin 2⎝ ⎛⎭⎪⎫x +π3=sin 2x +⎝ ⎛⎭⎪⎫12sin x +32cos x 2=54sin 2x +34cos 2x +32sin x cos x =34+1-cos 2x 4+34sin 2x =1+12⎝ ⎛⎭⎪⎫32sin 2x -12cos 2x =1+12sin ⎝ ⎛⎭⎪⎫2x -π6≥1-12=12,故选A. 4.(2020·贵阳市第一学期监测考试)已知函数f (x )=sin(2x +φ),其中φ∈(0,2π),若f (x )≤f ⎝ ⎛⎭⎪⎫π6对于一切x ∈R 恒成立,则f (x )的单调递增区间是( )A.⎣⎢⎡⎦⎥⎤k π,k π+π2(k ∈Z )B.⎣⎢⎡⎦⎥⎤k π-π3,k π+π6(k ∈Z ) C.⎣⎢⎡⎦⎥⎤k π+π6,k π+2π3(k ∈Z ) D.⎣⎢⎡⎦⎥⎤k π-π2,k π(k ∈Z ) 解析:选B.因为f (x )≤f ⎝ ⎛⎭⎪⎫π6对x ∈R 恒成立,则f ⎝ ⎛⎭⎪⎫π6为函数f (x )的最大值,即2×π6+φ=2k π+π2(k ∈Z ),则φ=2k π+π6(k ∈Z ),又φ∈(0,2π),所以φ=π6,所以f (x )=sin ⎝ ⎛⎭⎪⎫2x +π6.令2x +π6∈⎣⎢⎡⎦⎥⎤2k π-π2,2k π+π2(k ∈Z ),则x ∈⎣⎢⎡⎦⎥⎤k π-π3,k π+π6(k ∈Z ).故选B.5.(2020·昆明市三诊一模)已知函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx -π4(ω>0),x ∈⎣⎢⎡⎦⎥⎤0,π2的值域是⎣⎢⎡⎦⎥⎤-22,1,则ω的取值范围是( )A.⎝ ⎛⎦⎥⎤0,32 B.⎣⎢⎡⎦⎥⎤32,3 C.⎣⎢⎡⎦⎥⎤3,72 D.⎣⎢⎡⎦⎥⎤52,72 解析:选B.通解:因为x ∈⎣⎢⎡⎦⎥⎤0,π2,ω>0,所以ωx -π4∈⎣⎢⎡⎦⎥⎤-π4,ωπ2-π4.又当x ∈⎣⎢⎡⎦⎥⎤0,π2时,f (x )∈⎣⎢⎡⎦⎥⎤-22,1,所以π2≤ωπ2-π4≤5π4,解得32≤ω≤3,故选B. 优解:当ω=2时,f (x )=sin ⎝ ⎛⎭⎪⎫2x -π4.因为x ∈⎣⎢⎡⎦⎥⎤0,π2,所以2x -π4∈⎣⎢⎡⎦⎥⎤-π4,3π4,所以sin ⎝ ⎛⎭⎪⎫2x -π4∈⎣⎢⎡⎦⎥⎤-22,1,满足题意,故排除A ,C ,D ,选B.6.比较大小:sin ⎝ ⎛⎭⎪⎫-π18________sin ⎝ ⎛⎭⎪⎫-π10.解析:因为y =sin x 在⎣⎢⎡⎦⎥⎤-π2,0上为增函数且-π18>-π10>-π2,故sin ⎝ ⎛⎭⎪⎫-π18>sin ⎝ ⎛⎭⎪⎫-π10.答案:>7.已知函数f (x )=4sin ⎝ ⎛⎭⎪⎫2x -π3,x ∈[-π,0],则f (x )的单调递增区间是________.解析:由-π2+2k π≤2x -π3≤π2+2k π(k ∈Z ), 得-π12+k π≤x ≤5π12+k π(k ∈Z ), 又因为x ∈[-π,0],所以f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤-π,-7π12和⎣⎢⎡⎦⎥⎤-π12,0.答案:⎣⎢⎡⎦⎥⎤-π,-7π12和⎣⎢⎡⎦⎥⎤-π12,08.若函数f (x )=2sin ωx (0<ω<1)在区间⎣⎢⎡⎦⎥⎤0,π3上的最大值为1,则ω=________.解析:因为0<ω<1,0≤x ≤π3,所以0≤ωx <π3,所以f (x )在区间⎣⎢⎡⎦⎥⎤0,π3上单调递增,则f (x )max =f ⎝ ⎛⎭⎪⎫π3=2sin ωπ3=1,即sin ωπ3=12.又因为0≤ωx <π3,所以ωπ3=π6,解得ω=12.答案:129.已知函数f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π4.(1)求f (x )的单调递增区间;(2)当x ∈⎣⎢⎡⎦⎥⎤π4,3π4时,求函数f (x )的最大值和最小值.解:(1)令2k π-π2≤2x +π4≤2k π+π2,k ∈Z , 则k π-3π8≤x ≤k π+π8,k ∈Z .故f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π-3π8,k π+π8,k ∈Z .(2)当x ∈⎣⎢⎡⎦⎥⎤π4,3π4时,3π4≤2x +π4≤7π4,所以-1≤sin ⎝ ⎛⎭⎪⎫2x +π4≤22,所以-2≤f (x )≤1,所以当x ∈⎣⎢⎡⎦⎥⎤π4,3π4时,函数f (x )的最大值为1,最小值为- 2.10.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫2x -π6.讨论函数f (x )在区间⎣⎢⎡⎦⎥⎤-π12,π2上的单调性并求出其值域.解:令-π2≤2x -π6≤π2,则-π6≤x ≤π3. 令π2≤2x -π6≤32π,则π3≤x ≤5π6. 因为-π12≤x ≤π2,所以函数f (x )=sin ⎝ ⎛⎭⎪⎫2x -π6在区间⎣⎢⎡⎦⎥⎤-π12,π3上单调递增,在区间⎣⎢⎡⎦⎥⎤π3,π2上单调递减.当x =π3时,f (x )取得最大值为1.因为f ⎝ ⎛⎭⎪⎫-π12=-32<f ⎝ ⎛⎭⎪⎫π2=12, 所以当x =-π12时,f (x )min =-32. 所以f (x )的值域为⎣⎢⎡⎦⎥⎤-32,1.[B 级 综合练]11.(2020·湖北八校第一次联考)若函数f (x )=sin x +3cos x 在区间[a ,b ]上是减函数,且f (a )=2,f (b )=-2,则函数g (x )=cos x -3sin x 在区间[a ,b ]上( )A .是增函数B .是减函数C .可以取得最大值2D .可以取得最小值-2解析:选 D.f (x )=sin x +3cos x =2sin ⎝ ⎛⎭⎪⎫x +π3,g (x )=cos x -3sin x =2cos ⎝ ⎛⎭⎪⎫x +π3=2sin ⎝ ⎛⎭⎪⎫x +π2+π3.f (x )在区间[a ,b ]上是减函数,且f (a )=2,f (b )=-2,不妨令a +π3=π2,b +π3=3π2,则a +π2+π3=π,b +π2+π3=2π,故g (x )在[a ,b ]上既不是增函数,也不是减函数,g (x )在[a ,b ]上可以取得最小值-2,故选D.12.(多选)关于函数f (x )=sin|x |-|cos x |,下列结论正确的是( ) A .f (x )是偶函数B .f (x )在区间⎝ ⎛⎭⎪⎫π2,π上单调递减C .f (x )的最大值为 2D .当x ∈⎝ ⎛⎭⎪⎫-π4,π4时,f (x )<0恒成立解析:选ABD.因为f (-x )=sin|-x |-|cos(-x )|=sin|x |-|cos x |=f (x ),所以f (x )为偶函数,故A 正确;当x ∈⎝ ⎛⎭⎪⎫π2,π时,f (x )=sin|x |-|cos x |=sin x +cos x =2sin ⎝ ⎛⎭⎪⎫x +π4,又x ∈⎝ ⎛⎭⎪⎫π2,π,所以令t =x +π4,则t ∈⎝ ⎛⎭⎪⎫3π4,5π4,y =2sin t 单调递减,所以B 正确;因为f (x )为偶函数,所以求函数f (x )的最大值可只考虑当x ≥0时的情况,又易知当x ≥0时,2π是其一个周期,所以只需研究x ∈[0,2π]时的情况,。
三角函数的单调性与极值

三角函数的单调性与极值三角函数是数学中常见且重要的函数之一,它涵盖了正弦函数、余弦函数和正切函数等多种函数。
在学习三角函数时,我们需要研究它们的单调性和极值,这对我们理解和应用三角函数有着重要的意义。
本文将探讨三角函数的单调性和极值,并分别对正弦函数、余弦函数和正切函数进行讨论。
一、正弦函数的单调性与极值正弦函数是一个周期函数,它的定义域为实数集,值域为闭区间[-1, 1]。
我们可以通过观察正弦函数的图像来研究其单调性和极值。
正弦函数的图像在每个周期内呈现周期性变化,从图像上观察,我们可以得出以下结论:1. 正弦函数在定义域内是振荡函数,没有整体的单调性;2. 在每个周期内,正弦函数先增后减,在0到π的区间上,正弦函数单调递增;3. 在π到2π的区间上,正弦函数单调递减;4. 正弦函数在特定角度处达到极值,即在0、π、2π等处取得最大值1和最小值-1。
综上所述,正弦函数的单调性为在每个周期内先递增后递减,且在特定角度处取得极值。
二、余弦函数的单调性与极值余弦函数也是一个周期函数,它的定义域为实数集,值域为闭区间[-1, 1]。
我们同样可以通过观察余弦函数的图像来研究其单调性和极值。
余弦函数的图像同样呈现周期性变化,在观察图像的基础上,我们可以得出以下结论:1. 余弦函数在定义域内是振荡函数,没有整体的单调性;2. 在每个周期内,余弦函数先减后增,在0到π的区间上,余弦函数单调递减;3. 在π到2π的区间上,余弦函数单调递增;4. 余弦函数在特定角度处达到极值,即在0、π、2π等处取得最大值1和最小值-1。
综上所述,余弦函数的单调性为在每个周期内先递减后递增,且在特定角度处取得极值。
三、正切函数的单调性与极值正切函数是一个奇函数,它的定义域为实数集,值域为整个实数集。
我们同样可以通过观察正切函数的图像来研究其单调性和极值。
正切函数的图像呈现周期性变化,从图像上我们可以得出以下结论:1. 正切函数在定义域内是振荡函数,没有整体的单调性;2. 在每个周期内,正切函数存在无穷多个间断点,因此无法具体判断其单调性;3. 正切函数在特定角度处取得极值。
第六讲-三角函数的单调性及最值

第六讲 三角函数单调性及最值[学习目标]1.掌握y =sin x 的最大值与最小值,并会求简单三角函数的值域和最值. 2. 掌握y =sin x 的单调性,并能利用单调性比较大小.3.会求函数y =A sin(ωx +φ)的单调区间.[知识链接]1.怎样求函数f (x )=A sin(ωx +φ)的最小正周期?答 由诱导公式一知:对任意x ∈R ,都有A sin[(ωx +φ)+2π]=A sin(ωx +φ),所以A sin ⎣⎢⎡⎦⎥⎤ω⎝ ⎛⎭⎪⎫x +2πω+φ=A sin(ωx +φ), 即f ⎝⎛⎭⎪⎫x +2πω=f (x ), 所以f (x )=A sin(ωx +φ)(ω≠0)是周期函数,2πω就是它的一个周期. 由于x 至少要增加2π|ω|个单位,f (x )的函数值才会重复出现,因此,2π|ω|是函数f (x )=A sin(ωx +φ)的最小正周期.2.观察正弦曲线,正弦函数是否存在最大值和最小值?若存在,其最大值和最小值分别为多少?答 正弦函数存在最大值和最小值,分别是1和-1.[预习导引]正弦函数的图象和性质(-∞,+∞)或R 经典例题要点一 求函数的单调区间例1 求函数y =2sin ⎝ ⎛⎭⎪⎫π4-x 的单调递增区间.解 y =2sin ⎝ ⎛⎭⎪⎫π4-x =-2sin ⎝⎛⎭⎪⎫x -π4, 令z =x -π4,则y =-2sin z . 因为z 是x 的一次函数,所以要求y =-2sin z 的递增区间,即求sin z 的递减区间,即2k π+π2≤z ≤2k π+3π2(k ∈Z ). 所以2k π+π2≤x -π4≤2k π+3π2(k ∈Z ), 2k π+3π4≤x ≤2k π+7π4(k ∈Z ), 所以函数y =2sin ⎝ ⎛⎭⎪⎫π4-x 的递增区间为 ⎣⎢⎡⎦⎥⎤2k π+3π4,2k π+7π4(k ∈Z ). 规律方法 用整体替换法求函数y =A sin(ωx +φ)的单调区间时,如果式子中x 的系数为负数,先利用诱导公式将x 的系数变为正数再求其单调区间.再将最终结果写成区间形式.跟踪演练1 求下列函数的单调递增区间:(1)y =1+2sin ⎝ ⎛⎭⎪⎫π6-x ; (2)y =log 12sin x . 解 (1)y =1+2sin ⎝ ⎛⎭⎪⎫π6-x =1-2sin ⎝⎛⎭⎪⎫x -π6.令u =x -π6,则根据复合函数的单调性知,所给函数的单调递增区间就是y =sin u 的单调递减区间,即2k π+π2≤u ≤2k π+32π(k ∈Z ), 亦即2k π+π2≤x -π6≤2k π+3π2(k ∈Z ). 亦即2k π+23π≤x ≤2k π+53π(k ∈Z ), 故函数y =1+2sin ⎝ ⎛⎭⎪⎫π6-x 的单调递增区间是2k π+23π,2k π+53π(k ∈Z ). (2)由sin x >0,得2k π<x <2k π+π,k ∈Z .∵12<1,∴函数y =log 12sin x 的单调递增区间即为 u =sin x 的递减区间,∴2k π+π2≤x <2k π+π,k ∈Z . 故函数y =log 12sin x 的单调递增区间为 ⎣⎢⎡⎭⎪⎫2k π+π2,2k π+π(k ∈Z ). 要点二 函数的单调性的应用例2 利用三角函数的单调性,比较下列各组数的大小:(1)sin ⎝ ⎛⎭⎪⎫-π18与sin ⎝ ⎛⎭⎪⎫-π10; (2)sin 196°与cos 156°.π2<-π10<-π18<π2,解(1)∵-∴sin ⎝ ⎛⎭⎪⎫-π18>sin ⎝ ⎛⎭⎪⎫-π10. (2)sin 196°=sin(180°+16°)=-sin 16°,cos 156°=cos(180°-24°)=-cos 24°=-sin 66°,∵0°<16°<66°<90°,∴sin 16°<sin 66°;从而-sin 16°>-sin 66°,即sin 196°>cos 156°.规律方法 用正弦函数的单调性比较大小时,应先将异名化同名,把不在同一单调区间内的角用诱导公式转化到同一单调区间,再利用单调性来比较大小. 跟踪演练2 比较下列各组数的大小.(1)sin ⎝ ⎛⎭⎪⎫-376π与sin ⎝ ⎛⎭⎪⎫493π; (2)cos 870°与sin 980°.解 (1)sin ⎝ ⎛⎭⎪⎫-376π=sin ⎝ ⎛⎭⎪⎫-6π-π6=sin ⎝ ⎛⎭⎪⎫-π6, sin ⎝ ⎛⎭⎪⎫493π=sin ⎝⎛⎭⎪⎫16π+π3=sin π3, ∵y =sin x 在⎣⎢⎡⎦⎥⎤-π2,π2上是增函数, ∴sin ⎝ ⎛⎭⎪⎫-π6<sin π3,即sin ⎝ ⎛⎭⎪⎫-376π<sin 493π. (2)cos 870°=cos(720°+150°)=cos 150°=-sin 60°,sin 980°=sin(720°+260°)=sin 260°=sin(180°+80°)=-sin 80°,∵0°<60°<80°<90°,∴sin 80°>sin 60°,∴-sin 60°>-sin 80°,即cos 870°>sin 980°.要点三 正弦函数的最值(值域)例3 (1)求函数y =3-2sin x 取得最大值、最小值时的自变量x 的集合,并分别写出最大值、最小值;(2)求函数f (x )=2sin 2 x +2sin x -12,x ∈⎣⎢⎡⎦⎥⎤π6,5π6的值域. 解 (1)∵-1≤sin x ≤1,∴当sin x =-1,即x =2k π+3π2,k ∈Z 时,y 取得最大值5,相应的自变量x 的集合为⎩⎪⎨⎪⎧ x ⎪⎪⎪⎭⎪⎬⎪⎫x =2k π+3π2,k ∈Z .当sin x =1,即x =2k π+π2,k ∈Z 时,y 取得最小值1,相应的自变量x 的集合为⎩⎪⎨⎪⎧ x ⎪⎪⎪⎭⎪⎬⎪⎫x =2k π+π2,k ∈Z .(2)令t =sin x ,y =f (t ),∵x ∈⎣⎢⎡⎦⎥⎤π6,5π6, ∴12≤sin x ≤1,即12≤t ≤1. ∴y =2t 2+2t -12=2⎝⎛⎭⎪⎫t +122-1,∴1≤y ≤72, ∴函数f (x )的值域为⎣⎢⎡⎦⎥⎤1,72. 规律方法 (1)形如y =a sin x +b 的函数的最值或值域问题,利用正弦函数的有界性(-1≤sin x ≤1)求解.求三角函数取最值时相应自变量x 的集合时,要注意考虑三角函数的周期性.(2)求解形如y =a sin 2 x +b sin x +c ,x ∈D 的函数的值域或最值时,通过换元,令t =sin x ,将原函数转化为关于t 的二次函数,利用配方法求值域或最值即可.求解过程中要注意t =sin x 的有界性.跟踪演练3 求函数y =sin ⎝ ⎛⎭⎪⎫π3+4x +cos ⎝ ⎛⎭⎪⎫4x -π6的周期、单调区间及最大、最小值.解 ∵⎝ ⎛⎭⎪⎫π3+4x +⎝ ⎛⎭⎪⎫π6-4x =π2, ∴cos ⎝ ⎛⎭⎪⎫4x -π6=cos ⎝ ⎛⎭⎪⎫π6-4x =cos ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π3+4x =sin ⎝ ⎛⎭⎪⎫π3+4x . 从而原式就是y =2sin ⎝⎛⎭⎪⎫4x +π3,这个函数的最小正周期为2π4,即T =π2. 当-π2+2k π≤4x +π3≤π2+2k π(k ∈Z )时函数单调递增,所以函数的单调递增区间为⎣⎢⎡⎦⎥⎤-5π24+k π2,π24+k π2(k ∈Z ). 当π2+2k π≤4x +π3≤3π2+2k π(k ∈Z )时函数单调递减,所以函数的单调递减区间为⎣⎢⎡⎦⎥⎤π24+k π2,7π24+k π2(k ∈Z ). 当x =π24+k π2(k ∈Z )时,y max =2; 当x =-5π24+k π2(k ∈Z )时,y min =-2.1.函数y =2sin x 的单调增区间是( )A .[2k π-π2,2k π+π2](k ∈Z ) B .[2k π+π2,2k π+3π2](k ∈Z ) C .[2k π-π,2k π](k ∈Z )D.[2kπ,2kπ+π](k∈Z)答案 A解析 函数y =2x 为增函数,因此求函数y =2sin x 的单调增区间即求函数y =sin x 的单调增区间2.函数y =sin ⎝ ⎛⎭⎪⎫x +2π3,x ∈⎣⎢⎡⎦⎥⎤0,π2的值域是( ) A.⎣⎢⎡⎦⎥⎤-32,12 B.⎣⎢⎡⎦⎥⎤-12,32 C.⎣⎢⎡⎦⎥⎤32,1 D.⎣⎢⎡⎦⎥⎤12,1 答案 B解析 ∵0≤x ≤π2,∴2π3≤x +2π3≤7π6. ∴sin 7π6≤sin ⎝⎛⎭⎪⎫x +2π3≤sin 2π3,∴-12≤y ≤32. 故选B.3.下列不等式中成立的是( )A .sin ⎝ ⎛⎭⎪⎫-π8>sin ⎝ ⎛⎭⎪⎫-π10 B .sin 3>sin 2 C .sin 75π>sin ⎝ ⎛⎭⎪⎫-25π D .sin 2>cos 1 答案 D解析∵sin 2=sin ()π-2,cos 1=sin ⎝ ⎛⎭⎪⎫π2-1, 且(π-2)-⎝ ⎛⎭⎪⎫π2-1=π2-1>0,∴π2>π-2>π2-1>0,∴sin(π-2)>sin ⎝ ⎛⎭⎪⎫π2-1,即sin 2>cos 1. 4.求函数y =f (x )=sin 2x -4sin x +5的值域.解 设t =sin x ,则|t |≤1,f (x )=g (t )=t 2-4t +5(-1≤t ≤1)g (t )=t 2-4t +5的对称轴为t =2.开口向上,对称轴t =2不在研究区间[-1,1]内. g (t )在[-1,1]上是单调递减的,∴g (t )max =g (-1)=(-1)2-4×(-1)+5=10, g (t )min =g (1)=12-4×1+5=2,即g (t )∈[2,10].所以y =f (x )的值域为[2,10].(注:可编辑下载,若有不当之处,请指正,谢谢!)。
1.4.2三角函数单调性及最大最小值

函数
y
1
y=sinx
2
0
-1
y
1
y=cosx
2
图形 定义域 值域
2
3 2
2
5 2
x
0
-1
3 2
2
5 2
x
x 2k 时, ymax 1 2 最值 x 2k 时,ymin 1 2 x[- 2k , 2k ] 增函数 2 2 单调性 x[ 2k , 3 2k ] 减函数 2 2
x
2
…
0
p 3 p , k ? Z时取得最大值 + 2 k 1, … … … 2 2 2
-1
y=sinx (xR)
0 p 0 1 当且仅当x = - +2k p , k ? Z时取得最小值 1; 2
sinx
-1
, +2k ],kZ 其值从-1增大到1 增区间为 [[ +2k , ] 2 2 2 2 3 3 , +2k 减区间为 [[ +2k , ] ],kZ 其值从 1减小到-1 2 2 2
形如y = A sin(wx + j )及y = A cos(wx + j ( ) A>0,w > 0)的函数求单调区间的方法: 采用“换元法”整体代换 将“wx + j ”看成一个整体z,则通过求y = A sin z及y = A cos z的单调区间 注意:(1)w < 0时,必须用诱导公式转化,使x的系数为正 (2)A>0时,单调性相反
2
对称轴: 对称中心:(
x k , k Z
三角函数的单调性与值域-课件

题型三 函数的单调性 【例 3】 比较下列各组数的大小: (1)sin 250°与 sin 260°;(2)cos158π与 cos 194π; (3)sin π5与 cos-125π. 审题指导 比较三角函数值大小的一般思路是先判断三角函 数值的正负,若同号,再利用诱导公式转化到同一单调区间内的 同名函数值进行比较. 【解题流程】
名师点睛 1.y=sin x 与 y=cos x 单调性 (1)正弦函数与余弦函数在定义域上不单调,说“正弦函数(或 余弦函数)在第一象限是增(或减)函数”是错误的. (2)正弦函数 y=sin x(x∈R)的增区间为 2kπ-π2,2kπ+π2(k∈Z) 的含义是指在 k 取每一个整数时,正弦函数在该区间上为增函数, 而不是 k 取每一个整数时,正弦函数在这些并集区间上为增函数.
【变式 1】 求函数 y=3cosπ3-2x的单调递增区间. 解 由已知函数为 y=3cosx2-π3, 欲求函数 y=3cosπ3-2x的单调递增区间, 只需求函数 y=3cosx2-π3的单调递增区间.
由 2kπ-π≤2x-π3≤2kπ (k∈Z), 得 4kπ-43π≤x≤4kπ+23π (k∈Z), 函数 y=3cosπ3-2x的单调递增区间为 4kπ-43π,4kπ+23π (k∈Z).
• 第3课时 三角函数的单调性与值 域
【课标要求】 掌握正弦函数、余弦函数的图象,理解并掌握它们的奇偶性、 值域相关的性质. 【核心扫描】 1.了解三角函数的单调性和值域.(重点) 2.会求函数的单调区间和值域.(难点)
自学导引
1.正、余弦函数的单调性 正弦函数 y=sin x(x∈R)在
2kπ-2π,2kπ+π2
2.正(余)弦函数的对称性 (1)轴对称:对于正弦函数 y=sin x,x∈R,我们发现函数的 图象在每一个最值(最大或最小)点处都有对称轴,方程为 x=kπ+ π2,k∈Z,而对于余弦函数,将正弦函数的图象向左平移π2个单位 长度得到,因此其对称轴方程为 x=kπ,k∈Z. (2)中心对称:对于正弦函数 y=sin x,x∈R,其对称中心为(kπ, 0)(k∈Z),而对于余弦函数,其对称中心为kπ+π2,0(k∈Z).对 称轴和对称中心都有无数个.
三角函数单调区间

三角函数单调区间、最值●三角函数的单区间 ▲x y sin =的单调区间 单调增区间:z k k k ∈++-],22,22[ππππ单调减区间:z k k k ∈++],223,22[ππππ取最大值集合:⎭⎬⎫⎩⎨⎧∈+=z k k x ,22ππ取最小值集合:⎭⎬⎫⎩⎨⎧∈+-=z k k x ,22ππ●求复合三角函数的单调区间▲求)0,0()sin(>>+=ωϕωA x A y 的单调区间的方法 增区间求法:令ϕω+=x t ,那么原函数等价变形为t A y sin =,当z k k t k ∈+≤≤+-,2222ππππ时单调递增,即当z k k x k ∈+≤+≤+-,2222ππϕωππ时原函数单调递增,从而求得x 的范围,进而得到函数的单调增区间。
减区间求法:令ϕω+=x t ,那么原函数等价变形为t A y sin =,当z k k t k ∈+≤≤+,22322ππππ时单调递减,即当z k k x k ∈+≤+≤+,22322ππϕωππ时原函数单调递减,从而求得x 的范围,进而得到函数的单调减区间。
取最值时集合的求法:令ϕω+=x t ,那么原函数等价变形为t A y sin =,当z k k t ∈+=,22ππ时取得最大值,即当z k k x ∈+=+,22ππϕω时取得最大值,从而求得x 的取值集合,求最小值集合类似。
☆例题:求)43sin(2π+=x y 的单调增区间和单调减区间。
解:增区间:由Z k k x k ∈+≤+≤+-,224322πππππ得Z k k x k ∈+≤≤+-,ππππ3212324 所以原函数的增区间为Z k k k ∈++-]3212324[ππππ,减区间:由Z k k x k ∈+≤+≤+,2234322πππππ得Z k k x k ∈+≤≤+,ππππ321253212 所以原函数的减区间为Z k k k ∈++]321253212[ππππ,所以原函数的减区间为Z k k k ∈++-]3243212[ππππ, 当1)43sin(=+πx 时函数取得最大值,那么43π+x =ππk 22+, ππk x 243+=即,,3212Z k k x ∈+=ππ▲形如)cos()sin(ϕωϕω+++=x b x a y 的单调区间的求法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
零点: x
1
k (k Z )
探究:余弦函数的最大值和最小值
y
1
3 5 2
2 3
2
2
O
2
1
3 2
2
5 2
3
x
最大值: 当 最小值:当 零点: x
x 0 2k 时, 有最大值 y 1
x 2k 时, 有最小值 y 1
函数的单调性反映了函数在一个区间上的走向。
增函数:上升
减函数:下降
观察正余弦函数的图象,探究其单调性
探究:正弦函数的单调性
y
1
3 5 2
2 3
2
2
O
2
1
3 2
2
5 2
3
x
归纳:正弦函数的单调性
y
1
3 5 2
2 3
2
2
O
2
2 3
2
2
O
2
1
3 2
2
5 2
3
x
归纳:余弦函数的单调性 y
1
3 5 2
2 3
2
2
O
2
1
3 2
2
5 2
3
x
由余弦函数的周期性知:
在每个闭区间 [ 2k , 2k ](k Z) 都是增函数, 其值从-1增大到1 ;
(1) sin(
18
)与 sin(
10
) (2) cos(
23 17 )与 cos( ) 5 4
1 例3、求函数y sin ( x+ ),x R的单调增区间 2 3
1 例3、求函数y sin( x ), x [2 ,2 ]的单调递增区间 . 2 3
1
3 2
2
5 2
3
x
正弦函数在每个闭区间[
2
2k ,
2
2k ]( k Z )
都是增函数,其值从-1增大到1; 3 而在每个闭区间[ 2k , 2k ](k Z )上都是 2 2 减函数,其值从1减小到-1。
探究:余弦函数的单调性 y
1
3 5 2
2
k (k Z )
单调性的应用 : 一、求最值
例1. 写出下列函数取最大、最小值时的自变量x的集合,并写出 最大、最小值分别是什么.
(1)y cos x 1, x R; (2)y 3sin 2 x, x R.
练习1:求使下列函数取得最大值、最小值的自变量 X的集合,并写出最大值、最小值各是多少?
在每个闭区间 [2k , 2k ](k Z) 上都是减函数,
其值从1减小到-1。
探究:正弦函数的最大值和最小值
y
1
3 5 2
2 3
2
2
O
2
1
3 2
2
5 2
3
x
最大值: 当
x
2
2k 时, 有最大值 y 1
有最小值 y 时,
最小值:当x 2k
1.4.2正弦函数、余弦函数的性质
复习:正弦函数对称性
y
1
3 5 2
2 3
2
2
O
2
对称轴: x k , k Z 2
对称中心: ( k , 0)
1
3 2
2
5 2
3
x
kZ
复习:余弦函数对称性 y
1
3 5 2
2 3
2
(1)y 2sin x, x R
(2)
x y 2 cos , x R 3
• 求 y sin(2 x ) 函数的对称轴和对称中心 3 z 2 x y sin(2 x ) sin z 解(1)令 则 3 3
y sin z
2x
例 题
的对称轴为 z
3
2
2
k , k Z
k
x
解得:对称轴为
(2) y sin z
12
k
2
,k Z
的对称中心为 ( k ,0) , k Z
2x
z k
3
k
x
6
k
2
对称中心为 (
6
k
2
,0) , k Z
二、比较大小
例2:利用三角函数的单调性,比较下列各组数的大小:
2
O
2
1
3 2
25 23x对称轴:x k , k Z
2 k , 0) k Z
对称中心: (
复习:函数的单调性
函数 y f ( x),若在指定区间任取 x1、x2 ,且 x1 x2 ,都有:
f ( x1 ) f ( x2,则 ) f(x)在这个区间上是增函数. 1、__________ f ( x1 ) f ( x2,则 ) f(x)在这个区间上是减函数. 2、__________
