北大博雅自主招生数学真题
14-18年北清自招博雅领军数学真题-数论基础与整除

北大博雅15.1.已知n为不超过2015的正整数,且1234n n n n+++的个位数字为0,则满足条件的正整数n的个数为()A.1511B.1512C.1513D.前三个答案都不对清华领军2015.18.已知存在实数r,使得圆周222x y r+=上恰好有n个整点,则n可以等于()A.4B.6C.8D.12分类存疑北大博雅2016.4.函数1,,(,)1,,(),0,qx p q p q NP pf xQ+⎧==∈⎪=⎨⎪∉⎩则满足(0,1)x∈且1()7f x>的x的个数为()A.12B.13C.14D.前三个答案都不对4.【解答】D满足(0,1)x∈,且1()7f x>的x的个数为11,分别为1121312341523344555566,,,,,,,,,,。
【评析】这个函数是非常有名的黎曼函数的一部分,但是对于学生的要求很低,只需要准确理解题意即可,问题本身并不困难。
北大博雅2016.14.已知正整数,,,a b c d满足ab cd=,则a b c d+++有可能等于()A.101B.301C.401D.前三个答案都不对14.【解答】B考虑a=mn,b=pq,c=mp,d=nq则a+b+c+d=mn+pq+mp+nq=(m+q)(n+p),于是a+b+c+d不是质数即可。
如301=7×43=(1+6)×(1+42),于是a=1,b=252,c=42,d=6即得正确答案是B。
【评析】数论不定方程问题,其中的换元方法是数论中的经典。
北大博雅2017.1.若正整数,,a b c满足402a b c++=,则使得10n| abc的最大正整数n是()A.5B.6C.7D.以上答案均不正确【1】Da=25,b=25,c=352时,n 可取4,下面我们将说明n 不可能大于4:若n ≥5,先考虑5n |abc :由于a+b+4=402,而402并不是5的倍数,所以abc 不可能均为5的倍数。
北大博雅计划笔试真题

北大博雅计划笔试真题篇一:16年北京大学博雅计划数学试题XX年北京大学博雅计划数学试题选择题共20小题,在每小题的选项中,只有一项符合题目要求,选对得5分,选错扣1分,不选得0分.1.直线y??x?2与曲线y??ex?a相切,则a的值为:;A.?3B.?2C.?1D.前三个答案都不对2.已知三角形ABC的三边长分别为a,b,c,则下面4个结论中正确的个数为:;(1(2)以a2,b2,c2为边长的三角形一定存在;(3)以a?bb?cc?a,,为边长的三角形一定存在;(4)以|a?b|?1,|b?c|?1,|c?a|?1为边长的三222角形一定存在;D.前三个答案都不对3.设AB,CD是?O的两条垂直直径,弦DF交AB于点E,DE?24,EF?18,则OE等于:;ABCD.前三个答案都不对q?1,若x为有理数,p与q互素1?p4.函数f?x???p,则满足x??0,1?且f?x??的x的个数有:; 7?0,若x为无理数?前三个答案都不对5.若方程x?3x?1?0的根也是方程x?ax?bx?c?0的根,则a?b?2c的值为:; 242A.?13B.?9C.?5D.前三个答案都不对6.已知k?1,则等比数列a?log2k,a?log4k,a?log8k的公比为:;111A. B. C. D.前三个答案都不对 234?2?10??的值为:; 111111111A.? B.? C.?D.前三个答案都不对 163264XX?z?z1228.设a,b,c为实数a,c?0,方程ax?bx?c?0的两个虚数根为z1,z2,且满足为实数,则??1?z2k?0?z2?k 等于:;.0 C D.前三个答案都不对9.将12个不同物体分成3堆,每堆4个,则不同的分法种类为:;D.前三个答案都不对10.设A是以BC为直径的圆上的一点,D,E是线段BC 上的点,F是CB延长线上的点,已知BF?4,BD?2,BE?5,?BAD??ACD,?BAF??CAE,则BC的长为:;D.前三个答案都不对11.两个圆内切于K,大圆的弦AB与小圆切于L,已知AK:BK?2:5,AL?10,则BL的长为:;D.前三个答案都不对?x?是一个定义在实数R上的函数,满足2f?x??fx?1?1,?x?R,则f; ??? 前三个答案都不对 2313.从一个正9边形的9个顶点中选3个使得它们是一个等腰三角形的三个顶点的方法数有:;D.前三个答案都不对14.已知正整数a,b,c,d满足ab?cd,则a?b?c?d有可能等于:;D.前三个答案都不对15.三个不同的实数x,y,z满足x3?3x2?y3?3y2?z3?3z2,则x?y?z等于:;A.?1 D.前三个答案都不对16.已知a?b?c?1的最大值与最小值的乘积属于区间:;A.[10,11)B.[11,12)C.[12,13)D.前三个答案都不对17.在圆内接四边形ABCD中,BD?6,?ABD??CBD?30?,则四边形ABCD的面积等于:;ABCD.前三个答案都不对!?2!?…+XX!除以100所得余数为:;D.前三个答案都不对19.方程组x?y2?z3,x2?y3?z4,x3?y4?z5的实数解组数为:;D.前三个答案都不对x3?x3x3?x)??3x的所有实根的平方和等于: 20.方程(33D.前三个答案都不对篇二:XX北京大学“博雅人才培养计划”面试题目及对策XX北京大学“博雅人才培养计划”面试题目1.北京申办冬奥会有哪些机遇和挑战2.如何治理雾霾,有何建议3.中国传统文化将如何走出去4.微信在人际交往中的作用5.欧洲历史上的分与合6.如何看待中国申请冬奥会面试分为两个阶段,第二阶段为一对一考察理科生需在45分钟内,尝试解答一道物理题和一道数学题,然后分别接受一名物理考官和一名数学考官的一对一考察。
2018北京大学博雅计划真题解析版 w - 数学

数学【真题1】已知!C !()!k m m k m k =-0123201820182018201820182018C +3C +5C +7C ++4037C L 的值为.A.201820192⨯B.2018!C.20184036CD.前三个答案都不对【真题2】已知△ABC 面积为1,D,E 分别是边BC 、AC 上的点,且13BD BC =,13CE CA =,AD,BE 交于点P ,则四边形CDPE 的面积是. A.12 B.23 C.17D.前三个答案都不对 【真题3】[x ]为不超过x 的最大正整数,a n 为满足:x ∈[0,n ),[x [x ]]可能取到的所有值的个数,则2018n a n+取到最小值时n 的取值 . A.63B.1009C.2018D.前三个答案都不对【真题4】已知n 为不超过400的正整数,n 的所有正因数的乘积为n 3,则满足条件的n 有____个A.50B.51C.55D.前三个答案都不对 【真题5】三边长均为正整数的三角形,周长为n ,S n 表示符合该条件的三角形的个数,则20182015S S -=. A.-3 B.0C.3D.前三个答案都不对【真题6】已知a,b,c 为非负实数,a+b+c =3,求a+ab+abc 的最大值.A.3B.4C.D.前三个都不对【真题7】设a,b,c 为公差不为0的等差数列,点(3,2)P -,(2,3)Q ,过点P 作PM 垂直于直线ax+by+c =0,垂足为M ,则|MQ |的最小与最大值乘积为 .A.10B.C.D.前三个都不对 【真题8】15个人圆成一圈,选4人,两两不相邻,有多少种选法?A.1560B.450C.0D.前三个都不对【真题9】_____A.(6,7]B.(7,8]C.(8,9]D.前三个答案都不对【真题10】 设()123,,,,1,2,3i a a a a i =L L 是一组从小到大的非完全平方数(正整数)例如122,3a a ==则2018a 等于 . A.2061B.2062C.2063D.前三个都不对【真题11】 在立方体1111ABCD A B C D -中,1AD 中点为M ,1B C 中点为N ,CM 与1D N所成角的余弦值.A.12B.23C.34D.前三个答案都不对【真题12】4的根的个数共有_____个A.0B.1C.3D.前三个答案都不对【真题13】 P 是椭圆22154x y +=上的一点,则是 .A.B.C.D.前三个答案都不对【真题14】 方程222|1|0x x a a x -++-=三个根,则a 的取值范围为.A.(,1]-∞-B.[1,)∞C.[1,0)(0,1]-UD.前三个都不对【真题15】 122018122018,,,,,,,a a a b b b L L 互异对任意(1,2,,2018)i a i =L 满足122018()()()=2018i i i a b a b a b +++L ,求任意i b 则122018()()()i i i a b a b a b +++L A.2018 B.2018- C.0 D.前三个都不对【真题16】 在2018个正整数任取3个数不相邻的取法种数为_____________。
(完整版)北京大学2018年博雅计划数学真题

北京大学2018年博雅计划数学试卷选择题共20小题,在每小题的四个项中,只有一项符合题目要求,请把正确选项的代号填在表格中,选对得5分,选错扣1分,不选得0分。
1. 设n 为正整数,)!(!!k n k n C k n-=为组合数,则201820182201812018020184037...53C C C C ++++等于( )A. 201822018⋅B. 2018!C. 20184036C D. 前三个答案都不对【答案】D 解析:111111(21)222nn n nn nnk k k k k k knnnn nn n k k k k k k k k CkC C nCC n CC ----=======+=+=+=+∑∑∑∑∑∑∑, 201820182018122018120182018201820182018201720180135...4037(21)22018k k kk k k CC CCk C CC -===∴++++=+=⨯⨯+∑∑∑ 20172018201840362220192=⨯+=⨯,故选D 。
2. 设a ,b ,c 为非负实数,满足a +b +c =3,则a +ab +abc 的最大值为( )A. 3B. 4C. 23D. 前三个答案都不对 【答案】B解析:22(1)(4)(1(1))1144b c a a ab abc a b c a a ⎛⎫⎛⎫++-++=++≤+=+ ⎪ ⎪⎝⎭⎝⎭,对其求导得到2a =时取最大值为4。
3. 一个正整数n 称为具有3-因数积性质若n 的所有正因数的乘积等于3n ,则不超过400的正整数中具有3-因数积性质的数的个数为( )A. 55B. 50C. 51D. 前三个答案都不对 【答案】C解析:设n 的所有正因数的乘积为T ,即3T n =。
1n =显然符合题意;下面证明当2n ≥时,正整数n 的质因数的个数最多为2:假设n 的质因数的个数大于或等于3,即n 的全部质因数为12,,...,(3)k p p p k ≥,并设1212...k k n p p p ααα=,则n 的所有正因数的乘积中,(1,2,...)i i p i k α=至少在12112,,,...,,...,,...i i i i i i i i i i i i i i i k i k p p p p p p p p p p p p p p ααααααα-+这些因子中出现,即i i p α出现的次数大于或等于4,这样T 124412(...)k k p p p n ααα≥=,这与题意3T n =矛盾,所以假设不成立,即n 的质因数的个数最多为2。
2017年北大博雅计划数学试题及答案

【5】C
1471013…20142017 的数值即
lx1Cf1 +4xl<f4 +7xl<f'1 代.+2014xl俨14 +2017xl庐17
其中 a1, a4, a1,…, ll2014,ll2011是对应数宇出现的数位数,比如 2017 出现在原数字的笫 0 位,
2014 出现在第 4 位等。 注意到 10 的方幕除以 9 的余 数一定是 1' 1471013...20142017 =1+4+7+…+2014+2017 = 673 X1009 三 7(mod9)
=-9 , s
即
SMoD=— 92x.
故 liDOA 的内切圆半径是?雾 2
答案为 A.
【评析】此题导向非常明确:通过周长和内切圆半径来求得三角形面积。有了面积之后,再 通过共边定理获得另一个三角形的面积值。 较为容易。
【8】C.
9 +95+995+… +99 …95=(10-1)+(100 -5)+(1000-5)+… +(102017 -5)
故n的最大可能值 不大于5 .我们设法构造取到 5 的情形。 a,b,c 所含 5 的幕次和 不小于 5 。 幕次和为6的情形上已排除, 故幕次和为 5 。 由于a,b,c
中至少有一个不是 5 的倍数,故 a,b,c必有一个被 2 5 整除,一个被 125 整除。我们尽力使这
两数所含 2 的幕次更大。为此, 取a==IOO, b=250 , 那么 C == 52 。此时 a,b,c 所含 2 的幕
小于n。而由于2,4,8... 的倍数在正整数集中分布比5,25,125的倍数密,即2的幕次不小于 n更容易达到。 故我们考虑 5 的幕次。 不大 于 402 的 5 的正 整 数幕最 大是 125, 故 a,b,c 各自所 含 5 的 幕 次最 高 是 3 . 而
2017年北京大学博雅计划数学试题

2017年北京大学博雅计划数学试题一、选择题(本大题共20小题,每小题5分,共100分)1.正整数9959959995++++的十进制表示中数字1的个数为( ) A.2012 B.2013 C.2014 D.前三个答案都不对2. 将等差数列1,5,9,132017,,排成一个大数159132017 ,则该大数被9除的余数为( ) A.4 B.1 C.7 D. 前三个答案都不对3.一个三位数等于它的各位数字的阶乘之和,则此三位数的各位数字之和为( ) A.9 B.10 C.11 D. 前三个答案都不对4. 单位圆的内接五边形的所有边及所有对角线的平方和的最大值为( ) A.15 B.20 C.25 D. 前三个答案都不对5. 351cos )(1cos)(1cos )777πππ+++(的值为( )A.98B.78C.34D. 前三个答案都不对 6.已知()f x =11()(),()(()),1,k k f x f x f x f f x k +==≥则2017(2017)f 的值为( )B.2017D. 前三个答案都不对 7.已知正整数n 满足201720172017n n n ≠,且与有相同的个位数字,则2017-n 的最小值为( )A.4B.6C.8D. 前三个答案都不对8.一个盒子装有红,白,蓝,绿四种颜色的玻璃球,每种颜色的玻璃球至少有一个,从中随机拿出4个玻璃球,这4个球是红色的概率为1p ,恰好有三个红色和一个白色的概率为2p ,恰好有两个红色,一个白色和一个蓝色的概率为3p ,四种颜色各一个的概率为4p ,1234p p p p ===则这个盒子里的玻璃球的个数的最小值等于( ) A.17个 B.19个 C.21个D. 前三个答案都不对9.设111,,)()()a b c a b c b c a---和(均为正整数,则235a b c ++的最大值与最小值之差( )A.8B.15C.22D. 前三个答案都不对10.将正整数集合N +分成两个不相交的子集的并,使得每个子集都不包含无穷等差数列的不同方式有( ) A.0种 B.1种 C.无穷多种 D. 前三个答案都不对11.O 是凸四边形ABCD 对角线AC BD 和的交点,已知,,,AOB BOC COD DOA ∆∆∆∆的周长相同,,,AOB BOC COD ∆∆∆的内切圆半径分别为3,4,6,则DOA ∆的内切圆半径为( ) A.92B.5C.112D. 前三个答案都不对12.一群学生参加学科夏令营,每名同学至少参加一个学科考试。
北京大学自主招生数学试题及答案1
南方球队总得分为 =189
北方球队总得分为 =21
南方球队内部比赛总得分 =105
北方球队内部比赛总得分 =15
北方胜南方得分=21-15=6
北方球队最高得分=5+6=11
因为11×15=165<189
所以南方球队中至少有一支得分超过11分.
冠军在南方球队中
当x=8时
所有球队总得分为 =300
北京大学自主招生数学试题及答案
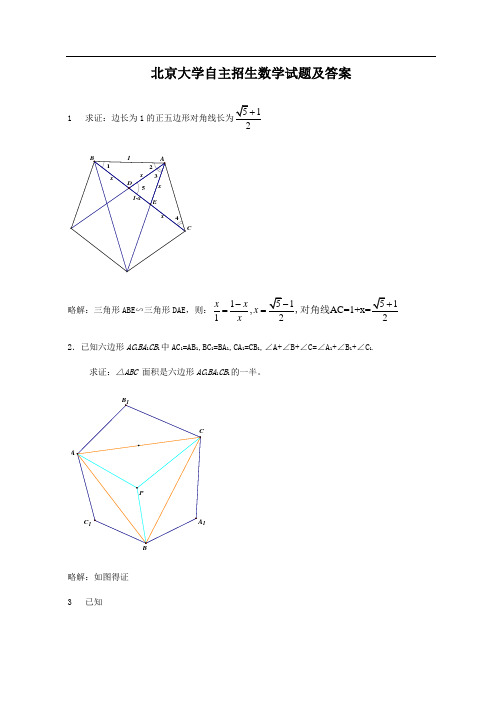
1 求证:边长为1的正五边形对角线长为
略解:三角形ABE∽三角形DAE,则:
2.已知六边形AC1BA1CB1中AC1=AB1,BC1=BA1,CA1=CB1,∠A+∠B+∠C=∠A1+∠B1+∠C1,
求证:△ABC面积是六边形AC1BA1CB1的一半。
略解:如图得证
3 已知
4 排球单循坏赛 南方球队比北方球队多9支 南方球队总得分是北方球队的9倍 求证 冠军是一支南方球队(胜得1分 败得0分)
解:设北方球队共有x支,则南方球队有x+9支
所有球队总得分为
南方球队总得分为
北方球队总得分为
南方球队内部比赛总得分
北方球队内部比赛总得分
解得:
因为 为整数
x=6或x=8
当x=6时
南方球队总得分为 =270
北方球队总得分分 =28
北方胜南方得分=30-28=2
北方球队最高得分=7+2=9
因为9×17=153<270
所以南方球队中至少有一支得分超过9分.
冠军在南方球队中
综上所述,冠军是一支南方球队
5 (理科)O-XYZ坐标系内xoy平面系内 绕y轴旋转一周构成一个不透光立体 在点(1,0,1)设置一光源xoy平面内有一以原点为圆心的圆C被光照到的长度为2π,求C上未被照到的长度。
自招2019北大博雅试题及答案

北大博雅试题及答案01、空间直角坐标系中,六个完全相同、均匀带电的正方形绝缘平板构成一个正方体,其中心O位于坐标原点,各棱方向与坐标轴平等,记与z轴平行的棱的中点为A,正方体与x轴的交点为B,则A、B、C三点的电场强度 DA、全部为B、全部不为0C、有两个满足至少在两个方向上的分量不为0D、有一个满足恰好在两个方向上的分量不为0解:答案:D根据对称性,O点的电场为零。
A点的电场Z分量为零,但X、Y分量不等于零。
B点的电场只有X分量。
02、如图,用轻绳悬挂一带电小球A,绳长为L,小球质量为m,现将一无穷远处的相同小球B移到图示位置,原小球偏转角度为θ,求移动小球过程中外力做的功解:答案:)cos1(3θ-=mgW如图位置处于平衡222sin2(2sin)2kqF mglθθ==电势能的增量221E4sin2(1cos)22sin2Pkqmg mgllθθθ∆===-重力势能的增量2E(1cos)Pmglθ∆=-则,外力做功12W E E3(1cos)P Pmglθ=∆+∆=-03、如图,有一等腰三棱镜,底角为θ,从侧面沿平行于底边的方向射入一光束,其折射后在底面发生全反射并从另一个侧面射出。
已知三棱镜的材料的折射率为2,求θ满足的条件。
解:第一次折射。
入射角0190iθ=-折射定律11sinsininr=解得1arcsin2r=光线在底面发生全反射的临界角C与折射率n的关系1sin Cn=解得045C=发生全反射的条件是21i rθ=+大于临界角C,则有452cosarcsin>+θθ04、长度分别为L1和L2的两根不可伸长的细绳悬挂着质量分别为m1和m2的两个小球,处于静止状态,如图所示,中间小球突然受到一水平方向的冲击力,瞬间获得水平向右的速度v,求此时两绳中的拉力。
解:m1相对于悬点O做圆周运动,根据牛顿定律,有211211vT m g T mL--= m2相对于m1做圆周运动,此时m1的向心力加速度为21vL,m1是一个非惯性系,故m2所受到的惯性力为22vL,方向竖直向下,根据牛顿定律,有22222212v v T m g m m L L --= 由上二式可得)(22122212111L v L v m g m L v m g m T ++++= )(2212222L v L v m g m T +++= 05、一平行板电容器,面积为S ,板间距为d ,与电动势为U 的恒定电源串联,现将一厚度为d ,面积为S 、相对介电常数为ε的电介质插入极板之间,求该过程中外力做的功。
2019北京大学博雅计划综合评价强基计划数学

2019年北京大学博雅计划笔试数学试卷和解答1、金字塔可以视为正四棱锥,底面正方形的边长为200米,如果一个游客处在距离底面中心200米的圆周上,则该游客可以同时看见金字塔两个侧面的概率为()A、13B、12C、32D、前三个答案都不对2、已知函数��=�sin �,�>0,�∈0若��与其反函数�−1�有两个交点,则实数a 的取值范围是()A、0,1B、1D、前三个答案都不对3、函数��=+1−x 21+x 2的值域为()A、−2,1B、−2C、−2D、前三个答案都不对4、三棱锥P-ABC 中,底面ABC 是边长为2的正三角形,PB ⊥底面ABC,PB=1,M,N 分别为AC,AB 的中点,则异面直线BM 和PN 所成角的正弦值为()A、64B、54C、104D、前三个答案都不对5、已知函数��满足��+�=x ,则�2=()B、A、12B、1C、−1D、前三个答案都不对6、平面直角坐标系xOy 中一点A �−22+y 2=1上一点关于直线y=kx 对称,则k 的值为()A、1B、12C、33D、前三个答案都不对7、已知x,y,z 为正实数,且满足x +y +z =1,则��4�+19�+�4�+ 9�+1的最大值为()A、1576B、11024C、11296D、前三个答案都不对8、已知a ,b ∈ℂ,且对任意满足的 =1的复数z,均有 4+� 2+�=1,则ab=()A、iB、-iC、1D、前三个答案都不对9、从6个男生,4个女生中各选2人,进行羽毛球男女混合双打比赛,则不同的组合方式的种数为()B、A、60B、90C、180D、前三个答案都不对10、在平面直角坐标系xOy 中,满足�2+4�2−44�2+�2−1≤0的点P x ,y 构成的平面图形的面积为()A、�2B、�C、32�D、前三个答案都不对11、满足方程�3+2n 2+8n −5=a 3的非负整数解组�,�的对数为()A、0对B、1对C、3对D、前三个答案都不对12、复数 1, 2和O 点在复平面内组成的三角形面积记为S,若 3=2 1+3 2,则复数 1, 2和 3点在复平面组成的图形面积为()A、2SB、5SC、13SD、前三个答案都不对13、已知x,y,z >0,且x +y +z =1,则�2�+�2�+�2的最小值为()A、�2+�2+�2B、3�2+�2+�2C、�+�+�2D、前三个答案都不对14、若0<x <1,则tan ��,tan 2��2,tan �2�2的大小关系为()A、tan 2��2>tan ��>tan �2�2B、tan 2��2>tan �2�2>tan ��B、tan ��>tan 2��2>tan �2�2D、前三个答案都不对15、已知数列��满足�1=1,��+1=na n+1,在n 为足够大的值时,以下成立的是()A、�−1≤a n ≤�+1B、n ≤a n ≤n +1C、C、2�≤a n ≤2�+1D、前三个答案都不对16、用�表示不超过实数x 的最大整数,则方程�3−�=3的实数解个数为()A、0B、1C、2D、前三个答案都不对17、n 时任意正整数,13+23+33+⋯+�3的个位数不可能是()A、4B、9C、2D、前三个答案都不对18、凸四边形ABCD 中AB =BC =CA ,∠ACD =10°,∠DAC =20°,则∠BDC 的大小为()A、60°B、70°C、75°D、前三个答案都不对19、若a >b >0,且a 3−b 3a 2−b 2,则a+b 的取值范围是()A、0,1B、0C、1D、前三个答案都不对20、1×1!+2×2!+⋯+672×672!被2019除的余数是()A、1B、2017C、2018D、前三个答案都不对答案:1、答案:A解析:如图,作为金字塔俯视图,其中ABCD 为底面正方形,O 为底面中心。
2016年北京大学博雅计划试题数学

(3)
以
������
+ 2
������ ,
������
+ 2
������
,
������
+ 2
������
为边长的三角形一定存在;
(4) 以 |������ − ������| + 1, |������ − ������| + 1, |������ − ������| + 1 为边长的三角形一定存在.
= 0 的两个虚数根 ������1, ������2 满足
������21 ������2
为实数,则
2015
∑
������=0
(
������1 ������2
)������
等于
(A) 1
(B) 0
(C) √3i
(D) 前三个答案都不对
9. 将 12 个不同物体分成 3 堆,每堆 4 个,则不同的分法种类为
(A) 101
(B) 301
(C) 401
(D) 前三个答案都不对
15. 三个不同的实数 ������, ������, ������ 满足 ������3 − 3������2 = ������3 − 3������2 = ������3 − 3������2,则 ������ + ������ + ������ 等于
(A) −13
(B) −9
(C) −5
(D) 前三个答案都不对
6. 已知 ������ > 0 且 ������ ≠ 1,则等比数列 ������ + log2������, ������ + log4������, ������ + log8������ 的公比是
2015年北京大学博雅计划数学试题及答案

2015年北京大学博雅计划数学试题一、选择题(本题共5小题,在每小题的四个选项中,只有一项符合题目要求,把正确选项的代号填在括号中,选对得10分,选错扣5分,不选得0分.)1.已知n 为不超过2015的正整数且1n +2n +3n +4n 的个位数为0,,则满足条件的正整数n 的个数为( )A .1511B .1512C .1513D .前三个答案都不对2.在内切圆半径为1的直角三角形ABC 中,∠C =900,∠B =300,内切圆与BC 切于D ,则A 到D 的距离AD 等于( )A . 4+23B .3+23C .3+43D .前三个答案都不对第2题图 第3题图3.正方形ABCD 内部一点P 满足PA: PB: PC=1:2:3,则∠APB 等于( )A .1200B .1350C .1500D .前三个答案都不对4.满足1112015x y +=,x y ≤的正整数对(x,y )的个数为() A .12 B .15 C .18 D .前三个答案都不对5.已知,,a b c Z ∈,且()()()a b b c c a a b c ---=++,则a b c ++可能为( )A .126B .144C .162D .前三个答案都不对二、填空题(本题共5小题,请把每小题的正确答案填在横线上,每题10分.)6.设α为复数,α表示α的共轭,已知-=23αα且2αα为纯虚数,则α的值为_______. 7.椭圆22221x y a b+=的一条切线与x,y 轴交于A 、B 两点,则三角形AOB 的面积的最小值为 _______.8.已知226450x y x y -+++=,则22+x y 的最小值是_______. 9.已知点集22{(x,y)1-x 1-y xy}M =⋅≥,则平面直角坐标系中区域M 的面积为 _______.10.现要登上10级台阶,每次可以登1级或2级,则不同的登法共有_______种.2015年北京大学博雅计划数学试题参考答案一、选择题1、B .提示:n 模4余1,2,3均可.2、D .提示:利用面积确定三边长,答案为5+233、B .提示:如图旋转将△APB 绕B 点顺时针旋转90°并连接PE ,∵将△APB 绕B 点顺时针旋转90°,得△BEC ,∴△BEC ≌△BPA ,∠APB=∠BEC ,∴△BEP 为等腰直角三角形,∴∠BEP=45°,∵PB=2,∴2∵PC=3,CE=PA=1,∴PC 2=PE 2+CE 2,∴∠PEC=90°,∴∠APB=∠BEC=∠BEP+∠PEC=45°+90°=135°.4、D . 提示:2222(2015)(2015)201551331x y --==⋅⋅,因此 (x,y)共有14对.5、C .提示: 注意()+()+()0a b b c c a ---=二、填空题6、23或3.提示: 根据已知sin()=336k r ππ⋅+,其中r 为α,k Z ∈,因此r=23或3,对应的 =3+3i α或=3i α.7、ab .提示:仿射变换.8、1/2提示:注意题中方程为两条互相垂直的直线.9、2+2π 提示:如图10、89.提示:递推.登上第1级:1种登上第2级:2种登上第3级:1+2=3种(前一步要么从第1级迈上来,要么从第2级迈上来)登上第4级:2+3=5种(前一步要么从第2级迈上来,要么从第3级迈上来)登上第5级:3+5=8种登上第6级:5+8=13种登上第7级:8+13=21种登上第8级:13+21=34种登上第9级:21+34=55种登上第10级:34+55=89种.故答案为:89.。
北京大学博雅计划数学真题版

北京大学 2021 年博雅方案数学试卷选择题共 20 小题,在每题的四个项中,只有一项切合题目要求,请把正确选项的代号填在表格中,选对得 5 分,选错扣 1 分,不选得 0 分。
1. 设 n 为正整数,C n k n!为组合数,那么 C202103C202115C20212...4037C20212021等于〔〕k!(n k)!A. 2021 22021B. 2021!C.C40362021D.前三个答案都不对【答案】 Dn n n n n n n分析:(2k1)C n k2kC n k C n k 2 nC n k11C n k2n C n k11C n k,k 0k 0k 0k 1k 0k 1k 0202120212021C202103C 202115C20212...4037C20212021(2 k 1)C2021k 2 2021C2021k1C2021kk0k 1k0 40362202122021202122021,应选D。
2.设 a, b,c 为非负实数,知足 a b c,那么a ab abc 的最大值为〔〕++=3++A. 3B. 4C. 3 2D.前三个答案都不对【答案】 B分析: a ab abc a(1b(1 c)) a 1(1 b c)2 a 1 (4a)2,对其求导获得 a 2 时取44最大值为 4。
3.一个正整数 n 称为拥有3-因数积性质假定n的所有正因数的乘积等于 n3,那么不超出400的正整数中拥有3- 因数积性质的数的个数为〔〕A. 55B. 50C. 51D.前三个答案都不对【答案】C分析:设 n 的所有正因数的乘积为T,即T n3。
n 1 明显切合题意;下边证明当 n 2 时,正整数n的质因数的个数最多为 2:假定n的质因数的个数大于或等于3,即n的所有质因数为p1, p2 ,..., p k (k3) ,并设 n p11 p22 ... p k k,那么 n 的所有正因数的乘积中, p i i (i1,2,...k) 起码在 p i i , p i i p1 , p i i p2 ,..., p i i p i1, p i i p i1..., p i i p k , p i i p2 ... p k这些因子中出现,即i 出现的次数大于或等于,这样 T12k)44,这与题意T n3p i4( p1p2... p k n 矛盾,因此假定不建立,即n 的质因数的个数最多为2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
辅
导
2与⾼考题的对比
2017年北京⼤学⾃主招⽣数学试题
1.保持了近年北⼤⾃招试题的风格.
(a)20道单选题,选对得5分,选错扣1分,不选得0分.
(b)时间紧张.三个⼩时内要完成语数外三科试题的解答,很少有学⽣能做完.
(c)D选项⼀律是“前三个答案都不对”,很有迷惑性,有时候甚⾄⽐较棘⼿.例如第5题,答案数字不怎
么整,考场上时间紧张的情况下,是否相信⾃⼰的判断选D,对考⽣来说是个考验;再⽐如第9题,
答案明显是个负整数,但由于D选项的存在,在只有A选项为负整数的情况下仍然需要进⾏估算.
(d)风格灵巧,强调多想少算.⽐如第1题,看出来配⽅的技巧就可以秒掉,如果硬算的话,考场上可能
就悲剧了.
(e)不追求知识点的全⾯覆盖.数论、函数、平⾯⼏何、三⾓等⼀向是北⼤各种⾃招相关的考试中的⾼频
考点,在2017年的⾃主招⽣考试中也依然是考察重点.⽽概率、统计、导数、⽴体⼏何等考点⼀向
被北⼤冷落,这场考试也不例外.
(f)经典试题有⼀定的重现率.⽐如第6题就是平⾯⼏何中的经典问题,第9题中⽤到的对数运算公式
在⾃招考试中也是屡见不鲜.
2.相对于近年北⼤的各场⾃招相关的考试来说,这份试卷的难度不⾼,在平均线以下.
3.有较好的区分度,可以达到北⼤⾃主选拔的⽬的.
1.有些试题即使放到⾼考中也不是难题,⽐如第19题、第20题.这类题基本每份⾃招试卷中都有,但⼀般
来讲数量较少.
2.有些试题的考点同时也是⾼考的重要考点,但是综合性较强,考⽣要想短时间内顺利解决的话,得有很好
的基本功.⽐如第18题,如果做成四次函数求最值就⿇烦了,代数变形之后换元,处理成⼆次函数才是
正道.再⽐如第14题,每⼀步可能都不难,⽤到的知识也都是⾼考要求的,但是步骤⼀多,考⽣可能就
会卡壳.
3.还有⼀多半的试题,或者考点不是⾼考重点要求的,⽐如数论,恐怕是⾃主招⽣中考察最多的知识点,但
⾼考却很少涉及;或者考点也许在⾼考范围内,但考法较为灵活,⽐如第12题,需要将多个变量之间的
本质关系想清楚才能顺利解决.
光
光
⼦
辅
导
1.⼀定要有针对性的训练.⽐如⾼考很少考到数论相关的问题,即使考到,最多也就⽤到奇偶性、简单的整
除之类常识性的知识,但是⾃主招⽣对于数论的要求却较⾼.事实上,数论相关的问题很容易体现出“多想
少算”的特点,⾮常符合⾃招的选拔需求.再⽐如说平⾯⼏何,⾼中⽣很可能还⽐不上初中⽣,毕竟⾼考中的平⾯⼏何问题都⾮常简单.如果平时没有针对性的训练,考场上遇到不熟悉的考点很容易抓瞎;遇到那种考点在⾼考范围内,但风格不太⼀样的试题,也很难顺利解决.
2.往年的⾃招真题,还有全国联赛的⼀试题、预赛题,都是很好的准备材料.平时多练习多思考多总结,考场上遇到原题或者改编题的可能性相当⼤,那就赚到了.
3.试题难度总体上会保持稳定.今年北⼤⾃主招⽣数学试题相对容易,只是正常波动,明年很可能⽐今年稍难.对此⼤家要有⼼理准备.
4.选择题的“考场技巧”平时要多练,毕竟北⼤这两年的⾃招、博雅全是选择题.必要的时候可以猜.事实上,⼀道题即使完全不会,也不能空着.有同学可能会问,选错不是倒扣1分吗?可是我们算算期望,⼀道题随机选择的得分期望是0.5分呀!如果能排除两个错误选项呢?期望只会更⾼.
1.已知实数a,b 满⾜(a 2+4)(b 2+1)=5(2ab −1),则b Åa +1
a
ã
的值为(
)
A.1.5
B.2.5
C.3.5
D.前三个答案都不对
解析
C .
2.函数f (x )= x 2−2 −1
2
|x |+|x −1|,x ∈[−1,2]上的最⼤值与最⼩值的差所在的区间是(
)
A.(2,3)
B.(3,4)
C.(4,5)
D.前三个答案都不对
解析
B .
3.不等式组
y ⩾2|x |−1,
y ⩽−3|x |+5
所表⽰的平⾯区域的⾯积为(
)
A.6
B.
335
C.
365
D.前三个答案都不对
解析C .
4.(1+cos π5)Å1+cos 3π
5ã的值为(
)
A.1+1
√
5 B.1+
1
4
C.1+1
√
3
D.前三个答案都不对
解析B .
光
⼦
辅
导
5.在圆周上逆时针摆放了4个点A,B,C,D ,已知BA =1,BC =2,BD =3,∠ABD =∠DBC ,则该圆的直径为(
)
A.2√5
B.2√6
C.2√7
D.前三个答案都不对
解析
D .
6.已知三⾓形三条中线长度分别为9,12,15,则该三⾓形⾯积为()
A.64
B.72
C.90
D.前三个答案都不对
解析
B .
7.已知x 为实数,使得2,x,x 2互不相同,且其中有⼀个数恰为另⼀个数的2倍,则这样的实数x 的个数为()
A.3
B.4
C.5
D.前三个答案都不对
解析
B .
8.设整数a,m,n 满⾜√a 2−4√5=√m −√
n ,则这样的整数组(a,m,n )的个数为(
)
A.0
B.1
C.2
D.前三个答案都不对
解析C .
9.设
S =
1log 12π+1log 13π+1log 15π+1
log 17
π,
则不超过S 且与S 最接近的整数为()
A.−5
B.4
C.5
D.前三个答案都不对
解析
A .
10.已知复数z 满⾜z +2
z 是实数,则|z +i |的最⼩值等于()A.√33 B.
√
22C.1 D.前三个答案都不对
解析
D .
11.已知正⽅形ABCD 的边长为1,P 1,P 2,P 3,P 4是正⽅形内部的4个点使得△ABP 1,△BCP 2,
△CDP 3和△DAP 4都是正三⾓形,则四边形P 1P 2P 3P 4的⾯积等于()A.2−√3 B.
√6−√
2
4C.1+√
38
D.前三个答案都不对
解析
A .
光
⼦
辅
导
12.已知某个三⾓形的两条⾼的长度分别为10和20,则它的第三条⾼的长度的取值区间为()
A.Å103,5ã
B.Å5,
203ã
C.Å203
,20ã
D.前三个答案都不对
解析
C .
13.正⽅形ABCD 与点P 在同⼀平⾯内,已知该正⽅形的边长为1,且|P A |2+|P B |2=|P C |2,则|P D |
的最⼤值为(
)
A.2+√
2
B.2√2
C.1+√
2 D.前三个答案都不对
解析
A .
14.⽅程log 4(2x +3x )=log 3(4x −2x )的实根个数为(
)
A.0
B.1
C.2
D.前三个答案都不对
解析
B .
15.使得x +
2x 和x 2+2
x
2都是整数的正实数x 的个数为()A.1 B.2
C.⽆穷多
D.前三个答案都不对
解析
A .
16.满⾜f (f (x ))=f 4(x )的实系数多项式f (x )的个数为(
)A.2 B.4
C.⽆穷多
D.前三个答案都不对
解析
D .
17.使得p 3+7p 2为平⽅数的不⼤于100的素数p 的个数为(
)
A.0
B.1
C.2
D.前三个答案都不对
解析
C .
18.函数f (x )=x (x +1)(x +2)(x +3)的最⼩值为(
)A.−1
B.−1.5
C.−2
D.前三个答案都不对
解析
A .
19.动圆与两圆x 2+y 2=1和x 2+y 2−6x +7=0都外切,则动圆的圆⼼轨迹是(
)
A.双曲线
B.双曲线的⼀⽀
C.抛物线
D.前三个答案都不对
解析
B .
光
⼦
辅
导
20.在△ABC 中,sin A =
45,cos B =413
,则该三⾓形是()A.锐⾓三⾓形 B.钝⾓三⾓形
C.⽆法确定
D.前三个答案都不对
解析
A .。
