斜齿圆柱齿轮传动的受力分析和强度计算
机械设计基础第五版斜齿圆柱齿轮传动受力分析

左旋
右旋
分别指向各自的轮心。
❖轴向力Fa的方向: 取决于齿轮的回转方
向和轮齿的螺旋方向。
用“主动轮左、右手定则”判断
例题分析Βιβλιοθήκη ❖讨论:Fa = Ft tan
1、斜齿轮轴向力Fa与tanβ成正比。
由于β↑→平稳性好,但β↑→Fa↑→轴承 要求高
β= 8°~20°
2、采用人字齿轮可 消除轴向力。
β= 15°~40°
1、各力大小 Fr
c Fa
长方体对角面即轮齿法面
Fn
αn Ft
β
β
Fr Fn αn
F’
T1 F’ ω1
Ft Fr = F’ tgαn
β
d1
Fa
F’
2
F’=Ft /cosβ
Fn
Fr=Fnsinn F´=Fncosn
Ft=F´cos
Fa=F´sin
圆周力 径向力 轴向力 法向力
Ft
=
2T1 d1
Fr
=
Ft tann cos
Fa = Ft tan
Fn
=
cos
Ft
n cos
2、主、从动轮受力关系
❖作用于主、从动轮上的各对力大小相等、方向相反。 即:
Ft1= - Ft2 Fr1= - Fr2 Fa1= - Fa2
3、各力方向
❖圆周力Ft的方向: 在主动轮上与转动方向
相反,在从动轮上与转向 相同。 ❖径向力Fr的方向:
主动轮左、右手螺旋定则
主动轮为右旋,握紧右 手,四指弯曲方向表示主动 轮的回转方向,拇指的指向 即为作用在主动轮上轴向力 Fa的方向;主动轮为左旋时, 则应以左手用同样的方法来 判断。 ❖★ 不能用在从动轮上
齿轮传动的受力分析

5 蜗杆传动的受力分析
普通蜗杆传动的承载能力计算2
蜗杆传动的受力分析与斜齿圆柱齿轮相似,轮齿在受到法向载荷Fn的情 况下,可分解出径向载荷Fr、周向载荷Ft、轴向载荷Fa。 在不计摩擦力时,有以下关系:
F = t1
2T 1 =F a2 d1 F = −F a1 t2
F 至于轴向力 α 的方向,则与 齿轮回转方向和螺旋线方向有关, 可用主动轮左、右手法则判断 (右图):左螺旋用左手,右螺旋 用右手,握住齿轮轴线,四指曲 指方向为回转方向,则大拇指的 Fα 1 指向为轴向力 的指向,从动轮 的轴向力 与其相反。 Fα 2
轴向力方向判断
4直齿锥齿轮传动
4 直齿圆锥齿轮的强度计算
2T F2 = 2 t d2 F = −F r1 r2
F = F 2 tan α r2 t
5蜗杆传动的受力分析
在分析蜗杆和蜗轮受力方向时,必须先指明主动轮和从动轮(一 般蜗杆为主动轮);蜗杆或蜗轮的螺旋方向:左旋或右旋;蜗杆的转 向和位置。
蜗杆与蜗轮轮齿上各方向判断如下:
① 圆周力的方向:主动轮圆周力与其节点速度方向相反,从动轮圆周 力与其节点速度方向相同; ② 径向力的方向:由啮合点分别指向各自轴心; ③ 轴向力的方向 :蜗杆主动时,蜗杆轴向力的方向由“主动轮左、右 手定则”判断,即右旋蜗杆用右手(左旋用左手),四指顺着蜗杆转 动方向弯曲,大拇指指向即蜗杆轴向力的方向。 蜗轮轴向力的方向与蜗杆圆周力方向相反。
1.受力分析 直齿锥齿轮的轮齿受力分析模型如下图,将总法向载荷集中作用于齿宽中 点处的法面截面内。Fn可分解为圆周力Ft1,径向力Fr1和轴向力Fa1三个分力。 各分力计算公式:
圆柱齿轮传动强度的计算

圆柱齿轮传动的强度计算1 直齿圆柱齿轮传动的强度计算1.齿面接触疲劳强度计算为了保证在预定寿命内齿轮不发生点蚀失效,应进行齿面接触疲劳强度计算。
因此,齿轮接触疲劳强度计算准则为:齿面接触应力σH小于或等于许用接触应力σHP,即σH≤σHP赫兹公式由于直齿轮在节点附近往往是单对齿啮合区,轮齿受力较大,故点蚀首先出现在节点附近。
因此,通常计算节点的接触疲劳强度。
图a表示一对渐开线直齿圆柱齿轮在节点接触的情况。
为了简化计算,用一对轴线平行的圆柱体代替它。
两圆柱的半径ρ1、ρ2分别等于两齿廓在节点处的曲率半径,如图b所示。
由弹性力学可知,当一对轴线平行的圆柱体相接触并受压力作用时,将由线接触变为面接触,其接触面为一狭长矩形,在接触面上产生接触应力,并且最大接触应力位于接触区中线上,其数值为式中σH-接触应力(Mpa)Fn-法向力(N)L-接触线长度(mm)rS-综合曲率半径(mm);±-正号用于外接触,负号用于内接触ZE-材料弹性系数(),,其中E1、E2分别为两圆柱体材料的弹性模量(MPa);m1、m2分别为两圆柱体材料的泊松比。
上式表明接触应力应随齿廓上各接触点的综合曲率半径的变化而不同,且靠近节点的齿根处最大(图c、d)。
但为了简化计算,通常控制节点处的接触应力。
节点处的参数(1)综合曲率半径由图可知,,代入rE公式得式中:,称为齿数比。
对减速传动,u=i;对增速传动,u=1/i。
因,则有(2)计算法向力(3)接触线长度L引入重合度系数Ze,令接触线长度将上述参数代入最大接触应力公式得接触疲劳强度计算公式令,称为节点区域系数。
则得(1) 齿面接触疲劳强度的校核公式齿面接触疲劳强度的校核公式为(2) 齿面接触疲劳强度设计公式设齿宽系数,并将代入上式,则得齿面接触疲劳强度的设计公式式中:d1-小齿轮分度圆直径(mm);ZE-材料弹性系数(),按下表查取;注:泊松比m1=m2=0.3Z H-节点区域系数,考虑节点处轮廓曲率对接触应力的影响,可由下左图查取。
齿轮传动的强度设计计算

1. 齿面接触疲劳强度的计算齿面接触疲劳强度的计算中,由于赫兹应力是齿面间应力的主要指标,故把赫兹应力作为齿面接触应力的计算基础,并用来评价接触强度。
齿面接触疲劳强度核算时,根据设计要求可以选择不同的计算公式。
用于总体设计和非重要齿轮计算时,可采用简化计算方法;重要齿轮校核时可采用精确计算方法。
分析计算表明,大、小齿轮的接触应力总是相等的。
齿面最大接触应力一般出现在小轮单对齿啮合区内界点、节点和大轮单对齿啮合区内界点三个特征点之一。
实际使用和实验也证明了这一规律的正确。
因此,在齿面接触疲劳强度的计算中,常采用节点的接触应力分析齿轮的接触强度。
强度条件为:大、小齿轮在节点处的计算接触应力均不大于其相应的许用接触应力,即:⑴圆柱齿轮的接触疲劳强度计算1)两圆柱体接触时的接触应力在载荷作用下,两曲面零件表面理论上为线接触或点接触,考虑到弹性变形,实际为很小的面接触。
两圆柱体接触时的接触面尺寸和接触应力可按赫兹公式计算。
两圆柱体接触,接触面为矩形(2axb),最大接触应力σHmax位于接触面宽中线处。
计算公式为:接触面半宽:最大接触应力:•F——接触面所受到的载荷•ρ——综合曲率半径,(正号用于外接触,负号用于内接触)•E1、E2——两接触体材料的弹性模量•μ1、μ2——两接触体材料的泊松比2)齿轮啮合时的接触应力两渐开线圆柱齿轮在任意一处啮合点时接触应力状况,都可以转化为以啮合点处的曲率半径ρ1、ρ2为半径的两圆柱体的接触应力。
在整个啮合过程中的最大接触应力即为各啮合点接触应力的最大值。
节点附近处的ρ虽然不是最小值,但节点处一般只有一对轮齿啮合,点蚀也往往先在节点附近的齿根表面出现,因此,接触疲劳强度计算通常以节点为最大接触应力计算点。
参数直齿圆柱齿轮斜齿圆柱齿轮节点处的载荷为综合曲率半径为接触线的长度为,3)圆柱齿轮的接触疲劳强度将节点处的上述参数带入两圆柱体接触应力公式,并考虑各载荷系数的影响,得到:接触疲劳强度的校核公式为:接触疲劳强度的设计公式为:•KA——使用系数•KV——动载荷系数•KHβ——接触强度计算的齿向载荷分布系数•KHα——接触强度计算的齿间载荷分配系数•Ft——端面内分度圆上的名义切向力,N;•T1——端面内分度圆上的名义转矩,N.mm;•d1——小齿轮分度圆直径,mm;•b ——工作齿宽,mm,指一对齿轮中的较小齿宽;•u ——齿数比;•ψd——齿宽系数,指齿宽b和小齿轮分度圆直径的比值(ψd=b/d1)。
斜齿轮

式中:YFa、YSa应按当量齿数zv=z/cos3查表确定 斜齿轮螺旋角影响系数Yβ的数值可查图确定
标准斜齿圆柱齿轮强度计算
四、齿面接触疲劳强度计算 斜齿轮齿面接触强度仍以节点处的接触应
标准斜齿圆柱齿轮强度计算4
力为代表,将节点处的法面曲率半径rn代入计 算。法面曲率半径以及综合曲率半径有以下关 系为: rt d sin t
L
L
因此,
b cos b
KFt KFt KFn pca bα L cos t cos b bα cos t cos b
载荷系数的计算与直齿轮相同,即:K=KA Kv Kα Kβ
标准斜齿圆柱齿轮强度计算
三、齿根弯曲疲劳强度计算 斜齿轮齿面上的接触线为一斜线。受载时,
标准斜齿圆柱齿轮强度计算3
轮齿的失效形式为局部折断(如右图)。
强度计算时,通常以斜齿轮的当量齿轮为对
象,借助直齿轮齿根弯曲疲劳计算公式,并引入
斜齿轮螺旋角影响系数Yβ,得: 校核计算公式: F
斜齿圆柱齿轮轮齿受载及折断KFtYFaYSa Y bmnα
F
2 KT1Y cos 2 YFaYSa 设计计算公式:m n 3 2 F d z1 α
KT1 H 2 3 R 1 0.5R d1 u
设计计算公式: d1 2.923 (
H
ZE
)2
KT1 R 1 0.5R 2 u
齿轮的结构设计
齿轮的结构设计 通过强度计算确定出了齿轮的齿数z、模数m、齿宽B、螺旋角、分度圆直 径d 等主要尺寸。
2
dα
u H
斜齿轮的[H]
标准锥齿轮传动的强度计算
齿轮传动的作用力及计算

11-4直齿圆柱齿轮传动的作用力及计算载荷:一、齿轮上的作用力:为了计算齿轮的强度,设计轴和选用轴承,有必要分析轮齿上的作用力。
当不计齿面的摩擦力时,作用在主动轮齿上的总压力将垂直于齿面,(因为齿轮传动一般都加以润滑,齿轮在齿啮合时,摩擦系数很小,齿面所受的摩擦力相对载荷很小,所以不必考虑),即为P175图11-5b所示的F n(沿其啮合线方向),Fn可分解为两个分力:圆周力:Ft=2T1/d1 N径向力:Fr=Fttgα N而法向力:Fn=Ft/cosα NT1:小齿轮上的扭矩 T1=9550000p/n1 n·mmP:传递的功率(KW) d1:小齿轮分度圆直径 mmα:压力角 n1:小齿轮的转速(r·p·m)Ft1:与主动轮运动方向相反;Ft2与从动轮运动方向一致。
各力的方向 Fr:分别由作用点指向各轮轮心。
Fn:通过节点与基圆相切(由法切互为性质)。
根据作用力与反作用力的关系,主从动轮上各对的应力应大小相等,方向相反。
二、计算载荷:Fn是根据名义功率求得的法向力,称为名义载荷,理论上Fn沿齿宽均匀分布,但由于轴和轴承的变形,传动装置的制造安装误差等原因,载荷沿齿宽的分布并不均匀,即出现载荷集中现象(如P176图11-6所示,齿轮相对轴承不对称布置,由于轴的弯曲变形,齿轮将相互倾斜,这时,轮齿左端载荷增大,轴和轴承刚度越小,b越宽,载荷集中越严重。
此外,由于各种原动机和工作机的特性不同,齿轮制造误差以及轮齿变形等原因,还会引起附加动载荷。
精度越低,圆周速度V越大,附加载荷越大。
因此在计算强度时,通常以计算载荷K·Fn代替名义载荷Fn,以考虑上两因素的影响。
K—载荷系数表达式11-311-5 直齿圆柱齿轮的齿面接触强度计算:一、设计准则:齿轮强度计算是根据齿轮失效形式来决定的,在闭式传动中,轮齿的失效形式主要是齿面点蚀,开式传动中,是齿轮折断,在高速变截的齿轮传动中,还会出现胶合破坏,因胶合破坏的计算方法有待进一步验证和完善。
第三节斜齿圆柱齿轮传动
轴向力Fa的方向用左、右手定则来判断:主动轮为右旋 齿轮时,用右手握轴,四指弯曲方向为主动轴的旋转方 向,伸直的大拇指指向为主动轮的轴向力Fa的方向;主 动轮为左旋齿轮时,左手握轴,判断方法相同。从动轮 的轴向力Fa的方向,与主动轮的相反。
斜齿轮受力分析例题:
分析斜齿轮1轮齿的旋向及齿轮1、2的受力
第三节斜齿圆柱齿轮传动
斜齿圆柱齿轮传动
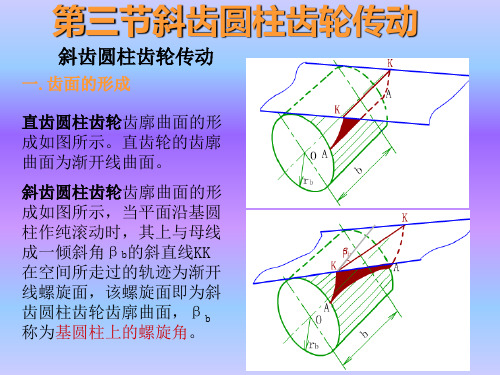
一.齿面的形成
直齿圆柱齿轮齿廓曲面的形 成如图所示。直齿轮的齿廓 曲面为渐开线曲面。
斜齿圆柱齿轮齿廓曲面的形 成如图所示,当平面沿基圆 柱作纯滚动时,其上与母线 成一倾斜角βb的斜直线KK 在空间所走过的轨迹为渐开 线螺旋面,该螺旋面即为斜 齿圆柱齿轮齿廓曲面,βb 称为基圆柱上的螺旋角。
数称为当量齿数,用 z v表示。铣刀 刀号应z v 按照选取
图 6-40
为确定当量齿数 z v ,如图4-30
所示。过斜齿轮分度圆上C点,作 斜齿轮法面剖面,得到一椭圆。 该剖面上C点附近的齿型可以视为 斜齿轮的法面齿型。以椭圆上点C
的曲率半径 作为虚拟直齿轮的
分度圆半径,并设该虚拟直齿轮 的模数和压力角分别等于斜齿轮 的法面模数和压力角,该虚拟直 齿轮即为当量齿轮,其齿数即为 当量齿数。
图a所示为一直齿条的情况,其上法面 和端面是同一个平面,所以有:
n t
对于斜齿条来说,因为轮齿倾斜了一个角 ,
于是就有端面与法面之分,如图b所示的斜齿条。
abc平面为端面,a'b'c为法面。 abc 即为端 面压力角,a 'b ' c为法面压力角。
由于 abc 和 a'b'c 这两个直角三角形等高,
所以
mn mt cos
斜齿圆柱齿轮传动的强度计算

一、齿轮的受力分析
直齿轮法面与端面重合受力分析比较简单,而斜齿轮转呈螺旋状,垂直轮齿的法平面与端面成β角。
在上图中Fn 分解为:
Fr --径向力指向轴心
Ft --圆周力,主动轮上与受力点方向速度相反,从动轮与速度相同
Fa --轴向力(方向根据左右手定则)
已知主动轮上驱动力矩T1时,有:
二、计算载荷
斜齿轮计算载荷:
式中:
Ft --主动轮上所受圆周力;
K--载荷系数;
b--齿轮宽度;
εα --斜齿轮端面重合度
三、齿根弯曲疲劳强度计算
当接触线通过齿顶边缘时,齿根出现最大弯曲应力,对斜齿轮很难用解析法进行精确计算。
斜齿轮齿根弯曲强度借助当量齿轮概念,直接应用直齿轮的公式。
校核与设计式:
式中:
K、T1、b、Фd 、d1、mn 、εα 同前;
Y β --螺旋角影响系数,根据β查表
YFa --斜齿轮齿形系数,按当量齿轮查表
Ysa --斜齿轮应力集中系数
四、齿面接触疲劳强度计算
以斜齿轮的法面参数代入进行计算。
校核与设计式:
(end)。
标准斜齿圆柱齿轮传动的强计算

Ft2FFar11 Fa2F1 t
Fr1 Ft1 Fa1 Fa Ft2
Fr2
2 Fr2
右
配对齿轮-旋向相反
(二) 计算载荷
1. 接触线长度: 接触线倾斜 + 重合度→接触线长度= 2.计算载荷:
b cos b
pca
KFn L
KFt
b cost
是端面重合度 图10 — 26
系数K类似与直齿
(三) 齿根弯曲疲劳强度计算
§10—7 标准斜齿圆柱齿轮传动的强度计算
(一) 作用力分析
1. 旋向:左、右旋 的判断(β-分度圆柱上的螺旋角)
右
左
2. Fn 的分解: Fn -圆周力Ft \径向力Fr
\轴向力Fa 与轴线平行并指向齿面
3. 作用力的大小:
Ft=2T1/d1 Fr=Ft·tgαn/cosβ Fa=Ft·tgβ
轴向力Fa的判断
F
Yfa、YSa由Zv=Z/cos3β查表
(四) 齿面接触疲劳强度计算
t
d
sin t
2
n
t cos b
综合曲率半径:
代入得:
1 1 1 2cos b u 1 n1 n2 d1 sin t u
H ZE
pcaZEFra bibliotekKFt b cost
2 cos b u 1 d1 sin t u
ZE
KFt u 1
bd1 u
2 cos b sin t cost
F
ZH
2 cos b ——区域系数 图10—30 sin t cost
齿面接触疲劳强度计算公式
H ZHZE
KFt
bd1
u 1 u
机械设计第11章斜齿与圆锥齿轮传动

(8-44)
4. 公式应用中的参数选择和注意事项
(1) 软齿面闭式齿轮传动在满足弯曲强度的条件下,为提 高传动的平稳性,小齿轮齿数一般取z1=20~40,速度较高时 取较大值;硬齿面的弯曲强度是薄弱环节,宜取较少的齿数, 以便增大模数,通常取z1 =17~20。
(2)为保证减小加工量,也为了装配和调整方便,大齿轮 齿宽应小于小齿轮齿宽。取b2=φdd1,则b1=b2+(5~10)。
图8-43表示一斜齿圆柱齿轮传动,取主动小齿轮作为研究对 象,设法向力Fn集中作用在分度圆柱上的齿宽中点P处。在法向 平面内的Fn可分解为径向力Fr、切向力Ft和轴向力Fa,F′是Ft和Fa 的合力,是Fn在P点分度圆柱切平面上的分力。
图8-43 斜齿圆柱齿轮传动的受力分析
切向力 径向力
轴向力 法向力
许用弯曲应力[σ]F:由表8-9得 σFlim1=330+0.45HBS1=(330+0.45×236)MPa=436.2 MPa σFlim2=184+0.74×HBS2=(184+0.74×190)MPa=324.6 MPa
由表8-10得,SFmin=1。所以
F1
Flim
SFmin
436.2MPa436.2MPa 1
法向力Fn分解为切于平均分度圆的切向力Ft和垂直分度圆锥母
线的分力F′,再将F′分解为径向力Fr和轴向力F(8-45)
Fr1=F′cosδ1=Ft1tanα cosδ1
(8-46)
Fa1=F′sinδ1 =Ft1tanαsinδ1
(8-47)
式中:dm1——小齿轮平均分度圆直径, dm1=d1(1-0.5b/R)。
由表8-10得SHmin=1,所以
斜齿圆柱齿轮的强度计算与结构设计PPT课件

轴向重合度(附加重合度)
B sin mn
端面重合度
1
2
[ z1( tgat1
tgt'
) z2( tgat2
tg
' t
)]
13
三、斜齿圆柱齿轮的当量齿数
——与斜齿轮法面齿形相当 的直齿轮的齿数
zv z / cos3
当量齿数应用:
d f 2 mz2 2.4m cos2 126 .353 mm
Rm 2
z12
z22
3 2
172 432 69.358 mm
35
齿顶角 齿根角 顶锥角
a
arctg
ha R
rctg
13 2.48 69.358
f
arctg hf R
rctg 1.2 3 69.358
2KT1 bmd1
YFS
[ F ]
对比,直齿轮的 弯曲强度公式!
24
25
2019/10/18
26
27
直齿圆锥齿轮机构
圆锥齿轮机构用来实现两相交轴之间
的传动,通常轴交角=δ1+δ2=90° 28
圆锥齿轮传动的特点
可传递交叉轴的运动, 常用Σ=90°;
一般使用场合:传动比 i≤3,v≤5m/s;
mm,00<β<200,i12=z2 / z1=5
16
③ 斜齿轮几何参数计算
a mn( z1 z2 ) 234 3( z1 5z1 )
2 cos
2 cos
先取β=200
468>3(z1+5z1)>468
《机械设计基础》第6章 齿轮传动(2)

斜齿轮传动的重合 度比直齿轮大
五、斜齿圆柱齿轮的当量齿数
用仿形法加工斜齿轮时,为便于选择刀号,应了 用仿形法加工斜齿轮时,为便于选择刀号, 解斜齿轮的法面齿形。 解斜齿轮的法面齿形。 一法平面与斜齿轮分度圆柱的交线为一椭圆, 一法平面与斜齿轮分度圆柱的交线为一椭圆, 如图,其长半轴a和短半轴b分别为: 如图,其长半轴a和短半轴b分别为:
⑵斜齿轮齿廓曲面的形成 发生面上与基圆柱母线成一角度β 的直线KK KK, 发生面上与基圆柱母线成一角度βb的直线KK, 在基圆柱上纯滚动时,直线KK KK在空间所展出的轨迹 在基圆柱上纯滚动时,直线KK在空间所展出的轨迹 为一渐开螺旋面,此曲面即为斜齿轮的齿廓曲面 斜齿轮的齿廓曲面。 为一渐开螺旋面,此曲面即为斜齿轮的齿廓曲面。
tan β =
πd
ps
, tan βb =
πdb
ps
所以: 所以:
tanβb=tanβcos αt β β
模数(m ⑵ 模数 n和mt) 由图可得, 由图可得, pn=ptcosβ pn=mnπ, pt=mtπ 因为 mn=mtcosβ 所以有 ⑶压力角(αn和αt) 压力角 由图可得, 由图可得,
五、斜齿圆柱齿轮的受力分析(如图) 斜齿圆柱齿轮的受力分析(如图)
由力矩平衡条件可得: 由力矩平衡条件可得: 圆周力: 圆周力: 径向力: 径向力: 轴向力: 轴向力:
2 T1 Ft = d1
Ft tanαn Fr = Fn′ tanαn = cosβ
Fa = Ft tanβ
的方向: 圆周力 Ft 的方向:在主动轮上 F t 对其轴之矩与转动 方向相反; 对其轴之矩与转向相同。 方向相反;在从动轮上 Ft 对其轴之矩与转向相同。 的方向:对两轮都是指向各自的轮心。 径向力 Fr 的方向:对两轮都是指向各自的轮心。
斜齿圆柱齿轮传动的强度计算

斜齿圆柱齿轮传动的强度计算
• 1.4 斜齿圆柱齿轮的当量齿数
图1-33 斜齿圆柱齿轮的当量齿轮
以ρ为分度圆半径、斜齿轮法面模数 mn为模数、法面压力角αn为压力角 作一直齿圆柱齿轮,其齿形可近似
• 1.5 斜齿圆柱齿轮的受力分析
如图1-34为斜齿圆柱齿轮传动中主动轮的受力分析图。图中Fn1作用在
轮齿的法面内,忽略摩擦力的作用,Fn1可分解为相互垂直的三个分力,
即圆周力Ft1、径向力Fr1、轴向力Fa1,大小分别为
圆周力
2
T 1 F t1
d1
(1-28)
径向力
tan
n
F F r1
t1 cos
端面尺寸可按直齿轮几何尺寸的计算公式直接计算。
斜齿圆柱齿轮传动的强度计算
• 1.3 正确啮合的条件
由斜齿轮齿廓曲面的形成可知,为保证斜齿轮正确啮合传动,除像直 齿轮一样保证两齿轮的端面模数、压力角相等外,两轮的螺旋角还应匹 配。对外啮合齿轮传动,两轮的螺旋角大小相等、方向相反;对于内啮 合,两轮的螺旋角应大小相等、方向相同。因此,斜齿轮正确啮合的条 件为:
• 1.2 主要参数及几何尺寸
4.齿顶高系数及顶隙系数 斜齿轮的齿顶高和齿根高不论从端面还是从法面来看都是相等的,即
将(1-24)带入上式得
h m h m
an n
at t
c m c m
nn
nt
h h cos
at
an
c c cos
t
n
(1-27)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第11章齿轮传动>>第十六节斜齿圆柱齿轮传动的受力分析和强度计算
受力分析图旋向判断图
右图表示斜齿轮传动中,主动和从动齿轮的受力情况。
当不计摩擦力时,轮齿所受的法向力可分解为三个相互垂直的分力
切向力N
轴向力N
径向力N
而法向力N
式中——小齿轮上传递的名义转矩,;
——小齿轮分度圆直径,;
——法面压力角。
主动轮上的切向力与齿轮回转方向相反;从动轮上的切向力与齿轮回转方向相同。
两轮的径向力的方向都指向各自的轮心。
至于轴向力的方向,则与齿轮回转方向和螺旋线方向有关,可用主动轮左、右手法则判断:左螺旋用左手,右螺旋用右手,握住齿轮轴线,四指曲指方向为回转方向,则大拇指的指向为轴向力的指向,从动轮的轴向力与其相反。
1.齿面接触强度计算
验算公式
设计公式
2.齿根弯曲强度计算
斜齿圆柱齿轮齿根弯曲强度按其法面上的当量直齿圆柱齿轮进行计算.
验算公式
设计公式。
