控制测量学水准网按条件平差算例
控制测量学第九章控制网平差

r nt
3
4
L1
p1 0 0
5 6
记:观测值
L n1
L2
相应权阵
p
nn
0
p2
0
7 8
Ln
0
0
pn
9
10
4 /7
v1
平差值改正数
V
n1
v2
vn
平差值
Lˆ
n1
Lˆ1 Lˆ2
Lˆn
L1
L2
Ln
v1 v2
vn
4
控制网平差
1 2 3 4 5 6 7 8 9
10
13 /7 4
2)平差值函数的权倒数
设有平差值函数为 f Lˆ1, Lˆ2,, Lˆn
它的权函数式为:
d
(
Lˆ1
)dLˆ1
(
Lˆ2
)dLˆ2
(
Lˆn
)dLˆn
f1dLˆ1 f2dLˆ2 fndLˆn
令
f T f1, f2, fn
则 d f T dLˆ
9
2) 改正数条件方程
10
以 Lˆi L(i v=i 1、i 2、… )代入n (1)得纯量形式为:
5 /7 4
a1v1 a2v2 anvn wa 0
b1v1 b2v2 bnvn wb 0
r1v1 r2v2 rnvn wr 0
(2)
1 2 3 4 5 6 7 8 9
控制网平差
第九章 控制网平差
1
2
3 4 5
[本章提要] 9.1 条件平差数学模型和公式
6
9.2 水准网按条件平差算例
7 8
9.3 附合导线按条件平差算例
水准网按条件平差算例
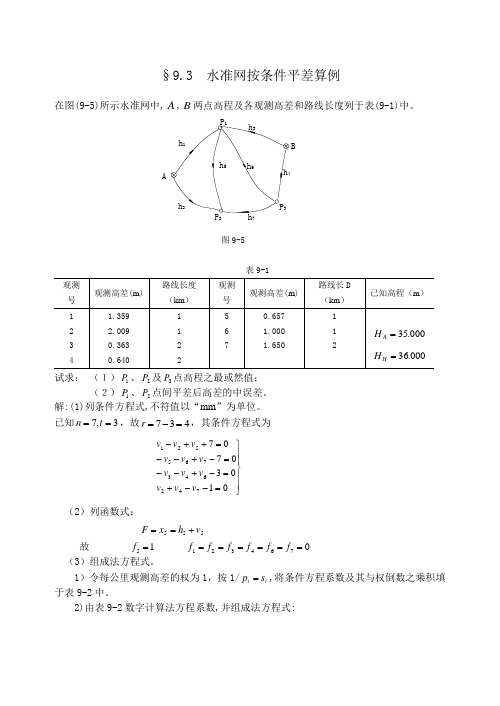
在图 表9-1试求: (1)1P 、2P 及3P 点高程之最或然值; (2)1P 、2P 点间平差后高差的中误差。
解:(1)列条件方程式,不符值以“mm ”为单位。
已知3,7==t n ,故437=-=r ,其条件方程式为⎪⎪⎭⎪⎪⎬⎫=--+=-+--=-+--=++-01030707742643765521v v v v v v v v v v v v(2)列函数式:555v h x F +==故 15=f 0764321======f f f f f f(3)组成法方程式。
1)令每公里观测高差的权为1,按1/i i s p =,将条件方程系数及其与权倒数之乘积填于表9-2中。
2)由表9-2数字计算法方程系数,并组成法方程式:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----------5221251021411013⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡d c b a k k k k +⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---1377=0 表9-2 条件方程系数表(4)法方程式的解算。
1)解算法方程式在表9-3中进行。
2)[]pvv 计算之检核。
[][]wk pvv -= []467.35=-wk由表9-3中解得[]47.35-=pvv ,两者完全一致,证明表中解算无误。
(5)计算观测值改正数及平差值见表9-4。
(6)计算321,,P P P 点高程最或然值。
359.3611=+=x H H A P m 012.3722=+=x H H A P m表9-4 改正数与平差值计算表(7)精度评定。
1)单位权(每公里观测高差)中误差2)21,P P 点间平差后高差中误差mm 0.3447.35±=±=μmmP m FF 2.252.00.31±=±=±=μ。
水准网平差实例

function tiaojian%条件方程的组成A=[1 -1 0 0 1 0 0;0 0 1 -1 1 0 0;0 0 1 0 0 1 1;0 1 0 -1 0 0 0];W=[7 8 6 -3]';%协因数阵的组成Q=diag([1.1 1.7 2.3 2.7 2.4 1.4 2.6]);P=inv(Q);%法方程组成Naa=A*Q*A';%求解联系数K和改正数K=-inv(Naa)*W;V=Q*A'*K;%计算观测值的平差值h=[1.359 2.009 0.363 1.012 0.657 0.238 -0.595]';adjh=h+V/1000;%精度评定VTPV=V'*P*V;r=4;var0=sqrt(VTPV/r);%计算单位权方差%评定观测值平差值函数的精度fs=[0 0 0 0 1 0 0]';%函数的系数Qss=fs'*Q*fs-(A*Q*fs)'*inv(Naa)*A*Q*fs;%观测值平差值函数的协因数varS=Qss*var0;%观测值平差值函数的方差%写输出结果文件fid=fopen('C:\Documents and Settings\陈岑\桌面\tiaojian.dat','w+'); fprintf(fid,'%s\n\n ',' ######水准网平差算例######'); fprintf(fid,'%s ','观测值改正数');fprintf(fid,'\n');for i=1:7fprintf(fid,' %s%1.0f ','V',i);fprintf(fid,'%15.3f\n',V(i));endfprintf(fid,'\n');fprintf(fid,'%s\n','观测值平差值');for i=1:7fprintf(fid,' %s%1.0f ','h',i);fprintf(fid,'%15.3f',h(i));fprintf(fid,'\n');endfprintf(fid,'\n');fprintf(fid,'%s ','单位权中误差');fprintf(fid,'\n');fprintf(fid,' %s %3.2f ','m0=',var0);fprintf(fid,'\n');fclose(fid);######水准网平差算例######观测值改正数V1 -0.243V2 2.855V3 -4.243V4 -0.145V5 -3.902V6 -0.615V7 -1.142观测值平差值h1 1.359h2 2.009h3 0.363h4 1.012h5 0.657h6 0.238h7 -0.595单位权中误差m0= 2.22-------------------------------------------------------------------------------------- 间接平差(水准网)function [B,l,P,h]=Finput%误差方程的组成B=[1 0;0 1;1 0;0 1;-1 1;-1 0];l=[0 0 4 3 7 2]';%协因数阵Q的组成Q=diag([1.1 1.7 2.3 2.7 2.4 4.0]);P=inv(Q);%观测值h=[1.359 2.009 0.363 1.012 0.657 -0.357]';function jianjie1[B,l,P,h]=Finput;%fafangchengdezuchengNbb=B'*P*B;% adjx Vadjx=inv(Nbb)*B'*P*l;V=B*adjx-l;%计算观测值的平差值adjh=h+V/1000;%精度评定VTPV=V'*P*V;r=4;var0=sqrt(VTPV/r);%计算单位权方差%写输出结果文件fid=fopen('C:\Documents and Settings\陈岑\桌面\jianjie1.dat','w+'); fprintf(fid,'%s\n\n ',' ######水准网间接平差算例######'); fprintf(fid,'%s ','观测值改正数');fprintf(fid,'\n');for i=1:6fprintf(fid,' %s%1.0f ','V',i);fprintf(fid,'%15.3f\n',V(i));endfprintf(fid,'\n');fprintf(fid,'%s\n','观测值平差值');for i=1:6fprintf(fid,' %s%1.0f ','adjh',i);fprintf(fid,'%15.3f',adjh(i));fprintf(fid,'\n');endfprintf(fid,'\n');fprintf(fid,'%s ','单位权中误差');fprintf(fid,'\n');fprintf(fid,' %s %3.2f ','m0=',var0);fprintf(fid,'\n');fclose(fid);######水准网间接平差算例######观测值改正数V1 -0.243V2 2.855V3 -4.243V4 -0.145V5 -3.902V6 -1.757观测值平差值adjh1 1.359 adjh2 2.012 adjh3 0.359 adjh4 1.012 adjh5 0.653 adjh6 -0.359单位权中误差m0= 2.22。
高程控制网平差

i
i
i
h h V 改厕厕短的改正数, 代入上式,得:
i
i
i
V1 V2 V3 V4 W 0
W H A h1 h2 h3 h4 H B
1.附合水准路线的条件数和条件方程式组成
观测值5个,待定水准点2 个,所以条件有3个,可 以列出3个条件方程:
h1
H B h1 h2 H A 0
V 1 V 3 V 2 W a 0 V 2 V 4 V 6 W b 0 V 4 V 5 V 3 W c 0
(二)观测值权的确定:
1.各水准路线都进行了往返观测,每公里水准路线的观测中误差为 ,
则m:i
R mi2
1 4n
n i
2 i
i
式中,为测往返测高程不符值,以mm为单位;R为测段长度,以km为单位;n
H A h2 h3 h5 H D 0
H B h1 h3 h4 H C 0
一般以1个已知点为起点,其它已知点为终点,所构成的附合 水准路线为已知点数减1,这样可以列出的条件方程式为已知 水准点个数减1.
2.闭合水准路线的条件数和条件方程式的组成
从一个水准点出发,经过若干水准测段,又回到该 水准点,这样的水准路线称为闭合水准路线。
V 1 V 7 V 8 W b 0
V 2 V 8 V 7 W c 0
V 3 V 5 V 8 W d 0
V 4 V 6 V 5 W e 0
2.闭合水准路线的条件数和条件方程式的组 成
图(c)是四边形状水准网,网中有4个待定点,没有已知点, 在平差计算时,只能确定个待定水准点之间的相互关系,如 果确定一个水准点的高程,就可以确定其他点的高程。因此, 该网的必要观测是3个,观测值总数是6个,又3个多余观测, 可以列出3个条件方程。为了让所列立的条件方程式互相独 立,没个条件方程都要求有一个其他方程没有用到的观测值, 即:
高程平差方法 举例说明

高程平差方法举例说明引言在工程建设中不免要对高程控制网进行高精度计算,手工计算对于较为简单的控制网还可适应,但对于较为复杂、节点较多的高程控制网来讲使用手工计算容易出现误差且非常耗时,因此我们针对高程控制网的平差计算原理进行了分析,并利用这一原理结合计算机技术进行了高效的控制网平差计算。
1 平差模型的建立1. 1 平差原理下面以一个水准网的算例来说明水准网间接平差原理,水准网如图1 所示:已知A 点高程HA=237. 483m,为求B、C、D 三点的高程,进行了水准测量,观测结果为见图1, h1、h2、h3、h4、h5 分别为观测值,对应的水准路线长度为S1、S2、S3、S4、S5。
取B、C、D 三点的高程值平差值为参数,其近似值为X01、X02、X03 其中:X01=HA+h1; X02=HA+h3; X03=HA+h5 于是观测值误差方程为v:常数项l:权P:如下:其中:改正数V= 系数阵A= 参数x= 常数项l=可以解出由此可以计算出高程平差值由上可知,水准网间接平差主要分为三个步骤:(1)高程近似值的计算;(2)列立观测值的误差方程;(3)解误差方程并求高程平差值。
1. 2 常数项矩阵的问题在求近似高程时,同一个未知点的近似高程并不是唯一的一个确定值,它的值随着计算时选择的线路不同而改变,因此得出的常数项矩阵L 也并不是唯一的,在下面的程序计算里面,输入已知数据时线路的排序不同,得出的常数项矩阵L 也不同,当然最后得到的高程改正数也不一样,由于进行平差计算时设的未知数就是未知点高程的近似值,因此在最后得到的未知点的高程平差值跟计算高程近似值时选择的线路无关,只要计算正确,最终得到的高程平差值也是正确的。
这一点可以在使用程序的过程中进行检验,无论线路排序如何改变,只要数据输入正确,得到的结果是一样的。
2 平差程序设计2. 1 关于程序语言的选用考虑到本软件所要解决的问题主要是数据的处理与计算,不涉及到计算机系统底层的操作,因此选用相对简单的Visual Basic 6. 0 来进行程序的编写,使用间接平差模型,在保证计算精度的同时,一来减少了代码编写的难度,二来提高了代码执行的效率。
测量平差--条件平差具体一个例子(成教院地质测量)

T1 = 67˚ 14′ 28.3″ T2= 141˚ 47′ 00.5″ T3 = 92˚ 51′ 33.8″ T4= 185˚ 11′ 54.0″ T5 = 249˚ 30′ 24.0″
(1)组成改正数条件方程及第3点平差后坐标函数式 改正数条件方程闭合差项:
(2)确定边角观测值的权
设单位权中误差 ˆ0 ˆ 2.5"
根据提供的标称精度公式 ˆ S = 5 mm +
5ppm•D计算测边中误差
根据(3-3-26)式,测角观测值的权为 Pβ = 1; 为不使测边观测值的权与测角观测值的权相差过大, 在计算测边观测值权时,取测边中误差和边长改正 值的单位均为厘米(cm)。
0.9221VS1 +0.6186VS 2 + 0.9988VS 3 0.0906VS 4 – 1.2502Vβ1 –1.5267Vβ2 – 0.9840Vβ3 – 0.9417Vβ4 – 1.7 = 0
0
0
0
0
1
1
1
1 1
A 0.3868 0.7857 0.0499 0.9959 1.8479 1.1887 0.7614 0.0857 0
X B(1) Xˆ12 Xˆ 23 Xˆ 34 Xˆ 45 XC(5) 0
YB(1) Yˆ12 Yˆ23 Yˆ34 Yˆ45 YˆC(5) 0
如何对角度和边长进行改正满足上述要求!!!
已知坐标(m)
B (187396.252 , 29505530.009)
C (184817.605 , 29509341.482)
解:
未知导线点个数n – 1 = 3,导线边数n = 4,观测角
水准网的条件平差

目录目录 (1)观测误差 (2)摘要: (2)关键词: (2)引言 (3)1水准测量 (4)1.1水准测量的原理 .............................................................................. •1.2水准网...................................................................................... •2条件平差 .. (6)2.1 衡量精度的指标 (6)2.2条件平差的原理 .............................................................................. •3水准网的平差 .. (14)3.1必要观测与多余观测 (14)3.2条件方程 (14)3.3条件平差法方程式 (14)3.4条件平差的精度评定 (15)3.5水准网的条件平差 (18)致谢 (20)参考文献 (21)观测误差由观测者、外界环境引起的偶然误差学生:xxx 指导教师:xxx摘要:对一系列带有偶然误差的观测值,采用合理的的方法消除它们间的不符值,得出未知量的最可靠值;以及评定测量成果的精度。
关键词:偶然误差;观测值;精度引言测量工作中,要确定地面点的空间位置,就必须进行高程测量,确定地面点的高程。
几何水准测量是高程测量中最基本、最精密的一种方法。
通过测量仪器,工具等任何手段获得的以数字形式表示的空间信息,即观测量。
然而,测量是一个有变化的过程,受仪器、观测值、外界环境因素的影响,观测的结果与客观上存在的一个能反映其真正大小的数值,即真值(理论值),有一定的差异。
可以说在测量中产生误差是不可避免的。
所以,观测值不能准确得到,在测量上称这种差异为观测误差。
根据其对观测结果影响的性质,可将误差分为系统误差和偶然误差两种。
测量程序设计_条件平差和间接平差

程序代码如下:
disp(‘-------水准网间接平差示例-------------’) disp(‘已知高程’) Ha = 5.015 % 已知点高程,单位m Hb = 6.016 % 已知点高程,单位m
A h2 D h1
C h6 E h7 B h4
h5
h3
disp(‘观测高差,单位m’)
L = [1.359; 2.009; 0.363; 1.012; 0.657; -0.357] disp(‘系数矩阵B’)
则: PV AT K
V P A K QA K
T
1 T
4、法方程: 将条件方程 AV+W=0代入到改正数方程V=QATK 中,则得到:
AQAT K W 0
r1 r1 r1
记作: 由于
N aa K W 0
rr
R( Naa ) R( AQAT ) R( A) r
Naa为满秩方阵, K Naa1W ( AQAT )1 ( AL A0 )
if H(1,1)+H(2,1)-H(3,1)+HA-HB==0 && H(2,1)H(4,1)==0 disp(‘检核正确') else disp(‘检核错误') end disp(‘平差后的高程值') HC = HA + H(1,1) HD = HA + H(1,1) + H(4,1)
二、间接平差的基本原理
其中l=L-d.
ˆ 设误差Δ和参数X的估计值分别为V 和 X
则有
ˆ V AX l
X0 为了便于计算,通常给参数估计一个充分接近的近似值
ˆ ˆ X X0 x
则误差方程表示为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在图h 5
h 2
A
P 2
h 1
P 1
h 6
h 7P 3
h 4
h 3
B
表9-1
观测号 观测高差(m )
路线长度(km ) 观测号 观测高差(m )
路线长D (km ) 已知高程(m )
1 2 3 4
1 1
2 2
5 6 7
1 1 2
000.35=A H 000.36=H H
试求: (1)1P 、2P 及3P 点高程之最或然值; (2)1P 、2P 点间平差后高差的中误差。
解:(1)列条件方程式,不符值以“mm ”为单位。
已知3,7==t n ,故437=-=r ,其条件方程式为
⎪⎪⎭
⎪
⎪
⎬⎫
=--+=-+--=-+--=++-01030707742643765521v v v v v v v v v v v v
(2)列函数式:
555v h x F +==
故 15=f 0764321======f f f f f f
(3)组成法方程式。
1)令每公里观测高差的权为1,按1/i i s p =,将条件方程系数及其与权倒数之乘积填于表9-2中。
2)由表9-2数字计算法方程系数,并组成法方程式:
⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----------5221251021411013⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡d c b a k k k k +⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡---1377=0 表9-2 条件方程系数表
观测号 a
b
c
d
s
s '
1 1 1 1
2 -1 1 0 0
3 -1 -1 -1
4 -1 1 0 0
5 1 -1 0 1 1
6 -1 1 0 0 7
1 -1 0 0 ∑
1
-1
-1
1
0 0
1
1 1
观测号 p
1
p
a
p
b
p
c
p
d
p
s
p
f
p
s '
1 1 1
1 1
2 1 -1
1
3 2 -2 -2 -2
4 2
-2 2 5 1 1 -1 1 1 6 1 -1 1 7
2 2 -2 ∑
1
-3
1
-1 -1
1
0 0
(4)法方程式的解算。
1)解算法方程式在表9-3中进行。
2)[]pvv 计算之检核。
[][]wk pvv -= []467.35=-wk
由表9-3中解得[]47.35-=pvv ,两者完全一致,证明表中解算无误。
(5)计算观测值改正数及平差值见表9-4。
(6)计算321,,P P P 点高程最或然值。
359.3611=+=x H H A P m 012.3722=+=x H H A P m
f
360.3543=+=x H H B P m
表9-3 高斯-杜力特表格
行的 符号
)(a
)(b
)(c
)(d
)(w
s
)(f
s '
∑
∑'
a
E b
1
⋅b 1⋅E
c
2
⋅c 2
⋅E d
3⋅d 3
⋅E
w
=
=
0 0
=
=
0 0
表9-4 改正数与平差值计算表
观测号
a b c d
p
1
a ak
b bk
c ck
d dk
v (mm)
h (mm)
平差值
x (m)
1 1 1
2 -1 1 1
3 -1 2
4 -1 1 2
5 1 -1 1
6 -1 1 1 7
1
-1
2
(7)精度评定。
1)单位权(每公里观测高差)中误差
2)21,P P 点间平差后高差中误差 )
(s a k b k c k d
k )(s '4
⋅w mm 0.34
47
.35±=±=μ。
