三角函数换底公式
三角函数变换公式大全

三角函数变换公式大全这篇文章给大家分享三角函数的变换公式以及初中常用的三角函数公式,一起看一下具体内容。
三角函数变换公式三角函数乘积变换和差公式sinAsinB=-[cos(A+B)-cos(A-B)]/2cosAcosB=[cos(A+B)+cos(A-B)]/2sinAcosB=[sin(A+B)+sin(A-B)]/2cosAsinB=[sin(A+B)-sin(A-B)]/2三角函数和差变换乘积公式sinA+sinB=2sin[(A+B)/2]cos[(A-B)/2]sinA-sinB=2cos[(A+B)/2]sin[(A-B)/2]cosA+cosB=2cos[(A+B)/2]cos[(A-B)/2]cosA-cosB=-2sin[(A+B)/2]sin[(A-B)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)三角函数两角和与差公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-cossinBcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)三角函数的转化公式sin(-α)=-sinαcos(-α)=cosαsin(π/2-α)=cosαcos(π/2-α)=sinαsin(π/2+α)=cosαcos(π/2+α)=-sinαsin(π-α)=sinαcos(π-α)=-cosαsin(π+α)=-sinαtanα=sinα/cosαtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα常用三角函数公式三角函数半角公式sin(A/2)=±√((1-cosA)/2)cos(A/2)=±√((1+cosA)/2)tan(A/2)=±√((1-cosA)/((1+cosA))三角函数倍角公式Sin2A=2SinA*CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1 tan2A=(2tanA)/(1-tanA^2)。
职业高中常用数学公式

职业高中常用数学公式三、指数部分与对数部分常用公式1、指数部分:⑵分数指数幂与根式形式的互化: ① nmnm a a= ② nmnm aa1=-)1*,(>∈n N n m 且、①10=a② a a n n =)( ③ ⎩⎨⎧=为偶数,当为奇数当n a n a a n n ||,2、对数部分:⑴1log =a a ;⑵01log =a ;⑶对数恒等式:N aNa =log 。
⑷N M N M a a a log log )(log +=⋅ ⑸N M NMa a a log log )(log -=; ⑹ M p M a pa log log =⑺换底公式:abb c c a log log log =﹡四、三角部分公式 1、弧度与角度⑴换算公式:1800=π,10=180πrad 1rad=π0180≈57018'=57.3002、角α终边经过点P ),(y x ,22y x r +=,则r y =αsin ,r x =αcos ,xy=αtan 1、 三角函数在各象限的正负情况:4、同角函数基本关系式:5、简化公式:①⎪⎩⎪⎨⎧-=-=--=-ααααααtan )tan(cos )cos(sin )sin( ②⎪⎩⎪⎨⎧-=-=--=-ααπααπααπtan )2tan(cos )2cos(sin )2sin( ③⎪⎩⎪⎨⎧-=--=-=-ααπααπααπtan )tan(cos )cos(sin )sin( ④ ⎪⎩⎪⎨⎧=+-=+-=+ααπααπααπtan )tan(cos )cos(sin )sin( ⑤⎪⎩⎪⎨⎧=+=+=+ααπααπααπtan )2tan(cos )2cos(sin )2sin(k k k (k Z ∈)⑥⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=-=-ααπααπααπcot )2tan(sin )2cos(cos )2sin(6、两角和与差的正弦、余弦、正切:⑴两角和与差的正弦:βαβαβαsin cos cos sin )sin(+=+βαβαβαsin cos cos sin )sin(-=-⑵两角和与差的余弦:βαβαβαsin sin cos cos )cos(-=+βαβαβαsin sin cos cos )cos(+=-⑶两角和与差的正切:βαβαβαtan tan 1tan tan )tan(-+=+βαβαβαtan tan 1tan tan )tan(+-=-7、二倍角公式:⑴二倍角的正弦:αααcos sin 22sin =⑵二倍角的余弦:ααα22sin cos 2cos -== α2sin 21-= 1cos 22-α⑶二倍角的正切:ααα2tan 1tan 22tan -=五、几何部分 1、 向量④向量的数量积:θcos ||||⋅⋅=⋅b a b a(其中θ为两个向量的夹角)﹡ ⑵代数方式的运算:设),(21a a a =,)(2,1b b b = ,①加法:),(2211b a b a b a ++=+②减法:),(2211b a b a b a --=-③数乘向量:),(21a a a λλλ=④向量的数量积:2211b a b a b a +=⋅(结果为实数)⑶两个向量平行与垂直的判定:设),(21a a a =,)(2,1b b b = ,①平行的判定:a ∥b ⇔a bλ=⇔1221b a b a =②垂直的判定:a ⊥b ⇔0=⋅b a⇔02211=+b a b a⑷其它公式:设),(21a a a =,)(2,1b b b =①向量的长度:2221||a a a +=﹡②设),(),,(2211y x B y x A ,则),(1212y y x x B A --=;|212212)()(|y y x x B A -+-=﹡③设),(),,(2211y x B y x A ,则线段AB 的中点M 的坐标为M )2,2(2121y y x x ++﹡④两个向量的夹角为θ,则222122212211||||cos b b a a b a b a b a ba +++=⋅= θ2、 直线部分⑴斜率公式:①)为直线的倾斜角,090(tan ≠=αααk②)(211212x x x x y y k ≠--=⑵直线方程的形式:① 点斜式:)(00x x k y y -=- (k 为斜率,),(00y x 为直线过的点); ② 斜截式:b kx y +=(k 为斜率,b 为直线在y 轴上的截距); ③ 一般式:)0(0≠=++A C By Ax (斜率BCb B A k -=-=,) ⑶两条直线平行或垂直的条件:① 两条直线斜率为21,k k ,且不重合则1l ∥2l ⇔21k k = ② 两条直线的斜率为21,k k ,则1l ⊥2l ⇔121-=⋅k k ⑷两条直线的夹角公式(设夹角为θ): ①21k k =时,1l ∥2l ,夹角θ=00; ②121-=⋅k k 时,1l ⊥2l ,则夹角θ=900; ⑷点),(00y x 到直线0=++C By Ax 的距离公式: ||2200BA CBy Ax d +++=⑸两平行线0:11=++C By Ax l 与0:22=++C By Ax l 间距离 ||2221B A C C d ++=3、圆部分⑴圆的方程:① 标准方程:222)()(r b y a x =-+-(其中圆心为),(b a ,半径为r ) ② 一般方程:022=++++F Ey Dx y x (其中圆心为)2,2(ED --,半径为2422FE D r -+=)六、数列1、 已知前n 项和公式n S :⎩⎨⎧∈≥-==-),2()1(11Z n n s s n s a n n n2、 等差数列:⑴通项公式d n a a n )1(1-+=(1a 是首项;d 为公差n 为项数;n a 为通项即第n 项)⑵等差公式:a ,A ,b 三数成等差数列,A 为a 与b 的等差中项,则)2(2b a A ba A +=+=或 ⑶前n 项和公式:① d n n n a S n 2)1(1-+=(已知n d a ,,1时应用此公式) ②2)(1n n a a n S +=(已知n a a n ,,1时应用此公式) ③特殊地:当数列为常数列,,,a a a ----时,na S n = 3、等比数列:⑴通项公式:11-=n n qa a⑵等比中项公式:若a ,A ,b 三数成等比数列,则A 为a 与b 的等比中项,则)(2b a A b a A ⋅±=⋅=或⑶前n 项和公式:①)1(1)1(1≠--=q qq a S nn (已知n q a ,,1时应用)②)1(1)1≠--=q qq a a S n n (已知n a a n ,,1时应用)③当1=q 时,数列为常数列,则1na S n =。
什么是换底公式换底公式怎么推导来的

什么是换底公式换底公式怎么推导来的换底公式是数学中常用的一种技巧,用于将不同底的对数转换为同底的对数。
它在解决一些复杂计算问题时具有很大的便利性,并且被广泛应用于各个领域。
本文将详细介绍什么是换底公式以及它是如何推导而来的。
1. 换底公式的定义换底公式是指将不同底的对数转换为同底的对数的公式。
具体来说,对于任意一个正实数a、b(a、b≠1),以及任意一个正实数x,换底公式可以表示为:logₐx = logₐb * log_bx其中,logₐx表示以底数a为底的x的对数,logₐb表示以底数a为底的b的对数,log_bx表示以底数b为底的x的对数。
2. 换底公式的推导过程为了推导换底公式,我们先从上述公式入手,根据对数的定义和性质进行推算。
首先,根据对数的定义,底数a为底的x的对数可以表示为a的多少次幂等于x。
即:a^logₐx = x。
其次,我们可以将a表示为b的对数的形式,即:a = b^log_ba。
将以上两个等式代入我们的初等换底公式中,得到:a^logₐx =(b^log_ba)^logₐb * log_bx。
在指数运算中,当相同底数的幂次相乘时,其底数保持不变,幂次相加。
根据此性质,上述等式可以进一步简化为:(b^log_ba)^logₐb *log_bx = b^{(log_ba)*(logₐb)} * log_bx。
为了使等式更加简洁,我们引入一个新的变量t,令t = log_ba。
代入上式得到:b^t * log_bx = b^{t * (logₐb)} * log_bx。
进一步观察整个等式,我们可以发现b^t与b^{t * (logₐb)}是相等的,即:b^t = b^{t * (logₐb)}。
由于底数相等,所以指数也必须相等。
根据这一条件,我们得到logₐb = 1。
将这个结果代入上面的等式,我们就可以得到最终的换底公式:a^logₐx = b^t * log_bx。
3. 换底公式的应用举例现在我们来看一些实际应用,以更好地理解换底公式。
三角函数

三角函数公式百科名片三角函数是数学中属于初等函数中的超越函数的一类函数。
它们的本质是任何角的集合与一个比值的集合的变量之间的映射。
通常的三角函数是在平面直角坐标系中定义的。
其定义城为整个实数城。
另一种定义是在直角三角形中,但并不完全。
现代数学把它们描述成无穷敖列的极限和微分方程的解,将其定义扩展到复数系。
[编辑本段]公式分类锐角三角函数公式sin α=∠α的对边/ 斜边cos α=∠α的邻边/ 斜边tan α=∠α的对边/ ∠α的邻边cot α=∠α的邻边/ ∠α的对边倍角公式Sin2A=2SinA•CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=(2tanA)/(1-tanA^2)(注:SinA^2 是sinA的平方sin2(A))三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin³acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-cos²a)cosa=4cos³a-3cosasin3a=3sina-4sin³a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos³a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)²]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)积化和差sinαsinβ= [cos(α-β)-cos(α+β)] /2cosαcosβ= [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2cosαsinβ = [sin(α+β)-sin(α-β)]/2双曲函数sinh(a) = [e^a-e^(-a)]/2cosh(a) = [e^a+e^(-a)]/2tg h(a) = sin h(a)/cos h(a)公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)= sinαcos(2kπ+α)= cosαtan(kπ+α)= tanαcot(kπ+α)= cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tanαcot(2π-α)= -cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)= cosαcos(π/2+α)= -sinαtan(π/2+α)= -cotαcot(π/2+α)= -tanαsin(π/2-α)= cosαcos(π/2-α)= sinαtan(π/2-α)= cotαcot(π/2-α)= tanαsin(3π/2+α)= -cosαcos(3π/2+α)= sinαtan(3π/2+α)= -cotαcot(3π/2+α)= -tanαsin(3π/2-α)= -cosαcos(3π/2-α)= -si nαtan(3π/2-α)= cotαcot(3π/2-α)= tanα(以上k∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用A·sin(ωt+θ)+ B·sin(ωt+φ) =√{(A^2 +B^2 +2ABcos(θ-φ)} • sin{ωt + arcsin[ (A•sinθ+B•sinφ) / √{A^2 +B^2; +2ABcos(θ-φ)} }√表示根号,包括{……}中的内容诱导公式sin(-α) = -sinαcos(-α) = cosαtan (—a)=-tanαsin(π/2-α) = cosαcos(π/2-α) = sinαsin(π/2+α) = cosαcos(π/2+α) = -sinαsin(π-α) = sinαcos(π-α) = -cosαsin(π+α) = -sinαcos(π+α) = -cosαtanA= sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍:奇变偶不变,符号看象限万能公式sinα=2tan(α/2)/[1+tan^(α/2)]cosα=[1-tan^(α/2)]/1+tan^(α/2)]tanα=2tan(α/2)/[1-tan^(α/2)]其它公式(1)(sinα)^2+(cosα)^2=1(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2证明下面两式,只需将一式,左右同除(sinα)^2,第二个除(cosα)^2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)(sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC其他非重点三角函数csc(a) = 1/sin(a)sec(a) = 1/cos(a)[编辑本段]内容规律三角函数看似很多,很复杂,但只要掌握了三角函数的本质及内部规律就会发现三角函数各个公式之间有强大的联系。
三角函数转换公式

三角函数转换公式1、诱导公式:sin(-α) = -sinα;cos(-α) = cosα;sin(π/2-α) = cosα;cos(π/2-α) = sinα;sin(π/2+α) = cosα;cos(π/2+α) = -sinα;sin(π-α) = sinα;cos(π-α) = -cosα;sin(π+α) = -sinα;cos(π+α) = -cosα;tanA= sinA/cosA;tan(π/2+α)=-cotα;tan(π/2-α)=cotα;tan(π-α)=-tanα;tan(π+α)=tanα2、两角和差公式:sin(A±B) = sinAcosB±cosAsinBcos(A±B) = cosAcosB sinAsinBtan(A±B) = (tanA±tanB)/(1 tanAtanB)cot(A±B) = (cotAcotB 1)/(cotB±cotA)3、倍角公式sin2A=2s inA•cosAcos2A=cosA2-sinA2=1-2sinA2=2cosA2-1tan2A=2tanA/(1-tanA2)=2cotA/(cotA2-1)4、半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))声屏障板:声屏障板声波在传播过程中,遇到声屏障板时,就会发生反射、透射和绕射三种现象。
通常我们认为屏障板能够阻止直达声的传播,并使统射声有足够的衰减,而透射声的影响可以忽略不计。
因此,声屏障板的隔声效果一般可采用减噪量表示,它反映了声屏障板上述两种屏蔽透声的本领。
换底公式的6个推论

换底公式的6个推论首先,我们来介绍一下换底公式:对于任意实数a,b,c,且a≠1,b≠1,有以下的换底公式:1. logₐb = logcₐ / logcₒb2. logₐ(b^c) = c * logₐb3. logₐ1 = 04. logₐa = 15. logₐ(ab) = logₐa + logₐb6. logₐ(b/c) = logₐb - logₐc接下来,我们将详细说明这些换底公式的推论:推论一: logₐb = 1 / logbₐ根据换底公式 logₐb = logcₐ / logcₒb,取c = b,并将logcₐ化简为1,得到 logₐb = logbₐ / logbₐ,再根据对数的倒数性质,可得 logₐb =1 / logbₐ。
推论二: loga(b^c) = logb(a^c)根据换底公式 logₐb = logcₐ / logcₒb,将c替换成a^c,可得loga(b^c) = log(a^c)ₐ / log(a^c)ₒb,再根据log的指数性质loga(b^c) = logₐ(b^c),log(a^c)ₐ = c,log(a^c)ₒb = c * log(a)ₒb,可得loga(b^c) = log(b)ₐ / log(b)ₒa^c = logb(a^c)。
推论三: loga1 = 0根据换底公式 logₐb = logₐ1 / logₐb,可以判断 logₐ1 = 0。
推论四: logaa = 1根据换底公式 logₐa = logₐa / logₐb,可以判断 logₐa = 1推论五: log(ab) = loga + logb根据换底公式 logₐb = logcₐ / logcₒb,取c = a * b,并将logcₐ化简为loga + logb,可得 log(ab) = loga + logb。
推论六: log(b/c) = logb - logc根据换底公式 logₐ(b/c) = logcₐ / logcₒ(b/c),取c = b,logcₐ化简为1 / logbₐ,logcₒ(b/c)化简为logbₒ(b) - logbₒ(c),可得 log(b/c) = logb - logc。
常用三角函数转换公式

常用三角函数转换公式三角函数转换公式汇总锐角三角函数公式sinα=∠α的对边/斜边cosα=∠α的邻边/斜边tanα=∠α的对边/∠α的邻边cotα=∠α的邻边/∠α的对边倍角公式Sin2A=2SinA?CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=(2tanA)/(1-tanA^2)(注:SinA^2是sinA的平方sin2(A))三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a=tana·tan(π/3+a)·tan(π/3-a)一个特殊公式(sina+sinθ)*(sina-sinθ)=sin(a+θ)*sin(a-θ)证明:(sina+sinθ)*(sina-sinθ)=2sin[(θ+a)/2]cos[(a-θ)/2]*2cos[(θ+a)/2]sin[(a-θ)/2]=sin(a+θ)*sin(a-θ)坡度公式我们通常半坡面的铅直高度h与水平高度l的比叫做坡度(也叫坡比),用字母i表示,即i=h/l,坡度的一般形式写成l:m形式,如i=1:5.如果把坡面与水平面的夹角记作a(叫做坡角),那么i=h/l=tana.常用三角函数公式1.万能公式令tan(a/2)=tsina=2t/(1+t^2)cosa=(1-t^2)/(1+t^2)tana=2t/(1-t^2)2.辅助角公式asint+bcost=(a^2+b^2)^(1/2)sin(t+r) cosr=a/[(a^2+b^2)^(1/2)]sinr=b/[(a^2+b^2)^(1/2)]tanr=b/a3.两角和差公式:sin(AB)=sinAcosBcosAsinBcos(AB)=cosAcosBsinAsinBtan(AB)=(tanAtanB)/(1tanAtanB)cot(AB)=(cotAcotB1)/(cotBcotA)4.半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA); cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA. sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a)) 5.积化和差sina*cosb=[sin(a+b)+sin(a-b)]/2cosa*sinb=[sin(a+b)-sin(a-b)]/2cosa*cosb=[cos(a+b)+cos(a-b)]/2sina*sinb=-[cos(a+b)-cos(a-b)]/26.和差化积sina+sinb=2sin[(a+b)/2]cos[(a-b)/2]sina-sinb=2sin[(a-b)/2]cos[(a+b)/2]cosa+cosb=2cos[(a+b)/2]cos[(a-b)/2] cosa-cosb=-2sin[(a+b)/2]sin[(a-b)/2]。
(整理)初等函数 三角函数

函数y=tanx,x∈(-π/2,π/2)的反函数,记作y=arctanx,叫做反正切函数。
反正切函数是反三角函数的一种。
同样,由于正切函数y=tanx在定义域上不具有一一对应的关系,所以不存在反函数。
注意这里选取是正切函数的一个单调区间。
1,定义域:R值域:(-π/2,π/2)单调性:增函数奇偶性:奇函数周期性:不是周期函数2,arctan(x+y) <= arctanx + arctany = arctan[Tan(arctanx + arctany)] = arctan[(x+y)/(1-xy)]反正切函数的大致图像如图所示,显然与函数y=tanx,x∈(-π/2,π/2)关于直线y=x 对称,且渐近线为y=π/2和y=-π/2反三角函数反三角函数主要是三个:y=arcsin(x),定义域[-1,1] ,值域[-π/2,π/2]图象用红色线条;y=arccos(x),定义域[-1,1] ,值域[0,π],图象用蓝色线条;y=arctan(x),定义域(-∞,+∞),值域(-π/2,π/2),图象用绿色线条;y=arccot(x),定义域(-∞,+∞),值域(0,π),图象用绿色线条;sin(arcsin x)=x,定义域[-1,1],值域 [-1,1] arcsin(-x)=-arcsinx 证明方法如下:设arcsin(x)=y,则sin(y)=x ,将这两个式子代入上式即可得其他几个用类似方法可得cos(arccos x)=x, arccos(-x)=π-arccos xtan(arctan x)=x, arctan(-x)=-arctanx反三角函数其他公式cos(arcsinx)=根号下1-x^2arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin(arcsinx)=cos(arccosx)=tan(arctanx)=cot(arccotx)=x当x∈[-π/2, π/2] 有arcsin(sinx)=xx∈[0,π], arccos(cosx)=xx∈(-π/2, π/2), arctan(tanx)=xx∈(0, π), arccot(cotx)=xx>0, arctanx=π/2-arctan1/x, arccotx类似若(arctanx+arctany)∈(-π/2, π/2), 则arctanx+arctany=arctan(x+y/1-xy)一般地,如果a(a大于0,且a不等于1)的b次幂等于N,那么数b叫做以a 为底N的对数,记作log aN=b,读作以a为底N的对数,其中a叫做对数的底数,N叫做真数。
三角函数转换公式大全

三角函数转换公式大全三角函数是高中数学中的重要内容,它们在数学和物理学中有着广泛的应用。
在学习三角函数的过程中,我们经常会遇到需要进行三角函数的转换,而掌握三角函数的转换公式是十分重要的。
本文将为大家详细介绍三角函数的转换公式,希望能对大家的学习有所帮助。
1. 正弦函数转换公式。
正弦函数是三角函数中的一种基本函数,其转换公式包括:(1)正弦函数的奇偶性,sin(-x)=-sinx,sin(π-x)=sinx;(2)正弦函数的周期性,sin(x+2kπ)=sinx,其中k为整数;(3)正弦函数的同角变换,sin(π/2-x)=cosx,sin(π/2+x)=cosx。
2. 余弦函数转换公式。
余弦函数也是三角函数中的一种基本函数,其转换公式包括:(1)余弦函数的奇偶性,cos(-x)=cosx,cos(π-x)=-cosx;(2)余弦函数的周期性,cos(x+2kπ)=cosx,其中k为整数;(3)余弦函数的同角变换,cos(π/2-x)=sinx,cos(π/2+x)=-sinx。
3. 正切函数转换公式。
正切函数是三角函数中的另一种基本函数,其转换公式包括:(1)正切函数的奇偶性,tan(-x)=-tanx,tan(π-x)=-tanx;(2)正切函数的周期性,tan(x+π)=tanx;(3)正切函数的同角变换,tan(π/2-x)=cotx,tan(π/2+x)=-cotx。
4. 余切函数转换公式。
余切函数是三角函数中的第四种基本函数,其转换公式包括:(1)余切函数的奇偶性,cot(-x)=-cotx,cot(π-x)=-cotx;(2)余切函数的周期性,cot(x+π)=cotx;(3)余切函数的同角变换,cot(π/2-x)=tanx,cot(π/2+x)=-tanx。
5. 正割函数和余割函数转换公式。
正割函数和余割函数是三角函数中的补充函数,其转换公式包括:(1)正割函数的奇偶性,sec(-x)=secx,sec(π-x)=-secx;(2)正割函数的周期性,sec(x+2kπ)=secx,其中k为整数;(3)余割函数的奇偶性,csc(-x)=-cscx,csc(π-x)=-cscx;(4)余割函数的周期性,csc(x+2kπ)=cscx,其中k为整数。
高一数学三角函数公式推导及三角函数公式

由基本性质4可得
log(a^n)(b^m)=[n*ln(a)]/[m*ln(b)]=(m/n)*{[ln(a)]/[ln(b)]}
再由换底公式
log(a^n)(b^m)=m/n*[log(a)(b)]
--------------------------------------------(性质及推导完)
tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)
tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)
·辅助角公式:
Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中
sint=B/(A^2+B^2)^(1/2)
tanα=sinα*secα
cotα=cosα*cscα
secα=tanα*cscα
cscα=secα*cotα
·倒数关系:
tanα·cotα=1
sinα·cscα=1
cosα·secα=1
直角三角形ABC中,
角A的正弦值就等于角A的对边比斜边,
所以log(a)(N)=log(b)(N)/log(b)(a)
性质二:(不知道什么名字)
log(a^n)(b^m)=m/n*[log(a)(b)]
推导如下
由换底公式[lnx是log(e)(x),e称作自然对数的底]
log(a^n)(b^m)=ln(a^n)/ln(b^n)
余弦等于角A的邻边比斜边
正切等于对边比邻边,
三角函数恒等变形公式
·两角和与差的三角函数:
cos(α+β)=cosα·cosβ-sinα·sinβ
新课标高中三角函数公式汇总

M = log a M − log a N ; N
n
(3) log a M = n log a M ( n ∈ R ) .
新课标高中三角函数公式汇总
1、诱导公式
2kπ + α → α : sin(2kπ + α ) = sin α , cos(2kπ + α ) = cos α , tan(2kπ + α ) = tan α
π
2
− α → α : sin(
π
2
− α ) = cos α
, cos(
π
2
− α ) = sin α ,
α +β
2
sin
α −β
2
2 2 a b c 8、正弦定理 = = = 2R sin A sin B sin C
9、余弦定理
cos α + cos β = 2 cos
α +β
cos
α −β
,
α +β
2
sin
α −β
2
a 2 = b 2 + c 2 − 2bc cos A ; b 2 = c 2 + a 2 − 2ca cos B ; 1 1 1 10、面积定理 S = ab sin C = bc sin A = ca sin B . 2 2 2
, cos(
tan(
− α → α : sin(−α ) = − sin α ,
cos(−α ) = cos α ,
tan(−α ) = − tan α
换底公式的6个推论

换底公式的6个推论换底公式是初中数学中的重要知识点,它是解决三角函数的周期性问题的有力工具。
换底公式有6个推论,本文将逐个介绍并解释这些推论的应用。
1. 推论一:sin(x) = cos(90° - x)换底公式的第一个推论是sin函数与cos函数的关系。
根据三角函数的定义,sin(x)表示角度x的正弦值,cos(x)表示角度x的余弦值。
推论一指出,对于任意角度x来说,它的正弦值等于90°减去该角度的余弦值。
这个推论的应用十分广泛,可以用来简化计算,特别是在求解不同角度的三角函数值时。
2. 推论二:cos(x) = sin(90° - x)推论二是推论一的逆命题,它指出,对于任意角度x来说,它的余弦值等于90°减去该角度的正弦值。
这个推论可以与推论一一起使用,互相验证结果的正确性。
3. 推论三:tan(x) = cot(90° - x)推论三是tan函数与cot函数的关系。
tan(x)表示角度x的正切值,cot(x)表示角度x的余切值。
推论三说明,对于任意角度x来说,它的正切值等于90°减去该角度的余切值。
这个推论可以用来简化计算,特别是在求解不同角度的三角函数值时。
4. 推论四:cot(x) = tan(90° - x)推论四是推论三的逆命题,它指出,对于任意角度x来说,它的余切值等于90°减去该角度的正切值。
这个推论可以与推论三一起使用,互相验证结果的正确性。
5. 推论五:sec(x) = csc(90° - x)推论五是sec函数与csc函数的关系。
sec(x)表示角度x的正割值,csc(x)表示角度x的余割值。
推论五说明,对于任意角度x来说,它的正割值等于90°减去该角度的余割值。
这个推论可以用来简化计算,特别是在求解不同角度的三角函数值时。
6. 推论六:csc(x) = sec(90° - x)推论六是推论五的逆命题,它指出,对于任意角度x来说,它的余割值等于90°减去该角度的正割值。
三角函数公式大全

三角函数诱导公式常用的诱导公式有以下几组:公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanα诱导公式记忆口诀※规律总结※上面这些诱导公式可以概括为:对于k·π/2±α(k∈Z)的个三角函数值,①当k是偶数时,得到α的同名函数值,即函数名不改变;②当k是奇数时,得到α相应的余函数值,即sin→cos;cos→sin;tan→cot,cot→tan.(奇变偶不变)然后在前面加上把α看成锐角时原函数值的符号。
(符号看象限)例如:sin(2π-α)=sin(4·π/2-α),k=4为偶数,所以取sinα。
三角函数转化公式

三角函数转化公式:倒数关系:tanα·cotα=1sinα·cscα=1cosα·secα=1商的关系:sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα平方关系:sin^2(α)+cos^2(α)=11+tan^2(α)=sec^2(α)1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式sin^2(α)+cos^2(α)=1tan α *cot α=1一个特殊公式(sina+sinθ)*(sina-sinθ)=sin(a+θ)*sin (a-θ)证明:(sina+sinθ)*(sina-sinθ)=2 sin[(θ+a)/2] cos[(a-θ)/2] *2 cos[(θ+a)/2] sin[(a-θ)/2]=sin(a+θ)*sin(a-θ)坡度公式我们通常半坡面的铅直高度h与水平高度l的比叫做坡度(也叫坡比), 用字母i表示,即 i=h / l, 坡度的一般形式写成 l : m 形式,如i=1:5.如果把坡面与水平面的夹角记作a(叫做坡角),那么 i=h/l=tan a.锐角三角函数公式正弦: sin α=∠α的对边/∠α的斜边余弦:cos α=∠α的邻边/∠α的斜边正切:tan α=∠α的对边/∠α的邻边余切:cot α=∠α的邻边/∠α的对边二倍角公式正弦sin2A=2sinA·cosA余弦1.Cos2a=Cos^2(a)-Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1即Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1=1-2Sin^2(a) 正切tan2A=(2tanA)/(1-tan^2(A))三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a) 三倍角公式推导sin(3a)=sin(a+2a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin^3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-cos^a)cosa=4cos^3a-3cosasin3a=3sina-4sin^3a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos^3a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)^2]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[ (a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)现列出公式如下: sin2α=2sinαcosα tan2α=2tanα/(1-tan^2(α)) cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) 可别轻视这些字符,它们在数学学习中会起到重要作用.包括一些图像问题和函数问题中三倍角公式sin3α=3sinα-4sin^3(α)=4sinα·sin(π/3+α)sin(π/3-α) cos3α=4cos^3(α)-3cosα=4cos α·cos(π/3+α)cos(π/3-α) tan3α=tan(α)*(-3+tan(α)^2)/(-1+3*tan(α)^2)=tan a · tan(π/3+a)· tan(π/3-a)半角公式sin^2(α/2)=(1-cosα)/2 cos^2(α/2)=(1+cos α)/2 tan^2(α/2)=(1-cosα)/(1+cosα) tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα万能公式sinα=2tan(α/2)/[1+tan^2(α/2)] cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)] tanα=2tan(α/2)/[1-tan^2(α/2)]其他sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0 cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2 tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0四倍角公式sin4A=-4*(cosA*sinA*(2*sinA^2-1))cos4A=1+(-8*cosA^2+8*cosA^4)tan4A=(4*tanA-4*tanA^3)/(1-6*tanA^2+tanA^4)五倍角公式sin5A=16sinA^5-20sinA^3+5sinAcos5A=16cosA^5-20cosA^3+5cosAtan5A=tanA*(5-10*tanA^2+tanA^4)/(1-10*tanA^2+5 *tanA^4)六倍角公式sin6A=2*(cosA*sinA*(2*sinA+1)*(2*sinA-1)*(-3+4 *sinA^2))cos6A=((-1+2*cosA^2)*(16*cosA^4-16*cosA^2+1)) tan6A=(-6*tanA+20*tanA^3-6*tanA^5)/(-1+15*tanA ^2-15*tanA^4+tanA^6)七倍角公式sin7A=-(sinA*(56*sinA^2-112*sinA^4-7+64*sinA^6 ))cos7A=(cosA*(56*cosA^2-112*cosA^4+64*cosA^6-7)) tan7A=tanA*(-7+35*tanA^2-21*tanA^4+tanA^6)/(-1 +21*tanA^2-35*tanA^4+7*tanA^6)八倍角公式sin8A=-8*(cosA*sinA*(2*sinA^2-1)*(-8*sinA^2+8* sinA^4+1))cos8A=1+(160*cosA^4-256*cosA^6+128*cosA^8-32*c osA^2)tan8A=-8*tanA*(-1+7*tanA^2-7*tanA^4+tanA^6)/(1 -28*tanA^2+70*tanA^4-28*tanA^6+tanA^8)九倍角公式sin9A=(sinA*(-3+4*sinA^2)*(64*sinA^6-96*sinA^4 +36*sinA^2-3))cos9A=(cosA*(-3+4*cosA^2)*(64*cosA^6-96*cosA^4 +36*cosA^2-3))tan9A=tanA*(9-84*tanA^2+126*tanA^4-36*tanA^6+t anA^8)/(1-36*tanA^2+126*tanA^4-84*tanA^6+9*tan A^8)十倍角公式sin10A=2*(cosA*sinA*(4*sinA^2+2*sinA-1)*(4*sin A^2-2*sinA-1)*(-20*sinA^2+5+16*sinA^4))cos10A=((-1+2*cosA^2)*(256*cosA^8-512*cosA^6+3 04*cosA^4-48*cosA^2+1))tan10A=-2*tanA*(5-60*tanA^2+126*tanA^4-60*tanA^6+5*tanA^8)/(-1+45*tanA^2-210*tanA^4+210*tanA ^6-45*tanA^8+tanA^10)N倍角公式根据棣美弗定理,(cosθ+ i sinθ)^n = cos(n θ)+ i sin(nθ) 为方便描述,令sinθ=s,cosθ=c考虑n为正整数的情形: cos(nθ)+ i sin(nθ) = (c+ i s)^n = C(n,0)*c^n + C(n,2)*c^(n-2)*(i s)^2 + C(n,4)*c^(n-4)*(i s)^4 + ... +C(n,1)*c^(n-1)*(i s)^1 + C(n,3)*c^(n-3)*(i s)^3 +C(n,5)*c^(n-5)*(i s)^5 + ... =>比较两边的实部与虚部实部:cos(nθ)=C(n,0)*c^n +C(n,2)*c^(n-2)*(i s)^2 + C(n,4)*c^(n-4)*(i s)^4 + ... i*(虚部):i*sin(nθ)=C(n,1)*c^(n-1)*(i s)^1 + C(n,3)*c^(n-3)*(i s)^3 +C(n,5)*c^(n-5)*(i s)^5 + ... 对所有的自然数n, 1. cos(nθ):公式中出现的s都是偶次方,而s^2=1-c^2(平方关系),因此全部都可以改成以c(也就是cosθ)表示. 2. sin(nθ): (1)当n是奇数时:公式中出现的c都是偶次方,而c^2=1-s^2(平方关系),因此全部都可以改成以s(也就是sinθ)表示. (2)当n是偶数时:公式中出现的c都是奇次方,而c^2=1-s^2(平方关系),因此即使再怎么换成s,都至少会剩c(也就是 cosθ)的一次方无法消掉. (例.c^3=c*c^2=c*(1-s^2),c^5=c*(c^2)^2=c*(1-s^2)^2) 半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a)) 和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtan B)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtan B)两角和公式tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)tan(α-β)=(tanα-tanβ)/(1+tanαtanβ)cos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβsin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ -cosαsinβ积化和差sinαsinβ =-[cos(α+β)-cos(α-β)] /2cosαcosβ = [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2cosαsinβ = [sin(α+β)-sin(α-β)]/2双曲函数sh a = [e^a-e^(-a)]/2ch a = [e^a+e^(-a)]/2th a = sin h(a)/cos h(a)公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)= sinαtan(2kπ+α)= tanαcot(2kπ+α)= cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三:任意角α与 -α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tanαcot(2π-α)= -cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)= cosαcos(π/2+α)= -sinαtan(π/2+α)= -cotαcot(π/2+α)= -tanαsin(π/2-α)= cosαcos(π/2-α)= sinαtan(π/2-α)= cotαcot(π/2-α)= tanαsin(3π/2+α)= -cosαcos(3π/2+α)= sinαtan(3π/2+α)= -cotαcot(3π/2+α)= -tanαsin(3π/2-α)= -cosαcos(3π/2-α)= -sinαtan(3π/2-α)= cotαcot(3π/2-α)= tanα(以上k∈Z)A·sin(ωt+θ)+ B·sin(ωt+φ) =√{(A² +B² +2ABcos(θ-φ)} · sin{ ωt + arcsin[ (A·sinθ+B·sinφ) / √{A^2 +B^2; +2ABcos(θ-φ)} }√表示根号,包括{……}中的内容三角函数的诱导公式(六公式)公式一sin(-α) = -sinαcos(-α) = cosαtan (-α)=-tanα公式二sin(π/2-α) = cosαcos(π/2-α) = sinα公式三 sin(π/2+α) = cosαcos(π/2+α) = -sinα公式四sin(π-α) = sinαcos(π-α) = -cosα公式五sin(π+α) = -sinαcos(π+α) = -cosα公式六tanA= sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍:奇变偶不变,符号看象限万能公式sinα=2tan(α/2)/[1+(tan(α/2))²]cosα=[1-(tan(α/2))²]/[1+(tan(α/2))²]tanα=2tan(α/2)/[1-(tan(α/2))²]其它公式(1) (sinα)^2+(cosα)^2=1(平方和公式)(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2证明下面两式,只需将一式,左右同除(sinα)^2,第二个除(cosα)^2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2) cot(C/2)(7)(cosA)^2;+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)(sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC 其他非重点三角函数csc(a) = 1/sin(a)sec(a) = 1/cos(a)(seca)^2+(csca)^2=(seca)^2(csca)^2。
三角函数公式定理及其推导两种方法
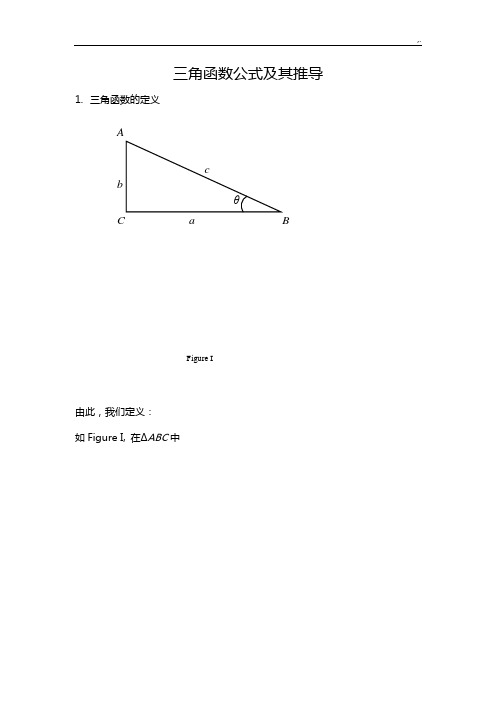
三角函数公式及其推导1.三角函数的定义AcbθC a BFigure I由此,我们定义:如Figure I, 在ΔABC中sin () cos () tan ()11 cot ()tan 11 sec ()cos 11 csc ()sin b c ac ba ab b ac a a cc b b cθθθθθθθθθθθθθθθ∠=∠=∠=∠===∠===∠===对边的正弦值:斜边邻边的余弦值:斜边对边的正切值:邻边邻边的余切值:对边斜边的正割值:邻边斜边的余割值:对边 备注:当用一个字母或希腊字母表示角时,可略写∠符号,但用三个子母表示时,不能省略。
在本文中,我们只研究sin 、cos 、tan 。
2. 额外的定义222222sin (sin )cos (cos )tan (tan )θθθθθθ===3. 简便计算公式22sin cos cos(90)cos sin sin(90)111tan tan tan(90)sin cos 1bA c cA b b a a A bθθθθθθθθ===-∠===-∠====-∠+=o o o 证明:2222222222901sin sin 1sin cos 1ABC ABC a b c a b c cB A θθ∆∠=∴+=∴+=∴+=∴+=o Q 在中,证完222222sin tan cos sin cos 1tan 1cos cos cos b b c a a cθθθθθθθθθ===+=+=4. 任意三角形的面积公式Ca b hd e如Figure II ,121sin 21sin ()2ABC S ah ab C ac B ∆===两边和其夹角正弦的乘积 5. 余弦定理:任意三角形一角的余弦等于两邻边的平方和减对边的平方之差与两邻边积的两倍之比。
证明:如Figure II,2222222222222222222222(cos )(sin )2cos cos sin =2cos (cos sin )2cos cos 22b d h a c B c B a ac B c B c Ba ac B c B B a c ac Bb ac a c b B ac ac=+=-+=-++-++=+---+-⇒==- 证完Figure II6. 海伦公式 证明:如Figure II ,1sin 212121212ABC S ab C∆=========2ABC a b c s S ∆===++=设:7. 正弦定理如 Figure III ,c 为ΔABC 外接圆的直径,sin 2 sin a A ca c r r ABC A=∴==∆Q (为的外接圆半径)同理:, sin sin 2sin sin sin b c c c B Ca b c r A B C ==∴===8.加法定理(1)两角差的余弦Figure IV 如Figure IV,AOC BOC AOB αβαβ∠=∠∠=∠∠=∠-∠令AO=BO=r点A 的横坐标为cos A x r α= 点A 的纵坐标为sin A y r α= 点B 的横坐标为cos B x r β= 点B 的纵坐标为sin B y r β=()()()()()()22222222222222222222222222sin sin cos cos sin sin 2sin sin cos cos 2cos cos sin sin 2sin sin cos cos 2cos cos sin cos sin cos 2sin sin 2cos cos 112s A B A B AB y y x x r r r r r r r r r r r r r αββααβαβαβαβαβαβαβαβααββαβαβ=-+-=-+-=+-++-=+-++-=+++--=+-()()()22in sin cos cos 22sin sin cos cos 21sin sin cos cos r r αβαβαβαβαβαβ+⎡⎤⎣⎦=-+⎡⎤⎣⎦=-+⎡⎤⎣⎦由余弦公式可得:()()()()2222222222cos 2cos 22cos 22cos 21cos AB AC BC AC BC ACBr r r r r r r r αβαβαβαβ=+-⋅∠=++⋅-=+-=--⎡⎤⎣⎦=--⎡⎤⎣⎦综上得:()cos sin sin cos cos αβαβαβ-=+ (2) 两角和的余弦()()()()cos cos sin sin cos cos sin sin cos cos cos cos sin sin αβαβαβαβαβαβαβαβ+=--⎡⎤⎣⎦=-+-=-+=-(3) 两角和的正弦()()()()()sin cos 90cos 90sin 90sin cos 90cos cos sin sin cos αβαβαβαβαβαβαβ+=︒-+⎡⎤⎣⎦=︒--⎡⎤⎣⎦=︒-+︒-=+(4) 两角差的正弦()()()()sin sin cos sin sin cos cos sin sin cos sin cos cos sin αβαβαβαβαβαβαβαβ-=+-⎡⎤⎣⎦=-+-=-+=-(5) 两角和的正切()()()sin tan cos cos sin sin cos cos cos sin sin cos sin sin cos cos cos cos cos sin sin cos cos sin sin cos cos sin sin 1cos cos tan tan 1tan tan αβαβαβαβαβαβαβαβαβαβαβαβαββαβααβαβαβαβ++=++=-+=-+=-+=- (6) 两角差的正切()()()()tan tan tan tan 1tan tan tan tan 1tan tan αβαβαβαβαβαβ-=+-⎡⎤⎣⎦+-=---=+ 9. 两倍角公式()()()()()()()222222222222sin 2sin sin cos sin cos 2sin cos cos 2cos cos cos sin sin cos sin 12sin 2cos 1sin 2tan 2cos 22sin cos cos sin 2sin cos cos cos sin cos 2sin cos sin 1cos 2tan 1ta αααααααααααααααααααααααααααααααααααααα=+=+==+=-=-=-=-==-=-=-=-2n α10. 积化和差公式()()()()1sin cos 2sin cos 21sin cos sin cos cos sin cos sin 21sin sin 2αβαβαβαβαβαβαβαβ==++-=++-⎡⎤⎣⎦()()()()()()()()1cos cos 2cos cos 21cos cos cos cos sin sin sin sin 21cos cos 21sin sin 2sin sin 21sin sin sin sin cos cos cos cos 21cos cos 2αβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβ==++-=++-⎡⎤⎣⎦==++-=+--⎡⎤⎣⎦ 11. 和差化积公式 (1)设:A=α+β, B=α-β,()()()()sin sin sin sin sin cos cos sin sin cos cos sin 2sin cos 2sin cos 222sin cos 22sin sin sin sin sin cos cos sin sin cos cos sin 2cos si A B A B A B A B αβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβα+=++-=++-=++-+--⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭+-⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭-=+--=+-+=n 2cos sin 222cos sin 22A B A B βαβαβαβαβ++-+-+⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭+-⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭(2)设:cos sin αα==∵22cos sin 1αα+=()()sin sin coscos sin sin cossinsin baθθθθαθαθαθ+=+=+=+12.其他常用公式()()()()()()()()()()()()()()000sin 360sin cos 360cos tan 360tan sin 90cos cos 90sin 1tan 90tan sin 90cos cos 90sin 1tan 90tan sin 90cos cos 90sin 1tan 90tan sin 180sin cos 180cos n n n θθθθθθθθθθθθθθθθθθθθθθθθθθθ+⨯=+⨯=+⨯=︒-=︒-=︒-=︒+=︒+=-︒+=--︒=--︒=-︒=-︒-=︒-=-()()()()()()()()tan 180tan sin 180sin cos 180cos tan 180tan sin sin cos cos tan tan tan 2190 1cos 1cos 11sin 1sin 1n θθθθθθθθθθθθθθθθθθθ︒-=-±︒=-±︒=-±︒=-=--=-=-+⨯︒⎡⎤⎣⎦-≤≤⇒≤-≤≤⇒≤不存在13. 特殊的三角函数值14. 关于机器算法在计算机中,三角函数的算法是这样的,其中x 用弧度计算()()13572102460sin 1!3!5!7!21!cos 0!2!4!6!2!n n nn x x x x x x n x x x x x x n +=∞=∞=-+-+=+=-+-+=∑∑L L推导公式:(a+b+c)/(sinA+sinB+sinC)=2R(其中,R为外接圆半径) 由正弦定理有a/sinA=b/sinB=c/sinC=2R所以a=2R*sinAb=2R*sinBc=2R*sinC加起来a+b+c=2R*(sinA+sinB+sinC)带入(a+b+c)/(sinA+sinB+sinC)=2R*(sinA+sinB+sinC)/(sinA+sinB+sinC)=2R 两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-cosAsinBcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)cot(A+B)=(cotAcotB-1)/(cotB+cotA)cot(A-B)=(cotAcotB+1)/(cotB-cotA)倍角公式Sin2A=2SinA?CosA对数的性质及推导用^表示乘方,用log(a)(b)表示以a为底,b的对数*表示乘号,/表示除号定义式:若a^n=b(a>0且a≠1)则n=log(a)(b)基本性质:1.a^(log(a)(b))=b2.log(a)(MN)=log(a)(M)+log(a)(N);3.log(a)(M/N)=log(a)(M)-log(a)(N);4.log(a)(M^n)=nlog(a)(M)推导1.这个就不用推了吧,直接由定义式可得(把定义式中的[n=log(a)(b)]带入a^n=b)2.MN=M*N由基本性质1(换掉M和N)a^[log(a)(MN)]=a^[log(a)(M)]*a^[log(a)(N)]由指数的性质a^[log(a)(MN)]=a^{[log(a)(M)]+[log(a)(N)]}又因为指数函数是单调函数,所以log(a)(MN)=log(a)(M)+log(a)(N)3.与2类似处理MN=M/N由基本性质1(换掉M和N)a^[log(a)(M/N)]=a^[log(a)(M)]/a^[log(a)(N)] 由指数的性质a^[log(a)(M/N)]=a^{[log(a)(M)]-[log(a)(N)]} 又因为指数函数是单调函数,所以log(a)(M/N)=log(a)(M)-log(a)(N)4.与2类似处理M^n=M^n由基本性质1(换掉M)a^[log(a)(M^n)]={a^[log(a)(M)]}^n由指数的性质a^[log(a)(M^n)]=a^{[log(a)(M)]*n}又因为指数函数是单调函数,所以log(a)(M^n)=nlog(a)(M)其他性质:性质一:换底公式log(a)(N)=log(b)(N)/log(b)(a)推导如下N=a^[log(a)(N)]a=b^[log(b)(a)]综合两式可得N={b^[log(b)(a)]}^[log(a)(N)]=b^{[log(a)(N)]*[log(b)(a)]}又因为N=b^[log(b)(N)]所以b^[log(b)(N)]=b^{[log(a)(N)]*[log(b)(a)]}所以log(b)(N)=[log(a)(N)]*[log(b)(a)]{这步不明白或有疑问看上面的} 所以log(a)(N)=log(b)(N)/log(b)(a)性质二:(不知道什么名字)log(a^n)(b^m)=m/n*[log(a)(b)]推导如下由换底公式[lnx是log(e)(x),e称作自然对数的底]log(a^n)(b^m)=ln(a^n)/ln(b^n)由基本性质4可得log(a^n)(b^m)=[n*ln(a)]/[m*ln(b)]=(m/n)*{[ln(a)]/[ln(b)]} 再由换底公式log(a^n)(b^m)=m/n*[log(a)(b)]--------------------------------------------(性质及推导完)公式三:log(a)(b)=1/log(b)(a)证明如下:由换底公式log(a)(b)=log(b)(b)/log(b)(a)----取以b为底的对数,log(b)(b)=1=1/log(b)(a)还可变形得:log(a)(b)*log(b)(a)=1平方关系:sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)·商的关系:tanα=sinα/cosαcotα=cosα/sinα·倒数关系:tanα·cotα=1sinα·cscα=1cosα·secα=1万能公式:sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]常用的诱导公式有以下几组:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:cos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα一般的最常用公式有:Sin(A+B)=SinA*CosB+SinB*CosASin(A-B)=SinA*CosB-SinB*CosACos(A+B)=CosA*CosB-SinA*SinBCos(A-B)=CosA*CosB+SinA*SinBTan(A+B)=(TanA+TanB)/(1-TanA*TanB) Tan(A-B)=(TanA-TanB)/(1+TanA*TanB) 平方关系:sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)·积的关系:sinα=tanα*cosαcosα=cotα*sinαtanα=sinα*secαsecα=tanα*cscαcscα=secα*cotα·倒数关系:tanα·cotα=1sinα·cscα=1cosα·secα=1直角三角形ABC中,角A的正弦值就等于角A的对边比斜边, 余弦等于角A的邻边比斜边正切等于对边比邻边,三角函数恒等变形公式·两角和与差的三角函数:cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·辅助角公式:Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)·倍角公式:sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) tan(2α)=2tanα/[1-tan^2(α)]·三倍角公式:sin(3α)=3sinα-4sin^3(α)cos(3α)=4cos^3(α)-3cosα·半角公式:sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)·降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2 cos^2(α)=(1+cos(2α))/2=vercos(2α)/2 tan^2(α)=(1-cos(2α))/(1+cos(2α)) ·万能公式:sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)] tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)] cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)] cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)] sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)] ·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·其他:sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0部分高等内容·高等代数中三角函数的指数表示(由泰勒级数易得):sinx=[e^(ix)-e^(-ix)]/(2i)cosx=[e^(ix)+e^(-ix)]/2tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)]泰勒展开有无穷级数,e^z=exp(z)=1+z/1!+z^2/2!+z^3/3!+z^4/4!+…+z^n/n!+…·三角函数作为微分方程的解:对于微分方程组y=-y'';y=y'''',有通解Q,可证明Q=Asinx+Bcosx,因此也可以从此出发定义三角函数。
三角函数指数函数与对数函数公式

三角函数指数函数与对数函数公式三角函数、指数函数和对数函数都是数学中重要的函数类型。
它们在各个科学领域中都有广泛的应用。
本文将从定义、性质、公式和应用等方面对三角函数、指数函数和对数函数进行详细介绍。
一、三角函数1.定义和性质三角函数是以单位圆上的点为基础,通过对角度的测量来定义的函数。
常见的三角函数包括正弦函数(sin)、余弦函数(cos)、正切函数(tan),以及它们的倒数函数:余切函数(cot)、正割函数(sec)和余割函数(csc)。
三角函数的定义和性质如下:- 正弦函数的定义:在单位圆上,点P的横坐标就是角度弧度的正弦值,即sinθ = y;- 余弦函数的定义:在单位圆上,点P的纵坐标就是角度弧度的余弦值,即cosθ = x;- 正切函数的定义:在单位圆上,点P的横纵坐标比值就是角度弧度的正切值,即tanθ = y /x;- 周期性:三角函数均具有周期性,即sin(θ + 2πk) = sinθ、cos(θ + 2πk) = cosθ、tan(θ + πk) = tanθ,其中k为整数。
2.重要公式三角函数有很多重要的公式,包括和差公式、倍角公式、半角公式等。
这些公式在解三角函数方程、化简三角函数表达式等方面非常有用。
以下是三角函数的一些重要公式:-和差公式:sin(α ± β) = sinαcosβ ± cosαsinβcos(α ± β) = cosαcosβ ∓ sinαsinβtan(α ± β) = (tanα ± tanβ) / (1 ∓ tanαtanβ)-倍角公式:sin2α = 2sinαcosαcos2α = cos^2α - sin^2αtan2α = (2tanα) / (1 - tan^2α)-半角公式:sin(α/2) = ±√[(1- cosα) / 2]cos(α/2) = ±√[(1 + cosα) / 2]二、指数函数1.定义和性质指数函数是以正实数为底数、以自然对数e为底的指数幂函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数没有换底公式一说,肯定是对数的换底公式:
log换底公式是:loga(N)=logb(N)/logb(a)。
证明:loga(N)=x,则a^x=N,两边取以b为底的对数,
logb(a^x)=logb(N),xlogb(a)=logb(N),x=logb(N)/logb(a),故此,loga(N)=logb(N)/logb(a)。
换底公式:logb(c)=loga(c)/loga(b) 可将不一样底的对数换为同底的对数 (括号前为底数,括号内为真数)如:log3(5)=lg5/lg3 (换为经常会用到对数)log3(5)=ln5/ln3 (换为自然对
数)log8(9)=log5(9)/log5(8) (换为任意数为底的对数,可将5换为任意正数)期望对你有很大帮助
log以a为底b的对数-loga(b)-=logc(b)/logc(a)也可写
lg(b)]/lg(a)其实就是常说的log以10为底b的对数。
换底公式是高中数学经常会用到对数运算公式,可将多异底对数式转化为同底对数式,结合其他的对数运算公式一起使用。
计算中经常会减少计算的难度,更快速的处理高中范围的对数运算。
