第二章拉普拉斯变换
合集下载
第二章 拉普拉斯变换

例5 求正弦函数 f (t ) sin k t
解 ℒ
st
(k R) 的拉氏变换
则
1 f (t ) 0 sin k t e dt 0 sin k t de s t s 1 st st e sin k t k e cos k tdt 0 0 s 1 s t 2 e cos k tdt 0 s 1 st st 2 e cos k t k e sin k tdt 0 0 s
f (t T ) f (t ) (t 0)
当 f (t ) 在一个周期上连续或分段连续时,则有
1 ℒ f (t ) s T 1 e
T
0
f (t )e s t dt
这是求周期函数拉氏变换公式
2.2 拉普拉斯变换的性质
2.2.1 线性性质 ℒ [ f 2 (t )] F2 ( s) , , 常数 设 ℒ [ f1 (t )] F1 ( s) , 则
Re s 0
n t 例4 求幂函数 n 1 的拉氏变换。
解: ℒ t 0
n
n 1 t e dt s n 1
n st
Re s 0
当 n 为正整数时,
n! ℒ t s n 1
n
Re s 0
0
2 k k sin k t e s t dt 2 2 s s
0
sin k t e s t dt
k 所以 ℒ sin k t 2 s k2
Re s 0
2.1.3 周期函数的拉普拉斯变换 可以证明:若 f (t ) 是周期为 T 的周期函数,即
积分变换-2 拉普拉斯变换

f (t + T ) = f (t) t > 0
且 f (t)在一个周期内分段连续,则有 T 1 st F(s) = f (t)e dt (Re s > 0) sT ∫ 0 1 e
2-2 Laplace变换的基本性质 Laplace变换的基本性质
1、线性性质 2、相似性质 3、延迟性质 4、位移性质 5、微分性质 6、积分性质 7、卷积与卷积定理
2-1 Laplace变换的概念 Laplace变换的概念
(1)Laplace变换实际上就是一种单边的广 Laplace变换实际上就是一种单边的广 义的Fourier变换。 义的Fourier变换。 (2)Laplace变换的复反演积分公式: Laplace变换的复反演积分公式 复反演积分公式:
1[F(s)] = 1 β + j∞F(s)est ds (t > 0) f (t) = L 2πj ∫β j∞
2-1 Laplace变换的概念 Laplace变换的概念
如何克服上述两个缺点? (1)单位阶跃函数
1, t ≥ 0 H(t) = 0, t < 0 用H(t)乘以 f (t),这样得到的 f (t)H(t),在
t < 0时就等于零,在 t ≥ 0 时仍为 f (t) , 就有可能使其积分区间由 ( ∞,+∞) 变为 [0,+∞)
2-1 Laplace变换的概念 Laplace变换的概念
Fourier变换的局限: Fourier变换的局限: (1)绝对可积的条件较强,许多简单的常见函数 (如单位阶跃函数、正弦函数、余弦函数以及线 性函数等)都不满足这个条件,都不能作古典的 Fourier变换。 Fourier变换。 (2)可以进行Fourier变换的函数必须在整个数轴 )可以进行Fourier变换的函数必须在整个数轴 上有定义,但在物理和无线电技术等实际应用中, 许多以时间t 许多以时间t作为自变量的函数往往在 t <0 时是无意义的或是不需要考虑的,像这样的函数 都不能取Fourier变换。 都不能取Fourier变换。
第二章 拉普拉斯变换

k 解:已知 L[sin kt ] = 2 由位移性质得 2 s +k
k L[e sin kt ] = ( s + a)2 + k 2 ì 0 t< t ï ï 例 3 求函数 u (t - t ) = í ï ï î1 t> t
- at
的 Laplace 变换
解:已知 L[u (t )] =
1 s
s= sk
k= 1
f (t ) =
å
n
Re s[ F ( s)e st ]
s = sk
k= 1
例 1 利用留数方法求 F ( s) = s 解: f (t ) = L- 1[
=
s2 + 1
的逆变换
s s st s st ] = e + e 2 s = j 2s s= - j s +1 2s
1 jt (e + e- jt ) = cos t 2
= 1+ (t - 1)et
t> 0
§2.4 卷积
一 、卷积的概念:
f 1 (t ) * f 2 (t ) =
ò
t
0
f1 (t ) f 2 (t - t )d t
交换律 f 1(t ) * f2 (t ) = f2 (t ) * f 1(t ) 结合律 f 1(t ) *[ f2 (t ) * f3 (t )] = [ f 1 (t )*] f2 (t ) * f3 (t ) 对加法的分配率 f 1(t ) *[ f2 (t ) + f3 (t )] = f 1(t ) * f2 (t ) + f 1(t ) * f3 (t ) 二、 卷积定理 设 f 1 (t ) 与 f 2 (t ) 都满足 Laplace 变换存在的条件,且 f (t ) * f 2 (t ) 的 Laplace 变 L[ f1 (t )] = F 1 ( s), L[ f 2 (t )] = F 2 ( s) 则 1 换一定存在,且 L[ f1 (t ) * f2 (t )] = F1 (s) F2 (s) -1 或 L [F1 (s) ?F2 (s)] f1 (t ) * f2 (t )
k L[e sin kt ] = ( s + a)2 + k 2 ì 0 t< t ï ï 例 3 求函数 u (t - t ) = í ï ï î1 t> t
- at
的 Laplace 变换
解:已知 L[u (t )] =
1 s
s= sk
k= 1
f (t ) =
å
n
Re s[ F ( s)e st ]
s = sk
k= 1
例 1 利用留数方法求 F ( s) = s 解: f (t ) = L- 1[
=
s2 + 1
的逆变换
s s st s st ] = e + e 2 s = j 2s s= - j s +1 2s
1 jt (e + e- jt ) = cos t 2
= 1+ (t - 1)et
t> 0
§2.4 卷积
一 、卷积的概念:
f 1 (t ) * f 2 (t ) =
ò
t
0
f1 (t ) f 2 (t - t )d t
交换律 f 1(t ) * f2 (t ) = f2 (t ) * f 1(t ) 结合律 f 1(t ) *[ f2 (t ) * f3 (t )] = [ f 1 (t )*] f2 (t ) * f3 (t ) 对加法的分配率 f 1(t ) *[ f2 (t ) + f3 (t )] = f 1(t ) * f2 (t ) + f 1(t ) * f3 (t ) 二、 卷积定理 设 f 1 (t ) 与 f 2 (t ) 都满足 Laplace 变换存在的条件,且 f (t ) * f 2 (t ) 的 Laplace 变 L[ f1 (t )] = F 1 ( s), L[ f 2 (t )] = F 2 ( s) 则 1 换一定存在,且 L[ f1 (t ) * f2 (t )] = F1 (s) F2 (s) -1 或 L [F1 (s) ?F2 (s)] f1 (t ) * f2 (t )
拉普拉斯变换

L[ f
(n)
(t )]
( n 2)
s n F ( s ) s n 1 f (0) s n 2 f (0) s f s L [ f (t )] s n 1i f ( i ) (0)
n i 0 n 1
(0) f
( n 1)
(0)
L [ t m ] 和 L cos kt , 练习: 利用(2.4)式,求
s 1
①
(m 1) m (m)
② Γ(1) 1
由上述性质,可知当 m为正整数时,有 (m 1) m ! ,
从而当 m 为正整数时,有 (Re (s) > 0)。
m! L [ t ] m 1 s
m
例6 求单位脉冲函数 (t ) 的拉氏变换
注:广义函数 (t )是用“分布”的概念定义的。具体说 来, ) f (t ) (t 满足条件:对任意连续函数 , 成立着 b 当 0 [ a, b] 0 f (t ) (t )dt f (0) 当0 [a, b] a
解:由
(t )
L (t )
的性质,可得
0
(t ) e st dt e st
t 0
1
注意:上式意味着积分区间包含了它的端点。
书上的附录Ⅱ(见 p106)给出了一些常见函数的拉氏变换。 请特别记住以下结果:
①
1 L 1 s
②
(m 1)
s m 1
§2.3 拉普拉斯逆变换( p72)
定理:若 s1、s2、…、sn 是F(s) 所有奇点,且当 s→∞时F(s)→0。则有
f (t ) L1[ F ( s)] Res[ F ( s) e st , sk ]
(n)
(t )]
( n 2)
s n F ( s ) s n 1 f (0) s n 2 f (0) s f s L [ f (t )] s n 1i f ( i ) (0)
n i 0 n 1
(0) f
( n 1)
(0)
L [ t m ] 和 L cos kt , 练习: 利用(2.4)式,求
s 1
①
(m 1) m (m)
② Γ(1) 1
由上述性质,可知当 m为正整数时,有 (m 1) m ! ,
从而当 m 为正整数时,有 (Re (s) > 0)。
m! L [ t ] m 1 s
m
例6 求单位脉冲函数 (t ) 的拉氏变换
注:广义函数 (t )是用“分布”的概念定义的。具体说 来, ) f (t ) (t 满足条件:对任意连续函数 , 成立着 b 当 0 [ a, b] 0 f (t ) (t )dt f (0) 当0 [a, b] a
解:由
(t )
L (t )
的性质,可得
0
(t ) e st dt e st
t 0
1
注意:上式意味着积分区间包含了它的端点。
书上的附录Ⅱ(见 p106)给出了一些常见函数的拉氏变换。 请特别记住以下结果:
①
1 L 1 s
②
(m 1)
s m 1
§2.3 拉普拉斯逆变换( p72)
定理:若 s1、s2、…、sn 是F(s) 所有奇点,且当 s→∞时F(s)→0。则有
f (t ) L1[ F ( s)] Res[ F ( s) e st , sk ]
第二章 拉普拉斯变换

s p1 或s p 2
a3 an a1s a2 s ( s p1 )( s p2 ) 或sp1 p2 ( s pn ) ( s p1 )( s p2 ) ( s p3 )
机械工程控制基础
例8
s 1 已知: F ( s) 3 2 求: f(t) s s s
a1s a2 a3 F ( s) 2 s s 1 s
s s 1
2
1 3 的两个复数根为: j 2 2
将上式两边同乘
s s 1
2
1 3 并令s= 2 j 2
1 3 1 3 得 j a1 ( j ) a 2 2 2 2 2
实部和虚部分别相等,得a1=-1,a2=0
1
6( s 2) 传递函数 ] 若R(s)=1,则 y (t ) L [ 2 s 7 s 12 12 1 6 L [ ] s3 s4 3t 4t 6e 12 e
1
机械工程控制基础
La(t )
0
1 2 st 1 t e dt 3 2 s
0 (t ) t0 t0
(单位)脉冲函数
L (t ) 1
机械工程控制基础
正弦函数 sinωt
Lsin(t ) 2 2 s
余弦函数 cosωt
s Lcos( t ) 2 2 s
3 2
( s 2s 3s 1) x0 ( s) (2s 1) xi ( s)
3 2
2s 1 x0 ( s) 3 机械工程控制基础 xi ( s) 2 s 2s 3s 1
(3) 几种典型时间函数的拉氏变换
单位阶跃函数
机械控制理论基础课件第2章拉普拉斯变换

械的
控位
移
制定
理理
论
若f(t)的拉氏变换为F(s),对于任一 常数a,有
L[eatf (t)] F(s a)
第二章 拉普拉斯变换的数学方法
机微
械分
控
定 理
制
理
论
设f(t)的拉氏变换为F(s),
则 L[df (t)] L[ f '(t)] sF(s) f (0 )
dt
其中f(0+)由正向使t 0时的f(t)值。
第二章 拉普拉斯变换的数学方法Leabharlann 一、复数和复变函数机
两复数相等当且仅当它们的实部和虚部分别相等.
械
复数 z 等于0当且仅当它的实部和虚部同时等于0.
控
说明 两个数如果都是实数,可以比较它们的大小, 如果 不全是实数, 就不能比较大小, 也就是说, 复数不能比
制 较大小.
理 共轭复数:实部相同而虚部绝对值相等符号相反的两
f (0 ) lim f (t) lim sF(s)
t 0
s
证明技巧:可利用微分定理来进
行证明
第二章 拉普拉斯变换的数学方法
机
械
终 值
控定
制理
理
论
若f(t)的拉氏变换为F(s),则终值
定理表示为:
lim f (t) lim sF(s)
t
s0
第二章 拉普拉斯变换的数学方法
机 拉普拉斯(Laplace)变换:
械 时域的微分方程
复数域的代数方程
控 优点:1、用图解法预测系统性能;
制
2、解微分方程时,可同时获得解的瞬态分量
和稳态分量。
理
第二章 拉普拉斯变换

1. 常用函数的拉氏变换
(1) 指数函数
0
t0
f
(t
)
Aet
t0
(2.6)
式中,A和α为常数。
其拉氏变换为
L[ Aet ] Aetestdt A e( s)tdt A
0
0
s
(2.7)
可以看出,指数函数在复平面内将产生一个极点。
第二章 拉普拉斯变换
(2) 阶跃函数
f
(t
)
0 A
t0 t 0
因此,正弦函数的拉氏变换为
L[ Asin t] A (e jt e jt )estdt 2j 0
A 2j
s
1 j
A 2j
s
1 j
A s2 2
(2.17)
类似地, Acost(如图2.3(b)所示)的拉氏变换可以导出如下:
L[ Acost] As s2 2
(2.18)
(5) 脉动函数
A
f
t
图2.1 单位阶跃函数
第二章 拉普拉斯变换
单位阶跃函数 u(t)
0
t0
u(t) 1
t 0
(2.10)
其拉氏变换为
L[u(t)] estdt 1
0
s
(2.11)
实际上,发生于t 0 时的阶跃函数,相当于在时间 t 0时,
把一个定常信号突然加到系统上。高度为A的阶跃函数,即式 (2.8)中的 f (t) ,当其发生在 t 0 时,可以写成 f (t) Au(t) 。
从拉氏变换 F(s)求时间函数 f (t) 的逆变换过程称为拉普拉斯 逆变换,简称为拉氏逆变换,其运算符号为 L1。
L1[F (s)] f (t) 1
教学课件:第二章拉普拉斯变换及其应用

信号处理
在信号处理中,拉普拉斯变换可以用于分析信号的频域特性,例如傅里 叶变换和Z变换等。
03
电路分析
在电路分析中,拉普拉斯变换可以用于分析线性时不变电路的响应,例
如求解一阶和二阶电路的零状态响应。
02 拉普拉斯变换的基本理论
拉普拉斯变换的公式和定理
拉普拉斯变换的定义
对于所有实数$s$,定义函数$f(t)$的拉普拉斯变换为$int_{0}^{infty}f(t)e^{-st}dt$。
拉普拉斯变换的线性性质
如果$f(t)$和$g(t)$的拉普拉斯变换存在,那么对于任意实数$a$和$b$,$(af(t)+bg(t))$的 拉普拉斯变换等于$aF(s)+bG(s)$,其中$F(s)$和$G(s)$分别是$f(t)$和$g(t)$的拉普拉斯变 换。
拉普拉斯变换的延迟性质
如果$f(t)$的拉普拉斯变换存在,那么$f(t-a)$的拉普拉斯变换等于$e^{-as}F(s)$,其中 $F(s)$是$f(t)$的拉普拉斯变换。
拉普拉斯变换的公式为:F(s) = ∫f(t)e^(-st) dt (s为复数,t为 实数)。
拉普拉斯变换的性质
线性性质
如果c1和c2是常数,f1(t)和f2(t) 是任意函数,那么c1f1(t) + c2f2(t)的拉普拉斯变换等于 c1F1(s) + c2F2(s)。
时移性质
如果f(t)的拉普拉斯变换为F(s), 那么f(at-b)的拉普拉斯变换为 a^(-b)F(s/a)。
THANKS FOR WATCHING
感谢您的观看
根轨迹的应用
03
根轨迹分析在控制系统分析和设计中具有重要应用,通过根轨
迹可以判断系统的稳定性、分析系统的性能指标等。
在信号处理中,拉普拉斯变换可以用于分析信号的频域特性,例如傅里 叶变换和Z变换等。
03
电路分析
在电路分析中,拉普拉斯变换可以用于分析线性时不变电路的响应,例
如求解一阶和二阶电路的零状态响应。
02 拉普拉斯变换的基本理论
拉普拉斯变换的公式和定理
拉普拉斯变换的定义
对于所有实数$s$,定义函数$f(t)$的拉普拉斯变换为$int_{0}^{infty}f(t)e^{-st}dt$。
拉普拉斯变换的线性性质
如果$f(t)$和$g(t)$的拉普拉斯变换存在,那么对于任意实数$a$和$b$,$(af(t)+bg(t))$的 拉普拉斯变换等于$aF(s)+bG(s)$,其中$F(s)$和$G(s)$分别是$f(t)$和$g(t)$的拉普拉斯变 换。
拉普拉斯变换的延迟性质
如果$f(t)$的拉普拉斯变换存在,那么$f(t-a)$的拉普拉斯变换等于$e^{-as}F(s)$,其中 $F(s)$是$f(t)$的拉普拉斯变换。
拉普拉斯变换的公式为:F(s) = ∫f(t)e^(-st) dt (s为复数,t为 实数)。
拉普拉斯变换的性质
线性性质
如果c1和c2是常数,f1(t)和f2(t) 是任意函数,那么c1f1(t) + c2f2(t)的拉普拉斯变换等于 c1F1(s) + c2F2(s)。
时移性质
如果f(t)的拉普拉斯变换为F(s), 那么f(at-b)的拉普拉斯变换为 a^(-b)F(s/a)。
THANKS FOR WATCHING
感谢您的观看
根轨迹的应用
03
根轨迹分析在控制系统分析和设计中具有重要应用,通过根轨
迹可以判断系统的稳定性、分析系统的性能指标等。
第二章 拉普拉斯变换

t
的 Fourier 变换
两点说明
(1) 像函数 F ( s ) 的存在域一般是一个右半平 Re s c 面 即只要复数 s 的实部足够大就可以了。 ,
因此在进行Laplace变换时,常常略去存在域, 只有在非常必要时才特别注明。
(2) 在 Laplace 变换中的函数一般均约定在 t < 0 时为零,
(1)
(2) (3)
[1] = [ u ( t ) ]
[ ( t ) ] 1; [t m ]
s m!
m 1
1 s
;
(4)[eat源自]1 sa
2
;
s ; .
(5)
Γ ( m 1) s
m 1
[ cos a t ]
[
sin a t
;
(6)
]
s a a s a
2
2
2
特点 变换的结果均为分式函数。
3、复数的向量表示法 4、复数的三角表示法 5、复数函数
首页
上页
返回
下页
结束
铃
2
1、复数域
1.1 虚单位:
实例 : 方程 x 1 在实数集中无解
2
.
对虚数单位的规定:
( 1 ) i 1;
2
(2) i 可以与实数进行四则运算
3
虚数单位的性质:
i i;
1 4 2 2
i 1;
4n 2
1,
i
4n 3
i.
4
1.2 复数的代数形式的定义:
对于 x , y R , 称 z x yi 或 z x iy 为复数 .
实部 记做:Rez=x
第二章 拉普拉斯变换

非重根si:
二重根sj:
1.对F(s)的分母做因式分解后,将F(s)分 解为三部分:
2.利用留数定理确定待定系数:
由此得到F(s)的常用函数组合:
3.利用Laplace变换的线性性质和复移位性 质,反变换F(s)得到f(t):
三、象函数包含有共轭复根
• 共轭复根的特点是两个根具有相同的实部 和符号相反的虚部,如: • 共轭复根在象函数的分母中可以表示为:
的形式,其中
。
的形式,其中
。
6. 初值定理: 若 和 均可以进行Laplace变
换,且
存在,则:
7. 终值定理: 若 和 且
均可以进行Laplace变换,
存在,则:Байду номын сангаас
说明:该定理只适用于像函数 在复平 面右半平面和虚轴上(除坐标原点外)没有 极点的情况。即: 的根不能是 正实数或纯虚数
第二章
第3小节
的
推论:若
,则
同理:
4. 延迟性质: 时间函数 数等于 若 在时间轴上平移 的像函数 ,则: ,其像函 。 乘以指数因子
5. 复移位性质: 原函数 乘以指数 ,其像函数等于 的像函数 在复数域平移a,其中a 为实常数可取正、负值。 若 ,则:
例: 可以拆分成 已知: 那么:
例: 可以拆分成 已知: 那么:
例:电阻、电感、电容串联 构成的电路如图,其中, 各元件初始状态皆为0,即:
当电压源上产生单位阶跃函 数的电压后,电路的输出会 产生怎样的响应函数。
解: 1. 列写电路的微分方程 输入信号: 输出信号: 串联电路:
2. 对微分方程进行拉氏变换 零初始条件下:
3.求解拉氏变换后的代数方程:
第二章拉普拉斯变换.ppt

K11 (s s1)r
(s
K12 s1)r1
...
K1r s s1
F2 (s)
(s s1)r F(s) K11 (s s1)K12 ... (s s1)i1K1i ...
(s s1)r1K1r (s s1)r F2(s)
K11
s2 2
cost 1 d sin t dt
线性、微分定理
Lcost
1
s
s2
2
s2
s
2
Example 3
sin t 1 d cost dt
线性、微分定理
?
Lsin t
1
s
s2
s
2
s2 / s2 2
cos
m
m1
s X c (s) an1s X c (s) a0 X c (s)
n
n1
用 s 替代微分,用1/s 替代积分
五、时域积分特性(定理)
f t Fs
n重f积t分dt n
s n
1
m1
F(s)
f
s nm1 (0 )
n (m)
1(t) F (s) 0 (t)e dt
st
s 1
2)e-at
eat F(s) 0eatestdt
sa 1
前一页 后一页
3)tn(n为整数)
tn F(s)
0t
nest dt
s
t n est
s
0
n
0t
n1est
第2章 拉普拉斯变换及其应用

j
这个平面就被 我们称为是S 域或复数域
+1
5
第二章 拉普拉斯变换及其应用
•
由于0
f
(t)e是st d一t 个定积分,
将在t 新函数
中消失。因此, 只取F(s决) 于 ,它是s 复
变数 的函数s。拉氏变换将原来的实变
量函数 转化为复f (变t) 量函数 。
• 拉氏变换是一种单值变换。 和 之间
第二章 拉普拉斯变换及其应用
自动控制原理
1
第二章 拉普拉斯变换及其应用
• 拉氏变换的概念 • 拉氏变换的运算定理 • 拉氏反变换 • 应用拉氏变换求解微分方程
2
第二章 拉普拉斯变换及其应用
2.1 拉氏变换的概念
Laplace变换是求解线性常微分方程常用的一 种数学工具。与线性常微分方程的经典求解 方法相比,Laplace变换有如下两个显著的特 点: • 只需一步运算就可以得到微分方程的通解
s(s 1)
s s 1
19
第二章 拉普拉斯变换及其应用
2.4 应用拉氏变换求解微分方程
例2-5 求典型一阶系统的单位阶跃响应的原函数。
T dc(t) c(t) r(t) dt
解:单位阶跃信号, r(t) 1(t) 则
R(s) 1 s
TsC(s) C(s) R(s) C(s) 1 1
其中,A、B是待定系数,将上式进行通分后可得:
A B A(s 1) Bs (A B)s A
s s 1 s(s 1)
s(s 1)
比较以上两式的分子,可得: A
B A
1
2
A
B
1
这个平面就被 我们称为是S 域或复数域
+1
5
第二章 拉普拉斯变换及其应用
•
由于0
f
(t)e是st d一t 个定积分,
将在t 新函数
中消失。因此, 只取F(s决) 于 ,它是s 复
变数 的函数s。拉氏变换将原来的实变
量函数 转化为复f (变t) 量函数 。
• 拉氏变换是一种单值变换。 和 之间
第二章 拉普拉斯变换及其应用
自动控制原理
1
第二章 拉普拉斯变换及其应用
• 拉氏变换的概念 • 拉氏变换的运算定理 • 拉氏反变换 • 应用拉氏变换求解微分方程
2
第二章 拉普拉斯变换及其应用
2.1 拉氏变换的概念
Laplace变换是求解线性常微分方程常用的一 种数学工具。与线性常微分方程的经典求解 方法相比,Laplace变换有如下两个显著的特 点: • 只需一步运算就可以得到微分方程的通解
s(s 1)
s s 1
19
第二章 拉普拉斯变换及其应用
2.4 应用拉氏变换求解微分方程
例2-5 求典型一阶系统的单位阶跃响应的原函数。
T dc(t) c(t) r(t) dt
解:单位阶跃信号, r(t) 1(t) 则
R(s) 1 s
TsC(s) C(s) R(s) C(s) 1 1
其中,A、B是待定系数,将上式进行通分后可得:
A B A(s 1) Bs (A B)s A
s s 1 s(s 1)
s(s 1)
比较以上两式的分子,可得: A
B A
1
2
A
B
1
第二章拉普拉斯变换

page 3
第二章 拉普拉斯变换
一、拉普拉斯变换的定义
设时间函数 f (t),,则t 0 的拉普f (拉t) 斯变换定义为
控 制
L[ f (t)] F(s) f (t) estdt 0
工
程
基 础
象函数(Image Function)
原函数(Original Function )
page 4
制 工
2
程
基 础
cost 1 (e jt e jt )
2
page17
第二章 拉普拉斯变换
三、使用MATLAB符号运算工具箱进行拉氏变换
MATLAB提供了 laplace()函数来实现拉氏变换。
例2-1 求解函数 ebt cosat c 的拉氏变换。
控 制
解:输入以下命令
工
程 %L0201.m
A s2
eTs
1 eTs
seTs
page24
第二章 拉普拉斯变换
三、周期函数的拉氏变换
若函数 f 是(t)以T 为周期的周期函数,L f t f t estdt 0
控 制
T f testdt 2T f testdt n1T f t estdt
第二章 拉普拉斯变换
(六)正弦函数
正弦函数(Sine Function)的数学表达式为
r(t) sin t (t≥0)
控 式中, 为正弦函数的角频率。
制
工 程 基
其拉氏变换为 L[sin t] sin t estdt 0
础
1 (e jt ejt )est d t 2j 0
s2 2
u(t或) 1(t)来表示。 其变化曲线
0
t
控 如图2-1-2所示。
拉普拉斯变换

三、一些常用函数的拉普拉斯变换
公式
1 1. L[u (t )] = (Re p > 0) p 1 − pb L[u (t − b)] = e (Re p > 0) p 1 at 2. L[e ] = (Re p > Re a ) p−a a 3. L[sin at ] = (Re p > Im a ) 2 2 p +a p L[cos at ] = 2 (Re p > Im a ) 2 p +a
(2) L[t sin t ]
5. 积分性
F ( p) L[ f (t )] = F ( p ) ⇒ L[ ∫0 f (u )du ] = , p ∞ f (t ) ∞ −1 若 ∫p F ( ρ )d ρ 存在 ⇒ = L [ ∫p F ( ρ )d ρ ] t f (t ) ∞ ⇔ L[ ] = ∫p F ( ρ )d ρ t
p →∞
f (0) = lim f (t )= lim pF ( p).
t →0 p →∞
终值定理 若 L[ f (t )] = F ( p ), L[ f ′(t )]与 lim f (t )
t →+∞
存在,则
f (+∞) = lim f (t )= lim pF ( p).
t →+∞ p →0
基本公式
+∞
1 α + i∞ pt ==== ∫α −i∞ F ( p)e dp = f (t )(t > 0) dp = idw 2π i
p =α + iw
二、求拉氏逆变换的方法
1、公式+性质法: 2、留数法:(p181定理)
f (t ) = L [ F ( p )] = ∑ Re s[ F ( p)e , pk ]
拉普拉斯变换

其中s j,f t t u t
0
0
f t e
j t
dt
f t e st dt
s 设F s G j
3
则F s
定义:
0
f t e st dt (s为复参量)
2.微分性质
若L f t F s ,则有L f t sF s f 0 .
证明: L f t
0
f t e-st dt
19
f t e
-st 0
sL f t f 0 .
2 f 0 1 , f 0 0 , f t k cos kt 解:
由性质2有
2 L k cos kt f t L
s2 L f t sf 0 f 0
如u t , cos kt ,t m 等函数都不满足傅氏积分定理中
的绝对可积条件,但它们满足拉氏定理中的条件2
9
事实上 u t 1 e 0t,M 1,c 0
cos kt 1 e , M 1,c 0
0t
tm 由于 lim t 0,所以t 充分大后有t m e t t e 故t m 是按指数级增长的函数 M 1,c 1
k 0
2 k 1b
2 kb
f t e dt
-st
令t 2kb,则
2 k 1b
2 kb
f t e dt
-st
2b
第二章拉普拉斯变换
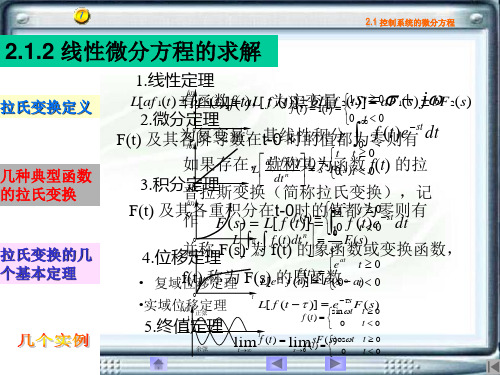
f (t )
F ( s)
解:将F(s)进行因式分解后得到
C3 C2 C1 C4 ( s 1) 2 s 1 s s 3 s2 2 C3 lim s F ( s) lim 2 3 s 0 s 0 ( s 1) ( s 3) s2 1 C 4 lim ( s 3) F ( s) lim 2 12 s 3 s 3 s ( s 1) s2 1 C 2 lim ( s 1) 2 F ( s) lim 2 s 11 s 11 s ( s 3) d d s2 3 C1 lim [(s 1) 2 F ( s)] lim [ ] 4 s 11 ds s 11 ds s ( s 3)
f (t )
的拉
拉氏变换的几 个基本定理
并称 4.位移定理 e at t 0 f (t ) at f(t) 称为 F(s) 的原函数。 L [ e f ( t )] F 0 at) 0 • 复域位移定理 (s
f(t)
0
n L t... f ( t ) dt s n F ( s) F(s) f(t) 的象函数或变换函数, n 为
s 0
0
2.1 控制系统的微分方程
例一
已知
f (t ) A,求F(s)。这里A是常数。
A s
解:因为A是常数,所以,根据线性定理则有
F ( s ) L[ A 1(t )] AL[1(t )]
例二
已知 f (t ) t ,求F(s)。
解:根据实域位移定理则有
e s F ( s) L[(t ) 1(t )] 2 s
将所求得的系数代入F(s)中
1 1 3 1 2 1 1 1 F ( s) 2 ( s 1) 2 4 s 1 3 s 12 s 3
拉普拉斯变换

t
目录 上页 下页 返回 结束
工程数学 --------- 积分变换
推论
1 Λ[∫ dt∫ dtL∫ f (t)dt] = n F(s) 0 0 0 s 象函数积分性质 ∞ f (t) − 1 Λ [∫ F(s)ds] = s t 或 ∞ f (t) ] = ∫ F(s)ds Λ[ s t 一般地 ∞ ∞ ∞ f (t) Λ[ n ] = ∫ ds∫ dsL∫ F(s)ds s s s t
Λ[ f (n) (t)] = snF(s) −sn−1 f (0) −L− f (n−1) (0)
特别地, 特别地, f (0) = f ′(0) =L= f (n−1) (0) = 0 , 当 时 有
Λ[ f (t)] = s F(s)
(n) n
工程数学 --------- 积分变换
目录 上页 下页 返回 结束
F(s) = ∫ f (t)e−stdt
0 +∞
在 平 R s) > c一 存 , 端 分 R s) ≥ c1 > c上 半 面 e( 定 在 右 积 在 e( 半 面 , 绝 收 而 一 收 , 且 R s) > c的 平 内 对 敛 且 致 敛 并 在 e(
F(s)为 析 数 解 积分变换 . 函 工程数学 ---------
F(s) = Λ[ f (t)]
工程数学 --------- 积分变换
目录 上页 下页 返回 结束
f (t)称 F(s)的 普 斯 变 (象 函 ), 记 为 拉 拉 逆 换 原 数 作
f (t) = Λ−1[F(s)]
注:
Λ[ f (t)] = Φ [ f (t)u(t)e−βt ]
工程数学 --------- 积分变换
目录 上页 下页 返回 结束
工程数学 --------- 积分变换
推论
1 Λ[∫ dt∫ dtL∫ f (t)dt] = n F(s) 0 0 0 s 象函数积分性质 ∞ f (t) − 1 Λ [∫ F(s)ds] = s t 或 ∞ f (t) ] = ∫ F(s)ds Λ[ s t 一般地 ∞ ∞ ∞ f (t) Λ[ n ] = ∫ ds∫ dsL∫ F(s)ds s s s t
Λ[ f (n) (t)] = snF(s) −sn−1 f (0) −L− f (n−1) (0)
特别地, 特别地, f (0) = f ′(0) =L= f (n−1) (0) = 0 , 当 时 有
Λ[ f (t)] = s F(s)
(n) n
工程数学 --------- 积分变换
目录 上页 下页 返回 结束
F(s) = ∫ f (t)e−stdt
0 +∞
在 平 R s) > c一 存 , 端 分 R s) ≥ c1 > c上 半 面 e( 定 在 右 积 在 e( 半 面 , 绝 收 而 一 收 , 且 R s) > c的 平 内 对 敛 且 致 敛 并 在 e(
F(s)为 析 数 解 积分变换 . 函 工程数学 ---------
F(s) = Λ[ f (t)]
工程数学 --------- 积分变换
目录 上页 下页 返回 结束
f (t)称 F(s)的 普 斯 变 (象 函 ), 记 为 拉 拉 逆 换 原 数 作
f (t) = Λ−1[F(s)]
注:
Λ[ f (t)] = Φ [ f (t)u(t)e−βt ]
工程数学 --------- 积分变换
第二章 拉氏变换

− f (t) = L 1[F(s)]
它表示对中括号中的函数求拉氏反变换。 它表示对中括号中的函数求拉氏反变换。 不同的原函数对应着不同的象函数;反过来, 不同的原函数对应着不同的象函数;反过来,不同 的象函数对应着不同的原函数。它们之间有一一对应 的象函数对应着不同的原函数。 的关系。 的关系。 以后我们用小写字母表示原函数, 以后我们用小写字母表示原函数,用大写的相同字 母表示象函数。 母表示象函数。如:
=∫ e
0−
∞
−(s+α)t
1 −(s+α)t ∞ 1 dt = − e = 0− s +α s +α
1 ∴ L[e ] = s +α 1 −1 −αt L[ ] =e s +α
−αt
③ (s) = L[δ (t)] = ∫ δ (t)e dt = ∫ δ (t)e dt F
−st −st 0− −∞
解 ① (s) = L[ε(t)] = ∫ ε(t)e−stdt : F
0− ∞
1 −st ∞ 1 = ∫ e dt = − e = 0+ 0+ s s
−st
∞
1 ∴ L[ε(t)] = s −1 1 L [ ] = ε(t) s
② (s) = L[e ] = ∫ e e dt F
0−
−αt
∞
−αt −st
ε(t)
eαt
1 s 1 s −α
t e (n为正整数 为正整数) 为正整数
n −αt
(1−αt)e−atδ (t)A源自A(1−e−αt )1
A s Aα s(s +α) n! sn+1
sin( ωt +φ)
cos(ωt +φ)
它表示对中括号中的函数求拉氏反变换。 它表示对中括号中的函数求拉氏反变换。 不同的原函数对应着不同的象函数;反过来, 不同的原函数对应着不同的象函数;反过来,不同 的象函数对应着不同的原函数。它们之间有一一对应 的象函数对应着不同的原函数。 的关系。 的关系。 以后我们用小写字母表示原函数, 以后我们用小写字母表示原函数,用大写的相同字 母表示象函数。 母表示象函数。如:
=∫ e
0−
∞
−(s+α)t
1 −(s+α)t ∞ 1 dt = − e = 0− s +α s +α
1 ∴ L[e ] = s +α 1 −1 −αt L[ ] =e s +α
−αt
③ (s) = L[δ (t)] = ∫ δ (t)e dt = ∫ δ (t)e dt F
−st −st 0− −∞
解 ① (s) = L[ε(t)] = ∫ ε(t)e−stdt : F
0− ∞
1 −st ∞ 1 = ∫ e dt = − e = 0+ 0+ s s
−st
∞
1 ∴ L[ε(t)] = s −1 1 L [ ] = ε(t) s
② (s) = L[e ] = ∫ e e dt F
0−
−αt
∞
−αt −st
ε(t)
eαt
1 s 1 s −α
t e (n为正整数 为正整数) 为正整数
n −αt
(1−αt)e−atδ (t)A源自A(1−e−αt )1
A s Aα s(s +α) n! sn+1
sin( ωt +φ)
cos(ωt +φ)
第2章第1节拉普拉斯变换

lim f ( t ) lim s F ( s )
t
AEEC
航空工程实验中心
自动控制原理
第二章 控制系统的数学模型
二.拉氏反变换
1. 定义:从象函数F(s)求原函数f(t)的运算称 为拉氏反变换。记为 L1 [ F ( s )] 。由F(s) 可按下式求出 1 C j 1 st f (t ) L [ F ( s)] F ( s )e ds(t 0) 2 j C j 式中C是实常数,而且大于F(s)所有极点的实 部。接按上式求原函数太复杂,一般都用查 拉氏变换表的方法求拉氏反变换,但F(s)必 须是一种能直接查到的原函数的形式。
0
0 t
f 2 ( ) d f1 (t )e st dt
令t , 则 L[ f1 (t ) f 2 ( ) d ]
0
0
f 2 ( ) d f1 ( )e s ( ) d
0
0
f 2 ( )e
s
1
即:
同理,对f(t)的二重积分的拉氏变换为 1 1 ( 1) 1 ( 2 ) 2 L[ f (t )dt ] 2 F ( s ) 2 f (0) f (0) s s s 若原函数f(t)及其各重积分的初始值都等于0 则有 1 n L[ f (t )dt ] n F ( s) s 即原函数 f(t)的n重积分的拉氏变换等于其象 n 函数除以 s 。
L[ h(t )] sL[ h(t )] h(0)
1 1 1 1 L[ h(t )] L[ h (t )] h(0) L[ f (t )] h(0) s s s s 1 1 1 F ( s ) f ( 0) s s
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f (t ) Me ( M和k为实常数)
kt
page
4
机电工程学院
第二章
拉普拉斯变换
如果复变函数 F ( s ) 是时间函数 f (t ) 的拉氏变换,则f (t ) 称为 F ( s ) 的拉氏逆变换,或拉氏反变换。记为 :
控 制 工 程 基 础
f (t ) L [ F ( s )]
1
page 21
机电工程学院
第二章
拉普拉斯变换
四、复数域位移定理(Complex-Shifting Theorem)
若 L[ f (t )] F ( s ),对于任意常数a(实数或复数),有
Le
控 制 工 程 基 础
at
f t F s a
page 22
机电工程学院
第二章
控 制 工 程 基 础
L f t
T 0
0
f t e st dt
st 2T st
f t e dt f t e dt
T
n 1T
nT
f t e st dt
n 0
n 1T
nT
f t e st dt
(0) f (t )dt
0
t
t 0
推论 若
L[ f (t )] F (s)
则
t t t 1 1 ( 1) 1 ( 2) n L f (t )(dt ) n F ( s ) n f (0) n 1 f (0) 0 0 0 s s s 1 (n) f (0) s
推论 若
L[ f (t )] F (s) ,则
d n f (t ) n n 1 n2 ( n 1) L s F ( s ) s f (0) s f (0) f (0) n dt ( n 1) (0) 0 时,有 特别地,当 f (0) f (0) f
控 制 工 程 基 础
page
2
机电工程学院
第二章
拉普拉斯变换
一、拉普拉斯变换的定义
设时间函数 f (t ), t 0 ,则 f (t ) 的拉普拉斯变换定义为
控 制 工 程 基 础
L[ f (t )] F ( s ) f (t ) e dt
st 0
象函数(Image Function)
控 制 工 程 基 础
数学表达式为
e at
0 t
r ( t) = (指数增长函数) r (t)= e-at (指数衰减函数) 其中a >0 。
其拉氏变换为
at
eat
图2-1-5 指数函数
1 L[e ] e e dt 0 sa 1 at at st L[e ] e e dt 0 sa
page 25
机电工程学院
第二章
拉普拉斯变换
( 1) ( 2) (n) f (0) f (0) f (0) 0 当初始条件为零时,
t 1 L f (t )dt F ( s ) 0 s
控 制 工 程 基 础
t t t 1 n L f (t )( dt ) n F ( s ) 0 0 0 s
机电工程学院
第二章
拉普拉斯变换
注:欧拉公式
控 制 工 程 基 础
e cos t j sin t
jt
page 16
机电工程学院
第二章
拉普拉斯变换
第二节 拉普拉斯变换的性质
一、线性性质(Linearity)
线性性质指同时满足叠加性和齐次性 。
控 制 工 程 基 础
叠加性 (Additivity Property):指当几个激励信号 同时作用于系统时,总的输出响应等于每个激励单独 作用所产生的响应之和。如 r1 c1,r2 c2 ,则
st
1 jt jt st (e e )e d t 2j 0 2 2 s
page 13
机电工程学院
第二章
拉普拉斯变换
(七)余弦函数 余弦函数(Cosine Function)的数学表达式为
r (t ) cos t
控 制 工 程 基 础
(t≥0)
page 26
机电工程学院
第二章
拉普拉斯变换
八、初值定理(Initial Value Theorem)
若 L[ f (t )] F (s) ,且 lim sF ( s ) 存在,则
控 制 工 程 基 础
L 1 e 2 t cos3t t 3 (t )
L1 L e 2 t Lcos3t L t 3 L t
1 1 s 6 2 4 1 s s2 s 9 s
page 19
机电工程学院
第二章
机电工程学院
第二章
拉普拉斯变换
主要内容 第一节 拉普拉斯变换简介
控 制 工 程 基 础
第二节 拉普拉斯变换的性质 第三节 拉普拉斯反变换 第四节 用拉普拉斯变换解线性微分方程
page
1
机电工程学院
第二章
拉普拉斯变换
第一节 拉普拉斯变换简介
拉普拉斯变换(Laplace Transform)(简称拉氏 变换)是一种解线性微分方程的简便运算方法。
L[ f
(n)
(t )] s F ( s )
n
page 24
机电工程学院
第二章
拉普拉斯变换
七、积分性质(Integration Property)
若L[ f (t )] F ( s)则 L
其中 f
控 制 工 程 基 础
(-1)
0
t
( 1) F ( s ) f (0) f (t )dt s s
拉普拉斯变换
二、延时定理(Time-Shift Theorem)
若有
L[ f (t )] F ( s )
,对任意实数 a ,则
as
控 制 工 程 基 础
L[ f (t a )] e
F (s)
page 20
机电工程学院
第二章
拉普拉斯变换
三、周期函数的拉氏变换
若函数 f (t ) 是以T 为周期的周期函数,即 f (t T ) f (t ) , 则有
原函数(Original Function )
page
3
机电工程学院
第二章
拉普拉斯变换
一个函数可以进行拉氏变换的充要条件是: (1)在t<0时, f (t ) 0 (2)在t≥0的任一有限区间内, f (t ) 是分段连续的;
控 制 工 程 基 础
(3)当t→﹢∞时, f (t ) 的增长速度不超过某一指数函数, 即
r3 r1 r2 c3 c1 c2 。
齐次性 (Homogeneity Property):指当输入信号乘 以某常数时,响应也倍乘相同的常数。如:r c ,
则 kr kc 。
page 17
机电工程学院
第二章
拉普拉斯变换 a和b为常数
若有
L[ f 1 (t )] F1 ( s )
(t )
1
控 制 工 程 基 础
0
图2-1-1 单位脉冲函数
t
t 0 (t ) 0 t 0
page
7
机电工程学院
第二章
拉普拉斯变换
函数具有如下重要性质
控 制 工 程 基 础
(t ) dt
0
0
(t ) dt 1
(t ) f (t ) dt f (0)
page
5
机电工程学院
第二章
拉普拉斯变换
二、典型时间函数的拉氏变换
常用的时间函数有:
控 制 工 程 基 础
单位脉冲函数、单位阶跃函数、单位斜坡函数、单位加 速度函数、指数函数、正弦函数、余弦函数、以及幂函数等。
page
6
机电工程学院
第二章
拉普拉斯变换
(一)单位脉冲函数
单位脉冲函数(Unit Impulse Function)也称为 函数或称狄 拉克函数(Dirac Function),其 变化曲线如图2-1-1, 数学表达式为:
控 制 工 程 基 础
n
(t≥0, n> -1且为整数)
其拉氏变换 为 n
L[t ] t e dt
n st 0
n! L[t ] n 1 s
n
单位阶跃函数 、 单位斜坡函数及单 位加速度函数分别 是幂函数 t n ( n 1) 当n=0、 n=1 及 n=2时的特例。
page 15
at
st
page 12
机电工程学院
第二章
拉普拉斯变换
(六)正弦函数 正弦函数(Sine Function)的数学表达式为 式中,
控 制 工 程 基 础
为正弦函数的角频率。
0
r (t ) sin t
(t≥0)
其拉氏变换 为
L[sin t ] sin t e dt
0
t
控 制 工 程 基 础
图2-1-2 单位阶跃函数
0 u (t ) 1
t0 t0
u(t ) 的拉氏变换为 L[u (t )]
0
u (t ) e dt e dt
st st 0
