第三章37概率
概率论答案 - 李贤平版 - 第三章

第三章 随机变量与分布函数1、直线上有一质点,每经一个单位时间,它分别以概率p 或p -1向右或向左移动一格,若该质点在时刻0从原点出发,而且每次移动是相互独立的,试用随机变量来描述这质点的运动(以n S 表示时间n 时质点的位置)。
2、设ξ为贝努里试验中第一个游程(连续的成功或失败)的长,试求ξ的概率分布。
3、c 应取何值才能使下列函数成为概率分布:(1);,,2,1,)(N k Nck f Λ==(2),,2,1,!)(Λ==k k c k f k λ 0>λ。
4、证明函数)(21)(||∞<<-∞=-x e x f x 是一个密度函数。
5、若ξ的分布函数为N (10,4),求ξ落在下列范围的概率:(1)(6,9);(2)(7,12);(3)(13,15)。
6、若ξ的分布函数为N (5,4),求a 使:(1)90.0}{=<a P ξ;(2)01.0}|5{|=>-a P ξ。
7、设}{)(x P x F ≤=ξ,试证)(x F 具有下列性质:(1)非降;(2)右连续;(3),0)(=-∞F 1)(=+∞F 。
8、试证:若αξβξ-≥≥-≥≤1}{,1}{12x P x P ,则)(1}{21βαξ+-≥≤≤x x P 。
9、设随机变量ξ取值于[0,1],若}{y x P <≤ξ只与长度x y -有关(对一切10≤≤≤y x ),试证ξ服从[0,1]均匀分布。
10、若存在Θ上的实值函数)(θQ 及)(θD 以及)(x T 及)(x S ,使)}()()()(ex p{)(x S D x T Q x f ++=θθθ,则称},{Θ∈θθf 是一个单参数的指数族。
证明(1)正态分布),(20σm N ,已知0m ,关于参数σ;(2)正态分布),(200σm N ,已知0σ,关于参数m ;(3)普阿松分布),(λk p 关于λ都是一个单参数的指数族。
但],0[θ上的均匀分布,关于θ不是一个单参数的指数族。
必修3第三章-概率-知识点总结和强化练习:

高中数学必修3 第三章 概率 知识点总结及强化训练一、 知识点总结3.1.1 —3.1.2随机事件的概率及概率的意义 1、基本概念:(1)必然事件:在条件S 下,一定会发生的事件,叫相对于条件S 的必然事件; (2)不可能事件:在条件S 下,一定不会发生的事件,叫相对于条件S 的不可能事件; (3)确定事件:必然事件和不可能事件统称为相对于条件S 的确定事件;(4)随机事件:在条件S 下可能发生也可能不发生的事件,叫相对于条件S 的随机事件;(5)频数与频率:在相同的条件S 下重复n 次试验,观察某一事件A 是否出现,称n 次试验中事件A出现的次数nA 为事件A 出现的频数;称事件A 出现的比例fn(A)=n n A为事件A 出现的概率:对于给定的随机事件A ,如果随着试验次数的增加,事件A 发生的频率fn(A)稳定在某个常数上,把这个常数记作P (A ),称为事件A 的概率。
(6)频率与概率的区别与联系:随机事件的频率,指此事件发生的次数nA 与试验总次数n 的比值n n A,它具有一定的稳定性,总在某个常数附近摆动,且随着试验次数的不断增多,这种摆动幅度越来越小。
我们把这个常数叫做随机事件的概率,概率从数量上反映了随机事件发生的可能性的大小。
频率在大量重复试验的前提下可以近似地作为这个事件的概率3.1.3 概率的基本性质 1、基本概念:(1)事件的包含、并事件、交事件、相等事件(2)若A ∩B 为不可能事件,即A ∩B=ф,那么称事件A 与事件B 互斥;(3)若A ∩B 为不可能事件,A ∪B 为必然事件,那么称事件A 与事件B 互为对立事件;(4)当事件A 与B 互斥时,满足加法公式:P(A ∪B)= P(A)+ P(B);若事件A 与B 为对立事件,则A ∪B 为必然事件,所以P(A ∪B)= P(A)+ P(B)=1,于是有P(A)=1—P(B)2、概率的基本性质:1)必然事件概率为1,不可能事件概率为0,因此0≤P(A)≤1; 2)当事件A 与B 互斥时,满足加法公式:P(A ∪B)= P(A)+ P(B);3)若事件A 与B 为对立事件,则A ∪B 为必然事件,所以P(A ∪B)= P(A)+ P(B)=1,于是有P(A)=1—P(B);4)互斥事件与对立事件的区别与联系,互斥事件是指事件A 与事件B 在一次试验中不会同时发生,其具体包括三种不同的情形:(1)事件A 发生且事件B 不发生;(2)事件A 不发生且事件B 发生;(3)事件A 与事件B 同时不发生,而对立事件是指事件A 与事件B 有且仅有一个发生,其包括两种情形;(1)事件A 发生B 不发生;(2)事件B 发生事件A 不发生,对立事件互斥事件的特殊情形。
概率论与数理统计课件第三章

f
(x,
y)
1
21 2
1
2
exp
1
2(1 2 )
(x
1)2
2 1
2
(x
1)( y 1 2
2 )
(y
2)2
2 2
其中1、2、1、 2、都是常数,且1 0, 2 0,1 1.
则称(X,Y)服从参数为1、2、1、的二2、维 正态分布,
记为
(X
,Y)
~
N (1,
2
,
2 1
,
2 2
2F(x, y) f (x, y) xy
(5)若(X,Y)为二维连续型随机向量,联合概率密度为f(x,y),则
F(x,y) P{X x,Y y}
返回
X
18
第
页
例5 设二维随机变量(X,Y)的概率密度为
Ae2(x y) , x 0, y 0
f (x, y)
0, 其他
(1)确定常数A;
分别为(X,Y)关于X和Y的边缘分布函数.
返回
X
25
第
页
例1 设二维随机向量(X,Y)的联合分布函数为
(1 e2x )(1 e3y ), x 0, y 0,
F(x, y)
0, 其他.
求边缘分布 FX (x), FY ( y)
当x
0时,FX
(x)
lim (1
y
e2 x
)(1
e3 y
)
1
e2 x
返回
X
14
第
例3 设随机变量Y~N(0,1),令
0, X 1 1,
| Y | 1
0,
|Y
|
概率论基础第三章答案

第三章 随机变量与分布函数1、直线上有一质点,每经一个单位时间,它分别以概率p 或p −1向右或向左移动一格,若该质点在时刻0从原点出发,而且每次移动是相互独立的,试用随机变量来描述这质点的运动(以n S 表示时间n 时质点的位置)。
2、设ξ为贝努里试验中第一个游程(连续的成功或失败)的长,试求ξ的概率分布。
3、c 应取何值才能使下列函数成为概率分布:(1);,,2,1,)(N k N c k f L ==(2),,2,1,!)(L ==k k c k f kλ 0>λ。
4、证明函数)(21)(||∞<<−∞=−x e x f x 是一个密度函数。
5、若ξ的分布函数为N (10,4),求ξ落在下列范围的概率:(1)(6,9);(2)(7,12);(3)(13,15)。
6、若ξ的分布函数为N (5,4),求a 使:(1)90.0}{=<a P ξ;(2)01.0}|5{|=>−a P ξ。
7、设}{)(x P x F ≤=ξ,试证)(x F 具有下列性质:(1)非降;(2)右连续;(3),0)(=−∞F 1)(=+∞F 。
8、试证:若αξβξ−≥≥−≥≤1}{,1}{12x P x P ,则)(1}{21βαξ+−≥≤≤x x P 。
9、设随机变量ξ取值于[0,1],若}{y x P <≤ξ只与长度x y −有关(对一切10≤≤≤y x ),试证ξ服从[0,1]均匀分布。
10、若存在Θ上的实值函数)(θQ 及)(θD 以及)(x T 及)(x S ,使)}()()()(exp{)(x S D x T Q x f ++=θθθ,则称},{Θ∈θθf 是一个单参数的指数族。
证明(1)正态分布),(20σm N ,已知0m ,关于参数σ;(2)正态分布),(200σm N ,已知0σ,关于参数m ;(3)普阿松分布),(λk p 关于λ都是一个单参数的指数族。
北师大版九年级数学上册第三章 概率的进一步认识用频率估计概率

摸到白球概率 m 0.65 0.62 0.593 0.604 0.601 0.599 0.601
n
00
摸到白球次数m 65 124 178 302 481 599 1803
摸到白球概率 m 0.65 0.62 0.593 0.604 0.601 0.599 0.601
n
(1)请估计:当 n 很大时,摸到白球的频率将会接近
0.6 (精确到 0.1); (2)假如你摸一次,估计你摸到白球的概率 P (白球) =
0.6 .
的概率是多少? 口袋中有 3 个红球、7 个白球,共 10 个球,则随机 摸出红球的概率是 3 .
10
一般地,如果一个试验有 n 种等可能的结果, 事件 A 包含其中的 m 种结果,那么事件 A 发生的 概率为:P A m
n
(2)一个口袋中有红球、白球共 10 个,这些球除颜 色外都相同. 如果不将球倒出来数,那么你能设计一 个试验方案,估计其中红球与白球的比例吗? 方案:每次随机摸出一个球并记录颜色,然后将球 放回,搅匀,当次数越多,试验频率将越稳定于理 论概率.
练一练
1. 判断正误
(1)连续掷一枚质地均匀硬币 10 次,结果 10 次全
部是正面,则正面向上的概率是 1.
错误
(2)小明掷硬币 10000 次,则正面向上的频率在 0.5
附近.
正确
(3)设一大批灯泡的次品率为 0.01,那么从中抽取
1000 只灯泡,一定有 10 只次品.
错误
想一想 (1) 一个口袋中有 3 个红球、7 个白球,这些球除颜色 外都相同,从口袋中随机摸出一个球,这个球是红球
抽屉原理:把 m 个物品任意放进 n 个空抽屉里( m >
概率论与数理统计统计课后习题答案(有过程)

概率论与数理统计统计课后习题答案(有过程)第一章习题解答1.解:(1)Ω={0,1,…,10};(2)Ω={,1,…,100n},其中n为小班人数;n(3)Ω={√,×√, ××√, ×××√,…},其中√表示击中,×表示未击中;(4)Ω={(x,y)}。
2.解:(1)事件AB表示该生是三年级男生,但不是运动员;(2)当全学院运动员都是三年级学生时,关系式是正确的;(3)全学院运动员都是三年级的男生,ABC=C成立;(4)当全学院女生都在三年级并且三年级学生都是女生时,=B成立。
3.解:(1)ABC;(2)AB;(3);(4);(5);(6)4.解:因,则P(ABC)≤P(AB)可知P(ABC)=0 所以A、B、C至少有一个发生的概率为P(A∪B∪C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)=3×1/4-1/8+0 =5/85.解:(1)P(A∪B)= P(A)+P(B)-P(AB)=0.3+0.8-0.2=0.9 P(A)=P(A)-P(AB)=0.3-0.2=0.1(2)因为P(A∪B)= P(A)+P(B)-P(AB)≤P(A)+P(B)=α+β, 所以最大值maxP (A∪B)=min(α+β,1);又P(A)≤P(A∪B),P(B)≤P(A∪B),故最小值min P(A∪B)=max(α,β)6.解:设A表示事件“最小号码为5”,B表示事件“最大号码为5”。
223由题设可知样本点总数,。
2C52C411所以;7.解:设A表示事件“甲、乙两人相邻”,若n个人随机排成一列,则样本点总数为n!,, 1若n个人随机排成一圈.可将甲任意固定在某个位置,再考虑乙的位置。
表示按逆时针方向乙在甲的第i个位置,。
则样本空间,事件所以8.解:设A表示事件“偶遇一辆小汽车,其牌照号码中有数8”,则其对立事件A表示“偶遇一辆小汽车,其牌照号码中没有数8”,即号码中每一位都可从除8以外的其他9个数中取,因此A包含的基本事件数为,样本点总数为104。
概率论第三章

若二维随机变量( 若二维随机变量(X,Y)具有概率密度 ) 1 1 x − µ1 2 f (x, y) = exp{− ) 2 [( 2 2(1− ρ ) σ1 2πσ1σ2 1− ρ x − µ1 y − µ2 y − µ2 2 )( ) +( ) ]} − 2ρ( 其中
µ1, µ2,σ1,σ2, ρ
3.1.2、二维随机变量的联合分布函数 、 维随机变量的联合 联合分布函数
二维随机变量( 二维随机变量(X,Y) ) ( X , Y )的联合分布函数 )的联合分布函数
一维随机变量X 一维随机变量 X的分布函数 的分布函数
F(x, y) = P(X≤ x,Y ≤ y) − ∞ < x, y < ∞
xi ≤3yj ≤2
求:F(3,2) = P(X≤ 3,Y ≤ 2) = ∑∑pij
1 1 1 1 = + 0+ 0+ + + 0 = 4 8 8 2
例2 设随机变量 Y ~ E (1) ,随机变量
0 , 若Y ≤ k ( k = 1,) 2 Xk = 1 , 若Y > k 的联合概率分布列。 求 X 1 和 X 2 的联合概率分布列。
第三章 多维随机变量及其分布
到现在为止, 到现在为止,我们只讨论了一维随机变量 及其分布. 及其分布. 但有些随机现象用一个随机变量来 描述还不够, 描述还不够,而需要用几个随机变量来描述 在打靶时, 在打靶时,命中点的位置是由一 对随机变量(两个坐标)来确定的. 对随机变量(两个坐标)来确定的. 飞机的重心在空 中的位置是由三个随 机变量(三个坐标) 机变量(三个坐标)来 确定的等等. 确定的等等.
1/ 4 x 1 1 解: (3)P( X < ,Y < ) = ∫0 [∫0 3xdy]dx 4 2
北师大版九年级上第三章:概率的进一步认识(精品)学案
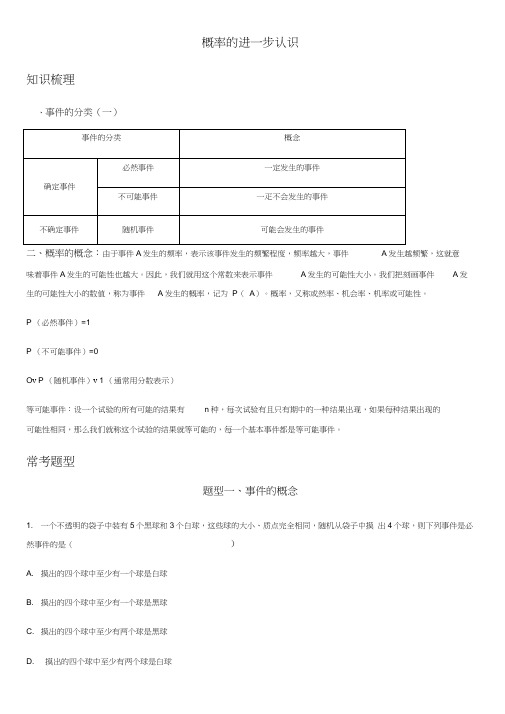
概率的进一步认识知识梳理、事件的分类(一)二、概率的概念:由于事件A发生的频率,表示该事件发生的频繁程度,频率越大,事件A发生越频繁,这就意味着事件A发生的可能性也越大。
因此,我们就用这个常数来表示事件A发生的可能性大小。
我们把刻画事件A发生的可能性大小的数值,称为事件A发生的概率,记为P(A)。
概率,又称或然率、机会率、机率或可能性。
P (必然事件)=1P (不可能事件)=0O v P (随机事件)v 1 (通常用分数表示)等可能事件:设一个试验的所有可能的结果有n种,每次试验有且只有期中的一种结果出现,如果每种结果出现的可能性相同,那么我们就称这个试验的结果就等可能的,每一个基本事件都是等可能事件。
常考题型题型一、事件的概念1. 一个不透明的袋子中装有5个黑球和3个白球,这些球的大小、质点完全相同,随机从袋子中摸出4个球,则下列事件是必然事件的是()A. 摸出的四个球中至少有一个球是白球B. 摸出的四个球中至少有一个球是黑球C. 摸出的四个球中至少有两个球是黑球D. 摸出的四个球中至少有两个球是白球2. 从标号分别为1、2、3、4、5的5张卡片中,随机抽出1张。
下列事件中,必然事件是(A、标号小于6 B 、标号大于6C标号是奇数 D 、标号是33、把下列事件进行分类A. 如果|a|=|b| ,那么a=bB. 三角形的内角和是360 °C. 明天太阳从西边升起D. 篮球队员在罚球线上投篮一次,未投中E. 实心铁球投入水中会沉入水底F. 抛出一枚硬币,落地后正面朝上抛掷一枚硬币四次,有两次正面朝上G. 打开电视频道,正在播放《十二在线》H. 射击运动员射击一次,命中十环I. 方程x2-2x-仁0 必有实数根J. 单项式加上单项式,和为多项式K. 13名同学中至少有两名同学的出生月份相同L. 体育课上,小刚跑完1000米所用时间为1分钟M. 扇形统计图中,所有百分比的和为100%(1)必然事件:⑵不可能事件:____________________________________________随机事件:______________题型二、频率概率(1)一次概率问题1 •端午节吃粽子是中华民族的传统习俗,妈妈买了2只红豆粽、3只碱水粽、5只咸肉粽,粽子除内部馅料不同外1 11 1 A. 10 B.5C.3D.22•甲、乙、丙三人站成一排拍照,则甲站在中间的概率是( )111A. 6 B • 3 C • 23.下列说法正确的是( )B. 随机抛一枚硬币,落地后正面一定朝上C. 同时掷两枚均匀的骰子,朝上一面的点数和为 61D. 在一副没有大小王的扑克牌中任意抽一张,抽到的牌是 6的概率是134.在一个不透明的布袋中装有若干个只有颜色不同的小球,如果袋中有红球5个,黄球4个,其余为白球,从袋1子中随机摸出一个球,“摸出黄球”的概率为 2 3,则袋中白球的个数为()A. 2 B . 3 C . 4 D . 125. 用2, 3, 4三个数字排成一个三位数,则排出的数是偶数的概率为 _______________6. 长度分别为3cm, 4cm, 5cm, 9cm 的四条线段,任取其 中三条能组成三角形的概率是(2)二次概率(用树状图求概率)1. 一个不透明的袋子中有三个完全相同的小球,把它们分别标号为1,2,3,随机摸出一个小球,记下标号后放回,再随机摸出一个小球并记下标号,两次摸出的小球标号的和是偶数的概率是()2 在一个不透明的袋子中,有 2个白球和2个红球,它们只有颜色上的区别,从袋子中随机地摸出一个球记下颜色 放回,再随机地摸出一个球 ,则两次都摸到白球的概率为 。
§37 特征函数

中南大学数学院 概率统计课程组
§3.6 条件分布与条件期望、 回归与第二类回归
在前一章中,对离散型随机变量,我 们曾经研究了ξ在已知发生的条件下的分布 问题,并称P(ξ =xi|η =yj)为条件分布,类似 的问题对连续型随机变量也存在。
设 ( ξ ,η ) 是二维连续型随机变量,由于
P{Y y} 0, 所以 P{ x | y}
其它.
当0 x 1,
f| ( y | x)
f (x, y) f (x)
1
2x
0,
,
x y x, 其它。
(3)
P{
1 |Y 2
0}
P{ 1 , 0}
2
P{ 0}
y
yx
(1
1) 2
1 2
2
3
1 11
4
2
1
0 1/2
x
y x
例25 设二维随机变量(,)服从二元正态分布:
~ (ξ,η) N(μ1,μ2,σ12,σ22,r)
[2] 盛骤,谢式千,潘承毅.概率论与数理统 计(3版).北京:高等教育出版社,2001,12.
[3] 梁之舜,邓集贤,杨维权,司徒荣,邓永录. 概率论与数理统计(2版).北京: 高等教育 出版社,1988,10.
[4] 韩旭里,王家宝,陈亚力,裘亚峥. 概率 论与数理统计.北京:科学出版社,2004.
f
( x,
y)
1, | y | x, 0, 其它.
0
x
1,
试求:(1) f (x) ; f ( y) (2) f| (x | y) ; f| ( y | x)
(3) P{ 1 | 0}.
2
求:(1) f (x), f ( y); (2) f| (x | y), f| ( y | x)
《概率论与数理统计答案》第三章

习题参考答案与提示
第三章 随机变量的数字特征习题参考答案与提示
1.设随机变量 X 的概率分布为
X
-3 0.1
0 0.2
1 0.3
5 0.4
pk 试求 EX 。
答案与提示: EX = 2 。 2.已知随机变量 X 的分布列为
X
0 0.1
1
p
2 0.4
3 0.2
Pk
答案与提示:(1)由归一性, p = 0.3 ; (2) EX = 1.7 ; (3) DX = 0.81 3.已知随机变量 X 的分布列为
后
答
D X −Y = 1−
26.设灯管使用寿命 X 服从指数分布,已知其平均使用寿命为 3000 小时,现有
—5—
案
若一周 5 个工作日里无故障可获利 10 万元,发生一次故障仍获利 5 万元,发生二次2π网
。
ww w
3 ; 2
.k
hd a
EZ =
1 , DZ = 3 ; 2
w. c
解:(1)由数学期望、方差的性质及相关系数的定义( ρ XY =
第三章
习题参考答案与提示
求:(1) Y = 2 X 的数学期望;(2) Y = e −2 X 的数学期望。 答案与提示:(1) EY = E 2 X = 2 ;(2) EY = Ee −2 X = 1/ 3 。
1 11.试证明事件在一次试验中发生的次数的方差不超过 。 4
答案与提示:事件在 n 次独立重复试验中发生的次数服从参数为 n , p 的二项分 布 B ( n, p ) ,当然在一次试验中发生的次数应服从 B (1, p ) ,即为(0-1)分布。
f ( x) = 1 − x− β e 2α
37似然率法医物证学

似然率(likelihood, LR)
表达 方式
用竖线分开条件与事件,竖线右边为条件,左边 为事件。似然率可写成LR=Pr(E∣Hp)/Pr(E∣Hd)
计算 公式
对于仅有一名个体留下的斑痕 LR=1/Pr(E∣Hd)= 1/P(X)
13个STR基因座特定表型组合在群体中出现的概率
遗传标记 TPOX
内容总结
综上所述,对法医个人识别科学证据的评估,至少需要考虑 遗传标记的系统效能和具体案件的鉴定结果,给法庭提供 量化的科学证据;
不同术语表达的概念与数值意义不同,在使用时需要特别 注意。
内容总结
术语 表达的概念
公式 公式中表型 频率的区别
用途
个人识别能力
遗传标记区别群体中随机 抽样的两名个体的能力
D3S1358 FGA
D5S818 CSF1PO D7S820 D8S1179
TH01 VWA D13S317 D16S539 D18S51 D21S11
现场血型STR表型 8-11 15-16 22-23 11-12 11-12 11-12 13-14 7-9 14-17 8-11 9-11 14-15 29-31
嫌疑人STR表型 8-11 15-16 22-23 11-12 11-12 11-12 13-14 7-9 14-17 8-11 9-11 14-15 29-31
表型频率P 0.323 0.242 0.103 0.154 0.190 0.143 0.075 0.294 0.131 0.105 0.144 0.086 0.092
LR = 1/P(X)
X指实际检测出的样本表型,因 此P(X)是特指这种表型在群体中 的频率
遗传标记的个案应用
数据形式 数值意义
概率论与数理统计实践考核37作业

概率论与数理统计实践考核37作业第⼀章随机事件与概率三、计算题1.设P (A )=0.4, P (B )=0.2, (|)0.3P B A =, 求P (AB )以及P (A |B ).解:由(|)0.3P B A =得:()0.3,()P AB P A =即()()0.31()P B P AB P A -=-, 解得:P (AB )=0.02. 从⽽, ()0.02(|)0.1()0.2P AB P A B P B ===.2.已知,()0.2,()0.3,A B P A P B ?==求:(1)(),()P A P B ;(2)P (AB );(3)()P AB ;(4) ()P A B ;(5)P (B -A ).解:(1)由概率的性质,知()1()0.8,P A P A =-=()1()0.7P B P B =-=; (2)因为A B ?,所以AB A =,P (AB )=P (A )=0.2; (3)()P AB =P (A -AB )=P (A )-P (AB )=P (A )-P (A )=0; (4) 因为A B ?,所以A B B =, ()P A B =P (B )=0.3;或者,()P A B =P (A )+P(B )-P (AB )=0.2+0.3-0.2=0.3; (5) P (B -A )=P (B )-P (AB )=0.3-0.2=0.1.3.若事件A 与B 互不相容,P (A )=0.6, P (A+B )=0.9, 求:(1)()P AB ;(2)(|)P A B ;(3)()P AB .解:(1) 因A 与B 互不相容,故AB =Φ,P (AB )=0,所以()P AB =1-P (AB )=1;(2) 因A 与B 互不相容,由加法公式:P (A+B )=P (A )+P (B ),得P (B )=0.3,从⽽ (|)P A B =()()()0.661()0.77()P AB P A P AB P B P B -===-;(3) ()P AB =1()1()10.90.1P AB P A B -=-+=-=.4.已知事件A 与B 相互独⽴,且P (A )=0.4, P (A+B )=0.6, 求(1)P (B );(2)()P AB ;(3)P (A|B ).解:(1)因为事件A 与B 相互独⽴,所以P (AB )=P (A )P (B ),()()()()()()()()P A B P A P B P AB P A P B P A P B +=+-=+- 0.6=0.4+P (B )-0.4P (B ),解得:P (B )=13;(2) 因为事件A 与B 相互独⽴,所以A 与B 也相互独⽴,故()P AB =4()()15P A P B =; (3) 因为事件A 与B 相互独⽴,所以P (A|B )=P (A )=0.4.四、应⽤题6.盒⼦中有8个红球和4个⽩球,每次从盒⼦中任取⼀球,不放回地抽取两次,试求:(1) 两次取出的都是红球的概率;(2)在第⼀次取出⽩球的条件下,第⼆次取出红球的概率;(3)第⼆次取到红球的概率.解:A 1“第⼀次取出的是红球”,A 2“第⼆次取出的是红球”,则 (1)由乘法公式得,两次取出的都是红球的概率为:121218714()()(|)121133P A A P A P A A ===; (2)在第⼀次取出⽩球的条件下,第⼆次取出红球的概率为:218(|)11P A A =; (3)由全概率公式得,第⼆次取到红球的概率为: 2121121()()(|)()(|)P A P A P A A P A P A A =+ 87482121112113 =+=. 第⼆章随机变量及其概率分布三、计算题1.设连续型随机变量X 的分布函数为20,0(),011,1x F x x x x=≤,求X 的概率密度函数.解:由分布函数与概率密度函数之间的关系()()F x f x '=知,当0当1x ≥或0x ≤时,()f x =0,所以,X 的概率密度为2,01()0,x x f x <2.设X 服从参数p =0.2的0-1分布,求X 的分布函数及P (X <0.5).解:X 的分布律为当0x <时,()()F x P X x =≤=0;当01x ≤<时,()()F x P X x =≤=(0)0.8P X ==;当1x ≥时,()()F x P X x =≤=(0)(1)0.80.21P X P X =+==+=.所以,X 的分布函数为0,0()0.8,011,1x F x x x=≤;⽽P (X <0.5)= P (X =0)=0.8.3.设随机变量X ~U (a , b ),求X 的密度函数与分布函数.解:X 的密度函数为1,()0,a xb f x b a ?<=-其它;分布函数()()x F x f t dt -∞=?,当x a <时,()()x F x f t dt -∞=?00xdt -∞==?;当a x b ≤<时,()()xF x f t dt -∞=?10a xax a dt dt b a b a-∞-=+=--??;当x b ≥时,()()xF x f t dt -∞=?1001abx ab dt dt dt b a-∞=++=-??.所以,X 的分布函数为0,(),1,x a x a F x a x b b ax b=≤4.设随机变量X ~N (3, 4),求:(1)P (2P (|X|>2);(4)P (X >3).解:(1)P (2(3)(2)()()22F F ---=Φ-Φ(0)(0.5)=Φ-Φ- (0)[1(0.5)]=Φ--Φ=0.1915;(2) P (-4(10)(4)()()22F F -----=Φ-Φ =(3.5)(3.5)2(3.5)1Φ-Φ-=Φ-=0.9996;(3) P (|X|>2)=1(||2)P X -≤=1(22)1[(2)(2)]P X F F --≤≤=--- =2323 1[()()]22----Φ-Φ=(0.5)(2.5)1Φ-Φ+=0.6977; (4)P (X >3)=1(3)P X -≤=33 1(3)1()1(0)2F --=-Φ=-Φ=0.5.5.已知随机变量X 的密度函数为2,01()0,kx x f x ?<<=??其它,求:(1)常数k ;(2)分布函数;(3)(10.5)P X -<<..解:(1)因为()1f x dx +∞-∞=?,所以123100|133k kkx dx x ===?,故k =3. 即随机变量X 的概率密度为23,01()0,x x f x ?<<=??其它;(2)当0x <时,()()xF x f t dt -∞=?=0,当01x ≤<时,()()x F x f t dt -∞=?=023003xdt t dt x -∞+=??,当1x ≥时,()()xF x f t dt -∞=?=01210301xdt t dt dt -∞++=.所以,随机变量X 的分布函数为30,0(),011,1x F x x x x=≤;(3)(10.5)P X -<<3(0.5)(1)0.500.125F F =--=-=;第三章多维随机变量及其概率分布三、计算题1.已知⼆维离散型随机变量(X , Y )的联合分布为:(1)确定常数C ;(2)求(X , Y )关于X ,Y 的边缘分布.解:(1)由概率分布的性质知,11111+++++=1464812C ,解得:C =18;(2)11113(0)46824P X ==++=,11111(1)481224P X ==++=,从⽽,(X , Y )关于X 的边缘分布为:111(0)442P Y ==+=,117(1)6824P Y ==+=,115(2)81224P Y ==+=,从⽽,(X, Y)关于Y的边缘分布为:2.已知⼆维离散型随机变量(X, Y)的联合分布为:求(X , Y )关于X ,Y 的边缘分布. 解:111(0)012126P X ==++=,,,,所以,(X , Y )关于X 的边缘分布为:,,,从⽽,(X , Y )关于Y 的边缘分布为:3.设⼆维离散型随机变量(X , Y )的等可能值为(0, 0), (0, 1), (1, 0), (1, 1).求: (1) (X , Y )的联合概率分布律; (2) (X , Y )关于X , Y 的边缘概率分布. 解:(1)由题设知:115(1)+04612P X ==+=111(3)0+1264P X ==+=111(5)012126P X ==++=11(1)01241212P Y ==+++=(2)006124P Y ==+++=1111P Y ==+++=所以,(X , Y )的联合概率分布为:(2) 与上⾯1,2题作法相同,可得(X , Y )关于X , Y 的边缘概率分布分别为:1(0,0)(0,1)(1,0)(1,1)4P X Y P X Y P X Y P X Y ============4.设⼆维随机变量(X , Y )只能取下列数组中的值:1(0,0),(1,1),(1,),(2,0)3--,且取这些值的概率依次为1115,,,631212.(1)写出(X , Y )的分布律;(2)求(X , Y )关于X ,Y 的边缘分布律.解:(1)由题设可得(X , Y )的分布律为:(2) ,,,所以,(X , Y )关于X 的边缘分布为:115(1)012312P X =-=++=1(0)6P X ==5(2)12P X ==,,,从⽽,(X , Y )关于Y 的边缘分布为:5.设⼆维随机变量(X , Y )的分布律为:试问:X 与Y 是否相互独⽴?为什么?157(0)061212P Y ==++=11()312P Y ==1.解:可求得(X , Y )关于X ,Y 的边缘概率分布分别为:因为所以,X 与Y 相互独⽴.第四章随机变量的数字特征三、计算题1.设随机变量X 的分布律为求:(1)EX ;(2)E (X 2);(3)E (3X 3+5).解:(1)EX =; (2)E (X 2)=;(3)E (3X 3+5)=3E (X 3)+5,⽽E (X 3)=,所以,.(,)()(),1,2;1,2.P X i Y j P X i P Y j i j =======(2)0.400.320.30.2-?+?+?=-222(2)0.400.320.3 2.8-?+?+?=333(2)0.400.320.30.8-?+?+?=-33(35)3()53(0.8)5 2.6E X E X +=+=?-+=2.设随机变量X 的分布律为求:期望EX 与⽅差DX ..解:;, .3.设随机变量X 的概率密度为6(1),01()0,x x x f x -<解:;, . 10.220.530.3 2.1EX =?+?+?=2222()10.220.530.3 4.9E X =?+?+?=222()() 4.9(2.1)0.49DX E X EX =-=-=()EX xf x dx +∞-∞=?1234100316(1)(2)|22x x dx x x =-=-=?22()()E X x f x dx +∞-∞=?13451003636(1)()|2510x x dx x x =-=-=?22()()DX E X EX =-31110420=-=4.设随机变量X的概率密度为||1()0,||1x f x x <=≥?,求:期望EX 与⽅差DX ..解:;,=.5.设随机变量X 的概率密度为,01()2,120,x x f x x x ≤≤??=-<其它,求:期望EX 与⽅差DX .解:=; =, =.第五章⼤数定律及中⼼极限定理三、计算题()EX xf x dx +∞-∞=10-==?22()()E X x f x dx +∞-∞=22110122-===?22()()DX E X EX =-1()EX xf x dx +∞-∞=?12231232010111(2)|()|133x dx x x dx x x x +-=+-=??22()()E X x f x dx +∞-∞=?12324134201011217(2)|()|4346x dx x x dx x x x +-=+-=?22()()DX E X EX =-161.已知随机变量X 服从均匀分布U [0,1],估计下列概率:(1){|0.5|P X -≥; (2) 13{}22P X -<<.解:因为X ~U [0,1],所以.(1)由切⽐雪夫不等式,得;(2).2.设X i (i =1, 2, ...,50)是相互独⽴的随机变量,且都服从泊松分布P (0.03), 令1i i Z X ==∑,试⽤中⼼极限定理计算(3)P Z ≥.解:因为X i ~P (0.03), 故EX i =DX i =0.03,且,11,212EX DX =={|0.5|P X -≥21112143DX ≤==13{}22P X -<<11{11}{||1}22P X P X =-<-<=-<21111111212DX ≥-=-=5011.5i i EZ EX ===∑,由中⼼极限定理知:.所以 ==1-0.8888=0.1112.3.设P (A )=0.4,现在进⾏1000次独⽴重复试验,(1)估计事件A 发⽣的次数在300~500之间的概率;(2)求事件A 发⽣的次数在300~500之间的概率.解:设随机变量X 表⽰1000次试验中A 发⽣的次数,由题意知:X ~B (1000,0.4), EX =400, DX =240.(1)由切⽐雪夫不等式得, =0.976.(2)因为n =1000很⼤,所以不能直接⽤⼆项分布计算. 由中⼼极限定理知,.≈1.4.设P (A )=0.5,利⽤中⼼极限定理求在100次重复独⽴试验中A ⾄少发⽣60次的概率.5011.5i i DZ DX ===∑~(1.51.5)Z N 近似,(3)P Z≥1(3)1(3)1P Z F =-<=-≈-Φ1(1.22)-Φ2(300500)(|400|100)1100DXP X P X <<=-<≥-~(400,240)X N近似(300500)21P X <<≈Φ-Φ=Φ-解:X 表⽰在100次重复独⽴试验中A 发⽣的次数,则X ~B (100,0.5),EX =50,DX =25,由中⼼极限定理:.所求概率为=1-0.9772=0.0228. 5.设X ~U [-1,1], Y ~N (0,14),且X 与Y 相互独⽴,估计概率P (-1. 第六章统计量及其抽样分布三、计算题 1.已知样本值如下:19.1, 20.0, 21.2, 18.8, 19.6, 20.5, 22.0, 21.6, 19.4, 20.3. 求样本均值x ,样本⽅差2s ,样本⼆阶中⼼矩2b .解:样本均值;样本⽅差; ~(50,25)X N近似(60)1(60)1P X P X ≥=-<≈-Φ14410,123EX DX ===14()0,E X Y EX EY +=+=7(),12D X Y DX DY +=+=2()75(11)(||1)1111212D X Y P X Y P X Y +-<+<=+<≥-=-=101120.2510i i x x ===∑102211() 1.165101i i s x x ==-=-∑样本⼆阶中⼼矩2.设总体2~(,)X N µσ,样本121,,...,,n n X X X X +来⾃总体X ,2,n n X S 表⽰12,,...,n X X X 的样本均值和样本⽅差..解:因为,,且与相互独⽴,所以. ⼜,由t 分布的定义知:t (n -1).102211() 1.048510i i b x x ==-=∑211~(,)n n i i X X N n nσµ==∑21~(,)n X N µσ+n X 1n X +211~(0, )n n n X X N n σ++-~(0,1)n N 222(1)~(1)nn S n χσ--~(1),t n -。
随机过程第三章-泊松过程

N (t)
定理3.6 设 X (t) Yi 是一复合泊松过程,其中泊松 i 1
过程 N(t) 的强度为 ,则
(1) X (t) 具有独立增量;
(2)若E(Yi ) 1, E(Yi2 ) 2 均存在,则
E[ X (t)] t1,
D[ X (t)] t2
证 (1) 令 t0 t1 tn ,由于N(t)具有独立增量性,故
的泊松分布,故
P{N (10) N (0) 1} (4.5)e4.5
二.复合泊松过程
定义3.6 称随机过程 {X (t),t 0}为复合泊松过程,如果对
于 t 0 ,它可以表示为如下形式
N (t)
X (t) Yi i 1
其中 {N(t),t 0} 是一个泊松过程, Y1, ,Yn 是一族独立同 分布的随机变量,并且与 {N(t),t 0} 独立.
(5)4 e5 4!(7)5 e7 (12)9 e12 9!
5! C94
5 12
4
1
5 12
94
.
(5) E[N(5)]=5, D N 5 5,
Cov[N(5), N(12)] D N 5 5.
例2 事件A的发生形成强度为 的泊松过程 {N(t),t 0}.如 果每次事件发生时以概率 p能够记录下来,并以 M (t)表示到 t时刻被记录下来的事件总数,证明{M (t),t 0} 是一个强度为
(1) N(0) 0;
(2) N(t) 有独立增量;
(3)对任意的 s,t 0,有
P{N (t s) N (s) n} (t)n et ,
n!
n 0,1,2,
由条件(3)可知泊松过程有平稳增量并且在任一长度为t
的区间中事件的个数服从参数(均值)为 t 的泊松分布.
概率论与数理统计-第37讲

n个独立 同分布的 均匀分布 随机变量 的和:
X1 X1 X2 X3
X1 X2 X1 X2 X3 X4
3
定理 (独立同分布的中心极限定理(CLT )):
设随机变量X1, X 2 ,, X n ,,相互独立且同分布,
E Xi ,D Xi 2,i
E Xi , D Xi 2, i 1, 2,,
n
n
E( Xi ) E(Xi ) n.
i 1
i 1
n
n
D( Xi ) D( Xi ) n 2.
i 1
i 1
n
近似
据CLT,有 Xi ~ N (n, n 2 ).
i 1
故CLT仅仅是分布类型上的一种近似.("万物归一")
5
定理 (德莫弗-拉普拉斯中心极限定理):
记nA为n重贝努里试验中事件A发生的次数, 并记事件A在每次试验中发生的概率为p (0 p 1).
近似
则对于充分大的n有 nA ~ N(np,np(1 p)).
即, 对于二项分布B(n, p),当n充分大时, 可用正态分布来近似.
分布相同,且E( Xi ) 100, D( Xi ) 322,i 1, 2,,55.
55
P{倒了55次后该瓶红酒仍有剩余} P{ Xi 6000}
根据独立同分布的CLT ,可知
i1
55
近似
Xi ~ N (55100,55 322 ).
i 1
55
P{
i1
Xi
6000}
600055100 32 55
2.11
0.9826.
《概率论与数理统计》第三章

§1 二维随机变量
定义:设E是一个随机试验,样本空间S={e}; 设X=X(e)和Y=Y(e)是定义
y
X e,Y e
在S上的随机变量,由它们构成的
向量(X,Y)叫做二维随机向量 或二维随机变量。
e S
x
定义:设(X,Y)是二维随机变量对于任意实数x,y,
二元函数
ቤተ መጻሕፍቲ ባይዱ
y
F(x, y) P(X x) (Y y)
1 4
1 i
,
ji
0, j i
(X,Y)的联合分布律为:
YX
1
1
1/4
23 4 1/8 1/12 1/16
2
0 1/8 1/12 1/16
3
0
0 1/12 1/16
4
0
0 0 1/16
例3:设有10件产品,其中7件正品,3件次品。现从中
任取一件产品,取后不放回,令
1 X 0
第一次取到的产品是次品 1
z f (x, y)为顶面的柱体体积。
所以 X,Y 落在面积为零的区域的概率为零。
例3:设二维随机变量(X,Y)具有概率密度:
2e(2x y) , x 0,y 0
y f (x, y) 0,
其他
1 求分布函数F(x, y);2求P{X 2,Y 3};
3求P(Y X )的概率
解: (1)当x>0,y>0时
f (x, y)xy
————————
概率微分
(4) f ( x, y)的作用 : 求二维随机变量(X,Y)取值
落在区域G内的事件的概率
P((X ,Y ) G) f ( x, y)dxdy
G
G
注:1在几何上,z f (x, y)表示空间一个曲面,
北师大版九年级数学上册《概率的进一步认识——用树状图或表格求概率》教学PPT课件(3篇)

例题精讲
知识点 1 利用画树状图法或列表法求复杂的等可能事件的概率 例1 (教材 P64 随堂练习)有三张大小一样而画面不同的画片,先将每 一张从中间剪开,分成上下两部分;然后把三张画片的上半部分都放在 第一个盒子中,把下半部分都放在第二个盒子中.分别摇匀后,从每个 盒子中各随机地摸出一张,求这两张恰好能拼成原来的一幅画的概率.
知识点 2 不同颜色球的数目不等的摸球游戏中的概 率
例2 (教材 P67 例 2)一个盒子中装有两个红球,两个白球 和一个蓝球,这些球除颜色外都相同,从中随机摸出一个球, 记下颜色后放回,再从中随机摸出一个球,求两次摸到的球 的颜色能配成紫色的概率.
【思路点拨】(红色和蓝色可以配成紫色)画树状图展示 所有 25 种等可能的结果数,再找出红色和蓝色的结果数,根 据概率公式求解.
不遗漏
2. 判断游戏公平性,先计算游戏双方获胜的概率,如果 概率相等,则游戏公平;如果不相等,则游戏不公平.
第三章 概率的进一步认识
3.1 用树状图或表格求概率
第3课时
教学目标
能借助画树状图或列表计算与转盘有关的配色游戏及数 目不等型游戏中的概率.(重难点)
课前预习
预习反馈
1. 用图中两个可自由转动的转盘做“配紫色”游戏:分别旋转两
上的数字之和为 5 的概率是 3 .
例题精讲 知识点 1 转盘配紫色游戏中的概率
例1 小明和小亮用下面两个可以自由转动的转盘做“配 紫色”游戏(红色和蓝色在一起能配成紫色),同时随机转动这 两个转盘,若能配成紫色,则小明胜,否则小亮胜,这个游 戏对双方公平吗?请用列表或画树状图的方法说明理由.
第37讲 概率

第37讲┃ 归类示例
[解析] (1)首先根据题意画出树状图,然后由树状图即可求 得所有等可能的结果; (2)由点Q在x轴上的有:点(0,0),(-2,0),利用概率公式 即可求得点Q在x轴上的概率; (3)因为当点Q在圆上或在圆外时,过点Q能作⊙O的切线, 由在⊙O外的有:点(-2,1),(-2,-2),在⊙O上的有:点 (0,-2),(-2,0),利用概率公式即可求得答案.
出现张数(张)
500
1000
2000
6500
第37讲┃ 归类示例
(1)求“紫气东来”奖券出现的频率; (2)请你帮助小明判断,抽奖和直接获得购 物券,哪种方式更合算?并说明理由.
第37讲┃ 归类示例
[解析] (1)根据概率的求法,找准两点: ①符合条件的情况数目;②全部情况的总数. 二者的比值就是其发生的概率. (2)算出每张奖券获得的购物券金额的平均数,与10比较即可. 500 1 解:(1) = 或5%; 10000 20 (2)平均每张奖券获得的购物券金额为 500 1000 2000 6500 100× +50× +20× +0× =14(元). 10000 10000 10000 10000 ∵14>10,∴选择抽奖更合算.
而乙胜的概率为
第37讲┃ 归类示例
游戏的公平性是通过概率来判断的,在得分相等的 前提下,如果对于参加游戏的每一个人获胜的概率相等, 则游戏公平,否则不公平;在概率不等的前提下,可将 概率乘相应得分,结果相等即公平,否则不公平.
第37讲┃ 归类示例 ► 类型之四 概率与频率之间的关系 命题角度: 用频率估计概率. 例4 [2013·青岛] 某商场为了吸引顾客,举行抽奖活动 ,并规定:顾客每购买100元的商品,就可随机抽取一张 奖券,抽得奖券“紫气东来”、“花开富贵”、“吉星高 照”,就可以分别获得100元、50元、20元的购物券,抽得 “谢谢惠顾”不赠购物券;如果顾客不愿意抽奖,可以直 接获得购物券10元.小明购买了100元的商品,他看到商场 公布的前10000张奖券的抽奖结果如下: 奖券种类 紫气东 来 花开富 贵 吉星高 照 谢谢惠 顾
北师大版九年级上册第三章概率的进一步认识知识点归纳及例题含答案

北师大版九年级上册第三章概率的进一步认识知识归纳及例题【学习目标】1.进一步认识频率与概率的关系,加深对概率的理解;2.会用列表和画树状图等方法计算简单事件发生的概率;3.能利用重复试验的频率估计随机事件的概率;4.学会运用概率知识解决简单的实际问题. 【知识点梳理】要点一、用树状图或表格求概率 1.树状图当一次试验要涉及3个或更多个因素时,为了不重不漏地列出所有可能的结果,通常采用树形图,也称树形图、树图.树形图是用树状图形的形式反映事件发生的各种情况出现的次数和方式,以及某一事件发生的可能的次数和方式,并求出概率的方法. 知识点诠释:(1)树形图法适用于各种情况出现的总次数不是很大时,求概率的问题;(2)在用树形图法求可能事件的概率时,应注意各种情况出现的可能性务必相同. 2.列表法当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法.列表法是用表格的形式反映事件发生的各种情况出现的次数和方式,以及某一事件发生的可能的次数和方式,并求出概率的方法. 知识点诠释:(1)列表法适用于各种情况出现的总次数不是很大时,求概率的问题; (2)列表法适用于涉及两步试验的随机事件发生的概率. 3.用列举法求概率的一般步骤(1)列举(列表、画树状图)事件所有可能出现的结果,并判断每个结果发生的可能性是否都相等; (2)如果都相等,再确定所有可能出现的结果的个数n 和其中出现所求事件A 的结果个数m ; (3)用公式计算所求事件A 的概率.即P (A )=. 知识点二、用频率估计概率 1.频率与概率的定义频率:在相同条件下重复n 次试验,事件A 发生的次数m 与试验总次数n 的比值.概率:事件A 的频率接近与某个常数,这时就把这个常数叫做事件A 的概率,记作P (A ). 2.频率与概率的关系事件的概率是一个确定的常数,而频率是不确定的,当试验次数较少时,频率的大小摇摆不定,当试验次数增大时,频率的大小波动变小,并逐渐稳定在概率附近.可见,概率是频率的稳定值,而频率是概率的近似值. 知识点诠释:(1)频率本身是随机的,在试验前不能确定,无法从根本上来刻画事件发生的可能性的大小,在大量nm nm重复试验的条件下可以近似地作为这个事件的概率;(2)频率和概率在试验中可以非常接近,但不一定相等;(3)概率是事件在大量重复试验中频率逐渐稳定到的值,即可以用大量重复试验中事件发生的频率去估计得到事件发生的概率,但二者不能简单地等同,两者存在一定的偏差是正常的,也是经常的. 3.利用频率估计概率当试验的可能结果不是有限个,或各种结果发生的可能性不相等时,一般用统计频率的方法来估计概率.知识点诠释:用试验去估计随机事件发生的概率应尽可能多地增加试验次数,当试验次数很大时,结果将较为精确.类型一、用树状图或表格求概率1.同时抛掷两枚均匀硬币,正面都同时向上的概率是( )A .B .C .D .【答案】B.【解析】可能性有(正,正),(正,反),(反,正),(反,反)4种,正面都同时向上的占1种,所以概率为. 【总结升华】利用树状图法列出所有的可能,看符合题意的占多少. 举一反三:【变式1】袋中装有一个红球和一个黄球,它们除了颜色外其余均相同,随机从中摸出一球,记录下颜色放回袋中,充分摇匀后,再随机从中摸出一球,两次都摸到黄球的概率是( ) A .B .C .D .【答案】C.【变式2】随机地掷两次骰子,两次掷得的点数相同的概率是( ). A .BC D【答案】 D.2. (2016•大庆)一个盒子装有除颜色外其它均相同的2个红球和3个白球,现从中任取2个球,则取到的是一个红球、一个白球的概率为( ) A .B .C .D .【思路点拨】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与取到的是一个红球、一个白球的情况,再利用概率公式求解即可求得答案.13141234141312143413【答案】C.【解析】解:画树状图得:∵共有20种等可能的结果,取到的是一个红球、一个白球的有12种情况, ∴取到的是一个红球、一个白球的概率为:=.故选C .【总结升华】此题考查了列表法或树状图法求概率.注意此题是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.举一反三:【变式1】从分别标有1到9数字的9张卡片中任意抽取一张,抽到所标数字是3的倍数的概率为( )A .B .C .D . 【答案】D.【变式2】如图是地板格的一部分,一只蟋蟀在该地板格上跳来跳去,如果它随意停留在某一个地方,则它停留在阴影部分的概率是_____.【答案】P (停在阴影部分)=. 类型二、频率与概率3.关于频率和概率的关系,下列说法正确的是( ) A. 频率等于概率 B. 当试验次数很大时,频率稳定在概率附近 C. 当试验次数很大时,概率稳定在频率附近 D. 试验得到的频率与概率不可能相等【思路点拨】对于某个确定的事件来说,其发生的概率是固定不变的,而频率是随着试验次数的变化而变化的. 【答案】B.【解析】事件的概率是一个确定的常数,而频率是不确定的,当试验次数较少时,频率的大小摇摆不定,当试验次数增大时,频率的大小波动变小,并逐渐稳定在概率附近. 【总结升华】概率是频率的稳定值,而频率是概率的近似值.1918291323类型三、利用频率估计概率4. 某商场设立了一个可以自由转动的转盘(如图),并规定:顾客购物10元以上能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据:(1)计算并完成表格:落在“铅笔”的频率(2)请估计,当很大时,频率将会接近多少?(3)转动该转盘一次,获得铅笔的概率约是多少?(4)在该转盘中,标有“铅笔”区域的扇形的圆心角大约是多少?(精确到 1°)【答案与解析】(1) 0.68、0.74、0.68、0.69、0.6825、0.701;(2) 0.70;(3) 由(1)的频率值可以得出P(获得铅笔)=0.70;(4) 0.70×360°=252°.【总结升华】(1)试验的次数越多,所得的频率越能反映概率的大小;(2)频数分布表、扇形图、条形图、直方图都能较好地反映频数、频率的分布情况,我们可以利用它们所提供的信息估计概率.5.(2015春•泰兴市期末)在一个暗箱里放有a个除颜色外都完全相同的红、白、蓝三种球,其中红球有4个,白球有10个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在20%.(1)试求出a的值;(2)从中任意摸出一个球,下列事件:①该球是红球;②该球是白球;③该球是蓝球.试估计这三个事件发生的可能性的大小,并将三个事件按发生的可能性从小到大的顺序排列(用序号表示事件).【思路点拨】(1)根据频率估计概率,可得到摸到红球的概率为20%,然后利用概率公式计算a的值;(2)根据概率公式分别计算出摸出一个球是红球或白球或蓝球的概率,然后根据概率的大小判断这三个事件发生的可能性的大小.【答案与解析】解:(1)a=4÷20%=20;(2)在一个暗箱里放有20个除颜色外都完全相同的红、白、蓝三种球,其中红球有4个,白球有10个,蓝求有6个,所以从中任意摸出一个球,该球是红球的概率=20%;该球是白球的概率==50%;该球是蓝球的概率==30%,所以可能性从小到大排序为:①③②.【总结升华】用频率估计概率,强调“同样条件,大量试验”. 举一反三:【变式1】为了估计池塘里有多少条鱼,从池塘里捕捞了1000条鱼做上标记,然后放回池塘里,经过一段时间,等有标记的鱼完全混合于鱼群中以后,再捕捞200条,若其中有标记的鱼有10条,则估计池塘里有鱼______________条. 【答案】条 .【变式2】一只箱子里原有3个球,其中2个白球,1个红球,它们除颜色外均相同.(1)从箱子中任意摸出两个球,用树状图或列表法列举出所有可能并求两次摸出球的都是白球的概率. (2)若从箱子中任意摸出一个球是红球的概率为,则需要再加入几个红球? 【答案】类型四、概率的简单应用6. 把一副扑克牌中的3张黑桃牌(它们的正面牌面数字分别是3、4、5)洗匀后正面朝下放在桌面上.(1)如果从中随机抽取一张牌,那么牌面数字是的概率是多少?(2)小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽出一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小李随机抽出一张牌,记下牌面数字.当张牌面数字相同时,小王胜;当张牌面数字不相同时,小李胜.现请你利用树状图或列表法分析游戏规则对双方是否公平?并说明理由.【思路点拨】(1)问属于古典概型;(2)问可以采用列表法或树状图法列出所有的可能,计算小王和小李各自取胜的概率,再去做判断. 【答案与解析】(1)P (抽到牌面数字4)=;(2)游戏规则对双方不公平,理由如下:53一共有9种可能的结果,每种结果发生的可能性相等,∴P(牌面数字相同)=;P(牌面数字不相同)=,∴小李胜的概率要大,游戏不公平.【总结升华】列表法可以不重不漏地列出所有可能的结果.举一反三:【变式】(2015•漳州)在一只不透明的袋中,装着标有数字3,4,5,7的质地、大小均相同的小球,小明和小东同时从袋中随机各摸出1个球,并计算这两个球上的数字之和,当和小于9时小明获胜,反之小东获胜.(1)请用树状图或列表的方法,求小明获胜的概率;(2)这个游戏公平吗?请说明理由.【答案】解:(1)根据题意画图如下:∵从表中可以看出所有可能结果共有12种,其中数字之和小于9的有4种,∵P(小明获胜)==;(2)∵P(小明获胜)=,∵P(小东获胜)=1﹣=,∵这个游戏不公平.23。
用树状图或表格求概率课件

3.1 用树状图或表格求概率
1
回顾与思考
频率与概率的关系
当试验次数很多时,一个事件 发生频率稳定在相应的概率附 近.因此,我们可以通过多次试验 ,用一个事件发生的频率来估计 这一事件发生的概率.
2
回顾与思考
概率
概率 事件发生的可能性,也称为事件发生的概率 (probability).
19
问题探究 2.用树状图来研究上述问题
开始
第一次
红
白
第二次
红 白红 白
所有可能出 (红, 红) (红, 白) (白, 红) (白, 白) 现的结果
答: (1)两次都摸到红球的概率是1/4; (2)两次摸到不同颜色的球的概率是2/4或者1/2。
20
用树状图或表格求概率 P62
小明、小颖和小凡做“石头、剪子、布”的游 戏。游戏规则如下: 有小明和小颖做“石头、剪 子、布”的游戏如果两人的手势相同,那么小凡 获胜;如果两人手势不同,那么按照“石头胜剪 子,剪子胜布,布胜石头”的规则决定小明和小 颖中的获胜者。
在上面投掷硬币的实验中。
(3),在第一枚硬币正面朝上的情况下, 第二枚硬币可能出现哪些结果? 他们发 生的可能性是否一样? 如果第一枚硬币 反面朝上呢?
答: 一正一反 一样
答: 一正一反 一样
利用树状图或表格,可以比较方便地 求出某些事件发生的概率.
10
例题欣赏
例1 随机掷一枚均匀的硬币两次,至少有 一次正面朝上的概率是多少?
必然事件发生的概率为1(或100%),记作P(必然事件)=1;
不可能事件发生的概率为0,记作P(不可能事件)=0;
不确定事件发生的概率介于0~1之间,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 随机变量及其概率分布 样本点ω:随机试验的可能结果 称全体样本点组成的集合为样本空间, 记为 Ω 随机事件A:样本空间中的子集 A ⊆Ω σ-代数F:样本空间的子集构成的集合,具有性质: Ω∈F 若A∈F 则 Ac∈F 若Ai∈F 则 ∪Ai ∈F
概率测度:定义在F上的实值函数, P: A → P{A}, A ∈ F , 满足: 1)非负性:P{A}>0, 2) 规范性:P{Ω}=1, 3)可列可加性: 设Ai ∈F 是两两不相容的事 件,则 P{∪Ai }= ∑P{Ai} , 称P{A} 为事件A 的概率, 0 ≤ P{A} ≤ 1. 称(Ω F P) 为概率空间,它是研究随机试验 的概率模型
⎧ X 1 + + X n − nμ ⎫ lim Pr ⎨ ≤ t ⎬ → Φ (t ) = n →∞ σ n ⎩ ⎭
∫
t
−∞
1 − x2 / 2 e dx 2π
于是,有 95% 的把握断言
−2≤ X1 + + X n − nμ ≤2
σ n
nμ − 2σ n ≤ X 1 +
+ X n ≤ nμ + 2σ n
dA q ΔA / A S ( A, q ) = ⋅ = lim dq A Δq →0 Δq / q
更一般的稳健性分析要考虑独立性的假设。这里 假设在操作过程中接连出现次品的次数之间是无 关的。事实上,有可能由于生产环境中的一些异 常的原因,如工作台的颤动或电压变化的冲击, 使得次品的二极管趋向于出现在一些批次中。这 时,独立随机变量概率模型的数学分析就不能完 全处理这个问题。 在下一节介绍的随机过程的模型可以描述某些具 有依赖性的问题。当然,有些依赖性的问题不容 易给出解析的表达式,随机模拟就成为常用的方 法。
2 . 当n = 153时,因为对于任何的 λ∈[128,178] 区间(153 /λ-2*1531/2/λ,153 /λ+2*1531/2/λ)总 会包含 1,所以对于任何的社区,只要它的平均 每月报警电话数在128到178次之间,一个月有 153次报警就属于正常的变化范围。 3. 因为,中心极限定理只要当 μ和 σ是有限的时 对于任何的分布都是正确的。所以,我们的结论 上对于报警电话之间的时间 间隔是指数分布的假 设是不灵敏的。
变量 n = 每个检验组内二极管的数目(决策变量) C = 一组元件的检验费用(分)(随机变量) A = 平均检验费用(分/个) q=一个二极管为次品的概率 假设:二极管质量相互独立 如果 n = 1, 则 A = 5分 否则 (n > 1), 都是好的, 则 C = 4 + n 如果检验结果有次品, 则 C = (4 + n) + 5 n A = (C 的平均值)/ n 目标: 求 n 的数值, 使 A 最小
P (ξ = k ) =
λk
k!
e
−λ
P (ξ t = k ) =
λt− e − λ t , t ≥ 0 F (t ) = ⎨ ⎩ 0, t < 0 ⎧ λ e − λt , t ≥ 0 p (t ) = ⎨ ⎩ 0, t < 0
均匀分布 离散的均匀分布 连续的均匀分布 正态分布
建模的方法:统计推断。 假设 X,X1,X2,X3,…是独立的随机变量,全部 有相同的分布。它的平均或期望值是 EX = Σxk P{X = xk}, 方差为 VX =Σ(xk – EX)2 P{X = xk}, 中心极限定理:当 n →∞时, X1+…+Xn 的分布越来 越接近于正态分布。特别是,如果 μ= EX,σ2 = VX,则对于所有的实数 t,有
2 几类常见的概率分布 两点分布 只有两种可能结果 (成功、失败)的实验 称为贝努里试验。 试验成功的概率为p 二项分布
⎧1 ξ = ⎨ ⎩0 成功 失败
⎧ p P (ξ = x) = ⎨ ⎩1 − p
x =1 x=0
ξ: n重贝努里试验成功的次数。
P (ξ = k ) = C p (1 − p )
当 n = 17 时 A 取最小值 A = 1.48 (分/个)。 结论:在次品的二极管出现得很少,每一 千的中只有三个的前提下,采用分组检验 次品二极管的方法非常经济。逐个检验的 花费是 5 分/个。使用每一组 17 个二极管 串联起来分组化验,在不影响质量的前提 下可以将检验的费用降低到三分之一,花 费只有1.5 分/个。
k n k
n−k
泊松分布 ξ: 在单位时间间隔内随机 事件发生的次数.(已知 单位时间内平均发生的 次数为λ.) 注:满足独立增量、平稳 性、普通性的随机过程) 在时间区间[0,t)内随机 事件发生的次数ξt服从泊 松分布,称为泊松过程 指数分布 泊松过程的随机事件陆续 发生的时间间隔, (已知平均时间间隔为1/λ)
组建模型:假设报警电话之间的时间 Xn 是指数分布。 期望:μ= 1/λ 方差:σ2=1/λ2 将 λ=171 和 n = 153 代入也就是说, 0.75 ≤ X1 + … + X153 ≤ 1.04 因此,观察值
X1 + … +X153 ≈ 1
在正常的变化范围之内。
结论:断言火灾报警率降低的证据是不充分的。 所观测到的报警电话的数量也许是正态随机 变量的正常的结果。自然,每月报警电话的 数量连续这样低,则我们就需要重新评估这 一情况。 灵敏性分析: 1. 当λ=171时,因为对于任何的 n ∈[147,198], 区间(n/171-2n1/2/171, n/171+2n1/2/171)总 会包含 1,所以有 95% 的时间这个社区每 月报警电话的次数在147到198之间。
问题1 在一个简单的掷骰子的游戏中,同时投掷 两个骰子,庄家将按照两个骰子所示的点数付 给你同等面值的人民币(元)。要付多少钱你 才愿意玩这个游戏? 注: EX=2*1/36+3*2/36+4*3/36+5*4/36+6*5/36 +7*6/36+8*5/36+9*4/36+9*4/36+10*3/36 +11*2/36+12*1/36=7
连续型 若 P(ξ ∈ [a, b]) = ∫a p ( x)dx 则称 函数 p(x) 为随机变量 ξ 的分布密度,
b
∫
+∞
−∞
p ( x)dx = 1
此时随机变量 ξ 的分布函数为 F ( x) = ∫−∞ p( x)dx 随机变量 ξ 的分布函数F(x)具有性质: 单调非降 左连续 规范性: F(- ∞)=0, F(+ ∞)=1
变量: n=飞机容量, g=机票价格, r=飞行费用, g=r/(an), a =利润调节因子(例如,a=60%, 表示 飞机60%的满员率就不亏本)。 m=预订票数量的限额 (>n), p=每位持票乘客不按时前来登机的概率,个人的 行为是独立的。 b=每位因满员不能飞走的乘客获得的赔偿金。
假设: 1. 预订票的乘客按时前来登机是随机的。 2. 维护公司的社会声誉可以通过使得持票按时前 来登机,但因为满员不能飞走的乘客人数限制 在一定范围内来实现。 3. 公司的经济利益由每次航班利润s的期望值(平 均利润)S体现, s=机票收入-飞行费用-赔偿金。 目标:确定预订票数量的最佳限额m,使公司利益 最大化,既要使得最大,且使得因飞机满员不 能飞走的乘客限制在一定数量以内。
灵敏度分析:质量管理程序的实行将依赖于 若干模型范围之外的因素。 1. 也许由于我们操作的特殊性对于10个或20 个一批的二极管或者 n 是 4 或 5 的倍数时检 验起来更容易。 验证:在 n = 10 和 n = 35 之间时检验的平 均花费 A 没有明显的变化。
2. 在检验过程中的次品率 q = 0.003 同样也是 必须考虑的。这个数值可能会随着工厂内的 环境条件而发生变化。 一般模型 A=4/n+6– 5 (1 – q)n 当n=17时,A对q的灵敏性 S(A,q)=0.16 所以,q 的微小的改变不会导致检验费用大 的变化。
4. 数值模拟
• 解析模拟方法
例3:航空公司的预订票策略 航空公司预订票业务承诺,预先订购机票的乘客 可以在登机时才付款。如果限定预订票的数量 恰好等于飞机的容量,则可能由于定了票的乘 客不按时前来登机,致使飞机因为不满员而利 润降低,甚至亏本。如果不限制预订票数量, 那么当持票按时前来登机的乘客超过飞机容量 时,必然会引起乘客的不满,导致公司在经济 和声誉方面受损。所以公司要确定预订票数量 的最佳限额。
一共有 n 个二极管,一个二极管为次品的概率是 0.003。换句话说,一个二极管是正品的概率为 0.997。假设每个二极管都是相互独立的,于是 一个检验组内的 n 个二极管全部是正品的概率为 p = 0.997n。 随机变量 C 的期望值是 EC = (4+n) 0.997n + [(4+n) + 5n] (1 – 0.997n) = (4+n) + 5n (1 – 0.997n) = 4 + 6n – 5n (0.997)n 由大数定律知,C的平均值≈C 的期望值 模型:每一个二极管的平均检验费用为 A = 4/n + 6 – 5(0.997)n
建模的方法:离散的概率模型。 对于任何的 n > 1, 随机变量 C 取两个可能数值中的一个: 如果所有的二极管都是好的, 则 C=4+n. 否则 C=(4+n)+5n, 用 p 表示所有的二极管都是正品的概率,则 C 的 平均或期望值是 EC =(4 + n)p +[(4 + n)+5n](1–p)
例2:火灾率
一个地区119 应急服务中心在过去的一年内 平均每月要收到171个房屋火灾的电话。基 于这个资料房屋的火灾率被估计为每月171 次。下一个月收到的火灾报警电话只有153 个。这是否表明房屋的火灾率实际上减少 了,或者它就是一个随机波动?
