八年级下册数学图形的旋转(2)课件
合集下载
八年级数学下册(北师大版)3.2.2图形的平移与旋转(旋转作图)课件

后作这两部分关于GH的轴
对称图形,这样就可以得
到整个图形。
G
F
旋转图案设计欣赏
课后任务:
1、旋转作图的步骤 : (1)明确题目要求:弄清旋转中心、方向和角度; (2)分析所作图形:找出构成图形的关键点; (3)旋转关键点:沿一定的方向和角度分别作出
各关键点的对应点; (4)作出新图形: 顺次连接作出的各点;
(5)写出结论: 说明所作出的图形.
2、“旋转”作图的条件 : (1)图形原来的位置; (2)旋转中心; (3)旋转方向; (4)旋转角度.
1.将△AOB绕点O旋转180°得到△DOC,则下列作图正确的是( )
2.如图,在正方形网格中有△ABC,△ABC绕点O按逆时针方向旋转90°后的 图案应该是( )
各关键点的对应点;
(4)作出新图形: 顺次连接作出的各点;
(5)写出结论: 说明所作出的图形.
目标检测1:
目标检测1:
3、如图,在方格纸上,△DEF是由△ABC绕定 点P顺时针旋转得到的,如果用(2,1)表示方格 纸上A点的位置,(1,2)表示B点的位置,那么 点P的位置为( A ) A.(5,2) B.(2,5) C.(2,1) D.(1,2)
第三章 图形的平移与旋转
3.2 图形的旋转(第二课时)
3.2.2 旋转作图
课前学习——知识回顾
1、“旋转”的定义: 在平面内,将一个图形绕着_一__个_定_点__沿_某_个_方__向_转动
_一_个__角_度__,这样的图形运动称为__旋_转__(变_换__) ___. 2、“旋转”的基本性质: (1)经过旋转,图形的___形_状__和_大_小_____不变; (2)经过旋转,图形上的每一点都绕_旋__转_中_心_沿相同 的方向转动了相同的__角__度__; (3)任意一对_对__应_点__与_旋_转__中_心__的连线所成的角都是 ___旋_转_角___,对应点到__旋_转__中_心___的距离相等.
初中数学八年级下册《9.1 图形的旋转》PPT课件 (2)
如 图 , 正 方 形ABCD是 正 方 形ABCD
按 顺 时 针 方 向 旋 转 45 而 成 的 。
(1) 若AB 4,
S 16 则 正 方 形ABCD
;
(2)BAB 45° , BAD 45° ;
(3) 若 连 接BB,
则BBA 67.5 ° 。
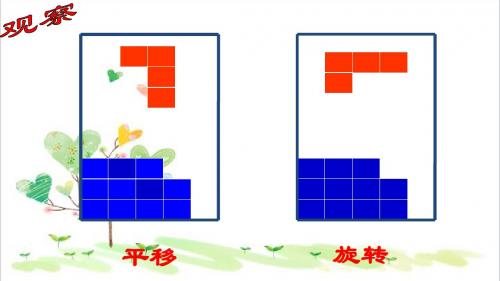
平移
旋转
..
图图形形的的
图形的旋转
在平面内,将一个图形绕一个定点 转动一定的角度,这样的图形运动称为 图形这的个旋定转点。称为旋转中心。
旋转的角度称为旋转角。
图形旋转的探究
A
在发图现形:旋转的过程中
A′
. . N . . M′
哪验些证发方生法了:改变? N 哪旋些转没的有有发关生结改论变:?
M B′
. 旋转角40°
C
B
将 ABC 绕点O顺时针旋转90°到 ABC 的位置
A
B&
O
A'
AOB是AOB绕 点O按 逆 时 针 方 向 旋 转
得 到 的 。 已 知AOB 20,AOB 24,
AB 3,OA 5, 则AB 3
,
OA 5 , 旋 转 角 44° 。
画出点A绕点O按逆时针方向旋转90 °后的图形。 A
O
画出点AB绕点O按逆时针方向旋转90 °后的图形。 A B
O
香港特别行政区区旗中央的紫荆花图案 是怎样形成的?
把这个图形绕点O旋转3次,每次旋转90度。
O
北师大版八年级下册数学图形的旋转作图课件

新知讲授
练习2:如图所示,四边形ABCD绕点O按顺时针方向旋转 后,顶点A旋转到了点A’处,请画出旋转后的四边形.
解:如图所示, 四边形A’B’C’D’就 是旋转后的四边形.
新知讲授
说一说:画旋转图形的一般步骤. (1)确定旋转 中心 、 旋转方向 和 旋转角 ; (2)将原图形中的 关键点 与旋转中心连接起来,然后按 旋转方向 分别将它们旋转一个角度,得到 关键点 的对应点; (3)按照原图形的顺序连接这些对应点,所得到的图形就是旋转 后的图形.
作业布置
基础作业-教材第79页习题3.5第1、2题 能力作业-教材第80页习题3.5第3、4题
最有价值的学习就是方法的收获!
A.点D B.点C C.点B D.点A
中考链接
(202X)如图,点A、B、C、D、O都在方格纸的格点上,
若△COD是由△AOB绕点O按顺时针方向旋转而得到的,则旋转的
角度为____9_0_°______.
课堂总结
说一说画旋转图形的一般步骤?
(1)确定旋转中心、旋转方向和旋转角; (2)将图形中的关键点与旋转中心连接起来,然后按旋转 方向分别将它们旋转一个角度,得到关键点的对应点; (3)按照原图形的顺序连接这些对应点,所得到的图形就 是旋转后的图形.
新知讲授
做一做:如图所示,你能对甲图案进行适当的运动变化,
使它与乙图案重合吗?写出你的操作过程.
乙
甲
还可以用
什么方法把
甲图案变成
乙图案?
B
A
答:先从点A到点B的方向平移线段AB的长度,再将甲图
案绕点A逆时针旋转70° ,即可与图案乙重合.
课堂练习
1.如图,在4×4的正方形网格中,△MNP绕某点旋转一 定的角度,得到△M1N1P1,则其旋转中心是( C )
3.2 图形的旋转 课件(共30张PPT)数学北师大版八年级下册

就是旋转角 .
感悟新知
知1-练
例1 [母题教材P77习题T1 ]如图 3-2-1, A, B, C 三点共 线,△ ACD 和△ BCE 都是等边三角形,△ ACE 经 过旋转后到达△ DCB 的位置 .
感悟新知
知1-练
解题秘方:紧扣“图形旋转时,固定不动的点是 旋转中心,转动的角是旋转角”进行 判断 .
感悟新知
(1)旋转中心是哪一点?
知1-练
解:点 C 是在△ ACE 旋转过程中不动的点,所 以点C 是旋转中心 .
感悟新知
知1-练
(2)旋转角是多少度? 解:△ ACE 旋转后到达△ DCB 的位置, AC 绕 点 C 旋转到 DC, AC 转过的角,即∠ ACD 就是 旋转角 . 因为△ ACD 是等边三角形, 所以∠ ACD=60°,即旋转角是 60° .
感悟新知
(4)你能求出∠ GDF 的度数吗?说明你的理由 .
知2-练
解:能,∠ GDF=45° . ∵△ DEC 绕点 D 顺时针旋转 90°到△ DGA 的位置, ∴∠ GDE=90° . 又∵∠ FDE=45°,∴∠ GDF= ∠ GDE- ∠FDE=90°-45° =45° .
感悟新知
知2-练
知3-练
感悟新知
解:(1)连接 OA, OB, OC, OD; (2)分别以 OB, OC 为边,作∠ BOM= ∠ CON= ∠ AOD; (3)分别在 OM, ON 上截取 OE=OB, OF=OC; (4)连接 DE, EF, FD,△ DEF 就是所求 作的三角形,如图 3-2-3 所示.
感悟新知
2. 旋转作图的一般步骤
知3-讲
(1)确定旋转中心、旋转方向和旋转角 .
(2)找出图形的关键点,一般是图形中的转折点 .
感悟新知
知1-练
例1 [母题教材P77习题T1 ]如图 3-2-1, A, B, C 三点共 线,△ ACD 和△ BCE 都是等边三角形,△ ACE 经 过旋转后到达△ DCB 的位置 .
感悟新知
知1-练
解题秘方:紧扣“图形旋转时,固定不动的点是 旋转中心,转动的角是旋转角”进行 判断 .
感悟新知
(1)旋转中心是哪一点?
知1-练
解:点 C 是在△ ACE 旋转过程中不动的点,所 以点C 是旋转中心 .
感悟新知
知1-练
(2)旋转角是多少度? 解:△ ACE 旋转后到达△ DCB 的位置, AC 绕 点 C 旋转到 DC, AC 转过的角,即∠ ACD 就是 旋转角 . 因为△ ACD 是等边三角形, 所以∠ ACD=60°,即旋转角是 60° .
感悟新知
(4)你能求出∠ GDF 的度数吗?说明你的理由 .
知2-练
解:能,∠ GDF=45° . ∵△ DEC 绕点 D 顺时针旋转 90°到△ DGA 的位置, ∴∠ GDE=90° . 又∵∠ FDE=45°,∴∠ GDF= ∠ GDE- ∠FDE=90°-45° =45° .
感悟新知
知2-练
知3-练
感悟新知
解:(1)连接 OA, OB, OC, OD; (2)分别以 OB, OC 为边,作∠ BOM= ∠ CON= ∠ AOD; (3)分别在 OM, ON 上截取 OE=OB, OF=OC; (4)连接 DE, EF, FD,△ DEF 就是所求 作的三角形,如图 3-2-3 所示.
感悟新知
2. 旋转作图的一般步骤
知3-讲
(1)确定旋转中心、旋转方向和旋转角 .
(2)找出图形的关键点,一般是图形中的转折点 .
八年级数学下册:9.1 图形的旋转 (共17张PPT)

BB A′ A
A′ B′ B′
O
课堂小结: 通过本节课的学习,你学到了什么?请谈一
谈体会和收获.
作业布置:
1.课本习题9.1第1、2题.
问题2
如图,已知点O和点 A.
(1)画出点A绕着点O按逆时针方向旋转100°后的点A′ ;
(2)你能画出线段AB绕点O按逆时针方向旋转100°后的 图形吗? (3)你能画出△ABC绕点O按逆时针方向旋转100°后的 A A 图形吗?
O O
CC
B
B
问题3
如图,已知线段AB绕点O旋转后的对应
线段是A′B′,你能确定旋转中心点O的位置吗?
A
B'
B
C
C' A' O
图形旋转的基本性质
1、图形的旋转不改变图形的形状、大小; 2、一个图形和它经过旋转后得到的图形中, 对应点到旋转中心距离相等,两组对应点 分别与旋转中心连线所成的角相等.
问题1
如图,在正方形ABCD中,E是BC上一
F A D
点,△ABE经过旋转后得到△ADF.
B
E
C
( )若连接EF ,那么△ AEF是什么三角形? ( 32 )如果点 G是 AB的中点,那么经过上述旋转 (1)旋转中心是哪一点?旋转角为多少度? 后,点G旋转到了什么位置?
9.1
图形的旋转
学习目标
1、通过具体的实例认识平面图形关于旋转中 心的旋转; 2、经历对生活中旋转现象的观察、分析的过 程,探索旋转的基本性质; 3、能画出简单图形关于给定旋转中心经过旋 转后的图形.
你能再举出生活中类似的例子吗?
探索活动一 1.将一块三角尺放在一张白纸上,画下它的外轮 廓,记为△ABC. 2.将三角尺绕直角顶点按逆时针方向旋转一定的 角度,再画下它的外轮廓,记为△ A′B′C . A
【最新】北师大版数学八年级下册第三章《图形的旋转 2》公开课课件.ppt

大小关系是( ∠AOD=∠BOE)
如图,如果旋转中心在△ABC
的外面点O处,逆时针转动 90°,将整个△ABC旋转到
C′
B′
△ A′ B′C′ 的位置,那么这两
个三角形的顶点、边与角是
如何对应的呢?
0 · 90°
A′ C
A B
例1、如图,△ABC是等边
A
三角形,D是BCห้องสมุดไป่ตู้一点,
△ABD经过旋转后到达
解: 方案一: 把正方形ABCD绕点D
顺时针旋转90°.
B
方案二: 把正方形ABCD绕点C
逆时针旋转90°.
A
方案三: 把正方形ABCD绕CD的 中点O旋转180°.
C F
·O
D
E
例3、如图11.2.7(1)点M是线段AB上一点, 将线段AB绕着点M顺时针方向旋转90,旋转后 的线段与原线段的位置有何关系?,如果逆时 针方向旋转90呢?
。2020年12月16日星期三2020/12/162020/12/162020/12/16
15、会当凌绝顶,一览众山小。2020年12月2020/12/162020/12/162020/12/1612/16/2020
16、如果一个人不知道他要驶向哪头,那么任何风都不是顺风。2020/12/162020/12/16December 16, 2020
图形的旋转
旋转木马
旋转飞机
动动脑筋:以上这些转运动有什么共同的特征?
荡秋千也是我们日常生活中 常见的旋转运动,我们一起来 仔细观察一下.
在平面内,将一个图形绕着一个定点沿 某个方向转动一个角度,这样的图形运 动称为旋转。
这个定点O 称为旋转中心
o 旋转中心
如图,如果旋转中心在△ABC
的外面点O处,逆时针转动 90°,将整个△ABC旋转到
C′
B′
△ A′ B′C′ 的位置,那么这两
个三角形的顶点、边与角是
如何对应的呢?
0 · 90°
A′ C
A B
例1、如图,△ABC是等边
A
三角形,D是BCห้องสมุดไป่ตู้一点,
△ABD经过旋转后到达
解: 方案一: 把正方形ABCD绕点D
顺时针旋转90°.
B
方案二: 把正方形ABCD绕点C
逆时针旋转90°.
A
方案三: 把正方形ABCD绕CD的 中点O旋转180°.
C F
·O
D
E
例3、如图11.2.7(1)点M是线段AB上一点, 将线段AB绕着点M顺时针方向旋转90,旋转后 的线段与原线段的位置有何关系?,如果逆时 针方向旋转90呢?
。2020年12月16日星期三2020/12/162020/12/162020/12/16
15、会当凌绝顶,一览众山小。2020年12月2020/12/162020/12/162020/12/1612/16/2020
16、如果一个人不知道他要驶向哪头,那么任何风都不是顺风。2020/12/162020/12/16December 16, 2020
图形的旋转
旋转木马
旋转飞机
动动脑筋:以上这些转运动有什么共同的特征?
荡秋千也是我们日常生活中 常见的旋转运动,我们一起来 仔细观察一下.
在平面内,将一个图形绕着一个定点沿 某个方向转动一个角度,这样的图形运 动称为旋转。
这个定点O 称为旋转中心
o 旋转中心
八年级数学下册(北师版)课件 3.2 第2课时 旋转作图

第3章 图形的平移与旋转
3.2 图形的旋转 第2课时 旋转作图
1.将△AOB绕点O旋转180°得到△DOC,则下列作图正确的是( C )
2.如图,在正方形网格中有△ABC,△ABC绕点O按逆时针方向旋转 90°后的图案应该是( A )
3.如图,将正方形图案绕中心O旋转180°后,得到的图案是( C)
(2)平移△ABC,使点A的对应点A2的坐标为(-2,-6),请画出平移后对 应的△A2B2C2的图形;
(3)若将△A1B1C绕某一点旋转后可得到△A2B2C2,请直接写出旋转中心 的坐标.
解:(1)(2)画图略
(3)旋转中心的坐标为(0,-2)
15.如图,你能对甲图案进行适当的运动变化,使它与乙图案重合吗? 写出你的操作过程.
(1)画出△OA′B′; (2)写出点A′,B′的坐标; (3)连接AA′,求AA′的长.
解:(1)如图 (2)A′(-2,4),B′(0,3) (3)AA′=2 10
14.如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的 三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,,请画出 △A1B1C的图形;
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1; (2)分别连接AB1,BA1后,求四边形AB1A1B的面积.
解:(1)如图,△A1B1C1即为所求作, (2)四边形 AB1A1B 的面积=4×12×3×2=12
13.如图,小正方形的边长都是1,点O,A,B都在格点上,将△OAB 绕O点逆时针方向旋转90°得到△OA′B′.
A.(5,2) B.(2,5) C.(2,1) D.(1形所在 的平面上可作为旋转中心的点共有__3__个.
3.2 图形的旋转 第2课时 旋转作图
1.将△AOB绕点O旋转180°得到△DOC,则下列作图正确的是( C )
2.如图,在正方形网格中有△ABC,△ABC绕点O按逆时针方向旋转 90°后的图案应该是( A )
3.如图,将正方形图案绕中心O旋转180°后,得到的图案是( C)
(2)平移△ABC,使点A的对应点A2的坐标为(-2,-6),请画出平移后对 应的△A2B2C2的图形;
(3)若将△A1B1C绕某一点旋转后可得到△A2B2C2,请直接写出旋转中心 的坐标.
解:(1)(2)画图略
(3)旋转中心的坐标为(0,-2)
15.如图,你能对甲图案进行适当的运动变化,使它与乙图案重合吗? 写出你的操作过程.
(1)画出△OA′B′; (2)写出点A′,B′的坐标; (3)连接AA′,求AA′的长.
解:(1)如图 (2)A′(-2,4),B′(0,3) (3)AA′=2 10
14.如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的 三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,,请画出 △A1B1C的图形;
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1; (2)分别连接AB1,BA1后,求四边形AB1A1B的面积.
解:(1)如图,△A1B1C1即为所求作, (2)四边形 AB1A1B 的面积=4×12×3×2=12
13.如图,小正方形的边长都是1,点O,A,B都在格点上,将△OAB 绕O点逆时针方向旋转90°得到△OA′B′.
A.(5,2) B.(2,5) C.(2,1) D.(1形所在 的平面上可作为旋转中心的点共有__3__个.
八年级数学下册 第三章 图形的平移与旋转 2 图形的旋转教学课件下册数学课件

种情况如题干图所示:F1C=1,F2B=DE=2, F2C=F2B+BC=5. 答案:1或5
12/12/2021
第二十五页,共三十三页。
3.△ABC是等边三角形,△ABP顺时针旋转后能与 △CBP′重合(chónghé),那么 (1)旋转中心是哪一点?
(2)旋转角是几度?
(3)连接PP′后,△BPP′是 什么三角形?
A
方向连续旋转45°、90°、
135°、180°、225°、
F
270°、315°前后的图形共
同组成的.
B
12/12/2021
第十二页,共三十三页。
E D
H
C
G
方法二:整个图形也可以
看成是图形的四分之一绕
A
中心位置连续旋转90°、
180°、270°前后(qiánhòu)
F
的图形共同组成的.
B
12/12/2021
BO C B
A
关系? 12/12/2021
第五页,共三十三页。
F
D E
O
【解析】1.旋转中心(zhōngxīn)是O点,旋转角是∠AOD.旋转角 还可以是∠BOE. 2.A旋转到点D的位置,点B旋转到点E的位置. 3.钟表的指针长短、形状没有变化,所以OA与OD是相等的. 同样,线段OB与OE是相等的. 4.因为四边形AOBC绕O点旋转到四边形DOEF的位置,在旋
(2)分针匀速旋转一周需要60分,因此旋转20分,分针
旋转的角度为
12/12/2021
36020120 60
第九页,共三十三页。
【跟踪训练】
1.将一个四边形进行(jìnxíng)旋转可得到如图 所示图形
(1)这个四边形旋转了几次?
12/12/2021
第二十五页,共三十三页。
3.△ABC是等边三角形,△ABP顺时针旋转后能与 △CBP′重合(chónghé),那么 (1)旋转中心是哪一点?
(2)旋转角是几度?
(3)连接PP′后,△BPP′是 什么三角形?
A
方向连续旋转45°、90°、
135°、180°、225°、
F
270°、315°前后的图形共
同组成的.
B
12/12/2021
第十二页,共三十三页。
E D
H
C
G
方法二:整个图形也可以
看成是图形的四分之一绕
A
中心位置连续旋转90°、
180°、270°前后(qiánhòu)
F
的图形共同组成的.
B
12/12/2021
BO C B
A
关系? 12/12/2021
第五页,共三十三页。
F
D E
O
【解析】1.旋转中心(zhōngxīn)是O点,旋转角是∠AOD.旋转角 还可以是∠BOE. 2.A旋转到点D的位置,点B旋转到点E的位置. 3.钟表的指针长短、形状没有变化,所以OA与OD是相等的. 同样,线段OB与OE是相等的. 4.因为四边形AOBC绕O点旋转到四边形DOEF的位置,在旋
(2)分针匀速旋转一周需要60分,因此旋转20分,分针
旋转的角度为
12/12/2021
36020120 60
第九页,共三十三页。
【跟踪训练】
1.将一个四边形进行(jìnxíng)旋转可得到如图 所示图形
(1)这个四边形旋转了几次?
八年级数学下册 《11.2图形的旋转》(2) 课件PPT

ABCD的边AB、BC上的点,BE=CF
,连接DF、CE.将中心O按逆时针方向旋转到△CDF的位
置,则旋转角是( C ). A.450 B.600 C.900 D.1200
O
F
A
EB
如图所示:正方形ABCD中E为BC的中点,将△ABE 旋转后得到△CBF.则旋转中心是__B_____; 旋转角=___9_0;0 AE与CF的位置关系是_互__相__垂__直; 如果正方形的面积为18cm2,△BCF的面积为 4cm2,则四边形AECD的面积是_1_4_c_m__2_
两组对应点分别与旋转中心的连线所成的角相等 (旋转角相等)
如图,将△OAB绕点O按逆时针方向旋转至△OA′B′, 使点B恰好落在边A′B′上.已知AB=4 cm, BB′=1 cm,则A′B长是__3___cm.
A′B=A′B′-BB′=AB-BB′ =4-1=3(cm).
(2013•晋江)如图,E、F分别是正方形
知识
链接
旋转的定 义 在平面内,将一个图形绕一个定点按某一个方向(逆时
针或顺时针方向)转动一定的角度,这样的变换叫做图 形的旋转,这个定点叫做旋转中心,这个角叫做旋转角 旋转后图形的位置是由旋转中心、旋转方向和旋转角确
旋定转的的。 性 质
一个图形和它经过旋转所得到的图形中
对应点到旋转中心的距离相等;
B
G
F
A
E
D
C①
G
F
D
E
G D
E F
小试牛刀
1、如图,在正方形ABCD中,E为DC边上的点,连结BE, 将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF, 若∠BEC=600,则∠EFD的度数为( )BA.100 B.150 C.200 D.250 2、(2013.山东聊城)如图,在等边△ABC中, AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,
苏科版八年级数学下册第九章《9.1 图形的旋转2》公开课课件

•
A
B'
B
C
C'
A' O
一个图形和它经过旋转所得到的图形中,对应点 到旋转中心距离相等,两组对应点与旋转中心连线所 成的角相等.
问题1 如图,在正方形ABCD中,E是BC上一
点,△ABE经过旋转后得到△ADF.
F
A
D
B E
C
后,(点((3G12)旋))如旋若转果转连到中接点了心EG什F是是,么哪A那位一B么的点置△中??AE旋点F转是,角什那为么么多三经少角过度形?上?述旋转
初中数学 八年级(下册)
9.1 图形的旋转
你能再举出生活中类似的例子吗?
探索活动一
1.将一块三角尺放在一张白纸上,画下它的外轮 廓,记为△ABC.
2.将三角尺绕直角顶点按逆时针方向旋转一定的 角度,再画下它的外轮廓,记为△A′B′C .
A A'
对应点:
B'
对应边:
对应角:
C
B
思考:什么叫做图形的旋转?
BB
A′
A
A′
A
B′ B′
O
课堂小结
将图形绕一个定点转动一定的角度,这样的图形 运动叫做图形的旋转。
这个定点叫做旋转中心;
旋转的角度叫做旋转角;
图形的旋转三要素:旋转中心,旋转方向,旋转角度.
一个图形和它经过旋转所得到的图形中,对应点到 旋转中心距离相等,两组对应点与旋转中心连线所成 的角相等.
• 15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年7月2021/7/312021/7/31206、提出一个问题往往比解决一个更重要。因为解决问题也许仅是一个数学上或实验上的技能而已,而提出新的问题,却需要有创造性的想像力,而且标志着科学的真正进步。2021/7/312021/7/31July 31, 2021
A
B'
B
C
C'
A' O
一个图形和它经过旋转所得到的图形中,对应点 到旋转中心距离相等,两组对应点与旋转中心连线所 成的角相等.
问题1 如图,在正方形ABCD中,E是BC上一
点,△ABE经过旋转后得到△ADF.
F
A
D
B E
C
后,(点((3G12)旋))如旋若转果转连到中接点了心EG什F是是,么哪A那位一B么的点置△中??AE旋点F转是,角什那为么么多三经少角过度形?上?述旋转
初中数学 八年级(下册)
9.1 图形的旋转
你能再举出生活中类似的例子吗?
探索活动一
1.将一块三角尺放在一张白纸上,画下它的外轮 廓,记为△ABC.
2.将三角尺绕直角顶点按逆时针方向旋转一定的 角度,再画下它的外轮廓,记为△A′B′C .
A A'
对应点:
B'
对应边:
对应角:
C
B
思考:什么叫做图形的旋转?
BB
A′
A
A′
A
B′ B′
O
课堂小结
将图形绕一个定点转动一定的角度,这样的图形 运动叫做图形的旋转。
这个定点叫做旋转中心;
旋转的角度叫做旋转角;
图形的旋转三要素:旋转中心,旋转方向,旋转角度.
一个图形和它经过旋转所得到的图形中,对应点到 旋转中心距离相等,两组对应点与旋转中心连线所成 的角相等.
• 15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年7月2021/7/312021/7/31206、提出一个问题往往比解决一个更重要。因为解决问题也许仅是一个数学上或实验上的技能而已,而提出新的问题,却需要有创造性的想像力,而且标志着科学的真正进步。2021/7/312021/7/31July 31, 2021
北师大版八年级下册数学3.2图形的旋转课件(共15张PPT)

某个方向转动一个角度,这样的图形
如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案? 把正方形ABCD绕CD的 2、探索旋转的基本性质; 把正方形ABCD绕CD的 1、通过具体实例认识平面图形的旋转; 5、经历有关旋转的观察、操作、分析等过程,积累
将∆ABC绕点O旋转到∆A'B'C'的位置 2、探索旋转的基本性质; 2、探索旋转的基本性质; 这节课,你的收获是什么?
把正方形ABCD绕CD的 在平面内,将一个图形绕一个定点按
某个方向转动一个角度,这样的图形
1、通过具体实例认识平面图形的旋转; 2、探索旋转的基本性质; 数学活动经验,增强动手能力。
运动称为旋转。 2、探索旋转的基本性质;
5、经历有关旋转的观察、操作、分析等过程,积累 1、通过具体实例认识平面图形的旋转;
经典习题
如图,正方形ABCD和正方形CDEF有公共边CD,请 设计方案,使正方形ABCD旋转后能与正方形CDEF 重合,你能写出几种方案?
解: 方案一: 把正方形ABCD绕点D
让我们的生活 一片灿烂
在变中寻找不变 ———人类永恒的追求
2、探索旋转的基本性质;
在平面内,将一个图形绕一个定点按 3、会进行简单的旋转画图;
2、探索旋转的基本性质; 查阅:http://baike. 在平面内,将一个图形绕一个定点按
2、探索旋转的基本性质; 2、探索旋转的基本性质; 某个方向转动一个角度,这样的图形
1、课本P79-80 1、2
某个方向转动一个角度,这样的图形 1、通过具体实例认识平面图形的旋转;
1、课本P79-80 1、2 这节课,你的收获是什么?
如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案? 把正方形ABCD绕CD的 2、探索旋转的基本性质; 把正方形ABCD绕CD的 1、通过具体实例认识平面图形的旋转; 5、经历有关旋转的观察、操作、分析等过程,积累
将∆ABC绕点O旋转到∆A'B'C'的位置 2、探索旋转的基本性质; 2、探索旋转的基本性质; 这节课,你的收获是什么?
把正方形ABCD绕CD的 在平面内,将一个图形绕一个定点按
某个方向转动一个角度,这样的图形
1、通过具体实例认识平面图形的旋转; 2、探索旋转的基本性质; 数学活动经验,增强动手能力。
运动称为旋转。 2、探索旋转的基本性质;
5、经历有关旋转的观察、操作、分析等过程,积累 1、通过具体实例认识平面图形的旋转;
经典习题
如图,正方形ABCD和正方形CDEF有公共边CD,请 设计方案,使正方形ABCD旋转后能与正方形CDEF 重合,你能写出几种方案?
解: 方案一: 把正方形ABCD绕点D
让我们的生活 一片灿烂
在变中寻找不变 ———人类永恒的追求
2、探索旋转的基本性质;
在平面内,将一个图形绕一个定点按 3、会进行简单的旋转画图;
2、探索旋转的基本性质; 查阅:http://baike. 在平面内,将一个图形绕一个定点按
2、探索旋转的基本性质; 2、探索旋转的基本性质; 某个方向转动一个角度,这样的图形
1、课本P79-80 1、2
某个方向转动一个角度,这样的图形 1、通过具体实例认识平面图形的旋转;
1、课本P79-80 1、2 这节课,你的收获是什么?
八年级下册数学图形的旋转(2)课件全文

700
850
课堂练习
3. 如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为 . 4. 如图,把Rt⊿ABC绕点A逆时针旋转40°,得Rt⊿AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′= 度.
1.6
20
课堂练习
5.下图是由正方形ABCD旋转而成。
(1)旋转中心是__________ (2) 旋转的角度是_________
点A
450
(3) 若正方形的边长是1,则C'D=_________
C'
D'
B'
B
A
C
D
课堂练习
结论总结
通过本节课的内容,你有哪些收获?
怎样在方格纸上画出一个图形绕某个点旋转后的图形。
旋转的性质
11.2图形的旋转 第2课时
学习目标: 1. 在方格纸中会画图形旋转后的新图形。 2. 探索已知点绕原点按逆时针方向旋转90 度时的坐标变化规律。 3.探索图形之间的旋转变化关系,培养学生分析问题,解决问题的能力。
线段OB的对应线段是线段______
∠A的对应角是______
线段AB的对应线段是线段______
∠B的对应角是______
旋转中心是点______
旋转的角度是 ______
点B的对应点是点_____
如图,是△AOB绕点O按逆时针方向旋转450所得的。
B’
0B’
A’B’
∠A’
∠B’
O
450
D'
D
A'
A
850
课堂练习
3. 如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为 . 4. 如图,把Rt⊿ABC绕点A逆时针旋转40°,得Rt⊿AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′= 度.
1.6
20
课堂练习
5.下图是由正方形ABCD旋转而成。
(1)旋转中心是__________ (2) 旋转的角度是_________
点A
450
(3) 若正方形的边长是1,则C'D=_________
C'
D'
B'
B
A
C
D
课堂练习
结论总结
通过本节课的内容,你有哪些收获?
怎样在方格纸上画出一个图形绕某个点旋转后的图形。
旋转的性质
11.2图形的旋转 第2课时
学习目标: 1. 在方格纸中会画图形旋转后的新图形。 2. 探索已知点绕原点按逆时针方向旋转90 度时的坐标变化规律。 3.探索图形之间的旋转变化关系,培养学生分析问题,解决问题的能力。
线段OB的对应线段是线段______
∠A的对应角是______
线段AB的对应线段是线段______
∠B的对应角是______
旋转中心是点______
旋转的角度是 ______
点B的对应点是点_____
如图,是△AOB绕点O按逆时针方向旋转450所得的。
B’
0B’
A’B’
∠A’
∠B’
O
450
D'
D
A'
A
北师大版数学八年级下册3.2《图形的旋转》 课件(共21张PPT)

(1)上面情景中的运动现象,有什么共 同的特征? (2)在运动过程中,摩天轮的座椅、钟 表的指针,风车的风叶其形状、大小、位 置是否发生变化呢?
“旋转”的定义:
在平面内,将一个图形绕( 一个定点 )按 ( 某个方向 )转动( 一个角度 ),这样的图形运
动称为旋转。
这个定点称为_旋__转___中__心___ 转动的角称为__旋__转__角____
总结归纳
“旋转”的基本性质:
(1)旋转不改变图形的_形__状__和___大__小___; (2)对应线段_相__等____,对应角_相__等___; (3)对应点到旋转中心的距离_相___等___;
(4)任意一对对应点与旋转中心的连线所成的角
都是__旋__转___角__。
练习3
下列(1)-(4)的四个三角形中,哪个不能由△ABC经过平移 或旋转得到?
如图,ABC是等边三角形,D是BC上一点, ABD经过旋转后到达 ACE的位置。
(1)旋转中心是哪一点?
A
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过
M.
上述旋转后,点M转到了什么位置4)连接DE,△ADE是什么三角形?
课堂小结
1、旋转的定义: “三要素” 一个定点 某个方向 一个角度
作业
1、基础作业:
课本P77习题3.4
2、提高作业:
学案练习题1、2
△ADE绕点A按_顺__时__针__方向旋转_9_0__度旋转到△ABE’
逆时针
270
思考:图形的旋转是由什么决定的?
旋转中心
旋转方向 旋转角度
三要素
△ABC绕点O按顺时针方向旋转一个
角度,得到△DEF。
H
H’
《图形的旋转》公开课教学PPT课件【北师大版八年级数学下册】

第三章第二节图形的旋转北师大版统编教材八年级数学下册新课导入观察思考观察思考新课讲解新课讲解fabdeo?你能否描述一下什么叫旋转
北师大版·统编教材八年级数学下册
第三章 · 第二节
图形的旋转
新课导入
观察思考
观察思考
新课讲解
新课讲解
• 你能否描述一下什么叫旋转?
B
D
F
A
E O
新课讲解
1.旋转的定义:
对应点到旋转中心的距离相等;
旋转不改变图形的形状和大小。
3. 旋转图形的形成描述:“五说明”
基本图形、旋转中心、方向、次数、旋转角.
“这个图案可以看成是
绕点 按 时针方向旋转 次,分别旋
转
前后的所有图形共同组成的。”
拓展延伸
Байду номын сангаас
再见
答:旋转7次得到,旋转角度分别等于45°, 90°, 135°, 180°, 225°, 270 °,315°.
图案欣赏
图案欣赏
E
O
知识归纳
知识点归纳
1. 旋转的定义:“四要素”
“四、三、五”
一个图形、一个定点、一个方向、一个角度. 2. 旋转的性质:“三特点” 对应点与旋转中心的连线所成的角都是旋转角;
随堂练习
拓展练习
拓展练习1
图案可以看作是一个菱形通过几次旋转 得到的?每次旋转了多少角度?
拓展练习
图案可以看作是一个菱形通过几次旋转得到的? 每次旋转了多少角度?
答:旋转5次得到,旋转角度分别等于60°, 120°, 180°, 240°, 300°.
拓展练习
拓展练习2:
下图可看作是一个等腰三角形通过几次旋转得到的?每次旋转多少度?
北师大版·统编教材八年级数学下册
第三章 · 第二节
图形的旋转
新课导入
观察思考
观察思考
新课讲解
新课讲解
• 你能否描述一下什么叫旋转?
B
D
F
A
E O
新课讲解
1.旋转的定义:
对应点到旋转中心的距离相等;
旋转不改变图形的形状和大小。
3. 旋转图形的形成描述:“五说明”
基本图形、旋转中心、方向、次数、旋转角.
“这个图案可以看成是
绕点 按 时针方向旋转 次,分别旋
转
前后的所有图形共同组成的。”
拓展延伸
Байду номын сангаас
再见
答:旋转7次得到,旋转角度分别等于45°, 90°, 135°, 180°, 225°, 270 °,315°.
图案欣赏
图案欣赏
E
O
知识归纳
知识点归纳
1. 旋转的定义:“四要素”
“四、三、五”
一个图形、一个定点、一个方向、一个角度. 2. 旋转的性质:“三特点” 对应点与旋转中心的连线所成的角都是旋转角;
随堂练习
拓展练习
拓展练习1
图案可以看作是一个菱形通过几次旋转 得到的?每次旋转了多少角度?
拓展练习
图案可以看作是一个菱形通过几次旋转得到的? 每次旋转了多少角度?
答:旋转5次得到,旋转角度分别等于60°, 120°, 180°, 240°, 300°.
拓展练习
拓展练习2:
下图可看作是一个等腰三角形通过几次旋转得到的?每次旋转多少度?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2. 如图,将△ABC绕点A逆时针旋转一定角度,得到 △ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC 的度数为( 850 )
课堂练习
3. 如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将
△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B
的对应点D恰好落在BC边上时,则CD的长为 1.6 .
点B的对应点是点___B_’_
线段OB的对应线段是线段__0_B__’_
B 线段AB的对应线段是线段__A__’_B_’
∠A的对应角是___∠__A_’
A
∠B的对应角是__∠__B__’
旋转中心是点____O__
旋转的角度是 __4__5_0 _
C B
D●
新课学习
A 例1.在图所示的方格纸上,
图案ABCDO是由等腰直角 三角形ABO和等腰直角三角 形CDO拼成的,画出这个图
●O 案绕点O按逆时针方向旋转
90°得到的图案
C
新课学习
A
B
D
●
A`
B` ●
●
C`
●O ● D`
新课学习
C
A
B
D
0
新课学习
C
A
B
0 D
变式练习
BB
CCC
AA
●
O
新课学习
A
D
E
B D`
C
新课学习
A
D
E
B D`
C
课堂练习
1. 如图,在直角△OAB中,∠AOB=30°,将△OAB绕点O 逆时针旋转100°得到△OA1B1,∠A1OB= 700 .
4. 如图,把Rt⊿ABC绕点A逆时针旋转40°,得
Rt⊿AB′C′,点C′恰好落在边AB上,连接BB′,则
∠BB′C′= 20 度.
B/
B
C/
A
C
课堂练习
5.下图是由正方形ABCD旋转而成。
(1)旋转中心是____点__A____
C
(2) 旋转的角度是__4_5_0_____
C'
B'
(3) 若正方形的边长是1,则
D
B C'D=____2___1__
D'
A
结论总结
通过本节课的内容,你有哪些收获?
怎样在方格纸上画出一个图形绕某个点旋转后 的图形。
zxxkw
11.2图形的旋转 第2课时
学习目标:
1. 在方格纸中会画图形旋转后的新图形。 2. 探索已知点绕原点按逆时针方向旋转90 度时的坐标变化规律。 3.探索图形之间的旋转变化关系,培养学 生分析问题,解决问题的能力。
如图,是△AOB绕点O按逆时针方向旋转450 所得的。
B'
A' D'
O
D
旋转角是:
温故知新
旋转的定义
在平面内,将一个图形绕一个定点按某一个方向(逆时 针或顺时针方向)转动一定的角度,这样的变换叫做图 形的旋转,这个定点叫做旋转中心,这个角叫做旋转角 旋转后图形的位置是由旋转中心、旋转方向和旋转角确 定的。
旋转的性质
一个图形和它经过旋转所得到的图形中
对应点到旋转中心的距离相等; 两组对应点分别与旋转中心的连线所成的角相等
课堂练习
3. 如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将
△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B
的对应点D恰好落在BC边上时,则CD的长为 1.6 .
点B的对应点是点___B_’_
线段OB的对应线段是线段__0_B__’_
B 线段AB的对应线段是线段__A__’_B_’
∠A的对应角是___∠__A_’
A
∠B的对应角是__∠__B__’
旋转中心是点____O__
旋转的角度是 __4__5_0 _
C B
D●
新课学习
A 例1.在图所示的方格纸上,
图案ABCDO是由等腰直角 三角形ABO和等腰直角三角 形CDO拼成的,画出这个图
●O 案绕点O按逆时针方向旋转
90°得到的图案
C
新课学习
A
B
D
●
A`
B` ●
●
C`
●O ● D`
新课学习
C
A
B
D
0
新课学习
C
A
B
0 D
变式练习
BB
CCC
AA
●
O
新课学习
A
D
E
B D`
C
新课学习
A
D
E
B D`
C
课堂练习
1. 如图,在直角△OAB中,∠AOB=30°,将△OAB绕点O 逆时针旋转100°得到△OA1B1,∠A1OB= 700 .
4. 如图,把Rt⊿ABC绕点A逆时针旋转40°,得
Rt⊿AB′C′,点C′恰好落在边AB上,连接BB′,则
∠BB′C′= 20 度.
B/
B
C/
A
C
课堂练习
5.下图是由正方形ABCD旋转而成。
(1)旋转中心是____点__A____
C
(2) 旋转的角度是__4_5_0_____
C'
B'
(3) 若正方形的边长是1,则
D
B C'D=____2___1__
D'
A
结论总结
通过本节课的内容,你有哪些收获?
怎样在方格纸上画出一个图形绕某个点旋转后 的图形。
zxxkw
11.2图形的旋转 第2课时
学习目标:
1. 在方格纸中会画图形旋转后的新图形。 2. 探索已知点绕原点按逆时针方向旋转90 度时的坐标变化规律。 3.探索图形之间的旋转变化关系,培养学 生分析问题,解决问题的能力。
如图,是△AOB绕点O按逆时针方向旋转450 所得的。
B'
A' D'
O
D
旋转角是:
温故知新
旋转的定义
在平面内,将一个图形绕一个定点按某一个方向(逆时 针或顺时针方向)转动一定的角度,这样的变换叫做图 形的旋转,这个定点叫做旋转中心,这个角叫做旋转角 旋转后图形的位置是由旋转中心、旋转方向和旋转角确 定的。
旋转的性质
一个图形和它经过旋转所得到的图形中
对应点到旋转中心的距离相等; 两组对应点分别与旋转中心的连线所成的角相等
