公考数量关系课程
公务员考试之数量关系
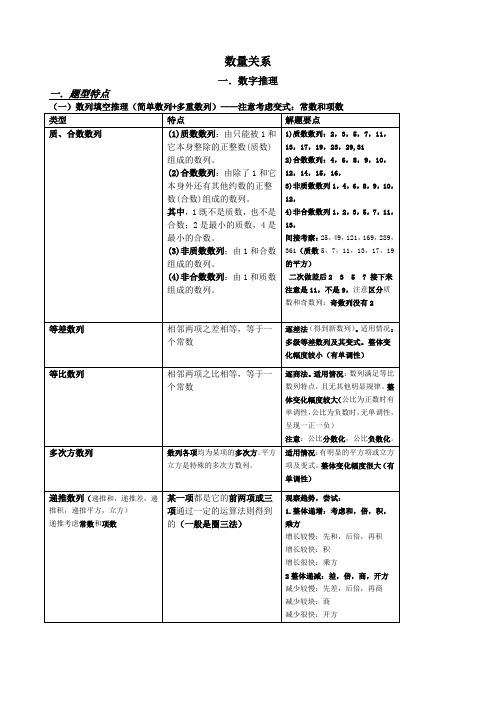
数量关系一.数字推理一.题型特点(一)数列填空推理(简单数列+多重数列)——注意考虑变式:常数和项数类型特点解题要点质、合数数列(1)质数数列:由只能被1和它本身整除的正整数(质数)组成的数列。
(2)合数数列:由除了1和它本身外还有其他约数的正整数(合数)组成的数列。
其中,1既不是质数,也不是合数;2是最小的质数,4是最小的合数。
(3)非质数数列:由1和合数组成的数列。
(4)非合数数列:由1和质数组成的数列。
1)质数数列:2,3,5,7,11,13,17,19,23,29,312)合数数列:4,6,8,9,10,12,14,15,16,3)非质数数列1,4,6,8,9,10,12,4)非合数数列1,2,3,5,7,11,13,间接考察:25,49,121,169,289,361(质数5,7,11,13,17,19的平方)二次做差后2 3 5 7 接下来注意是11,不是9,注意区分质数和奇数列:奇数列没有2等差数列相邻两项之差相等,等于一个常数逐差法(得到新数列)。
适用情况:多级等差数列及其变式。
整体变化幅度较小(有单调性)等比数列相邻两项之比相等,等于一个常数逐商法。
适用情况:数列满足等比数列特点,且无其他明显规律。
整体变化幅度较大(公比为正数时有单调性,公比为负数时,无单调性,呈现一正一负)注意:公比分数化,公比负数化。
多次方数列数列各项均为某项的多次方。
平方立方是特殊的多次方数列。
适用情况:有明显的平方项或立方项及变式。
整体变化幅度很大(有单调性)递推数列(递推和,递推差,递推积,递推平方,立方)递推考虑常数和项数某一项都是它的前两项或三项通过一定的运算法则得到的(一般是圈三法)观察趋势,尝试:1.整体递增:考虑和,倍,积,乘方增长较慢:先和,后倍,再积增长较快:积增长很快:乘方2整体递减:差,倍,商,开方减少较慢:先差,后倍,再商减少较块:商减少很快:开方根式数列数列中含根式的数列1根次之间存在关系2根次相同时,可以把根号外面的数化到根号里面去(或把根号里面的数化到外面去),看底数关系3根式的底数存在关系4.根次,底数分别存在一定的关系。
公务员考试数量关系真题及答案讲解

第一章 解题方法第一节 代入排除法 2 2 第二节 数字特性法 第三节 方程法 3 4 第四节 赋值法 5 第二章 比例问题67 67 62 63 64 64 65 22 28 28 24 29 2: ;6第一节 工程问题 第二节 经济利润问题 第三节 行程问题第三章 计数问题、几何问题第一节 容斥原理第二节 排列组合与概率 第三节 几何问题 第四章 其他问题第一节 最不利构造 第二节 数列构造 第三节 时间相关问题 第四节 植树、方阵问题 第五节 牛吃草问题数量关系第一章解题方法第一节代入排除法代入排除适合题型:(1)选项信息充分的题目(选项数据比较多,两个及两个以上,优先代入排除);(2)多位数问题、余数问题、年龄问题等;(3)从正面无法入手的题目,一般问题是“可能”或是“不可能”考虑代入排除。
【例 1】孙儿孙女的平均年龄是 10 岁,孙儿年龄的平方减去孙女年龄的平方所得的数值,正好是爷爷出生年份的后两位,爷爷生于上个世纪 40 年代。
问孙儿孙女的年龄差是多少岁?(A. 2)B. 4D. 8C. 6【例 2】三位运动员跨台阶,台阶总数在 100-150 级之间,第一位运动员每次跨 3 级台阶,最后一步还剩 2 级台阶。
第二位运动员每次跨 4 级台阶,最后一步还剩 3 级台阶。
第三位运动员每次跨 5 级台阶,最后一步还剩 4 级台阶。
则这些台阶总共有()级。
A.119 C.129B.121 D.131【例 3】某工厂有甲、乙、丙 3 条生产线,每小时均生产整数件产品。
其中甲生产线的效率是乙生产线的 3 倍,且每小时比丙生产线多生产 9 件产品。
已知 3 条生产线每小时生产的产品之和不到 100 件且为质数,则乙生产线每小时最多可能生产多少件产品?A.14 C.11B.12 D.8【例 4】有 A、B 两瓶混合液,A 瓶中水、油、醋的比例为 3:8:5,B 瓶中水、油、醋的比例为 1:2:3,将 A、B 两瓶混合液倒在一起后,得到的混合液中水、油、醋的比例可能为:A.4:5:2 C.3:7:7B.2:3:5 D.1:3:1第二节数字特性法奇偶特性:【基础】奇数±奇数=偶数;偶数±偶数=偶数;奇数±偶数=奇数;奇数×奇数=奇数;奇数×偶数=偶数;偶数×偶数=偶数。
公考行测数量关系-计数模型问题

1. 张、王、刘和李四人进行象棋比赛,每两人之间都要赛一局。
已知张胜了两局,王平了三局,问刘和李加起来最多胜了几局:根据单循环赛规则,一共是进行了场比赛。
王平了三局则有王的三局比赛结果都是平局,不会出现胜负,即刘、李与王比赛的结果均平;接下来张胜了两局,就一定是胜了刘、李,即刘、李均负;最后一局未确定结果的比赛就是刘对李,出现平局或者胜负,最多只有一方胜。
综上,故刘、李加起来最多胜利1局。
2. 某条道路的一侧种植了25棵杨树,其中道路两端各种有一棵,且所有相邻的树距离相等。
现在需要增种10棵树,且通过移动一部分树(不含首尾两棵)使所有相邻的树距离相等,则这25棵树中有多少棵不需要移动位置:本题为植树问题。
原间隔数为,现有间隔数为,两者最小公倍数为408,据此赋值该道路长度为408米。
那么可知原来每隔17米种一棵,而调整后为每隔12米种一棵。
注意到17和12的最小公倍数为204,即位于204米处的树不需要移动位置,加上首尾2棵,共3棵树不需要移动位置。
3. 某乒乓球俱乐部决定举办一场所有会员间的循环赛,经俱乐部委员会计算,所需比赛场数刚刚超过2000场,即使省略掉委员会委员们之间的比赛,场数仍有2001场,那么这个乒乓球俱乐部有多少委员:假设该俱乐部共有会员假设该俱乐部共有会员人,委员会委员人,根据题意可得,。
可知越小,的值越小,越符合比赛场数刚刚超过2000场。
从小到大代入验证。
将A项代若,则可得,可以解得,为整数解。
因此该俱乐部有6个委员。
其他选项代入,不符合题意。
4. 甲、乙、丙三人打羽毛球,每一局由两人上场,另一人做裁判。
第一局抽签决定裁判,往后每一局的比赛在上一局的胜者和上一局的裁判之间进行。
打了若干场之后,甲胜了10局,则乙和丙各负了8局,则他们至少打了多少局:甲胜了10场,乙和丙各负了8局,那么乙和丙进行了场比赛。
而这6场比不能连续进行,需要穿插每一场胜者与甲之间的比赛,因而还需要插入5场比赛,因此至少需要局数为局。
公务员考试数量关系

公务员考试数量关系单价×数量=总价单产量×面积=总产量速度×时间=路程总价÷数量=单价总产量÷面积=单产量路程÷速度=时间总价÷单价=数量总产量÷单产量=面积路程÷时间=速度效率×时间=工作总量图上距离÷实际距离=比例尺工作总量÷工作时间=工作效率实际距离×比例尺=图上距离工作总量÷工作效率=工作时间图上距离÷比例尺=实际距离本金×利率×时间=利息成活率=成活棵数/总棵数合格率=合格/总每份数×份数=总数总数÷每份数=份数总数÷份数=每份数加数+加数=和和-一个加数=另一个加数被减数-减数=差被减数-差=减数差+减数=被减数因数×因数=积积÷一个因数=另一个因数被除数÷除数=商被除数÷商=除数商×除数=被除数相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间运算定律加法交换律a+b=b+a加法结合律a+b+c=(a+b)+c=a+(b+c)=(a+c)+b乘法交换律ab=ba 乘法结合律abc=(ab)c=a(bc)=(ac)b乘法分配律a(b+c)=ab+ac减法的运算性质a-b-c=a-(b+c)除法的运算性质a÷b÷c=a÷(b×c)商不变的性质a÷b=(a×x)÷(b×x)=(a÷x)÷(b÷x)(x≠0)分数的基本性质比的基本性质a:b=(a×x):(b×x)=(a÷x):(b÷x)(x≠0)比例的基本性质:因为a:b=c:d所以ad=bc计算公式长方形的周长C=(a+b)×2 长方形的面积S=ab正方形的周长C=4a 正方形的面积S=a2平行四边形的面积S=ah 三角形的面积S=ah÷2梯形的面积S=(a+b)×h÷2圆的周长C=2πr或C=πd 圆的面积S=πr2或S=π(d÷2)2长方体的表面积S=(ab+ah+bh)×2 长方体的体积V=abh正方体的表面积S=6a2 正方体的体积V=a3圆柱体的表面积S=2πrh+πr2×2 圆柱体的体积V=Sh 或V=πr2 圆锥体的体积V=Sh÷3或V=πr2h÷3小学单位换算表【长度单位】1千米=1000米1米=10分米1厘米=10毫米1分米=10厘米【面积单位】1平方千米=100公顷1公顷=10000平方米1平方千米=1000000平方米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米【体积单位】1立方千米=1000000立方米1立方米=1000立方分米1立方分米=1000立方厘米1立方厘米=1000立方毫米【容积单位】1升=1000毫升1立方分米=1升1立方厘米=1毫升【重量单位】1吨=1000千克1千克=1000克【人民币单位换算】1元=10角1角=10分【时间换算】1世纪=100年1年=12月1日=24小时1时=60分1分=60秒注意:大月(31天)有:1、3、5、7、8、10、12等七个月;小月(30天)有:4、6、9、11等四个月;在平年时2月有28天,在闰年2月有29天。
公务员行测数量关系知识点整理

公务员行测数量关系知识点整理公务员考试中,行测的数量关系部分一直是众多考生的难点和重点。
数量关系涉及的知识点繁多,题型复杂,需要我们系统地学习和掌握。
下面就为大家整理一下常见的数量关系知识点。
一、数学运算1、整数特性整数特性是数量关系中的基础知识点。
包括整除特性、奇偶性、质数与合数等。
整除特性:若整数 a 除以非零整数 b,商为整数,且余数为零,我们就说 a 能被 b 整除。
比如,能被 2 整除的数的特征是个位是偶数;能被 3 整除的数,其各位数字之和能被 3 整除。
奇偶性:奇数±奇数=偶数,偶数±偶数=偶数,奇数±偶数=奇数。
质数与合数:质数是指在大于 1 的自然数中,除了 1 和它本身以外不再有其他因数的自然数。
合数是指自然数中除了能被 1 和本身整除外,还能被其他数(0 除外)整除的数。
2、方程与不等式方程是解决数量关系问题的常用工具。
通过设未知数,根据题目中的等量关系列出方程,然后求解。
一元一次方程:形如 ax + b = 0(a≠0)的方程。
二元一次方程组:由两个未知数,且未知数的次数都是 1 的方程组成。
不等式:用不等号(大于>、小于<、大于等于≥、小于等于≤)连接两个代数式的式子。
3、比例问题比例是指两个比相等的式子。
常见的有工程问题中的效率比、行程问题中的速度比等。
若 a:b = c:d,则 ad = bc。
4、行程问题行程问题是数量关系中的重点和难点。
基本公式:路程=速度×时间。
相遇问题:路程和=速度和×相遇时间。
追及问题:路程差=速度差×追及时间。
5、工程问题工程问题的核心是工作总量=工作效率×工作时间。
经常通过设工作总量为 1 或工作总量的最小公倍数来解题。
6、利润问题涉及成本、售价、利润、利润率等概念。
利润=售价成本,利润率=利润÷成本×100% 。
7、几何问题包括平面几何和立体几何。
【花生十三】25年公务员考试数量关系随堂笔记

小数点后尾数是0.6,x 可以是8、18、28……想买的笔总数尽量多,那需要多买便宜的,因此要x 尽量大,选项最大到22,x ≤22,x 最大取到18。
1.7x=1.7×18=30.6,代入方程3y+4z=10,4z 和10都是2的倍数,因此3y 也是2的倍数,3不是2的倍数,所以y 是2的倍数。
y=2时,z=1,总数为18+2+1=21.例题9(2020浙江)某会务组租了20多辆车将2220名参会者从酒店接到活动现场。
大车每次能送50人,小车每次能送36人,所有车辆送2趟,且所有车辆均满员,正好送完,则大车比小车?A .多5辆B .多2辆C .少2辆D .少5辆【答案】A【解析】设大车x 辆,小车y 辆。
所有车辆送2趟,则送1趟是:50x+36y=1110,整理得:25x+18y=555.25x 和555是5的倍数,18y 也得是5的倍数,18不是5的倍数,y 是5的倍数。
当y=5,不符合;当y=10,x=15,符合题目要求。
例题10(2022江苏)某企业年终评选了30名优秀员工,分三个等级,分别按每人10万元、5万元、1万元给与奖励。
若共发放奖金89万元,则获得1万元奖金的员工有多少?A .14人B .19人C .20人D .21人 【答案】B【解析】设获得3个奖项的优秀员工分别有x 、y 、z 人,根据题意,可列方程:⎩⎨⎧=++=++3089510z y x z y x 联立,整理可得:4z=61+5x ,61是奇数,4z 是偶数,奇数+奇数=偶数,所以5x 也是奇数,x=1、3、5……分别试解,当x=3时,z=19,y=18,符合题意,选B 。
例题11(2024联考)商店销售甲、乙、丙、丁四种商品,每件分别盈利15元、9元、4元和1元。
某日销售这四种商品共40件,共盈利201元。
四种商品每种至少销售1件,且甲、丁商品销量相同。
设甲效率为3,天,故选D。
例题9(2024联考)包粽子3小时,比李师傅多包14A.224C.320【答案】A5A+5B=6A+2B,解得A=3B方法二:假设工作总量为A=1.5份,B=0.5份,1.5份-0.5例题10(2019国考)有甲、乙、丙三个工作组,A工程如由甲、乙组共同工作3完成,需要整7天。
cctalk刘文超数量关系讲义

cctalk刘文超数量关系讲义
摘要:
一、课程简介
- 课程名称:CCTalk 刘文超数量关系讲义
- 课程内容:数量关系
- 适合人群:备考公务员、事业单位、银行、选调生、村官等考试的学员
二、课程目标
- 帮助学员掌握数量关系的基本解题方法
- 提高学员在考试中解决数量关系问题的效率和准确率
三、课程特色
- 讲师刘文超具有丰富的教学经验,擅长用生动形象的例子解释抽象的概念
- 课程内容详实,涵盖数量关系的各种题型和解题技巧
- 课程设置有答疑环节,学员可以在课程中提出自己的疑问,讲师会进行解答
四、课程内容
- 数量关系基本概念和公式
- 数量关系题型及解题技巧
1.数字推理
2.数列问题
3.比例问题
4.平均数问题
5.几何问题
6.其他问题
- 课程实战训练及答疑
正文:
CCTalk 刘文超数量关系讲义是一门针对备考公务员、事业单位、银行、选调生、村官等考试的学员开设的课程。
课程内容涵盖数量关系的基本概念和公式,以及各种题型和解题技巧。
通过学习本课程,学员可以掌握数量关系的基本解题方法,提高在考试中解决数量关系问题的效率和准确率。
课程由经验丰富的讲师刘文超主讲,他擅长用生动形象的例子解释抽象的概念,让学员更容易理解和掌握。
课程设置有答疑环节,学员可以在课程中提出自己的疑问,讲师会进行解答,帮助学员更好地消化和吸收课程内容。
课程内容详实,包括数字推理、数列问题、比例问题、平均数问题、几何问题等题型,以及比例问题、其他问题等。
课程还设有实战训练环节,让学员通过实际题目演练,更好地掌握课程内容。
公务员考试中的数量关系与数据分析

34
工作环境有所帮助。
增强时间管理能力:数量 关系题目往往需要在有限 的时间内完成,这需要公 务员具备良好的时间管理 能力,合理安排时间,提
高工作效率。
数量关系考察的能力
数学运算能力:包括基本的算术运算、代数运算等,是数量关系考察的基本能力。
逻辑思维:通过数量关系的题目,考察考生对问题进行分析、推理和解决的能力。
分布情况
占比与排名:计 算占比和排名, 了解数据在总体 中的比例和位置
相关性分析:通 过计算相关系数, 分析两个变量之
间的关联程度
回归分析:利用 回归方程,预测
因变量的取值
添加标题
添加标题
添加标题
添加标题
数据分析的实际应用
商业决策:数据分析帮助 企业做出更明智的商业决 策,例如市场趋势预测、 消费者行为分析等。
综合应用在考试中的题型及解题方法
数据分析题型:包括表格分析、 图表分析、数据推理等,解题方 法包括对比分析、趋势分析、结 构分析等。
综合应用题型:将数量关系和数 据分析结合起来,考察考生的综 合应用能力,解题方法需要结合 数量关系和数据分析的解题方法。
数量关系题型:包括计算问题、 比例问题、几何问题等,解题方 法包括代数法、方程法、比例法 等。
PART 03
数量关系的基本概念与 解题技巧
10
数量关系的概念
定义:数量关系是指数学中对象之间所存在的关系,如大小关系、相等关系、和差关系等。
解题技巧:掌握基本概念和公式,理解题意,分析数量关系,选择合适的数学模型进行计算。 重要性:数量关系是公务员考试中必考的知识点之一,掌握数量关系的基本概念和解题技巧 对于提高考试成绩至关重要。
PART 05
行测数量关系讲解

行测数量关系讲解数量关系题是公务员考试中非常重要的一类题型,在行测中占据了相当大的比重,是参加公务员考试的考生必须掌握的内容。
本文将为大家介绍数量关系的概念、分类、解题思路和常见的解题方法。
一、数量关系的定义数量关系是指在一组数据中,通过某种数学方法进行计算、分析、比较和推理,发现其中的联系、规律、趋势和问题,以达到求解问题的目的。
在数量关系的分析中,常常涉及到数字、数量、比例、百分数、平均数、中位数、标准差等概念。
数量关系题型按照计算方式可以分为比例关系、百分数关系、平均数关系、倍数关系等。
按照计算技巧可以分为等量代换法、解方程法、逆推法等。
1. 比例关系:通过分析两个或多个数据之间的比例来解决问题。
比例关系通常涉及到数字的增减和变化,需要注意比例的转化和比例的换算。
2. 百分数关系:通过百分数对数据的描述和比较来解决问题。
百分数关系是在比例关系的基础上进行转换的,需要掌握常见的百分数运算和百分数与小数之间的转换。
3. 平均数关系:通过平均数的计算和比较来解决问题。
平均数是一组数据的总和除以个数,可以反映数据的集中程度和趋势。
在平均数关系的解题中,需要注意加权平均数和修改后的平均数等概念。
三、数量关系的解题思路在解决数量关系题目时,一般可以采取如下的解题思路:1. 读懂题干和数据:理解问题的意义和数据的含义,把问题具体化和明确化。
2. 提取关键信息:找出题目中的关键数据、关键词语和关键推理,明确问题的要点和难点。
3. 分析数据关系:把数据进行分类、比较和分析,找出规律和趋势,掌握数据之间的数量关系。
4. 选择解题方法:根据数据的特点和要求,选择合适的计算方法和技巧,解决具体的问题。
5. 核对答案:对计算结果进行核对和评估,避免疏漏和错误。
四、常见的解题方法1. 等量代换法:通过等式两侧的等量代换来解决问题,比如将数据进行整体增减、分组代替和变量代入等。
2. 解方程法:通过方程的通解和特解来解决问题,比如利用一次方程、二次方程和联立方程等。
公务员考试行测数量关系知识点

公务员考试行测数量关系知识点公务员考试中的行政职业能力测验(简称行测)是众多考生需要攻克的难关,而其中的数量关系部分更是让许多人感到头疼。
数量关系主要考查考生对数学运算和数学思维的运用能力,涵盖了众多知识点和题型。
接下来,我们就详细梳理一下这部分的重要知识点。
一、数字推理数字推理是数量关系中的常见题型,要求考生通过分析给定的数字序列,找出其中的规律并推测出下一个数字。
1、等差数列这是最基础的规律之一。
相邻两项的差值相等,例如:1,3,5,7,9,差值均为 2。
2、等比数列相邻两项的比值相等。
比如:2,4,8,16,32,比值均为 2。
3、多次方数列数字是某个数的平方、立方或多次方。
例如:1,4,9,16,25 分别是 1、2、3、4、5 的平方。
4、组合数列数列由两个或多个简单数列组合而成,需要分别分析不同部分的规律。
5、递推数列通过前面若干项的运算得到下一项,如前两项相加等于第三项等。
二、数学运算数学运算包含了各种各样的实际问题和数学模型。
1、行程问题涉及速度、时间和路程之间的关系。
如相遇问题、追及问题等。
相遇问题:路程=速度和×相遇时间。
追及问题:路程差=速度差×追及时间。
2、工程问题工作总量=工作效率×工作时间。
常考的有合作完工问题,根据各自工作效率和合作方式来计算完成工作的时间。
3、利润问题涉及成本、售价、利润、利润率等概念。
利润=售价成本,利润率=利润÷成本×100% 。
4、排列组合问题排列是有顺序的,组合是无顺序的。
例如从 5 个人中选 3 个人排成一排,这是排列;从 5 个人中选 3 个人组成一组,这是组合。
5、概率问题计算某个事件发生的可能性大小。
古典概率:概率=有利事件数÷总事件数。
6、容斥原理用于解决集合之间的重叠问题。
两集合容斥:总数= A + B 既 A 又 B +既非 A 又非 B 。
三、解题方法1、方程法这是最基本也是最常用的方法。
公考-数量关系

数量关系代入排除法1.什么时候用?(1)看题型:①年龄:比如题目中出现2/3/4 个人(比如甲、乙、丙),已知他们年龄之间的关系。
②余数:题目中出现一个数除以几余几,或者分给每人三个余两个,分东西余几,有余数的词汇的时候。
③不定方程:比如x+y=10,未知数的个数比方程个数多,比如两个未知数只有一个方程,或者三个未知数只有两个方程。
④多位数:题目中出现三位数、四位数,告诉个/十/百位有变化,比如个位比十位大3,把个位和十位对调之后会发生怎样的变化等。
(2)看选项:①选项为一组数(比如例1):比如A 项是甲=10,乙=20,告诉了甲和乙两个值,就是一组数。
这类情况的问法一般是“分别/各是多少”,可以代两个/三个数,代入的未知数越多,题目越好验证。
②选项可以转化为一组数:问题问的是甲等于多少,比如A 项是10,但是条件明确告知乙等于甲的两倍(乙=2*甲),丙等于甲的一半(丙=甲/2)……,虽然选项只有甲可以代入,但是根据条件可以推出乙和丙(乙=20,丙=5),相当于转化为一组数。
(3)剩二代一:四个选项往往有两个选项错得比较明显,比如四个选项是3、4、5、6,根据应该是3 的倍数这一条件排除了选项中不是3 的倍数的选项(排除4 和5),四个选项只剩两个选项以后,没必要正常算,代入一个(比如代入3),如果3 对,选3,如果3 不对,直接选6。
剩下两个选项任意代入一个,对了就选,不对就选另一个。
排除不了再进行代入:①从好算的入手:比如选项有100 和135,从简单入手,就先代入100。
②问最值:比如选项有100 和135,如果问最多,先代135,因为如果100和135 都是对的,只代入100 验证了是正确的,就选了100 就错了。
问最多,从最大的开始代,问最小,从最小的开始代。
倍数特性法1.整除型:(1)理论:若A=B*C(B、C 均为整数),A、B、C 是三个量,则A 能被 B 或C 整除。
2.余数型:除以几之后余几。
【备战公务员考试】数量关系:用代入排除法、倍数特性法、方程法快速解题

数量关系:三大解题方法(第一课时)【注意】1.提前预习,学得轻松;做好复习,学得扎实。
2.学习任务:(1)课程内容:讲解三大解题方法,从方法的角度讲解数量关系应该如何做题,都是非常简单且很好认知的方法):代入排除法、倍数特性法(存在技巧)、方程法(列方程,比较好接受)。
(2)重点内容:有同学学习数量关系是一听就会、一做就废,之所以会出现这种尴尬的情况,是因为做题的时候没有形成思维,思维其实就是一种套路,遇到什么题型就应该怎么想。
①掌握代入排除法的适用范围及使用方法。
②掌握倍数特性法的基础知识,以及余数型和比例型的解题思路。
③掌握设未知数的技巧,熟悉不定方程的解题思路。
第一节代入排除法【注意】代入排除法(把选项代入题干,对则选,不对则排除):并不是所有的题目都能代入求解,一套题中有 1~2 题能代出来就不错了。
1.什么时候“代”。
2.怎么“代”。
3.代入排除的“逻辑”。
【知识点】什么时候“代”:分三个维度。
1.题型:(1)年龄问题(题干涉及年龄):①例:3 年前张三的年龄是他女儿的 17 倍,3 年后张三的年龄是他女儿的 5 倍,那么张三的女儿现在:A.2 岁B.3 岁C.4 岁D.5 岁答:题干都是关于年龄的表述,为年龄问题,将选项代入题干,代入的时候需要结合常识,如年龄差不变,如今年老师和 A 相差7 岁,若干年后仍差 7 岁;法定婚龄必须满足客观事实,必须在满足法定婚龄之后才能结婚生子,太小或不成年则是不允许的,哪怕数据能对上也不行,因为公务员考试要符合最基本的价值观、法律和法规。
问小张女儿现在的年龄,3 年前女儿是存在的,故排除 A、B 项(3 年前不能是 0 岁或没出生),代入 C 项:女儿 3 年前1 岁,张三才 17 岁,这不太现实、不满足法定婚龄,排除 C 项,D 项当选。
题干分为 3 年前、现在、3 年后这三个时间点,代入时间点进行验证,看能否对应。
考试的时候,A、B、C 项明显错误,D 项不需要再验证,行测题不能没有答案,验证是费劲不讨好,掉入思维的误区,若 D 项也验证错误,则更耽误了自己的时间。
《行测——数量关系》公务员考试复习指南

《行测——数量关系》公务员考试复习指南一、引言在公务员考试的行测科目中,数量关系部分往往是考生们倍感压力的一环。
它不仅考察考生的数学基础,还检验其逻辑思维能力和解题技巧。
为了帮助广大考生更好地应对这一挑战,本复习指南将详细解读数量关系部分的考查内容、复习策略及解题技巧,并结合具体例子进行深入讲解。
二、数量关系考查内容概述数量关系部分主要包括数字推理和数学运算两大模块。
数字推理主要考察考生对数列规律、数字特征等的识别和推理能力;数学运算则侧重于考查考生对基本数学运算、应用题等方面的掌握程度。
具体来说,数字推理可能涉及等差数列、等比数列、质数、合数等概念,而数学运算则可能包括代数运算、几何计算、概率统计等内容。
三、复习策略系统梳理基础知识数量关系部分涉及的知识点较多,考生需要首先系统梳理数学基础知识,包括代数、几何、数列、概率统计等。
对于每个知识点,考生都要确保理解其基本概念、公式和定理,并能够熟练运用。
熟悉题型和解题思路通过大量练习,考生需要熟悉各种数量关系的题型和解题思路。
特别是对于常见的题型,如数字推理中的等差数列、等比数列等,以及数学运算中的方程求解、比例计算等,考生要能够迅速识别并找到正确的解题方法。
注重练习和反思练习是提高解题能力的关键。
考生需要通过大量的练习来巩固所学知识,提高解题速度和准确性。
在练习过程中,考生要注重反思和总结,分析错题原因,找出自己的不足之处,有针对性地进行改进。
四、解题技巧与实例讲解数字推理解题技巧(1)观察法观察法是解答数字推理题的基本方法。
考生需要仔细观察数列或数字的特征,找出其中的规律。
例如,对于等差数列,考生可以通过观察相邻两项的差是否相等来判断其是否为等差数列;对于等比数列,则可以通过观察相邻两项的比值是否相等来判断。
【例1】1.3.7.13.( )A. 21B. 22C. 23D. 24解析:观察数列,发现从第二项开始,每一项与前一项的差分别为2、4、6.即一个等差数列。
省考国考公务员笔试课件-数量关系(226页)

数量关系数量关系是什么数量关系主要测查报考者理解、把握事物间量化关系和解决数量关系问题的能力,主要涉及数据关系的分析、推理、判断、运算等。
常见的题型有:数字推理、数学运算等。
61626364656667686970工程方程最值计算函数时间排列组合行程计算概率经济时间时间概率方程排列组合几何工程函数几何经济几何概率计算经济工程方程排列组合最值方程201620172018数学思维:选项特征、特殊取值、方程思想、定性分析数学模型:行程问题、工程问题、经济问题、几何问题、函数问题、排列组合问题概率问题、容斥问题、最值问题、不等问题、浓度问题、时间问题牛吃草问题、植树问题、方阵问题11-19的平方:112=121122=144132=169142=196152=225162=256172=289182=324192=361 15、25、……、95的平方化乘为除错位相加错位相减原则:你不是一个人在战斗技巧:尾数法范围性奇偶性顺序性适用范围:多位数问题余数问题年龄问题比例问题例1.有一个三位数,其百位数是个位数的2倍,十位数等于百位数和个位数之和,那么这三位数是:()A.211B.432C.693D.824例2.某个三位数的数值是其各位数字之和的23倍。
这个三位数为:()A.702 B.306 C.207 D.203例3.某汽车厂商生产甲、乙、丙三种车型,其中乙型产量的3倍与丙型产量的6倍之和等于甲型产量的4倍,甲型产量与乙型的2倍之和等于丙型产量的7倍。
则甲、乙、丙三型产量之比为()A.5:4:3B.4:3:2C.4:2:1D.3:2:1例4.有一些信件,把它们平均分成三份后还剩2封,将其中两份平均三等分还多出2封,问这些信件至少有多少封?( )A.20B.26C.23D.29例5.有四个学生恰好一个比一个大一岁,他们的年龄相乘等于93024,问其中最大的年龄是多少岁?()A.16岁B.18岁C.19岁D.20岁例6.有一堆围棋子,白子颗数是黑子的3倍,每次拿出5颗白子,3颗黑子,经过若干次后,剩下的白子是黑子的9倍。
公考”数量关系+资料分析“公式

4.3. 2. 22 3 31. 5.公式:利润=单价-成本;期望利润=定价-成本;实际利润=售价-成本;利润率=利润÷成本;售价=定价× 折扣;总售价=单价×销售量;总利润=单件利润×销售量相遇追及问题:相遇距离 S=(V 1+V 2)×相遇时间t ;追及距离 S=(V 1-V 2)×追及时间 t环形运动问题:环形周长 S=(V 1+V 2)×反向运动时间;环形周长 S=(V 1-V 2)×同向运动时间;环线型n 次相遇,共同行走的距离=n×环线长度流水行船问题:顺流速度=静水船速+水速;逆流速度=静水船速-水速;顺流航程 S=(V 船+V 水)×顺流时间 t ;逆流航程S=(V 船-V 水)×逆流时间 t两集合型:A+B-A∩B=满足条件 A 或 B 的情况数三集合标准型:A+B+C-A∩B -A∩C -B∩C+A∩B∩C=总数-一个条件都不满足的情况数三集合非标准型:A+B+C-只满足两个条件的情况数-2×满足三个条件的情况数=总数-一个条件都不满足的情况数常用面积公式:S 正方形 =a²,S 长方形 =ab ,S 圆=πr²,S 三角形 =ah ,S 平行四边形 =ah ,S =(a+b )h ,S n 360πr ² 常用表面积公式:正方体表面积=6a²,长方体表面积=2ab+2ac+2bc ,圆柱表面积=2πrh+2πr²,圆柱的侧面积=2πrh,球的表面积=4πr²常用体积公式:正方体体积=a³,长方体体积=abc ,球的体积=4 πr ³,圆柱的体积=πr²h,圆锥(棱锥) 的体积=1×底面积×高数资必备公式 = 梯形 扇形7.6.工作总量=工作效率×工作时间常用方法:①套用公式②给定时间型:只出现工作时间没有出现效率之间关系的,赋值工作总量为工作时间的最小公倍数;效率制约型:出现工作效率之间的关系,直接赋值工作效率为简单值公式:R=r +r +r ×r ,间隔基期量=现期量 (注:r 与 r 分别代表最近两年的增长率) 1 2 1 2 1+间隔增长率1 2 例:2016 年、2017 年和 2018 年当年,2018 年相对于 2017 年,以及 2017 年相对于 2016 年的增长率分别为 r 1 与 r 2。
公务员考试行测讲义-数量关系

【行测讲义】数量关系一、数量关系简介数量关系主要是考查应试者对数量关系的理解,其主要有两大题型,一是数字推理,二是数学运算。
数字推理主要是考察应试者对数字和运算的敏感程度。
本质上来看,是考察是考生对出题考官的出题思路的把握,因为在数字推理中的规律并非“客观规律”,而是出题考官的“主观规律”,也就是说,在备考过程中,不能仅从数字本身进行思考,还必须深入地理解出题者的思路与规律。
数学运算基本题型众多,每一基本题型都有其核心的解题公式或解题思路,应通过练习不断熟练。
在此基础上,有意识培养自己的综合分析能力,即在复杂数学运算题面前,能够透过现象看到本质,挖掘其中深层次的等量关系。
从备考内容来看,无论是数字推理还是数学运算,都需要从思路和技巧两方面来着手准备。
上篇数字推理数字推理的题目通常状况下是给你一个数列,但整个数列中缺少一项(中间或两边),要求应试者仔细观察这个数列各数字之间的关系,判断其中的规律,然后在四个选择答案中选择最合理的答案。
一、数字推理要点简述(一)解题关键点1.培养数字、数列敏感度是应对数字推理的关键2.熟练掌握各种基本数列(自然数列、平方数列、立方数列等)3.熟练掌握常见的简单数列,并深刻理解“变式”的概念(1)应掌握的基本数列如下:常数数列7,7,7,7, 7,7,7 …自然数列:1,2,3,4,5,6,7……奇数列:1,3,5,7,9,11……偶数列:2,4,6,8,10,12……自然数平方数列:1,4,9,16,25,36……自然数立方数列:1,8,27,64,125,216……等差数列:1,6,11,16,21,26……等比数列:1,3,9,27,81,243……质数数列2,3,5,7,11,13,17,19…《质数是指只能被1和其本身整除的数(1既不是质数,也不是合数)》合数数列4,6,8,9,10,12,14,15…合数是指除1和质数之外的自然数。
周期数列1,3,4,1,3,4…幂次数列1,4,9,16,25,…1,8,27,64,125,…递推数列1,1,2,3,5,8,13…对称数列1,3,2,5,2,3,1…1,3,2,5,-5,-2,-3,-1…4.进行大量的习题训练(二)熟练掌握数字推理的解题技巧1、观察题干,大胆假设。
《行测数量关系》课件

04
行测数量关系真题解析
历年真题回顾
1 2
2018年行测数量关系真题
考察了工程问题、溶液问题、概率问题等。
2019年行测数量关系真题
涉及了行程问题、排列组合问题、几何问题等。
3
2020年行测数量关系真题
主要考察了利润问题、年龄问题、概率问题等。
真题解析方法
掌握基本概念
理解并掌握数量关系中的基本概 念,如比例、百分比、平均数等
模拟试题三及答案解析
总结词
这道题目考察的是概率的计算方法,需要考生根据题 干中的信息,运用概率的计算公式计算出正确的概率 值。
详细描述
题目给出了一组数据和一组事件,要求考生根据这组 数据和事件,运用概率的计算公式计算出正确的概率 值。首先,考生需要仔细阅读题干,理解题目的要求 和数据、事件之间的关系。然后,运用概率的计算公 式,计算出每个事件发生的概率值。最后,比较计算 出的概率值与题目要求的概率值是否一致,并判断各 事件之间的关系是否符合题目的要求。
推理规则
理解推理规则,如三段论 、假言推理、选言推理等 ,是解决逻辑推理题目的 基础。
逻辑谬误
识别常见的逻辑谬误,如 偷换概念、假两难等,有 助于提高逻辑思维能力。
论证结构
掌握论证结构的分析方法 ,能够准确把握论证的核 心观点和论据。
图表分析知识
图表识别
数据可视化
能够识别并理解各种类型的图表,如 柱状图、折线图、饼图等。
THANKS
感谢观看
02
行测数量关系基础知识
数学基础知识
01
02
03
代数运算
包括方程求解、不等式求 解、函数等代数知识,是 解决数量关系题目的基础 。
公考数量关系总结

公考数量关系总结嘿,朋友们!说起公考中的数量关系,那可真是一场有趣又有点“烧脑”的挑战。
咱们先来瞧瞧这数量关系到底是个啥。
你就把它想象成一个神秘的宝库,里面藏着各种宝贝,可你得有正确的钥匙才能打开,拿到高分。
这钥匙呢,就是咱们的解题方法和技巧。
比如说行程问题,就像是你和朋友约好了在某个地方碰面,你得算好啥时候能到,走多快,花多长时间。
是不是感觉挺熟悉的?再比如说工程问题,就好比盖房子,几个人一起干活,各自的效率不同,得算出多久能完工。
还有那些排列组合的问题,哎呀,就像给一群调皮的小朋友排座位,得考虑怎么排才能让他们都满意,还不重样。
还有利润问题,这不就是做生意嘛,得算算成本多少,卖多少能赚钱。
那怎么才能搞定这些问题呢?首先,基础得打牢。
公式定理啥的,一定要烂熟于心。
这就像练武之人要扎马步,根基稳了,才能施展拳脚。
然后呢,多做题!别偷懒,别觉得烦。
题做多了,你就会发现,很多题目都是换汤不换药,套路都差不多。
还有啊,一定要学会总结错题。
做错的题目,可都是你的“财富”,好好分析为啥错,下次遇到类似的,就不会再掉坑里啦。
这就好比走路摔了一跤,你得记住这地方有个坑,下次绕着走。
另外,考试的时候,别死磕一道题。
时间宝贵着呢,要是一道题想半天都没头绪,赶紧放下,先做后面的。
可别为了一棵歪脖子树,放弃了整片大森林。
朋友们,公考的数量关系其实没那么可怕。
只要咱们用心去学,多练多总结,还怕拿不到高分?加油吧,相信自己一定能行!总之,数量关系就是公考中的一道坎,迈过去,前面就是光明大道。
别害怕,勇敢冲!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、某单位男女员工的人数之比是15:13。
按人数之比5:7:8,分为甲、乙、丙三个科室,其中甲科室男女员工的人数之比为4:3,乙科室为5:2。
则丙科室男女员工人数之比为:
A.1:2
B.2:3
C.5:9
D.5:8
2、某校组织师生春游,已知有397名师生出游,旅游公司有39座和17座两种客车,问要让所有人都有座位,且客车上没有空座,一共需要几辆车?
A.10辆
B.11辆
C.12辆
D.13辆
3、车间共用50名工人。
年底进行考核,有12人业务能力为优,10人政治表现为优。
没有一项考核成绩为优的有34人。
车间要向上级单位推荐2名两项考核均为优的工人作为先进个人的候选人,问有多少种推荐方案?
A12B15C18D21
4、甲、乙两工厂接到一批成衣订单,如一起生产,需要20天时间完成任务,如乙工厂单独生产,需要50天时间才能完成任务。
已知甲工厂比乙工厂每天多生产100件成衣,则订单总量是多少件成衣?
A8000B10000C12000D15000
5、某工程队原定10天完成一段道路工程,实际提前两天完成任务,问每天的工作量比计划平均提高了()
A15%B20%C25%D30%
6、一项复印工作,如果由复印机A、B单独完成,分别需50分钟、40分钟。
现两台复印机同时工作20分钟后,B机器损坏需要维修,余下工作由A机器单独完成,则完成这项复印工作共需时间()分钟。
A.5
B.15
C.20
D.25
7、某年2月份有5个星期日,4个星期六,则2月1日是
A星期四B星期五C星期六D星期日
8、有甲乙两个水池,其中甲水池中一直有水注入,如果分别用8台抽水机去抽空甲和乙水池,分别需要16小时和4小时,如给甲水池加5台,提前10小时抽完。
若共安排20台抽水机,则为了保证两个水池能同时抽空,在甲水池的抽水机比乙水池多多少台?
A.4
B.6
C.8
D.10
9、甲、乙、丙三个办公室的职工参加植树活动,三个办公室人均植树分别为4,5,6棵,三个办公室植树总数彼此相等。
问这三个办公室总共至少有多少职工?
A37B53C74D106
10、甲、乙两人从环形跑道的A点同时出发背向而行,6分钟后两人第一次相遇,相遇后两人的速度各增加10米每分钟,5分钟后两人第二次相遇。
问环形跑道的长度为多少米?
A600B500C400D300
11、某高校两校区相距2760米,甲,乙两同学从各自校区同时出发到对方校区,甲的速度为70米每分钟,乙的速度为110米每分钟,在路上二人第一次相遇后继续行进,到达对方校区后马上回返,那么两人从出发到第二次相遇需要多少分钟?
A.32
B.46
C.61
D.64
12、老王和老李沿着小公园的环形小路散步,两人同时出发,当老王走到一半路程时,老李走了100米;当老王回到起点时,老李走了5/6的路程。
问环形小路总长多少米?
A.200
B.240
C.250
D.300
13、张老师家四代同堂,且从父亲、张老师、儿子到孙子,每两代人的年龄差相同。
5年前张老师父亲的年龄是儿子的3倍,8年后张老师的年龄是孙子的5倍。
问今年四个人的年龄之和为:
A.168岁
B.172岁
C.176岁
D.180岁
14、一块三角形农田ABC(如下图所示)被DE、EF两条道路分成三块。
已知BD=2AD,CE=2AE,CF=2BF,则三角形ADE、三角形CEF和四边形BDEF的面积之比为:
A.1:3:3
B.1:3:4
C.1:4:4
D.1:4:5。
