纳什均衡(课堂作业)
纳什均衡计算题例题

选择题:在一个博弈中,如果所有玩家都不能通过改变策略来增加自己的收益,那么这个博弈的结果被称为:A. 优势策略均衡B. 纳什均衡(正确答案)C. 劣势策略均衡D. 混合策略均衡在一个两人零和博弈中,如果玩家A的策略改变不会导致其收益增加,同时玩家B的策略也是最优的,那么这个博弈处于:A. 非合作均衡B. 纳什均衡(正确答案)C. 合作均衡D. 优势策略均衡纳什均衡的概念是由哪位经济学家提出的?A. 亚当·斯密B. 约翰·纳什(正确答案)C. 阿尔弗雷德·马歇尔D. 保罗·萨缪尔森在一个博弈中,如果存在一个策略组合,使得每个玩家都不能通过单方面改变策略来增加收益,那么这个策略组合是:A. 劣势策略组合B. 优势策略组合C. 纳什均衡(正确答案)D. 混合策略组合下列哪个选项不是纳什均衡的特征?A. 每个玩家的策略都是最优的B. 玩家之间不能通过合作来增加收益C. 博弈的结果是可预测的(正确答案)D. 给定其他玩家的策略,每个玩家的策略都是最优反应在一个非合作博弈中,如果所有玩家都选择了最优策略,并且没有人愿意改变策略,那么这个博弈的结果是:A. 合作均衡B. 纳什均衡(正确答案)C. 混合策略均衡D. 优势策略均衡纳什均衡在博弈论中的重要性体现在:A. 它总是导致最优的社会结果B. 它是一种稳定的博弈结果,没有人愿意单方面改变策略(正确答案)C. 它总是导致公平的博弈结果D. 它是一种容易实现的博弈结果在一个博弈中,如果玩家A的策略改变会导致其收益减少,同时玩家B的策略也是最优的,那么这个博弈:A. 可能不是纳什均衡B. 一定是纳什均衡(正确答案)C. 一定是合作均衡D. 一定是混合策略均衡下列哪个选项描述了纳什均衡的一个可能结果?A. 所有玩家都获得了最大可能的收益B. 至少有一个玩家可以通过改变策略来增加收益C. 给定其他玩家的策略,每个玩家都没有动机改变策略(正确答案)D. 所有玩家都选择了劣势策略。
三方博弈纳什均衡例题

三方博弈纳什均衡例题全文共四篇示例,供读者参考第一篇示例:三方博弈是博弈论中一种常见的情形,指的是有三方参与并且彼此之间存在竞争和合作关系的博弈情况。
纳什均衡是博弈论中的一个重要概念,指的是在博弈中每个玩家都做出最佳决策的情况下所达到的一个稳定状态。
在三方博弈中,如果存在某种情况下所有玩家都无法通过改变自身策略而获益,这种状态就是三方博弈的纳什均衡。
下面我们通过一个例子来说明三方博弈纳什均衡的概念。
假设有三位学生A、B、C参加了一个考试竞赛,在这个竞赛中,他们可以选择合作作弊,也可以选择正当的考试。
如果三位学生都选择正当考试,那么每个人都能得到10分的成绩;如果某一位学生作弊而其他两人选择正当考试,那么作弊的学生可以得到15分,而其他两人得0分;如果所有人都选择作弊,那么每个人只能得到5分。
同理,对于学生B和C来说,选择作弊也是更有利的策略。
第二篇示例:三方博弈是博弈论中的一个重要概念,指的是有三个各自独立的决策者同时做出决策的情况。
在三方博弈中,每个决策者都会考虑其他两方的利益和行为,以最大化自己的利益。
纳什均衡是博弈论中一个非常重要的概念,是指在一个博弈当中,每个参与者都选择了最优的行动策略,没有任何一方可以通过改变自己的策略来获得更好的结果。
下面我们来看一个关于三方博弈纳什均衡的例题。
假设有三个玩家A、B、C,他们在一个零和博弈中,并且每个玩家都只有两种可行的策略,分别是合作和背叛。
博弈的收益矩阵如下表所示:| | 合作| 背叛|| ---- | ------ | ------ || 合作| 3,3,3 | 1,4,4 || 背叛| 4,4,1 | 0,2,2 |在这个收益矩阵中,每个元素表示每个玩家在不同组合下的收益,例如当A、B、C都选择合作时,他们的收益分别是3,当A、B、C都选择背叛时,他们的收益分别是2。
现在我们来分析一下这个博弈的纳什均衡。
我们来看一下玩家A的最佳策略。
玩家A会根据其他两个玩家的策略来选择自己的策略,如果B、C都选择合作,那么玩家A选择背叛可以得到更高的收益4;如果B、C都选择背叛,那么玩家A也选择背叛可以得到更高的收益4。
博弈论习题

由于老板在决定是否克扣工资欠可以完全清楚工人是否偷懒,因此这是一个 动态博弈,而且是一个完全信息的动态博弈。此外,由于双方都有关于得益 的充分信息,因此只是一个完全且完美信息的动态博弈。该博弈用扩展形表 示如下:
工人
偷懒
不偷懒
克扣
老板
不克扣
克扣
老板
不克扣
(40,40) )
(100,-20) )
(-10,110) )
而开辟第二战场可共选择的方案有两个:1.塞纳河东岸的布龙捏—加来—敦刻 尔克一带,这是英吉利海峡最狭窄的地方,只有几十公里,是一个理想的登陆地 点2.塞纳河西岸的诺曼底,但这里海面比较宽阔,渡海时间较长,容易被德军发 现。当时,德军在西线的总兵力是58个师,要布防在近5000公里的海岸线上, 因此,德军只能把主要兵力放在他们认为盟军可能的登陆地点的上述两个地方。 同时盟军在英国集结也由于受登陆舰船的限制,数量也有限,只能考虑集中有限 兵力重点进攻一个地方。所以,对德军和盟军怎样选择、怎样判断成为这次跨海 作战的关键。
在某工商管理学院 MBA 创业方案的讨论中,有三位同学准备创办 一个企业。同学甲经过多年经营拥有一定资本,同学乙拥有某项专
利所有权,同学丙有很快的社会交际和营销能力。该创业项目需投 资 100 万元,由甲进行投资,若乙和丙不愿参加,甲可以拥有这 100 万元的自由支配权若甲和丙不愿参加,乙可以将所拥有的专利 实行有价转让,而获利 80 万元 ; 若甲和乙不愿参加,丙 可以到其 它公司,在该项目生命期内工作收入 20 万元 ; 若甲和乙单独合作, 可将专利转换为成熟的生 产技术,再转卖可获利 200 万元 ; 若甲和 丙单独合作,则不可能获利 ; 若乙和丙单独合作,可将专利的转让 价格提高到 120 万元 ; 若甲、乙和丙三人合作,可获利 400 万元。 请把该问题用一个合作博弈给予表示
博弈论作业——精选推荐
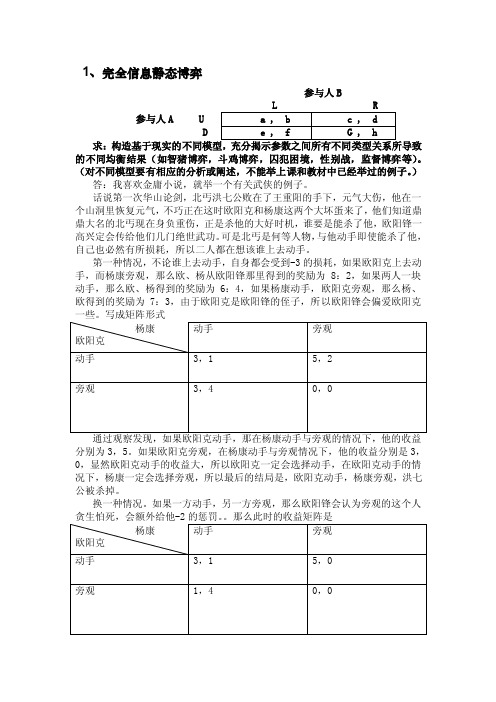
1、完全信息静态博弈参与人B参与人A UD求:的不同均衡结果(如智猪博弈,斗鸡博弈,囚犯困境,性别战,监督博弈等)。
(对不同模型要有相应的分析或阐述,不能举上课和教材中已经举过的例子。
)答:我喜欢金庸小说,就举一个有关武侠的例子。
话说第一次华山论剑,北丐洪七公败在了王重阳的手下,元气大伤,他在一个山洞里恢复元气,不巧正在这时欧阳克和杨康这两个大坏蛋来了,他们知道鼎鼎大名的北丐现在身负重伤,正是杀他的大好时机,谁要是能杀了他,欧阳锋一高兴定会传给他们几门绝世武功。
可是北丐是何等人物,与他动手即使能杀了他,自己也必然有所损耗,所以二人都在想该谁上去动手。
第一种情况,不论谁上去动手,自身都会受到-3的损耗,如果欧阳克上去动手,而杨康旁观,那么欧、杨从欧阳锋那里得到的奖励为8:2,如果两人一块动手,那么欧、杨得到的奖励为6:4,如果杨康动手,欧阳克旁观,那么杨、欧得到的奖励为7:3,由于欧阳克是欧阳锋的侄子,所以欧阳锋会偏爱欧阳克分别为3,5。
如果欧阳克旁观,在杨康动手与旁观情况下,他的收益分别是3,0,显然欧阳克动手的收益大,所以欧阳克一定会选择动手,在欧阳克动手的情况下,杨康一定会选择旁观,所以最后的结局是,欧阳克动手,杨康旁观,洪七公被杀掉。
换一种情况。
如果一方动手,另一方旁观,那么欧阳锋会认为旁观的这个人可见,如果欧阳克动手,那在杨康动手与旁观的情况下,他的收益分别为3,5。
如果欧阳克旁观,那在杨康动手与旁观的情况下,他的收益分别为1,0。
所以他一定会选择动手,对杨康来说,动手的收益分别为1,4,旁观的收益分别是0,0,所以他一定会选择动手,最终的结果一定是,欧、杨两人一起动手杀掉七公。
第三种情况。
由于洪七公是天下第一大帮丐帮帮主,杀掉他的人一定会得罪丐帮,得罪天下武林同道,以后难以立足江湖,自身会受到-3的损伤,此时的如果杨康选择旁观,那么它的收益分别为0,0。
所以杨康一定不会动手。
同样,欧阳克选择动手,收益分别是-1,1.如果选择旁观收益分别为1,0。
三方博弈纳什均衡例题

三方博弈纳什均衡例题博弈论是研究决策主体的行为发生直接相互作用时候的决策以及这种决策的均衡问题的理论。
在博弈论中,当参与博弈的决策主体超过两个时,我们称之为多方博弈。
纳什均衡是博弈论中的一个核心概念,它描述的是在给定其他参与者策略的情况下,每个参与者都选择自己的最优策略,从而使得所有参与者的策略构成一个稳定的状态。
下面,我们将通过一个具体的三方博弈的例子来详细解析纳什均衡的概念和应用。
例题:假设有三个公司A、B、C分别生产同类产品,并且它们的市场份额相当。
为了扩大自己的市场份额,每个公司都有两种策略可以选择:增加产量(进攻策略)或减少产量(保守策略)。
这三个公司的决策是相互影响的,每个公司的策略都会对其他两个公司的市场份额产生影响。
1.如果所有公司都选择增加产量,由于市场竞争的加剧,每个公司的市场份额都会下降,假设每个公司的收益都为-1(表示市场份额下降,收益减少)。
2.如果所有公司都选择减少产量,由于市场供应减少,每个公司的市场份额都会上升,假设每个公司的收益都为1(表示市场份额上升,收益增加)。
3.如果其中两家公司选择增加产量,而另一家公司选择减少产量,那么增加产量的两家公司的市场份额会略有上升,而减少产量的公司的市场份额会大幅下降。
假设增加产量的公司的收益为0,减少产量的公司的收益为-2。
4.如果其中两家公司选择减少产量,而另一家公司选择增加产量,那么增加产量的公司的市场份额会大幅增加,而减少产量的两家公司的市场份额会略有下降。
假设增加产量的公司的收益为2,减少产量的公司的收益为0。
基于以上情况,我们可以构建如下的收益矩阵:现在,我们来分析这个三方博弈的纳什均衡。
首先,我们考虑公司A的选择。
如果B和C都选择增加产量(策略为进攻),那么A的最优策略是减少产量(保守策略),因为这样可以避免市场份额的大幅下降。
如果B和C都选择减少产量(策略为保守),那么A的最优策略是增加产量(进攻策略),因为这样可以抓住市场机会增加自己的市场份额。
纳什均衡

弈
猜
-1, 1
硬
币
1, -1
1, -1 -1, 1
2, 1 0, 0
0, 0 1, 3
课堂习题
• 用划线法求出均衡解
C1
C2
C3
R1
0,4 4,0 5,3
R2 4,0 0,4 5,3
R3 3,5 3,5 6,6
箭头法
• 思路:
– 对博弈中的每一个策略组合进行分析,考察在每个策略组合 处各个博弈方能否通过单独改变自己的策略而增加得益
– 与划线法一样都是基于策略之间的相对优劣关系进行分析的, 所得到的结果也是一致的。
– 如果能,则从所分析的策略组合对应的得益数组引一箭头, 到改变策略后策略组合对应的得益数组
– 最后,只有指向,没有离开的策略组合为均衡解--稳定- -没有人愿意单独改变
箭头法
1, 0 0, 4
1, 3 0, 2
0, 1 2, 0
经典博弈故事之二--情侣博弈
•
大海和小丽正在热恋。难得的周末又到了,安排什么节目呢?周末晚上,
中国足球队要在世界杯外围赛中和伊朗队做生死之战。大海是个超级球迷,国
内的甲级联赛都不肯放过,何况是不争气的国家队的生死大战?也正好是这个
周末的晚上,俄罗斯一个著名芭蕾舞团莅临该市演出芭蕾舞剧《胡桃夹子》。
丽娟最崇尚钢琴、芭蕾这样的高雅艺术,对斯拉夫民族的歌唱和芭蕾更是崇拜
– 稳定的和自我强制的,所以是真正可预测的 – 反之,不具有一致预测性的博弈结果,则难以避免预测和行为之间的
矛盾,甚至是自我否定的。
•只有纳什均衡才具有一致预测的性质 •一致预测性是纳什均衡的本质属性 •一致预测并不意味着一定能准确预测,因为有多重均衡,预测不一致 的可能
耶鲁大学公开课博弈论课习题

耶鲁⼤学公开课博弈论课习题耶鲁⼤学公开课:博弈论习题集1(第1-3讲内容)Ben Polak, Econ 159a/MGT522a.由⼈⼈影视博弈论制作组Darrencui翻译1.严格劣势策略与弱劣势策略:严格劣势策略的定义是什么?弱劣势策略的定义是什么?请⽤⼀个包含两个参与⼈的博弈矩阵来举例说明,要求其中⼀个参与⼈有三个策略且三者之⼀为严格劣势策略;另⼀个参与⼈有三个策略但三者之⼀为弱劣势策略。
请指出你所举例⼦中的劣势策略。
2.迭代剔除(弱)劣势策略:请看下⾯的博弈2(a). 这个博弈中是否存在严格劣势策略和弱劣势策略?如果存在,请指出并说明。
(b). 剔除掉严格劣势策略和弱劣势策略之后,在简化的博弈中是否还有劣势策略呢?如果是,请指出并说明。
最后哪些策略不会被剔除呢?(c). 回顾你第⼀次剔除劣势策略时哪些策略是劣势策略并给出解释。
把它与第⼆次剔除的劣势策略作⽐较。
从中你能得出关于迭代剔除劣势策略的何种结论?3. 霍特林的选址博弈(也称霍特林模型):回顾⼀下课堂中所讲的选票博弈。
其中有两个参与⼈,每个参与⼈都从集合* +中选出⾃⼰的⽴场。
这⼗个⽴场均分全部的选票。
选民把选票投给与⾃⼰⽴场最接近的候选⼈。
如果两个候选⼈站在同⼀个⽴场上,那么持该⽴场选民的选票平均分给每个候选⼈。
候选⼈想要最⼤化⾃⼰的得票率。
举例来说,()。
⽽() [提⽰:回答这道题时不必画出整个矩阵](a).课堂中我们指出⽴场2严格优于⽴场1,⽽实际上还有其它的⽴场也是严格优于⽴场1的,请找出所有优于⽴场1的⽴场并作出解释。
(b).假设现在有三名候选⼈。
举例来说,()⽽()。
此时⽴场2是否严格优于⽴场1?⽴场3呢?请作出解释。
另外,假设我们剔除了⽴场1和10,但是该⽴场的选票依然存在。
在简化的博弈中,⽴场2是否严格劣于或弱劣于其它(纯)策略?请作出解释。
4. “到底谁的话语权更重”:由三⼈组成的评审委员会要决出⼀场全国艺术⼤赛的冠军。
平新乔课后习题详解(第10讲--策略性博弈与纳什均衡)

平新乔《微观经济学十八讲》第10讲策略性博弈与纳什均衡1 •假设厂商A与厂商B的平均成本与边际成本都是常数,MC A=10,MC B =8,对厂商产出的需求函数是Q D二500 -20 p(1)如果厂商进行Bertrand竞争,在纳什均衡下的市场价格是多少?(2)每个厂商的利润分别为多少?(3)这个均衡是帕累托有效吗?解:(1)如果厂商进行Bertrand竞争,纳什均衡下的市场价格是p B =10 一;,p A =10 , 其中;是一个极小的正数。
理由如下:假设均衡时厂商A和B对产品的定价分别为p A和p B,那么必有p A刃0 , p B K8,即厂商的价格一定要高于产品的平均成本。
其次,达到均衡时,p A和p B都不会严格大于10。
否则,价格高的厂商只需要把自己的价格降得比对手略低,它就可以获得整个市场,从而提高自己的利润。
所以均衡价格一定满足p A空10 , p B・「0。
但是由于p A的下限也是10,所以均衡时P A =10。
给定P A =10 ,厂商B的最优选择是令P B =10- ;,这里:是一个介于0到2 之间的正数,这时厂商B可以获得整个市场的消费者。
综上可知,均衡时的价格为P A =10 , P B =10 -;。
(2)由于厂商A的价格严格高于厂商B的价格,所以厂商A的销售量为零,从而利润也是零。
下面来确定厂商B的销售量,此时厂商B是市场上的垄断者,它的利润最大化问题为:max pq —cq ①其中p =10 _ q =500 -20 107、把这两个式子代入①式中,得到:max (10 —芯―)500 —20(10 —名卩解得;=0,由于;必须严格大于零,这就意味着;可以取一个任意小的正数,所以厂商B 的利润为:||500-20 10 -; 10-;。
(3)这个结果不是帕累托有效的。
因为厂商B的产品的价格高于它的边际成本,所以如果厂商B和消费者可以为额外1单位的产品协商一个介于8到10一;之间的价格,那么厂商B的利润和消费者的剩余就都可以得到提高,同时又不损害厂商A的剩余(因为A的利润还是零)。
4 纳什均衡

求解纳什均衡的反应函数法
当一个博弈可以用博弈矩阵表示出 来时,我们可以用划线法找出其纳什均 衡,但若一个博弈中参与人可选择的策 略有无穷多个,无法用博弈矩阵表示时, 要求出其纳什均衡,就要用到反应函数 法。 下面简要介绍库诺特寡头竞争模型 帮助大家理解反应函数法。
库诺特寡头竞争模型
关于风险厌恶的统计
究竟应取具有支付优势的NE还是取具有风险优 势的NE呢? 假设你是一个很穷的学生或者下岗职工,好不容 易在周末找了一个卖力气的工作。老板别出心裁的安 排了两种工资支付方式: 第一种:每天下班时领取100元; 第二种:由抛硬币决定你是领200元,还是一无 所得。 你会选择哪一种工资支付方式?(注:两种方式的期 望工资值相等)
假设:选民的政治态度从 0到 1排列,越往左代 表越支持劳工阶层,越往右代表越支持企业主 的利益。如下图所示:
民主党
0
· 1/2 3/4 · · 1/4
共和党
1
一个政党要想获胜,就要尽可能拉更多的 选民,因此与哪个政党所宣传的政治态度接近 的居民越多,哪个政党就获胜。
因此,我们会看到民主党会往右靠,宣布 他们也要照顾到中产阶级的利益,甚至兼顾企 业主发财;共和党也会向左靠,最终两党实际 纲领非常接近,这就是两党执政的稳定性。 (中庸之道与极端主义) 由于政客们在竞选时是怎样有利于拉选票 就怎样讲,当选就忘得一干二净,这就是两党 执政的欺骗性。
(2)商业中心区的形成
在城市街道上,我们常见到一些地 段上的商店十分拥挤,构成一个繁荣的 商业中心区,但另一些地段却十分冷僻, 没什么商店。对于这种现象,我们可以 运用杂货铺定位模型加以解释。 产品定位: 趋同化 差异化
博弈论3

定义 例题 案例研究 IEDS和纳什均衡之间的一般关系
定义: 定义:
局中人i的策略与其他局中人的策略向量, 如果它们满足
* * π i (si* , s −i ) ≥ π i (si , s −i )
对所有si,
则称是关于的最优反应。 策略向量 s* = s1* , s2*, …sN*, 如果满 足条件:
2. 决定生产的数量。为做出这个决定,公司必须权衡从增
加产量得到的好处——那样,它将出售较多产品——以及 这样做所需要的成本——即,这些大量的产品将以较低价 格出售(而它们不得不以较高的总成本生产)。当两家公 司满意地解决了这两件事时,将得到工业范围的——或纳 什—化利润的生产量
P=
α Q − β β
1
我们通过记 b = β 和 式;即,从这个观点出发我们将使用的逆需求函数为 P=a–bQ
a=
α 来简化这个(逆)需求曲线的表达 β
假设每家公司的成本函数相同,并且每单元成本不随生产 的单元数变化。更正规一些,每家公司具有常数边际成本 函数;生产数量Qi的成本为cQi,其中c > 0是常数边际成本, i = 1,2。 每家公司将生产多少?为做出该决策,每家公司必须采取 两步: 1. 对另一家公司的生产量进行预测。这一步将给于公司一 个有关可能的市场价格的想法;例如,如果它认为对手将 生产大量产品,那么,不管它自己生产多少,价格将偏低。
第5章 应用: 应用:古诺特双头卖主垄断
基本模型 古诺特古诺特-纳什均衡 卡特尔解
基本模型
古诺特提出的模型中,两家公司关于同类产品在市场上竞争。 两家公司在市场上面临单纯的需求曲线,假设需求曲线为 Q = α – βP 其中α > 0, β > 0。而Q = Q1 + Q2是由公司1和公司2生产的 总量。需求曲线的另一种理解方式是,如果Q=Q1+Q2 是 Q=Q 双寡头自身之间生产的量,由此产生的价格是
Game04纳什均衡

ui (s1 , s2 ,, si1, si , si1, sn ) ui (s1,, si1, si , si1,sn )
则称 (s1, s2,sn) 是博弈G的一个NE。
等价定义:
在博弈 G S1, S2,Sn;u1,u2,un 中,若策略组合 (s1, s2,sn )
– “cheap talk”:这种事先的口头宣告的交流方式 • 发出的信号(message)是没有成本的; • 博弈的分析不应该考虑这种信号的作用,为什 么?(见下页)
33
• 博弈人2的策略集变为:
– {Ff, Fo, Of, Oo}
(第1个数字:实际选择的策 略;第2个数字代表:宣布 的策略)
• 博弈支付没有变,实质博 弈、博弈结果不变
– 对应的NE就是强NE,否则为弱均衡;
• 强NE比弱NE更容易取舍(因为弱均衡有无差异的 策略存在);
• 强NE对博弈支付矩阵的微小改变不敏感。
16
NE的含义:
博弈G的NE指这样一个策略组合:
• 为了极大化自己的收益(效用),每个局中人所采 取的策略必定是其它局中人所采取策略的最优反应;
– 给定你的策略,我的策略是最优的;(同时)给定我 的策略,你的策略是最优的;
– 聚点就成为博弈的最终结果, 是多个NE解中的一个
• 如在一双行道上的两个相对 开车的人,各自既可选择左 行(L),也可右行(R); 共同的交通规则下,结果 (R,R)。
26
性别战
• 两NE: (F,F)和(O,O)
– 对两博弈人(夫妇), 这两均衡解不是无差异 的。
27
实验:性别战之一
• 假设你和你的女(男)朋友正在进行“性别战” 博弈。实验人群分为男、女生两组,男、女两类 实验者均做为博弈人1(丈夫)在看踢足球、看歌 剧这两个行动中进行选择。
博弈论中的纳什均衡-教案

博弈论中的纳什均衡-教案一、引言1.1博弈论的基本概念1.1.1博弈论的定义:博弈论是研究具有冲突和合作特点的决策制定过程。
1.1.2博弈论的应用:经济学、政治学、心理学等领域。
1.1.3博弈论的重要性:帮助理解竞争和合作中的决策行为。
1.1.4博弈论的局限性:假设理性人行为,实际中存在非理性行为。
1.2纳什均衡的提出1.2.2纳什均衡的意义:预测博弈结果,分析策略选择。
1.2.3纳什均衡的挑战:存在多个纳什均衡,选择合适的均衡。
1.2.4纳什均衡的应用:经济学、社会学、生物学等领域。
1.3教学目标和结构1.3.1教学目标:理解博弈论的基本概念,掌握纳什均衡的原理和应用。
1.3.3教学方法:讲授、案例分析、小组讨论。
1.3.4教学评估:课堂参与、案例分析报告、期末考试。
二、知识点讲解2.1博弈论的基本要素2.1.1参与者:博弈中的决策主体。
2.1.2策略:参与者可选择的行动方案。
2.1.3支付函数:参与者选择不同策略所得到的收益。
2.1.4结果:博弈的最终状态。
2.2纳什均衡的求解方法2.2.1纯策略纳什均衡:参与者选择确定的策略。
2.2.2混合策略纳什均衡:参与者以一定概率选择不同的策略。
2.2.3反复剔除劣势策略:通过剔除劣势策略找到纳什均衡。
2.2.4最佳响应动态:分析参与者对其他参与者策略的最佳响应。
2.3纳什均衡的应用实例2.3.1囚徒困境:两个囚犯选择合作或背叛的策略。
2.3.2鹰鸽博弈:参与者选择攻击或退让的策略。
2.3.3公地悲剧:多个参与者共享资源时的策略选择。
2.3.4供应链协调:供应商和零售商之间的策略选择。
三、教学内容3.1博弈论的基本模型3.1.1零和博弈:参与者的收益和损失相加为零。
3.1.2非零和博弈:参与者的收益和损失不相加为零。
3.1.3完美信息博弈:参与者了解其他参与者的策略和支付。
3.1.4不完美信息博弈:参与者不了解其他参与者的策略和支付。
3.2纳什均衡的性质和分类3.2.1稳定性:在纳什均衡下,参与者没有改变策略的动机。
贝叶斯纳什均衡例题

贝叶斯纳什均衡例题
贝叶斯纳什均衡 (Bayesian Nash Equilibrium) 是一种非合作的博弈理论。
在贝叶斯纳什均衡中,每个参与者根据其他参与者的策略和历史数据,计算出自己在给定其他参与者的策略下的最大收益,并采取最优策略。
以下是一个贝叶斯纳什均衡的例题。
假设有三个人,分别是 A、B、C,他们玩一个猜拳游戏。
游戏规则如下:
1. A 和 B 随机猜拳,胜负概率均为 50%。
2. 如果 A 和 B 获胜,则 C 获胜的概率为 25%。
3. 如果 A 和 B 失败,则 C 获胜的概率为 75%。
现在问,谁是游戏的胜者,如果 A 和 B 采取随机策略,而 C 采取最优策略。
根据贝叶斯纳什均衡的定义,我们需要计算出每个参与者在给定其他参与者策略下的最优策略。
首先,对于 A 和 B,由于他们是随机的,所以可以采取任何策略,因此他们的最优策略是随机。
其次,对于 C,他需要计算出自己在 A 和 B 随机策略下的最大收益。
根据游戏规则,如果 A 和 B 随机,则 C 的最大收益为 25%。
因此,C 的最优策略是采取赢的概率为 25% 的拳法。
最后,由于 C 已经采取了最优策略,A 和 B 将不得不采取随机策略。
因此,游戏的胜者是 C。
需要注意的是,贝叶斯纳什均衡只适用于非合作的博弈理论。
在合作博弈中,参与者之间的策略选择需要基于信任和相互利益。
1.3 纳什均衡应用举例

反应函数为:
1 q = R1 (q2 ) = (a − q2 − c) 2
* 1
1 * q2 = R2 (q1 ) = (a − q1 − c) 2
就是说一个企业每增加一个单位的产量,另一个 企业将减少1/2单位的产量。 返回斯坦克 1 * 尔伯格模型 故: q1* = q2 = (a − c) 3 (一)每个企业的纳什均衡利润分别为: (二)计算垄断企业的最优产量和均衡利润 x 1、利润函数: Ma Q π = Q(a − Q − c) 1 2 Q = (a − c) < q + q = (a − c) 2、最优产量: 2 3 3、垄断利润: π m = 1 (a − c)2 > 2 (a − c) 2
找纳什均衡,就是求函数极大值问题:对利 润函数求导,并令其等于零:
∂π 1 = P(q1 + q2 ) + q1 P′(q1 + q2 ) − C1′(q1 ) = 0 ∂q1
∂π 2 ′ = P (q1 + q2 ) + q2 P′(q1 + q2 ) − C2 (q2 ) = 0 ∂q2
以上两个方程都是两企业产量的函数,即反映出 两企业产量间的关系——称做反应函数。
* 2
a+b p =p = (0 < b < 2) 2−b
* 1 * 1
由此得均衡产量:
纳什均衡利润为:
(a − c + bc)2 π1 ( p , p ) = π 2 ( p , p ) = (2 − b) 2
* 1 * 2 * 1 * 2
1.3-5 公共问题
公共问题如牧场、海洋、大气、煤、石油等,他 们都存在两个关键特征:
* 价格组合 ( p1* , p2 ) 是纳什均衡价格,必须满足:
2023年网路安全题库及参考答案 (1)精选全文

精选全文完整版(可编辑修改)2023年网络安全题库及答案判断题:共 26题,每题 1分,合计 26分1.目前,我国商品和服务价格97%以上由市场定价。
对2.黑客攻击主要使用信息手段。
错对3.全面的网络安全保障要点、线、面相结合。
错对4.隐私是指不愿让他人知道自己的个人生活的秘密。
中国公民依法享有不愿公开或不愿让他人(一定范围之外的人)知悉的不危害社会的个人秘密的权利。
错对5.零信任是一种能力。
对错6.网络安全是整体的而不是割裂的,是开放的而不是封闭的,是动态的而不是静态的,是相对的而不是绝对的,是共同的而不是孤立的。
错对7.在战略方面,一定要树立正确的安全观。
对错8.安全事件分析方法就是采用定量分析方式。
错9.数据安全的要求是每个内部员工只能访问与其工作内容相关的应用和数据;所有的访问均能做到可控制、可管理、可追溯。
对错10.无知引起的最受累的错误,是形成了魔高一尺、道高一丈的局势。
对错11.人和机器最大的区别是,人的行为是会退化的。
对错12.对付黑客的时候要将其当作机器去考虑。
对错13.博弈系统只能用于网络安全。
错对14.数据是关于自然、社会现象和科学试验的定量或定性的记录,是科学研究最重要的基础。
错对15.设立国家网络安全宣传周的目的是发动群众。
错对16.数据的标准化、规范化和安全性是数据能够流动起来并创造价值的根本基础。
错对17.重要数据一般不包括个人信息和企业内部管理信息。
错对18.在网络空间安全学科的8个知识领域中,系统安全之上的3个是人文社科色彩浓厚的知识领域,占总知识领域数的60%,其余5个是理工科味道厚重的知识领域,占比40%。
对错19.数据分类具有多种视角和维度,其主要目的是便于数据管理和使用。
对20.在一定的条件下,数据是无限的,而应用则是有限的。
对错21.政务数据开放部署在政府专门的网站。
错对22.虽然可以精准预测黑客的几乎所有行为,但是,有些行为却是不可管理的。
错对23.对付不同的人,要用不同的方法。
02博弈中的纳什均衡与一致预期

R1
R2 R3
0,4 4,0
4,0
0,4
5,3
5,3
3,5
3,5
6,6
纳什均衡
纳什均衡:所有参与人的最优战略的组合:
给定该战略中别人的选择,没有人有积极性 改变自己的选择。 纳什均衡是局中人战略选择上构成的一种 “僵局”,给定其他局中人的选择不变,任 何一个局中人的选择是最好的,他也不会改 变其战略选择。 敌不动,我不动 例如:乒乓球,生气
考虑有N个人参与的游戏:每个人可任意放
最多100元到一部可以生钱的机器(可以选择 不放),机器把所有人放进去的钱的总和增 加到原来的三倍,然后再平均分给这N个人。 请猜出这N人博弈的纳什均衡并给出相应的 分析。
实验:
请三位男同学
大家拿出一张纸 写下任意一个人的名字 获胜者:选中大部分人选择的
“智猪博弈”(boxed pigs)
有些博弈没有占优均衡,但通过剔除“坏”战略, 我们可以预测博弈的结果。如“智猪博弈”
小猪
按
大猪
等待 2,4 0,0
按 等待
3,1 7,-1
这个博弈中,大猪的最优选择依赖 于小猪的选择,但小猪的最优选择 与大猪的选择无关。如果大猪知道 小猪的理性的,大猪将选择“按”。 均衡是“大猪按,小猪等待”。 “劣”战略:无论对方选择什么,如果 自己选择A得到的总是收益小于选择 B得到的收益,A就是相对于B的劣
B
不坦白 -8,-8 0,-10 -10,0 -1,-1
A
不坦白
无论对方如何选择,每个人的最优选择:坦白。 所以,我们可以预测,结果将是(坦白,坦白)
占优均衡
(dominant-strategy equilibrium)
贝叶斯精炼纳什均衡解经典例题和解答

贝叶斯精炼纳什均衡解经典例题和解答贝叶斯精炼纳什均衡(Bayesian refinement of Nash equilibrium)是博弈论中的一个概念,它结合了贝叶斯理论和纳什均衡的概念,用于描述在不完全信息博弈中玩家对其他玩家类型的不确定性。
这里我将为你提供一个经典的例题,并给出相应的解答。
考虑一个简化的拍卖场景,有两个潜在的买家:买家A和买家B。
拍卖的物品是一幅画,卖家想以尽可能高的价格卖出这幅画。
买家A和买家B对这幅画的估值分别服从正态分布,其均值和标准差如下:买家A的估值:均值为100,标准差为20买家B的估值:均值为120,标准差为15拍卖的规则如下:卖家首先设定一个底价p(reserve price),然后买家A和买家B分别出价。
如果买家A的出价高于底价p,并且买家B的出价也高于底价p,那么拍卖的赢家是出价最高的买家,并且他们需要支付自己的出价。
如果只有一个买家的出价高于底价p,那么这个买家获胜,并以底价p购买这幅画。
如果两个买家都没有出价高于底价p,那么拍卖失败,画作不会被卖出。
现在我们来解答这个问题:1. 假设卖家设定底价p为90,请计算在这个底价下,买家A和买家B的最优出价以及对应的期望收益。
为了计算买家A和买家B的最优出价,我们可以使用贝叶斯精炼纳什均衡的概念。
在这个场景中,买家A和买家B都面临不完全信息,即对方的估值是未知的。
我们需要通过贝叶斯理论来计算每个买家对对方估值的后验概率分布,然后根据这些概率分布来确定最优出价。
买家A的后验概率分布可以通过贝叶斯定理计算得到:P(v_A|p) = P(p|v_A) * P(v_A) / P(p)其中,v_A表示买家A对画作的估值,P(v_A)表示买家A对估值的先验概率分布(正态分布),P(p|v_A)表示在买家A估值为v_A的情况下,底价p被设定的概率,P(p)表示底价被设定为p的概率。
根据题目中给出的信息,买家A的估值服从均值为100,标准差为20的正态分布,我们可以计算P(v_A)。
第三讲 纳什均衡:案例分析

Conclusion
Revenue equivalent theorem
Best response functions
Conclusion
三、Hotelling’s model of electoral competition
Best response function
Best response function
Conclusion
The conclusion is that the competition between the candidates to secure a majority of the votes drives them to select the same position,equal to the median of the citizens’ favorite positions.
Firm 1’s best response function:
Firm 2’s best response function:
1 ( c q2 )ifq1 c b2 (q1 ) 2 0ifq1 c
Best response functions
基本假定
Constant unit cost:
Linear demand function:
Assume:
pifp D( p) 0ifp
Profit functions
Best response functions
Best response functions
四、The war of attrition
Best response function
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
纳什均衡的核心要素在于,我们做出决策的 时候总是要基于他人的决策,把他的决策看成一 个常数,选择策略最大化自己的收益。当每一个 人都这么做的时候,纳什均衡就产生了。判断纳 什均衡的标准是,给定其他人的最优策略,如果 每一个参与者都没有意愿改变自己的策略,那种 这些策略组合就是纳什均衡。
Thank you !
选
择
他们面临着两难的选择——坦白或抵赖。显然最 好的策略是双方都抵赖,结果是大家都只被判一年。 但是由于两人处于隔离的情况下无法串供,按照亚当 •斯密的理论,每一个人都是一个“理性的经济人” ,都会从利己的目的出发进行选择。这两个人都会有 这样一个盘算过程:假如他招了,我不招,得坐10年 监狱,招了才5年,所以招了划算;假如我招了,他 也招,得坐5年,他要是不招,我就只坐3个月,而他 会坐10年牢,也是招了划算。
综合以上几种情况考虑,不管他招不招 ,对我而言都是招了划算。两个人都会动这 样的脑筋,最终,两个人都选择了招?结果 都被判5年刑期。原本对双方都有利的策略( 抵赖)和结局(被判1年刑)就不会出现。这就 是著名的“囚徒困境”。 它实际上反映了一个很深刻的问题,这 就是个人理性与集体理性的矛盾。
今天,纳什均衡被广泛应用于各个领域 的研究,尤其在进行制度分析时,我们可应 用它得出一个很重要结论:一种制度(体制) 安排要发生效力,必须是一种纳什均衡。否 则,这种制度安排便不能成立。(据《诺贝 尔经济学奖经典理论》一书)
许多人知道有名的ABCD男女理论,由于男 性的节制性偏向,导致其一般会降一格选择异性 伙伴,因此实际社会中的典范完配是A男配B女, B男配C女,C男配D女,而A女与D男轮空。这个 时候发生了两个确定性,A女(鲜花)确定D牛粪 男是没人要的,而D男确定A女是追不到的。这种 确定导致了两个最有可能的均衡策略,A女如果 在某种情形下选择了D男,则D男必定会接收,而 D男去追A女则确定不会有成果,但反正D男也没 人要则追A与不追A都一样不会有丧失,所以D男 出于无聊或其它动机仍非常有可能追A女。
纳 什
均
衡
一农户在杀鸡前的晚上喂鸡,不经 意地说:快吃吧,这是你最后一顿! 第二日,见鸡已躺倒并留遗书:爷 已吃老鼠药,你们别想吃爷了,爷他妈 也不是好惹的。
当对手知道了你的决定之后,就能做出对自 己最有利的决定。——纳什均衡理论 所以保密、信息安全很重要!
纳什均衡
假设有n个局中人参与博弈,给定其他人策略的 条件下,每个局中人选择自己的纳什均衡最优策 略(个人最优策略可能依赖于也可能不依赖于他 人的战略),从而使自己利益最大化。所有局中 人策略构成一个策略组合(Strategy Profile)。 纳什均衡指的是这样一种战略组合,这种策略组 合由所有参与人最优策略组成。即在给定别人策 略的情况下,没有人有足够理由打破这种均衡。 纳什均衡,从实质上说,是一种非合作博弈状态 。
背景介绍
关键词:约翰•纳什、博弈论、囚徒困境
Байду номын сангаас
1994年诺贝尔经济学奖的获得者是美国普 林斯顿大学的约翰•纳什。纳什获得诺贝尔经 济学奖的原因是他在博弈论领域的贡献,他提 出了“纳什均衡”理论、关于博奕论,流传最 广的是一个叫做“囚徒困境”的故事:
囚徒困境
话说有一天,一个富翁在家中被杀,财物被盗 ;警方在此案的侦破过程中,抓到两个犯罪嫌疑人 张三和李四,并从他们的住处搜出被害人家中丢失 的财物。但是,他们矢口否认曾杀过人,辩称他们 只是顺手牵羊偷了点儿东西。于是警方将两人隔离 ,分别关在不同的房间进行审讯。警察分别对张三 和李四说,“由于你们的偷盗罪已有确凿的证据, 所以可以判你们1年刑期。但是,我可以和你做个 交易。如果你单独坦白杀人的罪行,我只判你3个 月的监禁,但你的同伙要被判10年刑。如果你拒不 坦白,而被同伙检举,那么你就将被判10年刑,他 只判3个月的监禁。但是,如果你们两人都坦白交 代,那么,你们都要被判5年刑。
纳什均衡现象
很多时候,当我们站在一个人的角度或是利 益点来考虑问题的时候,往往都只考虑了对于自 己单方面的最优方法,往往会忘记掉综合所有因 素自己的最优做法
鲜花插牛粪
为什么许多美女最后嫁给 了让许多男性跌碎眼镜的男 士,一些帅哥最后也好不到 哪里去。如果我们用纳什均 衡对这一现象进行剖析就有 许多有趣的结论。
