第六章第2部分(第四节-第七节)
第六章 经济增长与国际贸易

因为在这种情况下,国际贸
易只发生相应的数量变化或 规模的变动,国际相对价格 不变,规模收益不变,人均 收入也不会变动;
这样,恩格尔定律将不起作用,
社会需求不会从常用品向奢侈品, 消费结构保持稳定,由于生产可 能性曲线的形式和各个国家的消 费结构不变,国际贸易的格局则 不会改变,但贸易的数量增加了。
经济增长后,该国的生产可能性
曲线外扩,变成A’B’,新的相对价 格线为M’N’,且M’N’//MN,即x,y产 品相对价格在经济增长前、后不 变; M’N’与新的生产可能性曲线相切于 与Q’( x+∆x,y+∆y )点,Q’点为 新的生产产品组合点,它随生产 可能性曲线A’B’变化而变化;
在此基础上,我们来讨论经
横坐标轴表示一国具有出口能
力的X产品的产量,纵轴表示可 能进口产品Y的产量; 从供给方面来考虑,一国努力 生产并供给那些可能进口的产 品,就是生产进口替代品,所 以Y产品也称为进口替代品。
原来的生产可能性曲线为AB,
x、y两种产品的相对价格线为 MN,它与AB线相切于Q(x,y) 点,Q点为该国生产产品的组 合点;
相反,等产量曲线Y离N点更
远,ON>MP,这表明可能进口 的商品Y的产量增加了; 因此,在劳动要素不变,单 方面增加资本要素时,资本 密集型的产业将扩大,劳动 密集型的产业将缩小;
这时,如果出口产业是劳动
密集型的,就会出现超逆贸 易型增长;反之,如果出口 产业是资本密集型的,就会 出现超顺贸易型增长。
这样,在Q点,X商品的等产
量线变为X1 ,Y商品的等产量 线变Y1,这两条曲线的切线与 P点上的切线相互平行,其斜 率相同(资本增长后要素价格 比率相同)。
图6-5显示Q点是容易确定的,
化学第六章常见的金属单质 及其化合物

2FeCl3
2.与水反应
在高温条件下,铁能与水蒸气反应生成四氧化三铁和氢气,反应的化学方程
式为
高温
3Fe 4H2O(g)
图1-2 铝
二、铝
(二)铝的化学性质 1.与氧气反应 常温下,铝能够与空气中的氧气反应,表面生成一层致密而坚固的氧化
物薄膜,从而失去光泽,这层氧化物薄膜能阻止铝继续与氧气反应。 在点燃的条件下,铝能够与氧气发生剧烈反应,生成氧化铝(Al2O3),
放出大量的热,并发出耀眼的白光,反应的化学方程式为:
点燃
4Al 3O2
2Al2O3
二、铝
2.与酸反应
铝可以与稀盐酸、稀硫酸等反应,生成铝盐,并放出氢气,其实
质是铝与酸溶液中的氢离子反应,反应的离子方程式为:
2Al 6H
3.与碱反应
2Al3 3H2
铝可以与碱反应,生成偏铝酸盐和氢气。例如,铝和氢氧化钠溶
液反应,生成偏铝酸钠( NaAlO2)和氢气,反应的化学方程式为:
(一)金属的物理性质 纯金属在常温下一般都是固体(汞除外),具有金属光泽,大多呈银白
色或灰色(铜、金等少数金属除外),具有良好的导电性、导热性和延展性, 密度较大,熔点较高。 (二)金属的化学性质
金属在化学反应中,易失去最外层的电子而被氧化,变成阳离子。因此, 金属具有还原性,且活泼性越强的金属还原性越强:
图1-1 储存在煤油中的钠
一、钠
(二)钠的化学性质 钠原子的最外电子层上只有一个电子,其在化学反应中易失去最外层电子,
所以钠的化学性质非常活泼。 1.与氧气反应 在常温下,钠与氧气反应生成白色固体氧化钠( Na2O);在受热的情况下,
钠与氧气会发生剧烈反应,发出黄色火焰,并生成淡黄色固体过氧化钠 ( Na2O2 )。这两个反应的化学方程式分别为
第六章 位移法

ql 2 8
2)令B结点产生转角 B ( ) 。此时AB、BC杆 类似于B端为固端且产生转角 的单跨超静定梁。 B
9
A A
i i
B
B
i
C i
B 3i B
B
B
3i B
B
EI i l
C
3)杆端弯矩表达式
M BA 3i B M BC ql 2 3i B 8
F l/2 A B EI = 常数 l D l l
结点B只转动一个角度,没有水平和竖向位移。 力 法:六个未知约束力。 位移法:一个未知位移(θB)。
C
F
B
C
B
F
B
B
C
l
l/ 2
l/2
A
l/ 2
l/ 2
三次超静定图示刚架
力
法:三个未知约束力。
位移法:一个未知位移(θB)。
二、 位移法基本思路
(8-6)
位移法典型方程的物理意义:基本结构在荷载和 各结点位移共同作用下,各附加约束中的反力等于零, 反映了原结构的静力平衡条件。
二、位移法典型方程
对于具有n个独立结点位移的的结构,有n个基本 未知量,可建立n个平衡方程,位移法典型方程
r11Z1 r12 Z 2 r1n Z n R1P 0 r21Z1 r22 Z 2 r2 n Z n R2 P 0 rn1 Z1 rn 2 Z 2 rnn Z n RnP 0
r11 r 21 rn1
r12 r1n Z1 R1P 0 Z R 0 r22 r2 n 2 2P rn 2 rnn Z n RnP 0
有机化学第六章(高职高专)

键体系。
α 8
β7
α 1
2β
β6 5 α
3β 4α
萘的一元取代物只有两种,二元取代物两取代 基相同时有10种,不同时有14种。
2.萘及衍生物的命名
C2H5
CH3
C2H5
SO3H
1,6-二乙基萘 ; 4-甲基-1-萘磺酸
Br Br
1-溴萘 2-溴萘 α-溴萘 β-溴萘
3.萘的性质
(1) 取代反应 萘的取代反应较易发生在α位。
⑤烷基化试剂也可是烯烃或醇。例如:
+ CH2 CH2 AlCl3 + CH2CHCH3 H+
OH
C2H5 CH(CH3)2
(2) 酰基化反应
O + CH3C
Cl
AlCl3
O CH3 + CH3 C O AlCl3
CH3 C O
C CH3 + HCl O
CH3
C CH3 + CH3COOH
O 甲基对甲苯基酮
环的α位。如:
NO2
混酸
ห้องสมุดไป่ตู้NO2 NO2
NO2
+
NO2
二、其它稠环芳烃
8 91
7
2
9 10
8
1
6
37
2
5 10 4
65 43
芘
3,4-苯并芘
蒽
菲
所以,也可用下式表示苯的结构:
第四节 单环芳烃的物理性质
苯和同系物一般为无色液体,不溶于水,易溶 于有机溶剂,相对密度大多为0.86~0.93。
熔点除与相对分子质量有关外,还与结构的对 称性有关,通常结构对称性高的化合物,熔点较高。 芳香烃一般都有毒性,长期吸入它们的蒸气,会损 害造血器官及神经系统。
《平面构成》第六章

14
三、骨格的近似
近似构成
骨格的近似是指骨格线在形状、大小上有着相似的变化,基本形随着骨格的变 化而变化,从而形成新的表现形式。这种骨格的形式比较自由,富有艺术气质。
15
四、近似构成的应用实例
近似构成
近似构成使画面有序、统一而不失灵活性和自由性,赋予设计作品更多 的创意和生动感。近似构成在平面设计中有着广泛的应用。
7
二、基本形的重复
重复构成
在构成设计中,连续不断地使用同一 个基本形构成的画面称为基本形的重复。
基本形的重复分为绝对重复和相对重 复。绝对重复是指基本形始终不变的反复 使用,具有严谨、统一的观感,但易产生 平淡、呆板之感;相对重复则是指在整体 重复的前提下,部分要素产生规律性的变 化,于严谨中求变化,使画面更加灵活、 丰富。
27
二、发射构成的形式
(二)发射构成的形式
发射构成
发射构成根据发射点、发射方向、发射轨迹及发射物可分为以下几种类型。 1.以发射点进行分类 以发射点进行分类,发射构成可分为一点式和多点式发射。 一点式发射:发射点只有一个,呈现离心式或向心式分布。 多点式发射:发射点有多个,发射方向可以任意设定和变换。
平面设计
Plane Formation
目录页
Contents Page
第六章 平面构成的基本形式
第一节
重复构成 近似构成
第二节 第三节
渐变构成
2
目录页
Contents Page
第四节
发射构成 特异构成 密集构成
3
第五节 第六节
目录页
Contents Page
第七节
对比构成 肌理构成
第八节 第九节
8
分析化学 第六章 重量分析法和沉淀滴定法

通辽职业学院
3.电解法
利用电解原理,使待测金属离子在电极上还原析出, 然后称重,电极增加的重量即为金属重。 重量分析法优点:其准确度较高,相对误差一般为 0.1-0.2%。
缺点:
程序长、费时多,操作繁琐,也不适用于微量组 分和痕量组分的测定。
分析化学
通辽职业学院
二、沉淀重量法对沉淀形式和称量形式的要求
Ba2+ SO42SO42- Ba2+ SO42SO42-
沉淀
Ba2+
Cl
-
Ca2+
K+
Ba2+ SO42Cl SO42- Ba2+ SO4
2-
Ca2+
Na+ Cl
-
Ba2+ SO42吸附层 扩散层
分析化学
通辽职业学院
(2) 吸留和包藏 吸留(occlusion):在沉淀过程中,若生成沉淀 的速度过快,则表面吸附的杂质来不及离开沉淀表面 就被沉淀下来的离子所覆盖,而杂质就被包藏在沉淀 内部,从而引起共沉淀。 包藏(inclusion):在沉淀过程中,母液也可能 被包夹在沉淀当中,从而引起共沉淀。 (3)混晶 当杂质离子的半径与构晶离子的半径相近时,所形 成的晶体结构相同,则它们极易生成混晶。 如:BaSO4和PbSO4, AgCl和AgBr. BaSO4和KMnO4等。 分析化学
K sp
K ap
②对于MmAn型沉淀,溶度积的表达式为:
MmAn
mM + nA
[Mn ]m [Am- ]n Ksp
分析化学
通辽职业学院
(2)条件溶度积 MA M
OH
+
+
第六章老年人常见疾病的护理-PPT

言语障碍:表现为找词困难、用词不当或张冠 李戴。
智能障碍:出现抽象思维、概括、综合分析、 判断、计算等全面性智力减退。
⑵行为与人格改变 最早出现且引人注目得症状之一 表现为日渐加重得懒散、退缩、孤
僻,缺乏热情,主观、固执狭隘、敏感 多疑、行为粗俗等。
⑶精神行为症状
妄想:表现为异乎寻常得想法 幻觉:表现为幻听与幻视 身份识别障碍 抑郁 行为紊乱:表现为无目得徘徊、激越、反复
抱怨
⑷神经系统症状 早期:无症状体征 晚期:肌张力增高、震颤 严重时:癫痫样发作,肌强直,无法行走,
病理反射阳性。
⑸老年性痴呆病程分期
第一期:主要表现为记忆障碍,学习与掌握新信息 困难,近期记忆轻微受损,空间定向障碍,词汇减 少,生活尚能自理。此期约1-3年。
与语言沟通训练 妥善保管危险物品,预防外伤与压疮 专人瞧护 随身携带名片
二、阿尔茨海默病
阿尔茨海默氏病(AD),又称老年性痴呆 ,就是一种进行性认知障碍与记忆能力 损害为主得中枢神经系统退行性变性 疾病。
30岁以后均可发病,多发于50岁以后, 多数散发,25%有家族遗传史,女性略 高于男性
㈠病因与发病机制
副作用 消化道症状 ,体位性低血压,心律失常, 幻觉 、焦虑、错乱,剂未现象,开-关现象与异动 症等并发症。
左旋多巴与药物引起得并发症
病程
5 —10年
药效
并发症
认知功能 障碍 僵住现象 异动症
开关现象
剂末现象
3、多巴胺受体激动剂
作用:对早期病人可单用,也可与多巴制剂合 用治疗中、晚期病人。它不易引起异动症与 症状波动,并可推迟与减少多巴制剂得使用。
第六章 免疫应答

一、抗体产生的动力学
初次应答:指某种抗原首次进入机体内引起 初次应答: 抗体产生的过程。 抗体产生的过程。 再次应答:机体再次接触与第一次相同抗原时, 再次应答:机体再次接触与第一次相同抗原时, 体内产生抗体的过程为再次应答。 体内产生抗体的过程为再次应答。 回忆应答:抗原刺激机体产生抗体一段时间后, 回忆应答:抗原刺激机体产生抗体一段时间后, 在体内逐渐消失, 在体内逐渐消失,此时机体若再次接 触相同的抗原物质, 触相同的抗原物质,可使已消失的抗 体快速回升,称为抗体的回忆应答。 体快速回升,称为抗体的回忆应答。
细胞毒性T 细胞毒性T细胞主要通过两种方式杀伤靶细胞
1.CTL释放细胞毒蛋白对靶细胞的直接作用( 1.CTL释放细胞毒蛋白对靶细胞的直接作用(即 释放细胞毒蛋白对靶细胞的直接作用 穿孔素 -粒酶系统效应 ) 2.CTL上的膜结合 2.CTL上的膜结合Fas配体与靶细胞表面的Fas受 上的膜结合Fas配体与靶细胞表面的 配体与靶细胞表面的Fas受 体相互作用( FasL/Fas系统 体相互作用(即FasL/Fas系统 )
二、参与免疫应答的细胞及其表现形式
参与免疫应答主要是T 参与免疫应答主要是T、B细胞及巨噬细胞 等辅佐细胞。 等辅佐细胞。 表现形式为体液免疫 细胞免疫。 表现形式为体液免疫和细胞免疫。 体液免疫和 1.特异性 1.特异性 免疫应答特点: 2.具有一定免疫期 免疫应答特点: 2.具有一定免疫期 3.具有免疫记忆 3.具有免疫记忆
(二)再次应答的特点: 再次应答的特点:
1. 潜伏期显著缩短。 潜伏期显著缩短。 2.抗体含量高,且维持时间长。 2.抗体含量高,且维持时间长。 抗体含量高 3.再次应答产生的抗体大部分为IgG,而IgM很少。 3.再次应答产生的抗体大部分为 再次应答产生的抗体大部分为IgG, IgM很少 很少。
第六章 循环系统
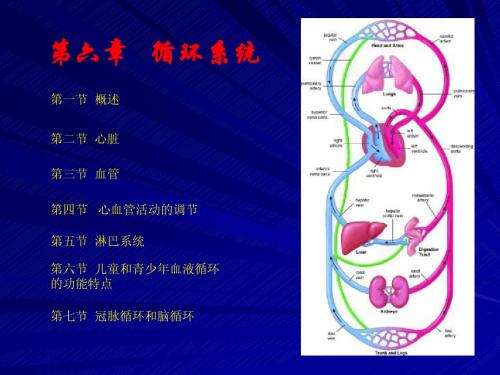
(四)心电图:
定义:用置于体表一定部位的引导电极测记 带心电变化的波形即心电图。 组成:一般有一个P波、一个QRS波群和T波、 有时在T波之后还出现一个小的U波。
P波:反映左右心房的兴奋 过程即心房去极化过程的 电位变化, QRS波群:代表左右心室 先后兴奋时的去极化过程, T波反映心室复极化过程的 电位变化 P-R间期:代表心房开始兴 奋到心室开始兴奋所需时
生理变异:
①年龄 ②性别 血压随年龄ቤተ መጻሕፍቲ ባይዱ增加而升高 男性高于女性
高血压和低血压对人体会造成什么样的危害?
(二)动脉血压的形成
*前提条件:封闭的血管系统中有足够的血液充盈。
*基本条件:心脏射血和外周阻力。
*重要条件:大动脉管壁的弹性。
心室收缩 心室舒张 ↓ 射血入主A + 外周阻力 大A回弹 (势能释放) ↓ 推血(1/3)流动 + 大A扩张(2/3) (动能消耗) (势能贮存+缓冲力) 推血继续流动 ↓ 血液对动脉壁的侧压 血液对动脉壁的侧压 上升到最大值=收缩压 降低到最小值=舒张压
2.正常起搏点与潜在起搏点
窦房结是正常心脏的起搏点,主导整 个心脏兴奋的部位,故称之为正常起搏点, 或正常起步点。正常情况下其它部位的自 律细胞都受窦房结的控制,并不表现出它 们的自动节律性,它们只是起着兴奋传导 作用,称之为潜在起搏点。
窦房结控制潜在起搏点的机制,是通过二种方式实现的。
①抢先占领:所谓抢先占领是指由于窦房结的自律性高于 潜在起搏点,所以潜在起搏点的4期自动去极化尚未达到 阈电位水平之前,它们已经受到窦房结发出并依次传布而 来的兴奋激动作用而产生了动作电位,因之其自身的兴奋 就不可能出现。
(2)复极化1期(快速复极化期)
膜电位迅速由30mV下降到0mV左右,占时约2ms,
化工安全工程课件第六章泄漏源及扩散模式

第八节 湍流扩散模型 一、湍流扩散微分方程的推导
若风向与X轴方向一致
二、无边界点源扩散模型
1. 瞬时泄漏点源的扩散模型 U=0 即无风条件下
U≠0 有风条件下
2. 连续泄漏点源的扩散模型 U=0 即无风条件下,连续泄漏各位置点浓度与时间无关
U≠0 有风条件下,连续泄漏各位置点浓度与时间无关
三、有边界点源扩散模型
第六节 易挥发液体蒸发的源模式
泄漏液体向大气蒸发,该蒸发过程的传质推动力为蒸发物质 的气液界面与大气间的浓度差。液体蒸发为气体的摩尔通量:
第七节 扩散模式(有毒有害ቤተ መጻሕፍቲ ባይዱ质在空气中扩散)
连续泄漏源泄漏 的扩散模式
瞬间泄漏源泄漏 的扩散模式
风速、大气稳定度、地面情况、泄漏源高度、泄漏物质的初 始状态、物料性质等因素均会对泄漏物质在大气中的扩散产 生影响。
a 对于光滑管,λ由雷诺数Re决定 (经验公式) b 对于粗糙管,λ由雷诺数Re和相对粗糙度ε/d决定(经验公式、查图)
U= 0→u Z= 5 →0
第四节 气体或蒸气经小孔泄露的源模式
泄漏后密度发生变化 可压缩流体
(势能变化忽略) 定义孔流系数:
令
第五节 闪蒸液体的泄漏源模式
闪蒸:瞬间完成的减压气化,不需加热。近似为绝热过程。
第一节 液体经小孔泄露的源模式
泄露形式
容器内流速忽略, 不考虑摩擦损失和 液位变化
考虑到因惯性引起的截面收缩及摩擦引起的速度减小,引入孔流系数C0。 C0=实际流量/理论流量
C0约为1
薄壁小孔C0约0.61
厚壁小孔或孔外伸有 一段短管C0约0.81
通常情况下C0难以求取,为保持足够的安全余量,可取1.
第二节 储罐中液体经小孔泄露的源模式
七年级上册数学第六章-《图形的初步知识》知识点及典型例题大全(精选.)

新浙教版七年级上册数学第六章《图形的初步知识》知识点及典型例题知识框图第一节几何图形:会区分平面图形与立体图形第二节线段、射线和直线:线段、射线和直线的概念及表示方法;直线的基本事实(经过两点有一条且只有一条直线,简单地说,两点确定一条直线)第三节线段的长短比较:度量法和叠合法;线段的基本事实(在所有连结两点的线中,线段最短,简单地说,两点之间线段最短)及两点间距离的概念第四节线段的和差:线段的中点以及三等分点等;线段的加减计算第五节角与角的度量:角的概念及表示方法;度、分、秒的相互换算及计算第六节角的大小比较:度量法和叠合法;角的分类第七节角的和差:角平分线的概念;角的加减计算第八节余角和补角:余角和补角的概念及性质;根据图形和文字,利用该性质进行简单的推理和计算第九节直线的相交:相交线的概念;对顶角的概念和性质;会用余角、补角、对顶角的性质进行推理和计算;两条直线互相垂直的概念、画法(一靠、二过、三画、四标)及表示法;垂线段最短的性质和点到直线的距离的概念考点一、与概念、性质、基本事实直接相关的题目考点二、关于角度的计算,注意一元一次方程在这种题目中的妙用。
若语言模糊,一定要分类讨论,多画图。
考点三、关于线段的计算,注意一元一次方程在这种题目中的妙用。
若语言模糊,一定要分类讨论。
考点四、与实际生活相关的线段问题考点五、关于规律性的角度、线段问题考点六、作图题将考点与相应习题联系起来考点一、与概念、性质、基本事实直接相关的题目 1、与课本、足球分别类似的图形是( )A.长方形、圆B.长方体、圆C.长方体、球D.长方形、球 2、如图,下列说法错误的是( )A.直线AB 与直线AC 是同一条直线B.线段AB 与线段BA 是同一条线段C.射线AB 与射线BA 是同一条射线D.射线AB 与射线AC 是同一条射线3、把一条弯曲的河道改成直道,可以缩短航程,其中的道理可以解释为( )A.线段有两个端点B.过两点可以确定一条直线C.两点之间,线段最短D.线段可以比较大小4、下列说法:① 过两点有且只有一条线段;② 连结两点的线段的长度叫做两点之间的距离;③ 两点之间线段最短;④ AB=BC ,则点B 是线段AC 的中点;⑤ 射线比直线短,正确的个数有( ) A.1个 B.2个 C.3个 D.4个5、如图所示,∠BAC=90°,AD ⊥BC ,则图中能表示点到直线距离的线段有( ) A.3条 B.4条 C.5条 D.6条6、在海上,灯塔位于一艘船的北偏东40°方向,那么这艘船位于这个灯塔的( )A.南偏西50°方向B. 南偏西40°方向C.北偏东50°方向D. 北偏东40°方向 7、在同一平面内有4个点,过每两点画一条直线,则直线的条数有( )注意分类讨论的数学思想 A.1条 B.4条 C.6条 D.1或4或6条8、如果α和β是对顶角且互补,那么它们所在的直线( )A.互相垂直B.互相平行C.即不垂直也不平行D.1或4或6条 9、如图,∠AOB=∠COD=90°,则∠AOC=∠BOD ,这是根据( )A.同角的余角都相等B.等角的余角都相等C.互为余角的两个角相等D. 直角都相等10、下列选项中,∠1与∠2是对顶角的是( )D CBA2121212111、下列各角中,属于锐角的是( ) A.13周角 B.18平角 C.65直角 D.12平角 12、如图所示,∠BAC=90°,AD ⊥BC ,则图中表示点B 到AC 的距离的线段是( )A. ABB. ADC. BDD.AC★★★用平面去截一个立方体,得到的截面不可能是………………………………………( ) A.三角形 B.正方形 C.长方形 D.圆形 ★★★如果点C 在线段AB 上,下列表达式:①AC=12AB ;②AB=2BC ;③AC=BC ;④AC+BC=AB 中,能表示点C 是线段AB 中点的有 ( )A.1个B.2个C.3个D.4个EDC B O A★★★下列四个图中的线段(或直线、射线)能相交的是……………………………………( )1()CDBA2()CD BA3()C D BA4()CDBAA.(1)B.(2)C.(3)D.(4) ★★★已知线段则线段的长度是( ) A.5B.1C.5或1D.以上都不对考点二、关于角度的计算,注意一元一次方程在这种题目中的妙用。
脂肪酸的生物合成及

O
CO2 E2-SH
CH3 – C - CH2 – C – S - ACP
O
O
(4)第一次还原(reduction): E4: - 酮酰-ACP还原酶(KR)
CH3–C-CH2–C–S-ACP
E4
C–S-ACP
精品课件
CH3–CH-CH2–
(5)脱水反应(dehydration):
E5:羟酰-ACP脱水酶(HD)
脂酰-ACP脱去ACP成为软脂酸。 • 酶以二聚体形式存在,反平行配置。P261
精品课件
精品课件
软脂酰-ACP硫酯酶
脂肪酸合Байду номын сангаас系结构模式
③
④
②
ACP
⑤
①
⑥
中央巯基 SH
外围巯基 SH
③
④
② ①
⑤ ⑥
①乙酰CoA:ACP转酰酶,AT ② 丙二酸单酰CoA:ACP转酰酶,MT
③β-酮(脂)酰-ACP合酶,KS ④ β-酮(脂)酰-ACP还原酶,KR ⑤β-羟(脂)酰-ACP脱水酶,H精D品课件⑥ 烯(脂)酰-ACP还原酶,ER
经酰胺 + 磷酸胆碱。
至今在动物体内尚未发现有 9 以上的去饱和 酶
必需脂肪酸
亚油酸(18, 9,12) (linoleic acid)
-亚麻酸(18, 9,12,15)
(linolenic acid)
花生四烯酸(20, 5,8,11,13) (半必需)是含量最丰富的多烯脂酸
精品课件
精品课件
DHA
二 脂肪(三酰甘油)的生物合成
脂肪酸合酶
(5)脱水
脂肪酸合酶 精品课件
(6)还原
脂肪酸合酶
第六章 挡土墙设计

4)地基为软弱土层时,可采用砂砾、碎 石、矿渣或灰土等材料予以换填。
5)当挡土墙修筑在陡坡上,而地基又为 完整、稳固、对基础不产生侧压力的坚硬 岸石时,可设置台阶基础,以减少基坑开 挖和节省圬工。
6)如地基有短段缺口(如深沟等)或挖基 困难(如需水下施工),可采用拱形基础。
a)墙趾或墙踵部分加宽;b)钢筋混凝土底板; c)换填地基;d)台阶基础;e)拱形基础
2.基础埋置深度
对于土质地基,基础埋置深度应符合下列要求: (1)无冲刷时,应在天然地面以下至少1m; (2)有冲刷时,应在冲刷线以下至少1m; (3)受冻胀影响时,应在冻结线以下不少于0.25m。当冻深超过1m时,采 用1.25m,但基底应夯填一定厚度的砂砾或碎石垫层,垫层底面亦应位于 冻结线以下不少于0.25m。
(四)沉降缝与伸缩缝
设计时,一般将沉降缝与伸缩缝合并设置,沿路线方向每隔10~15m设置 一道,兼起两者的作用,缝宽2~3cm,缝内一般可用胶泥填塞,但在渗 水量大,填料容易流失或冻害严重地区,则宜用沥青麻筋或涂以沥青的木 板等具有弹性的材料,沿内、外、顶三方填塞,填深不宜小于0.15m,当 墙后为岩石路堑或填石路堤时,可设置空缝。
附加力是季节性作用于挡土墙的各种力, 特殊力是偶然出现的力。
二、一般条件下库仑主动土压力计算 主动土压力:挡土墙向外移动时(位移或倾覆),
土压力随之减少,直到墙后土体沿破裂面下滑而处于极 限平衡状态,作用于墙背的土压力。
被动土压力:墙向土体挤压移动,土压力随之增大,
土体被推移向上滑动处于极限平衡状态,此时土体对墙 的抗力。
1. 破裂面交于内边坡时(库仑主动土压力公式的推导) (1).力的大小
第六章 合同法(总则)

第三节
一、合同的内容
合同的内容与形式
(一)当事人名称、姓名 (二)标的 (三)数量 (四)质量 (五)价款或报酬 (六)履行期限、地点和方式 (七)违约责任 (八)解决争议的方式 (九)其他内容
二、合同的形式
书面形式、口头形式、其他形式
第四节 合同成立的时间与地点
一、合同成立的时间
一般:自承诺生效时成立
(四)承诺的撤回 在承诺通知到达之前或与承诺通知同时到达。
(五)承诺的迟延与迟到 1.迟延承诺:受要约人超过承诺期限发出承诺。 (一般无效。除要约人及时通知受要约人该承诺 有效的以外,迟延承诺应视为新要约。) 2.迟到承诺:受要约人在承诺期限内发出承诺, 按照通常情况能够及时到达要约人,但因其他原 因致使承诺到达要约人时超过承诺期限的,为迟 到承诺(一般有效。要约人及时通知受要约人因 承诺超过期限不接受该承诺的除外)。
2.要约和要约邀请的区别 要约邀请:希望他人向自己发出要约的意思 表示。 (1)要约的内容应当具体明确,如果缺少某 一主要条款(如数量、价款),则属于要 约邀请。 (2)要约具有法律约束力,而要约邀请没有 法律约束力。
案例2--1甲向乙发出一封电报称:现有100吨白糖,每 吨售价2000元,如有意购买,请于6月1日前到我厂 提货。 问:该电报属于要约还是要约邀请?
(三)可撤销合同 1.可撤销合同的概念与特征 P132 2.可撤销合同的种类 (1)因重大误解订立的合同; (2)在订立合同时显失公平的; (3)一方以欺诈、胁迫或乘人之危订立的 合同;
3.撤销权的行使
(1)只有受损害方才有权撤销 (2)行使方式:意思表示 (3)行使期限:具有撤销权的当事人自知 道或应当知道撤销事由之日起1年内没有行使 撤销权的,撤销权消灭。
医学心理学第六章 心理治疗与心理咨询

2.神经症的心理病理学解释
焦虑是理解神经症的关键所在,焦虑是 一种弥漫性的恐惧体验,由于有焦虑体验者无 法意识到其恐惧的具体对象,所以焦虑称为 “无原因的恐惧”。焦虑来自对性冲动的压抑, 本能冲动得不到正常宣泄,就转化成焦虑或以 焦虑的形式得到宣泄。
二、心理分析的主要治疗方法
1、自由联想 (free association)
人本主义学派认为人基本上是真诚、 善良和可以信赖的,提出了“人 之初,性本善”的理论立足点。
人本主义心理学认为心理障碍的发 生是自我发生了扭曲,内在的 “向善性”发展受到阻抑。
以人为中心疗法的发展过程
• 以人为中心治疗 的发展大体分为四个阶段:
• 第一阶段:四十年代1942年罗杰斯《治疗与心理咨 询》出版,倡导非指导性治疗。
1、系统脱敏疗法(交互抑制法)
通过渐进性暴露于日益恐惧的刺激情境以逐 步消除恐惧反应的治疗方法,就叫系统脱敏疗 法。
基本原理
系统脱敏疗法的基本原则是交互 抑制,即在想象或呈现恐惧刺激 的同时,让来访者做出抑制焦虑 或恐惧的反应——松弛,松弛反 应便可削弱或破坏恐惧刺激同恐 惧反应间的联系。
具体实施分三步进行:
• (1)训练准备 • ①来访者心理准备。 • ②训练者自身准备。 • ③训练环境与仪器准备。 • (2)测定基线值与应激时生理反应值 • (3)训练技巧 • ①肌感练习。 • ②被动集中注意训练。 • ③塑造技术。 • ④双向练习与技能转换技术。 • ⑤布置家庭作业。 • ⑥结合传统放松训练。
评价
二十世纪60年代,人本主义心理治疗开始兴起,以 罗杰斯的以来访者为中心的疗法影响最大。
二十世纪70年代以后,认知心理治疗开始形成。
三、国外心理治疗的现状
第六章 挡土结构物上的土压力(4-7节)

Ka
sin( ) sin( ) cos cos( ) 1 cos( ) cos( )
2
(6 - 22)
12
Ka称为库伦主动土压力系数。它与、、 、有关,可查表6-1。 、 —填土的容重与内摩擦角; —墙背与竖直线之间的夹角。以竖直线为 准,逆时针为正,顺时针为负; —填土面与水平面之间的夹角。水平面以 上为正,水平面以下为负; —墙背与填土之间的摩擦角,其值一般取 为(1/3~2/3) 或按表6-2取值。
2
(二)库伦假设条件 平面滑裂面假设。 刚体滑动假设。 土楔体ABC整体处于极限平衡状态。
3
4
(三)滑动土楔体的受力分析 根据土楔体整体处于极限平衡状态的条 件,可得知E、R的方向。 根据楔体应满足静力平衡力三角形闭合 的条件,可知E、R的大小。 求极值,找出真正滑裂面,从而得出作 用在墙背上的总主动土压力Ea和被动土 压力Ep。
5
6
为了找出土中真正的滑裂面,可假设不 同角的几个滑裂面,分别算出维持各个 滑裂楔体保持极限平衡时的土压力E值。 对于主动状态来说,要求E值最大的滑裂 面是真正的滑裂面;对于被动状态来说, 需要E值最小的滑裂面是真正的滑裂面。 利用dE/d=0条件,即可求得作用于挡土 墙上的总土压力Ea或Ep
50
二、适用范围 (一)朗肯理论的应用范围 1.墙背与填土面条件 1)墙背垂直、光滑、墙后填土面水平,即 =0、=0和=0(图6-32a); 2)墙背垂直,填土面为倾斜平面,即=0、 0,但<且> (图6-32b); 3)坦墙(>cr)。计算面见图6-32c; 4)L形钢筋混凝土挡土墙(图6-32d)。
27
第六章 合同法律制度 《经济法》PPT课件

四、合同成立的时间和地点
(二)合同成立的地点 承诺生效的地点为合同成立的地点。 具体规定如下: ➢ 采用数据电文形式订立合同的,收件人的主营业地为合同成立的地
点;没有主营业地的,其住所地为合同成立的地点。当事人另有约定 的,按照其约定。 ➢ 当事人采用合同书形式订立合同的,双方当事人签字、盖章或者按指 印的地点为合同成立的地点,但当事人另有约定的除外。
(一)合同条款约定不明时的履行规则
仍不能确定的,适用下列规定履行: ➢ 质量要求不明确的,按照国家标准、行业标准履行;没有国家标准、 行业标准的,按照通常标准或者符合合同目的的特定标准履行 ➢ 价款或者报酬不明确的,按照订立合同时履行地的市场价格履行; 依法应当执行政府定价或者政府指导价的,按照规定履行 ➢ 履行地点不明确,给付货币的,在接受货币一方所在地履行;交付不 动产的,在不动产所在地履行;其他标的,在履行义务一方所在地履行 ➢ 履行期限不明确的,债务人可以随时履行,债权人也可以随时要求 履行,但应当给对方必要的准备时间 ➢ 履行方式不明确的,按照有利于实现合同目的的方式履行 ➢ 履行费用的负担不明确的,由履行义务一方负担;因债权人原因增加
的履行费用,由债权人负担。
(二)价格变动时的履行规则
执行政府定价或者政府指导价的,在合同约定的交付期限内政府价格调 整时,按照交付时的价格计价。 逾期交付标的物的,遇价格上涨时,按照原价格执行;价格下降时,按 照新价格执行。 逾期提取标的物或者逾期付款的,遇价格上涨时,按照新价格执行;价 格下降时,按照原价格执行,即执行对违约方不利的价格。
五、缔约过失责任
所谓缔约过失责任,是指在合同订立过程中,一方因违背其依据诚实 信用原则所产生的义务,使对方的信赖利益遭受损失,所应承担的损害 赔偿责任。 缔约过失责任的构成要件主要包括三个方面: ➢ 当事人一方实施了违反先合同义务的行为 ➢ 由于当事人一方违反先合同义务给对方造成了损失 ➢ 行为人主观上有过错
第六章芳香油植物资源

第六节.芳香油的提取方法
自植物中提取芳香油时,其方法有下述三种: (一)水蒸气蒸馏法:芳香油的沸点甚高, 但易随水蒸气蒸馏而出,此法操作容易,热度 又不会分解芳香油中的香成分,加之设备简单, 故应用最广泛。水蒸气蒸馏法所用设备型式很 多,可从植物根、茎、叶、枝、果、种子及部 分花类中提取芳香油。
水蒸馏法有以下三种: 水中蒸馏法:将原料直接放在水中,用直火 或封闭的蒸气管道加热,使芳香油蒸馏出来。 直接蒸馏法:即蒸锅内不放水,只放原料, 而 将水蒸气自另一蒸气锅通过多孔气管喷入蒸 馏锅的下部,再经过原料把芳香油蒸出。 水气蒸馏法:将原料放在蒸馏锅内设置的一 个多孔隔板上,锅内放水,水的高度在隔板之 下。当水蒸气通过多孔隔板和板上的原料时, 芳香油便可随水蒸气蒸馏出来。
E.芳香族醚类:是芳香族醇的羟基 上的氢被一有机根所取代而衍生的一种 有机化合物。如存在于石莒蒲中的胡椒 酚甲醚和榄香烯,存在于细辛中的α -细 辛醚和β -细辛醚 。
3.脂肪族直链化合 物
精油成分除萜类、芳香族化合物外,脂肪 族化合物为数不少。 A .醇类:属于脂肪族醇类的直链化合物 中有经过发酵的茶叶中有顺式 3- 己烯醇,具 有青草的清香。 2- 甲基正庚烯 -2- 醇 -6 存在于 咖罗木油中,具有青草鲜果香气。调香时常 用少量于配方中作为头香。
第四节.我国的芳香油植物资源
我国的芳香植物种类很多,在种子植物中有 60多个科l70余个属的植物含有芳香油,其中最 重要的有20余科,如: 松科(Pinaceae) 柏科 (Cupressaceae) 樟科 (Lauraceae) 芸香科(Rutaceae) 唇形科 (Labiatae) 桃金娘科(Myrtaceae) 伞形科(Umbelliferae) 菊科(Compositae) 败酱科(Valerianaceae) 木犀科(Oleaceae) 蔷薇科(Rosaceae) 莎草科 (Cyperaceae)
第六章管理信息系统的系统分析PPT课件

第二节 管理业务调查
❖ 开发和建立管理信息系统的根本目的在于提高管理 水平,严格地说,设计一个新的信息系统,应首先 进行组织的重新设计,应当把建立新系统看成是对 组织的一种有目的的改变过程。管理系统是信息系 统的环境。因此,对现行业务的调查十分重要,其 中包括:组织结构调查、管理功能调查和管理业务 流程调查等。
❖ 数据流程图具有抽象性和概括性。
❖ 抽象性表现在它完全舍去了具体的物质,只剩下数 据的流动、加工处理和存储。
❖ 概括性表现在它可以把信息中的各种不同业务处理 过程联系起来,形成一个整体。
❖ 数据流程图用四种符号表示:
1.外部实体
2.数据流
3.处理(功能)
4.数据存储 17
s
外部实体
D
数据流
P
处理
❖ 首先,画出顶层数据流程图。顶层数据流程图只有一 张,它说明了系统的总的处理功能、输入和输出。
❖ 其次,对顶层数据流程图中的“处理‘进行分解。
1.判定订货处理方式。根据用户信用情况(查信用手 册)、库存情况(查库存帐)和购货金额将订货单按 以下三种情况分别处理:
(1)货到付款
(2)有货再发
(3)先付款再发货
11
某企业物资管理业务流程图
车间
有关部门
用料计划
领料单
未批准的领料单
领料通知
库长
库存报表
库存账
已批准的领料单
用料流水账
订货单(合同) 崔货单
库工 缺料通知单
入库单
采购员 供货单位
补充订货单
12
提货通知单
(二)表格分配图
❖ 表格分配图可帮助分析员表示出系统中各种单据和报告都与 那些部门发生业务关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五节 定量资料的假设检验
一、样本均数与总体均数的比较
• 1.单样本t检验 • 2.单样本u检验
单样本t检验
• 例6.5 . 已知正常成年男子血红蛋白含量的均数 为140g/L。某医生随机抽取了某皮鞋厂16名男 性工人,并测得其血红蛋白含量,均数为 130.83g/L,标准差为12.74g/L。假定该样本血 红蛋白含量服从正态分布,且检验水准为α= 0.05。问该皮鞋厂工人的血红蛋白是否与正常 成年男性的血红蛋白平均水平不同?
(1)建立检验假设,确定检验水准
– H0:μ1=μ2=…=μk – H1:μ1、μ2、…、μk不全相等
– α=0.05
(2)计算检验统计量F值
F
MS组间 MS组内
SS组间 / 组间 SS组内 / 组内
14.81
1 组间 k 1 2
2 组内 N k 57
一、配对设计两样本的比较 ――――Wilcoxon符号秩和检验
• 例6.13 某医师为评价安眠药的疗效,随机选取 了10名失眠患者进行药物治疗,服药前后患者 的睡眠时间如下表,假设该资料不服从正态分
布,请评价该药物的疗效。
1.建立检验假设,确立检验水准
H0:治疗前后睡眠时间差值的总体中位数为0,Md = 0 H1:治疗前后睡眠时间差值的总体中位数不为0,Md ≠ 0 =0.05
假设检验(hypothesis test)
• 如果总体分布类型已知,检验问题仅涉 及总体分布的未知参数,属于参数检验。 • 若总体分布类型未知,检验是针对总体 分布函数的类型或某些特征的,属于非 参数检验。
一、假设检验基本思想
• 小概率事件 • 反证法原理
二、假设检验的基本步骤
1.检验假设,确立检验水准
– H0:μd=0 – H1:μd≠0 α=0.05
(2)选择检验方法,计算检验统计量t值
d 0 t 5.43, n 1 7 Sd / n
(3)确定P值,下结论 – t=5.43 > t 0.01/2,7=3.499 ,P<0.01,按照α=0.05的水 准,拒绝H0,接受H1,差异有统计学意义,可认为增 喝和不喝牛奶组的儿童身高增加有差别,喝牛奶组身 高增加的更多。
t X1 X 2 2.07 4.33 5.441, n1 n2 2 25 1 1 1 1 Sc2 ( ) 1.14 2 ( ) n1 n2 15 12
(3)确定P值,判断结果
– t=-5.441 > t0.001/2,25=3.725,P<0.001,按 照α=0.05的水准,拒绝H0,接受H1,差异 有统计学意义,可以认为健康人和肺气肿 患者痰中α1抗胰蛋白酶含量不同。
2. 选择检验方法,计算检验统计量
3. 确定P值,下结论
三、假设检验中的两类错误
• 第一类错误:当H0为真时,由于样本的随机性,根 据样本观测值却做出了拒绝了H0的判断,称为第一 类错误,也称为“弃真”的错误。其概率大小为显 著性水准。
• 第二类错误:当H0不真时,根据样本观测值却做出 了不拒绝H0的判断,称为第二类错误,即“存伪” 的错误,大小为。 • 要同时减少两类错误,只有增加样本含量。
四、行列表资料的卡方检验
A n 1 nR nc
2 2
( r 1)(c 1)
• 例6.12 某临床医师为比较研究三种治疗方法对降低血压的 疗效,将病情相似的272例患者随机地分到三个组进行治 疗,结果以有效、无效来表示。数据如下表。试比较三个 组的有效率是否相同?
三、配对设计四格表资料卡方检验
• McNemar检验
• 例6.11 某研究人员为研究两种检测方法的检出 率,将410份血样一分为二后,分别用甲、乙 两种方法检测其乙肝表面抗原HbsAg的表达情 况,结果如下表。试分析两种方法的检测结果 是否不同?
(1)建立检验假设,确定检验水准
– H0:B=C,即两种方法的总体检出率相同 – H1:B≠C,即两种方法的总体检出率不同
第七节 秩和检验
• 参数检验(parametric test):在总体分布类型 已知的情况下,对总体参数进行的假设检验。 • 非参数检验(nonparametric test):一种不依 赖于总体分布类型,不对总体参数进行检验的 方法,它检验的是分布而不是参数。
• 如果资料满足参数检验的条件,或者经 过变量变换可以符合参数检验条件的资 料,应该选择参数检验。 • 对于偏态分布资料、方差不齐的资料、 等级资料、一端或者两端不确切值的资 料等,才考虑非参数检验。
2.计算检验统计量
(1)求差值。 (2)按差值的绝对值由小到大进行编秩,冠以差值的正负号。
(3)分别求出正负秩和T+、T- ,取其中较小的作为统计量T。
本例,T+=51,T-=4,所以,统计量T=4。
3.确定P值,下结论
– 查T界值表,若检验统计量T在上下界值范围内,其P>α;若检验 统计量T在上下界值范围外,其P<α。
第四节 假设检验的原理和基本步骤
假设检验(hypothesis test)
• 假设检验:根据研究目的,预先对未知总体做 出一些假设,然后根据实测样本的信息去检验
假设的合理性,以决定对该假设的取舍,这种
关于总体的种种假设称为统计假设,处理假设
的统计方法称为假设检验。
• 又称为显著性检验(significance test)。
– α=0.05
(2)计算检验统计量2值
– b+c=118>40,所以选用公式:
(b c ) 2 (110 8) 2 2 88.17 bc 110 8
(3)确定P值,判断结果
– 根据卡方值和自由度,查卡方界值表,得P<0.005,按α=0.05的水 准,拒绝H0,接受H1,差异有统计学意义,可认为两种方法的检 出率不同,甲法检出率高于乙法。
(1)建立假设,确定检验水准
– H0:μ1=μ2 – H1:μ1≠μ2 – α =0.05
(2)选择检验方法,计算检验统计量t值
( n1 1) S12 ( n2 1) S 22 (15 1) 1.012 (12 1)1.14 2 S c2 1.14 n1 n2 2 15 12 2
度趋于无穷大时,2卡方分布渐近于正态分布。
• 2分布曲线下右侧尾部的面积记为时,横轴上相
应的卡方值即为2分布的分位数。
二、完全随机设计四格表资料的 卡方检验
• 例6.10 为研究吸烟和肺癌的关系,某研究者进行 了以医院为基础的病例对照研究,结果如下表所 示。试分析肺癌组和对照组的吸烟率是否有差别?
四、多个样本均数的比较
• 方差分析(Analysis of variance,ANOVA)
• 多个样本均数的比较不能直接用两两进行t检验 (会增加犯第一类错误的概率),而应该用方 差分析。
• 方差分析最早是由英国统计学家R.A.Fisher创 立的,又称为F检验。
单因素方差分析
• 例6.9 为研究一种降糖新药的疗效,某医师以 统一的纳入和排除标准选择了60名2型糖尿病 患者,按照完全随机设计方案将患者分为三组 即高剂量组、低剂量组与对照组,每组20人, 进行临床试验。对照组服用公认有效的降糖药 物,治疗1个月后测得其餐后2小时血糖下降值 (mmol/L),结果如下表。问治疗1个月后三 组患者的餐后2小时血糖下降值是否不同?
二、配对设计两样本均数的比较
• 配对设计主要情况:
1. 两同质受试对象配成对子分别接受两种不
同的处理措施;
2. 同一受试对象分别接受两种不同的处理;
3. 同一受试对象接受处理前后。
• 例6.6 某研究人员为研究牛奶是否有增加身 高的作用,把16名儿童按照年龄相近、性 别相同、身高体重相近等原则配成8对,每 对儿童中一个给予正常饮食,另一个除了 正常饮食外,每天增喝500ml牛奶,6个月 后测得其身高增长情况如下表,问增喝与 不喝牛奶组的儿童身高增加情况是否有差 别?
三、成组设计两样本均数的比较
• 成组t检验 • 成组u检验
成组t检验
• 例6.7 某呼吸内科医师分别测得15例健康人和12 例肺气肿患者痰中α1抗胰蛋白酶含量如下,问健 康人和肺气肿患者痰中α1抗胰蛋白酶含量是否不 同? – 健康人 2.7 2.2 4.1 4.3 2.6 1.9 1.7 0.6 1.9 1.3 1.5 1.7 1.3 1.3 1.9 – 患者 3.6 3.4 3.7 5.4 3.6 6.8 4.7 2.9 4.8 5.6 4.1 3.3
(3)确定P值,判断结果
– 根据卡方值和自由度,查卡方界值表,得 P>0.5,按α=0.05的水准,不拒绝H0,差异 无统计学意义,尚不能认为三种方法的总体 有效率不同。
行列表卡方检验的注意事项:
• 行列表卡方检验时要求理论频数不应小于1,并且 1≤T<5的格子数不能超过格子总数的1/5。
• 多个样本率或构成比的比较,结果为“拒绝H0,接受 H1”时,只能认为各总体率总的来说有差异,要进一步 进行两两比较判断哪两个总体之间有差异。 • 由于行列表卡方检验的计算公式与分类变量的顺序无 关,当行列变量中有一个变量是有序分类变量(即单 向有序行列表资料)时,不宜采用卡方检验,应改用 秩和检验或Ridit检验进行分析。
(1)建立检验假设,确定检验水准
– H0:1 =2,两个组的总体吸烟率相同 – H1:1≠2,两个组的总体吸烟率不同 – α=0.05
(2)选择检验方法,计算检验统计量2值
n=200>40, Tmin
nr min * nc min 100 96 48 5 n 200
(1)建立检验假设,确定检验水准 H0:1=2=3,即三种治疗方法的总体有效率相同 H1:1,2,3不全相同,即三种治疗方法的总体有效率 不同或不全相同 α=0.05 (2)选择检验方法,计算检验统计量2值
