反问题、tikhonov迭代正则化方法与应用
反问题概述及其数值求解方法阐述

反问题概述及其数值求解方法阐述姓名:赵天骐 学号:1014203026学院:电气与自动化工程学院 专业:电气工程1.反问题概述1.1什么是反问题近30年来,反问题不仅是学术领域中的一个话题,它已经被广泛的应用到工程学、医学、地质学、经济学、物理学等领域,无论在理论还是应用方面均取得了飞速的发展。
随着计算科学的发展,人们从计算的角度研究反问题,更加频繁地被应用于解决实际问题,比如其在石油勘测、医学图像处理、遥感技术、经济决策等领域。
但是,究竟什么是反问题?对此常常仁者见仁,智者见智。
它的严格定义很难给出,有点“只能意会,不能言传”的味道。
美国斯坦福大学的J. B. Keller (1976)提出:“若在两个问题中,一个问题的表述或处理涉及到或包含了有关另一个问题的全部或部分的知识,我们称其中一个为正问题(Direct problem),另一个为反问题(Inverse problem)。
”C. W. Groetsch则认为:”反问题是很难定义的,但是几乎每一个数学家都能马上判断出一个问题是正问题还是反问题。
”苏联学者Levrentiev则指出:“偏微分方程的反问题是指从偏微分方程解的某些泛函去确定偏微分方程的系数或右端项。
”T. Robinson的观点是:“在数学上,通常是有了方程而要求此方程的解。
现在的情况是有了方程的解,必须把对应的方程找出来。
我喜欢后者。
”事实上,上述对反问题的各种说法虽然揭示了反问题和正问题类似于对偶的一种关系,但没有直观地反映出反问题的一个主要特征。
通常情况下,反问题在Hadamard意义下是不适定的。
其学术性的描述为:在两个相互为逆的问题中,如果一个问题在Hadamard意义下是不适定的,特别是若问题的解不连续地依赖于原始数据,则称该不适定问题为反问题。
即通常意义下的反问题一般应该是Hadamard不适定的,这也正是我们研究反问题的困难所在。
那么,什么是Hadamard意义下不适定呢?1923年,Hadamard给出了相反的定义,即什么是适定的。
电阻抗成像技术中Tikhonov正则化方法应用与改进的研究

电阻抗成像技术中Tikhonov正则化方法应用与改进的研究本文介绍了一种新型的功能成像技术——电阻抗成像技术(Electrical Impedance Tomography,简称EIT技术).在近几十年来,EIT技术由于设备轻便、速度快、无伤害等被国内外学者广泛研究,这项技术的主要原理是利用不同组织电导率不同的特点,采用“电流激励-电压测量”的方式,通过测量边界电压获得目标体内部的电导率(电阻抗)分布或者变化的图像,具有很强的生物学、医学意义.但这种技术也有较大的局限性,成像质量不高、不稳定、数据误差较大等是制约其发展的主要原因.在数学上,电阻抗成像技术反问题可以看作是一类二阶椭圆型偏微分方程参数识别问题,所以常常带有反问题的不适定性等特点,因此本文针对电阻抗成像正问题和反问题进行了研究:第一章为绪论,主要介绍了电阻抗成像技术的基本原理和国内外研究现状,并对其研究的理论和实际意义、技术难点进行了说明,然后介绍了反问题和不适定性的相关概念,引出本文的研究结构.第二章研究了电阻抗成像技术的正问题,首先介绍了电阻抗成像技术的工作模式(电流的注入和电压的测量方式),并通过麦克斯韦方程组和相关边界条件推导了正问题的数理模型,选择了全电极模型并采用有限元方法对其求解.在有限元剖分时,得出了稀疏和加密两种剖分方式.第三章讨论了电阻抗成像技术的反问题,是本文的重点.在这一章中,首先采用常用的最小二乘法求解,发现解不稳定或失去实际意义,所以引入了正则化方法.对正则化方法的定义和原理进行说明后引出了本文主要研究的Tikhonov正则化方法,对其基本思想、求解过程进行了推导说明,并分析了解的相关性质.针对Tikhonov正则化方法的缺陷,对罚函数项进行改进,引入了变差函数,得到全变差正则化方法,并推导了牛顿迭代法的迭代格式.通过EIDORS 2D软件对两种正则化方法的成像质量进行简单比较后,引出本文的组合正则化方法,推导了罚函数项构造方式和迭代求解过程,随后介绍了选择正则化参数的高阶迭代收敛算法,并设计了相关算法.最后通过Matlab 进行了仿真研究.第四章得出了研究结论,并分析了本文存在的不足和未来继续研究的方向。
椭圆方程反问题的正则化方法研究

椭圆方程反问题的正则化方法研究椭圆方程反问题的正则化方法研究概述在实际工程和科学领域中,我们常常会面临一些反问题,即根据已知的观测数据来确定某个物理过程的未知参数或边界。
椭圆方程反问题是其中一类重要的反问题,涉及到椭圆型偏微分方程的参数估计和边界重构。
由于反问题的不适定性,常常会导致数值计算过程中的不稳定性和非唯一解。
因此,为了提高反问题的求解精度和稳定性,需要采用正则化方法。
一、椭圆方程及反问题的描述椭圆方程是一类重要的偏微分方程,具有广泛的应用。
一般来说,椭圆方程可以表示为:L[u] = f其中L是一个椭圆算子,u是未知函数,f是给定的函数。
椭圆方程求解的问题是确定未知函数u。
而椭圆方程反问题则是,在已知边界条件和观测数据的情况下,确定椭圆方程的参数或边界。
在实际应用中,椭圆方程反问题常常以以下几种形式出现: 1. 参数估计问题:已知椭圆方程的边界条件和观测数据,求解椭圆方程的参数。
例如,已知某个材料的传热模型和观测到的温度分布,求解该材料的热传导系数。
2. 边界重构问题:已知椭圆方程的边界条件和观测数据,求解椭圆方程的边界。
例如,已知某个地下水流动模型和观测到的水位数据,求解该地下水流动领域的边界。
二、椭圆方程反问题的正则化方法椭圆方程反问题的正则化方法是一种常用的数值求解方法,用于消除不适定性和提高求解精度。
正则化方法的核心思想是在目标函数中引入正则化项,通过平衡目标函数的拟合程度和正则化项的平滑度,来实现参数估计和边界重构。
常见的正则化方法包括Tikhonov正则化和迭代正则化。
1. Tikhonov正则化方法Tikhonov正则化方法是一种将L2范数引入目标函数的方法。
其目标函数可以表示为:J(u) = ||L[u] - f||^2 + α||u||^2其中||·||表示L2范数,α是正则化参数。
Tikhonov 正则化方法通过控制α的大小,使目标函数在拟合观测数据的同时,保持解的光滑性。
基于Tikhonov_正则化改进的IHB法求解Mathieu-Duffing_系统多重解

第 62 卷第 5 期2023 年9 月Vol.62 No.5Sept.2023中山大学学报(自然科学版)(中英文)ACTA SCIENTIARUM NATURALIUM UNIVERSITATIS SUNYATSENI基于Tikhonov正则化改进的IHB法求解Mathieu-Duffing系统多重解*王德亮1,2,刘济科1,刘广1,21. 中山大学航空航天学院,广东深圳 5181072. 深圳市智能微小卫星星座技术与应用重点实验室,广东深圳 518107摘要:增量谐波平衡法(IHB法)是研究强非线性振动系统的一种半数值半解析方法,然而已有研究表明,在求解含多重解的系统时该方法的收敛性强烈地依赖于初值的选择。
Tikhonov正则化常被用于优化问题中来解决可能出现的病态问题。
文章通过在原始的IHB法中引入Tikhonov正则化,提出一种改进的IHB法(TIHB法)来求解具有多重解的Mathieu-Duffing系统。
结果表明,改进的TIHB法可以快速、高效地获得系统的多个稳定或不稳定解,且算法的收敛性能要远远优于原始的IHB法。
关键词:非线性振动;IHB法;Tikhonov正则化;多重解中图分类号:V21 文献标志码:A 文章编号:2097 - 0137(2023)05 - 0078 - 07Multiple solutions of the Mathieu-Duffing system obtainedby the improved IHB method based on Tikhonov regularizationWANG Deliang1,2, LIU Jike1, LIU Guang1,21. School of Aeronautics and Astronautics,Sun Yat-sen University, Shenzhen 518107, China2. Shenzhen Key Laboratory of Intelligent Microsatellite Constellation, Shenzhen 518107, ChinaAbstract:The incremental harmonic balance method (IHB method) is a semi-numerical and semi-ana‐lytical method for strongly nonlinear dynamic systems. However, previous studies have shown that the convergence performance of the original IHB method in solving systems with multiple solutions strong‐ly depends on the selection of initial values. The Tikhonov regularization is often used in optimization problems to solve potential ill-posed problems. In this paper, by incorporating the Tikhonov regulariza‐tion into the original IHB method, an improved IHB method (TIHB method) is proposed to obtain the multiple solutions of the Mathieu-Duffing system. The results show that the improved TIHB method can obtain the stable and unstable solutions of the Mathieu-Duffing system quickly and efficiently, and the convergence performance of the TIHB method is much better than the original IHB method.Key words:nonlinear vibration; IHB method; Tikhonov regularization; multiple solution现实中的各种振动系统都含有非线性因素(陈予恕,1992;陈树辉,2007;Amabili,2008)。
地球物理反演中的正则化技术分析

地球物理反演中的正则化技术分析地球物理反演是一种通过观测地球上各种现象和数据,来推断地球内部结构和物质分布的方法。
在地球物理反演中,由于观测数据的不完整性和不精确性,常常需要借助正则化技术来提高反演结果的可靠性和准确性。
正则化技术是一种以一定规则限制解的优化方法。
通过在反演过程中引入附加信息或者假设,正则化技术可以帮助减小反演问题的不确定性,提高解的稳定性和可靠性。
在地球物理反演中,正则化技术有多种应用。
下面将介绍几种常见的正则化技术,并对其进行分析和比较。
1. Tikhonov正则化Tikhonov正则化是一种基本的正则化技术,它通过在目标函数中加入一个范数约束来限制解的空间。
常见的约束可以是L1范数和L2范数。
L1范数可以使解具有稀疏性,即解中的大部分分量为零,适用于具有稀疏特性的反演问题。
而L2范数可以使解具有平滑性,适用于具有平滑特性的反演问题。
2. 主成分分析正则化主成分分析正则化是一种通过将反演问题映射到低维空间来减小问题的维度的正则化技术。
它可以通过选择重要的主成分来实现数据降维,从而减少反演问题的不确定性。
主成分分析正则化在处理高维数据时可以提高反演的效率和精度。
3. 奇异值正则化奇异值正则化是一种基于奇异值分解的正则化技术。
通过对反演问题进行奇异值分解,可以将问题分解为多个低维子问题,从而减小高维问题的不确定性。
奇异值正则化适用于非线性反演问题,可以提高反演结果的稳定性和可靠性。
4. 稀疏表示正则化稀疏表示正则化是一种基于稀疏表示理论的正则化技术。
它通过将反演问题转化为对系数矩阵的优化问题,并引入L1范数约束,使得解具有稀疏性。
稀疏表示正则化适用于信号重构和图像恢复等问题,并在地震勘探和地球成像中有广泛应用。
在选择正则化技术时,需要考虑问题的特性和数据的特点。
不同的正则化技术适用于不同的问题,并且各自具有一些优势和限制。
因此,根据问题的具体要求和数据的特征,选择合适的正则化技术可以提高反演结果的可靠性和准确性。
基于非凸稀疏域约束条件的Tikhonov正则化方法

基于非凸稀疏域约束条件的Tikhonov 正则化方法摘要本文给出了一个奇特的正则化方法的理论分析用来解决(非线性)反问题,从而将正则化方法推广到稀疏域上。
我们考察特定的Tikhonov 正则化方法的稳定性和收敛性。
我们将这种正则化方法用于传统的连续的pl 空间,由于这是稀疏域上的正则化方法,所以我们将p 限定于0到1之间。
当1<p 时三角不等式不再成立并且我们会得到一个带有非凸限制条件的伪Banach 空间。
我们将要证明在传统的环境下最小值的存在性,稳定性和连续性。
除此之外,我们还将给出在各自的传统假设下拓扑Hilbert 空间下的收敛速度。
1.介绍本文是关于在稀疏域条件下正则化方法的理论分析。
我们将这种方法不妨设在 p l ))1,0((∈p 空间上并且是非线性的算子。
我们证明了Tikhonov 正则化方法的解的存在性,解得稳定性,对数据扰动解的收敛性。
除此之外,我们还将给出在各自的传统假设下拓扑Hilbert 空间下的收敛速度。
稀疏域上的反问题。
我们有等式y x F =)( )1( 这里F 是一个非线性算子。
为此我们将该式用Tikhonov 方法表示,求该等式的最小值 ),()(2x y x F αψ+- )2( 除了传统的正则化项)(x ψ,如2L 范数,全部变量或者是最大正则化熵等方法,还有一个具有潜质的新奇的稀疏域上的正则化方法.普遍的选择设置都是基础上的延拓,例如小波扩张,傅里叶分解活着各种结构的扩张,典型地这些扩张被用于图像或者频率数据,因此本文所涉及的扩张系数通常指的是稀疏域的扩张。
它可应用于各种潜在的应用。
比如,X 线断层摄影术(CT ,SPECT ,PET )。
这些通常的医学成像技术正是传统的反问题同时又可以通过积分算子来得出Radon 变换的具体形式。
这种图像重构的方法是通过基扩展来实现的,如小波和像素基,参考文献【5,6】,一个适用用的正则化方法都是引进适当的惩罚项)(x ψ,如1l 范数:∑=k k xx )(ψ, )3(这里的k 能够预示小波级数的系数。
线性反问题的正则化算法

线性反问题的正则化算法反问题,是相对于正问题而言的,是一个倒果求因的过程。
在地球物理,生命科学,材料科学,遥感技术,模式识别,信号(图象)处理,工业控制乃至经济决策等众多的科学技术领域中,都提出了“由效果、表现反求原因、原象”的反问题。
反问题是一个新兴的研究领域,有别于传统的定解的正问题,反问题研究由解的部分已知信息来求解问题中的某些未知量。
在许多实际问题中,需要通过输出的(部分)信息来获取或识别系统的某些性质。
反问题已经发展成为横跨数学、物理、生物、计算机等众多科学的一个热门研究领域。
反问题可以写成如下的数学模型:Fx=y其中f: x→y为从空间X到Y的一个映射,与正问题相比,反问题的研究起步较晚,发展还远不成熟,并且反问题研究的难度一般比相应的正问题要大。
这是因为反问题的求解往往违背了物理过程的自然顺序,从而使正问题中的许多良好性质不再满足。
这些困难主要体现在:与正问题相比,求解反问题面临的两个本质性的实际困难是: (l)原始数据可能不属于所论问题精确解所对应的数据集合,因而在经典意义下的近似解可能不存在; (2)近似解的不稳定性,即:原始资料的小的观测误差会导致近似解与真解的严重偏离。
也就是我们通常所说的Hadamard意义下不适定.Hadamard在1923年提出在经典意义下适定问题要满足下述三个条件:(l)该问题的解是存在的;(2)该问题的解是唯一的;(3)该问题的解对输入数据是稳定的。
上面的三个适定性条件无疑具有深刻的实际背景.首先对于实际问题,我们当然期望答案是存在唯一的.更重要的是,在实际获取的数据资料总是不可能是精确的。
除了前面提到的不适定性以外,反问题的研究还经常面临非线性的困扰。
即使正问题是线性的,它所对应的反问题也有可能表现为非线性,这为反演的研究和计算带来了很多麻烦。
为了求解非线性反问题,通常要线性化后反复进行正、反演迭代,在高维情况下需要十分巨人的计算量。
对于一个效率低下的算法在实际应用中将导致时间和人力、物力的极大浪费。
tikhonov正则化方法

tikhonov正则化方法Tikhonov正则化方法是一种用于解决线性反问题的数值稳定方法,也称为Tikhonov-Miller方法或Tikhonov-Phillips方法。
它由俄罗斯数学家Andrey Tikhonov在20世纪40年代提出,被广泛应用于信号处理、图像处理、机器学习、物理学等领域。
线性反问题指的是,给定一个线性方程组Ax=b,已知矩阵A和向量b,求解未知向量x。
然而,在实际应用中,往往存在多个解或无解的情况,而且解的稳定性和唯一性也很难保证。
这时候,就需要引入正则化方法来提高求解的稳定性和精度。
Tikhonov正则化方法的基本思想是,在原有的线性方程组中添加一个正则化项,使得求解的解更加平滑和稳定。
具体地说,Tikhonov 正则化方法可以用下面的形式表示:min ||Ax-b||^2 + λ||x||^2其中,第一项表示原有的误差项,第二项表示正则化项,λ是正则化参数,用来平衡两个项的重要性。
当λ越大时,正则化项的影响就越大,求解的解就越平滑和稳定;当λ越小时,误差项的影响就越大,求解的解就越接近原有的线性方程组的解。
Tikhonov正则化方法的求解可以通过最小二乘法来实现。
具体地说,可以将原有的线性方程组表示为Ax=b的形式,然后将其转化为最小二乘问题,即:min ||Ax-b||^2然后,再添加一个正则化项λ||x||^2,得到Tikhonov正则化问题。
由于这是一个二次最小化问题,可以通过求导等方法来求解。
Tikhonov正则化方法的优点在于,它可以有效地提高求解的稳定性和精度,减少过拟合和欠拟合的问题。
同时,它的求解也比较简单和直观,适用于各种线性反问题的求解。
然而,Tikhonov正则化方法也存在一些限制和局限性。
首先,正则化参数λ的选择比较困难,需要通过试错和经验来确定;其次,正则化项的形式也比较单一,往往不能很好地适应不同的问题和数据;最后,Tikhonov正则化方法只适用于线性反问题的求解,对于非线性问题和大规模问题的求解效果较差。
采用边界积分方程和tikhonov正则化方法延拓潜艇磁场

采用边界积分方程和tikhonov正则化方法延拓潜艇磁场边界积分方程和Tikhonov正则化方法是一种有效的手段,用于延拓潜艇磁场。
这种方法基于物理学原理和数学模型,可以通过计算潜艇表面的磁场分布,来推断潜艇内部的磁场分布。
本文将详细介绍这种方法的原理和应用。
一、边界积分方程边界积分方程是一种数学工具,用于描述物体表面的电磁场分布。
在潜艇磁场延拓中,我们可以将潜艇表面看作一个电磁场边界,通过边界积分方程来计算潜艇表面的磁场分布。
具体来说,我们可以将潜艇表面划分成若干个小面元,对每个小面元上的磁场进行积分,得到整个表面上的磁场分布。
这种方法可以有效地避免对潜艇内部结构的复杂计算,从而简化了问题的求解。
二、Tikhonov正则化方法Tikhonov正则化方法是一种数学工具,用于处理反问题。
在潜艇磁场延拓中,我们需要通过已知的潜艇表面磁场分布,来推断潜艇内部的磁场分布。
这是一个反问题,通常会受到噪声和不确定性的影响。
Tikhonov正则化方法可以通过引入正则化项,来限制解的复杂度,从而提高解的稳定性和精度。
三、应用实例潜艇磁场延拓方法在实际应用中具有广泛的应用价值。
例如,在海洋探测和海底勘探中,可以通过潜艇磁场延拓方法来推断海底地形和地质构造。
在潜艇隐身技术中,可以通过潜艇磁场延拓方法来预测潜艇的磁场特征,从而减少被敌方探测的可能性。
此外,潜艇磁场延拓方法还可以应用于磁共振成像、地球物理勘探等领域。
总之,边界积分方程和Tikhonov正则化方法是一种有效的手段,用于延拓潜艇磁场。
这种方法基于物理学原理和数学模型,可以通过计算潜艇表面的磁场分布,来推断潜艇内部的磁场分布。
在实际应用中,潜艇磁场延拓方法具有广泛的应用价值,可以为海洋探测、潜艇隐身技术、磁共振成像、地球物理勘探等领域提供有力的支持。
Tikhonov正则化参数的选取及两类反问题的研究的开题报告

Tikhonov正则化参数的选取及两类反问题的研究的开题报告题目:Tikhonov正则化参数的选取及两类反问题的研究一、研究背景和意义:随着科学技术的进步,反问题研究成为了最热门的研究领域之一。
反问题的研究涉及到的学科领域非常广泛,其中数学、物理和工程等领域是最为重要的。
反问题包括了许多子领域,如参数反问题、区域反问题、混合反问题等等。
其中参数反问题是最为基础和重要的子领域之一。
Tikhonov正则化方法在参数反问题中得到了广泛应用,因为它可以通过降低噪声波动和提高解的光滑性来改进问题的稳定性。
然而,在应用Tikhonov正则化方法时,如何选取正则化参数是一个非常重要的问题,因为不同的正则化参数会影响到结果的精度和稳定性。
此外,不同类型的反问题需要对正则化参数作出不同的选择,这也是一个需要进一步探究的问题。
因此,我们需要对Tikhonov正则化参数的选取以及在不同类型的反问题中的应用进行深入的研究。
二、研究内容和目标:本文将主要研究Tikhonov正则化参数的选取方法,探讨其在参数反问题和区域反问题中的应用。
具体研究内容包括以下几个方面:1. 对Tikhonov正则化方法的优化算法进行研究,包括最小二乘方法、正交匹配迭代算法等。
2. 针对参数反问题,研究不同类型的Tikhonov正则化方法与对应的正则化参数的选取方法,并比较其性能和精度。
3. 针对区域反问题,研究不同类型的Tikhonov正则化方法与对应的正则化参数的选取方法,并比较其性能和精度。
4. 开发相应的计算程序,实现研究结果的数值验证和实际应用。
通过以上研究,本文旨在实现以下目标:1. 系统性地总结不同类型的Tikhonov正则化方法与对应的正则化参数的选取方法,并探讨其适用范围和局限性。
2. 比较不同类型的Tikhonov正则化方法及其选取的正则化参数在参数反问题和区域反问题中的应用效果,提出相应改进措施,提高解的稳定性和精度。
3. 开发相应的计算程序,实现研究结果的数值验证和实际应用,为相关领域的研究提供参考。
两类偏微分方程反问题的正则化方法和算法研究

两类偏微分方程反问题的正则化方法和算法探究专业品质权威编制人:______________审核人:______________审批人:______________编制单位:____________编制时间:____________序言下载提示:该文档是本团队精心编制而成,期望大家下载或复制使用后,能够解决实际问题。
文档全文可编辑,以便您下载后可定制修改,请依据实际需要进行调整和使用,感谢!同时,本团队为大家提供各种类型的经典资料,如办公资料、职场资料、生活资料、进修资料、教室资料、阅读资料、知识资料、党建资料、教育资料、其他资料等等,想进修、参考、使用不同格式和写法的资料,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!And, this store provides various types of classic materials for everyone, such as office materials, workplace materials, lifestyle materials, learning materials, classroom materials, reading materials, knowledge materials, party building materials, educational materials, other materials, etc. If you want to learn about different data formats and writing methods, please pay attention!两类偏微分方程反问题的正则化方法和算法探究两类偏微分方程反问题的正则化方法和算法探究摘要:偏微分方程反问题的探究在科学和工程领域中具有重要的应用。
数值方法中的反问题正则化理论

数值方法中的反问题正则化理论数值方法是一种通过计算机进行数值计算的方法,广泛应用于科学、工程、金融等领域。
然而,在实际应用中,我们常常遇到一类称为“反问题”的难题:已知结果,求解问题。
在数值方法中,这个反问题可以通过正则化理论来解决。
正则化理论是一种可以在反问题中添加约束条件的方法,以提高求解问题的稳定性和准确性。
在本文中,我们将介绍数值方法中的反问题正则化理论,并探讨其在实际应用中的作用。
首先,让我们先来了解什么是反问题。
在数值计算中,我们通常希望通过已知的输入数据,推导出未知的参数或者状态。
然而,由于观测数据的限制、误差或者噪声,求解这类问题变得困难。
这种由结果推导出问题的过程,称为反问题。
在反问题中,我们经常遇到一个重要的挑战就是不稳定性。
由于输入数据的不确定性,求解的结果往往对输入数据的微小变化非常敏感。
这导致了数值计算结果的不稳定性和不准确性。
为了解决这个问题,我们可以引入正则化理论。
反问题正则化理论通过约束条件来提高反问题的稳定性和准确性。
常见的约束条件包括Tikhonov正则化、方程约束和边界约束等。
这些约束条件可以限制问题的解空间,对求解结果进行约束,从而提高反问题的稳定性。
Tikhonov正则化是反问题正则化理论中的一个重要方法。
它通过在原问题中添加一个正则化项,来限制问题的解。
Tikhonov正则化可以通过解析方法或者优化方法来求解,具体的求解过程可以参考相关的数值计算方法。
通过引入Tikhonov正则化,反问题可以得到稳定和准确的结果。
方程约束是另一种常见的反问题正则化方法。
它通过向反问题添加一组约束方程,对问题的解进行约束。
这些约束方程可以基于已知的物理规律、数学模型或者经验公式等。
通过引入方程约束,反问题可以得到满足约束条件的解。
边界约束是一种特殊的反问题正则化方法。
它通过限制问题解的边界条件,来提高问题的稳定性和准确性。
边界约束可以根据具体的问题设定,例如对解的范围、梯度等进行约束。
Tikhonov正则化的编程实现及其在气象中的应用
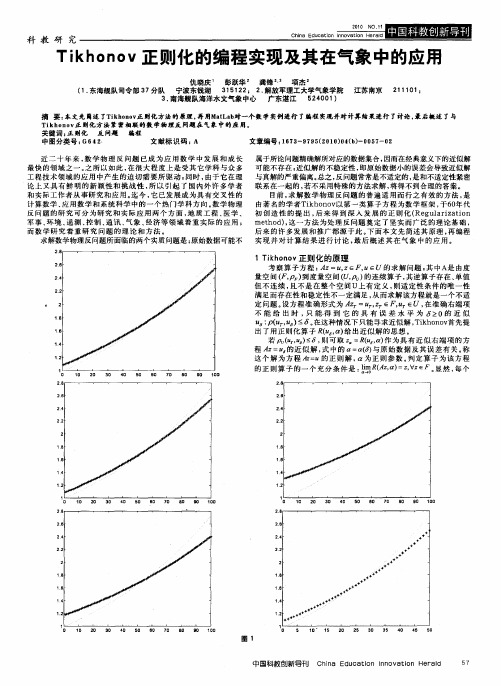
T h 则化 的编程 实现及其 在气象 中的应 用 n v正 i k oo
仇 晓庆 ’ 彭跃华 龚锋 。 项杰 - ( . 海舰队 司令 部 3 分队 宁波东钱 湖 3 1 2 2 解放军 理工大学气象 学院 江苏 南京 2 1 0 1东 7 1 2; . 5 l1 1 3 南海舰 队海洋水文 气象 中心 广 东湛江 5 4 0 ) . 2 0 1 摘 要: 本文先 筒述 了 i h n v 则化方法的原理 , Tk 00正 再 ̄M t a 对一个数 学实例进行 了壕程 实现 并对计算结果进行 了讨论 , 后概速 了与 aL b 最 T k o o  ̄ 则化方 法紧密相联 的数 学物理反 问题 在 气象 中的应 用。 ihn v 关键词 : 正则化 反问题 鳊程 中图分类 号 : 4 G6 2 文 献标 识码 : A 文章编 号 : 6 3 9 9 ( 0 O 0 ( ) O 5 - 2 1 7 - 7 52 1)4b- 0 7 0 近 二 十 年 来 , 学 物 理 反 问题 已成 为 应 用 数 学 中发 展 和 成 长 数 最 快 的 领域 之 一 。 所 以 如 此 , 很 大 程度 上 是 受其 它学 科 与 众 多 之 在 工 程 技 术领 域 的 应 用 中产 生 的 迫切 需 要 所 驱 动 ; 时 , 同 由于 它 在 理 论 上 又 具 有 鲜 明 的 新 颖性 和 挑 战性 , 以 引起 了 国 内 外许 多学 者 所 和 实 际 工作 者 从 事研 究 和 应 用 。 今 , 已发 展 成为 具 有 交 叉 性 的 迄 它 计 算数 学 、 用数 学 和 系 统科 学 中的 一 个 热 门学 科 方 向 。 学 物 理 应 数 反 问 题 的研 究 可分 为 研 究 和 实 际应 用 两 个 方 面 , 质 工 程 、 地 医学 、 军事、 环境 、 测 、 制 、 讯 、 象 、 遥 控 通 气 经济 等 领 域 着 重 实 际 的 应 用 ; 而 数 学 研 究 着 重 研 究 问题 的理 论和 方 法 。 求解数 学物理 反 问题 所面 临的 两个 实质 问题是 : 原始数 据可 能不 属于 所论 问题精 确解 所对应 的数据 集合 , 因而在 经典意 义下 的近似解 可 能不 存在 ; 近似 解 的不稳 定性 , 即原始 数据 小 的误 差会导 致近 似解 与真 解的严 重偏 离 。 之 , 问题常 常是不 适定 的 , 总 反 是和 不适定性 紧密 联 系在 一起 的 , 若不 采 用特殊 的 方法 求 解 , 得不 到 合理 的答 案 。 将 目前 , 解 数 学 物理 反 问题 的 普 遍 适 用 而行 之 有 效 的 方 法 , 求 是 由著 名的 学 者 T k o o 以第 一 类 算子 方程 为 数 学框 架 , O 代 ih n v 于6 年 初 创 造 性 的 提 出 , 来 得 到 深 入 发 展 的 正 则 化 ( g l rz to 后 Re u a ia i n meh d , 一 方 法 为 处理 反 问题 奠 定 了 坚 实而 广 泛 的 理论 基 础 , t o )这 后 来 的许 多发 展 和推 广 都 源 于此 。 面 本 文先 简 述 其 原理 , 编程 下 再 实 现 并 对 计 算 结 果 进 行 讨 论 , 后 概 述 其 在 气象 中 的应 用 。 最
正则化方法求解偶应力反问题

正则化方法求解偶应力反问题姚宇新;薛齐文【摘要】Tikhonov's regularization approach has been used to identify parameters for the inverse couple-stress problem based on Bregman distances and weighted Bregman distances in the construction of regularization terms for the Tikhonov's function. The inverse problem is formulated implicitly as an optimization problem with the cost functional of squared residues between calculated and measured quantities. A FE model is given, taking account of inhomogeneity and facilitating to sensitivity analysis for direct and inverse problems. Satisfactory numerical validation is given including a preliminary investigation of effect of noise data on the results and the computational efficiency for different regularization terms. Results show that the proposed method can identify parameters for the inverse couple-stress problem with high computational precision/efficiiency and the ability of anti-noisy data. It could improve computational efficiency for the weighted Bregman distances function as regularization terms.%引入Bregman函数及其加权函数作为正则项,应用Tikhonov正则化方法,对偶应力反问题相关参数进行识别.利用相关测量信息和计算信息构造最小二乘函数.在考虑材料非均质的同时,建立了便于敏度分析的偶应力正/反问题数值求解模型.给出了相关的数值算例,并对信息误差以及不同正则项的计算效率作了探讨.数值结果表明所提的求解策略不仅能够对相关的材料参数进行有效识别,而且具有较高的计算精度、较好的稳定性和一定的抗噪性.采用加权的Bregman距离函数作正则项可以提高计算效率.【期刊名称】《科学技术与工程》【年(卷),期】2011(011)033【总页数】4页(P8131-8134)【关键词】Bregman函数;偶应力;反问题;正则化【作者】姚宇新;薛齐文【作者单位】大连交通大学土木与安全工程学院,大连116028;大连交通大学土木与安全工程学院,大连116028;工业装备结构分析国家重点实验室,大连116023【正文语种】中文【中图分类】O343.1偶应力理论是研究具有微结构、一定特征尺度介质力学行为的重要工具之一。
正则化和反问题

正则化和反问题正则化(regularization)在线性代数理论中,不适定问题通常是由一组线性代数方程定义的,而且这组方程组通常来源于有着很大的条件数的不适定反问题。
大条件数意味着舍入误差或其它误差会严重地影响问题的结果。
反问题有两种形式。
最普遍的形式是已知系统和输出求输入,另一种系统未知的情况通常也被视为反问题。
许多反问题很难被解决,但是其他反问题却很容易得到答案。
显然,易于解决的问题不会比很难解决的问题更能引起人们的兴趣,我们直接解决它们就可以了。
那些很难被解决的问题则被称为不适定的。
一个不适定问题通常是病态的,并且不论是简单地还是复杂地改变问题本身的形式都不会显著地改善病态问题。
另一方面,病态问题不一定是不适定的,因为通过改变问题的形式往往可以改善病态问题。
在严格的数学意义上,我们通常不可能对不适定问题进行求解并得到准确解答。
然而,通过使用我们的先验知识,我们通常有希望能够得到一个接近准确解答的答案。
求解不适定问题的普遍方法是:用一族与原不适定问题相"邻近"的适定问题的解去逼近原问题的解,这种方法称为正则化方法。
如何建立有效的正则化方法是反问题领域中不适定问题研究的重要内容。
通常的正则化方法有基于变分原理的Tikhonov正则化、各种迭代方法以及其它的一些改进方法,这些方法都是求解不适定问题的有效方法,在各类反问题的研究中被广泛采用,并得到深入研究。
正则化:Normalization,代数几何中的一个概念。
通俗来说,就是给平面不可约代数曲线以某种形式的全纯参数表示。
即对于PC^2中的不可约代数曲线C,寻找一个紧Riemann面C*和一个全纯映射σ:C*→PC^2,使得σ(C*)=C严格的定义如下:设C是不可约平面代数曲线,S是C的奇点的集合。
如果存在紧Riemann 面C*及全纯映射σ:C*→PC^2,使得(1)σ(C*)=C(2)σ^(-1)(S)是有限点集(3)σ:C*\σ^(-1)(S)→C\S是一对一的映射则称(C*,σ)为C的正则化。
结构损伤识别中的正则化方法

结构损伤识别中的正则化方法代江【摘要】In light of the inverse problem of structural damage,the article describes the regularization method needed in solving,introduces various specific methods,which is helpful for understanding damage identification and regularization method and for promoting relevant research of damage identification.%针对结构损伤识别这一反问题,对求解所需的正则化方法进行了综述,介绍了多种具体方法,有助于加深对损伤识别问题和正则化方法的理解,进而促进损伤识别的相关研究。
【期刊名称】《山西建筑》【年(卷),期】2012(038)012【总页数】3页(P42-44)【关键词】损伤;识别;反问题;正则化【作者】代江【作者单位】新疆哈密矿务局勘察设计院,新疆哈密839003【正文语种】中文【中图分类】TU311.41 概述工程结构的可靠性问题关乎生命财产安全,在学术界和工程界都得到了很大的重视。
要确保结构的可靠,需要及时发现结构的损伤情况。
从一般意义上来看,结构发生损伤是一种正问题,对损伤进行识别是一类典型的反问题。
当前各类反问题研究中都面临一个突出障碍,就是不适定性[1]。
对结构的损伤识别问题来说,反演需要基于一定的原始资料,主要是位移、频率、振型等,这些资料一般是通过监测直接或者间接获得的。
由于测量误差、测试条件或技术水平有限等因素,造成反演出的损伤信息不能达到存在性、唯一性和稳定性的完全满足,出现不适定问题(损伤可能识别不出来;对应有多种损伤情况、不能唯一确定;识别结果不抗噪)[2,3]。
不适定问题的tikhnonov正则化方法

不适定问题的tikhnonov正则化方法《不适定问题的tikhnonov正则化方法》一、Tikhonov正则化方法简介Tikhonov正则化方法是一种在不确定性情况下,以满足已获知条件来确定未知参数的数学方法,也称为受限最小二乘法(RLS)或Tikhonov惩罚。
它是拟合未知数据,裁剪异常数据或选择特征的常用技术。
它结合了线性代数的误差拟合和函数的模型,通过比较数据和模型来实现,并且可以消除装配数据较大的噪声。
它广泛应用于各种领域,如机器学习,图像处理,测量信号处理,医学成像,数据拟合等。
二、不适定问题不适定问题指的是拟合数据时,没有明确地标定未知数据范围或转换规则,需要解决大量不完全未知因素时,所面临的问题。
在大量实际问题中,存在着许多模型参数或者说未知量,通常我们是模糊不清的,不知道未知量到底应该取多少值,这些未知量和现实世界紧密相连,因此,很难准确的给出未知量的取值范围,这样的问题就称之为不适定问题。
三、Tikhonov正则化解决不适定问题的方法Tikhonov正则化是极其重要的方法,可以有效地解决不适定问题。
它主要基于几何形式的最小二乘拟合方法,考虑多个参数逐步克服受限性,增加惩罚力度,以抑制不具可解释性,存在明显异常点的资料变化,有效影响拟合数据偏离未知数带来的影响,使数据拟合的更加准确,能够比较准确的拟合复杂的函数。
四、Tikhonov解不适定问题优势所在Tikhonov正则化的主要优点有两个:一是克服参数之间的相关性,从而减少误差拟合;二是增加惩罚力度,从而抑制异常点。
此外,他还可以从数据中提取出更多有用的信息,增强无关事实的辨认能力,减少参数数量,从而确保拟合信息具有更强的准确性和可靠性。
因此,Tikhonov正则化有助于更好地解决不适定问题,能够提高模型的分类概率,以达到解决不适定问题的最佳效果。
五、总结Tikhonov正则化方法是一种有效地解决不适定问题的方法,它可以通过比较有约束的正则误差与受限的最小二乘拟合的误差之间的差异来拟合数据,克服参数之间的相关性,准确作出拟合结果,提高模型的分类概率,减少参数数量,以达到解决不适定问题的最佳效果。
迭代Tikhonov正则化位场向下延拓方法及其在尕林格铁矿的应用

迭代Tikhonov正则化位场向下延拓方法及其在尕林格铁矿的应用赵亚博;刘天佑【摘要】解析延拓是一种广泛应用的位场处理方法,向下延拓可以压制深部地质体的影响,突出浅部异常。
但是,向下延拓滤波因子是一个高通滤波器,会造成下延结果震荡,从而限制了该方法在实际资料中的应用。
文中详细介绍并实现了迭代Tikhonov正则化向下延拓方法,在理论模型上将该方法与传统频率域延拓方法进行对比,表明迭代Tikhonov正则化向下延拓方法的有效性;并将该方法应用于青海尕林格铁矿区磁测资料的处理解释中,下延结果与钻探情况相符,说明在厚覆盖层的勘查区中,运用迭代Tikhonov正则化向下延拓方法能够有效地提高资料处理解释的效果。
%Analytic continuation for potential field is a widely used method for processing and interpretation, because downwardcon⁃tinuation can suppress the influence of deep geological bodies and protrude the shallow layer anomaly. However, the downward con⁃tinuation filter factor is a high⁃pass filter, leading to unstableness of the result, and therefore it can not be used to process the real data. The authors systematically studied and implemented the iterative Tikhonov regularization method for downward continuation of potential fields. In contrast to the continuation of potential field on the theoretical model, the iterative Tikhonov regularization method indicates better effectiveness than frequency domain. The authors also applied this method to Galingeiron deposit's magnetic data pro⁃cessing, and the results indicate that the iteration Tikhonov regularization method for downwardcontinuation of potential fields is wor⁃thy to use in heavy overburden exploration areas.【期刊名称】《物探与化探》【年(卷),期】2015(000)004【总页数】6页(P743-748)【关键词】重磁勘探;向下延拓;迭代Tikhonov正则化;尕林格铁矿【作者】赵亚博;刘天佑【作者单位】中国地质大学武汉地球物理与空间信息学院,湖北武汉 430074;中国地质大学武汉地球物理与空间信息学院,湖北武汉 430074【正文语种】中文【中图分类】P631上世纪70年代初,我国开始将计算机应用于地球物理勘探资料的处理解释。
地球物理反演中的正则化技术及应用

地球物理反演中的正则化技术及应用地球物理反演是研究地球内部结构和性质的重要手段。
正则化技术是地球物理反演过程中常用的数学方法,旨在解决反问题的不适定性和非唯一性,提高反演结果的稳定性和可靠性。
本文将介绍正则化技术的基本原理和常用方法,并探讨其在地球物理反演中的应用。
地球物理反演是根据观测数据推断地下地球结构和性质的过程。
然而,由于地球介质的复杂性以及观测数据的不完备性和噪声污染等因素的影响,地球物理反演问题往往是不适定的反问题。
也就是说,同一个目标模型可以对应多个不同的观测数据解释,使得反演结果存在非唯一性。
此外,反演过程中还可能存在数值不稳定性,即小的扰动可能导致大的误差放大。
为了克服不适定性和非唯一性问题,正则化技术在地球物理反演中得到广泛应用。
正则化通过向反演问题中引入附加信息,对反演结果进行约束,从而提高反演结果的稳定性和可靠性。
正则化的基本思想是在目标函数中同时考虑拟合数据的残差项和模型的先验信息项,通过调节两者之间的平衡,得到最优的反演结果。
在正则化技术中,最常用的方法是Tikhonov正则化。
Tikhonov正则化通过在目标函数中引入二阶范数(L2范数)惩罚项,对模型进行光滑约束,使得反演结果具有空间平滑性。
这种正则化方法在稳定性和保真性之间取得了良好的平衡,常用于地震波速度、重力场和磁场等反演问题。
除了Tikhonov正则化,还有一些其他常用的正则化技术,如L1范数正则化、TV正则化和脉冲响应正则化等。
L1范数正则化通过在目标函数中引入一阶范数惩罚项,将反演结果稀疏化,适用于具有稀疏结构的反演问题。
TV正则化是对图像进行处理的一种方法,通过将图像的梯度惩罚项添加到目标函数中,实现对反演结果的边缘保持和去噪。
脉冲响应正则化是将目标函数中的滤波器参数视作反演模型的参数,通过滤波器设计对反演结果进行约束。
这些正则化技术在地球物理反演中具有各自的优势和适用范围,根据具体的反演问题选择合适的正则化方法进行应用。
三类分数阶偏微分方程反问题的正则化方法和算法研究

三类分数阶偏微分方程反问题的正则化方法和算法研究三类分数阶偏微分方程反问题的正则化方法和算法研究摘要:分数阶偏微分方程广泛应用于自然科学和工程领域,其中反问题更是高度关注的研究领域之一。
本文旨在研究三类常见的分数阶偏微分方程反问题,在此基础上提出相应的正则化方法和算法,以提高问题求解的稳定性和精确度。
1. 引言分数阶偏微分方程被广泛用于描述复杂的自然现象和物理过程。
与传统的整数阶偏微分方程相比,分数阶偏微分方程能更好地刻画非局部和非线性的动态现象。
然而,由于分数阶导数的非局部性质,分数阶偏微分方程的反问题求解更加困难。
因此,正则化方法和算法在分数阶反问题的研究中具有重要意义。
2. 问题描述本文研究了三类常见的分数阶偏微分方程反问题:分数阶扩散方程反问题、分数阶波动方程反问题和分数阶常微分方程反问题。
这些反问题的求解都具有非唯一性和不稳定性,需要采用适当的正则化方法和算法来提高求解的可行性和精确度。
3. 正则化方法为了解决分数阶反问题的非唯一性和不稳定性,本文提出了以下几种正则化方法:(1)Tikhonov正则化方法:引入稳定函数和正则化参数,通过最小二乘逼近的方式求解反问题,得到稳定的解;(2)Truncated Singular Value Decomposition (TSVD)正则化方法:在奇异值分解的基础上,通过截断低奇异值保留高奇异值,减小反问题求解的不稳定性;(3)正则化梯度方法:通过求解正则化函数的梯度来逐步逼近真解,从而得到稳定的反问题解。
4. 正则化算法针对三类分数阶反问题,本文设计了相应的正则化算法:(1)分数阶扩散方程反问题的正则化算法:根据已知的边界条件和初始条件,采用Tikhonov正则化方法求解扩散系数,通过正则化函数的二阶导数近似求解散度项;(2)分数阶波动方程反问题的正则化算法:通过TSVD正则化方法求解波动方程的初始条件和边界条件,采用逆迭代法求解分数阶导数的近似;(3)分数阶常微分方程反问题的正则化算法:通过正则化梯度方法,采用逐步逼近的方式求解常微分方程的参数,并得到稳定的解。
