道路竖曲线参数计算
纵断面设计——竖曲线设计

纵断面设计——竖曲线设计纵断面上相邻两条纵坡线相交的转折处,为了行车平顺用一段曲线来缓和,这条连接两纵坡线的曲线叫竖曲线。
竖曲线的形状,通常采用平曲线或二次抛物线两种。
在设计和计算上为方便一般采用二次抛物线形式。
纵断面上相邻两条纵坡线相交形成转坡点,其相交角用转坡角表示。
当竖曲线转坡点在曲线上方时为凸形竖曲线,反之为凹形竖曲线。
一、竖曲线如图所示,设相邻两纵坡坡度分别为i1 和i2,则相邻两坡度的代数差即转坡角为ω= i1-i2 ,其中i1、i2为本身之值,当上坡时取正值,下坡时取负值。
当i1- i2为正值时,则为凸形竖曲线。
当i1 - i2 为负值时,则为凹形竖曲线。
(一)竖曲线基本方程式我国采用的是二次抛物线形作为竖曲线的常用形式。
其基本方程为:若取抛物线参数为竖曲线的半径,则有:(二)竖曲线要素计算公式竖曲线计算图示1、切线上任意点与竖曲线间的竖距通过推导可得:2、竖曲线曲线长:L = Rω3、竖曲线切线长:T= TA =TB ≈ L/2 =4、竖曲线的外距:E =⑤竖曲线上任意点至相应切线的距离:式中:x —为竖曲任意点至竖曲线起点(终点)的距离, m;R—为竖曲线的半径,m。
二、竖曲线的最小半径(一)竖曲线最小半径的确定1.凸形竖曲线极限最小半径确定考虑因素(1)缓和冲击汽车行驶在竖曲线上时,产生径向离心力,使汽车在凸形竖曲线上重量减小,所以确定竖曲线半径时,对离心力要加以控制。
(2)经行时间不宜过短当竖曲线两端直线坡段的坡度差很小时,即使竖曲线半径较大,竖曲线长度也有可能较短,此时汽车在竖曲线段倏忽而过,冲击增大,乘客不适;从视觉上考虑也会感到线形突然转折。
因此,汽车在凸形竖曲线上行驶的时间不能太短,通常控制汽车在凸形竖曲线上行驶时间不得小于3秒钟。
(3)满足视距的要求汽车行驶在凸形竖曲线上,如果竖曲线半径太小,会阻挡司机的视线。
为了行车安全,对凸形竖曲线的最小半径和最小长度应加以限制。
竖曲线高程计算公式(一)

竖曲线高程计算公式(一)竖曲线高程计算公式在土木工程和道路设计中,竖曲线是指公路或铁路沿纵向发生变化的曲线。
通过计算竖曲线的高程,我们可以确定道路或铁路的纵向轮廓,确保车辆或列车在垂直方向上的安全行驶。
本文将介绍竖曲线高程计算公式的相关内容,并提供示例说明。
标准竖曲线要素在计算竖曲线高程之前,我们需要了解一些标准竖曲线的要素,包括以下几个参数:1.起点高程(E1):竖曲线的起点高程,通常为已知值。
2.终点高程(E2):竖曲线的终点高程,也为已知值。
3.起点纵坡比(G1):起点的纵向坡度,表示每单位水平距离对应的竖向高度变化。
4.终点纵坡比(G2):终点的纵向坡度,同样表示每单位水平距离对应的竖向高度变化。
5.曲线长度(L):竖曲线的水平长度,即起点到终点之间的距离。
6.曲线中点(P):竖曲线的中点,即起点和终点之间的一半距离。
通常情况下的竖曲线高程计算公式在绝大多数情况下,我们可以使用以下公式来计算竖曲线的高程:E = E1 + G1 * P + (4 * (E2 - E1) - (G1 + G2) * L) *(P / L) * (1 - (P / L))其中,E为竖曲线的任意点的高程。
示例说明我们来通过一个具体的示例来解释竖曲线高程计算公式的应用。
假设一条道路的起点高程为100米,终点高程为150米,起点纵坡比为,终点纵坡比为,曲线长度为200米。
现在我们需要计算该曲线上距离起点100米处的高程。
根据上述公式,我们可以依次计算:•起点到终点的水平距离为200米,因此曲线中点P为100米。
•根据公式,可得到:E = 100 + * 100 + (4 * (150 - 100) - ( + ) * 200)* (100 / 200) * (1 - (100 / 200))化简后计算得到:E = 100 + 3 + (4 * 50 - * 200) * *= 100 + 3 + (200 - 10) *= 100 + 3 +=因此,在距离起点100米处的位置,竖曲线的高程为米。
《纵坡竖曲线》课件

纵坡与竖曲线的关系:在排水设计中,纵坡和竖曲线是相互影响的,需要协调好 两者的关系。
纵坡的作用:控制水流速度,防止水流过快导致冲刷和侵蚀。
竖曲线的作用:控制水流方向,防止水流过于集中导致冲刷和侵蚀。
协调方法:根据实际情况,合理设置纵坡和竖曲线的坡度、长度和位置,确保水 流平稳、均匀、安全地通过排水系统。
确定纵坡竖曲线的位置和长度
测量纵坡竖曲线的坡度和曲率
检查纵坡竖曲线的平整度和稳 定性
测量纵坡竖曲线的宽度和深度
控制点设置原 则:根据设计 图纸和现场实 际情况,合理
设置控制点
控制点类型: 包括高程控制 点、平面控制 点、坡度控制
点等
控制点测量: 采用全站仪、 水准仪等测量 仪器进行测量, 确保测量精度
纵坡计算公式:i = h/l,其中i为纵坡, h为高差,l为水平距 离
纵坡的表示方法: 通常用百分比表示,%之间 ,具体取值根据道路等 级和设计速度确定
纵坡的计算注意事项 :在计算纵坡时,需 要考虑地形、地质、 水文等因素,确保道 路的安全性和舒适性 。
施工人员必须佩戴安全帽、安全带等防护用品 施工过程中注意保持施工现场整洁,避免杂物堆积 施工过程中注意观察周围环境,避免发生意外事故 施工过程中注意遵守交通规则,避免发生交通事故
添加文档副标题
目录
01.
02.
03.
04.
05.
06.
纵坡是指道路在纵向上的坡度,通常用百分比表示。 纵坡的坡度决定了车辆行驶的速度和稳定性。 纵坡过大或过小都会对车辆行驶产生不利影响。 纵坡的设置需要考虑地形、地质、气候等因素。
竖曲线是道路 设计中的一种 特殊曲线,用 于连接不同坡
度的路段。
竖曲线的形状 通常是一个弧 形,其半径和 坡度可以根据 道路设计要求
各种曲线计算公式

一、公路平曲线坐标计算公式1、缓和曲线:Lb1 0{K,D}①T=A2/R ②L=J(K-O)+T ③B=T2 /2/A2 *180/π④M=(L-T)-(L5-T5)/40/A4+(L9-T9)/3456/A8-(L13-T13)/599040/A12+(L17-T17)/17542600/A165.N=(L3-T3)/6/A2-(L7-T7)/336/A6+(L11-T11)/42240/A10-(L15-T15) /9676800/A14+(L19-T19)/3530097000/A18⑥I=(L2-T2)*180/2/A2/π⑦X=C+Mcos(Q-ZB)-ZNsin(Q-ZB)+Dcon(Q+ZI+S)◢⑧Y=F+Msin(Q-ZB)+ZNcos(Q-ZB)+Dsin(Q+ZI+S)◢Goto 0注:A:缘和曲线参数 R:起点半径 J:曲率半径判定值(当曲率半径由小到大取1,否则取-1)(当起点半径到终点半径是由大或无穷大到小取+1,反之则取-1) K:欲求点里程 O:缘和曲线起点里程 C:缘和曲线起点X坐标Q:起始方位角(当J=-1时,方位角应+180。
) Z:偏角判定值(当J=1时,左偏为-1,右偏为1;当J=-1时,左偏为1,右偏为-1) D:距中桩的距离 S:斜交角度 F:缘和曲线起点Y坐标2、圆曲线Lb1 0{K,D}①L=K-0②X=C+R[sin(Q+L/R*180/π)-sinQ]+Dcos(Q+L/R*180/π+S)◢③Y=F-R[cos(Q+L/R*180/π)-cosQ]+Dsin(Q+L/R*180/π+S)◢ Goto 0注:K:欲求点里程 O:圆曲线起点里程 C:圆曲线起点X坐标 R:圆曲线半径 (左偏为负) Q:起始方位角 D:距中桩的距离 S:斜交角度 F:圆曲线起点Y坐标3、直线Lb1 0{K,D}①L=K-0②X=C+LcosQ+Dcos(Q+S)◢③Y=F+LsinQ+Dsin(Q+S)◢Goto 0注:K:欲求点里程 O:直线起点里程 C:直线起点X坐标 Q:起始方位角 D:距中桩的距离 S:斜交角度 F:直线起点Y坐标二、竖曲线计算公式Lb1 0①{K} ②L=K-(0-T)③H=M-IT+LI-ZL2 /2/R◢ Goto 0 注:K:欲求点里程;O:顶点里程;T:切线长;M:顶点高程;I:坡度;Z:竖曲线判定值三、预拱度计算公式Lb1 0①{K} ②H=D-(4D÷B2)×(B/2-(K-O)) 2◢ Goto 0注:D:跨中最大设计预拱度 H:要计算的预拱度 K:欲求点里程桩号(距支座的距离) O:起点桩号 B:本跨净长。
竖曲线半径定义

竖曲线半径定义
竖曲线半径是指道路设计中的一个参数,用于描述道路竖曲线的曲率大小。
竖曲线是指道路在垂直方向上的曲线,用来连接不同的高程。
竖曲线半径即为竖曲线的曲率半径,表示竖曲线所形成的圆弧的半径长度。
在道路设计中,竖曲线半径的大小很重要,它影响着道路的坡度和曲线的平顺程度。
竖曲线半径越大,曲线的变化越平缓,车辆过弯时的加速度和侧向力较小,行驶更加平稳。
相反,竖曲线半径越小,曲线的变化越急,车辆过弯时的加速度和侧向力较大,行驶则较为颠簸。
在道路设计中,根据道路的等级和设计速度等因素,会确定竖曲线的最小半径。
一般来说,在高速公路等高速道路上,竖曲线半径一般较大,以确保车辆能够平稳过弯;而在城市道路等低速道路上,由于车速较低,竖曲线半径可以较小。
此外,竖曲线半径的选择还需要考虑其他因素,如地形条件、车辆类型等。
竖曲线、缓和曲线计算公式
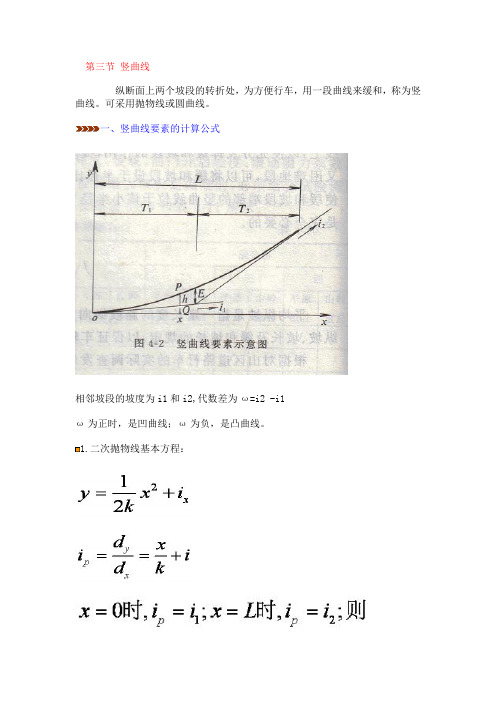
第三节竖曲线纵断面上两个坡段的转折处,为方便行车,用一段曲线来缓和,称为竖曲线。
可采用抛物线或圆曲线。
一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时,是凹曲线;ω为负,是凸曲线。
1.二次抛物线基本方程:或ω:坡度差(%);L:竖曲线长度;R:竖曲线半径2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: (前提:ω很小)L=Rω竖曲线切线长:T=L/2=Rω/2竖曲线上任一点竖距h:竖曲线外距:二、竖曲线最小半径(三个因素)1.缓和冲击对离心加速度加以控制。
ν(m/s)根据经验,a=0.5~0.7m/s2比较合适。
我国取a=0.278,则Rmin=V2/3.6 或Lmin=V2ω/3.62.行驶时间不过短 3s的行程Lmin=V.t/3.6=V/1.23.满足视距的要求分别对凸凹曲线计算。
(一)凸形竖曲线最小半径和最小长度按视距满足要求计算1.当L<ST时,Lmin = 2ST - 4/ω2.当L≥ST时,ST为停车视距。
以上两个公式,第二个公式计算值大,作为有效控制。
按缓和冲击、时间行程和视距要求(视距为最不利情况)计算各行车速度时的最小半径和最小长度,见表4-13。
表中:(1)一般最小半径为极限最小半径的1.5~2倍;(2)竖曲线最小长度为3s行程的长度。
(二)凹曲线最小半径和长度1.夜间行车前灯照射距离要求:1)L<ST2) L≥STL<ST Lmin = 2ST - 26.92/ω (4-14)L≥STω /26.92 (4-15)3s时间行程为有效控制。
例:设ω=2%=0.02;则L=ωR竖曲线最小长度L=V/1.2速度V=120km/h V=40km/h 一般最小半径R凸17000 700一般最小半径R凹6000 700 L凸340 14L凹120 14 例题4-3ω=-0.09 凸形;L=Rω=2000*0.09=180mT=L/2=90mE=T2/2R=2.03m起点桩号=k5+030 - T =K4+940起始高程=427.68 - 5%*90=423.18m桩号k5+000处:x1=k5+000-k4+940=60m切线高程=423.18+60*0.05=426.18m h1=x21/2R=602/2*2000=0.90m设计高程=426.18 - 0.90=425.28m 桩号k5+100处:x2=k5+100-k4+940=160m切线高程=423.18+160*0.05=431.18m h2=x22/2R=1602/2*2000=6.40m设计高程=431.18 - 6.40=424.78m第一节平面线形概述一、路线路线指路的中心线;路线在水平面上的投影叫路线的平面;路线设计:确定路线空间位置和各部分几何尺寸的工作;可分为平面设计、纵断面设计、横断面设计。
道路勘测课程设计计算说明书1

道路勘测设计课程设计道路勘测课程设计计算说明书指导老师:汪晓霞一、设计总说明1、目的和要求:通过本次课程设计,要求熟悉公路设计规范,理解、掌握《道路勘测设计》的基本概念,综合运用本课程和其他有关课程的基本知识和基本操作技能,使所学知识进一步巩固、深化和发展;学习道路路线设计的一般方法和步骤。
通过设计,培养学生初步具备正确的设计思想和动手的能力,使学生具有初步的工程设计概念;培养学生具备道路路线设计的基本技能。
根据设计所给资料,进行平、纵、横断面设计及其组合处理,完成土石方计算与调配,编制直线、曲线及转角一览表、路基设计表、路基土石方数量计算表;进行路面结构类型选择,并确定各结构层的合理厚度。
2、工程概况:本路为某矿区通往工业基地跨越重丘区一路线,主要为解决解放牌汽车运输问题,现年平均交通量990辆(折合重型载重汽车)平均年增长率为7.5%。
设计路线范围为11#~45#,路线起点11#高程为160m,终点45#高程204m。
本线一端接山区,另一端为微丘地形,中间为重丘过渡段(即本课题设计路段),该段地质情况基本稳定,除地表0.5-1.0米风化土层外,下部为石灰岩,地下水位一般较深对路基与边坡稳定影响不大。
二、道路参数1、道路技术等级的确定查《公路工程技术标准》以下简称《标准》)及其他相关资料,解放牌汽车以小客车为标准的折算系数为:1.5(包括:>19座的客车和载质量>2~7t的货车)。
当设计年限为15年,远景设计年平均交通量:)/(4087%)5.71(9905.1)1(11510日辆=+⨯=+=--n d N N γ式中:d N ——远景设计年平均日交通量,辆/日;0N ——预测初年平均日交通量,辆/日;γ——交通量年平均增长率,%;n ——远景设计年限。
查《公路工程技术标准》双车道三级公路应能适应将各种汽车折合成小客车的年平均日交通量为2000~6000辆。
本设计路线折合成小客车的远景设计年平均日交通量为4087辆,综合考虑公路工程技术标准和指标,确定该公路等级为三级公路。
铁路竖曲线要素计算公式

铁路竖曲线要素计算公式
铁路竖曲线要素计算公式包括:
1.曲线半径:R = (V^2) / (g x tan(α))
其中,R为曲线半径,V为设计速度,g为重力加速度(约等于9.8m/s^2),α为设定超高角(通常为2-7度)。
2.切线长度:TL = R x sin(α)
其中,TL为切线长度,R为曲线半径,α为设定超高角。
3.过渡曲线长度:GL = R x (cot(α/2) - tan(α/2))
其中,GL为过渡曲线长度,R为曲线半径,α为设定超高角。
4.过渡曲线进入曲线角度:θI = cos^(-1)(cos(α/2) / (1 + GL/R))
其中,θI为过渡曲线进入曲线角度,α为设定超高角,GL为过渡曲线长度,R为曲线半径。
5.过渡曲线退出曲线角度:θO = cos^(-1)(cos(α/2) / (1 -
GL/R))
其中,θO为过渡曲线退出曲线角度,α为设定超高角,GL为过
渡曲线长度,R为曲线半径。
以上是常见的铁路竖曲线要素计算公式,它们用于确定设计时的
曲线半径、切线长度、过渡曲线长度以及进入和退出曲线的角度。
这
些要素的计算是为了确保铁路的行车安全性和乘车舒适性而进行的。
拓展方面,还可以根据需要考虑其他要素,如设计超高、坡度等,以
满足不同的工程要求。
此外,曲线要素计算还可以考虑地形地貌、列
车运行参数、轨道几何要求等方面的因素,以使设计更加综合和实用。
两种形式的竖曲线计算方法及结果分析

三级公路
3 0
40 O
四级公路
2 0
20 o
k /h m R n l
其 中, R即竖 曲线的半径 , 将式 ( ) 4 代人式 ( ) : 1得
Y
1
=
凹 型
R J R
m
3O 0 0
l o 0o 0
l0 0 0
2O o 0
20 5
40 0
行 加宽处理 , 以满足交通量增长 的需要 。
配采用 A 一3 石 料选用抗 滑 、 C1 、 耐磨石 料) 改性乳 化沥青粘层 油 ; , 4 考虑到二 次抛物 的 曲率是连 续变 化 的, 于行 车来 说 , ) 对 抛
5 对 比两者基本 方程 , ) 二次抛物 线式竖 曲线计算公 式更为 简
种形式竖 曲线 之间相 互通 用的条件。
关键词 : 二次抛物线 , 圆曲线 , 曲线 , 竖 计算 , 比分 析 对
中图分类号 : 4 2 3 U 1 . 文献标识码 : A 由图 2可得 :
1 acai = rt 1 n () 6 () 7
() 8
O 引言
公路路线 纵断面为沿道路 中线竖 直剖切后 的展 开线 , 在纵 断 面的纵坡 变更 处 , 用竖 曲线 进行缓 和 , 采 其计 算形 式有 二次 抛 物 线 和圆曲线两种。JJ 1 - T 1 4公路路线设计规范 ( 0 9 以下简称《 旧规 范》 中规定 一般 采用 二 次抛 物 线或 圆 曲线 ; JG D 020 ) 而 T 2 -0 6 公路路 线设计 规范 ( 以下简 称《 规范》 中规 定宜 采 用 圆曲线 。 新 ) 但在 《 新规范》 的条文 说明中明确在实际设计工作 中 , 可根据计算 的方便 , 采用抛物线或 圆曲线 。
道路竖曲线计算

第二节 竖曲线设计纵断面上相邻两条纵坡线相交的转折处,为了行车平顺用一段曲线来缓和,这条连接两纵坡线的曲线叫竖曲线。
竖曲线的形状,通常采用平曲线或二次抛物线两种。
在设计和计算上为方便一般采用二次抛物线形式。
纵断面上相邻两条纵坡线相交形成转坡点,其相交角用转坡角表示。
当竖曲线转坡点在曲线上方时为凸形竖曲线,反之为凹形竖曲线。
一、竖曲线如图所示,设相邻两纵坡坡度分别为i 1 和i 2,则相邻两坡度的代数差即转坡角为ω= i 1-i 2 ,其中i 1、i 2为本身之值,当上坡时取正值,下坡时取负值。
当 i 1- i 2为正值时,则为凸形竖曲线。
当 i 1 - i 2 为负值时,则为凹形竖曲线。
(一)竖曲线基本方程式我国采用的是二次抛物线形作为竖曲线的常用形式。
其基本方程为:Py x 22=若取抛物线参数P 为竖曲线的半径 R ,则有:Ry x 22= Rx y 22=(二)竖曲线要素计算公式竖曲线计算图示1、切线上任意点与竖曲线间的竖距h 通过推导可得:==PQ h )()(2112li y l x R y y A A q p ---=-Rl 22=2、竖曲线曲线长: L = R ω3、竖曲线切线长: T= T A =T B ≈ L/2 =2ωR 4、竖曲线的外距: E =RT 22⑤竖曲线上任意点至相应切线的距离:Rx y 22=式中:x —为竖曲任意点至竖曲线起点(终点)的距离, m ;R —为竖曲线的半径,m 。
二、竖曲线的最小半径(一)竖曲线最小半径的确定1.凸形竖曲线极限最小半径确定考虑因素 (1)缓和冲击汽车行驶在竖曲线上时,产生径向离心力,使汽车在凸形竖曲线上重量减小,所以确定竖曲线半径时,对离心力要加以控制。
(2)经行时间不宜过短当竖曲线两端直线坡段的坡度差很小时,即使竖曲线半径较大,竖曲线长度也有可能较短,此时汽车在竖曲线段倏忽而过,冲击增大,乘客不适;从视觉上考虑也会感到线形突然转折。
高速公路坐标计算方法

高速公路坐标高程计算程序本软件简要说明:一、平曲线计算(主程序)1、J为起算点里程,C、D为起算点的X、Y坐标,F为起算点的切线方位角,R为圆曲线半径(左偏取负,右偏取正),A、B为第一、第二缓和曲线回旋参数,O为圆曲线长度,Ki为该分段的终点里程;2、对于直线段或圆曲线段,起算点可取直线或圆曲线上的任意一点;3、对于带第一、第二缓和曲线的平曲线段,起算点应取HY点;4、K为所求点的里程,T、P为第一偏距、偏角,S、Z为第二偏距、偏角,偏角取从该点的切线顺时针旋转的夹角;5、分段法则:直线单独分段;单一的圆曲线单独分段;缓和曲线1+圆曲线+缓和曲线2为一个整体单独分段,若不存在第一或第二缓和曲线(即不完全缓和曲线)仍然可以计算,A或B可取任意不为零的值;若不存在圆曲线,则O取零;6、无论任何时候A、B不能取零,否则可能导致被零除的错误;7、F、Q切线方位角输入输出均为度.分秒的格式,例如153°24′05.24″=153.240524。
Q改变时,可按照新方位角为基准,结合第一第二偏距、偏角重新计算所求点;8、输入平曲线参数后,默认为计算全线坐标,可修改来计算某段曲线,默认间距也可修改;9、可参考CAD图《平曲线计算图例》;10、生成的中桩CAD脚本设置成在世界坐标系下生成,注意的是世界坐标系与大地测量坐标系的区别是XY坐标是互换的,否则画出的图形与实际相反。
先打开CAD,设置好图层名称、颜色,并设置为当前层,然后单击CAD的工具==>运行脚本==>选中生成的脚本文件即可。
11、输出的坐标结果可以导入到EXCEL中,操作办法为:打开EXCEL,然后把坐标数据复制到单元格里,然后单击数据==>分列==>选中分隔符号==>下一步==>选中TAB键和逗号==>下一步==>完成即可。
下一次可直接在此表中粘贴,数据自动分列。
二、缓和曲线计算(辅助程序)1、本程序为辅助程序,用来从ZH点或HZ点计算整条完全的缓和曲线,若不知道HY点X、Y、Q参数,可用此程序计算出来,然后输入平曲线参数;2、参数设置参考平曲线计算;3、导出到EXCEL的办法同平曲线计算;三、直线计算(辅助程序)1、本程序为辅助程序,若已知P1(X1,Y1),P1-->P2的距离I及方位角J(度.分秒格式),可计算坐标P2(X2,Y2)。
道路勘测设计第三版答案

道路勘测设计第三版答案道路勘测设计第三版答案【篇一:道路勘测设计第三章课后习题参考答案】线计算3-9 某条道路变坡点桩号为k25+460.00,高程为780.72m,i1=0.8%,i2=5%,竖曲线半径为5000m。
(1)判断凸、凹性;(2)计算竖曲线要素;(3)计算竖曲线起点、k25+400.00、k25+460.00、k25+500.00、终点的设计高程。
l/2=105.00 m e=t2/2r=1.10 m(3)设计高程竖曲线起点桩号:k25+460-t=k25+355.00竖距:h=x2/2r=0.20 m设计高程:780.24+0.20=780.44 mk25+460:变坡点处设计高程=变坡点高程+e=780.72+1.10=781.82 m竖曲线终点桩号:k25+460+t=k25+565两种方法 1)从竖曲线起点开始计算横距:x=(k25+500)-(k25+355.00)=145m 竖距:h=x2/2r=2.10 m 切线高程(从3-10 某城市i级主干道,其纵坡分别为i1=-2.5%、i2=+1.5%,变坡点桩号为k1+520.00,标高为429.00m,由于受地下管线和地形限制,曲线中点处的标高要求不低于429.30m,且不高于429.40m,试确定竖曲线的半径,并计算k1+500.00、k1+520.00、k1+515.00点的设计标高。
竖曲线中点处的设计高程为变坡点高程加外距,则外距的取值范围为e=(429.30-429,429.40-429)=(0.30,0.40)设计高程计算:设计高程=429.50+0.07=429.57 mk1+520.00处:设计高程=429.00+0.36=429.36m设计高程=429.375+0.27=429.39 m3-11 某平原微丘区二级公路,设计速度80km/h,有一处平曲线半径为250m,该段纵坡初定为5%,超高横坡为8%,请检查合成坡度,若不满足要求时,该曲线上允许的最大纵坡度为多少?解答:根据《公路路线设计规范》,二级公路、设计速度80km/h,最大合成坡度值应取9.0% 22225%8%9.4349.0zhiii=++==%%,不满足要求允许的最大纵坡 22229%8%4.123zhiii=?+==%【篇二:道路勘测设计课后答案第三版杨少伟】二章汽车行驶特性2.1 已知某条道路的滚动阻力系数为0.015,如果东风eq-140型载重汽车装载90%时,挂iv档以30km/h的速度等速行驶,试求(1)h=0,(2)h=1500m海拔高度上所能克服的最大坡度。
路线设计中停车视距要求下的竖曲线半径计算

s= +
半 径值 的研究比较深入.但对竖曲线 的计 算及 研究还 比较 少。
式中 ,.s为停车视 距 ,m;S。为安全 距离 ,取 3 ̄5m;V为运行速
2停车视距 的概念及计 算
行车 视距 分为停车视距 、会车视距 、超车视距 、识别 视距
度 ,km/h;t为反应时间 .s; 为轮 胎与路面 之间的纵向摩阻系 数 ;i为路线纵坡(上坡 为正 ,下坡 为负 )。影响停车视距 的主要 因素有运行速度 I,、摩 阻系数 和 反应时间 t[31。
梁素平
(中交远洲交通 科技集 团有 限公司 ,石家庄 050000)
LIA NG Su—ping (China Roads Communications Technology Group Limited,Shijiazhuang050000,China)
【摘 要 】近年 来,设计质量越 来越受到 大家的重视 。公路路线的设计作 为公路设计的基础计 中停车视 巨的计 算 并通过 MATLAB对停车视距要求 下的竖曲线半径进 行计 算,对
表 2 停车视距计算参数及结果表
。\\\ R| |R¨ 一h2 I 7/ 62
图 1 凸竖 曲线半径计算 图 图 2凹竖 曲线半径计算图 图 1中 ,由于竖 曲线半 径比较 大 ,停车 视距很 小 ,昕 以 , 。 图中 啦均较小 ,因此认 为 S=S。+.s:。
凸 曲线半径计算如下 :
b 22-R—b. sin89。。
(2)
式(1)、式 (2)均 为一元四 次方程 ,本 文通过 MATLAB计
【文章 编 号 】1007—9467(2019)叭 一0136—02
各级公路的竖曲线最小长度和半径规定表6

第一节 纵坡及坡长设计
合成坡度
合成坡度是指由路线纵坡与弯道超高 横坡或路拱横坡组合而成的坡度,其 方向即流水线方向。
ib
i
i合
合成坡度可按矢量关系或勾股定理关 系导出:
i合 i2 ib2
式中: i合—合成坡度(%);i —公路平曲线处的纵坡(%); ib —公路平曲线处的超高横坡度(%)。
第二节 竖曲线设计
竖曲线
如图所示,设相邻两纵坡坡度分别为i1 和i2,则相 邻两坡度的代数差即转坡角为ω= i1-i2 ,其中i1、 i2为本身之值,当上坡时取正值,下坡时取负值。
当 i1- i2为正值时,则为凸形竖曲线。当 i1 - i2 为负值时,则为凹形竖曲线。
第二节 竖曲线设计
的竖曲线半径的最小值,该值只有在地形受限制迫不得已时 采用。
通常为了使行车有较好的舒适条件,设计时多采用大于极限 最小半径1.5~2.0倍,该值为竖曲线一般最小值。我国按照 汽车在竖曲线上以设计速度行驶3s行程时间控制竖曲线最小 长度。
各级公路的竖曲线最小长度和半径规定表3-6所列,在竖曲 线设计时,不但保证竖曲线半径要求,还必须满足竖曲线最
改正值: y x2 2R
第二节 竖曲线设计
计算竖曲线上任意点设计标高: 某桩号在凸形竖曲线的设计标高 =该桩号在切线上的设计标高-y 某桩号在凹形竖曲线的设计标高 =该桩号在切线上的设计标高+y
第三节 爬坡车道
爬坡车道:是陡坡路段正线行车道外侧增设的供载重车行
驶的专用车道。
设置爬坡车道的条件
第二节竖曲线设计竖曲线的最小半径竖曲线最小半径的确定凸形竖曲线极限最小半径确定考虑因素缓和冲击经行时间不宜过短满足视距的要求第二节竖曲线设计凹形竖曲线极限最小半径确定考虑因素缓和冲击前灯照射距离要求跨线桥下视距要求经行时间不宜过短第二节竖曲线设计凸凹形竖曲线都要受到上述缓和冲击视距及行驶时间三种因素控制
竖曲线最值点位置及曲线任意点高程准确计算

= 。 一 鬲T ’ 鬲 , , 。 。 + 而T 而
其 中, %, ,分别为前 、 后切点的里程 。
U
u
( 4 ) ’
\
1 竖 曲线 的几何 要素
由图 1可以得出 , 竖 曲线 的几何 要素如下 :
切 线长 :
=
/ 。
/
胁 n 旦 2
_
站, 此 时就需要确定竖 曲线实 际最低点 的位 置 。当工 程付诸 实施 时, 施 工方根据设计 图纸进 行 竖曲线 的测设 , 然而设 计 文件一 般
由图 1可以看出 , 最低点位 于坡度较缓 的一侧 。
需 要说明的是 , 最低点 与变 坡点 的距 离满 足 A L ≥0的 条件 ,
线上任意点 的准确 高程计 算公式 , 结果表 明理论 导出的竖 曲线高程计 算方法提高 了计算 精度 , 涵盖 了所 有 圆形 竖 曲线 类别 , 适 用
于铁路工程 、 公路工程及地铁工程领域 的设计和施 工 , 可为竖 曲线计算提供参 考借鉴。
关键词 : 竖 曲线 , 最值 点 , 位置 , 任 意点 , 高程 中图分类 号 : U 2 3 1 . 1 文献标识码 : A
探讨 了极值 点存 在的情况 , 并 给出了竖 曲线中极值 点位置 的计算 归为如下 四类 : 1 ) i 1 < 0< i 2 且l i l I ≥l i 2 I , 简称凹形一类竖 曲线 ; 公式 , 其公式 以弧长 的形式 给出 , 公式 中存在其 他未 知量 , 不便 于
2 ) i <i 2 ≤O且 l i l l >I i 2 I , 简称凹形二类竖 曲线 ;
3 ) i < 0< i 2 且l i J I <l i 2 I , 简 称凹形三类竖 曲线 ; 4 ) 0 ≤i 。 < i , 简称 凹形 四类竖 曲线 。 由图 2可 以得 出, 前后 两切点的里程分别为 :
道路竖曲线高程计算公式

道路竖曲线高程计算公式在道路工程中,竖曲线高程的计算可是个相当重要的环节。
说起这竖曲线高程计算公式,那可真是让不少人头疼,但别怕,咱们一起来把它弄明白。
我还记得有一次在一个道路施工的现场,我亲眼目睹了因为竖曲线高程计算不准确而导致的问题。
当时,工人们正在铺设一段新的道路,一切看起来都有条不紊地进行着。
可是,当铺设到一处竖曲线的位置时,问题出现了。
原本应该顺滑过渡的路面,却出现了明显的高低差,车辆行驶在上面颠簸得厉害。
经过一番调查,发现就是因为竖曲线高程的计算出现了偏差。
那到底什么是竖曲线高程计算公式呢?简单来说,竖曲线是在道路纵断面上两个坡段的转折处,为了行车的平稳和安全而设置的一段曲线。
而计算竖曲线高程,就是要确定在这个曲线上不同位置的高度。
竖曲线高程的计算公式主要涉及到一些关键的参数,比如竖曲线的半径、切线长、外距等等。
其中,最常用的公式是:竖曲线高程 = 切线高程 ±竖距而切线高程 = 变坡点高程 ±坡度 ×坡长这里的“±”要根据竖曲线的凹凸情况来确定,如果是凸形竖曲线就用“-”,凹形竖曲线就用“+”。
比如说,我们有一个道路的变坡点高程为 100 米,坡度为 5%,坡长为 200 米,竖曲线半径为 5000 米。
首先计算切线高程,切线高程 = 100 + 0.05 × 200 = 110 米。
接下来计算竖距,竖距 = (坡长的平方)÷(2 ×竖曲线半径)= (200×200)÷(2×5000)= 4 米。
如果这是一个凸形竖曲线,那么竖曲线高程 = 110 - 4 = 106 米。
在实际应用中,可不能马虎。
就像我在前面提到的那个施工现场,一点点的偏差都可能导致严重的后果。
而且,不同的道路设计要求和地形条件,都会对竖曲线高程的计算产生影响。
有时候,计算竖曲线高程还需要考虑到一些特殊情况。
比如说,如果道路有多个变坡点,那就需要依次计算每个竖曲线的高程,确保整个路段的过渡都平稳顺畅。
某一级公路k17+800-k20+500段计算书

内容提要本次毕业设计为模拟常德市石门县一级公路K17+800-K20+500段施工图设计,此一级公路本设计路段全长2700m ,设计行车时速是80km/h,双向四车道。
石门县一级公路本设计路段,路线平面设计2个交点,平曲线半径分别为1900m和1200m。
纵断面设计两个变坡点,设计了一凸一凹两竖曲线,竖曲线半径均为30000m。
路线最大纵坡为1.533%,为下坡;路线最小纵坡为0.412%,为上坡。
路基宽度24.5m,其中:行车道宽度为15.0m,中间带宽3.0m,两侧均设有0.75m的土路肩和2.5m的硬路肩。
行车道及硬路肩横坡度为2%,土路肩横坡度为3%。
边沟的深度和沟底宽度均为0.6m。
本次挡土墙设计共设计了3处,统一采用重力式的。
路面结构采用16cm厚的沥青混凝土面层、20cm厚的基层和35cm厚的底基层。
另外本次设计还在位于桩号K18+284、K19+648两处设置管径为1.5m的圆管涵洞。
本设计还运用纵横软件对路段土石挖填方进行了预算。
关键词:平面设计;挡土墙;涵洞;一级公路;路面CONTENT SUMMARYThis graduation design is a simulation of Changde Shimenn County highway K17+800-K20+500 section of the construction design, the design of the section of a highway length 2700m, designed driving speed is 80km/h, two-way four lane.The design section of Shimenn County highway, route 2 intersection plane design, horizontal curve radius are respectively two 1900m and 1200m. on design vertical section design, a convex and concave two vertical curve, vertical curve radius is the maximum longitudinal slope of 30000m. route 1.533%, route for the downhill minimum grade is 0.412%;, uphill roadbed width 24.5m, the lane width is 15.0m, the middle bandwidth of 3.0m, both sides are equipped with hard shoulder 0.75m soil shoulder and 2.5m. And the hard shoulder Lane cross slope is 2%, transverse slope soil shoulder 3%. edge The depth of the ditch and the width of the bottom of the ditch are 0.6m.. The design of the retaining wall has been designed 3, unified gravity type. The pavement structure adopts 16cm thick asphalt concrete surface layer, 20cm thick base and 35cm thick subbaseIn addition, the design is still located in the pile number K18+284, K19+648 two set of pipe diameter of 1.5m pipe culvert. This design also uses vertical and horizontal software to track the earth fill excavation budget Keywords: graphic design; retaining wall; culvert; highway; pavement目录内容提要 (I)CONTENT SUMMARY........................................ I I 1 设计总说明. (1)1.1 给定的原始资料 (1)1.2 设计依据 (1)1.4 工程相关情况 (2)1.5 技术指标 (2)2 路线平面设计 (4)2.1 公路等级的确定 (4)2.2 路线设计 (4)2.3 平曲线形要素值的确定 (4)2.4 路线曲线要素计算 (7)3路线纵断面设计 (10)3.1 纵坡设计的步骤 (10)3.2 纵断面的竖曲线设计技术指标 (10)3.3 竖曲线设计计算 (11)4 横断面设计 (13)4.1横断面的组成部分 (13)4.2横向坡度 (13)4.3弯道的超高和加宽 (13)4.4 曲线的加宽 (14)4.5横断面图的绘制 (14)5 土石方的计算 (16)5.1 横断面面积计算 (16)5.2 土石方数量计算 (16)5.3土方量计算 (16)6 路基及排水设计 (17)6.1路基宽度的确定 (17)6.2路基边坡 (17)6.3 路基压实标准 (18)6.4 路基填料 (18)6.5 排水设计 (18)7 挡土墙设计 (19)7.1.挡土墙设计 (19)7.2.挡土墙结构验算 (20)8 涵洞设计 (22)8.1涵洞类型选择 (22)8.2涵洞的位置及尺寸 (22)9 路面设计 (23)9.1 路面选择 (23)9.2 轴载换算 (23)9.3 结构组合与材料选取 (24)10 施工图预算编制 (31)11 总结 (32)参考文献 (33)1 设计总说明1.1 给定的原始资料(1)湖南省常德市石门县地形图;(2)石门县一级公路K17+800-K20+500段施工图设计任务书;(3)石门县相关的其它资料。
凹竖曲线最小半径

凹竖曲线最小半径凹竖曲线是指在平面内的一种特殊曲线形状,它的曲率在某一段区间内是凹的(曲率向外),而在另一段区间内是竖的(曲率向内)。
在道路设计、管道布置等领域中,凹竖曲线的应用非常广泛,它可以使曲线的转弯半径得以最小化,从而能够在有限的空间内实现更加灵活的布置。
本文将重点探讨凹竖曲线最小半径的计算方法及其在实际应用中的意义。
一、凹竖曲线的定义凹竖曲线是指在直线段之间,变半径曲线的转弯规则。
当曲线向外转弯时,曲率最小值对应的半径为凹竖曲线的最小半径。
二、凹竖曲线最小半径的计算方法凹竖曲线最小半径的计算方法主要包括两种:一是基于曲率变化率的计算方法,二是基于半径变化率的计算方法。
1. 基于曲率变化率的计算方法凹竖曲线最小半径可以通过计算曲率的变化率来确定。
曲率的变化率可以通过公式来计算,其推导过程较为复杂,在此不做详细介绍。
基于曲率变化率的计算方法可以较为准确地确定凹竖曲线的最小半径,但计算复杂度较高。
2. 基于半径变化率的计算方法凹竖曲线最小半径也可以通过计算半径的变化率来确定。
半径的变化率可以通过公式来计算,其计算方法相对简单。
具体的计算步骤如下:1) 首先,根据道路设计或管道布置的实际要求,确定起始点和终止点的位置。
2) 根据起始点和终止点的位置,计算直线段的长度。
3) 根据直线段长度和曲线段长度的要求,确定曲线段的长度。
4) 根据曲线段的长度,计算半径的变化率。
5) 根据半径的变化率和给定的参数,计算凹竖曲线的最小半径。
三、凹竖曲线最小半径的实际应用意义凹竖曲线最小半径的计算方法可以为道路设计和管道布置等领域的实际工程提供重要的参考依据。
凹竖曲线的最小半径的确定可以使曲线的转弯半径减小,从而能够在有限的空间内实现更加灵活的布置。
在狭窄的道路、弯曲的山路以及限制条件多的管道设计中,凹竖曲线的应用可以有效地解决空间布局难题,提高工程的安全性和效率。
综上所述,凹竖曲线最小半径的计算方法及其在实际应用中的意义是道路设计和管道布置等领域中的重要课题。
