一道经典的立体几何求角问题
初中求角度10题

初中求角度10题
当然,以下是10道适合初中学生的求角度的几何题目:
1.在△ABC中,已知∠A = 40°,∠B = 60°,求∠C的度数。
2.已知等腰三角形的一个底角为50°,求它的顶角的度数。
3.在△ABC中,AB = AC,∠A = 36°,求∠B和∠C的度数。
4.已知一个多边形的内角和为1080°,求这个多边形的边数及每个内角的度数。
5.在矩形ABCD中,若∠A = 60°,求∠B、∠C和∠D的度数。
6.已知菱形的两条对角线互相垂直,且其中一条对角线与菱形的一边的夹角为30°,
求这个菱形的各个内角的度数。
7.在△ABC中,若∠A = ∠B = ∠C,且∠A + ∠B + ∠C = 180°,求∠A、∠B和∠
C的度数。
8.已知等腰梯形ABCD中,AD∥BC,∠A = 60°,∠B = 45°,求∠C和∠D的度
数。
9.在△ABC中,若∠A = 2∠B = 3∠C,求∠A、∠B和∠C的度数。
10.已知一个正n边形的每个外角都等于45°,求这个正n边形的边数n。
立体几何求角

立体几何求角一•解答题(共8小题)1 如图,在正四棱锥P-ABCD中, PA=AB=a E是棱PC的中点.(1)求证:PC X BD;(2)求直线BE与PA所成角的余弦值.2. 如图,已知△BCD所在平面互相垂直,且/ BAC玄BCD=90 , AB=AC CB=CD点E, F分别在线段BD, CD上,沿直线丘卩将厶EFD向上翻折使得D与A重合(I)求证:AB丄CF;(H)求直线AE与平面ABC所成角.3. 如图,在直三棱柱ABC- A1B1O中,AB=AC=5 BB=BC=6 D, E分别是AA和B i C的中点.(1)求证:DEI BC(2)求三棱锥E- BCD的体积.4. 如图:ABCD是平行四边形,AP丄平面ABCD BE// AP, AB=AP=2 BE=BC=1 / CBA=60(1)求证:EC/平面PAD;(2)求证:平面PACL平面EBC(3)求直线PC与平面PABE所成角的正弦值.5. 如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA丄平面ABCD M N分别是AB PC 的中点,PA=AD=1 AB=2(1)求证:MIN/平面PAD(2)求证:平面PMC_平面PCD(3)求点D到平面PMC的距离.6. 如图,在四棱锥P- ABCD中, AD丄平面PDC AD// BC, PD丄PB, AD=1, BC=3, CD=4, PD=2(I)求异面直线AP与BC所成角的余弦值;(n)求证:PD丄平面PBC(川)求直线AB与平面PBC所成角的正弦值.7. 如图,已知三棱锥P- ABC PU平面ABC / ACB=90,/ BAC=60 , PA=AQ M 为PB 的中点.(I)求证:PC X BC(n)求二面角M- AC- B的大小.&如图,四棱锥P-ABCD中, PD丄底面ABCD且底面ABCD为平行四边形,若/ DAB=60 , AB=2, AD=1.(1)求证:PA X BD(2)若/ PCD=45,求点D到平面PBC的距离h.立体几何求角一•解答题(共8小题)1 如图,在正四棱锥P-ABCD中, PA=AB=a E是棱PC的中点.(1)求证:PC X BD;(2)求直线BE与PA所成角的余弦值.【解答】证明:(1厂••四边形ABCD为正方形,且PA=AB=a•••△PBC △PDC都是等边三角形,…(2分)•E是棱PC的中点,•BE X PC, DEI PC,又BE n DE=E•PC丄平面BDE・・(5 分)又BD?平面BDE•PC X BD・・(6 分)解:(2)连接AC,交BD于点O连OE四边形ABCD为正方形,•O是AC的中点•••(8分)又E是PC的中点•OEACP的中位线,•AP// OE•/ BEO即为BE与PA所成的角•••(10分)在Rt△BOE中, BE=「|, EO= . ,,-(12 分)•cos / BEO丄-.BE - 3•直线BE与PA所成角的余弦值为「(14分)32. 如图,已知△ABC和△BCD所在平面互相垂直,且/ BAC玄BCD=90 , AB=AC CB=CD 点E, F分别在线段BD CD上,沿直线丘卩将厶EFD向上翻折使得D与A重合(I)求证:AB丄CF;(H)求直线AE与平面ABC所成角.R【解答】解:(1)面ABCL 面BCD 面AB6面BCD=BC / BCD=90> CF 丄 BC,> FC 丄面ABC> AB 丄CF ・・(5 分)(2 ) 设 21' ' 1 ■ 1 I-'- - 'I 1,设 BE=t ,贝U ED=EA=2 — t , 又二「-J 匚一面ABC 丄面BCD面ABCri 面BCD 二BC =AH 丄面7分) AH1BC 丿又 AH!面 BCD AE^AH+EH ,.— 2 - t )二+t 2- t+丄, 2 2••• _〕.,•••点 E 是 BD 的中点,•••( 10 分)HE// BC, • HE!面ABC / BEA 为所求角的线面角…(12分)宀./■ . 口 •••( 14 分)所以直线AE 与平面ABC 所成角为」••( 15分).3. 如图,在直三棱柱 ABC- A 1B 1C 1中,AB=AC=5 BB=BC=6 D, E 分别是 AA 和BQ 的中点.(1) 求证:DEI BC ;(2) 求三棱锥 E - BCD 的体积.a取BC 的中点H,连接HE AH【解答】证明:(1 )取BC中点F,连结EF, AF,则EF A BCB的中位线,/•EF// BB, EF= BB,2•/AD// BB, AD」-BB,「. EF/ AD, EF=AD 二四边形ADEF是平行四边形,二DE// AF,2•/ AB=AC F 是BC的中点,•••AF丄BC, /• DEI BC.(2)T BB 丄平面ABC AF?平面ABC •- BB 丄AF,又•••AF丄BC BC?平面BCCB i , BB?平面BCCB i , BC A BB=B,•AF丄平面BCCB i , •DEL平面BCCB i ,•/ AC=5, BC=6 •CF丄:「=3 , •AF= ‘_「r「=4 , /. DE=AF=4 ■/ BC=BB=6 , •• S A BCE=^厂=9.•三棱锥E- BCD的体积 V=」S A BC E?DE==12.3 34. 如图:ABCD是平行四边形,AP丄平面ABCD BE/ AP, AB=AP=2 BE=BC=1 / CBA=60(1)求证:EC//平面PAD(2)求证:平面PACL平面EBC(3)求直线PC与平面PABE所成角的正弦值.Bi【解答】(1)证明:因为BE// PA,BE?平面 PAD PA?平面 PAD , 所以BE//平面 PAD 同理BC//平面 PAD 所以平面PAD//平面EBC因为EC?平面EBC 所以EC//平面PAD-( 4分)(2) 证明:因为 AB=2 BC=1, / CBA=60 , 由余弦定理得,AC=J ■,所以由勾股定理逆定理/ BCA=90 ,所以AC 丄BC ,又因为 BE X 平面 ABCD 所以BE X AC, 则有AC 丄平面EBC AC?平面PAC所以平面 BEC X 平面PAC •••( 8分)(3) 解:作CH X AB 于H ,连结PH, 又因为CH 丄PA 所以CH 丄平面PABE 所以/ HPC 即为线面角,5. 如图所示,四棱锥 P -ABCD 中 ,底面 ABCD 是矩形,PA 丄平面ABCD M N 分别是AB PC 的中点,PA=AD=1 AB=2(1) 求证:MIN/平面PAD(2) 求证:平面 PMC_平面PCD(3) 求点D 到平面PMC 的距离.【解答】(1)证明:设PD 的中点为E ,连接AE NE由N 为PC 的中点知EN 平行且等于1 DC 2又ABCD 是矩形,••• DC 平行且等于 AB, ••• EN 平行且等于一 AB2又M 是AB 的中点,• EN 平行且等于 AM• AMNE 是平行四边形• MN// AE,而 AE?平面 PAD NM?平面 PAD• MN//平面 PAD(2)证明:T PA=AD •- AE X PD,又••• PA 丄平面 ABCD CD?平面ABCD• CD 丄 PA 而 CD 丄 AD • CDL 平面 PAD• CD 丄 AE, •/ PD A CD=D • AE 丄平面 PCD•/ MN// AE, • MNL 平面 PCDPC 14 (13 分)* v ■ * x /A Nf E又MN?平面PMC•••平面 PMCL 平面 PCD(3) 解:设点D 到平面PMC 勺距离为h ,则•32 3•••点D 到平面PMC 的距离h^L -. 5【解答】解:(I)如图,由已知 AD// BC,故/ DAP 或其补角即为异面直线 AP 与BC 所成的角.因为AD 丄平面 PDC 所以AD ± PD.在 Rt △ PDA 中,由已知,得•川「||「||「|「-故..u. :.AP 5所以,异面直线 AP 与BC 所成角的余弦值为工.5证明:(n)因为 ADL 平面 PDC 直线 PD?平面PDC所以AD ± PD又因为BC// AD,所以PD 丄BC又PD 丄PB 所以PDL 平面 PBC解:(川)过点 D 作AB 的平行线交 BC 于点F ,连结PF , 则DF 与平面PBC 所成的角等于AB 与平面PBC 所成的角. 因为PD 丄平面PBC 故PF 为DF 在平面PBC 上的射影, 所以/ DFP 为直线DF 和平面PBC 所成的角. 由于 AD// BC DF// AB 故 BF=AD=16. 如图,在四棱锥 P - ABCD 中, AD 丄平面 PDC AD// BC, PD 丄PB, AD=1, (I)求异面直线 AP 与BC 所成角的余弦值;(H)求证:PD 丄平面PBCBC=3, CD=4, PD=2由已知,得 CF=BC- BF=2.又 ADL DC ,故 BC 丄 DC在 Rt △ DCF 中,可得匚—-F ■--.所以,直线AB 与平面PBC 所成角的正弦值为7. 如图,已知三棱锥 P- ABC PAL 平面 ABC / ACB=90,/ BAC=60 , PA=AC M 为 PB 的中点. (I)求证:PC L BC(H)求二面角 M- AC- B 的大小.P【解答】解:(I)证明:由 PA L 平面ABC ••• PA L BC,又因为/ ACB=90,即 BC L AC• BC 丄面 PAC • PC L BC.(H)取 AB 中点O,连结MO 过O 作HC L AC 于 H,连结 MH 因为M 是PB 的中点,所以 MO // PA , 又因为PAL 面ABC • MOL 面ABCMHO 为二面角 M- AC- B 的平面角.设 AC=2 贝U BC=^3, MO=1 OH 丽, 二面角 M- AC- B 的大小为300. P&如图,四棱锥 P -ABCD 中 , PD 丄底面ABCD 且底面ABCD 为平行四边形,若/ DAB=60 ,在 Rt △ MHO 中 tanAB=2, AD=1.(1)求证:PA I BD(2)若/ PCD=45,求点D到平面PBC的距离h.【解答】(1)证明:T AD=1, AB=2,Z DAB=60 ,•BD2=A B'+AE2 - 2AB?AD?cos60 °=3, .AD2+BE2=A B', •AD丄BD,-PD丄平面ABCD BD?平面ABCD•PD丄BD,又AD A PD=D•BD丄平面PAD PA?平面PAD•BD丄PA(2)解:由(1)可知BC丄BD•- PC=二CD=2 二,PB=「】L»= - , BC=1,2 2 2•BC+PB=PC , •PB丄BC,i V T•S A BC= •],・「=,•V D- BC L. r=",3 2 6又V3-BC[=V D-BCP, •.7 =匚•• ,6 3解得h=「.•••S A BC\:|尸,•••/ PCD=45 , • PD=CD=2。
第8章立体几何专题7 线面角的求解常考题型专题练习——【含答案】

线面角的求解【方法总结】1、线面角的范围:[0°,90°]2、线面角求法(一):先确定斜线与平面,找到线面的交点A为斜足;找线在面外的一点B,过点B向平面α做垂线,确定垂足O;连结斜足与垂足为斜线AB在面α上的投影;投影AO与斜线AB之间的夹角为线面角;把投影AO与斜线AB归到一个三角形中进行求解(可能利用余弦定理或者直角三角形)。
注意:以上第二步过面外一点向平面做垂线的方法有一下几种:1)线在面外的一点B与平面上某点的连线正垂直于面α,无需再做辅助线;2)题中已知有与面α垂直的直线,过线在面外的一点B直接做此垂线的平行线;3)过线在面外的一点B做两垂直平面交线的垂线,利用面面垂直的性质证明OB⊥面α(这两个垂直平面一个是面α,另一个是过点B且与α垂直的平面)。
3、线面角求法(二)用等体积法,求出斜线PA在面外的一点P到面的距离,利用三角形的正弦公式进行求解。
114、线面角求法(三)利用空间向量进行求解,高二再学。
【巩固练习】1、已知正方体1111ABCD A B C D -的体积为162,点P 在正方形1111D C B A 上,且1,A C 到P 的距离分别为2,23,则直线CP 与平面11BDD B 所成角的正切值为( )A.2 B.3 C.12D.13【答案】A【解析】易知22AB =;连接1C P ,在直角1CC P ∆中,可计算22112C P CP CC =-=;又1112,4A P A C ==,所以点P 是11A C 的中点;连接AC 与BD 交于点O ,易证AC ⊥平面11BDD B ,直线CP 在平面11BDD B 内的射影是OP ,所以CPO ∠就是直线CP 与平面11BDD B 所成的角,在直角CPO ∆中,2tan 2CO CPO PO ∠== .2、把正方形沿对角线折起,当以四点为顶点的三棱锥体积最大时,直线和平面所成的角的大小为A.B.C.D.[来源网ZXXK]【答案】C【解析】如图所示,当平面平面时,三棱锥的体积最大,取的中点,则平面,故直线和平面所成的角为,则,所以,故选C.3、如图,在三棱锥P-ABC中,,PA AB⊥PC BC⊥,,AB BC⊥22,AB BC==5PC=,则PA与平面ABC所成角的大小为_______.【答案】45︒【解析】如图,作平行四边形ABCD,连接PD,由AB BC⊥,则平行四边形ABCD是矩形.由BC CD⊥,BC PC⊥,PC CD C=,∴BC⊥平面PCD,而PD⊂平面PCD,∴BC PD⊥,同理可得AB PD⊥,又AB BC B⋂=,∴PD⊥平面11ABCD .,PD CD PD AD ⊥⊥,PAD ∠是PA 与平面ABC 所成角.由2,5CD AB PC ===得1PD =,又1AD BC ==,∴45PAD ∠=︒.∴PA 与平面ABC 所成角是45︒.4、已知三棱柱ABC -A 1B 1C 1的侧棱与底面边长都相等,A 1在底面ABC 内的射影为△ABC 的中心O ,则AB 1与底面ABC 所成角的正弦值为( )A .23B .13C .33D .23【答案】A【解析】作1A H ⊥面ABC 于点H ,延长11B A 到D ,延长BA 到E 使得111B A A D =,,BA AE =如图则有11A EAB ,又因为1A O ⊥面ABC ,故1A EO ∠为所求角,且111sin AO A EO A E∠=。
高考典型题型训练——立体几何中求角与距离

C A1EB1C1高考典型题型训练——立体几何中求角与距离1. 四棱锥P —ABCD 的底面是边长为a 的正方形,PB ⊥面ABCD. (1)若面PAD 与面ABCD 所成的二面角为60°,求这个四棱锥的体积;(2)证明无论四棱锥的高怎样变化,面PAD 与面PCD 所成的二面角恒大于90°2如图,直三棱柱ABC-A 1B 1C 1的底面ABC 为等腰直角三角形,∠ACB=900,AC=1,C 点到AB 1的距离为CE=23,D 为AB 的中点. (1)求证:AB 1⊥平面CED ;(2)求异面直线AB 1与CD 之间的距离;(3)求二面角B 1—AC —B 的平面角.3. 如图a—l—β是120°的二面角,A,B两点在棱上,AB=2,D在α内,三角形ABD是等腰直角三角形,∠DAB=90°,C在β内,∆ABC是等腰直角三角形∠ACB=.900(I)求三棱锥D—ABC的体积;(2)求二面角D—AC—B的大小;(3)求异面直线AB、CD所成的角.4. 在边长为a的正三角形的三个角处各剪去一个四边形.这个四边形是由两个全等的直角三角形组成的,并且这三个四边形也全等,如图①.若用剩下的部分折成一个无盖的正三棱柱形容器,如图②.则当容器的高为多少时,可使这个容器的容积最大,并求出容积的最大值.图①图②5. 已知三棱锥P—ABC中,PC⊥底面ABC,AB=BC,D、F分别为AC、PC的中点,DE⊥AP于E.(1)求证:AP⊥平面BDE;(2)求证:平面BDE⊥平面BDF;(3)若AE∶EP=1∶2,求截面BEF分三棱锥P—ABC所成两部分的体积比.6. 如图,几何体ABCDE中,△ABC是正三角形,EA和DC都垂直于平面ABC,且EA=AB=2a,DC=a,F、G分别为EB和AB的中点.(1)求证:FD∥平面ABC;(2)求证:AF⊥BD;(3) 求二面角B—FC—G的正切值.7. 如图,正方体ABCD—A1B1C1D1的棱长为1,P、Q分别是线段AD1和BD上的点,且D1P∶PA=DQ∶QB=5∶12.(1) 求证PQ∥平面CDD1C1;(2) 求证PQ⊥AD;A B C D E A 1 B 1C 1D 1 xyz(3)求线段PQ 的长.8. 如图4,在长方体ABCD -1111A B C D 中,AD=1AA =1,AB=2,点E 在棱AB上移动。
高考真题(立体几何中空间角问题[题目])
![高考真题(立体几何中空间角问题[题目])](https://img.taocdn.com/s3/m/9d2b391cdaef5ef7bb0d3c62.png)
解答题1. 如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是菱形,2,60AB BAD =∠=o .(Ⅰ)求证:BD ⊥平面;PAC(Ⅱ)若,PA AB =求PB 与AC 所成角的余弦值;(Ⅲ)当平面PBC 与平面PDC 垂直时,求PA 的长.2. 如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,四边形ABCD 中,AB ⊥AD ,AB +AD =4,CD =2,︒=∠45CDA .(I )求证:平面P AB ⊥平面P AD ;(II )设AB =AP .(i )若直线PB 与平面PCD 所成的角为︒30,求线段AB 的长;(ii )在线段AD 上是否存在一个点G ,使得点G 到点P ,B ,C ,D 的距离都相等?说明理由。
3. 如图5.在椎体P -ABCD 中,ABCD 是边长为1的棱形,且∠DAB =60︒,2PA PD ==,PB =2, E ,F 分别是BC ,PC 的中点.(1) 证明:AD ⊥平面DEF ;(2) 求二面角P -AD -B 的余弦值.4. 如图,已知正三棱柱111ABC A B C -的各棱长都是4,E 是BC 的中点,动点F 在侧棱1CC 上,且不与点C 重合.(Ⅰ)当CF =1时,求证:EF ⊥1A C ;(Ⅱ)设二面角C AF E --的大小为θ,求tan θ的最小值.A B DC FPE5. 如图,在圆锥PO中,已知PO=2,⊙O的直径2AB=,C是»AB的中点,D为AC 的中点.(Ⅰ)证明:平面POD⊥平面PAC;(Ⅱ)求二面角B PA C--的余弦值。
6. 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=12 PD.(I)证明:平面PQC⊥平面DCQ;(II)求二面角Q—BP—C的余弦值.8. 如图,四棱锥P ABCD -中,底面ABCD 为平行四边形,60DAB ∠=︒,2AB AD =,PD ⊥底面ABCD .(I )证明:PA BD ⊥;(II )若PD =AD ,求二面角A -PB -C 的余弦值.9. 在如图所示的几何体中,四边形ABCD 为平行四边形,∠ ACB =90︒,EA⊥平面ABCD,EF ∥AB,FG∥BC,EG∥AC.AB=2EF.(Ⅰ)若M是线段AD的中点,求证:GM∥平面ABFE;(Ⅱ)若AC=BC=2AE,求二面角A-BF-C的大小.10. 如图,在ABC ∆中,60,90,ABC BAC AD ∠=∠=o o 是BC 上的高,沿AD 把ABC ∆折起,使90BCD ∠=o 。
高中数学必修二立体几何角的问题-教师版(含几何法和向量法)

立体几何线线、线面、面面所成角的问题几何法1、两异面直线及所成的角:不在同一个平面的两条直线,叫做异面直线,已知异面直线a,b,经过空间任一点O 作直线a '∥a ,b '∥b ,我们把a '与b '所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角).如果两条异面直线所成的角是直角,我们就说这两条直线互相垂直.2、直线和平面所成的角:一条直线PA 和一个平面α相交,但不和这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点A 叫做斜足。
过斜线上斜足以外的一点向平面引垂线PO ,过垂足O 和斜足A 的直线 AO 叫做斜线在这个平面上的射影。
平面的一条斜线和它在平面内的摄影所成的锐角,叫做这条直线和这个平面所成的角。
一条直线垂直于平面,我们就说它们所成的角是直角。
一条直线和平面平行,或在平面内,我们说它们所成的角是00.3、二面角:从一条直线出发的两个半平面所组成的图形叫做二面角。
在二面角βα--l 的棱l 上任取一点O ,以点O 为垂足,在半平面α和β内分别作垂直于棱l 的射线OA 和OB ,则射线OA 和OB 构成的∠AOB 叫做二面角的平面角。
二面角的大小可以可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度。
常见角的取值范围:① 异面直线所成的角⎥⎦⎤ ⎝⎛20π,,直线与平面所成的角⎥⎦⎤⎢⎣⎡20π,,二面角的取值范围依次[]π,0② 直线的倾斜角[)π,0、到的角[)π,0、与的夹角的取值范围依次是⎥⎦⎤⎢⎣⎡20π,4、点到平面距离:求点到平面的距离就是求点到平面的垂线段的长度,其关键在于确定点在平面内的垂足,当然别忘了转化法与等体积法的应用. 向量法1、两异面直线及所成的角:设异面直线a ,b 的夹角为θ,方向向量为a ,b ,其夹角为ϕ,则有cos cos a b a bθϕ⋅==.2、直线和平面所成的角:设直线l 的方向向量为l ,平面α的法向量为n ,l 与α所成的角为θ,l 与n 的夹角为ϕ,则有sin cos l n l nθϕ⋅==.3、二面角:设1n ,2n 是二面角l αβ--的两个面α,β的法向量,则向量1n ,2n 的夹角(或其补角)就是二面角的平面角的大小.若二面角l αβ--的平面角为θ,则1212cos n n n n θ⋅=.4、点到平面距离:点P 是平面α外一点,A 是平面α内的一定点,n 为平面α的一个法向量,则点P 到平面α的距离为cos ,n d n nPA⋅=PA 〈PA 〉=.例题例1.长方体ABCD -A 1B 1C 1D 1中,AB =AA 1=2,AD =1,E 为CC 1的中点,则异面直线BC 1与AE 所成角的余弦值为( )A.1010B.3010C.21510D.31010 解析:建立空间直角坐标系如图.则A (1,0,0),E (0,2,1),B (1,2,0),C 1(0,2,2).BC 1→=(-1,0,2),AE →=(-1,2,1),cos 〈BC 1→,AE →〉=BC 1→·AE →|BC 1→|·|AE →|=3010.所以异面直线BC 1与AE 所成角的余弦值为3010.答案:B例 2.已知ABCD 是矩形,PA ⊥平面ABCD ,2AB =,4PA AD ==,E 为BC 的中点.(1)求证:DE ⊥平面PAE ;(2)求直线DP 与平面PAE 所成的角. 证明:在ADE ∆中,222AD AE DE =+,∴AE DE ⊥ ∵PA ⊥平面ABCD ,DE ⊂平面ABCD ,∴PA DE ⊥又PA AE A ⋂=,∴DE ⊥平面PAE (2)DPE ∠为DP 与平面PAE 所成的角在Rt PAD ∆,PD =Rt DCE ∆中,DE =在Rt DEP ∆中,2PD DE =,∴030DPE ∠=例3.如图,在四棱锥P ABCD -中,底面ABCD 是060DAB ∠=且边长为a 的菱形,侧面PAD 是等边三角形,且平面PAD 垂直于底面ABCD . (1)若G 为AD 的中点,求证:BG ⊥平面PAD ; (2)求证:AD PB ⊥;(3)求二面角A BC P --的大小.证明:(1)ABD ∆为等边三角形且G 为AD 的中点,∴BG AD ⊥ 又平面PAD ⊥平面ABCD ,∴BG ⊥平面PAD(2)PAD 是等边三角形且G 为AD 的中点,∴AD PG ⊥ 且AD BG ⊥,PG BG G ⋂=,∴AD ⊥平面PBG ,PB ⊂平面PBG ,∴AD PB ⊥(3)由AD PB ⊥,AD ∥BC ,∴BC PB ⊥ 又BG AD ⊥,AD ∥BC ,∴BG BC ⊥∴PBG ∠为二面角A BC P --的平面角在Rt PBG ∆中,PG BG =,∴045PBG ∠=例4.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,E 、F 分别为棱AA 1、BB 1的中点,G 为棱A 1B 1上的一点,且A 1G =λ(0≤λ≤1),则点G 到平面D 1EF 的距离为( D ) A.3 B.22C.32λ D.55练习:1、已知四边形ABCD 是空间四边形,,,,E F G H 分别是边,,,AB BC CD DA 的中点,(1)求证:EFGH 是平行四边形;(2)若BD=AC=2,EG=2。
立体几何中的求角问题
考向二:求线面所成角
题型一:直接利用垂直关系找射影
1.(2015浙江文)如图,在三棱柱中,
,
在地面的射影为的中点,是的中点。
(1)证明:平面
(2)求直线和平面所成角的正弦值.
2.(2016年浙江高考)如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=
3.
(1)求证:BF⊥平面ACFD;
(2)求直线BD与平面ACFD所成角的余弦值.
题型二:利用平行线和垂直关系找射影
3.(2017天津文)如图,在四棱锥中,平面,,
,,,,.
(1)求异面直线与所成角的余弦值;
(2)求证:平面
(3)求直线与平面所成角的正弦值.
题型三:构造垂直关系作射影
4.(2016天津文)如图,四边形是平行四边形,平面平面,,,,
,,,为的中点.
(1)求证:平面
(2)求证:平面平面
(3)求直线与平面所成角的正弦值.
B
A
3。
立体几何典型例题精选(含答案)
FEDCBA 立体几何专题复习热点一:直线与平面所成的角例1.(2014,广二模理 18) 如图,在五面体ABCDEF 中,四边形ABCD 是边长为2的正方形,EF ∥平面ABCD , 1EF =,,90FB FC BFC ︒=∠=,3AE =.(1)求证:AB ⊥平面BCF ;(2)求直线AE 与平面BDE 所成角的正切值.变式1:(2013湖北8校联考)如左图,四边形ABCD 中,E 是BC 的中点,2,1,5,DB DC BC ===2.AB AD ==将左图沿直线BD 折起,使得二面角A BD C --为60,︒如右图.(1)求证:AE ⊥平面;BDC(2)求直线AC 与平面ABD 所成角的余弦值.变式2:[2014·福建卷] 在平面四边形ABCD 中,AB =BD =CD =1,AB ⊥BD ,CD ⊥BD .将△ABD 沿BD 折起,使得平面ABD ⊥平面BCD ,如图1-5所示.(1)求证:AB ⊥CD ; (2)若M 为AD 中点,求直线AD 与平面MBC 所成角的正弦值.热点二:二面角例2.[2014·广东卷] 如图1-4,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC 于点F,FE∥CD,交PD于点E.(1)证明:CF⊥平面ADF;(2)求二面角D -AF -E的余弦值.变式3:[2014·浙江卷] 如图1-5,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED =90°,AB=CD=2,DE=BE=1,AC= 2.(1)证明:DE⊥平面ACD;(2)求二面角B -AD -E的大小.变式4:[2014·全国19] 如图1-1所示,三棱柱ABC -A1B1C1中,点A1在平面ABC内的射影D在AC 上,∠ACB=90°,BC=1,AC=CC1=2.(1)证明:AC1⊥A1B; (2)设直线AA1与平面BCC1B1的距离为3,求二面角A1 -AB -C的大小.热点三:无棱二面角例3.如图三角形BCD 与三角形MCD 都是边长为2的正三角形,平面MCD ⊥平面BCD ,AB ⊥平面BCD ,23AB =.(1)求点A 到平面MBC 的距离;(2)求平面ACM 与平面BCD 所成二面角的正弦值.变式5:在正方体1111ABCD A B C D -中,1K BB ∈,1M CC ∈,且114BK BB =,134CM CC =. 求:平面AKM 与ABCD 所成角的余弦值.变式6:如图1111ABCD A B C D -是长方体,AB =2,11AA AD ==,求二平面1AB C 与1111A B C D 所成二面角的正切值.高考试题精选1.[2014·四川,18] 三棱锥A-BCD及其侧视图、俯视图如图1-4所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.(1)证明:P是线段BC的中点;(2)求二面角A -NP -M的余弦值.2.[2014·湖南卷] 如图所示,四棱柱ABCD -A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.(1)证明:O1O⊥底面ABCD;(2)若∠CBA=60°,求二面角C1OB1D的余弦值.3.[2014·江西19] 如图1-6,四棱锥P -ABCD中,ABCD为矩形,平面P AD⊥平面ABCD.(1)求证:AB⊥PD. (2)若∠BPC=90°,PB=2,PC=2,问AB为何值时,四棱锥P -ABCD 的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.M OH FED C B A 立体几何专题复习 答案例1.(2014,广二模)(1)证明:取AB 的中点M ,连接EM ,则1AM MB ==,∵EF ∥平面ABCD ,EF ⊂平面ABFE ,平面ABCD 平面ABFE AB =, ∴EF ∥AB ,即EF ∥MB . ……………1分 ∵EF =MB 1=∴四边形EMBF 是平行四边形. ……………2分 ∴EM ∥FB ,EM FB =.在Rt △BFC 中,2224FB FC BC +==,又FB FC =,得FB =∴EM =……………3分在△AME中,AE =1AM =,EM =∴2223AM EM AE +==,∴AM EM ⊥. ……………4分 ∴AM FB ⊥,即AB FB ⊥. ∵四边形ABCD 是正方形,∴AB BC ⊥. ……………5分 ∵FB BC B =,FB ⊂平面BCF ,BC ⊂平面BCF ,∴AB ⊥平面BCF . ……………6分 (2)证法1:连接AC ,AC 与BD 相交于点O ,则点O 是AC 的中点, 取BC 的中点H ,连接,OH EO ,FH , 则OH ∥AB ,112OH AB ==. 由(1)知EF ∥AB ,且12EF AB =,∴EF ∥OH ,且EF OH =.∴四边形EOHF 是平行四边形.∴EO ∥FH ,且1EO FH == .……………7分 由(1)知AB ⊥平面BCF ,又FH ⊂平面BCF ,∴FH AB ⊥. ……………8分∵FH BC ⊥,,ABBC B AB =⊂平面ABCD ,BC ⊂平面ABCD ,∴FH ⊥平面ABCD . ……………9分 ∴EO ⊥平面ABCD . ∵AO ⊂平面ABCD ,∴EO ⊥AO . ……………10分 ∵AO BD ⊥,,EOBD O EO =⊂平面EBD ,BD ⊂平面EBD ,∴AO ⊥平面EBD . ……………11分∴AEO ∠是直线AE 与平面BDE 所成的角. ……………12分 在Rt △AOE中,tan AOAEO EO∠== ……………13分 ∴直线AE 与平面BDE……………14分 证法2:连接AC ,AC 与BD 相交于点O ,则点O 取BC 的中点H ,连接,OH EO ,FH , 则OH ∥AB ,112OH AB ==.由(1)知EF ∥AB ,且12EF AB =, ∴EF ∥OH ,且EF OH =. ∴四边形EOHF 是平行四边形.∴EO ∥FH ,且1EO FH ==. ……………7分 由(1)知AB ⊥平面BCF ,又FH ⊂平面BCF , ∴FH AB ⊥.∵FH BC ⊥,,ABBC B AB =⊂平面ABCD ,BC ⊂平面ABCD ,∴FH ⊥平面ABCD .∴EO ⊥平面ABCD . ……………8分 以H 为坐标原点,BC 所在直线为x 轴,OH 所在直线为y 轴,HF 所在直线为z 轴, 建立空间直角坐标系H xyz -,则()1,2,0A -,()1,0,0B ,()1,2,0D --,()0,1,1E -. ∴()1,1,1AE =-,()2,2,0BD =--,()1,1,1BE =--. ……………9分 设平面BDE 的法向量为=n (),,x y z ,由n 0BD ⋅=,n 0BE ⋅=, 得220x y --=,0x y z --+=,得0,z x y ==-.令1x =,则平面BDE 的一个法向量为=n ()1,1,0-. ……………10分 设直线AE 与平面BDE 所成角为θ, 则sin θ=cos ,n AE⋅=n AE nAE=. ……………11分∴cos θ==,sin tan cos θθθ== ……………13分 ∴直线AE 与平面BDE……………14分变式1:(2013湖北8校联考)(1)取BD 中点F ,连结,EF AF ,则11,,60,2AF EF AFE ==∠=……………2分由余弦定理知22222113121cos 60,222AE AF EF AE AE EF ⎛⎫+-⋅⋅=+=∴⊥ ⎪⎝⎭………4分又BD ⊥平面AEF ,,BD AE AE ∴⊥⊥平面BDC ………6分 (2)以E 为原点建立如图示的空间直角坐标系,则31),(1,,0)2A C -,11(1,,0),(1,,0)22B D --- ………8分设平面ABD 的法向量为n (,,)x y z =,由00n DB n DA ⎧⋅=⎪⎨⋅=⎪⎩得201302x x y =⎧⎪⎨+=⎪⎩,取3z =,则3,(0,3)y =-∴=-n . 136(1,,),cos ,224||||AC AC AC AC =--∴<>==-n n n ……11分故直线AC 与平面ABD 10. …………12分变式2:(2014福建卷)解:(1)证明:∵平面ABD ⊥平面BCD ,平面ABD ∩平面BCD =BD ,AB ⊂平面ABD ,AB ⊥BD ,∴AB ⊥平面BCD . …………3分 又CD ⊂平面BCD ,∴AB ⊥CD . …………4分 (2)过点B 在平面BCD 内作BE ⊥BD .由(1)知AB ⊥平面BCD ,BE ⊂平面BCD ,BD ⊂平面BCD ,∴AB ⊥BE ,AB ⊥BD . ……6分以B 为坐标原点,分别以BE →,BD →,BA →的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系(如图所示).依题意,得B (0,0,0),C (1,1,0),D (0,1,0),A (0,0,1),M ⎝⎛⎭⎫0,12,12. 则BC →=(1,1,0),BM →=⎝⎛⎭⎫0,12,12,AD →=(0,1,-1).…………7分 设平面MBC 的法向量n =(x 0,y 0,z 0), 则⎩⎪⎨⎪⎧n ·BC →=0,n ·BM →=0,即⎩⎪⎨⎪⎧x 0+y 0=0,12y 0+12z 0=0, 取z 0=1,得平面MBC 的一个法向量n =(1,-1,1). …………9分设直线AD 与平面MBC 所成角为θ,则sin θ=||cos 〈n ,AD →〉=|n ·AD →||n |·|AD →|=63. …………11分 即直线AD 与平面MBC 所成角的正弦值为63. …………12分例2.(2014,广东卷):(1):,,,,A ,,,,,,,,,,.(2):E EG//CF DF G,,,G GH AF H,EH,PD ABCD PD PCD PCD ABCD PCD ABCD CD D ABCD AD CD AD PCD CF PCD CF AD AF PC CF AF AD AF ADF ADAF A CF ADF CF DF EG DF ⊥⊂∴⊥=⊂⊥∴⊥⊂∴⊥⊥∴⊥⊂=∴⊥⊥∴⊥⊥∠解证明平面平面平面平面平面平面平面平面又平面平面解法一过作交于平面A 平面A 过作于连则00,CD 2,30,130,==1,21324,,,,,22333EG .,423EHG D AF E DPC CDF CF CD DECF CP EF DC DEDF DP CP DE EF AE AF EF DF AE EF EH HG AF --=∠=∴∠==∴=∴⋅=====⋅∴====为二面角的平面角设从而∥还易求得EF=从而易得故cos GH EHG EH ∴∠===12:,,,,,2,1(0,0,2),C(0,2,0),,(23,22,0),,,431,0),ADF CP (3,1,0),22AEF (x DP DC DA x y z DC A CF CP F DF CF F E n n λλλλ==-⊥===-=解法二分别以为轴建立空间直角坐标系设则设则可得从而易得取面的一个法向量为设面的一个法向量为2212212,y,z),0,0,419||||2n AE n AF n n n n n ⋅=⋅=⋅==⋅⨯利用且得可以是从而所求二面角的余弦值为变式3:(2014浙江卷)解:(1)证明:在直角梯形BCDE 中,由DE =BE =1,CD =2,得BD =BC =2, 由AC =2,AB =2,得AB 2=AC 2+BC 2,即AC ⊥BC . …………2分 又平面ABC ⊥平面BCDE ,从而AC ⊥平面BCDE ,所以AC ⊥DE .又DE ⊥DC ,从而DE ⊥平面ACD . …………4分 (2)方法一:过B 作BF ⊥AD ,与AD 交于点F ,过点F 作FG ∥DE ,与AE 交于点G ,连接BG . 由(1)知DE ⊥AD ,则FG ⊥AD .所以∠BFG 是二面角B - AD - E 的平面角.…………6分在直角梯形BCDE 中,由CD 2=BC 2+BD 2,得BD ⊥BC .又平面ABC ⊥平面BCDE ,得BD ⊥平面ABC ,从而BD ⊥AB .由AC ⊥平面BCDE ,得AC ⊥CD . 在Rt △ACD 中,由DC =2,AC =2,得AD = 6.在Rt △AED 中,由ED =1,AD =6,得AE =7.…………7分在Rt △ABD 中,由BD =2,AB =2,AD =6,得BF =2 33,AF =23AD .从而GF =23ED =23. …………9分在△ABE ,△ABG 中,利用余弦定理分别可得cos ∠BAE =5 714,BG =23. …………11分在△BFG 中,cos ∠BFG =GF 2+BF 2-BG 22BF ·GF=32. …………13分所以,∠BFG =π6,即二面角B - AD - E 的大小是π6.…………14分方法二:以D 为原点,分别以射线DE ,DC 为x ,y 轴的正半轴, 建立空间直角坐标系D - xyz ,如图所示.由题意知各点坐标如下:D (0,0,0),E (1,0,0),C (0,2,0),A (0,2,2),B (1,1,0).设平面ADE 的法向量为m =(x 1,y 1,z 1),平面ABD 的法向量为n =(x 2,y 2,z 2).可算得AD =(0,-2,-2),AE =(1,-2,-2),DB →=(1,1,0).…………7分由⎩⎨⎧m ·AD =0,m ·AE →=0,即⎩⎨⎧-2y 1-2z 1=0,x 1-2y 1-2z 1=0,可取m =(0,1,-2).…………9分由⎩⎪⎨⎪⎧n ·AD →=0,n ·DB →=0,即⎩⎨⎧-2y 2-2z 2=0,x 2+y 2=0, 可取n =(1,-1,2).…………11分于是|cos 〈m ,n 〉|=|m ·n ||m |·|n |=33×2=32. …………13分由题意可知,所求二面角是锐角,故二面角B - AD - E 的大小是π6.变式4:(2014全国卷)19.解:方法一:(1)证明:因为A 1D ⊥平面ABC ,A 1D ⊂平面AA 1C 1C AA 1C 1C ⊥平面ABC . 又BC ⊥AC ,所以BC ⊥平面AA 1C 1C . …………2分连接A 1C ,因为侧面AA 1C 1C 为菱形,故AC 1⊥A 1C .由三垂线定理得AC 1⊥A 1B . ……4分(注意:这个定理我们不能用) (2) BC ⊥平面AA 1C 1C ,BC ⊂平面BCC 1B 1,故平面AA 1C 1C ⊥平面BCC 1B 1.作A 1E ⊥CC 1,E 为垂足,则A 1E ⊥平面BCC 1B 1. …………6分又直线AA 1∥平面BCC 1B 1,因而A 1E 为直线AA 1与平面BCC 1B 1的距离,即A 1E = 3. 因为A 1C 为∠ACC 1的平分线,所以A 1D =A 1E = 3. …………8分 作DF ⊥AB ,F 为垂足,连接A 1F .由三垂线定理得A 1F ⊥AB ,故∠A 1FD 为二面角A 1 AB C 的平面角.…………10分由AD =AA 21-A 1D 2=1,得D 为AC 中点,DF =55,tan ∠A 1FD =A 1DDF=15,……12分 所以cos ∠A 1FD =14. …………13分所以二面角A 1 AB C 的大小为arccos 14. …………14分方法二:以C 为坐标原点,射线CA 为x 轴的正半轴,以CB 的长为单位长,建立如图所示的空间直角坐标系C - xyz .由题设知A 1D 与z 轴平行,z 轴在平面AA 1C 1C 内.(1)证明:设A 1(a ,0,c ).由题设有a ≤2,A (2,0,0),B (0,1,0),则AB →=(-2,1,0),AC →=(-2,0,0),AA 1→=(a -2,0,c ),AC 1→=AC →+AA 1→=(a -4,0,c ),BA 1→=(a ,-1,c ).由|AA 1→|=2,得(a -2)2+c 2=2,即a 2-4a +c 2=0.①又AC 1→·BA 1→=a 2-4a +c 2=0,所以AC 1⊥A 1B . …………4分(2)设平面BCC 1B 1的法向量m =(x ,y ,z ),则m ⊥CB →,m ⊥BB 1→,即m ·CB →=0,m ·BB 1→=0.因为CB →=(0,1,0),BB 1→=AA 1→=(a -2,0,c ),所以y =0且(a -2)x +cz =0.令x =c ,则z =2-a ,所以m =(c ,0,2-a ),故点A 到平面BCC 1B 1的距离为 |CA →|·|cos 〈m ,CA →〉|=|CA →·m ||m |=2c c 2+(2-a )2=c . …………6分又依题设,A 到平面BCC 1B 1的距离为3,所以c =3,代入①,解得a =3(舍去)或a =1, 于是AA 1→=(-1,0,3). …………8分 设平面ABA 1的法向量n =(p ,q ,r ), 则n ⊥AA 1→,n ⊥AB →,即n ·AA 1→=0,n ·AB →=0,-p +3r =0,且-2p +q =0.令p =3,则q =2 3,r =1,所以n =(3,2 3,1).…………10分 又p =(0,0,1)为平面ABC 的法向量,…………11分 故 cos 〈n ,p 〉=n ·p |n ||p |=14. …………13分所以二面角A 1 AB C 的大小为arccos 14. …………14分例3. 无棱二面角(2010年江西卷)解法一:(1)取CD 中点O ,连OB ,OM ,则OB ⊥CD ,OM ⊥CD .又平面MCD ⊥平面BCD ,则MO ⊥平面BCD ,所以MO ∥AB ,A 、B 、O 、M 共面.延长AM 、BO 相交于E ,则∠AEB 就是AM 与平面BCD 所成的角.OB =MO 3,MO ∥AB ,MO//面ABC ,M 、O 到平面ABC 的距离相等,作OH ⊥BC 于H ,连MH ,则MH ⊥BC ,求得:OH=OCsin600,利用体积相等得:A MBC M ABC V V d --=⇒=5分 (2)CE 是平面ACM 与平面BCD 的交线.由(1)知,O 是BE 的中点,则BCED 是菱形.作BF ⊥EC 于F ,连AF ,则AF ⊥EC ,∠AFB 就是二面角A -EC -B 的平面角,设为θ. ……7分因为∠BCE =120°,所以∠BCF =60°.sin 603BF BC =⋅=9分tan 2ABBFθ==,sin θ=…………11分所以,所求二面角的正弦值是5. …………12分 解法二:取CD 中点O ,连OB ,OM ,则OB ⊥CD ,OM ⊥CD ,又平面MCD ⊥平面BCD ,则MO ⊥平面BCD .以O 为原点,直线OC 、BO 、OM 为x 轴,y 轴,z 轴,建立空间直角坐标系如图. OB =OM ,则各点坐标分别为O (0,0,0),C (1,0,0),M (0,0,B (0,,0),A (0,,3),(1)设(,,)n xy z =是平面MBC 的法向量,则BC=(1,3,0),BM =,由n BC⊥得0x +=;由n BM ⊥得0+=;取(3,1,1),(0,0,n BA =-=,则距离2155BA n d n⋅==…………5分 (2)(CM =-,(1,CA =-.设平面ACM 的法向量为1(,,)n x yz =,由11n CM n CA⎧⊥⎪⎨⊥⎪⎩得0x x ⎧-+=⎪⎨-+=⎪⎩.解得x =,y z =,取1(3,1,1)n =.又平面BCD 的法向量为(0,0,1)n =,则1111cos ,5nn n n n n⋅<>==⋅ 设所求二面角为θ,则sin θ==.…………12分BA变式5:解析:由于BCMK 是梯形,则MK 与CB 相交于E .A 、E 确定的直线为m ,过C 作CF ⊥m 于F ,连结MF ,因为MC ⊥平面ABCD ,CF ⊥m ,故MF ⊥m .∠MFC 是二面角M -m -C 的平面角.设正方体棱长为a ,则34CM a =,14BK a =.在△ECM 中,由BK ∥CM 可得12EB a =,CF =,故tan 4MFC ∠=.因此所求角的余弦值为cos 21MFC ∠=. 变式6:解析:∵平面ABCD ∥平面1111A B C D ,∴平面1AB C 与平面1111A B C D 的交线m 为过点1B 且平行于AC 的直线.直线m 就是二平面1AB C 与1111A B C D 所成二面角的棱.又平面1AB C 与平面1AA ⊥平面1111A B C D ,过1A 作AH ⊥m 于H ,连结AH .则1AHA ∠为二面角1A m A --的平面角.可求得1tan AHA ∠=.高考试题精选1.(2014 四川卷)解:(1)如图所示,取BD 的中点O ,连接AO ,CO .由侧视图及俯视图知,△ABD ,△BCD 为正三角形,所以AO ⊥BD ,OC ⊥BD .因为AO ,OC ⊂平面AOC ,且AO ∩OC =O , 所以BD ⊥平面AOC .又因为AC ⊂平面AOC ,所以BD ⊥AC . 取BO 的中点H ,连接NH ,PH .又M ,N ,H 分别为线段AD ,AB ,BO 的中点,所以MN ∥BD ,NH ∥AO , 因为AO ⊥BD ,所以NH ⊥BD . 因为MN ⊥NP ,所以NP ⊥BD .因为NH ,NP ⊂平面NHP ,且NH ∩NP =N ,所以BD ⊥平面NHP .又因为HP ⊂平面NHP ,所以BD ⊥HP .又OC ⊥BD ,HP ⊂平面BCD ,OC ⊂平面BCD ,所以HP ∥OC . 因为H 为BO 的中点,所以P 为BC 的中点.…………5分 (2)方法一:如图所示,作NQ ⊥AC 于Q ,连接MQ .由(1)知,NP ∥AC ,所以NQ ⊥NP .因为MN ⊥NP ,所以∠MNQ 为二面角A - NP - M 的一个平面角.由(1)知,△ABD ,△BCD 为边长为2的正三角形,所以AO =OC = 3. 由俯视图可知,AO ⊥平面BCD .因为OC ⊂平面BCD ,所以AO ⊥OC ,因此在等腰直角△AOC 中,AC = 6. 作BR ⊥AC 于R因为在△ABC 中,AB =BC ,所以R 为AC 的中点,所以BR =AB 2-⎝⎛⎭⎫AC 22=102.因为在平面ABC 内,NQ ⊥AC ,BR ⊥AC , 所以NQ ∥BR .又因为N 为AB 的中点,所以Q 为AR 的中点, 所以NQ =BR 2=104.同理,可得MQ =104. 故△MNQ 为等腰三角形, 所以在等腰△MNQ 中, cos ∠MNQ =MN 2NQ =BD 4NQ =105.…………13分故二面角A - NP - M 的余弦值是105. …………14分 方法二:由俯视图及(1)可知,AO ⊥平面BCD .因为OC ,OB ⊂平面BCD ,所以AO ⊥OC ,AO ⊥OB .又OC ⊥OB ,所以直线OA ,OB ,OC 两两垂直.…………6分如图所示,以O 为坐标原点,以OB ,OC ,OA 的方向为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系O -xyz .则A (0,0,3),B (1,0,0),C (0,3,0),D (-1,0,0). 因为M ,N 分别为线段AD ,AB 的中点, 又由(1)知,P 为线段BC 的中点,所以M ⎝⎛⎭⎫-12,0,32,N ⎝⎛⎭⎫12,0,32,P ⎝⎛⎭⎫12,32,0,于是AB =(1,0,-3),BC =(-1,3,0),MN =(1,0,0),NP =⎝⎛⎭⎫0,32,-32.…………7分 设平面ABC 的一个法向量n 1=(x 1,y 1,z 1),由⎩⎪⎨⎪⎧n 1⊥AB ,n 1⊥BC ,得⎩⎪⎨⎪⎧n 1·AB =0,n 1·BC =0,即⎩⎨⎧(x 1,y 1,z 1)·(1,0,-3)=0,(x 1,y 1,z 1)·(-1,3,0)=0,从而⎩⎨⎧x 1-3z 1=0,-x 1+3y 1=0.取z 1=1,则x 1=3,y 1=1,所以n 1=(3,1,1). …………9分 设平面MNP 的一个法向量n 2=(x 2,y 2,z 2),由,⎩⎪⎨⎪⎧n 2⊥MN ,n 2⊥NP ,得⎩⎪⎨⎪⎧n 2·MN =0,n 2·NP =0,即⎩⎪⎨⎪⎧(x 2,y 2,z 2)·(1,0,0)=0,(x 2,y 2,z 2)·⎝⎛⎭⎫0,32,-32=0,从而⎩⎪⎨⎪⎧x 2=0,32y 2-32z 2=0. 取z 2=1,则y 2=1,x 2=0,所以n 2=(0,1,1). …………11分 设二面角A - NP - M 的大小为θ,则cos θ=⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|=⎪⎪⎪⎪⎪⎪(3,1,1)·(0,1,1)5×2=105.…13分故二面角A -NP -M 的余弦值是105.…………14分2.(2014 湖南卷)解:(1)如图(a),因为四边形ACC 1A 1为矩形,所以CC 1⊥AC .同理DD 1⊥BD . 因为CC 1∥DD 1,所以CC 1⊥BD .而AC ∩BD =O ,因此CC 1⊥底面ABCD .由题设知,O 1O ∥C 1C .故O 1O ⊥底面ABCD . …………4分 (2)方法一: 如图(a),过O 1作O 1H ⊥OB 1于H ,连接HC 1.由(1)知,O 1O ⊥底面ABCD ,所以O 1O ⊥底面A 1B 1C 1D 1,于是O 1O ⊥A 1C 1又因为四棱柱ABCD -A 1B 1C 1D 1的所有棱长都相等,所以四边形A 1B 1C 1D 是菱形,因此A 1C 1⊥B 1D 1,从而A 1C 1⊥平面BDD 1B 1,所以A 1C 1⊥OB 1,于是OB 1⊥平面O 1HC 1.进而OB 1⊥C 1H .故∠C 1HO 1是二面角C 1OB 1D 的平面角.不妨设AB =2.因为∠CBA =60°,所以OB =3,OC =1,OB 1=7.在Rt △OO 1B 1中,易知O 1H =OO 1·O 1B 1OB 1=237.而O 1C 1=1,于是C 1H =O 1C 21+O 1H 2=1+127=197. 故cos ∠C 1HO 1=O 1HC 1H =237197=25719.即二面角C 1OB 1D 的余弦值为25719.方法二:因为四棱柱ABCD -A 1B 1C 1D 1的所有棱长都相等,所以四边形ABCD 是菱形,因此AC ⊥BD .又O 1O ⊥底面ABCD ,从而OB ,OC ,OO 1两两垂直.如图,以O 为坐标原点,OB ,OC ,OO 1所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系O xyz ,不妨设AB =2.因为∠CBA =60°,所以OB =3,OC =1,于是相关各点的坐标为O (0,0,0) ,B 1(3,0,2),C 1(0,1,2). 易知,n 1=(0,1,0)是平面BDD 1B 1的一个法向量.设n 2=(x ,y ,z )是平面OB 1C 1的一个法向量,则⎩⎪⎨⎪⎧n 2·OB →1=0,n 2·OC →1=0,即⎩⎨⎧3x +2z =0,y +2z =0.取z =-3,则x =2,y =23,所以n 2=(2,23,-3). 设二面角C 1OB 1D 的大小为θ,易知θ是锐角,于是cos θ=|cos 〈,〉|=⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|=2319=25719.故二面角C 1OB 1D 的余弦值为25719.3.(2014 江西卷)19.解:(1)证明:因为ABCD 为矩形,所以AB ⊥AD .又平面P AD ⊥平面ABCD ,平面P AD ∩平面ABCD =AD , 所以AB ⊥平面P AD ,故AB ⊥PD .(2)过P 作AD 的垂线,垂足为O ,过O 作BC 的垂线,垂足为G ,连接PG .故PO ⊥平面ABCD ,BC ⊥平面POG ,BC ⊥PG .在Rt △BPC 中,PG =2 33,GC =2 63,BG =63.设AB =m ,则OP =PG 2-OG 2=43-m 2,故四棱锥P - ABCD 的体积为V =13×6·m ·43-m 2=m38-6m 2. 因为m 8-6m 2=8m 2-6m 4=-6⎝⎛⎭⎫m 2-232+83, 所以当m =63,即AB =63时,四棱锥P - ABCD 的体积最大.此时,建立如图所示的空间直角坐标系,各点的坐标分别为 O (0,0,0),B ⎝⎛⎭⎫63,-63,0,C⎝⎛⎭⎫63,263,0,D ⎝⎛⎭⎫0,263,0,P ⎝⎛⎭⎫0,0,63,故PC →=⎝⎛⎭⎫63,263,-63,BC →=(0,6,0),CD =⎝⎛⎭⎫-63,0,0. 设平面BPC 的一个法向量为n 1=(x ,y ,1),则由n 1⊥PC →,n 1⊥BC →,得⎩⎪⎨⎪⎧63x +2 63y -63=0,6y =0,解得x =1,y =0,则n 1=(1,0,1).同理可求出平面DPC 的一个法向量为n 2=⎝⎛⎭⎫0,12,1. 设平面BPC 与平面DPC 的夹角为θ,则cos θ=|n 1·n 2||n 1||n 2|=12·14+1=105.。
专题7:立体几何中各种角的求法基础练习题

专题7:立体几何中各种角的求法基础练习题1.如图,在四棱锥P ABCD -中,底面是边长为a 的正方形,侧棱,2PD a PA PC a ===,求二面角P BC D --的平面角的大小.2.已知正方体1111ABCD A B C D -,(1)证明:1//D A 平面1C BD ;(2)求异面直线1D A 与BD 所成的角.3.如图,AB 是圆O 的直径,点C 是弧AB 的中点,,D E 分别是,VB VC 的中点,求异面直线DE 与AB 所成的角.4.如图,直三棱柱111ABC A B C -的底面为直角三角形,两直角边AB 和AC 的长分别为4和3,侧棱1AA 的长为5.(1)求三棱柱111ABC A B C -的体积;(2)设M 是BC 中点,求直线1A M 与平面ABC 所成角的正切值.5.如图,在四棱锥P —ABCD 中,底面ABCD 是边长为2的正方形,P A ⊥平面ABCD ,E 为PD 的中点.(1)证明://PB 平面AEC ;(2)若三棱锥C —ADE 的体积为223,求PC 与底面所成角的大小. 6.如图,四棱锥P ABCD -的底面ABCD 是边长为2的菱形,PA ⊥底面ABCD ,120BAD ∠=︒,E ,F 分别是CD ,PC 的中点,4AP =.(1)求四棱锥F ABCE -的体积;(2)求BF 与底面ABCD 所成角的正切值.7.如图,正四棱锥S ABCD -中,4SA =,2AB =,E 为SC 中点.(1)求证://SA 平面BDE ;(2)求异面直线SA 与BE 所成角的余弦值.8.如图,在三棱柱ABC A B C '''-中,M 、N 、F 分别是A C '、BC 、A C ''的中点.(1)证明://MN 平面CFB ';(2)底面△A B C '''是边长为2的正三角形,C 在底面上的射影为F ,且=1CF ,当P 是CB '的中点时,求二面角P A C B '''--的大小.9.如图,AB 是⊙O 的直径,PA 垂直于⊙O 所在的平面,C 是圆周上不同于A ,B 的一动点.(1)证明:平面PAC ⊥平面PBC ;(2)若1PA AC ==,2AB =,求直线AB 与平面PBC 所成角的正弦值.10.如图所示,ABC ∆是正三角形,线段EA 和DC 都垂直于平面ABC ,设2==,DC a=,且F为BE的中点.EA AB a(1)求证:DF∕∕平面ABC;(2)求平面BDE与平面ABC所成的较小二面角的大小11.如图在四棱锥S-ABCD中,底面四边形ABCD为正方形,SD=CD=2a,SD⊥平面ABCD,E为SD的中点.(1)试判断BS与平面AEC的位置关系,并说明理由;--的余弦值.(2)求二面角E AC B12.如图平面SAC⊥平面ACB,SAC是边长为4的等边三角形,ACB△为直角三角形,∠ACB=90°,42BC=,求二面角S-AB-C的余弦值.参考答案1.二面角P BC D --的平面角的大小为45°.【分析】根据条件可知,PD DC PD AD ⊥⊥,知PD ⊥平面ABCD ,用,BC DC BC PD ⊥⊥,可知BC ⊥平面PDC ,找到二面角P BC D --的平面角,简单计算可得结果.【详解】,,PD a DC a PC ===,222PC PD DC ∴=+,PD DC ∴⊥.同理可证PD AD ⊥.AD DC D ⋂=,且,AD DC ⊂平面ABCDPD ∴⊥平面ABCD .由BC ⊂平面ABCD ,PD BC ∴⊥.又,BC DC PD DC D ⊥⋂=,,PD DC ⊂平面PDCBC ∴⊥平面PDC .PC ⊂平面PDC ,BC PC ∴⊥.PCD ∴∠为二面角P BC D --的平面角.在Rt PDC ∆中,,45PD DC a PCD ==∴∠=.∴二面角P BC D --的平面角的大小为45°. 【点睛】本题考查线线、线面之间的关系,熟练使用线面垂直的判定定理,考验分析问题能力以及逻辑推理能力,属中档题.2.(1)证明见解析;(2)3π. 【分析】(1)证明11//D A C B ,再根据线面平行的判定定理即可证明结论;(2)1C BD ∠即为异面直线1D A 与BD 所成的角,求出即可.【详解】(1)证:在正方体1111ABCD A B C D -中,11//AB C D ,且11AB C D =,∴四边形11ABC D 为平行四边形,∴11//D A C B ,又∵1D A ⊄平面1C BD ,1C B ⊂平面1C BD ;∴1//D A 平面1C BD ;(2)解:∵11//D A C B ,∴1C BD ∠即为异面直线1D A 与BD 所成的角,设正方体1111ABCD A B C D -的边长为a ,则易得11C B BD C D ==,∴1C BD ∆为等边三角形, ∴13C BD π∠=,故异面直线1D A 与BD 所成的角为3π. 【点睛】 本题主要考查线面平行的判定与异面直线所成的角,属于基础题.3.45︒【分析】根据题意,直径所对圆周角是直角,BC AC ∴⊥,又知点C 是弧AB 的中点,则等腰直角三角形,再根据中位线平行,找到异面直线所成角的平面角,即可求解.【详解】 AB 是圆O 的直径,BC AC ∴⊥.∵点C 是弧AB 的中点,,45BC AC ABC ∴=∴∠=︒.在VBC △中,,D E 分别为,VB VC 的中点,DE BC ∴∥,DE ∴与AB 所成的角为45ABC ∠=︒.故答案为:45︒【点睛】本题考查异面直线所成角问题,考查转化与化归思想,属于基础题.4.(1)30;(2)2.【分析】(1)由棱柱的体积公式运算即可得解;(2)连接AM ,由线面角的概念可得1A MA ∠就是直线1A M 与平面ABC 所成角,即可得解.【详解】(1)根据题意可知14362ABC S =⨯⨯=△, 所以三棱柱111ABC A B C -的体积16530ABC V S AA =⋅=⨯=△;(2)连接AM ,如图,1AA ⊥平面ABC ,1A MA ∴∠就是直线1A M 与平面ABC 所成角,ABC 是直角三角形,且M 是BC 中点,5,52A BC M ∴==, 115tan 252AA A MA AM ∴∠===, 所以直线1A M 与平面ABC 所成角的正切值为2.5.(1)证明见解析;(2)4π. 【分析】(1)作辅助线:连接BD 交AC 于点O ,连接OE ,OE 是三角形BDP 的中位线,则PB 平行于OE ,即可得到PB 平行于平面ACE ;(2)由 ,C ADE E ADC V V --=可得1132E ADC ADC V S PA -∆=⋅=即可得PA =角形PAC 中,PCA ∠即为PC 与底面所成角,解直角三角形即可。
立体几何中角的问题

立体几何中“角”的问题在《立体几何》的舞台上,空间的“角”是无可争议的第一主角,纵观近年高考试题中的立体几何的问题,几乎每年都有关于“角”的试题出现.根据“解法”的典型性,以下分三个部分展示与点评.一、两条异面直线所成的角.当两条异面直线不垂直时,寻找或构造两条异面直线所成的角,基本策略有四:一是通过构造平行四边形实现线段的平移;二是通过构造三角形的中位线实现线段的平移;三是通过构造同一平面的垂线推出平行直线;四是借助“补体”完成线段的平移以及沟通有关线段间的联系.例1 、在梯形ABCD中,AB=BC=1,AD=2,,沿对角线AC将折起,使点B在平面ACD内的射影O恰在AC上.(1)求证:平面BCD;(2)求异面直线BC与AD所成角.解:(1)略证:在梯形ABCD中,由题设得,即∴在空间图形中有①又平面ACD,∴由①得②而(已知)③∴由②,③得平面BCD.(2)解:由题设得AB=BC,∴O为AC中点.为实现线段的“平移”,取CD中点为E,AB中点为F,连结OE,OF,EF,则有OE//AD,OF//BC∴即为AD与BC所成角或其补角为求EF,在平面ABC内过点F作FH//BO交AC于H,连结HE,则平面ACD.∴即又,EO=1∴在中由余弦定理得,∴即所求异面直线所成角为60°.点评:对于(1)的证明,要认知并利用折叠前后的“不变”(不变的量或不变的关系)推理;对于(2),这里运用的是“通过构造三角形的中位线实现异面直线的平移”,此为实现线段平移的第一方略.例2、已知在正方体中,E、F分别是BD的中点,G在棱CD上,且.(1)求证:;(2)求异面直线EF与所成角的余弦值;(3)求二面角的大小(用反三角函数表示)解:(1)证:连结,,则由题设知EF为的中位线∴EF//BD1,且①又∵平面∴在平面上的射影为,∵∴(三垂线定理)②∴由①,②得;(2)解:为平移,延长CD至点P,使DP=CG,并连结,PB∵∴四边形为□∴③又由①知,④∴由③,④得为异面直线EF与所成角(或其补角)设正方体棱长为4a,则,∴即所求余弦值为;(3)取DC中点为M,连结FM,则,平面∴在平面作于N,连结FN,则.∴的邻外角为二面角的平面角设正方体棱长为4a,则FM=2a,在中,,在中,,∴∴所求二面角的大小为。
立体几何中有关的角的计算问题

立体几何中 有关的角的
计算问题
立体几何中的三类角:
1. 异面直线所成的角 θ
范围: 0ºθ≤90º 解题关键:找平行线 特殊情况: 垂直 转化为证明线线垂直 2. 直线和平面所成的角 θ 范围: 0º≤θ≤90º 解题关键:作垂线、找射影 特殊情况:垂直 转化为证明线面垂直
分析: SA=AC , E是SC的中点,AE⊥SC
DE⊥SC , SC⊥平面BDE SC⊥AD, SB⊥平面ABC
SB⊥AD, AD⊥平面SBC S
AD⊥DE AD⊥DC
E
所以∠EDC就是所求二面角
的平面角。 ∠EDC=60o。
D
B
C
A
例6.设△ABC和△DBC所在的平面互相垂直,
且AB=BC=BD=1, ∠CBA=∠DBC=120o.
故∠AED就是二面角A-SC-B的平面角。
设AC=a, 则AB=BC= 2 a
2
又SA ⊥平面ABC,所以∠SCA就是SC
E
与平面ABC所成的角,即∠SCA=60o
SA= 3a AD=
sin∠AED= 2 7
3 AE= 3
7
2
D
7
侧面SAC与SBC所成的二面角的大小为arcsin 2 7 。
7
例5.如图,SB⊥平面ABC,AB⊥AC,SB=AB, SA=AC,E是SC的中点,DE⊥SC,交BC于D, 求平面EAD和平面CAD所成的角的大小。
(2) A、D的连线与平面BCD所成的角;
(3)二面角A-BD-C的大小。
作图分析:
A
HM
C
OB
D
总 结:
在求解此三类角时,关键是找到它的平面 角,并加以证明和说明。如果原图中没有所求 角的平面角,则可以根据需要添加辅助线。添 加辅助线往往通过从图形中的特殊点,向投影 面或棱作垂线(或平行线)来实现的。添线过程 的科学性和合理性,以及确定垂足(或交点)的 位置对解题至关重要。
第8章立体几何专题7 线面角的求解常考题型专题练习——【含答案】

线面角的求解【方法总结】1、线面角的范围:[0°,90°]2、线面角求法(一):先确定斜线与平面,找到线面的交点A为斜足;找线在面外的一点B,过点B向平面α做垂线,确定垂足O;连结斜足与垂足为斜线AB在面α上的投影;投影AO与斜线AB之间的夹角为线面角;把投影AO与斜线AB归到一个三角形中进行求解(可能利用余弦定理或者直角三角形)。
注意:以上第二步过面外一点向平面做垂线的方法有一下几种:1)线在面外的一点B与平面上某点的连线正垂直于面α,无需再做辅助线;2)题中已知有与面α垂直的直线,过线在面外的一点B直接做此垂线的平行线;3)过线在面外的一点B做两垂直平面交线的垂线,利用面面垂直的性质证明OB⊥面α(这两个垂直平面一个是面α,另一个是过点B且与α垂直的平面)。
3、线面角求法(二)用等体积法,求出斜线PA在面外的一点P到面的距离,利用三角形的正弦公式进行求解。
114、线面角求法(三)利用空间向量进行求解,高二再学。
【巩固练习】1、已知正方体1111ABCD A B C D -的体积为162,点P 在正方形1111D C B A 上,且1,A C 到P 的距离分别为2,23,则直线CP 与平面11BDD B 所成角的正切值为( )A.2 B.3 C.12D.13【答案】A【解析】易知22AB =;连接1C P ,在直角1CC P ∆中,可计算22112C P CP CC =-=;又1112,4A P A C ==,所以点P 是11A C 的中点;连接AC 与BD 交于点O ,易证AC ⊥平面11BDD B ,直线CP 在平面11BDD B 内的射影是OP ,所以CPO ∠就是直线CP 与平面11BDD B 所成的角,在直角CPO ∆中,2tan 2CO CPO PO ∠== .2、把正方形沿对角线折起,当以四点为顶点的三棱锥体积最大时,直线和平面所成的角的大小为A.B.C.D.[来源网ZXXK]【答案】C【解析】如图所示,当平面平面时,三棱锥的体积最大,取的中点,则平面,故直线和平面所成的角为,则,所以,故选C.3、如图,在三棱锥P-ABC中,,PA AB⊥PC BC⊥,,AB BC⊥22,AB BC==5PC=,则PA与平面ABC所成角的大小为_______.【答案】45︒【解析】如图,作平行四边形ABCD,连接PD,由AB BC⊥,则平行四边形ABCD是矩形.由BC CD⊥,BC PC⊥,PC CD C=,∴BC⊥平面PCD,而PD⊂平面PCD,∴BC PD⊥,同理可得AB PD⊥,又AB BC B⋂=,∴PD⊥平面11ABCD .,PD CD PD AD ⊥⊥,PAD ∠是PA 与平面ABC 所成角.由2,5CD AB PC ===得1PD =,又1AD BC ==,∴45PAD ∠=︒.∴PA 与平面ABC 所成角是45︒.4、已知三棱柱ABC -A 1B 1C 1的侧棱与底面边长都相等,A 1在底面ABC 内的射影为△ABC 的中心O ,则AB 1与底面ABC 所成角的正弦值为( )A .23B .13C .33D .23【答案】A【解析】作1A H ⊥面ABC 于点H ,延长11B A 到D ,延长BA 到E 使得111B A A D =,,BA AE =如图则有11A EAB ,又因为1A O ⊥面ABC ,故1A EO ∠为所求角,且111sin AO A EO A E∠=已知底面为正三角形,且O为底面中点,解三角形可知:111336,333AO AB AA A O AA==∴=又在AEO∆中运用余弦定理,150EAO∠=︒则()()22212cos3EO EA AO EA AO EAO AB=+-⋅∠=故由勾股定理可得22113A E AO EO AB=+=则1623sin33A EO∠==故选A5、如图所示,已知AB为圆O的直径,且AB=4,点D为线段AB上一点,且13AD DB=,点C为圆O上一点,且3BC AC=.点P在圆O所在平面上的正投影为点D,PD=DB.(1)求证:CD⊥平面PAB;(2)求直线PC与平面PAB所成的角.【答案】(1)见解析;(2)301旗开得胜1【解析】(1)证明:连接CO ,由3AD =DB 知,点D 为AO 的中点. 又因为AB 为圆O 的直径,所以AC ⊥CB. 由3AC =BC 知,∠CAB =60°, 所以△ACO 为等边三角形.故CD ⊥AO. 因为点P 在圆O 所在平面上的正投影为点D ,所以PD ⊥平面ABC ,又CD ⊂平面ABC ,所以PD ⊥CD , 由PD ⊂平面PAB ,AO ⊂平面PAB ,且PD ∩AO =D , 得CD ⊥平面PAB.(2)由(1)知∠CPD 是直线PC 与平面PAB 所成的角, 又△AOC 是边长为2的正三角形,所以CD =3. 在Rt △PCD 中,PD =DB =3,CD =3,所以3tan 3CD CPD PD ∠==,∠CPD =30°, 即直线PC 与平面PAB 所成的角为30°.16、如图,在四棱锥P -ABCD 中,AP ⊥平面PCD ,//AD BC ,AB BC ⊥,12AP AB BC AD ===,E 为AD 的中点,AC 与BE 相交于点O .(1)证明:PO ⊥平面ABCD .(2)求直线BC 与平面PBD 所成角的正弦值.【答案】(1)证明见解析(2)2211【解析】 (1)证明:AP ⊥平面PCD ,CD ⊂平面PCD ,AP CD ∴⊥,//,AD BC 12BC AD =,E 为AD 的中点,则//BC DE 且BC DE =. ∴四边形BCDE 为平行四边形,//BE CD ∴,AP BE ∴⊥.1又,AB BC⊥12AB BC AD ==,且E 为AD 的中点,∴四边形ABCE 为正方形,BE AC ∴⊥,又,AP AC A =BE ∴⊥平面APC ,PO ⊂平面APC ,则BE PO ⊥.AP ⊥平面,PCD PC ⊂平面PCD ,AP PC ∴⊥,又22AC AB AP ==,PAC ∴∆为等腰直角三角形,O 为斜边AC 上的中点,PO AC ∴⊥且,ACBE O =PO ∴⊥平面ABCD .(2)高一学生可以用等体积法求解。
立体几何——二面角经典求法

∴AE⊥AD又BA⊥AD,平面ABC∩平面α=A,
∴∠BAE是平面ABC与α所成的角,
∴BE⊥平面α,∴BE⊥AE,∴ΔABC是RtΔ
Sin∠BAE=BE:AB= ,即平面ABC与α所成角的正弦值为 。
6、射影公式
由公式S射影=S斜面cosθ,作出二面角的平面角直接求出。运用这一方法的关键是从图中找出斜面多边形和它在有关平面上的射影,而且它们的面积容易求得。
(2)要求二面角A1-EC-D的大小,先要作出二面角的平面角,本题可用三垂线法,因FH⊥底面ABCD于H,过H作HM⊥EC于M,连FM,则由三垂线定理知FM⊥EC。
所以∠HMF为所求二面角A1-EC-D的平面角。
四、延伸法
例4. 如图10,设正三棱柱ABC-A'B'C'各棱长均为α,D为CC1中点,求平面A'BD与平面ABC所成二面角的度数。
例5如图12,设正方体ABCD-A1B1C1D1中,M为AA1上点,A1M:MA=3:1,求截面B1D1M与底面ABCD所成二面角。
本题应用“射影法”求截面B1D1M与底面ABCD所成二面角容易。它可以不作出所求二面角的平面角。
因是正方体,所以B1、D1、M在底面射影分别为B、D、A,设棱长为a.
三、垂线法:
例3如图6,设正方体ABCD-A1B1C1D1中,E、F分别是AB、C1D1的中点。
(1)求证:A1、E、C、F四点共面;
(2)求二面角A1-EC-D的大小。
(1)要证A1、E、C、F四点共面,可证:A、F//EC,取DC中点H,连AH、FH,则AH EC,又FH A1A。故A1F//AH,即A1F//EC,从而A、E、C、F四点共面。
立体几何——面角求法

二面角求法1 .定义法即在二面角的棱上找一点,在二面角的两个面内分别作棱的射线即得二面角的平面角.例1 . 正方体ABCD-A 1B 1C 1D 1中,求 二面角A-BD-C 1的正切值为 .解析:易知∠COC 1是二面角C-BD-C 1的平面角,且tan ∠COC 1=2。
例2.在锥体P-ABCD 中,ABCD 是边长为1的菱形,且∠DAB=60︒,PA PD ==,PB=2, E,F 分别是BC,PC 的中点.求:二面角P-AD-B 的余弦值.解:由(1)知PGB ∠为二面角P AD B --的平面角,在Rt PGA ∆中,2217()24PG =-=;在R t B G A ∆中,222131()24BG =-=;在PGB ∆中,222cos 27PG BG PB PGB PG BG +-∠==-⋅.2 三垂线法此法最基本的一个模型为:如图3,设锐二面角βα--l ,过面α 内一点P 作PA ⊥α于A ,作AB ⊥l 于B ,连接PB ,由三垂线定理得PB ⊥l ,则∠PBA 为二面角βα--l 的平面角,故称此法为三垂线法.D B 1图1AO A 1CBD 1C 1O 1A 图3 αβPBlGPASBSCSDSFE例3.如图4,平面α⊥平面β,α∩β=l ,A ∈α,B ∈β,点A 在直线l 上的射影为A 1,点B 在l 的射影为B 1,已知AB=2,AA 1=1,BB 1=2, 求:二面角A 1-AB -B 1的正弦值. 分析与略解:作A 1E ⊥AB 1于AB 1于E ,则可证A 1E ⊥平面AB 1B.过E 作EF ⊥AB 交AB 于F ,连接A 1F ,则得A 1F ⊥AB ,∴∠A 1FE 就是所求二面角的平面角.依次可求得AB 1=B 1B=2,A 1B=3,A 1E=22,A 1F=23, 则在Rt △A 1EF 中,sin ∠A 1FE=A 1E A 1F =63 .例4.如图所示,在四棱锥P-ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD,点E 在线段PC 上,PC ⊥平面BDE.(1)若PA=1,AD=2,求二面角B-PC-A 的正切值.解法一:由(1)得BD ⊥平面PAC, ∴BD ⊥AC.又四边形ABCD 为矩形, ∴四边形ABCD 是正方形.设AC 交BD 于O 点,∵PC ⊥平面BDE, ∴∠BEO 即为二面角B-PC-A 的平面角. ∵PA=1,AD=2,∴AC=2,BO=OC=,∴PC==3,图4B 1A αβA 1BlEF又OE===在直角三角形BEO中,tan∠BEO===3,∴二面角B-PC-A的正切值为3.例5. (2010重庆, 19, 12分) 如图, 四棱锥P-ABCD中, 底面ABCD为矩形, PA⊥底面ABCD, PA=AB=, 点E是棱PB的中点.(1) 若AD=, 求二面角A-EC-D的平面角的余弦值.(1) 过点D作DF⊥CE, 交CE于F, 过点F作FG⊥CE, 交AC于G, 则∠DFG为所求的二面角的平面角.由(Ⅰ) 知BC⊥平面PAB, 又AD∥BC, 得AD⊥平面PAB, 故AD⊥AE, 从而DE==. 在Rt△CBE中, CE==. 由CD=, 所以△CDE为等边三角形, 故F为CE的中点, 且DF=CD·sin=.因为AE⊥平面PBC, 故AE⊥CE, 又FG⊥CE, 知FG AE, 从而FG=, 且G点为AC的中点. 连结DG, 则在Rt△ADG中, DG=AC==.所以cos∠DFG==.3、向量法向量法解立体几何中是一种十分简捷的也是非常传统的解法,可以说所有的立体几何题都可以用向量法求解,用向量法解立体几何题时,通常要建立空间直角坐标系,写出各点的坐标,然后将几何图中的线段写成用坐标法表示的向量,进行向量计算解题。
高中数学立体几何---用空间向量求空间角专题训练(解析版)
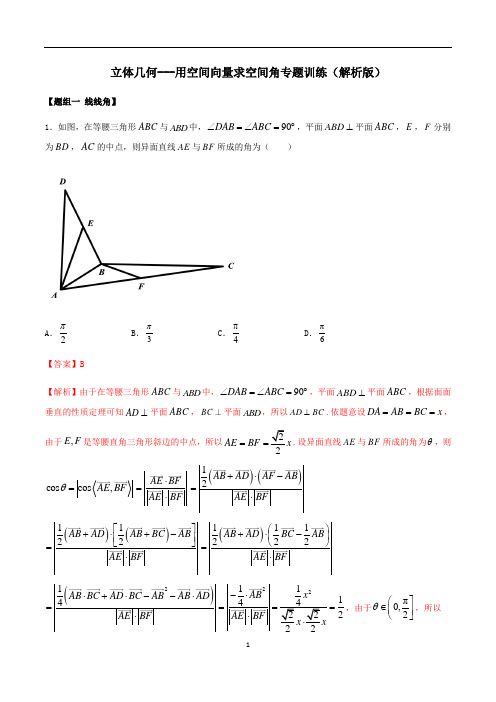
立体几何---用空间向量求空间角专题训练(解析版)【题组一 线线角】1.如图,在等腰三角形ABC 与ABD 中,90DAB ABC ∠=∠=︒,平面ABD ⊥平面ABC ,E ,F 分别为BD ,AC 的中点,则异面直线AE 与BF 所成的角为( )A .2πB .3πC .4πD .6π 【答案】B【解析】由于在等腰三角形ABC 与ABD 中,90DAB ABC ∠=∠=︒,平面ABD ⊥平面ABC ,根据面面垂直的性质定理可知AD ⊥平面ABC ,BC ⊥平面ABD ,所以AD BC ⊥.依题意设DA AB BC x ===,由于,E F是等腰直角三角形斜边的中点,所以2AE BF x ==.设异面直线AE 与BF 所成的角为θ,则cos cos ,AE BF θ=AE BF AE BF ⋅=⋅()()12AB AD AF AB AE BF +⋅-=⋅()()1122AB AD AB BC AB AE BF ⎡⎤+⋅+-⎢⎥⎣⎦=⋅()111222AB AD BC AB AE BF ⎛⎫+⋅- ⎪⎝⎭=⋅()214AB BC AD BC AB AB AD AE BF ⋅+⋅--⋅=⋅22111422AB x AE BF -⋅===⋅,由于π0,2θ⎛⎤∈ ⎥⎝⎦,所以π3θ=.故选:B 2.直三棱柱ABC —A ′B ′C ′中,AC =BC =AA ′,∠ACB =90°,E 为BB ′的中点,异面直线CE 与C A '所成角的余弦值是( )A B .C .D 【答案】D【解析】直三棱柱ABC A B C -'''中,AC BC AA ==',90ACB ∠=︒,E 为BB '的中点.以C 为原点,CA 为x 轴,CB 为y 轴,CC '为z 轴,建立空间直角坐标系,设2AC BC AA =='=,则(0C ,0,0),(0E ,2,1),(0C ',0,2),(2A ,0,0),(0CE =,2,1),(2C A '=,0,2)-,设异面直线CE 与C A '所成角为θ, 则||210cos 10||||58CE C A CE C A θ'==='∴异面直线CE 与C A '所成角的余弦值为10. 故选:D .3.已知直三棱柱111ABC A B C -,90ABC ∠=︒,12AB BC AA ===,1BB 和11B C 的中点分别为E 、F ,则AE 与CF 夹角的余弦值为( )A B .25 C .45 D 【答案】B【解析】如图所示:分别以1,,BA BC BB 为,,x y z 轴建立空间直角坐标系.故()0,2,0A ,()2,0,0C ,()0,0,1E ,()1,0,2F ,故()0,2,1AE =-,()1,0,2CF =-. 2cos ,5AE CFAE CF AE CF ⋅==⋅,即AE 与CF 夹角的余弦值为25. 故选:B .4.如图所示,四棱锥P ABCD -中,PB PD AD AB ===,60BAD ∠=︒,1CD CB ==,120BCD ∠=︒,点M N 、分别为PA AB 、的中点.(1)证明:平面DMN ∥平面PBC ;(2)若2PA =PA 与BC 所成角的余弦值.【答案】(1)证明见解析;(2)4 【解析】(1)如图,因为M N 、分别为PA AB 、的中点,所以//MN PB ,MN ⊄平面PBC ,∴//MN 平面PBC ;又AB AD =,60BAD ∠=︒,所以ABD △为正三角形,又CD BC =,120BCD ∠=︒,所以30CBD ∠=︒,BC AB ⊥,又DN AB ⊥,所以BC DN ,∴DN 平面PBC因为MN DN N ⋂=,所以平面DMN 平面PBC . (2)如图,取BD 中点O ,连结,,AO CO PO ,因为AD AB =,60DAB ∠=︒,所以ABD △为正三角形,所以AO BD ⊥,又因为BCD 为等腰三角形,所以CO BD ⊥,所以A O C 、、三点共线,所以AC BD ⊥,因为PB PD =,所以PO BD ⊥,1CD BC ==,120BCD ∠=︒,所以BD =,所以PB PD AD AB ====,32AO PO ==,又2PA =,所以222AO PO PA +=, 所以AO PO ⊥,又AOPO O =,所以PO ⊥平面ABCD . 以O 为坐标原点,,,OA OB OP 分别为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系,3,0,02A ⎛⎫ ⎪⎝⎭,30,0,2P ⎛⎫ ⎪⎝⎭,B ⎛⎫ ⎪ ⎪⎝⎭,1,0,02C ⎛⎫- ⎪⎝⎭, 33,0,22PA ⎛⎫=- ⎪⎝⎭,1,2BC ⎛⎫=- ⎪ ⎪⎝⎭, 设异面直线PA 与BC 所成角为α,所以cos ,||||3PA BC PA BC PA BC⋅〈〉===⋅ 所以异面直线PA 与BC【题组二 线面角】1.如图,在△ABC 中,D ,E 分别为AB ,AC 的中点,O 为DE 的中点,AB =AC BC =4.将△ADE 沿DE 折起到△A 1DE 的位置,使得平面A 1DE ⊥平面BCED ,如下图.(Ⅰ)求证:A 1O ⊥BD ;(Ⅱ)求直线A 1C 和平面A 1BD 所成角的正弦值;【解析】(Ⅰ)因为AB AC =,,D E 分别为,AB AC 中点,故可得AD AE =,故1A DE 为等腰三角形,又O 为DE 中点,故可得1AO DE ⊥,又因为平面A 1DE ⊥平面BCED ,且交线为DE , 又1AO ⊂平面1A DE ,故1AO ⊥平面BCED ,又BD ⊂平面BCDED , 故1AO BD ⊥.即证. (Ⅱ)过O 作OH BC ⊥,由(Ⅰ)可知1AO ⊥平面BCED , 又,OH OE ⊂平面BCED ,故可得11,AO OH AO OE ⊥⊥, 又因为,OH BC BC ⊥//DE ,故可得OH OE ⊥.综上所述:1,,OH OE OA 两两垂直,故以O 为坐标原点,1,,OH OE OA 分别为,,x y z 轴建立空间直角坐标系, 如下图所示:故可得()()()()10,0,2,2,2,0,0,1,0,2,2,0A C D B --, 则()()10,1,2,2,1,0A D BD =--=-设平面1A BD 的法向量为(),,n x y z =,故可得100n A D n BD ⎧⋅=⎪⎨⋅=⎪⎩,即2020y z x y --=⎧⎨-+=⎩, 取1x =,可得2,1y z ==-.故()1,2,1n =-.又()12,2,2AC =-, 故可得11122,?3n AC cos n AC n AC ⋅==. 设直线A 1C 和平面A 1BD 所成角为θ,故可得12,3sin cos n AC θ==.则直线A 1C 和平面A 1BD 所成角的正弦值为3.2.如图1,在ABC 中, D , E 分别为AB , AC 的中点,O 为DE 的中点,AB AC ==4BC =.将ABC 沿DE 折起到1A DE △的位置,使得平面1A DE ⊥平面BCED ,如图2.(1)求证:1AO BD ⊥; (2)求直线1AC 和平面1ABD 所成角的正弦值.【答案】(1)证明见解析;(2)3. 【解析】(1)连接1AO .图1中,AB AC =,D , E 分别为AB , AC 的中点,AD AE ∴=, 即11A D A E =,又O 为DE 的中点,1AO DE ∴⊥. 又平面1A DE ⊥平面BCED ,且平面1A DE 平面BCED DE =,1AO ⊂平面1ADE , 1AO ∴⊥平面BCED ,又BD ⊂平面BCED , 1AO BD ∴⊥. (2)取BC 中点G ,连接OG ,则OG DE ⊥.由(1)可知1AO ⊥平面BCED ,OG ⊂平面BCED 11,AO DE AO OG ∴⊥⊥. 以O 为原点,分别以1,,OG OE OA 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系,如图所示AB AC ==4BC =,112,1,2A D DE OD A O ∴==∴=∴==.()()()()10,0,2,2,2,0,2,2,0,0,1,0A B C D ∴--, ()()()11112,2,2,0,1,2,2,2,223A B A D AC AC ∴=--=--=-=,. 设平面1A BD 的法向量为(),,n x y z =,则11·0·0n A B n A D ⎧=⎪⎨=⎪⎩,即222020x y z y z --=⎧⎨--=⎩,令1z =,则2,1y x =-=-,()1,2,16n n ∴=--=,. 设直线1AC和平面1A BD 所成的角为θ,则 111sin cos ,323AC n ACn AC n θ-=〈〉===, 所以直线1AC 和平面1A BD 所成角的正弦值为3. 3.在矩形ABCD 中,3AB =,2AD =,点E 是线段CD 上靠近点D 的一个三等分点,点F 是线段AD 上的一个动点,且()01DF DA λλ=≤≤.如图,将BCE ∆沿BE 折起至BEG ∆,使得平面BEG ⊥平面ABED .(1)当12λ=时,求证:EF BG ⊥; (2)是否存在λ,使得FG 与平面DEG 所成的角的正弦值为13?若存在,求出λ的值;若不存在,请说明理由.【答案】(1)见解析(2) 12λ= 【解析】(1)当12λ=时,点F 是AD 的中点. ∴112DF AD ==,113DE CD ==. ∵90ADC ∠=︒,∴45DEF ∠=︒. ∵223CE CD ==,2BC =,90BCD ∠=︒, ∴45BEC ∠=︒.∴BE EF ⊥.又平面GBE ⊥平面ABED ,平面GBE ⋂平面ABED BE =,EF ⊂平面ABED ,∴EF ⊥平面BEG .∵BG ⊂平面BEG ,∴EF BG ⊥.(2)以C 为原点,,CD CB 的方向为x 轴,y 轴的正方向建立如图所示空间直角坐标系Cxyz .则()2,0,0E ,()3,0,0D ,()3,2,0F λ.取BE 的中点O ,∵2GE BG ==,∴GO BE ⊥,∴ 易证得OG ⊥平面BCE ,∵BE =OG(G .∴(2,12FG λ=--,(EG =-,(DG =-.设平面DEG 的一个法向量为(),,n x y z =,则20,0,n DG x y n EG x y ⎧⋅=-++=⎪⎨⋅=-++=⎪⎩令z =(0,n =-. 设FG 与平面DEG 所成的角为θ, 则sin cos ,FG n θ=13==, 解得12λ=或710λ=-(舍去)∴存在实数λ,使得DG 与平面DEG 所成的角的正弦值为13,此时12λ=. 4.如图,在直三棱柱ABC ﹣A 1B 1C 1中,△ABC 是边长为6的等边三角形,D ,E 分别为AA 1,BC 的中点.(1)证明:AE //平面BDC 1;(2)若异面直线BC 1与AC DE 与平面BDC 1所成角的正弦值.【答案】(1)详见解析;(2 【解析】(1)证明:取BC 1的中点F ,连接DF ,EF ,∵E 为BC 中点,∴EF ∥1CC ,112EF CC = 又∵D 为AA 1的中点,DA ∥1CC ,112DA CC =, ∴EF ∥DA ,EF DA =∴四边形ADFE 为平行四边形,∴AE ∥DF ,∵AE ⊄平面BDC 1,DF ⊂平面BDC 1,∴AE ∥平面BDC 1;(2)由(1)及题设可知,BC ,EA ,EF 两两互相垂直,则以点E 为坐标原点,EC ,EA ,EF 所在直线分别为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系,设AA 1=2t (t >0),则1(3,0,0),(3,0,2),(3,0,0),)B C t A C D t -,所以1(3,33,),(6,0,2),(3,BD t BC t AC ===-,故111|cos ,|4||||6BC AC BC AC BC AC ⋅<>===⋅解得t =,设平面BDC 1的法向量为(,,)m x y z =由100m BD m BC ⎧⋅=⎪⎨⋅=⎪⎩,得3060x x⎧+=⎪⎨+=⎪⎩, 令1x =,则(1,0,m =,又D ED ∴=, 所以cos ,||||(3ED m ED m ED m ⋅<>===, 设DE 与平面BDC 1所成角为θ,则sin θ=30|cos ,|20ED m <>=, ∴DE 与平面BDC 15.如图,四棱锥P ABCD -中,AP ⊥平面PCD ,AD BC ∥,2DAB π∠=,12AP AB BC AD ===,E 为AD 的中点,AC 与BE 相交于点O .(Ⅰ)求证:PO ⊥平面ABCD ;(Ⅱ)求直线AB 与平面PBD 所成角的正弦值.. 【解析】Ⅰ)由已知AP ⊥平面PCD ,可得AP PC ⊥,AP CD ⊥,由题意得,ABCD 为直角梯形,如图所示,BC DE ,所以BCDE 为平行四边形,所以BE CD ∥,所以AP BE ⊥.又因为BEAC ⊥,且AC AP A =, 所以BE ⊥面APC ,故BE PO ⊥.在直角梯形中,AC ==,因为AP ⊥面PCD ,所以AP PC ⊥,所以PAC 为等腰直角三角形,O 为斜边AC 上的中点,所以PO AC ⊥.且ACBE O =,所以PO ⊥平面ABCD(Ⅱ)法一:以O 为原点,分别以,,OB OC OP 为x 轴,y 轴,z 轴的建立直角坐标系.不妨设1BO = 0(0)1A -,,,()100B ,,,()001P ,,,0()21D -,,,设(,,)n x y z =是平面PBD 的法向量.满足00n PB n BD ⎧⋅=⎨⋅=⎩, 所以030x z x y -+=⎧⎨-+=⎩, 则令1x = ,解得(1,3,1)n =sin cos ,AB n θ=22211AB nAB n ⋅==⋅ 法二:(等体积法求A 到平面PBD 的距离)A PBD P ABD V V--=设AB=1,计算可得1PF =,PD= ,BD ,4PBD S =△ 1133PBD ABD S hS PO ⨯⨯=⨯⨯△△,解得h = sin h AB θ==【题组三 二面角】1.如图,平行四边形ABCD 所在平面与直角梯形ABEF 所在平面互相垂直,且11,//2AB BE AF BE AF ===,,,2,3AB AF CBA BC P π⊥∠==为DF 中点.(1)求异面直线DA 与PE 所成的角;(2)求平面DEF 与平面ABCD 所成的二面角(锐角)的余弦值.【答案】(1)6π(2【解析】在ABC ∆中,1,,23AB CBA BC π=∠==,所以2222cos 3AC BA BC BA BC CBA =+-⨯∠=所以222AC BA BC +=,所以AB AC ⊥又因为平面ABCD ⊥平面ABEF ,平面ABCD ⋂平面ABEF AB =,AC ⊂平面ABCD ,所以AC ⊥平面ABEF如图,建立空间直角坐标系{},,AB AF AC ,则1(0,0,0),(1,0,0),((1,1,0),(0,2,0),(22A B C D E F P--(1)3(1,0,3),(,0,2DA PE=-=设异面直线DA与PE所成的角为α,则3cos2DA PEDA PEα⋅===⨯⨯所以异面直线DA与PE所成的角为6π;(2)(0,2,0)AF=是平面ABCD的一个法向量,设平面DEF的一个法向量(,,)n x y z=,(2,1,3),(1,2,DE DF=-=则(,,)(2,1,20{(,,)(1,2,20n DE x y z x yn DF x y z x y⋅=⋅=+-=⋅=⋅=+-=,得z==,取1x=,则1,y z==故(1,1,3)n=是平面DEF的一个法向量,设平面DEF与平面ABCD 所成的二面角(锐角)为β,则2cos525AF nAF nβ⋅===⨯⨯.2.如图,梯形ABCS中,//AS BC,AB BC⊥,122AB BC AS===,D、E分别是SA,SC的中点,现将SCD∆沿CD翻折到PCD∆位置,使PB=(1)证明:PD ⊥面ABCD ;(2)求二面角E BD C --的平面角的正切值;(3)求AB 与平面BDE 所成的角的正弦值.【答案】(1)证明见解析;(23)3【解析】(1)梯形ABCS 中,//AS BC ,AB BC ⊥,122AB BC AS ===,D 、E 分别是SA ,SC 的中点,2DA =,四边形ABCD 为平行四边形,AB BC ⊥,2AB DA ==,BD =所以四边形ABCD 为正方形,CD DS ⊥,折叠后,CD DP ⊥,2PD =,PB =PBD 中,2224812PD BD PB +=+==,所以BD DP ⊥,,CD DB 是平面ABCD 内两条相交直线,所以PD ⊥面ABCD ;(2),,DA DC DP 两两互相垂直,以D 为原点,,,DA DC DP 分别为,,x y z 轴建立空间直角坐标系,如图所示:则(0,0,0),(2,0,0),(2,2,0),(0,2,0),(0,0,2),(0,1,1)D A B C P E (2,2,0),(0,1,1)DB DE ==,设平面BDE 的法向量为(,,)n x y z = 则2200DB n x y DE n y z ⎧⋅=+=⎨⋅=+=⎩,解得y z x z =-⎧⎨=⎩,令1z =,取(1,1,1)n =- 由(1)可知,PD ⊥面ABCD ,取平面ABCD 的法向量(0,0,2)DP =cos ,3DP n ==,根据图形,二面角E BD C --所以二面角E BD C --(3)(0,2,0)AB =,由(2)可得平面BDE 的法向量(1,1,1)n =- 设直线AB 与平面BDE 所成的角为θ,sin cos ,AB n θ-===.所以AB 与平面BDE3.如图四棱柱1111ABCD A BC D -中,//AD BC ,AB AD ⊥,2AD AB BC ==,M 为1A D 的中点.(1)证明://CM 平面11AA B B ;(2)若四边形11AA B B 是菱形,且面11AA B B ⊥面ABCD ,13B BA π∠=,求二面角1A CM A --的余弦值. 【答案】(1)证明见解析;(2)25. 【解析】(1)取1AA 的中点N ,连接MN ,BN ,∵M 为1A D 的中点,∴//MN AD 且12MN AD = 又//BC AD ,12BC AD = ,所以//BC MN 且MN BC =, 所以四边形MNBC 是平行四边形,从而//CM BN ,又BN ⊂平面11AA B B ,CM ⊄平面11AA B B ,所以//CM 平面11AA B B .(2)取11A B 的中点P ,连接AP ,1AB ,∵四边形11AA B B 为菱形,又13B BA π∠=,易知AP AB ⊥.又面11AA B B ⊥面ABCD ,面11AA B B 面ABCD AB =,AD AB ⊥∴AD ⊥平面11AA B B ,AD AP ⊥故AB ,AD ,AP 两两垂直以A 为原点,AB ,AD ,AP 所在直线分别为x ,y ,z 轴建立空间直角坐标系A xyz -(如图所示),不妨设4AB =.则()0,0,0A ,()0,4,0D ,()4,2,0C,,(1A -,(1,M -,(11,2,A M =,(CM =-,()4,2,0AC =设平面1ACM 的法向量为(),,m x y z =, 由100m A M m CM ⎧⋅=⎨⋅=⎩,得2050x y x ⎧+=⎪⎨-=⎪⎩,可得平面1ACM的一个法向量1,m ⎛= ⎝⎭, 设平面ACM 的法向量为()111,,n x y z =,由00n AC n CM ⎧⋅=⎨⋅=⎩,得111142050x y x +=⎧⎪⎨-+=⎪⎩, 可得平面ACM的一个法向量1,n ⎛=- ⎝⎭. ∴25142cos ,51m nm n m n -+⋅===⋅+ 所以二面角1A CM A --的余弦值为25. 4.已知平行四边形ABCD 中60A ∠=︒,22AB AD ==,平面AED ⊥平面ABCD ,三角形AED 为等边三角形,EF AB ∥.(Ⅰ)求证:平面⊥BDF平面AED ;(Ⅱ)若BC ⊥平面BDF①求异面直线BF 与ED所成角的余弦值;②求二面角B DF C --的正弦值.【答案】(Ⅰ)见解析;(Ⅱ)①45.【解析】(Ⅰ)平行四边形ABCD 中∵60A ∠=︒,22AB AD ==,由余弦定理可得BD ,由勾股定理可得BD AD ⊥,如图,以D 为原点建立空间直角坐标系O xyz -∴()0,0,0D ,()1,0,0A ,()B ,12E ⎛ ⎝⎭,()C -∴()=DB ,()1,0,0DA =,1,0,22DE ⎛= ⎝⎭∴0DB DA ⋅=,0DB DE ⋅=,∴DB DA ⊥,DB DE ⊥.又DA DE D ⋂=,∴DB ⊥平面AED .又∵DB ⊂平面BDF ,∴平面⊥BDF 平面AED .(Ⅱ)∵EF AB ∥,∴设()(),0EF AB λλλ==-=-∴12F λ⎛- ⎝⎭,()1,0,0BC =-. ∵BC ⊥平面BDF ,∴BC DF ⊥,∴102BC DF λ⋅=-=,∴12λ=.∴F ⎛⎝⎭.①0,BF ⎛= ⎝⎭,1,0,2ED ⎛=- ⎝⎭∴34cos cos ,BF ED θ=== ∴异面直线BF 与ED ②设(),,n x y z =为平面BDF 的法向量,则303022n DB y n DF y z ⎧⋅==⎪⎨⋅=+=⎪⎩可得()1,0,0n=,设(),,m x y z =为平面CDF 的法向量,则0302m DC x m DF y z ⎧⋅=-=⎪⎨⋅=+=⎪⎩可得()3,1,1m =-,∴3cos ,5m n ==sin θ= ∴二面角B DF C --. 5.如图,在四棱锥P ABCD -中,已知PA ⊥平面ABCD ,且四边形ABCD 为直角梯形,2ABC BAD π∠=∠=,2PA AD ==,1AB BC ==.(1)求平面PAB 与平面PCD 所成锐二面角的余弦值;(2)点Q 是线段BP 上的动点,当直线CQ 与DP 所成的角最小时,求线段BQ 的长.【答案】 【解析】以为正交基底建立如图所示的空间直角坐标系Axyz ,则各点的坐标为()()()()1,0,0,1,1,0,0,2,0,0,0,2B C D P .(1) 因为AD ⊥平面PAB ,所以是平面PAB 的一个法向量,.因为(1,1,2),(0,2,2)PC PD =-=-.设平面PCD 的法向量为(),,m x y z =,则0,0m PC m PD ⋅=⋅=,即20{220x y z y z +-=-=,令1y =,解得1,1z x ==. 所以()1,1,1m =是平面PCD 的一个法向量,从而3cos ,3||||AD m AD m AD m ⋅〈〉==,所以平面PAB 与平面PCD所成二面角的余弦值为3. (2) 因为(1,0,2)BP =-,设(,0,2)(01)BQ BP λλλλ==-≤≤,又(0,1,0)CB =-,则(,1,2)CQ CB BQ λλ=+=--,又(0,2,2)DP =-, 从而1cos ,||||10CQ DP CQ DP CQ DP ⋅〈〉==, 设[]12,1,3t t λ+=∈,则2222229cos ,5109101520999t CQ DP t t t 〈〉==≤-+⎛⎫-+ ⎪⎝⎭,当且仅当95t =,即25λ=时,|cos ,|CQ DP 〈〉因为cos y x=在0,2π⎛⎫ ⎪⎝⎭上是减函数,此时直线CQ 与DP 所成角取得最小值.又因为BP ==25BQ BP ==.6.如图,在三棱锥S 一ABC 中,SA =AB =AC =BC ,O为BC 的中点(1)求证:SO ⊥平面ABC(2)在线段AB 上是否存在一点E ,使二面角B —SC -E ?若存在,求B E BA 的值,若不存在,试说明理由【答案】(1)见解析(2)23【解析】(1)∵SB SC =,O 为BC 的中点,∴SO BC ⊥,设SB a =,则SO =,AO a =,SA =, ∴222SO OA SA +=,∴SO OA ⊥,又∵BC OA O ⋂=,∴SO ⊥平面ABC .(2)以O 为原点,以OA 所在射线为x 轴正半轴,以OB 所在射线为y 轴正半轴,以OS 所在射线为z 轴正半轴建立空间直角坐标系.则有()0,0,0O ,0,0,2S ⎛⎫ ⎪ ⎪⎝⎭,0,,02C a ⎛⎫- ⎪ ⎪⎝⎭,,0,02A a ⎛⎫ ⎪ ⎪⎝⎭,0,,02B a ⎛⎫ ⎪ ⎪⎝⎭. 假设存在点E 满足条件,设()01BE BA λλ=≤≤,则(),1,02E a a λ⎫-⎪⎪⎝⎭,则()62,02CE a λ⎛⎫=- ⎪ ⎪⎝⎭. 设平面SCE 的法向量为(),,n x y z =,由00n CE n SC ⎧⋅=⎨⋅=⎩,得()200x y y z λ+-=+=⎪⎩,故可取()2,n λ=-.易得平面SBC 的一个法向量为()1,0,0m =.所以,cos 5m nm n θ⋅===⋅,解得23λ=或2λ=-(舍). 所以,当23BE BA =时,二面角B SC E --. 7.在如图所示的几何体中,四边形ABCD 是正方形,四边形ADPQ 是梯形,PD ∥QA ,2PDA π∠=,平面ADPQ ⊥平面ABCD ,且22AD PD QA ===.(Ⅰ)求证:QB ∥平面PDC ;(Ⅱ)求二面角C PB Q --的大小;(Ⅲ)已知点H 在棱PD 上,且异面直线AH 与PB所成角的余弦值为15,求线段DH 的长. 【答案】(1)证明见解析;(2)56π;(3)32. 【解析】(1)平面ADPQ ⊥平面ABCD ,平面ADPQ ⋂平面ABCD AD =,PD ADPQ ⊂平面,PD AD ⊥,∴直线PD ⊥平面ABCD .由题意,以点D 为原点,分别以,,DA DC DP 的方向为x 轴,y 轴,z 轴的正向建立如图空间直角坐标系,则可得:()()()0,0,0,2,2,0,0,2,0D B C ,()()()2,0,0,2,0,1,0,0,2A Q P .依题意,易证:()2,0,0AD =-是平面PDC 的一个法向量, 又()0,2,1QB =-,∴ 0QB AD ⋅=, 又直线QB ⊄平面PDC ,∴ //QB PDC 平面.(2) ()()2,2,2,=0,22PB PC =--,. 设()1111,,n x y z =为平面PBC 的法向量,则1100n PB n PC ⎧⋅=⎪⎨⋅=⎪⎩,即111112220220x y z y z +-=⎧⎨-=⎩. 不妨设11z =,可得()10,1,1n =.设()2222,,n x y z =为平面PBQ 的法向量,又()()2,2,2,2,0,1PB PQ =-=-, 则2200n PB n PQ ⎧⋅=⎪⎨⋅=⎪⎩,即22222202220x z x y z -=⎧⎨+-=⎩. 不妨设22z =,可得()21,1,2n =,∴ 1212123cos<,2n n n n n n ⋅>==⋅, 又二面角C PB Q --为钝二面角,∴二面角C PB Q --的大小为56π. (3)设()()0,0,02H h h ≤≤,则()2,0,AH h =-,又()2,2,2PB =-, 又7cos<,15PB AH >=15=, ∴ 2625240h h -+=,解得32h =或83h =(舍去). 故所求线段DH 的长为32.8.已知在四棱锥C ABDE -中,DB ⊥平面ABC ,//AE DB ,ABC 是边长为2的等边三角形,1AE =,M 为AB 的中点.(1)求证:CM EM ⊥;(2)若直线DM 与平面ABC 所成角的正切值为2,求二面角B CD E --的大小.【答案】(1)证明见解析;(2)90.【解析】(1)证明:ABC为等边三角形,M为AB的中点,∴CM AB⊥,又DB⊥平面ABC,CM⊂平面ABC,∴DB CM⊥,DB AB B=,DB,AB平面ABDE,∴CM⊥平面ABDE,又EM⊂平面ABDE,∴CM EM⊥.(2)过点M作//Mz BD,易知Mz、MB、MC两两垂直;以M为原点,分别以MC、MB、Mz作为x轴、y轴、z轴建立空间直角坐标系,如图;DB⊥平面ABC,∴DMB∠直线DM与平面ABC所成角,∴tan2BDDMBBM∠==,∴22BD BM==,∴()0,1,0B,)C,()0,1,2D,()0,1,1E-,∴()3,1,0BC=-,()CD=-,()1,1CE=--,设平面BCD的一个法向量为()111,,m x y z=,则m BCm CD⎧⋅=⎨⋅=⎩即1111120yy z-=++=⎪⎩,令11x=,则()1,3,0m=,设平面CDE的一个法向量为()222,,n x y z=,则n CEn CD⎧⋅=⎨⋅=⎩即22222220y zy z⎧-+=⎪⎨++=⎪⎩,令2x=,则()3,1,2n=-,∴cos,0m nm nm n⋅==⋅,∴二面角B CD E--的大小为90.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一道经典的立体几何求角问题
边长为2的正ABC ∆,O 是重心,沿OB 把ABC ∆翻折使60.AOC ∠=o
(1)求OC 与AB 所成角的余弦值;
(2)求OC 与平面OAB 所成角的正弦值; (3)求二面角C OA B --的正弦值. 解:(1)如图,过点O 作OD ∥AB 交AM 于D , 则COD ∠或其补角即为OC 与
AB 所成的角。
易知,90AMB ∠=o
,OC =,1233OD AB ==,
1AM CM ==,,60,OA OC AOC AOC =∠=∴∆o Q 为正三角形。
222
1cos .23
AM CM AC CMA AM CM +-∴∠=
=⋅
2228
2cos 9
CD CM MD CM MD CMA ∴
=+-⋅⋅∠=
, 222cos 2OC OD CD COD OC OD +-∴∠==⋅
(2)用等体积法求。
设OC 与平面OAB 所成角为θ,易知
BM ⊥平面ACM ,
221211113333323O ABC B ACM O ACM B ACM ACM V V V V S BM ----∆=-==⨯⋅=⨯⨯⨯⨯⨯=
设点C 到平面OAB 的距离为d ,则由C
OAB O ABC V V -
-=得121
1332
d ⨯⨯⨯=
, 解得
d
=
s i n
.d OC θ=== (3)为了作图看得清,特将图形作了一定的转动。
由(1)知AOC ∆为正三角形,
∴取OA 的中点E ,连结CE ,则有CE OA ⊥。
在AOB ∆内作EF OA ⊥于E ,连接CF , 则CEF ∠为二面角C OA B --的平面角。
易知1CE =,30BAO ∠=o
,12tan 30,.3cos303
AE EF AE AF ∴=⋅==
=o o 在ACF ∆中,由余弦定理,222
42cos 3
CF AC AF AC AF FAC =+-⋅⋅∠=,
2221cos 23CE FE CF CEF CE FE +-∴∠==-
⋅,∴二面角C OA B --。
