投资学第6章风险与风险厌恶
投资学PPT 第6章--风险与风险厌恶

投资者的风险态度
风险厌恶(Risk aversion) 风险中性(Risk neutral) 风险爱好(Risk lover)
5
风险厌恶型投资者的无差异曲线 (Indifference Curves)
Expected Return
1 P
2
3
4 Increasing Utility Standard Deviation
36
无差异曲线
1 投资者效用函数: U E (r ) A 2 2 其中A为外生变量。 如此,为保持 U不变,可调整 E (r )和的组合 在E (r )和 空间中,为一系列的点 。 连结各点得到投资者的 无差异曲线。 其中U 为无差异曲线的确定等 价收益率。 投资者无差异曲线簇与 资本配置线相切的点, 为与投资者风险厌恶程 度相应的最优资产配置 水平
25
资产组合的动态调整(续)
Vanguard Fidelity Portfolio P Risk-Free Assets F Portfolio C
113,400/300,000 = 0.378 96,600/300,000 = 0.322 210,000/300,000 = 0.700 90,000/300,000 = 0.300 300,000/300,000 = 1.000
2 A
2 B
则该投资者认为“A占优于B”,或A比B有优势(A dominates B)。
19
占优原则(Dominance Principle)
期望回报 4 2 1 方差或者标准差 3
• 2 占优 1; 2 占优于3; 4 占优于3;
20
表 6.3 风险厌恶系数A=4的投资者的 可能组合效用值
21
证券投资风险厌恶与风险资产配置习题
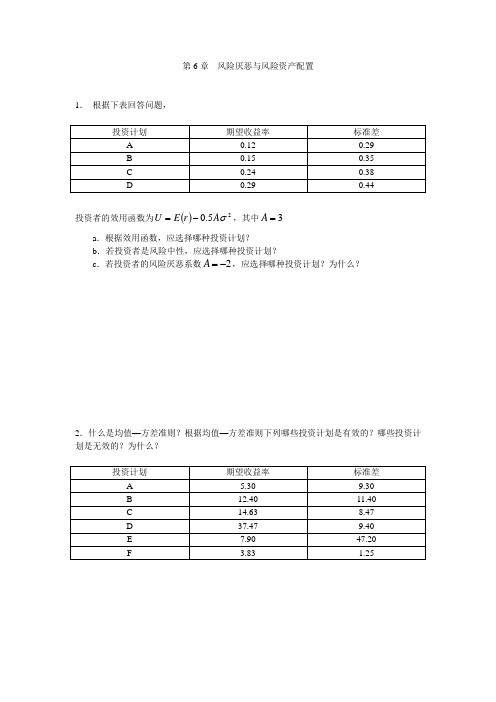
第6章 风险厌恶与风险资产配置
1. 根据下表回答问题,
投资者的效用函数为()2
5.0σA r E U -=,其中3=A
a .根据效用函数,应选择哪种投资计划?
b .若投资者是风险中性,应选择哪种投资计划?
c .若投资者的风险厌恶系数2-=A ,应选择哪种投资计划?为什么?
2.什么是均值—方差准则?根据均值—方差准则下列哪些投资计划是有效的?哪些投资计划是无效的?为什么?
3.某投资者可以选择收益率为4%的国库券,或者是年末现金流是24000美元的风险组合进行投资。
若该投资者要求的风险溢价为7.5%,那么该投资者对于风险组合能接受的最高出价是多少?
4.你计划投资100美元于期望收益率为13%,标准差为14%的风险资产和收益率为4%的国库券,
a.为构建期望收益率为8%的投资组合,你将如何构建投资组合?其构建的投资组合的标准差是多少?
b.为构建标准差为5%的投资组合,你将如何构建风险资产和国库券的投资比例?
c.由该风险资产和国库券形成的资本配置线(CAL)的斜率和截距是多少?
d.假设该投资者想借入资金,则必须支付9%的利率。
画出新的资本配置线。
对于借款分段的资本配置线的斜率是多少?
e.最终该投资者借入资金30美元投资于风险资产,其构建的投资组合的期望收益率和标准差是多少?。
博迪《投资学》视频课程(投资组合理论-风险厌恶与风险资产的资本配置)

第6章风险厌恶与风险资产的资本配置6.1 本章要点●明晰风险偏好和风险厌恶的涵义,了解如何评估风险厌恶程度●熟悉风险资产和无风险资产投资组合的特征:收益、风险、资本配置线●熟悉基于风险偏好和资本配置线的最优风险资产头寸选择6.2 重难点导学一、风险与风险厌恶(1)风险风险的存在意味着不确定性。
将某一初始财富用于投资时面临着风险,也就是投资回报具有不确定性。
投机是指在获取相应的报酬时承担一定的商业风险。
“相应的报酬”是指去除无风险收益之后的实际期望收益,这就是风险溢价,风险溢价是由于风险所得到的预期所得。
(2)风险态度(偏好)●风险厌恶●风险中性●风险喜爱(3)风险偏好与效用函数将风险厌恶引入效用函数:U=E(r)-0.005Aσ2,其中,E(r)为资产组合的期望收益,σ为收益标准差,A为投资者的风险厌恶指数。
风险厌恶者A>0。
与风险厌恶投资者相比,风险中性的投资者只是按期望收益率来判断风险投资,这意味着不存在风险妨碍(A=0)。
风险爱好者愿意参加公平游戏与赌博,这种投资者把风险的“乐趣”考虑在内(A<0)。
(4)风险厌恶效用函数:均值-方差准则投资组合A优于投资组合B,如果E(r A)≥E(r B),而且σA≤σB。
至少有一项不相等时,投资组合A优于B。
图6-1 投资组合P的风险和收益(5)风险厌恶效用函数:(效用)无差异曲线图6-2 无差异曲线二、风险资产与无风险资产投资组合的资本配置(1)资产组合:收益和风险①收益:资产组合的期望收益就是其组成资产期望收益率的加权平均值。
1()()n P i i i E r w E r ==∑②风险:资产组合风险的一种测度就是其收益率的标准差。
211cov(,)=n n n n pi j i j i j ij i j i j i i j i w w r r w w σρσσ=====∑∑∑∑(2)无风险资产:σ=0一般认为短期国库券可以作为无风险资产。
ch067版风险厌恶与风险资产的资本配置

• 假定无风险利率为5%,投资者面对以下三种不同 的投资组合如何选择呢?
•
表6-1 提供的风险投资组合(无风险利率为5%)
• 投资组合 风险溢价(%) 期望收益(%) 风险程度(SD)(%)
• L(低风险) 2
7
5
• M(中风险) 4
9
10
• H(高风险) 8
13
20
• 可以看出,风险随着期望收益而增加,那么最具 有吸引力的投资组合是哪个?
7-20
6.1.3 评估风险厌恶
• 考虑一个风险厌恶程度为A的投资者,他的全部财产就是 一块真实的不动产。假设在某任一年度里,发生泥石流损 害不动产,使得投资者的财产化为乌有的概率为p,这样 的事件带来的收益是-100%。另外,不动产保持原样的概 率就为1-p,认为这样的收益率为0。
r(损失)= -1(即-100%)
p
1-p
r(未损失)=0
• 这种情况下的期望收益和标准差是多少?
7-21
6.1.3 评估风险厌恶
• E (r)=p*(-1)+(1-p)*0= -p p
(6-2) -1-(-p)=p-1
1-p
0-(-p)=p
s2 r = p (p 1)2 (1 p) p2
• = p(1 p)
(6-3)
7-22
7-25
结论:经济学家预测投资者的风险厌恶程度A位于2和 4之间,而他们愿意为期望损失付出的代价(保险费率) 大概在损失的概率的2-3倍之间。
大量的股票指数投资组合中得到的期望收益率与标准 差的估计可以证实大多数投资者的风险厌恶程度在2—4之 间。
7-26
6.2风险资产与无风险资产投资组合的资本配置
6.1.3 评估风险厌恶
第六章 风险厌恶与风险资产的

S E(rc ) rf 18.2 7 0.36
c
30.8
有风险借贷对CAL的影响
E(r)
E(rp)=15%
rBf=9% rf=7% S=0.36
P
S=0.27
P 22%
通常投资者借入利率大于无
风险资产利率,假如借入利
率为9%,这样资本配置线的
斜率为:
E rp rfB 6 0.27
2、风险厌恶的投资者不会进行公平博弈() 3、波动越大的投资组合其效用越大() 4、越厌恶风险的投资者越倾向于持有无风
险资产() 5、风险厌恶型无差异曲线上,越上方的点
表示效用越大()
计算
1、一个投资组合的期望收益率为20%,标 准差为20%。国债能提供的无风险收益 率为7%。试计算风险规避系数A=4的投 资者更愿意投资国债还是风险投资组合?
单一风险资产和单一无风险资 产的投资组合
假险定设资义投产P资F的的风组投险合收资中益比风率例险为为r资p ,1期产-y望P收比益例率为为yE,(rp无),风标准
差为 p,无风险收益率为rf。若假设 E(rp ) 15%, p 20%, rf 7%
则为,:组成rc 整个y投rp资组(1合C,y)风rf险收益收益率rc
计算
2、考虑一风险投资组合,年末来自该资产 组合的现金流可能为7万美元或20万美元, 概率都是0.5。可供选择的国库券投资的 年利率为6%。如果投资者要求8%的风 险溢价,那么他愿意支付多少钱购买该 风险资产组合?
无风险资产的含义
无风险资产:如果投资者在期初 购买了一种无风险资产,那么他 将准确地知道在持有期期末这笔 资产的准确价值。无风险资产的 最终价值没有任何不确定性,无 风险资产的标准差,根据定义, 应为零。
博迪《投资学》(第9版)课后习题-风险厌恶与风险资产配置(圣才出品)

第6章风险厌恶与风险资产配置一、习题1.风险厌恶程度高的投资者会偏好哪种投资组合?a.更高风险溢价b.风险更高c.夏普比率更低d.夏普比率更高e.以上各项均不是答:e。
2.以下哪几个表述是正确的?a.风险组合的配置减少,夏普比率会降低b.借入利率越高,有杠杆时夏普比率越低c.无风险利率固定时,如果风险组合的期望收益率和标准差都翻倍,夏普比率也会翻倍d.风险组合风险溢价不变,无风险利率越高,夏普比率越高答:b项正确。
较高的借入利率是对借款人违约风险的补偿。
在没有额外的违约成本的完美市场中,这个增量值将与借款人违约选择权的价值相等。
然而,在现实中违约是有成本的,因此这部分的增量值会使夏普比率降低。
c项是不正确的,因为一个固定的无风险利率的预期回报增加一倍,风险溢价和夏普比率将增加一倍以上。
3.如果投资者预测股票市场波动性增大,股票期望收益如何变化?参考教材式(6-7)。
答:假设风险容忍度不变,即有一个不变的风险厌恶系数(A),则观察到的更大的波动会增加风险投资组合的最优投资方程(教材式6-7)的分母。
因此,投资于风险投资组合的比例将会下降。
4.考虑一个风险组合,年末现金流为70000美元或200000美元,两者概率相等。
短期国债利率为6%。
a.如果追求风险溢价为8%,你愿意投资多少钱?b.期望收益率是多少?c.追求风险溢价为12%呢?d.比较a和c的答案,关于投资所要求的风险溢价与售价之间的关系,投资者有什么结论?答:a.预期现金流入为(0.5×70000)+(0.5×200000)=135000(美元)。
风险溢价为8%,无风险利率为6%,则必要回报率为14%。
因此资产组合的现值为:135000/1.14=118421(美元)。
b.如果资产组合以118421美元买入,给定预期的收入为135000美元,则期望收益率E(r)满足:118421×[1+E(r)]=135000(美元)。
06风险与风险厌恶

- 风险爱好
效用 效用函数
U = E ( r ) - .005 A s 2 A 为投资者的风险厌恶指数
6-5
风险厌恶和效用价值:投资实例
U = E ( r ) - .005 A s 2 = 高 低 .22 - .005 A (34%) 2
风险厌恶
A
5
价值
-6.90
.6 (150-122)2 + .4(80=122)2 = 1,176,000
s = 34.293
6-3
风险投资与无风险投资
W1 = 150 盈利= 50
风险投资
100
1-p = .4
无风险国库券
W2 = 80 盈利= -20 盈利 = 5
风险溢价 = 17
6-4
风险厌恶与效用价值
投资者对风险的态度
sp2 = w12s12 + w22s22 + 2W1W2 Cov(r1r2) Cov(r1r2) = 证券1和证券资产组合的收益率是构成资产组合的每 种资产收益率的加权平均值,以资产组合比例 作为权数。 rp = W1r1 + W2r2 W1 = 在证券1上的投资比例 W2 = 在证券2上的投资比例 r1 = 证券1的期望收益率 r2 = 证券2的期望收益率
6-12
风险资产与无风险资产组合
规则4:当一项风险资产和一项无风险资产相组 合时,资产组合的标准差等于风险资产的标准 差乘以该资产组合投资于这部分的资产上的比 例。
s p = w风险资产 s
风险资产
6-13
投资组合风险
规则5:方差分别是s12和s22两项风险资产 以w1 和w2 的权重构成一个资产组合,该 资产组合的方差为:
ch06风险与风险厌恶

U = E ( r ) - .005 A σ 2 = .22 - .005 A (34%) 2 风险厌恶度 效用值 Risk Aversion A Value High 5 -6.90 3 4.66 Low 1 16.22
T-bill = 5%
6-7
风险厌恶,风险与收益的权衡
Equilibrium of Risk Aversion,Risk and return Aversion,
6-16
风险中性投资者的无差异曲线 Risk neutral: Indifference Curves
期望收益 Expected Return
风险中性型的 投资者对风险 无所谓,只关 心投资收益.
标准差 Standard Deviation
6-17
风险偏好投资者的无差异曲线 Risk Seeking : Indifference Curves
6-12
确定性等价收益率(Certainly 确定性等价收益率(Certainly equivalent rate) rate) 为使无风险资产与风险资产具有相同的效 用而确定的无风险资产的报酬率,称为风 险资产的确定性等价收益率. 由于无风险资产的方差为0 由于无风险资产的方差为0,因此,其效用 U就等价于无风险回报率,因此,U就是风 就等价于无风险回报率,因此,U 险资产的确定性等价收益率.
期望收益Expected Return 期望收益
风险偏好型的 投资者将风险 作为正效用的 商品看待,当 收益降低时候, 可以通过风险 增加得到效用 补偿.
标准差Standard Deviation 标准差
6-18
资产组合风险
Portfolio Risk
到现在为止,我们的讨论一直集中在个人全部资产组合的 风险与收益上.这样的资产组合是由各种类型的资产组成 的,除了在金融市场上的直接投资外,投资者还持有养老 基金,以储蓄形式进行的人寿保险计划,住宅,还有并非 最不重要的是他们自身技能带来的获利能力(人力资本). Investor portfolios are composed of diverse types of assets. In addition to direct investment in financial markets, investors have stakes in pension funds, life insurance policies with savings components, homes, and not least, the earning power of their skills (human capital).
风险厌恶与风险资产的配置概论课件

29
6.4 单一风险资产与单一无风险资产的投资组合
风险投资组合的比例为 y,无风险投资组合比例为 1-y,组成的整个投 资组合 C 的收益率 rC 为:
rc yrp (1 y)rf
整个投资组合的收益率期望值为:
E(rc ) yE(rp ) (1 y)rf rf y[E(rp ) rf )] E(rp ) 15%, p 22%, rf 7%,则 风险资产的风险溢价=E(rp ) p 8%。
风险、投机与赌博
赌博可以向投机转化:当参赌者要求有足够的风险 溢价作为参赌的条件,赌博就变成了投机。
貌似投机的赌博 主观认为有两种不同的前景,经济学家称为“异质 预期”。解决方法为交换信息、充分沟通。
6.1 风险与风险厌恶 6.1.1 风险、投机与赌博
风险:不确定性 投机:承担一定风险(considerable risk),获 取相应报酬(commensurate return) 赌博:为一不确定结果下注
风险、投机与赌博
投机:为获得相应的报酬而承担一定的商业风险。
注意: 1、明确“相应的报酬”和“一定的风险”含义。 “相应的报酬”是指除去无风险收益之后的实际期望收益,它 或者是超额收益或者是风险溢价。--比如,投资者如果选择股 票,他希望获得的是股票期望收益高于国库券期望收益的风险 溢价。 “一定的风险”是指足以影响决策的风险,当增加的收益不足 以补偿所冒的风险时,投资者会放弃产生正的风险溢价的机会。
2、风险厌恶。现代投资组合理论还假设,投资者是 风险厌恶的,即在其他条件相同的情况下,投资者将 选择标准差较小的组合。
3
本章主要内容
投资者的风险态度 投资组合的效用评分方法 单一风险资产与单一无风险资产的投资
组合 资本配置线(CAL) 最优资本配置比例 资本市场线(CML)
投资学6~7章课后习题

证券投资学课后作业张娟管实1101 U201113738第六章风险厌恶与风险资产配置1.选e. 风险厌恶程度高的投资者会选择风险小的投资组合,或者说更愿意持有无风险资产.更高的风险溢价听着可能会很有吸引力,但是其风险一般也会很大,不能抵消掉风险厌恶者的恐惧;风险更高,那风险厌恶程度高的投资者更加不会考虑;夏普比率是说单位风险所获得的风险溢价,虽然夏普比率高,表明单位风险获得的风险溢价高,但是对于风险厌恶者来说,总的风险很高,那么他们同样会拒绝。
另外,夏普比率没有基准点,其大小本身没有意义,只有在与其他组合的比较中才有意义。
2.选b. 由夏普比率的公式S=E(r p)−r f B,当借入利率r f B升高时,若其它保持不变,σp则夏普比率升高。
3.如果预测股票市场的波动性增大,则说明其风险增大;假设投资者的风险容忍度不变,投资比例不变,那么预期收益会增加。
根据6-7的公式得出的。
13. E(r c)=70%*18%+30%*8%=15%;σc=70%∗28%=19.6%14.15.我的报酬-波动比率为(0.18-0.8)/0.28=0.3571. 客户的报酬-波动比率和我的一样。
斜率为0.357117.a. y=0.8b. 标准差为22.4%18.当标准差不大于18%时,投资比例y<=0.18/0.28=0.6429,最大投资收益为0.6429*0.18+0.3571*0.08=0.1443=14.43%,其中A=3.5,解得y∗=0.3644,即36.44%投资于风险资产,19.y∗=E(r p)−r fAσP263.56%投资于无风险资产。
20. a. y∗=0.4578,即45.78%投资于股票,54.22%投资于短期国债。
b. y∗=0.3080,即30.8%投资于股票,69.2%投资于短期国债。
c.但投资者的风险厌恶程度相等时,风险越大,投资于无风险资产的比重变大。
21.a. 0.5b. 7.5%c. 标准差不超过12%,要想收益最大化,则令标准差为12%,算出y=0.12/0.15=0.822.y=0.5, E(r c)=0.5∗12%+0.5∗5%=8.5%23分别有两条无差异曲线与上面这条折线的上下部分相切。
ch06风险与风险厌恶

E(r)=p (-1)+(1-p) 0=-p
方பைடு நூலகம்为:
2 =p (-1+p)2 +(1-p) (0+p)2 =p(1-p)
效用值为:
1 1 U= E(r)- A 2 (r)=-p- Ap(1-p) 2 2
6-13
现在可以将风险厌恶者与个人愿意付出多少保险来 规避可能的损失联系在一起。假定一个保险公司在 对一年中的任何损失都提供保费率为v的财产保险, 个人按每美元的实际不动产价值付保费v给保险公司, 就可以不用承担风险,保险公司可以对任何损失进 行偿还,因此真实不动产可以在年末时仍然保持它 的原始价值。考虑这样条款所带来的确定负收益率 为-v,效用值为U=-v:
风险厌恶型的投资者会放弃公平博弈或更糟的投资组合,而更愿意考虑 无风险资产或正溢价的投机性投资。
效用评价公式:
U E (r )
1 A 2 2
其中,U 为效用值,A 为投资者的风险厌恶系数(A 越大表明该投资者 越厌恶风险,在冒同等风险的情况下必须给予其更大的风险溢价,否则 不愿意冒此风险)。系数 1/2 为一个约定俗成的分数项。收益率必须采用 小数形式而不是百分数形式。
6-4
我们可以把风险投资的效用值看成是投资者的“确 定等价收益率”。确定等价收益率就是为使无风险 投资与风险投资具有相同的吸引力而确定的无风险 投资收益率。只有当一个投资组合的确定等价收益 大于无风险投资收益时,这个投资才是值得的。 风险中性的投资者(A=0)只是根据期望收益率来判 断风险预期。风险的高低与风险中性投资者无关, 对他们来说,投资组合的确定等价收益率就是预期 收益率。 风险偏好者(A<0)更加愿意参加公平博弈与赌博, 这种投资者将风险的“乐趣”考虑在内之后反而使 他们的期望收益率升高。 均值-方差准则:如果E(rA)≥E(rB),σA≤σB,且至少 有一项不相等时,投资组合A优于B。
投资学课件:Chap006_风险厌恶与风险资产配置

线。
INVESTMENTS|
6-37
6.6被动策略:资本市场线
•从1926~2009年的历史数据上看,被动策
略提供的平均风险溢价为7.9%,标准差是20.8%,报酬-波动比率是0.38。
•一般风险厌恶系数在2.0-4.0之间。
投资者对风险厌恶程度越高(A越大),对风险要求的补偿就越高。确定等价收益率:风险资产的效用值,即无风险资产达到与风险资产相同的效用所需要的收益率。
INVESTMENTS|
6-9
6.1.2风险厌恶和效用价值
2、均值-方差(M-V)准则
•投资组合A优于投资组合B,如果:
ErEr与
sAsB
AB
•至少有一个条件严格成立。①期望收益率相同,风险低者更优。②风险水平相同,期望收益高者更优。
•投资组合的吸引力随着期望收益的增加和风险
的减少而增加。
•收益与风险同时增加是会怎么样呢?
INVESTMENTS|
6-6
表6.1可供选择的风险资产组合
(无风险利率= 5%)
投资者会根据风险收益情况为每个资产组合给出一个效用值分数。
INVESTMENTS|
6-7
6.1.2风险厌恶和效用价值
1、效用函数
资本配置:•是投资组合构建中最
控制风险:
•简化方法:只需控制投资于风险资产组合
重要的问题;
•在大量的投资资产种
和无风险资产组合的比重。
类中选择证券;
INVESTMENTS|
6-13
6.2风险资产与无风险资产组合的资本配置
基本资产配置:
风险与风险厌恶

风险与风险厌恶 资产组合的风险
风险与风险厌恶
风险的定性描述 单一前景的风险 风险、投机与赌博 风不确定性
风险无处不在 不确定性并不意味着损失
风险与风险厌恶
单一前景的风险
例子:投资10元,有两种选择,一种是确切的 得到10.5元,另一种是以60%的可能性得到15 元,以40%的可能性得到8元。对于第二种情 况,我们知道,它的预期回报是12.2元,比第 一种高1.7元,但是这种投资也有风险。 度量:度量预期回报与实际回报之间的差距, 差距越大,则风险越大。上例中,我们知道:
E [ w ] 12.2; D ( w ) 11.76; 3.43
风险与风险厌恶
风险、投机与赌博
赌博的预期回报低于投入 投机是为了获得较高报酬而承担风险 有时难以区分赌博、投机与投资之间的差别
风险与风险厌恶
风险厌恶与效用函数
投资者的分类 财富与效用的关系 效用函数 无差异曲线
风险与风险厌恶
风险与风险厌恶 资产组合的风险
资产组合的风险
单个资产的风险与资产组合的风险
保单的风险与收益 组合中的风险是可以对冲的 套期保值与分散化
资产组合的风险
案例
第六章风险与风险厌恶

第六章风险与风险厌恶1.考虑一风险资产组合,年末来自该资产组合的现金流可能为70000美元或200000美元,概率相等,均为0.5;可供选择的无风险国库券投资年利率为6%。
a.如果投资者要求8%的风险溢价,则投资者愿意支付多少钱购买该资产组合?b.假定现在投资者可以购买(a)中的资产组合数量,该投资的期望收益率为多少?c.假定现在投资者要求12%的风险溢价,则投资者愿意支付的价格是多少?d.比较(a)和(b)的答案,关于投资所要求的风险溢价与售价之间的关系,投资者有什么结论?a. 预期现金流为0 . 5×70 000+0.5×200 000=135 000美元。
风险溢价为8%,无风险利6%,要求的回报率为1 4%。
因此,资产组合的现值为:135 000/1.14=118 421美元b. 如果资产组合以118 421美元买入,给定预期的收入为135 000美元,而预期的收益率E(r)推导如下:118 421美元×[ 1 +E(r)]=135 000美元因此E(r) = 1 4%。
资产组合的价格被设定为等于按要求的回报率折算的预期收益。
c. 如果国库券的风险溢价现值为1 2%,要求的回报率为6%+ 1 2%= 1 8%。
该资产组合的现值就为135 000美元/ 1 . 1 8 = 114 407美元。
d. 对于一给定的现金流,要求有更高的风险溢价的资产组合必须以更低的价格售出。
预期价值的多余折扣相当于风险的罚金。
2.糖生产的正常年份异常年份股市的牛市股市的熊市糖的生产危机概率0.5 0.3 0.2收益率(%)best candy 25 10 -25 sugarcane 7 -5 20国库券 5 5 5A.它与best candy 股票的相关性怎样?B.目前sugarkane 公司股票是有用的套期保值资产吗?C.计算两种情形下的资产组合的收益率及其标准差。
然后用规则5。
评估σpD.两种计算标准差的方法是一致的吗?。
第6章 风险厌恶与风险资产的资本配置

Table 6.1 Available Risky Portfolios (Risk-free Rate = 5%) 提供的风险投资组合(无风险利率为5%)
Utility Function 效用函数
U = E ( r ) – 1/2 A σ2 Where U = utility 效用值 E ( r ) = expected return on the asset or portfolio 资产或投资组合的期望收益 A = coefficient of risk aversion 投资者的 风险厌恶系数 σ2 = variance of returns 收益方差
CHAPTER 6
Risk Aversion and Capital Allocation to Risky Assets 风险厌恶与风险资产 的资本配置
Risk and Risk Aversion 风险与风险厌恶
Speculation 投机
– Considerable risk 一定的风险
• Sufficient to affect the decision 足以影响决策
The Risk-Free Asset 无风险资产
Only the government can issue default-free bonds 只有政府才可以发行无违约风险的债券 – Guaranteed real rate only if the duration of the bond is identical to the investor’s desire holding period 只有当债券的偿还期等于投 资者愿意持有的期限时才能对投资者的实际 收益率提供担保 T-bills viewed as the risk-free asset 短期国库 券可以作为无风险资产 – Less sensitive to interest rate fluctuations 对利率的波动不敏感
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 2 占优 1; 2 占优于 4 占优于 占优于3; 占优于3;
17
风险厌恶系数A=4的投资者的 表 6.3 风险厌恶系数 的投资者的 可能组合效用值
18
图6.2 无差异曲线
19
6.1.3 评估风险厌恶
观察个体面临风险时的决策过程 观察为避免风险而愿意付出的代价
保险支付
20
表6.4 投资者愿意为灾难事件付出的保险
21
6.2 风险与无风险资产组合的资本配置
控制资产组合风险的方法: 控制资产组合风险的方法:
部分投资于无风险资产,部分投资于风险资产 部分投资于无风险资产, 记风险资产组合为P,无风险资产组合为F, 记风险资产组合为 ,无风险资产组合为 ,风 险资产在整个组合中的比重为y, 险资产在整个组合中的比重为 ,则我们可通 过y的调整来调整组合风险 的调整来调整组合风险
风险中性型的 投资者对风险 无所谓, 无所谓,只关 心投资收益。 心投资收益。
Standard Deviation
9
风险偏好( 风险偏好(Risk lover)投资者的无差异曲线 )
Expected Return
风险偏好型的 投资者将风险 作为正效用的 商品看待, 商品看待,当 收益降低时候, 收益降低时候, 可以通过风险 增加得到效用 补偿。 补偿。
A ∈ [2.0,4.0]
40
大盘股和1月期国库券的年平均收益率 图 6.8大盘股和 月期国库券的年平均收益率, 大盘股和 月期国库券的年平均收益率, 大盘股各段时期内的标准差和收益的变化
41
本章小结
投机与赌博 风险溢价、 风险溢价、公平博弈与投资者风险态度 投资者效用函数 确定等价收益率 降低资产组合风险的最有效方式是加大无风险 资产投资的比重 资本配置线的斜率为报酬与波动性比率 风险资产的最优头寸 消极投资策略
35
表6.6 无差异曲线的电子数据表计算
36
图6.7 无差异曲线 for U = .05 and U = .09 with A = 2 and A = 4
37
表6.7使用无差异曲线寻找最优的投资组 使用无差异曲线寻找最优的投资组 合
38
图6.8 用无差异曲线寻找最优的投资组合
39
6.6 消极策略:资本市场线 消极策略:
6
Байду номын сангаас
从风险厌恶型投资来看, 从风险厌恶型投资来看,收益带给他正的 效用,而风险带给他负的效用, 效用,而风险带给他负的效用,或者理解 为一种负效用的商品。 为一种负效用的商品。 根据微观经济学的无差异曲线, 根据微观经济学的无差异曲线,若给一个 消费者更多的负效用商品, 消费者更多的负效用商品,且要保证他的 效用不变,则只有增加正效用的商品。 效用不变,则只有增加正效用的商品。 根据均方准则,若均值不变,而方差减少, 根据均方准则,若均值不变,而方差减少, 或者方差不变,但均值增加, 或者方差不变,但均值增加,则投资者获 得更高的效用, 得更高的效用,此即风险厌恶者的无差异 曲线。 曲线。
4
投资者的风险态度
风险厌恶(Risk aversion) 风险中性(Risk neutral) 风险爱好(Risk lover)
5
风险厌恶型投资者的无差异曲线 (Indifference Curves) )
Expected Return
1 P 3
2
4 Increasing Utility Standard Deviation
23
资产组合的动态调整(续 资产组合的动态调整 续)
Vanguard Fidelity Portfolio P Risk-Free Assets F Portfolio C
113,400/300,000 = 0.378 96,600/300,000 = 0.322 210,000/300,000 = 0.700 90,000/300,000 = 0.300 300,000/300,000 = 1.000
3
6.1.2 风险厌恶与效用价值
引子:如果证券 可以无风险的获得回报 引子:如果证券A可以无风险的获得回报 率为10%,而证券B以 %的概率获得20% %,而证券 率为 %,而证券 以50%的概率获得 % 的收益, %的概率的收益为0, 的收益,50%的概率的收益为 ,你将选择 哪一种证券? 哪一种证券? 对于一个风险规避的投资者,虽然证券B的 对于一个风险规避的投资者,虽然证券 的 期望收益为 %,但它具有风险, %,但它具有风险 期望收益为10%,但它具有风险,而证券 A的无风险收益为 %,显然证券 优于证 的无风险收益为10%,显然证券A优于证 的无风险收益为 %,显然证券 券B。 。 结论: 结论:风险厌恶型的投资者会放弃公平博 或更糟的投资组合。 弈(fair play)或更糟的投资组合。 或更糟的投资组合
24
6.3 无风险资产
无风险资产只是一种近似 短期国库券可视为一种无风险资产, 短期国库券可视为一种无风险资产,但其 利率存在一定的低估 习惯以货币市场基金作为对绝大部分投资 者易接受的无风险资产
无风险利率有时可用LIBOR(伦敦银行同业拆放 伦敦银行同业拆放 无风险利率有时可用 利率 )来代替 来代替 LIBOR:LondonInterBankOfferedRate 指在伦敦的第一流银行借款给伦敦的另一家第 一流银行资金的利率。 一流银行资金的利率。
30
图6.5 借贷利率不同时的可行集 (弯折的 弯折的CAL) 弯折的
31
6.5 风险容忍度与资产配置
A=4时投资者不同风险资产比例(y)的效用水平 时投资者不同风险资产比例(y) 表6.5 A=4时投资者不同风险资产比例(y)的效用水平
32
效用作为风险资产投资比例y的函数 图6.6 效用作为风险资产投资比例 的函数
研究表明, 研究表明,资产配置可以解释投资收益的 94%。 。
22
例:资产组合的动态调整
Total portfolio value = $300,000 Risk-free value = 90,000 Risky (Vanguard & Fidelity) = 210,000 股权Vanguard (V) = 54% 股权 债券Fidelity (F) = 46% 债券
12
确定等价收益率(Certainty equivalent 确定等价收益率( rate) )
为使无风险投资与风险投资具有相同的吸 为使无风险投资与风险投资具有相同的吸 无风险投资与风险投资 引力而确定的无风险投资的报酬率 风险投资的报酬率, 引力而确定的无风险投资的报酬率,称为 风险资产的确定等价收益率。 风险资产的确定等价收益率。 确定等价收益率 由于无风险资产的方差为0,因此, 由于无风险资产的方差为 ,因此,其效用 U就等价于无风险回报率,因此,U就是风 就等价于无风险回报率, 就等价于无风险回报率 因此, 就是风 险资产的确定性等价收益率。 险资产的确定性等价收益率。
29
CAL的杠杆作用 的杠杆作用
以无风险利率借入款项并全部投资于风险资产。 以无风险利率借入款项并全部投资于风险资产。 若使用40%杠杆 则有: 杠杆,则有 若使用 杠杆 则有: E(rc)= (-0.4) (0.07) + (1.4) (0.15) = 18.2%
σc = (1.4) (0.22) = 30.8%
消极策略(passive strategy):决策不做任何直接或间 消极策略 : 接的证券分析 资本市场线(capital market line, CML):1月期短期国 资本市场线 : 月期短期国 库券与一个普通股指数所生成的资本配置线 消极策略合理性的原因: 消极策略合理性的原因: 积极策略的投资成本 Free rider(搭便车 收益 搭便车)收益 搭便车 投资者的历史风险厌恶态度
7
附录6A:圣彼德堡悖bei论 附录6A:圣彼德堡悖bei论 6A bei
期望收益无限的赌局, 期望收益无限的赌局,为何参加者愿意付 出的门票价格非常有限? 出的门票价格非常有限? 边际效用递减规律
8
风险中性( 风险中性(Risk neutral)投资者的无差异曲线 )
Expected Return
13
表6.2 各种风险厌恶投资者的投资组合的 效用值
准则: 准则:只有当资产组合的确定性等价收益大于无风险资产的 收益率时,这项投资才是值得的。 收益率时,这项投资才是值得的。
14
投资组合P的收益与风险权衡 图6.1 投资组合 的收益与风险权衡
15
均值方差准则( 均值方差准则(Mean-variance criterion) 若投资者是风险厌恶的,则对于证券A和 若投资者是风险厌恶的,则对于证券 和 证券B, 证券 ,如果
E(rA ) ≥ E(rB )
并且
σ ≤σ
2 A
2 B
则该投资者认为“ 占优于 占优于B”, 有优势(A 则该投资者认为“A占优于 ,或A比B有优势 比 有优势 dominates B)。 。
16
占优原则( 占优原则(Dominance Principle) )
期望回报 4 2 1 方差或者标准差 3
33
6.5 风险容忍度与资产配置
1 投资者效用函数:U = E (r ) − Aσ 2 2 A > 0:风险厌恶者 A = 0:风险中性者 A < 0:风险爱好者 求解效用最大化问题: 1 2 2 Max U = r f + y[ E ( rP ) − rf ] − Ay σ P y 2 E (rP ) − r f * ⇒ 最优风险资产配置比例y = 2 Aσ P
34
无差异曲线
1 投资者效用函数:U = E (r ) − Aσ 2 2 其中A为外生变量。 如此,为保持U不变,可调整E (r )和σ的组合 在E (r )和σ空间中,为一系列的点。 连结各点得到投资者的无差异曲线。 其中U为无差异曲线的确定等价收益率 投资者无差异曲线簇与资本配置线相切的点, 为与投资者风险厌恶程度相应的最优资产配置水平
