2014华杯赛决赛小学高年级组试题A答案详解
2014华赛决赛试题a卷及答案

2014华赛决赛试题a卷及答案2014华赛决赛试题A卷及答案一、选择题1. 已知函数f(x)=x^2-6x+8,求f(3)的值。
A. -1B. 1C. 3D. 5答案:B2. 一个等差数列的前三项分别是1, 4, 7,求第四项的值。
A. 10B. 11C. 12D. 13答案:A3. 已知一个圆的半径是5,求圆的面积。
A. 25πB. 50πC. 100πD. 125π答案:C4. 一个直角三角形的两条直角边长分别为3和4,求斜边的长度。
A. 5B. 6C. 7D. 8答案:A5. 已知一个等腰三角形的底边长为6,两腰相等,求等腰三角形的高。
A. 3B. 4C. 5D. 6答案:C二、填空题6. 已知一个数列的前三项是2, 5, 8,求第四项的值。
答案:117. 已知一个直角三角形的两条直角边长分别是6和8,求斜边的长度。
答案:108. 已知一个圆的直径是10,求圆的半径。
答案:59. 已知一个等差数列的前三项分别是2, 5, 8,求公差。
答案:310. 已知一个直角三角形的两条直角边长分别是5和12,求斜边的长度。
答案:13三、解答题11. 已知函数f(x)=2x^3-3x^2+1,求f(2)的值。
解:将x=2代入函数f(x)中,得到f(2)=2*(2)^3-3*(2)^2+1=16-12+1=5。
12. 已知一个等差数列的前三项分别是1, 3, 5,求第五项的值。
解:设等差数列的公差为d,则d=3-1=2。
因此,第五项的值为5+2=7。
13. 已知一个圆的半径是7,求圆的周长。
解:圆的周长C=2πr,其中r为半径。
将r=7代入公式,得到C=2π*7=14π。
14. 已知一个直角三角形的两条直角边长分别是7和24,求斜边的长度。
解:根据勾股定理,斜边的长度c=√(7^2+24^2)=√(49+576)=√625=25。
15. 已知一个等腰三角形的底边长为10,两腰相等,求等腰三角形的高。
解:设等腰三角形的高为h,两腰相等为a,则根据勾股定理,h^2+(10/2)^2=a^2。
14届华杯赛

第十四届华杯赛初赛试题及答案一、 选择题。
每小题10分,满分60分。
以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英语字母写在每题的圆括号内) 1. 下面的表情图片中。
没有对称轴的个数为( )(A ) 3 (B ) 4 (C ) 5 (D ) 62. 开学前6天,小明还没做寒假数学作业,而小强已完成了60道题。
开学时,两人都完成了数学作业,在这6天中,小明做的题的数目是小张的3倍,他平均每天做了( )道题。
(A ) 6 (B ) 9 (C ) 12 (D ) 153. 按照中国篮球职业联赛组委会的规定,各队队员的号码可以选择的范围是0~55号,但选择两位数的号码时,每位数字均不能超过5。
那么,可供每支球队选择的号码共有( )个。
(A ) 34 (B ) 35 (C ) 40 (D ) 56 4. 在19,197,2009这三个数中,质数的个数是( )。
(A ) 0 (B ) 1 (C ) 2 (D ) 3 1. 下面有四个算式:① 0.6+0.1●33●=0.7●33●② 0.625= 58③ 5 14 + 3 2 = 3+5 14+2 = 8 16 = 1 2 ④ 337 ×415 =1425其中正确的算式是( )(A )①和② (B )②和④ (C )②和③ (D )①和④6. A、B、C、D、E五个小朋友做游戏,每轮游戏都按照下面的箭头方向把原来手里的玩具传给另外一个小朋友:A→C ,B→E,C→A,D→B,E→D,开始时A、B拿着福娃,C、D、E拿着福牛,传递完5轮时,拿着福娃的小朋友是( )。
(A )C与D (B )A 与D (C )C 与E (D )A 与B 二、 填空题(每小题10分,满分40分)7.下面的算式中,同一个汉字代表同一个数字,不同的汉字代表不同的数字。
团团×圆圆=大熊猫则“大熊猫”代表的三位数是( )。
8.从4个整数中任意选出3个,求出它们的平均值,然后再求这个平均值和余下1个数的和,这样可以得到4个数:4、6、513 和423 ,则原来给定的4个整数的和为( )。
第二十二届华杯赛小高年级组决赛试题A解析

第二十二届华杯赛小高年级组决赛试题A解析第二十二届华杯赛小高年级组决赛试题A 解析1. 用[x]表示不超过x 的最大整数,例如[3.14]=3,则:201732017420175201762017720178[][][][][][]111111111111+++++的值为。
【考点】取整运算【专题】计算【难度】☆【解析】直接计算即可比较麻烦的简算方法:先看第一项20173(200215)361001454545[][][][691]691[]1111111111+??+===?+=?+ 第二项:20173(200215)481001606060[][][][891]891[]1111111111+??+===?+=?+ 所以原式=45607590105120691[]891[]1091[]1291[]1491[]1691[]111111111111++?++?++?++?++?+=(6810121416)914568910+++++?+ +++++ =60482. 从4个整数中任意选出3个, 求出它们的平均值, 然后再求这个平均值和余下1个数的和, 这样可以得到4个数:8,12,2103和193, 则原来给定的4个整数的和为。
【考点】平均数与求和【专题】计算【难度】☆【解析】假设这四个数为,,,a b c d每三个数的平均值为:()3,()3,()3,()3a b c a b d a c d b c d++÷++÷++÷++÷ 分别与余下的数的和为:21()38,()312,()310,()3933a b c d a b d c a c d b b c d d ++÷+=++÷+=++÷+=++÷+=将这四个式子左右两边分别相加得到:21()3()3()3()381210933a b c d a b d c a c d b b c d d ++÷++++÷++++÷++++÷+=+++()340a b c a b d a c d b c d a b c d +++++++++++÷++++= 3()3()40a b c d a b c d ?+++÷++++=2()40a b c d ?+++=20a b c d +++=3. 在3×3的网格中(每个格子是个1×1的正方形)放两枚相同的棋子,每个格子最多放一枚棋子, 共有种不同的摆放方法.(如果两种放法能够由旋转而重合, 则把它们视为同一种摆放方法).【考点】【专题】杂题【难度】☆【解析】这种题目因为情况不多,所以一一列举就是一种很好的办法,但是要注意不能重复和遗漏。
2014第十九届华杯初赛小学高年级组B卷(含解析)

第十九届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级B组)(时间:2014年3月15日8:00~9:00)一、选择题(每小题10分,满分60分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母填在答题卡相应题处.)1.平面上的四条直线将平面分割成八个部分,则这四条直线中至多有()条直线互相平行.A.0 B.2 C.3 D.42.在下列四个算式中:2÷=,0AB CD-=,4代表0~9中的不同数字,+=,A JI JE F⨯=,1G H那么两位数AB不可能是().A.54 B.58 C.92 D.963.淘气用一张正方形纸剪下了一个最大的圆(如图甲),笑笑用一张圆形纸剪下了七个相等的最大圆(如图乙),在这两种剪法中,哪种剪法的利用率最高?(利用率指的是剪下的圆形面积和占原来图形面积的百分率)下面几种说法中正确的是()A.淘气的剪法利用率高B.笑笑的剪法利用率高C.两种剪法利用率一样D.无法判断4.小华下午2点要到少年宫参加活动,但他的手表每个小时快了4分钟,他特意在上午10点时对好了表.当小华按照自己的表于下午2点到少年宫时,实际早到了().A.14 B.15 C.16 D.175.甲乙丙丁四个人今年的年龄之和是72岁.几年前(至少一年)甲是22岁时,乙是16岁.又知道,当甲是19岁的时候,丙的年龄是丁的3倍(此时丁至少1岁).如果甲乙丙丁四个人的年龄互不相同,那么今年甲的年龄可以有()种情况.A.4 B.6 C.8 D.106.有七张卡片,每张卡片上写有一个数字,这七张卡片摆成一排,就组成了七位数2014315.将这七张卡片全部分给甲、乙、丙、丁四人,每人至多分2张.他们各说了一句话:甲:“如果交换我卡片上的2个数字在七位数中的位置,那么新的七位数就是8的倍数”乙:“如果交换我卡片上的2个数字在七位数中的位置,那么新的七位数仍不是9的倍数”丙:“如果交换我卡片上的2个数字在七位数中的位置,那么新的七位数就是10的倍数”丁:“如果交换我卡片上的2个数字在七位数中的位置,那么新的七位数就是11的倍数”已知四人中恰有一个人说了谎,那么说谎的人是().A.甲B.乙C.丙D.丁二、填空题(每小题10 分,满分40 分.)7.算式33111324443100719(12345)522÷+÷+⨯÷++++⨯-的计算结果是______.8.海滩上有一堆栗子,这是四只猴子的财产,它们想要平均分配.第一只猴子来了,它左等右等别的猴子都不来,便把栗子分成四堆,每堆一样多,还剩下一个,它把剩下的一个顺手扔到海里,自己拿走了四堆中的一堆.第二只猴子来了,它也没有等别的猴子,于是它把剩下的栗子等分成四堆,还剩下一个,它又扔掉一个,自己拿走一堆.第三只猴子也是如此,等分成四堆后,把剩下的一个扔掉,自己拿走一堆;而最后一只猴子来,也将剩下的栗子等分成了四堆后,扔掉多余的一个,取走一堆.那么这堆栗子原来至少有______个.9.甲、乙二人同时从A地出发匀速走向B地,与此同时丙从B地出发匀速走向A地.出发后20分钟甲与丙相遇,相遇后甲立即调头;甲调头后10分钟与乙相遇,然后甲再次调头走向B地.结果当甲走到B 地时,乙恰走过A、B两地中点105米,而丙离A地还有315米.甲的速度是乙的速度的________倍,A、B两地间的路程是________米.10.从1,2,3,…,2014中取出315个不同的数(不计顺序)组成等差数列,其中组成的等差数列中包含1的有________种取法;总共有________种取法.第十九届华罗庚金杯少年数学邀请赛 初赛试卷(小学高年级B 组)参考答案参考解析1.平面上的四条直线将平面分割成八个部分,则这四条直线中至多有( )条直线互相平行. A .0B .2C .3D .4【考点】几何 【难度】☆☆ 【答案】C【解析】这是一道考前公开题.当四条直线相互平行的时候把平面分成五个部分,当三条直线平行,另一条直线与它们相交的时候四条直线恰好把平面分成八个部分.所以选择C2.在下列四个算式中:2AB CD ÷=,0E F ⨯=,1G H -=,4I J +=,A J 代表0~9中的不同数字,那么两位数AB 不可能是(). A .54B .58C .92D .96【考点】数论,数字谜专题中的横式数字谜问题 【难度】☆☆ 【答案】D【解析】首先可以确定的是0E F ⨯=,,E F ⇒中必有一个是0.那么4I J +=,I ⇒,J 只能为1,3;此时剩下的数字还有2,4,5,6,7,8,9.1G H -=,,G H ⇒相差1;讨论如下 若5427AB CD =⇒=,那么,G H 为8,9 若5829AB CD =⇒=,那么,G H 为6,7 若9246AB CD =⇒=,那么,G H 为7,8若9648AB CD =⇒=,此时,G H 无法取值.所以96AB ≠,选D .3.淘气用一张正方形纸剪下了一个最大的圆(如图甲),笑笑用一张圆形纸剪下了七个相等的最大圆(如图乙),在这两种剪法中,哪种剪法的利用率最高?(利用率指的是剪下的圆形面积和占原来图形面积的百分率)下面几种说法中正确的是( )A .淘气的剪法利用率高B .笑笑的剪法利用率高C .两种剪法利用率一样D .无法判断 【考点】几何 【难度】☆☆ 【答案】A【解析】根据提议,根据题意,如右甲图中正方形的面积为()2224r r =,圆的面积为2r π,所以淘气的剪法利用率为2278.5%44r r ππ=≈;如左乙图中3R r =,大圆面积为()2239r r ππ=,七个小圆面积和为27r π,所以笑笑的剪法利用率为2279r rππ=777.8%9≈;所以选A .4.小华下午2点要到少年宫参加活动,但他的手表每个小时快了4分钟,他特意在上午10点时对好了表.当小华按照自己的表于下午2点到少年宫时,实际早到了(). A .14B .15C .16D .17 【考点】行程,时钟问题【难度】☆☆ 【答案】B【解析】小华所带的“快表”每小时快了4分钟,说明准确时间走60分钟的时候,“快表”已经走了64分钟了,这样我们就可以得到6416==6015快表标准表;现在快表走了460=240⨯分钟,那么标准表走了2401516=225⨯÷分钟;所以实际上早到了24022515-=分钟,选B .5.甲乙丙丁四个人今年的年龄之和是72岁.几年前(至少一年)甲是22岁时,乙是16岁.又知道,当甲是19岁的时候,丙的年龄是丁的3倍(此时丁至少1岁).如果甲乙丙丁四个人的年龄互不相同,那么今年甲的年龄可以有()种情况.A.4B.6C.8D.10【考点】典型应用题中年龄问题【难度】☆☆【答案】B【解析】甲乙的年龄差是22166-=岁;当甲19岁时,13岁;至少一年前甲22岁,所以当甲19岁的时候,此时至少是4年前的年龄,那么甲今年至少是23岁;甲19岁时,丙的年龄是丁的3倍,假设丁为1岁,丙为3岁,此时四人的年龄和至少是19+13+1+3=36岁;且甲今年的年龄至多为()19+7236428-÷=岁;所以甲今年的年龄可能是23,24,25,26,27,28;共6种,所以选B.6.有七张卡片,每张卡片上写有一个数字,这七张卡片摆成一排,就组成了七位数2014315.将这七张卡片全部分给甲、乙、丙、丁四人,每人至多分2张.他们各说了一句话:甲:“如果交换我卡片上的2个数字在七位数中的位置,那么新的七位数就是8的倍数”乙:“如果交换我卡片上的2个数字在七位数中的位置,那么新的七位数仍不是9的倍数”丙:“如果交换我卡片上的2个数字在七位数中的位置,那么新的七位数就是10的倍数”丁:“如果交换我卡片上的2个数字在七位数中的位置,那么新的七位数就是11的倍数”已知四人中恰有一个人说了谎,那么说谎的人是().A.甲B.乙C.丙D.丁【考点】组合中的逻辑推理,数论中的整除问题【难度】☆☆☆【答案】C【解析】可以直接判断乙必定说的是真话,可以直接判断乙必定是说真话的,乙中的数字不管怎么变换都不可能是9的倍数因为七位数的数字之和为2+0+1+4+3+1+5=16,不是9的倍数;如果丙说真话,那么他手中的数字是0和5,可以实现对调位置后被10整除;如果甲说真话,那么他手中的数字只能是5和2,可以实现对调位置后被8 整除;如果丁说真话,那么他手中的数字只能是0和3,这样才能使得奇数位数字之和减去偶数位数字之和的差是11的倍数(2314015,(5012)(143)0+++-++=).综上,如果丙说真话,那甲和丁都是说谎话的人,两个人说谎话,不符合题意,所以说谎话的人是丙,选C.7.算式33111324443100719(12345)522÷+÷+⨯÷++++⨯-的计算结果是______.【考点】计算,繁分数计算【难度】☆☆☆【答案】4【解析】33111324443100719(12345)522÷+÷+⨯÷++++⨯- 74413143931007752219⨯+⨯+=⨯⨯- 741133310071953++=⨯⨯1213=⨯4=8.海滩上有一堆栗子,这是四只猴子的财产,它们想要平均分配.第一只猴子来了,它左等右等别的猴子都不来,便把栗子分成四堆,每堆一样多,还剩下一个,它把剩下的一个顺手扔到海里,自己拿走了四堆中的一堆.第二只猴子来了,它也没有等别的猴子,于是它把剩下的栗子等分成四堆,还剩下一个,它又扔掉一个,自己拿走一堆.第三只猴子也是如此,等分成四堆后,把剩下的一个扔掉,自己拿走一堆;而最后一只猴子来,也将剩下的栗子等分成了四堆后,扔掉多余的一个,取走一堆.那么这堆栗子原来至少有______个. 【考点】应用题,还原问题 【难度】☆☆☆ 【答案】253 【解析】有:()333{[11]1}4k 1444x ---=+,,x k 均为自然数;化简得:25617527k x +=,变形可得243162131327k k x +++=;经计算26k =,此时x 最小;所以2562617525327x ⨯+==.9.甲、乙二人同时从A 地出发匀速走向B 地,与此同时丙从B 地出发匀速走向A 地.出发后20分钟甲与丙相遇,相遇后甲立即调头;甲调头后10分钟与乙相遇,然后甲再次调头走向B 地.结果当甲走到B 地时,乙恰走过A 、B 两地中点105米,而丙离A 地还有315米.甲的速度是乙的速度的________倍,A 、B 两地间的路程是________米. 【考点】行程,多人相遇【难度】☆☆☆ 【答案】3,1890【解析】假设全程为s ,甲乙的速度关系已经得知,现在我们从甲丙的路程关系中入手;从乙开始到最后共走了11052s +米,那么甲就共走了13310531522s s ⎛⎫⨯+=+ ⎪⎝⎭米;丙共走了315s -;又知道甲丙相遇之时甲所走的路程正好是3131531522s s s +-=+米;此时丙走1131531522s s s ⎛⎫-+=- ⎪⎝⎭;说明从甲丙相遇后到甲走到B 地,丙恰好走了一半的路程,即()1131531522s s s ⎛⎫---= ⎪⎝⎭;这段时间乙共走的路程为:11111053152323s s s ⎛⎫+-⨯+= ⎪⎝⎭;所以乙丙的速度比是11:2:332s s =,所以甲乙丙速度比是6:2:3;全程113151189023s ⎛⎫=÷--= ⎪⎝⎭米.10.从1,2,3,…,2014中取出315个不同的数(不计顺序)组成等差数列,其中组成的等差数列中包含1的有________种取法;总共有________种取法. 【考点】数论计数 【难度】☆☆☆☆ 【答案】6,5490【解析】要形成等差数列,那么315个数中有314个公差,公差最小是1;公差最大是6,因为31461884201431472205⨯=<<⨯=;含有1的只有6种;公差为1的有:()201431511700--=种;公差为2的有:()20142314111386-⨯++=种; 公差为3的有:()20143314111072-⨯++=种; 公差为4的有:()2014431411758-⨯++=种; 公差为5的有:()2014531411444-⨯++=种; 公差为6的有:()2014631411130-⨯++=种; 共有1700138610727584441305490+++++=种.131315米A。
2019华杯赛决赛小学高年级组试题A答案详解

第十九届华罗庚金杯少年数学邀请赛决赛试题A (小学高年级组)一、填空题(每小题 10 分, 共80 分)1. 如右图, 边长为12米的正方形池塘的周围是草地, 池塘边A , B , C , D 处各有一根木桩, 且AB =BC =CD =3米. 现用长4米的绳子将一头羊拴在其中的某根木桩上. 为了使羊在草地上活动区域的面积最大, 应将绳子拴在 处的木桩上. 【考点】圆与扇形 【答案】B【解析】拴在B 处活动区域最大,为43圆。
2. 在所有是20的倍数的正整数中, 不超过2019并且是14的倍数的数之和是 . 【考点】最小公倍数,等差数列 【答案】14700【解析】[]14014,20=,141402014=⎥⎦⎤⎢⎣⎡,()1470014321140=+++⨯Λ.3. 从1~8这八个自然数中任取三个数, 其中没有连续自然数的取法有 种. 【考点】计数 【答案】20【解析】解法一:枚举法(1)三奇数:135、137、157、357,4个; (2)三偶数:246、248、268、468,4个;(3)两奇一偶:136、138、158、147、358、257,6个; (4)两偶一奇:247、258、146、148、168、368,6个; 共4+4+6+6=20种.解法二:排除法1~8中任取三个数,有5638 C 种不同的取法其中三个连续数有6种(123~678)两个连续数有5+4+4+4+4+4+5=30种(如124、125、126、127、128等) 则满足题意的取法有56—6—30=20种.4. 如右图所示, 网格中每个小正方格的面积都为1平方厘米. 小明在网格纸上画了一匹红鬃烈马的剪影(马的轮廓由小线段组成, 小线段的端点在格子点上或在格线上), 则这个剪影的面积为 平方厘米.【考点】格点与面积 【答案】56.5【解析】如图(见下页),通过分割和格点面积公式可得小马总面积为56.5个正方形,即面积为56.5平方厘米。
第二十二届“华杯赛”决赛小高组试题A详细解答

第二十二届华罗庚金杯少年数学邀请赛决赛试题A(小学高年级组)详细解答【解】:∵201711=183+411∴[201711×3] = [183×3+411×3]= 183×3+1类似地,可知:[201711×4]= 183×4+1;[201711×5]= 183×5+1[201711×6]= 183×6+2;[201711×7]= 183×7+2;[201711×8]= 183×8+2∴原式= 183×[3+4+5+6+7+8]+1+1+1+2+2+2=6048【答】:所求值为6048。
【解】:假设原来四个整数分别为a,b,c,d,则按照题意所求的四个数的表达式分别为:a+b+c3+d,a+b+d3+ca+c+d3+b,b+c+d3+a∵a+b+c3+d+a+b+d3+c+a+c+d3+b+b+c+d3+a=3(a+b+c+d)3+(a+b+c+d)=2(a+b+c+d)∴a+b+c+d=12×(8+12+1023+913)=12×(20+20) =20【答】:原来给定的4个整数的和为20。
【解】:分三种情形,共有10种不同摆法,如下图:(1)两个点都在第一行;(2)两个点不在同一行但相邻;(3)两个点不在同一行且不相邻;【答】:共有10种不同的摆放方法。
【解】:设甲的速度为V甲,乙的速度为V乙,AB两地距离为SAB,BC两地距离为SBC 根据题意可知:V甲=80÷2=40 (千米/小时) ,甲原来的速度的2倍为80(千米/小时) 所以,BC两地距离:SBC=2×80=160 (千米)又,乙从B地到C地花了2.5小时,所以,乙的速度为:V乙=SBC÷2.5=160÷2.5=64(千米/小时)【答】:乙的速度为64 千米/小时。
第20届小学数学华杯赛决赛A卷试题

第二十届华罗庚金杯少年数学邀请赛决赛试题A (小学高年级组)(时间: 2015年4月11日10:00~11:30)一、填空题(每小题 10分, 共80分)1、计算:84419×1.375+105519×0.92、下图是用六个正方形,六个三角形、一个正六边形组成的图案,正方形边长都是2cm ,这个图案的周长是____cm 。
3、某项工程需要100天完成,开始由10个人用30天完成了全部工程的15,随后再增加10个人来完成这项工程,那么能提前____天完成任务。
4、王教授早上8点到达车站候车,登上列车时,站台上的时钟的时针和分针恰好左右对称。
列车8点35分出发,下午2点15分到达终点站。
当王教授走下列车时,站台上时钟的时针和分针恰好上下对称,走出车站时恰好3点整。
那么王教授在列车上的时间共计____分钟。
5、由四个非零数字组成的没有重复数字的所有四位数的和为73326, 则这些四位数中最大的是____, 最小的是____。
6、如右图所示, 从长、宽、高分别为15 cm, 5 cm, 4 cm 的长方体中切割走一块长、宽、高分别为ycm, 5cm, xcm 的长方体(x, y 为整数), 余下部分的体积为120 cm³, 那么x 为 ___cm, y 为____cm7、一次数学竞赛有A, B, C三题, 参赛的39个人中, 每人至少答对了一道题. 在答对A的人中, 只答对A的比还答对其它题目的多5人; 在没答对A的人中, 答对B的是答对C的2倍; 又知道只答对A的等于只答对B的与只答对C的人数之和. 那么答对A的最多有___人。
8、甲,乙进行乒乓球比赛, 三局两胜制. 每局比赛中, 先得11 分且对方少于10分者胜; 10平多得2 分者胜. 甲、乙二人得分总和都是30分, 在不计比分先后顺序时, 三局的比分共有__种情况。
二、解答下列各题(每小题10分, 共40分, 要求写出简要过程)9、两个自然数之和为667, 它们的最小公倍数除以最大公约数所得的商等于120. 求这两个数.10、酒店有100个标准间, 房价为400元/天, 但入住率只有50%. 若每降低20元的房价, 则能增加5间入住. 求合适的房价, 使酒店收到的房费最高.11、如图, 长方形ABCD的面积是56 cm².BE=3cm, DF=2cm. 请你回答:三角形AEF的面积是多少?12、当N取遍1, 2, 3 ,… , 2015中所有的数时, 形如3ᴺ+N³的数中能够被7整除的有多少个?三、解答下列各题(每小题 15分, 共30分, 要求写出详细过程)13、在右图中, ABCD是平行四边形, AM = MB, DN=CN, BE=EF=FC, 四边形EFGH的面积是1, 求平行四边形ABCD的面积。
2014华杯赛试题及答案

2014华杯赛试题及答案一、选择题1. 以下哪个国家不是2014华杯赛参赛国家?A. 中国B. 韩国C. 日本D. 巴西答案:D. 巴西2. 2014华杯赛的比赛场馆在哪个城市?A. 北京B. 上海C. 广州D. 深圳答案:C. 广州3. 以下哪个球队是2014华杯赛的冠军?A. 中国国家队B. 日本国家队C. 韩国国家队D. 巴西国家队答案:A. 中国国家队4. 2014华杯赛共进行了多少场比赛?A. 8场B. 10场C. 12场D. 14场答案:C. 12场5. 谁是2014华杯赛的最佳球员?A. 张三B. 李四C. 王五D. 赵六答案:B. 李四二、填空题1. 2014华杯赛的主办国是()。
答案:中国2. 2014华杯赛的举办时间是()年。
答案:20143. 2014华杯赛的比赛形式是()。
答案:足球比赛4. 2014华杯赛的冠军是()。
答案:中国国家队5. 2014华杯赛的最佳球员是()。
答案:李四三、简答题1. 请简述2014华杯赛的比赛规则。
答案:2014华杯赛的比赛规则与普通足球比赛规则相同,两队各派出11名球员上场进行比赛,比赛时间为两个45分钟的半场和一个15分钟的中场休息时间。
比赛期间,球员需要遵守足球规则,以球队进球数多的一方获胜。
2. 请列举2014华杯赛的参赛国家。
答案:参赛国家包括中国、韩国、日本。
3. 你对2014华杯赛的印象如何?请简述你最难忘的瞬间。
答案:我对2014华杯赛的印象非常深刻。
最难忘的瞬间是中国国家队在决赛中以2:1的比分战胜日本国家队,成功捧起冠军奖杯。
那一刻,整个球场都沸腾了,观众们激动地欢呼雀跃,这是中国足球走向更高峰的一步。
四、解答题请回答以下问题:1. 2014华杯赛的举办地点和时间是什么?答案:2014华杯赛的举办地点是广州,时间是2014年。
2. 你认为2014华杯赛对于中国足球的发展有何意义?答案:2014华杯赛对于中国足球的发展具有重要意义。
第十九届华杯赛决赛试卷_小高C

7. 用八块棱长为1cm的小正方块堆成一立体,其俯视图如右图所示,问共有种不同的堆法(经旋转能重合的算一种堆法)。
第十九届华罗庚金杯少年数学邀请赛
决赛试题C(小学高年级组)
(时间: 2014年4月12日10:00~11:30)
一、填空题(每小题10分,共80分)
1.计算: .
2. 在右边的算式中,每个汉字代表0至9这十个数字中的一个,相同汉字代表相同数字、不同汉字代表不同数字.则“ ”所代表的四位数是.
3.如右图,在直角三角形ABC中,点F在AB上且 ,四边形EBCD是平行四边形,全平方数,求此自然数.
三、解答下列各题(每小题15分,共30分,要求写出详细过程)
13. 如右图,圆周上均匀地标出十个点.将1~10这十个自然数分别放到这十个点上.用过圆心的一条直线绕圆心旋转,当线上没有标出的点时,就把1~10分成两组.对每种摆放方式,随着直线的转动有五种分组方式.对于每种分组都有一个两组数和的乘积,记五个积中最小的值为K.问所有的摆放中,K最大为多少?
8. 如右图,在三角形ABC中, , , .连接CF交DE于P点,求 的值.
二、解答下列各题(每题10分,共40分,要求写出简要过程)
9.有三个农场在一条公路边,分别在下图所示的A, B和C处. A处农场年产小麦50吨, B处农场年产小麦10吨, C处农场年产小麦60吨.要在这条公路边修建一个仓库收买这些小麦.假设运费从A到C方向是每吨每千米1.5元,从C到A方向是每吨每千米1元.问仓库应该建在何处才能使运费最低?
第十八届华杯赛·小学高年级组·武汉

【分析】 原式
2.
3.
4.
5.
【考点】勾股定理 【答案】 110 【分析】 直角边有 101 条,斜边有 9 条,一共 110 条. 【考点】计数 【答案】 B 【分析】 和是 12,有 1 种;和是 10 有 1 种;和是 8,有 2 种;和是 6 有 2 种;和是 4, 有 1 种,一共 7 种,选 B. 【考点】完全平方数 【答案】 9 【分析】 5ab 4 是完全平方数,那么这个数末位是 2 或 8,在判断首位只能是 7,验证 722 5184 满足,那么 a b 9 【考点】容斥 【答案】 140 【分析】 5,8 40 个一周期,去的时候一共标记 40 个,回来时标记 25 个,重复标记 5 个,没有被标记的一共有 200 40 25 5 140 个.
一、填空题 1. 【考点】计算 【答案】2013
2012 2013 2007 2014 2013 . 2007 2012 2014 【考点】扶梯问题 【答案】36 2 【分析】 小孩的速度: 60 90 (米/秒) ,自动扶梯的速度是: 60 60 1 (米/秒) , 3 2 需要: 60 1 36 (秒) 3 【考点】行程 【答案】 3 : 40 【分析】 骑车 A:10 分钟共走 3 千米,骑车 B:10 分钟走 40 千米,速度比等于路程 比是 3 : 40 . 【考点】比例应用题 【答案】20 5 4 【分析】 猴大:猴二:猴三= 5 : 4 : 4 45 : 20 :16 ,则猴二为 9 9 20 29 45 16 20 .
A G F E
B
D
C
11. 影院正在放映《玩具总动员》 、 《冰河世纪》 、 《怪物史莱克》 、 《齐天大圣》四部动漫电影, 票价分别为 50 元、55 元、60 元、65 元。来影院的观众至少看一场,至多看两场。因 时间关系《冰河世纪》与《怪物史莱克》不能观看,若今天必有 200 人看电影所花的钱 一样多,则影院今天至少接待观众多少人?
第14届华杯赛决赛试题A卷试题及详解
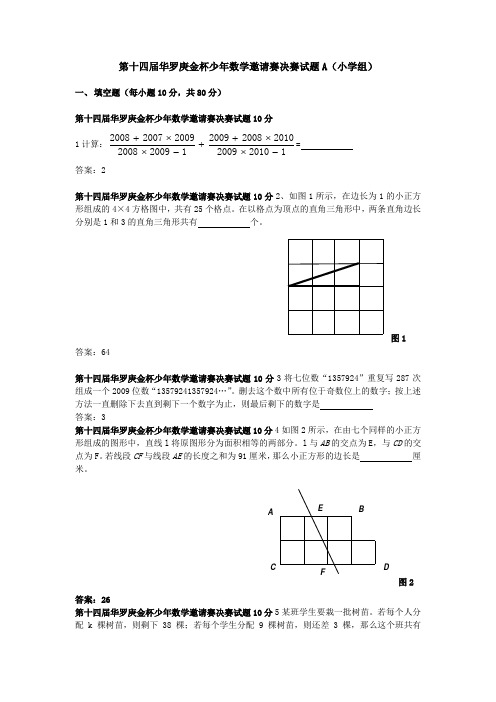
第十四届华罗庚金杯少年数学邀请赛决赛试题A (小学组)一、 填空题(每小题10分,共80分)第十四届华罗庚金杯少年数学邀请赛决赛试题10分 1计算:200820072009200920082010200820091200920101+⨯+⨯+⨯-⨯-=答案:2第十四届华罗庚金杯少年数学邀请赛决赛试题10分2、如图1所示,在边长为1的小正方形组成的4×4方格图中,共有25个格点。
在以格点为顶点的直角三角形中,两条直角边长分别是1和3的直角三角形共有 个。
图1答案:64第十四届华罗庚金杯少年数学邀请赛决赛试题10分3将七位数“1357924”重复写287次组成一个2009位数“13579241357924…”。
删去这个数中所有位于奇数位上的数字;按上述方法一直删除下去直到剩下一个数字为止,则最后剩下的数字是 答案:3第十四届华罗庚金杯少年数学邀请赛决赛试题10分4如图2所示,在由七个同样的小正方形组成的图形中,直线l 将原图形分为面积相等的两部分。
l 与AB 的交点为E ,与CD 的交点为F 。
若线段CF 与线段AE 的长度之和为91厘米,那么小正方形的边长是 厘米。
BEDFCA图2答案:26第十四届华罗庚金杯少年数学邀请赛决赛试题10分5某班学生要栽一批树苗。
若每个人分配k 棵树苗,则剩下38棵;若每个学生分配9棵树苗,则还差3棵,那么这个班共有名学生。
答案;41第十四届华罗庚金杯少年数学邀请赛决赛试题10分6已知三个合数A,B,C 两两互质,且A ×B ×C=11011×28,那么A+B+C 的最大值为答案:1626第十四届华罗庚金杯少年数学邀请赛决赛试题10分7方格中的图形符号“◇”,“○”,“▽”,“☆”代表填入方格中的数,相同的符号代表相同的数,如图3所示,若第一列,第三列,第二行,第四行的四个数的和分别是36,50,41,37,则第三行的四个数的和为图3答案:33(第14届华罗庚金杯少年数学邀请赛决赛第8题)已知1+2+3+⋯+n (n>2)的和的个位数为3,十位数为0,则n 的最小值是 【分析】 37二、解答下列各题(每题10分,共40分,要求写出简要过程) 第十四届华罗庚金杯少年数学邀请赛决赛试题10分第二大题1六个分数12,13,15,17,111,113的和在哪两个连续自然数之间?1.答案:在1和2之间。
五届华杯赛小高年级组试题及答案

2012年第十七届华杯赛小高年级组初赛试题答案第1题:176第2题:865第3题:3721第4题:3第5题:120第6题:60第7题:75第8题:2012第9题:6第10题:40442013第十八届华杯赛决赛小学高年级组试题A卷2013-04-25 14:23:54 来源:华杯赛官网2013第十八届“华杯赛”笔试决赛已经结束,全国试卷小高组分A、B、C卷外,其余组别都是分A、B卷,杭州智康1对1整理了第十八届“华杯赛”决赛所有试题及答案解析。
•2014年第十八届华罗庚金杯少年数学邀请赛初赛试卷B (小学高年级组)(时间: 2013 年3 月23 日10:00 ~ 11:00)一、选择题 (每小题 10 分, 满分60 分. 以下每题的四个选项中, 仅有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号内.)1. 一个四位数, 各位数字互不相同, 所有数字之和等于6, 并且这个数是11 的倍数, 则满足这种要求的四位数共有( )个.(A )6 (B )7 (C )8 (D )9【答案】A【解析】四个数字互不相同,且和为6,只能是0、1、2、3;又知这个四位数是11的倍数,所以奇数位的数字和和偶数位的数字和都是3,只能是0+3=1+2; 千位可能是1、2、3;确定千位后十位也随之确定。
每个对应的个位和百位有2种可能;共有6种。
2. 932232332333+⨯+⨯⨯++⨯⨯⨯⨯L L 14243个个位数字是( ). ?? ?????(A )2 (B )8 (C )4 (D )6【答案】B【解析】式子为10个数相加,这10个数的个位分别是2、6、8、4、2、6、8、4、2、6;易得和的个位是83. 在下面的阴影三角形中, 不能由右图中的阴影三角形经过旋转、平移得到的是图( )中的三角形.(A ) (B ) (C ) (D )【答案】B【解析】图中①、②、③三边应为顺时针关系,B 不合要求。
4. 某日, 甲学校买了56 千克水果糖, 每千克8.06 元. 过了几日, 乙学校也需要买同样的56 千克水果糖, 不过正好赶上促销活动, 每千克水果糖降价0.56 元, 而且只要买水果糖都会额外赠送5% 同样的水果糖. 那么乙学校将比甲学校少花( )元.(A )20 (B )51.36 (C )31.36 (D )10.36【答案】B【解析】甲花的钱是8.0656451.36⨯=元 乙花的钱是568.060.56=4001+5%-⨯()元;差是451.36-400=51.36元5. 甲、乙两仓的稻谷数量一样, 爸爸, 妈妈和阳阳单独运完一仓稻谷分别需要10 天, 12 天和15 天. 爸爸妈妈同时开始分别运甲、乙两仓的稻谷, 阳阳先帮妈妈, 后帮爸爸, 结果同时运完两仓稻谷, 那么阳阳帮妈妈运了( )天.(A )3 (B )4 (C )5 (D )6【答案】C【解析】三人的效率分别是111101215,,;共同运了2仓稻谷,需要1112++=8101215÷()天;妈妈运了1仓稻谷的812;小明帮妈妈运了412,需要5天; 6. 如图, 将长度为9 的线段AB 分成9 等份, 那么图中所有线段的长度的总和是( ).(A )132 (B )144 (C )156 (D )165【答案】D【解析】图中长度为1的线段有9条,长度为2的线段有8条,……1×9+2×8+3×7+…+9×1=165二、填空题(每小题 10 分, 满分40 分)7. 将乘积0.2430.325233⨯&&&&化为小数, 小数点后第2013 位的数字是________.【答案】9 【解析】243325233-3927879371079110.2430.325233====0.079119999999903727999991099999⨯⨯⨯⨯⨯⨯⨯⨯&&&&&& 循环节有5位,2013≡3(mod5),第2013位和第3位一样,是9.8. 一只青蛙8 点从深为12 米的井底向上爬, 它每向上爬3 米, 因为井壁打滑, 就会下滑1 米, 下滑1 米的时间是向上爬3 米所用时间的三分之一. 8 点17 分时, 青蛙第二次爬至离井口3 米之处, 那么青蛙从井底爬到井口时所花的时间为________分钟.【答案】22【解析】青蛙的运动状态如下图所示,从开始到第二次离井口3米的时间为17份,爬到井口的时间为22份。
2014华杯赛模考小学高年级试题解析

考试时间:60 分钟 一、选择题(每小题 10 分,满分 60 分,以下每题的四个选项中,仅有一个是正确的,请用 表示正确答案的英文字母作答。 ) 1、 有这样的正整数 n,使得 4n-7、9n-8 均为完全平方数。则符合要求的正整数 n 一共 有 个。 (网校兰海老师供题) (A)1 (B)2 (C)3 (D)4 【答案】A 【解析】设 4n 7 a2 ,9n 8 b2 。则 36n 63 (3a)2 , 36n 32 (2b)2 。那么
【解析】考虑到 33=3 11 ,所以 20 xy09 要满足既被 3 整除,又被 11 整除。 ①首先被 3 整除需要满足各位数字和能被 3 整除,即 2+0+x y 0 9=11+x+y 要 能被 3 整除,所以可能的情况有: x+y=1,4,7,10,13,16 。 ②然后看被 11 整除需要满足的条件,即奇数位数字之和与偶数位数字之和的差能 被 11 整 除 , 也 就 是 2+x+0, 0+y+9 的 差 能 被 11 整 除 。 首 先 看 差 等 于 0 的 情 况 ,
2
8、如图,三角形 ABC 是等腰直角三角形, D 是 BC 边的中点,已知 BC 20 厘米,那么阴 (网校张旷昊老师供题) 影部分的面积是 平方厘米。 (π 3)
A
B
D
C
【答案】 37.5 【解析】如下图所示,连结 DE,DF,△ABC 三角形内部两块阴影部分面积: 20 10 45 S1=SABC 2S白色扇形= 2 102 25 (平方厘米) 2 360 1 1 10 5 三角形外部的阴影面积 S2 = S圆 S AEDF = 52 2 12.5 (平方厘米) 2 2 2 所以总阴影面积为 37.5
2014第五届华杯赛精英赛(小中组)试卷答案

我们也可以通过这样的方式求得。所以我们只要保证正方形有最长的 2 条对角线就可以了, 而且正方形的两条对角线是相等的。与菱形平行时才等于 10,因此类似于图 1 这样放置的 对角线小于 10,所以可以知道下图 2 才是菱形中面积最大的正方形,在该图中正方形的对 角线长度是正三角形的边长,边长=10,所以面积为 50。 (杭州学而思陈世杰老师编辑)
【题型】最优方案 【答案】17,见图 6-1 【解析】要使任意 2×2 的方格中阴影方格数多于一半,且要涂的空白方格最少,则需要任 意 2×2 的方格中尽量有三个阴影方格,涂格方法不唯一。 (杭州学而思王海强老师编辑)
图 6-1 7.自然数 A 除本身以外最大的约数是 d ,自然数 A 2 除本身以外最大的约数是 d 2 ,那 么 A 的值是 . 【题型】数论中的因倍问题 【答案】7 【解析】 1.若 A 为偶数,则当 A+2 时,除本身以外最大的约数是 d+1,这与题目中的 d+2 不符合。故 A 为奇数。 2.若 A 为合数,由 1 分析可得 A 同时为奇数,所以设 A 2n1 1 ,其中 n1 为大于 1 的自然 数。由于 A 为奇数,所以除本身外最大的因数 d 也是奇数,同理可设 d 2n2 1 , n2 为大 于等于 0 的自然数。则 A 可以分解成如下算式:
第五届两岸四地华罗庚金杯少年数学精英邀请赛 笔试一试卷(小学高年级组)
(2014 年 7 月 23 日,60 分钟) 一、填空题Ⅰ(每题 8 分,共 32 分) 1.算式
(1 3 5 7 9) (10 12 14 16 18) 的计算结果是 (5 6 7 8 9)2
10
10
图 1.
图 2.
2014年国奥赛和华赛决赛试题

2014年国奥赛和华赛决赛试题2014年国奥赛决赛试题姓名: ________ 成绩: —+ — + — + -- =2 4 8 163、五个分数討磊、算罟中'第三大的分数是——4、如图,椒3,则阴影部分的面积是______________ 。
5、将数字1、2、3、4、5、6分别填入下列算式中的六个□中,使算式成立(此题有多个解,填入一个即可。
)□ X (7—□) -r□ —□+□=□6. 由棱长为1厘米的若干个立方体堆成一个长.宽、高分别11. 9. 7 (厘米)的长方体,将它的表面全部涂上红色,然后将只有一面是红色的立方体取出, 再将取出的立方体堆成一个长.宽.高都不同的实心长方体,那么这个新的长方体的表面积的最大值是___________________________ O7. 矿泉水.果汁.豆奶三种饮料共计180瓶,第一种取法是以瓶为单位刚好可以从中取出矿泉水瓶数的果汁瓶数的豆奶瓶数的土,共计取出60 瓶;第二种取法是以瓶为单位刚好可以从中取出矿泉水瓶数的丄,果汁瓶数4的;,豆奶瓶数的I,共计取出70瓶。
那么,这180瓶饮料中,果汁有3 2瓶。
8. 甲组10人和乙组9人一起去看电影,这两组人中有14人各带了一包花生米入场与本组的人共同食用,看完电影后发现,这两组总的消费(电影票钱和花生米钱之和)相同。
如果电影票每张18元,花生米每包的价格以元为单位也是整数,―那么,花生米每包的价格是7G©9、语文书和数学书共有88本,分给甲、乙两班使用,甲班得到的书中有彳是数学书,乙班得到的书中有#是语文书。
那么,语文书共有 _________________ 本。
10. 一套机器由主机、马达.机座三个套件组装而成。
车间一天可以生产2件主机.5件马达和7个机座,生产一件主机的时间可生产3件马达或5件机座。
那么生产380套机器,需时____________________________ 天。
2014年第19届华杯赛高年级组决赛A卷详解

【答案】15 【分析】如左下图,用 a、b、 c、d、 e、 f、 g 记所填的自然数, 并设这个和为 S, 则
3S (a b d e) (b c d f ) (e d f g ) 2 (a b c d e f g ) (d a c g ) 42 (6 0 1 2) 45.
8 7 6 56 种. 所以没有连续 3 2 1
4.
如右图所示, 网格中每个小正方格的面积都为 1 平方厘米. 小明在网格纸上画了一匹红鬃烈马的剪 影(马的轮廓由小线段组成 , 小线段的端点在格子点上或在格线上) , 则这个剪影的面积为 平方厘米.
【答案】56.5 【分析】见右图, 可将马的剪影分成七部分:阴影部分①, 面积为 31 平方厘米; 马头部分②, 面积为 6.5 平方厘米; 马肚部分④, 面积为 4 平方厘米; 马尾⑥, 面积为 1 平方厘米; 马后身③, 面积为 6.5 平方厘米; 马后腿⑤, 面积为 3 平方厘米; 马前腿⑦, 面积为 4.5 平方厘米.
6 20 1 v0 : v1 1: 1 5 : 6 , (t0 1) : t1 6 : 5 ,所以 t0 1 3 (小时). 60 5
30 4 72 1 2 小时 类似地, v0 : v2 1: 1 3 : 4 , t0 : t2 4 : 3 .所以后部分按原速走需用时 60 v0 3
14. 在右边的算式中,字母 a,b,c,d 和“□”代表十个数字 0 到 9 中的一个. 其中 a, b,c,d 四个 字母代表不同的数字,求 a,b,c,d 代表的数字之和.
a 4 6 c b d
+
□ □ □ □ □ □ □ 2
第十九届华杯赛决赛解答_小高C

第十九届华罗庚金杯少年数学邀请赛决赛试题C (小学高年级组)(时间: 2014 年4月12日)一、填空题 (每小题10分, 共80分)1. 计算: =-⨯++⨯-5213.23.0241225.095.22.3 . 【答案】1【解答】132319.06.075.025.0=+=+=原式 2. 在右边的算式中, 每个汉字代表0至9这十个数字中的一个, 相同汉字代表相同数字、不同汉字代表不同数字. 求“ 数学竞赛”所代表的四位数.【答案】1962【解答】由算式可得:4202赛竞赛竞学数+. 因为“赛”+“赛”和的个位数为4, 所以“赛”表示的数为2或7.若“赛”表示的数字为7, 则“竞”+“竞”和的个位数为1, 显然不存在满足这样的数.所以“赛”表示的数为2, “竞”+“竞”和的个位数为2, 所以“竞”表示的数字为1或6.若“竞”表示数字1, 则“学”表示的数字为0, “数”表示的数字为2; 此时, 2012=数学竞赛,但数和赛不能表示同一个数字,舍去; 若“竞”表示的数字为6, 则“学”表示的数字为9, “数”数字为1, 此时, 1962=数学竞赛.·· 3. 如右图, 在直角三角形ABC 中, 点F 在AB 上且FB AF 2=, 四边形EBCD 是平行四边形, 那么EF FD :为 .【答案】2:1【解答】连接FC , BD , 设kEF FD =, S S BFE =∆, 那么kS S BDF =∆,S k S S FBC BCD )1(+==∆∆. 由FB AF 2=可知kS S AFD 2=∆, 进而S k S A B C )41(+=∆, 得kk S S AFD ABC 2)41(+=∆∆. 又kk S S S BC FB S BC AB S S AFD FBC AFD AFD AFD ABC 2)1(33232+==⨯=⨯=∆∆∆∆∆∆, 所以)1(341k k +=+.解得, 2=k . 因此, EF FD 2=.4. 右图是由若干块长12厘米、宽4厘米、高2厘米的积木搭成的立体的正视图, 上面标出了若干个点. 一只蚂蚁从立体的左侧地面经过所标出的点爬到右侧的地面. 如果蚂蚁向上爬行的速度为每秒2厘米, 向下爬行的速度为每秒3厘米, 水平爬行的速度为每秒4厘米, 则蚂蚁至少爬行了________秒.【答案】40【解答】蚂蚁要从立体的左侧地面经所标出的点爬到右侧的地面, 向上至少爬行6212236⨯+⨯=厘米, 需要18秒钟, 向下至少爬行36厘米, 需要12秒钟, 平行爬行40122422=⨯+⨯⨯厘米, 需要10秒钟. 因此至少需要40秒钟.5. 设a , b , c , d , e 均是自然数, 并且e d c b a <<<<, 3005432=++++e d c b a , 则b a +的最大值为________.【答案】35【解答】因为 e d c b a <<<<, 所以b b a 2<+, 并且.32)(21532)(7267)1(62614)3(5)2(4)1(325432300++>+++=+++++≥++=+++++++≥++++=b a b b a b b a a b a b b b b a e d c b a 由此得到151135+<+b a . 所以b a +最大不能超过35. 另一方面, 令 22,20,19,18,17=====e d c b a , 则35=+b a 且满足3005432=++++e d c b a .最终得到, b a +的最大值为35.6. 现有甲、乙、丙三个容量相同的水池. 一台A 型水泵单独向甲水池注水, 一台B 型水泵单独向乙水池注水, 一台A 型和一台B 型水泵一起向丙水池注水. 已知注满乙水池比注满丙水池所需时间多4个小时, 注满甲水池比注满乙水池所需时间多5个小时, 则注满丙水池的三分之二需要________个小时.【答案】4【解答】A 型和B 型水泵一起向丙水池注水, 设注满水池需要t 小时, 则注满乙和甲水池需要的时间分别是 )4(+t 个小时和 )9(+t 个小时. 可列出方程:14191=⨯⎪⎭⎫ ⎝⎛+++t t t , 解得6=t , 4326=⨯. 7. 用八块棱长为1 cm 的小正方块堆成一立体, 其俯视图如右图所示, 问共有多少种不同的堆法(经旋转能重合的算一种堆法)?【答案】10【解答】底层已用了四块小方体, 考虑第二层分别有一、二、三、四块的情况. 见下图, 第二层有一块, 只有1种堆法; 第二层有两块, 有5种堆法; 第二层有三块, 有3种堆法; 第二层有四块, 只有1种堆法,总计有10种堆法.8. 如右图, 在三角形ABC 中, BF AF 2=, AE CE 3=, BD CD 4=. 连接CF 交DE 于P 点, 求DPEP 的值. 【答案】815 【解答】如右图所示, 设x SBDF =∆. 因为BD CD 4=, 所以x S FDC 4=∆,x S CFB 5=∆.因为BF AF 2=, 所以2==∆∆BF AF S S CFB CAF , 得x S CAF 10=∆. 因为31==∆∆CE AE S S EFC AFE , 所以x S EFC 215=∆. 因为DPPE S S S S CPD CEP DPF EFP ==∆∆∆∆, 所以815==∆∆FDC EFC S S DP PE . 9. 答案:A 处(1)讨论变化趋势,比较A 、B 两点设仓库可知A →B 运费越来越高,而B →A 则运费越来越低,同理可知C →B 运费越来越低,而B →C 则运费越来越高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十九届华罗庚金杯少年数学邀请赛
决赛试题A (小学高年级组)
一、填空题(每小题 10 分, 共80 分)
1. 如右图, 边长为12米的正方形池塘的周围是草地, 池塘边A , B , C , D 处各有一根木桩, 且AB =BC =CD =3米. 现用长4米的绳子将一头羊拴在其中的某根木桩上. 为了使羊在草地上活动区域的面积最大, 应将绳子拴在 处的木桩上. 【考点】圆和扇形 【答案】B
【分析】拴在B 处活动区域最大,为
4
3
圆。
2. 在所有是20的倍数的正整数中, 不超过2014并且是14的倍数的数之和是 . 【考点】最小公倍数,等差数列 【答案】14700
【分析】[]14014,20=,141402014=⎥⎦
⎤
⎢⎣⎡,()1470014321140=+++⨯Λ. 3. 从1~8这八个自然数中任取三个数, 其中没有连续自然数的取法有 种. 【考点】计数 【答案】20
【分析】解法一:枚举法
(1)三奇数:135、137、157、357,4个; (2)三偶数:246、248、268、468,4个;
(3)两奇一偶:136、138、158、147、358、257,6个; (4)两偶一奇:247、258、146、148、168、368,6个; 共4+4+6+6=20种. 解法二:排除法
1~8中任取三个数,有5638=C 种不同的取法
其中三个连续数有6种(123~678)
两个连续数有5+4+4+4+4+4+5=30种(如124、125、126、127、128等) 则满足题意的取法有56—6—30=20种.
4. 如右图所示, 网格中每个小正方格的面积都为1平方厘米. 小明在网格纸上画了一匹红鬃烈马的剪影(马的轮廓由小线段组成, 小线段的端点在格子点上或在格线上), 则这个剪影的面积为平方厘米.
【考点】格点和面积
【答案】56.5
【分析】如图(见下页),通过分割和格点面积公式可得小马总面积为56.5个正方形,即面积为56.5平方厘米。
2.5 0.5
3
12
1.5
1
16
4
3
2
0.5
3
0.5
2
1
1.5
边上点数÷2+内部点数—1 =4÷2+1—1=2
黑线圈中部分的面积也可用长方形(蓝框)减去两个三角形
5. 如果成立, 则“○”和“□”中可以填入的非零自然数之和最大为 .
【考点】最值,分数比较大小 【答案】77
【分析】
547<□,通分,将分母统一为□×5,54535⨯⨯<⨯□□□,□≥9 □○711<,通分能得到□□□○⨯<⨯⨯117711,○×□<77 乘积最大为76,要使和最大,应两数相差最多
76=1×76,当○=1,□=76时,两数之和最大,为1+76=77.
6. 如右图, 三个圆交出七个部分. 将整数0~6分别填到七个部分中, 使得每个圆内的四个数字的和都相等, 那么和的最大值是 . 【考点】数阵图,最值 【答案】15
【分析】要使圆内四个数字的和最大,则中间同时属于三个圆的区域填6, 同时属于两个圆的区域依次填入5、4、3 最后填入0、1、2即可,如下图。
7. 学校组织1511人去郊游, 租用42座大巴和25座中巴两种汽车. 如果要求恰好每人一座且每座一人, 则有 种租车方案. 【考点】不定方程
6 5 4 1 0
3 2
【答案】2
【分析】设大巴a辆,中巴b辆
根据题意列不定方程42a+25b=1511
1511÷25…11,则42a÷25…11,42a个位为6,经试验当a=8时,b=47
当a=8+25=33时,b=5,共2组整数解。
8. 平面上的五个点A, B, C, D , E 满足: AB = 8厘米, BC = 4厘米, AD = 5厘米, DE = 1厘米, AC = 12厘米, AE = 6厘米. 如果三角形EAB的面积为24平方厘米, 则点 A 到CD 的距离等于厘米
【考点】勾股定理
【答案】
13
60
【分析】(1)由题意AB = 8厘米, BC = 4厘米,AC = 12厘米,可知点A、B、C在同一条直线上;
(2)AD = 5厘米, DE = 1厘米, AE = 6厘米,可知点A、D、E在同一条直线上;
(3)三角形EAB的面积为24平方厘米,24
2
1
=
⨯
⨯AE
AB,可知AB和AE垂直。
画出下图
(4)问题转化为求直角三角形ACD斜边CD上的高,即AF的长度
2
2
2CD
AC
AB=
+,得出CD=13
2
1
2
1
⨯
⨯
=
⨯
⨯AF
CD
AD
AC,解得AF=
13
60
.
二、解答下列各题(每题10 分, 共40 分, 要求写出简要过程)
9. 把n 个相同的正方形纸片无重叠地放置在桌面上, 拼成至少两层的多层长方形(含正方形)组成的图形, 并且每一个上层正方形纸片要有两个顶点各自在某个下层的正方形纸片一边的中点上. 下图给出了n =6时所有的不同放置方法, 那么n =9时有多少种不同放置方法?
【考点】操作,计数
【答案】25
A B
D
C
F
E
【分析】当层数为2时:
(1)8+1:7种;(2)7+2:5种;(3)6+3:3种;(4) 5+4:1种; 当层数为3时:
(1)6+2+1:4种;(2)5+3+1:4种;(3)4+3+2:1种; 层数为4时无法满足,
因此共有7+5+3+1+4+4+1=25种不同的放置方法。
10. 有一杯子装满了浓度为16%的盐水. 有大、中、小铁球各一个, 它们的体积比为10:4:3. 首先将小球沉入盐水杯中, 结果盐水溢出 10%, 取出小球; 其次把中球沉入盐水杯中, 又将它取出; 接着将大球沉入盐水杯中后取出; 最后在杯中倒入纯水至杯满为止. 此时杯中盐水的浓度是多少?(保留一位小数) 【考点】浓度,比例 【答案】10.7%
【分析】大、中、小球体积比为10:4:3,盐水的10%对应小球“3份”体积, 则大球“10份”体积对应盐水的3
1
103%10=
⨯÷, 因此最终溢出的盐水量为杯子容积的31
,
此时杯中盐水的浓度为%7.10131-1%16≈÷⎪⎭
⎫
⎝⎛⨯.
11. 清明节, 同学们乘车去烈士陵园扫墓. 如果汽车行驶1个小时后, 将车速提高五分之一, 就可以比预定时间提前20分钟赶到; 如果该车先按原速行驶72千米, 再将速度提高三分之一, 就可以比预定时间提前30 分钟赶到. 那么从学校到烈士陵园有多少千米? 【考点】行程 【答案】216千米 【分析】比例法
(1)原速:后速=5:6 原时:后时=6:5
原时=6×20=120分=2小时,总时间为2+1=3小时; (2)原速:后速=3:4 原时:后时=4:3
原时=4×30=120分=2小时,按原速行驶72千米所用时间为3—1=1小时; 从学校到烈士陵园有72÷1×3=216千米.
12. 如右图, 在三角形 ABC 中, D 为 BC 的中点, AF =2BF , CE =3AE . 连接CF 交DE 于P 点, 求DP
EP
的值. 【考点】几何 【答案】3
【分析】连接EF ,DF
36
121312132432143
==⨯⨯===
∆∆∆∆BCF ACF
CDF
CEF
S S S S DP EP
三、解答下列各题(每小题 15 分,共30 分,要求写出详细过程)
13. 从连续自然数1, 2, 3, …, 2014中取出n 个数, 使这n 个数满足: 任意取其中两个数, 不会有一个数是另一个数的5倍. 试求n 的最大值, 并说明理由. 【考点】构造,最值 【答案】1679 【分析】尽可能多取数
(1)2014÷5=402……4,从2014取到403,有2014—402=1612个数; (2)402÷5=80……2,402到81不取;
(3)80÷5=16,从80取到17,有80—16=64个数; (4)16÷5=3……1,16到4不取; (5)最后取3、2、1; n =1612+64+3=1679.
14. 在右边的算式中, 字母a, b, c, d 和“□”代表十个数字0到9中的一个. 其中a, b, c, d 四个字母代表不同的数字, 求a, b, c, d 代表的数字之和. 【考点】数字谜 【答案】10,18,19 【分析】如下图
a=5
(1)当c=3时,b+d进位,取b+d=10或b+d=11
则a+b+c+d=5+3+10=18或a+b+c+d=5+3+11=19
(2)当c=4时,b+d不进位,只能取b+d=1,0+1=1符合要求此时a+b+c+d=5+4+1+0=10.。
