上海中考数学二模23题合集
2024年上海市中考数学徐汇区二模卷和参考答案

2023学年第二学期徐汇区学习能力诊断卷初三数学 试卷 2024.4(时间100分钟 满分150分)考生注意∶1.本试卷含三个大题,共25题;答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题(本大题共6题,每题4分,满分24分) 【下列各题的四个选项中,有且只有一个选项是正确的】 1.下列实数中,有理数是(A )3; (B )4; (C )5; (D )6. 2.下列单项式中,与单项式322b a 是同类项的是(A )4ab −; (B )232b a ; (C )233a b ; (D )c b a 222−. 3.已知一次函数b kx y +=的图像经过第一、二、四象限,那么直线k bx y +=经过 (A )第二、三、四象限; (B )第一、二、三象限; (C )第一、二、四象限; (D )第一、三、四象限.4.如表1,记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差.根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择 (A )甲; (B )乙; (C )丙; (D )丁. 5.如图,□ABCD 的对角线AC 、BD 相交于点O ,如果添加一个条件使得□ABCD 是矩形,那么下列添加的条件中正确的是 (A )︒=∠+∠90ADO DAO ; (B )ACD DAC ∠=∠; (C )BAC DAC ∠=∠; (D )ABC DAB ∠=∠. 6.如图,一个半径为cm 9的定滑轮由绳索带动重物上升,如果该定滑轮逆时针旋转了︒120,假设绳索(粗细不计)与滑轮之间没有滑动,那么重物上升的高度是 (A )π5 cm ; (B )π6 cm ; (C )π7cm ; (D )π8cm .表1 甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差统计表BOACD(第5题图)(第6题图)二、填空题(本大题共12题,每题4分,满分48分) 7.方程012=−−x x 的根是___▲___. 8.不等式组⎩⎨⎧>−−>−1)3(23,312x x x 的解集是___▲___.9.方程组⎩⎨⎧=−=+02,522y x y x 的解是____▲____.10.关于x 的一元二次方程012=−−mx x 根的情况是:原方程__▲___实数根.11.如果二次函数1422+−=x x y 的图像的一部分是上升的,那么x 的取值范围是▲_.12.如果反比例函数xy 4−=的图像经过点)2,(t t A −,那么t 的值是____▲_____. 13.如果从长度分别为2、4、6、7的四条线段中任意取出三条,那么取出的三条线段能构成三角形的概率是__▲__.14.小杰沿着坡比4.2:1=i 的斜坡,从坡底向上步行了130米,那么他上升的高度是▲米. 15.某校为了了解学生家长对孩子用手机的态度问题,随机抽取了100名家长进行问卷调查, 每位学生家长只有一份问卷,且每份问卷仅表明一种态度(这100名家长的问卷真实有效),将这100份问卷进行回收整理后,绘制了如图1、图2所示的两幅不完整的统计图.如果该校共有2000名学生,那么可以估计该校对手机持“严格管理”态度的家长有__▲__人.16.如图,梯形ABCD 中,AD BC //,CD AB =,AC 平分BAD ∠,如果AB AD 2=,a AB=,b AD =,那么AC 是_▲_(用向量a 、b 表示). 17.如图,在ABC ∆中,6==AC AB ,4=BC . 已知点D 是边AC 的中点,将ABC ∆沿直线BD 翻折,点C 落在点E 处,联结AE ,那么AE 的长是_▲__. 18.如图,点A 是函数)0(8<−=x x y 图像上一点,联结OA 交函数)0(1<−=x xy 图像于 点B ,点C 是x 轴负半轴上一点,且AO AC =,联结BC ,那么ABC ∆的面积是_▲_.(第16题图)D AB C(第17题图)AB C (第15题图1)不管询问 管理(第15题图2) 25℅ 从来 不管 严格 管理稍加 询问三、(本大题共7题,第19—22题每题10分;第23、24题每题12分;第25题14分;满分78分) 19.(本题满分10分)计算:212218−+−−π.20.(本题满分10分)解方程:21416222+=−−−+x x x x . 21.(本题满分10分)如图,⊙1O 和⊙2O 相交于点A 、B ,联结AB 、21O O 、2AO ,已知48=AB ,5021=O O ,302=AO .(1)求⊙1O 的半径长;(2)试判断以21O O 为直径的⊙P 是否经过点B ,并说明理由. 22.(本题满分10分)A 市“第××届中学生运动会”期间,甲校租用两辆小汽车(设每辆车的速度相同)同时出发送8名学生到比赛场地参加运动会,每辆小汽车限坐4人(不包括司机),其中一辆小汽车在距离比赛场地15千米的地方出现故障,此时离截止进场的时刻还有42分钟,这时唯一可利用的交通工具是另一辆小汽车.已知这辆车的平均速度是每小时60千米,人步行的平均速度是每小时5千米(上、下车时间忽略不计).(1)如果该小汽车先送4名学生到达比赛场地,然后再回到出故障处接其他学生,请你判断他们能否在截止进场的时刻前到达?并说明理由;(2)试设计一种运送方案,使所有参赛学生能在截止进场的时刻前到达比赛场地,并说明方案可行性的理由. 23.(本题满分12分) 如图,在菱形ABCD 中,点E 、G 、H 、F 分别在边AB 、BC 、CD 、DA 上,AF AE =,CH CG =,AE CG ≠. (1)求证:GH EF //; (2)分别联结EG 、FH ,求证:四边形EGHF 是等腰梯形.(第23题图)E A B C DFGH (第21题图)AB1O 2O24.(本题满分12分)如图,在平面直角坐标系xOy 中,抛物线)0(442>+−=a ax ax y 与x 轴交于点)0,1(A 和点B ,与y 轴交于点C .(1)求该抛物线的表达式及点B 的坐标;(2)已知点),0(m M ,联结BC ,过点M 作BC MG ⊥,垂足为G ,点D 是x 轴上的动点,分别联结GD 、MD ,以GD 、MD 为边作平行四边形GDMN .① 当23=m 时,且□GDMN 的顶点N 正好落在y 轴上,求点D 的坐标; ② 当0≥m 时,且点D 在运动过程中存在唯一的位置,使得□GDMN 是矩形,求m 的值.25.(本题满分14分)如图,在扇形OAB 中, 26==OB OA ,︒=∠90AOB ,点C 、D 是弧AB 上的动点(点C 在点D 的上方,点C 不与点A 重合,点D 不与点B 重合),且︒=∠45COD . (1)①请直接写出弧AC 、弧CD 和弧BD 之间的数量关系;②分别联结AC 、CD 和BD ,试比较BD AC +和CD 的大小关系,并证明你的结论; (2)联结AB 分别交OC 、OD 于点M 、N .①当点C 在弧AB 上运动过程中, BM AN ⋅的值是否变化,若变化请说明理由;若不变,请求BM AN ⋅的值;②当5=MN 时,求圆心角DOB ∠的正切值.(第25题图)BA CDO2023学年第二学期徐汇区初三年级数学学科学习能力诊断卷参考答案和评分标准一、选择题:(本大题共6题,每题4分,满分24分) 1.B ; 2.C ; 3.D ; 4.A ; 5.D ; 6.B . 二.填空题:(本大题共12题,满分48分) 7.1=x ; 8.2>x ; 9.⎩⎨⎧==1,2y x 或⎩⎨⎧−=−=1,2y x ; 10.有两个不相等的;11.1≥x ; 12.2±; 13.21; 14.50; 15.400;16.b a21+; 17.171710; 18.228−.三、(本大题共7题,第19、20、21、22题每题10分,第23、24题每题12分,第25题14分,满分78分)19. 解:原式21)12(22−+−−=1122++−=2=.20.解:去分母,得216)2(2−=−+x x ;化简,得01032=−+x x ; 解得 51−=x ,22=x ; 经检验,2=x 是原方程的增根;所以,原方程的根是5−=x .21.解:(1)联结1AO ,设21O O 与AB 的交点为C . ∵⊙1O 和⊙2O 相交于点A 、B ,∴2421==AB AC ,AB O O ⊥21; 在2ACO Rt ∆中,︒=∠902ACO ,∴182430222222=−=−=AC AO CO ;∴3218502211=−=−=CO O O CO ;在1ACO Rt ∆中,︒=∠901ACO , ∴402432222211=+=+=AC CO AO ;即⊙1O 的半径长为40.(2)以21O O 为直径的⊙P 经过点B .∵535030212==O O AO ,53301822==AO CO ; ∴22212AO CO O O AO =,又A O O C AO 212∠=∠; ∴21O AO ∆∽2ACO ∆;∴︒=∠=∠90221ACO AO O ; 取21O O 的中点P ,联结AP 、BP .∴1PO AP =; 又21O O 垂直平分AB ,1PO AP BP ==; ∴以21O O 为直径的⊙P 经过点B .22.解:(1)他们不能在截止进场的时刻前到达比赛场地.∵单程送达比赛场地的时间是:)(15)(25.06015分钟小时==÷; ∴送完另4名学生的时间是:)(42)(45315分钟分钟>=⨯:∴他们不能在截止进场的时刻前到达比赛场地. (2)方案不唯一.如:先将4名学生用车送达比赛场地,另外4名学生同时步行前往比赛场地, 汽车到比赛场地后返回到与另外4名学生的相遇处再载他们到比赛场地.(用 这种方案送这8名学生到达比赛场地共需时间约为4.40分钟).理由如下:先将4名学生用车送达比赛场地的时间是:)(15)(25.06015分钟小时==÷ 此时另外4名学生步行路程是:25,125,05=⨯(千米);设汽车与另外4名学生相遇所用时间为t 小时.则25.115605−=+t t ;解得5211=t (小时)13165=(分钟); 从相遇处返回比赛场地所需的时间也是13165(分钟);所以,送这8名学生到达比赛场地共需时间为:4.4021316515≈⨯+(分钟); 又424.40<;所以,用这种方案送这8名学生能在截止进场的时刻前到达比赛场地.23.证明:(1)联结BD .∵四边形ABCD 是菱形, ∴CD BC AD AB ===;又AF AE =,CH CG =,∴AD AF AB AE =,CDCHCB CG =; ∴BD EF //,BD GH //; ∴GH EF //.(2)∵BD EF //,∴AB AEBD EF =; ∵BD GH //,∴BCCGBD GH =;又AE CG ≠,∴GH EF ≠; 又GH EF //,∴四边形EGHF 是梯形; ∵AF AD AE AB −=−,即DF BE =; 又CH CD CG BC −=−,即DH BG =; ∵四边形ABCD 是菱形,∴D B ∠=∠; ∴DHF BGE ∆≅∆;∴FH EG =; ∴梯形EGHF 是等腰梯形.24.解:(1)由题意,得044=+−a a ;解得34=a ;∴抛物线的表达式为4316342+−=x x y ; ∵抛物线的对称轴是直线2=x ,∴点)0,3(B . (2)①由题意,得)4,0(C 、)23,0(M ,∴25=CM ; ∵四边形GDMN 是平行四边形,∴NM GD //; 又点N 在y 轴上,∴OD NM ⊥;∴OD GD ⊥; 在BOC Rt ∆中。
2019年上海各区初三二模数学试卷23题专题汇编(教师版)

2019年上海各区初三二模数学试卷23题专题汇编(教师版)崇明23.(本题满分12分,每小题满分各6分)如图7,在直角梯形ABCD 中,90ABC ∠=︒,AD BC ∥,对角线AC 、BD 相交于点O . 过点D 作DE BC ⊥,交AC 于点F . (1)联结OE ,若BE AOEC OF=,求证:OE CD ∥; (2)若AD CD =且BD CD ⊥,求证:AF DFAC OB=. 23.(本题满分12分,每小题满分各6分) 证明(1)∵90ABD ∠=︒,BC DE ⊥∴//AB DE ………………………………………………………………(1分) ∴AO BOOF OD=………………………………………………………………(2分) ∵BE AOEC OF =∴AO BEOF EC=……… ………………………………………………………(2分) ∴//OE CD …………………………………………………………………(1分) (2)∵BC AD //,//AB DE ,∴四边形ABED 为平行四边形 又∵90ABD ∠=︒∴四边形ABED 为矩形 ……………………………………………………(1分) ∴AD BE =,90ADE ∠=︒ 又∵CD BD ⊥∴90BDC BDE CDE ∠=∠+∠=︒︒=∠+∠=∠90BDE ADB ADE∴CDE ADB ∠=∠ …………………………………………………………(1分)AD CD =∴DCA DAC ∠=∠∴()A S A CDF ADO ..∆≅∆…………………………………………………(1分) ∴OD DF =DE AB //ABCDOE F图7∴AF BE ADAC BC BC==…………………………………………………………(1分) ∵BC AD //∴BODFBO OD BC AD ==…………………………………………………………(1分) ∴AF DFAC OB=…………………………………………………………………(1分) 奉贤23.(本题满分12分,每小题满分各6分)已知:如图8,正方形ABCD ,点E 在边AD 上,AF ⊥BE ,垂足为点F ,点G 在线段BF 上,BG=AF .(1)求证:CG ⊥BE ;(2)如果点E 是AD 的中点,联结CF ,求证:CF=CB .23.证明:(1)∵四边形ABCD 是正方形,∴AB BC =.90ABC. ··········· (1分) ∵AF ⊥BE ,∴90FAB FBA ∠+∠=︒.∵90FBA CBG ∠+∠=︒,∴FAB CBG ∠=∠. ································ (1分) 又∵AF BG =,∴△AFB ≅△BGC . ············································· (2分)∴AFB BGC ∠=∠. ······································································· (1分) ∵90AFB ∠=︒,∴90BGC ∠=︒,即CG ⊥BE . ······························· (1分) (2)∵ABF EBA ∠=∠,90AFB BAE ∠=∠=︒,∴△AEB ∽△FAB .∴AE AFAB BF=. ················································· (3分) ∵点E 是AD 的中点,AD AB =,∴12AE AB =.∴12AF BF =.··················· (1分) ∵AF BG =,∴12BG BF =,即FG BG =.············································ (1分) ∵CG ⊥BE ,∴CF CB =. ······························································· (1分)ABCD FG E 图8闵行(本题共2小题,每小题6分,满分12分)如图,已知四边形ABCD 是菱形,对角线BD AC 、相交于点O ,AC BD 2=,过点A 作CD AE ⊥,垂足为点E ,AE 与BD 相交于点F ,过点C 作AC CG ⊥,与AE 的延长线相交于点G . 求证:(1)DOA ACG ∆∆≌;(2)AG DE BD DF ⋅=⋅223.证明:(1)在菱形ABCD 中,AD = CD ,AC ⊥BD ,OB = OD .∴ ∠DAC =∠DCA ,∠AOD = 90°.……………………………(1分) ∵ AE ⊥CD ,CG ⊥AC ,∴ ∠DCA +∠GCE = 90°,∠G +∠GCE = 90°.∴ ∠G =∠DCA .…………………………………………………(1分) ∴ ∠G =∠DAC .…………………………………………………(1分) ∵ BD = 2AC ,BD = 2OD ,∴ AC = OD . ……………………(1分) 在△ACG 和△DOA 中,∵ ∠ACG =∠AOD ,∠G =∠DAC ,AC = OD ,∴ △ACG ≌△DOA . ……………………………………………(2分) (2)∵ AE ⊥CD ,BD ⊥AC ,∴ ∠DOC =∠DEF = 90°.…………(1分) 又∵ ∠CDO =∠FDE ,∴ △CDO ∽△FDE .…………………(1分)∴ CD OD DF DE=.即得 OD DF DE CD ⋅=⋅. ……………………(2分) ∵ △ACG ≌△DOA ,∴ AG = AD = CD . ……………………(1分)又∵ 12OD BD =,∴ 2DF BD DE AG ⋅=⋅.…………………(1分)嘉定23.(本题满分12分,第(1)小题6分、第(2)小题6分)如图6,在矩形ABCD 中,点E 是边AB 的中点,△EBC 沿直线EC 翻折,使B 点落在矩形ABCD 内部的点P 处,联结AP 并延长AP 交CD 于点F ,联结BP 交CE 于点Q . (1)求证:四边形AECF 是平行四边形; (2)如果PE PA =,求证:△APB ≌△EPC .23.(1)证明:由翻折得:EC 垂直平分BP ………………1分∴EQ BQ = ………………1分 ∵点E 为AB 的中点,∴EB AE = ………………1分 ∴EQ 是△ABP 的中位线,∴EC ∥AF ,……………1分 ∵四边形ABCD 是矩形∴AE ∥FC ………………1分 ∴四边形AECF 是平行四边形. ………………1分(2)∵AE ∥FC ,∴EQB APB ∠=∠ ………………1分由翻折得: ︒=∠90EQB ,︒=∠90EPC∴︒=∠=∠90EPC APB ………………1分 由翻折得:EB PE =,BEC PEC ∠=∠∵PE PA =,EB AE = ∴AE PE PA ==∴△AEP 是等边三角形,∴︒=∠=∠60AEP PAB …………1分 ∵︒=∠+∠+∠180BEC PEC AEP∴︒=∠60PEC ………………1分AB DCF PEQ图6∴PEC PAB ∠=∠ ………………1分 ∵PE PA =,∴△APB ≌△EPC ………………1分 黄埔23.(本题满分12分)如图6,已知四边形ABCD ,AD ∥BC ,对角线AC 、BD 交于点O ,DO =BO ,过点C 作CE ∥AC ,交BD 的延长线于点E ,交AD 的延长线于点F ,且满足DCE ACB ∠=∠. (1)求证:四边形ABCD 是矩形; (2)求证:DE ADEF CD=.23. 证明:(1)∵AD ∥BC ,∴AD DOBC BO=, ∵DO =BO ,∴AD BC =,--------------------(2分)∴四边形ABCD 是平行四边形. ------------------------------------------------------------------------(1分) ∵CE ⊥AC ,∴90ACD DCE ∠+∠=︒,∵DCE ACB ∠=∠,∴90ACB ACD ∠+∠=︒,即90BCD ∠=︒,------------------------(2分) ∴四边形ABCD 是矩形. --------------------------------------------------------------------------------------(1分)(2)∵四边形ABCD 是矩形,∴AC BD =,90ADC ∠=︒---------------------------------------(2分)∵AD ∥BC ,∴DE EFBD FC=.--------------------------------------------------------------------------------(1分) ∴DE EFAC FC =,------------------------------------------------------------------------------------------------(1分) ∴DE AC EF FC=,∵90ADC ACF ∠=∠=︒, ∴cot AC ADDAC FC CD∠==,----------------------------------------------------------------------------------(1分) ∴DE AD EF CD =.--------------------------------------------------------------------------------------------------(1分)ABC DEF图6OA B CDO E H F 第23题图金山22. 已知:如图,菱形ABCD 的对角线AC 与BD 相交于点O ,若DBC CAD ∠=∠.(1)求证:ABCD 是正方形.(2)E 是OB 上一点,CE DH ⊥,垂足为H ,DH 与OC 相交于点F ,求证:OF OE =.23.(1)证明:∥四边形ABCD 是菱形,∥BC AD //,DAC BAD ∠=∠2,DBC ABC ∠=∠2; (2分) ∥180=∠+∠ABC DAB ; (1分) ∥DBC CAD ∠=∠;∥ABC BAD ∠=∠, (1分) ∥1802=∠BAD ; ∥90=∠BAD ; (1分) ∥四边形ABCD 是正方形. (1分) (2)证明:∥四边形ABCD 是正方形;∥BD AC ⊥,BD AC =,AC CO 21=,BO DO 21=; (1分) ∥90=∠=∠DOC COB ,DO CO =; (1分) ∥CE DH ⊥,垂足为H ;∥90=∠DHE ,90=∠+∠DEH EDH ; (1分) 又∥90=∠+∠DEH ECO ;∥EDH ECO ∠=∠; (1分) ∥ECO ∆≌FDO ∆; (1分) ∥OF OE =. (1分)普陀23.(本题满分12分)已知:如图10,在四边形ABCD 中,AD BC <,点E 在AD 的延长线上, ACE BCD ∠=∠,EC ED EA =⋅2. (1)求证:四边形ABCD 为梯形; (2)如果EC ABEA AC=,求证:AB ED BC =⋅2.23.证明:(1)∵ ACE BCD ∠=∠,∴DCE BCA ∠=∠. ········································· (1分)∵EC ED EA =⋅2,∴ED ECEC EA=. ······················································ (1分) 又∵E ∠是公共角,∴△EDC ∽△ECA . ·············································· (1分) ∴DCE CAE ∠=∠. ········································································· (1分) ∴BCA CAE ∠=∠.∴AD ∥BC . ·················································································· (1分) ∵AD BC <,∴AB 与CD 不平行.∴四边形ABCD 是梯形. ····································································· (1分) (2)∵△EDC ∽△ECA .∴EC CDEA AC =. ∵EC AB EA AC=,∴AB DC =.··························································· (1分) ∴四边形ABCD 是等腰梯形. ···························································· (1分) ∴B DCB ∠=∠. ··········································································· (1分) ∵AD ∥BC .∴EDC DCB ∠=∠.图10A BCD E∴EDC B ∠=∠.∵ECD ACB ∠=∠,∴△EDC ∽△ABC . ········································ (1分) ∴ED DCAB BC=. ··············································································· (1分) ∴AB ED BC =⋅2. ······································································ (1分) 徐汇22. (本题满分(12分),第(1)题满分6分,第(2)小题满分6分) 如图,已知梯形ABCD 中,E AC AB BC AD ,,=∥是边BC 上的点,且CAD AED ∠=∠,DE 交AC 于点F(1) 求证:DAF ABE ∽△△(2) 当EC AE FC AC ⋅=⋅时,求证:BE AD = 23. :(1)BC AD // ACB CAD ∠=∠∴ AC AB = ACB B ∠=∠∴ 又CAD AED ∠=∠CAD AED ACB B ∠=∠=∠=∠∴ 又CED AED BAE B ∠+∠=∠+∠ CED BAE ∠=∠∴又BC AD // CED ADF ∠=∠∴ ADF BAE ∠=∠∴ CAD ABE ∠=∠ ABE ∆∴相似于DAF ∆(2)由(1)知ABE ∆∴相似于DAF ∆AF BE AD AB =∴AFADBE AB =∴ BC AD // FC AF EC AD =∴FCECAF AD =∴ FC ECBE AB =∴ 由(1)知:CED BAE CED B ∠=∠∠=∠,ABE ∆∴相似于ECF ∆ FC BE EC AB =∴ FCEC BE AB =∴ EC AE FC AC ⋅=⋅ FCECAE AC =∴AEAC BE AB =∴ 又AC AB = AE BE =∴ BAE B ∠=∠∴又AED B ∠=∠ AED BAE ∠=∠∴DE AB //∴ 又BC AD //∴四边形ABED 是平行四边形 BE AD =∴杨浦1、 (本题满分12分,第(1)小题6分,第(2)小题6分)已知:如图,在ABC 中,AB=BC ,∠ABC=90°,点D 、E 分别是AB 、BC 的中点,点F 、G 是边AC 的三等分点,DF 、EG 的延长线相交于H ,联结HA 、HC 求证:(1)四边形FBGH 是菱形 (2)四边形ABCH 是正方形23.证明(1):∵点F 、G 是边AC 的三等分点,∴F 、G 分别是AG 、CF 的中点, ∵点D 是AB 的中点,∴DF //BG ,即FH //BG . ........................ (2分)同理: GH // BF . ........................................................................... (1分) ∴四边形FBGH 是平行四边形. .................................................. (1分) ∵AB =BC ,∴∠BAC =∠ACB .∵点F 、G 是边AC 的三等分点,∴AF =CG .∴△ABF ≌△CBG . ∴BF =BG. .................................................... (1分) ∴平行四边形FBGH 是菱形. ....................................................... (1分)证明(2)联结BH ,交FG 于点O ,∵四边形FBGH 是平行四边形,∴OB =OH ,OF =OG . ............ (2分) ∵AF =CG ,∴OA =OC . ................................................................. (1分) ∴四边形ABCH 是平行四边形. .................................................. (1分) ∵∠ABC =90°,∴平行四边形ABCH 是矩形. .......................... (1分)∵AB =BC ,∴矩形ABCH 是正方形. (1分)长宁23.(本题满分12分,第(1)小题5分,第(2)小题7分)如图5,平行四边形ABCD 的对角线BD AC 、交于点O ,点E 在边CB 的延长线上,且︒=∠90EAC ,EC EB AE ⋅=2. (1)求证:四边形ABCD 是矩形;(2)延长AE DB 、交于点F ,若AC AF =,求证:BF AE =.23.(本题满分12分,第(1)小题5分,第(2)小题7分)证明:(1)∵EC EB AE ⋅=2 ∴AEEB EC AE =又 ∵CEA AEB ∠=∠ ∴AEB ∆∽CEA ∆ (2分) ∴EAC EBA ∠=∠∵︒=∠90EAC ∴︒=∠90EBA (1分) 又 ∵︒=∠+∠180CBA EBA ∴︒=∠90CBA (1分) ∵四边形ABCD 是平行四边形∴四边形ABCD 是矩形 (1分)(2)∵ AEB ∆∽CEA ∆ ∴ AC AB AE BE = 即 ACAE AB BE = , ECA EAB ∠=∠ (2分)∵四边形ABCD 是矩形 ∴BD AC =又 ∵BD OB 21=, AC OC 21= ∴OC OB = ∴ECA OBC ∠=∠ 又 ∵OBC EBF ∠=∠ ECA EBA ∠=∠ ∴EAB EBF ∠=∠又∵F F ∠=∠ ∴EBF ∆∽BAF ∆ (3分)∴AB BE AF BF = ∴ACAEAF BF =(1分) ∵AC AF = ∴AE BF = (1分)图5AB CDE FO宝山23.(本题满分12分,第(1)、第(2)小题满分各6分)如图,在矩形ABCD 中,E 是AB 边的中点,沿EC 对折矩形ABCD ,使B 点落在点P 处,折痕为EC ,联结AP 并延长AP 交CD 于F 点, (1)求证:四边形AECF 为平行四边形;(2)如果P A=PC ,联结BP ,求证:∥APB ≅∥EPC .第23题图23.(1)证明:由折叠得到EC 垂直平分BP , ………………1分 设EC 与BP 交于Q ,∥BQ=EQ ………………1分 ∥E 为AB 的中点, ∥AE =EB , ………………1分 ∥EQ 为∥ABP 的中位线,∥AF ∥EC , ………………2分 ∥AE ∥FC , ∥四边形AECF 为平行四边形; ………………1分 (2)∥AF ∥EC ,∥∥A PB =∥EQB =90° ………………1分由翻折性质∥E PC =∥EBC =90°,∥PEC =∥BEC ………………1分 ∥E 为直角∥APB 斜边AB 的中点,且AP =EP ,∥∥AEP 为等边三角形 , ∥BAP =∥AEP =60°, ………………1+1分︒=︒-︒=∠=∠60260180CEB CEP ………………1分 在∥ABP 和∥EPC 中, ∥BAP =∥CEP ,∥APB=∥E PC ,AP =EP ∥∥ABP ∥∥EPC (AAS ), ………………1分松江23.(本题满分12分,每小题各6分)如图,已知□ABCD 中,AB=AC ,CO ⊥AD ,垂足为点O ,延长CO 、BA 交于点E ,联结DE . (1)求证:四边形ACDE 是菱形;(2)联结OB ,交AC 于点F ,如果OF=OC ,求证:22AB BF BO =⋅.23.证明:(1)∵四边形ABCD 是平行四边形∴AB ∥DC ,AB=DC ………………………………………………………………(1分) ∵AB=AC ,∴AC=DC ……………………………………………………………(1分) ∵CO ⊥AD ,∴AO=DO …………………………………………………………(1分) ∵EO AOCO DO=,∴EO=CO ………………………………………………………(1分) ∴四边形ACDE 是平行四边形……………………………………………………(1分) ∵AC=DC ,∴四边形ACDE 是菱形……………………………………………(1分) (2)∵ OF=OC ,∴∠OFC=∠OCF ……………………………………………(1分) ∵AE=AC ,∴∠OCF=∠BEO∵∠OFC=∠BF A ,∴∠BF A=∠BEO …………………………………………(1分) ∵∠ABF=∠OBE …………………………………………………………………(1分) ∴△BF A ∽△BEO ,∴AB BFBO BE=………………………………………………(1分) ∴AB ·BE=BF ·BO ,∵AE=AC=AB ,∴BE=2AB ………………………………(1分) ∴22AB BF BO =⋅………………………………………………………………(1分)(第23题图)OECBA静安22.(本题满分10分,第(1)小题满分5分,第(2)小题满分5分)已知:如图5,在矩形ABCD 中,过AC 的中点M 作EF ⊥AC , 分别交AD 、BC 于点E 、F . (1)求证:四边形AECF 是菱形; (2)如果2CD BF BC =⋅,求∠BAF 的度数.22.(本题满分10分,第(1)小题5分,第(2)小题5分) 证明:(1)∵四边形ABCD 为矩形,∴AD //BC , ∴∠1=∠2...........................................(1分)∵点M 为AC 的中点,∴AM =CM .在△AME 与△CMF 中,12AM CM AME CMF ∠=∠⎧⎪=⎨⎪∠=∠⎩..............................................(1分) ∴△AME ≌△CMF ...........................................(1分) ∴AE =CF .∴四边形AECF 为平行四边形. ·································································· (1分) 又∵EF ⊥AC ,∴平行四边形AECF 为菱形. ····································································· (1分) (2)∵2CD BF BC =⋅,∴CD BC BF CD =.又∵四边形ABCD 为矩形,∴AB =CD ,∴AB BC BF AB =. ··········································································· (1分)又∵∠ABF =∠CBA ,∴△ABF ∽△CBA . ·················································································· (1分) ∴∠2=∠3. ···························································································· (1分) ∵四边形AECF 为菱形,∴∠1=∠4,即∠1=∠3=∠4. ····································································· (1分) ∵四边形ABCD 为矩形, ∴∠BAD =∠1+∠3+∠4=90°,∴即∠1=30°. ······················································································· (1分)图5CFEDA BM图5CF EDA B M 124323.(本题满分12分,第(1)小题满分8分,第(2)小题满分4分)已知:如图6,△ABC 内接于⊙O ,AB ﹦AC ,点E 为弦AB 的中点,AO 的延长线交BC 于点D ,联结ED .过点B 作BF ⊥DE 交AC 于点F .(1)求证:∠BAD ﹦∠CBF ; (2)如果OD ﹦DB .求证:AF =BF .证明:(1)∵AB ﹦AC , ∴AB AC =. ........................(1分)∵直线AD 经过圆心O , ..................................................(1分) ∴AD ⊥BC ,BD=CD . ....................................................(1分) ∵点E 为弦AB 的中点, ∴DE 是△ABC 的中位线. ∴DE ∥AC . ......................................................................(1分) ∵BF ⊥DE ,∴∠1=90°, ∴∠2=90°.......................................................................(1分) ∴∠CBF +∠ACB ﹦90°.∵AB ﹦AC ,∴∠ABC ﹦∠ACB , .....................................(1分)∴∠CBF +∠ABC ﹦90°..................................................(1分)又∵AD ⊥BC ,∴∠BAD +∠ABC ﹦90°,∴∠BAD ﹦∠CBF ..............................................................(1分)(2)联结OB .∵AD ⊥BC ,OD ﹦DB ,∴△ODB 是等腰直角三角形........................................................................................................(1分)∴∠BOD ﹦45°. ∵OB=OA ,∴∠OBA ﹦∠OAB .∵∠BOD ﹦∠OBA +∠OAB ,∴∠BAO=12∠BOD=22.5°. .....................................................................................................(1分)∵AB=AC ,且AD ⊥BC , ∴∠BAC=2∠BAO=45°. ∵∠2=90°,即BF ⊥AC ,∴在△ABF 中,∠ABF =180904545--=,................................................................................(1分)图6BCDEF OA· 图6 B C DE F O A·12OE第23题图 C A B D F∴∠ABF =∠BAC ,∴AF =BF ..........................................................................................................................................(1分) 虹口23.(本题满分12分,第(1)小题6分,第(2)小题6分)如图,在□ABCD 中,AC 与BD 相交于点O ,过点B 作BE ∥AC ,联结OE 交BC 于点F ,点F 为BC 的中点.(1)求证:四边形AOEB 是平行四边形;(2)如果∠OBC =∠E ,求证:=BO OC AB FC ⋅⋅.23.(1)证明:∵BE ∥AC ∴OC CFBE BF=∵点F 为BC 的中点 ∴CF=BF ∴OC=BE ∵四边形ABCD 是平行四边形 ∴AO=CO ∴AO=BE∵BE ∥AC ∴四边形AOEB 是平行四边形(2)证明:∵四边形AOEB 是平行四边形 ∴∠BAO =∠E ∵∠OBC =∠E ∴∠BAO =∠OBC∵∠ACB =∠BCO ∴△COB ∽△CBA ∴BO BC AB AC =∵四边形ABCD 是平行四边形 ∴AC =2OC ∵点F 为BC 的中点 ∴BC =2FC ∴BO FC AB OC= 即=BO OC AB FC⋅⋅青浦23.(本题满分12分,第(1)、(2)小题,每小题6分)已知:如图9,在菱形ABCD 中,AB =AC ,点E 、F 分别在边AB 、BC 上,且AE =BF ,CE 与AF 相交于点G . (1)求证:∠FGC =∠B ;(2)延长CE 与DA 的延长线交于点H ,求证:.23.证明:(1)∵四边形ABCD 是菱形, ∴AB =BC . ··········································································· (1分)∵AB =AC ,∴AB =BC =AC ,∴∠B =∠BAC =60°. ··························· (1分) 在△EAC 与△FBA 中,∵EA =FB ,∠EAC =∠FBA ,AC =BA , ∴△EAC ≌△FBA , ································································ (1分) ∴∠ACE =∠BAF ,·································································· (1分) ∵∠BAF+∠F AC =60°,∴∠ACE +∠F AC =60°,∴∠FGC =60°, ······· (1分) ∴∠FGC =∠B . ····································································· (1分) (2)∵四边形ABCD 是菱形,∴∠B =∠D ,AB =DC ,AB //DC , ················································ (1分) ∴∠BEC =∠HCD , ································································· (1分) ∴△BEC ∽△DCH , ······························································· (1分)∴=BE ECDC CH, ····································································· (1分) ∴⋅=⋅BE CH EC DC .∵AB =AC ,∴CD =AC , ··························································· (1分) ∵△EAC ≌△FBA , ∴EC =F A ,∴⋅=⋅BE CH AF AC . ························································· (1分)BE CH AF AC ⋅=⋅GF EDA BC图9。
上海中考数学二模23题合集
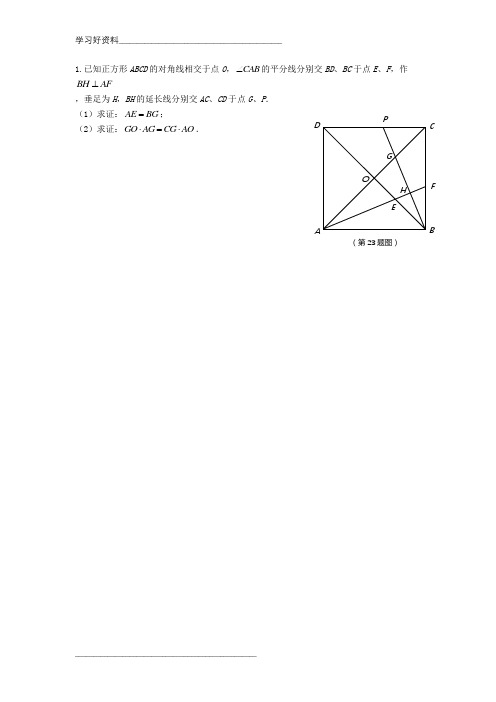
1.已知正方形ABCD的对角线相交于点O,CAB∠的平分线分别交BD、BC于点E、F,作BH AF⊥,垂足为H,BH的延长线分别交AC、CD于点G、P.(1)求证:;(第23题图)B C F2. 已知:如图,梯形ABCD 中,DC ∥AB ,AD=BC=DC ,AC 、BD 是对角线,E 是AB 延长线上一点,且∠BCE =∠ACD ,联结CE . (1)求证:四边形DBEC 是平行四边形; (2)求证:2AC AD AE =⋅.第23题图EDCBA3. 如图,在四边形ABCD 中,AB ∥DC ,E 、F 为对角线BD 上两点,且BE DF =, AF ∥EC .(1)求证:四边形ABCD 是平行四边形;(2)延长AF ,交边DC 于点G ,交边BC 的延长线 于点H ,求证:AD DC BH DG =.A BCEF第23题图DG H4. 如图5,在ABC ∆中,D 、E 分别是AC 、BC 边上的点,AE 与BD 交于点O ,且CD =CE ,12∠=∠.(1)求证:四边形ABED 是等腰梯形;(2)若EC =2,BE =1,21AOD ∠=∠,求AB 的长.图5 AB C DO E125. 如图6,BD 是平行四边形ABCD 的对角线,若∠DBC =45°,DE ⊥BC 于E ,BF ⊥CD 于F ,DE 与BF 相交于H ,BF 与AD 的延长线相交于G . 求证:(1)CD =BH ;(2)AB 是AG 和HE 的比例中项.A图66. 如图, BD是△ABC的角平分线, 点E、F分别在BC、AB上, 且DE∥AB, ∠DEF=∠A. (1)求证: BE=AF ;(2)设BD与EF交于点M, 联结AE, 交BD于点N,求证: BN·MD=BD·ND.M AFB E CD(静安)23.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分)已知:如图,四边形ABCD 是菱形,点E 在边CD 上,点F 在BC 的延长线上,CF =DE ,AE 的延长线与DF 相交于点G . (1)求证:∠CDF =∠DAE ;(2)如果DE =CE ,求证:AE =3EG .(闵行)23.(本题满分12分,其中每小题各6分)如图,已知在矩形ABCD 中,过对角线AC 的中点O 作 AC 的垂线,分别交射线AD 和CB 于点E 、F ,交边DC 于 点G ,交边AB 于点H .联结AF ,CE . (1)求证:四边形AFCE 是菱形; (2)如果OF = 2GO ,求证:2GO DG GC =⋅.(普陀)23.(本题满分12分)如图7,已知在四边形ABCD 中,AD ∥BC ,对角线AC 、BD 相交于点O ,BD 平分ABC ∠,过点D 作DF ∥AB 分别交AC 、BC 于点E 、F . (1)求证:四边形ABFD 是菱形;(2)设AC AB ⊥,求证:AC OE AB EF =.(第23题图)EDCGFA B(第23题图)AB CDE FGOH(松江)23.(本题满分12分,每小题满分各6分)如图,已知等腰△ABC 中,AB =AC ,AD ⊥BC ,CE ⊥AB ,垂足分别为D 、E . (1)求证:∠CAD =∠ECB ;(2)点F 是AC 的中点,联结DF ,求证:BD 2=FC ·BE .(徐汇)23.(本题满分12分)如图7,在ABC ∆中,AC AB =,点D 在边AC 上,DE BD AD ==,联结BE ,︒=∠=∠72DBE ABC .(1)联结CE ,求证:BE CE =;(2)分别延长CE 、AB 交于点F ,求证:四边形DBFE 是菱形.(杨浦)23.(本题满分12分,每小题各6分)已知:如图,在直角梯形纸片ABCD 中,DC //AB ,AB CD AD >>,∠A =90°,将纸片沿过点D 的直线翻折,使点A 落在边CD 上的点E 处,折痕为DF ,联结EF 并展开纸片. (1)求证:四边形ADEF 为正方形;(2)取线段AF 的中点G ,联结GE ,当BG =CD 时, 求证:四边形GBCE 为等腰梯形. CB ADEF(第23题图) (第23题图)图7ABC DE(第23题图)(闸北)23.(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分)如图,直角梯形ABCD中,∠B=90°,AD∥BC,BC=2AD,点E为边BC的中点.(1)求证:四边形AECD为平行四边形;(2)在CD边上取一点F,联结AF、AC、EF,设AC与EF交于点G,且∠EAF=∠CAD.求证:△AEC∽△ADF;(3)在(2)的条件下,当∠ECA=45°时.求:FG:EG的比值.(浦东)23.(本题满分12分,第(1)、(2)小题各6分)如图,已知:四边形ABCD是平行四边形,点E在边BA的延长线上,CE交AD于点F,∠ECA = ∠D.(1)求证:∆EAC∽∆ECB;(2)若DF = AF,求AC︰BC的值.(第23题图)AB CEDFG。
上海中考二模数学试题及答案

上海中考二模数学试题及答案一、选择题1. 若集合A = {1, 2, 3, 4, 5, 6, 7},B = {2, 4, 6, 8,10},则A ∩ B = ()A. {2, 4, 6}B. {1, 2, 3}C. {8, 10}D. {1, 3, 5, 7}2. 已知直线l与x轴交于点A,直线l与y轴交于点B,则下列说法中正确的是()A. 点(0, 0)在l上B. 点(0, 1)在l上C. A与B的横坐标之积小于0D. A、B的横坐标之积大于03. 方程(x-2)²-4 = 0的根是()A. 0B. 2C. 4D. 64. a1, a2, a3, ...是等差数列,若a1+a9=28,a5+a11=24,则该数列首项为()A. 1B. 2C. 3D. 45. 在Rt△ABC中,AB=12,AC=16,则BC的长度为()A. 4B. 8C. 12D. 16答案:1. A 2. D 3. B 4. C 5. B二、填空题1. 若a:b=2:3,且a:b:c=3:5:7,求c。
2. 设二次函数f(x)=-2x²+3x+4,若f(x)的图像与x轴交于点A、B,且AB=4,则A、B的横坐标分别为___。
3. 已知平行四边形ABCD中,AB=2a,AD=a+3,AC=4a-3,则BD 等于___。
4. 已知函数y=f(x)的图像关于原点对称,则f(-x)=___。
5. 若函数y=f(x)=ax²+x-1在区间[0, 1]上是增函数,则a的取值范围是___。
答案:1. 7 2. (-1, 3) 3. 2a-3 4. f(x) 5. a>0三、解答题1. 已知等差数列S的首项为a,公差为d,且S1 + S2 + S3 = 15,求S6的值。
解答:设等差数列的第n项是Sn,则有Sn = a + (n-1)d。
根据等差数列和公式,可以得到:S1 = aS2 = a + dS3 = a + 2dS6 = a + 5d给出条件S1 + S2 + S3 = 15,代入上面的式子可以得到:a + (a + d) + (a + 2d) = 153a + 3d = 15再考虑到S6 = a + 5d,将3a + 3d = 15带入可以得到:3a + 3d = 153(a + d) = 15a + d = 5将a + d = 5带入S6 = a + 5d:S6 = 5 + 5dS6 = 5(d + 1)所以S6的值为5(d + 1)。
2023年上海市静安区中考数学二模试卷(含解析)

2023年上海市静安区中考数学二模试卷学校:___________姓名:___________班级:___________考号:___________第I卷(选择题)一、选择题(本大题共6小题,共24.0分。
在每小题列出的选项中,选出符合题目的一项)1. 化简(−x3)2的结果是( )A. −x6B. −x5C. x6D. x52. 下列无理数中,在−2与0之间的数是( )A. −1−2B. 1−2C. −1+2D. 1+23. 下列关于9的算术平方根的说法正确的是( )A. 9的算术平方根是3与−3B. 9的算术平方根是−3C. 9的算术平方根是3D. 9的算术平方根不存在4. 甲、乙两名射击运动员分别进行了相同次数的射击训练,如果将甲、乙两人射击环数的平均数分别记作−x甲和−x乙,方差分别记作S2甲和S2乙,那么下列描述能说明甲运动员成绩较好且更稳定的是( )A. −x甲>−x乙且S2甲<S2乙B. −x甲>−x乙且S2甲>S2乙C. −x甲<−x乙且S2甲<S2乙D. −x甲<−x乙且S2甲>S2乙5. 某种型号油电混合动力汽车计划从甲地开往乙地,如果纯用电行驶,则电费为25元,如果纯燃油行驶,则燃油费为75元.已知每行驶1千米,纯燃油费用比纯用电费用多0.6元.如果设每行驶1千米纯用电的费用为x元,那么下列方程正确的是( )A. B. C. D. .6. 下面是“作∠AOB的平分线”的尺规作图过程:①在OA、OB上分别截取OD、OE,使OD=OE;②分别以点D、E为圆心,以大于1DE的同一长度为半径作弧,两弧交于∠AOB内的一点C;2③作射线OC.OC就是所求作的角的平分线.该尺规作图可直接利用三角形全等说明,其中三角形全等的依据是( )A. 三边对应相等的两个三角形全等B. 两边及它们的夹角对应相等的两个三角形全等C. 两角及它们的夹边对应相等的两个三角形全等D. 两角及其中一个角的对边对应相等的两个三角形全等第II卷(非选择题)二、填空题(本大题共12小题,共48.0分)7. 1的倒数是______ .58. 计算:______ .9. 已知f(x)=x−1,那么f(3)=______ .10. 方程2x−1=x的解是______ .11. 如果关于x的一元二次方程x2−3x+c=0有两个不相等的实数根,那么c的取值范围为______ .12. 我国明代珠算家程大位的名著《直指算法统宗》里有一道著名的算术题:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”其意思就是:100个和尚分100个馒头,正好分完,其中,大和尚一人分3个,小和尚三人分1个.那么大和尚有______ 人. 13. 毕业典礼上,李明、王红、张立3位同学合影留念,3人随机站成一排,那么王红恰好站在中间的概率是______ .14. 已知半径分别是2和6的两圆的圆心距为6,那么这两个圆有______ 个公共点.15.如图,已知四边形ABCD中,点P、Q、R分别是对角线AC、BD和边CD的中点.如果设A D=a,B C=b,那么向量PQ=______ (用向量a、b表示).16.某旅游风景区为满足不同游客的需求,推出了100、150、200(单位:元)三种价格的套票.景区统计了这三种套票一年的销售情况,并将销售量数据绘制成扇形统计图(如图所示).那么这一年销售的套票的平均价格是______ 元.17.如图,在△ABC中,AB=AC,将△ABC绕着点B旋转后,点C落在AC边上的点E处,点A落在点D处,DE与AB相交于点F,如果BE=BF,那么∠DBC的大小是______ .18. 在平面直角坐标系xOy中,我们定义点A(x,y)的“关联点”为,如果已知点A在直线y=x+3上,点B在⊙O的内部,⊙O的半径长为32(如图所示),那么点A的横坐标x的取值范围是______ .三、解答题(本大题共7小题,共78.0分。
2024上海初三二模数学试卷分类《23题几何证明题》

第23题图上海市2024届初三二模数学试卷分类汇编——23题几何证明题【2024届·宝山区·初三二模·第23题】1.(本题满分12分,第(1)小题6分,第(2)小题6分)如图10,在⊙O 中,直径AB 垂直于弦CD ,垂足为点E ,联结AC 、DO ,延长DO 交AC 于点F .(1)求证:2AF OF DF =⋅;(2)如果8CD =,2BE =,求OF 的长.【2024届·崇明区·初三二模·第23题】2.(本题满分12分,第(1)小题6分,第(2)小题6分)如图,已知在四边形ABCD 中,//AB CD ,对角线AC 平分DAB ∠,点O 是AC 上一点,以OA 为半径的⊙O 过B 、D 两点.(1)求证:四边形ABCD 是菱形;(2)设⊙O 与AC 交于点E ,联结DE 并延长,交AB 的延长线于点F ,若2AB AC EC =⋅,求证:AE EF =.图10图8图9【2024届·奉贤区·初三二模·第23题】3.(本题满分12分,第(1)小题6分,第(2)小题6分)如图8,在四边形ABCD 中,//AB DC ,B ADC ∠=∠,点E 、F 分别在边AB 、BC 上,且ADE ∠=CDF ∠.(1)求证:CF CB AE AB ⋅=⋅;(2)联结AC 、EF ,如果//EF AC ,求证:四边形ABCD 是菱形.【2024届·虹口区·初三二模·第23题】4.(本题满分12分,第(1)小题6分,第(2)小题6分)如图9,在Rt ABC ∆中,90C ∠=︒,延长CB 至点D ,使得DB CB =,过点A 、D 分别作//AE BC ,//DE BA ,AE 与DE 相交于点E ,联结BE .(1)求证:BE CD ⊥;(2)联结AD 交BE 于点F ,联结CE 交AD 于点G .如果FBA ADB ∠=∠,求证:23AG AB =.图8图7【2024届·黄浦区·初三二模·第23题】5.(本题满分12分)如图8,M 、N 分别是平行四边形ABCD 边AD 、BC 的中点,对角线BD 交AN 、CM 分别于点P 、Q .(1)求证:13PQ BD =;(2)当四边形ANCM 是正方形时,试从内角大小和邻边的数量关系的角度探究平行四边形ABCD 的形状特征.【2024届·嘉定区·初三二模·第23题】6.(本题满分12分,第(1)小题6分,第(2)小题6分)如图7,在梯形ABCD 中,//AD BC ,AB DC =,点P 在四边形ABCD 内部,PB PC =,联结PA 、PD .(1)求证:APD ∆是等腰三角形;(2)已知点Q 在AB 上,联结PQ ,如果//AP CD ,AQ AP =,求证:四边形AQPD 是平行四边形.第23题图第23题图【2024届·金山区·初三二模·第23题】7.(本题满分12分,第(1)小题6分,第(2)小题6分)如图,已知:D 是ABC ∆的边BC 上一点,点E 在ABC ∆外部,且BAE CAD ∠=∠,ACD ADC∠=∠ADE =∠,DE 交AB 于点F .(1)求证:AB AE =;(2)如果AD AF =,求证:2EF BF AB =⋅.【2024届·静安区·初三二模·第23题】8.(本题满分12分,第(1)小题6分,第(2)小题6分)已知:如图,直线EF 经过矩形ABCD 顶点D ,分别过顶点A 、C 作EF 的垂线,垂足分别为点E 和点F ,且DE DF =,联结AC .(1)求证:2AD AE AC =⋅;(2)联结BE 和BF ,求证:BE BF =.【2024届·闵行区·初三二模·第23题】9.(本题满分12分,第(1)小题4分,第(2)小题8分)沪教版九年级第二学期的教材给出了正多边形的定义.......:各边相等、各角也相等的多边形叫做正多边形.同时还提到了一种用直尺和圆规作圆的内接正六边形和圆的内接正五边形的方法,但课本上并未证明.我们现开展下列探究活动.活动一:如图1,展示了一种用尺规作⊙O 的内接正六边形的方法.①在⊙O 上任取一点A ,以A 为圆心、AO 为半径作弧,在⊙O 上截得一点B ;②以B 为圆心,AO 为半径作弧,在⊙O 上截得一点C ;再如此从点C 逐次截得点D 、E 、F ;③顺次联结AB 、BC 、CD 、DE 、EF 、FA .(1)根据正多边形的定义.........,我们只需要证明,.(请用符号语言表示,不需要说明理由),就可证明六边形ABCDEF 是正六边形.活动二:如图2,展示了一种用尺规作⊙O 的内接正五边形的方法.①作⊙O 的两条互相垂直的直径PQ 和AF ;②取半径OP 的中点M ;再以M 为圆心、MA 为半径作弧,和半径OQ 相交于点N ;③以点A 为圆心,以AN 的长为半径作弧,与⊙O 相截,得交点B .如此连续截取3次,依次得分点C 、D 、E ,顺次联结AB 、BC 、CD 、DE 、EA ,那么五边形ABCDE 是正五边形.(2)已知⊙O 的半径为2,求边AB 的长,并证明五边形ABCDE 是正五边形.(参考数据:22sin 22.52-︒=,21cos 22.52+︒=,1025sin 364-︒=,51cos364+︒=,1025sin 724+︒=.)第23题图2第23题图1第23题图【2024届·浦东新区·初三二模·第23题】10.(本题满分12分,第(1)小题6分,第(2)小题6分)已知:如图,在菱形ABCD 中,点E 是边DC 上的任意一点(不与点D 、C 重合),AE 交对角线BD 于F ,过点E 作//EG BC 交BD 于点G .(1)求证:2DF FG BF =⋅;(2)当2BD DF AD DE ⋅=⋅时,求证:AE DC ⊥.【2024届·普陀区·初三二模·第23题】11.(本题满分12分)已知:如图7,四边形ABCD 中,//AB CD ,点E 在边AD 上,CE 与BA 的延长线交于点F ,FA AEAB ED=.(1)求证:四边形ABCD 为平行四边形;(2)联结FD ,分别延长FD 、BC 交于点G ,如果2FC FD FG =⋅,求证:AD CG BF CD ⋅=⋅.图7第23题图图7已知:如图,在四边形ABCD 中,//AD BC ,点E 是对角线AC 上一点,EA ED =,且DAB DEC ∠=∠=DCB ∠.(1)求证:四边形ABCD 是菱形;(2)延长DE 分别交线段AB 、CB 的延长线于点F 、G ,如果GB BC =,求证:22AD EF GD =⋅.【2024届·松江区·初三二模·第23题】13.(本题满分12分,第(1)小题6分,第(2)小题6分)如图7,已知AB 是⊙1O 与⊙2O 的公共弦,12O O 与AB 交于点C ,12O O 的延长线与⊙2O 交于点P ,联结PA 并延长,交⊙1O 于点D .(1)联结1O A 、2O A ,如果AB AD AP ==,求证:12O A O A ⊥;(2)如果123PO PO =,求证:PA AD =.第23题图第23题图如图,在菱形ABCD 中,点E 、G 、H 、F 分别在边AB 、BC 、CD 、DA 上,AE AF =,CG CH =,CG AE ≠.(1)求证://EF GH ;(2)分别联结EG 、FH ,求证:四边形EGHF 是等腰梯形.【2024届·杨浦区·初三二模·第23题】15.(本题满分12分,第(1)小题6分,第(2)小题6分)已知:如图,在梯形ABCD 中,//AD BC ,AB CD =,BD BC =,DBC ∠的平分线交AD 延长线于点E ,交CD 于点F .(1)求证:四边形BCED 是菱形;(2)联结AC 交BF 于点G ,如果AC CE ⊥,求证:2AB AG AC =⋅.第23题图已知:在梯形ABCD 中,//AD BC ,BD AD ⊥,点E 在边AD 上(点E 不与点A 、D 重合),点F 在边CD 上,且ABD EBF C ∠=∠=∠.(1)求证:AB BEBD BF=;(2)联结EF ,与BD 交于点G ,如果BG EG =,求证:四边形BEDF 为等腰梯形.。
2019年上海各区初三二模数学试卷23题专题汇编(学生版)
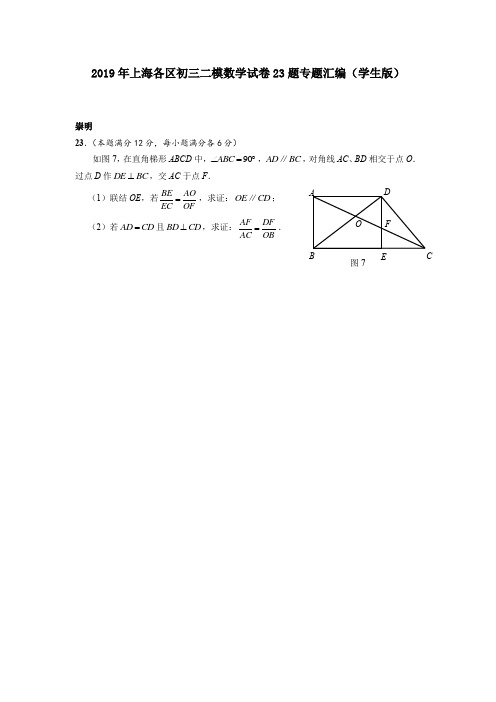
2019年上海各区初三二模数学试卷23题专题汇编(学生版)崇明23.(本题满分12分,每小题满分各6分)如图7,在直角梯形ABCD 中,90ABC ∠=︒,AD BC ∥,对角线AC 、BD 相交于点O . 过点D 作DE BC ⊥,交AC 于点F . (1)联结OE ,若BE AOEC OF=,求证:OE CD ∥; (2)若AD CD =且BD CD ⊥,求证:AF DFAC OB=.ABCDOE F图7奉贤23.(本题满分12分,每小题满分各6分)已知:如图8,正方形ABCD ,点E 在边AD 上,AF ⊥BE ,垂足为点F ,点G 在线段BF 上,BG=AF .(1)求证:CG ⊥BE ;(2)如果点E 是AD 的中点,联结CF ,求证:CF=CB .ABCD FG E 图8闵行(本题共2小题,每小题6分,满分12分)如图,已知四边形ABCD 是菱形,对角线BD AC 、相交于点O ,AC BD 2=,过点A 作CD AE ⊥,垂足为点E ,AE 与BD 相交于点F ,过点C 作AC CG ⊥,与AE 的延长线相交于点G . 求证:(1)DOA ACG ∆∆≌;(2)AG DE BD DF ⋅=⋅2嘉定23.(本题满分12分,第(1)小题6分、第(2)小题6分)如图6,在矩形ABCD 中,点E 是边AB 的中点,△EBC 沿直线EC 翻折,使B 点落在矩形ABCD 内部的点P 处,联结AP 并延长AP 交CD 于点F ,联结BP 交CE 于点Q . (1)求证:四边形AECF 是平行四边形; (2)如果PE PA ,求证:△APB ≌△EPC .AB DCF PEQ图6黄埔23.(本题满分12分)如图6,已知四边形ABCD,AD∥BC,对角线AC、BD交于点O,DO=BO,过点C作CE∥AC,交BD的延长线于点E,交AD的延长线于点F,且满足DCE ACB∠=∠.(1)求证:四边形ABCD是矩形;(2)求证:DE ADEF CD=.AB CDEF图6OA B CD OE HF 第23题图金山22. 已知:如图,菱形ABCD 的对角线AC 与BD 相交于点O ,若DBC CAD ∠=∠.(1)求证:ABCD 是正方形.(2)E 是OB 上一点,CE DH ⊥,垂足为H ,DH 与OC 相交于点F ,求证:OF OE =.普陀23.(本题满分12分)已知:如图10,在四边形ABCD 中,AD BC <,点E 在AD 的延长线上, ACE BCD ∠=∠,EC ED EA =⋅2. (1)求证:四边形ABCD 为梯形; (2)如果EC ABEA AC=,求证:AB ED BC =⋅2.图10A BCD E徐汇22. (本题满分(12分),第(1)题满分6分,第(2)小题满分6分) 如图,已知梯形ABCD 中,E AC AB BC AD ,,=∥是边BC 上的点,且CAD AED ∠=∠,DE 交AC 于点F(1) 求证:DAF ABE ∽△△(2) 当EC AE FC AC ⋅=⋅时,求证:BE AD =杨浦1、(本题满分12分,第(1)小题6分,第(2)小题6分)V中,AB=BC,∠ABC=90°,点D、E分别是AB、BC的中点,已知:如图,在ABC点F、G是边AC的三等分点,DF、EG的延长线相交于H,联结HA、HC求证:(1)四边形FBGH是菱形(2)四边形ABCH是正方形长宁23.(本题满分12分,第(1)小题5分,第(2)小题7分)如图5,平行四边形ABCD 的对角线BD AC 、交于点O ,点E 在边CB 的延长线上,且︒=∠90EAC ,EC EB AE ⋅=2. (1)求证:四边形ABCD 是矩形;(2)延长AE DB 、交于点F ,若AC AF =,求证:BF AE =.图5 AB C DE FO宝山23.(本题满分12分,第(1)、第(2)小题满分各6分)如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,联结AP并延长AP交CD于F点,(1)求证:四边形AECF为平行四边形;(2)如果P A=PC,联结BP,求证:∥APB≅∥EPC.第23题图松江23.(本题满分12分,每小题各6分)如图,已知□ABCD 中,AB=AC ,CO ⊥AD ,垂足为点O ,延长CO 、BA 交于点E ,联结DE . (1)求证:四边形ACDE 是菱形;(2)联结OB ,交AC 于点F ,如果OF=OC , 求证:22AB BF BO =⋅.(第23题图)O EBA22.(本题满分10分,第(1)小题满分5分,第(2)小题满分5分)已知:如图5,在矩形ABCD 中,过AC 的中点M 作EF ⊥AC , 分别交AD 、BC 于点E 、F . (1)求证:四边形AECF 是菱形; (2)如果2CD BF BC =⋅,求∠BAF 的度数.23.(本题满分12分,第(1)小题满分8分,第(2)小题满分4分)已知:如图6,△ABC 内接于⊙O ,AB ﹦AC ,点E 为弦AB 的中点,AO 的延长线交BC 于点D ,联结ED .过点B 作BF ⊥DE 交AC 于点F .(1)求证:∠BAD ﹦∠CBF ; (2)如果OD ﹦DB .求证:AF =BF .图5CFEDA BM图6BCDEF OA·OE 第23题图CABD F虹口23.(本题满分12分,第(1)小题6分,第(2)小题6分)如图,在□ABCD中,AC与BD相交于点O,过点B作BE∥AC,联结OE交BC于点F,点F为BC的中点.(1)求证:四边形AOEB是平行四边形;(2)如果∠OBC =∠E,求证:=BO OC AB FC⋅⋅.青浦23.(本题满分12分,第(1)、(2)小题,每小题6分)已知:如图9,在菱形ABCD 中,AB =AC ,点E 、F 分别在边AB 、BC 上,且AE =BF ,CE 与AF 相交于点G . (1)求证:∠FGC =∠B ;(2)延长CE 与DA 的延长线交于点H ,求证:.BE CH AF AC ⋅=⋅GF EDA BC图9。
上海中考数学二模23题几何证明题及习题练习(2018-2013)-排版后

初中数学讲义几何证明题授课教师:教师联系电话:2013-2018年,上海市二模23题共考80道题目,其中考察内容和解题技巧的具体数目及占比如下图;其中相似三角形、比例线段、平行四边形及特殊的平行四边形、全等三角形是重点考察内容。
其中最核心的解题技巧是“等积化等比”、等量替换;“平行+中点”、“平行+角平分线”、“平行+等角”、旋转型、三线合一等上述技巧是非常典型的解题技巧,应该通过练习熟练掌握。
有个一隐形的技巧就是判定后必定用性质(例如:判定完全等用全等的性质、判定完相似用相似的性质、判定完平行四边形用平行四边形的性质…………)常用技巧讲解及练习: 技巧一:“平行+中点”首先,这是一个证明全等的重要方式,另外通过两个三角形全等,我们可以进一步说明该四边形是平行四边形。
例题:例1. (2017 闵行区)如图,在△ABC 中,∠C =90°,点D 为边BC 上一点,点E 为边AB 的中点,过点A 作AF ∥BC ,交DE 的延长线于点F ,联结BF 1) 求证:四边形ADBF 是平行四边形;D例2. (2014 嘉定宝山区)如图,在直角梯形ABCD 中,AD ∥BC ,∠DAB =∠ABC =90°,E 是CD 的中点,联结AE 并延长交BC 的延长线于F 1) 联结BE ,求证:BE =EF ;2) 联结BD 交AE 于M ,当AD =1,AB =2,AM =EM ,求CD 的长;练习:1. (2016 浦东区)如图,已知:四边形ABCD 是平行四边形,点E 是边BA 的延长线上,CE 交AD 于点F ,∠ECA =∠D 1) 求证:△EAC ∽△ECB ; 2) 若DF =AF ,求AC:BC 的值;FDB2. (2018 杨浦区)已知,如图,在平行四边形ABCD 中,点G 为对角线AC 的中点,过点G 的直线EF分别交边ABCD 于点E 、F ,过点G 的直线MN 分别交边AD 、BC 于点N 、M ,且∠AGE =∠CGN 1) 求证:四边形ENFM 是平行四边形;2) 当四边形ENFM 是矩形时,求证:BE =BN ;3. (2015 崇明区)如图,△ABC 中,BC =2AB ,点D 、E 分别是BC 、AC 的中点,过点A 作AF ∥BC交线段DE 的延长线于点F ,取AF 的中点G ,联结DG ,GD 与AE 交于点H 1) 求证:四边形ABDF 是菱形; 2) 求证:HA 2=HE ∙HCBGB技巧二:“平行+等角”“平行+等角”是一个很重要判定平行四边形的方法,切记切记 例题:例3. (2015 奉贤区)已知:如图,在四边形ABCD 中,AB ∥CD ,点E 是对角线AC 上一点,∠DEC =∠ABC ,且CD 2=CE ∙CA1) 求证:四边形ABCD 是平行四边形;2) 分别过点E 、B 作AB 和AC 的平行线交于点F ,联结CF ,若∠FCE =∠DCE ,求证:四边形EFCD 是菱形;例4. (2016 长宁区)如图,BD 是△ABC 的角平分线,点E 、F 分别在边BC 、AB 上,且DE ∥AB ,∠DEF =∠A 1) 求证:BE =AF ;2) 设BD 与EF 交于点M ,联结AE 交BD 于点N ,求证:BN ∙MD =BD ∙NDBB练习:4. (2013 长宁区)如图,△ABC 中,∠ACB =90°,D 、E 分别是BC 、BA 的中点,联结DE ,F 在DE 延长线上,且AF =AE1) 求证:四边形ACEF 是平行四边形; 2) 若四边形ACEF 是菱形,求∠B 的度数;技巧三:“平行+角平分线”“平行+角平分线”必出等腰三角形 例题:例5. (2013 闸北区)已知:如图,△ABC 中,点D 、E 、F 分别在BC 、CA 、AB 上,AF FB=BD DC=AE EC,若BE 平分∠ABC ,说明四边形DBFE 的形状,证明FDB练习:5.(2013 杨浦区)如图,在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,联结DE1)求证:四边形ABED是菱形;2)若∠ABC=60°,CE=2BE,试判断△CDE的形状,并说明理由;技巧四:旋转型旋转型涉及到全等和相似的技巧例题:例6.(2014 奉贤区)已知:如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE1)求证:△ABE∽△ACD;2)求证:BC∙AD=DE∙AC;CBD B例7. (2013 奉贤区)如图,已知等边△ABC ,点D 是BC 延长线上的一个动点,以AD 为一边作等边△ADE ,过点E 作BC 的平行线,分别交AB 、AC 的延长线于点F 、G ,联结BE 1) 求证:△AEB ≌△ADC ;2) 如果BC =CD ,判断四边形BCGE 的形状,说明理由;例8. (2016 徐汇区)如图,在△ABC 中,AB =AC ,点D 在边AC 上,AD =DB =DE ,联结BE ,∠ABC =∠DBE =72° 1) 联结CE ,求证:CE =BE ;2) 分别延长CE 、AB 交于点F ,求证:四边形DBFE 是菱形;FEA练习:6. (2015 宝山区)如图,已知△ABC 和△ADE 都是等边三角形,点D 在边BC 上,点E 在边AD 的右侧,联结CE 1) 求证:∠ACE =60°;2) 在边AB 上取一点F ,使BF =BD ,联结DF 、EF ,求证:四边形CDFE 是等腰梯形;7. (2014 闵行区)已知:如图,四边形ABCD 是平行四边形,分别以AB 、AD 为腰作等腰△ADE 和等腰△ABF ,且顶角∠BAF =∠DAE ,联结BD 、EF 相交于点G ,BD 与AF 相交于点H 1) 求证:BD =EF ;2) 当线段FG 、GH 和GB 满足怎样的数量关系时,四边形ABCD 是菱形,证明之;BB技巧五:等积换等比等积换等比的目的是为了判断使用比例线段继续做还是用相似判定 比例线段:例9. (2017 静安区)已知:如图,在菱形ABCD 中,点E 在边BC 上,点F 在BA 的延长线上,BE =AF ,CF ∥AE ,CF 与边AD 相交于点G 1) 求证:FD =CG ; 2) 求证:CG 2=GF ∙FC例10. (2017 松江区)如图,点D 、E 分别是△ABC 边BC 、AB 上的点,AD 、CE 相交于点G ,过点E作EF ∥AD 交BC 于点F ,且CF 2=CD ∙CB ,联结FG 1) 求证:GF ∥AB ;2) 如果∠CAG =∠CFG ,求证:四边形AEFG 是菱形;BB练习:8. (2016 崇明区)已知正方形ABCD 的对角线相交于点O ,∠CAB 的平分线分别交BD 、BC 于点EF ,作BH ⊥AF ,垂足为H ,BH 的延长线分别交AC 、CD 于点G 、P 1) 求证:AE =BG ; 2) 求证:GO ∙AG =CG ∙AO ;相似:例11. (2016 虹口区)如图,在四边形ABCD 中,AB ∥DC ,EF 为对角线BD 上两点,且BE =DF ,AF∥EC1) 求证:四边形ABCD 是平行四边形;2) 延长AF ,交边DC 于点G ,交边BC 的延长线于点H ,求证:AD ∙DC =BH ∙DG ;FB练习:9. (2015 静安区)如图,梯形ABCD 中,AB ∥CD ,AD =BC ,E 是CD 的中点,BE 交AC 于点F ,过点F 作FG ∥AB ,交AE 于点G 1) 求证:AG =BF ;2) 当AD 2=AC ∙CF 时,求证:AB ∙AD =AG ∙AC ;10. (2013 徐汇区)如图,四边形ABCD 是平行四边形,在边AB 的延长线上截取BE =AB ,点F 在AE的延长线上,CE 和DF 交于点M ,BC 和DF 交于点N 1) 求证:四边形DBEC 是平行四边形;2) 如果AD 2=AB ∙AF ,求证:CM ∙AB =DM ∙CN ;ABA技巧五:等积式的数字替换 例题:例12. (2018 普陀区)已知:如图,梯形ABCD 中,AD ∥BC ,DE ∥AB ,DE 与对角线AC 交于点F ,FG ∥AD ,且FG =EF 1) 求证:四边形ABED 是菱形;2) 联结AE ,AC ⊥ED ,求证:12AE 2=EF ∙ED例13. (2018 松江区)如图,已知梯形ABCD 中,AB ∥CD ,∠D =90°,BE 平分∠ABC ,交CD 于点E ,F 是AB 的中点,联结AE 、EF ,且AE ⊥BE 1) 求证:四边形BCEF 是菱形; 2) 求证:BE ∙AE =2AD ∙BC ;B例14.(2017 闵行区)如图,在△ABC中,∠C=90°,点D为边BC上一点,点E为边AB的中点,过点A作AF∥BC,交ED的延长线于点F,联结BF1)求证:四边形ADBF是平行四边形;2)当∠ADF=∠BDF时,求证:BD∙BC=2BE2;特殊平行四边形类题目菱形例15. (2016 普陀区)如图,已知在四边形ABCD 中,AD ∥BC ,对角线AC 、BD 相较于点O ,BD 平分∠ABC ,过点D 作DF ∥AB 分别交AC 、BC 于点E 、F 1) 求证:四边形ABDF 是菱形;2) 设AC ⊥AB ,求证:AC ∙OE =AB ∙EF ;例16. (2015 普陀区)如图,在△ABC 中,点D 、E 分别在边BC 、AC 上,BE 、AD 相交于点G ,EF ∥AD 交BC 于点F ,且BF 2=BD ∙BC ,联结FC 1) 求证:FG ∥CE ;2) 设∠BAD =∠C ,求证:四边形AGFE 是菱形;DBB11. (2015 虹口区)如图,四边形ABCD 是平行四边形,点E 为DC 延长线上一点,联结AE ,交边BC于点F ,联结BE 1) 求证:AB ∙AD =BF ∙ED ;2) 若CD =CA ,且∠DAE =90°,求证:四边形ABEC 是菱形.12. (2014 虹口区)已知:如图,在□ABCD 中,AE 是BC 边上的高,将△ABE 沿BC 方向平移,使点E与点C 重合,得△GFC . 1) 求证:BE =DG ;2) 若∠BCD =120˚,当AB 与BC 满足什么数量关系时,四边形ABFG 是菱形?证明你的结论.FE B例题:例17. (2017 普陀区)已知:如图,在平行四边形ABCD 中,AC 为对角线,E 是边AD 上一点,BE ⊥AC 交AC 于点F ,BE 、CD 的延长线交于点G ,且∠ABE =∠CAD 1) 求证:四边形ABCD 是矩形;2) 如果AE =EG ,求证:AC 2=BC ∙BG ;D例18.(2017 奉贤区)已知:如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,点E是BD的中点,CE的延长线交边AB于点F,且∠CED=∠A1)求证:AC=AF;2)在边AB下方画∠GBA=∠CED,交CF的延长线于点G,联结DG,在图中画出图形,证明四边形CDGB是矩形;练习:13.(2017 长宁区)如图,在△ABC中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在BC边上,联结AD交PQ于点E,且CPCD =QEBD,点G在BC的延长线上,∠ACG的平分线CF交直线PQ于点F1)求证:PC=PE;2)当P是边AC的中点时,求证:四边形AECF是矩形;A14.(2014 徐汇区)已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E是BC的中点,F是CD上的点,联结AE、EF、AC1)求证:AO∙OF=OC∙OE;2)若点F是DC的中点,联结BD交AE于点G,求证:四边形EFDG是菱形;正方形:例题:例19. (2015 闵行区)如图,已知梯形ABCD 中,AD ∥BC ,∠A =90°,AB =AD ,点E 在边AB 上,且DE ⊥CD ,DF 平分∠EDC ,交BC 于点F ,联结CE 、EF 1) 求证:DE =DC ;2) 如果BE 2=BF ∙BC ,求证:∠BEF =∠CEF ;例20. (2015 徐汇区)已知:如图,正方形ABCD ,BM 、DN 分别是正方形的两个外角平分线,∠MAN =45°,将∠MAN 绕着正方形的顶点A 旋转,边AM 、AN 分别交两条角平分线于点M 、N ,联结MN1) 求证:△ABM ∽△AND ;2) 联结BD ,当∠BAM 的度数为多少时,四边形BMND 是矩形,证明之;E例21. (2014 浦东区)如图,正方形ABCD 中,点E 是边AD 的中点,联结BE ,过点A 作AF ⊥BE ,分别交BE 、CD 于点H 、F ,联结BF 1) 求证:BE =BF ;2) 联结BD ,交AF 于点O ,联结OE ,求证:∠AEB =∠DEO ;练习:15. (2015 长宁区)如图,正方形ABCD 中,点E 、F 分别在边BC 、CD 上,AE =AF ,AC 和EF 交于点O ,延长AC 至点G ,使得AO =OG ,联结EG 、FG 1) 求证:BE =DF ;2) 求证:四边形AEGF 是菱形;BB16. (2015 松江区)如图,已知正方形ABCD 中,点E 在CD 边上,过C 点作AE 的垂线交于点P ,联结DF ,过点D 作DF 的垂线交AF 于点G ,联结BG 1) 求证:△ADG ≌△CDF ;2) 如果E 为CD 的中点,求证:BG ⊥AF ;17. (2013 松江区)已知在△ABC 中,∠BAC =90°,AB =AC ,点D 在边BC 上,以AD 为边作正方形ADEF ,联结CF 、CE 1) 求证:FC ⊥BC ;2) 如果BD=AC ,求证:CD=CE ;FB辅助线:例22. (2015 普陀区)如图,在△ABC 中,点D 、E 分别在边BC 、AC 上,BE 、AD 相交于点G ,EF ∥AD 交BC 于点F ,且BF 2=BD ∙BC ,联结FC 1) 求证:FG ∥CE ;2) 设∠BAD =∠C ,求证:四边形AGFE 是菱形;例23. (2018 黄浦区)如图,点E 、F 分别是菱形ABCD 边AD 、CD 的中点 1) 求证:BE =BF ;2) 当△BEF 是等边三角形时,求证:∠D=2∠A ;BC例24. (2016 静安区)已知:如图,四边形ABCD 是菱形,点E 在边CD 上,点F 在BC 延长线上,CF =DE ,AE 的延长线与DF 相交于点G 1) 求证:∠CDF=∠DAE ; 2) 如果DE=CE ,求证:AE=3EG ;例25. (2014 嘉定区)如图,在直角梯形ABCD 中,AD ∥BC ,∠DAB =∠ABC =90°,E 为CD 的中点,联结AE 并延长交BC 的延长线于F ; 1) 联结BE ,求证BE =EF ;2) 联结BD 交AE 于M ,当AD =1,AB =2,AM =EM 时,求CD 的长;B例26.(2017 宝山区)如图,在矩形ABCD中,E是AD边上的中点,BE⊥AC,垂足为点F,联结DF1)求证:CF=2AF;2)求tan∠CFD的值;例27.(2015 闵行区)如图,已知梯形ABCD中,AD∥BC,∠A=90°,AB=AD,点E在边AB上,且DE⊥CD,DF平分∠EDC,交BC于点F,联结CE、EF1)求证:DE=DC;2)如果BE2=BF∙BC,求证:∠BEF=∠CEF;E例28. (2015 杨浦区)已知:如图,Rt △ABC 和Rt △CDE 中,∠ABC =∠CDE =90°,且BC 于CD 共线,联结AE ,点M 为AE 的中点,联结BM ,交AC 于点G ,联结MD ,交CE 于点H 1) 求证:MB =MD ;2) 当AB =BC ,DC =DE 时,求证:四边形MGCH 为矩形;例29. (2013 杨浦区)如图,在梯形ABCD 中,AD ∥BC ,AB =AD ,∠BAD 的平分线AE 交BC 于点E ,联结DE1) 求证:四边形ABED 是菱形;2) 若∠ABC =60°,CE =2BE ,试判断△CDE 的形状,并说明理由;ACB。
2024年上海市虹口区中考二模数学试题(解析版)

虹口区2023学年度初三年级第二次学生学习能力诊断练习数学 练习卷(满分150分,考试时间100分钟)注意:1.本练习卷含三个大题,共25题.答题时,请务必按答题要求在答题纸规定的位置上作答,在草稿纸、本练习卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.]1. 下列各数中,无理数是( )A. B. 3.14159 C. D. 【答案】C【解析】【分析】本题主要考查的是对无理数定义的应用,熟练掌握理解无理数的定义是解此题的关键.根据无理数的定义(无理数是指无限不循环小数)判断即可.【详解】解:A、是分数,不是无理数,故本选项错误;B 、3.14159是小数,不是无理数,故本选项错误;C 是无理数,故本选项正确;D 、是循环小数,不是无理数,故本选项错误;故选C .2. 关于一元二次方程无实数根,则实数的取值范围是( )A. B. C. D. 【答案】D【解析】【分析】根据一元二次方程判别式与根情况的关系,列代数式求解即可.【详解】解:一元二次方程无实数根,的211 1.22111.2x 220x x m -+=m 1m <1m £m 1≥1m >220x x m -+=则判别式解得,故选:D .【点睛】此题考查了一元二次方程判别式与根情况的关系,解题的关键是掌握相关基础知识,一元二次方程的判别式,当时有两个不相等的实数根,当时,有两个相等的实数根,当时,无实数根.3. 已知二次函数,如果函数值随自变量的增大而减小,那么的取值范围是( )A. B. C. D. 【答案】A【解析】【分析】本题考查二次函数的性质,熟练掌握二次函数的增减性是解题关键.根据二次函数,可得函数图象开口向下,对称轴为,函数值随自变量的增大而减小,则,得以解答.【详解】解:二次函数,,函数图象开口向下,对称轴为,时,函数值随自变量的增大而减小,故选:A .4. 下列事件中,必然事件是( )A. 随机购买一张电影票,座位号恰好是偶数B. 抛掷一枚质地均匀的硬币,落地后反面朝上C. 在只装有2个黄球和3个白球的盒子中,摸出一个球是红球D. 在平面内画一个三角形,该三角形的内角和等于【答案】D【解析】【分析】本题考查是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.根据事件发生的可能性大小判断.的()224240b ac m ∆=-=--<1m >()200ax bx c a ++=≠24b ac ∆=-0∆>Δ0=Δ0<()24y x =--y x x 4x ≥4x ≤4x ≥-4x ≤-()24y x =--()24y x =--4x =y x 4x ≥()24y x =--10-< ∴()24y x =--4x =∴4x ≥y x 180︒【详解】解:A 、随机购买一张电影票,座位号是偶数,是随机事件;B 、抛掷一枚质地均匀的硬币,反面朝下,是随机事件;C 、在只装有2个黄球和3个白球的盒子中,摸出一个球是红球,是不可能事件;D 、在平面内画一个三角形,该三角形的内角和等于,是必然事件;故选D .5. 如图,在正方形中,点、分别在边和上,,,如果,那么的面积为( )A. 6B. 8C. 10D. 12【答案】B【解析】【分析】本题主要考查了正方形的性质,平行四边形的性质与判定,先根据正方形的性质得到,进而证明四边形是平行四边形,得到,则,最后根据三角形面积计算公式求解即可.【详解】解:∵四边形是正方形,∴,∵,∴四边形是平行四边形,∴,∴,∴,故选:B .6. 在中,,.如果以顶点为圆心,为半径作,那么与边所在直线的公共点的个数是( )A. 3个B. 2个C. 1个D. 0个.180︒ABCD E F BC AD 2BE =6AF =AE CF ABE 90AD BC AB CD ABE =∠=︒∥,,AECF 6AF CE ==8AB BC BE CE ==+=ABCD 90AD BC AB CD ABE =∠=︒∥,,AE CF AECF 6AF CE ==8AB BC BE CE ==+=1128822ABE S AB BE =⋅=⨯⨯=△ABCD Y 5BC =20ABCD S = C BC C C AD【答案】B【解析】【分析】本题考查了平行四边形的面积,直线与圆的位置关系d 、r 法则,熟练掌握法则是解题的关键.根据面积公式计算点C 到的距离d ,比较d 与半径的大小判断即可.【详解】解:如图,∵在平行四边形中,,,设点C 到的距离为d ,∴点C 到的距离,∴直线与圆C 相交,即有2个交点,故选:B .二、填空题:(本大题共12题,每题4分,满分48分)[请将结果直接填入答题纸的相应位置]7.=___.【答案】﹣2【解析】【分析】根据立方根的定义,求数a 的立方根,也就是求一个数x ,使得x 3=a ,则x 就是a 的立方根.【详解】∵(-2)3=-8,,故答案为:-28. 分解因式:_______.【答案】【解析】【分析】根据平方差公式因式分解即可求解.【详解】解:AD BC ABCD 5BC =20ABCD S = AD AD 2054d =÷= 45BC<=AD 2-229a b -=()()33a b a b +-229a b -=()()33a b a b +-故答案为:.【点睛】本题考查了因式分解,熟练掌握因式分解的方法是解题的关键.9. 解不等式:,的解集为________.【答案】【解析】【分析】本题主要考查的是解一元一次不等式;按照去括号、移项、合并同类项、系数化为1的步骤解一元一次不等式即可求解.【详解】解:去括号,移项,合并同类项,化系数为1,故答案为:.10. 函数的定义域是 【答案】>【解析】【分析】定义域是指该函数的自变量的取值范围,根据二次根号下被开方数≥0;分式中分母不为0;即可解答.【详解】定义域是指该函数的自变量的取值范围,二次根号下被开方数≥0;分式中分母不为0;∴∴故答案为11. 将抛物线先向右平移3个单位,再向下平移4个单位后,所得到的新抛物线的表达式为________.【答案】【解析】【分析】本题主要考查的是二次函数的图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.并()()33a b a b +-()5232x x +≤+2x ≤()5232x x +≤+5263+≤+x x5362x x -≤-24x ≤2x ≤2x≤y =10x +>1x >-1x >-()221y x =-+()253y x =--用规律求函数解析式.根据平移规律“左加右减,上加下减”写出新抛物线解析式.【详解】解:抛物线先向右平移3个单位,再向下平移4个单位后,所得到的新抛物线的表达式为,即.故答案为:.12. 在一个不透明袋子中,装有2个红球和一些白球,这些球除颜色外其他都一样,如果从袋中随机摸出一个球是红球的概率为,那么白球的个数是________.【答案】6【解析】【分析】本题考查了概率的定义.解题的关键与难点在于理解概率的定义,求出球的总数.随机摸出一个球是红球的概率是,可以得到球的总个数,进而得出白球的个数.【详解】解:设红、白球总共n 个,记摸出一个球是红球为事件A ,,白球有个故答案为:.13. 某校为了解该校1200名学生参加家务劳动的情况,随机抽取40名学生,调查了他们的周家务劳动时间并制作成频数分布直方图,那么估计该校周家务劳动时间不少于2小时的学生大约有________名.【答案】780【解析】【分析】本题主要考查了用样本估计总体,根据条形统计图获取信息是解题的关键.根据条形统计图直接得出家务劳动时间不少于2小时的学生有26名,进而估计该校1200名学生参加家务劳动时间不少于2小时的学生人数即可求解.()221y x =-+()22314y x =--+-()253y x =--()253y x =--0.2520.25n=()20.25P A n==8n ∴=∴826-=6【详解】解:由题意得:被调查的40人中,家务劳动时间不少于2小时的学生有26名,该校周家务劳动时间不少于2小时的学生大约有(名),故答案为:780.14. 一根蜡烛长30厘米,点燃后匀速燃烧,经过50分钟其长度恰为原长的一半.在燃烧的过程中,如果设蜡烛的长为(厘米),燃烧的时间为(分钟),那么关于的函数解析式为________(不写定义域).【答案】【解析】【分析】本题主要考查由实际问题列一次函数的解析式,解题的关键是理解题意.根据题意先求出蜡烛燃烧的速度为(厘米/分),即可直接进行求解.【详解】解:由题意可得:蜡烛长30厘米,经过50分钟其长度恰为原长的一半,经过50分钟蜡烛燃烧的长度为15厘米,蜡烛燃烧的速度为(厘米/分),蜡烛的长为蜡烛燃烧前长度减去燃烧的长度,,故答案为:.15. 如图,正六边形螺帽的边长是,那么这个扳手的开口的值是______.【答案】【解析】【分析】本题考查解直角三角形,等腰三角形的性质,含角的直角三角形的性质.由螺帽是正六边形,可得是含角的直角三角形,再根据即可求出和.【详解】解:如图,连接,则,过点作于∴26120078040⨯=y t y t 300.3y t=-15500.3÷=∴∴15500.3÷=300.3y t \=-300.3y t =-4cm a 30︒ACD 30︒4AC =AD AB AB a AB =C CD AB ⊥D螺帽是正六边形,,.故答案为:16. 如图,在梯形中,,,点、分别是边、的中点,连接,设,,那么用向量、表示向量________.【答案】【解析】【分析】本题考查了平面向量的问题,熟练掌握三角形法则是解题的关键,根据梯形的中位线定理及向量的三角形法则解答即可.【详解】解:,,,,, 120ACB ∴∠=︒CD AB ⊥AC BC=1120602ACD ∴∠=⨯︒=︒AD BD =4AC = 4AD AC ∴===22a AB AD ∴===⨯=ABCD AD BC ∥2BC AD =E F AB CD AC AB a =AC b = a b EF = 3344a b -+ AB a = AC b =BC BA AC a b \=+=-+ ,2AD BC BC AD = ∥111222AD BC a b \==-+,点、分别是边、的中点,,,,故答案为:.17. 如图,在中,,,.点在边上,,以点为圆心,为半径作.点在边上,以点为圆心,为半径作.如果和外切,那么的长为________.【答案】##【解析】【分析】本题考查的是圆和圆的位置关系、解直角三角形的知识,作于点H ,连接,先求出,设,在中,根据勾股定理列方程即可解决.【详解】解:作于点H ,连接,,,,在中,,11112222DC DA AC AD AC a b b a b \=+=-+=-+=+ E F AB CD 111222EA BA AB a \==-=- 111244DF DC a b \==+ 11111332224444EF EA AD DF a a b a b a b æöæöç÷ç÷\=++=-+-+++=-+ç÷ç÷èøèø3344a b -+ ABCD Y 7AB =8BC =4sin 5B =P AB 2AP =P AP P Q BC Q CQ Q P Q CQ 37149214PH BC ⊥PQ 43PH BH ==,CQ a =Rt QPH △PH BC ⊥PQ 7AB = 2AP =725BP \=-=Rt BPH 4sin 5B =,,设,和外切,半径为2,,在中,,,解得:,故答案为:.18. 如图,在扇形中,,,点在半径上,将沿着翻折,点的对称点恰好落在弧上,再将弧沿着翻折至弧(点是点A 的对称点),那么的长为________.【答案】##【解析】【分析】本题考查翻折性质,圆的基本性质,等边三角形判定与性质、勾股定理的应用,连接,由翻折得,证出是等边三角形,设,在中,根据勾股定理列方程并解出进而求出结论.【详解】解:连接,455PH \=43PH BH \==,CQ a =P Qe Q P 2PQ a \=+Rt QPH △4,835PH HQ a a ==--=-()()222452a a ∴+-=+3714a =3714AOB 105AOB ∠=︒8OA =C OA BOC BC O D AB AD CD 1A D 1A 1OA 8-8-+OD 1105OB BD AC A C BOC BDC ==∠=∠=︒,,OBD AC a =Rt COD AC OD由翻折得:,,,是等边三角形,,,设,则,在中,,,解得:(舍去),,故答案为:.三、解答题:(本大题共7题,满分78分)19.先化简,再求值:,其中.【答案】【解析】【分析】本题主要考查分式的化简求值,分母有理化,掌握分式的基本性质与运算法则是解题的关键,注意化简过程中能因式分解要先因式分解.先算括号内的减法,把除法变成乘法,算乘法,最后代入求值即可.【详解】解:1105OB BD AC A C BOC BDC ==∠=∠=︒,,OC CD =OB OD = OBD ∴△60OBD ∴∠=︒3601051056090OCD \Ð=°-°-°-°=°AC a =1882OC a CD A O a =-==-,Rt COD 8OC CD a ==-()()222888a a ∴-+-=12888a a =-=+>(128288OA OA AC ∴=-=--=8-22214133m m m m m -+⎛⎫÷- ⎪++⎝⎭m 1m m -22214133m m m m m -+⎛⎫÷- ⎪++⎝⎭()()2134333m m m m m m -+⎛⎫=÷- ⎪+++⎝⎭;当.20. 解方程组:【答案】【解析】【分析】将第二个方程进行因式分解得到,然后令因式和因式分别为0即可求解.【详解】解:由题意可知: 对方程②进行因式分解得:即或∴原方程组化为 或 解得或故原方程组的解为:或.【点睛】本题考查了因式分解的方法及二元方程组,熟练掌握常见的二元一次方程组的解法是解决此类题的关键.21. 如图,一次函数图像在反比例函数图像相交于点和点,与轴交于点.点在反比例函数图像上,过点作轴的垂线交一次函数图像于点.()()21133m m m m m --=÷++()()21331m m m m m -+=⨯+-1m m-=m =1m m -222-620x y x xy y =⎧⎨--=⎩121242,22x x y y ==⎧⎧⎨⎨==-⎩⎩()(2)0+-=x y x y 2x y -x y +222-620x y x xy y =⎧⎨--=⎩①②()(2)0+-=x y x y 20x y -=0x y +=2620x y x y -=⎧⎨-=⎩260x y x y -=⎧⎨+=⎩1142x y =⎧⎨=⎩2222x y =⎧⎨=-⎩1142x y =⎧⎨=⎩2222x y =⎧⎨=-⎩(),2A m ()2,4B -y C ()1,D n -D x E(1)求反比例函数和一次函数的解析式;(2)求面积.【答案】(1)反比例函数为,一次函数解析式 (2)【解析】【分析】此题考查了反比例函数综合题,涉及的知识有:待定系数法确定反比例函数和一次函数解析式,三角形面积.()利用待定系数法求解即可;()先分别求出、、的坐标,进而利用三角形面积公式解答即可.【小问1详解】解:设反比例函数为,把点代入得,,∴反比例函数为,把点,点代入,得,,∴,,∴点,点,设一次函数解析式,的CDE 8y x=-2y x =--9212C D E k y x=()2,4B -k y x=428k =-⨯=-8y x=-(),2A m ()1,D n -8y x =-82m =-881n =-=-4m =-8n =()4,2A -()1,8D -y cx d =+把点,点代入得,解得,∴一次函数解析式;【小问2详解】∵一次函数解析式,∴把点代入,得,∴,∴点,∵轴,∴点横坐标为,把代入得,∴∴,∴22. 根据以下素材,完成探索任务.探究斜坡上两车之间距离素材1图①是某高架入口的横断面示意图.高架路面用表示,地面用表示,斜坡用表示.已知,高架路面离地面的距离为25米,斜坡长为65米.素如图②,矩形为一辆大巴车的侧面示意图,长为10米,长为的()4,2A -()2,4B -4224c d c d-=+⎧⎨=-+⎩12c d =-⎧⎨=-⎩2y x =--2y x =--()0,2C -,()1,D n -8y x =-881n =-=-8n =()1,8D -DE x ⊥E 1-1x =-2y x =--121y =-=-()1,1E --,189DE =+=119191222CDE S DE =⋅=⨯⨯= .BM AN AB BM AN ∥BM BH AB ECKG CK EC 3.5材2米.如图③,该大巴车遇堵车后停在素材1中的斜坡上,矩形的顶点与点重合,点与指示路牌底端点之间的距离为米,且.小张驾驶一辆小轿车跟随大巴车行驶,小张的眼睛到斜坡的距离为1米.任务一如图①,求斜坡的坡比.问题解决任务二如图③,当小张正好可以看到整个指示路牌(即、、在同一条直线上)时,试求小张距大巴车尾的距离.【答案】任务一:斜坡的坡比;任务二:米【解析】【分析】本题考查的是解直角三角形坡度坡角问题及相似三角形判定与性质,矩形判定与性质,任务一:根据勾股定理求出第三边进而求出坡度;任务二:作交延长线于点O ,作于点Q ,交于点R ,通过解直角三角形结合矩形判定与性质求出相关线段长度,再证明,根据性质求出结论即可.【详解】解:任务一:如图①,由题意得:在中,25米,斜坡长为65米,(米),斜坡的坡比;任务二:如图③,作交延长线于点O ,作于点Q ,交于点R ,为ECKG K B B P BP 6.5BP BM ⊥FD AB P E F EC CD AB 1:2.4i =12.5PO DB ⊥DB FQ PO ^CE FER FPQ ∽Rt ABH △BH AB 60AH \=∴AB 251:2.460BH i AH ===PO DB ⊥DB FQ PO ^CE则四边形为矩形,四边形为矩形,米,米,,为米,,解得:米,米,米,米,,,,,,解得:,经检验,是原方程的解,米.23. 如图,在中,,延长至点,使得,过点、分别作,,与相交于点,连接.CRQO FDCR,1RQ CO FR DC FD CR OQ\=====,3.51 2.5ER\=-=,90ABH PBO O HÐ=ÐÐ=Ð=°BP 6.525cos cos6.565BOPBO ABH\Ð==Ð=2.5BO=6PO\==615PQ∴=-=10 2.512.5RQ CO==+=,EC AB PQ AB^^ER PQ\∥FER FPQ\∽ER FRPQ FQ\=2.5512.5FRFR\=+12.5FR=12.5FR=12.5CD FR\==Rt ABC△90C∠=︒CB D DB CB=A DAE BC∥DE BA∥AE DE E BE(1)求证:;(2)连接交于点,连接交于点.如果,求证:.【答案】(1)证明见解析(2)证明见解析【解析】【分析】本题考查平行四边形的判定与性质,矩形的判定与性质,勾股定理等,解题的关键是掌握平行四边形和矩形的判定方法.(1)先证四边形是平行四边形,得出从而证出四边形是矩形,即可证明结论;(2)设,算出,证明,求出 ,进而证出结论;【小问1详解】证明:,,四边形是平行四边形,,,,又,点D 在的延长线上,,四边形是平行四边形,又,四边形是矩形,;【小问2详解】解:如图,BE CD ⊥AD BE F CE AD G FBA ADB ∠=∠AG AB =AEDB AE CB =AEBC EF BF a ==AE =AEG DCG V ∽△AGAB = AE BD DE BA ∥∴AEDB ∴AE BD = BD CB =∴AE CB = AE BD CB ∴AE CB ∥∴AEBC 90C ∠=︒∴AEBC ∴BE CD ⊥四边形是平行四边形,,设,,,,,,,,,,,在中,,,,在中,,AEDB ,EF BF AF DF \==EF BF a ==FBA ADB Ð=Ð tan tan FBA ADB \Ð=ÐAE BF BE BD\=AE BD = 222AE a \=AE ∴=BD BC AE \==AE CD AEG DCG \ ∽12AE AG CD DG \==Rt DBF △DF ==AD \=AG \=Rt ABC △AB ==.24. 新定义:已知抛物线(其中),我们把抛物线称为的“轮换抛物线”.例如:抛物线的“轮换抛物线”为.已知抛物线:的“轮换抛物线”为,抛物线、与轴分别交于点、,点在点的上方,抛物线的顶点为.(1)如果点的坐标为,求抛物线的表达式;(2)设抛物线的对称轴与直线相交于点,如果四边形为平行四边形,求点的坐标;(3)已知点在抛物线上,点坐标为,当时,求的值.【答案】(1) (2) (3)或【解析】【分析】本题考查的是二次函数综合题,重点考查二次函数的性质、平行四边形性质及相似三角形性质,(1)将点代入表达式,求出m 的值,根据“轮换抛物线”定义写出即可;AG AB \=AG AB \=2y ax bx c =++0abc ≠2y cx ax b =++2y ax bx c =++2231y x x =++223y x x =++1C ()2445y mx m x m =+-+2C 1C 2C y E F E F 2C P E ()0,12C 2C 38y x =+Q PQEF E ()4,M n -2C N 12,72⎛⎫-- ⎪⎝⎭PMN PEF △∽△m 241y x x =+-20,3E ⎛⎫- ⎪⎝⎭1m =-1732()0,1E(2)根据轮换抛物线定义得出抛物线表达式及点E 、F 坐标,并求出P 、Q 坐标,根据平行四边形性质得出列方程并解出m 值,进而解决问题;(3)先求,结合求出的点P 、E 、F 坐标得出及,根据相似三角形性质得出关于m 的方程,解方程即可解决.【小问1详解】解:抛物线:与轴交于点坐标为,当,代入,得,,抛物线表达式为,抛物线的“轮换抛物线”为表达式为;【小问2详解】解:抛物线:,当时,,即与y 轴交点为,抛物线:的“轮换抛物线”为,抛物线表达式为,同理抛物线与y 轴交点为,抛物线对称轴为直线,当时,,抛物线的顶点坐标为,当时,,抛物线的对称轴与直线交点,点在点的上方,,解得:,2C PQ EF =()4,45M m --2PN 2PF 1C ()2445y mx m x m =+-+y E ()0,10x =1y =1m =451m \-=-∴1C 241y x x =-+∴1C 2C 241y x x =+-1C ()2445y mx m x m =+-+0x =y m =()0,E m 1C ()2445y mx m x m =+-+2C ∴2C ()2445y mx mx m =++-2C ()0,45F m -2C 422m x m=-=-2x =-5y =-∴2C ()25P --,2x =-382y x =+=∴2C 38y x =+()2,2Q - E F 45m m \>-53m <,四边形为平行四边形,,即,解得:,;【小问3详解】解:点在抛物线上,当时,,即,点坐标为,,,,,,,,,,解得:.25. 在梯形中,,点在射线上,点在射线上,连接、相交于点,.()4553EF m m m \=--=- PQEF PQ EF \=()2553m --=-23m =-20,3E ⎛⎫∴- ⎪⎝⎭ ()4,M n -2C 4x =-()244545y mx mx m m =++-=-()4,45M m -- N 12,72⎛⎫-- ⎪⎝⎭()25P --,()0,E m ()0,45F m -()222125225724PN æöç÷\=-++-+=ç÷èø()()22222455416PF m m =-+-+=+()115325322PEF P S EF x m m =×=-´=- ()111557242222PMN M P S PN x x æöç÷=×-=´-+´-+=ç÷èø PMN PEF ∽222PEF PMN S PF PF S PN PN æöç÷\==ç÷èø 25341652524m m -+\=12171,32m m =-=ABCD AD BC ∥E DA F AB CE DF P EPF ABC ∠=∠(1)如图①,如果,点、分别在边、上.求证:;(2)如图②,如果,,,.在射线的下方,以为直径作半圆,半圆与的另一个交点为点.设与弧的交点为.①当时,求和的长;②当点为弧的中点时,求的长.【答案】(1)见解析(2)①;;②【解析】【分析】(1)根据等腰梯形的性质可得,,,根据三角形的外角性质得出,进而可得,即可证明,根据相似三角形的性质,即可求解;(2)①同(1)证明,如图所示,过点作于点,连接,得出,,解直角三角形,分别求得,,进而根据相似三角形的性质求得的长;②根据题意画出图形,根据垂径定理得出,根据题意可设,,则,得出,设,则,则,在中,得出,根据得出,即可求解.【小问1详解】证明:∵梯形中,,,∴,,,又∵,∴AB CD =E F ADAB AF DF DE CE =AD CD ⊥5AB =10BC =3cos 5ABC ∠=DA DE O O CE G DF EG Q 6DE =EG AF Q EG AF EG =215AF =15B DCB DCE BCE ∠=∠=∠+∠A EDC ∠=∠DEC BCE ∠=∠FPE CED EDP ∠=∠+∠ADF DCE ∠=∠ADF DCE ∽ADF PDE ∽A AM BC ⊥M DG cos DEC ∠=sin DEC ∠=EG EP AF OQ EQ ⊥EPF ABC α∠=∠=ODQ OQD β∠=∠=90αβ+=︒43tan tan 34αβ==12FR a =9AR a =15AF a =Rt DFR 16DR a =1697AD DR AR a a a =-=-=1a =ABCD AD BC ∥AB CD =B DCB DCE BCE ∠=∠=∠+∠A EDC ∠=∠DEC BCE ∠=∠FPE CED EDP ∠=∠+∠EPF ABC∠=∠ADF DCE∠=∠∴,∴;【小问2详解】解:∵,∵,则∴∴∵∴又∵∴,如图所示,过点作于点,连接,∵,∴,则,,∵∴∵∴又∵∴,在中,∴∴,ADF DCE ∽AF DF DE CE=EPF ABC ∠=∠DPC EPF∠=∠180FPC DPC ∠+∠=︒180FPC B ∠+∠=︒180ECB PFB ∠+∠=︒ECB AFD∠=∠AD BC∥ECB DEC∠=∠EDP FDA∠=∠ADF PDE ∽A AM BC ⊥M DG 5AB =3cos 5ABC ∠=3BM =4AM =4sin 5AM ABC AB ∠==,AD BC AD CD⊥∥4CD AM==10BC =1037AD MC BC BM ==-=-=6DE =1AE=Rt EDC 6,4ED CD ==EC ===cos DE DEC EC ∠===sin DC DEC EC ∠===∵为直径∴∴,∴,∵∴∴②过点作于点,∵∴∵∴设,,则ED 90DGE ∠=︒cos 6EG ED DEC =⨯∠==sin 6DG ED DEC =∠==sin sin DG DG PD DPG ABC ====∠∠3cos 5PG PD DPG =∠==EP EG PG =-=ADF PDE∽AF AD PE PD=215D A PE AF PD ⋅===F FR AD ⊥R EQGQ =OQ EQ⊥OQ OD=ODQ OQD∠=∠EPF ABC α∠=∠=ODQ OQD β∠=∠=90αβ+=︒∵,则设,则∴∵∴设,则,∴,在中,∴又∵∴∴【点睛】本题考查了解直角三角形,等腰梯形的性质,相似三角形的性质与判定,垂径定理,熟练掌握以上知识是解题的关键.3cos os cos 5DPG EPF ABC ∠=∠=∠=35PG PD =3,5PG k PD k ==4GD k =43tan tan 34αβ==AD BC∥RAF α∠=12FR a =9AR a =15AF a =Rt DFR 3tan 4RF DR β==16DR a=1697AD DR AR a a a =-=-=7=1a =15AF =。
上海数学中考二模复习第23题相似专题

1.已知:如图,在△ABC中,AB=AC=6,BC=4,AB的垂直平分线交AB于点E,交BC的延长线于点D.(1)求CD的长;(2)求点C到ED的距离.2.如图,已知在▱ABCD中,AE⊥BC,垂足为E,CE=AB,点F为CE的中点,点G在线段CD上,联结DF,交AG于点M,交EG于点N,且∠DFC=∠EGC.(1)求证:CG=DG;(2)求证:CG2=GM•AG.3.如图,已知在正方形ABCD中,对角线AC与BD交于点O,点M在线段OD 上,联结AM并延长交边DC于点E,点N在线段OC上,且ON=OM,联结DN 与线段AE交于点H,联结EN、MN.(1)如果EN∥BD,求证:四边形DMNE是菱形;(2)如果EN⊥DC,求证:AN2=NC•AC.4.如图,已知四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB,垂足为点H,交AC于E,联结HO并延长交CD于点G,(1)求证:∠DHO=1∠BCD;2(2)求证:HG•AE=2DE•CG.5.如图,已知,在平行四边形ABCD中,E为射线CB上一点,联结DE交对角线AC于点F,∠ADE=∠BAC.(1)求证:CF•CA=CB•CE;(2)如果AC=DE,求证:四边形ABCD是菱形.6.如图,CD是直角△ABC斜边AB上的中线,点E位于边AC上,且∠ADE=∠B-∠A.(1)求证:△CDE∽△ABC;(2)当DA:EA=√6:1时,求△CDE与△ABC的面积比.7.如图,在△ACB中,∠ABC=90°,点D是斜边AC的中点,四边形CBDE是平行四边形.(1)如图1,延长ED交AB于点F,求证:EF垂直平分AB;(2)如图2,联结BE、AE,如果BE平分∠ABC,求证:AB=3BC.8.如图,在▱ABCD中,∠BAD的平分线交边BC于点E,交DC的延长线于点F,点G在AE 上,联结GD,∠GDF=∠F.(1)求证:AD2=DG•AF;(2)联结BG,如果BG⊥AE,且AB=6,AD=9,求AF的长.9.如图,在▱ABCD中,点G是边BC延长线上一点,联结AG分别交BD和CD于点E和F,联结DG.(1)求证:AE2=EF•EG;(2)如果∠ABD=∠AGD,求证:四边形ABGD是等腰梯形.10.如图,已知四边形ABCD中,AD∥BC,对角线AC、BD相交于点O,AC 平分∠BAD,BD平分∠ABC,点E在边BC的延长线上,联结OE,交边CD 于点F.(1)求证:四边形ABCD是菱形;(2)如果OE⊥CD,求证:CE•OF=CF•OE.11.如图,已知在梯形ABCD中,AD∥BC,对角线BD平分∠ABC,点G在底边BC上,联结DG交对角线AC于F,∠DGB=∠DAB.(1)求证:四边形ABGD是菱形;(2)联结EG,求证:BG•EG=BC•EF.12.已知:如图,在梯形ABCD中,AD∥BC,∠B=90°,E是AC的中点,DE 的延长线交边BC于点F.(1)求证:四边形AFCD是平行四边形;(2)如果2AE2=AD•BC,求证:四边形AFCD是菱形.13.已知:如图,梯形ABCD中,AD∥BC,AB=DC,点E在下底BC上,∠AED=∠B.(1)求证:CE•AD=DE2;(2)求证:CEAD =AB2AE2.14.如图,在梯形ABCD中,AD∥BC,AB=CD,过点A作AE⊥BC,垂足为点E,过点E作EF⊥CD,垂足为点F,联结DE,且DE平分∠ADC.(1)求证:△ABE≌△ECF;(2)联结BD,BD与AE交于点G,当AB2=BG•BD时,求证EC2=BE•BC.15.如图,已知在直角梯形ABCD中,AD∥BC,∠ABC=90°,AE⊥BD,垂足为E,联结CE,作EF⊥CE,交边AB于点F.(1)求证:△AEF∽△BEC;(2)若AB=BC,求证:AF=AD.16.如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.(1)求证:AC2=CD•BC.(2)过E做EG⊥AB,延长EG至点F,使FG=EG,若∠B=30°,求证:四边形AFEC是菱形17.已知:如图,在四边形ABCD中,AB∥DC,对角线AC、BD交于点O,过点C作CE⊥CD交AB的延长线于点E,联结OE,OC=OE.(1)求证:OE=1AC;2(2)如果DB平分∠ADC,求证:四边形ABCD是菱形.18.已知:如图,在正方形ABCD中,联结BD,E是边AB上一点,BF⊥DE,垂足为点F,且EF•BD=BE•BF.(1)求证:∠ADE=∠BDE;(2)延长DF与CB的延长线交于点G,求证:BG=BC+AE.19.在平面直角坐标系xOy(如图)中,二次函数f(x)=ax2-2ax+a-1(其中a 是常数,且a≠0)的图象是开口向上的抛物线.(1)求该抛物线的顶点P的坐标;(2)我们将横、纵坐标都是整数的点叫做“整点”,将抛物线f(x)=ax2-2ax+a-1与y轴的交点记为A,如果线段OA上的“整点”的个数小于4,试求a的取值范围;(3)如果f(-1)、f(0)、f(3)、f(4)这四个函数值中有且只有一个值大于0,试写出符合题意的一个函数解析式;结合函数图象,求a的取值范围.20.已知:四边形ABCD是正方形,点E是BC边的中点,点F在边AB上,联结DE、EF.(1)如图1,如果tan∠BEF=1,求证:EF⊥DE;2(2)如图2,如果tan∠BEF=34,求证:∠DEF=3∠CDE.21.已知:如图,在▱ABCD中,点E、F分别在边BC、边BC的延长线上,四边形AEFD是菱形,菱形的对角线AF分别交DE、DC于点P、Q,AFBF =EFPF.求证:(1)四边形ABCD为矩形;(2)BE•DQ=FQ•PE.。
(完整版)上海市2019年初三中考数学二模汇编_23题几何证明

上海市2019年中考二模数学汇编:23题几何证明 闵行 23.(本题共2小题,每小题6分,满分12分)如图,已知四边形ABCD 是菱形,对角线AC 、BD 相交于点O ,BD = 2AC .过点A 作AE ⊥CD ,垂足为点E ,AE 与BD 相交于点F .过点C 作CG ⊥AC ,与AE 的延长线相交于点G . 求证:(1)△ACG ≌△DOA ;(2)2DF BD DE AG ⋅=⋅.宝山23.(本题满分12分,第(1)、第(2)小题满分各6分)如图,在矩形ABCD 中,E 是AB 边的中点,沿EC 对折矩形ABCD ,使B 点落在点P 处,折痕为EC ,联结AP 并延长AP 交CD 于F 点, (1)求证:四边形AECF 为平行四边形;(2)如果PA=PC ,联结BP ,求证:△APB ≅△EPC .ABCDOE GF(第23题图)A B CDOE H F第23题图23.(本题满分12分,每小题满分各6分)如图7,在直角梯形ABCD 中,90ABC ∠=︒,AD BC ∥,对角线AC 、BD 相交于点O . 过点D 作DE BC ⊥,交AC 于点F . (1)联结OE ,若BE AOEC OF=,求证:OE CD ∥; (2)若AD CD =且BD CD ⊥,求证:AF DFAC OB=. 奉贤23.(本题满分12分,每小题满分各6分)已知:如图8,正方形ABCD ,点E 在边AD 上,AF ⊥BE ,垂足为点F ,点G 在线段BF 上,BG=AF .(1)求证:CG ⊥BE ;(2)如果点E 是AD 的中点,联结CF ,求证:CF=CB . 金山22. 已知:如图,菱形ABCD 的对角线AC 与BD 相交于点O ,若DBC CAD ∠=∠.(1)求证:ABCD 是正方形.(2)E 是OB 上一点,CE DH ⊥,垂足为H ,DH 与OC 相交于点F ,求证:OF OE =.ABCDOE F图7ABCD FGE 图823.(本题满分12分)已知:如图10,在四边形ABCD 中,AD BC <,点E 在AD 的延长线上, ACE BCD ∠=∠,EC ED EA =⋅2. (1)求证:四边形ABCD 为梯形; (2)如果EC ABEA AC=,求证:AB ED BC =⋅2. 杨浦23. 已知:在ABC 中,AB=BC ,∠ABC=90°,点D 、E 分别是边AB 、BC 的中点,点F 、G 是边AC 的三等分点,DF 、EG 的延长线相交于点H ,联结HA 、HC. 求证:(1)四边形FBGH 是菱形;(2)四边形ABCH 是正方形.长宁23.(本题满分12分,第(1)小题5分,第(2)小题7分)图10A BCD E如图5,平行四边形ABCD 的对角线BD AC 、交于点O ,点E 在边CB 的延长线上,且︒=∠90EAC ,EC EB AE ⋅=2. (1)求证:四边形ABCD 是矩形;(2)延长AE DB 、交于点F ,若AC AF =,求证:BF AE =. 黄浦嘉定23.静安图5AB CDE FO松江徐汇答案 闵行23.证明:(1)在菱形ABCD 中,AD = CD ,AC ⊥BD ,OB = OD .∴ ∠DAC =∠DCA ,∠AOD = 90°.……………………………(1分) ∵ AE ⊥CD ,CG ⊥AC ,∴ ∠DCA +∠GCE = 90°,∠G +∠GCE = 90°.∴ ∠G =∠DCA .…………………………………………………(1分) ∴ ∠G =∠DAC .…………………………………………………(1分) ∵ BD = 2AC ,BD = 2OD ,∴ AC = OD . ……………………(1分) 在△ACG 和△DOA 中,∵ ∠ACG =∠AOD ,∠G =∠DAC ,AC = OD ,∴ △ACG ≌△DOA . ……………………………………………(2分) (2)∵ AE ⊥CD ,BD ⊥AC ,∴ ∠DOC =∠DEF = 90°.…………(1分) 又∵ ∠CDO =∠FDE ,∴ △CDO ∽△FDE .…………………(1分)∴ CD OD DF DE=.即得 OD DF DE CD ⋅=⋅. ……………………(2分) ∵ △ACG ≌△DOA ,∴ AG = AD = CD . ……………………(1分)又∵ 12OD BD =,∴ 2DF BD DE AG ⋅=⋅.…………………(1分)宝山23.(1)证明:由折叠得到EC 垂直平分BP , ………………1分 设EC 与BP 交于Q ,∴BQ=EQ ………………1分 ∵E 为AB 的中点, ∴AE =EB , ………………1分 ∴EQ 为△ABP 的中位线,∴AF ∥EC , ………………2分 ∵AE ∥FC , ∴四边形AECF 为平行四边形; ………………1分 (2)∵AF ∥EC ,∴∠A PB =∠EQB =90° ………………1分由翻折性质∠E PC =∠EBC =90°,∠PEC =∠BEC ………………1分 ∵E 为直角△APB 斜边AB 的中点,且AP =EP ,∴△AEP 为等边三角形 , ∠BAP =∠AEP =60°, ………………1+1分︒=︒-︒=∠=∠60260180CEB CEP ………………1分 在△ABP 和△EPC 中, ∠BAP =∠CEP ,∠APB=∠E PC ,AP =EP ∴△ABP ≌△EPC (AAS ), ………………1分 崇明23.(本题满分12分,每小题满分各6分) 证明(1)∵90ABD ∠=︒,BC DE ⊥∴//AB DE ………………………………………………………………(1分)∴AO BOOF OD=………………………………………………………………(2分) ∵BE AOEC OF =∴AO BEOF EC=……… ………………………………………………………(2分) ∴//OE CD …………………………………………………………………(1分) (2)∵BC AD //,//AB DE ,∴四边形ABED 为平行四边形 又∵90ABD ∠=︒∴四边形ABED 为矩形 ……………………………………………………(1分) ∴AD BE =,90ADE ∠=︒ 又∵CD BD ⊥∴90BDC BDE CDE ∠=∠+∠=︒︒=∠+∠=∠90BDE ADB ADE∴CDE ADB ∠=∠ …………………………………………………………(1分)AD CD =∴DCA DAC ∠=∠∴()A S A CDF ADO ..∆≅∆…………………………………………………(1分) ∴OD DF =DE AB // ∴AF BE AD AC BC BC==…………………………………………………………(1分) ∵BC AD //∴BODFBO OD BC AD ==…………………………………………………………(1分) ∴AF DFAC OB=…………………………………………………………………(1分) 奉贤22.证明:(1)∵四边形ABCD 是正方形,∴AB BC =.90ABC. ············· (1分) ∵AF ⊥BE ,∴90FAB FBA ∠+∠=︒.∵90FBA CBG ∠+∠=︒,∴FAB CBG ∠=∠. ·········································· (1分) 又∵AF BG =,∴△AFB ≅△BGC . ···························································· (2分) ∴AFB BGC ∠=∠. ····························································································· (1分) ∵90AFB ∠=︒,∴90BGC ∠=︒,即CG ⊥BE . ··········································· (1分) (2)∵ABF EBA ∠=∠,90AFB BAE ∠=∠=︒,∴△AEB ∽△FAB .∴AE AFAB BF=. ································································· (3分) ∵点E 是AD 的中点,AD AB =,∴12AE AB =.∴12AF BF =.·························· (1分) ∵AF BG =,∴12BG BF =,即FG BG =.·························································· (1分) ∵CG ⊥BE ,∴CF CB =. ···················································································· (1分)金山23.(1)证明:∵四边形ABCD 是菱形,∴BC AD //,DAC BAD ∠=∠2,DBC ABC ∠=∠2; (2分) ∴ 180=∠+∠ABC DAB ; (1分) ∵DBC CAD ∠=∠;∴ABC BAD ∠=∠, (1分) ∴ 1802=∠BAD ; ∴ 90=∠BAD ; (1分) ∴四边形ABCD 是正方形. (1分) (2)证明:∵四边形ABCD 是正方形;∴BD AC ⊥,BD AC =,AC CO 21=,BO DO 21=; (1分) ∴ 90=∠=∠DOC COB ,DO CO =; (1分) ∵CE DH ⊥,垂足为H ;∴ 90=∠DHE , 90=∠+∠DEH EDH ; (1分) 又∵ 90=∠+∠DEH ECO ; ∴EDH ECO ∠=∠; (1分)∴ECO ∆≌FDO ∆; (1分) ∴OF OE =. (1分)普陀 23.证明:(1)∵ ACE BCD ∠=∠,∴DCE BCA ∠=∠. ······················································ (1分)∵EC ED EA =⋅2,∴ED ECEC EA=. ······································································· (1分) 又∵E ∠是公共角,∴△EDC ∽△ECA . ····························································· (1分) ∴DCE CAE ∠=∠. ································································································· (1分) ∴BCA CAE ∠=∠.∴AD ∥BC . ············································································································· (1分) ∵AD BC <,∴AB 与CD 不平行.∴四边形ABCD 是梯形. ··························································································· (1分)(2)∵△EDC ∽△ECA .∴EC CDEA AC =. ∵EC AB EA AC=,∴AB DC =.·············································································· (1分) ∴四边形ABCD 是等腰梯形. ··············································································· (1分) ∴B DCB ∠=∠.··································································································· (1分) ∵AD ∥BC .∴EDC DCB ∠=∠. ∴EDC B ∠=∠.∵ECD ACB ∠=∠,∴△EDC ∽△ABC . ····················································· (1分) ∴ED DCAB BC=. ········································································································ (1分) ∴AB ED BC =⋅2. ····························································································· (1分) 杨浦23.(1)证明略 (2)证明略 长宁 23.(本题满分12分,第(1)小题5分,第(2)小题7分)证明:(1)∵EC EB AE ⋅=2 ∴AEEB EC AE =又 ∵CEA AEB ∠=∠ ∴AEB ∆∽CEA ∆ (2分) ∴EAC EBA ∠=∠∵︒=∠90EAC ∴︒=∠90EBA (1分) 又 ∵︒=∠+∠180CBA EBA ∴︒=∠90CBA (1分) ∵四边形ABCD 是平行四边形∴四边形ABCD 是矩形 (1分)(2)∵ AEB ∆∽CEA ∆ ∴ AC AB AE BE = 即 ACAE AB BE = , ECA EAB ∠=∠ (2分)∵四边形ABCD 是矩形 ∴BD AC =又 ∵BD OB 21=, AC OC 21= ∴OC OB = ∴ECA OBC ∠=∠ 又 ∵OBC EBF ∠=∠ ECA EBA ∠=∠ ∴EAB EBF ∠=∠又∵F F ∠=∠ ∴EBF ∆∽BAF ∆(3分)∴ABBEAF BF =∴ACAEAF BF =(1分)∵AC AF =∴AE BF = (1分) 黄浦嘉定静安松江徐汇。
2023年上海市松江区中考二模数学试卷(含答案解析)

2023年上海市松江区中考二模数学试卷学校:___________姓名:___________班级:___________考号:___________A.12二、填空题7.计算:23a a⋅=__________.8.因式分解:a2﹣3a=_______.三、解答题9.不等式组26 {2 xx>--+>15.已知相交两圆的半径长分别为一个符合条件的r 的值:16.一辆客车从甲地驶往乙地,米)与行驶的时间x (小时)之间的函数关系如图所示.已知私家车的速度是时,客车的速度是60千米17.已知ABCD 中,AB =4,∠ABC 则边AD 的长为_______.18.我们定义:二次项系数之和为作互为友好函数,那么224y x =+五、解答题19.计算:()1121823π--+-+20.解方程组:2221024x y x xy y --=⎧⎨++=⎩BC=,求cot B的值;(1)如果3=,求四边形ABCD(2)如果AB BC22.某校对六年级学生进行了一次安全知识测试,请根据所给信息,回答下列问题:(1)扇形图中,B等级所在扇形的圆心角为(2)此次测试成绩的中位数处在等级(3)该校决定对D等级的学生进行安全再教育,学生中,需接受安全再教育的约有多少人?23.如图,已知正方形⊥,垂足为点DN AE(1)求证:AM MN =;(2)连接BE ,求MBE ∠正弦值.24.在平面直角坐标系()21(0)y x t t =-->的顶点为(1)若抛物线经过点A ,求抛物线解析式;(2)将线段OB 绕点B 顺时针旋转坐标;(3)设抛物线的对称轴与直线45BOD ∠=︒,求t 的值.25.如图,AB 是半圆O 射线AO '交半圆O 于点(1)如图,如果点O '恰好落在半圆(2)如果30DAB ∠=o ,求(3)如果3,1OA O D =='参考答案:的重心,∵点G是ABCAC∴点D,E分别为,当120x x <<,根据图象可得:12>y y ,故答案为:>.【点睛】本题考查的是反比例函数的图象与性质,熟练的利用数形结合的方法解题是关键.故答案为:4(答案不唯一).【点睛】本题考查了圆与圆的位置关系:设两圆的圆心距为d,两圆半径分别为R 、,r 当两圆外离d R r ⇔>+;两圆外切d R r ⇔=+;两圆相交()R r d R r R r ⇔-<<+≥;两圆内切()d R r R r ⇔=->;两圆内含()d R r R r ⇔<->.16.()4,0【分析】观察图象得:点A 的实际意义是两车此时相遇,甲乙两地之间的距离为600千米,再根据两车行驶的路程之和等于600千米,即可求解.【详解】解:观察图象得:点A 的实际意义是两车此时相遇,甲乙两地之间的距离为600千米,因为私家车的速度是90千米/时,客车的速度是60千米/时,∴9060600x x +=,解得4x =,∴点A 的坐标是()4,0.故答案为:()4,0【点睛】本题主要考查了函数图象,明确题意准确从函数图象获取信息是解题的关键.17.5或11【分析】由平行四边形的性质和角平分线的定义证出∠ABE =∠AEB ,得出AE =AB =4,同理:DF =CD =4,再分两种情况计算即可.【详解】∵BE 平分∠ABC ,∴∠ABE =∠CBE ,∵四边形ABCD 是平行四边形,∴AD ∥CB ,CD =AB =4,∴∠AEB =∠CBE ∴∠ABE =∠AEB ,∴AE =AB =4,同理:DF =CD =4,分两种情况:①如图1所示:∵,AD BC AD CD ⊥∥,∴90AEC D BCD ∠=∠=∠=︒∴四边形ADCE 是矩形,∵,AD BC AD CD ⊥∥,∴90AEC D BCD ∠=∠=∠=︒,∴四边形ADCE 是矩形,∵1tan 2DE DAE AD ∠==又∵AM MN =,∴12DN AN MN ==,∵NDE ADN ADE ∠+∠=∠∴NDE DAN ∠=∠,∴1tan 2NE NDE DN ∠==,∴12NE DN =,设NE a =,则2DN a =在Rt DEN 中,DE =∴3ME MN NE a =+=,∴5EC DE a ==,在Rt BCE 中,5BE =∴3sin 5ME a MBE BE a ∠==∵旋转,∴,90OB OC OBC =∠=∴BEO OBC BDC ∠=∠=∠∴90OBE CBD ∠=︒-∠∴BEO CDB≌∴1,OE BD BE CD ===由2y x =-+,令0y =,得∴2OA OH ==,AH =∴OAH △是等腰直角三角形∵BD y ∥轴,∴DFH 是等腰直角三角形,∴2DF FH t ==-,则过点O 作OE AH ⊥,则2ED EH DH =-=-∴EOH EOD DOH ∠=∠+∠∵BOD FOB DOH ∠=∠+∠∴EOD FOB∠=∠又,OE ED BF OF⊥⊥∴tan tan EOD FOB∠=∠即DE FB OE OF=()211t -∵点O '恰好落在半圆O 上,∴OO OA '=,∵点O '与点O 关于直线AC 对称∴AO OA CO CO ==='',O AC '∠=∴OAO ' 是等边三角形, O C BC'=∴60OAO '∠=︒,∴(11802COO BOC OAO '∠=∠=︒-∠∴60AOO BOC '∠=∠=︒,∵,30OA OD OAD =∠=︒,∴,30120ODA OAD AOD ︒∠=∠=∠=在Rt AON △中,sin 30ON OA =⋅︒∵ON AD ⊥,∴223AD AN a ==,又∵2O A OA a '==,∴()232O D a '=-,∴23O N a a '=-,在Rt O ON ' 中,2OO ON ON '=+由轴对称可得:12O E OE OO ''==∴FN FM=∴1212AFD OFA AD FM S AD S AO AO FN ⨯==⨯ ,又∵AFD OFA S DF S OF = ,43AD DF AO OF ∴==,即43DF OF =,又∵3OF DF OD +==,∴97OF =;当O '在半圆O 外时,由对称性可得:如图:作FM AO '⊥于M ,FN AO ⊥∴FN FM =,∴1212AFD OFA AD FM S AD S AO AO FN ∆∆⨯==⨯,又∵AFD OFA S DF S OF ∆∆=,AD DF AO OF∴=,又∵31AD O A O D OA O D '''=-=-=-∴23DF OF =,即23DF OF =,。
2024年上海市杨浦区中考数学二模试卷及答案解析

2024年上海市杨浦区中考数学二模试卷一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.(4分)下列根式中,的同类二次根式是()A.B.C.D.2.(4分)已知a>b,下列不等式成立的是()A.﹣a>﹣b B.2﹣a<2﹣b C.2a<2b D.a﹣b<0 3.(4分)如果k<0,b<0,那么一次函数y=kx+b的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限4.(4分)已知一组数据a,2,4,1,6的中位数是4,那么a可以是()A.0B.2C.3D.55.(4分)下列命题中,真命题的是()A.四条边相等的四边形是正方形B.四个内角相等的四边形是正方形C.对角线互相垂直的平行四边形是正方形D.对角线互相垂直的矩形是正方形6.(4分)如图,在△ABC中,AB≠AC,∠BAC=120°,将△ABC绕点C逆时针旋转,点A、B分别落在点D、E处,如果点A、D、E在同一直线上,那么下列结论错误的是()A.∠ADC=60°B.∠ACD=60°C.∠BCD=∠ECD D.∠BAD=∠BCE 二、填空题:(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置上】7.(4分)计算:6a3÷2a2=.8.(4分)在实数范围内因式分解x2﹣3=.9.(4分)函数的定义域是.10.(4分)如果关于x的方程x2﹣6x+m=0有两个实数根,那么m的取值范围是.11.(4分)布袋中有大小、质地完全相同的5个小球,每个小球上分别标有数字1,2,3,4,5,如果从布袋中随机抽一个小球,那么这个小球上的数字是合数的概率是.12.(4分)若反比例函数的图象在每一个象限中,y随着x的增大而减小,则m的取值范围是.13.(4分)根据上海市统计局数据,上海市2021年的地区生产总值约是4.32万亿,2023年的地区生产总值约是4.72万亿,设这两年上海市地区生产总值的年平均增长率都为x,根据题意可列方程.14.(4分)如图,在平行四边形ABCD中,E是边AD的中点,CE与对角线BD相交于点F,设向量,向量,那么向量=.(用含、的式子表示)15.(4分)近年来越来越多的“社区食堂”出现在街头巷尾,它们是城市服务不断丰富的缩影.已知某社区食堂推出了15元、18元、20元三种价格的套餐,每人限购一份.据统计,3月16日该食堂销售套餐共计160份,其中15元的占总份数的40%,18元的卖出40份,其余均为20元,那么食堂这一天卖出一份套餐的平均价格是元.16.(4分)如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交边BC于点D,如果BD =4CD,那么tan B=.17.(4分)如图,已知一张正方形纸片的边长为6厘米,将这个正方形纸片剪去四个角后成为一个正八边形,那么这个正八边形的边长是厘米.18.(4分)已知矩形ABCD中,AB=5,以AD为半径的圆A和以CD为半径的圆C相交于点D、E,如果点E到直线BC的距离不超过3,设AD的长度为m,则m的取值范围是.三、解答题:(本大题共7题,满分78分)19.(10分)计算:()﹣1+()0﹣2+|1﹣|.20.(10分)解方程组:.21.(10分)如图,已知在△ABC中,AB=AC=9,,点G是△ABC的重心,延长AG交边BC于点D,以G为圆心,GA为半径的圆分别交边AB、AC于点E、F.(1)求AG的长;(2)求BE的长.22.(10分)寒假期间,小华一家驾车去某地旅游,早上6:00点出发,以80千米/小时的速度匀速行驶一段时间后,途经一个服务区休息了1小时,再次出发时提高了车速.如图,这是她们离目的地的路程y(千米)与所用时间x(小时)的函数图象.根据图象提供的信息回答下列问题:(1)图中的a=,b=;(2)求提速后y关于x的函数解析式(不用写出定义域);(3)她们能否在中午12:30之前到达目的地?请说明理由.23.(12分)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BD=BC,∠DBC的平分线交AD延长线于点E,交CD于点F.(1)求证:四边形BCED是菱形;(2)联结AC交BF于点G,如果AC⊥CE,求证:AB2=AG•AC.24.(12分)定义:我们把平面内经过已知直线外一点并且与这条直线相切的圆叫做这个点与已知直线的点切圆.如图1,已知直线l外有一点H,圆Q经过点H且与直线l相切,则称圆Q是点H与直线l的点切圆.阅读以上材料,解决问题;已知直线OA外有一点P,PA⊥OA,OA=4,AP=2,圆M是点P与直线OA的点切圆.(1)如果圆心M在线段OP上,那么圆M的半径长是(直接写出答案).(2)如图2,以O为坐标原点、OA为x轴的正半轴建立平面直角坐标系xOy,点P在第一象限,设圆心M的坐标是(x,y).①求y关于x的函数解析式;②点B是①中所求函数图象上的一点,联结BP并延长交此函数图象于另一点C.如果CP:BP=1:4,求点B的坐标.25.(14分)已知以AB为直径的半圆O上有一点C,CD⊥OA,垂足为点D,点E是半径OC上一点(不与点O、C重合),作EF⊥OC交弧BC于点F,联结OF.(1)如图1,当FE的延长线经过点A时,求的值;(2)如图2,作FG⊥AB,垂足为点G,联结EG.①试判断EG与CD的大小关系,并证明你的结论;②当△EFG是等腰三角形,且,求的值.2024年上海市杨浦区中考数学二模试卷参考答案与试题解析一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.【分析】将各式化为最简二次根式后判断被开方数是否相同即可.【解答】解:与不是同类二次根式,则A不符合题意;与不是同类二次根式,则B不符合题意;=2,它与不是同类二次根式,则C符合题意;=3,它与不是同类二次根式,则D不符合题意;故选:C.【点评】本题考查同类二次根式,熟练掌握其定义是解题的关键.2.【分析】根据不等式的性质逐项判断即可.【解答】解:已知a>b,两边同乘﹣1得﹣a<﹣b,则A不符合题意;两边同乘﹣1,再同时加2得2﹣a<2﹣b,则B符合题意;两边同乘2得2a>2b,则C不符合题意;两边同时减b得a﹣b>0,则D不符合题意;故选:B.【点评】本题考查不等式的性质,此为基础且重要知识点,必须熟练掌握.3.【分析】根据一次函数图象与系数的关系进行判断即可.【解答】解:当一次函数k<0,b<0,经过第二三四象限,不经过第一象限,故选:A.【点评】本题考查了一次函数的性质,熟练掌握一次函数的性质是解答本题的关键.4.【分析】当总数个数是奇数的话,按从小到大的顺序,取中间的那个数就是这组数据的中位数.而一组数a,2,4,1,6的中位数是4,所以前3个数是1,2,4,那么剩下的两个就是a,6,这样就知道a与4的大小关系.【解答】解:根据题意,得a,2,4,1,6的中位数是4,所以前3个数是1,2,4,那么剩下的两个就是a,6,所以a可以是大于或大于4的任意一个数.故选:D.【点评】本题考查了中位数的意义.如果总数个数是奇数的话,按从小到大的顺序,取中间的那个数;如果总数个数是偶数个的话,按从小到大的顺序,取中间那两个数的平均数.5.【分析】根据矩形、菱形、正方形的判定定理判断即可.【解答】解:A、四条边相等的四边形是菱形,不一定是正方形,故本选项命题错误,不符合题意;B、四个内角相等的四边形是矩形,不一定是正方形,故本选项命题错误,不符合题意;C、对角线互相垂直的平行四边形是是菱形,不一定是正方形,故本选项命题错误,不符合题意;D、对角线互相垂直的矩形是正方形,命题正确,符合题意;故选:D.【点评】本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.6.【分析】由旋转的性质可得△ABC≌△DEC,则CD=CA,∠BAC=∠EDC=120°,得出∠ADC=60°,进而得出△ADC是等边三角形,即可判断选项A,B,D结论正确.【解答】解:∵将△ABC绕点C逆时针旋转,点A、B分别落在点D、E处,∴△ABC≌△DEC,∴CD=CA,∠BAC=∠EDC=120°,得∴∠ADC=60°,故A正确;∴△ADC是等边三角形,∴∠ACD=60°,故B正确,∴∠DAC=60°,∠BAE=60°,∵∠BCE=∠ACD=60°,∴∠BAD=∠BCE,故D正确;∵∠ECD=∠BCA,BC不一定平分∠ACD,∴∠BCD不一定等于∠ECD,故选:C.【点评】本题考查旋转的性质,熟练掌握旋转的想知识解题关键.二、填空题:(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置上】7.【分析】根据整式除法的运算法则计算即可.【解答】解:6a3÷2a2=3a.故答案为:3a.【点评】本题考查了整式的除法,熟练掌握整式除法的运算法则是关键.8.【分析】根据平方差公式分解因式即可.【解答】解:.故答案为:.【点评】本题考查了实数范围内分解因式,掌握a2﹣b2=(a+b)(a﹣b)是解题的关键.9.【分析】本题考查了函数式有意义的x的取值范围.一般地从两个角度考虑:分式的分母不为0;偶次根式被开方数大于或等于0;当一个式子中同时出现这两点时,应该是取让两个条件都满足的公共部分.【解答】解:根据题意得到:x﹣1>0,解得x>1.故答案为:x>1.【点评】判断一个式子是否有意义,应考虑分母上若有字母,字母的取值不能使分母为零,二次根号下字母的取值应使被开方数为非负数.易错易混点:学生易对二次根式的非负性和分母不等于0混淆.10.【分析】由方程有两个实数根结合根的判别式,即可得出Δ=36﹣4m≥0,解之即可得出m的取值范围.【解答】解:∵关于x的方程x2﹣6x+m=0有两个实数根,∴Δ=(﹣6)2﹣4m=36﹣4m≥0,解得:m≤9.故答案为:m≤9.【点评】本题考查了根的判别式,牢记“当△≥0时,方程有两个实数根”是解题的关键.11.【分析】直接由概率公式求解即可.【解答】解:∵布袋中有大小、质地完全相同的5个小球,每个小球上分别标有数字1,2,3,4,5,其中4是合数,∴从布袋中随机抽一个小球,这个小球上的数字是合数的概率是,故答案为:.【点评】本题考查了概率公式以及合数,用到的知识点为:概率=所求情况数与总情况数之比.12.【分析】根据反比例函数的性质可得m﹣1>0,再解不等式即可.【解答】解:∵图象在每一个象限中y随着x的增大而减小,∴m﹣1>0,解得:m>1,故答案为:m>1.【点评】此题主要考查了反比例函数的性质,关键是掌握对于反比例函数(k≠0),(1)k>0,反比例函数图象在一、三象限;(2)k<0,反比例函数图象在第二、四象限内.13.【分析】根据上海市2021年的地区生产总值约是4.32万亿,2023年的地区生产总值约是4.72万亿,列方程即可.【解答】解:根据题意得,4.32(1+x)2=4.72,故答案为:4.32(1+x)2=4.72.【点评】本题考查了由实际问题抽象出一元二次方程,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列出方程.14.【分析】根据平面向量的平行四边形法则结合相似三角形对应边成比例即可求解.【解答】解:∵量,向量,∴,∵四边形ABCD是平行四边形,∴DE∥BC,∴△DEF∽BCF,∴,∵E是边AD的中点,AD=BC,∴,∴BF=BD,∴,故答案为:.【点评】本题考查了平面向量,相似三角形的判定与性质,平行四边形的性质,正确得出BF=BD是解题的关键.15.【分析】分别用单价乘以相应的百分比,计算即可得解.【解答】解:其中18元的占总份数的40÷160=25%,其中20元的占总份数的1﹣40%﹣25%=35%,15×40%+18×25%+20×35%=17.5(元),即食堂这一天卖出一份套餐的平均价格是17.5元.故答案为:17.5.【点评】本题考查了百分数的应用,解题的关键是求出相应的百分比.16.【分析】连接AD,根据垂直平分线的性质可知AD=DB,根据勾股定理求出AC的值,即可求解tan B.【解答】解:连接AD,∵BD=4CD,设CD=x,则BD=4x,BC=5x,∵AB的垂直平分线交边BC于点D,∴AD=DB=4x,∴AC===x,∴tan B==,故答案为:.【点评】本题考查解直角三角形,正确记忆相关知识点是解题关键.17.【分析】根据正方形和正八边形的性质以及勾股定理列方程求解即可》【解答】解:如图,设EF=x厘米,则AE=AQ==(3﹣x)厘米,由勾股定理得,AQ2+AE2=QE2,即(3﹣x)2+(3﹣x)2=x2,解得x=6﹣6,或x=﹣6﹣6(舍去),即正八边形的边长为(6﹣6)厘米,故答案为:(6﹣6).【点评】本题考查正多边形和圆,掌握正方形,正八边形的性质以及勾股定理是正确解答的关键.18.【分析】如图,当E在AB的左侧时,连接AC,AE,CE,过E作ER⊥BC于R,作ES ⊥AB于S,如图,当E在AB的右侧时,连接AC,AE,CE,过E作EH⊥BC于H,交AD于Q,再分别求解m的值,从而得到答案.【解答】解:如图,当E在AB的左侧时,连接AC,AE,CE,过E作ER⊥BC于R,作ES⊥AB于S,∵已知矩形ABCD,AB=5,AD=m,∴四边形ERBS为矩形,AD=CB=m,AB=CD=5,∵ES=BR,ER=BS=3,∴AS=5﹣3=2,∵A,C为圆心,∴AC是DE的垂直平分线,∴AD=AE=m,CD=CE=5,∵ER=3,∴CR==4,∴ES=BR=4﹣m,在Rt△AES中,m2=(4﹣m)2+22,解得:m=,如图,当E在AB的右侧时,连接AC,AE,CE,过E作EH⊥BC于H,交AD于Q,∵已知矩形ABCD,AB=5,AD=m,∴AD=CB=m,AB=CD=5,四边形CDQH为矩形,∴QH=CD=5,同理可得:AD=AE=m,CD=CE=5,∵EH=3,∴QD=CH==4,∴AQ=m﹣4,∵EQ=5+3=8在Rt△AEQ中,m2=(m﹣4)2+82,∴m=10,综上所述:点E到直线BC的距离不超过3,则≤m≤10;故答案为:≤m≤10.【点评】本题主要考查了矩形的判定与性质,勾股定理的应用,两圆的位置关系,线段的垂直平分线的性质等,确定临界点是解答本题的关键.三、解答题:(本大题共7题,满分78分)19.【分析】根据实数的运算和指数幂运算法则计算即可.【解答】解:原式=+1﹣+﹣1=﹣2=.【点评】本题考查的是实数的运算和指数幂,熟练掌握其运算法则是解题的关键.20.【分析】先化简组中的第二个方程,得两个二元一次方程与组中的第一个方程得新方程组,求解即可.【解答】解:,由②,得(x﹣2y)2=4,∴x﹣2y=±2.当x+2y=12,x﹣2y=2时,x=7,y=2.5;当x+2y=12,x﹣2y=﹣2时,x=5,y=3.5.∴原方程组的解为或.【点评】本题考查了二元二次方程组,把组中的二元二次方程化为一元一次方程,掌握二元一次方程组的解法是解决本题的关键.21.【分析】(1)由重心的性质得到D是BC中点,AG=AD,由锐角的余弦求出BD=3,由勾股定理求出AD==6,得到AG=×6=4;(2)连接EG,过G作GH⊥AE于H,由等腰三角形的性质得到AE=2AH,由锐角的余弦求出AH的长,即可得到AE的长,即可得到BE的长.【解答】解:(1)∵G是△ABC的重心,∴D是BC中点,AG=AD,∵AB=AC,∴AD⊥BC,∵cos B==,AB=9,∴BD=3,∴AD==6,∴AG=×6=4;(2)连接EG,过G作GH⊥AE于H,∵GA=GE,∴AE=2AH,∵∠AHG=∠ADB=90°,∠GAH=∠BAD,∴∠AGH=∠B,∴cos∠AGH=cos B=,∴=,∵AG=4,∴GH=,∴AH==,∴AE=2AH=,∴BE=9﹣=.【点评】本题考查解直角三角形,等腰三角形的性质,三角形的重心,关键是由重心的性质得到AG=AD,由锐角的余弦求出GH的长.22.【分析】(1)根据图象求出a的值,根据“离目的地的路程=家与目的地之间的距离﹣行驶的路程”可计算b的数值;(2)利用待定系数法求解即可;(3)当y=0时求出对应x的值,计算出到达目的地的时间,从而作出判断即可.【解答】解:(1)a=2+1=3,b=480﹣80×2=320,故答案为:3,320.(2)设提速后y关于x的函数解析式为y=kx+b(k、b为常数,且k≠0).将坐标(3,320)和(5,120)代入y=kx+b,得,解得,∴提速后y关于x的函数解析式为y=﹣100x+620.(3)能.理由如下:当她们到达目的地时,y=0,得﹣100x+620=0,解得x=6.2,6.2小时=6时12分,∴她们于12:12分到达目的地.【点评】本题考查一次函数的应用,掌握待定系数法求函数的解析式是本题的关键.23.【分析】(1)根据角平分线定义可得∠DBF=∠CBF,根据平行线的性质可得∠CBF=∠DEF,等量代换可得∠DBF=∠DEF,于是BD=DE,又因为BC∥DE,所以四边形BCED是平行四边形,再根据邻边相等的平行四边形是菱形即可得证;(2)如图,设BD与AC交于点H,根据等腰梯形的性质可得∠ABC=∠DCB,根据BD=BC,可得∠BCD=∠BDC,根据菱形的性质和垂直的定义可得∠DFG=90°,∠DHG=90°,根据四边形的内角和为360°,可得∠BDC+∠HGF=180°,又因为∠BGA+∠HGF=180°,可得∠BGA=∠BDC,于是∠ABC=∠BGA,再根据∠BAC=∠GAB即可得到△ABC ∽△AGB,利用相似三角形对应边的比相等即可得证.【解答】证明:(1)∵BF平分∠DBC,∴∠DBF=∠CBF,∵AD∥BC,∴∠CBF=∠DEF,∴∠DBF=∠DEF,∴BD=DE,∵BC∥DE,∴四边形BCED是平行四边形,∵BD=BC,∴平行四边形BCED是菱形;(2)如图,连接AC,交BD于点H,交BE于点G,在梯形ABCD中,AD∥BC,AB=CD,∴∠ABC=∠DCB,∵BD=BC,∴∠BCD=∠BDC,∴∠ABC=∠BDC,∵四边形BCED是菱形,∴BE⊥CD,BD∥CE,∴∠DFG=90°,∵AC⊥CE,∴AC⊥BD,∴∠DHG=90°,∵∠BDC+∠HGF+∠DHG+∠DFG=360°,∴∠BDC+∠HGF=180°,∴∠BGA+∠HGF=180°,∴∠BGA=∠BDC,∴∠ABC=∠BGA,∵∠BAC=∠GAB,∴△ABC∽△AGB,∴,∴AB2=AG•AC.【点评】本题考查了等腰梯形性质、等腰三角形的判定和性质、菱形的判定和性质定理、相似三角形的判定和性质等知识,熟练掌握相关知识是解答本题的关键.24.【分析】(1)作MB⊥x轴于点B,则MB=MP=r,可证得△OBM∽△OAP,从而,从而,从而求得r;(2)①根据圆心M到P的距离等于点P到x轴的距离得出(x﹣4)2+(y﹣2)2=y2,化简得出结果;②设点B(m,n),C(a,b),从而得出n=①,接PA,作BD⊥x轴,作CE⊥PA,交BD于D,可证得△CEP∽△CDB,从而,即,从而得出a=,b=,代入解析式得出=()2+1②,由①②得出m,n,进而得出结果.【解答】解:如图1,作MB⊥x轴于点B,则MB=MP=r,∵PA⊥x轴,∴MB∥PA,∴△OBM∽△OAP,∴,∴,∴r=,故答案为:;(2)①由题意得,圆心M到P的距离等于点P到x轴的距离,∴(x﹣4)2+(y﹣2)2=y2,∴y=;②如图2,设点B(m,n),C(a,b),∴n=①,连接PA,作BD⊥x轴,作CE⊥PA,交BD于D,∴PA∥BD,∴△CEP∽△CDB,∴,∴,∴a=,b=,∴=()2+1②,由①②得,,,∴B(8,5)或(0,5).【点评】本题考查了圆的切线的性质,相似三角形的判定和性质,勾股定理,解一元二次方程等知识,解决问题的关键是作辅助线,构造相似三角形.25.【分析】(1)利用垂径定理,直角三角形的性质,全等三角形的判定与性质解答即可;(2)①延长FE交⊙O于点M,延长FG交⊙O于点N,延长CD交⊙O于点H,连接MN,OH,ON,OM,利用垂径定理,三角形的中位线定理得到EG=MN,利用垂径定理得到CD=DH=CH,再利用四边形的内角和定理和邻补角的性质得到∠AOC=∠EFG,再利用相等的圆心角所对的弧相等的性质,等弧对等弦的性质得到CH=MN,则结论可得;②利用分类讨论的方法分三种情况解答:Ⅰ.当EF=EG时,利用全等三角形的判定与性质和勾股定理解答即可;Ⅱ.当FG=EF时,过点E作EH⊥AB于点H,利用直角三角形的边角关系定理和勾股定理解答即可;Ⅲ.当FG=EG时,则FG=4k,连接FC,利用矩形的判定与性质和勾股定理解答即可.【解答】解:(1)当FE的延长线经过点A时,∵EF⊥OC,∴AE=FE=AF,∠A+∠AOE=90°.∵CD⊥OA,∴∠C+∠AOE=90°,∴∠A=∠C.在△AOE和△COD中,,∴△AOE≌△COD(ASA),∴AE=CD,∴CD=AF,∴;(2)①EG与CD的大小关系为:EG=CD.理由:延长FE交⊙O于点M,延长FG交⊙O于点N,延长CD交⊙O于点H,连接MN,OH,ON,OM,如图,∵OE⊥FM,∴EF=EM.∵AB为直径,FG⊥AB,∴FG=GN.∴EG为△FMN的中位线,∴EG=MN.∵AB为直径,CD⊥OA,∴CD=DH=CH.∵OC=OH,OA⊥CH,∴∠COH=2∠COD.∵∠FEO=∠FGO=90°,∴∠EFG+∠EOG=180°.∵∠AOC+∠EOG=180°,∴∠AOC=∠EFG,∴∠COH=2∠EFG.∵∠MON=2∠EFG,∴∠MON=∠COH,∴.∴CH=MN,∴EG=CD;②∵,sin∠COD=,∴设CD=4k,则OC=5k,∴OD==3k.Ⅰ.当EF=EG时,由(2)①知:EG=CD=4k,∴EF=4k,OF=OC=5k,∵EF⊥OC,∴OE==3k.∴OE=OD,∴=1;Ⅱ.当FG=EF时,过点E作EH⊥AB于点H,如图,在Rt△FEO和Rt△FGO中,,∴Rt△FEO≌Rt△FGO(HL),∴OE=OG,设OE=OG=m,∵,∴,∴EH=m,∴OH=m,∴HG=m.∵EH2+GH2=EG2,∴,∴m=k,∴OE=k.Ⅲ.当FG=EG时,则FG=4k,连接FC,如图,∵CD=FG=4k,CD⊥AB,FG⊥AB,∴四边形CDGF为矩形,∴CF=DG.在Rt△CDO和Rt△FGO中,,∴Rt△CDO≌Rt△FGO(HL),∴OD=OG=3k,∴FC=DG=6k,设OE=x,则CE=OC﹣OE=5k﹣x,∵EF2=CF2﹣CE2,EF2=OF2﹣OE2,∴(6k)2﹣(5k﹣x)2=(5k)2﹣x2,∴x=k,∴OE=k.∴=.综上,当△EFG是等腰三角形,且,的值为1或或.【点评】本题主要考查了圆的有关性质,圆周角定理,垂径定理,直角三角形的性质,直角三角形的边角关系定理,勾股定理,全等三角形的判定与性质,等腰三角形的性质,矩形的判定与性质,三角形的中位线定理,添加适当的辅助线和利用分类讨论的思想方法解答是解题的关键。
2023学年上海市宝山区第二学期初三二模数学试卷及参考答案(2024届上海初三二模)

图12023学年第二学期二模九年级数学试卷(宝山)考生注意:1.本试卷共25题.2.试卷满分150分.考试时间100分钟.3.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.4.除第一、二大题外,其余各题如无特殊说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.二次根式1-x 有意义,则x 的取值范围是(▲)(A )0>x ;(B )0≥x ;(C )1>x ;(D )1≥x .2.如果关于x 的一元二次方程20x x m --=有两个相等的实数根,那么实数m 的值是(▲)(A )1-;(B )41-;(C )41;(D )1.3.下列函数中,y 的值随x 值的增大而减小的是(▲)(A )122+=x y ;(B )122+-=x y ;(C )1+=x y ;(D )1+-=x y .4.先后两次抛掷同一枚质地均匀的硬币,两次都是正面向上的概率是(▲)(A )41;(B )31;(C )21;(D )61.5.上海发布微信公众号可查询到上海市实时空气质量状况.下面是三月某一周连续七天的空气质量指数(AQI ):28,26,26,37,33,40,117,这组数据的下列统计量中,能比较客观地反映这一周空气质量平均水平的是(▲)(A )平均数;(B )中位数;(C )众数;(D )方差.6.如图1,△ABC 中,∠C =90°,AB =5,21=tanB ,如果以点C 为圆心,半径为R 的⊙C 与线段AB 有两个交点,那么⊙C 的半径R 的取值范围是(▲)(A )52≤<R ;(B )52≤≤R ;(C )525≤≤R ;(D )50≤<R .二、填空题(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置上】7.计算:26a a ÷=▲.8.因式分解:m 2-3m =▲.9.不等式x -12<0的解集是▲.10.方程x x -=-2的解是▲.11.我国天文学家算出了仙女星系“体重”.仙女星系是距离银河系最近的大型漩涡星系,是研究星系形成和演化的绝佳案例.计算得到仙女星系质量约为11400亿倍太阳质量.把数据11400亿用科学记数法表示应是▲.12.某厂生产了1000只灯泡.为了解这1000只灯泡的使用寿命,从中随机抽取了50只灯泡进行检测,结果有28只灯泡的使用寿命超过了2500小时,那么估计这1000只灯泡中使用寿命超过2500小时的灯泡的数量为▲只.13.《孙子算经》记载了这样一个题目:今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?其大意是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木多出1尺.那么长木的长度为▲尺.14.如图2,街心花园有A 、B 、C 三座小亭子,A 、C 两亭被池塘隔开,A 、B 、C 三亭所在的点不共线.设AB 、BC 的中点分别为M 、N .如果MN=3米,那么AC =▲米.15.如图3,正六边形ABCDEF ,连接OE 、OD ,如果,,b OE a OD ==那么=AB ▲.16.为传承海派文化,社区准备举办沪剧爱好者观摩演出活动.把某场馆的一个正方形区域改造成一个由矩形和半圆形组成的活动场地(如图4),矩形ABCD 是观众观演区,阴影部分是舞台,CD 是半圆O 的直径,弦EF 与CD 平行.已知EF 长8米,舞台区域最大深度为2米,如果每平方米最多可以坐3名观众,那么观演区可容纳▲名观众.图2图4图317.如图5,边长分别为5,3,2的三个正方形拼接在一起,它们的一边在同一直线上,那么图中阴影三角形①和②的面积之比21S S 的比值为_______.18.如图6,菱形ABCD 的边长为5,cosB =54,E 是边CD 上一点(不与点C 、D 重合),把△ADE 沿着直线AE 翻折,如果点D 落在菱形一条边的延长线上,那么CE 的长为▲.三、解答题:(本大题共7题,满分78分)19.(本题满分10分)计算:21382183-----().20.(本题满分10分)解方程:12113+=+xx .21.(本题满分10分,第(1)小题满分5分,第(2)小题满分5分)如图7,在平面直角坐标系xOy 中,直线3y x =+与x 轴、y 轴分别交于点A 、B ,与反比例函数xky =的图像交于点C (2,m ).(1)求反比例函数的解析式;(2)过点C 作x 轴的平行线l ,如果点D 在直线l 上,且CD =3,求△ABD 的面积.xOBAy图7C 图6图522.(本题满分10分)小明家院内靠墙安装了一个遮阳篷(如图8),图9是它的侧面示意图,遮阳篷长AC=6米,与水平面的夹角为17.5°,靠墙端A离地高度AB=5米,已知该地区冬至正午太阳光照入射角∠CDF=36.9°,夏至正午太阳光照入射角∠CEF=82.4°,因此,点D、E 之间的区域是一年四季中阳光不一定照射到的区域,求该区域深度DE的长.(结果精确到0.1米)参考数据:sin17.5°≈0.3,cos17.5°≈0.95,tan17.5°≈0.32;sin36.9°≈0.6,cos36.9°≈0.8,tan36.9°≈0.75;sin82.4°≈0.99,cos82.4°≈0.13,tan82.4°≈7.5.23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图10,在⊙O中,直径AB垂直于弦CD,垂足为点E,联结AC、DO,延长DO交AC于点F.(1)求证:AF2=OF·DF;(2)如果CD=8,BE=2,求OF的长.图10图8图924.(本题满分12分,第(1)小题满分4分,第(2)小题满分4分,第(3)小题满分4分)在平面直角坐标系xOy 中(如图11),已知开口向下的抛物线422+-=x ax y 经过点P (0,4),顶点为A .(1)求直线PA 的表达式;(2)如果将△POA 绕点O 逆时针旋转90°,点A 落在抛物线上的点Q 处,求抛物线的表达式;(3)将(2)中得到的抛物线沿射线PA 平移,平移后抛物线的顶点为B ,与y 轴交于点C .如果AB PC 2=,求PBC tan ∠的值.25.(本题满分14分,第(1)小题①满分4分,第(1)小题②满分4分,第(2)小题满分6分)已知AB 是半圆O 的直径,C 是半圆O 上不与A 、B 重合的点,将弧AC 沿直线AC 翻折,翻折所得的弧交直径AB 于点D ,E 是点D 关于直线AC 的对称点.(1)如图12,点D 恰好落在点O 处.①用尺规作图在图12中作出点E (保留作图痕迹),联结AE 、CE 、CD ,求证:四边形ADCE 是菱形;②联结BE ,与AC 、CD 分别交于点F 、G ,求FGBE的值;(2)如果AB =10,OD =1,求折痕AC 的长.图12备用图xOP (0,4)y 图11参考答案一、选择题(本大题共6题,每题4分,满分24分)1.D ;2.B ;3.D ;4.A ;5.B ;6.A .二、填空题(本大题共12题,每题4分,满分48分)7.4a ;8.)3(-m m ;9.1<x ;10.2-=x ;11.121014.1⨯;12.560;13.6.5;14.6;15.b a -;16.150;17.254;18.13401或.三、解答题(本大题共8题,满分78分)19.(本题满分10分)解:原式=)()(223124--+-……………………………………(2分+2分+2分+2分)=2.……………………………………………………………………………(2分)20.(本题满分10分)解:)1(2)1(23+++=⋅x x x x ……………………………………………………………(3分)01322=+-x x ………………………………………………………………………(2分)0)1)(12(=--x x ……………………………………………………………………(1分)12121==x x …………………………………………………………………………(2分)经检验12121==x x ,都是原方程的解,……………………………………………(1分)所以,原方程的根是12121==x x .………………………………………………(1分)21.(本题满分10分,其中第(1)小题5分,第(2)小题5分)解:(1)由直线3y x =+经过C (2,m ),可得,5=m 于是C (2,5),…………(2分)由点C 在反比例函数xky =的图像上,可得,10=k …………(2分)所以,反比例函数的解析式是.10xy =…………(1分)(2)点D 在过点C 且平行于x 轴的直线l 上,则D (a ,5),………(1分)过点A 作AE ⊥l ,垂足为点E ,直线l 与y 轴交于点F,点D 在点C 左侧或右侧总有)(21BF AE CD S S S BCD ACD ABD -⋅⋅=-=∆∆∆………(2分)由A (-3,0),B (0,3)29)25(321=-⋅⋅=∆ABD S .………(2分)22.(本题满分10分)解:过点C 作CG ⊥AB ,垂足为点G ,.………………(1分)在Rt △ACG 中,ACAGACG =∠sin ,………………(1分)∵AC=6米,∴8.13.06sin =⨯≈∠⋅=ACG AC AG .…………(1分)∵AB =5米,∴BG =3.2米,…………………………………………(1分)∵CG ∥BF ,AB ⊥BF ,CH ⊥BF ,∴CH =BG =3.2米,……………………………………………………(1分)过点C 作CH ⊥BF ,垂足为点H ,.……………………………………………………(1分)在Rt △CDH 中,CDHCHDH ∠=tan ,……………(1分)∴,27.475.02.3≈≈DH …………………………………(1分)同理43.0≈EH ,………………………………………………………(1分)∴8.343.027.4≈-=-=EH DH DE 米.……………………………(1分)答:该区域深度DE 的长为3.8米.EF D 11D 2lxOBAy 图7C23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)(1)证明:联结AD ,………………………(1分)∵直径AB 垂直于弦CD ,∴CD DE CE 21==,………………………(1分)∵AB ⊥CD ,∴AC =AD ,∵AB ⊥CD ,∴∠FAO =∠DAO ,…………………………(1分)∵OA=OD ,∴∠DAO =∠ODA ,∴∠FAO =∠ODA ,……………………………………………………………(1分)∵∠AFO =∠AFD ,∴△AFO ∽△AFD ,……………………………………………………………(1分)∴AFDFOF AF =,∴AF 2=OF·DF.…………………………………………………………………(1分)(2)∵CD DE CE 21==,CD =8,∴CE =DE =4,………………………………………………………………………(1分)在Rt △DEO 中,222OD DE OE =+,由BE =2,设OD=OB =r ,则OE =r -2,2224)2(r r =+-,r =5,……………(1分)∴OE =3,AE =8,在Rt △ADE 中,54482222=+=+=DE AE AD ,……………(1分)∵△AFO ∽△AFD ,∴ADAOAF DF OF AF ==,……………………………………………………………(1分)设AF =y ,OF =x ,∴5455=+=y x x y ,……………………………………………………………(1分)解得1125=x ,∴1125=OF …………………………………………………………………………(1分)24.(本题满分12分,第(1)小题满分4分,第(2)小题满分4分,第(3)小题满分4分)解:(1)由aa x a x ax y 141(4222-+-=+-=,可得)(a a A 141-,………(1分)由题意设直线PA 的表达式为)0(4≠+=k kx y ,…………………………………(1分),(a a A 141-代入得,aa k 144-=+,1-=k ,…………………………………(1分)所以,直线PA 的表达式为4+-=x y .………………………………………………(1分)(2)由抛物线开口向下且过点P (0,4),△POA 绕点O 逆时针旋转90°,点A 的对应点Q 如图所示,过点A 、Q 分别作AM ⊥y 轴,QN ⊥y 轴,垂足分别为点M 、N ,于是QON AOM ∆≅Δ,则由,(a a A 141-得),(aa Q 141-,…(1分)代入422+-=x ax y 得01282=-+a a ,…………………………(1分)21-=a ,或(舍去)41=a ,……………………………(1分)所以,a 的值为21-.………………………………………(1分)(3)由(2)得6)2(21422122++-=+--=x x x y ,)6,2(-A ,…(1分)设平移后的抛物线表达式为m m x y -+--=4)(212,则)4,(m m B -,)421,0(2+--m m C ,……………(1分)点B 在点A 的上方,点C 在点P 的下方,如图所示,于是,22)2()2(22+=+++=m m m AB ,m m m m PC +=+---=22214214)(,由AB PC 2=,可得)2(2212+-=+m m m ,解得(舍去)或24-=-=m m ………………………(1分)于是)8,4(-B ,)0,0(C 过点C 作CD ⊥PA ,垂足为点D ,数学王老师微信:wang3927666在Rt △CDP 中,∠DPC =45°,PC =4,可得22==DP CD ,24)48()40(22=-++=BP ,于是26=+=BP DP BD ,所以,在Rt △CDB 中,312622tan ===∠BD CD PBC .……………(1分)25.(本题满分14分,第(1)小题①满分4分,第(1)小题②满分4分,第(2)小题满分6分)解:(1)①尺规作图略………(1分)证明:∵E 是点D 关于直线AC 的对称点,∴AE =AD ,CE =CD ,…………………………………(1分)∵AD =CD ,∴AE =AD =CE =CD ,……………………………………………(1分)∴四边形ADCE 是菱形.…………………………………………(1分)②∵四边形ADCE 是菱形,数学王老师微信:wang3927666∴CE ∥AD ,………………………………………………………………………(1分)∴21==AB CE AF CF ,同理AF CF EF FG =,21==AB AD BE EG ,……………………………………………(1分)∴EG FG 31=,BE EG 21=,…………………………………………………(1分)∴BE FG 61=,∴61=BE FG .……………………………………………………(1分)(2)Ⅰ.当点D 在点O 右侧,数学王老师微信:wang3927666作点D 关于直线AC 的对称点E ,联结DE 、AE ,过点O 作OG ⊥AE ,垂足为点G ,过点C 作CH ⊥AB ,垂足为点H ,…(1分)∴90=∠=∠OHC AGO ,∵AE =AD ,DE ⊥AC ,∴21∠=∠,∵AO =CO ,∴23∠=∠,∴2232∠=∠+∠=∠COH ,第13页∵2221∠=∠+∠=∠OAG ∴OAG COH ∠=∠,∵AO =CO ,∴COH OAG ≅∆,∴AG =OH ,…(1分)∵AB =10,OD =1,∴AD=AE=6,∵OG ⊥AE ,∴321==AE AG ,……………………(1分)∴OH=3,AH =8,在Rt △COH 中,4352222=-=-=OH CO CH ,……………………(1分)在Rt △ACH 中,54482222=+=+=CH AH AC .…………………(1分)Ⅱ.当点D 在点O 左侧,同理可得AC=70.…………………………………(1分)综上所述:折痕AC 的长为7054或者.。
2023年上海市黄浦区中考二模数学试题(含答案解析)

2023年上海市黄浦区中考二模数学试题学校:___________姓名:___________班级:___________考号:___________A.任选两个角,测量它们的角度;B.测量四条边的长度;C.测量两条对角线的长度;D.测量两条对角线的交点到四个顶点的距离.【答案】D【分析】利用矩形的判定定理逐个选项查看即可.【详解】选项A中任意两个角只能判定一对角互补或相等,或两个直角,有可能为直角梯形,判断四边形为矩形需要3个角是直角,选项A错误;选项B中,四条边的关系为对边相等,可能仅是平行四边形,选项B错误;选项C中,对角线长度相等但是不是平行四边形时,仅为普通四边形,选项C错误;选项D中,根据对角线交点到四个顶点的距离分别相等,判断对角线互相平分则为平行四边形,又通过对角线相等判断为矩形.故选D.【点睛】矩形的判定定理有3条,三个角是直角的四边形;对角线相等的平行四边形;有一个角是直角的平行四边形.熟练的应用判定定理是解题的关键.二、填空题【答案】170【分析】根据频数直方图可知40人中有34再估计200人中完成时间少于90分钟的人数即可.【详解】解:由题意得:4102020017040++⨯=(人)【点睛】本题考查三角形的重心,属于中考常考题型.16.在直角坐标平面内,已知点EF GH ∥ ,∴四边形EFGH 时平行四边形,3EH FG ∴==,∴四边形EFGH 的周长为如图2,当OEF HOG ≌1EF OG ∴==,OF GH =,3FG = ,312OF FG OG ∴=-=-=,2GH ∴=,90EFO ∠=︒ ,90OEF EOF ∴∠+∠=︒,90HOG EOF ∴∠+∠=︒,(180EOH HOG ∴∠=︒-∠+∠三、解答题将12y =代入③,得23x =所以,原方程的解是101x y =⎧⎨=-⎩,1132x y =⎧⎨=⎩.【点睛】此题考查了二元二次方程组,熟练掌握二元二次方程组的解法是解题的关键.21.小丽与妈妈去商场购物,商场正在进行打折促销,规则如下:优惠活动一:任选两件商品,第二件半价(两件商品价格不同时,低价商品享受折扣);优惠活动二:所有商品打八折.(两种优惠活动不能同享)(1)如果小丽的妈妈看中一件价格600元的衣服和一双500元的鞋子,那么她选择哪个优惠活动会更划算?请通过计算说明;(2)如果小丽的妈妈想将之前看中的鞋子换成一条裤子,当裤子价格(裤子价格低于衣服价格)低于多少元时,小丽会推荐妈妈选择优惠活动二?为什么?【答案】(1)选择伏惠活动一更划算,见解析(2)当裤子价格低于400元时,推荐选择优惠活动二,见解析【分析】(1)分别计算出两种优惠活动的总价格,再比较那个价格更低即可得解答;(2)按照优惠活动列出不等式解答.【详解】(1)解:选择优惠活动一更划算,理由如下:活动一价格:6005000.5850+⨯=(元),活动二价格:()6005000.8880+⨯=(元),∵850880<,∴选择优惠活动一更划算.(2)解:当裤子价低于400元时,推荐选择优惠活动二,设裤子的价格为(600)x x <元,则活动一的价格为()6000.5x +元;活动二的价格为()4800.8x +元,由题意,得6000.54800.8x x +>+,解,得400x <.∴当裤子价格低于400元时,推荐选择优惠活动二.【点睛】本题考查了方案选择问题,一元一次不等式与实际问题,审清题意找出等量关系是解题的关键.(1)求弦AB 的长;(2)求图中阴影部分面积(结果保留【答案】(1)23AB =(2)23S π=阴∵弦AB 垂直平分OP ,∴112OQ OP ==.在Rt OBQ △中,=BQ ∵半径OP 垂直AB ,∴AQ BQ=∵ BC BP =,∴BC BP =,BOC ∠=又∵OC OB =,∴OBC △是等边三角形.∴60BCO ∠=︒,(1)求证:BF DE =;(2)延长AB 交射线EF 于点【答案】(1)见解析(2)见解析AF AE =,90EAF ∠=∴45AFE AEF ∠=∠=︒,四边形ABCD 是正方形,∴45ADB BDC =∠=∠°,∴135ADE AFG ∠=∠= ,由(1)知EAD BAF ∠=∠ADE AFG ∴ ∽,(1)求抛物线的表达式;(2)设抛物线与x轴的另一个交点为(3)点D坐标是()0,4的长.【答案】(1)2y x=+(2)点P的坐标是3 2⎛-⎝(3)410MN=【分析】(1)先利用一次函数解析式求出点物线的表达式即可;(2)先求出抛物线的对称轴是直线在AC的垂直平分线上,由PB PA=,求出a(3)先说明点M,()2,34+-m m m,点(1)已知3sin 5DBC ∠=,①当4EC =时,求BCH V 的面积;②以点H 为圆心,HM 为半径作圆有且仅有一个公共点,求CE (2)延长AH 交边BC 于点P 【答案】(1)①725BHC S =;②(2)102xx-【分析】(1)①联结AC 交函数可得,CO BO 的长,再由CEGD 是平行四边形,可得继而得到BE ME =,再由EH 485H x r BH ==-,45OH =后分两种情况:当两圆外切时,当两圆内切时,即可求解;∵四边形ABCD 是菱形,∴OC BO ⊥.在Rt BOC 中,10BC =,∴sin 6CO BC DBC =⋅∠=,∴8BO =,∵EH BD ⊥,∴EH CO ∥,∴BH BE BO BC =,即104810BH -=∴245BH =.∴1122BHC S OC BH =⨯=⨯ ②在菱形ABCD 中,AB 又∵GD CE =,∴四边形CEGD 是平行四边形,∴EG D C ∥,∴EG AB ∥,∴EMB ABD ∠=∠.又∵ABD CBD ∠=∠,由(1)得:HM BH =,EG HQ EN AB ∴∥∥,∴,HQP CEN QHP ∠=∠∠=∴HQP CEN ∽ ,∴HP HQ CN CE=,又∵EH BD ⊥,∴11022x HQ BE -==.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016.4各区二模23题合集
(崇明)23.(本题满分12分,其中每小题各6分)
已知正方形ABCD 的对角线相交于点O ,CAB ∠的平分线分别交BD 、BC 于点E 、F ,作
BH AF ⊥,垂足为H ,BH 的延长线分别交AC 、CD 于点G 、P .
(1)求证:AE BG =;
(2)求证:GO AG CG AO ⋅=⋅.
(奉贤)23.(本题满分12分,每小题满分各6分)
已知:如图,梯形ABCD 中,DC ∥AB , AD=BC=DC ,AC 、BD 是对角线,E 是AB 延长线上一点,且∠BCE =∠ACD ,联结CE . (1)求证:四边形DBEC 是平行四边形; (2)求证:2AC AD AE =⋅.
(虹口)23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)
如图,在四边形中,∥,、为对角线上两点,且,
∥.
(1)求证:四边形是平行四边形;
(2)延长,交边于点,交边的延长线 于点,求证:.
ABCD AB DC E F BD BE DF =AF EC ABCD AF DC G BC H AD DC BH DG =(第23题图)
A
B
C
D
P
G O
F
H E
第23题图
E
D
C
B
A
A B
C
E
F
第23题图
D
G H
(黄浦)23.(本题满分12分,第(1)、(2)小题满分各6分)
如图5,在ABC ∆中,D 、E 分别是AC 、BC 边上的点,AE 与BD 交于点O ,且CD =CE ,12∠=∠.
(1)求证:四边形ABED 是等腰梯形;
(2)若EC =2,BE =1,21AOD ∠=∠,求AB 的长.
(嘉定宝山)23.(本题满分12分,每小题满分各6分)
如图6,BD 是平行四边形ABCD 的对角线,若∠DBC =45°,DE ⊥BC 于E ,BF ⊥CD 于F ,DE 与BF 相交于H ,BF 与AD 的延长线相交于G . 求证:(1)CD =BH ;
(2)AB 是AG 和HE 的比例中项.
(金山)23.(本题满分12分, 每小题满分各6分)
如图, BD 是△ABC 的角平分线, 点E 、F 分别在BC 、AB 上, 且DE ∥AB , ∠DEF =∠A . (1)求证: BE =AF ;
(2)设BD 与EF 交于点M , 联结AE , 交BD 于点N ,
求证: BN ·MD =BD ·ND .
图5 A
B C
D
O E
12H F
B E D A
C G 图6
M
A
F
B
E C
D
(静安)23.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分)
已知:如图,四边形ABCD 是菱形,点E 在边CD 上,点F 在BC 的延长线上,CF =DE ,AE 的延长线与DF 相交于点G . (1)求证:∠CDF =∠DAE ;
(2)如果DE =CE ,求证:AE =3EG .
(闵行)23.(本题满分12分,其中每小题各6分)
如图,已知在矩形ABCD 中,过对角线AC 的中点O 作 AC 的垂线,分别交射线AD 和CB 于点E 、F ,交边DC 于 点G ,交边AB 于点H .联结AF ,CE . (1)求证:四边形AFCE 是菱形; (2)如果OF = 2GO ,求证:2GO DG GC =⋅.
(普陀)23.(本题满分12分)
如图7,已知在四边形ABCD 中,AD ∥BC ,对角线AC 、BD 相交于点O ,BD 平分ABC ∠,过点D 作DF ∥AB 分别交AC 、BC 于点E 、F . (1)求证:四边形ABFD 是菱形;
(2)设AC AB ⊥,求证:AC OE AB EF =.
(第23题图)
E
D
C
G
F
A B
(第23题图)
A
B C
D
E F
G
O
H
O
F
E
D
C
B
A
(松江)23.(本题满分12分,每小题满分各6分)
如图,已知等腰△ABC 中,AB =AC ,AD ⊥BC ,CE ⊥AB ,垂足分别为D 、E . (1)求证:∠CAD =∠ECB ;
(2)点F 是AC 的中点,联结DF ,求证:BD 2=FC ·BE .
(徐汇)23.(本题满分12分)
如图7, 在ABC ∆中,AC AB =,点D 在边AC 上,DE BD AD ==,联结BE ,︒=∠=∠72DBE ABC .
(1)联结CE ,求证:BE CE =;
(2)分别延长CE 、AB 交于点F ,求证:四边形DBFE 是菱形.
(杨浦)23.(本题满分12分,每小题各6分)
已知:如图,在直角梯形纸片ABCD 中,DC //AB , AB CD AD >>,∠A =90°,将纸片沿过点D 的直线翻折,使点A 落在边CD 上的点E 处,折痕为DF ,联结EF 并展开纸片. (1)求证:四边形ADEF 为正方形;
(2)取线段AF 的中点G ,联结GE ,当BG =CD 时, 求证:四边形GBCE 为等腰梯形.
C
B A
D
E
F
(第23题图) (第23题图)
图7
A
B
C D
E
(第23题图) A B C D
E
(闸北)23.(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分) 如图,直角梯形ABCD 中,∠B=90°,AD ∥BC ,BC=2AD ,点E 为边BC 的中点. (1)求证:四边形AECD 为平行四边形;
(2)在CD 边上取一点F ,联结AF 、 AC 、 EF ,设AC 与EF 交于点G ,且∠EAF=∠CAD .求证:△AEC ∽△ADF ;
(3)在(2)的条件下,当∠ECA=45°时.求:FG:EG 的比值.
(浦东)23.(本题满分12分,第(1)、(2)小题各6分)
如图,已知:四边形ABCD 是平行四边形, 点E 在边BA 的延长线上,CE 交AD 于点F ,∠ECA = ∠D .
(1)求证:∆EAC ∽∆ECB ; (2)若DF = AF ,求AC ︰BC 的值.
(第23题图)
A
B
C
E
D F G。
