相平面分析资料

合集下载

非线性-第二章

第2章相平面分析方法212.1相平面分析的概念2.2 线性系统的相平面分析2.3 非线性系统的相平面分析2.1 相平面分析的概念211i 2.1.1 相平面图（Phase portraits ）二阶自治系统1112(,)xf x x =&(2.1)a 2212(,)xf x x =&(2.1)b 以状态x 1与x 2为坐标的平面，称为相平面。

给定一对初值(0)=x (0)x 0，可以确定系统的一个解，在相平面中得到一条相平面轨线。

对不同初值的一簇相平面轨线称为系统的相平面图（相图）。

例2.1质量-弹簧系统k =1m=1&&系统的动态方程x x +=假设质点初始位置在x 0，其解为0()cos x t x t ==−&0()sin xt x t 相轨线方程2&22x xx +=图2.1 质量-弹簧系统相平面图相图的作用：一旦得到系统的相图，则系统对应于不同初值的特性即21展漏无遗。

从例2.1可以看出，系统的相轨线既不趋于零也不趋于无穷，而是以原点为中心的同心圆，表示系统处于临界稳定状态。

2.1.2 奇异点(Singular point)满足=奇异点是相平面上的一个平衡点。

112212(,)0(,)0f x x f x x=对线性系统，奇异点通常只有一个。

对非线性系统，则经常存在多个孤立的奇异点。

20.630x xx x +++=&&&例2.2二阶非线性系统两个奇异点：收敛区0x =3x =−奇异点是相平面不稳定奇异点的重要特征。

线性系统的稳定性完全由奇异点的本质决定，而非线性系统则会存在一些复杂22特征。

图2.2 系统相平面图2.2 线性系统的相平面分析0x axbx ++=&&&考虑下面二阶线性系统(2.2)系统的解为121212(),t tx t k e k e λλλλ=+≠111212(),ttx t k e k te λλλλ=+=系统(22)(2.2)只有一个奇异点（设b ≠0），但奇异点附近的系统轨线根据参数a 和b 的不同表现出不同的特征。

相平面分析实验报告(3篇)

第1篇一、实验目的1. 理解相平面的概念及其在控制系统中的应用；2. 掌握相平面分析方法，通过分析相轨迹图，了解系统的动态特性；3. 分析饱和非线性环节对控制系统性能的影响。

二、实验原理相平面分析是一种研究非线性系统动态特性的方法。

它通过将系统的状态变量绘制在二维平面上，形成相轨迹图，从而直观地观察系统的运动规律。

在相平面上，系统的状态变量可以是系统的位置和速度，也可以是系统的其他两个相互独立的变量。

本实验主要研究带有饱和非线性环节的控制系统。

饱和非线性环节具有上限和下限，当输入信号超出这个范围时，系统的输出将不再改变。

在相平面上，饱和非线性环节表现为相轨迹的折线。

三、实验设备1. PC机一台；2. MATLAB软件；3. Simulink模块库。

四、实验步骤1. 建立控制系统模型根据实验要求，建立带有饱和非线性环节的控制系统模型。

首先，建立系统的传递函数，然后添加饱和非线性环节模块。

2. 设置仿真参数设置仿真参数，包括仿真时间、采样时间等。

3. 运行仿真运行仿真，观察系统输入饱和非线性环节前后的相轨迹图。

4. 分析相轨迹图对比有无非线性环节的相轨迹图，分析饱和非线性环节对系统性能的影响。

5. 求解超调量在输入单位阶跃信号的情况下，计算系统的超调量。

五、实验结果与分析1. 相轨迹图分析在饱和非线性环节的影响下，系统的相轨迹图发生了明显的变化。

当输入信号超出饱和非线性环节的上下限时，相轨迹图出现折线。

这表明饱和非线性环节限制了系统的运动范围，影响了系统的动态性能。

2. 系统性能分析通过对比有无非线性环节的相轨迹图，可以发现饱和非线性环节对系统的超调量和上升时间有一定影响。

当饱和非线性环节存在时，系统的超调量增大，上升时间变长。

这是因为饱和非线性环节限制了系统的运动范围，导致系统在达到稳定状态之前需要更多的能量。

3. 超调量计算在输入单位阶跃信号的情况下，系统的超调量为：超调量 = (终值 - 原始值) / 原始值其中，终值为系统稳定后的输出值，原始值为输入信号的幅值。

相平面法ppt课件

有可能出现在x轴上。
11
忽略高阶无穷小，一般情况下令 x10 x20 0
则有
P( x1,
x2 )
P( x1, x1
x2 )
(0,0)
x1
P( x1, x2
x2 )
(0,0)
x2
Q( x1,
x2 )
Q( x1, x1
x2 )
(0,0)
x1
Q( x1, x2
x2 )
(0,0)
x2
令 a P( x1, x2 )
平面上绘制一系列的等倾线。
8
x2
1
( x10 , x20 )
2
3 x1
4
图8-27 用等倾线法绘制相轨迹
1,2 ,表3示,相轨迹通过这些等倾线时切线的斜率。
相平面中所有等倾线上的短线，组成了相轨迹的切线场。从相轨迹起始点 ( x10, x20 ) 出发，平滑的将相邻等倾线上的短线连起来，即得系统相轨迹。
§8.4 相平面法
相平面法是Poincare在1885年首先提出来的，它是一种求解一、二阶常微分方程的图解法。这种方法的实质是将系统的运动过程形象地转化为相平面上一个点的移动，通过研究这个点移动的轨迹，就能获得系统运动规律的全部信息。由于它能比较直观、准确、全面地表征系统的运动状态，因而获得广泛应用。
1,2
2
5）纯虚根
(a d ) 0, ad bc 0
奇点称为中心点。 x2
0
x1
图8-32 纯虚根对应的相轨迹
18
2、极限环
相平面图上的一根孤立的封闭相轨迹称为极限环。它对应系统的自激振荡状态。极限环把相平面划分为内部平面和外部平面两部分，相轨迹不能从环内穿越环进入环外，反之也不能。

第7章_2相平面法

12
极限环的分类稳定极限环当 t → ∞ 时，在极限环邻域内的所有轨迹都收敛于该极限环，这样的极限环称为稳定极限环稳定极限环。稳定极限环它表示系统的运动是一种稳定的带固有周期的自持振荡。在系统设计时，应尽可能减小极限环，以满足稳态精度的要求。
13
& x
极限环外部稳定极限环内部不稳定
5
4 负阻尼情形
−1 < ζ < 0
jω
& x
λ1
0
σ
λ2
0
x
不稳定焦点
λ1,2 = −ζωn ± jωd
6
ζ < −1
jω
& x
λ1 λ2
0
σ
0
x
不稳定节点正实特征根 −ζωn ± ωn ζ 2 − 1
7
5 给定二阶线性系统的微分方程
2 && + 2ζωn x − ωn x = 0 & x
I区
II区
27
& e
a=0
KM
−e0
0
e0
e
a=0
II区
28
− KM
III区 I区
& e
KM
−e0
0
e0
e
− KM
III区 I区 II区
29
2 输入信号为 r (t ) = R + vt 时 a）v > KM ， M = e0 ）稳态误差为无穷大！
& e
v + KM
A
v − KM
−e0
0
e0
2
1 无阻尼情形（ζ = 0 ）

相平面

第八章非线性控制系统分析
第一讲
第八章非线性控制系统分析
第一讲
本节课基本要求相平面法分析法了解非线性系统基本概念、特点。掌握几种常见的非线性迹。
重点：掌握几种常见的非线性特性
难点：相轨迹绘制
主要内容：
8-1 非线性控制系统概述
1．非线性控制系统
非线性：指元件或环节的静特性不是按线性规律变化。非线性系统：如果一个控制系统，包含一个或一个以上具有非线性静特性的元件或环节，
第一讲
注意：
1)坐标轴 x 和 x& 应选用相同的比例尺，以便于根据等倾线斜率准确绘制等倾线上一
点的相轨迹切线。
2)在相平面的上半平面，由于 x& > 0 ，则 x 随 t 增大而增加，相轨迹的走向应是由左
向右，在相平面的下半平面 x& < 0 ，则 x 随 t 增大而减小，相轨迹的走向应由右向左。
e(t) ≤ a e(t) > a
200
第八章非线性控制系统分析
第一讲
(3)饱和特性
⎧ke(t)
y (t )
=
⎪ ⎨
⎪⎩kasigne(t)
e(t) ≤ a e(t) > a
signe(t)
=
⎩⎨⎧+−
1 1
e(t) > 0 e(t) < 0
式中 a − 线性区宽度 k − 线性区特性的斜率
(4)间隙特性
⎪
y(t)
=
⎪⎪ ⎨
0
− a < e(t) < ma, e&(t) < 0
bsigne(t)
e(t) ≥ a
⎪ ⎪
b
e(t) ≥ ma, e&(t) < 0

第七章相平面法2010

7.6 相平面法
一、相平面的基本概念二、相轨迹的绘制三、由相轨迹求系统的瞬态响应四、奇点与极限环五、非线性系统的相平面分析
1
一、相轨迹的基本概念
解决两个问题： 1.什么是相轨迹？ 2.相轨迹的几个重要性质。
2
（一）相轨迹的基本概念
相平面法是状态空间法在二维空间特殊情况下的应用。它是一种通过图解法求解一阶或二阶线性或非线性系统的准确方法。它可以给出某一平衡状态稳定性的信息和系统运动的直观图像。所以，它属于时间域的分析方法。
12
等倾线与相轨迹
x n2 x 2n
设系统参数 ξ=0.5，ω＝1。求得对应于不同α 值的等倾线
x
－ 1.2 － 1.4
k＝－ 1
A
B
－ 1.6 － 1.8 －2
C D
－ 2.5 －3
0
－ 1.4 － 1.2
－ 0.8－ 0.6－ 0.4－ 0.20
1 0.5
－4 －6
对于二阶时不变系统，可用以下常微分方程来描述：
x f (x, x) 0
设: x1 x x2 x
x1 x x2 则: x2 x f (x1 , x2 )
3
相平面、相轨迹、相平面图
x
定义：
X
(t
)

x1 x2

为状态变量。
0
x
我们将 (x , x ) 构成的直角平面叫做相平面。
－ 11 x
9 4 2
13
用等倾线法相轨迹绘制
14
三、由相轨迹求系统的瞬态响应
相轨迹是消去时间后画出的，尽管它直观地给出了系统状态的运动轨迹，但却将时间信息隐含其中，使时间信息变得不直观了。有时我们希望给出时间响应以便得到与时间有关的性能指标，这就需通过相轨迹求出时间信息。

7-2相平面法

bx cx 0 x
当c > 0时，上述微分方程又可以表示为
2 2 n x n x 0 x
线性二阶系统的特征根
b b 4c s1 2
2
b b 2 4c s2 2
相轨迹方程为
dx bx cx dx x
假设由初始条件确定的点为图中的A点。则过A点作斜率为[ (1) + (1.2) ] / 2 = 1.1的直线，与a = 1.2的等倾线交于B点。再过B 点作斜率为的[ (1.2 ) + (1.4) ] / 2 = 1.3 直线，与a = 1.4的等倾线交于C点。如此依次作出各等倾线间的相轨迹线段，最后即得系统近似的相轨迹。
x t4
(x, x0)
t3
0 t2 0
t1
x
x
t1
t2 t3 t4
4
当t变化时，系统状态在相平面上移动的轨迹称为相轨迹。
t
而与不同初始状态对应的一簇相轨迹所组成的图叫做相平面图。利用相平面图分析系统性能的方法称为相平面法。
7.3.2 相平面图的绘制
绘制相平面图可以用解析法、图解法和实验法。 1. 解析法解析方法一般用于系统的微分方程比较简单或可以分段线性化的方程。应用解析法求取相轨迹方程时一般有二种方法：一种是对式（7-35）直接进行积分。显然，这只有在上述方程可以进行积分时才能运用。另一种方法是先求出x和对t的函数关系，然后消去t， 5 从而求得相轨迹方程。下面举例加以说明。
x
0
x
22
④ = 0。系统特征根为一对纯虚根。系统的自由运动为等幅正弦振荡。给定初始点，系统的相平面图为围绕坐标原点的一簇椭圆（参阅例7-1），系统相平面图:

第2章相平面分析201-资料

(x,x)
x
(x,x)
0
x
相轨迹对称于原点
f( x ,x ) f( x , x )
2.相平面上的奇点
由相轨迹的斜率方程 d xd x 可f( 知x ,,相x )平x 面上的点
只要不(同x,时x)满足
,则x 该点0 ,相f轨(x 迹,x 的) 斜0 率是唯一确定
的。
这样的点称为普通点。通过普通点的相轨迹只有一条。
用xf来(x表)示。
x(t)
x
t
x
方程的解
1.相轨迹：如果我们取 x 和作x为平面的直角坐标，则
系统在每一时刻的 (x,均x)相应于平面上的一点。当 t 变化时，这一点在平面x上将x 绘出一条相应的轨迹-----相轨迹。
它描述系统的运动过程。
2.相平面: x x平面称为相平面。对于一个系统，初始条件
f(x,x) xf(x,x)
x 给定一个 α值 ,可由上式求得一条等倾线 ; 给定一组 α值 ,则可求得一组等倾线族 ,它们确定了相平面中相轨迹斜率的分布 .
设系统方程为: x 2x 2x 0
上式改写为:
x dx 2x 2x 0
一、相轨迹的共同特性
1.相轨迹的对称性
相轨迹的对称性可以从对称点上相轨迹的斜率来判断。设二阶系统的方程为：
改写为：
xfx,x0
x = d x = d x d x = x d x , x d x fx ,x
d t d xd t d x d x
两边除以 dx 可x得： dt
dx f x,x----相轨迹的
dx
x 斜率方程

相平面

dx

x
横轴上的点皆为奇点。
积分法

由于相轨迹方程表示成
dx dx
f ( x, x)

x

当 f ( x, x) ( x) 即仅是x的函数

则有 x d x ( x)dx 两边分别积分，即解出该方程的相轨迹
例：

x M

x
d
x

M
可解得
dx

x
2
2
因此

T c c Kx (1)
而 e r c (或c r e)
代入（1）式，得

T (r e) (r e) Kx (2)
e 0

T e e KM T r r
e 0

T e e KM T r r
非线性控制系统的相平面分析法
描述函数对非线性环节有限定条件，并且不能直接分析初始条件对非线性系统的影响。也就是说，它只能用于非线性系统的稳定性分析。
相平面以运动中的两个重要的状态量（速度和位置）作为坐标，将运动的变迁过程表现在平面上，不仅可直观地表现线性系统运动特点，更为非线性系统提供了一种有效的分析手段。
II区是欠阻尼运动，相应的奇点（0，0）是
稳定的焦点。轨迹越过区域边界，运动规律
随之改变。由于两个线性方程具有共同的奇
点。且在I区内，运动最终以过阻尼形式收
敛于该奇点。
e
II
I
II
0
e
r
e GN
xK
s(Ts 1)
M -M
C
c(s) K

自动控制原理之非线性控制系统的相平面分析总结

7-5 非线性控制系统的相平面分析一、线性控制系统的相平面分析1、阶跃响应设线性二阶控制系统如图7-38所示。

若系统开始处于平衡状态。

试求系统在阶跃函数)(1)(0t R t r ⋅=　作用下，在ee -平面上的相轨迹。

建立系统微分方程式，由图示系统可得Ke c cT =+ 因为c r e -=，代入上式得r r T Ke e eT +=++ （7-31）对于->⋅=0),(1)(0t t R t r 时，0)()(==t r t r因此上式可写成0=++Ke e e T （7-32）方程（7-32）与（7-22）式相仿。

因为假设系统开始处于平衡状态，所以误差信号的初始条件是0)0(R e =和0)0(=e。

e e -平面上的相轨迹起始于)0,(0R 点，而收敛于原点(系统的奇点)。

当系统特征方程的根是共轭复数根，并且位于左半平面时，其相轨迹如图7-39(a)所示。

根据ee -平面上的相轨迹就可方便的求得c c -平面上系统输出的相轨迹，如图7-39(b)所示。

由图7-39可见，欠阻尼情况下系统的最大超调量P σ及系统在稳态时的误差为零。

因为e e -平面相轨迹最终到原点，即奇点；所以在cc -平面上相轨迹最终到达0R c =的稳态值，则奇点坐标为)0,(0R 。

2、斜坡响应对于斜坡输入t V t r 0)(=；当0>t 时，)(t r 的导数0)(V t r= 及0)(=t r 。

因此，方程（7-31）可以写成0V Ke e eT =++ 或 0)(0=-++KV e K e e T 令v e K V e =-0，代入上式，则有0V Ke ee T =++ννν （7-33）在v v ee -平面上，方程（7-33）给出了相平面图与在e e -平面上方程（7-32）给出的相平面图是相同的。

应当指出，特征方程式的根确定了奇点的性质，在v v ee -平面上的奇点的位置是坐标原点，而在e e -平面上奇点坐标为)0,(0K V 点。

相平面法ppt课件

9
绘制相轨迹的目的是为了分析系统的运动特性；由于系统的平衡点有无穷根相轨迹离开或到达，因此平衡点附近的相轨迹，最能反映系统的运动特性。平衡点又称为奇点。
另一反映系统运动特性的相轨迹是极限环（奇线）。极限环是相平面上一根孤立的封闭的相轨迹，反映了系统的自激振荡状态，它将无穷大的相平面分为两个部分，有利于与奇点特性一起分析系统的运动特性。
e
y
0.5 0.5
e e 0 e e 0
e
区域（1）区域（2）
（1）
0
e
（2）
e e 0
28
区域（1）：
e 0.5 e 0.5t c1 e 0.25t 2 c1t c2
代入初始条件 e(0) 6, e，(0有) 0
e
0 （2）
（1）
A(6,0) e
e e 0
c1 0, c2 6
1,2
2
根据特征方程根的性质，可将奇点分为如下几种情况：
13
a d (a d )2 4(ad bc)
1,2
2
1) 同号相异实根
(a d )2 4(ad bc)
当 a d时，0 两根同负，奇点称为稳定的节点；当 a d时，0 两根同正，奇点称为不稳定的节点。
图。
6
令
P( Q(
x1 x1
, ,
x2 x2
) )
0 0
联立求解出的点 ( x10 , x称20为) 系统的平衡点。
相轨迹的特点：
1、相平面上除平衡点外的任意一点只有一根相轨迹通过。 2、由式 dx2 Q可知0 ，相轨迹在平衡点附近切线斜率不定，
dx1 P 0 意味着有无穷多根相轨迹到达或离开平衡点。

7-2相平面法

为自变量，为因变量的一阶微分方程。以x1为自变量，以x2为因变量的一阶微分方程。二阶系统常微分方程方程的解既可用x与的关系来表示方程的解既可用的关系来表示，统常微分方程方程的解既可用与t的关系来表示，也可的关系来表示。实际上，用x2与x1的关系来表示。实际上，看作一个质点的运动方程，则x1(t)代表质点的位置，x2(t)代表质点的速度。方程，代表质点的位置，代表质点的速度。代表质点的位置代表质点的速度
或பைடு நூலகம்
等倾线是过相平面原点的一些直线。等倾线是过相平面原点的一些直线。当ζ = 0.5、ωn = 1 、时的等倾线分布图 :
9
a= −1
x
−1.2 B −1.4 −2 −3 −6
2 ɺ ωn x =− x α + 2ξω n = −1/(a +1)
A
C
a= −1，k = −∞ ， a= −2，k = 1 ， a= −3，k = 1/2 ，
2
描述二阶系统常微用x1、x2描述二阶系统常微分方程方程的解方程的解，分方程方程的解，也就是用质点的状态来表示该质点的运动。点的状态来表示该质点的运动。在物理学中，状态又称为相在物理学中，状态又称为相。把由x 把由 1—x2所组成的平面坐标系称为相平面相平面，坐标系称为相平面，系统的一个状态则对应于相平面上的一个点。个点。变化时，当t变化时，系统状态在相变化时相轨迹。平面上移动的轨迹称为相轨迹平面上移动的轨迹称为相轨迹。
x 0 x
0
x
x
14
2。线性二阶系统。描述线性二阶系统自由运动的微分方程为
ɺɺ + bx + cx = 0 ɺ x

非线性系统的分析-相平面1PPT课件

ii.作等倾线分布图 iii.从初始点出发,沿相邻等倾线间的
ai
ai
ai1 2
平均斜率依次作短直线便可画得。
2021
7
说明：等倾线未必都是直线，另外，为保证精度，等倾线分布要有适当密度，密度可不一样。
例如 x2 nxn2x0 令 0.5, n1
i.等斜线方程:
y n2 x 1 x
i.等斜线分布图.
止条件。
2021
43
(1) 具有死区特性的非线性控制系统
2021
44
取
作为状态变量，
因为
，
2021
45
给定参数T=1, K k =1，根据二阶线性系统相
轨迹分析结果，可得奇点类型
区域 I：奇点(-△，0)为稳定焦点，相轨迹为向心
螺旋线(
);
区域 II：奇点(x，0)，x∈(-△, △)为稳定焦点，
x+axbx0
则该线性化系统的奇点的性质取决于特征根在复平面
上的位置。设特征根为 1 , 2 ，根据 1 , 2 在复平面
的位置，可以有以下几种情况：
2021
12
①一对具有负实部的共轭复根每条相轨迹都
以震荡方式无限地“卷向”平衡点，这种类型的奇点称为稳定焦点。
②一对具有正实部的共轭复根每条相轨迹都以
态，系统的相轨迹是围绕平衡点的一组封闭曲线。这种奇点称为中心点。
2021
15
⑥特征根为两个符号相反的实根。此时每条相轨迹都是先趋近平衡点，随后在尚未达到平衡点之前又远离平衡点而去，只有4条孤立的相轨迹除外，其中
两条趋于平衡点，另两条从平衡点散出，这时奇点称为鞍点。
2021
16

《相平面分析》课件

傅里叶级数和傅里叶变换
傅里叶级数和傅里叶变换是对信号进行频谱分析的重要工具，它们可以将信号分解成一系列频率成分。
RC、RL、RCL电路的相平面分析
相平面分析可以应用于分析RC、RL和RCL等电路，帮助理解电路的频率响应、稳定性和传递函数。
线性时不变系统的相平面分析
相平面分析是研究线性时不变系统的常用方法，通过分析系统的零极点分布和频率响应，可以了解系统的特性。
相平面分析的未来发展趋势
相平面分析作为一种重要的信号处理和控制系统分析方法，随着科学技术的发展，将继续发展并得到更广泛的应用。
极性和共轭
复数的极性表示复数的模和角度，共轭用于表示复数的共轭对称性质，在相平面分析中有重要的应用。
大角度相位移
大角度相位移是相平面分析中的一个重要概念，描述了信号在复平面上的相位偏移，可以用于分析系统的稳定性。
时域和频域之间的转换
相平面分析提供了在时域和频域之间转换的方法，可以将信号从时域表示转换为频域表示，或者反之。
Karnaugh图和相平面分析的关系
相平面分析和Karnaugh图是两种不同的分析方法，可以互补使用，帮助理解逻辑电路和时域系统的行为。
相平面分析的局限性和不足
相平面分析虽然是一种重要的分析工具，但它也有一些局限性，例如无法分析非线性和时变系统，以及对大规模系统的分析需要较高的计算复杂度。
相平面坐标系概述
相平面坐标系通过使用实部和虚部来表示复数，以一种直观的方式将信号和系统表示在平面上。
欧拉公式和复参数
欧拉公式是描述复数的重要公式，它将复数表示为指数和三角函数的关系，复参数在相平面分析中起着重要作用。
相平面上的运算
在相平面上，可以进行复数的加减乘除运算，这些运算在相平面分析中用于计算信号的频谱和系统的响应。

第7章--相平面法

若输出的一次谐波分量为
y1 (t) A1 cost B1 sint Y1 sin(t 1 )
输入的正弦量为 X sin t
则描述函数的数学表达式如式（7-75）所示：
返回子目录
N

Y1 X

e
e e0 e e0
e r c
得到 Te e Ku Tr r
假定
1 1 1
2 KT
2 kKT
54
（1）阶跃输入 r(t)=R
• 系统方程变为
Te e Ke 0
Te e kKe 0
图7-51 阶跃输入下得相轨迹
55
（2）输入信号r(t)=Vt+R
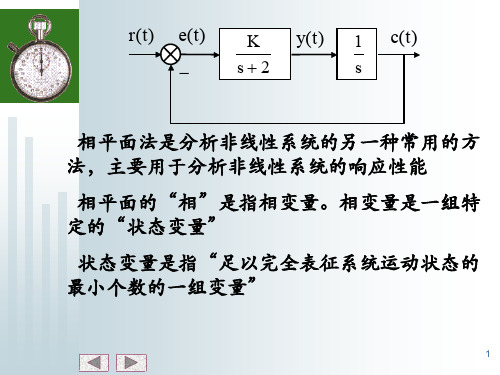
• 其中y(t)与c(t)两个状态变量之间满足导函数关系
d
•
y(t) c(t) dt
•
• 将相变量定义为满足导函数关系的一组状态变量。显然，相变量也不唯一
• 相平面法仅适用于研究二阶或一阶系统
2
c
o
a)
c(t)
c
o
t b)
o
c(t)
t
c)
3
• 图c是响应的时域曲线，图b是它的导函数曲线，图a是以t为参变量,将输出响应特性及其导函数特性绘在相平面上的曲线--输出响应特性的“相轨迹”曲线输出特性上既包含输出量大小的信息，也包含它的导函数信息，特性上点的切线斜率就是该点的导数
34
1、在 c>h的区域
系统方程为
Tc(t) c(t) KM
c(t)

k1

k e(1/T )t 2

KMt
其中 k1 c0 (c0 KM )T k2 (c0 KM )T

相平面02

7.2 相平面法相平面法是一种在时域中求解二阶微分方程的图解法。

它不仅能分析系统的稳定性和自振荡，而且能给出系统运动轨迹的清晰图像。

相平面法一般适用于二阶非线性系统的分析。

7.2.1 相平面的基本概念1. 相平面和相轨迹设一个二阶系统可以用下面的常微分方程),(=+xxfx（7-1）来描述。

其中),(xxf 是x和x 的线性或非线性函数。

在一组非全零初始条件下()0(x 和)0(x不全为零)，系统的运动可以用解析解)(tx和)(tx 描述。

如果取x和x 构成坐标平面，则系统的每一个状态均对应于该平面上的一点，这个平面称相平面。

当t变化时，这一点在x-x 平面上描绘出的轨迹，表征系统状态的演变过程，该轨迹就叫做相轨迹（如图7-8(a)所示）。

相平面和相轨迹曲线簇构成相平面图。

相平面图清楚地表示了系统在各种初始条件下的运动过程。

例如，研究以方程22=++xxxωξω（7-2）描述的二阶线性系统在一组非全零初始条件下的运动。

当0=ξ时式（7-2）变为2=+xxω（7-3）初始条件为)0(xx=，)0(xx=，方程（7-3）对应有一对虚根，即ωjp±=-2,1式（7-3）的解为图7-8 相轨迹)sin(ϕω+=tAx（7-4）式中，2220ωxxA+=，arctanxxωϕ=设x为描述二阶线性系统的一个变量，取x为描述系统的另一状态变量，即)cos(ϕωω+==tAdtdxx （7-5）从式（7-4）、式（7-5）中消去变量t，可得出系统运动过程中两个状态变量的关系为222)(Axx=+ω这是一个椭圆方程。

椭圆的参数A取决于初始条件x和x 。

选取不同的一组初始条件，可得到不同的A，对应相平面上的相轨迹是不同的椭圆，这样便得到一个相轨迹簇。

0=ξ时的相平面图如图7-9所示，表明系统的响应是等幅周期运动。

图中箭头表示时间t增大的方向。

2.相轨迹的性质相平面的上半平面中，0>x ，相迹点沿相轨迹向x轴正方向移动，所以上半部分相轨迹箭头向右；同理，下半相平面0<x ，相轨迹箭头向左。

自动控制原理--系统的相平面分析

xx00
x
x 0.5x 2x 0
s2 0.5s 2 0
s1 1.19, s2 1.69 鞍点
x 系统奇点特性及其相平面图
• •
P2
P1
x
2
2．奇线-极限环
在相平面图上表现为一个孤立的封闭的相轨迹，其他轨迹都趋向或者离开这个相轨迹，这个相轨迹称之为极限环。极限环在系统运动状态上表现为自振荡。
即系统的奇点为:
e e 0
e
y
(R,0)
•e
t
a) e
e
R•
(R,0)
•e
t
c)
b)
典型二阶线性系统阶跃输入相平面图及时域曲线
二、斜坡响应
Ty y Ke
Rs Es
K
sTs 1
Ys
因为 e r y,e r y,e r y
典型二阶线性系统结构图
在斜坡输入作用下 r(t) Vt, r(t) 0，r(t) V
e)
x x
x x
x x
j
0 b)
j
0
d) j
0 f)
典型二阶系统奇点特性及其相平面图
x x
x x
x x
关于奇点的结论： ①线性二阶系统有一个奇点，如果是零输入系统，奇点就是原点。 ②除奇点外，不同初始点的相轨迹不相交。 ③根据线性系统根的分布，判断奇点类型，可以确定奇点附近的相轨迹，可以分析系统的运动状态。 ④对于非线性二阶系统，可能存在多个奇点，在确定奇点位置后，可以在奇点处对系统进行线性化，然后确定奇点附近的相轨迹。
此时，
e
e0区域内，Te
e
0 ，e(T
d2e de
dt 2 dt