中考几何动点问题12种模型全总结PPT
合集下载
中考数学复习专题-动点问题ppt

230、积极的人在每一次忧患中都看到一个机会,而消极的人则在每个机会都看到某种忧患。
•
231、出门走好路,出口说好话,出手做好事。
•
232、旁观者的姓名永远爬不到比赛的计分板上。
•
233、怠惰是贫穷的制造厂。
•
234、莫找借口失败,只找理由成功。(不为失败找理由,要为成功找方法)
•
235、如果我们想要更多的玫瑰花,就必须种植更多的玫瑰树。
为何值时,S最大,并求最大 值。
析-
典 已知:如图①,在Rt△ABC中,∠C=90°,
AC=4cm,BC=3cm,点P由B出发沿BA方向向点A
例 匀速运动,速度为1cm/s;点Q由A出发沿AC方向
向点C匀速运动,速度为2cm/s;连接PQ.若设运 动的时间为t(s),解答下列问题 :
分 ⑷当t为何值时,△APQ是
时, PQ∥BC?”类型的 题目结论变条件,寻找 解题思路;必要时画出
相应的图形。
典 已知:如图①,在Rt△ABC中,∠C=90°,
AC=4cm,BC=3cm,点P由B出发沿BA方向向点A
例 匀速运动,速度为1cm/s;点Q由A出发沿AC方向
向点C匀速运动,速度为2cm/s;连接PQ.若设运 动的时间为t(s),解答下列问题 :
•
225、积极思考造成积极人生,消极思考造成消极人生。
•
226、人之所以有一张嘴,而有两只耳朵,原因是听的要比说的多一倍。
•
227、别想一下造出大海,必须先由小河川开始。
•
228、有事者,事竟成;破釜沉舟,百二秦关终归楚;苦心人,天不负;卧薪尝胆,三千越甲可吞吴。
•
229、以诚感人者,人亦诚而应。
•
中考数学总复习课件(专题3:动点型问题)

MN 1 x2 S 16 2( 1 x2
8. 8)
1
x2
8.
2
2
根据二次函数的图形和性质,这个函数的图形是开口向下,
对称轴是y轴,顶点是(0,8),自变量的取值范围是0<x
<4.
故答案选C.
(三)面动问题 【例题 4】(2014·玉林市)如图,边长分别为1和2的两个等边 三角形,开始它们在左边重合,大三角形固定不动,然后把 小三角形自左向右平移直至移出大三角形外停止.设小三角形 移动的距离为x,两个三角形重叠的面积为y,则y关于x的函 数图象是( )
解:(1)①当△BPQ∽△BAC时,
∵ BP BQ , BP=5t,QC=4t,
BA BC
AB=10 cm,BC=8 cm,
∴ 5t 8 4t ,∴t=1.
10 8
②当△BPQ∽△BCA时,
∵
BP BC
BQ , BA
∴
5t 8 4t , 8 10
∴
t 32 . 41
∴t=1或 t 32 时,△BPQ与△ABC类似.
41
(2)如图a,过点P作PM⊥BC于点M,AQ,CP相交于点N.
则有PB=5t,PM=3t,CM=8-4t,
∵∠NAC+∠NCA=90°,
∠PCM+∠NCA=90°,
∴∠NAC=∠PCM且∠ACQ=∠PMC=90°.
∴△ACQ∽△CMP.
∴ AC QC .
CM PM
∴ 6 4t , 解得 t 7 ,
题型一 建立动点问题的函数关系式(或函数图象)
【例题 1】(2014·黑龙江省)如图,在平面直角坐标系中,边 长为1的正方形ABCD中,AD边的中点处有一动点P,动点P 沿P→D→C→B→A→P运动一周,则P点的纵坐标y与点P走
中考常见动点问题解题方法(共29张PPT)

AE
10-2t
t
30o
2t
30o
B
F
D
C
(3)当t为何值时,△DEF为直角三角形?请说明理由.
1单位/s
解析:
2单位/s
②当∠DEF=90o时
30o
由(2)知EF∥AD
5
∴∠ADE=∠DEF=90o
∵∠A=90o-∠C=60o
1
∴AD= AE
2
1
2
即10-2t= t
A
E 10-2t
60o
t
2t
则t=4
10、阅读一切好书如同和过去最杰出的人谈话。01:48:2201:48:2201:488/23/2021 1:48:22 AM
11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。21.8.2301:48:2201:48Aug-2123-Aug-21
最小值时,△APD中AP边上的高为 _________
3、如图,⊙O的半径为2,点A、B、C
在⊙O上,OA⊥OB, ∠AOC=60°,P是OB上
的一动点,则PA+PC的最小值是________
两个动点(一)
例、如图,∠AOB=45°,P是∠AOB内一
特点:已知一个定点位于平面内两相交直线之间,
点,PO=10,Q、R分别是OA、OB上的动点,
∵点D'和点D关于x轴对称,
∴点D'的坐标为(0,-2).
设直线CD'的解析式为y=kx+b,
∵直线CD'过点C(-3,2),D'(0,-2),
4
2 = -3 + ,
几何图形动点问题2大类12小类模型全梳理-

MO的长度,过点M作MN⊥BC于点N,在△AOM和△COP′中,
例3题图
∠AOM=∠COP′,OA=OC,∠OAM=∠OCP′,
∴△AOM≌△COP′,∴OM=OP′= 1 MP′,∴CP′=AM=4-1
2
=3,BP′=1,∴P′N=4-1-1=2,∴MP′= 22 +32 = 13 ,
1 ∴OM=2
例2题图
例2题解 图
类型2 线圆最值 【模型分析】 (i) 如图,AB为 O的一条定弦,点C为圆上一动点. (1)如图①,若点C在优弧 AB上,当CH⊥AB且CH过圆心O时,线段CH即为点C到 弦AB的最大距离,此时△ABC的面积最大; (2)如图②,若点C在劣弧AB上,当CH⊥AB且CH 的延长线过圆心O时,线段CH即为点C到弦AB的最大距离,此时△ABC的面积最大.
A. 4
B. 5
C. 6
D. 7
例5题图
【解析】如解图,分别作点P关于OA、OB的对称点C、D,连接 CM、OC、DN、OD,∵点P关于OA的对称点为C,∴PM=CM, OP=OC,∠COA=∠POA,∵点P关于OB的对称点为D,∴PN =DN,OP=OD,∠DOB=∠POB,∴OC=OD=OP=6, ∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+ 2∠POB=2∠AOB=60°,△PMN的周长为PM+PN+MN= CM+DN+MN,连接CD分别交OA,OB于点M′,N′,∵CM+ DN+MN≥CM′+DN′+M′N′,当M与M′,N与N′重合时, △PMN的周长最小,即为线段CD的长度,∵∠COD=60°, OC=OD,∴△COD是等边三角形,∴CD=OC=OD= 6.∴△PMN的周长的最小值为6.
中点,点M在BC边上,且BM=6,P为对角线BD上一点,则PM-PN的最大值为
中考总复习动点问题精品PPT教学课件

E
(P)
D (Q)
F两点,若△BEF与题
(1)中的△APQ相似, 试求a的值.
2020/12/8
(F) C 综上:当a=2或6或12时,
△BEF与△APQ相似 4
3、如图,在矩形ABCD中,AB=20厘米,BC=4厘米,点P从点A开 始沿折线A—B—C—D以4厘米/秒的速度移动,点Q从点C开 始沿CD以1厘米/秒的速度移动,如果点P和Q分别从点A、C 同时出发,当其中一个点到达D点时,另一点也随之停止运 动.设运动时间为t(秒).
厘米的等边三角形,质点P从点A沿AB—
A
BD作匀速运动,质点Q从点D同时出发沿
DC—CB—BA作匀速运动.
3a
Q
(P)
(21)如果问质点题(P、1) Q运中 3a
的 动的质速点度P、分Q别分是别同4厘时米沿/ B F
原 秒路、返5厘回米,/质秒点,请P的说速出 度 经不过变12,秒质后点△QA的PQ速是度哪 3a F 改 一类变三为角a厘形米?/(秒按,角经的过 3大秒小后分,类P)、Q分别到达E、
2020/12/8
1
1、如图,已知正三角形
ABC的高为9厘米,⊙O的
半径为r厘米,当圆心O
A
从点A出发,沿线路AB—
BC—CA运动,回到点A时,
⊙O随着点O的运动而停
止.
B
C
(1)当r=9厘米时,⊙O
在移动过程中与△ABC三
边有几个切点?
当r=9厘米时,⊙O在移动过程
中与△ABC三边有三个切点.
2020/12/8
温馨提示:本文内容皆为可修改式文档,下载后,可根据读者的需求 作修改、删除以及打印,感谢各位小主的阅览和下载
第35讲动点问题专题PPT课件
③如答图2-35-10,当4≤x<6时,CD=6-x, ∵∠BCE=90°,∠PDC=60°,
④当x≥6时,y=0.
②如答图2-35-5,作DH⊥AB于点H. 在Rt△ADH中,∵AD=x,∠DAH=∠ACO=30°,
在Rt△BDH中, ∴矩形BDEF的面积为
∴当x=3时,y有最小值为
分层训练
A组
3.(202X衢州)如图2-35-3,正方形ABCD的边长为4,点
E是AB的中点,点P从点E出发,沿E→A→D→C移动至终
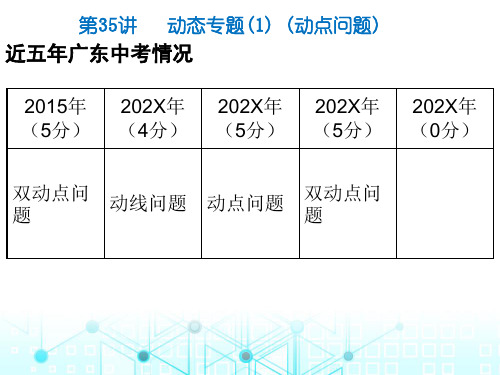
第35讲 动态专题(1) (动点问题)
近五年广东中考情况
2015年 202X年 202X年 202X年 202X年 (5分) (4分) (5分) (5分) (0分)
双动点问 题
动线问题
的运动中,一些图 形位置、数量关系的“变”与“不变”的问题.常用 的数学思想是方程思想、数学建模思想、函数思想、 转化思想等;常用的数学方法有分类讨论法、数形 结合法等.
(3)在直线l移动过程中,l上是否存在一点Q,使以B, C,Q为顶点的三角形是等腰直角三角形?若存在,直 接写出Q点的坐标;若不存在,请说明理由.
解:(1)在Rt△BOC中,OB=3,
设CO=4k,则BC=5k, ∵BC2=CO2+OB2,∴25k2=16k2+9, ∴k=1或-1(不符,舍去).∴BC=5,OC=4. ∵四边形ABCD是菱形,∴CD=BC=5.∴D(5,4). (2)①如答图2-35-6,当0≤t≤2时,直线l扫过的图形 是四边形OCQP,S=4t.
②如图2-35-2②,当点E在OC的延长线上时, △DCE是等腰三角形,则只有CD=CE, ∠DBC=∠DEC=∠CDE= ∠ACO=15°, ∴∠ABD=∠ADB=75°.∴AB=AD= 综上所述,满足条件的AD的值为2或
④当x≥6时,y=0.
②如答图2-35-5,作DH⊥AB于点H. 在Rt△ADH中,∵AD=x,∠DAH=∠ACO=30°,
在Rt△BDH中, ∴矩形BDEF的面积为
∴当x=3时,y有最小值为
分层训练
A组
3.(202X衢州)如图2-35-3,正方形ABCD的边长为4,点
E是AB的中点,点P从点E出发,沿E→A→D→C移动至终
第35讲 动态专题(1) (动点问题)
近五年广东中考情况
2015年 202X年 202X年 202X年 202X年 (5分) (4分) (5分) (5分) (0分)
双动点问 题
动线问题
的运动中,一些图 形位置、数量关系的“变”与“不变”的问题.常用 的数学思想是方程思想、数学建模思想、函数思想、 转化思想等;常用的数学方法有分类讨论法、数形 结合法等.
(3)在直线l移动过程中,l上是否存在一点Q,使以B, C,Q为顶点的三角形是等腰直角三角形?若存在,直 接写出Q点的坐标;若不存在,请说明理由.
解:(1)在Rt△BOC中,OB=3,
设CO=4k,则BC=5k, ∵BC2=CO2+OB2,∴25k2=16k2+9, ∴k=1或-1(不符,舍去).∴BC=5,OC=4. ∵四边形ABCD是菱形,∴CD=BC=5.∴D(5,4). (2)①如答图2-35-6,当0≤t≤2时,直线l扫过的图形 是四边形OCQP,S=4t.
②如图2-35-2②,当点E在OC的延长线上时, △DCE是等腰三角形,则只有CD=CE, ∠DBC=∠DEC=∠CDE= ∠ACO=15°, ∴∠ABD=∠ADB=75°.∴AB=AD= 综上所述,满足条件的AD的值为2或
中考数学动态几何问题课件 (共37张PPT)

2 2
1
1
S△BCD= BD· CF= × 4× - x 2 + 3x =-x2+6x,
2 2 2
1
1
1
则S=S△OAD+S△ACD+S△BCD=4+(2x-4)+(-x2+6x)=-x2+8x=-(x-4)2+16(2<x<6), 因为a=-1<0,所以当x=4时,四边形ABCD的面积S取最大值,最大值为16.
难点突破
6、 在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB 相交于点E,DF与线段AC(或AC的延长线)相交于点F. (1)如图①,若DF⊥AC,垂足为F,AB=4,求BE的长; (2)如图②,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.
∴ ∠BEC+ ∠AEN的值不变
难点突破
难点突破 5、如图,长方形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD上的 E点处,折痕的一端G点在边BC上. (1)如图①,当折痕的另一端F在AB边上且AE=4时,求AF的长; (2)如图②,当折痕的另一端F在AD边上且BG=10时. ①求证:EF=EG;②求AF的长;
由折叠知△A1DE≌△ADE, 所以A1D=AD=1.
由 A1B+A1D≥BD,得 A1B≥BD-A1D= 5-1. 故 A1B 长的最小值是 5-1.
难点突破
2、如图,在△ABC中,∠C=90°,AB=10 cm,BC=8 cm,点P从点A沿AC向点C以1 cm/s的速度
运动,同时点Q从点C沿CB向点B以2 cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边 形PABQ面积的最小值为( C )
1
1
S△BCD= BD· CF= × 4× - x 2 + 3x =-x2+6x,
2 2 2
1
1
1
则S=S△OAD+S△ACD+S△BCD=4+(2x-4)+(-x2+6x)=-x2+8x=-(x-4)2+16(2<x<6), 因为a=-1<0,所以当x=4时,四边形ABCD的面积S取最大值,最大值为16.
难点突破
6、 在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB 相交于点E,DF与线段AC(或AC的延长线)相交于点F. (1)如图①,若DF⊥AC,垂足为F,AB=4,求BE的长; (2)如图②,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.
∴ ∠BEC+ ∠AEN的值不变
难点突破
难点突破 5、如图,长方形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD上的 E点处,折痕的一端G点在边BC上. (1)如图①,当折痕的另一端F在AB边上且AE=4时,求AF的长; (2)如图②,当折痕的另一端F在AD边上且BG=10时. ①求证:EF=EG;②求AF的长;
由折叠知△A1DE≌△ADE, 所以A1D=AD=1.
由 A1B+A1D≥BD,得 A1B≥BD-A1D= 5-1. 故 A1B 长的最小值是 5-1.
难点突破
2、如图,在△ABC中,∠C=90°,AB=10 cm,BC=8 cm,点P从点A沿AC向点C以1 cm/s的速度
运动,同时点Q从点C沿CB向点B以2 cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边 形PABQ面积的最小值为( C )
2020年中考数学复习 初中数学动态几何问题 (29张PPT)

ACB=90°,AC=6,BC=8,点D 以每秒1个单位长度的速度由点A向点B匀速运动,到达B点即停止 运动,M,N分别是AD,CD的中点,连结MN,设点D运动的时间为 t.
(3)若△DMN是等腰三角形,求t的值.
[解析] (3)根据等腰三角形的腰的情况 进行分类讨论,从而求出t的值.
初中数学动态几何问题
动态几何问题是指以几何知识和图形为背景,蕴涵一些运动变化的 几何元素,主要研究几何图形在运动中所遵循的规律,如图形的形状、 位置、数量关系等.
就运动对象而言,有点动(点在线段或弧线上运动)、线动(直线或线 段的平移、旋转)和面动(部分图形的平移、旋转、翻折)等,而且在运动 过程中大多是动中有静,动静结合.
(3)根据题意可知,MD=12AD,DN=12DC,MN=12AC=3.
i)当MD=MN=3时,△DMN为等腰三角形,此时AD=AC=6,
∴t=6;
ii)当MD=DN时,AD=DC,
1 过D作DH⊥AC交AC于H,则AH=2AC=3, ∵AC=6,BC=8, ∴AB=10,
∵cosA=AAHD=AACB=35,
例 2 已知:如图①,抛物线 y=ax2+bx+c 与 x 轴正半轴交 于 A,B 两点,与 y 轴交于点 C,直线 y=x-2 经过 A、C 两 点,且 AB=2.
(2)若直线 DE 平行于 x 轴并从 C 点开始以每秒 1 个单位的 速度沿 y 轴正方向平移,且分别交 y 轴、线段 BC 于点 E、D, 同时动点 P 从点 B 出发,沿 BO 方向以每秒 2 个单位的速度运 动.当点 P 运动到原点 O 时,直线 DE 与点 P 都停止运动,连结
位长度的速度由点A向点B匀速运动,到达B点即停止运动,M,N分别是AD,CD 的中点,连结MN,设点D运动的时间为t.
(3)若△DMN是等腰三角形,求t的值.
[解析] (3)根据等腰三角形的腰的情况 进行分类讨论,从而求出t的值.
初中数学动态几何问题
动态几何问题是指以几何知识和图形为背景,蕴涵一些运动变化的 几何元素,主要研究几何图形在运动中所遵循的规律,如图形的形状、 位置、数量关系等.
就运动对象而言,有点动(点在线段或弧线上运动)、线动(直线或线 段的平移、旋转)和面动(部分图形的平移、旋转、翻折)等,而且在运动 过程中大多是动中有静,动静结合.
(3)根据题意可知,MD=12AD,DN=12DC,MN=12AC=3.
i)当MD=MN=3时,△DMN为等腰三角形,此时AD=AC=6,
∴t=6;
ii)当MD=DN时,AD=DC,
1 过D作DH⊥AC交AC于H,则AH=2AC=3, ∵AC=6,BC=8, ∴AB=10,
∵cosA=AAHD=AACB=35,
例 2 已知:如图①,抛物线 y=ax2+bx+c 与 x 轴正半轴交 于 A,B 两点,与 y 轴交于点 C,直线 y=x-2 经过 A、C 两 点,且 AB=2.
(2)若直线 DE 平行于 x 轴并从 C 点开始以每秒 1 个单位的 速度沿 y 轴正方向平移,且分别交 y 轴、线段 BC 于点 E、D, 同时动点 P 从点 B 出发,沿 BO 方向以每秒 2 个单位的速度运 动.当点 P 运动到原点 O 时,直线 DE 与点 P 都停止运动,连结
位长度的速度由点A向点B匀速运动,到达B点即停止运动,M,N分别是AD,CD 的中点,连结MN,设点D运动的时间为t.
中考数学复习专题动点问题PPT课件
(2)若点P从点A沿射线AB运动,速度仍是1cm/s。
当t为何值时,△PBC为等腰三角形?
D
C
4 P
A
7
B
小组合作交流讨论
第2页/共21页
D
C
4 P
A
7
B
当BP=BC时
D(钝角)
C
4
∟
30°
A
7
B 23 E
P当CB=CP时D源自C4A7
B
P
当BP=BC时
(锐角)
D
C
E4
A
7
B
P
当PB=PC时
第3页/共21页
∠B=90°,AD=24cm,BC=26cm,动点P从点A开始沿AD边 向点D,以1cm/秒的速度运动,动点Q从点C开始沿CB向点B
以3厘米/秒的速度运动,P、Q分别从点A点C同时出发,当其
中一点到达端点时,另一点也随之停止运动,设运动时间为t秒,
求:
1)t为何值时,四边形PQCD为平行四边形 2) t为何值时,等腰梯形?
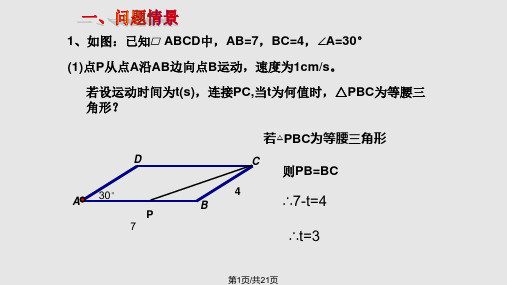
1、如图:已知 ABCD中,AB=7,BC=4,∠A=30°
(1)点P从点A沿AB边向点B运动,速度为1cm/s。
若设运动时间为t(s),连接PC,当t为何值时,△PBC为等腰三 角形?
D
A 30° P
7
若△PBC为等腰三角形
C
则PB=BC
4 B
∴7-t=4
∴t=3
第1页/共21页
如图:已知 ABCD中,AB=7,BC=4,∠A=30°
∴方程无解。 即点D都不可能在线段QP的中垂线 上。
第12页/共21页
3、(2009中考)如图在边长为2cm的正方形ABCD中, 点Q为BC边的中点,点P为对角线AC上一动点,连接 PB、PQ,则 △PBQ 周长的最小值是-----cm (结果不取近 似值)
2023中考英语专题:中考中常见的动点问题及解题方法(共24张PPT)

BC边运动,其中一个点到达终点时,另一点也随之停止运动。当运动时
间为t秒,连结MN,将△BMN沿MN翻折,B点恰好落在AC边上的P处,
求t的值及点P的坐标;
y
C
P
N
t4 3
P 1,2 3 3
A
MO B x
典例探究
【题型3】直线上的动点问题
例 3 如图,二次函数 y ax2 bx c的图象与x轴交于A、B两点,与y轴
致
动时间为t秒,求S与t的之间函数关系式并写出自变量取值范围; (3)在(2)的条件下,当t为何值时,∠MPB与∠BCO互余,求
用
求出此时直线OP与直线AO所夹锐角的正切值。
y
y
A HB
A HB
M
M
O
Cx
图1
O Cx 图2
数学活动室
2.如图,在平面直角坐标系中,点A( 3 ,0),B(3 3,2),C (0,2),动点D以每秒1个单位的速度从点O出发沿OC向终点C
在动点的运动过程中观察图形的变化情况,理解图形在不同 位置的情况,做好计算推理的过程。在变化中找到不变的性质是 解决“动点”探究题的基本思路,这也是动态几何数学问题中最 核心的数学本质。
梳理体系
1、研究背景图形: 2、分析运动过程,分段,定范围(关注四要素) (1)根据起点、终点、确定时间范围; (2)速度(注意速度是否变化) (3)状态转折点,确定分段,常见状态转折点为拐点; (4)所求目标——明确方向。 3、分析结合特征,表单,设计方法求解。 画出符合题意的图形,表达线段长,根据几何特征列方程求解, 结合范围验证结果。
用
y F
C
B
3 m 13 3
6
D
初三数学几何动点题及方法精选幻灯片

5
【思路分析】本题和上题有所不同,上一题会给出一个条件使得动点静 止,而本题并未给出那个“静止点”,所以需要我们去分析由D运动产生的 变化图形当中,什么条件是不动的。由题我们发现,正方形中四条边的垂 直关系是不动的,于是利用角度的互余关系进行传递,就可以得解。
6
【思路分析】这一问是典型的从特殊到一般的问法,那么思路很简 单,就是从一般中构筑一个特殊的条件就行,于是我们和上题一样找 AC的垂线,就可以变成第一问的条件,然后一样求解。
A
D
N
B
M
C
2
【思路分析】解决动点问题,首先就是要找谁在动,谁没在动, 通过分析动态条件和静态条件之间的关系求解。对于大多数题目 来说,都有一个由动转静的瞬间,就本题而言,M,N是在动,意 味着BM,MC以及DN,NC都是变化的。但是我们发现,和这些动态的 条件密切相关的条件DC,BC长度都是给定的,而且动态条件之间也 是有关系的。所以当题中设定MN//AB时,就变成了一个静止问 题。由此,从这些条件出发,列出方程,自然得出结果。
A
M
D
60°
B P
Q C
11
以上三类题目都是动点问题,这一类问题的关键就在于当动点移动中出现 特殊条件,例如某边相等,某角固定时,将动态问题化为静态问题去求 解。如果没有特殊条件,那么就需要研究在动点移动中哪些条件是保持不 变的。当动的不是点,而是一些具体的图形时,思路是不是一样呢?接下 来我们看另外两道题.
A
M
D
G
E
FN
B
C
图2 14
【思路分析】如果△BEF任意旋转,哪些量在变化,哪些量不变呢?在△BEF的
旋转过程中,始终不变的依然是G点是FD的中点。可以延长一倍EG到H,从而构造
【思路分析】本题和上题有所不同,上一题会给出一个条件使得动点静 止,而本题并未给出那个“静止点”,所以需要我们去分析由D运动产生的 变化图形当中,什么条件是不动的。由题我们发现,正方形中四条边的垂 直关系是不动的,于是利用角度的互余关系进行传递,就可以得解。
6
【思路分析】这一问是典型的从特殊到一般的问法,那么思路很简 单,就是从一般中构筑一个特殊的条件就行,于是我们和上题一样找 AC的垂线,就可以变成第一问的条件,然后一样求解。
A
D
N
B
M
C
2
【思路分析】解决动点问题,首先就是要找谁在动,谁没在动, 通过分析动态条件和静态条件之间的关系求解。对于大多数题目 来说,都有一个由动转静的瞬间,就本题而言,M,N是在动,意 味着BM,MC以及DN,NC都是变化的。但是我们发现,和这些动态的 条件密切相关的条件DC,BC长度都是给定的,而且动态条件之间也 是有关系的。所以当题中设定MN//AB时,就变成了一个静止问 题。由此,从这些条件出发,列出方程,自然得出结果。
A
M
D
60°
B P
Q C
11
以上三类题目都是动点问题,这一类问题的关键就在于当动点移动中出现 特殊条件,例如某边相等,某角固定时,将动态问题化为静态问题去求 解。如果没有特殊条件,那么就需要研究在动点移动中哪些条件是保持不 变的。当动的不是点,而是一些具体的图形时,思路是不是一样呢?接下 来我们看另外两道题.
A
M
D
G
E
FN
B
C
图2 14
【思路分析】如果△BEF任意旋转,哪些量在变化,哪些量不变呢?在△BEF的
旋转过程中,始终不变的依然是G点是FD的中点。可以延长一倍EG到H,从而构造
初三几何动点问题ppt课件

精选ppt课件
20
一、教学模式
1、课堂教学模式(新授课) ①概念方法习题化(定义、法则、公式、定理、方法和思想等)不直接 叙述概念 ②习题设置题组化 ③题组设计层次化(由易到难从不同角度不同层次进行训练) ④题目处理变式化(不能就题论题采用一题多解或一题多变的形式深入 灵活地强化训练) ⑤问题解决自主化
精选ppt课件
22
三、教学思路
整体设计:时间、内容、单元、知识、方法与技能等 分类设计:知识、方法与技能要体现基础性、针对性、
层次性、典型性、 综合性、发展性,因材施教。 分层设计:以人为本,在课程内容、巩固练习、基本技能、
目标评价、作业布置等方面有梯度。 整体提高:对学困生:不厌其差,不厌其烦,不厌其慢
精选ppt课件
13
四、画龙点睛
5、需要掌握知识 (1)不等式,一元二次方程及其根的判别式 (2)反比例函数、一次函数和二次函数的图象 与性质 (3)三角形、四边形、梯形面积公式 (4)勾股定理及其逆定理 (5)等腰三角形、直角三角形、相似三角形、 (特殊)平行四边形、梯形的判定与性质、特殊 角三角函数
对优秀生:引导激励,自主学习,自我发展
精选ppt课件
23
四、教学设计
精选ppt课件
24
五、课堂教学
引入新课——温故知新 讲授新课——举一反三 巩固新知——趁热打铁 归纳小结——画龙点睛 布置作业——触类旁通
精选ppt课件
25
六、例题教学
源于教材。就是要吃透教材,正确体会新教材编写意图,弄清配备 例题的功能,强化解题的规范性。
整合教材。就是要研究教材,研究不同版本教材,取长补短,择优选 用。
跳出教材。就是要更新教材,把每一个例题当成一个课题去研究,去 探究题目源头,寻找变化规律,拓宽解题思路,总结解题方法,提炼数 学思想。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考几何动点问题12种模型全总结PPT
1.利用垂线段最短求最值
2.利用将军饮马求最值
3.同侧线段和最小值问题
4.同侧差最大值问题
5.异侧差最大值问题
6.“一点两线”型(两动点+一定点)
7.“两点两线”型(两动点+两定点)
8.利用圆的相关性质求线段最值
9.点圆最值
10.直径对直角
11.四点共圆
12.特定条件问题
1.利用垂线段最短求最值
2.利用将军饮马求最值
3.同侧线段和
1.利用垂线段最短求最值
2.利用将军饮马求最值
3.同侧线段和最小值问题
4.同侧差最大值问题
5.异侧差最大值问题
6.“一点两线”型(两动点+一定点)
7.“两点两线”型(两动点+两定点)
8.利用圆的相关性质求线段最值
9.点圆最值
10.直径对直角
11.四点共圆
12.特定条件问题问题
4.同侧差最大值问题
5.异侧差最大值问题
6.“一点两线”型(两动点+一定点)
7.“两点两线”型(两动点+两定点)
8.利用圆的相关性质求线段最值
9.点圆最值
10.直径对直角
11.四点共圆
12.特定条件问题。
