多种类型的回归模型

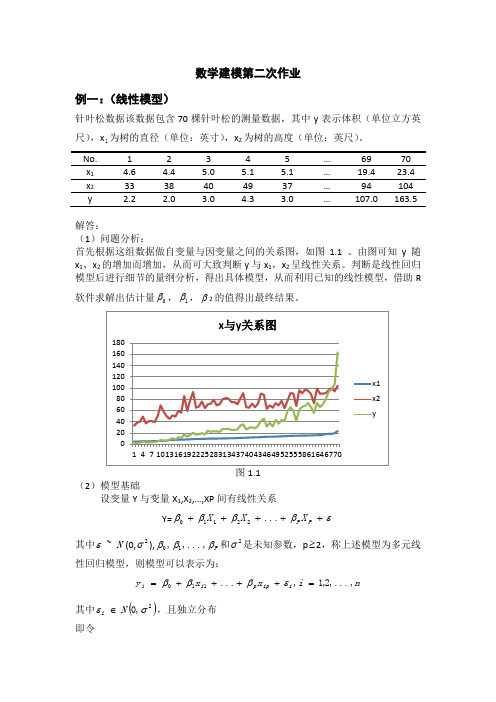
数学建模第二次作业

例一：（线性模型）

针叶松数据该数据包含70棵针叶松的测量数据，其中y 表示体积（单位立方英尺），x 1为树的直径（单位：英寸），x 2为树的高度（单位：英尺）。 x 1 4.6 4.4 5.0 5.1 5.1 … 19.4 23.4 x 2 33 38 40 49 37 … 94 104 解答：

（1）问题分析：

首先根据这组数据做自变量与因变量之间的关系图，如图1.1 。由图可知y 随x 1、x 2的增加而增加，从而可大致判断y 与x 1，x 2呈线性关系。判断是线性回归模型后进行细节的量纲分析，得出具体模型，从而利用已知的线性模型，借助R 软件求解出估计量0β，1β，β2的值得出最终结果。

图1.1

（2）模型基础

设变量Y 与变量X 1,X 2,…,XP 间有线性关系

Y=εββββ+++++P P X X X (22110)

其中N ~ε(0,2σ),P βββ,...,,10和2σ是未知参数，p ≥2，称上述模型为多元线性回归模型，则模型可以表示为：

n i x x y i ip p i i ,...,2,1,...110=++++=εβββ

其中()

2,0σεN i ∈，且独立分布 即令

⎥

⎥

⎥⎥

⎦⎤⎢⎢⎢⎢⎣⎡=n y y y y 2

1，⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=p ββββ 10，⎥⎥⎥

⎥⎥⎦

⎤

⎢⎢⎢⎢

⎢⎣⎡=np n n p p x x x x x x x x x X ...1...1 (12)

1

222

2111211

，⎥

⎥⎥⎥

⎦⎤⎢⎢⎢⎢⎣⎡=n εε

εε 21

则多元线性回归模型可表示为

εβ+=X Y ,

其中Y 是由响应变量构成的n 维向量，X 是n ⨯（p+1）阶设计矩阵，β是p+1维

向量，并且满足

E （ε）=0，Var （ε）=2σI n

与一元线性回归类似，求参数β的估计值β

ˆ，就是求最小二乘函数 Q （β）=

()()ββX y X y T

--

达到最小的β的值。

β的最小二乘估计

()

y X X X T T 1

ˆ-=β

从而得到经验回归方程

P P X X Y βββ

ˆˆˆˆ11+++=

（3）问题求解：

由于体积与长度的量纲不一致，为了使等式两边量纲统一，首先利用excel 软件对数据进行预处理，即对y 进行三次开方的处理。

其中，选择线的性模型为：i i i i x x y εβββ+++=221103，i=1,…,70

3

y 计算结果如下表1.1

0β=0.0329

1β=0.1745 2β=0.0142

根据计算结果可以将x 1,x 2的值带入回归方程求解y 值，将所得y 值（实验值）与真实y 值（观测值）进行比较达到检验模型模拟优度的目的，得下图1.2

图1.2

由图1.2得，回归系数和回归方程检验都是显著的，模型模拟结果较好。 则该题结果为：i

i i x x y 2130142.01745.000329.0++=

（4）模型评价：

①模型优点：选取线性回归模型有效反应了自变量与因变量之间的内在关系，在利用线性模型的基础上，注意到保持等式两边量纲的一致性，体现模型的严谨性。

②模型缺点：当x 值增大时，y 实验值增长速度加快，模拟出现偏差。

例二：（非线性模型）欧洲野兔

No. 1 2 4 5 … 70 71 X 15 15 18 28 … 768 860 y 21.66 22.75 31.25 44.79 … 232.12 246.70

这组数据包含71组观测值，其中y 为在澳大利亚的欧洲野兔干燥眼球重量（单位：毫克）的对数值，x 为野兔相应的年龄（单位：天）。、

解答：

（1）问题分析：要求澳大利亚的欧洲野兔年龄与干燥眼球重量之间的关系，首先应该大致分析两者之间的线性关系。确定其大致性关系后进一步具体化分析，得出澳大利亚的欧洲野兔年龄与干燥眼球重量之间的具体模型并建立函数模型，通过对未知参数的求解得出最终结果。本题中，通过spss 模型进行初步估计后建模具体求解 （2）问题求解：

利用spss 软件对野兔年龄(自变量x)与干燥眼球重量（因变量y ）进行画图初步分析，所得结果如图2.1

图2.1

由图2.1可知，x、y两者呈非线性关系，故需用非线性回归模型进行进一步估计。

（2）由（1）知x、y两者呈非线性关系，则用曲线估计中的线性、对数、逆模型、

二次项、立方、幂次、复合、S、logistic、增长、指数分布等11种模型进行拟合，

所得结果如表2.1，拟合效果图见图2.2.

表2.1

模型汇总和参数估计值

因变量:重量

模型汇总参数估计值方程

R 方 F df1 df2 Sig. 常数b1 b2 b3 线性.762 217.236 1 68 .000 82.217 .264

对数.970 2184.028 1 68 .000 -173.394 62.940

倒数.636 118.830 1 68 .000 186.705 -3748.419

二次.950 636.309 2 67 .000 37.172 .689 -.001

三次.979 1016.731 3 66 .000 17.289 1.035 -.002 1.061E-6 复合.559 86.313 1 68 .000 76.813 1.002

幂.936 999.744 1 68 .000 7.021 .571

S .860 416.599 1 68 .000 5.279 -40.205

增长.559 86.313 1 68 .000 4.341 .002

指数.559 86.313 1 68 .000 76.813 .002

Logistic .559 86.313 1 68 .000 .013 .998