九下第二单元易错题
九年级英语下学期unit-2常错题复习课件

【易错题】中考九年级历史下第二单元第二次工业革命和近代科学文化试卷(附答案)

一、选择题1.某同学以“科学家与成就”为主题设计了如下四个探究题目。
其中正确的是A.牛顿与万有引力定律B.莱特兄弟与火车C.达尔文与电的应用D.爱迪生与进化论2.在1750—1850年间欧洲的人口从1.4亿增加到2.65亿,到1900年猛增到4亿。
这主要是由于A.欧洲城市扩大与发展B.欧洲开放的移民政策C.两次工业革命的开展D.欧洲国家联合的结果3.“江河的水往低处流、爬山和上楼梯觉得很累”。
这些日常现象都和那种理论有关( )A.德漠克里特的原子论B.亚里士多德的逻辑学C.牛顿的万有引力定律D.达尔文的进化论4.右下表摘自吴于廑、齐世荣主编的《世界史·近代史编》,对该表格解读正确的是1861~1900年主要资本主义国家工业年平均增长率(%)A.主要资本主义国家经济发展不平衡B.美、德后来居上,工业总产值超过英、法C.第一次世界大战一触即发D.英、法两国基本没有参与第二次工业革命5.一位19世纪的法国伟大批判现实主文作家曾说过:“拿破仑用剑所未能完成的事业,我要用笔来完成。
”马克思、恩格斯称赞他“是超群的小说家”材料中的“他”是A.巴尔扎克B.列夫托尔斯泰C.高尔基D.伏尔泰6.有这样一段广告词:“一个苹果让牛顿吸引了世界,一壶沸水让瓦特转动了世界,一个元素让爱迪生点燃了世界。
”“爱迪生点燃了世界”是指A.发现万有引力定律B.发明内燃机C.改良蒸汽机D.研制成功耐用碳丝灯泡7.1876年,一位俄国地主写道:“解放法令颁布15个月后,当我再看到农民时,我只有敬慕他们。
他们同以前的主人交谈时,就像一个平等的人在同另一个平等的人交谈。
”俄国农民的这种变化主要是因为A.人人都得到了一小块份地B.从法律上获得了人身自由C.完全摆脱封建地主的控制D.俄国走上了资本主义道路8.如图反映了1870年和1900年的世界石油产量。
以下选项中,导致1870年至1900年世界石油产量发生变化的是A.斯蒂芬森的蒸汽机车B.瓦特改良的蒸汽机C.内燃机的发明和使用D.爱迪生发明白炽灯泡9.飞上天空是人类自古以来的梦想。
【易错题】中考九年级历史下第二单元第二次工业革命和近代科学文化试题(带答案)(2)

一、选择题1.有位著名的生物学家以充分的事实证明了物种的可能性,并以自然选择的理论解释了生物的进化,从根本上推翻了“神创论”和“物种不变论”,从而完整地确立了生物进化学说。
他是()A.牛顿B.达尔文C.爱因斯坦D.伏尔泰2.打破了千百年来“上帝创造万物”的神创论,在生物科学领域掀起了一场伟大革命的著作是A.《天工开物》B.《物种起源》C.《农政全书》D.《自然哲学的数学原理》3.一个伟人就是一座丰碑。
下列组合,不正确的是A.牛顿——近代自然科学的奠基人——《自然哲学的数学原理》B.贝多芬——近代伟大的音乐家——《英雄交响曲》C.列夫·托尔斯泰——19世纪俄国革命的镜子——《高老头》D.达尔文——近代生物学的莫基者——《物种起源》4.下图反映了某时期英国域市人口和农村人()A.新航路的开辟B.君主立宪制的确立C.工业革命的发展D.海外殖民地的扩大5.历史学家使用“城市化的浪潮”“教育的大众化”“人口数量的激增”等来描述19世纪后期()A.欧洲资本主义萌芽产生B.早期资产阶级革命爆发C.第一次工业革命的开始D.工业化国家的社会巨变6.右下表摘自吴于廑、齐世荣主编的《世界史·近代史编》,对该表格解读正确的是1861~1900年主要资本主义国家工业年平均增长率(%)年份英国美国法国德国1861~1873 3.3 5.0未统计 3.81874~1890 1.7 5.2 2.1 3.51891~1900 1.6 3.5 2.6 4.8A.主要资本主义国家经济发展不平衡B.美、德后来居上,工业总产值超过英、法C.第一次世界大战一触即发D.英、法两国基本没有参与第二次工业革命7.一位19世纪的法国伟大批判现实主文作家曾说过:“拿破仑用剑所未能完成的事业,我要用笔来完成。
”马克思、恩格斯称赞他“是超群的小说家”材料中的“他”是A.巴尔扎克B.列夫托尔斯泰C.高尔基D.伏尔泰8.分析材料,可以得出的结论是在第二次工业革命过程中A.英国依然是工业头号强国B.法国增长率在四国中始终最小C.美德工业增长速度超越英法D.德国增长速度始终超过美国9.下列国家中,其科学家和发明家为第二次工业革命作出了突出贡献的有()①英国②美国③德国④意大利⑤日本A.①②③④B.①②④⑤C.①③④⑤D.②③④⑤10.1908年,采用流水装配线大规模作业的福特T型车面世,以其低廉的价格使汽车作为一种实用工具走入了寻常百姓之家,美国亦自此成为了“车轮上的国度”。
九年级英语下学期unit-2常错题复习课件

郑州市九年级语文下册第二单元易错题集锦

郑州市九年级语文下册第二单元易错题集锦选择题1、下列加点词语的含义相同的一项是()A.①我要拿点儿颜色..出来给那些放出狗来到处乱跑的人看看。
②有些动物善于通过改变身上的颜色..来隐蔽自己。
B.①他是个荒唐..的家伙,长官!②在这里可以听到最荒唐..的新闻。
C.①“我早晚要收拾..你!”奥楚蔑洛夫向他恐吓说。
②我来收拾..残局!D.①(奥楚蔑洛夫)裹紧大衣,穿过市场的广场径自..走了。
②他什么话也没说,拿着铁锹径自..出了家门。
答案:D试题分析:A.①句中的“颜色”是指显示利害的脸色或行动。
句②中的“颜色”指的是色彩。
B.①句中的“荒唐”指行为放荡。
②句中的“荒唐”指思想、言行不符合常理人情,使人感到离奇。
C.①句中的“收拾”是折磨,惩治。
②句“收拾”是整理,整顿。
D.句子中的“径自”都是表示自己直接行动。
据此,答案为D。
2、下列各句中加点词语书写完全正确的一项是()A.每当他们夜晚独对星空时,浮华和名利都被过滤掉,他们的心灵惦记..的是最初那两扇柴门,那是故乡的眼睛。
B.她的瘦以及她的黄发丝,都让人无原无故....地产生一种怜悯。
C.趁个假日,我出了城,经自..寻春去了。
D.他之容易接受,是由于他的流畅的旋律与扬溢..的感情和才华。
答案:AB.无缘无故。
C.径自。
D.洋溢。
故选A。
3、下列词语中没有错别字的一项是( )A.哄笑羼水千钧之力无缘无故B.荤菜荒唐望眼欲穿无精打彩C.惦记门槛提心掉胆如坐针毡D.坎肩洋溢不屑置辨一想天开答案:AB项中的“彩”应为“采”;C项中的“掉”应为“吊”;D项中的“辨”应为“辩”,“一”应为“异”。
4、下列说法错误的一项是()A.《蒲柳人家》一文的作者是刘绍案,其主要作品有《京门脸子》《蛾眉》《运河的桨声》等。
B.《变色龙》的作者契诃夫是俄国作家、戏剧家。
其主要作品有小说《第六病室》《装在套子里的人》,剧本《万尼亚舅舅》《樱桃园》,等等。
C.《孔乙己》《社戏》和《藤野先生》里的“我”都是作者自己。
【易错题】湘教版九年级数学下册《第二章圆》单元检测试卷含答案解析.doc

【易错题解析】湘教版九年级数学下册 第二章圆 单元检测试卷一、单选题(共10题;共30分)1•下列说法正确的是()A.过一点A 的圆的圆心可以是平面上任意点B.过两点A 、B 的圆的圆心在一条直线上C.过三点A 、B 、C 的圆的圆心有且只有一点D.过四点A 、B 、C 、D 的圆不存在2.如图,AB 是O0的直径,AC 是O0的切线,A 为切点,连接BC,若ZABC=45°,则下列结论正确的是( )3.已知OO 的半径为4,圆心0到直线I 的距离为3,则直线I 与O0的位置关系是() A.相交 B.相切 C.相离 D.无法确定4.如图,已知AB 是OO 的直径,D, C 是劣弧EB 的三等分点,ZBOC=40°,那么ZAOE=(C. AC<AB iD. AC=- BCD. 120°D. 60°)D.2 V3)D. 10 cmA. AC>ABB. AC=ABA. 1B. V3C. 27.00的弦AB 的长为8cm,弦AB 的弦心距为3 cm,则©0的直径为A. 4 cmB. 5 cmC. 8 cm8.若圆锥的侧面展开图是一个半径为a 的半圆,则圆锥的高为()A. a B •空 a C. 3a3B. 60° C. 80°A. 20°B. 40°C. 50°6. (2016>南京)已知正六边形的边长为2,则它的内切圆的半径为(9.如图,点A,B,P 在G)0上,且ZAPB=50°,若点M 是G)0上的动点,要使ABM 为等腰三角形,则所有符 合条件的点M 有()A. 1个B. 2个C. 3个D. 4个10.如图,在半径为6cm 的O0中,点A 是劣弧BC 的中点,点D 是优弧BC 上一点,且ZD=30°,下列 四个结论:①0A1BC ; @BC=6 V3cm :③sinZAOB=乎;④卩4边形 ABOC 是菱形.其中正确结论的序号是()二、填空题(共10题;共30分)11.如图,SB 是的直径,C 是O0上的点,过点C 作的切线交AB 的延长线于点D .12. 如图,在平面直角坐标系中,OM 与x 轴相切于点A (8, 0),与y 轴分别交于点B (0, 4)和点C (0,26),则圆心M 的坐标为 ___________ . 13. 在平面直角坐标系内,以点P( - 1,0)为圆心、V5为半径作圆,则该圆与y 轴的交点坐标是 _____________ •24.圆内接正六边形的边长是8cm,则该正六边形的半径为 ___________15.如图,菱形ABCD 中,对角线AC 二2>/3,BD=2,以A 为圆心,AB 为半径画圆弧BD,则图中阴影部分 的面积为 _______________ .如图,以G(0,l)为圆心,半径为2的圆与x 轴交于A 、B 两点,与y 轴交于C 、D 两点,B.①②③④C.②③④D.①③④若ZA=32°,贝ZD =P _______ 度.点E为O G上一动点,CF丄4E于F ,则弦AB的长度为__________________ ,当点E在G) G上运动的过程17. 如图5, AB是半圆0的直径,E是BC的屮点,0E交弦BC于点D,已知BC=8cm z DE=2cm,则AD的长为_______ cm.18. 如图,在AABC中,AB二10, AC=8, BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P, Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是___________ •19. 如图所示,在AABC中,BC=4,以点A为圆心,2为半径的G)A与BC相切于点D,交AB于点E,交AC于点F,且ZEAF=80°,则图中阴影部分的面积是_____________ ・20.如图,在(DO中,AB是直径,点D是<30上一点,点C是AD的中点,CE±AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE, CB于点P, Q,连接AC,关于下列结论:①ZBAD=ZABC;①②GP=GD;③点P是AACQ的外心,其屮结论正确的是____________ (只需填写序号).三、解答题(共7题;共60分)21.如图,已知AB是O0的直径,CD丄AB ,垂足为点E,如果BE=OE , AB=12,求△ ACD的周长PB是O0的切线,A、B为切点,AC是O0的直径,若ZPAB=40°,求ZP的度数.22.如图,已知PA、C B23.如图,I是AABC的内心,ZB AC的平分线与AABC的外接圆相交于点D,交BC于点E.(1) 求证:BD=ID;(2) 求证:ID1 2=DE>DA.24.如图,已知AB为O0的直径,PA, PC是O0的切线,A, C为切点,ZBAC=30°. (I )求ZP的大小;(II)若AB=2,求PA的长(结果保留根号).25.如图所示,菱形ABCD的顶点A、B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,ZBAD=60°, 点A 的坐标为(一2, 0).1 求线段AD所在直线的函数表达式.2 动点P从点A出发,以每秒2个单位长度的速度,按照ATDTCTB的顺序在菱形的边上匀速运动, 设运动时间为t秒.求t为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?2&如图,已知直线PA 交。
九年级英语下学期unit-2常错题复习课件

彩票中奖辅助器
[单选]出现呕血时,胃内滞留血量大于()A.100mlB.500mlC.150mlD.350mlE.250ml [多选]总管线较短,投资较省,能量消耗较小,但供水独立性较差,上区受下区限制,水泵分散设置,管理维护不便的给水方式是()。A.分区并联给水方式B.并联直接给水方式C.分区串联给水方式D.分区水箱减压给水方式 [名词解释]声级计 [单选]在建筑施工现场()是导致事故发生的最主要因素。A.人的因素B.物的因素C.环境因素D.不可测知的因素 [单选,A1型题]一胎龄35周早产儿,冬天出生,现年龄为1个月2d。母乳喂养,体重已由出生时2.0kg增至3.0kg。现首先应添加的辅食及其添加目的是()A.米汤,以补充热量B.菜汤,以补充矿物质C.米糊,以补充热量D.鱼肝油,以补充维生素AE.鱼肝油,以补充维生素D [多选]SS7信令协议有哪两种?()A.ISUPB.SIGTRANC.TUPD.BICC [问答题,简答题]试述过量空气系数、空燃比和分子变更系数的定义。 [判断题]河流选取标准通常不是一个固定值,而是一个范围值;通常在高密度区采用高标准,低密度区采取低标准。A.正确B.错误 [判断题]记帐方法有单式记帐法和复式记帐法两类,银行会计核算使用复式记帐法。A.正确B.错误 [单选]柴油机装设调速器的主要目的是当外界负荷变化,通过改变()来维持或限制柴油机规定转速()。A.喷油压力B.喷油定时C.循环供油量D.喷油时间 [单选]当重心在浮心之右时,船舶会产生()。A.首倾B.尾倾C.左倾D.右倾 [问答题,简答题]多啦A梦的作者是谁? [单选]下列属于软件著作权中的财产权有()。A.修改权B.署名权C.转让权D.许可权 [单选]胶结类型中的基底胶结是指胶结物含量高,岩石颗粒之间()。A、大面积接触B、全部接触C、很少接触D、中等接触 [单选]“计算机集成制造系统”英文简写是()。A.CADB.CAMCIMSD.ERP [单选,A1型题]既能祛风解表,又能胜湿,止痛,止痉的药物是()A.荆芥B.防风C.香薷D.紫苏E.桂枝 [单选]最简单基本的心血管监测是()A.心输出量B.中心静脉压C.心率D.肺动脉压E.心电图 [单选]如果已知甲资产的风险大于乙资产的风险,则可以推出的结论是()。A.甲资产的预期收益率大于乙资产的预期收益率B.甲资产的方差大于乙资产的方差C.甲资产的标准差大于乙资产的标准差D.甲资产的标准离差率大于乙资产的标准离差率 [单选]产后72小时内血容量增加().A.1%~5%B.5%~10%C.10%~15%D.15%~25%E.25%~30% [单选]双务合同与单务合同是以()为标准进行划分的。A.合同当事人双方权利义务的分担方式B.法律上是否规定一定的名称C.是否以交付标的物为成立要件D.合同的成立是否需要特定的形式 [单选]为了达到管理优化的目的,提高管理效益,必须对管理进行充分的系统分析,这就是管理的()。A.系统原理B.人本原理C.整分合原理D.弹性原理E.排队论原理 [填空题]在认识论层次上研究信息的时候,必须同时考虑到()、()和()三个方面的因素。 [单选,A2型题,A1/A2型题]男性,30岁,复治肺结核,涂阳,下列治疗措施不必要的是()A.4~5联抗结核治疗B.加强营养支持C.抗结核同时注意保肝D.6个月以上化疗E.使用糖皮质激素减轻肺部炎症 [单选]选择显影剂使用剂量的原则是()A.为了保证显影质量,尽可能加大使用剂量B.为了减少不必要的辐射,尽可能减少用量C.每个病人需尽量使用相同剂量D.在满足显影质量的前提下,尽可能减少使用剂量E.根据受检者的身高 [单选]气割金属时,金属在切割氧流中的燃烧应是()。A.放热反应B.吸热反应C.分解反应D.还原反应 [单选]大多数花卉喜微酸性环境,无特殊要求时,营养液的pH值一般在()范围较好。A、4、5—5、5B、7、6—8、0C、6、0—6、5D、7、0—7、4 [单选]下述哪种情况下可出现睾丸鞘膜积液()A.睾丸肿瘤B.附睾炎C.原发病因不清D.睾丸外伤E.以上都是 [单选,A2型题,A1/A2型题]下列疾病需采用严密隔离的是()A.疟疾B.破素不是癔症的发病原因()。A.遗传因素B.个性特征C.精神因素D.幼年的创伤性经历E.受教育程度 [单选]在潮汐河段,由于转流的原因,船舶离泊时潮流来自于船尾,则采用()驶离。A.开尾B.开首C.绞锚D.平行 [单选]非凹陷性水肿见于A.特发性水肿B.药物性水肿C.营养不良性水肿D.肝原性水肿E.黏液性水肿 [单选,A1型题]有关血栓闭塞性脉管炎,不恰当的是()A.病变以下肢为多B.病变局限于小动脉C.为一种慢性、持续性、进行性疾病D.由于血栓形成而导致血管腔闭塞E.间歇性跛行为早期症状之一 [单选]患者男性,55岁,因外伤致截瘫,护士告知家属应注意预防压疮,尤其是骶尾部更易发生,家属在进行局部皮肤按摩的时候,有一些不正确的做法,请指出A.用手鱼际部分按摩B.用手蘸50%乙醇少许C.鱼际部分需紧贴皮肤D.由轻至重、由重至轻按摩E.压力均匀,以皮肤紫红为度 [单选]以下属于皮肤复合感觉的是()A.冷B.触C.痛D.湿E.温 [单选]对肝右叶门脉血管的描述,哪一项错误A.门脉右前、后叶支可清晰显示B.门脉右支与胆囊长轴或垂直关系C.门脉右干、右前叶支与右后叶下段支构成"Y"形结构D.门脉右前叶支与胆囊长轴构成平行关系E.门脉右干及前后叶支构成"Y"形结构 [填空题]在不同类型的原油中,()原油是石油的低凝产品和优质道路沥青的宝贵原料。 [单选]具有强筋壮骨,和胃健脾用于治疗和预防小儿佝偻病、软骨病的是()A.龙牡壮骨颗粒B.琥珀抱龙丸C.牛黄抱龙丸D.肥儿丸E.一捻金 [单选]判断营养状态的方法错误的是()A.皮肤B.皮下脂肪C.毛发D.体重指数E.消耗增加 [单选]对多发性骨髓瘤诊断具有决定性意义的检查是()A.骨髓穿刺涂片形态学检查B.外周血涂片检查C.血沉测定D.血清钙、磷和碱性磷酸酶测定E.血清免疫电泳 [名词解释]列车长
九年级英语下学期unit-2常错题复习课件

对于获取与选择报价的方法,下列哪一项不是要考虑的关键因素:A.要联系供应商的数量B.采购公司的规模C.使用的方法或流程D.评估报价的标准 水电站厂房的水轮机层一般要求高于下游最高尾水位。A.正确B.错误 栀子不具有的功效是A.泻火除烦B.清热利尿C.凉血解毒D.滋阴润燥E.消肿止痛 以下哪位学者首先论述了牙颌面畸形AngleB.LfunterC.FauchardD.CelsusE.Hippocrates 能破坏中止燃烧的物质是灭火剂.A.正确B.错误 新生儿护理中的重要环节是。A.抚触B.洗澡C.喂食D.睡眠 2014年8月,甲公司销售一批货物给乙公司,签订购销合同,合同上未注明该批货物的金额,已知同类货物的市场价是500000元。计算甲企业应缴纳的印花税元。A.150B.5C.0D.250 (S1-S2)/(S1+S2),提示()A.对比度B.图像均匀度C.信噪比D.对比噪声比E.空间分辨力 在疾病三级预防中,做好早期发现、早期诊断、早期治疗的“三早”预防工作在A.第一级预防B.第二级预防C.第三级预防D.第一级预防和第二级预防E.第二级预防和第三级预防 治疗肝经湿热型阴道炎的首选方剂是。A.肾气丸合萆薢渗湿汤B.龙胆泻肝汤C.阳和汤D.仙方活命饮E.归脾汤合二妙散 下列关于行政主体的表述中正确的有()。A.行政主体跟行政机关是等同的B.行政主体包括行使行政职权的社会组织或个人C.行政主体是指行政法律关系的主体D.行政主体是享有行政职权、实施行政活动并能独立承担行政责任的组织E.能够以自己的名义行使行政职权,是判断行政机关及其他组织能 财政的主体是,是为实现政府职能服务的。A.社会B.政府(或者说国家)C.货币D.银行 自然应激在第一阶段即可结束,强烈而持久的应激源才会发展到第三阶段。A.正确B.错误 社区的基本类型? 下面对CT扫描方法的叙述,错误的是
上海市2020〖人教版〗九年级数学下册第二章二次函数【易错题解析】

上海市2020年〖人教版〗九年级数学下册第二章二次函数【易错题解析】创作人:百里安娜创作日期:202X.04.01审核人:北堂王会创作单位:明德智语学校一、单选题(共10题;共30分)1.下列函数不属于二次函数的是()A. y=(x﹣1)(x+2)B. y= (x+1)2 C. y=2(x+3)2﹣2x2 D. y=1﹣ x22.抛物线y = -(x+1)2+3的顶点坐标()A. (1,3) B. (1,-3) C. (-1,3) D. (-1,-3)3.在抛物线y= ﹣4x﹣4上的一个点是().A. (4,4) B. (,)C. (3,﹣1) D. (﹣2,﹣8)4.函数y1=ax2+b,y2= (ab<0)的图象在下列四个示意图中,可能正确的是()A. B.C. D.5.把抛物线向右平移个单位,再向上平移个单位,得到抛物线()A.B.C.D.6.关于二次函数,下列说法正确的是()A. 图像与轴的交点坐标为 B. 图像的对称轴在轴的右侧 C. 当时,的值随值的增大而减小 D. 的最小值为-37.若函数y=a 是二次函数且图象开口向上,则a=()A. ﹣2B. 4C. 4或﹣2D. 4或38.已知二次函数,则下列说法正确的是( )A. y有最小值0,有最大值-3B. y有最小值-3,无最大值C. y有最小值-1,有最大值-3 D. y有最小值-3,有最大值09.如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是()A. ﹣4<k<B. ﹣2<k< C. ﹣4<k<﹣1 D. ﹣2<k< +110.定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为 [m,1-m,-1]的函数的一些结论:①当m=-1时,函数图象的顶点坐标是(1,0);②当m>0时,函数图象截x轴所得的线段长度大于1;③当m<0时,函数在x>时,y随x的增大而减小;④不论m取何值,函数图象经过一个定点.其中正确的结论有()A. 4个B. 3个C. 2个D. 1个二、填空题(共10题;共30分)11.二次函数的图象与y轴交于点(0,1),则b的值为________.12.二次函数y=ax2+bx+c的图象如图所示,当函数值y<0时,自变量x的取值范围是________.13.已知二次函数y=mx2+2mx+2的图象与x轴只有一个交点,则m的值是________.14.二次函数y=mx2+(m+2)x+m+2的图象与x轴只有一个交点,那么m的值为________ .15.(•咸宁)如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(﹣1,p),B (4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是________.16.将抛物线,绕着它的顶点旋转,旋转后的抛物线表达式是________.17.如图,抛物线y=ax2﹣2与y轴交于点A,过点A与x轴平行的直线交抛物线y=﹣ x2于点B,C,则S△BOC=________.18.(•内江)二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b﹣2c|,Q=|2a﹣b|﹣|3b+2c|,则P,Q的大小关系是________.19.如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y= x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是________.20.(•鄂州)已知正方形ABCD中A(1,1)、B(1,2)、C(2,2)、D (2,1),有一抛物线y=(x+1)2向下平移m个单位(m>0)与正方形ABCD的边(包括四个顶点)有交点,则m的取值范围是________.三、解答题(共8题;共60分)21.抛物线y=-x2+bx+c过点(0,-3)和(2,1),试确定抛物线的解析式,并求出抛物线与x轴的交点坐标.22.如图,抛物线y=ax2+bx+c经过A(1,0),B(4,0),C(0,3)三点,求抛物线的解析式.23.某商人如果将进货价为8元的商品按每件10元出售,每天可销售100件,现采用提高售出价,减少进货量的办法增加利润,已知这种商品每涨价1元其销售量就要减少10件,问他将售出价定为多少元时,才能使每天所赚的利润最大?并求出最大利润.24.已知:二次函数y=(n﹣1)x2+2mx+1图象的顶点在x轴上.(1)请写出m与n的关系式,并判断已知中函数图象的开口方向;(2)是否存在整数m,n的值,使函数图象的对称轴与x轴的交点横坐标为整数?若存在,请求出m,n的值;若不存在,请说明理由;(3)若y关于x的函数关系式为y=nx2﹣m2x﹣2n﹣2①当n≠0时,求该函数必过的定点坐标;②探索这个函数图象与坐标轴有两个交点时n的值.25.如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).求(1)抛物线的解析式;(2)两盏景观灯P1、P2之间的水平距离.26.根据下列要求,解答相关问题.请补全以下求不等式﹣2x2﹣4x>0的解集的过程.①构造函数,画出图象:根据不等式特征构造二次函数y=﹣2x2﹣4x;并在下面的坐标系中(图1)画出二次函数y=﹣2x2﹣4x的图象(只画出图象即可).②求得界点,标示所需,当y=0时,求得方程﹣2x2﹣4x=0的解为多少?;并用锯齿线标示出函数y=﹣2x2﹣4x图象中y>0的部分.③借助图象,写出解集:由所标示图象,可得不等式﹣2x2﹣4x>0的解集为﹣2<x<0.请你利用上面求一元一次不等式解集的过程,求不等式x2﹣2x+1≥4的解集.27.如图,抛物线与轴交于、两点(点在点的左侧),点的坐标为,与轴交于点,作直线.动点在轴上运动,过点作轴,交抛物线于点,交直线于点,设点的横坐标为.(Ⅰ)求抛物线的解析式和直线的解析式;(Ⅱ)当点在线段上运动时,求线段的最大值;(Ⅲ)当以、、、为顶点的四边形是平行四边形时,直接写出的值.28.某公司销售一种新型节能电子小产品,现准备从国内和国外两种销售方案中选择一种进行销售:①若只在国内销售,销售价格y(元/件)与月销量x (件)的函数关系式为y=-x+150,成本为20元/件,月利润为W内(元);②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳x2元的附加费,月利润为W外(元).(1)若只在国内销售,当x=1000(件)时,y每件多少元?;(2)分别求出W内、W外与x间的函数关系式(不必写x的取值范围);(3)若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值.答案解析部分一、单选题1.【答案】C2.【答案】C3.【答案】B4.【答案】C5.【答案】D6.【答案】D7.【答案】B8.【答案】B9.【答案】C10.【答案】B二、填空题11.【答案】012.【答案】-1<x<313.【答案】214.【答案】115.【答案】x<﹣1或x>416.【答案】17.【答案】418.【答案】P>Q19.【答案】﹣2<k<20.【答案】2≤m≤8三、解答题21.【答案】解:∵抛物线y=-x2+bx+c过点(0,-3)和(2,1),∴,解得,抛物线的解析式为y=-x2+4x-3,令y=0,得-x2+4x-3=0,即x2-4x+3=0,∴x1=1,x2=3,∴抛物线与x轴的交点坐标为(1,0)、(3,0)22.【答案】解:设抛物线解析式为y=a(x﹣1)(x﹣4),把C(0,3)代入得a•(﹣1)(﹣4)=3,解得a= ,所以抛物线解析式为y= (x﹣1)(x﹣4),即y= x2﹣x+3.23.【答案】解:由题意得,y=(x-8)[100-10(x-10)]=-10(x-14)2+360(10≤a<20),∵a=-10<0∴当x=14时,y有最大值360答:他将售出价(x)定为14元时,才能使每天所赚的利润(y)最大,最大利润是360元.24.【答案】解:(1)∵二次函数y=(n﹣1)x2+2mx+1图象的顶点在x轴上,∴4m2﹣4(n﹣1)=0,∴n﹣1=m2,∴n=m2+1,∵n﹣1≠0,且m2≥0∴n ﹣1>0,∴图象开口向上;(2)∵y=(n﹣1)x2+2mx+1,∴对称轴x=,要使为整数,∵m,n为整数,∴只要m=±1,此时n=2,∴存在m=±1,n=2,符合要求;(3)①y=nx2﹣(n﹣1)x﹣2n﹣2=n(x2﹣x﹣2)+x﹣2,令x2﹣x﹣2=0,得x=﹣1或2,所以必过的定点为(2,0),(﹣1,﹣3),②若n=0,则y=x﹣2,直线与坐标轴有两个交点,若n≠0:b2﹣4ac=(n﹣1)2+4n(2n+2)=(3n+1)2≥0,当抛物线过原点时,n=﹣1,此时图象与坐标轴有两个交点,当抛物线不过原点时,n=时,b2﹣4ac=0,图象与x轴,y轴各有1个交点,综上,当n=0或﹣1或时,函数图象与坐标轴有两个交点.25.【答案】解:(1)抛物线的顶点坐标为(5,5),与y轴交点坐标是(0,1)设抛物线的解析式是y=a(x-5)2+5把(0,1)代入y=a(x-5)2+5得a=-∴y=-(x-5)2+5=(0≤x≤10)(2)由已知得两景观灯的纵坐标都是4∴4=-(x-5)2+5∴(x-5)2=1,解得x1=,x2=∴两景观灯间的距离为5米.26.【答案】解:①图所示:;②方程﹣2x2﹣4x=0即﹣2x(x+2)=0,解得:x1=0,x2=﹣2;则方程的解是x1=0,x2=﹣2,图象如图1;③函数y=x2﹣2x+1的图象是:当y=4时,x2﹣2x+1=4,解得:x1=3,x2=﹣1.则不等式的解集是:x≥3或x≤﹣1 27.【答案】解:(I)∵抛物线过A、C两点,∴代入抛物线解析式可得,解得,∴抛物线解析式为y=﹣x2+2x+3,令y=0可得,﹣x2+2x+3=0,解x1=﹣1,x2=3,∵B点在A点右侧,∴B点坐标为(3,0),设直线BC解析式为y=kx+s,把B、C坐标代入可得,解得,∴直线BC解析式为y=﹣x+3;(Ⅱ)∵PM⊥x轴,点P的横坐标为m,∴M(m,﹣m2+2m+3),N(m,- m+3),∵P在线段OB上运动,∴M点在N点上方,∴MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣)2+ ,∴当m= 时,MN有最大值,MN的最大值为;(Ⅲ)∵PM⊥x轴,∴MN∥OC,当以C、O、创作人:百里安娜创作日期:202X.04.01M、N为顶点的四边形是平行四边形时,则有OC=MN,当点P在线段OB上时,则有MN=﹣m2+3m,∴﹣m2+3m=3,此方程无实数根,当点P不在线段OB 上时,则有MN=﹣m+3﹣(﹣m2+2m+3)=m2﹣3m,∴m2﹣3m=3,解得m= 或m= ,综上可知当以C、O、M、N为顶点的四边形是平行四边形时,m的值为或28.【答案】解:(1)x=1000,y=-×1000+150=140;(2)W内=(y-20)x=(-x+150-20)x=-x2+130x.W外=(150-a)x-x2=-x2+(150-a)x;(3)W内=-x2+130x=-(x-6500)2+422500,由W外=-x2+(150-a)x 得:W外最大值为:(750-5a)2,所以:(750-5a)2=422500.解得a=280或a=20.经检验,a=280不合题意,舍去,∴a=20.创作人:百里安娜创作日期:202X.04.01。
【易错题】中考九年级历史下第二单元第二次工业革命和近代科学文化试题含答案

一、选择题1.他在《人间喜剧》里给我们留下了一部法国社会,特别是巴黎上流社会的变迁史。
“他”是A.但丁B.莎士比亚C.巴尔扎克D.列夫·托尔斯泰2.一个伟人就是一座丰碑。
下列组合,不正确的是A.牛顿——近代自然科学的奠基人——《自然哲学的数学原理》B.贝多芬——近代伟大的音乐家——《英雄交响曲》C.列夫·托尔斯泰——19世纪俄国革命的镜子——《高老头》D.达尔文——近代生物学的莫基者——《物种起源》3.它被后人誉为“社会百科全书”,它真实地反映了法国大革命后,资本主义社会的贪婪、掠夺和一切建立在金钱基础上社会关系。
这部作品可用来研究社会转型期发展情况,这部作品是()A.《战争与和平》B.《人间喜剧》C.《英雄交响曲》D.《罗密欧与朱丽叶》4.《寂静的舂天》的章节标题有“不必要的大破坏”“死亡的河流”“自天而降的灾难”等,书中警示的是A.人口问题B.环境问题C.毒品问题D.战争问题5.观察下图,导致19世纪末20世纪初石油开采量发生变化的原因是①蒸汽机的产生②汽车的发明③飞机的研制④核能的利用A.①②B.③④C.①④D.②③6.下列图片属于第二次工业革命成果的是A.B.C.D.7.《新编剑桥世界近代史》中指出,他用数学的理论来表述法拉第的想法,完美阐释了电磁场理论。
这位伟大的科学家是()A.牛顿B.麦克斯韦C.达尔文D.爱因斯坦8.1908年,采用流水装配线大规模作业的福特T型车面世,以其低廉的价格使汽车作为一种实用工具走入了寻常百姓之家,美国亦自此成为了“车轮上的国度”。
福特T型车普及的主要原因是A.生产技术的进步B.蒸汽机的发明C.电力时代的到来D.内燃机的应用9.甘地在《印度自治》中说:“正是由于机器使印度赤贫遍野。
曼彻斯特给我们造成的伤害难以估量。
由于曼彻斯特,印度的手工业差不多消亡了。
”材料反映出( )A.甘地具有反工业化倾向B.印度手工业即将消亡C.甘地倡导“回到纺车去”D.甘地致力于解决民生问题10.1840—1920年英国农业人口占全国总人口的百分比变化表年份1840187019001920百分比2214.88.47.1导致表格中农业人口百分比变化的主要原因是()A.圈地运动蓬勃进行B.殖民帝国开始建立C.工业化进程的影响D.资产阶级革命成功11.某历史学家认为“19 世纪 80 年代,世界交通领域里的一场革命源于一种新动力的发明”。
(易错题)初中数学九年级数学下册第二单元《相似》测试题(含答案解析)
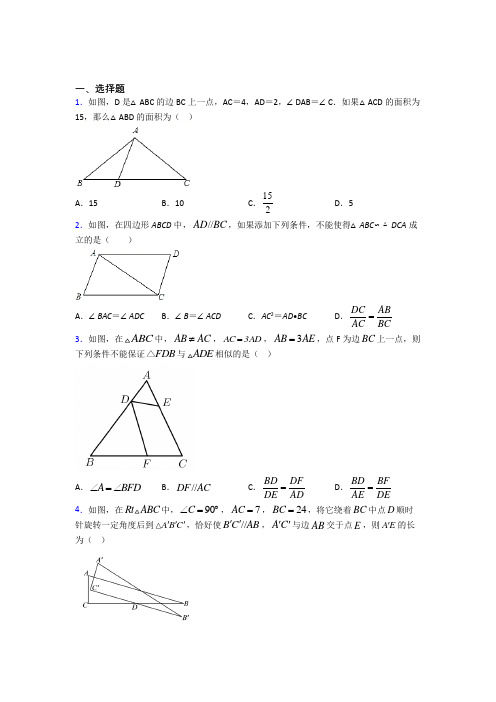
一、选择题1.如图,D 是△ABC 的边BC 上一点,AC =4,AD =2,∠DAB =∠C .如果△ACD 的面积为15,那么△ABD 的面积为( )A .15B .10C .152D .52.如图,在四边形ABCD 中,//AD BC ,如果添加下列条件,不能使得△ABC ∽△DCA 成立的是( )A .∠BAC =∠ADCB .∠B =∠ACDC .AC 2=AD •BC D .DC AB AC BC= 3.如图,在ABC 中,AB AC ≠,AC 3AD =,3AB AE =,点F 为边BC 上一点,则下列条件不能保证FDB △与ADE 相似的是( )A .A BFD ∠=∠B .//DF AC C .BD DF DE AD = D .BD BF AE DE = 4.如图,在Rt ABC 中,90C ∠=︒,7AC =,24BC =,将它绕着BC 中点D 顺时针旋转一定角度后到A B C ''',恰好使//B C AB '',A C ''与边AB 交于点E ,则A E '的长为( )A .72B .4924C .8425D .91255.如图,点D 在ABC 的边AC 上,添加下列哪个条件后,仍无法判定ABC ADB ∽△△( )A .C ABD ∠=∠B .CBA ADB ∠=∠C .AB AD AC AB = D .AB BC AC BD = 6.若点C 为线段AB 的黄金分割点,且AC BC >,则下列各式中不正确的是( ). A .::AB AC AC BC =B .352BC AB -= C .512AC AB +=D .0.618AC AB ≈ 7.如图,AB 为⊙O 的直径,AC 交⊙O 于E 点,BC 交⊙O 于D 点,CD =BD ,∠C =70°,现给出以下四个结论:①∠A =45°;②AC =AB ;③AE =BE ;④2CE •AB =BC 2,其中正.确.结论有( )A .1个B .2个C .3个D .4个8.大自然巧夺天工,一片小心树叶也蕴含着“黄金分割”.如图,P 为AB 的黄金分割点(AP >PB ),如果AP 的长度为8cm ,那么AB 的长度是( )A .5B .12-5C .12+45D .45 9.已知如图,DE 是△ABC 的中位线,AF 是BC 边上的中线,DE 、AF 交于点O .现有以下结论: ①DE ∥BC ;②OD =14BC ;③AO =FO ;④AOD S =14ABC S .其中正确结论的个数为( )A .1B .2C .3D .410.如图在ABC 中,其中D 、E 两点分别在AB 、AC 上,且31AD =,29DB =,30AE =,32EC =.若50A ∠=︒,则图中1∠、2∠、3∠、4∠的大小关系正确的是( ).A .13∠=∠B .24∠∠=C .23∠∠=D .14∠<∠ 11.下列判断中,不正确的有( )A .三边对应成比例的两个三角形相似B .两边对应成比例,且有一个角相等的两个三角形相似C .有一个锐角相等的两个直角三角形相似D .有一个角是100°的两个等腰三角形相似12.如图,△ABC 中,DE ∥BC ,25AD AB =,DE =3,则BC 的长为( )A .7.5B .4.5C .8D .6二、填空题13.如图,△ABC 中,∠C =90°,BC =8cm ,AC =6cm ,点P 沿BC 边以2cm/s 的速度从点B 向点C 移动,同时点Q 沿CA 边以1cm/s 的速度从点C 向点A 移动.若以点C 、P 、Q 构成的三角形与△ABC 相似,则运动时间为____________秒.14.已知5a=6b (a≠0),那么-a a b 的值为_______. 15.如图,已知点M 是△ABC 的重心,AB =123,MN ∥AB ,则MN =__________16.若 14b a b =-,则a b的值为__________. 17.如图,在ABC 纸片中,13AB AC ==,24BC =,D 是BC 边上任意一点,将ABD △沿AD 折叠得到AED ,AE 交BC 于点F ,当DEF 是直角三角形时,则BD 的长为________.18.如图,在正方形ABCD 中,15AB =,点,E F 分别为AB ,DC 上的点,将正方形沿EF 折叠,使点A 落在A '处,点D 落在D 处,FD '交BC 于点G ,A D ''交BC 于点H ,若10DF =,203CG =,则BH 的长为___________.19.如图,在矩形ABCD 中,AB =2,BC =a ,点E 在边BC 上,且BE =35a .连接AE ,将△ABE 沿AE 折叠,若点B 的对应点B′落在矩形ABCD 的边上,则a 的值为______.20.如图,正方形ABCD 中,BE =EF =FC ,CG =2GD ,BG 分别交AE ,AF 于M ,N .下列结论:①AF ⊥BG ;②BN 43=NF ;③38BM MG =;④S 四边形CGNF 12=S 四边形ANGD .其中正确的结论的序号是___________.三、解答题21.已知:E 是矩形ABCD 的边AB 上一个动点,直线EF DE ⊥交BC 于点F .(1)求证:ADE ∽BFE △;(2)若直线EF 经过C 点,且3AD =,10AB =,是否存在这样的点E ,使ADE 和BFE △相似?若存在,请求出AE 的长度;若不存在,请说明理由.(3)连结DF ,若3AD =,2AE =,当ADE 和EFD △相似时,则AB =______. 22.如图,建筑物BC 上有一个旗杆AB ,小明和数学兴趣小组的同学计划用学过的知识测量该建筑物的高度,他们制订了测量方案,并利用课余时间完成了实地测量,测量方法如下:在该建筑物底部所在的平地上有一棵小树ED ,小明沿CD 后退,发现地面上的点F 、树顶E 、旗杆顶端A 恰好在一条直线上,继续后退,发现地面上的点G 、树顶E 、建筑物顶端B 恰好在一条直线上,已知旗杆3AB =米,4DE =米,5DF =米,1.5FG =米,点、、A B C 在一条直线上,点C D F G 、、、在一条直线上,AC ED 、均垂直于CG ,根据以上信息,请求出这座建筑物的高BC .23.如图,AB 是O 的直径,C ,D 是O 上两点,且AD 平分CAB ∠,作DE AB⊥于E .(1)求证://AC OD;(2)求证:12OE AC=.24.已知平行四边形ABCD中6AB=,AE与BC延长线相交于E、与CD相交于F,2EF AF=,求FD的长度.25.图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,点A、B、C、D均在格点上.在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,不要求写画法,要求保留必要的作图痕迹.(1)在图①中以线段AD为边画一个三角形,使它与ABC相似.(2)在图②中画一个三角形,使它与ABC相似(不全等).(3)在图③中的线段AB上画一个点P,使23 APPB=.26.黄金分割为“最美丽”的几何比率,广泛应用于图案设计,下图是一个包装盒的俯视图,线段AB是这个俯视图的中轴线.某公司想在中轴线AB上找到黄金分割点,安装视频播放器.(1)请你用尺规作图的方式找出这个点(作出一点即可,保留作图痕迹);(2)请证明你找到的点是黄金分割点.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】首先证明△ABD∽△CBA,由相似三角形的性质可得:△ABD的面积:△ACB的面积为1:4,因为△ACD的面积为15,进而求出△ABD的面积.【详解】∵∠DAB=∠C,∠B=∠B,∴△ABD∽△CBA,∵AC=4,AD=2,∴△ABD的面积:△ACB的面积=(AD)2=1:4,AC∴△ABD的面积:△ACD的面积=1:3,∵△ACD的面积为15,∴△ABD的面积=5.故选:D.【点睛】本题考查了相似三角形的判定和性质:相似三角形的面积比等于相似比的平方,是中考常见题型.2.D解析:D【分析】利用相似三角形的判定定理,在AD∥BC,得∠DAC=∠BCA的前提下,需添加一角或夹这角的两边对应成比例进行排查即可.【详解】解:A.∵AD∥BC,∴∠DAC=∠BCA,当∠BAC=∠ADC时,则△ABC∽△DCA;B.∵AD∥BC,∴∠DAC=∠BCA,当∠B=∠ACD时,则△ABC∽△DCA;C .∵AD ∥BC ,∴∠DAC =∠BCA ,由AC 2=AD •BC 变形为AC AD BC AC =,则△ABC ∽△DCA ; D .∵AD ∥BC ,∴∠DAC =∠BCA ,当DC AB AC BC=时,不能判断△ABC ∽△DCA . 故选择:D .【第讲】 本题考查三角形相似问题,掌握相似三角形的判定定理,会根据判定定理进行添加条件使三角形相似解题关键.3.C解析:C【分析】先根据已知条件可证得ADE ACB ∽,由此可得AED B ∠=∠,再利用相似三角形的判定对选项逐个判断即可.【详解】解:∵AC 3AD =,3AB AE =, ∴AD AE 1AC AB 3==, 又∵A A ∠=∠, ∴ADE ACB ∽,∴AED B ∠=∠, A 选项:∵A BFD ∠=∠,B B ∠=∠,∴BFD BAC ∽,故选项A 正确;B 选项:∵//DF AC ,∴C BFD ∠=∠,∠=∠A BDF ,∴BFD BCA △∽△,故选项B 正确; C 选项:BD DF DE AD=无法证明FDB △与ADE 相似; D 选项:∵BD BF AE DE=, AED B ∠=∠, ∴BFD EDA △∽△,故选项D 正确;故选:C .【点睛】 本题考查了相似三角形的判定及性质,熟练掌握相似三角形的判定是解决本题的关键. 4.D解析:D【分析】过点D 作DF ⊥AB 于F ,易证四边形EFDC´是矩形,可得C´E=DF ,由勾股定理求得AB 的长,根据已知和相似三角形的判定可证明△ACB ∽△DFB ,可得AC AB DF BD=,J 进而求得DF 值,由A´E=A´C´﹣C´即可求解.【详解】解:过点D 作DF ⊥AB 于F ,则∠DFB=90°,∵△ABC 绕着BC 中点D 顺时针旋转一定角度后到A B C ''',恰好使//B C AB '',∴∠C=∠C´=∠A´EB=90°,AC=A´C´=7,CD=BD=12,∴四边形EFDC´为矩形,∴C´E=DF ,∵在Rt △ACB 中,∠C=90°,AC=7,BC=24, ∴222272425AC BC +=+=,∵∠C=∠DFE ,∠B=∠B ,∴△ACB ∽△DFB ,∴AC AB DF BD =即72512DF =, ∴DF=8425=C´E , ∴A´E=A´C´﹣C´E=7﹣8425=9125, 故选:D .【点睛】本题考查了旋转的性质、矩形的判定与性质、相似三角形的判定与性质、勾股定理等知识,熟练掌握这些知识的灵活运用,添加恰当的辅助线是解答的关键.5.D解析:D【分析】根据三角形相似的判定方法一一判断即可.【详解】解:A 、根据两角对应相等两三角形相似,可以判定△ABC ∽△ADB ;B 、根据两角对应相等两三角形相似,可以判定△ABC ∽△ADB ;C 、根据两边成比例夹角相等两三角形相似即可判定△ABC ∽△ADB ;D 、无法判断三角形相似.故选:D .【点睛】本题考查相似三角形的判定,解题的关键是熟练掌握基本知识,属于中考常考题型. 6.C解析:C【分析】根据黄金分割点的定义逐项排除即可.【详解】解:∵点C 为线段AB 的黄金分割点,且AC BC >,∴2AC BC AB =⋅,∴::AB AC AC BC =,则选项A 正确;∵点C 为线段AB 的黄金分割点,且AC BC >,∴510.618AC AB AB -=≈,则选项C 错误;选项D 正确; 5135BC AB AC AB AB AB --=-=-=,则选项B 正确. 故选:C .【点睛】 本题考查了成比例线段,熟练掌握黄金分割的定义成为解答本题关键.7.B解析:B【分析】连结AD 、BE ,DE ,如图,根据圆周角定理得∠ADB=90°,则AD ⊥BC ,加上CD=BD ,根据等腰三角形的判定即可得到AC =AB ;再根据等腰三角形的性质和三角形内角和定理可计算出∠BAC=40°;由AB 为直径得到∠AEB=90°,则∠ABE=50°,根据圆周角定理可判断AE BE ≠;接着证明△CED ∽△CBA ,利用相似比得到CD CE AC BC=,然后利用等线段代换即可判断④.【详解】解:连接AD ,∵AB 是⊙O 的直径,∴∠ADB=90°.∵CD=BD ,∴AD 是BC 的垂直平分线,∴AC=AB ,故②正确;∵AC=AB ,∴∠ABC=∠C=70°,∴∠BAC=40°,故①错误;连接BE ,DE ,∵AB 为⊙O 的直径,∴∠AEB=90°,∵∠BAC=40°,∴∠ABE=50°,∴∠BAC≠∠ABE ,∴AE≠BE ,∴AE BE ≠,故③错误;∵四边形ABDE 是圆内接四边形,∴∠CDE=∠CAB ,∴△CDE ∽△CAB , ∴CD CE AC BC=, ∴CE•AC=CD·BC , ∴CE•AB=12BC·BC , ∴2CE •AB =BC 2,故④正确.故选B .【点睛】本题考查了相似三角形的判定和性质,圆周角定理,根据题意作出辅助线,构造出圆周角是解题的关键.8.D解析:D【分析】根据黄金分割的定义得到AB ,然后把AP=8代入后可求出AB 的长. 【详解】∵P 为AB 的黄金分割点(AP >PB ),∴AB ,∴)8414==(cm ), 故选:D .【点睛】本题考查了黄金分割以及分母有理化.把线段AB 分成两条线段AC 和BC (AC >BC ),且使AC 是AB 和BC 的比例中项(即AB :AC=AC :BC ),叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点.其中AB .并且线段AB 的黄金分割点有两个. 9.C解析:C【分析】①根据三角形中位线定理进行判断;②根据三角形中位线定理进行判断;③根据三角形中位线定理进行判断;④由相似三角形△ADO ∽△ABF 的面积之比等于相似比的平方进行判断.【详解】∵DE 是△ABC 的中位线,∴DE ∥BC ,故①正确;∴DE=12BC , ∴OD=12BF , ∵AF 是BC 边上的中线,∴BF=12BC , ∴OD=12BF=14BC ,故②正确; ∵DE 是△ABC 的中位线,∴AD=DB ,DE ∥BC ,∴AO =FO ,故③正确;④∵DE ∥BC ,即DO ∥BF ,∴△ADO ∽△ABF , ∴22ADO ABF 1124S AD S AB ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭, 又∵AF 是BC 边上的中线,∴ABF ABC 12SS =, ∴ADO ABC18S S =,故④错误. 综上所述,正确的结论是①②③,共3个.故选:C .【点睛】本题考查了三角形中位线定理、相似三角形的判定与性质.本题利用了“相似三角形的面积之比等于相似比的平方”的性质.正确的识别图形是解题的关键.10.C解析:C【分析】根据31AD =,30AE =,可得21∠<∠;根据题意,通过计算AB 和CD ,可得12AD AEAC AB,即证明ADE ACB ∽,即可得到各个角度的大小关系. 【详解】∵31AD =,30AE =∴21∠<∠ ∵31AD =,29DB =,30AE =,32EC =∴60AB AD BD =+=,62AC AE EC =+= ∴12AD AE AC AB ∵50A ∠=︒∴ADE ACB ∽∴14∠=∠,23∠∠= ∴13∠>∠,24∠<∠故选:C .【点睛】本题考查了相似三角形的知识;解题的关键是熟练掌握相似三角形的性质,从而完成求解.11.B解析:B【分析】由相似三角形的判定依次判断可求解.【详解】解:A 、三边对应成比例的两个三角形相似,故A 选项不合题意;B 、两边对应成比例,且夹角相等的两个三角形相似,故B 选项符合题意;C 、有一个锐角相等的两个直角三角形相似,故C 选项不合题意;D 、有一个角是100°的两个等腰三角形,则它们的底角都是40°,所以有一个角是100°的两个等腰三角形相似,故D 选项不合题意;故选:B .【点睛】本题考查了相似三角形的判定,熟练运用相似三角形的判定是本题的关键.12.A解析:A【分析】先判断△ADE ∽△ABC ,然后利用相似比求BC 的长.【详解】解:∵DE ∥BC ,∴△ADE ∽△ABC , ∴25DE AD BC AB ==, ∴5515.3222BC DE ==⨯=. 故选:A .【点睛】 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形,灵活运用相似三角形的性质表示线段之间的关系;也考查了等腰三角形的性质.二、填空题13.或【分析】首先设点P 移动t 秒时△CPQ 与△ABC 相似然后分别从当即时△CPQ ∽△CBA 与当即时△CPQ ∽△CAB 去分析求解即可求得答案【详解】设点P 移动t 秒时△CPQ 与△ABC 相似∵点P 从点B 以2c 解析:125或3211【分析】 首先设点P 移动t 秒时△CPQ 与△ABC 相似,然后分别从当CP CQ CB CA =,即8286t t -=时,△CPQ ∽△CBA ,与当CQ CP CB CA =,即8286t t -=时,△CPQ ∽△CAB ,去分析求解即可求得答案.【详解】设点P 移动t 秒时△CPQ 与△ABC 相似,∵点P 从点B 以2cm/s 的速度向点C 移动,点Q 以1cm/s 的速度从点C 向点A 移动, ∴BP =2tcm ,CQ =tcm ,则CP =CB−BP =8−2t (cm ),∵∠C 是公共角,∴当CP CQ CB CA=,即8286t t -=时,△CPQ ∽△CBA , 解得:t =125; 当CQ CP CB CA=,即8286t t -=时,△CPQ ∽△CAB , 解得:t =3211,∴点P移动125s或3211s时△CPQ与△ABC相似.故答案为:125或3211【点睛】此题考查了相似三角形的判定.此题难度适中,注意掌握数形结合思想、分类讨论思想以及方程思想的应用.14.6【分析】由等式可用a表示出b代入求值即可【详解】解:∵5a=6b(a≠0)∴b=a∴故答案为:6【点睛】本题主要考查比例的性质由已知等式用a 表示出b是解题的关键解析:6【分析】由等式可用a表示出b,代入求值即可.【详解】解:∵5a=6b(a≠0),∴b=56a,∴1651--66aa b a aa===,故答案为:6.【点睛】本题主要考查比例的性质,由已知等式用a表示出b是解题的关键.15.【分析】根据三角形重心的性质可得AD=BD=CM:CD=2:3由MN∥AB可得△CMN∽△CDB再根据相似三角形的性质求解即可【详解】解:∵点M是△ABC的重心∴AD=BD=CM:CD=2:3∵MN解析:【分析】根据三角形重心的性质可得AD=BD=12AB=CM:CD=2:3,由MN∥AB可得△CMN∽△CDB,再根据相似三角形的性质求解即可.【详解】解:∵点M是△ABC的重心,∴AD=BD=12AB=CM:CD=2:3,∵MN∥AB,∴△CMN∽△CDB,∴23MN CM DB CD ==,23=,解得MN =.故答案为:【点睛】本题考查了三角形的重心和相似三角形的性质,熟练掌握上述知识是解题的关键. 16.5【分析】根据比例的性质可用b 表示a 代入可得答案【详解】解:由得4b=a-b 得a=5b ∴=5故答案是:5【点睛】本题考查了比例的性质利用比例的性质得出b 表示a 是解题关键解析:5【分析】根据比例的性质,可用b 表示a ,代入可得答案.【详解】 解:由14b a b =-,得4b=a-b . 得a=5b , ∴5a b b b==5, 故答案是:5.【点睛】 本题考查了比例的性质,利用比例的性质得出b 表示a 是解题关键.17.或7【分析】是直角三角形时有两种情况:∠EDF=90°或∠EFD=90°通过找相似三角形然后利用对应边成比例即可得到结果【详解】解:如图当∠EDF=90°时过A 作AG ⊥BC 于G 则DE ∥AG ∵AG ⊥B 解析:263或7. 【分析】 DEF 是直角三角形时,有两种情况:∠EDF=90°或∠EFD=90°,通过找相似三角形,然后利用对应边成比例即可得到结果.【详解】解:如图,当∠EDF=90°时,过A 作AG ⊥BC 于G ,则DE ∥AG ,∵13AB AC ==,24BC =,AG ⊥BC , ∴1122BG BC ==, 在直角三角形ABG 中,2213125AG =-=,由折叠可知∠B=∠E ,BD=ED ,AE=AB=13,∵DE ∥AG ,∴∠FAG=∠E=∠B ,∴Rt △AFG ∽Rt △BAG ,∴AB BG AF AG =,即13125AF =, ∴6512AF = ∴6591131212EF =-=, 由∠B=∠E ,∠EDF=∠ABG=90°,可知△ABG ∽△FED ,∴AB BG EF DE =,即13129112DE =, ∴7DE =,即7BD =;如图,当∠EFD=90°时,由折叠可知∠B=∠E ,BD=ED ,AE=AB=13,由于∠EFD=90°,因此AF ⊥BC ,在直角三角形ABF 中,2213125AF =-=,∴1358EF =-=,∵∠B=∠E ,∠AFB=∠EFD=90°,∴△ABF ∽△DEF , ∴AB BF DE EF =,即13128DE =, ∴263DE =,即263BD =; 综上,263BD =或7BD =, 故答案为:263或7. 【点睛】 本题考查了相似三角形的性质和判定以及折叠问题,找到相似三角形是解题的关键,要注意分类讨论.18.【分析】根据正方形的性质得到AB=AD=DC=BC=15∠A=∠D=∠C=∠B=90°根据折叠的性质得到∠D=∠D´=90°DF=DF´=10根据勾股定理可得FC 的长从而得到D´G 根据相似三角形的判 解析:254【分析】根据正方形的性质得到AB=AD=DC=BC=15,∠A=∠D=∠C=∠B=90°,根据折叠的性质得到∠D=∠D´=90°,DF=DF´=10,根据勾股定理可得FC 的长,从而得到D´G ,根据相似三角形的判定得到△HGD´∽△FGC ,从而得到HG GD FG GC '=,可得HG 的长,由BH=BC-HG-CG 即可得出结论.【详解】解:∵四边形ABCD 为正方形,∴AB=AD=DC=BC=15,∠A=∠D=∠C=∠B=90°,由折叠的性质,得∠D=∠D´=90°,DF=DF´=10,在Rt △FCG 中,FC=DC-DF=15-10=5,CG=203,∴253==, ∴D´G=D´F-FG=10-253=53, ∵∠D´=∠C=90°,∠HGD´=∠FGC ,∴△HGD´∽△FGC ,∴HG GD FG GC '=, ∴HG=255·253320123FG GD GC =='⨯, ∴BH=BC-HG-CG=15-2512-203=254. 故答案为254. 【点睛】本题考查了相似三角形的判定与性质,勾股定理,折叠的性质及正方形的性质.证得△HGD´和△FGC 相似是解题的关键.19.或【分析】分两种情况:①点落在AD 边上根据矩形与折叠的性质易得即可求出a 的值;②点落在CD 边上证明根据相似三角形对应边成比例即可求出a 的值【详解】解:分两种情况:①当点落在AD 边上时如图1四边形AB 解析:103或253. 【分析】分两种情况:①点'B 落在AD 边上,根据矩形与折叠的性质易得=AB BE ,即可求出a 的值;②点'B 落在CD 边上,证明''ADB B CE ∆∆,根据相似三角形对应边成比例即可求出a 的值.【详解】解:分两种情况:①当点B '落在AD 边上时,如图1.四边形ABCD 是矩形,90BAD B ∴∠=∠=︒,将ABE ∆沿AE 折叠,点B 的对应点B '落在AD 边上,'1452BAE B AE BAD ∴∠=∠=∠=︒, AB BE ∴=,325a ∴=, 103a ∴=;②当点'B 落在CD 边上时,如图2.∵四边形ABCD 是矩形,90BAD B C D ∴∠=∠=∠=∠=︒,AD BC a ==.将ABE ∆沿AE 折叠,点B 的对应点'B 落在CD 边上,'90B AB E ∴∠=∠=︒,'2AB AB ==,'35BE B E a ==, 2224DB B A AD a ''∴-=-3255EC BC BE a a a =-=-=. 在ADB '∆与B CE '∆中,9090B AD EB C AB D D C ∠=∠=︒-∠''⎧⎨∠=∠=︒'⎩, ''ADB B CE ∴∆∆, '''DB AB CE B E ∴=242355a a a -=, 解得153a =,253a =-(舍去). 综上,所求a 的值为10325. 故答案为10325 【点睛】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质,勾股定理,相似三角形的判定与性质.进行分类讨论与数形结合是解题的关键.20.①③【分析】①易证△ABF ≌△BCG 即可解题;②易证△BNF ∽△BCG 即可求得的值即可解题;③作EH ⊥AF 令AB=3即可求得MNBM 的值即可解题;④连接AGFG 根据③中结论即可求得S 四边形CGNF 和解析:①③【分析】①易证△ABF ≌△BCG ,即可解题;②易证△BNF ∽△BCG ,即可求得BN NF 的值,即可解题; ③作EH ⊥AF ,令AB=3,即可求得MN ,BM 的值,即可解题;④连接AG ,FG ,根据③中结论即可求得S 四边形CGNF 和S 四边形ANGD ,即可解题.【详解】解:①∵四边形ABCD 为正方形,∴AB=BC=CD ,∵BE=EF=FC ,CG=2GD ,∴BF=CG ,∵在△ABF 和△BCG 中,90AB BC ABF BCG BF CG ︒=⎧⎪∠=∠=⎨⎪=⎩,∴△ABF ≌△BCG ,∴∠BAF=∠CBG ,∵∠BAF+∠BFA=90°,∴∠CBG+∠BFA=90°,即AF ⊥BG ;①正确;②∵在△BNF 和△BCG 中,90CBG NBF BCG BNF ︒∠=∠⎧⎨∠=∠=⎩, ∴△BNF ∽△BCG ,32BN BC NF CG ∴==, BN 32NF =,②错误; ③作EH ⊥AF ,令AB=3,则BF=2,BE=EF=CF=1,2213AF AB BF =+=1122ABF AF BN AB BF S ∆=⋅=⋅,6132413,3N 1B 133NF BN === 3AN 91AF NF =∴=-, ∵E 是BF 中点,∴EH 是△BFN 的中位线,313213,NH EH ==∴,BN ∥EH , 1113AH AN MN AH EH∴==,,解得:MN=2713, ∴BM=BN-MN=313,MG=BG-BM=813, 38BM MG ∴=,③正确; ④连接AG ,FG ,根据③中结论,则713 11142712213S 13CFG GNF CGNF S S CG CF NF NG ∆∆=+=⋅+⋅=+=四边形, 11633512226213ANG ADG ANGD S S S AN GN AD DG ∆∆=+=⋅+⋅=+=四边形, S 12CGNF S ≠四边形,④错误; 故答案为 ①③.【点睛】本题考查了正方形的性质,全等三角形的判定和性质,考查了相似三角形的判定和对应边成比例的性质,本题中令AB=3求得AN ,BN ,NG ,NF 的值是解题的关键.三、解答题21.(1)证明见解析;(2)存在,1AE =或9;(3)4或132【分析】(1)根据两角对应相等的两个三角形相似判断即可;(2)设AE x =,则10BE x =-,利用相似三角形的性质,构建方程求解即可; (3)连接DF .分两种情形:当ADE EDF ∽△时,当ADE △∽EFD △时,分别构建方程求解即可.【详解】(1)∵四边形ABCD 是矩形∴90A B ∠=∠=︒,∵EF DE ⊥∴90DEF ∠=︒,∴AED BFE ∠=∠∴ADE ∽BFE △;(2)设AE x =,则10BE x =-, 由题意得:3BF BC AD ===∵ADE ∽BFE △ ∴AD AE BE BF =, ∴3103x x =- 解得:1x =或9 经检验,1x =或9是分式方程的根,∴1AE =或9;(3)连接DF .当ADE ∽EDF 时 则AD AE DE EF = ∴32DF AD EF AE == ∵ADE ∽BEF∴32AD DE EB EF == ∵3AD =∴2BE =∴224AB AE BE =+=+=当ADE ∽EFD △时则AD AE EF DE = ∴23DE AE EF AD == ∵ADE ∽BEF ∴23AD DE EB EF == ∵3AD = ∴92BE = ∴913222AB AE EB =+=+= 综上所述,满足条件的AB 的值为4或132 故答案为:4或132. 【点睛】 本题考查了相似三角形、矩形、分式方程的知识;解题的关键是熟练掌握相似三角形、矩形、分式方程的性质,从而完成求解.22.这座建筑物的高BC 为 14米【分析】根据两组相似三角形ACF EDF ∆∆∽和BCG EDG ∆∆∽,利用对应边成比例,列出CD 和BC 的关系式,然后解方程求出BC 的长.【详解】解:由题意可得90ACF EDF AFC EFD ︒∠∠∠∠==,=,ACF EDF ∴∆∆∽,AC CF ED DF∴=, 即3545BC CD ++=, 554BC CD -∴=, 由题意可得,90BCG EDG BGC EGD ︒∠∠∠∠==,=,BCG EDG ∴∆∆∽,BC CG ED DG∴=, 即5 1.545 1.5BC CD ++=+, 6.54( 6.5)BC CD ∴+=,556.54264BC BC -∴=⨯+, 14BC ∴=,∴这座建筑物的高BC 为 14米.【点睛】本题考查相似三角形的应用,解题的关键是利用相似三角形对应边成比例的性质列式求边长.23.(1)证明见解析;(2)证明见解析.【分析】(1)先根据圆的性质、等腰三角形的性质可得OAD ODA ∠=∠,再根据角平分线的性质可得OAD CAD ∠=∠,从而可得ODA CAD ∠=∠,然后根据平行线的判定即可得证; (2)如图(见解析),先根据圆周角定理可得90ACB ∠=︒,再根据垂直的定义可得90OED ∠=︒,然后根据平行线的性质可得DOE BAC ∠=∠,最后根据相似三角形的判定与性质即可得证.【详解】(1)12OA OD AB ==, OAD ODA ∠=∠∴, AD 平分CAB ∠,OAD CAD ∴∠=∠,ODA CAD ∴∠=∠,//AC OD ∴;(2)如图,连接BC ,由圆周角定理得:90ACB ∠=︒,DE AB ∵⊥,90OED ∴∠=︒,由(1)已证://AC OD ,DOE BAC ∴∠=∠,在DOE △和BAC 中,90OED ACB DOE BAC ∠=∠=︒⎧⎨∠=∠⎩, DOE BAC ∴~,12OE OD AC AB ∴==, 12OE AC ∴=.【点睛】本题考查了圆周角定理、等腰三角形的性质、平行线的判定与性质、相似三角形的判定与性质等知识点,较难的是题(2),通过作辅助线,构造相似三角形是解题关键. 24.2FD =【分析】先根据平行四边形的性质得出AD ∥BE ,AB=CD=6,再根据平行线的性质得出∠DAE=∠AEB ,∠D=∠ECF ,根据相似三角形的判定定理可知△AFD ∽△EFC ,进而得到FD 的长.【详解】证明:∵四边形ABCD 是平行四边形,∴//AD BE ,6AB CD ==,∴DAE AEB ∠=∠,DCE D ∠=∠,∴ADF ECF , ∴12AF DF FE FC ==, ∴2FD =.【点睛】本题考查的是平行四边形的性质及相似三角形的判定与性质,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;或依据基本图形对图形进行分解、组合.25.(1)见解析;(2)见解析;(3)见解析【分析】(1)连接DE ,则DE//BC ,由相似三角形的判定方法可知△ADE ∽△ABC ;(2)如图②,根据勾股定理和相似三角形的判定方法可知△DEF ∽△ABC ;(3)连接DE ,BE ,DE 交AB 于点P ,则DE//BC ,根据平行线分线段成比例定理可知23AP AD PB DC ==. 【详解】解:(1)如图①;(2)如图②;(3)如图③.【点睛】本题考查了相似三角形的判定,平行四边形的判定与性质,以及勾股定理等知识,熟练掌握相似三角形的判定方法是解答本题的管家.①两角分别相等的两个三角形相似;②两边成比例,且夹角相等的两个三角形相似;③三边成比例的两个三角形相似. 26.(1)图见解析;(2)见解析【分析】(1)过点B 作AB 的垂线,并用圆规在垂线上截取BC ,使BC=12AB ,连接AC ,以C 为圆心,BC 为半径画弧,交AC 于点D ,以A 为圆心,AD 为半径画弧,交AB 于E ,则点E 即为线段AB 的黄金分割点;(2)设BC=a ,则AB=2a ,AC=225AB BC a +=,通过计算证明2AE BE AB =⋅即可解决问题.【详解】(1)如图:点E 即为所求;(2)设BC=a ,则AB=2a ,∴225AB BC a +=,∵CD=BC=a ,∴5a -a ,∵2222(5625)AE a a a a =-=-,222(25)625AB BE a a a a a a ⋅=⋅+=-, ∴2AE BE AB =⋅,∴点E 是线段AB 的黄金分割点.【点睛】此题考查黄金分割,黄金分割的作图,勾股定理,正确掌握黄金分割的知识并熟练应用解决问题是解题的关键.。
九年级英语下学期unit-2常错题复习课件

[单选]6[综合知识试题1]某图的邻接矩阵如下所示,则该图为()。A.B.C.D.ABCD [单选,A2型题,A1/A2型题]不索取和非法收受患者财物;不收受医疗器械、药品、试剂等生产、经营企业或人员以各种名义、形式给予的回扣、提成;不违规参与医疗广告宣传和药品医疗器械促销”体现了哪项基本行为规范()A.廉洁自律,恪守医德B.遵纪守法,依法执业C.严谨求实,精益求精 [判断题]使命是一个组织存在的理由或价值。组织的每一个成员都非常清楚这一点,所以没有必要形成文件。()A.正确B.错误 [单选]慢性胃炎脾胃湿热证的治法是()A.温中散寒,和胃止痛B.健脾益气,温中和胃C.养阴益胃,和中止痛D.清利湿热,醒脾化浊E.化瘀通络,和胃止痛 [单选]下列关于仓库流量的计算公式正确的是()。A.仓库流量=入库货量/出库货量B.仓库流量=出库货量/入库货量+出库货量C.仓库流量=(入库货量+出库货量)/存货量D.仓库流量=(入库货量+出库货量)/(入库货量+出库货量+存货量) [问答题,简答题]维修用电设备时,应采取哪些安全措施? [多选]关于航空运输市场的含义下列说法正确的是()A.航空运输市场是一种特定的市场B.是航空运输产品和服务交易的场所C.是指航空运输产品供求关系的总和D.是在一定时空条件下对航空运输产品和服务需求的总和E.供求关系的无法测量的市场 [单选]()是指在工程建设项目或政府采购项目中,具备独立工作流程、能够单独实施的工作单元。A.最小工作单元B.最小合同单元C.招标合同单元D.最小分解单元 [单选,A2型题,A1/A2型题]旋转阳极启动的定子线圈安装在()A.控制台内B.球管内阳极端C.球管内阴极端D.高压发生器内E.管套中央部 [单选,A1型题]27岁初产妇,胎儿娩出后无阴道流血,胎盘娩出后阴道流血不断,时多时少,1小时内阴道流血量超过600ml,血压70/50mmHg,脉搏126次/分。紧急措施应是()A.为宫颈裂伤,立即缝合B.为阴道血肿,立即处理C.检查凝血功能,并输纤维蛋白原D.静注麦角新碱加强宫缩E.手入宫 [判断题]受教育权是一种内容广泛的民事权利,既包括财产权,又包括人格权。A.正确B.错误 [单选,A2型题,A1/A2型题]右心衰竭引起皮肤发绀的机制是()。A.肺循环血液中还原血红蛋白增多B.体循环静脉血中还原血红蛋白增多C.肺循环血液中还原血红蛋白减少D.体循环静脉血中还原血红蛋白减少E.血液中高铁血红蛋白减少 [问答题,简答题]往复式压缩机实际压缩循环分哪几个过程? [填空题]液氨充装系数:在10℃充装液氨时,只可装容器体积的()。在0℃充装时,允许装料为容器的()。当在-10℃充装时则更少,装料不可超过容器体积的()。只有这样,才能保证在设计温度()下,容器内仍有10%的气相空间。 [单选]如果迎角和其他因素保持不变,空速变为原来的2倍,则升为将().A.不变B.是原来的2倍C.是原来的4倍 [单选]卵泡刺激素的主要作用是().A.促进卵泡生长发育和成熟B.促进黄体形成C.促进黄体分泌雌激素和孕激素D.促进排卵E.促进卵泡分泌孕激素和雌激素 [单选]1978~1991年中国房地产发展的主要特点是针对传统住房制度的核心(),提出了以大幅度提高租金为基本环节的改革思路。A、国家统包B、无偿分配C、高租金D、低租金 [单选]泵的轴承箱的的温度要求不大于()。A.65℃B.70℃C.80℃ [单选]锚的抓力大小决定于:()。A.锚型、锚重、锚杆的仰角、抛锚方法B.底质、水底地形、出链长度、水深C.船舶的排水量和风、流、浪等外力的大小D.A和B正确 [单选]茶叶加工道德根源于()A.先天的人性B.阶级斗争C.经济关系D.生存需要工 [填空题]晶片尺寸较小的探头发射的超声波束,其远场覆盖面积()。 [填空题]涂料通常储存期限在()年以内,温度升高通常会()储存期限。 [问答题,案例分析题]B企业拟在A市郊区原A市卷烟厂厂址处(现该厂已经关闭)新建屠宰量为120万头猪/年的项目(仅屠宰,无肉类加工),该厂址紧临长江干流,A市现有正在营运的日处理规模为3万t的城市污水处理厂,距离B企业1.5km。污水处理厂尾水最终排入长江干流(长江干流在A市段 [填空题]沙波由()、()、()组成 [单选]在25℃时,0.01mol∙kg糖水的渗透压为π1,0.01mol∙kg食盐水的渗透压为Π2,则两者的渗透压()。A.无法比较B.Π1>Π2C.Π1=Π2D.Π1<Π2 [单选]下列不属于基金销售机构职责规范的是()。A.严格账户管理B.基金托管人应制定业务规则并监督实施C.签订销售协议,明确权利和义务D.禁止提前发行 [多选]有关先天性髋关节脱位治疗后的并发症,下列哪些是恰当的A.再脱位常由于前倾角过小所致B.股骨上端骨折也常由于手术所致C.坐骨神经损伤常由于手术所致D.股骨头缺血性坏死与复位前牵引不够或内收肌、髂腰肌未松解,复位后股骨头承受过大压力有关E.髋关节骨性关节病亦与软 [单选]如果饭店资源丰富、实力雄厚,可选择()市场策略。A.差异B.无差异C.密集性D.集中性 [判断题]安消防要求,门禁系统必须断电开锁,门也一定要选外开式。A.正确B.错误 [单选]银屑病的有关叙述,正确的是()A.可致脱发B.不易复发C.临床上无瘙痒症状发生D.有同形反应E.病理改变无角化不全 [单选]加氢气密性试验时应控制压力()。A、稍低于操作压力B、等于控制压力C、稍高于操作压力D、等于工厂公用工程部所提供的高压氮气压力 [填空题]执行机构绝缘电阻应合格,通电试合时动作平衡,开度指示()。 [单选]一3岁男孩,消瘦明显,右上腹饱满,触及巨大肿块,B.超探及右上腹巨大分叶状肿块,边界清晰,内回声不均,肝右叶向上推移,右肾下移至盆腔,可能是A.右腹膜后神经纤维瘤B.肾母细胞瘤C.神经母细胞瘤D.肾上腺皮质腺癌E.肝母细胞瘤 [单选,A2型题,A1/A2型题]患者右侧肢体无力一年余,查体右上肢下运动神经元瘫,肌力4级,右下肢上运动神经元瘫,肌力3级,其病变部位为()。A.左上胸髓部B.右上胸髓部C.双侧颈膨大部D.左侧颈膨大部E.右侧颈膨大部 [单选]接受长期胰岛素治疗的病人最常见的问题是()A.抗体诱发的胰岛素耐药性B.脂肪萎缩C.胰岛素注射部位产生局部变态反应D.胰岛素注射部位感染E.低血糖 [单选]3DES在DES的基础上使用两个56位的密钥K1和K2,发送方用K1加密,K2解密,再用K1加密。接收方用K1解密,K2加密,再用K1解密,这相当于使用()倍于DES的密钥长度的加密效果。A.1B.2C.3D.6 [单选]关于交通性睾丸鞘膜积液,下列正确的是()A.平卧后鞘膜积液可逐渐缩小B.站立后透光试验仍阴性C.单纯抽液治疗可获得良好疗效D.精索鞘膜积液同时伴有睾丸鞘膜积液称之为交通性鞘膜积液E.单纯鞘膜翻转术也可获得满意的治疗效果 [单选,A1型题]哪种疾病用青霉素治疗可引起赫氏反应()。A.流行性脑脊髓膜炎B.草绿色链球菌心内膜炎C.大叶性肺炎D.气性坏疽E.梅毒 [多选]关于工程无法按规定期限竣工验收情况下的缺陷责任期的起计日期,下列说法正确的有()。A.承包人原因所致的,从实际通过竣工验收之日起计B.承包人原因所致的,在承包人提交竣工验收报告30天后,工程自动进入缺陷责任期C.发包人原因所致的,从实际通过竣工验收之日起计D.发包 [单选]注册消防工程师职业道德原则的特点中,对社会本质最直接、最集中反应的特点是()。A.稳定性B.独特性C.本质性D.基准性
九年级英语下学期unit-2常错题复习课件

(易错题)初中数学九年级数学下册第二单元《相似》测试(有答案解析)

一、选择题1.如图,已知点D ,E 是AB 的三等分点,DF ,EG 将ABC 分成三部分,且////DF EG BC ,图中三部分的面积分别为1S ,2S ,3S ,则123::S S S 的值为( )A .1:2:3B .1:2:4C .1:3:5D .2:3:4 2.如图,在△ABC 中,点D 在BC 边上,连接AD ,点E 在AC 边上,过点E 作//EF BC ,交AD 于点F ,过点E 作//EG AB ,交BC 于G ,则下列式子一定正确的是( )A .AE EF EC CD =B .BF EG CD AB= C .AF BC FD GC = D .CG AF BC AD = 3.如图,在ABC 中,中线BE ,CD 相交于点O ,连接DE ,下列结论:①12DE BC =;②12S S =△DOE △COB ;③AD OE AB OB=;④16ODE ADC S S =△△.其中结论正确的是( ).A .①②B .①③C .①②③D .①③④ 4.如图,在Rt ABC 中,90C ∠=︒,7AC =,24BC =,将它绕着BC 中点D 顺时针旋转一定角度后到A B C ''',恰好使//B C AB '',A C ''与边AB 交于点E ,则A E '的长为( )A .72B .4924C .8425D .91255.如图,在ABC ∆中,,D E 分别是边,BC AC 上的点,且11,BD BC AE AC n m ==,连接,AD BE 交于点F ,则AF AD的值为( )A .1m n -B .1m m n +-C .1n m n +-D .1n m - 6.如果两个相似三角形的对应高之比是1:2,那么它们的周长比是( )A .1:2B .1:4C .1:2D .2:17.如图,ABC 是等边三角形,被一平行于BC 的矩形所截(即:FG ∥BC),若AB 被截成三等分,则图中阴影部分的面积是ABC 的面积的( )A .19B .29C .13D .498.如图在ABC 中,其中D 、E 两点分别在AB 、AC 上,且31AD =,29DB =,30AE =,32EC =.若50A ∠=︒,则图中1∠、2∠、3∠、4∠的大小关系正确的是( ).A .13∠=∠B .24∠∠=C .23∠∠=D .14∠<∠ 9.如图,在矩形OABC 中,点A 和点C 分别在y 轴和x 轴上.AC 与BO 交于点D ,过点C 作CE BD ⊥于点E ,2DE BE =.若5CE =,反比例函数(0,0)k y k x x=>>经过点D ,则k =( )A .2B .352C .36D .30 10.下列判断中,不正确的有( )A .三边对应成比例的两个三角形相似B .两边对应成比例,且有一个角相等的两个三角形相似C .有一个锐角相等的两个直角三角形相似D .有一个角是100°的两个等腰三角形相似11.已知两个三角形相似,其中一个三角形的两个内角分别为72,63︒︒,则另一个三角形的最小内角为( )A .72︒B .63︒C .45︒D .不能确定 12.如图,要使ABC ACD ∆∆,需补充的条件不能是( )A .ADC ACB ∠=∠B .ABC ACD ∠=∠ C .AD AC AC AB= D .AD BC AC DC ⋅=⋅ 二、填空题13.如图,点О是正方形ABCD 的中心,DE 与О相切于点E ,连接,BE 若10,DE =102BE =,则О的面积是________________.14.如图,////AB GH CD ,点H 在BC 上,AC 与BD 交于点G ,2AB =,3CD =,则GH 的长为 .15.如图,直线////AF BE CD ,直线AC 交BE 于B ,直线FD 交BE 于E ,2AB cm =,1BC cm =, 1.8EF cm =,求DE 的长为______cm .16.已知线段=AB 6,点c 是线段AB 的黄金分割点,AC BC >.那么AC BC -=________.17.如图,D 是ABC 的边BC 上一点,4AB =,2AD =,DAC B ∠=∠.如果ABD △的面积为6,那么ACD △的面积为_______.18.如图,AB 是⊙O 的直径,AB =20cm ,弦BC =12cm ,F 是弦BC 的中点.若动点E 以2cm/s 的速度从A 点出发沿着AB 方向运动,设运动时间为t (s )(0≤t≤10),连接EF ,当△BEF 是直角三角形时,t (s )的值为_______.19.如图,菱形ABCD 的对角线AC ,BD 相交于点O ,过点A 作AH ⊥BC 于点H ,AH 交OB 于点E ,若OB =4,S 菱形ABCD =24,则OE 的长为_____.20.如图,90A B ∠=∠=︒,AB a ,AD BC <,在边AB 上取点P ,使得PAD △,PBC 与PDC △两两相似,则AP 长为___________.(结果用含a 的代数式表示)三、解答题21.如图,AB 是ABC 的内接圆O 的直径,点D 在半圆上,DC 与AB 交于点E ,12∠=∠,过点C 作CF DC ⊥交DB 的延长线于点F ,交圆O 于点G .(1)当105DF =,:1:2AE EC =时,求圆O 的半径.(2)在(2)的条件下,连接DG 交BC 于点M ,则:OMB DGF S S =△△______.(直接写出答案)22.作图题:如图所示,图中的小方格都是边长为1的正方形,△ABC 与△A 'B 'C '是以点O 为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点O ;(2)△A 'B 'C '与△ABC 的位似比是 ;(3)以位似中心O 为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A 'B 'C '关于点O 中心对称的△A "B "C ",并直接写出△A "B "C "各顶点的坐标. 23.已知:△ABC 在坐标平面内,三个顶点的坐标为A (0,3)、B (3,4)、C (2,2).(正方形网格中,每个小正方形边长为1个单位长度)(1)画出△ABC 向下平移4个单位得到的△A 1B 1C 1;(2)以B 为位似中心,在网格中画出△A 2BC 2,使△A 2BC 2与△ABC 位似,且位似比2:1,直接写出C 2点坐标是 ;(3)△A 2BC 2的面积是 平方单位.24.如图,已知平行四边形ABCD ,过点A 的直线交BC 的延长线于E ,交BD 、CD 于F 、G .(1)若3AB =,4BC =,2CE =,求CG 的长;(2)证明:2AF FG FE =⋅.25.如图,△ABC 中,E 、F 分别是边AB 、AC 的中点,EF =a ,动点P 在射线EF 上,BP 交CE 于D ,∠CBP 的平分线交CE 于Q ,(1)当CQ =12CE 时,求EP+BP 的值.(2)当CQ =13CE 时,求EP+BP 的值. (3)当CQ =1n CE 时,直接写出EP+BP 的值.26.如图,已知AB 为O 直径,C 为O 外一点,(连结,AC BC 交O 于点F ,取弧BF 的中点D ,连接AD 交BC 于点E ,过点E 作EH AB ⊥于H ,且满足BH BC BE AB ⋅=⋅.(1)求证:AC 是O 的切线;(2)若8,10CF BF ==,求AC 和EH 的长【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据题意易得ADF AEGABC ,则有13AD AB =,23AE AB =.进而可求得119ABC S S =,213ABC S S =,359ABC S S =,最后即可求出结果.【详解】∵DF ∥EG ∥BC ,∴ADF AEG ABC ,∵D 、E 是AB 的三等分点, ∴13AD AB =,23AE AB =, ∴119ABC S S =,49AEG ABC S S =.∵21411993AEG ABC ABC ABC S S S S S S =-=-=,34599ABC AEG ABC ABC ABC S S S S S S =-=-=. ∴123115::::1:3:5939ABC ABC ABC S S S S S S ==.故选C .【点睛】 本题主要考查相似三角形的判定与性质,掌握面积比等于相似比的平方是解题的关键. 2.C解析:C【分析】根据平行线分线段成比例性质进行解答便可.【详解】解:∵EF ∥BC ,∴AF AE FD EC =, ∵EG ∥AB ,∴AE BG EC GC =, ∴AF BC FD GC=, 故选:C .【点睛】本题考查了平行线分线段成比例性质,关键是熟记定理,找准对应线段.3.D解析:D【分析】先判断DE 为ABC 的中位线,则根据三角形中位线性质得到//DE BC ,12DE BC =,于是可对①进行判断;证明DOE △∽COB △,利用相似比得到12OE DE OD OB BC OC ===,14DOE COBS S =△△,则可对②进行判断;加上12AD AB =,则可对③进行判断;利用三角形面积公式得到13ODE DCE S S =△△,12DCE ADC S S =△△,则可对④进行判断.【详解】解:∵BE 、CD 为ABC 的中线,∴DE 为ABC 的中位线,∴//DE BC ,12DE BC =,所以①正确; ∵//DE BC ,∴DOE △∽COB △, ∴12OE DE OD OB BC OC ===,214DOE COB S DE S CB ⎛⎫== ⎪⎝⎭△△,所以②错误; ∵12AD AB =, ∴AD OE AB OB=,所以③正确; ∵:1:2OD OC =, ∴13ODE DCE S S =△△, ∵AE CE =, ∴12DCE ADC S S =△△, ∴16ODE ADC S S =△△,所以④正确. 故选D .【点睛】本题考查相似三角形的性质和判定,解题的关键是熟练运用相似三角形的性质和判定定理. 4.D解析:D【分析】过点D 作DF ⊥AB 于F ,易证四边形EFDC´是矩形,可得C´E=DF ,由勾股定理求得AB 的长,根据已知和相似三角形的判定可证明△ACB ∽△DFB ,可得AC AB DF BD=,J 进而求得DF 值,由A´E=A´C´﹣C´即可求解.【详解】解:过点D 作DF ⊥AB 于F ,则∠DFB=90°,∵△ABC 绕着BC 中点D 顺时针旋转一定角度后到A B C ''',恰好使//B C AB '',∴∠C=∠C´=∠A´EB=90°,AC=A´C´=7,CD=BD=12,∴四边形EFDC´为矩形,∴C´E=DF ,∵在Rt △ACB 中,∠C=90°,AC=7,BC=24,∴222272425AC BC +=+=,∵∠C=∠DFE ,∠B=∠B ,∴△ACB ∽△DFB , ∴AC AB DF BD =即72512DF =, ∴DF=8425=C´E , ∴A´E=A´C´﹣C´E=7﹣8425=9125, 故选:D .【点睛】本题考查了旋转的性质、矩形的判定与性质、相似三角形的判定与性质、勾股定理等知识,熟练掌握这些知识的灵活运用,添加恰当的辅助线是解答的关键.5.C解析:C【分析】过D 作DG ∥AC 交BE 于G ,易证△BDG ∽△BCE ,△DGF ∽△AEF,利用三角形相似的性质即可解答.【详解】解:过D 作DG ∥AC 交BE 于G ,则△BDG ∽△BCE , ∴DG BD CE BC=, ∵1BD BC n =, ∴1DG BD CE BC n ==,∵1AE AC m =, ∴1m CE AC m-=, ∴DG=11m CE AC n mn-⋅= ∵DG ∥AC ,∴△DGF ∽△AEF ,∴111m AC DF DG m mn AF AE n AC m--===, ∴1AD m n AF n +-=,即1AF n AD m n =+-, 故选:C .【点睛】本题考查了相似三角形的判定与性质、比例性质,熟练掌握相似三角形的判定与性质,添加辅助线构造相似三角形是解答的关键.6.A解析:A【分析】根据相似三角形对应高的比等于相似比,周长的比等于相似比解答.【详解】解:∵对应高之比是1:2,∴相似比=1:2,∴对应周长之比是1:2.故选:A .【点睛】本题主要考查相似三角形的性质,周长的比等于相似比.7.C解析:C【分析】AB 被截成三等分,可得AB=3AE ,AF=2AE ,由EH ∥FG ∥BC ,可得△AEH ∽△AFG ∽△ABC ,则S △AEH :S △AFG :S △ABC =AE 2:AF 2:AB 2,S 阴影= S △AFG - S △AEH =13S △ABC . 【详解】∵AB 被截成三等分,∴AB=3AE ,AF=2AE ,∵EH ∥FG ∥BC ,∴△AEH ∽△AFG ∽△ABC ,∴S △AEH :S △AFG :S △ABC =AE 2:AF 2:AB 2=AE 2:(2AE )2:(3AE )2=1:4:9,∴S △AEH =19S △ABC , S △AFG =4 S △AEH , S 阴影= S △AFG - S △AEH =3 S △AEH =3×19 S △ABC =13S △ABC . 故选择:C .【点睛】 本题考查阴影部分面积问题,关键是利用相似三角形的面积比等于相似比的平方,找到阴影面积与△AEH 的关系,由△AEH 与△ABC 的关系来转化解决问题.8.C解析:C【分析】根据31AD =,30AE =,可得21∠<∠;根据题意,通过计算AB 和CD ,可得12AD AE AC AB ,即证明ADE ACB ∽,即可得到各个角度的大小关系. 【详解】∵31AD =,30AE =∴21∠<∠∵31AD =,29DB =,30AE =,32EC =∴60AB AD BD =+=,62AC AE EC =+= ∴12AD AE AC AB ∵50A ∠=︒∴ADE ACB ∽∴14∠=∠,23∠∠= ∴13∠>∠,24∠<∠故选:C .【点睛】本题考查了相似三角形的知识;解题的关键是熟练掌握相似三角形的性质,从而完成求解. 9.B解析:B【分析】作DF ⊥OC 于F ,根据矩形的性质和相似三角形的性质求得OD=3,OE=5,根据勾股定理求得30OC =,然后通过三角形相似求得DF 和OF ,从而求得D 的坐标,代入解析式即可求得k 的值.【详解】解:作DF ⊥OC 于F ,在矩形OABC 中,∠OCB=90°,OD=BD ,90,OCE BCE ∴∠+∠=︒∵CE ⊥OB ,90,CEO BEC ∴∠=∠=︒90,OCE COE ∴∠+∠=︒,COE BCE ∴∠=∠,COE BCE ∴∽,CE OE BE CE∴= ∴2,CE BE OE =∵2DE BE =,5,CE = 设,BE x =则DE=2x ,3,OD BD x ==∴OE=5x ,∴255,x x =解得,x=1(负根舍去),∴OD=3,OE=5,∴()22225530,OC OE CE =+=+= ∵∠OFD=∠OEC=90°,∠DOF=∠EOC ,∴△DOF ∽△COE , ∴,DF OF OD CE OE OC== 5530OF ==∴22OF DF ==∴D 的坐标为22⎛⎝⎭, ∵反比例函数k y x =(k >0,x >0)经过点D ,∴k == 故选:B .【点睛】本题考查了矩形的性质,勾股定理,三角形相似的判定和性质,反比例函数图象上点的坐标特征,求得D 的坐标是解题的关键.10.B解析:B【分析】由相似三角形的判定依次判断可求解.【详解】解:A 、三边对应成比例的两个三角形相似,故A 选项不合题意;B 、两边对应成比例,且夹角相等的两个三角形相似,故B 选项符合题意;C 、有一个锐角相等的两个直角三角形相似,故C 选项不合题意;D 、有一个角是100°的两个等腰三角形,则它们的底角都是40°,所以有一个角是100°的两个等腰三角形相似,故D 选项不合题意;故选:B .【点睛】本题考查了相似三角形的判定,熟练运用相似三角形的判定是本题的关键.11.C解析:C【分析】根据相似三角形的性质、三角形的内角和定理可得出另一个三角形的三个内角度数,由此即可得.【详解】由相似三角形的性质得:另一个三角形的两个内角分别为72,63︒︒,则另一个三角形的第三个内角为180726345︒-︒-︒=︒,因此,另一个三角形的最小内角为45︒,故选:C .【点睛】本题考查了相似三角形的性质、三角形的内角和定理,熟练掌握相似三角形的性质是解题关键.12.D解析:D【分析】要使两三角形相似,已知有一组公共角,则可以再添加一组角相等或添加该角的两边对应成比例.【详解】∵∠DAC=∠CAB∴当∠ACD=∠ABC 或∠ADC=∠ACB 或AD :AC=AC :AB 时,△ABC ∽△ACD .故选:D【点睛】本题考查相似三角形的判定方法的开放性的题,相似三角形的判定方法:①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.二、填空题13.25【分析】连接EO 可知EO ⊥ED 延长DE 到点F 作BF ⊥DF 根据题意可知△DEO ∽△DFB 在△EFB 中根据勾股定理求解得出半径的长然后再根据圆的面积公式求解即可;【详解】如图:连接EO 可知EO ⊥ED解析:25π【分析】连接EO ,可知EO ⊥ED ,延长DE 到点F ,作BF ⊥DF ,根据题意可知△DEO ∽△DFB ,在△EFB 中,222EB EF FB =+,根据勾股定理求解得出半径的长,然后再根据圆的面积公式求解即可;【详解】如图:连接EO ,可知EO ⊥ED ,延长DE 到点F ,作BF ⊥DF ,∵∠FDB=∠EDO ,∠DEO=∠DFB ,∴△DEO ∽△DFB ,∵EO=r ,ED=10,EB=∵DO=OB , ∴12DO EO DE DB FB DF===, ∴EF=10,FB=2r , 在△EFB 中,222EB EF FB =+,(22=1004r +,∴ r=5,∴ 圆的面积为225r ππ=,故答案为:25π【点睛】本题考查了圆的面积公式、相似三角形的判定、勾股定理等知识,熟练掌握这些公式是解题的关键;14.【分析】根据平行线分线段成比例定理由AB ∥GH 得出由GH ∥CD 得出将两个式子相加即可求出GH 的长【详解】解:即①即②①②得解得故答案为:【点睛】本题考查了平行线分线段成比例定理熟练运用等式的性质进行 解析:65【分析】根据平行线分线段成比例定理,由AB ∥GH ,得出GH CH AB BC=,由GH ∥CD ,得出3GH BH BC=,将两个式子相加,即可求出GH 的长. 【详解】解://AB GH ,GH CH AB BC∴=, 即2GH CH BC=①, //GH CD ,GH BH CD BC∴=, 即3GH BH BC=②, ①+②, 得23GH GH CH BH BC BC+=+, CH BH BC +=,123GH GH ∴+=, 解得65GH =. 故答案为:65【点睛】本题考查了平行线分线段成比例定理,熟练运用等式的性质进行计算.本题难度适中. 15.09【分析】直接根据平行线分线段成比例定理求解即可【详解】解:∵∴即:∴DE=09cm 故答案为:09【点睛】此题主要考查了平行线分线段成比例定理熟练运用定理是解答此题的关键解析:0.9【分析】直接根据平行线分线段成比例定理求解即可.【详解】解:∵////AF BE CD , ∴AB EF BC DE= 即:2 1.8=1DE∴DE=0.9cm故答案为:0.9【点睛】 此题主要考查了平行线分线段成比例定理,熟练运用定理是解答此题的关键16.【分析】根据黄金比值为进行计算即可得到答案【详解】解:∵点C 为线段AB 的黄金分割点AB=6∴AC=×6=3-3BC=6-(3-3)=9-3AC-BC=3-3-(9-3)=6-12;故答案为:【点睛】解析:12【分析】进行计算即可得到答案. 【详解】解:∵点C 为线段AB 的黄金分割点,AB=6,∴,BC=6-(),(;故答案为:12【点睛】本题考查的是黄金分割的知识和二次根式的计算,理解黄金分割的概念,找出黄金分割中成比例的对应线段是解决问题的关键.17.【分析】先证明△ACD ∽△BCA 再根据相似三角形的性质得到:△ACD 的面积:△ABC 的面积为1:4再结合△ABD 的面积为6然后求出△ACD 的面积即可【详解】解:∵∠C=∠C ∴△ACD ∽△BCA ∴∴即解析:2【分析】先证明△ACD ∽△BCA ,再根据相似三角形的性质得到:△ACD 的面积:△ABC 的面积为1:4,再结合△ABD 的面积为6,然后求出△ACD 的面积即可.【详解】解:∵DAC B ∠=∠,∠C=∠C∴△ACD ∽△BCA ∴12AD AB = ∴21124ACD ABC S S⎛⎫== ⎪⎝⎭ ,即164ACD ACD ABD ACD ACD S S S S S ∆∆∆∆∆==++,解得:ACD S ∆=2. 故答案为2.【点睛】本题主要考查了相似三角形的判定和性质、掌握相似三角形的面积比等于相似比的平方解答本题的关键.18.5或82【分析】求出BF 和AO 的长分为两种情况①∠EFB =90°②∠FEB=90°分别利用三角形中位线的性质以及相似三角形的判定和性质求出AE 的长再求出t 即可【详解】∵AB 是⊙O 的直径∴∠C=90° 解析:5或8.2【分析】求出BF 和AO 的长,分为两种情况,①∠EFB=90°,②∠FEB=90°,分别利用三角形中位线的性质以及相似三角形的判定和性质求出AE 的长,再求出t 即可.【详解】∵AB 是⊙O 的直径,∴∠C=90°, ∵AB=20cm ,弦BC=12cm ,F 是弦BC 的中点,∴BF=12BC=6cm , 有两种情况:①当∠EFB=90°时,如图:∵AB 是⊙O 的直径,∴∠C=90°,∵∠EFB=90°,∴AC ∥EF ,∵F 为BC 的中点,∴E 为AB 的中点,即E 和O 重合,∵AB=20cm ,∴AE=AO=12AB=10cm , ∴1052t ==; ②当∠FEB=90°时,如图:∵∠B=∠B ,∠FEB=∠C=90°,∴△FEB ∽△ACB ,∴BE BF BC AB =, ∴61220BE =, 解得:BE=3.6(cm ),∵AB=20cm ,∴AE=AB-BE=16.4cm ,∴16.48.22t ==; 故答案为:5或8.2.【点睛】本题考查了圆周角定理,三角形中位线定理,相似三角形的性质和判定等知识点,分类讨论是解此题的关键.19.225【分析】依据菱形的面积即可得到AH=48进而得出BH的长再根据相似三角形的对应边成比例即可得到BE的长进而得出OE的长【详解】解:∵菱形ABCD的对角线ACBD相交于点OOB=4∴BD=8又∵解析:2.25【分析】依据菱形的面积,即可得到AH=4.8,进而得出BH的长,再根据相似三角形的对应边成比例,即可得到BE的长,进而得出OE的长.【详解】解:∵菱形ABCD的对角线AC,BD相交于点O,OB=4,∴BD=8,又∵S菱形ABCD=24,∴2 241BD AC,∴AC=6,CO=3,∴Rt△BCO中,BC=5,又∵AH⊥BC,∴24BC AH,∴ 4.8AH,∴Rt ABH中,2222548 1.4BH AB AH.,∵∠EBH=∠CBO,∠BHE=∠BOC=90°,∴△BEH∽△BCO,∴BH BEBO BC ,即1.445BE,∴ 1.75BE,∴4 1.75 2.25EO BO BE,故答案为:2.25.【点睛】本题主要考查了菱形的性质以及相似三角形的判定与性质,利用相似三角形的性质是解决问题的关键.20.或【分析】根据△PAD△PBC都是直角三角形△PAD△PBC△PDC两两相似利用相似三角形性质分类讨论即可;【详解】∵△PAD△PBC都是直角三角形△PAD△PBC△PDC两两相似∴△PDC是直角三解析:12a或13a【分析】根据△PAD,△PBC都是直角三角形,△PAD,△PBC,△PDC两两相似,利用相似三角形性质分类讨论即可;【详解】∵△PAD,△PBC都是直角三角形,△PAD,△PBC,△PDC两两相似,∴△PDC 是直角三角形,当90DPC ∠=︒时,∴90APD BPC ∠+∠=︒,∵90BPC BCP ∠+∠=︒,∴APD BCP ∠=∠,∵90A B ∠=∠=︒,∴△△APD BCP ,当△△APD PDC 时,∴APD PDC ∠=∠,此时CD ∥AB ,90ADC ∠=︒,四边形ABCD 是矩形,∴AD=BC ,与题意矛盾,故不存在这种情况;当△△APD PCD 时,∴ADP PDC ∠=∠,APD PCD ∠=∠,∴PCD BCP ∠=∠,过点P 作PM CD ⊥于M ,∴90PMD A ∠=∠=︒,90PMC B ∠=∠=︒,在△PAD 和△PMD 中,A PMD ADP MDP PD PD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△△PAD PMD ≅,∴PA=PM ,在△PBC 和△PMC 中,B PMC BCP MCP CP CP ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△△PBC PMC ≅,∴PB=PM , ∴12PA PB AB ==, ∵AB a , ∴12AP a =;当90PDC ∠=︒时,当△△△ADPDCP BCP 时,60APD DPC BPC ∠=∠=∠=︒,∴30ADP ∠=︒, ∴12AP PD =, 在△DPC 和△BPC 中,PDC B DPC BPC PC PC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△△DPC BPC ≅,∴PD=PB , ∴12AP PB =, ∴1133AP AB a ==; ∴AP 的长为12a 或13a . 【点睛】 本题主要考查了相似三角形的性质应用,结合全等三角形证明求解是解题的关键.三、解答题21.(1)254;(2)544 【分析】(1)连接AD ,利用“HL”证明Rt △ADB ≅Rt △ACB ,推出AB ⊥DC ,DE=CE ,再证明BE 为△DCF 的中位线,利用锐角三角函数的定义得到AD 1BD 2=,再利用勾股定理即可求得⊙O 的半径;(2)同理先求得DE=5, DC=10,利用勾股定理可求得CG=152,证明△OBM ~△GCM ,推出56OM MG =,推出OBM GBM 56S S =,设OBM 5S a =,则GBM 6S a =,利用三角形的中线平分此三角形的面积,即可推出DGF 44S a =,即可求得答案.【详解】(1)连接AD ,∵∠1=∠2,∴AD=AC ,∵AB 为⊙O 的直径,∴∠ADB=∠ACB=90︒,∴Rt △ADB ≅Rt △ACB(HL),∴DB=CB ,∠1=∠3,∴AB ⊥DC ,∴DE=CE ,∵CF ⊥DC ,∴BE ∥FC ,∴BE 为△DCF 的中位线,∴DB=12DF=55, ∵AE :EC=1:2, ∴AE AD 1tan 3tan 1EC BD 2∠∠====, ∴AD=552, ∴AB=()222252555522AD BD ⎛⎫+=+= ⎪⎝⎭, ∴⊙O 的半径为254; (2)连接BG ,∵CF ⊥DC ,∴∠ACG=90︒,∴DG 为⊙O 的直径,∵DE 1tan 3EB 2∠==,∴EB=2DE ,∵222DE EB BD +=,即(2224DE DE +=, ∴DE=5,则DC=2DE=10,∵222DC CG GD +=,即22225102CG ⎛⎫+= ⎪⎝⎭, ∴CG=152, ∵BO ∥GC ,∴△OBM ~△GCM , ∴OM OB MG CG=, 则25541562OM OB MG CG ===, ∴OBM GBM 56S S =, 设OBM 5Sa =,则GBM 6S a =, ∴GBO 5611Sa a a =+=, ∵点O 为直径DG 的中点, ∴DBO GBO 11SS a ==, ∴DBG GBO 222S S a ==, ∵点B 为线段DF 的中点,DGF DBG 244S S a ==,∴OBM DGF 554444S a S a ==. 故答案为:544. 【点睛】本题考查了圆周角定理,相似三角形的判定和性质,勾股定理的应用,三角形中位线的判定和性质,三角形的中线的性质等知识点,解题的关键是灵活运用所学知识解决问题. 22.(1)画图见解析;(2)1:2;(3)画图见解析;A "(6,0),B "(3,-2),C "(4,-4)【分析】(1)连接CC′并延长,连接BB′并延长,两延长线交于点O ;(2)由OB=2OB′,即可得出△A′B′C′与△ABC 的位似比为1:2;(3),连接B′O 并延长,使OB″=OB′,延长A′O 并延长,使OA″=OA′,C′O 并延长,使OC″=OC′,连接A″B″,A″C″,B″C″,则△A″B″C″为所求,从网格中即可得出△A″B″C″各顶点的坐标.【详解】解:(1)图中点O为所求;(2)△A′B′C′与△ABC的位似比等于1:2;故答案为:1:2;(3)△A″B″C″为所求;A″(6,0);B″(3,-2);C″(4,-4).【点睛】此题考查了作图-位似变换,画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.23.(1)图见解析;(2)图见解析,2C(1,0);(3)10【分析】(1)利用平移的性质得出对应点的坐标即可画出平移后的图形;(2)利用位似图形的性质得出对应点的坐标即可画出平移后的图形,进而可得点C2的坐标;(3)根据所画图形判断出△A2BC2为等腰直角三角形,利用三角形的面积公式即可求解.【详解】解:(1)如图所示:△A1B1C1,即为所求;(2)如图所示:△A2BC2即为所求,C2点坐标为(1,0),故答案为:(1,0);(3)∵A2C2=BC222+=A2224225+=62210∴A2C22+BC22= A2B2,∴△A2BC2是等腰直角三角形,且∠A2C2B=90°,∴△A2BC2的面积位为:1×(252=10平方单位,2故答案为:10.【点睛】本题考查平移变换和位似变换的性质、勾股定理及其逆定理、三角形的面积公式,掌握变换性质,正确得出变换后的对应点的位置是解答的关键.24.(1)CG=1;(2)见解析【分析】(1)根据平行四边形的性质得到AB ∥CD ,证明△EGC ∽△EAB ,根据相似三角形的性质列出比例式,代入计算即可;(2)分别证明△DFG ∽△BFA ,△AFD ∽△EFB ,根据相似三角形的性质证明即可.【详解】(1)解:∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴△EGC ∽△EAB , ∴CG EC AB EB =,即2324CG =+, 解得,CG=1;(2)证明:∴AB ∥CD ,∴△DFG ∽△BFA , ∴FG DF FA FB=, ∴AD ∥CB , ∴△AFD ∽△EFB , ∴AF DF FE FB =, ∴FG AF FA FE=, 即2AF FG FE =⋅.【点睛】本题考查了平行四边形的性质,相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.25.(1)2a ;(2)4a ;(3)2an ﹣2a .【分析】(1)延长BQ 交EF 的延长线于点G ,根据三角形中位线定理求出BC ,证明△BQC ∽△GQE ,根据相似三角形的性质得到EG=BC=2a ,根据角平分线的定义、平行线的性质得到PB=PG ,得到答案;(2)(3)仿照(1)的解法解答.【详解】解:(1)如图1,延长BQ 交EF 的延长线于点G ,∵E 、F 分别是边AB 、AC 的中点,∴EF 是△ABC 的中位线,∴BC=2EF=2a ,EF ∥BC ,∴△BQC ∽△GQE , ∴1EG EQ BC QC==, ∴EG=BC=2a ,∵BQ 是∠CBP 的平分线,∴∠PBQ=∠CBQ ,∵EF ∥BC ,∴∠EGQ=∠CBQ ,∴∠PBQ=∠EGQ ,∴PB=PG ,∴PE+PB=PE+PG=EG=2a ;(2)如图2,延长BQ 交EF 的延长线于点M ,由(1)可知,△BQC ∽△MQE ,∴1.2BC CQ EM EQ ==, ∴EM=2BC=4a ,∴PE+PB=PE+PM=EM=4a ;(3)如图2,当1CQ CE n=时,则EQ=(n-1)CQ , 由EF ∥BC 得,△MEQ ∽△BCQ , ∴1EM EQ n BC QC==-, ∴EM=(n-1)BC=2a (n-1),即EP+BP=2an-2a .【点睛】本题考查了相似三角形的判定与性质、角平分线的定义、平行线的性质,延长BQ 构造出相似三角形,求出EP+BP=EM 并得到相似三角形是解题的关键.26.(1)见解析;(2)AC =;4EH =【分析】(1)根据条件可证明△EBH ∽△CBA ,推出90CAB EHB ∠=∠=︒即可.(2)证明△AFC ∽△BFA ,可得AF 2=FC•FB ,求出AF ,再利用勾股定理求出AC ,证明EH=EF ,在Rt △BEH 中,利用勾股定理构建方程即可解决问题.【详解】(1)证明:∵BH BC BE AB ⋅=⋅, ∴BH BE BA BC=, ∵EBH CBA ∠=∠,∴EBH CBA ∽, ∴EHB CAB ∠=∠, ∵EH AB ⊥, ∴90EHB ∠=︒, ∴90CAB EHB ∠=∠=︒, ∴AC AB ⊥, ∴AC 是O 的切线.(2)解:连接AF .∵AB 是直径,∴90AFB AFC ∠=∠=︒,∵90,90C CAF CAF FAB ∠+∠=︒∠+∠=︒,∴C FAB ∠=∠,∴AFC BFA ∽,∴280AF FC FB =⋅=, ∴45AF = ∴22228(45)12,10(45)65AC AB =+==+=∵DF BD =,∴FAD DAB ∠=∠,∵,EF AF EH AB ⊥⊥,∴EF EH =,设EH EF x ==,∵AE AE =,∴()Rt AEF Rt AEH HL ≌, ∴5,25AF AH BH ===在Rt EBH △中,∵222BE EH BH =+, ∴222(10)(25)x x -=+,∴4x =,∴4EH =.【点睛】本题考查了相似三角形的判定和性质,圆周角,切线的判定等知识,解题的关键是正确作出辅助线,寻找相似三角形解决问题.。
河南省九年级语文下册第二单元易错知识点总结

河南省九年级语文下册第二单元易错知识点总结选择题1、下列句子中无语病的一项是()A.有些家长为自己的孩子购置了多功能电话手表,是一种可以双向通话,能准确定位,并具有防水功能的电子设备。
B.随着人们对非物质文化遗产保护意识的不断增强,使得四川特有剧种——“川剧”的传承与发展迎来了难得的历史机遇。
C.最近,来自“一带一路”沿线20多个国家的在华留学生,评选出中国“新四大发明”:高铁、网购支付宝和共享单车。
D.傅雷以深厚的学养真挚的父爱,倾听着万里之外儿子的每一次心跳和儿子前进路上可能出现的困难,传送着自己的惦念。
答案:CA.句式杂糅,去掉“有些家长为自己的孩子购置了”;B.成分残缺,去掉“随着”或“使”杂糅;D.搭配不当,去掉“和儿子前进路上可能出现的困难”。
故选C。
2、下列句子中加点成语使用恰当的一项是()A.井盖所在位置是进出家门的必经之路,年轻人经过此处还需放慢步伐留意结冰处,老年人经过时就更为战战..兢兢..。
B.他自信,若是再次遇到那个匪徒,绝对能拳打脚踢....轻而易举的将他擒住。
C.正在千钧之力....的时刻,一位不知名的解放军战士奋不顾身跳进冰冷的河水中,救起了落水儿童。
D.听到这消息,他觉得天在旋,地在转,头重脚轻,身子情不自禁....地摇晃起来。
答案:AA.战战兢兢:形容非常害怕而微微发抖的样子也形容小心谨慎的样子;使用正确;B.拳打脚踢:用拳打,用脚踢,应为“三拳两脚”;C.千钧之力:常用来形容器物之重或力量之大,应为“千钧一发”;D.“情不自禁”改为“不由自主”。
故选A。
3、下列对孔乙己的性格特征概括得最恰当的一项是()A.好喝懒做、迂腐穷酸、看不起人、非偷则窃、麻木不仁。
B.穷困潦倒、好喝懒做、满腹经纶、麻木不仁、善良诚恳。
C.自命清高、好喝懒做、迂腐穷酸、麻木不仁、善良诚恳。
D.自命清高、好喝懒做、好为人师、麻木不仁、善良诚恳。
答案:CA.“看不起人”不是孔乙己的性格特点,是酒馆的掌柜,周围的酒客等人的特点;B.知道“茴”字的几种写法算不得“满腹经纶”;D.他告诉我“茴”字的几种写法,并不是“好为人师”,而是出于显摆与虚荣;故选C。
河南省九年级语文下册第二单元重点易错题

河南省九年级语文下册第二单元重点易错题选择题1、下列各组加点字注音无误的一项是()A.俯.身(fǔ)拽.起(zhuài)睹.(dǔ)B.锱.铢(zī)顷.刻(qīnɡ)腮.(sāi)C.脑髓.(suí)铃.铛(línɡ)呕.(ǒu)D.脖颈.(jǐnɡ)盘桓.(huán)绞.(jiǎo)答案:AB.顷应读(qǐnɡ);C.髓应读(suǐ);D.颈应读(gěng)2、下列加点字的注音完全正确的一项是()A.醋.栗(cù)恐吓.(xià)巡.警(xún)B.戳.到(chuō)乞丐.(gài)崽.子(zǎi)C.魁梧.(wǔ)混.蛋(hún)咳嗽.(sou)D.赫.然(chì)径.直(jìng)畜.生(chù)答案:BA.吓hè;C.梧wu;D.赫hè;故选B。
3、下列加点字的注音完全正确的一项是( )A.颓.唐(tuí) 品行.(háng) 不屑.置辩(xiè)B.夹.袄(jiā)恐吓.(hè) 千钧.之力(jūn)C.坎.肩(kǎn)捯.气(dǎo)一气呵.成(hē)D.驾驭.(yù) 礼聘.(pìn) 形影.不离(yǐnɡ)答案:D关于字音,要求学生平时的学习中注意字音的识记和积累,特别是多音字。
D项正确。
ABC三项修改为:A.品行.(xíng);B.夹.袄(jiá);C.捯.气(dáo)。
4、下列说法不正确的一项是()A.“今天的青年,更能认识创新之于国家的意义。
”这个句子的主干是“青年认识意义”。
B.“振兴中华”“声名狼藉”“衣冠楚楚”是同一结构的短语。
C.“今天下午你是打球,还是游泳?”这个句子的标点使用正确。
D.“每个人勇于开拓创新,‘中国制造’就能更上层楼。
”这是个假设关系的复句答案:B本题考查语法知识,包括对句子成分、词语结构、标点符号和复句类型的考查。
【易错题】中考九年级历史下第二单元第二次工业革命和近代科学文化试题及答案

一、选择题1.他在《人间喜剧》里给我们留下了一部法国社会,特别是巴黎上流社会的变迁史。
“他”是A.但丁B.莎士比亚C.巴尔扎克D.列夫·托尔斯泰2.分析材料,可以得出的结论是在第二次工业革命过程中A.英国依然是工业头号强国B.法国增长率在四国中始终最小C.美德工业增长速度超越英法D.德国增长速度始终超过美国3.在一次宴会上,一位贵妇人问达尔文:“您看我也是猴子变的吗?”达尔文微笑着说:“是的。
不过,您是一只漂亮的猴子变的!”他俩的对话与什么理论有关A.万有引力定律B.适者生存原理C.相对论D.生物进化论4.科幻电影《流浪地球》讲述了“流浪的地球”差一点被木星引力捕获而亡的故事。
与之相关的理论是( )A.德谟克利特的原子论B.亚里土多德的逻辑学C.牛顿的万有引力定律D.牛顿的光学分析5.在英国,人们称达尔文为“生物学领域的牛顿”,是因为()A.他们都对近代科学的发展做出了重要贡献B.他们都提出了进化学说C.他们都是英国的科学家D.他们都发现了万有引力6.《新编剑桥世界近代史》中指出,他用数学的理论来表述法拉第的想法,完美阐释了电磁场理论。
这位伟大的科学家是()A.牛顿B.麦克斯韦C.达尔文D.爱因斯坦7.对于神学来说,这是一次致命的危机,他不仅仅否定了上帝造人造万物,而且彻底否定了神学的神圣性。
引发材料中“致命的危机”的理论来自于A.马克思B.牛顿C.达尔文D.巴尔扎克8.乔治从美国芝加哥邮政大厦给远在纽约的妈妈发了一封电报,电文如下:“亲爱的妈妈:今晚我将开汽车到机场,乘坐8点的飞机飞往伦敦,不能与您共度圣诞佳节。
请原谅!您的儿子:乔治”乔治发这封电报的时间最早可能在A.19世纪中期B.19世纪末期C.20世纪初期D.20世纪中期9.资产阶级启蒙思想家严复主张维新变革,所宣传的“物竞天择,适者生存”的思想来源于()A.爱因斯坦的科学理论B.牛顿的科学理论C.达尔文的进化论D.伏尔泰的启蒙思想10.日本是近代亚洲惟一没有沦为殖民地、半殖民地、而走上了资本主义发展道路的国家,它之所以避免了类似其他亚洲国家的厄运,是因为它成功实施了()A.大化改新B.明治维新C.天皇专制D.幕府将军的统治11.有位著名的生物学家以充分的事实证明了物种的可能性,并以自然选择的理论解释了生物的进化,从根本上推翻了“神创论”和“物种不变论”,从而完整地确立了生物进化学说。
九年级英语下学期unit-2常错题复习课件

பைடு நூலகம்
澳门漂亮女赌徒
[单选]甲与乙订立了一份合同,约定甲供给乙狐皮围脖200条,总价6万元,但合同未规定狐皮围脖的质量标准和等级,也未封存样品。甲如期发货,乙验收后支付了货款。后乙因有20条围脖未能销出,便以产品质量不合格为由,向法院起诉,其诉讼代理人在审理过程中又主张合同无效。本案中, [单选]目前我国已基本形成了以()为中心、国家统一会计制度为基础的法规体系。A.会计法B.注册会计师法C.会计管理条例D.会计师管理条例 [单选]()决定着矿粒按密度分层的效果。A..水B.风C.大气压D.床层运动状态 [多选]关节镜下可观察到的关节结构有()。A.滑膜形态B.软骨C.韧带D.内外侧半月板E.血管、神经 [单选]某一竖直角为17°23,40,化为弧度值为()。A.0.72B.0.304C.0.605 [名词解释]起动风速 [单选]具有健脾养胃,消食止泻的作用,用于小儿腹胀便泄、面黄肌瘦、食少倦怠、小便短少的药物是()A.止泻灵颗粒B.健脾消食丸C.小儿泻速停颗粒D.肥儿宝颗粒E.健脾康儿片 [多选]关于航空运输市场的含义下列说法正确的是()A.航空运输市场是一种特定的市场B.是航空运输产品和服务交易的场所C.是指航空运输产品供求关系的总和D.是在一定时空条件下对航空运输产品和服务需求的总和E.供求关系的无法测量的市场 [单选,A1型题]情感对于情绪来说具有的特点是()。A.强烈而冲动B.伴有明显的行为变化C.伴有明显的生理变化D.稳定而深刻E.带有明显的情境性 [单选]港口与航道工程施工总承包特级和一级资质企业,经理应具有()以上从事工程管理工作经历或具有本专业高级职称。A.5年B.8年C.10年D.15年 [问答题]学生的权利有哪些? [判断题]装置引蒸气时应先开回水阀,再开进气阀。A.正确B.错误 [单选]一般认为,社会学创立于()A.1840年B.1839年C.1848年D.1789年 [单选]近海航区,系指中国渤海、黄海及东海距岸不超过()海里的海域。A.100B.150C.200D.250 [问答题,简答题]形式运算阶段的思维方式有哪些特征? [单选]先天性胆管扩张称为A.硬化性胆管炎B.瓷状胆囊Caroli病D.先天性胆总管囊肿 [单选]下列各项中,不属于事业单位净资产项目的是()。A.事业结余B.固定基金C.专用基金D.应缴预算款 [多选]下列属于行政事业单位负债的是()。A.应交税金B.应收及预付款项C.借入款项D.对外投资E.应缴款项 [单选]下列除哪一项外,都与温病的发病有密切关系?()A.感受外邪B.正气强弱及邪正力量的对比C.失治、误治D.外界环境中的自然因素 [单选]职业品德是()职业习惯喝心理的体现。A.消费者B.从业者C.市场监督者D.制定政策者 [多选]先天性巨结肠最有意义的诊断依据是A.腹胀B.出生后不久即出现便秘C.呕吐D.可见肠型及蠕动波E.以上都是 [单选]当年播种,当年开花结果,然后死亡的植株是()。A.一年生植物B.两年生植物C.多年生植物D.木本植物 [单选]以下不属于《建设工程质量管理条例》规定的工程竣工验收所具备工程技术档案和施工管理资料的是()。A.工程竣工图B.质量检验评定资料C.监理会议纪要D.施工日志 [单选]风湿性心脏瓣膜病二尖瓣狭窄不可能有下列哪项心电图改变().A.左房增大,P波增宽超过0.11s,有切迹B.心房颤动C.右室肥厚的心电图图形D.左室肥厚的心电图图形E.右束支传导阻滞 [单选]由婴儿到成人,上颌骨宽度增长约为()。A.1.0倍B.1.6倍C.3.2倍D.0.8倍E.2.0倍 [问答题]一架装载如下的飞机的地板的最小承载限制是多少?货盘尺寸-长37.5宽35货盘重量-34磅系留装置-23磅货物重量-1,255.4磅 [单选]流脑的主要传播途径()A.空气、飞沫B.玩具及用品C.动物传播D.通过饮用水传播E.通过食物传播 [填空题]氨合成反应的单程合成率与()()()有关。 [名词解释]简化原则 [单选]女,21岁,2周前感冒,持续发热37.8~38.5℃,10天前出现情绪不稳定,打人毁物,胡言乱语,自语自笑。曾抽搐一次,大小便失禁。入院体检:T38℃,P100次/分,BP140/90mmHg,下肢肌张力增高,可疑病理征,CSF:潘氏阳性。EEG:弥漫性e波以额颞为主,伴阵发尖波。最不应当忽 [单选,A1型题]青霉紊G最适于治疗()。A.伤寒、副伤寒B.肺炎杆菌性肺炎C.布氏杆菌病D.溶血性链球菌感染E.细菌性痢疾 [单选]下列对于性病性淋巴肉芽肿的诊断有意义,但除了()A.有不洁性交史或配偶感染史B.衣原体培养阳性C.男性龟头、包皮处可见小丘疹、疱疹,无自觉症状D.低丙种球蛋白血症 [问答题,简答题]高危病人管理? [判断题]出口电池产品的制造商在电池产品出口前,应向国家质检总局申请备案。()A.正确B.错误 [单选]当代汽车使用的制动液是()型制动液。A、天然B、合成C、高温D、冷却 [单选]某孕妇,28岁。孕1产0,妊娠38周,宫口开全2小时30分,先露高位+2。胎方位LOT,宫缩30″~40″/4~5分,诊断为第二产程延长。造成这种情况最常见的原因是下列哪一项()A.宫缩乏力B.产妇衰竭C.中骨盆平面狭窄D.骨盆出口狭窄E.胎儿过大 [单选]《部标》规定:快速列车始发前供电时间不少于()。A、2小时B、1.5小时C、0.5小时D、1小时 [单选]某产品的单位变动成本为6元,单位售价为10元,销售数量预计为150万件,企业为该产品确定的目标利润为200万元,那么该产品分担的固定成本应()。A.不高于600万元B.不低于600万元C.不低于400万元D.不高于400万元 [单选,A1型题]下列哪项提示左心功能衰竭()A.交替脉B.水冲脉C.短绌脉D.奇脉E.重搏脉 [单选]关于病原携带状态,下列不正确的是()A.可以出现在显性感染后,也可出现在隐性感染后B.是许多传染病的重要传染源C.并非所有的传染病都有病原携带者D.并非所有的病原携带者都能排出病原体E.机体有免疫反应,但不足以清除病原体
(易错题)初中数学九年级数学下册第二单元《相似》检测(包含答案解析)

一、选择题1.如图,在平行四边形ABCD中,:2:1AE BE ,F是AD的中点,射线EF与AC交于点G,与CD的延长线交于点P,则AGGC的值为().A.5:8B.3:8C.3:5D.2:52.下列四个选项中的三角形,与图中的三角形相似的是()A.B.C.D.3.如图,在▱ABCD中,M、N为BD的三等分点,连接CM并延长交AB与点E,连接EN 并延长交CD于点F,则DF:FC等于().A.1:2 B.1:3 C.2:3 D.1:44.如图所示,在矩形ABCD中,AB=2,BC=2,对角线AC、BD相交于点O,过点O 作OE垂直AC交AD于点E,则AE的长是()A .2B .3C .1D .1.55.如图,矩形ABCD 中,AD m =,AB n =,要使BC 边上至少存在一点P ,使ABP △、APD △、CDP 两两相似,则m 、n 间的关系式一定满足( )A .12m n ≥B .m n ≥C .32m ≥D .2m n ≥ 6.如图,已知////AB CD EF ,它们依次交直线1l 、2l 于点A 、D 、F 和点B 、C 、E ,如果:3:1AD DF =,10BE =,那么CE 等于( )A .103B .203C .52D .1527.如图,已知在ABC 中,D 为BC 上一点,//EG BC ,分别交AB ,AD ,AC 于点E ,F ,G ,则下列比例式正确的是( )A .AE EF BE BD = B .EF AF DC AD = C .AC FG CG DC = D .AE FG AB DC= 8.已知a 3b 4=,则下列变形错误的是( ) A .34a b = B .34a b = C .4a=3b D .43b a = 9.已知如图,DE 是△ABC 的中位线,AF 是BC 边上的中线,DE 、AF 交于点O .现有以下结论:①DE ∥BC ;②OD =14BC ;③AO =FO ;④AOD S =14ABC S .其中正确结论的个数为( )A .1B .2C .3D .410.如图,在ABC 中,点D 、E 分别在边AB 、AC 上,则在下列五个条件中:①AED B ∠=∠;②//DE BC ;③AD AE AC AB=;④AD BC DE AC ⋅=⋅,能满足ADE ACB 的条件有( )A .1个B .2个C .3个D .4个11.已知P 是线段AB 的黄金分割点,且51AB =+,则AP 的长为( ). A .2 B .51- C .2或51-D .35- 12.如图,四边形ABCD 是正方形,E 是BC 的中点,连接AE 与对角线BD 相交于点G ,连接CG 并延长,交AB 于点F ,连接DE 交CF 于点H .以下结论:①CDE BAE ∠=∠;②CF DE ⊥;③AF BF =;④22CE CH CF =⋅.其中正确结论的个数有( )A .1B .2C .3D .4二、填空题13.如果x :y =3:2,那么x y x-的值是__.14.己知034x z y ==≠,则345x y z x y z -+=++________. 15.如图,ABC 中,1BC =.若113AD AB =,且11//D E BC ,照这样继续下去,12113D D D B =,且22//D E BC ;23213D D D B =,且33//DE BC ;…;1113n n n D D D B --=,且//n n D E BC 则101101=D E _________.16.如图,△ABC 中,D 在AC 上,且AD :DC=1:n ,E 为BD 的中点,AE 的延长线交BC 于F ,那么FC:BF 的值为______(用含有n 的代数式表示).17.如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点A ,在近岸取点D ,B ,使得A ,D ,B 在一条直线上,且与河的边沿垂直,测得10m BD =,然后又在垂直AB 的直线上取点C ,并量得30m BC =.如果20m DE =,则河宽AD 为_________m .18.如图,已知△ABC 中,∠B =90°,BC =3,AB =4,D 是边AB 上一点,DE ∥BC 交AC 于点E ,将△ADE 沿DE 翻折得到△A ′DE ,若△A ′EC 是直角三角形,则AD 长为_____.19.如图,Rt △ABC 中,AC =5,BC =12,O 为BC 上一点,⊙O 分别与边AB 、AC 切于E 、C ,则⊙O 半径是________.20.如图,在△ABC 中,AE AF EB FC=,动点P 在射线EF 上,BP 交CE 于点D ,∠CBP 的平分线交CE 于点Q ,当CQ =13CE 时,EP +BP =20,则BC 的长为________.三、解答题21.如图,在每个小正方形的边长为1的网格中,△ABC 的项点A ,B ,C 均落在格点上:(I )AC 的长等于_________;(II )点P 落在格点上,M 是边BC 上任意一点,点B 关于直线AM 的对称点为B ',当PB '最短时,请在如图所示的网格中,用无刻度的直尺,画出点B ',并简要说明点B '的位置是如何找到的.(不要求证明)22.已知:E 是矩形ABCD 的边AB 上一个动点,直线EF DE ⊥交BC 于点F .(1)求证:ADE ∽BFE △;(2)若直线EF 经过C 点,且3AD =,10AB =,是否存在这样的点E ,使ADE 和BFE △相似?若存在,请求出AE 的长度;若不存在,请说明理由.(3)连结DF ,若3AD =,2AE =,当ADE 和EFD △相似时,则AB =______. 23.如图,在平面直角坐标系xoy 中,直线2y x b =+经过点()2,0A -,与y 轴交于点B ,与反比例函数()0k y x x =>的图象交于点C(m ,6),过B 作BD y ⊥轴,交反比例函数()0k y x x=>的图象于点D ,连接AD ,CD . (1)求b ,k 的值;(2)求△ACD 的面积;(3)在坐标轴上是否存在点E(除点O 外),使得△ABE 与△AOB 相似,若存在,请求出点E 的坐标;若不存在,请说明理由.24.如图1,在△ABC 中,AD ⊥BC ,DE ⊥A B ,DF ⊥AC .(1)若AD 2 =BD ·DC , ①求证:∠BAC =90°;②连接EF ,若AB =4,DC =6,求EF .(2)如图2,若AD =4,BD =2,DC =4,求EF .25.如图,ABC 内接于⊙O ,AB AC =,过点C 作AB 的垂线CD ,垂足为点E ,交O 于点F ,连接AD ,并使AD BC ∥.(1)求证:AD 为O 的切线;(2)若5AC =,2BE =,求AD 的长.26.如图,已知△ABC 中,BC =10,BC 边上的高AH =8,四边形DEFG 为内接矩形. (1)当矩形DEFG 是正方形时,求正方形的边长.(2)设EF =x ,矩形DEFG 的面积为S ,求S 关于x 的函数关系式,当x 为何值时S 有最大值,并求出最大值.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】证明AFE △≌△()DFP AAS ,推出=AE DP ,由:2:1AE BE =,设BE k =,2AE k =,推出3AB CD k ==,5PC k =,由//AE BC ,可得AG AE GC CP=的值. 【详解】∵四边形ABCD 是平行四边形,∴//AB PC ,AB CD =,∴AEF P ∠=∠,∵AFE DFP ∠=∠,AF DF =,∴AFE △≌△()DFP AAS ,∴=AE DP ,∵:2:1AE BE =,设BE k =,2AE k =,∴3AB CD k ==,5PC k =,∵//AE BC , ∴2255AG AE k GC CP k ===, 故选:D .【点睛】 本题考查了平行四边形的性质,全等三角形的判定和性质,平行线分线段成比例定理等知识,解题的关键是学会利用已知条件证明三角形全等、利用参数解决问题,属于中考常考2.B解析:B【分析】由于已知三角形和选择项的三角形都放在小正方形的网格中,设正方形的边长为1,所以每一个三角形的边长都是可以表示出,然后根据三角形的对应边成比例即可判定选择项.【详解】解:设小正方形的边长为1,那么已知三角形的三边长分别为,,所以三边之比为1:2A、三角形的三边分别为2,,三边之比为3,故本选项错误;B、三角形的三边分别为2,4,1:2C、三角形的三边分别为2,32:3D44,故本选项错误.故选:B.【点睛】此题主要考查了相似三角形的判定,属于基础题,掌握三边对应成比例的两个三角形相似是解答本题的关键,难度一般.3.B解析:B【分析】由题意可得DN=NM=MB,据此可得DF:BE=DN:NB=1:2,再根据BE:DC=BM:MD=1:2,AB=DC,故可得出DF:FC的值.【详解】解:由题意可得DN=NM=MB,AB//CD,AB//BC∴△DFN∽△BEN,△DMC∽△BME,∴DF:BE=DN:NB=1:2,BE:DC=BM:MD=1:2,又∵AB=DC,∴DF:AB=1:4,∴DF:FC=1:3故选:B.【点睛】本题考查相似三角形的性质,两相似三角形对应线段成比例,要注意比例线段的应用.4.D解析:D【分析】先求出AC,进而求出OA,再证明△AOE∽△ADC,得到AE OAAC AD,即可求解.解:∵四边形ABCD 是矩形,∴∠ABC =∠ADC =90°,AD =BC =2,CD =ABOA =OC =12AC ,∴AC=∴OA =2, ∵OE ⊥AC , ∴∠AOE =90°,∴∠AOE =∠ADC ,又∵∠OAE =∠DAC ,∴△AOE ∽△ADC , ∴AE OA AC AD=,即22AE =, ∴AE =1.5.故选:D .【点睛】本题考查了矩形的性质,勾股定理,相似三角形的性质与判定等知识,能根据已知条件判定△AOE ∽△ADC 是解题关键.5.D解析:D【分析】由于△MNP 和△DCP 相似,可得出关于MN 、PC 、NP 、CD 的比例关系式.设PC=x ,那么NP=m-x ,根据比例关系式可得出关于x 的一元二次方程,由于NC 边上至少有一点符合条件的P 点,因此方程的△≥0,由此可求出m 、n 的大小关系.【详解】解:若设PC=x ,则NP=m-x ,∵△ABP ∽△PCD ,AB BP PC CD ∴=即,n m x x n-= 即x 2-mx+n 2=0方程有解的条件是:m 2-4n 2≥0,∴(m+2n )(m-2n )≥0,则m-2n≥0,∴m≥2n .故选:D .【点睛】本题是存在性问题,可以转化为方程问题,利用判断方程的解的问题来解决. 6.C解析:C【分析】 根据平行线分线段成比例得到BC AD CE DF =,代入已知解答即可. 【详解】解:∵////AB CD EF , ∴BC AD CE DF=, ∵:3:1AD DF =,10BE =, ∴1031CE CE -=, 解得:CE=52, 故选:C .【点睛】 本题考查平行线分线段成比例、比例的性质,掌握平行线分线段成比例是解答的关键,注意对应线段的顺序.7.D解析:D【分析】根据相似三角形的判定推出△AEF ∽△ABD ,△AFG ∽△ADC ,△AEG ∽△ABC ,再根据相似三角形的性质得出比例式即可.【详解】A 、∵EG ∥BC ,即EF ∥BD ,∴△AEF ∽△ABD , ∴AE EF AB BD=, ∵AB BE ≠,故本选项不符合题意;B 、∵EF ∥BD ,∴△AEF ∽△ABD , ∴EF AF BD AD=, ∵BD ≠DC ,故本选项不符合题意;C 、∵EG ∥BC ,即FG ∥DC ,∴△AFG ∽△ADC , ∴AG FG AC DC =,∵AG ACAC CG≠,故本选项不符合题意;D、∵EG∥BC,∴△AEG∽△ABC,∴AE AGAB AC=,∵FG∥DC,∴△AFG∽△ADC,∴AG FGAC DC=,∴AE FGAB DC=,故本选项符合题意;故选:D【点睛】本题考查了相似三角形的性质和判定,能正确的识别图形、灵活运用定理进行推理是解此题的关键.8.A解析:A【分析】根据两内项之积等于两外项之积对各选项分析判断即可得解.【详解】解:由34ab=得,4a=3b,A、由等式性质可得:ab=12,原变形错误,故这个选项符合题意;B、由等式性质得到4a=3b,原变形正确,故这个选项不符合题意;C、由等式性质可得:4a=3b,原变形正确,故这个选项不符合题意;D、由等式性质可得:4a=3b,原变形正确,故这个选项不符合题意;故选:A.【点睛】本题考查比例的性质.熟练掌握内项之积等于外项之积是解题的关键.9.C解析:C【分析】①根据三角形中位线定理进行判断;②根据三角形中位线定理进行判断;③根据三角形中位线定理进行判断;④由相似三角形△ADO∽△ABF的面积之比等于相似比的平方进行判断.【详解】∵DE是△ABC的中位线,∴DE∥BC,故①正确;∴DE=12BC , ∴OD=12BF , ∵AF 是BC 边上的中线,∴BF=12BC , ∴OD=12BF=14BC ,故②正确; ∵DE 是△ABC 的中位线,∴AD=DB ,DE ∥BC ,∴AO =FO ,故③正确;④∵DE ∥BC ,即DO ∥BF ,∴△ADO ∽△ABF , ∴22ADO ABF 1124S AD S AB ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭, 又∵AF 是BC 边上的中线,∴ABF ABC 12SS =, ∴ADO ABC18S S =,故④错误. 综上所述,正确的结论是①②③,共3个.故选:C .【点睛】本题考查了三角形中位线定理、相似三角形的判定与性质.本题利用了“相似三角形的面积之比等于相似比的平方”的性质.正确的识别图形是解题的关键.10.B解析:B【分析】根据相似三角形的判定逐个判断即可得.【详解】①在ADE 和ACB △中,AED B A A ∠=∠⎧⎨∠=∠⎩, ADEACB ∴,则条件①能满足; ②//DE BC ,ADE ABC ∴,则条件②不能满足;③在ADE 和ACB △中,AD AE AC AB A A⎧=⎪⎨⎪∠=∠⎩,ADE ACB ∴,则条件③能满足;④由AD BC DE AC ⋅=⋅得:AD DE AC BC=, 对应的夹角ADE ∠与C ∠不一定相等,∴此时ADE 和ACB △不一定相似,则条件④不能满足;综上,能满足的条件有2个,故选:B .【点睛】 本题考查了相似三角形的判定,熟练掌握判定方法是解题关键.11.C解析:C【分析】若点P 是靠近点B的黄金分割点,则AP AB =,然后代入数据计算即可;若点P 是靠近点A 的黄金分割点,先求出BP ,再利用线段的和差即可求出AP .【详解】解:若P 是靠近点B的黄金分割点,则)12AP AB ===; 若P 是靠近点A的黄金分割点,则)111222BP AB ==⨯=,∴121AP AB BP =-=-=;故选:C .【点睛】是解题的关键. 12.D解析:D【分析】证明△ABE ≌△DCE ,可得结论①正确;由正方形的性质可得AB=AD=BC=CD ,BE=CE ,∠DCE=∠ABE=90°,∠ABD=∠CBD=45°,可证△ABE ≌△DCE ,△ABG ≌△CBG ,可得∠BCF=∠CDE ,由余角的性质可得结论②;证明△DCE ≌△CBF 可得结论③,证明△CHF ∽△CBF 即可得结论④正确.【详解】解:∵四边形ABCD 是正方形,点E 是BC 的中点,∴AB=AD=BC=CD ,BE=CE ,∠DCE=∠ABE=90°,∠ABD=∠CBD=45°,∴△ABE ≌△DCE (SAS )∴∠DEC=∠AEB ,∠BAE=∠CDE ,DE=AE ,故①正确,∵AB=BC ,∠ABG=∠CBG ,BG=BG ,∴△ABG ≌△CBG (SAS )∴∠BAE=∠BCF ,∴∠BCF=∠CDE ,且∠CDE+∠CED=90°,∴∠BCF+∠CED=90°,∴∠CHE=90°,∴CF ⊥DE ,故②正确,∵∠CDE=∠BCF ,DC=BC ,∠DCE=∠CBF=90°,∴△DCE ≌△CBF (ASA ),∴CE=BF ,∵CE=12BC=12AB , ∴BF=12AB , ∴AF=BF ,故③正确,∵∠BCF+∠BFC=90°,∠DEC=∠BFC∴∠BCF+∠DECC=90°,∴∠CHE=90°∴∠CHE=∠FBC又∠DEC=∠BFC∴△CHF ∽△CBF ∴CH CE BC CF= ∵BC=2CE , ∴2BC CE CE CE CH CF CF== ∴22CE CH CF =⋅故选:D .【点睛】本题考查了正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质,直角三角形的性质,勾股定理等知识,熟练运用这些性质进行推理是本题的关键.二、填空题13.【分析】根据已知条件得出再把化成然后代值计算即可得出答案【详解】∵∴∴故答案为:【点睛】此题考查了比例的性质熟练掌握比例的性质是解题的关键解析:13【分析】 根据已知条件得出23y x =,再把x y x -化成1y x -,然后代值计算即可得出答案. 【详解】∵:3:2x y =, ∴23y x =, ∴211133x y y x x -=-=-=. 故答案为:13. 【点睛】此题考查了比例的性质,熟练掌握比例的性质是解题的关键.14.【分析】可设则x=3ky=kz=4k 代入所求式子中求解即可【详解】解:设则x=3ky=kz=4k 则===故答案为:【点睛】本题考查比例的性质分式的求值熟练掌握比例的性质巧妙设参数是解答的关键 解析:43【分析】 可设=34x z y k ==,则x=3k ,y=k ,z=4k ,代入所求式子中求解即可. 【详解】 解:设=34x z y k ==,则x=3k ,y=k ,z=4k , 则345x y z x y z -+++ =3344354k k k k k k-+⨯++ =1612k k=43, 故答案为:43. 【点睛】本题考查比例的性质、分式的求值,熟练掌握比例的性质,巧妙设参数是解答的关键. 15.【分析】由D1E1∥BC 可得△AD1E1∽△ABC 然后由相似三角形的对应边成比例证得继而求得D1E1的长又由D1D2=可得AD2=继而求得D2E2的长同理可求得D3E3的长于是可得出规律则可求得答案 解析:10121()3- 【分析】由D 1E 1∥BC ,可得△AD 1E 1∽△ABC ,然后由相似三角形的对应边成比例,证得111D E AD BC AB =,继而求得D 1E 1的长,又由D 1D 2= 113D B ,可得AD 2= 59AB ,继而求得D 2E 2的长,同理可求得D 3E 3的长,于是可得出规律,则可求得答案.【详解】解:∵D 1E 1∥BC ,∴△AD 1E 1∽△ABC , ∴111D E AD BC AB=, ∵BC=1,AD 113AB =, ∴D 1E 113=, ∵D 1D 2=113D B , ∴AD 2= 59AB , 同理可得:22254211()993D E ==-=-, 3331921()273D E ==-, ∴21().3n n n D E =-∴101101D E =10121()3-. 故答案为:10121()3-.【点睛】 此题考查了相似三角形的判定与性质.得到规律21().3nn n D E =-是关键. 16.n+1【分析】作DG 平行于AF 交BC 于G 由平行线分线段成比例定理比例的性质求得;然后根据三角形中位线的定义知BF=FG 所以由等量代换证得结论【详解】证明:如图作交BC 于G ∵AD :DC=1:n ∴AD :解析:n+1【分析】作DG 平行于AF 交BC 于G .由平行线分线段成比例定理、比例的性质求得1AC FC n AD FG==+;然后根据三角形中位线的定义知BF=FG ,所以由等量代换证得结论. 【详解】证明:如图,作//DG AF 交BC 于G∵AD :DC=1:n ,∴AD :AC=1:(n+1).∵//DG AF ,∴AC FC CD GC=, 根据比例的性质知,1AC FC n AD FG ==+, 又E 是BD 的中点,∴EF 是△BGD 的中位线,∴BF=FG .∴FC:BF=FC BF =1FC n FG=+. 故填:n+1.【点睛】 本题考查了平行线分线段成比例.列比例式时,一定要找准对应线段,以防错解. 17.20【分析】证出ADE 和ABC 相似然后根据相似三角形对应边成比例列式求解即可【详解】解:∵AB ⊥DEBC ⊥AB ∴DE ∥BC ∴ADE ∽ABC ∴即解得:AD =20m 故答案为:20【点睛】本题考查了相似三解析:20【分析】证出ADE 和ABC 相似,然后根据相似三角形对应边成比例列式求解即可. 【详解】解:∵AB ⊥DE ,BC ⊥AB ,∴DE ∥BC ,∴ADE ∽ABC , ∴AD DE AB BC=,即201030AD AD =+, 解得:AD =20m .故答案为:20.【点睛】 本题考查了相似三角形的应用,利用相似三角形对应边成比例列出比例式是解题的关键. 18.或【分析】先根据勾股定理得到AC =5再根据平行线分线段成比例得到AD :AE =AB :AC =4:5设AD =x 则AE =A′E =xEC =5﹣xA′B =2x ﹣4在Rt △A ′BC 中根据勾股定理得到A′C 再根据△ 解析:78或258 【分析】 先根据勾股定理得到AC =5,再根据平行线分线段成比例得到AD :AE =AB :AC =4:5,设AD =x ,则AE =A ′E =54x ,EC =5﹣54x ,A ′B =2x ﹣4,在Rt △A ′BC 中,根据勾股定理得到A ′C ,再根据△A ′EC 是直角三角形,根据勾股定理得到关于x 的方程,解方程即可求解.【详解】解:在△ABC 中,∠B =90°,BC =3,AB =4,∴AC =5,∵DE ∥BC ,∴AD :AB =AE :AC ,即AD :AE =AB :AC =4:5,设AD =x ,则AE =A ′E =54x ,EC =5﹣54x ,A ′B =24x ﹣,在Rt △A ′BC 中,A ′C∵△A ′EC 是直角三角形,∴①当A '落在边AB 上时,∠EA ′C =90°,∠BA ′C =∠ACB ,A ′B =3×cot ∠ACB =39344⨯=, ∴AD =1974248⎛⎫-= ⎪⎝⎭;②点A在线段AB的延长线上(22(24)3x-+)2+(5﹣54x)2=(54x)2,解得x1=4(不合题意舍去),x2=25 8.故AD长为78或258.故答案为:78或258.【点晴】本题考查了勾股定理和平行线等分线段成比例定理,掌握相关知识是解决问题的关键.19.【分析】连接EO根据切线性质定理得OE⊥AB可得到△BEO∽△BCA根据相似三角形的性质可求出圆半径的长【详解】解:∵⊙O分别与边ABAC切于EC连接OE则OE⊥ABBC⊥AC∴∠BEO=∠BCA又解析:10 3【分析】连接EO,根据切线性质定理得OE⊥AB,可得到△BEO∽△BCA,根据相似三角形的性质,可求出圆半径的长.【详解】解:∵⊙O 分别与边AB 、AC 切于E 、C ,连接OE ,则OE ⊥AB ,BC ⊥AC∴∠BEO=∠BCA ,又∠B=∠B∴△BEO ∽△BCA ∴=BO OE AB AC 又AC=5,BC=12,∴AB=22AC BC +=13,设圆的半径为r ,∴12r r =135- ∴r=103 ∴圆的半径是103 , 故答案为:103.【点睛】此题考查了切线的性质及相似三角形的判定与性质,解题关键在于熟练掌握切线性质定理及相似三角形的性质与判定定理.20.10【分析】延长BQ 交射线EF 于点M 先证明△BCQ ∽△MEQ 然后可得=根据EM=20即可得出答案【详解】解:如图延长BQ 交射线EF 于点M ∵EF 是ABAC 的中点∴EF 是△ABC 的中位线∴EF ∥BC ∴∠解析:10【分析】延长BQ 交射线EF 于点M ,先证明△BCQ ∽△MEQ ,然后可得EM BC =2EQ CQ =,根据EM=20,即可得出答案.【详解】解:如图,延长BQ 交射线EF 于点M ,∵E ,F 是AB ,AC 的中点,∴EF 是△ABC 的中位线,∴EF ∥BC ,∴∠BME=∠MBC ,∵BQ 平分∠CBP ,∴∠PBM=∠MBC ,∴∠BME=∠PBM ,∴BP=PM ,∴EP+BP=EM=20,∵CQ =13CE , ∴2EQ CQ=, ∵EF ∥BC ,∴△BCQ ∽△MEQ , ∴EM BC =2EQ CQ =, ∵EM=20, ∴202BC=,即BC=10, 故答案为:10.【点睛】 本题考查了相似三角形的判定和性质,三角形中位线定理,判定△BCQ ∽△MEQ 是解题关键.三、解答题21.(I 29II )见解析.【分析】(I )利用勾股定理即可解决问题.(2)连接AP ,想办法在AP 上取一点B′,使得AB′=2时,PB′的值最小.方法:取格点G ,H ,连接GH 交AP 于点B′,由平行线分线段成比例定理可知AB′=2,点B′即为所求.【详解】解:(I )222529AC =+=.故答案为29.(II )如图,点B′即为所求.取格点G ,H ,连接GH 交AP 于点B′,由平行线分线段成比例定理可知AB′=2,点B′即为所求.【点睛】本题考查作图-复杂作图,勾股定理,平行线分线段成比例定理,轴对称等知识,解题的关键是理解题意,灵活运用所学知识解决问题.22.(1)证明见解析;(2)存在,1AE =或9;(3)4或132【分析】(1)根据两角对应相等的两个三角形相似判断即可;(2)设AE x =,则10BE x =-,利用相似三角形的性质,构建方程求解即可;(3)连接DF .分两种情形:当ADE EDF ∽△时,当ADE △∽EFD △时,分别构建方程求解即可.【详解】(1)∵四边形ABCD 是矩形∴90A B ∠=∠=︒,∵EF DE ⊥∴90DEF ∠=︒,∴AED BFE ∠=∠ ∴ADE ∽BFE △;(2)设AE x =,则10BE x =-, 由题意得:3BF BC AD ===∵ADE ∽BFE △∴AD AE BE BF =, ∴3103x x =- 解得:1x =或9 经检验,1x =或9是分式方程的根,∴1AE =或9;(3)连接DF .当ADE ∽EDF 时 则AD AE DE EF = ∴32DF AD EF AE == ∵ADE ∽BEF ∴32AD DE EB EF == ∵3AD =∴2BE =∴224AB AE BE =+=+=当ADE ∽EFD △时 则AD AE EF DE = ∴23DE AE EF AD == ∵ADE ∽BEF ∴23AD DE EB EF == ∵3AD = ∴92BE = ∴913222AB AE EB =+=+= 综上所述,满足条件的AB 的值为4或132 故答案为:4或132. 【点睛】 本题考查了相似三角形、矩形、分式方程的知识;解题的关键是熟练掌握相似三角形、矩形、分式方程的性质,从而完成求解.23.(1)4,6;(2)4.5;(3)存在,理由见解析.【分析】(1)把A(-2,0),代入y =2x +b 得到b 的值,再把C(m ,6)代入y =2x +b ,求出m 的值,进而即可得到答案;(2)先求出B 的坐标,再求出点 D 的纵坐标,根据S △ACD =S △ABD +S △BCD ,进而即可求解;(3)分两种情况①△AOB ∽△EAB ,②△AOB ∽△ABE ,分别列出比例式,进而即可求解【详解】(1)∵直线y =2x +b 经过点A(-2,0),∴-4+b =0,∴b =4,∴直线y =2x +4.把C(m ,6)代入y =2x +4中,得6=2m +4,解得m =1,∴C(1,6).把C(1,6)代入反比例函数()0k y x x=>中,得k =6. (2)令x =0,得y =2x +4=4,∴B(0,4).∵BD ⊥y 轴于B ,∴D 点的纵坐标为4,把y =4代入反比例函数y =6x 中,得x =32, ∴D (32,4), ∴BD =32, ∴S △ACD =S △ABD +S △BCD =4.5;(3)存在.当∠BAE =90°时,如图①,∵∠BAE =∠BOA =90°,∠ABE =∠OBA ,∴△AOB ∽△EAB , ∴AB BO EB BA=,∵=∴BE =5,∴OE =1,∴E(0,-1);当∠ABE =90°时,如图②,∵∠ABE =∠AOB =90°,∠OAB =∠BAE ,∴△AOB ∽△ABE ,∴AB AO AE BA = ∴AE =2AB AO=10, ∴OE =AE -AO =10-2=8,∴E(8,0). ∴存在点E(除点O 外),使得△ABE 与△AOB 相似,其坐标为(8,0)或(0,-1).① ②【点睛】本题主要考查一次函数与反比例函数的综合以及相似三角形的判定和性质,掌握待定系数法以及相似三角形的性质,是解题的关键.24.(1)①见解析;②32)105【分析】 (1)①依据∠ADB =∠CDA =90°,BD AD AD CD=,即可得到△ABD ∽△CAD ,再根据相似三角形的性质,即可得到∠BAC =90°; ②先判定四边形AEDF 是矩形,得出EF =AD ,再根据射影定理可得BD =2,最后根据勾股定理,求得Rt △ABD 中,AD 22AB BD -3EF =3(2)根据勾股定理得到AC =42AB =5AE AF AC AB =,∠EAF =∠CAB ,即可判定△AEF ∽△ACB ,进而得出=EF AF BC AB ,即可得到EF 610 【详解】(1)①证明:∵AD ⊥BC ,∴∠ADB =∠CDA =90°.∵AD 2 =BD ·DC ,∴BD AD AD CD=. ∴△ABD ∽ △CAD .∴∠BAD =∠C .又∵∠B +∠BAD =90° ,∴∠B +∠C =90°.∴∠BAC = 90°.②∵DE ⊥AB ,DF ⊥AC ,∠BAC =90°.∴∠EAF =∠AED =∠AFD =90°.∴四边形AEDF 是矩形.∴EF =AD .∵∠BAC =90°,AD ⊥BC ,∴AB 2=BD ⋅BC .∵AB =4,DC =6,即42=BD ⋅(BD +6).解得BD =2.∴Rt △ABD 中,AD∴EF=(2)∵在Rt △ABD 中,AD =4,BD =2,∴AB =∵AD =4,DC =4,DF ⊥AC ,∴AC=.∴AF =12AC = ∵DE ⊥AB ,DF ⊥AC ,AD ⊥BC ,∴AD 2=AE ⋅AB ,AD 2=AF ⋅AC .∴AE ⋅AB =AF ⋅AC . 即AE AF AC AB=. 又∵∠EAF =∠CAB ,∴△AEF ∽△ACB . ∴=EF AF BC AB .∴6EF =.解得EF 【点睛】本题主要考查了相似三角形的判定与性质,解题时注意:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形,或依据基本图形对图形进行分解、组合.25.(1)证明见解析;(2)【分析】(1)连接AO后交DC于点H,交BC于点G,由垂径定理可知AG⊥BC,然后根据互余关系得到∠HAE=∠HCG,然后利用平行关系得到∠ADE=∠HCG=∠HAE,等量代换后可得∠HAE +∠EAD=90°;(2)根据AC和BE可算出AE,然后在Rt△AEC中算出EC,然后证明△AED∽△BEC,然后利用比例关系算出DE,在Rt△AED中计算AD即可.【详解】解:(1)如图,连接AO交DC于点H,交BC于点G,则AG⊥BC∵AG⊥BC,AB⊥DC,∠AHE=∠CHG∴∠HAE=∠HCG∵AB⊥DC∴∠ADE+∠EAD=90°∵AD∥BC∴∠ADE=∠HCG=∠HAE∴∠HAE +∠EAD=90°∴AD为O的切线(2)∵AC=AB,AC=5,BE=2∴AE=3在Rt△AEC由勾股定理可得:22=4EC AC AE-=∵AD∥BC∴△AED∽△BEC∴BE ECAE DE=∴DE=6在Rt△AED由勾股定理可得:22AD=35DE AE+=【点睛】本题主要考查圆的相关定理,掌握切线的证明方法,灵活转化角关系是证明切线的关键,在圆中计算线段长度,找准相似三角形,结合勾股定理,是解题的关键.26.(1)409;(2)()254204S x=--+,当x=4时,S有最大值20【分析】(1)GF∥BC得△AGF∽△ABC,利用相似三角形对应边上高的比等于相似比,列方程求解;(2)根据相似三角形的性质求出GF=10−54x,求出矩形的面积,运用二次函数性质解决问题.【详解】(1)设HK=y,则AK=AH﹣KH=AH﹣EF=8﹣y,∵四边形DEFG为矩形,∴GF∥BC,∴△AGF∽△ABC,∴AK:AH=GF:BC,∵当矩形DEFG是正方形时,GF=KH=y,∴(8﹣y):8=y:10,解得:y=409;(2)设EF=x,则KH=x.∴AK=AH﹣EF=8﹣x,由(1)可知:8108GF x-=,解得:GF=10﹣54 x,∴s=GF•EF=(10﹣54x)x=﹣54(x﹣4)2+20,∴当x=4时S有最大值,并求出最大值20.【点睛】本题考查了相似三角形的性质,二次函数的最值,矩形的性质的应用,注意:矩形的对边相等且平行,相似三角形的对应高的比等于相似比,题目是一道中等题,难度适中.。
(易错题)初中数学九年级数学下册第二单元《相似》检测题(包含答案解析)

一、选择题1.如图,在四边形ABCD中,//AD BC,如果添加下列条件,不能使得△ABC∽△DCA成立的是()A.∠BAC=∠ADC B.∠B=∠ACD C.AC2=AD•BC D.DC AB AC BC=2.如图,在正方形ABCD中,点E是边BC的中点,连接AE,EF AE⊥交CD边于点F,已知4AB=,则CF的长为()A.1 B.5C.3 D.23.如图,已知D、E分别为AB、AC上的两点,且DE∥BC,AE=2CE,AB=12,则AD的长为()A.4 B.6 C.5 D.84.如图,练习本中的横格线都平行且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C都在横格线上.若线段AB=6,则线段AC的长为()A.12 B.18 C.24 D.305.如图,在矩形、三角形、正五边形、菱形的外边加一个宽度一样的外框,保证外框的边界与原图形对应边平行,则外框与原图一定相似的有()A.1个B.2个C.3 D.4个6.如图△BCD中,BE⊥CD,AE=CE=3,BE=DE=4.BC=5,DA的延长线交BC于F,则AF=()A.1 B.0.6 C.1.2 D.0.87.有下列四种说法:其中说法正确的有()①两个菱形相似;②两个矩形相似;③两个平行四边形相似;④两个正方形相似.A.4个B.3个C.2个D.1个8.如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O,点P是BD上的一个动点,过点P作EF∥AC,分别交正方形的两条边于点E,F,连接OE,OF,设BP=x,△OEF的面积为y,则能大致反映y与x之间的函数关系的图像为()A .B .C .D . 9.如图,地面上点A 处有一只兔子,距它10米的B 处有一根高1.6米的木桩,大树、木桩和兔子刚好在一条直线上.一只老鹰在9.6米高的树顶上刚好看见兔子,则大树C 离木桩B( )米.A .60B .50C .40D .45 10.已知线段a 、b 有52a b a b +=-,则:a b 为( ) A .5:1 B .7:2 C .7:3 D .3:711.已知P 是线段AB 的黄金分割点,且51AB =+,则AP 的长为( ). A .2 B .51- C .2或51-D .35- 12.如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,E 为BC 的中点,连接AE 交BD 于点F ,若1OF =,则BD 的长为( )A .5B .6C .7D .8二、填空题13.如图所示,在ABC ∆中,4BC =,E ,F 分别是AB ,AC 的中点.(1)线段EF 的长为_____;(2)若动点P 在直线EF 上,CBP ∠的平分线交CE 于点Q ,当点Q 把线段EC 分成的两线段之比是1∶2时,线段EP 、BP 之间的数量关系满足EP BP +=_____.14.已知线段=AB 6,点c 是线段AB 的黄金分割点,AC BC >.那么AC BC -=________.15.如图,在ABC 中,//DE BC ,若9AB =,8AC =,3AD =,则EC 的长是______.16.目前,某市正积极推进“五城联创”,其中扩充改造绿地是推进工作计划之一.现有一块直角三角形绿地,量得两直角边长分别为a=3米和b=4米,现要将此绿地扩充改造为等腰三角形,且扩充部分为含以b 为直角边的直角三角形,则扩充后等腰三角形的周长为____________米17.如图,ABC 是等边三角形,被一平行于BC 的矩形所截,AB 被截成三等分,则图中阴影部分的面积是ABC 的面积的______.18.如图,在Rt ABC ∆中,90ACB ∠=︒,//CD AB ,ABC ∠的平分线BD 交AC 于点E ,若10AB =,6BC =,则AE =_______.19.如图,在矩形ABCD 中,AB =2,BC =a ,点E 在边BC 上,且BE =35a .连接AE ,将△ABE沿AE折叠,若点B的对应点B′落在矩形ABCD的边上,则a的值为______.20.如果23a cb d==,其中20b d+≠,那么22a cb d+=+________.三、解答题21.如图,已知在矩形ABCD中,AD=2,AB=3,点E,F分别在边AB,BC上,且BF=FC,连接DE,EF,并以DE,EF为边作▱DEFG.(1)求▱DEFG对角线DF的长;(2)求▱DEFG周长的最小值;(3)当▱DEFG为矩形且AE﹥BE时,连接BG,分别交EF,CD于点P,Q,求BP:QG的值.22.如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C,D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:(1)①猜想如图1中线段BG .线段DE 的长度关系及所在直线的位置关系; ②将图1中的正方形CEFG 绕着点C 按顺时针(或逆时针)方向旋转任意角度α,得到如图2,如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断;(2)将原题中正方形改为矩形(如图4-6)且AB a ,BC b =,CE ka =,(),0CG kb a b k =≠>,第(1)题①中得到C 的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由;(3)在第(2)题图5中,连接DG 、BE ,且3a =,2b =,12k =,求22BE DG +的值.23.如图,在平面直角坐标系中,每个小正方形的边长都是1个单位长度,ABC 的顶点都在格点上.(1)以原点O 为位似中心,在第三象限内画出将ABC 放大为原来的2倍后的位似图形111A B C △.(2)已知ABC 的面积为72,则111A B C △的面积是_________. 24.下图是由边长为1的小正方形组成的5×4网格,A 、B 、C 、D 、E 、F 、P 、Q 均为网格格点,请用无刻度直尺作图,保留作图痕迹,不写画法.(1)在线段AB 上找到一点M ,使△AQM ≌△BPM.(2)在线段CD 上找点N ,使△ECN ∽△FDN.25.如图,在等边ABC ∆中,点D 是边AC 上一动点(不与点,A C 重合),连接BD ,作AH BD ⊥于点H ,将线段AH 绕点A 逆时针旋转60︒至线段AE ,连接CE(1)①补全图形;②判断线段BH 与线段CE 的数量关系,并证明;(2)已知4AB =,点M 在边AB 上,且1BM=,作直线HE . ①是否存在一个定点P ,使得对于任意的点D ,点P 总在直线HE 上,若存在,请指出点P 的位置,若不存在,请说明理由;②直接写出点M 到直线HE 的距离的最大值.26.△ABC 在边长为1的正方形网格中如图所示.(1)以点C 为位似中心,作出△ABC 的位似图形△A 1B 1C 1,使其位似比为1:2.且△A 1B 1C 1位于点C 的异侧,并表示出A 1的坐标.(2)作出△ABC 绕点C 顺时针旋转90°后的图形△A 2B 2C 2.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】利用相似三角形的判定定理,在AD ∥BC ,得∠DAC =∠BCA 的前提下,需添加一角或夹这角的两边对应成比例进行排查即可.【详解】解:A .∵AD ∥BC ,∴∠DAC =∠BCA ,当∠BAC =∠ADC 时,则△ABC ∽△DCA ;B .∵AD ∥BC ,∴∠DAC =∠BCA ,当∠B =∠ACD 时,则△ABC ∽△DCA ;C .∵AD ∥BC ,∴∠DAC =∠BCA ,由AC 2=AD •BC 变形为AC AD BC AC =,则△ABC ∽△DCA ; D .∵AD ∥BC ,∴∠DAC =∠BCA ,当DC AB AC BC=时,不能判断△ABC ∽△DCA . 故选择:D .【第讲】本题考查三角形相似问题,掌握相似三角形的判定定理,会根据判定定理进行添加条件使三角形相似解题关键. 2.A解析:A【分析】根据相似三角形的性质与判定即可求出答案.【详解】解:由题意可知:2BE CE ==,∵90AEF B C ∠=∠=∠=︒,∴BAE AEB AEB CEF ∠+∠=∠+∠,∴BAE CEF ∠=∠,∴AEB EFC ∆∆∽, ∴AB BE CE CF =, ∴422CF=, ∴1CF =,故选:A .【点睛】本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定,本题属于基础题型.3.D解析:D【分析】先根据平行线分线段成比例定理得出比例式,代入后得出AD=23AB ,代入求出即可. 【详解】解:∵DE ∥BC , ∴AD AE AB AC =, ∵AE=2CE , ∴2223AE CE AC EC EC ==+ 又AB=12, ∴AD=23AB=8, 故选:D .【点睛】 本题考查了平行线分线段成比例定理,能根据定理得出正确的比例式是解此题的关键. 4.C解析:C【分析】根据已知图形构造相似三角形,进而得出△ABD ∽△ACE ,即可求出AC 的长.【详解】解:如图所示:过点A 作平行线的垂线,交点分别为D ,E ,可得:△ABD ∽△ACE ,则AB AD AC AE =, 即628AC =, 解得:AC=24,故选:C .【点睛】此题主要考查了相似三角形的应用,根据题意得出△ABD ∽△ACE 是解题关键. 5.C解析:C【分析】根据相似多边形的判定定理对各个选项进行分析,从而确定最后答案.【详解】矩形的原图与外框不相似,因为其对应角的度数一定相同,但对应边的比值不一定相等,不符合相似的条件;锐角三角形的原图与外框相似,因为其对应角均相等,对应边均对应成比例,符合相似的条件;正五边形相似,因为它们的边长都对应成比例、对应角都相等,符合相似的条件;菱形的原图与外框相似,因为其对应角均相等,对应边均对应成比例,符合相似的条件. 综上,外框与原图一定相似的有3个,故选:C .【点睛】本题主要考查了相似图形的概念,注意边数相同、各角对应相等、各边对应成比例的两个多边形是相似多边形.6.B解析:B【分析】根据条件和判断Rt △CEB ≌Rt △AED ,然后得到角相等,证明△BEC ∽△BFA ,利用比例关系计算.【详解】解:∵AE=3,BE=4∴BA=BE-AE=1∴在Rt △CEB 与Rt △AED 中AE CE AD CB =⎧⎨=⎩∴Rt △CEB ≌Rt △AED∴∠EBC=∠BAF ∵∠ADE+∠EAD=90°,∠BAF=∠EAD∴∠EBC+∠BAF=90°∵∠BEC=∠BFA=90°∴△BEC ∽△BFA ∴AF BA CE BC =即135AF = ∴AF=0.6故选:B【点睛】 本题考查相似和全等的结合,通过全等得到角关系,然后证相似得到比例关系计算边长即可..7.D解析:D【分析】直接利用相似图形的判定方法分别判断得出答案.【详解】解:①两个菱形不一定相似,因为对应角不一定相等;②两个矩形不一定相似,因为对应边不一定成比例;③两个平行四边形不一定相似,因为形状不一定相同;④两个正方形相似,正确.故选:D .【点睛】本题考查了相似多边形的判定,正确掌握判定方法是解题的关键.8.C解析:C【分析】根据题意易得BO =EF 与x 的关系,进而分两种情况,依情况来判断函数图像即可.【详解】解:∵四边形ABCD 是正方形,边长为2,∴AC BD ==12BO OD BD ===①当P 在OB 上时,即0x ≤≤∵EF ∥AC ,∴△BEF ∽△BAC , ∴EF BP AC OB=, ∴22EF BP x ==, ∵OP x =,∴)2122y x x x =⨯⨯=-+;②当P 在OD x <≤∵EF ∥AC ,∴△DEF ∽△DAC , ∴EF DP AC OD =,=,∴)2EF x =,∵BP=x , ∴OP x =∴()()2122223242y x x x x =-⋅-=-+-, 这是一个二次函数,根据二次函数的性质可知:二次函数的图像是一条抛物线,开口向下,故选C .【点睛】本题主要考查相似三角形的性质与判定、二次函数的图像与性质及正方形的性质,关键是利用三角形相似和面积来列出二次函数的解析式,进而求解.9.B解析:B【分析】如图,证明△ABE ∽△ACD ,根据相似三角形的性质列式求解即可.【详解】解:如图,根据题意得,△ABE ∽△ACD ,∴AB BE AC CD= ∵AB=10m ,BE=1.6m ,CD=9.6m∴10 1.6=9.6AC ∴AC=60m ∴BC=AC-AB=60-10=50m故选:B .【点睛】此题主要考查了相似三角形的应用,善于观察题目的信息是解题以及学好数学的关键. 10.C解析:C【分析】把比例式化成乘积式求出ab 之间的关系即可.【详解】∵52a b a b +=- ∴2()5()a b a b +=-解得37a b =∴:7:3a b =故选C.【点睛】本题考查比例的性质,熟练利用比例的性质转换比例式和乘积式是解题的关键. 11.C解析:C【分析】若点P 是靠近点B 的黄金分割点,则12AP AB =,然后代入数据计算即可;若点P 是靠近点A 的黄金分割点,先求出BP ,再利用线段的和差即可求出AP .【详解】解:若P 是靠近点B 的黄金分割点,则)111222AP AB ==⨯=;若P 是靠近点A 的黄金分割点,则)12BP AB ===,∴121AP AB BP =-=-=;故选:C .【点睛】是解题的关键. 12.B解析:B【分析】根据平行四边形的性质知AD=2BE ,BC ∥AD ,BO=OD ,设BF=a ,得DF=a+2,由BC ∥AD 知△BEF ∽△DAF ,据此得=BF DF 12=BE DA ,得出BF 的长,从而得出BD 的长. 【详解】解:∵点E 是BC 中点,∴BC=2BE ,∵四边形ABCD 是平行四边形,∴BC=AD ,BC ∥AD ,BO=OD ,∴AD=2BE ,设BF=a ,∵OF=1,∴BO=DO=a+1,则DF=a+2,∵BC ∥AD∴△BEF ∽△DAF ,12∴==BF BE DF DA ∴1,22=+a a 解得a=2,经检验a=2是原方程的解∴BF=2,∴BO=DO=3,∴BD=6故选:B .【点睛】本题主要考查相似三角形的判定与性质,解题的关键是掌握平行四边形的性质和相似三角形的判定与性质.二、填空题13.22或8【分析】(1)运用中位线性质求解即可;(2)延长BQ 交射线EF 于M 根据三角形的中位线平行于第三边可得EF ∥BC 根据两直线平行内错角相等可得∠M=∠CBM 再根据角平分线的定义可得∠PBM=∠C解析:2 2或8【分析】(1)运用中位线性质求解即可;(2)延长BQ 交射线EF 于M ,根据三角形的中位线平行于第三边可得EF ∥BC ,根据两直线平行,内错角相等可得∠M=∠CBM ,再根据角平分线的定义可得∠PBM=∠CBM ,从而得到∠M=∠PBM ,根据等角对等边可得BP=PM ,求出EP+BP=EM ,再根据CQ=13CE 求出EQ=2CQ ,然后根据△MEQ 和△BCQ 相似,利用相似三角形对应边成比例列式求解即可.【详解】解:(1)∵E ,F 分别是AB ,AC 的中点 ∴1=2EF BC ∵BC=4∴EF=2;(2)如图,延长BQ 交射线EF 于M ,∵E 、F 分别是AB 、AC 的中点,∴EF ∥BC ,∴∠M=∠CBM ,∵BQ 是∠CBP 的平分线,∴∠PBM=∠CBM ,∴∠M=∠PBM ,∴BP=PM ,∴EP+BP=EP+PM=EM ,∵点Q 把线段EC 分成的两线段之比是1:2,∴CQ=13CE , ∴EQ=2CQ , 由EF ∥BC 得,△MEQ ∽△BCQ , ∴2EM EQ BC CQ==, ∴EM=2BC=2×4=8,即EP+BP=8,当CQ=2EQ 时,同法可得,EM=2,EP+PB=EM=2.故答案为:EP+BP=8或EP+PB=2.故答案为:2;8或2.【点睛】本题考查了三角形中位线定理、相似三角形的判定与性质,角平分线的定义,平行线的性质,延长BQ 构造出相似三角形,求出EP+BP=EM 并得到相似三角形是解题的关键,也是本题的难点.14.【分析】根据黄金比值为进行计算即可得到答案【详解】解:∵点C 为线段AB 的黄金分割点AB=6∴AC=×6=3-3BC=6-(3-3)=9-3AC-BC=3-3-(9-3)=6-12;故答案为:【点睛】 解析:512【分析】 根据黄金比值为512进行计算即可得到答案. 【详解】解:∵点C 为线段AB 的黄金分割点,AB=6,∴,BC=6-(),(;故答案为:12【点睛】本题考查的是黄金分割的知识和二次根式的计算,理解黄金分割的概念,找出黄金分割中成比例的对应线段是解决问题的关键.15.【分析】先根据相似三角形的判定与性质可得从而可得AE 的长再根据线段的和差即可得【详解】解得则故答案为:【点睛】本题考查了相似三角形的判定与性质熟练掌握相似三角形的判定与性质是解题关键 解析:163【分析】 先根据相似三角形的判定与性质可得AD AE AB AC =,从而可得AE 的长,再根据线段的和差即可得.【详解】//DE BC ,ADE ABC ∴,AD AE AB AC∴=, 9AB =,8AC =,3AD =,398AE ∴=, 解得83AE =, 则816833EC AC AE =-=-=, 故答案为:163. 【点睛】本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题关键. 16.16或10+2或【分析】分三种情形讨论即可①AB=BE1②AB=AE3③E2A=E2B 分别计算即可【详解】解:如图在Rt △ABC 中∵∠ACB=BC=3AC=4∴①当BA=BE1=5时CE1=2∴∴△解析:16或10+25或403【分析】 分三种情形讨论即可,①AB=BE 1,②AB=AE 3,③E 2A=E 2B ,分别计算即可.【详解】解:如图在Rt △ABC 中,∵∠ACB=90,BC=3,AC=4 ∴225AB BC AC =+=①当BA=BE 1=5时,CE 1=2, ∴221125AE AC CE =+=∴△ABE 1周长为(5②当AB=AE 3=5时,CE 3=BC=3,BE 3=6,∴△ABE 3周长为16米.③当E 2A=E 2B 时,作E 2H ⊥AB ,则BH=AH=2.5, ∵∠B=∠B ,∠ACB=∠BHE 2=90∘,∴△BAC ∽△BE 2H ,∴2BE BH BC AB= ∴BE 2=256, ∴△ABE 2周长为25402563⨯+=米. 综上所述扩充后等腰三角形的周长为16或5403米 故答案为:16或5403【点睛】本题考查等腰三角形的定义、勾股定理、相似三角形的性质与判定、三角形周长等知识,正确理解题意是解题的关键,运用了分类讨论的数学思想,注意漏解.17.【分析】根据题意易证△AEH ∽△AFG ∽△ABC 利用相似三角形的性质解决问题即可【详解】解:∵AB 被截成三等分∴△AEH ∽△AFG ∽△ABC ∴∴S △AFG :S △ABC=4:9S △AEH :S △ABC= 解析:13【分析】根据题意,易证△AEH ∽△AFG ∽△ABC ,利用相似三角形的性质解决问题即可.【详解】解:∵AB 被截成三等分,∴△AEH ∽△AFG ∽△ABC , ∴11,,23AE AE AF AB ==, ∴S △AFG :S △ABC =4:9,S △AEH :S △ABC =1:9, ∴S 阴影部分的面积=49S △ABC -19S △ABC =13S △ABC , ∴图中阴影部分的面积是ABC 的面积的13. 故答案为:13. 【点睛】 本题主要考查了利用三等分点求得各相似三角形的相似比,从而求出面积比计算阴影部分的面积,难度适中.18.5【分析】首先由勾股定理求出AC 再证明得到进而列方程求解即可【详解】解析:5【分析】首先由勾股定理求出AC ,再证明~ABE CDE ∆∆,得到AB AE CD CE=,进而列方程求解即可.【详解】 90ACB ∠=︒,10AB =,6BC =,8AC ∴==,∴设AE x =,则8CE x =-, BD 平分ABC ∠,ABD DBC ∴∠=∠,又//AB CD ,ABD BDC ∴∠=∠,DBC BDC ∴∠=∠,6BC CD ∴==,//AB CD ,∴~ABE CDE ∆∆, AB AE CD CE ∴= 1068x x∴=- 解得5x =,5AE ∴=故答案为:5. 【点睛】此题主要考查了相似三角形和判定与性质,熟练掌握并能灵活运用相似三角形和判定与性质定理是解答此题的关键.19.或【分析】分两种情况:①点落在AD 边上根据矩形与折叠的性质易得即可求出a 的值;②点落在CD 边上证明根据相似三角形对应边成比例即可求出a 的值【详解】解:分两种情况:①当点落在AD 边上时如图1四边形AB 解析:103或25. 【分析】分两种情况:①点'B 落在AD 边上,根据矩形与折叠的性质易得=AB BE ,即可求出a 的值;②点'B 落在CD 边上,证明''ADB B CE ∆∆,根据相似三角形对应边成比例即可求出a 的值.【详解】解:分两种情况:①当点B '落在AD 边上时,如图1.四边形ABCD 是矩形,90BAD B ∴∠=∠=︒,将ABE ∆沿AE 折叠,点B 的对应点B '落在AD 边上,'1452BAE B AE BAD∴∠=∠=∠=︒,AB BE∴=,325a∴=,103a∴=;②当点'B落在CD边上时,如图2.∵四边形ABCD是矩形,90BAD B C D∴∠=∠=∠=∠=︒,AD BC a==.将ABE∆沿AE折叠,点B的对应点'B落在CD边上,'90B AB E∴∠=∠=︒,'2AB AB==,'35BE B E a==,2224DB B A AD a''∴-=-3255EC BC BE a a a=-=-=.在ADB'∆与B CE'∆中,9090B AD EBC AB DD C∠=∠=︒-∠''⎧⎨∠=∠=︒'⎩,''ADB B CE∴∆∆,'''DB ABCE B E∴=242355aa a-=,解得153a=,253a=-(舍去).综上,所求a的值为10325.故答案为10325【点睛】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质,勾股定理,相似三角形的判定与性质.进行分类讨论与数形结合是解题的关键.20.【分析】根据已知条件得出再根据b+2d≠0即可得出答案【详解】解:∵∴∵b+2d≠0∴;故答案为:【点睛】本题考查了比例的性质熟练掌握比例的性质是解题的关键 解析:23 【分析】 根据已知条件得出2223a c b d ==,再根据b+2d≠0,即可得出答案. 【详解】解:∵23a c b d ==, ∴2223a cb d ==, ∵b+2d≠0,∴2223a cb d +=+; 故答案为:23. 【点睛】 本题考查了比例的性质,熟练掌握比例的性质是解题的关键.三、解答题21.(1)10(2)62 (3)35. 【分析】(1)▱DEFG 对角线DF 的长就是Rt △DCF 的斜边的长,由勾股定理求解;(2)▱DEFG 周长的最小值就是求邻边2(DE+EF )最小值,DE+EF 的最小值就是以AB 为对称轴,作点F 的对称点M ,连接DM 交AB 于点N ,点E 与N 点重合时即DE+EF=DM 时有最小值,在Rt △DMC 中由勾股定理求DM 的长;(3)用等腰直角三角形判定与性质,三角形相似的判定与性质和勾股定理求解.【详解】解:(1)如图1所示:连接DF ,∵四边形ABCD 是矩形,∠C=90°,AD=BC ,AB=DC ,BF=FC ,AD=2,∴FC=1,∵AB=3;∴DC=3,在Rt △DCF 中,由勾股定理得DF=22221310FC DC +=+=,故▱DEFG 对角线DF 的长10.(2)如图2所示:作点F 关直线AB 的对称点M ,连接DM 交AB 于点N ,连接NF ,ME ,点E 在AB 上是一个动点,①当点E 不与点N 重合时点M 、E 、D 可构成一个三角形,∴ME+DE >MD ,②当点E 与点N 重合时点M 、E (N )、D 在同一条直线上,∴ME+DE=MD ,由①和②DE+EF 的值最小时就是点E 与点N 重合时,∵MB=BF ,∴MB=1,∴MC=3,又∵DC=3,∴△MCD 是等腰直角三角形,∴MD=22223332MC DC +=+=,∴NF+DN=MD=32,∴262DEFG C NF DF =+=();(3)设AE=x ,则BE=3-x ,∵▱DEFG 为矩形,∴∠DEF=90°,∴∠AED+∠BEF=90°,∵∠BEF+∠BFE=90°,∴∠AED=∠BFE ,又∵∠A=∠EBF=90°,∴△DAE ∽△EBF (AA )∴AE AD BF BE =, ∴213x x=-,解得:x=1(舍去),或x=2,即AE=2,BE=1, 过点G 作GH ⊥DC ,如图3所示:∵▱DEFG 为矩形,∴∠A=∠EBF=90°,∵AD=AE=2,BE=BF=1,∴在Rt △ADE 和Rt △EFB 中,由勾股定理得:==,==,∴∠ADE=45°,又∵四边形DEFG 是矩形,∴EF=DG ,∠EDG=90°,∴,∠HDG=45°,∴△DHG 是等腰直角三角形,∴DH=HG=1,在△HGQ 和△BCQ 中有GHQ BCQ HQG CQB ∠∠⎧⎨∠∠⎩==, ∴△HGQ ∽△BCQ (AA ),∴12HG HQ CB CQ ==, ∵HC=HQ+CQ=DC-DH=2,∴HQ=23, 又∵DQ=DH+HQ ,∴DQ=25133+=, ∵AB ∥DC ,EF ∥DG ,∴∠EBP=∠DQG ,∠EPB=∠DGQ ,∴△EBP ∽△DQG (AA ), ∴35BP EB QG DQ ==. 【点睛】本题考查了矩形的性质,轴对称的性质,相似三角形的判定与性质,等腰三角形的判定与性质;重点掌握相似三角形的判定与性质,难点是作辅助线.22.(1)①BG DE =,BG DE ⊥.②BG DE =,BG DE ⊥仍然成立.详见解析;(2)BG DE ⊥成立,BG DE =不成立,详见解析;(3)654. 【分析】(1)①利用正方形的性质,证明BCG DCE ≌△△,利用全等三角形的性质可得:BG=DE ,∠CBG=∠CDE ,再证明:∠EDC+∠DGO=90°,从而可得结论;②同①,先证明:BCG DCE ≌△△,利用全等三角形的性质可得:BG DE =,CBG CDE ∠=∠,再证明:90CDE DHO ∠+∠=︒,从而可得结论;(2)利用矩形的性质,证明BCG DCE △∽△,可得:CBG CDE ∠=∠,再证明90CDE DHO ∠+∠=︒,从而可得结论;(3)连接,,BD GE 利用BG DE ⊥,结合勾股定理证明:2222BE DG BD GE +=+,再把3a =,2b =,12k =代入,即可得到答案. 【详解】解:(1)①BG DE =,BG DE ⊥.理由如下:如图1,延长BG 交DE 于O ,∵四边形ABCD 、CGFE 是正方形,∴BC=CD=AB ,CG=CE ,∠BCD=∠ECD=90°,∵在BCG 和DCE 中BC CD BCG DCE CG CE =⎧⎪∠=∠⎨⎪=⎩,∴BCG DCE ≌△△,∴BG=DE ,∠CBG=∠CDE ,∵∠CBG+∠BGC=90°,又∵∠DGO=∠BGC ,∴∠EDC+∠DGO=90°,∴∠DOG=1809090︒-︒=︒,∴BG ⊥DE ,即BG=DE ,BG ⊥DE ;②BG DE =,BG DE ⊥仍然成立.如图2,∵四边形ABCD 、四边形CEFG 都是正方形,∴BC CD =,CG CE =,90BCD ECG ∠=∠=︒,∴BCG DCE ∠=∠,∵在BCG 与DCE 中,,BC CD BCG DCE CG CE =⎧⎪∠=∠⎨⎪=⎩∴BCG DCE ≌△△,∴BG DE =,CBG CDE ∠=∠,又∵BHC DHO ∠=∠,90CBG BHC ∠+∠=︒,∴90CDE DHO ∠+∠=︒,∴90DOH ∠=︒,∴BG DE ⊥.(2)BG DE ⊥成立,BG DE =不成立.如图5,∵四边形ABCD 、四边形CEFG 都是矩形,且AB CD a ==,BC b =,CG kb =,(),0CE ka a b k =≠>, ∴BC CG b DC CE a==,90BCD ECG ∠=∠=︒, ∴BCG DCE ∠=∠, ∴BCG DCE △∽△,∴CBG CDE ∠=∠,又∵BHC DHO ∠=∠,90CBG BHC ∠+∠=︒,∴90CDE DHO ∠+∠=︒,∴90DOH ∠=︒,∴BG DE ⊥.显然:.BG DE ≠(3)如图5,连接,,BD GE∵BG DE ⊥,∴222OB OD BD +=,222OE OG GE +=,222OB OE BE +=,222OG OD DG += ∴22222222BE DG OB OE OG OD BD GE +=+++=+,又∵3a =,2b =,12k =,CE ka =,CG kb =, 2222222211323321222BD GE ⎛⎫⎛⎫⎛⎫∴=+=⨯+⨯=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,, ∴22222236523124BD GE ⎛⎫+=+++= ⎪⎝⎭,∴22654BE DG +=. 【点睛】 本题考查的是勾股定理的应用,正方形,矩形的性质,三角形全等的判定与性质,三角形相似的判定与性质,掌握以上知识是解题的关键.23.(1)画图见解析;(2)14【分析】(1)给A 、B 、C 三点坐标乘以-2,得到A 1、B 1、C 1的坐标,再描点连接即得到111A B C △;(2)给ABC 的面积乘以4即得111A B C △的面积.【详解】(1)如图,111A B C △为所作.(2)ABC 的面积为72,位似比为2:1, ∴111A B C △的面积是272142⨯=. 故答案为:14.【点睛】 此题考查位似图形和坐标变换.当位似中心为坐标原点时,位似图形的对应点之坐标比(即横坐标与横坐标之比,纵坐标与纵坐标之比)的绝对值等于位似比.当比值为负时,图形分居原点两侧;当比值为正时,图形在原点一侧.24.(1)见解析(2)见解析【分析】(1)连接PQ,AB 交点即为所求;(2)找到F 点关于CD 的对称点F’,连接CD,EF’,交点即为所求.【详解】(1)如图,M 点为所求;(2)如图,N 点为所求.【点睛】此题主要考查网格中作图,解题的关键是熟知熟知网格的特点、对称性、全等三角形与相似三角形的判定方法.25.(1)①见解析;②BH CE =,证明见解析;(2)①存在,点P 是边BC 的中点;②3【分析】(1)①按要求画出图形即可;②根据全等三角形对应边相等来回答;(2)①点P 为直线HE 与BC 的交点;②通过△BPM ∽△BAP 问题可解;【详解】(1)①如图;②BH CE =证明ABH ACE ∆≅∆即可(2)①存在点P 是边BC 的中点,理由:设直线HE 与边BC 交于点P可由60ACB AEP ︒∠=∠=得点,,,A E C P 共圆, 因为90AEC ︒∠=,所以90APC ︒∠=,即P 是BC 的中点.②如图, 当MP ⊥HE 时,MP 最大,理由:4,2,1AB BP BM ===,BM BP BP AB ∴=, B B ∠∠=,∴△BPM ∽△BAP ,∴∠BMP=∠BPA=90︒ ,2222213BP BP BP ∴=-=-=【点睛】本题考查等腰三角形的性质,全等三角形的判定和性质,点到直线的距离,旋转,相似三角形的判定和性质,勾股定理和圆的有关知识知识,综合性较强.26.(1)图见解析;(3,﹣3);(2)图见解析.【分析】(1)首先找到A 、B 、C 点对应点A 1、B 1、C 1,然后连接即可;(2)利用网格特点和旋转的性质画出A 、B 的对应点A 2、B 2即可【详解】解:(1)如图,△A 1B 1C 1所作,点A 1的坐标为(3,﹣3);(2)如图,△A 2B 2C 2为所作.【点睛】本题考查了作图-位似变换:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.也考查了旋转变换.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二单元错题
一、单选题
1、Why did you leave the room with the door ?
A、opening
B、opened
C、to be opening
D、open
2、Don’t you remember me ?
A、Yes, I don’t
B、Yes. I do
C、No. I do
D、No. I don’t
3、Linda has bought a large house a swimming pool.
A、with
B、in
C、on
D、from
4、Not only you but also he the secret.
A、knows
B、is know
C、know
D、isn’t know
5、There great changes in our hometown in the past twenty years.
A、are
B、were
C、has been
D、have been
6、She is very and has never played jokes with others.
A、outgoing
B、serious
C、careful
D、quiet
7、He used to watch TV or computer games at home on weekends.
A、to play
B、playing
C、play
D、played
8、The man left his home a terrible rainy night. A、in B、at C、for D、on
9、The little boy has got used to up early. A、get B、getting C、got D、gets
10、She is so busy that she has time to see her parents
A、often
B、always
C、even
D、hardly
11、Must I stop smoking ? For your health , I’m afraid you
A、can
B、have to
C、need
D、should
12、The speech contest is coming . I feel really nervous. Be brave! There is nothing
A、to do
B、to talk aboput
C、to work on
D、to be afraid of
13、Don’t you like history? .It’s difficult and boring.
A、Yes, I do
B、No, I don’t
C、Yes, I don’t
D、No, I do
14、The terrible traffic accident caused a lot of A、die B、died C、dead D、deaths
15、Tom did’t use to have long hair ,did he ? . But now hia hair is long
A、Yes, he didn’t
B、No, he did
C、Yes, he did
D、No,he didn’t
16、I didn’t answer the telephone because I a shower at that moment.
A、have taken
B、will take
C、was taking
D、am taking
17、He works very hard present. However , he used to pay no attention his lessons.
A、at ; to
B、to ;to
C、to ; at
D、at ; at
18、He used to in the morning ,but now he is used to at night
A、reading ; read
B、read ; read
C、reading ; reading
D、read ;reading
19、Please turn off the light. OK, Mom. I won’t leave the room the light
A、when ; on
B、with ; on
C、with ; off
D、when ;off
20、Do you always spend lots of time playing computer games?
No, but I spend much time my homework
A、In; on
B、on; on
C、on ; in
D、in; in
22、He is terrified of alone in the street at night.
A、to walk
B、having walk
C、walking
D、walked
23、I used to in the morning ,but now I’m used to before going to bed.
A、reading ; read
B、read ; read
C、reading ; reading
D、read ;reading
24、I like taking lots of notes in class and go over them after class.
But first of all, you should pay attention to the teacher in class
A、hear
B、hearing
C、listen to
D、listening to
二、根据要求完成句子
1、Let us have a break , ?(完成反意疑问句)
2、It seems that he has changed a lot.(改为同义句) He changed a lot.
3、She has to buy a computer. (改为一般疑问句) she to buy a computer.
4、This kind of machine (被用来) make clothes
5、There used to be a lot of trees here. ( 改为否定句) There be many trees.
6、He used to sleep the windows (开着窗户)
7、She used to live in Beijing Hutong (完成反意疑问句)
She used to live in Beijing Hutong ,
8、I show great interest in his speech. (改为同义句) I his speech.
9、He went to the supermarket alone. (改为同义句) He went to the supermarket
10、你还害怕在公众面前说话吗?
You still speaking a group?
11、We can speak better than before. (改为同义句) We speak better than before
12、It seems that they have known each other. (改为同义句)
They have known each other
13、The old man used to be a soldier.(改为同义句) The old man was a soldier in the
14、他的情绪终于平静下来了。
(in the end)
15、不但是我,他昨天也迟到了。
(as well as)
16、The students don’t have much time to play with their friends , (完成反意疑问句)
三、用所给词语的适当形式填空
1、Most children like to eat (candy)
2、He (be afraid of) failing in the math tese.
3、She has made a final (decide) to be a teacher in the western part of China.
4、I’m still afraid to (speak) in front of a group.
5、You don’t have enough (pride) of the Great Wall
6、He has given away the secret (descide) to other。
