缓和曲线、圆曲线测设计算例题
圆曲线和缓和曲线坐标推算公式附带例题

圆曲线和缓和曲线坐标推算公式一、直线上的坐标推算式中:Xm 、Ym ——直线段起点M 坐标Li ——直线段上任意点i 到线路起点M 的距离 a 0——直线段起点M 到JD1的方位角 二、圆曲线上任一点的坐标推算①、圆曲线上任一点i 相对应的圆心角:i i L R180πϕ︒=式中:Li ——圆曲线上任一点i 离开ZY 或YZ 点的弧长②、圆曲线上任一点i 的直角坐标:⎩⎨⎧-)(==i iii cos 1R Y Rsin X ϕϕ(可不计算).③、圆曲线ZY 或YZ 点到任一点i 的偏角:i ii L R902πϕ︒∆==④、圆曲线ZY 或YZ 点到任一点i 的弦长:)sin(2)2sin(2C i i iR R ∆=ϕ=⑤、圆曲线ZY 或YZ 点到任一点i 的弦长的方位角:i jd y z jd zy i a a ∆±→→或=⑥、所以圆曲线上任意点i 的坐标为:⎩⎨⎧++i i YZ ZY iii YZ ZY i sina C Y Y cosa C X X 或或==例题:已知一段圆曲线,R=3500m ,Ls =,交点里程K50+,ZY 点到JD 方向方位角为A=129°23′″,右偏9°3′″,ZY 点里程K49+,YZ 点里程K50+,起点坐标为x =,y =,求K50+200处中点坐标及左右各偏的坐标。
解:K50+200处的曲线长度为Li =K50+200相对应的方位角:"'︒⨯⨯︒︒52.39165393.3223500180L R 180i===ππa K50+200相对应的偏角:"'︒⨯⨯︒︒∆76.19382393.322350090L R 902i ii ====ππϕK50+200到zy 点的弦长:m 279.32276.19382sin 35002Rsin 2C i i ==="'︒⨯⨯∆ zy 点到K50+200中桩的方位角: K50+200左、右偏的方位角: 所以K50+200处的坐标为: K50+200左偏的坐标为: K50+200右偏的坐标为:三、缓和曲线上任一点的坐标推算切线角:πβ︒⨯1802RL L s 2i i = 缓和曲线上任意点i 的偏角:πβδ︒⨯180RL 6L 3s 2i ii ==缓和曲线ZH 或HZ 点到任意点i 的方位角为:i jd HZ jd ZH a a i δ±→→或=缓和曲线上任意点i 的坐标为:⎪⎪⎩⎪⎪⎨⎧-s 3ii 2s 25i i i 6RL L y L 40R L L x == 缓和曲线ZH 或HZ 点到任意点i 的弦长:22i y x C +=所以缓和曲线上任意点i 的坐标为:⎩⎨⎧++i i HZ ZH iii HZ ZH i sina C Y Y cosa C X X 或或==例题:已知一段缓和曲线,ZH 点到JD 方向方位角为A=183°17′″,线路左偏43°31′02″,ZH 点里程为K52+,ZH 点坐标x =,y =,R =960m ,Ls =120m ,求K52+100处的中点坐标及左右各偏的坐标。
缓和曲线的计算方法三种课件

b0
20
ls 3R
此外还有极坐标法、弦线支距法、长弦偏角 法。
缓和曲线的计算方法三种
要注意:点是位于缓和曲线上,还是位于圆曲线上。
位于缓和曲线
位于圆曲线
缓和曲线的计算方法三种
(1)当点位于缓和曲线上,有:
x y
l l5
40
R
2
l
2 s
l3 l7 6 Rl s 336 R
3l
3 s
(2)当点位于圆曲线上,有:
xRsinq yR(1c os)p
缓和曲线的计算方法三种
2、偏角法(整桩距、短弦偏角法) 要注意:点是位于缓和曲线,还是位于圆曲线。
位于圆曲线 位于缓和曲线
缓和曲线的计算方法三种
2、偏角法(整桩距、短弦偏角法)
(1)当点位于缓和曲线上,有:
总偏(常 角量 )0 6lR s
偏角
l2 ls2
0
距离:用曲线长l来代替弦长。放样出第1点后, 放样第2点时,用偏角和距离l交会得到。
缓和曲线的计算方法三种
(2)当点位于圆曲线上
方法:架仪HY (或YH),后视ZH(或HZ),拨角b0,即找 到了切线方向,再按单圆曲线偏角法进行。
缓和曲线的计算方法三种
(2)测设方法。(见例题)
例题:如图,设某公路的交点桩号为K0+518.66,右 转角αy=180018'36",圆曲线半径R=100m,缓和曲 线长ls=10m,试测设主点桩。(作为实习课内容)
解:(一)计算测设元素
p=0.04m;q=5.00m;
02lR s 1800205153
缓和曲线的计算方法三种
2、回旋缓和曲线(spiral curve)基本公式
带有缓和曲线圆曲线逐桩坐标计算例题
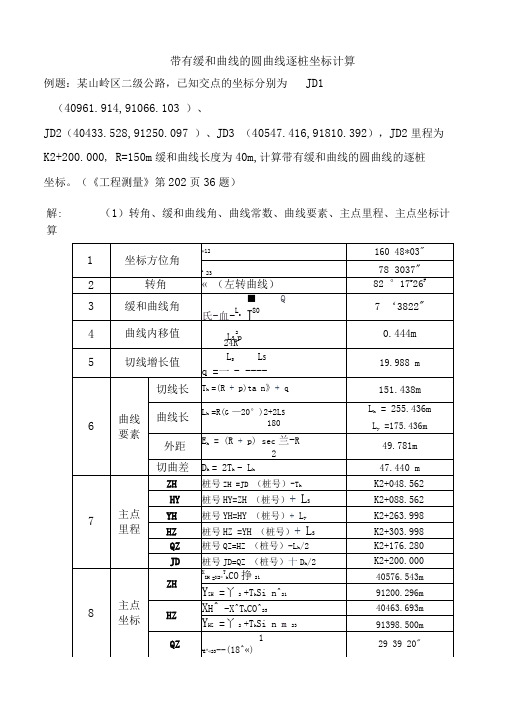
带有缓和曲线的圆曲线逐桩坐标计算
例题:某山岭区二级公路,已知交点的坐标分别为 JD1
(40961.914,91066.103 )、
JD2(40433.528,91250.097 )、JD3 (40547.416,91810.392),JD2里程为 K2+200.000, R=150m 缓和曲线长度为40m,计算带有缓和曲线的圆曲线的逐桩
坐标。
(《工程测量》第202页36题) (1)转角、缓和曲线角、曲线常数、曲线要素、主点里程、主点坐标计
解: 算
方法一:偏角法(坐标正算)(2)第一缓和段坐标计算% =73822 :12 = 160 48 03
K2+088.562
(4)第二缓和段坐标计算.0 = 7 38 22
方法二:切线支距法(坐标系转换)
(2)第一缓和段坐标计算
:-12 =160 48 03
X i 二X ZH• xcos〉12 ysi n〉12Y 二Y ZH xsi n〉12 - ycos〉12(本题为左转曲线)
(3)圆曲线段坐标计算
:o =7 3822 p=0.444mq=19.988m
12 =160 48 03 ZH(40576.543,91200.296
X i = X ZH xcos:12 ysin :12Y =Y ZH xsin:12-ycos:12
(4)第二缓和段坐标计算
F =78 30 37
X i =X HZ—xcos:23 - ysi n〉23 Y =Y HZ - xs in 乜—ycos:23 (本题为左转曲线)。
两圆曲线之间的缓和曲线的点位计算及测设方法

x′i co sΒ0 sinΒ0 y′i = - sinΒ0 co sΒ0
xi- x0 yi- y0
3 测设方法
311 以 (YH ) 为测站点
(1) 以 (YH ) 作为测站点, 必须要标定出后视方向, 连接A、(YH ) 两点其连线与 y′方向的夹角为 Α, 若
圆弧 A~ (YH ) 的长为 l1, 则 Α= 90°-
© 1995-2004 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved.
坐标系 x- (ZH ) - y, 则 (YH ) 点在 x- (ZH ) - y 坐标下的坐标
x0= l0-
l30
40R
2 1
y0=
l20 6R 1
将 x′方向与 x 方向的夹角记为 Β0, 将 (ZH ) 点与 (YH ) 点相连, 其连线方向与 x 方向的夹角为 ∆o, 如
图 1 所示。
根据缓和曲线的特性:
缓和曲线是工程测量中较常见的一种, 本文不做介绍。而对两圆曲线间增设缓和曲线的点位坐标参数方
程进行了推算并提出了几种测设点位方法, 供同行们参考。
2 公式推导
图 1A~ B 是线路的一段曲线, A~ (YH ) 是半径为 R 1 的圆曲线, (H Y)~ B 是半径为 R 2 的圆曲线, 从 (YH )~ (H Y) 是一段缓和曲线半径从 R 1 变化到 R 2, 其长度为 l12 (缓和曲线也称为 l12) , 则缓和曲线的 半径变化率 C 可以这样表示
则 Β0=
l0 2R
1
·
18Π0°, ∆0
=
1 3
Β0=
l0 6R
1
关于公路测量中圆曲线、缓和曲线(完整缓和曲线和非完整缓和曲线)的计算示例

关于公路测量圆曲线、缓和曲线(完整缓和曲线和非完整缓和曲线)的计算示例新浪微博:爱疯记录仪例:某道路桥梁中,A匝道线路。
已知交点桩号及坐标:SP,K9+000(2957714.490,485768.924);JD1,K9+154.745(2957811.298,485889.647);EP,K9+408.993(2957786.391,486158.713)。
SP—JD1方位角:51°16′25″;转角:右44°00′54.06″;JD1—EP方位角:95°17′20″。
由图纸上“A匝道直线、曲线及转角表”得知:K9+000—K9+116.282处于第一段圆曲线上,半径为385.75m;K9+116.282—K9+151.282处于第一段缓和曲线上,K9+151.282的半径为300m,缓和曲线要素A1=217.335,Ls1=35m;K9+151.282—K9+216.134处于第二段圆曲线上,半径为300m;K9+216.134—K9+251.134处于第二段缓和曲线上,K9+251.134的半径为1979.5,缓和曲线要素A2=111.245,Ls2=35m;K9+251.134—K9+408.933处于第三段圆曲线上,半径为1979.5m。
求:K9+130、K9+200、K9+230、K9+300的中桩坐标,切线方位角,左5米边桩的坐标,右10米边桩的坐标。
解:首先,我们知道要求一个未知点的坐标,必须知道起算点坐标,起算点至未知点的方位角,起算点至未知点的直线距离,然后利用坐标正算的计算公式,就可以直接求出未知点的坐标。
那么,关于圆曲线和缓和曲线(包括完整缓和曲线和非完整缓和曲线)的计算,我们需要知道如何求出起算点至圆曲线或缓和曲线上某点的方位角和直线距离。
下面,先列出关于圆曲线和缓和曲线中角度和距离计算的相关公式。
附:A匝道直线、曲线及转角表。
】下载地址:/view/f0677e38cdbff121dd36a32d7375a417866fc18f1 / 102 / 10y 轴。
缓和曲线计算题集(第二篇)

缓和曲线计算题集2一、已知某道路曲线第一切线上控制点ZD1和JD1,ZD1坐标为:(3162630.051,39389768.043),JD1坐标为(3162606.831,39390001.897)该曲线设计半径R=1000m,缓和曲线长L0=100m,JD1里程为DK0+275.004,转向角α左=23°03′38″。
请计算道路曲线主点ZH、HY、QZ点坐标,及第一缓和曲线和圆曲线上中桩点K0+100、K0+180的坐标,共计算5个点。
解:转角:23 03 38 方位角:275 40 14曲线五大桩里程和坐标一、直缓桩号ZH=00+020.9205 ,坐标X=3162581.7254 , 坐标Y=39390254.7371二、缓圆桩号HY=00+120.9205 ,坐标X=3162593.262 , 坐标Y=39390155.416 ,三、曲中桩号QZ=00+272.1618 ,坐标X=3162626.9124 , 坐标Y=39390008.1136 ,四、圆缓桩号YH=00+423.4031 ,坐标X=3162682.3721 , 坐标Y=39389867.5625 ,五、缓直桩号HZ=00+523.4031 ,坐标X=3162728.9689 , 坐标Y=39389779.0949 ,曲线要素表切线长T1=254.0835 切线角βo1=2.8648外失距E=21.0217 内移量p1=0.4166 曲线长L=502.4826 切垂距q1=49.9958 切曲差Dh=5.6844里程坐标X 坐标YK1+100 3162590.3585 39390176.1337K1+180 3162603.7508 39390097.2838二、某平原区二级公路上,有一弯道R=250m,缓和曲线L=80m,交点桩号为JD=K17+568.38,偏角α=38°30′00″。
求S曲线要素和桩点里程。
圆曲线及缓及曲线坐标推算公式附带例题
圆曲线和缓和曲线坐标计算公式一、直线上的坐标计算X i=X m L i cosa0Y i=Y m L i sina0式中: Xm、Ym——直线段起点M 坐标Li——直线段上任意点i 到线路起点 M 的距离a0——直线段起点M 到 JD1 的方向角二、圆曲线上任一点的坐标计算①、圆曲线上任一点i 相对应的圆心角:i=180L iR式中: Li——圆曲线上任一点 i 走开 ZY或 YZ点的弧长②、圆曲线上任一点i 的直角坐标:X i=Rsin i(可不计算) . Y i=R(1 cos i)③、圆曲线 ZY 或 YZ 点到任一点 i 的偏角: i = i=90L i2R④、圆曲线 ZY 或 YZ 点到任一点 i 的弦长: C i =2Rsin( i ) 2R sin( i )2 ⑤、圆曲线 ZY 或 YZ 点到任一点 i 的弦长的方向角: a i = a zy jd 或 y z jdiX i =X ZY 或 YZ C i cosa i⑥、所以圆曲线上任意点 i 的坐标为:C i sina iY i=YZY 或YZ例题:已知一段圆曲线 ,R=3500m ,Ls =553.1m ,交点里程 K50+154.734, ZY 点到 JD 方向方向角为 A=129° 23′ 18.3″,右偏 9° 3′ 15.8″, ZY 点里程K49+877.607, YZ 点里程 K50+430.707,起点坐标为 x =389823.196, y =507787.251,求 K50+200 处中点坐标及左右各偏 12.5m 的坐标。
解: K50+200 处的曲线长度为 Li = 322.393mK50+200 相对应的方向角: a =180L i = 180322.393=5 16 39.52R3500 K50+200 相对应的偏角:i =i = 90L i =90 322.393=2 38 19.762 R3500K50+200 到 zy 点的弦长: C i =2Rsin i =2 3500 sin2 38 19.76 =322.279m zy 点到 K50+200 中桩的方向角: a i = a zyjdi =129 23 18 .3 2 38 19 .76 =132 1 38 .06K50+200 左、右偏 12.5m 的方向角:a 左= A i a90 =134 39 57.82 90 =44 39 57.82 a 右=A i a90 =134 39 57.82 90 =134 39 57.82所以 K50+200 处的坐标为:X i =X ZY C i cosa i =389823.196 322.279 cos132 1 38.06 =389607.4354 Y i =Y ZY C i sina i =507787.251 322.279 sin132 1 38.06 =508026.6484K50+200 左偏 12.5m 的坐标为:X 左=X i=12.5 cos44 39 57.82=12.5cosa左389607.4354 389616.3256 =Y i=12.5=Y左12.5sina左508026.6484 sin44 39 57.82 508035.4656 K50+200 右偏 12.5m 的坐标为:X 右=X i=389607.4354 12.5 cos134 39 57.82=389598.648212.5cosa右=Y i=12.5=Y右12.5sina右508026.6484 sin134 39 57.82 508035.5386 三、缓和曲线上任一点的坐标计算2切线角:i=Li180缓和曲线上任意点i 的偏角:i =i=L2i 1803 6RL s缓和曲线 ZH 或 HZ 点到任意点i 的方向角为: a i=a ZH jd或 HZ jd ix i=L iL5i 40R2 L2s缓和曲线上任意点 i 的坐标为: 3y i=L i6RL s缓和曲线 ZH 或 HZ 点到任意点 i 的弦长:C i=x2 y2所以缓和曲线上任意点 i 的坐标为:X i=X ZH或HZ C i cosa i Yi=YZH或 HZ C i sina i例题:已知一段缓和曲线, ZH 点到 JD 方向方向角为 A=183°17′08.9″,线路左偏 43° 31′02″,ZH 点里程为 K52+001.615,ZH 点坐标 x =388071.927,y= 508789.089, R =960m ,Ls =120m ,求 K52+100 处的中点坐标及左右各偏 12.5m 的坐标。
测量道路圆缓曲线

测量道路圆缓曲线道路工程测量(圆曲线缓和曲线计算公式)一、主点(major point) 的测设1、曲线要素的计算若已知:转角α及半径R ,则:切线长:;曲线长:外距:;切曲差:2、主点的测设(1)主点里程的计算ZY 里程=JD 里程-T ;YZ 里程=ZY 里程+LQZ 里程=YZ 里程-L/2 ;JD 里程=QZ 里程+D/2 (用于校核)(2)测设步骤:1)JDi 架仪,照准JDi-1 ,量取T ,得ZY 点;照准JDi+1 ,量取T ,得YZ 点。
2)在分角线方向量取 E ,得QZ 点。
二、单圆曲线详细测设有整桩号法和整桩距法。
一般采用整桩号法。
1、切线支距法(tangent off-set method)(1) 以ZY 或YZ 为坐标原点,切线为X 轴,过原点的半径为Y 轴,建立坐标系。
(2) 计算出各桩点坐标后,再用方向架、钢尺去丈量。
特点:测点误差不积累;宜以QZ 为界,将曲线分两部分进行测设。
[ 例题] 设某单圆曲线偏角α=34°12′00″,R=200m ,主点桩号为ZY :K4+906.90 ,QZ :K4+966.59 ,YZ :K5+026.28 ,按每20m 一个桩号的整桩号法,计算各桩的切线支距法坐标。
(一)主点测设元素计算=61.53m ;=119.38m ;=9.25m ;=3.68m 。
(二)主点里程计算ZY=K4+906.90 ;QZ=K4+966.59 ;YZ=K5+026.28 ;JD= K4+968.43 (检查)(三)切线支距法(整桩号)各桩要素的计算表曲线桩号ZY(YZ )至桩圆心角φi 切线支距法坐标(m) 的曲线长(m) 小数度( °) X i (m) Yi (m) ZY K4+906.904906.9 0 0 0 0 K4+920 4920 13.1 3.752873558 13.090635 0.428871637 K4+940 4940 33.1 9.4 82451509 32.949104 2.732778823 K4+960 4960 53.1 15.21202946 52.478356 7.007714876 QZ K4+96 6.59 ———————————————————————K4+980 4980 46.28 13.25824338 45.868087 5.330745523 K5+000 5000 26.28 7.528665428 26.204441.724113151 K5+020 5020 6.28 1.799087477 6.2789681 0.098587899 YZ K5+026.28 5026.28 0 00 0 注:表中曲线长。
圆曲线和缓和曲线坐标推算公式(附带例题)
圆曲线和缓和曲线坐标推算公式一、直线上的坐标推算⎩⎨⎧++0i m i0i m i sina L Y Y cosa L X X == 式中:Xm 、Ym ——直线段起点M 坐标Li ——直线段上任意点i 到线路起点M 的距离 a 0——直线段起点M 到JD1的方位角 二、圆曲线上任一点的坐标推算①、圆曲线上任一点i 相对应的圆心角:i i L R180πϕ︒=式中:Li ——圆曲线上任一点i 离开ZY 或YZ 点的弧长②、圆曲线上任一点i 的直角坐标:⎩⎨⎧-)(==i iii cos 1R Y Rsin X ϕϕ(可不计算).③、圆曲线ZY 或YZ 点到任一点i 的偏角:i ii L R902πϕ︒∆==④、圆曲线ZY 或YZ 点到任一点i 的弦长:)sin(2)2sin(2C i i iR R ∆=ϕ=⑤、圆曲线ZY 或YZ 点到任一点i 的弦长的方位角:i jd y z jd zy i a a ∆±→→或=⑥、所以圆曲线上任意点i 的坐标为:⎩⎨⎧++i i YZ ZY iii YZ ZY i sina C Y Y cosa C X X 或或==例题:已知一段圆曲线,R=3500m ,Ls =553.1m ,交点里程K50+154.734,ZY 点到JD 方向方位角为A=129°23′18.3″,右偏9°3′15.8″,ZY 点里程K49+877.607,YZ 点里程K50+430.707,起点坐标为x =389823.196,y =507787.251,求K50+200处中点坐标及左右各偏12.5m 的坐标。
解:K50+200处的曲线长度为Li =322.393mK50+200相对应的方位角:"'︒⨯⨯︒︒52.39165393.3223500180L R 180i ===ππa K50+200相对应的偏角:"'︒⨯⨯︒︒∆76.19382393.322350090L R 902i ii ====ππϕ K50+200到zy 点的弦长:m 279.32276.19382sin 35002Rsin 2C i i ==="'︒⨯⨯∆ zy 点到K50+200中桩的方位角:"'︒"'︒+"'︒∆+→06.38113276.193823.1823129a a i jd zy i ===K50+200左、右偏12.5m 的方位角:"'︒︒-"'︒︒-+82.5739449082.573913490a a ===左i A "'︒︒+"'︒︒++82.57391349082.573913490a a ===右i A所以K50+200处的坐标为:⎩⎨⎧"'︒⨯++"'︒⨯++6484.50802606.381132sin 279.322251.507787sina C Y Y 4354.38960706.381132cos 279.322196.389823cosa C X X i i ZY ii i ZY i ======K50+200左偏12.5m 的坐标为:⎩⎨⎧"'︒⨯++"'︒⨯++4656.50803582.573944sin 5.126484.508026sina 5.21Y Y 3256.38961682.573944cos 5.124354.389607cosa 5.21X X i i ======左左左左 K50+200右偏12.5m 的坐标为:⎩⎨⎧"'︒⨯++"'︒⨯++5386.50803582.5739341sin 5.126484.508026sina 5.21Y Y 6482.38959882.5739341cos 5.124354.389607cosa 5.21X X i i ======右右右右 三、缓和曲线上任一点的坐标推算切线角:πβ︒⨯1802RL L s 2i i =缓和曲线上任意点i 的偏角:πβδ︒⨯180RL 6L 3s 2i ii ==缓和曲线ZH 或HZ 点到任意点i 的方位角为:i jd HZ jd ZH a a i δ±→→或=缓和曲线上任意点i 的坐标为:⎪⎪⎩⎪⎪⎨⎧-s 3ii 2s 25i i i 6RL L y L 40R L L x ==缓和曲线ZH 或HZ 点到任意点i 的弦长:22i yx C +=所以缓和曲线上任意点i 的坐标为:⎩⎨⎧++i i HZ ZH iii HZ ZH i sina C Y Y cosa C X X 或或==例题:已知一段缓和曲线,ZH 点到JD 方向方位角为A=183°17′08.9″,线路左偏43°31′02″,ZH 点里程为K52+001.615,ZH 点坐标x =388071.927,y =508789.089,R =960m ,Ls =120m ,求K52+100处的中点坐标及左右各偏12.5m 的坐标。
圆曲线和缓和曲线坐标推算公式(附带例题)

圆曲线和缓和曲线坐标推算公式一、直线上的坐标推算⎩⎨⎧++0i m i0i m i sina L Y Y cosa L X X == 式中:Xm 、Ym ——直线段起点M 坐标Li ——直线段上任意点i 到线路起点M 的距离 a 0——直线段起点M 到JD1的方位角 二、圆曲线上任一点的坐标推算①、圆曲线上任一点i 相对应的圆心角:i i L R180πϕ︒=式中:Li ——圆曲线上任一点i 离开ZY 或YZ 点的弧长②、圆曲线上任一点i 的直角坐标:⎩⎨⎧-)(==i iii cos 1R Y Rsin X ϕϕ(可不计算).③、圆曲线ZY 或YZ 点到任一点i 的偏角:i ii L R902πϕ︒∆==④、圆曲线ZY 或YZ 点到任一点i 的弦长:)sin(2)2sin(2C i i iR R ∆=ϕ=⑤、圆曲线ZY 或YZ 点到任一点i 的弦长的方位角:i jd yz jd zy i a a ∆±→→或=⑥、所以圆曲线上任意点i 的坐标为:⎩⎨⎧++i i YZ ZY iii YZ ZY i sina C Y Y cosa C X X 或或==例题:已知一段圆曲线,R=3500m ,Ls =553.1m ,交点里程K50+154.734,ZY 点到JD 方向方位角为A=129°23′18.3″,右偏9°3′15.8″,ZY 点里程K49+877.607,YZ 点里程K50+430.707,起点坐标为x =389823.196,y =507787.251,求K50+200处中点坐标及左右各偏12.5m 的坐标。
解:K50+200处的曲线长度为Li =322.393mK50+200相对应的方位角:"'︒⨯⨯︒︒52.39165393.3223500180L R 180i ===ππa K50+200相对应的偏角:"'︒⨯⨯︒︒∆76.19382393.322350090L R 902i ii ====ππϕ K50+200到zy 点的弦长:m 279.32276.19382sin 35002Rsin 2C i i ==="'︒⨯⨯∆ zy 点到K50+200中桩的方位角:"'︒"'︒+"'︒∆+→06.38113276.193823.1823129a a i jd zy i ===K50+200左、右偏12.5m 的方位角:"'︒︒-"'︒︒-+82.5739449082.573913490a a ===左i A "'︒︒+"'︒︒++82.57391349082.573913490a a ===右i A 所以K50+200处的坐标为:⎩⎨⎧"'︒⨯++"'︒⨯++6484.50802606.381132sin 279.322251.507787sina C Y Y 4354.38960706.381132cos 279.322196.389823cosa C X X i i ZY ii i ZY i ======K50+200左偏12.5m 的坐标为:⎩⎨⎧"'︒⨯++"'︒⨯++4656.50803582.573944sin 5.126484.508026sina 5.21Y Y 3256.38961682.573944cos 5.124354.389607cosa 5.21X X i i ======左左左左 K50+200右偏12.5m 的坐标为:⎩⎨⎧"'︒⨯++"'︒⨯++5386.50803582.5739341sin 5.126484.508026sina 5.21Y Y 6482.38959882.5739341cos 5.124354.389607cosa 5.21X X i i ======右右右右 三、缓和曲线上任一点的坐标推算切线角:πβ︒⨯1802RL L s 2i i=缓和曲线上任意点i 的偏角:πβδ︒⨯180RL 6L 3s 2i ii ==缓和曲线ZH 或HZ 点到任意点i 的方位角为:i jd H Z jd ZH a a i δ±→→或=缓和曲线上任意点i 的坐标为:⎪⎪⎩⎪⎪⎨⎧-s 3ii 2s 25i i i 6RL L y L 40R L L x ==缓和曲线ZH 或HZ 点到任意点i 的弦长:22i yx C +=所以缓和曲线上任意点i 的坐标为:⎩⎨⎧++i i HZ ZH iii HZ ZH i sina C Y Y cosa C X X 或或==例题:已知一段缓和曲线,ZH 点到JD 方向方位角为A=183°17′08.9″,线路左偏43°31′02″,ZH 点里程为K52+001.615,ZH 点坐标x =388071.927,y =508789.089,R =960m ,Ls =120m ,求K52+100处的中点坐标及左右各偏12.5m 的坐标。
道路工程测量(圆曲线缓和曲线计算)

内容:理解线路勘测设计阶段的主要测量工作(初测控制测量、带状地形图测绘、中线测设和纵横断面测量);掌握路线交点、转点、转角、里程桩的概念和测设方法;掌握圆曲线的要素计算和主点测设方法;掌握圆曲线的切线支距法和偏角法的计算公式和测设方法;了解虚交的概念和处理方法;掌握缓和曲线的要素计算和主点测设方法;理解缓和曲线的切线支距法和偏角法的计算公式和测设方法;掌握路线纵断面的基平、中平测量和横断面测量方;了解全站仪中线测设和断面测量方法。
重点:圆曲线、缓和曲线的要素计算和主点测设方法;切线支距法和偏角法的计算公式和测设方法;路线纵断面的基平、中平测量和横断面测量方法难点:缓和曲线的要素计算和主点测设方法;缓和曲线的切线支距法和偏角法的计算公式和测设方法。
§ 9.1 交点转点转角及里程桩的测设一、道路工程测量概述分为:路线勘测设计测量 (route reconnaissance and design survey) 和道路施工测量 (road construction survey) 。
(一)勘测设计测量 (route reconnaissance and design survey)分为:初测 (preliminary survey) 和定测 (location survey)1、初测内容:控制测量 (control survey) 、测带状地形图 (topographical map of a zone) 和纵断面图 (profile) 、收集沿线地质水文资料、作纸上定线或现场定线,编制比较方案,为初步设计提供依据。
2、定测内容:在选定设计方案的路线上进行路线中线测量 (center line survey) 、测纵断面图 (profile) 、横断面图 (cross-section profile) 及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查,为施工图设计提供资料。
(二)道路施工测量 (road construction survey)按照设计图纸恢复道路中线、测设路基边桩和竖曲线、工程竣工验收测量。
曲线计算公式及例题

一、圆曲线坐标计算公式β=180°/π×L/R(L= βπR/180°)弧长公式β为圆心角△X=sinβ×R△Y=(1-cosβ) ×RC= 弦长X=X1+cos (α±β/2)×CY=Y1+sin (α±β/2)×Cβ代表偏角,(既弧上任一点所对的圆心角)。
β/2是所谓的偏角(弦长与切线的夹角)△X 、△Y 代表增量值。
X 、Y 代表准备求的坐标。
X1、Y1代表起算点坐标值。
α代表起算点的方位角。
R 代表曲线半径二、缓和曲线坐标计算公式β= L2/2RLS ×180°/πC= L - L5/90R2L S 2X=X1+cos (α±β/3)×CY=Y1+sin (α±β/3)×C L 代表起算点到准备算的距离。
LS 代表缓和曲线总长。
X1、Y1代表起算点坐标值。
三、直线坐标计算公式X=X1+cosα×LY=Y1+sinα×LX1、Y1代表起算点坐标值α代表直线段方位角。
L 代表起算点到准备算的距离。
1)左右边桩计算方法X 边=X中+cos(α±90°) ×LY 边=Y中+sin(α±90°) ×L在计算左右边桩时,先求出中桩坐标,在用此公式求左右边桩。
如果在线路方向左侧用中桩方位角减去90°,线路右侧加90°,乘以准备算的左右宽度。
例题:直线坐标计算方法α(方位角)=18°21′47″DK184+714.029,求DK186+421.02里程坐标X1=84817.831 Y1=352.177 起始里程解:根据公式X=X1+cosα×LX=84817.831+COS18°21′47″×(86421.02—84714.029)=86437.901Y=Y1+sinα×LY=352.177+sin18°21′47″×(86421.02—84714.029)=889.943求DK186+421.02里程左右边桩, 左侧3.75m, 右侧7.05m. 解:根据公式线路左侧计算:X 边=X中+cos(α±90°) ×LX 边=86437.901+cos(18°21′47″- 90°) ×3.75=86439.082Y 边=Y中+sin(α±90°) ×LY 边=889.943+sin(18°21′47″- 90°) ×3.75=886.384线路右侧计算:X 边=X中+cos(α±90°) ×LX 边=86437.901+cos(18°21′47″+ 90°) ×7.05=86435.680Y 边=Y中+sin(α±90°) ×LY 边=889.943+sin(18°21′47″+90°) ×7.05=896.634四、例题:缓和曲线坐标计算方法α(ZH点起始方位角)=18°21′47″X1=86437.901 Y1=889.941 起始里程DK186+421.02曲线半径2500 缓和曲线长120m求HY 点坐标, 也可以求ZH 点到HY 点任意坐标解:根据公式β=L2/2RLS×180°/πβ={1202/(2×2500×120) }×(180°/π)= 1°22′30.36″C=L-L5/90R2LS2C=120-1205/(90×25002×1202)=119.997X=X1+cos(α±β/3)×CX=86437.901+cos(18°21′47″-1°22′30.36″/3)×119.997=86552.086Y=Y1+sin(α±β/3)×CY=889.941+sin(18°21′47″-1°22′30.36″/3)×119.997=926.832求DK186+541.02里程左右边桩, 左侧3.75m, 右侧7.05m. 解:根据公式线路左侧计算:X 边=X中+cos(α±90°) ×LX 边=86552.086+cos{(18°21′47″-1°22′30.36″)- 90°}×3.75=86553.182Y 边=Y中+sin(α±90°) ×LY 边=926.832+sin{(18°21′47″-1°22′30.36″)- 90°}×3.75=923.246线路右侧计算:X 边=X中+cos(α±90°) ×LX 边=86552.086+cos{(18°21′47″-1°22′30.36″)+ 90°}×7.05=86550.026Y 边=Y中+sin(α±90°) ×LY 边=926.832+sin{(18°21′47″-1°22′30.36″)+ 90°}×7.05=933.574缓和曲线方位角计算方法α=(起始方位角±β偏角)= 18°21′47″-1°22′30.36″=16°59′16.64″注:缓和曲线在计算坐标时, 此公式只能从两头往中间推, 只能从ZH 点往HY 点推,HZ 点往YH点推算, 如果YH 往HZ 点推算坐标, 公式里的β为β2/3.五、例题:圆曲线坐标计算方法α(HY点起始方位角)= 16°59′16.64″X1=86552.086 Y1=926.832曲线半径2500 曲线长748.75 起始里程DK186+541.02求YH 点坐标, 也可以求QZ 点坐标或任意圆曲线一点坐标. 解:根据公式β=180°/π×L/Rβ= 180°/π×748.75/2500=17°09′36.31″△X=sinβ×R△X=sin17°09′36.31″×2500=737.606△Y=(1-cosβ) ×R△Y=(1-cos17°09′36.31″) ×2500=111.290C= 弦长C=745.954X=X1+cos(α±β/2)×CX= 86552.086 +cos(16°59′16.64″+360°-17°09′36.31″/2) ×745.954=87290.023 Y=Y1+sin(α±β/2)×CY=926.832+ sin(16°59′16.64″+360°-17°09′36.31″/2) ×745.954=1035.905圆曲线方位角计算方法α=(起始方位角±β偏角)= 16°59′16.64″+360°-17°09′36.31″=359°49′40.33″求DK187+289.77里程左右边桩, 左侧3.75m, 右侧7.05m. 解:根据公式线路左侧计算:X 边=X中+cos(α±90°) ×LX 边=87290.023+cos(359°49′40.33″-90°) ×3.75=87290.012 Y 边=Y中+sin(α±90°) ×LY 边=1035.905+sin(359°49′40.33″-90°) ×3.75=1032.155线路右侧计算:X 边=X中+cos(α±90°) ×LX 边=87290.023+cos(359°49′40.33″+90°) ×7.05=87290.044 Y 边=Y中+sin(α±90°) ×LY 边=1035.905+sin(359°49′40.33″+90°) ×7.05=1042.955。
圆曲线和缓和曲线坐标推算公式(附带例题)

圆曲线和缓和曲线坐标推算公式一、直线上的坐标推算⎩⎨⎧++0i m i0i m i sina L Y Y cosa L X X == 式中:Xm 、Ym ——直线段起点M 坐标Li ——直线段上任意点i 到线路起点M 的距离 a 0——直线段起点M 到JD1的方位角 二、圆曲线上任一点的坐标推算①、圆曲线上任一点i 相对应的圆心角:i i L R180πϕ︒=式中:Li ——圆曲线上任一点i 离开ZY 或YZ 点的弧长②、圆曲线上任一点i 的直角坐标:⎩⎨⎧-)(==i iii cos 1R Y Rsin X ϕϕ(可不计算).③、圆曲线ZY 或YZ 点到任一点i 的偏角:i ii L R902πϕ︒∆==④、圆曲线ZY 或YZ 点到任一点i 的弦长:)sin(2)2sin(2C i i iR R ∆=ϕ=⑤、圆曲线ZY 或YZ 点到任一点i 的弦长的方位角:i jd yz jd zy i a a ∆±→→或=⑥、所以圆曲线上任意点i 的坐标为:⎩⎨⎧++i i YZ ZY iii YZ ZY i sina C Y Y cosa C X X 或或==例题:已知一段圆曲线,R=3500m ,Ls =553.1m ,交点里程K50+154.734,ZY 点到JD 方向方位角为A=129°23′18.3″,右偏9°3′15.8″,ZY 点里程K49+877.607,YZ 点里程K50+430.707,起点坐标为x =389823.196,y =507787.251,求K50+200处中点坐标及左右各偏12.5m 的坐标。
解:K50+200处的曲线长度为Li =322.393mK50+200相对应的方位角:"'︒⨯⨯︒︒52.39165393.3223500180L R 180i ===ππa K50+200相对应的偏角:"'︒⨯⨯︒︒∆76.19382393.322350090L R 902i ii ====ππϕ K50+200到zy 点的弦长:m 279.32276.19382sin 35002Rsin 2C i i ==="'︒⨯⨯∆ zy 点到K50+200中桩的方位角:"'︒"'︒+"'︒∆+→06.38113276.193823.1823129a a i jd zy i ===K50+200左、右偏12.5m 的方位角:"'︒︒-"'︒︒-+82.5739449082.573913490a a ===左i A "'︒︒+"'︒︒++82.57391349082.573913490a a ===右i A 所以K50+200处的坐标为:⎩⎨⎧"'︒⨯++"'︒⨯++6484.50802606.381132sin 279.322251.507787sina C Y Y 4354.38960706.381132cos 279.322196.389823cosa C X X i i ZY ii i ZY i ======K50+200左偏12.5m 的坐标为:⎩⎨⎧"'︒⨯++"'︒⨯++4656.50803582.573944sin 5.126484.508026sina 5.21Y Y 3256.38961682.573944cos 5.124354.389607cosa 5.21X X i i ======左左左左 K50+200右偏12.5m 的坐标为:⎩⎨⎧"'︒⨯++"'︒⨯++5386.50803582.5739341sin 5.126484.508026sina 5.21Y Y 6482.38959882.5739341cos 5.124354.389607cosa 5.21X X i i ======右右右右 三、缓和曲线上任一点的坐标推算切线角:πβ︒⨯1802RL L s 2i i=缓和曲线上任意点i 的偏角:πβδ︒⨯180RL 6L 3s 2i ii ==缓和曲线ZH 或HZ 点到任意点i 的方位角为:i jd H Z jd ZH a a i δ±→→或=缓和曲线上任意点i 的坐标为:⎪⎪⎩⎪⎪⎨⎧-s 3ii 2s 25i i i 6RL L y L 40R L L x ==缓和曲线ZH 或HZ 点到任意点i 的弦长:22i yx C +=所以缓和曲线上任意点i 的坐标为:⎩⎨⎧++i i HZ ZH iii HZ ZH i sina C Y Y cosa C X X 或或==例题:已知一段缓和曲线,ZH 点到JD 方向方位角为A=183°17′08.9″,线路左偏43°31′02″,ZH 点里程为K52+001.615,ZH 点坐标x =388071.927,y =508789.089,R =960m ,Ls =120m ,求K52+100处的中点坐标及左右各偏12.5m 的坐标。
缓和曲线连同圆曲线测设

实习报告
班级:
组别:
姓名:
学号:
指导教师:
年月日
前言
1、曲线元素计算
(1)设计元素
R=缓和曲线长l0= 转向角α
JD里程:DK+
(2)转向角测量
日期:年月日 仪器Байду номын сангаас号仪器编号
班级组别观 测 者记 录 者
置镜点
盘 位
目标
水平度盘读数
(° ′ ″)
半测回角值
(° ′ ″)
一测回角值
(° ′ ″)
JD
L
ZD1
ZD2
R
ZD2
ZD1
(3)缓和曲线常数
(4)曲线综合要素
2、曲线主要点里程推算
(1)里程推算
JD DK +
-T
ZH DK +
+l0
HY DK +
+(L-2l0)/2
QZ DK +
+(L-2l0)/2
YH DK +
+l0
HZ
(2)计算检核
ZH DK +
+2T
DK +
-q
HZ DK +
3、分弦偏角计算(圆曲线段不足20米的破弦)
NO
分弦(m)
分弦偏角(°′″)
δ1
δ2
δ3
δ4
δ5
3、偏角法测设曲线资料计算
日期:年月日 仪器型号仪器编号
班级组别观 测 者记 录 者
点 号
里 程
正反拨
偏角(°′″)
平盘读数(°′″)
备注
ZH(0)
道路工程测量(圆曲线缓和曲线计算)

内容:理解线路勘测设计阶段的主要测量工作(初测控制测量、带状地形图测绘、中线测设和纵横断面测量);掌握路线交点、转点、转角、里程桩的概念和测设方法;掌握圆曲线的要素计算和主点测设方法;掌握圆曲线的切线支距法和偏角法的计算公式和测设方法;了解虚交的概念和处理方法;掌握缓和曲线的要素计算和主点测设方法;理解缓和曲线的切线支距法和偏角法的计算公式和测设方法;掌握路线纵断面的基平、中平测量和横断面测量方;了解全站仪中线测设和断面测量方法。
重点:圆曲线、缓和曲线的要素计算和主点测设方法;切线支距法和偏角法的计算公式和测设方法;路线纵断面的基平、中平测量和横断面测量方法难点:缓和曲线的要素计算和主点测设方法;缓和曲线的切线支距法和偏角法的计算公式和测设方法。
§9.1交点转点转角及里程桩的测设一、道路工程测量概述分为:路线勘测设计测量(routereconnaissanceanddesignsurvey)和道路施工测量(roadconstructionsurvey)。
(一)勘测设计测量(routereconnaissanceanddesignsurvey)分为:初测(preliminarysurvey)和定测(locationsurvey)1、初测内容:控制测量(controlsurvey)、测带状地形图(topographicalmapofazone)和纵断面图(profile)、收集沿线地质水文资料、作纸上定线或现场定线,编制比较方案,为初步设计提供依据。
2、定测内容:在选定设计方案的路线上进行路线中线测量(centerlinesurvey)、测纵断面图(profile)、横断面图(cross-sectionprofile)及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查,为施工图设计提供资料。
(二)道路施工测量(roadconstructionsurvey)按照设计图纸恢复道路中线、测设路基边桩和竖曲线、工程竣工验收测量。
圆曲线、缓和曲线计算例题《精选》

圆曲线坐标计算公式β=180°/π×L/R(L= βπ R/180°)弧长公式β为圆心角△X=sinβ×R△Y=(1-cosβ)×RC= 弦长X=X1+cos (α ±β/2)×CY=Y1+sin (α ±β/2)×Cβ代表偏角,(既弧上任一点所对的圆心角)。
β/2是所谓的偏角(弦长与切线的夹角)△X、△Y代表增量值。
X、Y代表准备求的坐标。
X1、Y1代表起算点坐标值。
α代表起算点的方位角。
R 代表曲线半径缓和曲线坐标计算公式β= L2/2RLS ×180°/πC= L - L5/90R2LS2X=X1+cos (α ±β/3)×CY=Y1+sin (α ±β/3)×CL代表起算点到准备算的距离。
LS代表缓和曲线总长。
X1、Y1代表起算点坐标值。
直线坐标计算公式X=X1+cosα×L Y=Y1+sinα×LX1、Y1代表起算点坐标值α代表直线段方位角。
L代表起算点到准备算的距离。
左右边桩计算方法X边=X中+cos(α±90°)×LY边=Y中+sin(α±90°)×L在计算左右边桩时,先求出中桩坐标,在用此公式求左右边桩。
如果在线路方向左侧用中桩方位角减去90°,线路右侧加90°,乘以准备算的左右宽度。
例题:直线坐标计算方法α(方位角)=18°21′47″X1=84817.831 Y1=352.177 起始里程DK184+714.029求DK186+421.02里程坐标解:根据公式X=X1+cosα×LX=84817.831+COS18°21′47″×(86421.02—84714.029)=86437.901Y=Y1+sinα×LY=352.177+sin18°21′47″×(86421.02—84714.029)=889.943求DK186+421.02里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算:X边=X中+cos(α±90°)×LX边=86437.901+cos(18°21′47″- 90°)×3.75=86439.082Y边=Y中+sin(α±90°)×LY边=889.943+sin(18°21′47″- 90°)×3.75=886.384线路右侧计算: X边=X中+cos(α±90°)×LX边=86437.901+cos(18°21′47″+ 90°)×7.05=86435.680 Y边=Y中+sin(α±90°)×L Y边=889.943+sin(18°21′47″+90°)×7.05=896.634例题:缓和曲线坐标计算方法α(ZH点起始方位角)=18°21′47″X1=86437.901 Y1=889.941起始里程DK186+421.02曲线半径2500缓和曲线长120m求HY点坐标,也可以求ZH点到HY点任意坐标解:根据公式β=L2/2RLS×180°/πβ={1202/(2×2500×120)}×(180°/π)= 1°22′30.36″C=L-L5/90R2LS2C=120-1205/(90×25002×1202)=119.997X=X1+cos(α±β/3)×CX=86437.901+cos(18°21′47″-1°22′30.36″/3)×119.997=86552.086Y=Y1+sin(α±β/3)×CY=889.941+sin(18°21′47″-1°22′30.36″/3)×119.997=926.832求DK186+541.02里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算:X边=X中+cos(α±90°)×LX边=86552.086+cos{(18°21′47″-1°22′30.36″)- 90°}×3.75=86553.182Y边=Y中+sin(α±90°)×LY边=926.832+sin{(18°21′47″-1°22′30.36″)- 90°}×3.75=923.246线路右侧计算: X边=X中+cos(α±90°)×LX边=86552.086+cos{(18°21′47″-1°22′30.36″)+ 90°}×7.05=86550.026Y边=Y中+sin(α±90°)×LY边=926.832+sin{(18°21′47″-1°22′30.36″)+ 90°}×7.05=933.574缓和曲线方位角计算方法α=(起始方位角±β偏角)= 18°21′47″-1°22′30.36″=16°59′16.64″注:缓和曲线在计算坐标时,此公式只能从两头往中间推,只能从ZH点往HY点推,HZ点往YH 点推算,如果YH往HZ点推算坐标,公式里的β为β2/3.例题:圆曲线坐标计算方法α(HY点起始方位角)= 16°59′16.64″X1=86552.086Y1=926.832 曲线半径2500曲线长748.75起始里程DK186+541.02求YH点坐标,也可以求QZ点坐标或任意圆曲线一点坐标.解:根据公式β=180°/π×L/Rβ= 180°/π×748.75/2500=17°09′36.31″△X=sinβ×R△X=sin17°09′36.31″×2500=737.606△Y=(1-cosβ)×R△Y=(1-cos17°09′36.31″)×2500=111.290C=弦长C=745.954X=X1+cos(α±β/2)×CX= 86552.086 +cos(16°59′16.64″+360°-17°09′36.31″/2) ×745.954=87290.023Y=Y1+sin(α±β/2)×CY=926.832+ sin(16°59′16.64″+360°-17°09′36.31″/2) ×745.954=1035.905圆曲线方位角计算方法α=(起始方位角±β偏角)= 16°59′16.64″+360°-17°09′36.31″=359°49′40.33″求DK187+289.77里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算: X边=X中+cos(α±90°)×LX边=87290.023+cos(359°49′40.33″-90°)×3.75=87290.012Y边=Y中+sin(α±90°)×LY边=1035.905+sin(359°49′40.33″-90°)×3.75=1032.155线路右侧计算: X边=X中+cos(α±90°)×LX边=87290.023+cos(359°49′40.33″+90°)×7.05=87290.044Y边=Y中+sin(α±90°)×LY边=1035.905+sin(359°49′40.33″+90°)×7.05=1042.955。
(完整版)缓和曲线、圆曲线测设计算例题
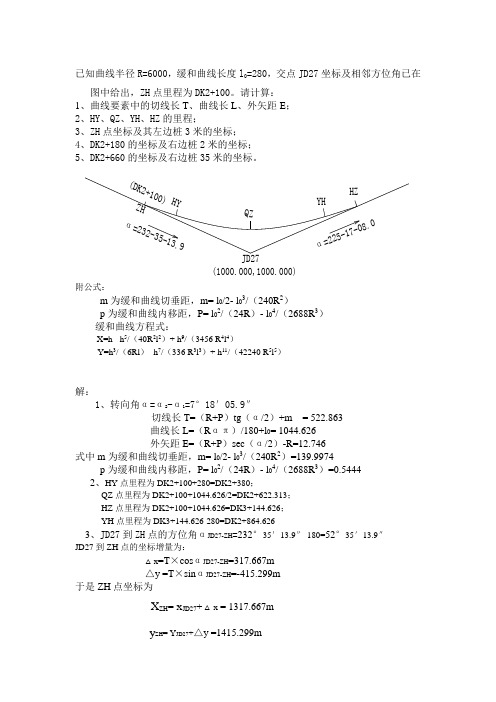
已知曲线半径R=6000,缓和曲线长度l 0=280,交点JD27坐标及相邻方位角已在图中给出,ZH 点里程为DK2+100。
请计算:1、曲线要素中的切线长T 、曲线长L 、外矢距E ;2、HY 、QZ 、YH 、HZ 的里程;3、ZH 点坐标及其左边桩3米的坐标;4、DK2+180的坐标及右边桩2米的坐标;5、DK2+660的坐标及右边桩35米的坐标。
永州α=225-17-08.0JD27(D K 2+100)(1000.000,1000.000)α=232-35-13.9H Z Q ZHZ H Y YH附公式:m 为缓和曲线切垂距,m= l 0/2- l 03/(240R 2)p 为缓和曲线内移距,P= l 02/(24R )- l 04/(2688R 3)缓和曲线方程式:X=h - h 5/(40R 2l 2)+ h 9/(3456 R 4l 4)Y=h 3/(6Rl )- h 7/(336 R 3l 3)+ h 11/(42240 R 5l 5)解:1、转向角α=α2-α1=7°18′05.9″切线长T=(R+P )tg (α/2)+m = 522.863曲线长L=(R απ)/180+l 0= 1044.626外矢距E=(R+P )sec (α/2)-R=12.746式中m 为缓和曲线切垂距,m= l 0/2- l 03/(240R 2)=139.9974p 为缓和曲线内移距,P= l 02/(24R )- l 04/(2688R 3)=0.54442、HY 点里程为DK2+100+280=DK2+380;QZ 点里程为DK2+100+1044.626/2=DK2+622.313;HZ 点里程为DK2+100+1044.626=DK3+144.626;YH 点里程为DK3+144.626-280=DK2+864.6263、JD27到ZH 点的方位角αJD27-ZH =232°35′13.9″-180=52°35′13.9″ JD27到ZH 点的坐标增量为:△x =T ×cos αJD27-ZH =317.667m△y =T ×sin αJD27-ZH =-415.299m于是ZH 点坐标为X ZH = x JD27+ △x = 1317.667my ZH = Y JD27+△y =1415.299mZH点到左边桩3米的方位角αZH-左边桩= 232°35′13.9″-90=142°35′13.9″左边桩3米的坐标为:X左= x ZH+ 3×cosαZH-左边桩= 1315.284mY左= y ZH +3×sinαZH-左边桩=1417.122m4、DK2+180的坐标及右边桩2米的坐标:DK2+180在缓和曲线上,计算过程为:ZH点到JD27的方位角αZH-JD1= =232°35′13.9″DK2+180到ZH点的缓和曲线长度h为180-100=80根据缓和曲线方程式:X=h - h5/(40R2l2)+ h9/(3456 R4l4)=80.000Y=h3/(6Rl)- h7/(336 R3l3)+ h11/(42240 R5l5)=0.0508由X和Y可以求出DK5+900与ZH的距离D和它的偏角δ:D=√(X2+ Y2)=80.000δ=arctg(Y/ X)=0°02′11.0″于是DK2+180的坐标(X1,Y1)为:X1= 1317.667+Dcos(232°35′13.9″-δ)=1269.022Y1 = 1415.299+Dsin(232°35′13.9″-δ)=1351.788DK2+300右边桩2米的坐标(X2,Y2)为:X2= 1269.022+2×cos(232°35′13.9″-3δ+90)=1270.608Y2= 1351.788+2×sin(232°35′13.9″-3δ+90)=1350.5705、圆曲线点DK2+660计算过程为:曲中点QZ的里程推算为DK2+622.313, DK2+660到QZ的圆曲线长度为660-622.313=37.687,所对应的圆心角为O′=(180*37.687)/(πR)=0°21′35.6″, JD27到圆心O的方位角αJD27-O=225°17′08.0″-(180-7°18′05.9″)/2=138°56′10.95″圆心O的坐标为:X3 =1000+(E+R)cos(138°56′10.95″)=-3533.494Y3= 1000+(E+R)sin(138°56′10.95″)=4949.753DK2+660的坐标(X4,Y4)为:X4= X3++ R cos(138°56′10.95″+180- O′)=965.544Y4 = Y3+Rsin(138°56′10.95″+180- O′)=980.035DK2+660右边桩35米的坐标(X5,Y5)为:X5= X3++ (R+35)×cos(138°56′10.95″+180- O′)=991.788Y5= Y3+(R+35)×sin(138°56′10.95″+180- O′)=956.878。
带有缓和曲线的圆曲线逐桩坐标计算例题

338
1938 52
2
22
+140
538
27 17 14
+160
738
34 55 36
QZ:
K2
4108 43
8
+180
42 33 58
+200
+220
+240
+260
YH:K2
74 39 04
79
(4)第二缓和段坐标盘算
(本题为左转曲线)
桩号
Xi
Yi
YH:
K2+2
40
2
7
+280
90
2
+300
带有缓和曲线的圆曲线逐桩坐标盘算
例题:某山岭区二级公路,已厚交点的坐标分离为JD1(40961.914,91066.103).
JD2(40433.528,91250.097).JD3(40547.416,91810.392),JD2里程为K2+200.000,R=150m,缓和曲线长度为40m,盘算带有缓和曲线的圆曲线的逐桩坐标.(《工程测量》第202页36题)
158 15 16
(3)圆曲线段坐标盘算
桩号
弧长
偏角
方位角(左转)
弦长
X
Y
HY:
K2
153 09 41
9
91215.104
+100
38
2 11 04
150 58 37
+120
338
6 00 15
147 09 26
+140
538
9 49 26
143 20 15
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
缓和曲线、圆曲线测设计算例题
已知曲线半径R=6000,缓和曲线长度l0=280,交点JD27坐标及相邻方位角已在图中给出,ZH点里程为DK2+100。
请计算:
1、曲线要素中的切线长T、曲线长L、外矢距E;
2、HY、QZ、YH、HZ的里程;
3、ZH点坐标及其左边桩3米的坐标;
4、DK2+180的坐标及右边桩2米的坐标;
5、DK2+660的坐标及右边桩35米的坐标。
永州
(DK2+100)HYHZYH
QZ
08-715-.0α=232-
附公式:
m为缓和曲线切垂距,m= l0/2- l03/(240R2)
p为缓和曲线内移距,P= l02/(24R)- l04/(2688R3)
缓和曲线方程式:
X=h - h5/(40R2l2)+ h9/(3456 R4l4)
Y=h3/(6Rl)- h7/(336 R3l3)+ h11/(__ R5l5)
解:
1、转向角α=α2-α1=7°18′05.9″
切线长T=(R+P)tg(α/2)+m = 522.863
曲线长L=(Rαπ)/180+l0= 1044.626
外矢距E=(R+P)sec(α/2)-R=12.746
式中m为缓和曲线切垂距,m= l0/2- l03/(240R2)=139.9974
p为缓和曲线内移距,P= l02/(24R)- l04/(2688R3)=0.5444
2、HY点里程为DK2+100+280=DK2+380;
QZ点里程为DK2+100+1044.626/2=DK2+622.313;
HZ点里程为DK2+100+1044.626=DK3+144.626;
YH点里程为DK3+144.626-280=DK2+864.626
3、JD27到ZH点的方位角α
JD27到ZH点的坐标增量为:
△x=T×cosα
△y =T×sinα
于是ZH点坐标为
yZH= YJD27+△y =1415.299m Z35-
1.922=αJD27(1000.000,1000.000)JD27-ZH=232°35′13.9″-180=52°35′13.9″ JD27-ZH=317.667m JD27-ZH=-415.299m XZH= xJD27+ △x =
1317.667m
ZH点到左边桩3米的方位角α
左边桩3米的坐标为:ZH-左边桩= 232°35′13.9″-90=142°35′13.9″X左= xZH+ 3×cosα
Y左= yZH +3×sinαZH-左边桩= 1315.284m ZH-左边桩=1417.122m
4、DK2+180的坐标及右边桩2米的坐标:
DK2+180在缓和曲线上,计算过程为:
ZH点到JD27的方位角αZH-JD1= =232°35′13.9″
DK2+180到ZH点的缓和曲线长度h为180-100=80
根据缓和曲线方程式:
X=h - h5/(40R2l2)+ h9/(3456 R4l4)=80.000
Y=h3/(6Rl)- h7/(336 R3l3)+ h11/(__ R5l5)=0.0508
由X和Y可以求出DK5+900与ZH的距离D和它的偏角δ:
D=√(X2+ Y2)=80.000
δ=arctg(Y/ X)=0°02′11.0″
于是DK2+180的坐标(X1,Y1)为:
X1= 1317.667+Dcos(232°35′13.9″-δ)=1269.022
Y1 = 1415.299+Dsin(232°35′13.9″-δ)=1351.788
DK2+300右边桩2米的坐标(X2,Y2)为:
X2= 1269.022+2×cos(232°35′13.9″-3δ+90)=1270.608
Y2= 1351.788+2×sin(232°35′13.9″-3δ+90)=1350.570
5、圆曲线点DK2+660计算过程为:
曲中点QZ的里程推算为DK2+622.313, DK2+660到QZ的圆曲线长度为660-622.313=37.687,所对应的圆心角为O′=(180*37.687)/(πR)=0°21′35.6″,JD27到圆心O的方位角αJD27-O=225°17′08.0″-(180-7°18′05.9″)/2=138°56′10.95″
圆心O的坐标为:
X3 =1000+(E+R)cos(138°56′10.95″)=-3533.494
Y3= 1000+(E+R)sin(138°56′10.95″)=4949.753
DK2+660的坐标(X4,Y4)为:
X4= X3++ R cos(138°56′10.95″+180- O′)=965.544
Y4 = Y3+Rsin(138°56′10.95″+180- O′)=980.035
DK2+660右边桩35米的坐标(X5,Y5)为:
X5= X3++ (R+35)× cos(138°56′10.95″+180- O′)=991.788 Y5= Y3+(R+35)×sin(138°56′10.95″+180- O′)=956.878。
