数字控制振荡器NCO
fpga_nco

基于FPGA和SRAM的数控振荡器的设计与实现佟力永,肖山竹1 引言数控振荡器是数字通讯中调制解调单元必不可少的部分,同时也是各种数字频率合成器和数字信号发生器的核心。
随着数字通信技术的发展,对传送数据的精度和速率要求越来越高。
如何得到可数控的高精度的高频载波信号是实现高速数字通信系统必须解决的问题,可编程逻辑器件和大容量存储器的发展为这一问题的解决带来了曙光。
本文介绍如何用FPGA(现场可编程逻辑门阵列)和SRAM(静态随机存储器)实现高精度数控振荡器。
2 NCO概述NCO(Numerical Controlled Oscillator)即数控振荡器用于产生可控的正弦波或余弦波,其实现的方法目前主要有计算法和查表法等。
计算法以软件编程的方式通过实时计算产生正弦波样本,该方法耗时多且只能产生频率相对较低的正弦波,而需要产生高速的正交信号时,用此方法无法实现。
因此,在实际应用中一般采用最有效、最简单的查表法,即事先根据各个NCO正弦波相位计算好相位的正弦值,并以相位角度作为地址把该相位的正弦值数据存储在表中,然后通过相位累加产生地址信息读取当前时刻的相位值在表中对应的正弦值,从而产生所需频率的正弦波。
用查表法实现NCO的性能指标取决于查表的深度和宽度,即取决于表示相位数据的位数(查表存储器地址线的位数)和表示正弦值数据的位数(查表存储器数据线的位数)。
改善NCO性能最简单和最根本的方法是加大查找表的深度和宽度。
目前,用查找表法实现NCO的普遍做法是用片内ROM作为查找表,由于片内资源的限制,查找表的深度和宽度一般不会很大(通常为256×8bits),大大限制了NCO性能的提高,用独立的大容量SRAM作为查找表,把查找表从片内移到片外,可以较好解决这个问题,基于这种思想,笔者成功地用FPGA (Xilinx公司的XC2V1000型门阵列)和SRAM(Cypress公司的CY7C1021型存储器)实现了NCO。
软件无线电系统中NCO的设计与实现

相位抖动实现的原理是在 NCO 相位累加器后面加上 一个在(0,2B ) 分布的随机数,然后再截取并查表,使 寻址的最后一位随机地抖动,破坏舍弃误差的周期,达到
抑制杂散的目的。B 位的伪随机数可以采用移位寄存器结 构的 m 序列发生器来产生。 1. 3 利用 CORDIC 算法实现 NCO
另一种实现 NCO 的方法是采用基于坐标旋转数字式 计 算 机 ( Coordinate Rotation Digital Computer, CORDIC ) 的算 法,CORDIC 算 法 最 初 是 由 Voider 和 Walther 提 出 的[3],用来解决平 面 直 角 坐 标 与 极 坐 标 之 间 的 自 由 变 换。
CORDIC 算法的基本思想是采用逐次逼近的算法实现三角 函数的计算,该算法的优点是只进行加减运算和移位,结
合并行处理和加流水线,可以实现每一个时钟周期输出一
个经过 n 位迭代的结果。 在直角坐标系中,点( x,y)经过角度 z 的旋转后得到
新的坐标( xnew ,ynew ): xnew = x·co(s z)- y·sin( z) ynew = y·co(s z)+ x·sin( z)
位累加器的位数 N 取的都很大,但是 N 增大,会使 ROM
查找表容量相应变大,实际中成本和体积限制了 ROM 的
容量,因此通常截取累加器输出的高 Y 位去寻址 ROM 来
满足要求。对低位的舍弃不可避免地产生误差。不同的输
出幅度位数 D,其量化误差对 NCO 的输出也会产生影响,
降低信号的信噪比( SNR)。而在系统设计中,相位截取
经过 n 次迭代 (z n)趋近于零,而 (x n),(y n)趋近于
co(s ωt),sin( ωt),其中 ωt 为输入相位地址 (z 0)所对应的 相位角。
数字控制振荡器
背景知识:在实际的通信系统中,携带数字信息的信号通常是由某种类型的载波调制方式发送的,传送信号的带宽限制在以载波为中心的一个频段上,如双边带调制,或在邻近载波的频段上,如单边带调制。
无论何种调制方式,在发送端均需要一个高频载波将信息调制上去,以减小信号衰落,相干解调时在接收端也需要一个与发送端同频同相的高频载波将信息从高频上解调下来。
为了产生这个高频载波,在数字电路中是采用数控振荡器(NCO),也称为直接数字频率合成器〔DDS),它的输出频率和相位可以受人为控制,从而满足各种需要。
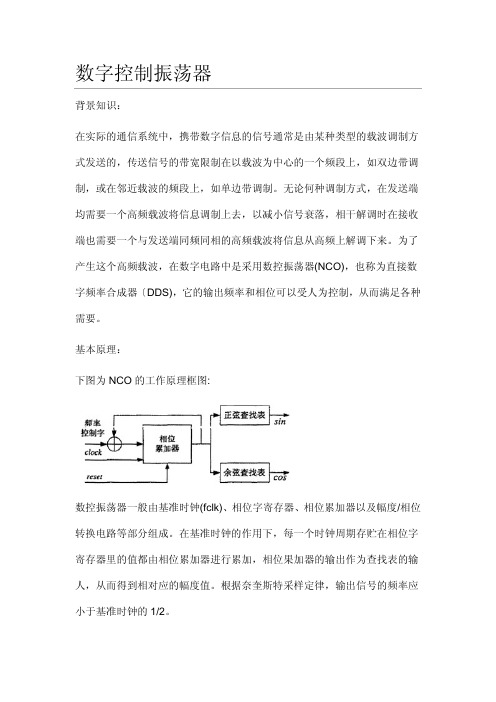
基本原理:下图为NCO的工作原理框图:数控振荡器一般由基准时钟(fclk)、相位字寄存器、相位累加器以及幅度/相位转换电路等部分组成。
在基准时钟的作用下,每一个时钟周期存贮在相位字寄存器里的值都由相位累加器进行累加,相位果加器的输出作为查找表的输人,从而得到相对应的幅度值。
根据奈奎斯特采样定律,输出信号的频率应小于基准时钟的1/2。
相位累加器输出(△Ф)的数值和系统的频率(fclk)决定了输出频率(fout),它门的关系如下:N是相位寄存器的位数,N值的大小决定了频率分辨率(fres ),有在这里假设,fclk=128MHz, N=32,可以计算出NCO的频率分辨率fres=0.0298Hz相位累加器是决定NCO电路性能的一个关键部分。
我们可以采用了Altera 的加法器宏功能模块形成一个32bit的累加器,它以流水线处理方式进行工作。
相位/幅度转换电路是NCO电路中的另一个关键部分,在设计中面临的主要问题就是资源的开销。
一般电路采用ROM结构,相位累加器的输出是一种数字式锯齿波,通过取它的若干位作为ROM的地址输人,而后通过查表和运算,ROM就能输出所需波形的量化数据。
在APEX器件中,ROM由EAB实现,ROM表的尺寸随着地址位数或数据位数的增加成指数递增关系,因此在满足信号性能的前提条件下,如何减少资源的开销就是一个重要的问题。
NCO,调制信号,FPGA

摘要:本文首先描述NCO的基本工作原理,然后介绍利用NCO产生调频信号(FM)、频移键控信号(FSK)、相移键控信号(PSK)、调幅信号(AM)和幅度键控信号(ASK)等多种调制信号的方法,最后以调幅信号(AM)为例介绍调制信号在FPGA中的实现。
关键词:NCO,调制信号,FPGA1 引言数控振荡器(NCO)产生时间离散和幅度离散的正弦信号和余弦信号,典型情况下用在通信系统中,在I-Q 混频器中用作正交载波发生器,也常用在数字锁相环中,在通信接收机中用于载波同步。
NCO还可作为频移键控(FSK)或相移键控(PSK)调制器,此时输出信号的频率或相位变化直接与输入数据相对应。
在模拟调制中,利用NCO可以直接产生调频信号(FM),但要产生调幅信号(AM)则要进行一定的处理。
2 NCO基本工作原理产生数字正弦信号的方法有许多种。
通用的方法是在单位圆上累加相位增量产生角度位置,然后用累加相位值作为ROM查找表的地址,完成从极坐标到笛卡尔坐标的转换。
可以使用乘法器减少ROM的容量,对于给定的精度,乘法器的使用可以指数降低存储器的使用量,但是需要更多的逻辑单元(LE)。
产生数字正弦信号的另一个方法是使用坐标旋转数字计算(CORDIC)算法确定正弦和余弦的值,CORDIC 算法用累加相位值作为输入,然后通过一系列二进制移位和比较确定对应角度的笛卡尔坐标。
在所有的方法中,相位增量累加的频率和输入相位增量的大小直接决定正弦信号的频率,而输出信号的值用二进制补码表示。
NCO生成的正弦信号用下列公式定义:s(nT)=Asin[2p(f0+f FM)nT+f PM+f DITH]其中:T是时钟周期,f O是由相位增量输入值f INC决定的未调制输出频率,f FM是由频率调制输入值f FM决定的频率调制参数,f PM是相位调制输入值,f DITH是内部抖动相位值,A=2N-1,N是幅值精度。
对于给定的相位增量f INC,输出频率f O由下列公式决定:f0=f INC*f clk/2M Hz其中:f clk是时钟频率,M是相位累加器精度。
使用MCC学习PIC单片机 – NCO 数控振荡器
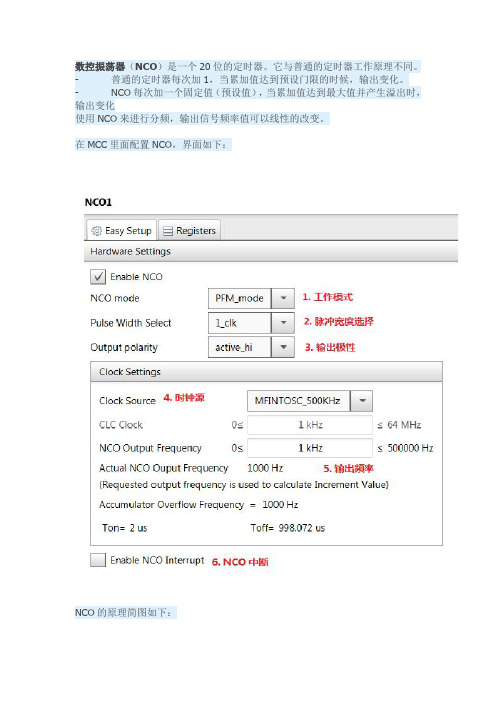
数控振荡器(NCO)是一个20位的定时器。
它与普通的定时器工作原理不同。
-普通的定时器每次加1,当累加值达到预设门限的时候,输出变化。
-NCO每次加一个固定值(预设值),当累加值达到最大值并产生溢出时,输出变化使用NCO来进行分频,输出信号频率值可以线性的改变。
在MCC里面配置NCO,界面如下:NCO的原理简图如下:NCO输入时钟源多种时钟源,可供选择。
NCO工作模式固定占空比模式:每次累加器溢出,产生一次电平翻转(图中D触发器构成的二分频电路)。
输出信号频率为翻转频率的1/2,占空比固定为50%。
脉冲频率模式:输出脉冲宽度可选择,宽度为(1/2/4…/128)个输入时钟周期。
输出信号周期为累加器溢出两次溢出的间隔周期。
NCO输出方式:PIN脚输出产生中断驱动其他外设输出状态bit位MCC生成代码:代码在nco1.c文件中。
初始化NCO1CON,NCO1CLK,NCO1ACC和NCO1INC寄存器,使能NCO。
void NCO1_Initialize(void){//Set the NCO to the options selected in the GUI//EN disabled;POL active_hi;PFM PFM_mode;NCO1CON=0x01;//CKS MFINTOSC_500KHz;PWS1_clk;NCO1CLK=0x03;//NCO1ACCU=0x00;//NCO1ACCH=0x00;//NCO1ACCL=0x00;//NCO1INCU=0x00;//NCO1INCH=0x08;//NCO1INCL=0x31;//Enable the NCO moduleNCO1CONbits.EN=1;//Clearing IF flag before enabling the interrupt.PIR7bits.NCO1IF=0;//Enabling NCO1interrupt.PIE7bits.NCO1IE=1;}查询输出状态bool NCO1_GetOutputStatus(void){//Return output status on accumulator over flow return(NCO1CONbits.OUT);}当NCO累加器溢出时产生中断void NCO1_ISR(void){//Clear the NCO1interrupt flagPIR7bits.NCO1IF=0;}。
DDS信号发生器设计

DDS信号发生器设计DDS(Direct Digital Synthesis)信号发生器是一种数字信号发生器,通过数字方式产生任意频率、任意波形的信号。
在信号处理中,DDS信号发生器具有重要的作用,例如在通信系统、音频信号生成、测试测量仪器等领域都需要使用到DDS信号发生器。
DDS信号发生器基本原理是通过数字的方式产生一个频率为Fs的正弦波,然后对该正弦波进行相位和幅度的调制,从而得到所需要的信号。
具体来说,DDS信号发生器主要由相位累加器、相位查找表、数字控制振荡器(NCO)以及低通滤波器等组成。
首先是相位累加器,它主要用于产生相位信息。
通过一个计时器不断累加一个步进量,得到一个连续变化的相位值。
相位累加器的工作原理是通过一个加法器加上步进量,然后将结果输出给相位查找表。
接下来是相位查找表,它主要用于存储正弦波的值。
相位查找表中存储了一个完整周期的正弦波值,根据相位累加器的输出值,可以从相位查找表中读取相应的正弦波值。
然后是数字控制振荡器(NCO),它主要用于控制频率。
通过调整相位累加器的步进量,可以改变输出信号的频率。
当相位累加器的步进量为1时,输出信号的频率为Fs。
当步进量为2时,输出信号的频率为Fs/2,以此类推。
最后是低通滤波器,它主要用于去除由于相位调制引起的高频成分。
由于DDS信号发生器在频率上是离散的,会产生一些高频的杂散信号。
通过使用低通滤波器,可以去除这些高频成分,得到我们所需要的信号。
综上所述,DDS信号发生器通过数字方式产生信号,具有灵活性高、调制精度高的优点。
在DDS信号发生器的设计中,需要注意一些关键参数的选择,例如采样率、分辨率、时钟稳定性等。
此外,还需要注意信号输出的波形质量、相位噪声、非线性失真等指标的优化。
在实际应用中,DDS信号发生器通常需要结合外部DAC(数字模拟转换器)芯片进行实现。
DAC芯片将数字信号转换为模拟信号,从而输出到各种应用中。
总而言之,DDS信号发生器是一种重要的数字信号发生器,通过数字方式产生任意频率、任意波形的信号。
NCO和DDS技术

波形和其波形序列指令都存在仪器所带的RAM中。
任意波形发生器
波形生成序列通常从 TTL硬件触发器开始。各种波形由许多 单个的样本构成,而生成采样率由仪器的采样时钟确定。从
内部采样时钟时基(100 MHz VCXO)中导出采样时钟有几种
不同模式,包括DDS定时Div/N时钟,以及几种提供不同外部 时钟的模式。另外,对于用于仪器的锁相环的频率基准,也
真思考如何为以后的发展开好头。
Thank you
函数发生器
函数发生器产生固定波形,如正弦波、方波(矩形波)阶梯波 或三角波(锯齿波),频率可调节。函数发生器无需来自计 算机或大容量存储缓冲器的连续输入,因为设备本身能够产 生这些波形。 函数发生器可以基于模拟技术,也可以基于数字技术。模拟 函数发生器利用模拟硬件来产生简单的函数,并在需要指定 频率的静态正弦波或方波时经常使用。而数字函数发生器采 用直接数字综合( DDS),DAC,数字信号处理,以及一个单 周期存储缓冲器来产生信号。 DDS技术依赖数字控制的方法, 利用单基准时钟频率来实现一个模拟频率源。DDS能够实现 高精度和高分辨率,高温度稳定度,高宽带,以及随机的和 相位连续的频率切换。 许多信号源通过对一个内部时基进行整数分频来产生时钟信 号,这被称为除N方法。但是,用除N方法来产生时钟,只能 产生有限的时钟频率。AWG,甚至几个时钟频率产生器,可 以采用DDS技术来产生具有非常精细的更新频率时钟信号, 而这是除NCO方法无法实现的。
CORDIC算法(参见论文-苏凯雄.基于FPGA的数控振荡器的设计与实现)
Walther JS于1971年提出了统一的CORDIC形式。 假定初始向量V1(x1 ,y1)旋转角度θ后得到向量V2(x2,y2),即:
基于FPGA的数控振荡器设计

个 时钟脉 冲到来 时 , 加法器 将上 个 时钟 周期 内寄存 器所 寄存 的值 与输 入 参 数 K 相 加 , 和 存 人 寄 存 其 器 作 为相 位加法 器 的当前 相位值 输 出 , 当前 相位 若
*
收稿 日期 :0 9年 1 月 1 20 2 5日, 修回 日期 :0 0年 1 1 21 月 7日
uain wi a t sⅡ b sdo h h lt t Qu ru o h a e n t et eNCO’ b scp icpe S ai rn il.Th e ut ftes lt np o et a h e ini c re t ers lso i ai rv h tted sg o rc h mu o s
1 引 言
随着 微 电子 技 术 和数 字 集 成 技 术 的发展 以及
2 NCO 的基 本 原 理
数 控振荡 器 主 要 是 由相 位 累加 器 和 波 形数 据
各种新 型器件 的不 断涌 现 , 控振 荡器 已成为 数字 数
通信 中调制 解 调 必 不 可 少 的 部 分 , 时 也 是 DD 同 S ( i c D gtl y t ei r) D r t ii n h s es 的核 心 。它可 根 据需 e aS z
图 1 NC 结 构 框 图 O
电子测量 、 频 通信 、 调 电子 对抗 等 领 域 。本 文 根 据
N O 的基 本 原 理 , 用 Qu ru I软 件 实 现 了 C 利 ats 1
1 )相位 累加 器是 NC 的核 心 , 于 实现 相位 O 用
的累加并 存储 累加 结果 。它 由两个 N 位 加 法器 和
Ab ta t Nu eia o to cl tr NC s rc m r l nrl c c Os iao ( O)i ii l in lg n r trwhc a e iso rt u ha ihfe l sadgt g a e e ao ihh sasre f as me i,s c shg — r q e c e ou in,hg u p twa esa izt n,fs rq e c wi hn u n yrs l t o iho t u v tbl a i i o atfe u n ys t ig,ec c t.Thsp p rraie h O ’ fn t nsr— i a e el st eNC S u ci i z o e
nco工作原理

nco工作原理NCO工作原理NCO(Numerically Controlled Oscillator)是一种数字控制振荡器,它可以通过数字信号来控制频率和相位。
在通信系统、雷达系统、无线电系统等领域中,NCO被广泛应用于频率合成、数字调制解调等方面。
本文将详细介绍NCO的工作原理。
一、NCO的基本结构NCO由两个主要部分组成:数字控制器和振荡器。
其中,数字控制器负责接收输入信号,并将其转换为相应的数字控制信号,然后将这些信号传递给振荡器。
振荡器则根据这些数字控制信号产生一个特定的频率和相位的输出信号。
二、数字控制器1. 数字输入NCO通常接收一个或多个32位宽度的二进制输入数据流。
这些数据可以是任何形式的数据,如音频、视频或其他类型的数据。
2. 相位累加器相位累加器是NCO中最重要的部分之一。
它负责计算当前输出信号的相位,并根据输入数据流中每个样本所代表的相位变化量进行更新。
具体来说,在每个时钟周期内,相位累加器会将其当前值与输入数据流中下一个样本值进行加法运算,从而计算出下一个输出信号的相位。
相位累加器的初始值可以是任何值,通常设置为0。
3. 数字控制信号生成NCO的数字控制器还负责生成一系列数字控制信号,这些信号用于控制振荡器的频率和相位。
具体来说,数字控制信号可以分为以下几种类型:(1)频率控制信号频率控制信号用于调节振荡器输出信号的频率。
在每个时钟周期内,数字控制器会根据输入数据流中每个样本所代表的频率变化量来更新频率控制信号。
(2)相位调节信号相位调节信号用于调节振荡器输出信号的相位。
在每个时钟周期内,数字控制器会根据输入数据流中每个样本所代表的相位变化量来更新相位调节信号。
4. 数字控制信号传输数字控制信号需要通过某种方式传输到振荡器中。
常见的传输方式有以下两种:(1)并行传输:将所有数字控制信号同时传输到振荡器中。
(2)串行传输:将所有数字控制信号按照一定顺序依次传输到振荡器中。
用于数字频率合成器的NCO实现与优化

数 控振 荡 器是 数 字通 讯 中调 制 解 调 单 元 必 不 可少 的部 分 ,同 时也是 各种 数字 频率合 成 器和数 字 信号 发生 器 的核心 。随着数 字通 信技 术 的发展 ,对 传 送 数据 的精 度和 速率 要求越 来 越高 。为 了迎合 通
如图 1 所示的 N C O包 括 相位 累加 器 、相 位 求
和模 块 以及 波 形发生 器 。
相位精度的位数成指数关系 ,以 = 1 6为例 ,查
询 表会 达到 8 Mb … ,考 虑 到 芯 片 面 积 、功耗 以及
收 稿 日期 :2 0 1 3— 0 3—1 5
作者简介 :时述有 ( 1 9 6 3 一) ,男 ,辽宁丹东人 ,教授级高级实验师 ,研究方 向:电子技术应用 。
・
2 67 ・
辽 东学 院学报 (自然科 学版 )
第2 O卷
f w
一 ,
pw
频
塞
\
/
波
1 r
● I
f
控
。 、
P
形
发 生 器
FG
/ \
a W
f w
f w
制
字
F W
p
. . PA Fra bibliotekPS B 图1 N C O 的结 构原 理图
溢 出相 位 累加 器 以 为 时钟 ,根 据 频率 控 制 ( 步长 ) 字 . 厂 产 生相 位 变 化 信息 ,相 位 累 加器 的值
为 =∑o v e  ̄ o m 厂 ,每个 时钟 周 期分 辨 率 为 比特 的 频率控制字被加入相位累加器 中,输出信号的频率 0 = 7 7 " …+ 孚( n . 2 + k ・ 2 ) ( 1 ) 等于 = x f / 2 s - ,其分辨 率 为 / 。相位 求 第 一 部 分 的 宽 度 为 3, 用 来 表 征 三 角 函 数 的 和模块 将相 位 累加器 的值 与宽 度 为 p 外 部输 入 相 0 . 2 5 7 r 对 称性 ,因 此 仅 [ 0 ,0 . 2 5 7 r ] 范 围 内 的相 位控制字 P的值相加获得相位控制信息。高分辨率 位值需要计算 。其他相位范 围内的正弦和余弦值可 的相 位序列 通 常 被 截 断 为 宽度 为 P的 内部 相 位 通 过交换 和 y值 ,并 运用 减 号得 到 ,相 应 的 映 值 ,通 常 P ≤ 。波 形发 生 器产 生 正 弦和 余 弦 幅度 射 关 系见表 1 。 值 序列 , P和 。 由 于 表 示 的 范 围 不 同 必 须 满 足 表 1 输 出 映射 关 系表
通信应用中的数字上变频和下变频

通信应用中的数字上变频和下变频数字上变频器(DUC)和数字下变频器(DDC)不仅仅是通信应用(如软件无线电)中的关键,而且在需要窄带信号高速流的应用中也是重要的。
另外,DDC结构容易控制所有取样速率下的混淆防止分样。
做为1个例子,让我们看看数字记录5MHz带宽(中心在50MHz)信号的问题。
此信号可以是来自RF-IF模拟下变频器的信号或者是直接从天线接收的信号。
为了满足尼奎斯特准则,我们需要以105ms/s取样率取样此信号。
然而,为了合理地捕获此信号,应该在较高的取样率(至少200ms/s)取样此信号。
假设ADC为16位,在该速率下被取样的信号会产生400MB/s数据。
也许更难办的是以这样高速率采集和存储数据缺乏商业可用的方案。
大多数可用的PC基数字器仅能在大约几分之几秒内存储此数据。
数字下变频DDC在持续时间期间可以数字记录RF信号。
在此实例中,我们仅需要记录5MHz信号(中心频率50MHz),而不是ADC的整个尼奎斯特带宽。
DDC允许除去其余数据,并降低数据率。
在现场可编程门阵列(FPGA)中实现时,简单的数字下变频分为3个性质不同的步:频率变换、滤波和分样(图1)。
频率变换和滤波第1步是频率变换。
5MHz频带需要降低变换到基带,靠乘或与载频(fc)正弦信号混频实现这种变换。
用数字控制振荡器(NCO)数字产生正弦波。
NCO通常也称之为本机振荡器(LO),它可以在精确频率和相位下产生取样波形。
随着信号从50MHz变频到基带,信号拷贝也从50 MHz变频到100 MHz。
基于此原因,新的基带信号必须滤波,去除较高频率的信号。
然而,到此我们的任务没有完成。
我们仍有1个在200ms/s取样的低频基带信号。
传输额外不必要数据时不希望PC总线过载,我们重新取样信号来降低有效取样率。
这靠分样实现,在规则的时间间隔内从数字化的信号中去除数据点。
在此例中,取样从200ms/s 下降到10ms/s,每20个取样去除19个取样。
数字下变频中基于CORDIC算法的NCO设计

数字下变频中基于CORDIC算法的NCO设计刘刚;蒋伟进;董胡;钟新跃【摘要】在数字下变频中传统数字控制振荡器(Numerically Controlled Oscillator,NCO)模块都是基于查找表结构的,该结构在FPGA内部实现需要占用大量ROM资源,针对这一问题,提出采用坐标旋转数字计算(Coordinate Rotation DigitalComputer,CORDIC)算法进行NCO设计,相比传统的NCO设计,该方法具有输出信号频谱纯度高、能够直接混频而不需要乘法器等优点.设计中采用变象限映射方法解决CORDIC算法无法全周期覆盖的问题,采用流水线技术解决串行迭代带来难以实时输出的问题.经过Modelsim仿真分析,实际输出值与理论值之间的相对误差在10-4~ 10-5数量级范围内,满足数字下变频中NCO的性能需要.【期刊名称】《无线电工程》【年(卷),期】2017(047)012【总页数】4页(P71-74)【关键词】数字下变频;坐标旋转数字计算方法;流水线;数字控制振荡器;现场可编程门阵列【作者】刘刚;蒋伟进;董胡;钟新跃【作者单位】长沙师范学院信息与工程系,湖南长沙410100;湖南商学院计算机与信息工程学院,湖南长沙410205;长沙师范学院信息与工程系,湖南长沙410100;长沙师范学院信息与工程系,湖南长沙410100【正文语种】中文【中图分类】TN911在软件无线电接收机中,数字下变频器是把ADC数字化后的高速数字中频信号变为低速的基带信号,便于后续的相关处理。
数字下变频器在这里起到前端ADC和后端通用DSP器件之间的桥梁作用,其性能的优劣会对整个软件无线电系统的性能产生直接的影响[1]。
因此,数字下变频技术成为软件无线电接收机的关键技术之一,成为制约软件无线电性能的重要器件之一[1]。
文献[2-3]中采用基于多相滤波结构来设计实现数字下变频器,虽然在一定程度上能够节省FPGA内部资源和实现高速数据流下数字下变频,但在性能上还有较大的提升空间,因为只有改进和优化数字下变频中NCO这一核心模块才能大幅度提高数字下变频的性能。
dds滤波算法

dds滤波算法DDS滤波算法是一种数字信号处理中常用的滤波算法,它可以有效地去除信号中的噪声和干扰,提取出我们所关注的信号成分。
DDS滤波算法的全称是Direct Digital Synthesis,直接数字合成。
它的原理是通过数字信号处理器(DSP)对输入信号进行采样和处理,然后再通过数字模拟转换器(DAC)将处理后的信号转换为模拟信号输出。
DDS滤波算法的核心是一个数字控制振荡器(NCO),它可以根据输入信号的频率和相位信息生成一个与之相对应的数字信号。
NCO的输出信号经过数字滤波器进行滤波处理,去除掉不需要的频率成分,最后通过DAC转换为模拟信号输出。
DDS滤波算法的优点是可以实现高精度的频率和相位控制,同时具有较低的噪声和失真。
DDS滤波算法的实现过程可以分为以下几个步骤:首先,需要对输入信号进行采样。
采样频率的选择要根据输入信号的最高频率成分来确定,一般要满足奈奎斯特采样定理,即采样频率要大于输入信号最高频率的两倍。
接下来,对采样得到的离散信号进行数字滤波处理。
数字滤波器可以选择不同的类型,如低通滤波器、高通滤波器、带通滤波器等,根据需要选择合适的滤波器类型和参数。
然后,将滤波后的信号输入到NCO中进行数字合成。
NCO根据输入信号的频率和相位信息生成一个与之相对应的数字信号。
NCO的输出信号经过数字滤波器进行滤波处理,去除掉不需要的频率成分。
最后,通过DAC将处理后的信号转换为模拟信号输出。
DAC的选择要根据输出信号的要求来确定,一般要考虑到输出信号的动态范围、失真和噪声等因素。
DDS滤波算法在实际应用中具有广泛的应用领域。
例如,在通信系统中,可以利用DDS滤波算法对接收到的信号进行滤波处理,去除掉噪声和干扰,提取出有效的信息。
在音频处理中,可以利用DDS滤波算法对音频信号进行滤波处理,提高音质和清晰度。
在雷达信号处理中,可以利用DDS滤波算法对雷达回波信号进行滤波处理,提取出目标信号。
高精度解调算法

高精度解调算法1. 引言高精度解调算法是一种用于信号处理的技术,旨在提取出原始信号中的有用信息。
它在许多领域中都有广泛应用,包括通信、雷达、无线电和音频处理等。
在本文中,我们将介绍高精度解调算法的基本原理、常见的应用场景以及一些常用的解调算法。
2. 基本原理高精度解调算法的基本原理是将输入信号进行变换和处理,以提取出所需的信息。
下面是一些常见的高精度解调算法:2.1 相位锁定环路(PLL)相位锁定环路是一种常见的高精度解调算法,它通过比较输入信号和参考信号之间的相位差来实现频率和相位的同步。
PLL通常由相位检测器、低通滤波器、数字控制振荡器(NCO)和反馈环组成。
2.2 调频解调器调频解调器是一种用于接收和解码调频(FM)信号的算法。
它通过检测输入信号中频率的变化来恢复出原始信息。
常见的调频解调器算法包括Costas环路和Foster-Seeley鉴频器。
2.3 脉冲编码调制解调器(PCM)脉冲编码调制解调器是一种用于数字通信的算法,它将模拟信号转换为数字信号。
PCM解调器通过检测输入信号中的脉冲位置来恢复出原始信息。
常见的PCM解调器算法包括差分解码和自适应等化器。
3. 应用场景高精度解调算法在许多领域中都有广泛应用。
下面是一些常见的应用场景:3.1 通信系统在通信系统中,高精度解调算法用于接收和处理传输过程中的信号。
它可以帮助提高接收端对传输数据的准确性和稳定性。
3.2 雷达系统雷达系统使用高精度解调算法来处理接收到的雷达信号,以提取出目标物体的位置、速度和其他相关信息。
3.3 无线电系统无线电系统使用高精度解调算法来接收和处理无线电信号。
它可以帮助识别不同频率、幅度和相位的无线电信号,并恢复出原始信息。
3.4 音频处理音频处理中的高精度解调算法用于提取音频信号中的频率和相位信息。
它可以帮助改善音频的质量和清晰度。
4. 常用解调算法除了上述提到的相位锁定环路、调频解调器和脉冲编码调制解调器等算法,还有一些其他常用的高精度解调算法:4.1 直接数字合成(DDS)直接数字合成是一种通过数字控制振荡器(NCO)生成任意波形的算法。
数字锁相环原理

数字锁相环原理数字锁相环(Digital Phase-Locked Loop,简称DPLL)是一种常见的数字信号处理技术,广泛应用于通信、雷达、导航、测量等领域。
它通过对输入信号进行频率和相位的跟踪和控制,实现信号的精确同步和解调。
本文将介绍数字锁相环的基本原理及其工作过程。
数字锁相环由相位比较器、数字控制振荡器(NCO)、低通滤波器和反馈控制电路等组成。
其工作原理可以简单描述为,首先,输入信号与NCO产生的参考信号经相位比较器比较,得到相位误差信号;然后,相位误差信号经过低通滤波器滤波处理,得到控制电压;最后,控制电压作用于NCO,调整其输出频率和相位,使得输入信号与参考信号同步。
整个过程不断迭代,直至达到稳定状态。
在数字锁相环中,相位比较器起着关键作用。
它能够准确比较输入信号和参考信号的相位差,并将其转换为数字形式的相位误差信号。
常见的相位比较器有边沿比较器、恒定增益比较器等,它们在不同应用场景下具有各自的优势和特点。
另外,NCO也是数字锁相环中的核心部件之一。
它能够根据控制电压实时调整输出信号的频率和相位,实现对输入信号的精确跟踪和同步。
NCO通常由相位累加器、频率控制器和相位控制器组成,通过对这些部件的协同工作,实现对输出信号的高精度控制。
低通滤波器在数字锁相环中也扮演着重要角色。
它能够滤除控制电压中的高频噪声,使得NCO的调节过程更加平稳和稳定。
低通滤波器的设计与参数选择对数字锁相环的性能影响巨大,需要根据具体应用需求进行合理设计和优化。
最后,反馈控制电路用于将经过滤波处理的控制电压反馈给NCO,实现闭环控制。
它能够实时监测和调节NCO的输出,保证数字锁相环在动态和静态条件下都能够稳定工作。
反馈控制电路的设计和调试是数字锁相环工程实践中的重要环节,直接关系到系统性能和稳定性。
综上所述,数字锁相环作为一种重要的数字信号处理技术,在现代通信和控制系统中发挥着不可替代的作用。
通过对其基本原理和工作过程的深入理解,可以更好地应用和优化数字锁相环,为工程实践提供有力支持。
基于FPGA的正交数控振荡器(Nco)的设计与实现

资 源 的 基 于 R M 查找 表 的 设计 方 法 。针 对 正 交 数 控 振 荡 器 N O 的 主 要 部 件 正 余 弦存 储 表 、 变模 计 数 器 进 行 了 算 O C 可
法 设 计 和 电路 设 计 , 在 A ea公 司的 F G 上 进 行 了验 证 , 形 仿 真 结 果 表 明 了 电路 设 计 的 正 确 性 。采 用 查找 表 的 并 hr PA 波
ZHANG n n A— i g,ZH AO i g Pn
( e a m n l t n nier g X ’ U i r o P s n eeo u i t n , ’f7 0 2 ,C ia D p r e tfEe r i E gnei , i伽 nv s f ot adT l mm n ai s Xia 1 1 1 hn ) t o coc n e s c c o t
中图 分 类 号 : N 5 T 72
文献标识码 : A
文 章 编 号 :1 7 — 2 6 2 1 ) 7 0 4 — 4 6 4 6 3 (0 1 1— 19 0
De i n n m p e e a i n fo t o o lNu e i a nt o s g a d i l m nt to o r h g na m rc lCo r l Os il t r ( c l o NCo )b s d n FPG a ae o A
u tbl t o n fe tv y i p o e he y t m u to c lbiiy a d y tm n e r t p a e me h d ca e ciel m r v t s se f nci n s a a lt n s se i t g ai on, mak s t e NCO un to e h f ci n
基于FPGA的正交数控振荡器_NCO_的设计与实现_张阿宁

基于FPGA 的正交数控振荡器(NCO )的设计与实现张阿宁,赵萍(西安邮电学院电子工程学院,陕西西安710121)摘要:在研究数控振荡器NCO 工作原理的基础上,通过分析对比几种不同的NCO 设计方法,采用了算法简单、节省资源的基于ROM 查找表的设计方法。
针对正交数控振荡器NCO 的主要部件正余弦存储表、可变模计数器进行了算法设计和电路设计,并在Altera 公司的FPGA 上进行了验证,波形仿真结果表明了电路设计的正确性。
采用查找表的方法可以有效提高系统功能的可扩展性和系统的可集成性,使得NCO 功能模块可以通过配置存储表、频率控制字来满足多种应用场合下的NCO 设计需要,可以广泛地应用于各种现代通信系统中。
关键词:软件无线电;数控振荡器;现场可编程门阵列;直接数字频率合成中图分类号:TN752文献标识码:A文章编号:1674-6236(2011)17-0149-04Design and implementation of orthogonal Numerical ControlOscillator (NCO )based on FPGAZHANG A -ning ,ZHAO Ping(Department of Electronic Engineering ,Xi ’an University of Posts and Telecommunications ,Xi ’an 710121,China )Abstract:This paper introduces the working principle of NCO ,through analysis and comparison of several different NCO design method ,uses a kind of simple and save resources based on ROM look -up table design method.According to orthogonal NCO main part is sine and cosine storage table and the variable mode counter ,algorithm and circuit design are presented ,and the test and waveform simulation results in Altera company ’s FPGA show the correctness of the circuit ing the look -up table method can effectively improve the system function scalability and system integration ,makes the NCO function module can through the configuration storage table ,frequency control word to meet many application situation's NCO design needs ,can widely used in all kinds of modern communication system.Key words:software radio ;Numerical Control Oscillator (NCO );Field Programmable Gata Array (FPGA );Direct Digital Synthesis (DDS )收稿日期:2011-07-18稿件编号:201107075作者简介:张阿宁(1979—),女,陕西西安人,助理工程师。
基于CPLD器件的数控振荡器(NCO)的设计

;
( 二进制编码) 经查找表查出, 完成相位到幅值转换。波形存
储器 的输出送到 D A转 换 器 , / / D A转换 器将 数字量形 式 的 收稿 日期 :05 1 — 8 第一作者 20 — 0 2 孛星沛 男 3岁 2
2 2 波形幅值存储器模块 的实现 .
设 计正( ) 找表分别 由两个 R M 宏模块 L P 余 弦查 O M 一
弦波信 号。
பைடு நூலகம்
在 MA UJ 平 台上进 行 了仿 真。这种 NX 的设 计 采用 Ⅺ S (3
直接数字频率合 成 ( D ) 术 , D S是 一 种非 常实 用 的 D 8技 而 D
2 N∞ 的设计 实现
本文在 N 0的硬件实现中, C 为了系统级综合和仿真 。 采 用 4M 的时钟速率和 9 0 位宽的频率控制字 k 由文献[ ] , 2 和 [] 分 析 D S的频 率 分 辨 率 满 足: 3的 D = /N= 2
i - .■ ● . J L1 t ∞ O -
田 8 NC 模 块仿 翼 波 形 O
7 .2 HZ 也就是说通过 改变 频率 控制 字 k来 改变 输 出正 8 1k ,
频率合成技 术 ,D 在 相对带 宽、 DS 频率 转换 时间、 高分辨 力 、 相位连续性 、 正交输出 以及集成化等一 系列性 能指标 方面远 远超过 了传统频 率合 成技术所能达到 的水平 , 为系统提供 了
用。
存器的数据输入端。累加寄存器将加法器在上一个时钟脉 冲作用后所产生的新相位数据反馈到加法器的输入端 , 以使
加法器在下一个时钟脉 冲的作用下继续与频率控制字 相加 。 这样 , 累加器在时钟 作用下 , 相位 不断 对频率 控制字进 行线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本文设计的 NCO 工作时钟为 100MHz,相位累加器的位数为 16 位,输入的频率控制字为 4CCCH,根据公式:
因此在实际设计中,采用的是图 2 所示的由 16 级 CORDIC 运算单元组成的流水线结构, 正常工作时只需 1 个时钟周期就能输出 1 个数据,为数据实现高速实时处理提供了前提。每 一级实现的功能是根据式(5)进行一次迭代,移位的位数等于当前的迭代级数,加减法选择 由该级中 Z 的最高位(符号位)决定,得到下一级的 X 、Y 和 Z 的值。经过 16 级流水线运 算后,Z 的值变为 0,X 和 Y 的值则为初始值 z0 的余弦和正弦值。每一级电路结构主要包 括 2 个移位器和 3 个加(减)法器,级与级之间直接相连,不需要额外的寄存器。θi 的值为 arctan(2-i),可将该小数转换为二进制数后,存储于存储单元中,为每一级流水线提供查 找表。若对于 16 级的流水线结构,则的范围是 0~15。
数控振荡器的 FPGA 实现
图 1 是数控振荡器的顶层电路。由图可见,频率控制字寄存器将接收到的的频率控制字 送入相位累加器,相位累加器对系统时钟进行计数,每到达输入频率控制字的值即对相位进 行累加,随后将累加值送入相位相加器,与相位控制字寄存器接收到的初始相位进行相加, 得到当前的相位值。其中,相位累加器是决定 NCO 性能的一个关键模块,可以利用 FPGA 器 件的进位链实现快速、高效的电路结构。然而,由于进位链必须位于临近的逻辑阵列块 CLB 和逻辑单元 LC 内,所以长的进位链会减少其它逻辑使用的布线资源;同时,过长的进位链 也会制约整个系统速度的提高。因此,设计中采用进位链和流水线技术相结合的办法。所谓 流水线技术,即把在一个时钟内要完成的逻辑操作分成几步较小的操作,并插入几个时钟周 期来提高系统的数据吞吐率。采用以上做法实现的相位累加器既能保证具有较高的资源利用 率,又能大幅提高系统的性能和速度。
足够的精度
为了避免使用大容量存储器,可以考虑利用算法来产生正余弦样本。基于矢量旋转的 CORDIC 算法正好满足了这一需求,该算法主要用于计算三角函数、双曲函数及其它一些基 本函数运算。它有线性的收敛域和序列的特性,只要迭代次数足够,即可保证结果有足够的 精度。
运算公式
Walther JS 于 1971 年提出了统一的 CORDIC 形式。假定初始向量 V1(x1 ,y1)旋转角度 θ 后得到向量 V2(x2,y2):
数控振荡器的基本实现原理
数控振荡器的作用是产生正交的正弦和余弦样本。传统方法是采用查表法(LUT),即事 先根据各个正余弦波相位计算好相位的正余弦值,并按相位角度作为地址存储该相位的正余 弦值,构成一个幅度 P 相位转换电路(即波形存储器)。在系统时钟的控制下,由相位累加器 对输入频率字不断累加,得到以该频率字为步进的数字相位,再通过相位相加模块进行初始 相位偏移,得到要输出的当前相位,将该值作为取样地址值送入幅度 P 相位转换电路,查表 获得正余弦信号样本。对于一个相位位数为 n ,输出信号幅度位数为 M 的数控振荡器,所 需查找表大小为 M×2n 。为了提高数控振荡器的频率分辨率,往往需要扩大波形存储器的 容量,造成存储资源的大量消耗。而且,当需要外挂 RAM 来存储波形时,由于受到 RAM 读 取速度的影响,数控振荡器的输出速率必然受到制约。因此,当需要设计高速、高精度的数 控振荡器时,不宜采用查表法。
结语
研究了正交数字混频器中数控振荡器的设计与实现方法,着重分析了如何在 FPGA 器件 中利用 CORDIC 迭代算法产生正余弦信号。结果表明,基于 CORDIC 迭代算法的数控振荡器, 仅用移位寄存器和加法器就可产生正余弦信号,不但省去了传统 NCO 庞大的存储器资源,而 且保留了一般数控振荡器频率分辨率高、频率变化速度快、相位可连续线性变化、生成的正 弦 P 余弦信号正交特性好等特点,非常适用于在正交数字混频器中进行高速高精度的数字调 制解调。
数字控制振荡器(NCO,numerically controlled oscillator)是软件无线电、直接数 据频率合成器(DDS,Direct digital synthesizer)、快速傅立叶变换(FFT,Fast Fourier Transform) 等的重要组成部分,同时也是决定其性能的主要因素之一,用于产生可控的正 弦波或余弦波。随着芯片集成度的提高、在信号处理、数字通信领域、调制解调、变频调速、 制导控制、电力电子等方面得到越来越广泛的应用。
经过上述相位的处理之后,即可获得具有所设定初始相位的一定频率的正余弦相位序 列,将此序列送入基于 CORDIC 算法的波形发生器,最终获得两路正交的正余弦输出序列。
NCO 的顶层电路结构
CORDIC 迭代算法的一种最直接的实现方法是,只设计一级 CORDIC 运算迭代单元,然后 在系统时钟的驱动下,将本级的输出作为本级的输入,通过同一级迭代完成运算。这种方法 虽然很直观,但是为了将计算结果提供给下一级运算而导致占用了大量的寄存器,带来许多 额外的资源消耗。而最大的缺点是运算速度较慢(需要 n-1 个时钟周期才能输出一个数据), 不利于数据的高速实时处理。
数控振荡器的仿真结果及性能分析
利用 ALTERA 公司的 QuartusII 软件,采用 VHDL 硬件描述语言对上述数控振荡器结构进 行描述,在 Modlesim 上通过功能仿真,结果正确后综合出电路网表,最后将程序下载至 ALTERA 公司生产的 Stratix 器件 EP1S20B780C6 实现。Leabharlann 数字振荡器高精度范围
在正交数字混频器中,采用数字频率合成技术,可以将数字处理延续到正交调制之后或 正交解调之前,滤波器和增益控制就可以用数字方法实现,I、Q 两路也就不会存在增益的 不平衡,加上数控振荡器(NCO)的低正交误差,可以使系统误差降低到数据的最低比特(LSB) 的高精度范围。
调制灵活性
此外,正交数字混频器更容易与数字信号处理技术结合,使得数字调制更加灵活,进而 实现软件无线电所要求的软件可更改的调制解调。 数控振荡器是正交数字混频器的核心部 分,它具有频率分辨率高、频率变化速度快、相位可连续线性变化和生成的正弦 P 余弦信号 正交特性好等特点。而且 NCO 的相位、幅度均已数字化,可以直接进行高精度的数字调制解 调。随着数字通信的发展,传送的数据速率越来越高。如何得到一个可数控的高频载波信号 是实现高速数字通信系统必须解决的问题。
CORDIC 迭代算法的流水线结构
设计中还应该注意迭代序列所能覆盖的角度范围,若直接采用 n 级迭代序列:0 ,1 , 2 ,…,n - 1 ,则迭代所能覆盖的角度范围仅有- 99.9°~99.9°。本设计采用了增加迭 代次数的方法来扩大角度覆盖范围,即增加两个 i = 0 的迭代,将迭代序列扩展为 0,0,0, 1,2,…,n-1,从而使角度覆盖范围也扩大到-π~π。
即: 若 每 次 旋 转 的 角 度 θ 是 正 切 值 为 2 的 倍 数 , 即 θi=arctan(2-i) , 则 cosθi=(1+2-2i)-1/2 。假设以 δi 代表矢量的旋转方向,+1 表示逆时针旋转,-1 表示顺 时针旋转,故第 i 步旋转可用下式表示: 其中:(1+2-2i)-1/2 为模校正因子。对于字长一定的运算,该因子是一个常数,用 K 表示,以 16 bits 字长为例,则: 可见,迭代运算不能使幅值比例因子恒为 1。为了抵消因迭代产生的比例因子的影响, 可将输入数据 X,Y 校正后再参与运算,以避免在迭代运算中增加校正运算,降低 CORDIC 算法的速度。由此运算迭代式可以简化成: 公式(5)运算仅通过加法器及移位器就可以实现。此外,若用 Zi 表示第 i 次旋转时与目 标角度之差, 则: 经过 n 次旋转后,式(5)的 n 次迭代可以得到以下结果: 本文介绍的数控振荡器的设计是在式(7)的基础上,给定 x0=K ,y0=0,则迭代结果为: 将所需产生的角度值作为 z0 输入,通过式(5)、(6)的迭代运算,迭代结果输出的 xn 和 yn 就是所需要的三角函数值。
其中:Φword 为输入的频率控制字;fclk 为工作时钟;N 为相位累加器位数,可算出 NCO 输出的正余弦信号的频率;fout 为 30MHZ ;频率分辨率 Δf ≈1.5 kHz。频率分辨率说 明了若通过输入频率控制字来改变输出正余弦信号的频率时,可以达到 1.5 kHz 的最小步 进。另外,也可以根据实际需要的频率改变输入频率控制字值。当然,NCO 输出频率的上限 要受到 Nyquist 定律的限制,即 fout 的最大值为 fclkP2,实际设计一般不大于 0.4fclk。 图 3 为数控振荡器的部分仿真时序图。
