静定刚架内力计算
合集下载
03结构力学 第三章 静定结构的内力计算3.3 静定刚架的内力计算(邓军)

剪力图: 剪力符号规定与直梁中的规定相同;剪力图可画在杆件的任一 侧,但剪力图上要标明正负号。 轴力图:
轴力仍以受拉为正,受压为负;轴力图可画在杆件的任一侧或 与纵坐标对称地画在杆件的两边,但需在轴力图上标明正负号。
§3.3 静定刚架的计算
例1 绘制如图所示门式刚架在半跨均布荷载作用下的内力图。
§3.3 静定刚架的计算
§3.3 静定刚架的计算
§3.3 静定刚架的计算
§3.3 静定刚架的计算
静定刚架的组成及类型
平面刚架是由直杆(梁和柱)组成的平面结构。
刚架中的结点部分或全部是刚节点。
在刚节点处,各杆件连成一个整体,杆件之间不能发生相对 移动和相对转动,刚架变形时各杆之间的夹角保持不变,因 此刚节点能够承受弯矩、剪力和轴力。
解:
1)求支座反力 由整体平衡方程可得
M A 0, 6 3 12FyB 0 M B 0, 6 9 12FyA 0
X 0, FxA FxB 0
取铰C右边部分为隔离体
MC 0, 6.5FxB 6FyB 0
求得
FyB =1.5kN() FyA=4.5kN() FxA =1.384 kN()
§3.3 静定刚架的计算
2)作弯矩图
求出杆端弯矩(设弯矩方正向为使刚架内侧受拉)后,画于受 拉一侧并连以直线,再叠加简支梁的弯矩图。
以DC杆为例
M DC 1.384 4.5 6.23kN m, MCD 0
CD中点弯矩为 1.3845.5 133 1 1 4.5 6 1.388kN m 22
(2)为计算静定刚架位移和分析超静定刚架打下基础。
2)刚架各杆内力的求法
从力学观点看,刚架是梁的组合结构,因此刚架的内力求法 原则上与梁的内力计算相同。 通常是利用刚架的整体或个体的平衡条件求出各支座反力和 铰接点处的约束反力,然后用截面法逐个计算杆件内力。
轴力仍以受拉为正,受压为负;轴力图可画在杆件的任一侧或 与纵坐标对称地画在杆件的两边,但需在轴力图上标明正负号。
§3.3 静定刚架的计算
例1 绘制如图所示门式刚架在半跨均布荷载作用下的内力图。
§3.3 静定刚架的计算
§3.3 静定刚架的计算
§3.3 静定刚架的计算
§3.3 静定刚架的计算
静定刚架的组成及类型
平面刚架是由直杆(梁和柱)组成的平面结构。
刚架中的结点部分或全部是刚节点。
在刚节点处,各杆件连成一个整体,杆件之间不能发生相对 移动和相对转动,刚架变形时各杆之间的夹角保持不变,因 此刚节点能够承受弯矩、剪力和轴力。
解:
1)求支座反力 由整体平衡方程可得
M A 0, 6 3 12FyB 0 M B 0, 6 9 12FyA 0
X 0, FxA FxB 0
取铰C右边部分为隔离体
MC 0, 6.5FxB 6FyB 0
求得
FyB =1.5kN() FyA=4.5kN() FxA =1.384 kN()
§3.3 静定刚架的计算
2)作弯矩图
求出杆端弯矩(设弯矩方正向为使刚架内侧受拉)后,画于受 拉一侧并连以直线,再叠加简支梁的弯矩图。
以DC杆为例
M DC 1.384 4.5 6.23kN m, MCD 0
CD中点弯矩为 1.3845.5 133 1 1 4.5 6 1.388kN m 22
(2)为计算静定刚架位移和分析超静定刚架打下基础。
2)刚架各杆内力的求法
从力学观点看,刚架是梁的组合结构,因此刚架的内力求法 原则上与梁的内力计算相同。 通常是利用刚架的整体或个体的平衡条件求出各支座反力和 铰接点处的约束反力,然后用截面法逐个计算杆件内力。
结构力学二3-静定结构的内力计算

以例说明如下
例 绘制刚架的弯矩图。 解:
E 5kN
由刚架整体平衡条件 ∑X=0 得 HB=5kN← 此时不需再求竖向反力便可 绘出弯矩图。 有:
30
20 20 75 45
40
0
MA=0 , MEC=0 MCE=20kN· m(外) MCD=20kN· m(外) MB=0 MDB=30kN· m(外) MDC=40kN· m(外)
有突变
铰或 作用处 自由端 (无m)
m
Q图
M图
水平线
⊕
⊖㊀
Q=0 处 突变值为P 如变号 无变化
有极值 尖角指向同P 有极值 有突变 M=0 有尖角
斜直线
→
↑
利用上述关系可迅速正确地绘制梁的内力图(简易法)
简易法绘制内力图的一般步骤:
(1)求支反力。 (2)分段:凡外力不连续处均应作为分段点, 如集中力和集中力偶作用处,均布荷载两端点等。 (3)定点:据各梁段的内力图形状,选定控制 截面。如集中力和集中力偶作用点两侧的截面、均 布荷载起迄点等。用截面法求出这些截面的内力值, 按比例绘出相应的内力竖标,便定出了内力图的各 控制点。
说明:
(a)M图画在杆件受拉的一侧。 (b)Q、N的正负号规定同梁。Q、N图可画在杆的 任意一侧,但必须注明正负号。 (c)汇交于一点的各杆端截 面的内力用两个下标表示,例如: MAB表示AB杆A端的弯矩。 MAB
例 作图示刚架的内力图
RB↑
←HA
VA→
CB杆:
由∑ X=0 可得: M = CD RB=42kN↑ HA=48kN←, H (左) A=6×8=48kN← 由∑M144 VA=22kN↓ 48 A=0 可得: MEB=MEC=42×3 ↑ (2)逐杆绘M图 R=126kN = 126 · m (下) B 192 MDC=0 CD杆: M =42 × 6-20 × 3 由 ∑Y=0 可得: CB MCD=48kN·m(左) =192kN· m(下) VA=42-20=22kN↓
3静定结构的内力计算

工程中的单跨静定梁,按其支座情况可分为三种: (1)简支梁:该梁的一端为固定铰支座,另一端为可动铰支座。 (2)外伸梁:一端或两端向外伸出的简支梁称为外伸梁。 (3)悬臂梁:该梁的一端为固定端支座,另一端为自由端。
①简支梁
②外伸梁
③悬臂梁
3
二、梁的内力
1、内力计算法——截面法
P1
A
m
FAx
K
n
P2 B
8
斜梁介绍
工程中,斜梁和斜杆是常遇到的,如楼梯梁、刚架中的斜杆等。斜梁 受均布荷载时有两种表示方法: (1)按水平方向分布的形式给出(人群、雪荷载等),用 q 表示。 (2)按沿轴线方向分布方式给出(自重),用 q’ 表示。
q 与 q’间的转换关系:
qdx = qds q = q
cos
dM dx
= FQ
无荷载区段 平行轴线
FQ图
M图
斜直线
均布荷载区段 集中力作用处 集中力偶作用处
↓↓↓↓↓↓
+ -
二次抛物线
凸向即q指向
发生突变
+P -
出现尖点
尖点指向即P的指向
无变化
发生突变
m
两直线平行
注备
FS=0区段M图 FS=0处,M 平行于轴线 达到极值
12
三、叠加法作弯矩图
1. 叠加原理: 几个载荷共同作用的效果,等于各个载荷单独
吊杆
带拉杆的三铰拱
拉杆折线形
拉杆
花篮螺丝
带吊杆的三铰拱
3、三铰拱的内力计算
1)、拱的内力计算原理仍然是截面法。 2)、拱通常以受压为主,因此规定轴力以受压为正。 3)、计算时常将拱与相应简支梁对比,通过对比完成计算。
45
①简支梁
②外伸梁
③悬臂梁
3
二、梁的内力
1、内力计算法——截面法
P1
A
m
FAx
K
n
P2 B
8
斜梁介绍
工程中,斜梁和斜杆是常遇到的,如楼梯梁、刚架中的斜杆等。斜梁 受均布荷载时有两种表示方法: (1)按水平方向分布的形式给出(人群、雪荷载等),用 q 表示。 (2)按沿轴线方向分布方式给出(自重),用 q’ 表示。
q 与 q’间的转换关系:
qdx = qds q = q
cos
dM dx
= FQ
无荷载区段 平行轴线
FQ图
M图
斜直线
均布荷载区段 集中力作用处 集中力偶作用处
↓↓↓↓↓↓
+ -
二次抛物线
凸向即q指向
发生突变
+P -
出现尖点
尖点指向即P的指向
无变化
发生突变
m
两直线平行
注备
FS=0区段M图 FS=0处,M 平行于轴线 达到极值
12
三、叠加法作弯矩图
1. 叠加原理: 几个载荷共同作用的效果,等于各个载荷单独
吊杆
带拉杆的三铰拱
拉杆折线形
拉杆
花篮螺丝
带吊杆的三铰拱
3、三铰拱的内力计算
1)、拱的内力计算原理仍然是截面法。 2)、拱通常以受压为主,因此规定轴力以受压为正。 3)、计算时常将拱与相应简支梁对比,通过对比完成计算。
45
静定结构的内力计算 教程

拆成单个杆,求出杆两端的弯矩,按与单跨梁相同的方法画弯矩图 (1)无荷载分布段(q=0), FQ图为水平线,M图为斜直线。 (2)均布荷载段(q=常数), FQ图为斜直线,M图为抛物线,且凸向与荷 载指向相同。 (3)集中力作用处,FQ图有突变,且突变量等于力值; M图有尖点,且指 向与荷载相同。 (4)集中力偶作用处, M图有突变,且突变量等于力偶值; FQ图无变化。
工程力学
第十四章
静定结构的内力计算
b、求D点的内力 先求计算参数:
xD 3m
dy 4 f 4 4 tg D 2 ( L 2 x) 2 (12 2 3) 0.667 dx L 12 MD D 3342' Cos D 0.832
4 4 yD 2 (12 3) 3 3m 12
工程力学
第十四章
静定结构的内力计算
3、杆端内力的计算 先求出刚架的支座反力,再利用截面法求出各杆杆端内力 (1)在待求内力的截面截开,取任一部分为隔离体。 (2)画隔离体的受力图。 (3)利用隔离体的平衡条件,求出截面上的剪力、轴力和弯矩。 (4)利用结点的平衡条件校核刚结点杆端内力值。 4、刚架弯矩图的绘制
i i
与右图简支梁的支座反力:
Pb l Pa l
F
0 AY
i i
F
0 BY
i i
FAY F
0 AY
0 FBY FBY
工程力学
第十四章
静定结构的内力计算
分析推力H 式:
FAY l1 P 1 (l1 a1 ) H f
上式中的分子
FAY l1 P 1 (l1 a1 )
MEC=0kN•m CE杆上为均布荷载,弯矩图为抛物线 。 利用叠加法求出中点截面弯矩MCE中=30+60=90kN•m
工程力学31 静定平面刚架的内力计算

35
F
C
XE E
B
YE
YE
A
XE
33
FP
FP a
D
F
2FPa 2FP 0
A
E0
FP 2FP
FP
C
D
F
FP
B
0 XE E
FP
2FP YE
FP
2FP
34
C
B
FRB FP FP
变形曲线
结构的变形曲线:
1. 必须符合支座的约束条件和杆件的联结条件; 2. 必须正确反映结点线位移和角位移的方向; 3. 必须正确反映杆件的弯曲方向。
静定平面刚架的内力
1
31
❖ 由多根直杆组成 ❖ 杆件之间的结点多为刚结点
2
刚结点
❖变形特点:限制相对的转动和移动 ❖受力特点:可传递弯矩、剪力和轴力
3
32
悬臂刚架 简支刚架
三铰刚架
4
3 ❖内力类型:弯矩、剪力、轴力 ❖计算方法:截面法 ❖内力的符号规定:
弯矩:取消正负规定,弯矩图画在受拉一侧。 剪力:符号规定不变。 轴力:符号规定不变。 轴力图和剪力图习惯上同号画在同侧,标明正负
(2) 作M图
10
(3) 作FQ图
由隔离体平衡条件求杆端剪力
FQAD 1.384kN
FQBE 1.384kN
FQDC
1 6.23 6 3 3.83kN
6.23
FQCD
1 6.23
6.23
6 3
1.86kN
FQCE
1 6.23
6.23
0.985kN
11
1.384 4.5
1.384
(4) 作FN图 由结点平衡条件求杆端轴力
F
C
XE E
B
YE
YE
A
XE
33
FP
FP a
D
F
2FPa 2FP 0
A
E0
FP 2FP
FP
C
D
F
FP
B
0 XE E
FP
2FP YE
FP
2FP
34
C
B
FRB FP FP
变形曲线
结构的变形曲线:
1. 必须符合支座的约束条件和杆件的联结条件; 2. 必须正确反映结点线位移和角位移的方向; 3. 必须正确反映杆件的弯曲方向。
静定平面刚架的内力
1
31
❖ 由多根直杆组成 ❖ 杆件之间的结点多为刚结点
2
刚结点
❖变形特点:限制相对的转动和移动 ❖受力特点:可传递弯矩、剪力和轴力
3
32
悬臂刚架 简支刚架
三铰刚架
4
3 ❖内力类型:弯矩、剪力、轴力 ❖计算方法:截面法 ❖内力的符号规定:
弯矩:取消正负规定,弯矩图画在受拉一侧。 剪力:符号规定不变。 轴力:符号规定不变。 轴力图和剪力图习惯上同号画在同侧,标明正负
(2) 作M图
10
(3) 作FQ图
由隔离体平衡条件求杆端剪力
FQAD 1.384kN
FQBE 1.384kN
FQDC
1 6.23 6 3 3.83kN
6.23
FQCD
1 6.23
6.23
6 3
1.86kN
FQCE
1 6.23
6.23
0.985kN
11
1.384 4.5
1.384
(4) 作FN图 由结点平衡条件求杆端轴力
静定梁与静定刚架

(二)绘内力图:
H A
=0
V
A =130KN
X 0 Y 0 M 0
C
NC 0 QC 130 KN M C 130 KN .M
第3章 例题: 试绘制图示外伸梁的内力图。
解:
10KN/m A HA=0 4m C 2m D B E 30KN.m 20KN
(1)计算支座反力
2m
2kN E
2m F
F
2m
G 2kN
2m
(b)
A
4kN/m B
C
G 2kN
G
B
11kN 4
4kN
4
(d)
8 7
(e) 9
4 M(kN.m) 2 2
Q(kN)
2
第3章 例题2: 图示三跨静定梁,全长承受均布荷载q,试确定铰E、F的位置,使中 间一跨支座的负弯矩与跨中正弯矩数据数值相等。
第3章
3.3 静定平面刚架的内力计算 一、刚架的组成 1、刚架的特征 由若干梁和柱用刚结点联结而成的结构。具有刚结点是 刚架的主要特征。 2、刚架的应用 刚架在工程上有广泛的应用。
(1)斜梁的倾角为常数,而曲梁各截面的的倾角是变量。 (2)计算曲梁的倾角时,可先写出曲梁的轴线方程y=f(x),而后对x求一 阶导数,进而确定倾角:
dy tan ; dx
tan1 (tan )
(3)角以由x轴的正方向逆时针转到切线方向时为正,反时针方向为负。
例题:试求图示曲梁C截面的内力值。已知曲梁轴线方程为:
y 4f 4 4 (l x) x 2 (12 1.5) 1.5 1.75m l2 12
4f 4 4 tan yx 1.5 2 (l 2 x) x1.5 2 (12 2 1.5) 1 l 12 2 450 sin con 0.707 2
静定刚架的内力计算及内力图

静定刚架的内力计算及内力图(步骤)求如图所示的刚架内力图:qXD解:(1)求支座反力。
ΣΧ=0 求得XD=q α() ΣMA=0 求得YD=32q α () ΣY=0解得YA=12q α()(2)画轴力图N N AB =-12 q α(压) N AC =- q α(压) N CD =-32q α(压) 求轴力可以从任一侧求,可设为正(即拉),按平衡求出为正值即为拉,负值即为压。
注:轴力图画在哪侧皆可,但一定要标出正负号。
轴力图N 如下;q α32q α(3)剪力图VV AE =0 V EB =- q α V DC =q α V BC =12q α V CB =-32q α v cd=q α 特点:没有荷载部分为平直线,有均布荷载部分为斜直线。
剪力图V 如下剪力图画在哪侧皆可,(4)画弯矩图(刚架内侧受拉为正,外侧受拉为负)区段叠加的控制点为 1 端部 2均布荷载的起止点 3其他的位置可分开求或叠加(一般在一个段内有集中力作用在均布荷载的位置上时,在集中力处分开。
) 先求每根杆两端的弯矩,用虚线连接,段间空载的直接连接,有力的叠加。
M 图特点:1均布荷载:抛物线 2无荷载:直线 3集中力:与力一致的方向产生尖点叠加大小 集中力点处:力的方向叠加Fab l(特别地,当α=b 时代入式子为fl 41) 均布荷载中点:28qlM AB =0 M BA =q α2(左) M DC =0 M CD = q α×2α=2q α2(右)M BC = q α2(上) M CBCD受力处E l22a 0,再用直线连接即可。
注:不管是简支梁与否,受力处的叠加都是加上M=Fabl。
受均布荷载的中点处叠加的弯矩的大小是向力的方向移动M=28ql 注:此处所说的简支是两端有支撑即可。
静定梁和刚架内力分析

(0<x<l ) (0≤x<l)
M
(-)
(c)
x
2.作剪力图和弯矩图:
由剪力方程可知,当 0 <x <l,时(即 AB 段上),剪力为 常数,因此剪力图为一条水平的直线;由弯矩方程可知,AB 梁段上沿着轴线方向弯矩呈线性变化,因此,弯矩图为一条斜 直线,只需求出两个端截面上
F A FQ x m m l
在列平衡方程求解内力时,需事先确定截面内力的方向, 而此时截面内力为未知力,因此,一般假定截面内力沿其正向 作用,则计算得到的正负号就是该截面内力的正负号。 另外,在利用截面法求解前,通常先确定支座反力,因支 座反力并无正负规定,在求支反力前可任意假设正方向。
若结果为正,则表示支反力实际方向与假设方向相同;
上所有外力对该截面形心的力矩的代数和。
其中外力对横截面形心之矩正负号选取规律为: (1)力——不论横截面左侧还是右侧,只要向上就取正,
反之取负;
(2)力偶——横截面左侧顺时针或右侧逆时针取正,反之 取负。 利用上述结论,可以不画分离体的受力图、不列平衡方 程,直接得出横截面的剪力和弯矩。这种方法称为直接法。 直接法将在以后求指定截面内力中被广泛使用。
2
求梁指定截面上的内力的方法: 剪力:梁任一横截面上的剪力在数值上等于该截面一侧梁段 上所有外力在平行于截面方向投影的代数和。 其中外力正负号选取规律为: 横截面左侧梁段上向上的外力取正,横截面右侧梁段上
向下的外力取正;反之取负。
简记为左上右下取正,反之取负。
弯矩:梁任一横截面上的弯矩在数值上等于该截面一侧梁段
若外力或外力偶矩使所考虑的梁段产生向下凸的变形(即 上部受压,下部受拉)时,等式右方取正号,反之,取负号。 此规律可简化记为“下凸弯矩正”或“左顺,右逆弯矩 正” ,相反为负。
第七章静定结构的内力计算

C
B
q a
qa 2
qa
A
a
qa
2
1.求支反力 2.分段 3.截面法求各段杆端内力值 4.用直线或曲线连接各段 5.标出数据、正负、图名
M CB
qa2 2
(下拉)
M CA
qa2 2
(右拉)
qa 2
C2
B
qa 2
2
qa 2
8
A
M
内力图的作法——剪力图
C
B
qa 2
qa
FQAC qa
FQCA 0
3m 1m
5kN
A
C
D
B
5kN 4kN
5m
4kN
5kN
FQDA
M DA
FDA
截面法计算D截面杆端内力
5kN
A
C
D
FNDC
M DC
FDC
4kN
3m 1m
B
5kN 4kN
5m
4kN
截面法计算D截面杆端内力
3m 1m
5kN
A
C
D
B
5kN 4kN
5m
4kN
FNDB
M DB
FQDB
5kN
4kN
内力图的作法——弯矩图
超静定结构
对于具有多余约束的几何不变体系,却不 能由静力平衡方程求得其全部反力和内力,这 类结构称为超静定结构
杆件类型
杆件
内力:轴力、剪力、弯矩 梁式杆
类型:梁、刚架、拱
链杆
内力:轴力 类型:桁架
梁
概念:是一种受弯构件,其轴线为直线, 有单跨和 多跨之分
单跨静定梁
6-2-2静定平面刚架的内力计算和内力图绘制.

(1)刚架任一横截面上的弯矩,其数值等于该截面任一边刚架
上所有外力对该截面形心之矩的代数和。力矩与该截面上规定的 正号弯矩的转向相反时为正,相同时为负。 (2)刚架任一横截面上的剪力,其数值等于该截面任一边刚架上 所有外力在该截面方向上投影的代数和。外力与该截面上正号剪 力的方向相反时为正,相同时为负。
作用点、分布荷载作用的起点和终点等)和杆件的连接点作为控
制截面,按刚架内力计算规律,计算各控制截面上的内力值。
国家共享型教学资源库
四川建筑职业技术学院
(3)按单跨静定梁的内力图的绘制方法,逐杆绘制内力图, 即用区段叠加法绘制弯矩图,由微分关系法绘制剪力图和轴 力图;最后将各杆的内力图连在一起,即得整个刚架的内力 图。
M BE 0
M EB FBx 4.5 62.1 kN m (右侧受拉)
M CE 0
M EC M EB 62.1 kN m
(上侧受拉)
四川建筑职业技术学院
国家共享型教学资源库
(3)绘剪力图。
FS AD FS DA 13.8 kN
FS BE FS EB 13.8 kN
四川建筑职业技术学院
例6-3 绘制图所示简支刚架的内力图。
解 (1)求支座反力。 FAx=16 kN, FBx=12 kN, FBy=24 kN
国。将刚架分为AC、CE、CD和DB
四段,取每段杆的两端为控制截面。这些截面上的内力为
MAC=0 MCA=-2kN/m×6m×3m=-36kN· m (左侧受拉) MCD= MCA=-36 kN· m (上侧受拉) MDC=-12kN×6m +12 kN· m =-60 kN· m (上侧受拉) MDB=-12kN×6m =-72 kN· m (右侧受拉) MBD=0 FSAC=0 FSCA=-2kN/m×6m=-12 kN FSCE= FSEC=16kN FSED=FSDE=-24kN FSDB=FSBD=12kN FNAC=FNCA=-16kN FNCD=FNDC=-12kN FNDB=FNBD=-24kN
工程力学中静定结构的内力计算

a
a
B XB X
YB
∑X=0 XC=XB=25kN ∑Y=0 YC=60-55=5kN ∑X=0 XA=25-40= -15kN
a
5kN
25kN
C
2m
y
25kN Fs 图
C
60kN
55kN
A
20kN· m
15k B N A 5kN
4m
25kN
B 4m
C
25kN 55kN
X
C
P2 P1 k y H A VA a3 b3 B VB H x 三铰拱与相应之简 支梁反力比较: VA =VA ° P3 B VB ° VB =VB ° HA=HB=H= MC°/f k C
P3
a2
a1 b1
b2
H=0
A VA°
P1
k1
P2 C
t
Mk
P1
y
n
k
Nk
∑Mk(F)=0, MK=[VAxk - P1 (xk- a1 )]-Hyk
FVb ×16 – 20 × 4 – 5 ×8 ×12=0
FVa=25KN FVb=35KN FHa=FHb
ΣMc=0
P=20Kn
FHa×4+20 ×4 – 25 ×8=0
FHc
FVc
FHa=30KN
FHa
4m 4m
FVa=25KN
4m
Σ Mo=0 . Mad=0 ΣХ=0. FQad+30=0
桁架的名称
上弦杆
桁高
斜杆 竖杆 下弦杆 跨度
1、按桁架的外形分为:
桁架的分类
a、三角形桁架
b、矩形桁架
《结构力学》静定结构内力计算

只承受竖向荷载和弯矩
FP1 A
FP2
B
C
基本部分:能独立承受外载。 附属部分:不能独立承受外载。
FP
A
B
C
■作用在两部分交接处的集 中力,由基本部分来承担。
FP1
FP2
A B
■基本部分上的荷载不影响附 属部分受力。
■附属部分上的荷载影响基本 部分受力。
先算附属部分, 后算基本部分。
例 确定x值,使支座B处弯矩与AB跨中弯矩相等,画弯矩图
ql ql/2
FQ图 ql
7ql/4 ql
5ql/4 ql/2
3ql/4
ql/2
练习
10kNm 20kN 10kN
10kN/m
1m 1m 1m 1m
1m 1m 10kN/m
10kNm
20kN 10kN 0
0
30kN
10kNm
20kN 10kNm
10kNm
10kNm
20kN 10kN 0
0
30kN
2m 2m
解 (1)求支反力
q=20kN/m FP=40kN
70kN
50kN
(2)取隔离体,求截面内力
MC C FQC
FP=40kN
B 50kN
(2)叠加法作弯矩图
120kNm
+
40kNm
40kNm
=
120kNm
40kNm
40kNm M图
例 试绘制梁的弯矩图。
40kNm
FP=40kN q=20kN/m
26
26
8 FQ图(kN)
6
12
M图(kNm)
24 12
例
解 (1)求支反力
静定结构的内力分析

40
第 三 章80 静定结构的内力计算
D
FNDE FNED
E
30
30
FNDC
FNEB
FQ
40 kN
FN 30 kN
80 kN
练习:
第三章
静定结构的内力计算
解: (1) 求支座反力。
F=qa
C
D
由 X 0
E
FxA q 2a 0
q
a B
得 FAx 2qa
a
由 M A 0
FxA
A
FyB
2qa a F a FyB 2a 0
首先进行定性分析。
由内力图的外观校核。杆上无分布荷载FS图为水 平直线;M图为斜直线。杆上有分布荷载FS图为斜直 线;M图为二次抛物线。 FS图为零的截面M为极值。 杆上集中荷载作用的截面, FS图上有突变;M图上有折 弯。根据这些特征来检查,本题的M图、FS图均无误。
第 三 章 静定结构的内力计算
6
FA=58 kN 26
10
18 FB=12 kN
q ME
FQE
MF
FS 图 ( kN )
FQF
第 三 章 静定结构的内力计算
二、 多跨静定梁 (multi-span statically determinate beam)
附属部分--依赖基本
基本部分--不依赖其它
部分的存在才维持几
部分而能独立地维持其
据
3.外力与杆轴关系(平行,垂直,重合) 4.特殊部分(悬臂部分,简支部分)
5.区段叠加法作弯矩图
第 三 章 静定结构的内力计算
结点平衡条件的应用:
一、铰结点: (集中力偶只能作用于杆端处)
M
《结构力学》第三章 静定结构内力计算(1)

技巧:“求谁不管谁”:不考虑待求未知力,而考虑其
它未知力有什么特点,具体分为下面两种情况:
(a)其余未知力平行,在其垂直方向投影。
(b)其余未知力汇交于一点,对该点取矩。
X 0,X A 0;
1
1
MB
0,YA
l ql
l 2
0,YA
ql 2
Y
0,YA
YB
ql
0,YB
1 2
ql
step2:求指定截面内力 (1)取脱离体:从指定c截面截开梁,取左半脱离体为 研究对象,受力如图所示:
轴力、剪力 符号规定
梁、拱的弯 矩符号通常 假定使下侧 受拉为正
2、杆件任一截面上内力的计算---截面法
沿计算截面用一假想截面将构件切开,任取一侧 脱离体为研究对象,利用脱离体的静力平衡条 件,可建立三个平衡方程:
X 0,Y 0,M 0
由此就可求得杆件任一截面上的内力。
注意:
• 脱离体要与周围的约束全部断开,并用相应的约束力 代替。例如,去掉辊轴支座、铰支座、固定支座时应 分别添加一个、二个以及三个支座反力,等等。
(二)简支结构
通过一铰、一链杆或三根链杆与基础相连的结构。
(三)三铰结构
若结构体系(不含基础)有两个刚片,其与基础 的连接满足三刚片法则,则称该体系为三铰结 构。
(四)组合结构
多次运用几何不变体系的简单组成规则构成的结 构。
2、静定结构内力分析(即绘制内力图) 方法
有三种常用的绘制内力图的方法。
(2)熟记几种常见单跨梁的弯矩图,如悬臂梁、简
支梁等。特别记住简支梁在均布荷载、集中力以及集 中力偶作用下的弯矩图。
(1)
(2) (3)
梁长均为L
静定刚架内力计算

-3
3m
3m 9kN
cos 2 5
lDC lEC 3.35m
-
0.45
-
5.82
-
N图(kN)
9
6D
ααQQC1CCN.CENC7DE9D↓C↓↓47α↓k.↓1N↓α6↓/m3.58 E
1.79 3.13QDC2
Q 2
EC
NC 9E
校∑Q核NX∑Q∑QNXMCCNMMECEDEDCE=XC(D=CE==N1C3=2=6.C07-3-66+EYN.9.-+4+N55Q(7D5333k83.kC.C(.E.8N131.31kN×DCc532.)63N×o18×=)kkks23cQ4N3NN+1o×.D4.0s3+7C5.5149×1=.×+57.()51973s02+..si.5n51i3n8+6.+03+315(+..1731Q2.975)E9QsC50in=C3E.5=008)00cos
绘制图示刚 架的弯矩图
仅绘M图,并不需要 求出全部反力.
先由AD ∑Y=0
得 YA=80kN
A ↓↓↓↓↓↓↓↓↓↓
D 120
E q=20kN/m
80kN 90
120 ↓↓↓↓↓↓↓↓
F
C
180 MEA=80×6-½ ×2200×k6N²=120
60
120
62.5
180
再由整体
∑X=0 得 XB=20kN
状特征和绘制内力图的叠加法。
4.会恰当选取分离体和平衡方程计算静定结构的内力。如何选取视具体情况(结构情 况、荷载情况)而定。当不知如何下手时,宜考察结构的几何组成。
3m
3m 9kN
cos 2 5
lDC lEC 3.35m
-
0.45
-
5.82
-
N图(kN)
9
6D
ααQQC1CCN.CENC7DE9D↓C↓↓47α↓k.↓1N↓α6↓/m3.58 E
1.79 3.13QDC2
Q 2
EC
NC 9E
校∑Q核NX∑Q∑QNXMCCNMMECEDEDCE=XC(D=CE==N1C3=2=6.C07-3-66+EYN.9.-+4+N55Q(7D5333k83.kC.C(.E.8N131.31kN×DCc532.)63N×o18×=)kkks23cQ4N3NN+1o×.D4.0s3+7C5.5149×1=.×+57.()51973s02+..si.5n51i3n8+6.+03+315(+..1731Q2.975)E9QsC50in=C3E.5=008)00cos
绘制图示刚 架的弯矩图
仅绘M图,并不需要 求出全部反力.
先由AD ∑Y=0
得 YA=80kN
A ↓↓↓↓↓↓↓↓↓↓
D 120
E q=20kN/m
80kN 90
120 ↓↓↓↓↓↓↓↓
F
C
180 MEA=80×6-½ ×2200×k6N²=120
60
120
62.5
180
再由整体
∑X=0 得 XB=20kN
状特征和绘制内力图的叠加法。
4.会恰当选取分离体和平衡方程计算静定结构的内力。如何选取视具体情况(结构情 况、荷载情况)而定。当不知如何下手时,宜考察结构的几何组成。
第3章_静定结构的内力分析
第3章
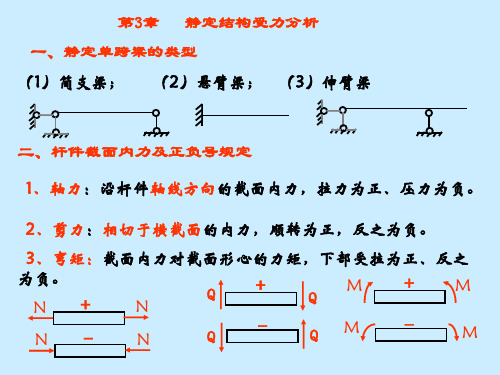
静定结构受力分析
一、静定单跨梁的类型
(1)简支梁;
(2)悬臂梁; (3)伸臂梁
二、杆件截面内力及正负号规定 1、轴力:沿杆件轴线方向的截面内力,拉力为正、压力为负。 2、剪力:相切于横截面的内力,顺转为正,反之为负。
3、弯矩:截面内力对截面形心的力矩,下部受拉为正、反之 为负。 + + M M Q Q + N N - - M M Q Q - N N
C 60
B
叠加法绘制直杆弯矩图 一、简支梁弯矩图的叠加方法
MA
A
q L
MB
B
MA
MAB中 1 qL2 MB 8
若MA、MB在杆的两侧,怎么画?
MA MB q
A
MA
MAB中
B MB
+
A 1 qL2 8
B
MAB中= ( MA + MB)/2
MA A
P a b
MB B MA M Pab L MB
L
M怎么计算?
C A 3.75kN 2m
D
4m
B
2m 0.25kN
ND左 = -10kN
求截面C、D左、D右的内力。 解:1、求支座反力 2、C截面的内力 取C截面以左为对象:
QD左 = 3.75-2×2 =-0.25kN MD左 = 3.75×6-2×2×5
=2.5kNm
4、D右截面的内力 取D右截面以右为对象:
三、内力图的校核
除一般校核平衡条件和荷载、内力微分关系外,重点是校核 刚结点处的平衡条件,即∑X = 0 , ∑Y = 0,∑M = 0
例1:作图示刚架的弯矩图。 2kN/m C A B 5m 4m
16
4
C
B MCB = 0 MBC = 2×4×2 =16kNm(上拉) MBA = 2×4×2 = 16kNm(右拉) MAB =2×4×2 = 16kNm(右拉)
静定结构受力分析
一、静定单跨梁的类型
(1)简支梁;
(2)悬臂梁; (3)伸臂梁
二、杆件截面内力及正负号规定 1、轴力:沿杆件轴线方向的截面内力,拉力为正、压力为负。 2、剪力:相切于横截面的内力,顺转为正,反之为负。
3、弯矩:截面内力对截面形心的力矩,下部受拉为正、反之 为负。 + + M M Q Q + N N - - M M Q Q - N N
C 60
B
叠加法绘制直杆弯矩图 一、简支梁弯矩图的叠加方法
MA
A
q L
MB
B
MA
MAB中 1 qL2 MB 8
若MA、MB在杆的两侧,怎么画?
MA MB q
A
MA
MAB中
B MB
+
A 1 qL2 8
B
MAB中= ( MA + MB)/2
MA A
P a b
MB B MA M Pab L MB
L
M怎么计算?
C A 3.75kN 2m
D
4m
B
2m 0.25kN
ND左 = -10kN
求截面C、D左、D右的内力。 解:1、求支座反力 2、C截面的内力 取C截面以左为对象:
QD左 = 3.75-2×2 =-0.25kN MD左 = 3.75×6-2×2×5
=2.5kNm
4、D右截面的内力 取D右截面以右为对象:
三、内力图的校核
除一般校核平衡条件和荷载、内力微分关系外,重点是校核 刚结点处的平衡条件,即∑X = 0 , ∑Y = 0,∑M = 0
例1:作图示刚架的弯矩图。 2kN/m C A B 5m 4m
16
4
C
B MCB = 0 MBC = 2×4×2 =16kNm(上拉) MBA = 2×4×2 = 16kNm(右拉) MAB =2×4×2 = 16kNm(右拉)
结构力学第4章静定刚架的内力计算

GDCB部分: 见图(c)右。计算如下:
FX 0
FCx 1kN (←)
MC 0
FBy
1 (q 6 3 8 6 1 4 4
FP
2)
30kN(↑)
MB 0
FCy
1 4
(q
4
2
q
2
1
8
2
1
4
FP
2) 2kN(↑)
2)作内力图:
结构力学
结构力学教研室
青岛理工大学工程管理系
第四章
静定刚架的内力分析
§4.1 概 述
组成刚架的杆件主要产生弯曲变形, 可承受弯矩。
刚架的构造特点: 具有刚结点
(a)
(b)
(c)
刚结点的特点:
能传递力矩 (弯矩)
静定刚架有如下几种最简形式, 较复杂的刚架一般是由若干简 单刚架按基本组成规则构成的。
由 M A 0 得:
1 L L qL
FBy
q L
2
4
8
(↑)
(a)
由 M B 0 得:
FAy
1 q L
L (L 24
L) 2
3qL 8
(↑)
(b)
如取截面I-I以右部分,由 MC 0
得:
FBx
1 L
FBy
L 2
qL(←)
16
再由整体的平衡方程 FX 0
(右侧受拉)
结点C:
MCD
FNCD FQCD MCB
FQCB
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、悬臂刚架绘制弯矩图,可以不求 反力,由自由端开始作内力图。
例题 6 悬臂刚架
如静定刚架仅绘制其弯矩图,往往并不需要求出全部反 力,只需求出与杆轴线垂直的反力。 一、悬臂刚架绘制弯矩图可以不求反力,由自由端开始作 内力图。 q ↓↓↓↓↓↓↓↓↓ ql² ½ql² 2q 2q
↓↓↓↓↓
q
l
l
6q
↓↓↓↓↓↓↓↓↓
B
q
qa2/2
qa2/8
注意:BC杆CD杆的 A 剪力等于零,弯矩图 于轴线平行
a
a
qa
返回
三、三铰刚架弯矩图,往往只须求 一水平反力,然后由支座作起。
例题 8 三铰刚架
三、三铰刚架弯矩图
1 反力计算 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓ 0 1 整体 C 2 2 MA= qa +2qa -2aYB=0 (1) 2 右半边 qa 1/2qa2 MC=0.5qa2+2aXB -aYB=0 (2) 解方程(1).(2)可得 A XB=0.5qa YB=1.5qa qa/2 XA 3 再由整体平衡 a a A Y X=0 解得 XA=-0.5qa Y=0 解得 YA=0.5qa 2 绘制弯矩图 a a
⑴M图与荷载情况不符。如图a所示刚架上DE段,有向左的均布荷 载,该段弯矩图应向左凸;C点有向下的集中力作用,弯矩图应向 下尖;AB段上A处只产生竖向反力,所以AB段只受轴力,该段弯矩 图等于零。正确的弯矩图如图b所示。 又如图c所示刚架上C截面上有集中力偶作用,弯矩图应发生突变 , 突变前后两条线平行。因为XB=0,YB通过C截面。所以由C截面以右 可得MC右=0。正确的弯矩图如图d所示。 ⑵M图与结点性质、约束情况不符。如图2-4e所示刚架上,铰结点C 、铰支座A和B处无集中力偶作用,该处截面弯矩等于零。正确的弯 矩图如图f所示。
返回
2m
2m
ql²
二、简支型刚架弯矩图,往往 只须求出一个与杆件垂直的反 力,然后由支座作起。
例题 7 简支刚架
二、简支型刚架弯矩图
简支型刚架绘制弯 矩图往往只须求出一个 于杆件垂直的反力,然后 由支座作起
↓↓↓↓↓↓↓↓↓↓↓↓
l/2
q
ql2/2 ql2/2
D
qa2/2
C
q l
l/2
q l
a
l
• ①分别取左、右半边建立仅含有中间铰 约束力的矩平衡方程,由这两个方程求 出中间铰约束力; • ②再由支座反力。
例题 2
反力计算2
先求中间铰的约束力 a O1
YA
q ↓↓↓↓↓↓↓↓↓↓ C XD a a X1 Y1 YD Y1 a
E
YB a
O2
q ↓↓↓↓↓↓↓↓↓↓↓ YA C
X1
E YB
qa2/2
qa2 q
B
B Xqa/2
YB
注:三铰刚架绘制弯矩图往往只须求一水平反力,然后由 支座作起!!
画三铰刚架弯矩图
M
O
C
M
M/2 M/2
a A a a B
A
C
B
RA
XB
YB
Mo=m-2a×XB=0, 得 XB=M/2a
注: 1:三铰刚架仅半边有荷载,另半边为二力体,其反力沿两
铰连线,对o点取矩可求出B点水平反力,由B支座开始作弯矩图。 2:集中力偶作用处,弯矩图发生突变,突变前后两条线平行。 3:三铰刚架绘制弯矩图时,关键是求出一水平反力!!
⑶作用在结点上的各杆端弯矩及结点集中力偶不满足平衡条件。 如图g所示刚架,若取结点C为分离体,将发现它不满足结点的力矩 平衡条件。另外AC段上A处只产生竖向反力,所以AC段只受轴力, 该段弯矩图等于零。正确的弯矩图如图2-4h所示。
§4.5刚架弯矩图绘制
• 如静定刚架仅绘制其弯矩图,往往并不 需要求出全 部反力,只需求出与杆轴线 垂直的反力。
§4.1 刚架的组成特征
一、刚架的特点 ①刚架的内部空间大,便于使用。 ②刚结点将梁柱联成一整体,增大了结构的刚度, 变形小。 ③刚架中的弯矩分布较为均匀,节省材料。
§4.2 刚架的反力计算
• 1、悬臂刚架、简支刚架的反力由整体的 三个平衡条件便可求出。
2、三铰刚架的反力计算:
一般方法 ①整体对左底铰建立矩平衡方程,右半边对中间 铰建立矩平衡方程,这两个方程求出右底铰的支座 反力; ②再由整体的两个投影平衡方程求出左支座的两 个支座反力。 ③校核。
X 0, X
D
0
返回
3、主从刚架求反力:
• 需要分析其几何组成顺序,确定基本部 分和附属部分。先计算附属部分,在计 算基本部分。
例题 3
反力计算3
由附属部分ACD 由整体
M
D
4 X A 2×2 4×2×1 0
X A 3kN
4kN/m
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
Q kN
2m
4m
+
6 N kN
返回
例题 5
内力计算2
作刚架Q、N图的另一种方法:首先作出M图;然后取杆件 为分离体,建立矩平衡方程,由杆端弯矩求杆端剪力;最后取 结点为分离体,利用投影平衡由杆端剪力求杆端轴力。 qa2/2 q qa2/2 C C B B 2 Q QBC CB qa /2 ∑MC=qa2/2+ QBCa=0 qa2/8 QBC=QCB=-qa/2 qa2/2
例题 4
内力计算1
QDA=8kN QDB=8kN QDC=-6kN NDC QDC NDA=0 NDB=6kN NDC=0 8kN (左拉) MDB=16kN.m(右拉) MDC=24kN.m(下拉) MDC=8kN.m
QDA MDA MDC 6kN
NDA
QDA=8kN NDB MDB D NDA=0 QDB QDB=8kN 6kN D 0 MDC=8kN.m (左拉) NDB=6kN 8kN.m B 8kN 8kN MDB=16kN.m(右拉)
例题 1
反力计算1
三铰刚架的反力计算
整体对右底铰建立矩方程 2 qa qa =3kN M 0 2 aY 0 Y B A A 2 4 左半边平衡 qa qa 2(kN ) × M a X 1 . 5 a 0 X C 4 A A 6 整体平衡 Y YA +YB qa 0 YB 3qa 4 9kN
5
5
返回
§4.4 刚架弯矩图对误判别
• 利用前述内力图与荷载、支承和联结之 间的对应关系,可在绘制内力图时减少 错误,提高效率。另外,根据这些关系, 常可不经计算直观检查M图的轮廓是否 正确。鉴于静定平面刚架M图的重要性, 而初学者又常易搞错,故掌握M图正误 判别是很有益的。下面结合例子说明画 M图时容易出现的错误:
O
2 qL /4 q
C
qL2/4 整体对O点建立平衡方 程得 ∑MO=ql×1.5l- 2lXA=0 得 XA=3ql/4 RB
l
A
=3/4ql XA
l l 三铰刚架弯矩图
B
YA
返回
四、主从结构绘制弯矩图时,可以利 用弯矩图与荷载、支承及连结之间的 对应关系,不求或只求部分约束力。 以铰支座、铰结点、自由端作为切入 点,先作附属部分,后作基本部分。
学习目的和要求
不少静定结构直接用于工程实际。另外静定结构还是解算超静定 结构的基础。所以,静定结构的内力计算是十分重要的,是结构力 学的重点内容之一。通过本章学习要求达到: 1.重视和熟练掌握结构的支座反力的计算。它的计算错误将导致 内力计算的错误。 2.能熟练的绘制静定刚架的弯矩图和剪力图,尤其是弯矩图的绘 制要十分的熟练。 3.绘制弯矩图有许多技巧,都要掌握。但最重要的是掌握截面内 力计算、内力图的形状特征和绘制内力图的叠加法。 4.会恰当选取分离体和平衡方程计算静定结构的内力。如何选取 视具体情况(结构情况、荷载情况)而定。当不知如何下手时 ,宜考察结构的几何组成。
A
a
↑↑↑↑↑↑↑↑
↑↑↑↑↑↑↑↑
M图 a qa/2
QCA
q
NCB
QAC
0 NCA ∑X=0,NCB = 0 ∑Y=0,NCA=qa/2
∑MC=qa2/2+ qa2/2 -QACa=0 QAC=(qa2/2+ qa2/2 )/a =qa ∑MA=0 Q CA=(qa2/2 - qa2/2 )/a =0
8kN 6kN -6kN 8kN 16kN.m
B 24kN.m
NDC=0 C MDC=24kN.m(下拉)
6kN
0
4m ∑X = 8-8 = 0 ∑Y = -6-(-6) = 0
校核:
6kN
∑M = 24-8 - 16 = 0
2m
1m
A 8kN QDC=-6kN
作内力图
8kN
1m
8 6
- +
16 8 24 6kN 8kN 6kN M kN.m
q=4kN/m 6 D α C
↓↓↓↓↓↓
1.5m
1.79
+
3.58
+
4.5
6
E
3m
-
M图(kN.m)
2kN
A
3kN
B
2kN
2
-
Q图(kN)7.16
+
2
4kN/m N 3m 3m CEC 9kN D ↓↓↓↓↓↓↓ CN α 3.58 1.79 C α CE ααQ 7.16 Q CD 6D sin 1 cos 2 l DC l EC 3.35m E 5 5 1.79 Q EC NC 3.13 2 0.45 2 QDC 9 E - 3 3.13 ∑M =6+3 × 1.5+3.35Q (C + 3.× (3.58 +1.79 0 N 13)4 cos )= sin0 EC X CE Q = - 7.16kN 2 + 7.16 1 0 - EC X 2 + N N 0 . 45 kN EC X N cos +1.79sin + 2 0 CE E=6- DC 5 5=0 ∑M 3 × 4× × 1.5+3.35Q CE ∑ M =6 - Q 3.35 = 0 + 0.45) sin + (1.79 3.58) cos 5.82 Y ( 3.13 D CD 校核 N 3 . 13 kN Q = 3.58kN DC NCE 5.82kN - EC Q =1.79(kN)=Q - 3 CD 3.58 DC 2 1.79× 0 9 N图(kN)
