相交线与平行线培优专题

合集下载

完整版)相交线和平行线提高题与常考题型和培优题(含解析)

完整版)相交线和平行线提高题与常考题型和培优题(含解析)相交线和平行线是初中数学中重要的几何概念，涉及到很多考试题型，包括提高题和常考题，也是培优题的内容。

以下是一些选择题和填空题。

1.在图中，已知AB∥CD，CD⊥EF，且∠1=124°，则∠2=（）A．56°B．66°C．24°D．34°2.如图，是婴儿车的平面示意图，其中AB∥CD，∠1=120°，∠3=40°，那么∠2的度数为（）A．80°B．90°C．100°D．102°3.在图中，直线a∥b，若∠2=55°，∠3=100°，则∠1的度数为（）A．35°B．45°C．50°D．55°4.在图中，△ABC的面积为2，将△ABC沿AC方向平移至△DFE，且AC=CD，则四边形AEFB的面积为（）A．6B．8C．10D．125.在图中，点D、E、F分别在AB，BC，AC上，且EF∥AB，要使DF∥BC，只需再有条件（）A．∠1=∠2B．∠1=∠DFEC．∠1=∠AFDD．∠2=∠AFD6.在图中，与∠1是同旁内角的是（）A．∠2B．∠3C．∠4D．∠57.在图中，以下条件不能判定直线a与b平行的是（）A．∠1=∠2 B．∠2=∠3 C．∠3=∠5 D．∠3+∠4=180°8.在图中，直线a、b被直线c所截，下列条件能使a∥b 的是（）A．∠1=∠6 B．∠2=∠6 C．∠1=∠3 D．∠5=∠79.在图中，将一副三角板叠放在一起，使直角的顶点重合于点O，AB∥OC，DC与OB交于点E，则∠DEO的度数为（）A．85°B．70°C．75°D．60°10.在图中，AB∥CD，AE平分∠CAB交CD于点E，若∠C=50°，则∠AED=（）A．65°B．115°C．125°D．130°11.在图中，AB∥CD，DA⊥AC，垂足为A，若∠ADC=35°，则∠1的度数为（）A．65°B．55°C．45°D．35°12.在图中，直线a∥b，∠1=85°，∠2=35°，则∠3=（）A．85°B．60°C．50°D．35°13.在图中，已知BD∥AC，∠1=65°，∠A=40°，则∠2的大小是_______。

九年级数学下册2023年中考专题培优训练平行线与相交线【含答案】

九年级数学下册2023年中考专题培优训练平行线与相交线一、单选题（每题3分，共30分）(共10题；共30分)a∥b AC⊥b 1．（3分）（2022·兰州）如图，直线，直线c与直线a，b分别相交于点A，B，，垂∠1=52°∠2=足为C．若，则（）A．52°B．45°C．38°D．26°2．（3分）（2022·青海）数学课上老师用双手形象的表示了“三线八角”图形，如图所示（两大拇指代表被截直线，食指代表截线）.从左至右依次表示（）A．同旁内角、同位角、内错角B．同位角、内错角、对顶角C．对顶角、同位角、同旁内角D．同位角、内错角、同旁内角AB∠13．（3分）（2022·贵阳）如图，将菱形纸片沿着线段剪成两个全等的图形，则的度数是（）A．40°B．60°C．80°D．100°∥4．（3分）（2022·鄂州）如图，直线l1l2，点C、A分别在l1、l2上，以点C为圆心，CA长为半径画弧，交l1于点B，连接AB.若∠BCA＝150°，则∠1的度数为（）A．10°B．15°C．20°D．30°AB∥CD，AE∥CF，∠BAE=75°∠DCF5．（3分）（2022·长沙）如图，，则的度数为（）65°70°75°105°A．B．C．D．a∥b c a，b A，C B b AB⊥AC 6．（3分）（2022·泸州）如图，直线，直线分别交于点，点在直线上，，若∠1=130°∠2，则的度数是（）30°40°50°70°A．B．C．D．Rt△ABC∠C=90°，∠BAC=30°7．（3分）（2022·山西）如图，是一块直角三角板，其中．直尺的一DE∥CB∠DAB边DE经过顶点A，若，则的度数为（）A．100°B．120°C．135°D．150°∠ABC∠DEF8．（3分）（2022·盐城）小明将一块直角三角板摆放在直尺上，如图所示，则与的关系是（）A．互余B．互补C．同位角D．同旁内角9．（3分）（2022·朝阳）将一个三角尺按如图所示的方式放置在一张平行四边形的纸片上，∠EFG＝90°，∠EGF＝60°，∠AEF＝50°，则∠EGC的度数为（）A．100°B．80°C．70°D．60°AB CD10．（3分）（2022·潍坊）如图是小亮绘制的潜望镜原理示意图，两个平面镜的镜面与平行，入AB∠1=40°10′∠6射光线l与出射光线m平行．若入射光线l与镜面的夹角，则的度数为（）100°40′99°80′99°40′99°20′A．B．C．D．二、填空题（每空3分，共18分）(共6题；共18分)a∥b∠1=110°∠211．（3分）（2022·眉山）如图，已知，，则的度数为 .∥∥12．（3分）（2022·济宁）如图，直线l1，l2，l3被直线l4所截，若l1l2，l2l3，∠1＝126°32'，则∠2的度数是．13．（3分）（2022·绵阳）两个三角形如图摆放，其中∠BAC＝90°，∠EDF＝100°，∠B＝60°，∠F＝40°，BC∥EFDE与AC交于M，若，则∠DMC的大小为．14．（3分）（2022·湘西）1.如图，直线a∥b，点C、A分别在直线a、b上，AC⊥BC，若∠1＝50°，则∠2的度数为．15．（3分）（2021·泰州）如图，木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住，∠EGB＝100°，∠EHD＝80°，将木棒AB绕点G逆时针旋转到与木棒CD平行的位置，则至少要旋转 °.AB CD16．（3分）（2021·湘西）如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为、CD//BE∠1=20°，若，的度数是 .三、解答题（共8题，共72分）(共8题；共72分)17．（6分）（2022·陕西）如图，在△ABC中，点D在边BC上，CD=AB，DE∥AB，∠DCE=∠A.求证：DE=BC.18．（8分）（2022·金华）图1是光伏发电场景，其示意图如图2，EF为吸热塔，在地平线EG上的点B，B'处各安装定日镜(介绍见图3).绕各中心点(A，A')旋转镜面，使过中心点的太阳光线经镜面反射3后到达吸热器点F处.已知AB=A'B'=1m，EB=8m，EB'=8 m，在点A观测点F的仰角为45º（1）（4分）点F的高度EF为 m.（2）（4分）设∠DAB=α，∠D'A'B'=β，则α与β的数量关系是 .19．（8分）（2021·泰州）如图（1）（4分）如图①，O为的中点，直线l1、l2分别经过点O、B，且l1∥l2，以点O为圆心，OA长为半径画弧交直线l2于点C，连接AC.求证：直线l1垂直平分AC；（2）（4分）如图②，平面内直线l1∥l2∥l3∥l4，且相邻两直线间距离相等，点P、Q分别在直线l1、l4上，连接PQ.用圆规和无刻度的直尺在直线l4上求作一点D，使线段PD最短.（两种工具分别只限使用一次，并保留作图痕迹）AB//DE，AB=DE，BF=CE 20．（8分）（2021·常州）如图，B、F、C、E是直线l上的四点， .△ABC≌△DEF（1）（4分）求证：；△ABC△A′BC（2）（4分）将沿直线l翻折得到 .△A′BC①用直尺和圆规在图中作出（保留作图痕迹，不要求写作法）；②连接，则直线与l 的位置关系是▲ .A ′D A ′D 21．（10分）（2021·绵阳）如图，点是的边上的动点，，连接，并将M ∠ABC BA BC =6MC 线段绕点逆时针旋转得到线段 .MC M 90°MN（1）（5分）如图1，作，垂足在线段上，当时，判断点是MH ⊥BC H BC ∠CMH =∠B N 否在直线上，并说明理由；AB （2）（5分）如图2，若，，求以、为邻边的正方形的面积 .∠ABC =30°NC//AB MC MN S 22．（10分）（2022·宁波模拟）有一组对边平行，一个内角是它对角的两倍的四边形叫做倍角梯形.（1）（3分）已知四边形ABCD 是倍角梯形，AD ∥BC ，∠A ＝100°，请直接写出所有满足条件的∠D 的度数；（2）（3分）如图1，在四边形ABCD 中，∠BAD+∠B ＝180°，BC ＝AD+CD.求证：四边形ABCD 是倍角梯形；（3）（4分）如图2，在（2）的条件下，连结AC ，当AB ＝AC ＝AD ＝2时，求BC 的长.23．（12分）（2022·鹿城会考）在Rt △ABC 中，AB=，BC=，过点C 作CG AB ，CF 平分3545∥∠ACD 交射线BA 于点F ，D 是射线CG 上的一个动点，连接AD 交CF 于点E.（1）（4分）求CF 的长.（2）（4分）当△ACE 是等腰三角形时，求CD 的长.（3）（4分）当B 关于AD 的对称点B'落在CF 上时，求的值.DEAE 24．（10分）（2022·宁波模拟）如图（1）（3分）【基础巩固】ABCD AD//BC，∠ACD=∠B△ABC∼△DCA 如图①，在四边形中，，求证：；（2）（3分）【尝试应用】ABCD E BC∠AED∠C BE=2，EC=4如图②，在平行四边形中，点在上，与互补，AE，求的长；（3）（4分）【拓展提高】ABCD E∠AED∠C F CD 如图③，在菱形中，为其内部一点，与互补，点在上，EF//AD AD=2EF AE=3，CF=1DE，且，，求的长.答案解析部分1．【答案】C2．【答案】D3．【答案】C4．【答案】B5．【答案】C6．【答案】B7．【答案】B8．【答案】A9．【答案】B10．【答案】C11．【答案】110º12．【答案】53°28′13．【答案】110°14．【答案】40°15．【答案】2016．【答案】40°17．【答案】证明：∵DE∥AB，∴∠EDC=∠B.又∵CD=AB，∠DCE=∠A，∴△CDE≌△ABC(ASA).∴DE=BC.18．【答案】（1）9（2）α-β=7.5°19．【答案】（1）证明：如图①，连接OC，∵OB=OA，l1∥l2，∴直线l1平分AC，由作图可知：OB=OA=OC，∴∠ACB=90°，∴l2垂直AC，∵l1∥l2，∴l1垂直AC，即直线l1垂直平分AC（2）解：如图②，以l2与PQ的交点O为圆心，OP长为半径画弧交直线l3于点C，连接PC并延长交直线l4于点D，此时线段PD最短，点D即为所求.BF=CE20．【答案】（1）证明：∵，∴BC=EF，AB//DE∵，∴∠ABC=∠DEF，AB=DE又∵，∴△ABC≌△DEF△A′BC（2）解：①如图所示，即为所求；；②平行N AB21．【答案】（1）解：结论：点在直线上；∠CMH=∠B∠CMH+∠C=90°∵，，∠B+∠C=90°∴，∠BMC=90°CM⊥AB∴，即 .CM90°BA N AB∴线段逆时针旋转落在直线上，即点在直线上.CD⊥AB D（2）解：作于，MC=MN∠CMN=90°∵，，∠MCN=45°∴，NC//AB∵，∠BMC=45°∴，BC=6∠B=30°∵，，CD=3MC=2CD=32∴，，S=MC2=18MC MN S=18∴，即以、为邻边的正方形面积 . 22．【答案】（1）满足条件的∠D的度数为160°或130°DE∥AB（2）证明：过点D作，交BC于点E，∠BAD+∠B=180°∵，AD∥BC∴，DE∥AB∵，∴四边形ABED为平行四边形，∴ ，，AD =BE ∠B =∠DEC =∠ADE ∵ ，BC =BE +CE ∴ ，BC =AD +CE 又∵ ，BC =AD +CD ∴ ，，CE =CD BC >AD ∴ ，∠CDE =∠DEC ∴ ，∠ADC =∠ADE +∠CDE =2∠B ∴四边形ABCD 是倍角梯形；（3）解：如图所示：过点A 作交BC 于点E ，AE ∥DC∵ ，AB =AC ∴ ，∠B =∠ACB ∵ ，AD =AC ∴ ，∠ACD =∠D ∵ ，，AD ∥BC AE ∥DC ∴四边形AECD ∴ ，，∠ACB =∠DAC ∠AEC =∠D =2∠B 设，则，∠B =α∠D =∠ACD =2α∵ ，∠DAC +∠D +∠ACD =180°∴ ，α+2α+2α=180°∴ ，α=36°∴ ，∠B =∠ACB =36°∴ ，∠BAC =∠AEB =108°∵ ，∠B =∠B ∴ ，△ABE ∽△CBA ∴，AB BC =BE AB 设，AE =BE =CD =x 则，BC =2+x∴ ，22+x =x 2∴ ，22=x(x +2)∴ 或（舍去），x =5−1x =−5−1∴ .CD =5−1∴ .BC =AD +CD =2+5−1=5+123．【答案】（1）解：∵Rt △ABC ，AB=，BC=，3545∴AC=AB 2+BC 2=55∵CG ∥AB ，∴∠GCF=∠AFC ，∵CF 平分∠ACD ，∴∠GCF=∠ACF ，∴∠ACF=∠AFC ，∴AF=AC=，55∴BF=，55+35=85∴在Rt △BCF ，CF=；BC 2+BF 2=(45)2+(85)2=20（2）解：①如图，当CE=AE 时，可得∠ACF=∠CAE ，∴∠CAE=∠CFA ，∵∠ACE=∠FCA ，∴△ACE ∽△FCA∴CE AC =AC CF ∴CE 55=5520∴CE =254∴CF =554∵CD ∥AB∴△CDE ∽△FAE∴CD AF =CE EF 即CD 55=2555∴CD =25511②如图，当AC=CE 时CE =AC =55∴EF =20−55∵CD AF =CE EF ∴CD 55=5520−55∴-CD =100+255综上所述，CD=25511（3）解：如图，过点B’作B’M ⊥AB 于M ，DN ⊥BF 于N ，交BB'于点H ，连接AB’由（1）可知tan ∠F=12设B’M=x ，则FM=2x∴AM =55−2x在Rt △AB’M 中，AB '2=AM 2+B 'M2∴(35)2=(55−2x )2+x2解得：x 1=25+2(舍去)，x 2=25−2∴BM=45+4∴tan∠B'BM=25−245+4由垂直可得∠BNH=∠DNA，∵∠BHN=∠DHB'，∴∠ADN=∠B’BM∴tan∠ADN=tan∠B'BM=25−245+4∴ANDN=25−245+4∴AN=35−5∴CD=5由①DEAE=CDAF=555=524．【答案】（1）证明：∵AD// BC，∴∠ACB=∠CAD，又∵∠ACD=∠B，∴△ABC∽△DCA.（2）解：∵四边形ABCD为平行四边形，∴AD//BC，AB// DC，∴∠DAE=∠AEB，∠C+∠B=180°又∵∠AED+∠C=180°，∴∠AED=∠B，∴△ABE∽△DEA∴BEAE=AEAD∵BE=2，EC=4，∴AD=BC=6，∴AE2=BE⋅AD=12，∴AE=23（3）解：如图，延长FE交AB于点G，∵EF//AD，∴∠DFE=∠C，∵AG// DF，∴四边形AGFD为平行四边形，∴AG=DF，AD=GF，由(2)可知﹐△AGE∽△DEA，∴AEGE=ADAE=DEAG∵AD=2EF∴AE2=GE⋅AD=AD22即，AD=2AE∴CD=AD=2AE=32∴AG=DF=32−1∴DE=2AG=2DF=6−2。

相交线与平行线培优专题一

l 3l 2l 1O相交线与平行线一、知识要点1、平面内两条直线的位置关系：相交或平行。

（1）相交线：如果两条直线有一个公共点，则称为两相交直线；（2）平行线：如果两条直线没有公共点，则称为平行直线。

2、两条直线的垂直：如果两条直线相交所成的角为直角，则称这两条直线互相垂直。

3、两条直线垂直的两个重要结论：（1）过一点有且只有一条直线与已知直线垂直；（2）直线外一点与直线上各点连结的所有线段中，垂线段最短。

4、平行公理：经过直线外一点，有且只有一条直线与这条直线平行。

5、两条直线平行的判定：（1）两直线没有公共点；（2）同时与第三条直线平行；（3）被第三条直线所截，同位角相等；（4）被第三条直线所截，内错角相等；（5）被第三条直线所截，同旁内角互补；（6）垂直于同一直线。

6、两平行直线被第三直线所截，有：（1）同位角相等；（2）内错角相等；（3）同旁内角互补。

例1、三条直线相交于一点，共可组成几对对顶角？若三条直线两两相交，但未必相交于一点呢？一般地，n(n 2)条直线两两相交，共可组成几对对顶角？例2、10条直线两两相交，最多将平面分成多少块不同的区域？例3、如图，平行直线EF 、MN 被相交直线AB 、CD 所截，请问图中有多少对同旁内角？其中互补的有多少对？例4、有10条公路（假设公路是笔直的，并且可以无限延伸），无任何三条公路交于同一个岔口，现有31名交警，刚好满足每个岔口有且只有一名交警执勤，请你画出公路示意图.例5、设a,b,c为锐角三角形 ABC的边长，而为对应边上的三条高线长，求证：h a+,h b+,h c＜a+b+c例6、如图，直线a∥b，直线 AB交 a与 b于 A，B，CA平分∠1，CB平分∠ 2，求证：∠C=90°例7、如图1，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，在C、D之间有一点P，如果P点在C、D之间运动时，问∠PAC，∠APB，∠PBD之间的关系是否发生变化？若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠PAC，∠APB，∠PBD之间的关系又是如何？例8、如图（1），∠ABC=120o，∠BCD=85o， ED,求∠CDE的度数。

七年级数学竞赛培优(含解析)专题24 相交线与平行线

专题24 相交线与平行线阅读与思考在同一平面内，两条不同直线有两种位置关系：相交或平行.当两条直线相交或两条直线分别与第三条直线相交，就产生对顶角、同位角、内错角、同旁内角等位置关系角，善于从相交线中识别出以上不同名称的角是解相关问题的基础，把握对顶角有公共顶点，而同位角、内错角、同旁内角没有公共顶点且有一条边在截线上，这是识图的关键．两直线平行的判定方法和重要性质是我们研究平行线问题的主要依据． 1．平行线的判定(1)同位角相等、内错角相等，或同旁内角互补，两直线平行； (2)平行于同一直线的两条直线平行；(3)在同一平面内，垂直于同一直线的两条直线平行． 2．平行线的性质(1)过直线外一点，有且只有一条直线和这条直线平行； (2)两直线平行，同位角相等、内错角相等、同旁内角互补；(3)如果一条直线和两条平行线中的一条垂直，那么它和另一条也垂直. 熟悉以下基本图形：例题与求解【例1】 (1) 如图①，AB ∥DE ，∠ABC ＝080，∠CDE ＝0140，则∠BCD ＝__________.（安徽省中考试题）(2) 如图②，已知直线AB ∥CD ，∠C ＝0115，∠A ＝025，则∠E ＝___________.（浙江省杭州市中考试题）DB图②FECA解题思路：作平行线，运用内错角、同旁内角的特征进行求解.【例2】如图，平行直线AB ，CD 与相交直线EF ，GH 相交，图中的同旁内角共有( )． A ．4对 B ．8对 C ．12对 D ．16对（“希望杯”邀请赛试题）解题思路：每一个“三线八角”基本图形都有两对同旁内角，从对原图进行分解入手．A BCDGHEFF DE BCA例2题图例3题图【例3】如图，在△ABC 中，CE ⊥AB 于E ，DF ⊥AB 于F ，AC //ED ，CE 是∠ACB 的平分线，求证：∠EDF ＝∠BDF .（天津市竞赛试题）解题思路：综合运用垂直定义、角平分线、平行线的判定与性质，由于图形复杂，因此，证明前注意分解图形．【例4】如图，已知AB ∥CD ，∠EAF ＝41∠EAB ，∠FCF ＝41∠ECD .求证：∠AFC ＝43∠AEC . （湖北省武汉市竞赛试题）DEC AB 图1解题思路：分别过点E ，F 作平行线，利用平行线的性质找角之间的关系.ABFCD E例4题图例5题图【例5】如图，已知∠1＝ ∠2，∠C ＝∠D ，求证：∠A ＝∠F .解题思路：从角出发，导出两直线的位置关系，再推出新的角的关系，新的两直线的位置关系，是解这类问题的基本思路.【例6】(1)已知平面内有4条直线a ，b ，c 和d ，直线a ，b 和c 相交于一点，直线b ，c 和d 也相交于一点，试确定这4条直线共有多少个交点？并说明你的理由．(2)作第5条直线e 与(1)中的直线d 平行. 说明：以这5条直线的交点为端点的线段有多少条？（“希望杯”邀请赛试题）解题思路：(1)先设直线a ，b ，c 的交点为P ，直线b ，c ，d 的交点为Q ，证得P 与Q 实为同一点，得出结论．(2)绘出图形，帮助解答，注意平行线的性质.FA BC1 DE 2能力训练A 级1．在同一平面内有1a ，2a ，3a …，10a 十条直线，如果1a //2a ，2a ⊥3a ，3a //4a ，4a ⊥5a ，5a //6a ，6a ⊥7a ，…，那么1a 与10a 的位置关系是____________.2．如图，已知AE ∥BD ，∠1＝0130，∠2＝030，则∠C ＝__________．（湖南省常德市中考试题）3．如图，直线a ，b 都与直线c 相交，下列命题中，能判断a ∥b 的条件是_____________（把你认为正确的序号填在横线上）①∠1＝∠2； ②∠3＝∠6； ③∠1＝∠8；④∠5＋∠8＝0180．（陕西省中考试题）第4题图21第3题图第2题图7865432121DA ECBab4. 将两张矩形纸片如图所示摆放，使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一边上，则∠1＋∠2__________.（山东省烟台市中考试题）5．下面四个命题中正确的是( )．A ．相等的两个角是对顶角B ．和等于0180的两个角互为邻补角 C ．连结两点的最短线是过这两点的直线D ．两条直线相交所成的四个角都相等，则这两条直线互相垂直（“希望杯”邀请赛试题）6．下列命题①两条相交直线组成的四个角相等，则这两直线垂直．②两条相交直线组成的四个角中，若有一个直角，则四角都相等． ③两条直线相交，一角的两邻补角相等，则这两直线垂直． ④两条直线相交，一角与其邻补角相等，则这两直线垂直．其中正确的有( )．A ．4个B ．3个C ．2个D ．1个7．如图，DH ∥EG ∥BC ，且DC ∥EF ，那么图中与∠BFE 相等的角(不包括∠BFE )的个数是( )． A.2 B ．4 C ．5 D ．6（山东省菏泽地区中考试题）8．如图，AB ∥CD ∥EF ∥GH ，AE ∥DG ，点C 在AE 上，点F 在DG 上，设与∠ɑ相等的角的个数为m （不包括∠a 本身），与∠β互补的角的个数为n ．若a ≠β，则m ＋n 的值是( )．A. 8B. 9C. 10D. 11第8题图第7题图βαCFG AGDHBBEDHE9．如图，已知AB ∥ED ，∠NCB ＝030，CM 平分∠BCE ，CN ⊥CM ，求∠B 的度数．10.如图，已知E 是AB ，CD 外一点，∠D ＝∠B ＋∠E ，求证：AB ∥CD .ABED NCM11.平面上有10条直线，无任何3条交于一点，要使它们出现31个交点，怎样安排才能办到？（吉林省竞赛试题）ABEDC12.如图，已知CD ∥EF ，∠1＋∠2＝∠ABC ，求证：AB //GF .（重庆市竞赛试题）B 级1. 如图，∠A ＝060，∠1＝∠2，则∠ADC 的度数是___________. 2．如图，直线a ∥b ，那么x 的度数是____________.（五城市联赛试题）ba第1题图第2题图第3题图x48°30°30°120°21C'D'EABADBCDC F3．如图，把一个长方形纸片沿EF 折叠后，点D ，C 分别落在D '，C '的位置，若∠EFB ＝065，则∠AED '＝__________.（山东省中考试题）4．如图，已知DE ∥BC ，∠2＝070，∠1＝040，那∠EBA 的度数是_____________.AC21EBDlk4321第4题图第5题图5. 如图，直线k ∥l ，∠4－∠3＝∠3－∠2＝∠2一∠3＝d ＞0．其中∠3＜090，∠1＝050，则∠4最大可能的整数值是( )．A. 1070B ．1080C ．1090D ．11006. 如图，AB ∥CD ∥EF ，EH ⊥CD 于H ，则∠BAC ＋∠ACE ＋∠CEH 等于( )． A ．1800B ．2700C ．3600D ．4500(北京市竞赛试题）7．如图，两直线AB ，CD 平行，则∠1＋∠2＋∠3＋∠4＋∠5＋∠6＝ ( )． A ．6300B. 7200C ．8000D. 9000（“希望杯”邀请赛试题）BDFAC654321HACBDEF GH第6题图第7题图8．两条直线a ，b 互相平行，直线a 上顺次有10个点A 1，A 2…，A 10，直线b 上顺次有9个点B 1，B 2，…，B 3，将a 上每一个点与b 上每一个点相连可得线段．若没有三条线段相交于同一点，则这些线段的交点个数是( )A. 90B.1620C.6480D.20069．如图，已知两条平行线AB ，CD 被直线EF 所截，交点分别为G ，H ，P 为HD 上任意一点，过P 点的直线交HF 于O 点，求证：∠HOP ＝∠AGF －∠HPO .O PA BCD10．如图，在△ABC 中，AB ＝7，AC ＝11，点M 是BC 的中点，AD 是∠BAC 的平分线，MF ∥AD .求FC 的长．(2013年“《数学周报》”杯竞赛试题)D FMBC11．平面上有七条两两不平行的直线，试证：其中必有直线的交角小于260．（莫斯科八年级竞赛试题）12．⑴如图①，MA 1∥NA 2，则∠A 1＋∠A 2＝_________.如图②，MA 1∥NA 3，则∠A 1＋∠A 2＋∠A 3＝_________. 如图③，MA 1∥NA 4，则∠A 1＋∠A 2＋∠A 3＋∠A 4＝_________. 如图④，MA 1∥NA 5，则∠A 1＋∠A 2＋∠A 3＋∠A 4＋∠A 5＝_________.从上述结论中你发现了什么规律？请在图②，图③，图④中选一个证明你的结论.（2）如图5，n NA ||MA 1，则=∠++∠+∠+∠n A A A A 321 .（3）利用上述结论解决问题：如图已知CD ||AB ，AB E ∠和CDE ∠的平分线相交于F ，140E =∠，求B FD ∠的度数.A 6A nA 5A 4A 2A 1 MNA 2（第21题）A 1MNA 3A 2 A 1MNA 3A 4A 2 A 1MNA 3 A 5A 4 A 2 A 1MNA 3 图①图②图③ 图④图⑤FEBACD图⑥专题24 相交线与平行线例1 （1）40° 过点 C 作CF ∥AB ，则∠BCF ＝∠ABC ＝80°．∠DCF ＝180°—140°＝40°，∴∠BCD ＝80°－40°=40°.（2）90° 过点E 作EM ∥AB ，∴AB ∥CD ，∴EM ∥CD ，∠AEM =180°—25°=155°. ∠CEM =180°—115°=65°，∴∠E =∠AE —∠CEM =155°-65°=90°.例2 D 提示：原图可分解为8个基本图形.例3 提示：由DF ∥CE 得，∠BDF =∠BCE ，∠FDE =∠DEC ，AC ∥DE ，得∠DEC =∠ECA .例4 过E 作EM ∥AB .∴AB ∥于CD ，∴EM ∥CD . ∴∠AEC =∠AEM +∠CEM =∠EAB +∠ECD .同理：∠AFC =∠FAB +∠FCD .∴∠AEC =∠FAB +∠FCD +∠EAF +∠ECF =∠AFC +¼∠EAB +14+∠ECD =∠AFC +¼∠AEC .故∠AFC =¾∠AEC .例5 提示：先证BD ∥CE ，再证DF ∥BC .例6 （1）直线a ，b ，c ，d 共有1个交点，理由如下：设直线a ，b ，c 的交点为P ，直线b ，c ，d 的交点为Q .这意味着点P 和点Q都是直线b 和c 的交点.而两条不同直线至多有一个交点.因此P和Q 必为同一个点.即4条直线a ，b ，c 和d 相交于同一个点.因此这4条直线只有一个交点.(2)不妨设（1）中交点为O .因为作的第5条直线e 与（1）中的直线d 平行，所以直线e 和直线d 没有公共点，因此这些e 不过点O .而直线a ，b ，c 与直线e 必然都相交.如图所示.设直线e 与直线a ，b ，c 分别相交于点A ，B ，C .这时有A ，B ，C ，O 共四个不同的点.可以连出OA ，OB ，OC ，AB ，AC ，BC 共6条不同的线段.A 级1. 1a //10a2.20°3.①②③④4.90°5.D6.B7.C8.D提示：m =5，n =6，m +n =5+6=11. 9.60° 10.提示：过点E 作EF ∥AB . 11如图所示.12.作CK ∥FG ，延长GF ，CD 交于H 点，则∠1+∠2=∠ABC ，故∠ABC +∠BCK =180°，即CK ∥AB ，AB ∥GF .B级1.120°2.72°3.50°4.30°5.C 提示：∠2=50°+d，∠3=50°+2d，∠4=50°+3d，又∵∠3=50°+2d<90°，∴d<20°，∠4=50°+3d<110°.故∠4的最大整数值为109°.6.B7.D8.B 提示：由题意知每一个交点由a上两点和b上两点所确定.在a上取两点有种情况，在b上取两点有种情况，故交点个数为45*36=1620个.9.提示：过点O作CD的平行线.10.如图，设N是AC的中点，连接MN，则MN∥AB.又MF∥AD，∴∠FMN=∠BAD=∠DAC=∠MFN.∴FN=MN=½AB.因此FC=FN+NC=½AB+12AC=½(AB+AC）=½（7+11）=9.11.提示：在平面上任取一点O，将已知的七条直线平移过点O，它们把以O为圆心的圆周角分成14个彼此相邻的角a₁,a₂,……，。

培优第6讲相交线平行线专题

N
l1
P
γ β
A B α D
l2
M
E
C
∠α=∠β+∠γ
N
l1 A
l2
B
β αγ
P
M
E
C
D
∠β=∠α+∠γ
5、如图，直线l与m相交于点C，∠C=∠β，AP、 BP交于点P，且∠PAC=∠α，∠PBC=∠γ，说明：∠APB=α+∠β+∠γ．
解：连接CP并延长到点F.
∵∠APF+∠APC=180° F
若点P在C、D两点的外侧运动时（P点与点C、D不重合），则有两种情形：（1 ）如图结论：∠APB ＝∠PAC-∠PBD ，理由是： ∵ l1∥l2， ∴∠1=∠PAC，又∵∠1 +∠2＝180° （邻补角定义），又∵∠APB +∠PBD+∠2=180°， ∴∠1=∠APB +∠PBD 2 1 ∴∠PAC=∠APB +∠PBD 即∠APB＝∠PAC-∠PBD .
专题二、平行线的性质与判定
C 4 2
1 A
D
我们已经学过哪两种基本作图？
专题三、尺规作图
1、作一条线段等于已知线段； 2、作一个角等于已知角。作一个角等于已知角的应用：已知：如图，在△ABC中，点P在AB边上，作直线PQ∥BC。（尺规作图，不写作法，保留作图痕迹）（2）如图2，有结论：∠APB ＝∠PBD-∠PAC ，
理由是：∵l1∥l2，
∴∠1=∠PBD，
又∵∠1+∠2 ＝180°， ∠APB+∠PAC+∠2＝180°， ∴∠1=∠APB+∠PAC ∴∠PBD=∠APB+∠PAC 即∠APB＝∠PBD-∠PAC

七年级数学.培优专题24 相交线与平行线_答案

专题24 相交线与平行线例1 （1）40° 过点 C 作CF ∥AB ，则∠BCF ＝∠ABC ＝80°．∠DCF ＝180°—140°＝40°，∴∠BCD ＝80°－40°=40°.（2）90° 过点E 作EM ∥AB ，∴AB ∥CD ，∴EM ∥CD ，∠AEM =180°−25°=155°. ∠CEM =180°−115°=65°，∴∠E =∠AEM −∠CEM =155°−65°=90°.例2 D 提示：原图可分解为8个基本图形.例3 提示：由DF ∥CE 得，∠BDF =∠BCE ，∠FDE =∠DEC ，AC ∥DE ，得∠DEC =∠ECA . 例4 过E 作EM ∥AB .∴AB ∥于CD ，∴EM ∥CD .∴∠AEC =∠AEM +∠CEM =∠EAB +∠ECD .同理：∠AFC =∠FAB +∠FCD .∴∠AEC =∠FAB +∠FCD +∠EAF +∠ECF =∠AFC +14∠EAB +14+∠ECD =∠AFC +14∠AEC .故∠AFC =34∠AEC .例5 提示：先证BD ∥CE ，再证DF ∥BC .例6 （1）直线a ，b ，c ，d 共有1个交点，理由如下：设直线a ，b ，c 的交点为P ，直线b ，c ，d 的交点为Q .这意味着点P 和点Q都是直线b 和c 的交点.而两条不同直线至多有一个交点.因此P 和Q 必为同一个点.即4条直线a ，b ，c 和d 相交于同一个点.因此这4条直线只有一个交点.(2)不妨设（1）中交点为O .因为作的第5条直线e 与（1）中的直线d 平行，所以直线e 和直线d 没有公共点，因此这些e 不过点O .而直线a ，b ，c 与直线e 必然都相交. 如图所示.设直线e 与直线a ，b ，c 分别相交于点A ，B ，C .这时有A ，B ，C ，O 共四个不同的点.可以连出OA ，OB ，OC ，AB ，AC ，BC 共6条不同的线段.A 级1.a 1∥a 102.20°3.①②③④4.90°5.D6.B7.C8.D 提示：m =5，n =6，m +n =5+6=11.9.60° 10.提示：过点E 作EF ∥AB . 11如图所示.12.作CK ∥FG ，延长GF ，CD 交于H 点，则∠1+∠2=∠ABC ，故∠ABC +∠BCK =180°，即CK ∥AB ，AB ∥GF .B 级1.120°2.72°3.50°4.30°5.C 提示：∠2=50°+d ，∠3=50°+2d ，∠4=50°+3d ，又∵∠3=50°+2d <90°，∴d <20°，∠4=50°+3d <110°.故∠4的最大整数值为109°.6.B7.D8.B 提示：由题意知每一个交点由a 上两点和b 上两点所确定.在a 上取两点有12×10×9=45种情况，在b 上取两点有12×9×8=36种情况，故交点个数为45×36=1620个.9.提示：过点O 作CD 的平行线.10.如图，设N 是AC 的中点，连接MN ，则MN ∥AB .又MF ∥AD ，∴∠FMN =∠BAD =∠DAC =∠MFN .∴FN =MN =12AB .因此FC =FN +NC =12AB +12AC =12（AB +AC ）=12（7+11）=9. 11.提示：在平面上任取一点O ，将已知的七条直线平移过点O ，它们把以O 为圆心的圆周角分成14个彼此相邻的角a 1,a 2,……，a 14其中的每一个都和原来某两条直线交角中的一个相等，假设a i (i =1,2,……,14)都大于180°7，则a 1+a 2+……+a 14>14×180°7=360°，与a 1+a 2+……+a 14=360°矛盾，由此可推出结论.12.(1)180° 360° 540° 720° 证明略.（2）（n -1）180°（3）过F作FG∥AB，则AB∥FG∥CD.则∠BFD=1（∠ABE+∠CDE），又∠ABE+∠CDE+∠E=360°，得∠ABE+∠CDE=220°，故∠2BFD=110°。

相交线与平行线培优辅导

1、下列说法正确的有。

①平面内，过直线上一点有且只有一条直线垂直于已知直线; ②平面内，过直线外一点有且只有一条直线垂直于已知直线;③不相交的两条直线是平行线; ④在平面内,有且只有一条直线垂直于已知直线. ⑤若线段AB 与CD 没有交点,则AB ∥CD; ⑥若a ∥b,b ∥c,则a 与c 不相交.2、如果两个角的两边分别垂直，而其中一个角比另一个角的4倍少30°，那么这两个角分别为。

3、一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，那么两次拐弯的角度是（）A.第一次右拐50 ，第二次左拐130B.第一次左拐50 ，第二次右拐50 C .第一次左拐50 ，第二次左拐130 D .第一次右拐50 ，第二次右拐50 4、下面说法中正确的是____________________（填序号）（1）过已知直线外一点，有且只有一条直线与已知直线平行.(2) 平行于同一直线的两条直线互相平行.(3)垂直于同一直线的两条直线互相平行.（4）不相交的两条直线必平行.（5）两条直线被第三条直线所截，同位角相等.（6）两条平行线被第三条直线所截，一对内错角的平分线互相平行.5、如图，l ∥m ，等腰直角三角形ABC 的直角顶点C 在直线m 上，若∠β＝30°，则∠α的度数为。

6、如图，将长方形纸片ABCD 折叠，使点D 与点B 重合，点C 落在点C '处，折痕为EF 。

如果20ABE ∠=︒，那么EFB ∠= 度7、如图，将矩形纸片ABCD 折叠，使点A 与C 重合，折痕为EF ；且∠EFC=65°，则∠BEC=8、如图，已知： AC DE ⊥于E ，AC BC ⊥，AB FG ⊥于G ，21∠=∠。

求证：AB CD ⊥9、如下图所示，AB ∥DE ，若∠ABC=80°，∠CDE=140°，则BCD=_______度.10、如下图，AB ∥CD,由B 点出发作n 条直线1BB ，21B B ，32B B ，…，D B n 1-，则∠1ABB -∠B 21B B +∠321B B B -…+∠D B n 1-C ＝．11、如图，已知∠1=∠2，∠3=∠4，CE//AB ，试说明：AD//BC.（8分）12、如图：已知∠BEF=∠CFE ，∠1=∠2，请指出AB 和CD 的位置关系并说明理由。

相交线与平行线专题培优练习

相交线与平行线专题培优练习1余角与补角1.了解互余、互补、临补的概念2.了解对顶角的概念，掌握对顶角相等的性质3.掌握同角或等角的余（补）角相等的性质1.若一个角的补角是这个角的余角的三倍，则这个角是________2.如图，已知AO⊥CO，BO⊥DO，且∠BOC=50°，则∠AOD=_________3.如果∠1和∠2互为补角，且∠1＞∠2，那么∠2的余角是________4.如图，直线CD和∠1和∠AOB两边相交于点M、N，已知∠CMO+∠CNO=180°。

（1）试找出图中所有与∠CMO、∠CNO相等的角（2）写出图中所有互补的角。

5.若一个角的余角与这个角的补角纸币是2:7，求这个角的邻补角。

BCOMNA6.如图AB∥CD，AC⊥BC，AC≠BC，则图中与∠BAC互余的角有__________7.如图，AB∥CD,那么图中共有同位角________对8.如图，平面上有A、B、C、D五个点，其中点B、C、D及点A、E、C分别在同一条直线上，那么以这五个点中的三个点为顶点的三角形有9.如果∠1和∠2互为补角，且∠1＞∠2，那么∠2的余角是_________(表示出来)10.如果一个角的余角比这个角的补角的13还小10°，求这个角的余角及这个角的补角。

2探索平行线的平行条件1.了解同位角、内错角、同旁内角的概念2.会寻找出同位角、内错角、同旁内角3.会用同位角、内错角、同旁内角之间的数量关系来说明两直线平行4.熟练地运用平行线的判定判断两条直线的位置关系，正确的进行分析推理1.如图所示，已知直线AB，CD被直线EF所截，如果∠BMN=∠DNF，∠1=∠2，那么MQ ∥NP．为什么？2．如图所示，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置，若∠EFB=65°，则∠AED′等于3.已知：如图，∠A0B的两边0A、0B均为平面反光镜，∠A0B=40°．若平行于OB的光线经点Q反射到P，则∠QPB=4.一条公路修到湖边时需拐弯绕湖而过，如果第一次拐的角∠A是120°，第二次拐的角是∠B是150°，第三次拐的角是角∠C，这时的道路恰好和第一次拐弯之前的道路平行，那么∠C是多少度？。

相交线与平行线培优专题.docx

第五章相交线与平行线培优专题训练1．已知：如，AB∥ EF∥ CD， EG平分∠ BEF，∠ B+∠ BED+∠ D =192°，∠B-∠ D=24°，求∠ GEF的度数。

A BGE FC D2．如，已知AB∥ CD，且∠ B=40°，∠ D=70°，求∠ DEB 的度数。

解： E 作 EF∥ ABC DA BEF3．如，直 AB 与 CD 相交于 O， EFAB于 F， GHCD于 H，求 EF与 GH 必相交。

分析：欲EF 与 GH 相交，直接很困，可考用反法。

明：假EF 与 GH 不相交。

∵EF、 GH 是两条不同的直∴ EF∥ GH∵EFAB∴GHABE GAD FHOCB又因 GHCD 故 AB∥ CD (垂直于同一直的两直平行 )（ 4）与已知AB 和 CD 相交矛盾。

所以 EF与 GH 不平行，即EF与 GH 必相交注：本用：(1)垂直于同一条直的两直平行。

(2)两条平行中的一条直垂直于第三条直，那么另一条直也平行于第三条直；4．平面上n 条直两两相交且无 3 条或 3 条以上直共点，有多少个不同交点解： 2 条直生个交点，第 3 条直与前面 2 条均相交，增加个交点，平面上 3 条直共有个交点；第 4 条直与前面 3 条均相交，增加个交点，平面上 4 条直共有个交点；⋯n 条直共有交点个数：。

5． 6 个不同的点，其中只有 3 点在同一条直上， 2 点确定一条直，能确定多少条直解： 6 条不同的直最多确定：条直，除去共的3 点中重合多算的 2 条直，即能确定的直15-2=13 条。

另法： 3 点所在的直外的3 点最多能确定 3 条直，3 点与直上的3 点最多有 3×3=9 条直，加上3 点所在的直共有：3+9+1=13 条注：一般地，平面上n 个点最多可确定直的条数：1+2+3+⋯ +(n-1)= 1n(n-1)26． 10 条直两两相交，最多将平面分成多少不同的区域解： 2 条直最多将平面分成 2+2=4 个不同区域；3 条直中的第3 条直与另两条直相交，最多有两个交点，此直被两点分成3 段，每一段将它所在的区域一分二，区域增加 3 个，即最多分成2+2+3=7 个不同区域；同理： 4 条直最多分成2+2+3+4=11 个不同区域；⋯∴10 条直最多分成推广： n 条直两两相交，最多将平面分成1 1 2+2+3+4+⋯+n=1+n(n+1)=22区域个不同区域。

吴忠中学七年级数学下册第五章《相交线与平行线》经典测试(专题培优)

吴忠中学七年级数学下册第五章《相交线与平行线》经典测试（专题培优）一、选择题1．下列命题：①相等的角是对顶角；②同角的余角相等；③垂直于同一条直线的两直线互相平行；④在同一平面内，如果两条直线不平行，它们一定相交；⑤同位角相等；⑥如果直线a ∥b ，b ⊥c ，那么a ⊥c ，其中真命题的个数是（）A ．4个B ．3个C ．2个D ．以上都不对B 解析：B【分析】利用对顶角的定义、余角的定义、两直线的位置关系等知识分别判断后即可确定正确的选项．【详解】解：①相等的角不一定是对顶角，故错误，是假命题；②同角的余角相等，正确，为真命题；③在同一平面内，垂直于同一条直线的两直线互相平行，故错误，是假命题； ④在同一平面内，如果两条直线不平行，它们一定相交，正确，为真命题；⑤两直线平行，同位角相等，故错误，是假命题；⑥如果直线a ∥b ，b ⊥c ，那么a ⊥c ，正确，为真命题，故选：B ．【点睛】本题考查了命题与定理的知识，解题的关键是了解对顶角的定义、余角的定义、两直线的位置关系等知识，属于基础题，难度不大．2．如图，两个直角三角形重叠在一起，将ABC 沿AB 方向平移2cm 得到DEF ，2cm CH =，4cm EF =，下列结论：①//BH EF ；②AD BE =；③BD CH =：④C BHD ∠=∠；⑤阴影部分的面积为26cm ．其中正确的是（）A ．①②③④B ．②③④⑤C ．①②③⑤D ．①②④⑤D解析：D【分析】根据平移的性质可直接判断①②③，根据平行线的性质可判断④，阴影部分的面积=S 梯形BEFH ，于是可判断⑤，进而可得答案．【详解】解：因为将ABC 沿AB 方向平移2cm 得到DEF ，所以//BH EF ，AD BE =，DF ∥AC ，故①②正确；所以C BHD ∠=∠，故④正确；而BD 与CH 不一定相等，故③不正确；因为2cm CH =，4cm EF BC ==，所以BH=2cm ，又因为BE=2cm ，所以阴影部分的面积=S △ABC －S △DBH = S △DEF －S △DBH =S 梯形BEFH =()12422⨯+⨯=26cm ，故⑤正确；综上，正确的结论是①②④⑤．故选：D ．【点睛】本题考查了平移的性质，属于基础题目，正确理解题意、熟练掌握平移的性质是解题的关键．3．如图a 是长方形纸带，26DEF ∠=︒，将纸带沿EF 折叠成图b ，再沿BF 折叠成图c ，则图c 中的CFE ∠的度数是（）A ．102°B ．112°C ．120°D ．128°A解析：A【分析】根据两条直线平行，内错角相等，则∠BFE=∠DEF=26°，根据平角定义，则∠EFC=154°（图a ），进一步求得∠BFC=154°-26°=128°（图b ），进而求得∠CFE=128°-26°=102°（图c ）．【详解】解：∵AD ∥BC ，∠DEF=26°，∴∠BFE=∠DEF=26°，∴∠EFC=154°（图a ），∴∠BFC=154°-26°=128°（图b ），∴∠CFE=128°-26°=102°（图c ）．故选：A ．【点睛】本题考查了翻折变换，平行线的性质和平角定义，根据折叠能够发现相等的角是解题的关键．4．下列图中的“笑脸”，由如图平移得到的是（）A．B．C．D． D解析：D【分析】根据平移的性质，不改变图形的形状和大小，经过平移，对应点所连的线段平行且相等，对应线段平行且相等．【详解】解：A、B、C都是由旋转得到的，D是由平移得到的．故选：D．【点睛】本题考查平移的基本性质是：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．5．现有以下命题：①斜边中线和一个锐角分别对应相等的两个直角三角形全等；②一组对边平行，另一组对边相等的四边形是平行四边形；③在圆中，平分弦的直径垂直于弦；④平行于同一条直线的两直线互相平行．其中真命题的个数为（）A．1个B．2个C．3个D．4个B解析：B【分析】根据全等三角形的判定、平行四边形的判定、垂径定理、平行线的性质一一判断即可．【详解】①斜边中线和一个锐角分别对应相等的两个直角三角形全等，是真命题；②一组对边平行，另一组对边相等的四边形是平行四边形，是假命题，比如等腰梯形；③在圆中，平分弦的直径垂直于弦，是假命题（此弦非直径）；④平行于同一条直线的两直线互相平行，是真命题；故选B．【点睛】本题考查命题与定理、全等三角形的判定、平行四边形的判定、垂径定理、平行线的性质等知识，解题的关键是熟练掌握基本概念．6．如图，△ABC经平移得到△EFB，则下列说法正确的有（）①线段AC的对应线段是线段EB；②点C的对应点是点B；③AC∥EB；④平移的距离等于线段BF的长度．A．1 B．2 C．3 D．4D解析：D【分析】根据平移的特点分别判断各选项即可．【详解】∵△ABC经平移得到△EFB∴点A、B、C的对应点分别为E、F、B，②正确∴BE是AC的对应线段，①正确∴AC∥EB，③正确平移距离为对应点连线的长度，即BF的长度，④正确故选：D【点睛】本题考查平移的特点，注意，在平移过程中，一定要把握住对应点，仅对应点的连线之间才有平行、相等的一些关系．7．如图，下列条件：13241804523623①，②，③，④，⑤中能判断∠=∠∠+∠=∠=∠∠=∠∠=∠+∠l l的有( )直线12A．5个B．4个C．3个D．2个B解析：B【分析】根据平行线的判定定理对各小题进行逐一判断即可．【详解】解：①∵∠1=∠3，∴l1∥l2，故本小题正确；②∵∠2+∠4=180°，∴l1∥l2，故本小题正确；③∵∠4=∠5，∴l1∥l2，故本小题正确；④∠2=∠3不能判定l1∥l2，故本小题错误；⑤∵∠6=∠2+∠3，∴l1∥l2，故本小题正确．故选B．【点睛】本题考查的是平行线的判定，熟记平行线的判定定理是解答此题的关键．8．如图，已知AB CD ∕∕，AF 交CD 于点E ，且,40BE AF BED ⊥∠=︒，则A ∠的度数是（）A ．40︒B ．50︒C ．80︒D ．90︒B解析：B【分析】直接利用垂线的定义结合平行线的性质得出答案．【详解】解：∵,40BE AF BED ⊥∠=︒，∴50FED ∠=︒，∵AB CD ∕∕，∴50A FED ∠=∠=︒．故选B ．【点睛】此题主要考查了平行线的性质以及垂线的定义，正确得出FED ∠的度数是解题关键． 9．如图，一副直角三角板图示放置，点C 在DF 的延长线上，点A 在边EF 上，//AB CD ，90ACB EDF ∠=∠=︒，则CAF ∠=（）A ．10︒B ．15︒C ．20︒D ．25︒B解析：B【分析】根据平行线的性质可知，BAF=EFD=45∠∠ ，由BAC=30∠ 即可得出答案。

相交线与平行线》培优

相交线与平行线》培优例一：在图中，已知AB∥CD，EF分别交AB，CD于M，N，且∠EMB=50°，MG平分∠BMF，MG交CD于G。

求∠1的度数。

解：根据题意，可得∠XXX∠XXX°，又因为MG平分∠BMF，所以∠XXX∠FMG=25°。

又因为AB∥CD，所以∠1=∠XXX∠EMG-∠EMN=130°-50°=80°。

例二：在图中，已知CD⊥AB于D，DE∥BC，EF⊥AB于F，求证：∠XXX∠BCD。

解：由题意，可得∠XXX∠FED，又因为CD⊥AB，所以∠BCD=90°-∠BAC。

又因为DE∥BC，所以∠BAC=∠BED。

故有∠XXX∠XXX∠BCD。

例三：在图中，已知∠1=∠2，∠A和∠F，请问∠C=∠D 相等吗？试写出推理过程。

解：无法确定∠C和∠D是否相等。

因为∠1=∠2，所以∠BAC=∠XXX。

但是在这个条件下，无法推出∠C和∠D是否相等，因为图中只给出了∠A和∠F的大小关系，而没有给出具体数值。

例四：在图中，已知∠ABC和∠ACB的平分线交于点O，EF经过点O且平行于BC，分别与AB，AC交于点1) 若∠ABC＝50°，∠ACB＝60°，求∠BOC的度数；2) 若∠ABC＝a，∠ACB＝β，用a，β的代数式表示∠BOC的度数；3) 在第(2)问的条件下，若∠ABC和∠ACB邻补角的平分线交于点O，其他条件不变，请画出相应图形，并用a，β的代数式表示∠BOC的度数。

解：(1) 因为∠ABO=∠XXX，所以∠BOC=180°-∠ABC-∠ACB=70°。

2) 因为∠ABO=∠XXX，所以∠BOC=180°-∠ABC-∠ACB=180°-(a+β)/2.3) 如下图所示，因为∠ABO=∠XXX，∠ABO和∠XXX互为邻补角，所以∠ABO+∠XXX°，即∠BOC=90°-(a+β)/2.例五：已知∠A=(90+x)°，∠B=(90-x)°，∠CED=90°，射线EF∥AC，2∠C-∠D=m°1）判断AC与BD的位置关系，并说明理由；2）如图1，当m=30°时，求∠C、∠D的度数；3）如图2，求∠C、∠D的度数（用含m的代数式表示）。

《易错题》初中七年级数学下册第五章《相交线与平行线》经典题(专题培优)

一、选择题1．下列语句不是命题的是（）．A ．两直线平行，同位角相等B ．作直线AB 垂直于直线CDC ．若a b =，则22a b =D ．等角的补角相等B解析：B【分析】根据“判断一件事情的语句叫做命题”进行判断即可得到答案．【详解】解：A 、两直线平行，同位角相等，是命题，不符合题意；B 、作直线AB 垂直于直线CD 是描述了一种作图的过程，故不是命题，符合题意；C 、正确，是判断语句，不符合题意；D 、正确，是判断语句，不符合题意．故选：B ．【点睛】主要考查了命题的概念．判断一件事情的语句叫做命题．2．如图，下列条件中，不能判断直线a ∥b 的是（）A ．∠1＝∠3B ．∠2＝∠3C ．∠4＝∠5D ．∠2+∠4＝180°B解析：B【分析】根据平行线的判定定理逐项判断即可．【详解】A 、当∠1＝∠3时，a ∥b ，内错角相等，两直线平行，故正确；B 、∠2与∠3不是同位角，也不是内错角，无法判断，故错误；C 、当∠4＝∠5时，a ∥b ，同位角相等，两直线平行，故正确；D 、当∠2+∠4＝180°时，a ∥b ，同旁内角互补，两直线平行，故正确．故选：B ．【点睛】本题考查了平行线的判定，熟记判定定理是解题的关键．3．下列所示的四个图形中，∠1和∠2是同位角的是（）A ．②③B ．①②③C ．①②④D ．①④C解析：C【分析】根据同位角的定义逐一判断即得答案．【详解】图①中的∠1与∠2是同位角，图②中的∠1与∠2是同位角，图③中的∠1与∠2不是同位角，图④中的∠1与∠2是同位角，所以在如图所示的四个图形中，图①②④中的∠1和∠2是同位角．故选：C ．【点睛】本题考查了同位角的定义，属于基础概念题型，熟知概念是关键．4．如图，1∠与2∠是同位角的共有（）个A ．1个B ．2个C ．3个D ．4个B解析：B【分析】根据同位角的概念对每个图形一一判断，选出正确答案即可．【详解】图1：1∠与2∠是同位角；图2：1∠与2∠不是同位角；图3：1∠与2∠不是同位角；图4：1∠与2∠是同位角；只有图1、图4中1∠与2∠是同位角．故选：B ．【点睛】本题主要考查同位角的概念，熟记同位角的概念是解题关键．5．已知//AB CD ，∠EAF=13∠EAB ，∠ECF=13∠ECD ，若∠E=66°，则∠F 为（）A ．23°B ．33°C ．44°D ．46°C解析：C【分析】如图（见解析），先根据平行线的性质、角的和差可得66EAB EC C D AE ∠+∠=∠=︒，同样的方法可得F FAB FCD ∠=∠+∠，再根据角的倍分可得,2323FAB EAB FCD ECD ∠=∠∠=∠，由此即可得出答案．【详解】如图，过点E 作//EG AB ，则////EG AB CD ，,EAB CE C A D G G E E ∴∠=∠∠∠=，66AEG EAB ECD CE A C G E ∴∠+=∠+=∠=∠∠︒，同理可得：F FAB FCD ∠=∠+∠，11,33EAF EAB ECF ECD ∠=∠∠=∠， ,2323FAB EAB FCD ECD ∴∠=∠∠=∠， ()266443333222F FAB FCD EAB ECD EAB ECD ∴∠=∠+∠=∠+∠=∠+∠=⨯︒=︒，故选：C ．【点睛】本题考查了平行线的性质、角的和差倍分，熟练掌握平行线的性质是解题关键． 6．如图，△ABC 经平移得到△EFB ，则下列说法正确的有（）①线段AC的对应线段是线段EB；②点C的对应点是点B；③AC∥EB；④平移的距离等于线段BF的长度．A．1 B．2 C．3 D．4D解析：D【分析】根据平移的特点分别判断各选项即可．【详解】∵△ABC经平移得到△EFB∴点A、B、C的对应点分别为E、F、B，②正确∴BE是AC的对应线段，①正确∴AC∥EB，③正确平移距离为对应点连线的长度，即BF的长度，④正确故选：D【点睛】本题考查平移的特点，注意，在平移过程中，一定要把握住对应点，仅对应点的连线之间才有平行、相等的一些关系．7．下列命题是真命题的有（）个①对顶角相等，邻补角互补②两条直线被第三条直线所截，同位角的平分线平行③垂直于同一条直线的两条直线互相平行④过一点有且只有一条直线与已知直线平行A．0 B．1 C．2 D．3B解析：B【分析】根据平行线的性质定理、平行公理、对顶角和邻补角的概念判断即可．【详解】解：对顶角相等，邻补角互补，故①是真命题；两条平行线被第三条直线所截，同位角的平分线平行，故②是假命题；在同一平面内，垂直于同一条直线的两条直线互相平行，故③是假命题；过直线外一点有且只有一条直线与已知直线平行，故④是假命题；故正确的个数只有1个，【点睛】本题考查的是平行的公理和应用，命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．8．如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠1=35°，则∠2的度数为（）A．10°B．20°C．25°D．30°C解析：C【解析】分析：如图，延长AB交CF于E，∵∠ACB=90°，∠A=30°，∴∠ABC=60°．∵∠1=35°，∴∠AEC=∠ABC﹣∠1=25°．∵GH∥EF，∴∠2=∠AEC=25°．故选C．9．下列命题中，属于假命题的是（）A．如果三角形三个内角的度数比是1:2:3，那么这个三角形是直角三角形B．内错角不一定相等C．平行于同一直线的两条直线平行>-，则a一定小于0DD．若数a使得a a解析：D【分析】利用三角形内角和对A进行判断；根据内错角的定义对B进行判断；根据平行线的判定方法对C进行判断；根据绝对值的意义对D进行判断．【详解】解：A、如果三角形三个内角的度数比是1：2：3，则三个角的度数分别为30°，60°，90°，所以这个三角形是直角三角形，所以A选项为真命题；B、内错角不一定相等，所以B选项为真命题；C、平行于同一直线的两条直线平行，所以C选项为真命题；D、若数a使得|a|＞-a，则a为不等于0的实数，所以D选项为假命题．故选：D．本题考查了命题与定理：命题的“真”“假”是就命题的内容而言．任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．10．如图，将△ABE 向右平移50px 得到△DCF ，如果△ABE 的周长是400px（1px=0.04cm ），那么四边形ABFD 的周长是（）A ．16cmB ．18cmC ．20cmD ．21cm C解析：C【分析】根据平移的性质可得DF=AE ，然后判断出四边形ABFD 的周长=△ABE 的周长+AD+EF ，然后代入数据计算即可得解．注意：1px = 0.04cm ．【详解】∵1px = 0.04cm ，∴50px=2cm ，400px=16cm ，∵△ABE 向右平移2cm 得到△DCF ，∴DF=AE ，∴四边形ABFD 的周长=AB+BE+DF+AD+EF=AB+BE+AE+AD+EF=△ABE 的周长+AD+EF ．∵平移距离为2cm ，∴AD=EF=2cm ，∵△ABE 的周长是16cm ，∴四边形ABFD 的周长=16+2+2=20cm ．故选：C ．【点睛】本题考查了平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．二、填空题11．如图，直线AB ，CD 相交于点O ，AO 平分COE ∠，且50EOD ∠=︒，则DOB ∠的度数是________．【分析】根据求出利用AO 平分求得即可得到∠DOB=【详解】∵∴∵AO 平分∴∴∠DOB=故答案为：【点睛】此题考查求一个角的补角角平分线的性质对顶角相等正确理解补角定义求出是解题的关键解析：65︒【分析】根据180COE EOD ∠+∠=︒，50EOD ∠=︒，求出130COE ∠=︒，利用AO 平分COE ∠，求得65AOC ∠=︒，即可得到∠DOB=65AOC ∠=︒．【详解】∵180COE EOD ∠+∠=︒，50EOD ∠=︒，∴130COE ∠=︒，∵AO 平分COE ∠，∴65AOC ∠=︒,∴∠DOB=65AOC ∠=︒,故答案为：65︒．【点睛】此题考查求一个角的补角，角平分线的性质，对顶角相等，正确理解补角定义求出130COE ∠=︒是解题的关键．12．如图，直线AB 与CD 相交于点O ，EO ⊥CD 于点O ，OF 平分∠AOD ，且∠BOE ＝50°，则∠DOF 的度数为__．【分析】利用垂直定义可得∠COE ＝90°进而可得∠COB 的度数再利用对顶角相等可得∠AOD 再利用角平分线定义可得答案【详解】解：∵EO ⊥CD 于点O ∴∠COE ＝90°∵∠BOE ＝50°∴∠COB ＝90解析：70︒【分析】利用垂直定义可得∠COE ＝90°，进而可得∠COB 的度数，再利用对顶角相等可得∠AOD ，再利用角平分线定义可得答案．【详解】解：∵EO ⊥CD 于点O ，∴∠COE ＝90°，∵∠BOE ＝50°，∴∠COB ＝90°+50°＝140°，∴∠AOD ＝140°，∵OF 平分∠AOD ，∴∠FOD ＝12∠AOD ＝70°，故答案为：70°．【点睛】此题主要考查了垂直定义，关键是理清图中角之间的和差关系．13．两个角的两边两两互相平行，且一个角的12等于另一个角的13，则这两个角中较小角的度数为____︒．72【分析】如果两个角的两边互相平行则这两个角相等或互补根据题意这两个角只能互补然后列方程求解即可【详解】解：设其中一个角是x°则另一个角是(180-x)°根据题意得解得x=72∴180-x=108解析：72【分析】如果两个角的两边互相平行，则这两个角相等或互补．根据题意，这两个角只能互补，然后列方程求解即可．【详解】解：设其中一个角是x°，则另一个角是(180-x)°，根据题意，得11(180)23x x =-，解得x=72，∴180-x=108°；∴较小角的度数为72°．故答案为：72．【点睛】本题考查了平行线的性质，一元一次方程的应用，运用“若两个角的两边互相平行，则两个角相等或互补”，而此题中显然没有两个角相等这一情况是解决此题的突破点． 14．阅读下面材料：在数学课上，老师提出如下问题：如图，需要在A 、B 两地和公路l 之间修地下管道．请你设计一种最节省材料的修路方案：小丽设计的方案如下：如图，（1）连接AB ；（2）过点A 画线段AC ⊥直线l 于点C ，所以线段BA 和线段AC 即为所求．老师说：“小丽的画法正确”请回答：小丽的画图依据是___．两点之间线段最短；直线外一点到这条直线上所有点连结的线段中垂线段最短（或垂线段最短）【分析】根据线段的概念和垂线的性质即可求解【详解】由垂线段最短可知点A 到直线l 的最短距离为AC 由两点之间线段最短可解析：两点之间线段最短；直线外一点到这条直线上所有点连结的线段中，垂线段最短（或垂线段最短）【分析】根据线段的概念和垂线的性质即可求解．【详解】由垂线段最短可知，点A 到直线l 的最短距离为AC ，由两点之间线段最短可知，点B 到点A 的最短距离为AB ．故答案为：两点之间线段最短；直线外一点到这条直线上所有点连结的线段中，垂线段最短（或垂线段最短）；【点睛】本题考察线段的概念和垂线的性质，熟练掌握其概念和性质是解题的关键．15．如图，//EF AD ，//AD BC ，CE 平分BCF ∠，120DAC ∠=︒，20ACF ∠=︒，FEC ∠为______°．20【分析】根据平行线的性质可得进而可得∠ACB ＝60°根据角平分线的性质和角的和差可得∠BCE 根据平行线的性质可得∠FEC 【详解】∵∴∵∴∵又∵∴∵平分∴∠BCE ＝∠ECF ＝∠BCF ＝20°∵∴∴解析：20【分析】根据平行线的性质可得180DAC ACB ∠+∠=︒，进而可得∠ACB ＝60°，根据角平分线的性质和角的和差可得∠BCE ，根据平行线的性质可得∠FEC ．【详解】∵//AD BC ，∴180DAC ACB ∠+∠=︒．∵120DAC ∠=︒，∴180********ACB DAC ∠=︒-∠=︒-︒=︒．∵60BCF ACF ACB ∠+∠=∠=︒．又∵20ACF ∠=︒，∴602040BCF ACB ACF ∠=∠-∠=︒-︒=︒．∵CE 平分BCF ∠，∴∠BCE ＝∠ECF ＝12∠BCF ＝20° ∵//EF BC ，∴20FEC BCE ∠=∠=︒，∴20FEC ∠=︒．故答案为：20．【点睛】本题主要考查平行线的性质，涉及到角的和差，角平分线的性质，解题的关键是求得∠BCE ．16．直线//,a b Rt ABC ∆的直角顶C 点在直线a 上，若135∠=︒，则2∠等于_______．【分析】先根据直角为90°即可得到∠3的度数再根据平行线的性质即可得出∠2的度数【详解】解：∵Rt △ABC 的直角顶点C 在直线a 上∠1=35°∴∠3=90°-35°=55°又∵a ∥b ∴∠2=∠3=55解析：55【分析】先根据直角为90°，即可得到∠3的度数，再根据平行线的性质，即可得出∠2的度数．【详解】解：∵Rt △ABC 的直角顶点C 在直线a 上，∠1=35°，∴∠3=90°-35°=55°，又∵a ∥b ，∴∠2=∠3=55°，故答案为：55°．【点睛】本题主要考查了平行线的性质，直角三角形两个锐角互余的性质，解题时注意：两直线平行同位角相等．17．如图，AC ⊥AB ，AC ⊥CD ，垂足分别是点A 、C ，如果∠CDB=130°，那么直线AB 与BD 的夹角是________度．50【分析】先根据平行线的判定可得再根据平行线的性质两直线的夹角的定义即可得【详解】∵∴∵∴∴直线AB 与BD 的夹角是50度故答案为：50【点睛】本题考查了平行线的判定与性质两直线的夹角的定义熟练掌握解析：50【分析】先根据平行线的判定可得//AB CD ，再根据平行线的性质、两直线的夹角的定义即可得．【详解】∵AC AB ⊥，AC CD ⊥，∴//AB CD ，∵130CDB ∠=︒，∴18050ABD CDB ∠=︒-∠=︒，∴直线AB 与BD 的夹角是50度，故答案为：50．【点睛】本题考查了平行线的判定与性质、两直线的夹角的定义，熟练掌握平行线的判定与性质是解题关键．18．如图是某公园里一处矩形风景欣赏区ABCD ，长AB=50米，宽BC=30米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小路的宽均为1米，那么小明沿着小路的中间出口A到出口B所走的路线（图中虚线）长为______米．98【解析】∵利用已知可以得出此图形可以分为横向与纵向分析水平距离等于AB铅直距离等于（AD-1）×2又∵长AB=50米宽BC=25米∴小明沿着小路的中间出口A到出口B所走的路线（图中虚线）长为50解析：98【解析】∵利用已知可以得出此图形可以分为横向与纵向分析，水平距离等于AB，铅直距离等于（AD-1）×2，又∵长AB=50米，宽BC=25米，∴小明沿着小路的中间出口A到出口B所走的路线（图中虚线）长为50+（25-1）×2=98米，故答案为98．19．如图，直线AB，CD相交于点O，OA平分∠EOC，∠EOD=120°，则∠BOD=__________°．30°【分析】先利用补角的定义求出∠EOC=60°再根据角平分线的性质计算【详解】解：∵∠EOD=120°∴∠EOC=60°（邻补角定义）∵OA平分∠EOC∴∠AOC=∠EOC=30°（角平分线定义解析：30°【分析】先利用补角的定义求出∠EOC=60°，再根据角平分线的性质计算．【详解】解：∵∠EOD=120°，∴∠EOC=60°（邻补角定义）．∠EOC=30°（角平分线定义），∵OA平分∠EOC，∴∠AOC=12∴∠BOD=30°（对顶角相等）．故答案为：30．【点睛】本题考查由角平分线的定义，结合补角的性质，易求该角的度数．20．假设一家旅馆一共有30个房间，分别编以1～30三十个号码，现在要在每个房间的钥匙上刻上数字，要求所刻的数字必须使服务员很容易辨认是哪一个房间的钥匙，而使局外人不容易猜到．现在有一种编码的方法是：在每把钥匙上刻上两个数字，左边的一个数字是这把钥匙原来的房间号码除以5所得的余数，而右边的一个数字是这把钥匙原来的房间号码除以7所得的余数．那么刻的数是25的钥匙所对应的原来房间应该是__________号．12【分析】根据编码的方法分析在1～30中除以5余2的数有712172227而其中除以7余5的数只有12故可求得答案【详解】解：∵1～30中除以5余2的数有712172227而其中除以7余5的数只有解析：12【分析】根据编码的方法分析，在1～30中，除以5余2的数有7，12，17，22，27，而其中除以7余5的数只有12，故可求得答案．【详解】解：∵1～30中，除以5余2的数有7，12，17，22，27，而其中除以7余5的数只有12，∴刻的数是25的钥匙所对应的原来房间应该是12，故答案为：12．【点睛】此题考查了带余数除法的知识．此题难度适中，解题的关键是理解题意，抓住1～30中，除以5余2的数有7，12，17，22，27，而其中除以7余5的数只有12．三、解答题21．如图，点D 、E 分别为AB 、AC 上的点，点F 、G 为BC 上的点，连接DE ，连接DG 、EF 交于点H ．已知12180∠+∠=︒，3B ∠=∠，若66C ∠=︒，求DEC ∠的度数．请你将下面解答过程填写完整．解：∵12180∠+∠=︒∴//AB ________∴3ADE ∠=∠（________________________）∵3B ∠=∠∴_______B =∠∴//DE BC （____________________________）∴180C DEC ∠+∠=︒∵66C ∠=︒∴114DEC ∠=︒解析：见解析．【分析】先根据平行线的判定可得//AB EF ，再根据平行线的性质可得3ADE ∠=∠，从而可得ADE B ∠=∠，然后根据平行线的判定与性质可得．【详解】解：∵12180∠+∠=︒，∴//AB EF ，∴3ADE ∠=∠（两直线平行，内错角相等），∵3B ∠=∠，∴ADE B ∠=∠，∴//DE BC （同位角相等，两直线平行），∴180C DEC ∠+∠=︒，∵66C ∠=︒，∴114DEC ∠=︒．【点睛】本题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解题关键．22．如图，直线AB ，CD 相交于点O ，OA 平分∠EOC ．（1）∠AOC 的对顶角为______，∠AOC 的邻补角为______；（2）若∠EOC ＝70°，求∠BOD 的度数；（3）若∠EOC ：∠EOD ＝2：3，求∠BOD 的度数．解析：（1）∠BOD ，∠BOC 或∠AOD ；（2）∠BOD ＝35°；（3）∠BOD ＝36°．【分析】（1）根据对顶角、邻补角的意义，结合图形即可得出答案；（2）根据角平分线的意义和对顶角的性质，即可得出答案；（3）根据平角、按比例分配，角平分线的意义、对顶角性质可得答案．【详解】（1）根据对顶角、邻补角的意义得：∠AOC 的对顶角为∠BOD ， ∠AOC 的邻补角为∠BOC 或∠AOD ，故答案为：∠BOD ，∠BOC 或∠AOD（2）∵OA 平分∠EOC.∠EOC ＝70°，∴∠AOE ＝∠AOC 12=∠EOC ＝35°， ∵∠AOC ＝∠BOD ，∴∠BOD ＝35°，（3）∵∠EOC ：∠EOD ＝2：3，∠EOC+∠EOD ＝180°，∴∠EOC ＝180°×25=72°，∠EOD ＝180°×35=108°， ∵OA 平分∠EOC ， ∴∠AOE ＝∠AOC 12=∠EOC ＝36°，又∵∠AOC ＝∠BOD ，∴∠BOD ＝36°．【点睛】本题考查对顶角、邻补角、角平分线、平角的意义和性质，通过图形具体理解这些角的意义是正确计算的前提．23．如图，直线AB ，CD 相交于点O ，EO AB ⊥，垂足为O ，35EOC ∠=︒，求AOD ∠的度数．解析：125°．【分析】由两直线垂直，求得∠AOE=90°；由∠AOC 与∠EOC 互余，∠EOC=35°，即可得到∠AOC 的度数；再由∠AOD 与∠AOC 互补，即可得出∠AOD 的度数．【详解】∵EO ⊥AB ，∴∠AOE=90°，又∵∠EOC=35°，∴∠AOC=∠AOE-∠EOC=90°-35°= 55°，∴∠AOD=180°-∠AOC=180°-55°=125°．【点睛】本题主要考查补角、余角和垂直的定义．解题的关键是熟练利用补角、余角关系求角的度数．24．如图，直线AB 、CD 相交于点O ，OE 平分BOD ∠，72AOC ∠=︒，OF CD ⊥．∠互余的角是______；（1）与BOF∠的度数．（2）求EOF解析：（1）∠BOD、∠AOC；（2）54°【分析】（1）根据垂直的定义得到∠FOD＝90°，于是得到∠BOF+∠BOD＝90°，根据对顶角的性质得到∠BOD＝∠AOC，等量代换得到∠BOF+∠AOC＝90°，即可得到结论．（2）根据已知条件得到∠BOF＝90°﹣72°＝18°，再由OE平分∠BOD，得出∠BOE＝1∠BOD＝36°，因此∠EOF＝36°+18°＝54°．2【详解】解：（1）∵OF⊥CD，∴∠FOD＝90°，∴∠BOF+∠BOD＝90°，∵∠BOD＝∠AOC，∴∠BOF+∠AOC＝90°，∴图中互余的角有∠BOF与∠BOD，∠BOF与∠AOC．故答案为：∠BOD、∠AOC；（2）∵直线AB和CD相交于点O，∴∠BOD＝∠AOC＝72°，∵OF⊥CD，∴∠BOF＝90°﹣72°＝18°，∵OE平分∠BOD，∠BOD＝36°，∴∠BOE＝12∴∠EOF＝36°+18°＝54°．【点睛】本题考查了对顶角、垂线以及角平分线的定义；弄清各个角之间的关系是解题的关键．25．已知：如图，DE∥BC，BE∥FG．求证：∠1＝∠2．解析：证明见解析．【分析】由//DE BC ，利用“两直线平行，内错角相等”可得出1CBE ∠=∠，由//BE FG ，利用“两直线平行，同位角相等”可得出2CBE，进而可证出12∠=∠．【详解】证明：//DE BC ，1CBE ∴∠=∠．//BE FG ，2CBE ，12∠∠∴=．【点睛】本题考查了平行线的性质，牢记平行线的各性质定理是解题的关键．26．如图，已知BC AE ⊥，DE AE ⊥，23180∠+∠=︒．（1）请你判断1∠与ABD ∠的数量关系，并说明理由；（2）若170∠=︒，BC 平分ABD ∠，试求ACF ∠的度数．解析：（1）∠1=∠ABD ，证明见解析；（2）∠ACF=55°．【分析】（1）先根据在平面内，垂直于同一条直线的两条直线互相平行得出BC ∥DE ，再根据平行线的性质结合23180∠+∠=︒可得∠2=∠CBD ，从而可得CF ∥DB 得出∠1=∠ABD ；（2）利用平行线的性质以及角平分线的定义，即可得出∠2的度数，再根据∠ACB 为直角，即可得出∠ACF ．【详解】解：（1）∠1=∠ABD ，理由：∵BC ⊥AE ，DE ⊥AE ，∴BC ∥DE ，∴∠3+∠CBD=180°，又∵∠2+∠3=180°，∴∠2=∠CBD ，∴CF ∥DB ，∴∠1=∠ABD ．（2）∵∠1=70°，CF ∥DB ，∴∠ABD=70°，又∵BC 平分∠ABD ， ∴1352DBC ABD ︒∠=∠=， ∴∠2=∠DBC=35°，又∵BC ⊥AG ， ∴∠ACF=90°-∠2=90°-35°=55°．【点睛】本题主要考查了平行线的判定与性质，平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．27．试用举反例的方法说明下列命题是假命题．例如：如果ab <0，那么a +b <0．反例：设a =4，b =-3，ab =4⨯（-3）=-12<0，而a +b =4+（-3）=1>0，所以这个命题是假命题．（1）如果a +b >0，那么ab >0．（2）如果a 是无理数，b 也是无理数，那么a +b 也是无理数．解析：（1）见解析；（2）见解析．【分析】（1）此题是一道开放题，可举的例子多，但只举一例就可．如果a+b ＞0，那么ab ＞0；所举的反例就是，a 、b 一个为正数，一个为负数，且正数的绝对值大于负数．（2）可利用平方差公式找这样的无理数，比如【详解】解：（1）取a=2，b=-1，则a+b=1＞0，但ab=-2＜0．所以此命题是假命题．（2）取，，a 、b 均为无理数．但a+b=2是有理数，所以此命题是假命题．【点睛】本题主要锻炼了学生的逆向思维．在证明几何题的过程中，有时需从反例上先去判断，然后再证明．28．如图，已知直线AB 及直线AB 外一点P ，按下列要求完成画图和解答：（1）连接PA ，PB ，用量角器画出∠APB 的平分线PC ，交AB 于点C ；（2）过点P 作PD ⊥AB 于点D ；（3）用刻度尺取AB 中点E ，连接PE ；（4）根据图形回答：点P 到直线AB 的距离是线段的长度．解析：（1）答案见解析；（2）答案见解析；（3）答案见解析；（4）PD．【详解】试题分析：(1)、用量角器量出∠APB的度数，然后求出一半的度数得出答案；(2)、根据垂线的作法得出答案；(3)、用刻度尺量出AB的长度，然后找出中点，从而得出答案；(4)、点到直线的距离是指点到直线垂线段的长度．试题(1)、如图所示；(2)、如图所示；(3)、如图所示；(4)、PD．。

人教版初一数学7年级下册第5章(相交线与平行线)压轴培优(三)(含答案)

七年级数学下册第五章《平行线与相交线》压轴培优（三）1．如图，直线AB和CD交于点O，∠COF＝90°，OC平分∠AOE，∠COE＝40°．（1）求∠BOD的度数；（2）OF平分∠BOE吗？请说明理由．2．如图1，O为直线AB上一点，过点O作射线OC，∠AOC＝30°，将一直角三角板（∠M＝30°）的直角顶点放在点O处，一边ON在射线OA上，另一边OM与OC都在直线AB的上方，将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周．（1）几秒后ON与OC重合？（2）如图2，经过t秒后，MN∥AB，求此时t的值．（3）若三角板在转动的同时，射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周，那么经过多长时间OC与OM重合？请画图并说明理由．（4）在（3）的条件下，求经过多长时间OC平分∠MOB？请画图并说明理由．3．完成下面推理过程．在括号内的横线上填空或填上推理依据如图，已知：∠3＝∠BAE，AC⊥BE，∠1＝∠2，∠3+∠4＝180°，求证：AB∥CD，AD∥BE证明：∵AC⊥BE（已知）；∴∠3＝90° ；∴∠BAE＝∠3＝90°；又∵∠3+∠4＝180°（已知）；∴∠4＝180°﹣∠3＝90°；∴∠ ＝∠BAE ；∴AB∥CD ；∵∠1＝∠2（已知）；∴∠1+∠CAE＝∠2+∠CAE ；即∠BAE＝∠CAD；∴∠3＝∠CAD；∴AD∥BE ．4．探究题：（1）如图1，若AB∥CD，则∠B+∠D＝∠E，你能说明理由吗？（2）反之，若∠B+∠D＝∠E，直线AB与直线CD有什么位置关系？简要说明理由；（3）若在（1）条件下，将点E移至图2的位置，此时∠B、∠D、∠E之间有什么关系？直接写出结论；（4）若在（1）条件下，将点E移至图3的位置，此时∠B、∠D、∠E之间有什么关系？直接写出结论．5．已知AB∥CD，定点E、F分别在直线AB，CD上，在平行线AB，CD之间有一动点P．（1）如图1所示时，试问∠AEP，∠EPF，∠PFC满足怎样的数量关系？并说明理由．（2）当∠EPF满足0°＜∠EPF＜180°，试问∠AEP，∠EPF，∠PFC又满足怎样的数量关系？（直接写出结论）．（3）当∠EPF满足0°＜∠EPF＜180°，且EQ，FQ分别平分∠PEB和∠PFD，①若∠EPF＝60°，则∠EQF＝ °．②猜想∠EPF与∠EQF的数量关系．（直接写出结论）6．完成下面的证明．如图，已知AB∥CD∥EF，写出∠A，∠C，∠AFC的关系，并说明理由．解：∠AFC＝．理由如下：∵AB∥EF（已知），∴∠A＝（两直线平行，内错角相等）．∵CD∥EF（已知），∴∠C＝．∵∠AFC＝ ﹣ ，∴∠AFC＝（等量代换）．7．如图，D，E，F，G，H，I是三角形ABC三边上的点，连接EI，EF∥BC，GH∥AC，DI∥AB．（1）判断∠GHC与∠FEC是否相等，并说明理由．（2）若∠FEC+∠FGH＝210°，求∠A+∠C的度数．（3）若EI平分∠FEC，∠C＝α，∠B＝β，试用含α，β的代数式表示∠EID的度数．8．直线AB∥CD，直线EF分别交AB、CD于点A、C，CM是∠ACD的平分线，CM 交AB于点N．（1）如图①，过点A作AC的垂线交CM于点M，若∠MCD＝55°，求∠MAN的度数；（2）如图②，点G是CD上的一点，连接MA、MG，∠MGD+∠EAB＝180°，MC 平分∠AMG．①∠AMG和∠EAB满足怎么样的数量关系时EC⊥AM？②若∠AMG＝36°，求∠ACD的度数．9．如图，直线AB，CD被直线EF，MN所截．（1）若AB∥CD，EF∥MN，∠1＝115°，试求∠3和∠4的度数；（2）本题隐含着一个规律，请你根据（1）的结果填空：如果一个角的两边分别和另一个角的两边平行，那么这两个角；（3）利用（2）的结论解答：如果两个角的两边分别平行，其中一个角是另一个角的2倍，求这两个角的度数．10．如图，已知直线AB与CD相交于点O，OP是∠BOC的平分线，∠AOE＝90°，∠DOF＝90°（1）图中除直角外，请写出两对相等的角并说明理由．（2）如果∠AOD＝40°，求∠BOF的度数．11．如图，两条射线AM∥BN，线段CD的两个端点C、D分别在射线BN、AM上，且∠A＝∠BCD＝108°．E是线段AD上一点（不与点A、D重合），且BD平分∠EBC．（1）求∠ABC的度数．（2）请在图中找出与∠ABC相等的角，并说明理由．（3）若平行移动CD，且AD＞CD，则∠ADB与∠AEB的度数之比是否随着CD位置的变化而发生变化？若变化，找出变化规律；若不变，求出这个比值．12．如图，点C在∠AOB的边OA上，过点C的直线DE∥OB，CF平分∠ACD，CG⊥CF于C．（1）若∠O＝40°，求∠ECF的度数；（2）试说明CG平分∠OCD；（3）当∠O为多少度时，CD平分∠OCF？并说明理由．13．推理填空．已知DG⊥BC，AC⊥BC，EF⊥AB，∠1＝∠2，求证：CD⊥AB．证明：∵DG⊥BC，AC⊥BC，∴∠DGB＝∠ACB＝90°，∴DG∥AC．（）∴∠2＝．（）∵∠1＝∠2．（已知）∴∠1＝∠ ．（等量代换）∴EF∥CD．（）∴∠AEF＝∠ADC．（）∵EF⊥AB，∴∠AEF＝90°，∴∠ADC＝90°，∴CD⊥AB．（）14．如图1，已知直线PQ∥MN，点A在直线PQ上，点C、D在直线MN上，连接AC、AD，∠PAC＝50°，∠ADC＝30°，AE平分∠PAD，CE平分∠ACD，AE与CE相交于E．（1）求∠AEC的度数；（2）若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置，此时A1E平分∠AA1D1，CE平分∠ACD1，A1E与CE相交于E，∠PAC＝50°，∠A1D1C＝30°，求∠A1EC的度数．（3）若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置，其他条件与（2）相同，求此时∠A1EC的度数．15．如图，已知点E，F为四边形ABDC的边CA的延长线上的两点，连接DE，BF，作∠BDH的平分线DP交AB的延长线于点P．若∠1＝∠2，∠3＝∠4，∠5＝∠C．（1）判断DE与BF是否平行？并说明理由；（2）试说明：∠C＝2∠P．参考答案1．解：（1）由∠COE＝40°，OC平分∠AOE，∠AOC＝40°，∠BOD＝∠AOC＝40°；（2）OF平分∠BOE，理由如下：由∠COE＝40°，∠COF＝90°得∠EOF＝90°﹣40°＝50°，又∵∠BOF＝∠DOF﹣∠BOD＝90°﹣40°＝50°，∴∠EOF＝∠BOF，∴OF平分∠BOE．2．解：（1）∵30÷3＝10，∴10秒后ON与OC重合；（2）∵MN∥AB∴∠BOM＝∠M＝30°，∵∠AON+∠BOM＝90°，∴∠AON＝60°，∴t＝60÷3＝20∴经过t秒后，MN∥AB，t＝20秒．（3）如图3所示：∵∠AON+∠BOM＝90°，∠BOC＝∠BOM，∵三角板绕点O以每秒3°的速度，射线OC也绕O点以每秒6°的速度旋转，设∠AON＝3t，则∠AOC＝30°+6t，∵OC与OM重合，∵∠AOC+∠BOC＝180°，可得：（30°+6t）+（90°﹣3t）＝180°，解得：t＝20秒；即经过20秒时间OC与OM重合；（4）如图4所示：∵∠AON+∠BOM＝90°，∠BOC＝∠COM，∵三角板绕点O以每秒3°的速度，射线OC也绕O点以每秒6°的速度旋转，设∠AON＝3t，∠AOC＝30°+6t，∵∠BOM+∠AON＝90°，∴∠BOC＝∠COM＝∠BOM＝（90°﹣3t），由题意得：180°﹣（30°+6t）＝（90°﹣3t），解得：t＝秒；即经过秒时间OC平分∠MOB．3．证明：∵AC⊥BE（已知）；∴∠3＝90° （垂直的定义）；∴∠BAE＝∠3＝90°；又∵∠3+∠4＝180°（已知）；∴∠4＝180°﹣∠3＝90°；∴∠4＝∠BAE（等量代换）；∴AB∥CD（同位角相等，两直线平行）；∵∠1＝∠2（已知）；∴∠1+∠CAE＝∠2+∠CAE（等式的性质）；即∠BAE＝∠CAD；∴∠3＝∠CAD；∴AD∥BE（内错角相等，两直线平行）；故答案为：垂直的定义；4；等量代换；同位角相等，两直线平行；等式的性质；内错角相等，两直线平行．4．解：（1）如图1，作EF∥AB，∵AB∥CD，∴∠B＝∠1，∵AB∥CD，EF∥AB，∴EF∥CD，∴∠D＝∠2，∴∠B+∠D＝∠1+∠2，又∵∠1+∠2＝∠E，∴∠B+∠D＝∠E．（2）如图1，作EF∥AB，∵EF∥AB，∴∠B＝∠1，∵∠E＝∠1+∠2＝∠B+∠D，∴∠D＝∠2，∴EF∥CD，又∵EF∥AB，∴AB∥CD．（3）如图2，过E作EF∥AB，∵EF∥AB，∴∠BEF+∠B＝180°，∵EF∥CD，∴∠D+∠DEF＝180°，∵∠BEF+∠DEF＝∠E，∴∠E+∠B+∠D＝180°+180°＝360°．（4）如图3，∵AB∥CD，∴∠B＝∠BFD，∵∠D+∠E＝∠BFD，∴∠D+∠E＝∠B．5．解：（1）如图1，过点P作PG∥AB，∵PG∥AB，∴∠EPG＝∠AEP，∵AB∥CD，∴PG∥CD，∴∠FPG＝∠PFC，∴∠AEP+∠PFC＝∠EPF；（2）如图1，由（1）知当P点在EF的左侧时，∠AEP，∠EPF，∠PFC满足数量关系为：∠EPF＝∠AEP+∠PFC；如图2，当P点在EF的右侧时，∠AEP，∠EPF，∠PFC满足数量关系为：∠AEP+∠EPF+∠PFC＝360°；（3）①如图3，若当P点在EF的左侧时，∵∠EPF＝60°，∴∠PEB+∠PFD＝360°﹣60°＝300°，∵EQ，FQ分别平分∠PEB和∠PFD，∴，∴∠EQF＝∠BEQ+∠QFD＝＝150°；如图4，当P点在EF的右侧时，∵∠EPF＝60°，∴∠PEB+∠PFD＝60°，∴∠BEQ+∠QFD＝＝＝30°；故答案为：150°或30°；②如图3，EQ，FQ分别平分∠PEB和∠PFD，设：∠BEQ＝，∠QFD＝，则∠EPF＝180°﹣2∠BEQ+180°﹣2∠DFQ＝360°﹣2（∠BEQ+∠PFD），∵∠EQF＝∠BEQ+∠DFQ，∴∠EPF+2∠EQF＝360°；如图4，EQ，FQ分别平分∠PEB和∠PFD，∴，∵∠EPF＝∠BEP+∠PFD，∴∠EPF＝2（∠BEQ+∠DFQ），∵∠BEQ+∠DFQ＝∠EQF，∴∠EPF＝2∠EQF；综合以上可得∠EPF与∠EQF的数量关系为：∠EPF+2∠EQF＝360°或∠EPF＝2∠EQF．6．解：∠AFC＝∠A﹣∠C．理由如下：∵AB∥EF（已知），∴∠A＝∠AFE　（两直线平行，内错角相等）．∵CD∥EF（已知），∴∠C＝∠CFE．∵∠AFC＝∠AFE﹣∠CFE，∴∠AFC＝∠A﹣∠C（等量代换）．故答案为：∠A﹣∠C，∠AFE，∠CFE，∠AFE，∠CFE，∠A﹣∠C．7．解：（1）∠GHC＝∠FEC，理由：∵EF∥BC，∴∠FEC+∠C＝180°，∵GH∥AC，∴∠GHC+∠C＝180°，∴∠GHC＝∠FEC；（2）∵GH∥AC，∴∠FGH+∠A＝180°，∵EF∥BC，∴∠FEC+∠C＝180°，∴∠FGH+∠FEC+∠C+∠A＝360°，∵∠FEC+∠FGH＝210°，∴∠A+∠C＝360°﹣210°＝150°；（3）∵EF∥BC，∴∠FEC+∠C＝180°，∠FEI＝∠EIC，∴∠FEC＝180°﹣α，∵EI平分∠FEC，∴∠FEI＝∠FEC＝90°﹣，∴∠FEI＝∠EIC＝90°﹣，∵DI∥AB，∴∠DIC＝∠B＝β，∴∠EID＝∠EIC﹣∠DIC＝90°﹣﹣β．8．解：（1）∵CM是∠ACD的平分线，∠MCD＝55°，∴∠ACD＝2∠MCD＝110°，又∵AB∥CD，∴∠BAC＝180°﹣110°＝70°，又∵AM⊥EF，∴∠MAN＝90°﹣70°＝20°；（2）①当∠AMG＝∠EAB＝90°时EC⊥AM，理由如下：∵CM是∠ACD的平分线，MC平分∠AMG，∴∠ACM＝∠GCM，∠AMC＝∠GMC，又∵CM＝CM，∴△AMC≌△GMC（ASA），∴∠CGM＝∠CAM，∵EC⊥AM，∴∠CGM＝∠CAM＝90°，∴∠MGD＝90°，∵∠MGD+∠EAB＝180°，∴∠EAB＝∠BAF＝90°，∵AB∥CD，∴∠ACG＝90°，∴∠AMG＝360°﹣90°﹣90°﹣90°＝90°；②∵MC平分∠AMG且∠AMG＝36°，∴∠CMG＝18°，∵MC平分∠ACG，∴∠MCG＝∠ACG，∵∠CAB+∠EAB＝180°，∠MGD+∠EAB＝180°，∴∠BAC＝∠MGD，∵AB∥CD，∴∠BAC+∠ACD＝180°，设∠ACD＝α，则∠MCG＝∠ACD＝α，∠BAC＝∠MGD＝180°﹣α，∵∠MGD是△CMG的外角，∴∠MGD＝∠CMG+∠MCG，即180°﹣α＝α+18°，解得α＝108°，∴∠ACD＝108°．9．解：如图所示：（1）∵AB∥CD，∴∠1＝∠2，又∵EF∥MN，∴∠2＝∠3，又∵∠1＝115°，∴∠3＝115°，又∵∠3+∠4＝180°，∴∠4＝180°﹣115°＝65°；（2）相等或互补，理由如下：∵∠1的两边是GB和GF，∠3的两边是HC和HM，GB∥HC，GF∥HM，∴∠1＝∠2，∠2＝∠3，∴∠1＝∠3；又∵∠1的两边是GB和GF，∠4的两边是HC和HN，GB∥HC，GF∥HN，∴∠1＝∠2，∠2+∠4＝180°，∴∠1+∠4＝180°；故答案为相等或互补．（3）设一个角为x，则另一个角为，依题意得，（舍去），，解得：x＝120°，∴另一个角为60°即两个角的度数分别为120°和60°．10．解：（1）∵OP是∠BOC的平分线，∴∠BOP＝∠COP，∠AOD＝∠BOC（对顶角相等）；（2）∠DOF＝90°，∴∠AOD+∠BOF＝90°，∴∠BOF＝90°﹣∠AOD＝90°﹣40°＝50°．11．解：（1）∵AM∥BN，∴∠A+∠ABC＝180°．∴∠ABC＝180°﹣∠A＝180°﹣108°＝72°．（2）与∠ABC相等的角是∠ADC、∠DCN．∵AM∥BN，∴∠ADC＝∠DCN，∠ADC+∠BCD＝180°．∴∠ADC＝180°﹣∠BCD＝180°﹣108°＝72°．∴∠DCN＝72°．∴∠ADC＝∠DCN＝∠ABC．（3）不发生变化．∵AM∥BN，∴∠AEB＝∠EBC，∠ADB＝∠DBC．∵BD平分∠EBC，∴∠DBC＝∠EBC，∴∠ADB＝∠AEB，∴＝．12．解：（1）∵DE∥OB，∠O＝40°，∴∠ACE＝∠O＝40°，∵∠ACD+∠ACE＝180°，∴∠ACD＝140°，∵CF平分∠ACD，∴∠ACF＝∠ACD＝70°，∴∠ECF＝∠ACE+∠ACF＝110°．（2）∵CG⊥CF，∴∠FCG＝90°，∴∠DCG+∠DCF＝90°，又∵∠GCO+∠DCG+∠DCF+∠ACF＝180°，∴∠GCO+∠FCA＝90°，∵∠ACF＝∠DCF，∴∠GCO＝∠GCD，即CG平分∠OCD．（3）当∠O＝60°时，CD平分∠OCF．理由如下：当∠O＝60°时，∵DE∥OB，∴∠DCO＝∠O＝60°，∴∠ACD＝120°，又∵CF平分∠ACD，∴∠DCF＝60°，∴∠DCO＝∠DCF，即CD平分∠OCF．13．证明：∵DG⊥BC，AC⊥BC（已知）∴∠DGB＝∠ACB＝90°（垂直定义）∴DG∥AC（同位角相等，两直线平行）∴∠2＝∠ACD（两直线平行，内错角相等）∵∠1＝∠2（已知）∴∠1＝∠ACD（等量代换）∴EF∥CD（同位角相等，两直线平行）∴∠AEF＝∠ADC（两直线平行，同位角相等）∵EF⊥AB（已知）∵∠AEF＝90°（垂直定义）∴∠ADC＝90°（等量代换）∴CD⊥AB（垂直定义）．故答案为：同位角相等，两直线平行，∠ACD，两直线平行，内错角相等，ACD，同位角相等，两直线平行，垂直定义．14．解：（1）如图1所示：∵直线PQ∥MN，∠ADC＝30°，∴∠ADC＝∠QAD＝30°，∴∠PAD＝150°，∵∠PAC＝50°，AE平分∠PAD，∴∠PAE＝75°，∴∠CAE＝25°，可得∠PAC＝∠ACN＝50°，∵CE平分∠ACD，∴∠ECA＝25°，∴∠AEC＝180°﹣25°﹣25°＝130°；（2）如图2所示：∵∠A1D1C＝30°，线段AD沿MN向右平移到A1D1，PQ∥MN，∴∠QA1D1＝30°，∴∠PA1D1＝150°，∵A1E平分∠AA1D1，∴∠PA1E＝∠EA1D1＝75°，∵∠PAC＝50°，PQ∥MN，∴∠CAQ＝130°，∠ACN＝50°，∵CE平分∠ACD1，∴∠ACE＝25°，∴∠CEA1＝360°﹣25°﹣130°﹣75°＝130°；（3）如图3所示：过点E作FE∥PQ，∵∠A1D1C＝30°，线段AD沿MN向左平移到A1D1，PQ∥MN，∴∠QA1D1＝30°，∵A1E平分∠AA1D1，∴∠QA1E＝∠2＝15°，∵∠PAC＝50°，PQ∥MN，∴∠ACN＝50°，∵CE平分∠ACD1，∴∠ACE＝∠ECN＝∠1＝25°，∴∠CEA1＝∠1+∠2＝15°+25°＝40°．15．解：（1）DE∥BF，理由是：∵∠3＝∠4，∴BD∥CE，∴∠5＝∠FAB，∵∠5＝∠C，∴∠C＝∠FAB，∴AB∥CD，∴∠2＝∠BGD，∵∠1＝∠2，∴∠1＝∠BGD，∴DE∥BF；（2）∵AB∥CD，∴∠P＝∠PDH，∵DP平分∠BDH，∴∠BDP＝∠PDH，∴∠BDP＝∠PDH＝∠P，∵∠5＝∠P+∠BDP，∴∠5＝2∠P，∵∠C＝∠5，∴∠C＝2∠P．。

第五章相交线与平行线(过关测试)【培优卷】(解析版)

第五章相交线与平行线（培优卷）考试时间:120分钟满分：120分一、单选题（每小题3分，共18分）1．已知三角形ABC ，过AC 的中点D 作AB 的平行线，根据语句作图正确的是（）A ．B ．C ．D ．【答案】B 【分析】根据中点的定义，平行线的定义判断即可．【详解】解：过AC 的中点D 作AB 的平行线，正确的图形是选项B ，故选：B ．【点睛】本题考查作图——复杂作图，平行线的定义，中点的定义等知识，解题关键是理解题意，灵活运用所学知识解决问题．2．如图，直线1l ，2l 被3l 所截得的同旁内角为a ，b ，要使12l l ∥，只要使（）A ．90a b +=°B ．a b=C ．116033a b +=°D ．090a °<£°，90180b °£<°【答案】C【分析】由同旁内角互补两直线平行即可判定出12l l ∥，变形后即可得到正确的选项．【详解】解：当180°a b +=，即116033a b +=°时，12l l ∥，故C 正确．故选：C ．【点睛】本题主要考查了平行线的判定，熟练掌握平行线的判定方法是解本题的关键．3．在同一平面内，两条直线的位置关系可能是（）A ．相交或垂直B ．垂直或平行C ．平行或相交D ．相交或垂直或平行【答案】C 【分析】根据两条直线有一个交点的直线是相交线，没有交点的直线是平行线，可得答案．【详解】在同一平面内，两条直线有一个交点，两条直线相交；在同一平面内，两条直线没有交点，两条直线平行，故C 正确；故选：C ．【点睛】本题主要考查了同一平面内，两条直线的位置关系，注意垂直是相交的一种特殊情况，不能单独作为一类．4．（2021·安徽·统考中考真题）设a ，b ，c 为互不相等的实数，且4155b a c =+，则下列结论正确的是（）A ．a b c>>B ．c b a >>C ．4()a b b c -=-D ．5()a c a b -=-【答案】D【分析】举反例可判断A 和B ，将式子整理可判断C 和D ．【详解】解：A ．当5a =，10c =，41655b a c =+=时，c b a >>，故A 错误；B ．当10a =，5c =，41955b a c =+=时，a b c >>，故B 错误；C ．4()a b b c -=-整理可得1455b a c =-，故C 错误；D ．5()a c a b -=-整理可得4155b a c =+，故D 正确；故选：D ．【点睛】本题考查等式的性质，掌握等式的性质是解题的关键．5．已知直线a 、b 、c 在同一平面内，则下列说法错误的是( )A ．如果a ∥b ，b ∥c ，那么a ∥cB ．a ⊥b ，c ⊥b ，那么a ∥cC ．如果a 与b 相交，b 与c 相交，那么a 与c 一定相交D ．如果a 与b 相交，b 与c 不相交，那么a 与c 一定相交【答案】C【分析】根据如果两条直线都与第三条直线平行，那么这两条直线也互相平行，同一平面内，垂直于同一条直线的两直线平行进行分析即可．【详解】A．如果a∥b，b∥c，那么a∥c，说法正确；B．a⊥b，c⊥b，那么a∥c，说法正确；C．如果a与b相交，b与c相交，那么a与c一定相交，说法错误；D．如果a与b相交，b与c不相交，那么a与c一定相交，说法正确．故选C．【点睛】此题主要考查了平行公理及推论，关键是熟练掌握所学定理．6．一副直角三角尺叠放如图所示，现将30°的三角尺ABC固定不动，将45°的三角尺BDE绕顶点B逆时Ð所有符合条件的针转动，点E始终在直线AB的上方，当两块三角尺至少有一组边互相平行时，则ABE度数为（）A．45°，75°，120°，165°B．45°，60°，105°，135°C．15°，60°，105°，135°D．30°，60°，90°，120°【答案】A【分析】分DE∥AB，DE∥AC，BE∥AC，AC∥BD，分别画出图形，根据平行线的性质和三角板的特点求解．【详解】解：如图，①DE∥AB，∴∠D+∠ABD=180°∴∠ABD=90°∴∠ABE=45°；②DE∥AC，∵∠D=∠C=90°，∴B ，C ，D 共线，∴∠ABE=∠CBE+∠ABC=180°-45°+30°=165°；③BE ∥AC ，∴∠C=∠CBE=90°，∴∠ABE=∠ABC+∠CBE=120°；④AC ∥BD ，∴∠ABD=180°-∠A=120°，∴∠ABE=∠ABD-∠DBE=75°，综上：∠ABE 的度数为：45°或75°或120°或165°．【点睛】本题考查了三角板中的角度计算，平行线的性质，解题的关键是注意分类讨论，做到不重不漏．二、填空题（每小题3分，共18分）7．“若0ab ＞，则0a ＞，0b ＞”_____命题（选填“是”或“不是”）．【答案】是【分析】根据命题的定义判断即可．【详解】若0ab ＞，则0a ＞，0b ＞是一个命题.故答案为：是．【点睛】本题主要考查了命题的判断，掌握定义是解题的关键．即是表示判断一件事情的句子是命题. 8．有一个密码箱，密码由三个数字组成，甲、乙、丙三个人都开过，但都记不清了．甲记得：这三个数字分别是7，2，1，但第一个数字不是7；乙记得：1和2的位置相邻；丙记得：中间的数字不是1．根据以上信息，可以确定密码是__．【答案】127【分析】先根据第一个数字不是7，得出第一个数字是1或2，再根据1和2相邻，进而得出第三个是7，即可得出结论．【详解】解：∵三个数字分别是7，2，1，但第一个数字不是7，∴第一个数为1或2，∵1和2的位置相邻，∴前两个数字是1，2或2，1，第三位是数字7，∵中间的数字不是1，∴第一个数字只能是1，第二个数字为2，即密码为127，故答案为：127【点睛】此题主要考查了推理与论证，判断出第三个数是7是解本题的关键．9．（2022秋·黑龙江佳木斯·七年级校考期中）将直角梯形ABCD平移得梯形EFGH，若===，则图中阴影部分的面积为_________平方单位．10,2,4HG MC MG【答案】36【分析】根据图形可知图中阴影部分的面积等于梯形ABCD的面积减去梯形EFMD的面积，恰好等于梯形EFGH的面积减去梯形EFMD的面积．【详解】根据平移的性质得S梯形ABCD =S梯形EFGH，Q DC = HG = 10，MC= 2，MG = 4，\DM = DC - MC = 10 - 2 = 8，\S阴影= S梯形ABCD-S梯形EFMD=S梯形EFGH-S梯形EFMD =S梯形HGMD=()12DM HG MG+g=12×(8+10)×4= 36．故答案为：36．【点睛】主要考查了梯形的性质和平移的性质，要注意平移前后图形的形状和大小不变，本题的关键是能得到：图中阴影部分的面积等于梯形ABCD的面积减去梯形EFMD的面积，恰好等于梯形EFGH的面积减去梯形EFMD的面积．10．把命题“等角的余角相等”改写成“如果……那么……”的形式:__________________________. 是______命题(填“真”或“假”)【答案】如果两个角是两个相等角的余角，那么这两个角相等. 真【分析】根据命题由题设和结论组成,把条件“两个角是同角的余角”写在如果的后面,把结论“这两个角相等"写在那么的后面即可【详解】命题“同角的余角相等”改写成“如果..,那么."的形式是“如果两个角是同角的余角,那么这两个角相等”如果两个角是同角的余角,那么这两个角相等是真命题【点睛】此题考查命题与定理，掌握三角形的性质是解题关键11．如图所示，在△ABC中，∠C＝90°，AC＝BC＝5，现将△ABC沿着CB的方向平移到△A′B′C′的位置．若平移的距离为2，则图中阴影部分的面积为________．【答案】8【分析】图中阴影部分的面积等于大三角形的面积减小三角形的面积，根据面积公式计算即可．【详解】解：∵∠C=90°，AC=BC=5，平移的距离为2，∴BC′=DC′=3∴阴影面积=5×5÷2-3×3÷2=8．故答案为8．【点睛】本题考查平移的性质，比较简单，解答此题的关键是利用平移的性质得出小三角形的底和高．12．（2022秋·重庆·七年级重庆市綦江中学校考阶段练习）如图，直线MN∥PQ，点A在直线MN与PQ之间，点B在直线MN上，连接AB．∠ABM的平分线BC交PQ于点C，连接AC，过点A作AD⊥PQ交PQ于点D，作AF⊥AB交PQ于点F，AE平分∠DAF交PQ于点E，若∠CAE=45°，∠ACB=52∠DAE，则∠ACD的度数是_____．【答案】27°##27度【分析】延长FA与直线MN交于点K，通过角度的不断转换解得∠BCA=45°，然后结合图形，利用各角之间的关系求解即可．【详解】解：延长FA与直线MN交于点K，由图可知∠ACD=90°-∠CAD=90°-(45°+∠EAD)=45°-12∠FAD=45°-12(90°-∠AFD)=12∠AFD，∵MN∥PQ，∴∠AFD=∠BKA=90°-∠KBA=90°-(180°-∠ABM)=∠ABM-90°，∴∠ACD=12∠AFD=12(∠ABM-90°)=∠BCD-45°，即∠BCD-∠ACD=∠BCA=45°，∴∠ACD=90°-(45°+∠EAD)=45°-∠EAD=45°-25∠BCA=45°-18°=27°，故∠ACD的度数是27°，故答案为：27°．【点睛】本题利用平行线、垂直、角平分线综合考查角度的计算，理解题意，综合运用这些知识点是解题关键．三、解答题（每小题6分，共30分）13．（2022秋·福建福州·七年级统考期末）如图，已知AGF ABC Ð=Ð，12180Ð+Ð=°．（1）试判断BF 与DE 的位置关系，并说明理由；（2）若BF AC ^，2140Ð=°，求AFG Ð的度数．【答案】（1）//BF DE ，理由见解析；（2）50°【分析】（1）根据已知条件，先证明 FG//BC ，继而得 ∠1=∠3 ，根据 ∠1+∠2=180° 等量代换得 ∠3+∠2=180° ，从而得证；（2）由（1）的结论，求得 ∠1 ，再根据 BF ⊥AC ，求得 ∠1 的余角即可．【详解】解：()1//BF DE ，理由如下：AGF ABC Ð=ÐQ ，//GF BC \，13\Ð=Ð，12180Ð+Ð=°Q ，32180\Ð+Ð=°，//BF DE \；()2//BF DE Q ，BF AC ^，DE AC \^，12180Ð+Ð=°Q ，2140Ð=°，140\Ð=°，904050AFG \Ð=°-°=°．【点睛】本题考查了平行线的性质与判定，求一个角的余角，熟练平行线的性质与判定是解题的关键．14．学习了两条直线平行的判定方法1后，谢老师接着问：“由同位角相等，可以判断两条直线平行，那么能否利用内错角相等来判定两条直线平行呢？”如图，直线AB 和CD 被直线EF 所截，∠2＝∠3，AB ∥CD 吗？说明理由．现请你补充完下面的说理过程：答：AB ∥CD理由如下：∵∠2＝∠3（已知）且（）∴∠1＝∠2∴AB ∥CD （）【答案】∠1＝∠3；对顶角相等；同位角相等，两直线平行【分析】根据已知条件及对顶角相等得出∠1＝∠2，由同位角相等，两直线平行即可证明．【详解】解：AB ∥CD理由如下：∵∠2＝∠3（已知）且∠1＝∠3（对顶角相等）∴∠1＝∠2∴AB ∥CD （同位角相等，两直线平行），故答案为：∠1＝∠3；对顶角相等；同位角相等，两直线平行．【点睛】题目主要考查对顶角相等及平行线的判定，理解题意，熟练掌握平行线的判定是解题关键．15．如图，己知点P 、Q 分别在AOB Ð的边OA OB 、上，按下列要求画图：(1)画射线PQ；(2)过点P画垂直于射线OB的线段PC，垂足为点C；(3)过点Q画直线QM平行于射线OA．【答案】(1)见解析(2)见解析(3)见解析【分析】根据题意过用直尺作图，分别P画垂直于射线OB的射线PC，垂足为点C；过点Q画直线QM平行于射线OA．【详解】（1）如图，射线PQ为所求；（2）如图，线段PC为所求；（3）如图，直线QM为所求【点睛】此题主要考查了基本作图，正确把握相关定义是解题关键．16．指出下列命题的题设和结论，并判断它们是真命题还是假命题，如果是假命题，举出一个反例．（1）两个角的和等于平角时，这两个角互为补角；（2）内错角相等；（3）两条平行线被第三条直线所截，内错角相等．【答案】（1）题设：如果两个角的和等于平角时，结论：那么这两个角互为补角；是真命题；（2）题设：如果两个角是内错角，那么这两个角相等；是假命题，反例见解析；（3）题设：如果两条平行线被第三条直线所截，结论：那么内错角相等．是真命题．【分析】（1）根据将命题写成“如果…，那么…”的形式，“如果”后面写题设，“那么”后面写结论可得题设和结论，根据平角的定义可得该命题是真命题；（2）根据将命题写成“如果…，那么…”的形式，“如果”后面写题设，“那么”后面写结论可得题设和结论，根据平行线的性质可得该命题是假命题；利用相交直线被第三条直线所截，内错角不相等可举反例；（3）根据将命题写成“如果…，那么…”的形式，“如果”后面写题设，“那么”后面写结论可得题设和结论，根据平行线的性质可得该命题是真命题；．【详解】（1）题设：如果两个角的和等于平角，结论：那么这两个角互为补角；是真命题；（2）题设：如果两个角是内错角，那么这两个角相等；是假命题，如图∠1与∠2是内错角，∠2＞∠1；（3）题设：如果两条平行线被第三条直线所截，结论：那么内错角相等．是真命题．【点睛】本题考查了命题与定理的相关知识．将命题写成“如果…，那么…”的形式，就是要明确命题的题设和结论，“如果”后面写题设，“那么”后面写结论．关键是明确命题与定理的组成部分，会判断命题的题设与结论．17．如图，AE⊥BC，FG⊥BC，∠1＝∠2，求证：AB∥CD．【答案】见解析【分析】首先由AE⊥BC，FG⊥BC可得AE∥FG，根据两直线平行，同位角相等及等量代换可推出∠A=∠2，利用内错角相等，两直线平行可得AB∥CD．【详解】证明：如图，设BC与AE、GF分别交于点M、N.∵AE⊥BC，FG⊥BC，∴∠AMB=∠GNB=90°，∴AE∥FG，∴∠A=∠1；又∵∠2=∠1，∴∠A=∠2，∴AB∥CD．【点睛】本题考查了平行线的性质及判定，熟记定理是正确解题的关键．四、解答题（每小题8分，共24分）18．如图，点O是直线AB上一点，OD平分∠AOC，∠BOE=3∠COE,∠DOE=81°，求∠BOE，∠AOD的度数.【答案】∠BOE=27°，∠AOD=72°．【分析】设∠COE=x ，则∠AOD=81°-x ，则∠BOE=3x ，∠AOC=2 ∠AOD ，由∠AOC+∠BOC=180° ，列方程2()81x °-+4x=180°，解方程求解即可．【详解】解：设∠COE=x ，∵∠BOE=3∠COE ，OD 平分∠AOC ，∠DOE DOC COE=Ð+Ð81ADO DOC DOE COE x\Ð=Ð=Ð-Ð=°-Q ∠BOE=3∠COE ，则∠BOE=3x ，∠AOC=2()81x °-，∵O 是直线AB 上一点，∴ ∠AOC+∠BOC=180° ，∴2()81x °-+4x=180°，解得9x =°∠AOD=81°-972°=°∴∠BOE=27°，∠AOD= 72°．【点睛】本题考查的是角平分线的定义，角的和差运算，邻补角的含义，解本题的关键是运用方程的思想解决几何问题．19．如图，直线AB ，CD 相交于点O ，OB 平分∠EOD ．(1)若∠BOE ：∠EOC ＝1：4，求∠AOC 的度数；(2)在（1）的条件下，画OF ⊥CD ，请直接写出∠EOF 的度数．【答案】(1)30°(2)30°或150°【分析】（1）设BOE x Ð=，则4EOC x Ð=，先根据角平分线的定义可得BOD BOE x Ð=Ð=，22EOD BOE x Ð=Ð=，再根据邻补角的定义求出x 的值，从而可得BOD Ð的度数，然后根据对顶角相等即可得；（2）先求出60,90EOD FOD Ð=°Ð=°，再分①点F 在AB 的上方和②点F 在AB 的下方两种情况，根据角的和差即可得．【详解】（1）解：由题意，设BOE x Ð=，则4EOC x Ð=，OB Q 平分EOD Ð，22EOD BOE x \Ð=Ð=，BOD BOE x Ð=Ð=，180EOD EOC Ð+Ð=°Q ，24180x x \+=°，解得30x =°，30BOD \Ð=°，由对顶角相等得：30AOC BOD Ð=Ð=°．（2）解：由（1）可知，23060EOD Ð=´°=°，OF CD ^Q ，90FOD \Ð=°，由题意，分以下两种情况：①如图，当点F 在AB 的上方时，则150EOF EOD FOD Ð=Ð+Ð=°；②如图，当点F 在AB 的下方时，则30EOF FOD EOD Ð=Ð-Ð=°；综上，EOF Ð的度数为30°或150°．【点睛】本题考查了与角平分线有关的计算、对顶角相等、一元一次方程的应用，较难的是题（2），正确分两种情况讨论是解题关键．20．如图，已知直线,,AB CD AC 上的点M ，N ，E 满足ME NE ^，90,AME CNE ACD Ð+Ð=Ð°的平分线CG 交MN 于G ，作射线GF AB ∥．(1)直线AB 与CD 平行吗？为什么？(2)若66CAB Ð=°，求CGF Ð的度数．【答案】(1)平行，理由见解析(2)123°【分析】（1）利用已知条件和三角形内角和定理，通过等量代换可得180A ACD Ð+Ð=°，由同旁内角互补，两直线平行，可得//AB CD ；（2）利用,66AB CD CAB Ð=°∥，求出ACD Ð，再利用角平分线的定义求出GCD Ð，再证GF CD ∥，利用两直线平行，同旁内角互补，即可求出CGF Ð．（1）解：//AB CD ．理由如下：∵ME NE ^，∴90MEN Ð=°，∴90AEM CEN Ð+Ð=°，∵180A AEM AME Ð+Ð+Ð=°，180ACD CEN CNE Ð+Ð+Ð=°，∴360A ACD AEM CEN AME CNE Ð+Ð+Ð+Ð+Ð+Ð=°，∵90AME CNE Ð+Ð=°，90AEM CEN Ð+Ð=°，∴180A ACD Ð+Ð=°，∴//AB CD ；（2）解：∵66AB CD CAB ∥，Ð=°，∴180114ACD CAB Ð=°-Ð=°，∵CG 平分ACD Ð，∴1572GCD ACD Ð=Ð=°，∵AB CD GF AB ∥，∥，∴GF CD ∥．∴180CGF GCD Ð+Ð=°，∴18057123CGF Ð=°-°=°．【点睛】本题考查平行线的判定与性质，角平分线的定义，三角形内角和定理，垂直的定义等，熟练掌握平行线的判定定理和性质定理是解题的关键．五、解答题（每小题9分，共18分）21．如图，//AC BD ，BC 平分ABD Ð，设ACB Ð为a ，点E 是射线BC 上的一个动点．（1）若30a =°时，且BAE CAE Ð=Ð，求CAE Ð的度数；（2）若点E 运动到1l 上方，且满足100BAE Ð=°，:5:1BAE CAE ÐÐ=，求a 的值；（3）若:()1BAE CAE n n ÐÐ=>，求CAE Ð的度数（用含n 和a 的代数式表示）．【答案】（1）60°；（2）50°；（3）18021n a °--或18021n a°-+【分析】（1）根据平行线的性质可得CBD Ð的度数，再根据角平分线的性质可得ABE 的度数，应用三角形内角和计算BAC Ð的度数，由已知条件BAE CAE Ð=Ð，可计算出CAE Ð的度数；（2）根据题意画出图形，先根据:5:1BAE CAE ÐÐ=可计算出CAE Ð的度数，由100BAE Ð=°可计算出BAC Ð的度数，再根据平行线的性质和角平分线的性质，计算出CBD Ð的度数，即可得出结论；（3）根据题意可分两种情况，①若点E 运动到1l 上方，根据平行线的性质由a 可计算出CBD Ð的度数，再根据角平分线的性质和平行线的性质，计算出BAC Ð的度数，再:BAE CAE n ÐÐ=，BAE BAC CAE Ð=Ð+Ð，列出等量关系求解即可等处结论；②若点E 运动到1l 下方，根据平行线的性质由a 可计算出CBD Ð的度数，再根据角平分线的性质和平行线的性质，计算出BAC Ð的度数，再:BAE CAE n ÐÐ=，BAE BAC CAE Ð=Ð-Ð列出等量关系求解即可等处结论．【详解】解：（1）30a =°Q ，//AC BD ，30CBD \Ð=°，BC Q 平分ABD Ð，30ABE CBD \Ð=Ð=°，1801803030120BAC ABE a \Ð=°-Ð-=°-°-°=°，又BAE CAE Ð=ÐQ ，111206022CAE BAC \Ð=Ð=´°=°；（2）根据题意画图，如图1所示，100BAE Ð=°Q ，:5:1BAE CAE ÐÐ=，20CAE \Ð=°，1002080BAC BAE CAE \Ð=Ð-Ð=°-°=°，//AC BD Q ，180100ABD BAC \Ð=°-Ð=°，又BC Q 平分ABD Ð，111005022CBD ABD \Ð=Ð=´°=°，50CBD a \=Ð=°；（3）①如图2所示，//AC BD Q ，CBD ACB a \Ð=Ð=，BC Q 平分ABD Ð，22ABD CBD a \Ð=Ð=，1801802BAC ABD a \Ð=°-Ð=°-，又:BAE CAE n ÐÐ=Q ，():BAC CAE CAE n \Ð+ÐÐ=，(1802):CAE CAE n a °-+ÐÐ=，解得18021CAE n a°-Ð=-；②如图3所示，//AC BD Q ，CBD ACB a \Ð=Ð=，BC Q 平分ABD Ð，22ABD CBD a \Ð=Ð=，1801802BAC ABD a \Ð=°-Ð=°-，又:BAE CAE n ÐÐ=Q ，():BAC CAE CAE n \Ð-ÐÐ=，(1802):CAE CAE n a °--ÐÐ=，解得18021CAE n a°-Ð=+．综上CAE Ð的度数为18021n a °--或18021n a°-+．【点睛】本题主要考查平行线的性质和角平分线的性质，两直线平行，同位角相等．两直线平行，同旁内角互补．两直线平行，内错角相等．合理应用平行线的性质是解决本题的关键．22．如图，//AB CD ，C 在D 的右侧，BE 平分ABC Ð，DE 平分ADC Ð，,BE DE 所在直线交于点E ，80ADC Ð=°．（1）若50ABC Ð=°，求BED Ð的度数；（2）将线段BC 沿DC 方向平移，使得点B 在点A 的右侧，其他条件不变，若120ABC Ð=°，求BED Ð的度数．【答案】（1）65°；（2）20°或160°【分析】1）作//EF AB ，如图1，利用角平分线的定义得到25ABE Ð=°，40EDC Ð=°，利用平行线的性质得到25BEF ABE Ð=Ð=°，40FED EDC Ð=Ð=°，从而得到BED Ð的度数；（2）作//EF AB ，如图2，利用角平分线的定义得到60ABE Ð=°，40EDC Ð=°，利用平行线的性质得到120BEF Ð=°，40FED EDC Ð=Ð=°，从而得到BED Ð的度数；如图3，利用//AB CD 得到240Ð=°，然后根据三角形外角性质可计算出BED Ð．【详解】解：（1）作//EF AB ，如图1，BE Q 平分ABC Ð，DE 平分ADC Ð，1252ABE ABC \Ð=Ð=°，1402EDC ADC Ð=Ð=°，//AB CD Q ，//EF CD \，25BEF ABE Ð=Ð=°Q ，40FED EDC Ð=Ð=°，254065BED \Ð=°+°=°；（2）作//EF AB ，如图2，BE Q 平分ABC Ð，DE 平分ADC Ð，1602ABE ABC \Ð=Ð=°，1402EDC ADC Ð=Ð=°，//AB CD Q ，//EF CD \，180120BEF ABE Ð=°-Ð=°Q ，40FED EDC Ð=Ð=°，12040160BED \Ð=°+°=°．如图3，BE Q 平分ABC Ð，DE 平分ADC Ð，11602ABC \Ð=Ð=°，1402EDC ADC Ð=Ð=°，//AB CD Q ，240\Ð=°，12BED Ð=Ð+ÐQ ，604020BED \Ð=°-°=°．如图4，BE Q 平分ABC Ð，DE 平分ADC Ð，1602ABE ABC \Ð=Ð=°，12402ADC Ð=Ð=°，//AB CD Q ，160ABE \Ð=Ð=°，3240Ð=Ð=°Q ，而12BED Ð=Ð+Ð，604020BED \Ð=°-°=°．综上所述，BED Ð的度数为20°或160°．【点睛】本题考查了平移的性质：解题的关键是把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同；新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行（或共线）且相等．也考查了平行线的性质．六、解答题（本大题共12分）23．（2022秋·贵州黔西·七年级校考阶段练习）已知：直线EF 分别与直线AB ，CD 相交于点G ，H ，并且∠AGE+∠DHE ＝180°．（1）如图1，求证：AB ∥CD ；（2）如图2，点M 在直线AB ，CD 之间，连接GM ，HM ，求证：∠M ＝∠AGM+∠CHM ；（3）如图3，在（2）的条件下，射线GH 是∠BGM 的平分线，在MH 的延长线上取点N ，连接GN ，若∠N＝∠AGM ，∠M ＝∠N+12∠FGN ，求∠MHG 的度数．【答案】（1）见解析；（2）见解析；（3）60°【分析】（1）根据已知条件和对顶角相等即可证明；（2）如图2，过点M 作MR ∥AB ，可得AB ∥CD ∥MR ．进而可以证明；（3）如图3，令∠AGM ＝2α，∠CHM ＝β，则∠N ＝2α，∠M ＝2α+β，过点H 作HT ∥GN ，可得∠MHT ＝∠N ＝2α，∠GHT ＝∠FGN ＝2β，进而可得结论．【详解】（1）证明：如图1，∵∠AGE+∠DHE ＝180°，∠AGE ＝∠BGF ．∴∠BGF+∠DHE ＝180°，∴AB ∥CD ；（2）证明：如图2，过点M 作MR ∥AB ，又∵AB ∥CD ，∴AB ∥CD ∥MR ．∴∠GMR ＝∠AGM ，∠HMR ＝∠CHM ．∴∠GMH ＝∠GMR+∠RMH ＝∠AGM+∠CHM ．（3）解：如图3，令∠AGM ＝2α，∠CHM ＝β，则∠N ＝2α，∠M ＝2α+β，∵射线GH 是∠BGM 的平分线，∴()111809022FGM BGM AGM a Ð=Ð=°-Ð=°-，∴∠AGH ＝∠AGM+∠FGM ＝2α+90°﹣α＝90°+α，∵12M N FGN Ð=Ð+Ð，∴1222FGN a b a +=+Ð，∴∠FGN ＝2β，过点H 作HT ∥GN ，则∠MHT ＝∠N ＝2α，∠GHT ＝∠FGN ＝2β，∴∠GHM＝∠MHT+∠GHT＝2α+2β，∠CHG＝∠CHM+∠MHT+∠GHT＝β+2α+2β＝2α+3β，∵AB∥CD，∴∠AGH+∠CHG＝180°，∴90°+α+2α+3β＝180°，∴α+β＝30°，∴∠GHM＝2（α+β）＝60°．【点睛】本题考查了平行线的判定与性质，对顶角的性质，角平分线的性质，解决本题的关键是掌握平行线的判定与性质．。

七年级下数学相交线与平行线培优训练(含解析)

相交线与平行线培优训练（含解析）一、单选题1．如图，已知直线AB 、CD 被直线AC 所截，AB ∥CD ，E 是平面内任意一点（点E 不在直线AB 、CD 、AC 上），设∠BAE=α，∠DCE=β．下列各式：①α+β，②α﹣β，③180°﹣α﹣β，，④360°﹣α﹣β，∠AEC 的度数可能是（）A ． ①②③B ． ①②④C ． ①③④D ． ①②③④【答案】B【解析】试题解析：点E 有4种可能位置．（1）如图，由AB ∥CD ，可得1AOC DCE β∠=∠=，11AOC BAE AE C ∠=∠+∠， 1AE C βα∴∠=-．（2）如图，过2E 作AB 平行线，则由AB ∥CD ，可得2212BAE DCE αβ∠=∠=∠=∠=，， 2AE C αβ∴∠=+．（3）如图，由AB ∥CD ，可得33BOE DCE β∠=∠=， 333BAE BOE AE C ∠=∠+∠，3AE C αβ∴∠=-．（4）如图，由AB ∥CD ，可得444360BAE AE C DCE ∠+∠+∠=︒， 4360AE C αβ∴∠=︒--．AEC ∴∠的度数可能为360βααβαβαβ-+-︒--，，，．故选：D ．2．如图， //AB CD ，用含123∠∠∠，，的式子表示4∠，则4∠的值为（）A ． 123∠+∠-∠B ． 132∠+∠-∠C ． 18031?2+∠-∠-∠D ． 231180∠+∠-∠-【答案】D【解析】试题解析：过点E 作EG ∥AB ，过点F 作FH ∥CD ，∵AB ∥CD ，∴AB ∥CD ∥EG ∥FH ，∴∠1=∠AEG ，∴∠GEF=∠2-∠1，∵EG ∥FH ，∴∠EFH=180°-∠GEF=180°-（∠2-∠1）=180°-∠2+∠1，∴∠CFH=∠3-∠EFH=∠3-（180°-∠2+∠1）=∠3+∠2-∠2-180°，∵FH ∥CD ，∴∠4=∠3+∠2-∠1-180°，故选：D ．3．下列说法：①平方等于其本身的数有0，±1；②32xy 3是4次单项式；③将方程x−10.3−x+20.5=1.2中的分母化为整数，得10x−103−10x+205=12；④平面内有4个点，过每两点画直线，可画6条．其中正确的有（）A ． 1个B ． 2个C ． 3个D ． 4个【答案】A【解析】根据负数没有平方根，可知①不正确；根据单项式的意义，可知次数为所有字母因式的指数和，故②正确；根据分数的基本性质，可知将方程x−10.3−x+20.5=1.2中的分母化为整数，得10x−103−10x+205=1.2，故③不正确；根据两点确定一条直线，可知平面内有4个点，过每两点画直线，条数不确定：当四个点在同一直线上时，只有一条；当只有每任意三点不在同一直线上的四个点才能画6条直线，故④不正确．故选：A.点睛：本题考查了数的平方，单项式的概念，方程的分母化为整数，点与直线条数的关系．4．如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30︒角直角三角板的斜边与纸条一边重合，含45︒角的三角板的一个顶点在纸条的另一边，则1∠的度数是（）A．14°B．15°C．20°D．30°【答案】B【解析】分析：过A点作AB∥a，利用平行线的性质得AB∥b，所以∠1=∠2，∠3=∠4=30°，加上∠2+∠3=45°，易得∠1=15°．详解：如图，过A点作AB∥a，∴∠1=∠2，∵a∥b，∴AB∥b，∴∠3=∠4=30°，而∠2+∠3=45°，∴∠2=15°，∴∠1=15°．故选：B．点睛：本题考查了平行线的性质，解题时注意：两直线平行，内错角相等．5．下列说法不正确的是（）A．过任意一点可作已知直线的一条平行线B．在同一平面内两条不相交的直线是平行线C．在同一平面内，过直线外一点只能画一条直线与已知直线垂直D．直线外一点与直线上各点连接的所有线段中，垂线段最短【答案】A【解析】试题分析：平面内，过直线外一点有且只有一条直线与已知直线平行，故A不正确；在同一平面内两条不相交的直线是平行线，这是平行线的概念，故B正确；在同一平面内，过直线外一点只能画一条直线与已知直线垂直，故C正确；直线外一点与直线上各点连接的所有线段中，垂线段最短，故D正确；故选：A.6．6．如图所示，AB∥CD，EF，HG相交于点O，∠1=40°，∠2=60°，则∠EOH的角度为（）A．80°B．100°C．140°D．120°【答案】B【解析】试题分析：如图，根据平行线的性质，可知∠3=∠2=60°，然后根据三角形的外角等于不相邻两内角的和，可得∠EOH=100°.故选：B7．如图，直角三角形ABC的直角边AB=6，BC=8，将直角三角形ABC沿边BC的方向平移到三角形DEF的位置，DE交AC于点G，BE＝2，三角形CEG的面积为13.5，下列结论：①三角形ABC平移的距离是4；②EG=4.5；③AD∥CF；④四边形ADFC的面积为6．其中正确的结论是（）A．①②B．②③C．③④D．②④【答案】B【解析】分析：(1)对应线段的长度即是平移的距离；(2)根据EC的长和△CEG的面积求EG；(3)平移前后，对应点的连线平行且相等；(4)根据平行四边形的面积公式求.详解：(1)因为点B，E是对应点，且BE＝2，所以△ABC平行的距离是2，则①错误；②根据题意得，13.5×2＝(8－2)EG，解得EG＝4.5，则②正确；③因为A，D是对应点，C，F是对应点，所以AD∥CF，则③正确；④平行四边形ADFC的面积为AB·CF＝AB·BE＝6×2＝12，则④错误.故选B.点睛：本题考查了平移的性质，平移的性质有：①平移只改变图形的位置，不改变图形的形状和大小；②平移得到的图形与原图形中的对应线段平行(或在同一条直线上)且相等，对应角相等；对应点连线平行(或在同一条直线上)且相等.8．如图，AB∥CD，EG⊥AB，垂足为G．若∠1＝50°，则∠E＝（）.A．60°B．50°C．40°D．30°【答案】C【解析】试题分析：先根据对顶角相等求出∠1的对顶角，然后根据两直线平行，同位角相等，求出直角三角形的一个内角，然后可求得∠E=90°-50°=40°.故选：C9．①如图1,AB∥CD,则∠A +∠E +∠C=180°；②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E－∠1=180° ；④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )A．、1个B．2个C．3个D．4个【答案】C【解析】①如图1，过点E作EF∥AB，因为AB∥CD，所以AB∥EF∥CD，所以∠A+∠AEF=180°，∠C+∠CEF=180°，所以∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°，则①错误；②如图2，过点E作EF∥AB，因为AB∥CD，所以AB∥EF∥CD，所以∠A=∠AEF，∠C=∠CEF，所以∠A+∠C=∠AEC+∠AEF=∠AEC，则②正确；③如图3，过点E作EF∥AB，因为AB∥CD，所以AB∥EF∥CD，所以∠A+∠AEF=180°，∠1=∠CEF，所以∠A+∠AEC-∠1=∠A+∠AEC-∠CEF=∠A+∠AEF=180°，则③正确；④如图4，过点P作PF∥AB，因为AB∥CD，所以AB∥PF∥CD，所以∠A+∠APF，∠C+∠CPF，所以∠A=∠CPF+∠APC=∠C+∠APC，则④正确；故选C.10．给出下列说法：（1）两条直线被第三条直线所截，同位角相等；（2）不相等的两个角不是同位角；（3）平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交；（4）从直线外一点到这条直线的垂线段，叫做该点到直线的距离；（5）过一点作已知直线的平行线，有且只有一条。

数学第五章相交线与平行线的专项培优练习题(含答案

同理，可以推导当n条直线相交时，交点数是，即
，
，
，
本题的答案为：1， .
【点睛】
本题考查了平面内直线两两相交交点数的计算，涉及到一种很重要的数学方法数学归纳法的初步应用接触，此方法在推导证明中比较常用.
13．【解析】
【分析】
首先过点E作EM∥AB，过点F作FN∥AB，由AB∥CD，即可得EM∥AB∥CD∥FN，然后根据两直线平行，同旁内角互补，由∠BED=110°，即可求得∠ABE+∠CDE=25
13．如图，平分平分，则 ______．
14．与的两边互相垂直，且，则的度数为_________.
15．如图，图①是长方形纸带，∠DEF=25°，将纸带沿EF折叠成图②，则图②中的∠CFG的度数是_____________．
16．两个角的两边分别平行,一个角是50°,那么另一个角是__________.
∴∠ABF+∠CDF= （∠ABE+∠CDE）=125°，
【详解】
∵四边形ABCD是矩形，
∴AD∥BC，
∴∠BFE=∠DEF=26°，
∴∠CFE=∠CFG-∠EFG=180°-2∠BFE-∠EFG=180°-3×26°=102°，
故选：A．
【点睛】
本题考查了翻折变换（折叠问题）、矩形的性质、平行线的性质；熟练掌握翻折变换和矩形的性质，弄清各个角之间的关系是解决问题的关键．
17．如图，已知EF∥GH，A、D为GH上的两点，M、B为EF上的两点，延长AM于点C，AB平分∠DAC，直线DB平分∠FBC，若∠ACB=100°，则∠DBA的度数为________．
18．如图所示，AB∥CD，EC⊥CD．若∠BEC＝30°，则∠ABE的度数为_____．

相交线与平行线的计算与证明能力训练培优卷

相交线与平行线的计算与证明能力训练培优卷（解答题20题）1．如图，点A、B、C、D在一条直线上，CE与BF交于点G，∠A＝∠1，CE∥DF，求证：∠E ＝∠F．2．如图，直线AB∥CD，BC平分∠ABD，∠1＝54°，求∠2的度数．3．光线在不同介质中传播速度不同，从一种介质射向另一种介质时会发生折射．如图，水面AB与水杯下沿CD平行，光线EF从水中射向空气时发生折射，光线变成FH，点G在射线EF上，已知∠HFB＝20°，∠FED＝45°，求∠GFH的度数．4．阅读理解：如图①，图形l外一点P与图形l上各点连接的所有线段中，若线段PA1最短，则线段PA1的长度称为点P到图形l的距离．例如：图②中，线段P1A的长度是点P1到线段AB的距离；线段P2H的长度是点P2到线段AB的距离．解决问题：如图③，平面直角坐标系xOy中，点A、B的坐标分别为（8，4），（12，7），点P从原点O出发，以每秒1个单位长度的速度向x轴正方向运动了t秒．（1）当t＝4时，求点P到线段AB的距离；（2）t为何值时，点P到线段AB的距离为5？（3）t满足什么条件时，点P到线段AB的距离不超过6？（直接写出此小题的结果）5．如图，AB∥CD，△EFG的顶点F，G分别落在直线AB，CD上，GE交AB于点H，GE平分∠FGD．若∠EFG＝90°，∠E＝35°，求∠EFB的度数．6．如图，AB∥CD，点E是CD上一点，∠AEC＝42°，EF平分∠AED交AB于点F，求∠AFE 的度数．7．如图，AB∥CD，∠1＝∠2．求证：AM∥CN．8．如图，在四边形ABCD中，AD∥BC，∠B＝80°．（1）求∠BAD的度数；（2）AE平分∠BAD交BC于点E，∠BCD＝50°．求证：AE∥DC．9．如图，AB∥CD，∠B＝∠D，直线EF与AD，BC的延长线分别交于点E，F，求证：∠DEF ＝∠F．10．如图，直线EF 分别与直线AB ，CD 交于点E ，F ．EM 平分∠BEF ，FN 平分∠CFE ，且EM ∥FN ．求证：AB ∥CD ．11．如图，已知AB ∥CD ，直线分别交AB 、CD 于点E ，F ，∠EFB ＝∠B ，FH ⊥FB ．（1）已知∠B ＝20°，求∠DFH ；（2）求证：FH 平分∠GFD ；（3）若∠CFE ：∠B ＝4：1，则∠GFH 的度数．12．已知AM ∥CN ，点B 为平面内一点，AB BC ⊥于B ．（1）如图1，直接写出∠A 和∠C 之间的数量关系是______________；（2）如图2，过点B 作BD AM ⊥于点D ，求证：ABD C ∠=∠．13.已知AB ∥CD ，点C 在点D 的右侧，∠ABC ，∠ADC 的平分线交于点E （不与B ，D 点重合）．∠ABC=n °，∠ADC=80°．（1）若点B 在点A 的左侧，求∠BED 的度数（用含n 的代数式表示）；（2）将（1）中的线段BC 沿DC 方向平移，当点B 移动到点A 右侧时，请画出图形并判断∠BED 的度数是否改变．若改变，求出∠BED 的度数（用含n 的代数式表示）若不变说明理由14．长江汛期即将来临，防汛指挥部在一危险地带两岸各安置了一探照灯，便于夜间查看江水及两岸河堤的情况．如图1，灯A射线自AM顺时针旋转至AN便立即回转，灯B射线自BP顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视．若灯A转动的速度是a度/秒，灯B转动的速度是b度/秒，且a、b满足|a﹣3b|+（a+b﹣4）2＝0．假定这一带长江两岸河堤是平行的，即PQ∥MN，且∠BAN＝45°（1）求a、b的值；（2）若灯B射线先转动20秒，灯A射线才开始转动，在灯B射线到达BQ之前，A灯转动几秒，两灯的光束互相平行？（3）如图2，两灯同时转动，在灯A射线到达AN之前．若A射出的光束与B射出的光束交于点C，过C作CD⊥AC交PQ于点D，则在转动过程中，∠BAC与∠BCD的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请求出其取值范围．15．已知直线AB∥CD．（1）如图1，直接写出∠ABE，∠CDE和∠BED之间的数量关系是．（2）如图2，BF，DF分别平分∠ABE，∠CDE，那么∠BFD和∠BED有怎样的数量关系？请说明理由．（3）如图3，点E在直线BD的右侧，BF，DF仍平分∠ABE，∠CDE，请直接写出∠BFD和∠BED 的数量关系．16．如图，已知l1∥l2，MN 分别和直线l1、l2交于点A 、B ，ME 分别和直线l1、l2交于点C 、D ，点P 在MN 上（P 点与A 、B 、M 三点不重合）．（1）如果点P 在A 、B 两点之间运动时，∠α、∠β、∠γ之间有何数量关系请说明理由；（2）如果点P 在A 、B 两点外侧运动时，∠α、∠β、∠γ有何数量关系（只须写出结论）．17．实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.(1)如图,一束光线m 射到平面镜a 上,被a 反射到平面镜b 上,又被b 反射.若被b 反射出的光线n 与光线m 平行,且∠1=50°,则∠2= °，∠3= °.(2)在(1)中,若∠1=55°,则∠3= °;若∠1=40°,则∠3= °.(3)由(1)、(2),请你猜想:当两平面镜a 、b 的夹角∠3= °时,可以使任何射到平面镜a 上的光线m ,经过平面镜a 、b 的两次反射后,入射光线m 与反射光线n 平行.你能说明理由吗?321nm b aP D C B A O x y 18．如图，在平面直角坐标系中，点A ，B 的坐标分别为A （m ，0）， B （n ，0）且m 、n 满足|m+2|+n 5-=0，现同时将点A ，B 分别向上平移3个单位，再向右平移2个单位，分别得到点A ，B 的对应点C ，D ，连接AC ，BD ，CD ．（12分）(1)求点C ，D 的坐标及四边形OBDC 的面积；(2)点P 是线段BD 上的一个动点，连接PC ，PO ，当点P 在BD 上移动时（不与B ，D 重合）DCP BOP CPO∠+∠∠的值是否发生变化，并说明理由。

相交线与平行线拓展与探究(培优篇)(含答案)

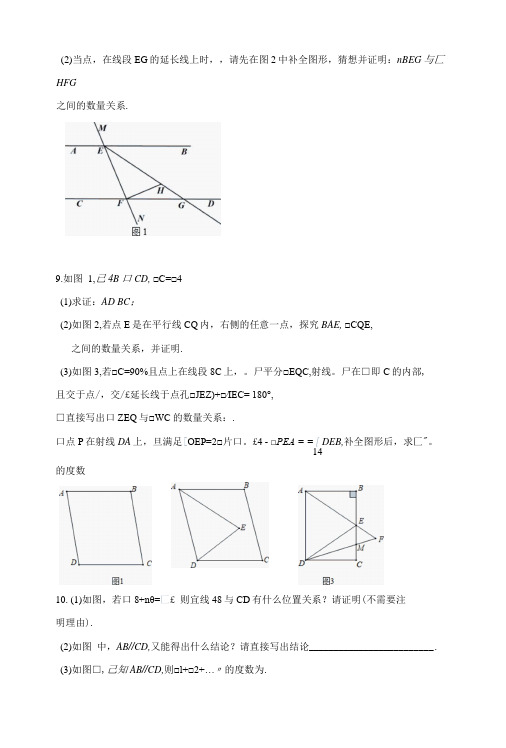
(2)当点，在线段EG的延长线上时，，请先在图2中补全图形，猜想并证明：nBEG与匚HFG之间的数量关系.9.如图1,已 4B口CD,□C=□4(1)求证：AD BC；(2)如图2,若点E是在平行线CQ内，右侧的任意一点，探究BAE,□CQE,之间的数量关系，并证明.(3)如图3,若□C=90%且点上在线段8C上，。

尸平分□EQC,射线。

尸在□即C的内部,且交于点/，交/£延长线于点孔□JEZ)+□∕IEC= 180°,□直接写出口ZEQ与□WC的数量关系：.口点P在射线DA上，旦满足[OEP=2□片口。

£4 - □PEA = = [ DEB,补全图形后，求匚"。

14的度数10. (1)如图，若口8+nθ=匚£ 则宜线48与CD有什么位置关系？请证明(不需要注明理由).(2)如图中，AB//CD,又能得出什么结论？请直接写出结论_________________________ .(3)如图□,己知AB//CD,则□l+□2+…〃的度数为.(1)如图1,求证：ABHCD ；(2)如图2,作的平分线交CD 于点/，点G 为上一点，连接FG,若NC~G 的平分线交线段AG 于点"，连接AC,若NACE = ∕β4C+∕BGM,过点〃作切交尸G的延长线于点且3NE-5Z4FH = 18。

，求/£4b+ NGWH 的度数.12.已知，45二CQ,点E 为射线EG 上一点. (1)如图 1,若口区4F=25°, ΠEDG=45o f W ∣J ∖2AED=.(2)如图2,当点£在bG 延长线上时，此时C 。

与力£交于点〃，贝I 」/4、EAF 、EDG 11.已知, AE∕∕BD, ZA = AD.图1(1)如图1,求证：ABHCD ；(2)如图2,作的平分线交CD 于点/，点G 为上一点，连接FG,若NC~G 的平分线交线段AG 于点"，连接AC,若NACE = ∕β4C+∕BGM,过点〃作切交尸G的延长线于点且3NE-5Z4FH = 18。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第五章相交线与平行线培优专题训练
1．已知：如图， AB∥EF∥CD，EG平分∠BEF，∠B+∠BED+∠D =192°，
∠B-∠D=24°，求∠GEF的度数。

2．如图，已知AB∥CD，且∠B=40°，∠D=70°，求∠DEB的度数。

解：过E作EF∥AB
3．如图，直线AB与CD相交于O，EF AB于F，GH CD于H，
求证EF与GH必相交。

分析：欲证EF与GH相交，直接证很困难，可考虑用反证法。

证明：假设EF与GH不相交。

∵EF、GH是两条不同的直线
∴EF∥GH
∵EF AB
∴GH AB
又因GH CD 故AB∥CD (垂直于同一直线的两直线平行) 图（4）
这与已知AB和CD相交矛盾。

所以EF与GH不平行，即EF与GH必相交
评注：本题应用结论：
(1) 垂直于同一条直线的两直线平行。

(2) 两条平行线中的一条直线垂直于第三条直线，那么另一条直线也平行于第三条直线；
4．平面上n条直线两两相交且无3条或3条以上直线共点，有多少个不同交点？
解：2条直线产生个交点，
第3条直线与前面2条均相交，增加个交点，这时平面上3条直线共有个交点；
第4条直线与前面3条均相交，增加个交点，这时平面上4条直线共有个交点；
…
则n条直线共有交点个数：。

5． 6个不同的点，其中只有3点在同一条直线上，2点确定一条直线，问能确定多少条直线？
解：6条不同的直线最多确定：条直线，除去共线的3点中重合多
算的2条直线，即能确定的直线为15-2=13条。

另法：3点所在的直线外的3点间最多能确定3条直线，这3点与直线上的3点最多有3×
3=9条直线，加上3点所在的直线共有：3+9+1=13条
评注：一般地，平面上n 个点最多可确定直线的条数为：1+2+3+…+(n-1)=2
1n(n-1) 6．10条直线两两相交，最多将平面分成多少块不同的区域？
解：2条直线最多将平面分成2+2=4个不同区域；
3条直线中的第3条直线与另两条直线相交，最多有两个交点，此直线被这两点分成3段，每一段将它所在的区域一分为二，则区域增加3个，即最多分成2+2+3=7个不同区域；同理：4条直线最多分成2+2+3+4=11个不同区域；
…
∴ 10条直线最多分成个不同区域。

推广：n 条直线两两相交，最多将平面分成2+2+3+4+…+n=1+21n(n+1)=2
1(n 2+n+2)块不同的区域
思考：平面内n 个圆两两相交，最多将平面分成多少块不同的区域？
7．平面上有5个点，其中仅有3点在同一直线上，过每2点作一条直线，一共可以作直线（）条
A ．6
B ． 7
C ．8
D ．9
8．平面上三条直线相互间的交点个数是（）
A ．3
B ．1或3
C ．1或2或3
D ．不一定是1，2，3
9．平面上6条直线两两相交，其中仅有3条直线过一点，则截得不重叠线段共有（）
A ．36条
B ．33条
C ．24条
D ．21条
10．已知平面中有n 个点C B A ,,三个点在一条直线上，E F D A ,,,四个点也在一条直线上，除些之外，再没有三点共线或四点共线，以这n 个点作一条直线，那么一共可以画出38条不同的直线，这时n 等于（）
（A ）9 （B ）10 （C ）11 （D ）12
11．若平行直线AB 、CD 与相交直线EF 、GH 相交成如图示的图形，则共得同旁内角（）
A ．4对
B ．8对
C ．12对
D ．16对
12．如下第6题图，已知FD ∥BE ，则∠1+∠2-∠3=( )
A ．90°
B ．135°
C ．150°
D ．180°
第13题
13．如图，已知AB ∥CD ，∠1=∠2，则∠E 与∠F 的大小关系；
14．平面上有5个点，每两点都连一条直线，问除了原有的5点之外这些直线最多还有交点
15．如图，已知AB ∥CD ∥EF ，PS GH 于P ，∠FRG=110°，则∠PSQ ＝。

16．已知A 、B 是直线L 外的两点，则线段AB 的垂直平分线与直线的交点个数是。

17．平面内有4条直线，无论其关系如何，它们的交点个数不会超过个。

18．如图，已知CB AB ，CE 平分∠BCD ，DE 平分∠CDA ，
∠EDC+∠ECD =90°，
求证：DA AB
19．一直线上5点与直线外3点，每两点确定一条直线，最多确定多少条不同直线？
20.观察如图所示中的各图，寻找对顶角（不含平角）：
（1）如图a ，图中共有＿＿＿对对顶角；
（2）如图b ，图中共有＿＿＿对对顶角；
（3）如图c ，图中共有＿＿＿对对顶角.
（4）研究（1）～（3）小题中直线条数与对顶角的对数之间的关系，若有n 条直线相图a 图b 图c
交于一点，则可形成多少对对顶角？
（5）若有2018条直线相交于一点，则可形成多少对对顶角？
21．将一副三角尺的两个直角顶点O重合在一起，如图所示放置，∠B＝45°，∠A＝60°.如果重叠在一起的角是∠BOC.
(1)若∠BOC＝60°，则∠AOD的度数是__ __；
(2)若∠BOC＝80°，则∠AOD的度数是__ __；
(3)通过上面的求解，你能否得到一个结论？请直接写出这个结论．。