不规则物体的质心计算和展示.ppt
合集下载
高二物理竞赛课件:质心(center of mass) 质心运动定理

一、质点对定点的角动量
说角动量时,
t 时刻, 如图 ,
必须指明是对 哪个固定点的
定义 L r P 为质点对固定点o 的角动量
大小:L rP 方向:垂直于
sri,nP
rmv sin
组成的平面
[SI] kgm 2/s
o r
L
P
m
力对定点的力矩
说力矩时,也
t 时 刻,如图,
必须指明是对 哪个固定点的
例 已知1/4圆M, m由静止下滑,求
t1→t2 过程中M移动的距离 S。 解: 选(M+m)为体系
水平方向: 合外力=0,质心静止
t1时刻
m
t2时刻
Mபைடு நூலகம்
M
m
x -R O
体系质心
X1
MxmR Mm
x-S -S O
体系质心
X
2
M
x
M
SmS
m
质心静止 X1 X 2
M
移动的距离
S
m Mm
R
思路:与处理动量定理 动量守恒问题相同
等于质点角动量的增量。
M 和L 是对惯性系中的同一固定点的。
角动量定理 Mdt dL
t2
Mdt ΔL
t1
若 M 0 则 L 0 角动量守恒定律
讨论
1)动量守恒与角动量守恒
是相互独立的定律。 如行星运动
2)有心力—力始终指向一点
直升飞机
动量不守恒 角动量守恒
质点在有心力作用下运动时角动量守恒
M r F 0 角动量守恒
o
F
mi
ri c质心
rc
o
重心是指各质点所受重力的合力作用点。
质点系统质心运动-PPT资料20页

• 質心(質量中心) :
– 為簡單描述多質點系統的運動情形,假想全
部系統的質量集中於某一特殊位置,此假想
的位置稱為系統的質心。
–
質心的質量為系統全部質量的總和。mc
mi
i
– 質點系統受外力而運動時,質心的移動情形 可代表系統整體的移動情形;但無法顯示出 系統的轉動情形。
博学之,审问之,慎寺之,明辩之,
2
笃行之。精心整理,欢迎收藏
質心運動可代表質點系統運動(1)
• 各質點所受力可分為 兩部分:
– 來自系統外的作用力, 稱為外力,
– 系統內其他質點對該 質點的作用力,稱為 內力。
• 由牛頓第三運動定律知,內力必成對存在。 兩力的量值相等但方向相反,故系統的內力 總和為零。
博学之,审问之,慎寺之,明辩之,
16
笃行之。精心整理,欢迎收藏
博学之,审问之,慎寺之,明辩之,
17
笃行之。精心整理,欢迎收藏
博学之,审问之,慎寺之,明辩之,
18
笃行之。精心整理,欢迎收藏
博学之,审问之,慎寺之,明辩之,
19
笃行之。精心整理,欢迎收藏
谢谢!
20
3
笃行之。精心整理,欢迎收藏
質心運動可代表質點系統運動(2)
• 系統所受的合力 = 系統各質點所受力的 向量和 =系統各質點所受的外力合力
F 外m 1a1m 2a2m 3a3
• 若假想全部系統的質量集中於某一特殊 位置 C (質心) ,則
F 外 m 1a 1 m 2a 2 m 3a 3 M a c
• 質心的加速度 a c ,等於假想把系統全部
的質量集中在質心,且總外力 F 外 作用在
質心時所產生的加速度。
质心运动(课堂PPT)

m1l1m2l2(杠杆关系)
m1 x1
l1
xC
l2
m2 x2
x
xC就是m1和m2的质心位置
m 1 (x C x 1) m 2(x 2 x C ) xCm 1 m x1 1 m m 2 2x2m 1x1M m 2x 4 2
二.质心坐标
推广到3维质点系,若n个质点的位矢为
r1,r2, rn,
质点系总质量 Mmi
作用在质点系上的合外力等于质点系 的总质量与质心加速度的乘积
质心的运动状态变化只由系统所受 的合外力决定,与内力无关。
(质心运动定理本身只对惯性系成立!)
10
质心的运动满足: F r合外Marc
质心能作为质点系 整体运动的代表!
11
五.质心动量变化定理
质心运动定理:
F 合 外 d(M dv C t)M a c
2
旋轮线:教材P25习题1.4
• 质点系运动 质心运动+各质点相对于质心的运动3
§6-1 质心动量定理
一. 质心
质心 — 质点系统的质量中心
对质点系, 总有一特殊点,其运动和质点系的所 有质量集中于该处的质点运动相同 质心
以质点系各点质量为权重的系统位置的平均值
以两质点系统为例:
若有一点xC,使
若质心系是非惯性系,则质心系中有:
F 合 F 外 惯 m a '(c质心系中的质心运动定律) 而a 'c0(质 心系中质心的加速度为零)
F 合 外 F 惯 0
在质心非惯性系中惯性力和外力完全抵消,
故系统总动量守恒,且恒为零。
16
§6-2. 质心动能定理
M aCF 合 外
若F合
外 0x,则 a C0
m1 x1
l1
xC
l2
m2 x2
x
xC就是m1和m2的质心位置
m 1 (x C x 1) m 2(x 2 x C ) xCm 1 m x1 1 m m 2 2x2m 1x1M m 2x 4 2
二.质心坐标
推广到3维质点系,若n个质点的位矢为
r1,r2, rn,
质点系总质量 Mmi
作用在质点系上的合外力等于质点系 的总质量与质心加速度的乘积
质心的运动状态变化只由系统所受 的合外力决定,与内力无关。
(质心运动定理本身只对惯性系成立!)
10
质心的运动满足: F r合外Marc
质心能作为质点系 整体运动的代表!
11
五.质心动量变化定理
质心运动定理:
F 合 外 d(M dv C t)M a c
2
旋轮线:教材P25习题1.4
• 质点系运动 质心运动+各质点相对于质心的运动3
§6-1 质心动量定理
一. 质心
质心 — 质点系统的质量中心
对质点系, 总有一特殊点,其运动和质点系的所 有质量集中于该处的质点运动相同 质心
以质点系各点质量为权重的系统位置的平均值
以两质点系统为例:
若有一点xC,使
若质心系是非惯性系,则质心系中有:
F 合 F 外 惯 m a '(c质心系中的质心运动定律) 而a 'c0(质 心系中质心的加速度为零)
F 合 外 F 惯 0
在质心非惯性系中惯性力和外力完全抵消,
故系统总动量守恒,且恒为零。
16
§6-2. 质心动能定理
M aCF 合 外
若F合
外 0x,则 a C0
质心运动定理新ppt课件

★ 例题结果讨论 Fx m2e 2 cost
Fy (m1 m2 )g m2e 2 sin t
1) 机座的约束力由两部分组成,一部分由重力(主动力)引起的,称为 静约束力(静反力),另一部分是由于转子质心运动变化引起的,称为附 加动约束力。
2) 附加动约束力的最大值和最小值:
驱动汽车行驶的力
maC Fie F1 F2 Fr
9
★ 质心运动守恒的实例分析 放在光滑板上的电动机的质心运动
10
例题6
电动机的外壳和定子的 总质量为 m1 ,质心C1与转子 转轴 O1 重合 ;转子质量 为 m2 ,质心 O2 与转轴不 重合 ,偏心距 O1O2 = e 。 若转子以等角速度 旋转。
0 时 时
2
Fxmin m2e 2
Fymin (m1 m2)g m2e2
时 Fxmax m2e 2 当Fymin<0时不固定时跳起。
3
2
时
Fymax (m1 m2 )g m2e2
3) 附加动约束力与2成正比,当转子的转速很高时,其数值可以达到静约束
质心完全取决于质点系各质点的质量大小及其位置的分布,而 与所受的力无关,重心只在质点系受重力作用时才存在。 5
2 质心运动定理
由质心公式
rC
mr
M
得:
MC mii
根据质点系的动量定义有:
K mii MC
将上式求导: dK dt
M
dC
dt
M
d 2rc dt 2
力的几倍,甚至几十倍,而且这种约束力是周期性变化的,必然引起机座和基
础的振动,还会引起有关构件内的交变应力。
高二物理竞赛质心与质心运动定理课件

5003
x 1.5103 N
§4-1 动量守恒定律
[例]质量为m的人由小车一端走向另一端,小
车质量为M、长为 l ,求人和车各移动了多
少距离?(不计摩擦)
解: 水平方向上车和人系统动量守恒
设分车别和为人V和相对v 地 面速度
MV mv 0
m v
V
M
即
V
m
v
M
X x
§4-1 动量守恒定律
mi ri
i
m
x
mi zi
zc
i
m
zc
zdm m
§4-1 动量守恒定律
[例]证明一匀质杆的质心位置C在杆的中点
解:设杆长为l,质量为m,单位长度质量为
建立如图的坐标系
取线元dx
l 2
质量 dm dx m dx
dm l 2
O x dx x
l
xC
1 m
xdm 1
l
m
l2 m
xdx 0
R sinRd
yC 0 R 2R
m R
y
dl
R d
O
x
质心不在铁丝上,但相对于铁丝的位置是确
定的
yC
ydl
m
§4-1 动量守恒定律
人相对于车的速度为
v'
v
V
M
m
v
M
V
m
v
M
设人在时间 t 内走到另一端
l t v'dt M m t v dt M m x
v
0
M0
M
x M l M m
V
M
X
l
x
m M
m
x 1.5103 N
§4-1 动量守恒定律
[例]质量为m的人由小车一端走向另一端,小
车质量为M、长为 l ,求人和车各移动了多
少距离?(不计摩擦)
解: 水平方向上车和人系统动量守恒
设分车别和为人V和相对v 地 面速度
MV mv 0
m v
V
M
即
V
m
v
M
X x
§4-1 动量守恒定律
mi ri
i
m
x
mi zi
zc
i
m
zc
zdm m
§4-1 动量守恒定律
[例]证明一匀质杆的质心位置C在杆的中点
解:设杆长为l,质量为m,单位长度质量为
建立如图的坐标系
取线元dx
l 2
质量 dm dx m dx
dm l 2
O x dx x
l
xC
1 m
xdm 1
l
m
l2 m
xdx 0
R sinRd
yC 0 R 2R
m R
y
dl
R d
O
x
质心不在铁丝上,但相对于铁丝的位置是确
定的
yC
ydl
m
§4-1 动量守恒定律
人相对于车的速度为
v'
v
V
M
m
v
M
V
m
v
M
设人在时间 t 内走到另一端
l t v'dt M m t v dt M m x
v
0
M0
M
x M l M m
V
M
X
l
x
m M
m
不规则物体的质心计算和展示解剖
§三 质心 质心运动定理 §1 质心 §2 质心参考系 §3 质心运动定理
高速闪光灯拍摄的扳手在光滑桌面上作运动的情况
§1 质心
运动员跳水
投掷手榴弹
若令系统总动量 p mivi mvc
水平上抛三角板
其中 m mi m1 m2
为质点系的总质量
质点系的整体运动可以等效为一个假想质点C 的运动。
vc
drc dt
如何确定这个 点的位置?
vc
mivi m
mi
dri dt
m
mi dri mdt
vi
dri dt
rc
mi ri m
n
rc
mi ri
i 1 n
mi
点C的位矢是质点系各质 点位矢的质量加权平均。
质心(质量中心):质点系 质量分布的平均位置。
i 1
直角坐标系中,各分量的表达式
0
x1
3
x2
o
x2 x
yc
my1 0 0 3m
y1 3
n
对质量连续分布的物体,
将其分为n个小质元
rc
直角坐标系中的分量表达式
ri mi
i 1
m
1 m
rdm
1
1
1
xc m xdm, yc m ydm, zc m zdm
线分布:dm m dl l
面分布:dm m dS S
体分布:dm m dV V
b
2 b x(a a x)dx
xc 0
b ab
1 ab 2
同理
x(a
a b
x)dx
b
aa x b
2 ydxdy
yc
0
高速闪光灯拍摄的扳手在光滑桌面上作运动的情况
§1 质心
运动员跳水
投掷手榴弹
若令系统总动量 p mivi mvc
水平上抛三角板
其中 m mi m1 m2
为质点系的总质量
质点系的整体运动可以等效为一个假想质点C 的运动。
vc
drc dt
如何确定这个 点的位置?
vc
mivi m
mi
dri dt
m
mi dri mdt
vi
dri dt
rc
mi ri m
n
rc
mi ri
i 1 n
mi
点C的位矢是质点系各质 点位矢的质量加权平均。
质心(质量中心):质点系 质量分布的平均位置。
i 1
直角坐标系中,各分量的表达式
0
x1
3
x2
o
x2 x
yc
my1 0 0 3m
y1 3
n
对质量连续分布的物体,
将其分为n个小质元
rc
直角坐标系中的分量表达式
ri mi
i 1
m
1 m
rdm
1
1
1
xc m xdm, yc m ydm, zc m zdm
线分布:dm m dl l
面分布:dm m dS S
体分布:dm m dV V
b
2 b x(a a x)dx
xc 0
b ab
1 ab 2
同理
x(a
a b
x)dx
b
aa x b
2 ydxdy
yc
0
数学分析课件8.5质心380.00KB

x, y为
l
x
xd s , ds
l
y
l
yd s ds
l
【数学分析课件】
2
若曲线段方程为 y f x a 此曲线段的质心坐标为
x b , f ' x 在 a , b 连续,则
x
l
xd s ds
l
b a
x 1 y ' dx
2 2
。
由对称性知
x 0
。
y 1 y ' dx
2
y
r r
2
r r
y 1 y ' dx
2
s
2 s
【数学分析课件】
2r
。
5
例 2: 知 一 抛 物 线 段 y x 已
2
1
x 1 ,曲 线 段 上
任 一 点 出 的 密 度 与 该 点 到 y轴 的 距 离 成 正 比 , x 1 处 的 密 度 为 5, 求 此 曲 线 段 的 质 量 。
解: 设密度函数为
x cx ,
c 5
c是 常 数 。
将 x 1, 1 5 代 入 上 式 , 得
故
x 5 x.
【数学分析课件】 6
故所求的质量为 m
1 1
x d s
1 1
5 x 1 2 x dx 5 5
l l
xdm
l
, m
y
l
y ( x )d s
大学物理质心质心运动定律课件

x2 2xC
第三章 动量守恒和能量守恒
14
物理学
第五版
3-9 质心 质心运动定律
例4 用质心运动定律 来讨论以下问题.
y F
一长为l、密度均匀的
柔软链条,其单位长度的质
量为 .将其卷成一堆放在
地面. 若手提链条的一端,
y c
yC o
以匀速v 将其上提.当一端
被提离地面高度为 y 时,求手的提力.
Rcosθ
x
yC
1 m'
ydm
y 2πR2 sind 2πR2
第三章 动量守恒和能量守恒
8
物理学
第五版
3-9 质心 质心运动定律
而 y R cosθ
y
Rsin θ Rdθ
R θ dθ O
Rcosθ
x
π
所以 yC R
其质心位矢:
2
0 rC
cos
R
sin
2j
d
R
2
第三章 动量守恒和能量守恒
θ=104.6o.求水分子的质心.
yH
d oC Od
H
52.3o
x
52.3o
第三章 动量守恒和能量守恒
4
物理学
第五版
3-9 质心 质心运动定律
解 yC=0
n
xC
mi sin 37.7o mO 0 mHd sin 37.7o mH mO mH
xC rC
6.810 12 6.810 12
itn1求m一i d阶drti导数,
得
n n
m'vC mivi pi
n
再对时间
t
i 1
求一阶导数,
质心学习教程.pptx
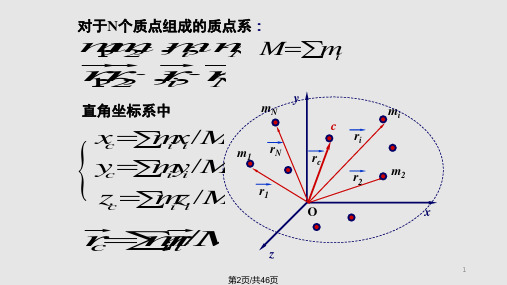
F i M ac
动定理
不管物体的质量如何分布,也不管外力作用在物体 的什么位置上,质心的运动就象是物体的质量全部 都集中于此,而且所有外力也都集中作用其上的一 个质点的运动一样。
9
第10页/共46页
10
第11页/共46页
§2-2 动量定理 动量守恒定律
一、 动量定理(theorem of momemtum)
刻的动量分别为:
初 始时刻
m
m v d m u
F
dm m+dm
u
末时刻
( m d m ) v ( d v )
v
t
v d v
tdt
22
第23页/共46页
变质量问题
对系统利用动 量定 理 m ( m d v d m d m ) v d v d ( d v ) m v ( m d v u d m u F m ) dtF dt
Ft(mv)
于是
(mv)
F
79.6N
t
作用力F的方向与△(mv)的方向相同,图(b)
中的θ角可由下式求得:
(mv) mv2
sin75 sin
29
21
第22页/共46页
动量定理
2. 变质量物体的运动方程
物体m与质元dm在t时刻的速度以及在t+dt时刻
合并后的共同速度如图所示:
把物体与质元作为系统考虑,初始时刻与末时
第15页/共46页
例题2-2 质量m=3t的重锤,从高度h处自由落到受锻压 的 工 件 上 , 工 件 发 生 形 变 。 如 果 作 用 的 时 间 (1)t , (2)t=0.01s 。试求锤对工件的平均冲力。
解:以重锤为研究对象,分析受力,作受力图:
详细版《理论力学》第十章 质心运动定理.ppt

质心运动定理的表示方法
直角坐标表示法:
自然表示法:
maCx
m
d 2 xC dt 2
FixE
maCy
m
d 2 yC dt 2
FiyE
maCz
m
d 2zC dt 2
FizE
maC
m dvC dt
FiE
maCn
m vC2
FinE
maCb 0 FibE
︵。︵
10
HOHAI UNIVERSITY ENGINEERING MECHANICS
练习1: 质量50kg,长度2 2m的均质杆A端搁在光滑水平面
上,另一端B与水平杆BD铰接并用铅直绳BE悬挂。已知系统
静止于图示位置,在绳突然剪断瞬间,B点的加速度为
7.35m/s2,方向铅垂向下。试求此瞬时水平面对AB杆的反力。
BD杆质量不计。
解:1.
2.
受力分析; 运动分析;
y
以B为基点,分析A点加速度:
得:
FN
FN
mg
maCy
mg m aB 2 ︵。︵
例3: 质量m,半径r的均质圆轮在一个力偶作用下,沿
水平面纯滚动。已知某时刻轮上最前点A的加速度为
aA,方向如图。试求:(1)质心的加速度;(2)圆 轮所受摩擦力的大小。
解:
aO
3aA 2
2.受力分析
M
C aO mg
3.质心运动定理
maO F
FN F
F
3 2
ma
A
︵。︵
23
HOHAI UNIVERSITY ENGINEERING MECHANICS
设电动机轴以匀角速ω转动,求螺栓和基础作用于电
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例:已知半圆环质量为M,半径为R 求:它的质心位置?
解:建立坐标系如图,
由对称性 xc 0
线密度 l M R
dm M Rd R
取dl → dm=ldl
y R sin
dl=Rd
yc
ydm M
R sin M R
M
Rd
R0
sin d
R ( cos ) R (11) 2R
0
质心不在物体上,但 相对半圆环位置固定
z
未落地部分:质量
m l
z,质心的坐标为
1 2
z
,
o
整条绳的质心坐标为
zc
1 m
(
m l
z
1 2
z
)
z2 2l
v
2g(l z)
质心的加速度为
ac
d vc dt
d dt
(
z l
v)
v2 l
z l
dv dt
zz
z
质心的速度为
vc
d zc dt
z l
dz dt
z l
v
ac
2g(1
l
)
l
g
2g
3 l
但质心却依然存在。 ③ 除非重力场均匀,否则系统的质心与重心通常不重合。
•作用在物体上各部分的重力方向平行;重力加速度可以视为常数。
•小线度物体(其上 g各处相等),质心和重心是重合的。
对于地球上体积不太大的物体,重心与质心的位置是重合的。 但当物体的高度和地球半径相比较不能忽略时,两者就不重合了, 如高山的重心比质心要低一些。
卡戎(冥卫一)和冥王星组成双星系统,
它们的共同质心在冥王星表面以外。
§3 质心运动定理
1、p系统的m总i动vi 量 mvc
系统内各质点的动量的矢量和等于
z ··
·
·
· C×vC rC · ri
·vi · mi
系统质心的速度与系统质量的乘积
O
y
2、质心运 动定理
F外
dP dt
d dt
(mvC
)
m
d vC dt
x
V1 : V2 : V3 R13 : R23 : R33 64 : 8 : 1
设小球质量为m0,则质量和质心坐标分别为:
o
大球: m1 64m0 , x1 0, y1 0
中球:m2 8m0 ,x2 R / 2, y2 0
三个球体可视为质量
小球:m3 m0 , x3 R / 2, y3 R / 4
m d m 2 R2 2 sin d 2 R2 0
半球壳质心的位置
xc 0,
yc
ydm
2 2 R3 sin cos d
0
1R
m
2 R2
2
例:计算如图所示的面密度σ为恒量的直角三角形的质心的位置。 解:取如图所示的坐标系
取微元ds=dxdy,质量为dm=σds=σdxdy ∴ 质心的x 坐标为
i 1
m
1 m
rvdm
1
1
1
xc m xdm, yc m ydm, zc m zdm
线分布:dm m dl l
面分布:dm m dS S
体分布:dm m dV V
•坐标系的选择不同,质心的坐标也不同; •密度均匀,形状对称的物体,其质心在物体的几何中心处; •质心不一定在物体上,例如:圆环的质心在圆环的轴心上。
★质心的运动代表着质点系整体的运动,与单个质点的运动相同。 这正是将实际物体抽象为质点模型的实质。
质点系的任何运动一般都可分解为 质心的运动和相对于质心的运动
§2 质心参考系
质心参考系是固结在质心上的平动参考系。
质心在其中静止,一般选取质心作为坐标系的原点。
r' r r
i
i
c
N
r
r
rc
n 点C的位矢是质点系各质
rc
mi ri
i 1 n
点位矢的质量加权平均。 质心(质量中心):质点系
mi 质量分布的平均位置。
i 1
直角坐标系中,各分量的表达式
n
mi xi
xc
i 1 n
,
mi
i 1
n
mi yi
yc
i 1 n
,
mi
i 1
n
mi zi
zc
i 1 n
mi
i 1
对两质点系统,质心位
N
mi ri mi
mi (ri rc ) mi ri ' 0
z z'
ri'
rc x' ri
i 1
求导
N
m i
v' i
i 1
0
i 1
x
mi
y'
y
从质心系中来看,系统总动量=0,零动量参考系 动量守恒
质 质心心系系中不的一速定度是惯v性' 系,v只有v合外力为零时质心系才是惯性系。
i
i
c
在讨论碰撞及天体运动时经常用到质心系。
x
r F外
marC
质心运动定律:作用在系统上的合外力等于系统的总质量与系统
质心加速度的乘积。
与描述质点运动的牛顿第二定律在形式上完全相同。 整体的运动→单个质点的运动。 质心的运动与内力无关,仅取决于外力,如大力士不能自举其身。
若质点系受到的外力的矢量和为零,则质心静止或作匀速直线运动
例:柔绳下落 一质量m 长度为 l 均匀柔绳竖直悬挂,其下端
系统的总质量为 m m1 m2 m3 57m0
各自集中在质心(球 心)处的三个质点。
xc
m1 x1
m2 x2 m
m3 x3
0 4m0 R m0 R / 57m0
2
7R 114
yc
m1 y1
m2 y2 m
m3 y3
0 0 m0 R / 57m0
4
1 R 228
实例
★重心(Center of Gravity)和质心( Center-of-Mass)是两个不同的 概念: ① 重心是重力的作用点,质心是系统质量分布的中心。 ② 当物体远离地球而不受重力作用时,重心这个概念就失去意义,
作业: P-139 38,39
方法2 用质心的概念
外力=0,系统质心保持静止
o
x10
x20 x
设初始船和车的坐标分别为x10和x20,根据质心坐标的定义得
t0时刻 m1x10 m2 x20 (m1 m2 )xc
t 时刻 m1(x10 x1) m2 (x20 x2 ) (m1 m2 )xc
两式相减得 m1x1 m2x2 0 车的相对位移 x2 (l1 l2 )
§三 质心 质心运动定理 §1 质心 §2 质心参考系 §3 质心运动定理
高速闪光灯拍摄的扳手在光滑桌面上作运动的情况
§1 质心
运动员跳水
若令系统总动量
p
投掷m手iv榴i 弹mvc
水平上抛三角板
其中 m mi m1 m2 L L 为质点系的总质量
质vrvrcc点系ddrv的tcmm整ivr体i 运如动点何mm可的i确d位以d定rvti置等这?效个为mmd一itd个rvi 假vrr想rci 质 d点drvtiCmm的i rri运动。
2 3
ab2 )
b
∴ 质心的坐标为 b , a
ab
ab
3
3 3
例:半径为R的大球内有一个半径为R/2的球形空腔,空腔的下部
放置了一个半径为R/4的小球。已知大球和小球的质量密度相同。
求:系统的质心。
y
解:该系统可看成由质量分布均匀(无空腔)的
大、中、小三个球体组成,它们各自的质心分
别处于球心处。中球的质量为负。
xc
xdm dm
x dxdy dxdy
xdxdy dxdy
( xdy)dx
从图中看出三角形斜边的方程为
yaa x
b
2 b x(a a x)dx
xc 0
b ab
1 ab 2
同理
x(a
a b
x)dx
b
aa x b
2 ydxdy
yc
0
0
ab
a 3
2( 1 2
ab2
a 3b
b3 )
(ab2
刚刚与地面接触。今使之自静止状态下落,
求:绳下落到所剩的长度为 z 时,地面对绳的作用力。
z
解:取整条绳子为研究对象,将柔绳视为 质点系,采用质心运动定理求解。
m
设地面对绳子的作用力N ,绳子的质心加速度
lz
ac , 建立如图所示坐标系,对整个绳子:
N mg mac
l
质心的坐标:未落地部分+已落地部分
即第二块碎片的落地点的水 平距离为碎片质心与第一块 碎片水平距离的两倍。
小结
•质心 rc
n
mi ri /
n
mi
i 1
i 1
质心位置的计算,区别质心与重心
系统的运动=整体的运动+各质点相对于质心的运动
••质 *质心心运参动考定系理:F零c动量M参dd考vtc系 Mac
质心的运动与内力无关
演示
置总满足关系式:m1d1 =
· · m2d2 m1
C× m2
o
d1
d2
例:任意三角形的每个顶点有一质量m,求质心。
y (x1, y1)
xc
mx1
mx2 3m
0
x1
3
x2
o
x2 x
yc
my1 0 0 3m
y1 3
