分段平均周期图法
FFT和功率谱估计

FFT和功率谱估计1.用Fourier变换求取信号的功率谱---周期图法clf;Fs=1000;N=256;Nfft=256;%数据的长度和FFT所用的数据长度n=0:N-1;t=n/Fs;%采用的时间序列xn=sin(2*pi*50*t)+2*sin(2*pi*120*t)+randn(1,N);Pxx=10*log10(abs(fft(xn,Nfft).^2)/N);%Fourier振幅谱平方的平均值,并转化为dBf=(0:length(Pxx)-1)*Fs/length(Pxx);%给出频率序列subplot(2,1,1),plot(f,Pxx);%绘制功率谱曲线xlabel('频率/Hz');ylabel('功率谱/dB');title('周期图 N=256');grid on;Fs=1000;N=1024;Nfft=1024;%数据的长度和FFT所用的数据长度n=0:N-1;t=n/Fs;%采用的时间序列xn=sin(2*pi*50*t)+2*sin(2*pi*120*t)+randn(1,N);Pxx=10*log10(abs(fft(xn,Nfft).^2)/N);%Fourier振幅谱平方的平均值,并转化为dBf=(0:length(Pxx)-1)*Fs/length(Pxx);%给出频率序列subplot(2,1,2),plot(f,Pxx);%绘制功率谱曲线xlabel('频率/Hz');ylabel('功率谱/dB');title('周期图 N=256');grid on;2.用Fourier变换求取信号的功率谱---分段周期图法%思想:把信号分为重叠或不重叠的小段,对每小段信号序列进行功率谱估计,然后取平均值作为整个序列的功率谱clf;Fs=1000;N=1024;Nsec=256;%数据的长度和FFT所用的数据长度n=0:N-1;t=n/Fs;%采用的时间序列randn('state',0);xn=sin(2*pi*50*t)+2*sin(2*pi*120*t)+randn(1,N);Pxx1=abs(fft(xn(1:256),Nsec).^2)/Nsec; %第一段功率谱Pxx2=abs(fft(xn(257:512),Nsec).^2)/Nsec;%第二段功率谱Pxx3=abs(fft(xn(513:768),Nsec).^2)/Nsec;%第三段功率谱Pxx4=abs(fft(xn(769:1024),Nsec).^2)/Nsec;%第四段功率谱Pxx=10*log10(Pxx1+Pxx2+Pxx3+Pxx4/4);%Fourier振幅谱平方的平均值,并转化为dBf=(0:length(Pxx)-1)*Fs/length(Pxx);%给出频率序列subplot(2,1,1),plot(f(1:Nsec/2),Pxx(1:Nsec/2));%绘制功率谱曲线xlabel('频率/Hz');ylabel('功率谱/dB');title('平均周期图(无重叠) N=4*256');grid on;%运用信号重叠分段估计功率谱Pxx1=abs(fft(xn(1:256),Nsec).^2)/Nsec; %第一段功率谱Pxx2=abs(fft(xn(129:384),Nsec).^2)/Nsec;%第二段功率谱Pxx3=abs(fft(xn(257:512),Nsec).^2)/Nsec;%第三段功率谱Pxx4=abs(fft(xn(385:640),Nsec).^2)/Nsec;%第四段功率谱Pxx5=abs(fft(xn(513:768),Nsec).^2)/Nsec;%第四段功率谱Pxx6=abs(fft(xn(641:896),Nsec).^2)/Nsec;%第四段功率谱Pxx7=abs(fft(xn(769:1024),Nsec).^2)/Nsec;%第四段功率谱Pxx=10*log10(Pxx1+Pxx2+Pxx3+Pxx4+Pxx5+Pxx6+Pxx7/7);%Fourier振幅谱平方的平均值,并转化为dBf=(0:length(Pxx)-1)*Fs/length(Pxx);%给出频率序列subplot(2,1,2),plot(f(1:Nsec/2),Pxx(1:Nsec/2));%绘制功率谱曲线xlabel('频率/Hz');ylabel('功率谱/dB');title('平均周期图(重叠1/2) N=1024');grid on;3.用Fourier变换求取信号的功率谱---welch方法%思想:welch法采用信号重叠分段,加窗函数和FFT算法等计算一个信号序列的自功率谱(PSD)和两个信号序列的互功率谱(CSD),采用MATLAB自%带的函数psdclf;Fs=1000;N=1024;Nfft=256;n=0:N-1;t=n/Fs;window=hanning(256);noverlap=128;dflag='none';randn('state',0);xn=sin(2*pi*50*t)+2*sin(2*pi*120*t)+randn(1,N);Pxx=psd(xn,Nfft,Fs,window,noverlap,dflag);f=(0:Nfft/2)*Fs/Nfft;plot(f,10*log10(Pxx));xlabel('频率/Hz');ylabel('功率谱/dB');title('PSD--Welch方法');grid on;4.功率谱估计----多窗口法(multitaper method ,MTM法)%思想:利用多个正交窗口获得各自独立的近似功率谱估计,综合这些得到一个序列的功率谱估计;相对于普通的周期图有更大的自由度;MTM法采用一个参数:时间带%宽积NW,这个参数用以定义计算功率谱所用窗的数目为2*NW-1,NW越大,时间域分辨率越高而频率分辨率越低,使得功率谱估计的波动减小;随着NW 的增大%,每次估计中谱泄露增多,总功率谱估计的偏差增大clf;Fs=1000;N=1024;Nfft=256;n=0:N-1;t=n/Fs;randn('state',0);xn=sin(2*pi*50*t)+2*sin(2*pi*120*t)+randn(1,N);[Pxx1,f]=pmtm(xn,4,Nfft,Fs); %此处有问题subplot(2,1,1),plot(f,10*log10(Pxx1));xlabel('频率/Hz');ylabel('功率谱/dB');title('多窗口法(MTM)NW=4');grid on;[Pxx,f]=pmtm(xn,2,Nfft,Fs);subplot(2,1,2),plot(f,10*log10(Pxx));xlabel('频率/Hz');ylabel('功率谱/dB');title('多窗口法(MTM)NW=2');grid on;5.功率谱估计----最大熵法(maxmum entmpy method,MEM法)%思想:假定随机序列为平稳高斯过程利用已知的自相关序列rxx(0),rxx(1),rxx(2)...rxx(p)为基础,外推自相关序列rxx(p+1),rxx(p+2)...保证信息熵最大clf;Fs=1000;N=1024;Nfft=256;n=0:N-1;t=n/Fs;window=hanning(256);randn('state',0);xn=sin(2*pi*50*t)+2*sin(2*pi*120*t)+randn(1,N);[Pxx1,f]=pmem(xn,14,Nfft,Fs); %此处有问题subplot(2,1,1),plot(f,10*log10(Pxx1));xlabel('频率/Hz');ylabel('功率谱/dB');title('最大熵法(MEM)Order=14');grid on;%采用Welch方法估计功率谱noverlap=128;dflag='none';subplot(2,1,2)psd(xn,Nfft,Fs,window,noverlap,dflag);xlabel('频率/Hz');ylabel('功率谱/dB');title('Welch方法估计功率谱');grid on;6.功率谱估计----多信号分类法(multiple signal classification,music法)%注:适用于白白噪声中的多正弦波频率估计%思想:将数据自相关矩阵看成是由信号自相关矩阵和噪声自相关矩阵两部分组成,求他们的矩阵特征值向量clf;Fs=1000;N=1024;Nfft=256;n=0:N-1;t=n/Fs;randn('state',0);xn=sin(2*pi*100*t)+2*sin(2*pi*200*t)+randn(1,N);pmusic(xn,[7,1.1],Nfft,Fs,32,16);xlabel('频率/KHz');ylabel('功率谱/dB'); title('Welch方法估计功率谱');grid on;。
利用经典谱估计法估计信号的功率谱(随机信号)

随机信号利用经典谱估计法估计信号的功率谱作业综述:给出一段信号“asd.wav”,利用经典谱估计法的原理,通过不同的谱估计方法,求出信号的功率谱密度函数。
采用MATLAB语言,利用MATLAB语言强大的数据处理和数据可视化能力,通过GUI的对话框模板,使操作更为简便!在一个GUI界面中,同时呈现出不同方法产生出的功率谱。
这里给出了几种不同的方法:BT法,周期图法,平均法以及Welch法。
把几种不同方法所得到的功率谱都呈现在一个界面中,便于对几种不同方法得到的功率谱作对比。
一.题目要求给出一段信号及采样率,利用经典谱估计法估计出信号的功率谱。
二.基本原理及方法经典谱估计的方法,实质上依赖于传统的傅里叶变换法。
它是将数据工作区外的未知数据假设为零,相当于数据加窗,主要方法有BT法,周期图法,平均法以及Welch法。
1. BT法(Blackman-Tukey)● 理论基础:(1)随机序列的维纳-辛钦定理由于随机序列{X(n)}的自相关函数Rx(m)=E[X(n)X(n+m)]定义在离散点m 上,设取样间隔为,则可将随机序列的自相关函数用连续时间函数表示为等式两边取傅里叶变换,则随机序列的功率谱密度(2)谱估计BT法是先估计自相关函数Rx(m)(|m|=0,1,2…,N-1),然后再经过离散傅里叶变换求的功率谱密度的估值。
即其中可有式得到。
2. 周期图法● 理论基础:周期图法是根据各态历经随机过程功率谱的定义来进行谱估计的。
在前面我们已知,各态历经的连续随机过程的功率谱密度满足式中是连续随机过程第i个样本的截取函数的频谱。
对应在随机序列中则有由于随机序列中观测数据仅在的点上存在,则的N点离散傅里叶变换为:因此有随机信号的观测数据的功率谱估计值(称“周期图”)如下:由于上式中的离散傅里叶变换可以用快速傅里叶变换计算,因此就可以估计出功率谱。
3.平均法:● 理论基础:平均法可视为周期图法的改进。
周期图经过平均后会使它的方差减少,达到一致估计的目的,有一个定理:如果是不相关的随机变量,且都有个均值及其方差,则可以证明它们的算术平均的均值为。
谱估计(复习大纲)

第一章 经典谱估计经典谱估计方法是以傅里叶变换为基础的方法,主要有两类:周期图法和布莱克曼—图基法(简称BT 法,又称为谱估计的自相关法)。
这两类方法都与相关函数有着密切的联系,由维纳——欣钦定理可知,功率谱和相关函数之间的关系是一对傅里叶变换,因而可以从观测数据直接估计相关函数,根据估计出来的相关函数,求它的傅立叶变换,就可以得到功率谱的估计值。
一、 相关函数和功率谱若 ==x x m n m )(常数,)(),(2121n n r n n r xx xx -=即)](*)([)(n x k n x E k r xx += 则称)}({n x 为广义平稳序列。
若)}({n x 和)}({n y 均为广义平稳序列,且)(),(2121n n r n n r xy xy -=即)](*)([)(n y k n x E k r xy +=,则称)}({n x 和)}({n y 为广义联合平稳序列。
广义平稳随机序列)}({n x 的相关函数)(k r xx 和它的功率谱密度)(ωxx P 之间是傅立叶变换对的关系,即∑+∞-∞=-=k kj xx xx d ek r P ωωω)()( (1.6)⎰-=ππωωωπd eP k r kj xx xx )(21)( (1.7)这一关系式常称为维纳——欣钦定理。
由自相关函数和功率谱密度的定义,不难得出它们的一些基本性质,主要有:1、当)}({n x 为复序列时,)(*)(k r k r xx xx =-;若)}({n x 为实序列,则相关函数为偶函数,即)()(k r k r xx xx =-。
2、相关函数的极大值出现在0=k 处,即)0()(xx xx r k r ≤。
3、若)(n x 含有周期性分量,则)(k r xx 也含有同一周期的周期性分量,否则,当∞→k 时,0)(→k r xx 。
4、当)(n x 为实序列时,)(ωxx P 为非负实对称函数,即)()(ωωxx xx P P =-和0)(≥ωxx P 。
随机信号分析

随机信号是一种不能用确定的数学关系式来描述的、无法预测未来时刻精确值的信号,也无法用实验的方法重复再现。
换言之,随机信号是指不能用确定性的时间函数来描述,只能用统计方法研究的信号。
其统计特性:概率分布函数、概率密度函数。
统计平均:均值、方差、相关。
随机信号分为平稳和非平稳两大类。
平稳随机信号又分为各态历经和非各态历经。
1) 各态历经信号——指无限个样本在某时刻所历经的状态,等同于某个样本在无限时间里所经历的状态的信号。
2) 平稳随机信号——其均值和相关不随时间变化。
注:各态历经信号一定是随机信号,反之不然。
工程上的随机信号通常都按各态历经平稳随机信号来处理。
仅在离散时间点上给出定义的随机信号称为离散时间随机信号,即随机信号序列。
平稳随机信号在时间上的无限的,故其能量是无限的,只能用功率谱密度来描述随机信号的频域特性。
1. 随机信号的数字特征 均值、均方值、方差若连续随机信号x(t)是各态历经的,则随机信号x(t)的均值可表示为:⎰→∞==TT x dt t x Tt x E 0)(1lim)]([μ均值描述了随机信号的静态分量(直流)。
随机信号x(t)的均方值表达式为:dt t x TTT x)(1lim22⎰→∞=ψ2xψ表示信号的强度或功率。
随机信号x(t)的均方根值表示为:⎰→∞=T T x dt t x T 02)(1limψ x ψ也是信号能量的一种描述。
随机信号x(t)的方差表达式为:⎰-==-→∞Tx T x x dx t x Tx E 0222])([1lim])[(μσμ2xσ是信号的幅值相对于均值分散程度的一种表示,也是信号纯波动分量(交流)大小的反映。
随机信号x(t)的均方差(标准差)可表示为⎰-=→∞T x T x dx t x T 02])([1limμσ 它和2x σ意义相同。
平稳随机过程统计特征的计算要求信号x(t)无限长,而实际上只能用一个样本即有限长序列来计算。
随机信号的线性谱估计方法

实验三 随机信号的线性谱估计方法
谱估计的峰值位置仍处于 0.6π 处,说明相位变化对谱估计的性能没有影响。
2 = 1 ,其它输入同步骤 1,观察信噪比变化对谱估计性能的影响。 (4)改变 σ w
图6
σ 2 = 1 时矩形窗功率谱估计
当增大高斯白噪声的方差时,对谱估计的峰值没有产生影响,但是影响了旁 瓣的宽度和幅值。改变信噪比对频谱的影响较小。
一、实验目的
1. 2. 利用自相关函数法和周期图法实现随机信号的功率谱估计。 观察数据长度、自相关序列长度、信噪比、窗函数、平均次数等对谱估计的 分辨率、稳定性、主瓣宽度和旁瓣宽度的影响。 3. 4. 学习使用FFT提高谱估计的运算速度。 体会线型谱估计方法的优缺点。
二、实验原理和方法
假设信号x(n)为平稳随机过程,其自相关序列定义为
四、 思考题
1. 证明:式(3-4)可以表示为:
ˆ( − m)e jwm ] − φ ˆ(0) ,其中 Re al[•] 表示取实部。 ˆ ( w) = 2 Re al[ ∑ φ P
0
M −1
证明: 先将(3-14)改写为三项相加的形式
ˆ ( w) = P
M −1
0 − M +1
− M +1
∑ φˆ(m)e− jwm =
对比上图,加矩形窗时,当 K=20 时可将两个正弦频率分量临界分辨出来;加
Hamming窗时,当K=10时可将两个正弦频率分量临界分辨出来。 重复4
经典功率谱估计实验报告(3篇)

第1篇一、实验目的1. 理解经典功率谱估计的原理和方法;2. 掌握BT法、周期图法、Bartlett法和Welch法等经典功率谱估计方法;3. 通过MATLAB仿真,验证各种方法的性能和特点;4. 分析实验结果,总结经典功率谱估计方法的优缺点。
二、实验原理功率谱估计是信号处理中的一个重要方法,用于分析信号的频率成分。
经典功率谱估计方法主要包括BT法、周期图法、Bartlett法和Welch法等。
1. BT法:先估计自相关函数,然后进行傅里叶变换得到功率谱;2. 周期图法:直接对样本进行傅里叶变换,得到功率谱;3. Bartlett法:将信号分成L段,计算每段的自相关函数,然后进行傅里叶变换得到功率谱;4. Welch法:对信号进行分段,计算每段的自相关函数,然后进行傅里叶变换得到功率谱,并对结果进行加权平均。
三、实验环境1. 操作系统:Windows 10;2. 编程语言:MATLAB;3. 实验数据:随机信号样本。
四、实验步骤1. 生成随机信号样本;2. 使用BT法进行功率谱估计;3. 使用周期图法进行功率谱估计;4. 使用Bartlett法进行功率谱估计;5. 使用Welch法进行功率谱估计;6. 对比分析各种方法的估计结果。
五、实验结果与分析1. BT法:BT法是一种较为精确的功率谱估计方法,其估计结果与真实功率谱较为接近。
但是,BT法需要计算样本的自相关函数,计算量较大。
2. 周期图法:周期图法是一种简单易行的功率谱估计方法,但其估计结果存在较大误差。
当样本长度N较大时,周期图法的估计结果逐渐接近真实功率谱。
3. Bartlett法:Bartlett法在Bartlett窗口的宽度较大时,估计结果较为准确。
但是,当Bartlett窗口的宽度较小时,估计结果误差较大。
4. Welch法:Welch法是一种改进的周期图法,通过分段和加权平均,提高了估计精度。
Welch法在估计精度和计算量之间取得了较好的平衡。
(实验六 随机信号功率谱分析)

实验报告实验课程:数字信号处理实验开课时间:2020—2021 学年秋季学期实验名称:随机信号功率谱分析实验时间: 2020年9月30日星期三学院:物理与电子信息学院年级:大三班级:182 学号:1843202000234 姓名:武建璋一、实验预习实验目的要求深刻理解随机信号的特性,掌握随机信号功率谱估计的基本原理,灵活运用各种随机信号功率谱估计的基本方法。
实验仪器用具装有Matlab的计算机一台实验原理功率谱估计是随机信号处理中的一个重要的研究和应用领域.功率谱估计基本上可以非参数估计的经典方法和参数估计的近代方法.典型功率谱估计是基于FFT 算法的非参数估计,对足够长的记录数据效果较好。
在工程实际中,经典功率谱估计法获得广泛应用的是修正期图发。
该方法采取数据加窗处理再求平均的办法。
通过求各段功率谱平均,最后得到功率谱计P(m),即:式中:为窗口函数ω[k]的方差。
K表示有重叠的分数段。
由于采用分段加窗求功率谱平均,有效地减少了方差和偏差,提高了估计质量,使修正周期图法在经典法中得到普遍应用。
但在估计过程存在两个与实际不符的假设,即(1)利用有限的N个观察数据进行自相关估计,隐含着在已知N个数据之外的全部数据均为零的假设。
(2)假定数据是由N个观察数据以N为周期的周期性延拓。
同时在计算过程中采用加窗处理,使得估计的方差和功率泄露较大,频率分辨率较低,不适用于短系列的谱分析和对微弱信号的检测。
近代谱估计是建立在随机信号参数模型的基础上,通过信号参数模型或预测误差滤波器(一步预测器)参数的估计,实现功率谱估计。
由于既不需要加窗,又不需要对相关函数的估计进行如经典法那样的假设,从而减少公里泄露,提高了频谱分辨率。
常用的参数模型有自回归(AR)模型、滑动平均(MA)模型、自回归滑动平均(ARMA)模型。
其中AR模型是基本模型,求解AR模型的参数主要有L—D算法和Burg算法。
1.某随机信号由两余弦信号与噪声构成x(t)=cos(20*pi*t)+cos(40*pi*t)+s(t)式中:s(t)是均值为0、方差为1的高斯白噪声。
数字信号处理中的功率谱密度估计

数字信号处理中的功率谱密度估计数字信号处理(Digital Signal Processing,简称DSP)是一种对连续时间信号进行数字化处理的技术,广泛应用于通信、音频、图像、雷达等领域。
在数字信号处理中,功率谱密度估计是一项重要的技术,用于分析信号的频率成分和能量分布。
一、引言功率谱密度(Power Spectral Density,PSD)是信号功率在频域上的分布,它反映了信号在不同频率上的能量强弱情况。
在数字信号处理中,由于信号是以数字形式存在的,因此需要通过一定的方法来估计信号的功率谱密度。
二、频谱估计方法频谱估计方法是用于估计信号功率谱密度的技术。
常见的频谱估计方法包括周期图法、自相关法、Burg方法、Welch方法等。
1. 周期图法周期图法是一种直接估计信号周期图的方法,通过将信号分成若干段进行快速傅里叶变换(Fast Fourier Transform,FFT),然后将各段频谱进行平均得到功率谱密度估计。
2. 自相关法自相关法是通过信号与自身进行相关计算,得到自相关函数,并通过傅里叶变换得到功率谱密度估计。
自相关法能够较好地估计周期性信号的功率谱密度。
3. Burg方法Burg方法是一种模型拟合的方法,通过拟合信号的自回归(Auto-regressive,AR)模型,从而得到信号的频谱估计。
Burg方法适用于非平稳信号,并且能够较好地估计窄带信号的功率谱密度。
4. Welch方法Welch方法是一种经典的频谱估计方法,它将信号分段,对每段信号进行窗函数加权,然后通过傅里叶变换得到每段信号的功率谱密度估计,最后将所有段的功率谱密度进行平均得到最终的估计结果。
三、功率谱密度估计的应用功率谱密度估计在数字信号处理中具有广泛的应用。
以下列举几个常见的应用领域:1. 通信领域在通信系统中,功率谱密度估计用于信号频谱分析、频率选择性衰落分析、频带分配等。
准确的功率谱密度估计可以提供可靠的信号分析结果,对系统性能评估和调试具有重要意义。
功率谱密度

∑x x
n n+m
=
N−m ˆ φ xx (m) N m N
N ˆ′ (m)] = ( N − m ) 2Var[φ ˆ ( m)] < Var[φ ˆ ( m)] Var[φ xx xx xx N
ˆ′ (m)] = φ ( m) − E[φ ˆ′ (m)] = φ xx (m), 有偏估计,偏倚Bias[φ xx xx xx
1 1 2 ∗ X N ( e jω ) X N X (ω ) ( e jω ) = N N
( X N (ω ) = ∑ x(n)e − jωn )
ˆ 1 2 X N (ω )是周期性的,直接将X N (ω )的模的平方除以N求得的功率谱的估计为周期图Pxx (ω ) = I N (ω ) = X (ω ) N ˆ 1 E[φ xx (m)] = N w(m) = 1 N
Dr. JI ZHEN
11
4.1周期图法的改进-窗口处理法
适当设计窗口谱函数W1 (e jω )与周期图卷积, ˆ 1 π Pxx (ω ) = I N (θ )W1 (e j (ω −θ ) )dθ ∫ 2π −π ˆ 1 π E[ Pxx (ω )] = E[ I N (θ )]W1 (e j (ω −θ ) )dθ ∫ 2π −π 1 π 而E[ I N (θ )] = Pxx (φ )W (e j (θ −φ ) )dφ ∫ π − 2π ˆ E[ Pxx (ω )] = Pxx (ω ) *W (e jω ) *W1 (e jω ) 如果W1 (e jω )的主瓣宽度大于W (e jω )的主瓣宽度,可以进一步平滑谱估计,减少方差。
ˆ ˆ Pxx (ω ) = Pxx (−ω ) = =
激光测速中多普勒频移的测定

激光测速中多普勒频移的测定孟影;梁平;王彦;黄其林【摘要】Doppler signal has characteristics of constant frequency and random values of phase and amplitude. In order to obtain the power spectrum of Doppler signal, the power spectrum is estimated via Welch-method, Doppler spectrum is thinned via Goertzel and corrected with energy centro-baric method. Real-time Doppler signal is simulated.The results demonstrate that variances and deviations of the estimation with Welch-method can gain better effect when the overlap number is half of window function length, frequency spectrum thinned can enhance the resolution of power spectrum, and frequency spectrum correction can make Doppler shift close to the real value.%多普勒信号具有频率不变、相位和幅度随机取值的特点.为了获得多普勒信号的功率谱,用Welch法对功率谱进行估算,采用Goertzel对功率谱进行细化和能量重心校正.对实测多普勒信号进行仿真,结果表明:当重叠数是窗函数长度1/2时,用Welch法估算得到的方差和偏差能够达到较好的效果;频谱细化可以提高功率谱的分辨率;频谱校正使得多普勒频移更接近真实值.【期刊名称】《安徽工业大学学报(自然科学版)》【年(卷),期】2012(029)002【总页数】5页(P150-153,161)【关键词】激光多普勒;周期图;频谱细化;频谱校正【作者】孟影;梁平;王彦;黄其林【作者单位】安徽工业大学电气信息学院,安徽马鞍山243002;安徽工业大学电气信息学院,安徽马鞍山243002;安徽工业大学电气信息学院,安徽马鞍山243002;安徽工业大学电气信息学院,安徽马鞍山243002【正文语种】中文【中图分类】TN249声音在声源与接收器之间相对运动时,接收器收到的声音频率不等于声源发出的声音频率,该频差为多普勒频差(频移)[1-2]。
分段统计出次图教程
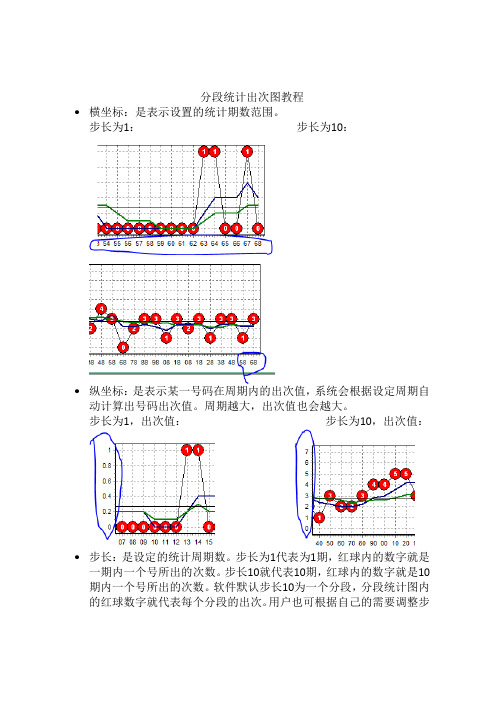
分段统计出次图教程∙横坐标:是表示设置的统计期数范围。
步长为1: 步长为10:∙纵坐标:是表示某一号码在周期内的出次值,系统会根据设定周期自动计算出号码出次值。
周期越大,出次值也会越大。
步长为1,出次值: 步长为10,出次值:∙步长:是设定的统计周期数。
步长为1代表为1期,红球内的数字就是一期内一个号所出的次数。
步长10就代表10期,红球内的数字就是10期内一个号所出的次数。
软件默认步长10为一个分段,分段统计图内的红球数字就代表每个分段的出次。
用户也可根据自己的需要调整步长的期数。
拐点:它只是表示在趋势线和移动平均线上,走向发生变化的一个点。
线5拐点就是从当前期往后数第5个数,线10拐点就是从当前期往后数第10个数,其它周期依此类推。
5.退期:是用来分析计划期内某一号码还有多少次出的机会。
示以当前期为界,依据设置的数向后退N期得到退到某期的期数。
假设胆8,我们设定步长为20,退期为10,那么我们根据拐点发生变化,分析预测胆8在未来20期内要出6次,而软件显示退期的10期已经出了4次,从而预测在未来20‐10=10期内,胆8还有6‐4=2次出机会。
(具体参见软件中“新3D分析”、“遗漏分析”模块)6.出次移动平均线:(1)线5:蓝色出次移动平均线,设置为5周期,它的值是5大周期内所有出次的和的平均值。
计算方法如下:上图线5这点平均值:,如果你判定蓝色线5上涨,平均值就要>2.6 , 那么下一点平均值: ,通过对比,明显看出,有4个数是相同的,要>2.6, 那么下周期出次必须? >1。
所以1出次就称为拐点,是发生变化的点。
★这是种定性分析方法,只要判断出线5上涨,我们就可以大胆预测下一周期(5期)某号码的至少要出多少次。
我们是找上涨的趋势图才有用,因为我们要看它出号的,下跌就没必要抓这个号了。
(2)线10:绿色出次移动平均线,设置为10周期,它的值是10大周期内所有出次的和的平均值。
计算方法如下:上图线10这点平均值:,如果你判定绿色线10上涨,平均值就要>2.4 , 那么下一点平均值:,通过对比,明显看出,有9个数是相同的,要>2.4, 那么下周期出次必须? >3。
周期图法的功率谱估计_黄英

2013 年 09 月第 12 卷第 09 期总第 290 期
1
周期图法的功率谱估计
黄 英
(苏州经贸职业技术学院,江苏 苏州 215009) 摘 要:功率谱估计是数字信号处理的重要研究内容之一。对目前用得较多且最具代表性的周期图法进行研究,并针对它谱 分辨率比较低等缺点,利用 Matlab 实现了几种改进的周期图法。 关键词:谱估计;周期图;Matlab DOI:10.3969/j.issn.1671-6396.2013.09.001
Matlab 程序示例: %信号 t = 0:0.001:0.6; y = sin(2*pi*50*t)+sin(2*pi*120*t) ; x = y+randn(size(t) ) ; N=length(x) ; %观察数据点数 n=1:1:N; %参数设置 Fs=1000; %每百年采样 100 次 nfft=512; %傅里叶变换点数 %window=hamming(25) ; window=boxcar(100) ; noverlap=20 range='half'; %计算序列的 psd nw=3.5;p=0.99; [Pxx,Pxxc,f]=pmtm(x,nw,nfft,Fs,p) ; plot_Pxx=10*log10(Pxx) ; %功率谱 dB plot(f,plot_Pxx) xlabel('Hz') ; ylabel('功率谱 dB') ; title('用多窗口法计算的功率谱') ; grid on; (下转第 8 页)
论
著
noverlap=20 range='half'; %计算序列的 psd [Pxx,f]=pwelch(x,window,noverlap,nfft,Fs,range) ; plot_Pxx=10*log10(Pxx) ; %功率谱 dB plot(f,plot_Pxx) xlabel('Hz') ; ylabel('功率谱 dB') ; title('用 welch 法计算的功率谱') ; grid on;
用matlab做经典功率谱估计

用matlab做经典功率谱估计经典功率谱估计1、直接法:直接法又称周期图法,它是把随机序列x(n)的N个观测数据视为一能量有限的序列,直接计算x(n)的离散傅立叶变换,得X(k),然后再取其幅值的平方,并除以N,作为序列x(n)真实功率谱的估计。
Matlab代码示例:clear;Fs=1000; %采样频率n=0:1/Fs:1;%产生含有噪声的序列xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n));window=boxcar(length(xn)); %矩形窗nfft=1024;[Pxx,f]=periodogram(xn,window,nfft,Fs); %直接法plot(f,10*log10(Pxx));2、间接法:间接法先由序列x(n)估计出自相关函数R(n),然后对R(n)进行傅立叶变换,便得到x(n)的功率谱估计。
Matlab代码示例:clear;Fs=1000; %采样频率n=0:1/Fs:1;%产生含有噪声的序列xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n));nfft=1024;cxn=xcorr(xn,'unbiased'); %计算序列的自相关函数CXk=fft(cxn,nfft);Pxx=abs(CXk);index=0:round(nfft/2-1);k=index*Fs/nfft;plot_Pxx=10*log10(Pxx(index+1));plot(k,plot_Pxx);3、改进的直接法:对于直接法的功率谱估计,当数据长度N太大时,谱曲线起伏加剧,若N 太小,谱的分辨率又不好,因此需要改进。
3.1、Bartlett法Bartlett平均周期图的方法是将N点的有限长序列x(n)分段求周期图再平均。
Matlab代码示例:clear;Fs=1000;n=0:1/Fs:1;xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n));nfft=1024;window=boxcar(length(n)); %矩形窗noverlap=0; %数据无重叠p=0.9; %置信概率[Pxx,Pxxc]=psd(xn,nfft,Fs,window,noverlap,p);index=0:round(nfft/2-1);k=index*Fs/nfft;plot_Pxx=10*log10(Pxx(index+1));plot_Pxxc=10*log10(Pxxc(index+1));figure(1)plot(k,plot_Pxx);pause;figure(2)plot(k,[plot_Pxx plot_Pxx-plot_Pxxc plot_Pxx+plot_Pxxc]);3.2、Welch法Welch法对Bartlett法进行了两方面的修正,一是选择适当的窗函数w(n),并再周期图计算前直接加进去,加窗的优点是无论什么样的窗函数均可使谱估计非负。
高速铁路0.01~120_m波段轨道不平顺功率谱密度函数的构建

第 54 卷第 6 期2023 年 6 月中南大学学报(自然科学版)Journal of Central South University (Science and Technology)V ol.54 No.6Jun. 2023高速铁路0.01~120 m 波段轨道不平顺功率谱密度函数的构建陈宪麦1, 2,董春敏1,魏子龙3,李赛1,杨飞3,孙宪夫3(1. 中南大学 土木工程学院,湖南 长沙,410075;2. 高速铁路建造技术国家工程研究中心,湖南 长沙,410075;3. 中国铁道科学研究院集团有限公司 基础设施检测研究所,北京,100081)摘要:目前国内外铁路轨道不平顺功率谱密度(power spectral density, PSD)函数的表达式多种多样,但因检测仪器有效测量范围有限,其表征波段范围往往较窄,常以短波、中波或中长波等形式呈现,因此,开展更宽波段轨道不平顺功率谱密度函数的研究对铁道工程领域的科学研究和工程应用具有参考价值。
本文对波磨小车与综合检测列车测得的高速铁路轨道(面)不平顺数据进行预处理,采用改进的周期图方法计算和分析其功率谱密度,总结其宽带和周期性成分特征;基于计算所获得的中位轨道不平顺功率谱密度,提出短波[0.01,1) m 、中长波[1,120] m 以及更宽波段0.01~120 m 的轨道不平顺功率谱密度函数的拟合公式,并将本文提出的拟合谱与既有的典型谱进行比对分析。
研究结果表明:高速铁路功率谱密度存在多个周期性成分,短波不平顺周期性成分主要与钢轨接头以及波磨相关,中长波不平顺周期性成分主要与无砟轨道结构和32 m 简支梁桥的构造形式有关;所提出的短、中长波以及0.01~120 m 波段的拟合公式能够很好地表征轨道不平顺功率谱密度的宽带波长特性,且参数少,形式简洁,适用性强。
关键词:高速铁路;轨道不平顺;波段;功率谱密度函数;拟合中图分类号:U213.7 文献标志码:A 文章编号:1672-7207(2023)06-2111-11Development on power spectral density function of trackirregularity of 0.01−120 m waveband of high-speed railwayCHEN Xianmai 1, 2, DONG Chunmin 1, WEI Zilong 3, LI Sai 1, YANG Fei 3, SUN Xianfu 3(1. School of Civil Engineering, Central South University, Changsha 410075, China;收稿日期: 2022 −08 −28; 修回日期: 2022 −10 −02基金项目(Foundation item):国家自然科学基金资助项目(51478482);中国国家铁路集团有限公司科技研究开发计划重点项目(N2019G012) (Project(51478482) supported by the National Natural Science Foundation of China; Project(N2019G012) supported by the Key Program of Science and Technology Research and Development Plan of China National Railway Group Co. Ltd.)通信作者:陈宪麦,博士,副教授,从事轨道工程研究;E-mail :*******************.cnDOI: 10.11817/j.issn.1672-7207.2023.06.003引用格式: 陈宪麦, 董春敏, 魏子龙, 等. 高速铁路0.01~120 m 波段轨道不平顺功率谱密度函数的构建[J]. 中南大学学报(自然科学版), 2023, 54(6): 2111−2121.Citation: CHEN Xianmai, DONG Chunmin, WEI Zilong, et al. Development on power spectral density function of track irregularity of 0.01−120 m waveband of high-speed railway[J]. Journal of Central South University(Science and Technology), 2023, 54(6): 2111−2121.第 54 卷中南大学学报(自然科学版)2. National Engineering Research Center of High-speed Railway Construction Technology,Changsha 410075, China;3. Infrastructure Inspection Research Institute, China Academy of Railway Sciences, Beijing 100081, China) Abstract:At present, there are various expressions for the power spectral density(PSD) function of railway track irregularity at home and abroad. However, due to the limitation of the test accuracy of the detection instruments, the range of its characteristic bands is often narrow, and it is usually presented in the form of shortwave, medium wave or medium-long wave. Therefore, the research on the power spectral density function of railway track irregularity with the wider band has reference value for scientific research and engineering application in the fieldof railway engineering. Based on the short-wave irregularity data and the medium-long wave irregularity data of the high-speed railways, the power spectral density was calculated and analyzed using the improved periodic graph method, and the characteristics of their broadband and periodic components were summarized. Based on the calculated power spectral density of the medium track irregularity, the fitted formulas of the power spectral density function for shortwave [0.01, 1) m, medium-long wave [1, 120] m, and wider band 0.01~120 m were presented. The proposed fitting formula was compared with the existing typical spectrum. The results show that there are several periodic components in the power spectral density of high-speed railways, the short wave irregularity periodic components are mainly related to the wave wear and rail joints, the medium and long wave irregularity periodic components are mainly related to the ballastless track structure and the construction form of 32 m simply supported beam bridges. The fitted formulas of short, medium and long waves bands and 0.01−120 m bands can well characterize the broadband wavelength characteristics of the power spectral density of track irregularity with fewer parameters, simpler form and better applicability.Key words: high-speed railway; track irregularity; waveband; power spectral density(PSD) function; fitting轨道不平顺是轮轨系统的激扰源,是引起机车车辆产生振动和轮轨动作用力的关键因素,对列车的行车安全性、平稳性、车辆和轨道部件的寿命、养护维修以及周边环境品质等都产生不利影响。
采用Welch法作谱估计

《测试信号分析与处理》仿真实验实验二:采用Welch法作谱估计1.实验目的:a. 掌握We l c h算法的概念、应用及特点;b. 了解谱估计在信号分析中的作用;c. 能够利用We l c h法对信号作谱估计,对信号的特点加以分析。
2.实验内容:a. 读入实验数据。
b. 编写一利用We l c h法作谱估计的算法程序。
c. 将计算结果表示成图形的形式,给出信号谱的分布情况图。
3.算法讨论及分析算法1:直接采用matlab中自相关函数[Px, F]=pwelch(x,, window,Noverlap,Nfft, fs)式中,x -随机信号,长度为NWindow -选用的窗函数Noverlap -估计x 的功率谱时每一段叠合的长度Nfft -对x 作FFT 时的长度fs -抽样频率算法2:该算法为有偏估计,利用FFT计算相关函数,4.实验结果及分析实验结果如图2-1所示,图2-1中上图为采用算法2,数据点为0~2048,中图也是使用的算法2,但是图中只是绘出1024个点,下图使用算法1,即matlab自带的算法。
图2-1 实验结果图1 不同的分段点数对Welch 谱估计结果有何影响?分段数K 增大,每组数据量M 减小,则会造成谱估计的偏差增大,曲线平滑;反之, 曲线起伏激烈, 谱线的尖峰保留。
从图2-2中的K 值大于图2-3的K 值,图2-2中的曲线比图2-3的曲线平滑,但是图2-3的尖峰效果比图2-2好。
图2-2 K =N/1100时的频谱图图2-3 K=N/3000时的频谱图2 不同的数据重叠长度Welch 对谱估计结果有何影响?如果数据交叠使用,分段数K 比平均周期图法增大,则估计方差比平均周期图法小,数据交叠长度越大,分段数K 越大,则估计方差会越小,图形会变得平滑,如图2-4所示,上图数据重叠度大,K 大,则曲线相对平滑。
从式(1)也可以看出,式(1)为谱估计的方差。
()()24sin ˆvar 1sin xxx M S K M ωσωω⎡⎤⎛⎫⎡⎤⎢⎥=+ ⎪⎣⎦⎢⎥⎝⎭⎣⎦(1)图2-4 使用不同的重叠度得到的谱估计图(上:重叠度为97%,下:重叠度为3%)3 不同的窗函数对Welch谱估计结果有何影响?使用窗函数,会使Welch谱估计的图形变得平滑,但是,不同的窗函数不同,则其主瓣宽度不同。
功率谱图应用

1.基本方法周期图法是直接将信号的采样数据x(n)进行Fourier变换求取功率谱密度估计的方法。
假定有限长随机信号序列为x(n)。
它的Fourier变换和功率谱密度估计存在下面的关系:式中,N为随机信号序列x(n)的长度。
在离散的频率点f=kΔf,有:其中,FFT[x(n)]为对序列x(n)的Fourier变换,由于FFT[x(n)]的周期为N,求得的功率谱估计以N为周期,因此这种方法称为周期图法。
下面用例子说明如何采用这种方法进行功率谱用有限长样本序列的Fourier变换来表示随机序列的功率谱,只是一种估计或近似,不可避免存在误差。
为了减少误差,使功率谱估计更加平滑,可采用分段平均周期图法(Bartlett法)、加窗平均周期图法(Welch 法)等方法加以改进。
2. 分段平均周期图法(Bartlett法)将信号序列x(n),n=0,1,…,N-1,分成互不重叠的P个小段,每小段由m个采样值,则P*m=N。
对每个小段信号序列进行功率谱估计,然后再取平均作为整个序列x(n)的功率谱估计。
平均周期图法还可以对信号x(n)进行重叠分段,如按2:1重叠分段,即前一段信号和后一段信号有一半是重叠的。
对每一小段信号序列进行功率谱估计,然后再取平均值作为整个序列x(n)的功率谱估计。
这两种方法都称为平均周期图法,一般后者比前者好。
程序运行结果为图9-5,上图采用不重叠分段法的功率谱估计,下图为2:1重叠分段的功率谱估计,可见后者估计曲线较为平滑。
与上例比较,平均周期图法功率谱估计具有明显效果(涨落曲线靠近0dB)。
3.加窗平均周期图法加窗平均周期图法是对分段平均周期图法的改进。
在信号序列x(n)分段后,用非矩形窗口对每一小段信号序列进行预处理,再采用前述分段平均周期图法进行整个信号序列x(n)的功率谱估计。
由窗函数的基本知识(第7章)可知,采用合适的非矩形窗口对信号进行处理可减小“频谱泄露”,同时可增加频峰的宽度,从而提高频谱分辨率。
功率谱估计模型法汇总

功率谱估计模型法汇总1.短时傅里叶变换(STFT)短时傅里叶变换是一种常见的功率谱估计方法,它将信号分成若干小段,并分别对每一小段进行傅里叶变换。
通过将时域信号转换为频域信号,可以得到信号在不同频率上的能量分布。
然后,对每一小段的频谱进行平均,得到整个信号的频谱估计结果。
2.自相关法自相关法是一种通过计算信号与其自身的相关性来估计功率谱的方法。
自相关函数表示信号在不同时刻的相似程度,通过对自相关函数进行傅里叶变换,可以得到信号的功率谱估计结果。
自相关法适用于平稳信号的功率谱估计。
3.平均周期图法(APM)平均周期图法是一种通过信号的周期平均来估计功率谱的方法。
该方法将信号分成若干个周期,并对每个周期的波形进行傅里叶变换。
然后,对每个周期的频谱进行平均,得到整个信号的频谱估计结果。
平均周期图法适用于具有明显周期性的信号,如正弦信号或周期性脉冲信号。
4.基于模型的方法基于模型的方法是一种通过对信号进行建模来估计功率谱的方法。
常见的模型包括自回归模型(AR)和最大似然估计(MLE)模型。
通过拟合信号模型,可以得到模型参数,进而估计信号的功率谱。
基于模型的方法适用于非平稳信号的功率谱估计。
5.基于窗函数的方法基于窗函数的方法是一种通过对信号进行加窗来估计功率谱的方法。
常见的窗函数包括矩形窗、汉明窗和凯泽窗等。
通过对信号进行加窗,可以抑制信号的频谱泄漏效应,提高功率谱估计的精度。
除了以上列举的几种方法,还存在其他一些功率谱估计模型,如周期图法、周期图平均法、波尔兹曼机等。
每种方法都有其适用的场景和优缺点。
在实际应用中,根据信号特性和需求选择合适的功率谱估计模型非常重要。
总而言之,功率谱估计模型是信号处理领域中常用的方法,用于分析信号的频谱特征。
不同的模型适用于不同的信号特性,根据实际需求选择合适的估计方法可以提高功率谱估计的准确性和可靠性。
计算信号频率的算法

计算信号频率的算法信号频率是指信号在单位时间内完成的周期数,是衡量信号变化速度的重要指标。
在实际应用中,我们常常需要计算信号的频率,以便进行信号处理、通信调制等工作。
本文将介绍一些常用的计算信号频率的算法。
一、基于周期的频率计算算法1. 平均周期法平均周期法是最常用的计算信号频率的方法之一。
它基于信号的周期性特征,通过测量多个周期的平均值来计算频率。
算法步骤:(1)选择一个合适的时间窗口,长度为T;(2)在该时间窗口内,测量信号通过的周期数N;(3)计算平均周期T_avg = T / N;(4)频率f = 1 / T_avg。
2. 自相关法自相关法是利用信号与自身进行相关分析的方法。
通过计算信号与其自身的互相关函数,找出信号的周期性特征,从而计算信号的频率。
算法步骤:(1)将信号与自身进行互相关运算;(2)找出互相关函数的峰值点,该点对应的横坐标即为信号的周期;(3)频率f = 1 / 周期。
二、基于傅里叶变换的频率计算算法傅里叶变换是一种常用的信号分析方法,可以将信号从时域转换到频域。
基于傅里叶变换的频率计算算法可以从频域的角度来计算信号的频率。
1. 快速傅里叶变换(FFT)FFT是一种高效的计算傅里叶变换的算法,可以将信号从时域转换到频域。
通过对信号进行FFT计算,可以得到信号的频谱图,从而计算出信号的频率。
算法步骤:(1)选择一个合适的采样窗口长度N;(2)对信号进行N点FFT计算,得到频谱图;(3)找出频谱图中的峰值点,该点对应的横坐标即为信号的频率。
2. 周期图法周期图法是一种基于傅里叶变换的频率计算方法,可以用来估计非周期信号的频率。
它通过将信号分解成多个周期分量,再进行傅里叶变换,从而得到信号的频率。
算法步骤:(1)选取一段信号数据,长度为N;(2)将N点信号数据分解成多个周期分量;(3)对每个周期分量进行傅里叶变换,得到频谱图;(4)找出频谱图中的峰值点,该点对应的横坐标即为信号的频率。
第五章功率谱估计1-2节

经FFT变换,得:
ˆ ˆ ˆ Pxx (k ) FFT xx (m) xx (m)e
m0 L -1 -j 2 km L
k 0,1, 2, L -1
29/113
三、相关图法功率谱估计质量
用x(n)的N 个有限值得到 ˆ 自相关函数的估计 ( m),
13/113
(a)间接法(BT法)
BT法又称为相关图法 对信号序列估计求其自相关函数值 对自相关函数的估计进行加权 对加权的自相关函数做傅里叶变换 获得功率谱估计。
直到1965年快速傅里叶变换算法(FFT) 问世以前,是最流行的谱估计方法。
14/113
(b)直接法(又称周期图 (periodogram)法)
对观测到的数据样本直接进行傅里叶变换 取模的平方,再除以N 得到功率谱估计。 不用估计自相关函数,且可以用FFT进行计算, 在FFT出现以后,周期图法才得到了广泛的应 用。
15/113
(2)现代谱估计
其基本思想是根据已有的观测数据,建 立信号所服从的模型,从而在观测不到 的区间上,信号的取值服从模型的分布 情况,不再认为是零。 主要讨论参数模型(AR、MA、ARMA) 法。
N
2 xx (l ) xx (l m)xx (l - m) (N - m - l )
N - m -1 2 l -( N - m -1) N - m -1 2 l -( N - m -1)
N - m
N
所以在实际中必须兼顾分辨率与方差的要求来适当选择信号仍然是均值为方差为的白噪声观察数据长度为了利用平均周期法估计其功率谱将它分成段分别按照平均周期图法估计其功率谱得到功率谱曲线如图从图中可以看出随着分段数的增加功率谱估计值在附近的幅度愈来愈小显示出分段平均对周期图方差减少有明显效果
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• The signal sequence x (n), n = 0,1, ..., N-1, is divided into K small non-overlapping segments, each of small non-overlapping segments has L samples, then K * L = N.To subdivide the existing record data :
• Power spectrum estimation is using of finite data to estimate the power spectrum of signal,it is widely used in radar, sonar, communications, geological exploration, astronomy, biomedical engineering and other fields.
Averaged Periodogram
• The method of Average Periodogram is divided a longer data sequence of random signal x (n) into m segments.Then using the Fourier analysis to transform them section by section.Finally, Periodogram averaging.
averaged periodogram(non-overlapping) N=4*256 30 Power spectrum /dB 20 10 0 -10
0
50
100
200 250 300 350 400 Frequency/Hz averaged periodogram(overlapping) N=1024
The averaged periodogram
School of Information Science and Technology Yunnan University
Power spectrum estimation
• Random signal is unlimited in time,and infinited in sample.Therefore,the energy of random signal is infinite,it is a power signal. The power signal does not meet the conditions of absolute integrable of Fourier transform. Strictly speaking,its Fourier transform does not exist. Analysis of random signals in the frequency domain,it is no longer a simple spectrum, but the power spectrum.
xi (n) = x(n + iL),
i=0,1,…,k-1,n= 0,1,…,L-1
The periodogram of the th segmnet is
S
B
(e
jw
) =
1 N
∑
பைடு நூலகம்
K − 1 i = 0
|∑
L − 1
x ( n + iL )e
−
jw n
|2
n = 0
T h e r e a r e t w o m e t h o d s o f Av e r a g e d Periodogram.The one is segmented overlapping method of small sample .The other is segmented non-overlapping method of big sample。Signal x (n) can also be devided for overlapping segments,such as by 2:1.They are half overlap.Power spectrum estimate every small segments,then average them.
150
450
500
30 Power spectrum/dB 20 10 0 -10
0
50
100
150
200 250 300 Frequency/Hz
350
400
450
500
• • • • •
• • •
• •
clf;Fs=1000; %segmented non-overlapping method N=1024;Nsec=256;n=0:N-1;t=n/Fs; randn('state',0); xn=sin(2*pi*50*t)+2*sin(2*pi*120*t)+randn(1,N); pxx1=abs(fft(xn(1:256),Nsec).^2)/Nsec; pxx2=abs(fft(xn(257:512),Nsec).^2)/Nsec; pxx3=abs(fft(xn(515:768),Nsec).^2)/Nsec; pxx4=abs(fft(xn(769:1024),Nsec).^2)/Nsec; Pxx=10*log10((pxx1+pxx2+pxx3+pxx4)/4); f=(0:length(Pxx)-1)*Fs/length(Pxx); subplot(2,1,1),plot(f(1:Nsec/2),Pxx(1:Nsec/2)); xlabel('Frequency/Hz');ylabel('Power spectrum /dB'); title('averaged periodogram(non-overlapping) N=4*256'); grid on
• • • • • • • • • • • • •
%segmented overlapping method pxx1=abs(fft(xn(1:256),Nsec).^2)/Nsec; pxx2=abs(fft(xn(129:384),Nsec).^2)/Nsec; pxx3=abs(fft(xn(257:512),Nsec).^2)/Nsec; pxx4=abs(fft(xn(385:640),Nsec).^2)/Nsec; pxx5=abs(fft(xn(513:768),Nsec).^2)/Nsec; pxx6=abs(fft(xn(641:896),Nsec).^2)/Nsec; pxx7=abs(fft(xn(769:1024),Nsec).^2)/Nsec; Pxx=10*log10((pxx1+pxx2+pxx3+pxx4+pxx5+pxx6+pxx7)/7); %Averaged Periodogram and tramsformed to dB f=(0:length(Pxx)-1)*Fs/length(Pxx); subplot(2,1,2),plot(f(1:Nsec/2),Pxx(1:Nsec/2)); xlabel('Frequency/Hz'); ylabel('Power spectrum/dB'); title('averaged periodogram(overlapping) N=1024'); grid on
• Using two methods of averaged periodogram to estimate power spectral density of signals.f1=50Hz,f2=120Hz, w(t) is Gaussian white noise,Sampling frequency Fs=1000Hz,Signal length N=1024.
