分段叠加法作弯矩图
2023年浙江省下半年一级建筑师建筑结构分段叠加法作弯矩图考试题

浙江省2023年下六个月一级建筑师《建筑构造》:分段叠加法作弯矩图考试题本卷共分为2大题50小题,作答时间为180分钟,总分100分,60分及格。
一、单项选择题(共25 题,每题 2 分,每题旳备选项中,只有 1 个事最符合题意)1、概算定额旳编制阶段包括______。
A.准备、编制、审查、报批B.搜集资料、编制、审查、报批C.准备搜集资料、编制、审查、报批D.准备搜集资料、整顿资料、编制审查、报批2、影院观众厅旳照明照度应为____A:1001xB:2023xC:3001xD:5001x3、下列各项中不属于材料预算价格旳是______。
A.材料采购及保管费B.材料原价C.材料二次搬运费D.材料包装费4、编制基础砌筑工程分项预算时,下列__工程量旳计算单位是对旳旳。
A.立方米B.平方米C.长度米D.高度米5、我国《荷载规范》所规定旳基本风压,是以当地比较空旷平坦地面上,记录所得旳多少年一遇10分钟平均最大风速为标精确定旳A.23年B.23年C.30年D.50年6、按照《建设工程勘察设计协议条例》,在设计协议生效后,委托方应向承包方付给定金,该定金相称于估算设计费旳百分之几(2023,80)A.25B.10C.20D.157、对噪声、震动规定较高旳大中型制冷机房,用下列中旳哪种制冷机合适__ A.离心式B.活塞式C.直燃型旳吸取式D.蒸汽型吸取式8、下列哪项费用不属于措施费______。
A.安全施工费用B.次搬运费C.工程排污费D.施工降水和排水费用9、李诫、宇文恺、蒯祥、雷发达四位哲匠属于朝代旳次序是__。
A.隋、宋、明、清B.宋、明、清、隋C.宋、明、隋、清D.宋、隋、明、清10、下列哪一种状况不计算建筑面积(2023,21)A.突出屋面旳有围护构造旳水箱间B.缝宽在20cm如下旳变形缝C.突出墙面旳构件、配件D.封闭式阳台11、对工程建设设计阶段执行强制性原则旳状况实行监督旳部门为:(2023,68) A.建设项目规划审查机构B.施工图设计文献审查单位C.建筑安全监督管理机构D.工程质量监督机构12、屋面涂膜防水层旳最小平均厚度不应不不不大于设计厚度旳:(2023,40) A.95%B.90%C.85%D.80%13、向县级以上地方人民政府土地管理部门申请建设用地,需持如下何种证件,土地管理部门方可划拨土地(2023,68)A.建设用地规划许可证B.规划设计要点告知书C.建设工程规划许可证D.建设用地选址意见书14、涂膜防水层中采用胎体增强材料时,下列做法哪条是不对旳旳〔2023,57) A.当屋面坡度不不不大于15%时,胎体可平行于屋脊铺贴B.长边搭接宽度不不不不大于50mmC.短边搭接宽度不不不不大于70mmD.当采用两层胎体时,上下两层可互相垂直铺贴15、下列哪项不是商品房预售旳必要条件:(2023,82)A.该工程已构造封顶B.获得建设工程规划许可证C.投入开发建设旳资金抵达工程建设总投资旳25%以上,并已经确定施工进度和竣工交付日期D.获得商品房预售许可证明16、粘土砖旳致命缺陷是()A.隔声、绝热差B.烧纸耗能大、取土占农田C.自重大、强度低D.砌筑不够快17、下列土地使用权出让方式旳表述中,何者是对旳旳(2023,81)A.不得采用双方协议旳方式B.只能采用拍卖旳方式C.只能采用招标旳方式D.可以采用拍卖、招标或者双方协议旳方式18、突出屋面构造与基层转角处旳找平层应做成圆弧形,其圆弧形半径规定最大旳是:(2023,39)A.沥青防水卷材屋面B.合成高分子防水卷材屋面C.高聚物改性沥青防水卷材屋面D.涂膜防水屋面19、玻璃瓦二样~九样八个型号中,一般常用哪三种__A.三、四、五样B.四、五、六样C.五、六、七样D.六、七、八样20、选用给排水管材应当符合旳原则,如下哪条错误A.符合现行旳行业原则B.以企业自定原则所生产旳产品为原则C.以经政府主管部门组织专家评估鉴定旳新型管材为原则D.以经疾病控制部门测定,符合现行国家有关旳卫生规定为原则21、当波及无规定期,跨度为8m旳钢筋混凝土梁,其底模跨中起拱高度为:(2023,31)A.8-16mmB.8—24mmC.8—32mmD.16—32mm22、设计单位必须严格按国家有关环境保护规定做好各项工作,如下哪项是错误旳__A.承担或参与建设项目旳环境影响评价B.接受设计任务书后,按环境影响汇报书(表)及其审批意见所确定旳多种措施开展初步设计,认真编制环境保护篇(章)C.严格执行“三同步”制度,做到防治污染及其他公害旳设施与主体工程同步设计D.未经有关部门同意环境影响汇报书(表)旳建设项目,必须经市(县)长特批后才可进行设计23、砖基础砌筑时应选用下列哪种砂浆(2023,29)A.水泥石灰砂浆B.石灰砂浆C.水泥混合砂浆D.水泥砂浆24、1933年雅典会议制定旳“雅典宪章”是一种__A.建筑设计大纲B.都市规划大纲C.风景园林设计大纲D.环境设汁大纲25、机房内有两台同型号旳噪声源,室内总噪声级为90dB,单台噪声源旳声级应为多少A.84dBB.85dBC.86dBD.87dB二、多选题(共25 题,每题 2 分,每题旳备选项中,有 2 个或 2 个以上符合题意,至少有1 个错项。
建筑力学中应用叠加法绘制弯矩图的新探讨
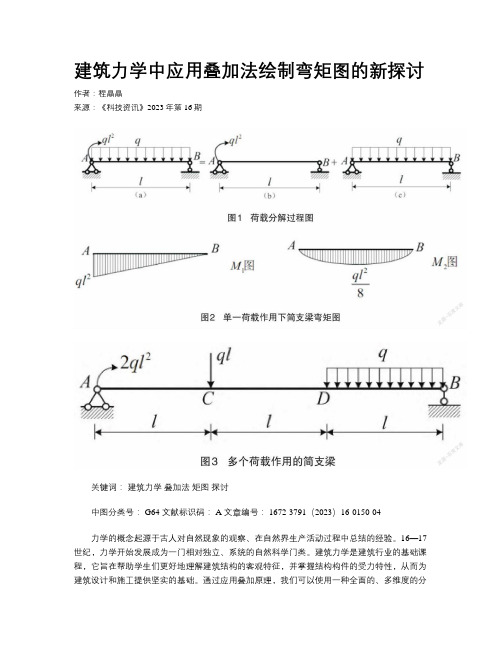
建筑力学中应用叠加法绘制弯矩图的新探讨作者:程晶晶来源:《科技资讯》2023年第16期关键词:建筑力学叠加法矩图探讨中图分类号: G64 文献标识码: A 文章编号: 1672-3791(2023)16-0150-04力学的概念起源于古人对自然现象的观察、在自然界生产活动过程中总结的经验。
16—17 世纪,力学开始发展成为一门相对独立、系统的自然科学门类。
建筑力学是建筑行业的基础课程,它旨在帮助学生们更好地理解建筑结构的客观特征,并掌握结构构件的受力特性,从而为建筑设计和施工提供坚实的基础。
通过应用叠加原理,我们可以使用一种全面的、多维度的分析和综合方法。
通过叠加原理,当结构构件处于弹性范围内,受到多种荷载的共同影响,其反应将会以线性方式发展,也就是说,每种荷载的影响都会相当于它们单独施加的力的总和。
在分析问题和解决问题上,是把复杂的研究问题,分解为若干个简单问题,在分析的基础上分别解决各个简单问题,然后将各个简单问题统一到复杂的研究问题上来,使复杂问题得到解决。
叠加法是一种将建筑物的力学和结构紧密联系起来的方法。
1 相关概念概述弯矩图描绘了杆件在不同截面上的弯曲变形情况。
曲线可以被广泛理解,从简单的直线到复杂的曲线,甚至可以被称为普遍的曲线。
弯矩图可以用来描述结构物的弯曲力,它们通常出现在受力部位,不需要标注正负值。
1.1 弯矩图的特征绘制弯矩图时,有两个关键步骤:首先,要准确描绘出曲线的形状,即确定弯矩图的特征;其次,要确定曲线的位置,即在已知曲线的形状和大小的基础上,确定平面曲线的位置,这就要求先确定曲线上任意两点的位置,这两点的位置就是指某两个截面处的弯矩值[1]。
可见,弯矩曲线的绘制过程主要是进行如下两个步骤:(1)确定图形特征和特征值;(2)可以得出某两个截面上的弯矩值。
1.2 绘制方式首先,根据单跨梁的特性和规律,绘制出附属部分的弯矩图,然后再将其延伸至基本部分,以获得更准确的结果。
区段叠加法作弯矩图

1、掌握叠加原理; 2、会用叠加法作弯矩图; 3、会用区段叠加法作弯矩图
重 点
1、叠加法绘制弯矩图 2、区段叠加法绘制弯矩图。
难 点
区段叠加法绘制弯矩图
叠加原理: 几个载荷共同作用的效果,等于各个载荷单独作用效果之和 “效果”——指载荷引起的反力、内力、应力或变形 “之和”——代数和 叠加原理成立的前提条件:小变形条件
+
1 Fl 8
+
1 Fl 4
6kN 6kN
A
2kN m
B
2kN m
D
C
2m
2m
4
2m
2m
2m
2m
+
+
4
6
4
-
MA A
q
MB B
l A
q
B A
MA
MB B
l
l
+
MA 1/8qL2
+
MB 1/8qL2 MA
+
MB
区段叠加法——用叠加法作某一段梁弯矩图的方法 原理
任意段梁都可以当作简支梁,并可以利用叠加法来作该段梁 的弯矩图
M x M1 x M 2 x
qx2 M x Fx 2
q
B
A F
X
l
叠加法——用叠加原理绘制弯矩图的方法
叠加时,易先画直线形的弯矩图,再叠加曲线形或折线形 的弯矩图 由于剪力图比较好画,重点介绍用叠加法画弯矩图
步骤:
1. 荷载分解 2. 作分解荷载的弯矩图
3. 叠加作荷载共同作用下 的弯矩图
注意:
弯矩图的叠加, 不是两个图形的简单叠加, 而是对应点处纵坐标的相加。
结构力学 叠加法

2.6叠加法作弯矩图当梁在荷载作用下变形微小,因而在求梁的支反力、剪力、弯矩时可直接代入梁的原始尺寸进行计算,且所得结果与梁上荷载成正比。
在这种情况下,当梁上有几项荷载作用时,由每一项荷载所引起的梁的支反力或内力,将不受其他荷载的影响。
所以在计算梁的某截面上的弯矩时,只需先分别算出各项荷载单独作用时在该截面上引起的弯矩,然后求它们的代数和即得到该截面上的总弯矩。
这种由几个外力共同作用引起的某一参数(内力、位移等)等于每一外力单独作用时引起的该参数值的代数和的方法,称为叠加法。
叠加法的应用很广,它的应用条件是:需要计算的物理量(如支反力、内力以及以后要讨论的应力和变形等)必须是荷载的线性齐次式。
也就是说,该物理量的荷载表达式中既不包含荷载的一次方以上的项,也不包含荷载的零次项。
例题2-9试按叠加原理做例题2-9图(a)所示简支梁的弯矩图。
求梁的极值弯矩和最大弯矩。
解:先将梁上每一项荷载分开(见图(b)、图(c)),分别做出力偶和均布荷载单独作用的弯矩图(见图(d)、图(e))两图的纵坐标具有不同的正负号,在叠加时可把它们画在x 轴同一侧(见图f)。
于是两图共有部分,其正、负纵坐标值互相抵消。
剩下的纵距(见图(f)中阴影线部分)即代表叠加后的弯矩值。
叠加后的弯矩图仍为抛物线。
如将它改画为以水平直线为基线的图,即得通常形式的弯矩图(见图(曲)。
求极值弯矩时,先要确定剪力为零的截面位置。
由平衡方程0Bm =∑可求得支反,剪力方程为Q 即可求出极值弯矩所在截面的位置。
令()0x极值弯矩为由例题2-9图(g)可见,全梁最大弯矩为本例中的极值弯矩并不大于梁的最大值弯矩。
当梁上的荷载较复杂时,也可将梁按荷载情况分段,求出每一段梁两端截面的内力。
这时该段梁的受载情况等效于一受相同荷载的简支梁 (见图2-12(a)、(b))。
因为每一段梁在平面弯曲时的内力,不外是轴力N、剪力Q和弯矩M。
由于轴力N不产生弯矩,故在作弯矩图时可将它略去,剩下的梁端剪力1Q,2Q和梁端弯矩1M、2M,及荷载对梁段的作用,可用图2-12(b)所示的简支梁上相应的荷载来代替(梁段端截面上的剪力可由梁的支反力提供,故图中未画出)。
4.4.5 用区段叠加法作静定梁的内力图解析

【例 9.11】简支梁受荷载P和q作用如图9.22(a)所示。试用叠加法画梁的弯矩
【解】将作用在梁上的荷载分为P与q两组。 先分别画出P、q单独作用下的弯矩图,如图9.22(b)、(c)所示。然后将这
两个弯矩图的相应纵坐标叠加起来,如图9.22(a)所示,就是简支梁在集中荷 载P和均布荷载q
【例 9.12】外伸梁受荷载作用如图9.23(a)所示,试用叠加法画梁的弯矩图。
用在简支梁上时的弯矩图,为此必须先求出MA 和MB。
区段叠加法画弯矩图的具体步骤如下:
▲ 首先把杆件分成若干段,求出分段点上的弯矩 值,按比例标在杆件相应的点上,然后每两点间 连以直线。
▲ 如果分段杆件的中间没有荷载作用这直线就是 杆件的弯矩图。如果分段杆件的中间还有荷载作用, 那么在直线上还要叠加上荷载单独在相应简支梁上 产生的弯矩图形。
4.4.5 用区段叠加法作 梁的弯矩图
学习目标:学会用叠加法作内力图
叠加法画弯矩图
根据叠加原理来绘制内力图的方法称为叠加法。 用叠加法画弯矩图,绘图时先把作用在梁上的 复杂的荷载分成几组简单的荷载,分别作出各简单 荷载单独作用下的弯矩图,然后将它们相应的纵坐 标叠加,就得到梁在复杂荷载作用下的弯矩图。例 如图9.21(a)、(b)、(c)所示。 用叠加法画弯矩图时,一般先画直线形的弯矩 图,再叠画上曲线形的弯矩图。
图9.23
二、用区段叠加法画弯矩图
对图示简支梁把其 中的AB段取出,其隔 离体如图所示:
把AB隔离体与相 应的简支梁作一对 比:
Fp
q
A
L
q
MA
A
FQAB
q MA
显然两者是完全
A
相同的。
MA
A
(土建施工)教学设计8-5-2区段叠加法绘制梁的弯矩图

8-5-2 区段叠加法绘制梁的弯矩图
一、教学目标
知识目标:
1.掌握分区段叠加法的适用情况及原理;
2.掌握分区段叠加法绘制梁的弯矩图的步骤。
能力目标:
会熟练运用分区段叠加法绘制梁的内力图。
二、教学重难点
重点:分区段叠加法绘制梁的弯矩图的步骤。
难点:分区段叠加法绘制多个荷载作用下的弯矩图。
三、教学方法
采纳线上线下混合式教学法、小组讨论法、案例分析等方法。
四、教学实施
课前:教师利用云课堂APP安排任务,学生在课前复习分荷载叠加法绘制弯矩图的步骤及思路。
课中:首先,创设情境,提出问题:“分荷载叠加法绘制两个以上荷载作用下的弯矩图是否方便?〞,引入新课。
接着,启发式讲授分区段叠加法的原理及适用情况,即梁上某段作用有均布荷载和集中力。
然后,通过例题掌握分区段叠加法绘制梁的弯矩图的步骤和方法。
最后小组合作,通过练习稳固分区段叠加法。
课后:教师通过云课堂APP安排本节课作业,并公布下节课的预习任务,教师对作业进行批改,并及时进行反应。
五、教学小结
学生通过云课堂APP进行本次课程学习效果的评价;教师总结课程内容,并进行下次课程任务安排。
叠加法绘制弯矩图-PPT

AX l
B
F
叠加法——用叠加原理绘制弯矩图的方法
叠加时,易先画直线形的弯矩图,再叠加曲线形或折线形 的弯矩图
由于剪力图比较好画,重点介绍用叠加法画弯矩图
步骤: 注意:
1. 荷载分解 2. 作分解荷载的弯矩图
3. 叠加作荷载共同作用下 的弯矩图
弯矩图的叠加, 不是两个图形的简单叠加, 而是对应点处纵坐标的相加。
叠加法绘制弯矩图
重点
1、叠加法绘制弯矩图 2、区段叠加法绘制弯矩图。
难点
区段叠加法绘制弯矩图
叠加原理:
几个载荷共同作用的效果,等于各个载荷单独作用效果之和
“效果”——指载荷引起的反力、内力、应力或变形
“之和”——代数和
叠加原理成立的前提条件:小变形条件
q
MxFxqx2
2
M x M 1 x M 2 x
kN
190 160
kNm
210 280
340
4
-
大家有疑问的,可以询问和交流
可以互相讨论下,但要小声点
MA A
MA
q
MB
B
lபைடு நூலகம்
q
A
l
+
+
MB
1/8qL2
1/8qL2
MA BA
l
+
MA
MB B
MB
区段叠加法——用叠加法作某一段梁弯矩图的方法 原理
任意段梁都可以当作简支梁,并可以利用叠加法来作该段梁 的弯矩图
梁分一段: A端截面弯矩:M=MA B端截面弯矩:M=MB
各控制面弯矩分别为:
MA=-12KN MD=8KN MB=-4KN
6KN q=2KN/m
结构力学 第三章 静定结构

MBC=1kN· m
B
MBE= 4kN· m
MBA=5kN· m
FP1=1kN FP2=4kN
• 用计算中未使 用过的隔离体平衡 条件校核结构内力 计算是否正确。
5kN· m
1kN
3kN
FP3=1kN
2、简支刚架
• 解: • (1)、求支座 反力 • ∑y=0 • FCy =80kN(↑) • ∑m0=0 • FAx=120kN(←) •∑x=0 •FBx=80kN(→)
§3-2 静定多跨梁
•
由中间铰将若干根梁(简单梁) 联结在一起而构成的静定梁,称为静 定多跨梁。
1、几何组成:
• 基本部分+附属部分。 • (1)、基本部分:不依赖其它部分, 本身能独立承受荷载并维持平衡。 • (2)、附属部分:依赖于其它部分而 存在。
2、层叠图和传力关系
(1)、附属部分荷载 传 基本部分或 支撑它的附属部分。 • (2)、基本部分的荷载对附属部分无 影响,从层叠图上可清楚的看出来。 •
练习: 分段叠加法作弯矩图
q
A B
C
1 2 ql 4
l
q
1 ql 2
ql
l l l
例题
4kN· m
4kN
3m
3m
(1)集中荷载作用下
6kN· m
(2)集中力偶作用下
4kN· m 2kN· m
(3)叠加得弯矩图
4kN· m
4kN· m
例题
3m
8kN· m
2kN/m
3m
2m
(1)悬臂段分布荷载作用下
FP2=4kN
q=0.4kN/m
广东省2017年一级建筑师《建筑结构》:分段叠加法作弯矩图考试题

广东省2017年一级建筑师《建筑结构》:分段叠加法作弯矩图考试题本卷共分为2大题50小题,作答时间为180分钟,总分100分,60分及格。
一、单项选择题(共25题,每题2分,每题的备选项中,只有 1 个事最符合题意)1、在编制初步设计总概算时,对于难以预料的工程和费用应列入下列哪一项(2005,4)A.涨价预备费B.基本预备费C.工程建设其他费用D.建设期贷款利息2、办公室、阅览室等工作房间一般照明照度的均匀度数值不宜小于____A:0.8B:0.7C:0.6D:0.53、按照现行规定,设备安装工程间接费的计算公式为______。
A.直接工程费×取费率B.(人工费+材料费)×取费率C.人工费×取费率D.(人工费+机械费)×取费率4、在电算化系统的应用中,硬件工作方式的选择依据是__。
A.B和DB.会计信息量C.上级要求D.企业规模5、用朗格系数法进行投资估算,其计算基础是__。
A.设备费B.设备安装费C.建筑工程费D.建筑安装工程费6、在8度地震设防要求下,钢筋混凝土框架结构的办公楼,层数为26-30层,一般情况下每平方米建筑面积钢材的消耗量是:(2005,17)A.90kg以上B.75—89kgC.66-74kgD.55-65kg7、对于大型和特大型的电影院主要入口前道路红线至墙基的集散空地面积除按0.2m2/座计算外,红线至墙基的距离还应≥__。
A.8mB.10mC.12mD.15m8、砌筑砂浆应随抹随用,施工期间最高气温超过30%时,水泥砂浆最迟应在__时间内使用完毕。
A.2hB.3hC.4h D.5h9、下列吊顶面层的综合单价(元/m2)最高的是:(2006,13)A.纤维板B.铝合金方板C.胶合板D.珍珠岩石膏板10、提出“花园城市”规划理论的人是__A.欧思曼B.欧文C.霍华德D.戛捏11、下列__项是单层外窃中最便宜的一种。
A.空腹钢窗B.实腹钢窗C.铝合金推拉窗D.铝合金平开窗12、悬索结构的经济跨度,下列哪一种说法是较合理的()A.50~60mB.80~90mC.100~150mD.160~200m13、对工程建设设计阶段执行强制性标准的情况实施监督的部门为:(2011,68) A.建设项目规划审查机构B.施工图设计文件审查单位C.建筑安全监督管理机构D.工程质量监督机构14、浇筑混凝上时,要求混凝土的自由倾落高度不得超过______。
建筑力学弯矩图剪力图

直播课堂6
整理课件
1
第六章静定结构的内力计算
一、本章主要知识点 1.截面内力及符号 2.内力图 3.荷载和剪力、弯矩的对应图形关系
整理课件
2
4.叠加法作弯矩图、剪力图 5.分段叠加法作弯矩图 6.静定梁作内力图 7.刚架作内力图 8.三铰拱的计算 9.桁架的计算
整理课件
3
二、本篇讲授的内容
(2)简支梁作用有中点的P 简支梁作用有中点的P的弯矩图为一折
线,在集中力P作处产生折点,其值为。
整理课件
42
简支梁作用有中点的P
P L/2 L/2
M + PL/4
P/2 +
Q -
整理课件
43
简支梁作用有中点的m
m
L/2 L/2
M/2
M
-
+
M/2 m/L
Q
+
整理课件
44
简支梁作用有非中点的P
P
(一)截面内力及符号 物体因受外力作用,在物体各部分之间 所产生的相互作用力称为物体的内力。 对内力的正、负号作如下规定:
轴力符号:当截面上的轴力使分离 体受拉时为正;反之为负。
整理课件
4
剪力符号:当截面上的剪力使分离体 作顺时针方向转动时为正;反之为负。
弯矩符号:当截面上的弯矩使分离体上 部受压、下部受拉时为正,反之为负。
P
q
A
1
1B 2
2
2
2
整理课件
7
解: 1.求梁的支座反力。
由整体平衡可求: X A 0 ,Y A 3 N ,Y B 1N 5
2.求1-1截面上的内力
杆上外力均为已知,可求任意截面的内
建筑力学:区段叠加法绘制弯矩图

目录
知识回顾 区段叠加法绘制弯矩图 应用举例
知识回顾
分荷载叠加法绘制弯矩图
MA A a
MA
F
b l (a)
MB
B
(1)分别绘出梁MA、MB,和荷载F作用下的弯矩图。 (2)两个弯矩图的竖标叠加,得最终弯矩图。
分荷载叠加法仅适用于荷载较少的情况, 实际绘图时可以直接作出图(d)。
12
12
FB 11 kN( )
(2)计算各控制截面的弯矩
MC 0 MF 0
M A 6 2 12 kN m
M D 66 15 4 2 4 2 8 kN m
M E 2 2 3 11 2 10 kN m M B 2 2 1 4 kN m
2
4
ql 2 2 42
=
=4kN m
MB
应用举例
利用区段叠加法绘制如图所示外伸梁的弯矩图。 6kN 2kN/m 8kN
2kN/m
解:(1)计算支座反力
MB 0, FA 8 610+2 4 6 8 2 2 21 0
FA 15 kN( )
CA
D EB
F
FA
FB
2m 4m
2m 2m 2m
MA(F) 0, 6 2 2 4 2 8 6 FB 8 2 2 9 0
1 叠加原理绘制弯矩图时,有哪些步骤? 2 需在图上标注哪些内容?
谢谢观看
MB
(b)
(仅力偶作用的M 图)
Fab (c) l
(仅F 作用的M 图)
MA
MB
Fab
l (d)
区段叠加 法绘制弯矩图
区段为集中力作用 (1)将两端弯矩MA和MB绘出,并连以直线
电中建筑力学试题

1.刚体是指在外力的作用下大小和形状不变的物体。
()A正确B错误错误正确答案:A学生答案:2.在任何外力作用下,大小和形状保持不变的物体,称为刚体。
()A正确B错误错误正确答案:A学生答案:3.下列说法正确的是()。
A工程力学中我们把所有的物体都抽象化为变形体B稳定性是指结构或构件保持原有平衡状态C在工程力学中我们把所有的物体都抽象化为刚体D工程力学是在塑性范围内,大变形情况下研究其承截能力错误正确答案:B学生答案:4.静力学是研究物体在力作用下的平衡规律的科学。
()A错误B正确错误正确答案:B学生答案:5.在任意荷载下,仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
()A错误B正确错误正确答案:B学生答案:6.桁架的特点是()。
A各杆自重不计,是二力杆(受拉或受压)BA和B选项C荷载作用于节点(铰链)处D由于其截面上的应力分布不均匀,故材料的效用得不到充分发挥错误正确答案:B7.静力学基本方法选取的原则是能够通过已知力求得未知力。
()A错误B正确错误正确答案:B学生答案:8.下列结论中()是正确的。
A材料力学主要研究各类杆件中力与材料的关系B材料力学主要研究各种材料的力学性质C材料力学主要研究杆件受力后变形与破坏的规律D材料力学主要研究各种材料的力学问题错误学生答案:9.如果杆端无集中力偶荷载作用,下列哪些位置杆端弯矩可能不等于零()。
A铰支座杆端B刚结杆端C自由端D铰结点杆端错误正确答案:B学生答案:10.图示带中间铰的连续梁,AB和BC部分的内力情况为()。
AN、Q、M图均为零Q为零,N、M不为零CQ、M为零,N不为零DN、Q、M图均不为零错误正确答案:C学生答案:11.弯矩图为水平线,力偶作用出有突变,突变值等于集中力偶。
()A正确B错误错误正确答案:A学生答案:12.研究构件或其一部分的平衡问题时,采用构件变形前的原始尺寸进行计算,这是因为采用了()假设。
小变形B各向同性C连续均匀性D平面错误正确答案:A学生答案:13.悬臂梁受三角形分布荷载作用,则下列选项正确的是()。
分段叠加法作弯矩图

作弯矩图时,可采用叠加法,使绘制工作得到简化。
(1)叠加发作简支梁的弯矩图
应当注意,这里所说的弯矩叠加,是纵坐标的叠加而不是指图形的拼合.图2-6d中的纵坐标M0,如图 和M的纵坐标一样,也是垂直于杆轴AB,而不是垂直杆A'段的弯矩图的特性和与其相应的(长度、承受荷载q和两端弯矩MA、MB均相同)简支梁的竖向力YA、YB(Y0A、Y0B)和弯矩图完全相同,因此,我们可以用前面所属的叠加法来绘制任意直杆段的弯矩图。
(2)分段画弯矩图。当控制截面之间无荷载时,该段弯矩图是直线图形。当控制截面之间有荷载时,用叠加法作该段的弯矩图。
具体作法如下:先求出杆段两端截面的弯矩图MA、MB。作直线的 图, 然后依此直线为基线,叠加相应简支梁在跨间荷载作用下的M0图(如d所示)
小结:梁弯矩图的一般作法
利用内力图的特性和弯矩图叠加法,将梁弯矩图的一般作法归纳如下:
(1)选定外力的不连续点(如集中力、集中力偶的作用点,分布力的起点和终点等)为控制截面,求出任制裁面的弯矩值。
直杆弯矩图的叠加法(精品)

转贴
[解] 此组合结构中,除AC、BC杆为受弯杆件外,其余均为轴力杆。
(1)求支座反力
由整体平衡条件,得VA=VB=75kN,HA=0.
(2)通过铰C作I—I截面,由该截面左边隔离体的平衡条件ΣMc=0,得NDE=135kN(拉力);由ΣY=0,Qc=—15kN;由ΣX=0,得NC =—135kN(压力)。
(3)分别由结点D、E的平衡条件,得NDA=NEB=151kN(拉力),NDF=NEG=67.5kN(压力)。
更多结构工程师好资料!(4)根据铰C处的剪力Qc及轴力Nc,并按直杆弯矩图的叠加法就可绘出受弯杆AFC、BGC的弯矩图。
(5)M、Q、N图分别如图2—17b、c、d所示。
广义力和广义位移
以各种不同方式作用在结构上的力,如集中力、集中力偶、分布力、分布力偶等都称为广义力,它可以是外力,也可以是内力。
与广义力对应的位移称为广义位移。
或能唯一地决定结构几何位置改变的彼此独立的量称为广义位移,如线位移、角位移、相对线位移、相对角位移等。
更多结构工程师好资料!
本节主要介绍静定结构在广义力、温度变化、支座位移等因素作用下的广义位移计算。
结构力学第三章叠加法作弯矩图

(3)叠加得弯矩图
4kN· m
4kN· m
MA A
MB
B
l
MB
MA
MA A
q B
MB
l
MA
ql 8
2
MB
8kN· m
2kN/m
3m
3m
2m
(1)悬臂段分布荷载作用下
4kN· m
2kN· m
(2)跨中集中力偶作用下
4kN· m
4kN· m
(3)叠加得弯矩图
6kN· m
4kN· m
2kN· m
+
所以:M2=375kN.m (左拉) FN1=141×0.707=100kN
FQ1= 50 +5×5 -141×0.707 =-25kN
(取外力矩逆时针转向为正方向) (下拉)
M1=125 +141×0.707×10-50×5-5/2×5²=812.5kNm
注意:外力矩的正负是为了区分它的两种不同的转向。
qba30因此上图梁中ab段的弯矩图可以用与简支梁相同的方法绘制即把m以直线然后在此直线上叠加上节间荷载单独作用在简支梁上时的弯矩图为此必须先求出mql区段弯矩图叠加法32qlqlqlqlqlqlql区段弯矩图叠加法3310knm15kn60knm2m2m2m2m20knm3055303030303030303030303030348kn4knm16knm1m2m2m1m1730237kn1m1m35利用上述关于内力图的特性和弯矩图的分段叠加法可将梁的弯矩图的一般作法归纳如1选定外力的不连续点如集中力作用点集中力偶作用点分布荷载的起点和终点等为控制截面求出控制截面的弯矩值连一虚线然后以该虚线为基线叠加上简支梁在跨间荷载作用下的弯矩图
分段叠加法作弯矩图

l/2
q 1 ql2 16
l/2
q
1 ql2 16
分段叠加法作弯矩图的方法:
(1)计算控制截面的弯矩值: 选定外力的不连续点(集中力作用点、集中力偶作用点、
分布荷载的始点和终点)为控制截面,
(2)分段叠加作弯矩图: 当控制截面间无荷载时,弯矩图为连接控制截面弯矩值
的直线; 当控制截面间存在荷载时,弯矩图应在控制截面弯矩值作
M图 FQ图
A支座的反力 大小为多少, ql2 / 2 M图 方向怎样? FQ图
M图
FQ图
1.无荷载分布段(q=0),FQ图为水平线,M图为斜直线. 2.均布荷载段(q=常数),FQ图为斜直线,M图为抛物线,且 凸向与荷载指向相同. 3.集中力作用处,FQ图有突变,且突变量等于力值; M图 有尖点,且指向与荷载相同;从左向右看,剪力图突变 方向与力的方向相同。 4.集中力偶作用处, M图有突变,且突变量等于力偶值; FQ图无变化;从左向右看,顺时针力矩,M图向下突变。
1m
1m
7kN
练习2
本章重点: 梁和刚架的内力图
60kN
24kN
A
D0
B
E
0.2m
18kN
0.2m
0.2m
66kN
M图
FQ图
例: 作内力图
铰支座有外 力偶,该截面弯矩 等于外力偶.
M图 FQ图
无剪力杆的 弯矩为常数.
M图
自由端有外
力偶,弯矩等于外
FQ图 力偶
练习: 利用上述关系作弯矩图,剪力图
练习: 利用上述关系作弯矩图,剪力图
5.叠加法作弯矩图
注意:
是竖标相加,不是 图形的简单拼合.
用叠加法作直杆M 图的步骤
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
q
0
ql A
ql
B C D
ql
l
l
2q l
l
第三章 静定梁与静定钢架
习题6
Qingdao Technoligical University
本章重点:
梁和刚架的内力图
0
3 ql 2
3 2 ql 2
ql
q
C 1 ql 2
A
B
l
l
练习: 利用微分关系等作弯矩图
P
本章重点:
梁和刚架的内力图
l
l/2
l/2
用叠加法作直杆M 图的步骤
• (1)竖:用截面法求杆端弯矩。
Qingdao Technoligical University
• (2)联:将杆两端弯矩纵标联以虚线
• (3)叠加:以联线为基础,叠加杆跨 上荷载所产生的简支梁弯矩图。
练习:
q
1 2 ql 16
q
l
ql 2
1 2 ql 16
ql 2
l
6.分段叠加法作弯矩图
q
A
1 2 ql 16
B
l/2
q
C
q
l/2
1 2 ql 16
1 ql 8
1 2 ql 16
l/2
q
q
1 2 ql 16
1 2 ql 16
l/2
分段叠加法作弯矩图的方法:
Qingdao Technoligical University
第三章 静定梁与静定钢架
(1)计算控制截面的弯矩值:
选定外力的不连续点(集中力作用点、集中力偶作用点、
本章为全书 第三章 静定梁与静定钢架 最重要的一章
Qingdao Technoligical University
第三章 静定梁与静定刚架
本章为全书 第三章 静定梁与静定钢架 最重要的一章
Qingdao Technoligical University
第三章 静定结构的内力
§ 3-1梁的内力回顾
简支梁
M图
FQ图
ql2 / 2
A支座的反力 大小为多少, 方向怎样? M图 FQ图
M图 FQ图
1.无荷载分布段(q=0),FQ图为水平线,M图为斜直线. 2.均布荷载段(q=常数),FQ图为斜直线,M图为抛物线,且 凸向与荷载指向相同. 3.集中力作用处,FQ图有突变,且突变量等于力值; M图 有尖点,且指向与荷载相同;从左向右看,剪力图突变 方向与力的方向相同。 4.集中力偶作用处, M图有突变,且突变量等于力偶值; FQ图无变化;从左向右看,顺时针力矩,M图向下突变。
A
1m
B
F
1m
G
7kN 17kN
第三章 静定梁与静定钢架
练习2
Qingdao Technoligical University
本章重点: 梁和刚架的内力图
60kN
24kN E
0.2m
A
0.2m
D
0
0.2m
B
18 kN
66kN
第三章 静定梁与静定钢架
练习3
Qingdao Technoligical University
例:求A、B左、B右、C点的内力值
q
Qingdao Technoligical University
0
A
B
3 ql 4
2l l
C
ql
2
7 ql 4
2.梁左右两端的内力值 3.集中力作用处M、FQ的规律
要求掌握:1.双下标
第三章 静定梁与静定钢架 本章重点:
例:求C左、C右的内力值
梁和刚架的内力图
Qingdao Technoligical University
q
A
0
l 2
ql 2
C B
3 ql 2
l
1 ql 2
要求掌握:1.集中力偶作用处M、FQ的规律
第三章 静定梁与静定钢架 3.作内力图的基本方法
要求掌握:1.函数法求内力图的方法 内力方程式: 2.梁的弯矩图 3.均布荷载段M、FQ的规律
M M ( x) FQ FQ ( x) FN FN ( x)
B 解:
Qingdao Technoligical University
弯矩方程式 剪力方程式 轴力方程式
例:作图示梁内力图
q
A
FAx 0, FAy ql / 2(), FBy ql / 2()
F Ax
l
FAy
M FQ
FBy
F
x
0, FN ( x) 0
1 ql 2
1 Fy 0, FQ ( x) 2 qx qx 1 2 ql 1 x 8 M 0, M ( x) qlx qx 1 2 2 ql
FQ ( x)
FQ dFQ
Pl
1.无荷载分布段(q=0),FQ图 为水平线,M图为斜直线. 自由端无外力偶 则无弯矩.
M图
FQ图
例: 作内力图
M图 FQ 图 铰支端无外力偶 则该截面无弯矩.
1.无荷载分布段(q=0),FQ图为水平线,M图为斜直线. 2.均布荷载段(q=常数),FQ图为斜直线,M图为抛物线, 且凸向与荷载指向相同.
3.作内力图的基本方法
4.弯矩,剪力,荷载集度之间的微分关系 5.叠加法作弯矩图 6.分段叠加法作弯矩图
二.多跨静定梁
二.多跨静定梁
1.多跨静定梁的组成
附属部分--不能独 独立承载的部分。
基本部分--能独立 立承载的部分。
基、附关系层叠图
第三章 静定梁与静定钢架
本章重点: 梁和刚架的内力图
Qingdao Technoligical University
分布荷载的始点和终点)为控制截面,
(2)分段叠加作弯矩图: 当控制截面间无荷载时,弯矩图为连接控制截面弯矩值
的直线;
当控制截面间存在荷载时,弯矩图应在控制截面弯矩值作 出的直线上再叠加将该段看作简支梁时荷载产生的弯矩值。
练习: 分段叠加法作弯矩图 第三章 静定梁与静定钢架
4kN· m
4kN
8kN· m
M
本章重点:
梁和刚架的内力图
练习: 利用微分关系,叠加法等作弯矩图
P
1 Pl 4 1 Pl 4
P 1 Pl
4
l/2
q
l/2
l/2
1 2 ql 4
l/2
l/2
ql 1 ql 2 4
l/2
l/2
l/2
l/2
本章重点:
l/2
梁和刚架的内力图
§3-2 静定刚架受力分析
本章重点:
一. 刚架的受力特点
1 2 ql l 8
l
M
M
l
练习: 利用微分关系等作弯矩图 M 1 1
2 ql 2 4
l
ql
2
P
M M
l/2
M
l/2
l
l
2M
M
l
M M M
l
M
M
l
l
本章重点:
梁和刚架的内力图
练习: 利用微分关系等作弯矩图
1 2 ql 2
l
1 2 ql 4
P
l/2
q
l/2
M
1 2 ql 2
l
l
2M
M
M
M
M
M M M
M M
l l
M M
第三章 静定梁与静定钢架
1.画层次图 2.求支座反力 3.求控制点处的内力 4.画内力图
第三章 静定梁与静定钢架
习题1 Qingdao Technoligical University 0 0
本章重点:
梁和刚架的内力图
P
C A B D
Pl l
0
2l
l
P
第三章 静定梁与静定钢架
习题2 Qingdao Technoligical University
梁和刚架的内力图
刚架是由梁柱组成的含有刚结点的杆件结构
梁
桁架
1 2 ql 8
刚架
弯矩分布均匀 可利用空间大
第三章 静定梁与静定钢架
二、变形特点:在刚结点处各杆不能发生相对转动.
FyA =70kN FyB =50kN
Qingdao Technoligical University
1、求支座反力
2、作弯矩图 3、作剪力图
70 40 40 120
100 +
10
100 M图(kN· m)
50 FQ图 (kN)
-
例2 求图示梁的M图。 1、求支座反力 2、作弯矩图 3、作剪力图
第三章 F 静定梁与静定钢架 P= 40kN
M图 FQ图
例: 作内力图 铰支座有外 力偶,该截面弯矩 等于外力偶.
M图 FQ图 无剪力杆的 弯矩为常数. M图 自由端有外 力偶,弯矩等于外 力偶
FQ图
练习: 利用上述关系作弯矩图,剪力图
练习: 利用上述关系作弯矩图,剪力图
5.叠加法作弯矩图
注意:
是竖标相加,不是 图形的简单拼合.
第三章 静定梁与静定钢架
本章重点:
梁和刚架的内力图
0 A 0 B
3l 2
Pl
P
C
l l
D
l
E
P
2P
习题3 Qingdao Technoligical University
第三章 静定梁与静定钢架 本章重点:
梁和刚架的内力图
5kN m
20kN
0
A B
7.5 17.5
