蛛网模型(差分方程)汇总
蛛网模型

承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载).我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题.我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出.我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性.如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理.我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等).我们参赛选择的题号是(从A/B/C/D中选择一项填写):我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名.以上内容请仔细核对,提交后将不再允许做任何修改.如填写错误,论文可能被取消评奖资格.)日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):市场经济的分析摘要商品价格与产量的波动是市场经济的常态,认识我国商品价格与产量的波动规律,为宏观调控提供理论依据,是经济学研究的主要课题之一. 本文利用市场供求关系的需求函数和供应函数的图形,建立蛛网模型,并借助差分方程将模型结果用公式表示,再对结果进行分析.最后可将该模型进行适当推广,以实现对市场经济的调控作用.同时提出了相应的政策建议.关键字:市场经济市场供求关系蛛网模型政策建议一、问题重述在市场经济中有关商品的价格是由消费者的需求关系来决定,而下一期商品的数量又是由生产者的供应关系来决定,这就导致了市场经济中商品的数量与价格在震荡,即当供大于求的时候会导致价格的下降,价格的下降导致产量的减少,产量的减少又会导致供不应求,商品的供不应求导致商品的价格的上涨,这时候又会增加产量,产量的增加又会导致供大于求,数量与价格就在此之间震荡.问题一:描述商品数量与价格的变化规律.问题二:商品数量与价格的振荡在什么条件下趋向稳定?问题三:当不稳定时政府能采取什么干预手段使之稳定?二、模型的假设1.该市场经济并没有经过政府的宏观调控.2.该市场经济遵循上述所提出的供求规律,即价格与产量的变化规律.3.近似的认为斜率大的曲线弹性小,斜率小的曲线弹性大.4.假设价格与产量紧密,可以用确定的关系来表现.三、符号的约定四、问题的分析4.1 名词解释1)需求关系:商品数量与商品价格的关系,商品数量的增加会导致商品价格的降低.2)供应关系:商品价格与商品数量的关系,商品价格的提高会导致商品数量的增加.3)需求函数f的斜率a(取绝对值)表示商品供应量减少1个单位时价格的上涨幅度.4)供应函数h的斜率B表示价格上涨1个单位时(下一时期)商品供应的增加量.5)平衡点:市场的商品数量与商品价格关于平衡点震荡,趋于平衡点.4.2 问题的背景分析随着社会主义市场经济的逐步完善,绝大多数产品的价格已经推向市场,对生产者来说,市场价格会影响下一个时间周期的产出决策,也就是说生产者要做出的产出决策只能受当时的市场价格影响,而产品则要到下一个时间周期才能售出,可见市场供应量对价格的反应是滞后的.但市场的需求量对价格变化的反应是瞬时的,所以必须讨论价格波动对下一个时间周期产量的影响,以及由此而产生的均衡的变动,即必须进行动态均衡分析.商品的价格是由消费者的需求关系决定的,这样的需求和供应关系决定了市场经济中商品的价格和数量必然是振荡的,在现实世界里这样的振荡会出现不同的形式,有的振幅减小趋向平稳,有的则振幅越来越大导致经济崩溃.当然政府会对后者采取干预手段.4.3 问题分析商品的价格是由消费者的需求关系决定的,这样的需求和供应关系决定了市场经济中商品的价格和数量必然是振荡的,面对这一震荡关系,必须对市场进行分析,让生产者能够更好的了解市场,也让政府能够掌握市场的趋向,使得政府能够实行宏观调控,让市场能够更好的发展.面对上文所提到的问题,再根据对社会主义市场经济的深入了解,根据社会主义市场经济的发展特点,即滞后性,编者建立了蛛网模型,利用蛛网模型对上述问题进行分析,编者还建立了方程模型,对蛛网模型进行检验.五、模型的建立5.1.蛛网模型的建立蛛网模型有3种表现形态:一是收敛型蛛网.当市场受到外力的干扰偏离原有的均衡状态后,实际价格和实际产量会围绕均衡水平上下波动,但波动的幅度会越来越小,最终会回到原来的均衡点.二是发散性蛛网.当市场受到外力的干扰使得产量的价格偏离原有的均衡状态后,在实际价格和实际产量相互决定的周期循环运动过程中,其运动轨迹呈现出向外发散的蛛网形态,最终使价格和产量越来越远离原来的均衡点.三是封闭性蛛网.当市场受到外力的干扰使得产量和价格偏离原有的均衡状态后,在实际价格和实际产量相互决定的周期循环运动过程中,其运动轨迹旱现封闭形状,产量和价格与均衡点始终保持一定距离,永远达不到稳定的均衡水平.下文只对蛛网模型的两种表现形态进行分析,一是收敛型蛛网,二是发散性蛛网,对于封闭性蛛网不予以考虑.5.1.1 收敛型蛛网在外力的干扰下,市场会偏离原来的均衡状态,在这种情况下,商品实际价格和实际产量会围绕均衡水平上下波动,但会逐渐减小幅度,最终会回到原来的均衡点,此时,与需求曲线斜率相比,供给曲线斜率要大一些,这时呈现的即为收敛型蛛网模型.如图1所示:图1 收敛性蛛网5.1.2 发散性蛛网市场在外力的干扰下,会使得商品的价格偏离原有的均衡状态,其实际价格和实际产量的波动会偏离原来的均衡点越来越远,其轨迹呈现出向外发散的蛛网形态,此时,与需求曲线斜率相比,供给曲线斜率的绝对值要小一些,这时呈现的即为发散型蛛网模型,如图2 所示:图2 发散性蛛网5.2 差分方程模型的建立由()k k y f x =和1()k k x h y +=(1()k k y g x +=)可建立差分方程:1[()]k k x h f x +=1[()]k k y f h y +=设000(,)p x y 点满足:0000(),()y f x x h y ==,在000(,)p x y 点附近取函数(),()f x h x 的一阶近似:00()0k k y y x x αα=-->100()0k k x x y y ββ+=+->合并两式得:100()k k x x x x αβ+-=--上式是关于k x 的一阶线性差分方程.当然它是原来方程的近似模型.为了处理方便.适当取用其近似形式是合理的.其中α为f 函数在0p 点处的切线斜率:1β为g 函数在点0p 处切线的斜率.六、模型的求解6.1 蛛网模型的求解对蛛网模型的求解主要是求解蛛网模型中的两模型,一、收敛型蛛网模型;二、发散型蛛网模型.6.1.1 收敛型蛛网模型求解由()k k y f x =和1()k k x h y +=可以得到1()k k y g x +=.设1x 偏离0x ,则11223x y x y x →→→→→ ;当00,k k x x y y →→时,即1230P P P P →→→→ ,那么可以知道0p 是稳定平衡点.并且由上述式子可以推出f 函数和g 函数的曲线斜率的绝对值为f g K K <.图形如下:图3 收敛型蛛网模型由图中可以看出f g K K <,也可以看出0p 就是此图形的稳定平衡点.6.1.2 发散型蛛网模型求解由()k k y f x =和1()k k x h y +=可以得到1()k k y g x +=.设1x 偏离0x ,则11223x y x y x →→→→→ 当00,k k x x y y →→时,即1230P P P P →→→→ ,那么可以知道0p 是不稳定平衡点.并且由上述式子可以推出f 函数和g 函数的曲线斜率的绝对值为f g K K >.图形如下:图4 发散型蛛网模型由图中可以看出f g K K >,也可以看出0p 就是此图形的不稳定平衡点.6.2差分方程模型的求解由上文的模型分析可知,编者可以把在P0点附近用直线近似曲线,即:()k k y f x =⇒00()0k k y y x x αα=-->1()k k x h y +=⇒100()0k k x x y y ββ+=+->合并两式得: 100()k k x x x x αβ+-=--把上式经过1k -次迭代得:)()(0101x x x x k k --=-+αβ分析上式可以得到:当1αβ<时,即1/αβ<⇒0k x x →,说明了0p 点稳定.当1αβ>时,即1/αβ>⇒k x →∞,说明了0p 点不稳定.七、结果分析和结果检验7.1 结果分析基于问题一的回答:当供大于求的时候会导致价格的下降,价格的下降导致产量的减少,产量的减少又会导致供不应求,商品的供不应求导致商品的价格的上涨,这时候又会增加产量,产量的增加又会导致供大于求,数量与价格就在此之间震荡基于问题二的分析:由模型求解可知:00()0k k y y x x αα=-->α为商品数量减1单位, 价格上涨幅度100()0k k x x y y ββ+=+->β为价格上涨1单位(下时段),供应的增量由上述式子可以看出α是消费者对需求的敏感程度,就是说α小,有利于经济的稳定. β是生产者对价格的敏感程度,就是说β小,有利于经济的稳定.由,αβ和上述求解的模型知当1αβ<,那么经济就是稳定的,否则经济是不稳定的.基于问题三的分析;面对经济不稳定的情况,政府一个如何去做,由模型的求解可知,影响经济的稳定性情况是,αβ这两因素,只要把,αβ这两因素的其中一个调小,或者两个一起调小,就可以让经济趋于稳定.方法一:使 α 尽量小,如 α=0,⇒需求曲线变为水平.0α=即政府可以以行政手段控制商品价格不变.方法二:使 β 尽量小,如 β =0,⇒供应曲线变为竖直.0β=即政府可以靠经济实力控制商品数量不变.7.2 结果检验已知f K α=,1/g K β=,那么由差分方程模型可知0p 稳定时,f g K K <.0p 不稳定时,f g K K >,从这个结果可以看出差分方程模型与蛛网模型是一致的,就是说蛛网模型所求出的结果是经得起检验的.八、模型的评价8.1 模型的优点1. 全面的回答了本文的问题,并给出了模型的解.2. 由蛛网模型和方程模型得出结果吻合,误差较小.3. 此蛛网模型还可以加以推广,得到更加广泛的应用8.2 模型的缺点1. 蛛网模型是根据市场的上一期价格对下一期进行预测,而实际生产者除了2. 据市场的上一期价格还可以根据自身经验逐步修正自己的预期价格,这就会使结果有一定的偏差.3. 此模型的建立有片面性,有些因素未考虑,是函数的大致趋势九、模型的推广在生产者管理水平提高的情况下,即1()k k x h y +=⇒112k k k y y x h -++⎛⎫= ⎪⎝⎭的情况下,生产者根据当前时段和前一时段的价格决定下一时段的产量.那么供应函数变为1010[()/2]k k k x x y y y β+--=+-,而需求函数不变,即00()k k y y x x α-=--,合并两函数得:9 21022(1)1,2,k k k x x x x k αβαβαβ++++=+=0x 为平衡点,编者将在0,k k x x →∞→的条件下,讨论平衡点的稳定.求解方程21022(1)k k k x x x x αβαβαβ++++=+,得它的通解为1122k k k x c c λλ=+,其中(c 1, c 2由初始条件确定),12,λλ为方程220λαβλαβ++=的根.由上述方程可以看出在0,k k x x →∞→的条件下,0x 要想稳定,必须满足1,21λ< ,由方程220λαβλαβ++=解出12,λλ得1,2λ= 化简得:1,2λ=把方程1,2λ=1,21λ<得:2αβ<即0x 要想稳定,需要满足2αβ<,这比原来的1αβ<,条件放宽了,也就是说在生产者管理水平提高的情况下,即生产者根据当前时段和前一时段的价格决定下一时段的产量,会有助于经济的稳定.十、参考文献[1]李忠民,张世英. 非线性蛛网模型的动态分析[J].数量经济技术经济究,1997,(02).[2]么海涛.蛛网模型的数学研究[期刊论文]-北京信息科技大学学报(自然科学版). 2011(2).[3]刘广智,李宝营,宋科. 用蛛网模型分析市场经济趋于稳定的条件[J].大连轻工业学院学报,1999,(04):357-360.[4]王慧贤. 蛛网模型一市场供求稳定性分析[J].长春师范学院学报,2003,(02):5-6.。
蛛网模型

——动态分析方法
第1页
动态模型:蛛网模型
• 蛛网模型所考察的是价格波动对下一个周期产量 的影响,以及由此而产生的均衡变动。 • 所分析的产品具有如下特点: • 本期的产量决定本期价格,而本期的价格决定 下期的产量。 • 换句话说,上期的价格决定本期的产量,本期的 产量决定本期的价格。
第2页
• 若用P、Q分别表示价格和产量,D和S分 别表示需求函数和供给函数,t表示时期, 则上述关系可用公式表述为: • Pt==D(Qt) • Qt==S(Pt-1) • • • • 蛛网模型有三种形式: 封闭式蛛网模型 收敛式蛛网模型 发散式蛛网模型
第3页
• 一、封闭式蛛网模型
• 封闭式模型的条件:需求曲线和供给曲线的斜率的
第5页
二、收敛式模型
• 条件:供给曲线比需求曲线陡峭。 • 特点:价格和产量以越来越小的幅度上下波动, 在达到均衡时停止。
价格 价格 S
D
P1 P3 P2
产量 Q3 Q2 1 2
:需求曲线比供给曲线陡峭。生产者对价格 的反应程度大于消费者。 • 特点:价格和产量以越来越大的幅度波动,离均 衡点越来越远。
绝对值相等。 • 特点:价格从高到低、产量从低到高均按同一幅度不断 波动,永远达不到均衡状态。
D
S
P1
P3
P2
年份
Q3
Q2
0
1
2
3 第4页
图形说明
• 假定P1为第一年的价格,生产周期为一年,供 给对价格的反应滞后一年,第二年的产量为Q2, 但它只能按P2的价格才能全部卖掉,这样,第 二年的价格为P2。 • 根据第二年的较低的价格,第三年的产量减少 到Q3,但这一较低的产量可按照较高的价格P1 出售,因此,第三年的价格又与第一年的价格 相同。如果其他条件不变,上述循环过程就会 不断持续下去。 • 生产者和消费者对价格的反应是一致的。
蛛网模型在农产品

第二章: 第二章:差分方程
蛛网模型中的差分方程: 蛛网模型中的差分方程: (1)需求函数: )需求函数: 当期的产量决定当期的价格 (2)供给函数: )供给函数: 当期的价格决定下期的产量 (3)由此建立差分方程: )由此建立差分方程:
第二章: 第二章:差分方程
将点列 连接起来,就会形成蛛网一样的折线如下图。 连接起来,就会形成蛛网一样的折线如下图。 这个图形就是蛛网模ห้องสมุดไป่ตู้。 这个图形就是蛛网模型。 当 当
第一章: 第一章:蛛网模型理论
蛛网模型可以用以下三个联立的方程式来表示: 蛛网模型可以用以下三个联立的方程式来表示:
需求函数: 需求函数: 供给函数: 供给函数: 供求相等: 供求相等:
第一章: 第一章:蛛网模型理论
蛛网模型的三种情况: 蛛网模型的三种情况: (1)收敛型蛛网模型 ) 供给曲线斜率> 稳定) 供给曲线斜率>需求曲线斜率 (稳定) (2)发散型蛛网模型 ) 供给曲线斜率< 不稳定) 供给曲线斜率<需求曲线斜率 (不稳定) (3)封闭型蛛网模型 ) 供给曲线斜率=需求曲线斜率 上下波动) 供给曲线斜率 需求曲线斜率 (上下波动)
k f < k g , P0 是稳定的
k f < k g , P0 是不稳定的
第三章: 第三章:蛛网模型在农产品价格 中的应用实例 数据来源: 数据来源: 2001-2009中国小麦市场 中国小麦市场 应用软件: 应用软件: Mathematica
第三章: 第三章:蛛网模型在农产品价格 中的应用实例
数据→需求和供给函数 差分方程 数据 需求和供给函数→差分方程 需求和供给函数 差分方程→ Mathematica建模 发散性蛛网模型 建模→发散性蛛网模型 建模 →预测 预测2010年中国小麦市场 预测 年中国小麦市场
市场经济中的蛛网模型

对角 化
若有某个| j | 1时, x* 0是不稳定的 ;
对于二阶常系数差分方程
xk 2 a1 xk 1 a2 xk 0
(14)
引 入 变 换 k xk 1 , 则(14 )式 等 价 于 y yk x k 1 y a x a y 1 k k 1 2 k
附录:差分方程简介
一阶常系数差分方程
xk 1 axk b
(11)
在给定初值x0后,我们很容易通过迭代逐步求解出每 一个xk,即求解了差分方程. 在很多时候,我们了解此差分方程在k充分大的解的性态. 这就涉及到差分方程的平衡点及其稳定性的概念. 平衡点
解代数方程 x ax b 得 x b /(1 a).
(14)
由通解的表达式我们容易得到(14)的平衡点x*=0的稳 定性结论:
| 1 | 1且 | 2 | 1时, (14 )的平衡点 * 0是稳定的 x ; | 1 | 1或 | 2 | 1时, (14)的平衡点 * 是不稳定的 x ;
xk 2 a1 xk 1 a2 xk b (15)
∙
若f 的图像陡些.
y f g 经济学中的 蛛网模型
y1
∙
P0(x0,y0)
x
结论: P0是不稳定的平衡点.
实际上,需求曲线 f 和供应曲线 g 的具体形式通常是 根据根据各个时段商品的数量和价格的一系列统计 资料得到的.一般来说, f 取决于消费者对这种商品的 需要程度和他们的消费水平, g 则与生产者的生产能 力、经营水平等因素有关.比如:当消费者收入增加时, f 会向上移动;当生产能力提高时, g 将向右移动. 一旦 f 和 g 的函数关系即需求曲线和供应曲线确 定下来后,我们完全能够象上面的图解法一样确 定平衡点的稳定性.记它们在平衡点处的斜率的 绝对值分别为Kf 和Kg .则
差分方程在经济学中的应用

第四节 差分方程在经济学中的应用本节介绍差分方程在经济学中的几个简单应用,以期望读者有一些初步了解.一、 存款模型设S t 为t 期存款总额,i 为存款利率,则S t 与i 有如下关系式:S t +1=S t +iS t =(1+i )S i , t =0,1,2,…,其中S 0为初始存款总额.二、 动态供需均衡模型(蛛网定理)普通市场上一般商品的价格能影响消费者对该种商品的需求量,需求量与价格呈反向 变化.设D t 表示t 期的需求量,S t 表示t 期的供给量,P t 表示商品t 期价格,则传统的动态供 需均衡模型为:⎪⎩⎪⎨⎧=+=+=-)3(,)2()1(,,111t t t t t t S D P b a S bP a D 其中a ,b ,a 1,b 1均为已知常数.上述各方程的经济意义是:(1)式表示t 期(现期)需求依赖于同期价格;(2)式表示t 期(现期)供给依赖于(t -1)期(前期)价格.这里实际上假定该种商品生产行为既不是瞬时的,也不是连续的,而是要求有一个固定的生产周期.生产者总认为:本期的市场价格将在下一周期内保持不变,并按现期价格安排下一周期的生产.因此,第t 期的供给量S t ,实际上由前一周期价格P t -1决定,也就是说,供给量滞后于价格一个周期.(3)_式为供需均衡条件. 若在供需平衡的条件下,而且价格保持不变,即P t =P t -1=P e ,那么由(1)(2)(3)式,我们即得静态均衡价格:P e =bb a a --11. 显然,若将需求曲线与供给曲线画在同一坐标平面上,其交点(P e ,Q e )即为该种商品的静态均衡点.一般地,将动态供需均衡模型的(1)(2)两式代入(3)式,便得到动态供需均衡模型的等价差分方程:P t -bb 1P t -1=b a a -1. (11-4-1) 这是一个一阶常系数非齐次线性差分方程,可求得(11-4-1)的一个特解t P =bb a a --11 =P e , 从而,方程(11-4-1)的通解为: P t =A (b b 1)t +P e , 这里A 为任意常数.若初始价格P 0已知时,将其代入通解,可求得任意常数A =P 0-P e ,此时,通解改写为P t =(P0-Pe )(1b b )t +Pe . (11-4-2) 如果初始价格P 0=P e ,那么Pt =Pe ,这表明没有外部干扰发生,价格将固定在常数值Pe 上,这就是前面所说的静态均衡.如果初始价格P0≠Pe ,那么价格Pt 将随t 的变化而变化.显然,由通解(11-4-2)式可知,当且仅当︱1b b︱<1时,有 10e e e lim lim ()()t t t t b P P P P P b →+∞→+∞⎡⎤=-+=⎢⎥⎣⎦, 也就是说,动态价格Pt 随着t 的无限增大逐渐地振荡趋近于静态均衡价格Pe .图11-1是普通商品的价格与供需关系图.图11-1图11-1形状类似于蜘蛛网,故称此模型为蛛网模型(或蛛网定理).三、 凯恩斯(K e yn e s .J .M)乘数动力学模型设Y t 表示t 期国民收入,C t 为t 期消费,I t 为t 期投资,I 0为自发(固定)投资,ΔI 为周期固定投资增量.凯恩斯国民经济收支动态均衡模型为:⎪⎩⎪⎨⎧+=+=+=-)3(,)2()1(,0,1I I I bY a C I C Y tt t t t t ∆ 其中(1)式为均衡条件,即国民收入等于同期消费与同期投资之和;(2)式为消费函数,即现期消费水平依赖于前期国民收入(消费滞后于收入一个周期),a (≥0)为基本消费水平,b 为边际消费倾向(0<b <1);(3)式为投资函数,这里仅考虑为固定投资.在(1)(2)(3)式中消去C t 和I t ,得到一阶常系数非齐次线性差分方程:Y t -bY t -1=a +I 0+ΔI . (11-4-3)可求得(11-4-3)的一个特解t Y =bI I a -++10∆, 从而,方程(11-4-3)的通解为 Y t =A ·b t +b I I a -++10∆,其中A 为任意常数.我们称系数b-11为凯恩斯乘数. 四、 哈罗德(Harrod .R .H)经济增长模型设S t 为t 期储蓄,Y t 为t 期国民收入,I t 为t 期投资,s 称为边际储蓄倾向(即平均储蓄倾向),0<s <1,k 为加速系数.哈罗德宏观经济增长模型为:11,01,(1)(),0,(2),(3)t t t t t tt S sY s I k Y Y k S I --=<<⎧⎪=->⎨⎪=⎩ 其中s ,k 为已知常数.(1)式表示t 期储蓄依赖于前期的国民收入;(2)式表示t 期投资为前两期国民收入差的加速,且预期资本加速系数k 为常数;(3)式为均衡条件.经整理后得齐次差分方程Y t -k s k + Y t -1=0, (11-4-4) 其通解为Y t =A (1+k s )t , (11-4-5) 其中A 为任意常数,k s >0,哈罗德称之为“保证增长率”.其经济意义就是:如果国民收入Y t 按保证增长率ks 增长,那么就能保证t 期储蓄与t 期投资达到动态均衡,即I t =S t , t =0,1,2,….假定t -1期收入Y t -1满足于通解(11-4-5),而t 期收入Y t 由于某种外部干扰使其不满足于(11-4-5),而是Y t =A (1+k s )t +B (B ≠0,称为外部干扰), 不妨设B >0,那么有I t =k (Y t -Y t -1)=k [k s A (1+k s )t -1+B ] =sA (1+ks )t -1+kB =sY t -1+kB=S t +kB .因kB >0,故I t >S t .这就表示:总投资将大于总供给(由储蓄提供),从而对收入产生一个向上的压力,迫使收入较以前增加得更多.这就充分地说明了,“保证增长率”保证了国民收入的增长.五、 萨缪尔森(Samu e lson P .A)乘数加速数模型设Y t 为t 期国民收入,C t 为t 期消费,I t 为t 期投资,G 为政府支出(各期均相同).萨缪尔森将乘数和加速数两个参数同时引进而得到国民经济收支均衡模型(也称为乘数-加速数模型):⎪⎩⎪⎨⎧>-=<<=++=--)3(,0),()2(,10,)1(,11k C C k I b bY C G I C Y t t tt t t t t 其中G >0为常数,b 称为边际消费倾向(常数),k 为加速数.将(2)(3)两式代入(1)并经整理后得:Y t -b (1+k )Y t -1+bkY t -2=G . (11-4-6)这是关于Y t 的二阶常系数非齐次线性差分方程.不难求得其特解t Y =b G-1. 其经济意义为:国民收入的均衡值等于凯恩斯乘数b -11与政府支出自发投资G 的乘积.方程(11-4-6)对应的齐次方程为Y t -b (1+k )Y t -1+bkY t -2=0, (11-4-7)其特征方程为λ2-b (1+k )λ+bk =0, (11-4-8)特征方程的判别式Δ=b 2(1+k )2-4bk =b [b (1+k )2-4k ],当Δ>0时,(11-4-8)有两相异实根:λ1=21[b (1+k )-∆],λ2=21[b (1+k )+ ∆].方程(11-4-7)的通解为:Y A (t )=A 1·λ1t +A 2·λ2t (A 1,A 2为任意常数).当Δ=0时,(11-4-8)有一对相等实特征根:1(1)2b k λ=+,方程(11-4-7)的通解为:12()()tA Y t A A t λ=+⋅,(A 1,A 2为任意常数).当Δ<0时,(11-4-8)有一对共轭复根:λ=21[b (1+k )+i ∆],λ=21[b (1+k )-i ∆],方程(11-4-7)的通解为:Y A(t )=γt (A 1cos ωt +A 2sin ωt ),A 1,A 2为任意常数;γ和ω由下式确定⎪⎩⎪⎨⎧∈+==),0(,)1(arctan ,πωωγk b bk ∆.综合上述,方程(11-4-6)的通解为:⎪⎪⎪⎩⎪⎪⎪⎨⎧<-++=-+⋅+>-+⋅+=,0,1sin cos (,0,1)(,0,121212211∆∆∆当当当b G t A t A b G t A A b G A A Y t t t t t ωωγλλλ, 其中Δ=b [b (1+k )2-4k ],A 1,A 2为任意常数,λ1,λ2及λ,γ和ω均如前面所述.若求出Y t ,由所给模型就不难确定C t 和I t .习题11-41. 设Y t 为t 期国民收入,C t 为t 期消费,I 为投资(各期相同).卡恩(Kahn)曾提出 如下宏观经济模型:1,,01,0,t t t t Y C I C Y αβαβ-=+⎧⎨=+<<>⎩其中α,β均为常数,试求Y t 和C t .2. 设Y t ,C t ,I t 分别表示t 期的国民收入、消费和投资,三者之间满足如下关系:⎪⎩⎪⎨⎧>+=≥<<+=+=+,0,,0,10,,1γγβαβαt t t t t t t t I Y Y Y C I C Y这里α,β,γ均为常数.求Y t ,C t ,I t .3. 设Y t 为t 期国民收入,S t 为t 期储蓄,I t 为t 期投资,三者之间满足如下关系:⎪⎩⎪⎨⎧>=>-=≥<<+=-,0,,0),(,0,10,1δδγγβαβαt tt t t t t I S Y Y I Y S , 这里α,β,γ,δ均为常数,试求Y t ,S t ,I t .4. 挪威数学家汉逊(Hanssen .J .S)研究局部化理论模型遇到如下的差分方程:D n +2(t )-4(ab +1)D n +1(t )+4a 2b 2D n (t )=0,这里a ,b 为常数,而D n (t )为未知函数,若1+2ab >0,试求方程的解.5. 梅茨勒(Metzler .L .A)曾提出如下的库存模型:⎪⎩⎪⎨⎧-=<<=++=---),(,10,,211t t tt t t t t Y Y S Y U S U Y βββα, 其中Y t 为t 期总收入,U t 为t 期销售收入,S t 为t 期库存量.α和β为常数.试求Y t ,U t ,S t 关于t 的表达式.。
差分方程模型

′( x * ) < 1 f f ′( x ) > 1
*
xk +1 = bx k (1 xk ) 的平衡点及其稳定性
平衡点 x = f ( x) = bx(1 x) 稳定性
f ′( x * ) < 1
b = r +1
另一平衡 点为 x=0
1 x =1 b
*
f ′( x * ) = b (1 2 x * ) = 2 b
现 象
问 题
描述商品数量与价格的变化规律 商品数量与价格的振荡在什么条件下趋向稳定 当不稳定时政府能采取什么干预手段使之稳定
蛛网模型
xk~第k时段商品数量;yk~第k时段商品价格 时段商品数量; 第 时段商品价格 第 时段商品数量 消费者的需求关系 生产者的供应关系
y
需求函数
yk = f ( xk )
t z t = ( c 1 + c 2 t + + c d t d 1 ) λ 1 + c d +1 λ td +1 + + c p λ tp
– 有相等实根场合λ1=…= λd 有相等实根场合λ
– 复根场合λ1=a+bi=rei, λ2=a-bi=re-i 复根场合λ
t z t = r t ( c 1 e it + c 2 e it ) + c 3 λ 3t + + c p λ p t = r t ( c 1 c o s t + c 2 s in t ) + c 3 λ 3t + + c p λ p
β ~ 价格上涨 单位 (下时段 供应的增量 价格上涨1单位 下时段 单位, 下时段)供应的增量 α ~ 消费者对需求的敏感程度 β ~ 生产者对价格的敏感程度 α小, 有利于经济稳定 β 小, 有利于经济稳定
蛛网模型的差分方程分析

蛛网模型的差分方程分析
蛛网模型的基本假设是:商品的本期d t Q 决定于前一期的价格1-t P ,即供给函数
)(1-=t d t P f Q ,商品的本期的需求量d t Q 决定于本期的价格t P ,即需求函数为)(t d t P f Q =。
根据以上假设条件,蛛网模型可以用以下三个联立的方程式表示:
t d t P Q ∙-=βα(本期需求函数)
1-∙+-=t s t P Q γδ(本期供给函数)
s t d t Q Q =
式中,γδβα,,,均为常数,且均大于零。
由以上方程组可以得到等式:1-∙+-=∙-t t P P γδβα即:βδαβγ+=+-1t t P P 。
解这个差分方程:因为01≠+βγ,所以解为γ
βδαβγ+++-=t t P )(。
所以当γβ>时(即需求函数的斜率大于供给函数的斜率),若∞→t ,γβδα++=
t P 。
说明价格收敛于γ
βδα++=e P 。
在静态模型中,e P 就是其稳定价格。
当γβ=时,即需求函数的斜率等于供给函数的斜率,∞→t ,γβδαβγ+++±=t P ,即价格以距离β
γ围绕稳定价格e P 变化。
当γβ<时,∞→t ,t P 发散。
t e t P P )(||β
γ=-,随着时间变化,价格t P 距离稳定价格e P 越来越远,以至无穷大。
蛛网模型

需求弹性大,则税负转嫁就很困难,且向前转给消 费者的少,向后转给原供应者的多;需求弹性小, 则税负容易转嫁,且向前转给消费者的多,向后转 给原供应者的少;需求完全无弹性,税负可能全部 向前转嫁给消费者;需求完全有弹性,税负可能全 部向后转嫁给原供应者。需求弹性越大,转嫁的可 能性越小;需求弹性越小,转嫁的可能快越大,税 负转嫁与需求弹性成反比
如果商品的供给弹性大于需求弹性, 则政府对该种商品征税后,赋税将 主要由消费者负担。 例如:粮食
如果商品的供给弹性 小于需求弹性,则政府 对该种商品征税后,赋 税将主要由生产者自己 负担。 例如:钻石,黄金。
为什么飞机票经常打折,火车票却很少打折?
第一:这与价格弹性有关。飞机票价格下跌需求就增加,总的 利润就会提高,这是所谓的“薄利多销”。然而火车票却是供 不应求,即使涨价,也会有很多人愿意购买,因为火车成本低, 涨价也不会涨得太厉害。
谢谢观赏!
为什么飞机票打折而火车票不打折 呢?
总体来说,飞机票是供大于求,所以航空公司总 是会采取打折的办法以吸引客源。而火车票是供 不应求,所以火车有时候总是宁愿空跑也不愿打 折。火车是国有制机构,是国家专制机构操作, 而飞机是处在几大航运公司的竞争下的,所以竞 争之下必有经营的不同手段而导致机票打折的现 象出现。然而本来就供不应求的火车票是没有多 大必要打折的。所以飞机票总是出现打折而火车 票不愿打折。
模蛛 型网
Co Cobweb model
在经济学中
蛛网模型(Cobweb model)
运用弹性原理解释某些生 的商品在失去均衡时发生 的不同波动情况的一种动 态分析理论
28—市场经济中的蛛网模型

目录市场经济中的蛛网模型 (2)摘要 (2)一、问题重述 (3)二、模型条件假设 (3)三、符号约定 (3)四、问题分析 (3)五、模型建立和求解 (3)5.1蛛网模型建立和求解 (3)5.2差分方程模型建立和求解 (5)六、模型分析 (6)七、模型推广 (8)八、参考文献 (9)市场经济中的蛛网模型摘要在市场经济中商品的价格是由消费者的需求关系决定,商品数量越多,价格越低;而下一生产周期商品的数量是由生产者的供应关系决定,商品价格越低,生产的数量就越少.这样的需求和供应关系就决定了市场经济中商品的价格和数量是存在震荡的.本文首先用图形方法建立蛛网模型,对市场经济中商品的价格和数量存在的震荡现象进行分析,给出市场经济趋于稳定的条件为需求曲线f 在0P 点斜率的绝对值f K 小于供应曲线g 在0P 点斜率的绝对值g K ;然后用差分方程建立模型,得到当1αβ<或1αβ<时,市场经济趋于稳定;并对模型结果进行分析解释,讨论当市场经济不稳定时政府可以采取控制物价和宏观调控的干预措施;最后对模型作适当评价和推广.一、问题重述根据某种商品市场需求和供应关系求解以下问题:(1)描述商品数量与价格的变化规律.(2)商品数量与价格的振荡在什么条件下趋向稳定?(3)当不稳定时政府能采取什么干预手段使之稳定?二、模型条件假设针对本问题可做以下假设:(1)假设在同一生产周期内不会严重的自然灾害.(2)假设在同一生产周期内消费者生活习惯不会有大的改变.三、符号约定表1 符号约定四、问题分析商品的价格是由消费者的需求关系决定,商品数量越多,价格越低,而下一时期商品的数量由生产者的供应关系决定,商品价格越低,生产的数量就越少.这样的需求和供应关系决定了市场经济中商品的价格和数量必然是震荡的.本题先用图形方法建立蛛网模型,对上述现象进行分析,给出市场经济趋于稳定的条件;然后用差分方程建立模型,对模型结果进行解释,并讨论当市场经济不稳定时政府采取的干预措施;最后对上述模型作适当评价和推广.五、模型建立和求解5.1蛛网模型建立和求解在商品的一个生产周期内,其价格k y 取决于数量k x ,设存在消费者需求关系为()k k y f x = (1)因为商品的数量越多价格越低,所以该需求曲线f 是一条下降曲线.下一生产周期商品的数量1k x +由上一生产周期商品的价格k y 决定,设存在生产者供应关系1()k k x h y +=或1()k k y g x += (2)因为价格越高生产产量才越大,所以该供应曲线g 是一条上升曲线.将两条曲线分别画在同一坐标内,可以发现两条曲线相交于000(,)P x y 点,则该点即为平衡点,因为在某个生产周期内有0k x x =,则由需求关系和供应关系可知,01010,,,k k k y y x x y y ++===,即商品的数量和价格将永远保持在000(,)P x y 点.但在实际情况下,,x y 不可能停在0P 点,故将1x 点偏离0x 点分析问题如图1所示.图1数量价格关系图在图1中,价格1y 由曲线f 上的1P 点决定,下一生产周期的2x 由曲线g 上的2P 点决定,2y 由曲线f 上的3P 点决定,依次下去可得到点列111(,)P x y ,221(,)P x y ,322(,)P x y ,432(,),P x y ,即1230P P P P →→→→,这表明000(,)P x y 点为平衡点,即市场经济将趋于稳定.当曲线f 和曲线g 的斜率发生改变时,存在另外一种情况如图2所示.图2 数量价格关系图在图2中,按类似方法分析可得点列关系为1230P P P P →→→⨯,这表明000(,)P x y 点不是平衡点,即市场经济将趋于不稳定.两图中折线1234PP P P 形似蛛网,故这种需求曲线和供应曲线分析市场经济稳定性的图示法在经济学上称为蛛网模型.实际上,需求曲线f 和供应曲线g 的具体形式通常是根据各个阶段商品数量和价格的一些列统计资料得到的.f 取决于消费者对这种商品的需求程度和他们的消费水平,g 则与生产者的生产能力、经营水平等因素有关.对于蛛网模型中,需求曲线和供应曲线交点000(,)P x y 稳定性的判断,可根据两条曲线在点000(,)P x y 的斜率关系来判断:当曲线f 在0P 点斜率的绝对值f K 小于曲线g 在0P 点斜率的绝对值g K 时,0P 点是稳定点.当曲线f 在0P 点斜率的绝对值f K 大于曲线g 在0P 点斜率的绝对值g K 时,0P 点是不稳定点.5.2差分方程模型建立和求解在0P 点附近取函数f 和g 的线性近似分别为00()(0)k k y y x x αα-=--> (3)100()(0)k k x x y y ββ+-=-> (4)两式消去k y ,合并可得1010()()k k x x x x αβ+-=-- (5)因为(5)是一阶线性差分方程,对k 递推可得到,当k →∞时0k x x →,则使得稳定的条件是1αβ<或1αβ< (6)当k →∞时0k x x →,则使得不稳定的条件是1αβ>或1αβ> (7)分析可知方程模型与蛛网模型的一致,且f K α=和1g K β=.六、模型分析对于α和β的含义,需求函数f 的斜率的绝对值α表示商品供应量减少1个单位时价格的上涨幅度;供应函数h 的斜率β表示价格上涨1个单位时生产周期商品供应的增加量.所以α的数值反映消费者对商品需求的敏感度,如果这种商品是生活必需品,消费者处于持币待购状态,商品量少缺,人们立即蜂拥购买,那么α会比较大;反之,若这种商品非必需品,消费者购买心理稳定,或者消费水平低下,则α值小.β的数值反映生产经营者对商品价格的敏感度,如果他们目光短浅,热衷于追逐于一时的高利润,价格稍有上涨立即大量增加生产,那么β值会比较大;反之,若他们素质较高,有长远的计划,则β较小.根据α、β的意义很容易对商场经济稳定与否的条件(6)、(7)做出解释.对于供应函数g ,当β固定时,α越小,需求曲线越平,表明消费者对商品需求的敏感程度越小,越利于经济稳定.对于需求函数f ,当α固定时,β越小,供应曲线越陡,表明生产者对价格的敏感程度越小,越利于经济稳定.反之,α、β当较大,表明消费者对商品的需求和生产者对商品的价格都很敏感,则会导致经济不稳定.从上述分析还可以看到,当市场经济趋向不稳定时政府有两种干预办法.一种办法是使α尽量小,极端情情况是0α=,即需求曲线水平,如图3所示,这时不论供应曲线如何(即不论β多大),总是稳定的.这相当于政府控制物价,无论商品数量多少,价格都不会改变.图3数量价格关系图 另外一种办法是使β尽量小,极端情况0β=,即供应曲线竖直,如图4所示,于是不论需求曲线如何变化(即不管α多大),也总是稳定的.这相当于控制市场上商品数量,当供应少于需求时,政府从外地购买或调拨,投入市场;当供过于求时,政府收购过剩部分,维持商品上市不变.y 0图4 数量价格关系图 七、模型推广如果生产者的管理水平更高一些,他们在决定商品生产数量1k x +时,不是仅根据前一时期的价格k y ,而是根据前两个时期的价格k y 和1k y +.为了简单起见不妨设取二者的平均值11()2k k k y y x +++=,则供应函数为 1()2k k k y y y g ++= (8)在0P 点附近取线性近似时可表示为1010()(2)2k k k k x x y y y β++-=+- (9) 因为需求函数不改变,β仍为原来的含义,则由(3)与(9)式得到21022(1)k k k x x x x αβαβαβ++++=+ (10)方程的通解为1122k k k x c c λλ=+ (1c ,2c 由初始条件确定) (11)特征根1λ和2λ为特征方程220λαβλαβ++=的根,即为1,2λ= (12)当8αβ>时有24αβλ=<- (13) 从而,22λ>,则2λ在单位圆外.当8αβ<时有1,21λ=< (14)平衡点稳定条件为 2αβ<与原有模型中0P 点稳定的条件相比,保持经济稳定的参数α、β的范围放大了(α、β得含义未变).可以想到,这是生产经营者的生产管理水平提高,对市场经济稳定起着有利影响的必然结果.八、参考文献[1] 韩中庚,《数学建模方法与应用》,北京;高等教育出版社,2009.[2]中南大学,数学模型-市场经济中的蜘蛛网模型(图片),,2015年7月.。
蛛网模型

经济应用模型——蛛网模型数理学院班级:姓名:学号:蛛网模型摘要:本文首先从蛛网模型的经济学定性分析出发,分析了蛛网波动的三种类型.然后分别在连续时间的条件下以时滞微分方程的形式和在离散化时间条件下以差分方程的形式两种角度建立模型,对传统的蛛网模型进行了定量分析并讨论了均衡点趋于稳定的条件.关键词:蛛网模型;差分方程;时滞微分方程;稳定性一、蛛网模型介绍蛛网理论(cobweb theorem),又称蛛网模型,是利用弹性理论来考察价格波动对下一个周期产量影响的动态分析,它是用于市场均衡状态分析的一种理论模型. 蛛网理论是20世纪30年代出现的一种关于动态均衡分析方法.许多商品特别是某些生产周期较长的商品(如猪肉,棉花等),他们的的市场价格、数量会随时间的变化而发生变化,呈现时涨时跌、时增时减、交替变化的规律. 1930年美国的舒尔茨、荷兰的丁伯根和意大利的里奇各自独立提出,由于价格和产量的连续变动用图形表示犹如蛛网,1934年英国的尼古拉斯·卡尔多将这种理论命名为蛛网理论.蛛网模型理论是在现实生活中应用较多、较广的动态经济模型,它在一定范围内揭示了市场经济的规律,对实践具有一定的指导作用.根据产品需求弹性与供给弹性的不同关系,将波动情况分成三种类型:收敛型蛛网(供给弹性小于需求弹性)、发散型蛛网(供给弹性大于需求弹性)和封闭型蛛网(供给弹性等于需求弹性).近年来,许多学者对经典的蛛网模型进行了广泛的的研究并做了一些改进,建立了更符合实际经济意义的蛛网模型.在这些研究中,对蛛网模型的假设基本上是基于单一商品市场上,将时间离散化后,从差分方程的角度入手, 研究蛛网模型的稳定性,并通过讨论模型平衡点的稳定性,得到了蛛网模型稳定的条件.实际上,价格是影响商品需求量、供给量因素,但并非唯一因素,例如人们对某种商品的需求量不仅与商品的价格有关,也与人们当期的可支配收入、当期价格上涨率等有关;另一方面,由于市场信息的滞后作用,生产者在进行市场价格与供给预测时,不仅会考虑前一期的价格,还会考虑到前几期甚至更长一段时期商品价格的综合趋势,因此考虑时滞效应的非均衡蛛网模型更具有实际意义.本文建立了蛛网理论的数学模型,给出了相应的数学分析与论证,使蛛网理论有了一个更加完备的理论基础,同时也为这一理论的量化分析提供了新的思路.二、蛛网模型在西方经济学中的定性分析蛛网模型考察的是生产周期较长的商品.蛛网模型的基本假设条件是:商品的本期产量s t Q 决定于前一期的价格1-t P ,即供给函数为)(1-=t s t P f Q .商品本期的需求量d t Q 决定于本期的价格t P ,即需求函数为)(t d t P g Q =.文中用t P 、t Q 、d t Q 、s t Q 分别表示t 时刻的价格、数量、需求量、供给量.蛛网模型是一个动态模型,它根据供求曲线的弹性分析了商品的价格和产量波动的三种类型:“收敛型蛛网”、“发散型蛛网”和“封闭型蛛网”.第一种类型:如图2-1所示,相对于价格轴,需求曲线斜率的绝对值大于供给曲线斜率的绝对值.当市场受到干扰偏离原有的均衡状态以后,实际价格和实际产量会围绕均衡水平上下波动,但波动的幅度越来越小,最后会恢复到原来的均衡点.相应的蛛网称为“收敛型蛛网”.由于某种原因的干扰,如恶劣的气候条件,实际产量由均衡水平e Q 减少为1Q .根据需求曲线,消费者愿意以价格1p 购买全部产量1Q ,于是,实际价格上升为1p . 根据第一期较高的价格水平1p ,按照供给曲线,生产者将第二期的产量增加为2Q ;在第二期,生产者为了出售全部产量2Q ,接受消费者支付的价格2p ,于是实际价格下降为2p .根据第二期较低的价格2p ,生产者将第三期的产量减少为3Q ;在第三期,消费者愿意支付3p 的价格购买全部的产量3Q ,于是实际价格又上升为3p .根据第三期的较高的价格3p ,生产者又将第四期的产量调整为4Q .依此类推,如图2-1所示,实际价格和实际产量的波动幅度越来越小,最后恢复到均衡点E 所代表的水平.由此可见,图2-1中均衡点E 状态是稳定的.也就是说,由于外在的原因,当价格与产量发生波动而偏离均衡状态()e e Q P 、时,经济体系中存在着自发的因素,能使价格和产量自动的恢复均衡状态.在图2-1中,产量与价格变化的路径就形成了一个蜘蛛网似的图形.从图2-1中可以看到,只有当供给曲线斜率的绝对值大于需求曲线斜率的绝对值时,即供给曲线比需求曲线较为陡峭时,才能得到蛛网稳定的结果,相应的蛛网被称为“收敛型蛛网”.在这里,我们看到,除第一期受到外在原因干扰外,其它各期都不会再受新的外在原因干扰,从而前一期的价格能够唯一决定下一期的产量.按照动态的逻辑顺序,我们还看到,生产者片面地根据上一期的价格决定供给量, 消费者被动地消费生产者提供的全部生产量,而价格则由盲目生产出来的数量所决定.第二种类型:如图2-2所示,相对于价格轴,需求曲线斜率的绝对值小于供给曲线斜率的绝对值.当市场受到外力干扰偏离原有的均衡状态以后,实际价格和实际产量会围绕均衡水平上下波动,但波动的幅度越来越大,最后会偏离原来的均衡点.相应的蛛网称为“发散型蛛网”.假定在第一期由于某种原因的干扰,实际产量由均衡水平e Q 减少为1Q .根据需求曲线,消费者愿意支付价格1p 购买全部产量1Q ,于是实际价格上升为1p ,根据第一期较高的价格水平1p ,按照供给曲线,生产者将第二期的产量增加为2Q ;在第二期,生产者为了出售全部产量2Q ,接受消费者支付的价格2p ,于是实际价格下降为2p .根据第二期较低的价格2p ,生产者将第三期的产量减少为3Q ;在第三期,消费者愿意支付3p 的价格购买全部的产量3Q ,于是实际价格又上升为3p ;根据第三期的较高的价格3p ,生产者又将第四期的产量调整为4Q .依此类推,如图2-2所示,实际价格和实际产量的波动幅度越来越大,最后偏离均衡点E 所代表的水平.由此可见,图2-2中均衡点E 所代表的均衡状态是不稳定的.从图2-2可看出,当相对于价格轴,需求曲线斜率的绝对值小于供给曲线斜率的绝对值时,即相对于价格轴而言,需求曲线比供给曲线较为平缓时,才能得到蛛网不稳定的结果.所以供求曲线的上述关系是蛛网不稳定的条件,当市场由于受到干扰偏离原有的均衡状态以后,实际价格和实际产量会围绕均衡水平上下波动,但波动的幅度越来越大,偏离原来的均衡点越来越远.相应的蛛网称为“发散型蛛网”.第三种类型:如图2-3所示,相对于价格轴,需求曲线斜率的绝对值等于供给曲线斜率的绝对值时.市场受到外力干扰偏离原有的均衡状态以后,实际价格和实际产量会按照同一幅度围绕均衡水平上下波动,既不偏离,也不趋向均衡点.相应的蛛网称为“封闭型蛛网”.对于图2-3中,不同时点的价格与供求量之间的解释与前两种情况类似,故从略.从图2-3可看出,当相对于价格轴,需求曲线斜率的绝对值等于供给曲线斜率的绝对值时,即相对于价格轴而言,供求曲线具有相同的陡峭与平缓程度时,蛛网以相同的幅度上下波动,相应的蛛网称为“封闭型蛛网”.三、蛛网模型的数学分析3.1 连续时间条件下的蛛网模型的数学分析在连续时间的条件下,建立起微分方程形式的蛛网模型,研究蛛网模型的稳定性,并对模型结果进行了经济解释.我们考虑基于单一商品的市场的蛛网模型,并假设:时间是连续变量,价格、商品数量随时间连续变化.设某商品价格是时间t 的函数()p p t =,供给量S 由供给函数()S f p =决定,记做()t S .供给是由多种因素决定的, 这里我们略去价格以外的因素, 只讨论供给与价格的关系.考虑到商品生产者对商品信息了解到商品价格的调节有个时间滞后,假定供给是某一时期价格()p t t -∆的线性函数:()()0S t S p t t α=+-∆,()1 其中, 0S 、α是大于零的常数,0t ∆>,α可表示商品的边际供给量.在传统的蛛网理论中,需求是价格的函数,价格作为影响需求的唯一因素,这对正确反映商品价格变化规律具有一定局限性,为更好的反映商品价格变化过程,考虑影响需求的其他因素如价格上涨等.假设需求与价格及价格的上涨率都有关系,需求与价格、价格上涨率负相关.为此建立的需求函数为:()()0.dP D t D P t dtβγ=-- ()2 其中, 0D 、β是大于零的常数,β表示商品的边际需求量. γ的大小反映了商品需求对价格上涨率的依赖程度.需求量与供给量之差()S D -称为过量需求,即需求大于供给的部分.供给者时刻都在确定价格()t P ,根据商品市场在正常的情况下, 商品供需的变化引起价格的变动, 价格的涨速与第t 段时间过剩的需求正相关, 即()()()()000,t dp D S D u S u du dtμ⎡⎤=-+-⎢⎥⎣⎦⎰ ()3 所以有 ()()()22.d p D t S t dtμ=- ()3* 其中,0μ>为价格的调节系数, 反映价格依据超额需求的变动而进行调节时的调整速度和幅度的度量参数.将()1式、()2式代入()3*式可得 ()()()2002.d p dp p t t p t D S dt dtμγμμβμ=--∂-∆-+- ()4 在()4式中,令()()p t x t =,()dp y t dt=,则有()()()()()()()()00,5.dx t y t dt dy t y t x t t x t D S dt μγμμβμ⎧=⎪⎪⎨⎪=--∂-∆-+-⎪⎩当00D S >时,系统()5有唯一平衡点00,0D S αβ⎛-⎫ ⎪+⎝⎭.当需求量等于供给量,即市场出清时的价格为均衡价格,即 βα+-=00_S D p 为均衡价格. 系统()5在00,0D S αβ⎛-⎫ ⎪+⎝⎭处线性近似系统为: ()()()()()(),+.du t v t dt dv t Au t Bu t t Cv t dt⎧=⎪⎪⎨⎪=-∆+⎪⎩ ()6其中,,,A B C μβμαμγ=-=-=-系统()6的特征方程为: ()20.t C A e B λλλ∆---= ()7令z t λ=∆,()7式可化为()2+=0z z mz n e ω++,其中,m C t =-∆,2n A t =-∆,2B t ω=-∆.记()()()2,+z H z h z t z mz n e ω==++,显然()()2,h z t z mz n t =+++ω具有主项2z t .令()()()+H i F iG σσσ=,则 ()()2cos sin ,F n m σσσσσω=--+()()2sin +cos .G n m σσσσσ=-由于函数()()2sin +cos G n m σσσσσ=-的所有零点都是实数,又因为 22μγαβ<≤,0,0,0αβγ>≥≥,则对于()G σ的每一个零点k σ都有不等式()()'0k k F G σσ>成立:如果22μγαβ<≤,0,0,0αβγ>≥≥,那么系统()5的平衡点00,0D S αβ⎛-⎫ ⎪+⎝⎭是局部渐进稳定的.通过对系统()5的分析,可得到如下结论:如果边际商品供给小于边际商品需求,边际商品需求不大于22μγ,并且商品需求对商品价格上涨率的依赖程度γ满足一定条件,那么无论时滞t ∆多么大,商品价格随着时间的变化,稳定的趋于均衡价格_00D S p αβ-=+.也就是说,无论供给者从了解商品需求到调控生产量的时间滞后有多长,对价格的调整有多么不同,只要这些调控的幅度不是很大,商品的价格总是能够回到使供需相等的均衡价格水平;反之,如果边际商品供给大于边际商品需求,边际商品需求不大于22μγ,当时滞t ∆取一定值时,系统会出现Hopf 分支,也就是说,价格会围绕均衡价格上下波动,而且商品的价格最终不能回到均衡价格.3.2 离散时间条件下的蛛网模型的数学分析最简单的市场经济模型是单一商品市场模型,在时间离散化后的条件下,假设商品的供给量、需求量,只与该商品的价格有关,由需求量等于供给量建立的方程,即均衡方程,求得其解即是均衡价格.若进一步假定需求、供给是价格的线性函数,可以得到传统线性蛛网模型.最后在需求、供给是价格的非线性函数的条件下,可以得到非线性蛛网模型.3.2.1 蛛网模型的线性分析由蛛网模型的基本假设条件,本期的需求量是本期价格的线性函数,即t t P Q ⋅-=βαd ,β表示商品价格减少1个单位时需求量的上涨幅度;而本期的供给量是由上一期的价格决定的,为上一期价格的线性函数,即1s -⋅+-=t t P Q γδ,γ表示商品价格增加1个单位时供给量的上涨幅度.该模型可以用以下三个联立的方程式来表示:d ,t t Q P αβ=-⋅ ()8s 1,t t Q P δγ-=-+⋅ ()9 d s .t t Q Q = ()10式中,β、∂、γδ和均为常数,且均大于零.d t Q 为第t 期的需求量,s t Q 为第t 期的供给量,t P 为第t 期的价格,1-t P 为第1-t 期的价格.将前面的()8式和()9式代入()10式可得1-.t t P P αβδγ-⋅=-+⋅ ()11由此可得第t 期的产品价格为⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-+++⎪⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+++⎪⎪⎭⎫ ⎝⎛-=++⎥⎦⎤⎢⎣⎡++⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=++⎪⎪⎭⎫ ⎝⎛-=----233222111βγβγβδαβγβγβδαβγβδαβδαβγβγβδαβγt t t t t P P P P P2101t t P γαδγγγβββββ-=⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+=-++-+-++-⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 011t t P γβγαδγββγβ⎛⎫-- ⎪⎛⎫⎛⎫+⎝⎭=-+⋅ ⎪ ⎪+⎝⎭⎝⎭+ 01.t t P γαδγββγβ⎡⎤⎛⎫⎛⎫+=-+--⎢⎥ ⎪ ⎪+⎢⎥⎝⎭⎝⎭⎣⎦()12 又因为在市场均衡时,均衡价格为1-==t t e P P P ,所以,由()11式可得均衡价格为γβδα++=e P ()13 均衡价格是一种理想状态,即在此价格水平下,每个人的需求都得到满足,而且不会有商品卖不出去.将()13式代入()12式可得()t 001.t t e te e P P P P P P γγββγβ⎡⎤⎛⎫⎛⎫=-+--⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎛⎫=--+ ⎪⎝⎭()14分析()14式,可以得到以下三种情形第一种情况,若1<βγ,当∞→t 时,则此时e t P P →.也就是说,价格t P 随着时间的推移,其波动幅度愈来愈小,最终趋向于均衡价格e P .事实上,此时因需求弹性P P e d βαβ-=,供给弹性PP e S γδγ+-=,当1<βγ时,可推得s d e e >,即供给弹性的绝对值小于需求弹性的绝对值(需求曲线斜率的绝对值小于供给曲线斜率的绝对值),蛛网模型是收敛的.在收敛性蛛网中,价格变动引起的需求量变动大于价格变动引起的供给量的变动,因而任何超额需求或超额供给只需较小的价格变动即可消除.同时价格变动引起的下一期供给量的变动较小,从而对当期价格发生变动的作用较小,这意味着超额需求或超额供给偏离其均衡量的幅度以及每期成交价格偏离均衡价格的幅度,在时间序列中将是逐渐缩减的,并最终趋向其均衡产量e Q 和均衡价格e P .第二种情况,若1>βγ,当∞→t 时,则此时∞→t P .这说明,需求曲线斜率的绝对值(β)小于供给曲线斜率的绝对值(γ)时,或供给弹性较大而需求弹性较小时,市场价格将振荡至无穷大,蛛网模型是发散的.在发散型蛛网中,价格变动引起的供给量的变动大于价格变动引起的需求量的变动.当出现超额供给时,为使市场上供给者卖出所有的产品,要求价格大幅度下跌,这将会导致下一期的供给量减少,以致该期出现大量的供给短缺,供给的严重不足导致价格大幅度上扬,由此导致下一期供给量大幅度增加和价格大幅度下跌.在这种情况下,一旦失去均衡,以后各期的供给过剩或短缺的波动幅度以及成交价格波动的幅度,都将离均衡价格e P 越来越远.第三种情况,若1=βγ,当∞→t 时为常数.这说明,相对于价格轴,需求曲线斜率的绝对值(β)等于供给曲线斜率的绝对值(γ)时,即市场价格一旦偏离均衡状态,则以后各期的价格及产量的变动序列就表现为围绕均衡值循环往复地上下振荡,既不进一步偏离,又不进一步逼近均衡价格e P .这就是“封闭型蛛网”的情形.从上面的讨论,我们可以看出,均衡点最终能否趋于稳定状态关系到该模型的分类,因此我们有必要对均衡点趋于稳定的条件作进一步讨论.3.2.2 蛛网模型的非线性分析记第t 时段商品的数量为t x ,价格为t y ,自然数t 表示时段, ,2,1=t .这里把时间离散化为时段,每个时段相当于商品的一个生产周期,蔬菜、水果是一个种植周期,肉类是牲畜的饲养周期.价格与产量紧密相关,可以用一个确定的关系来表现,即设().t t y f x =该函数反映消费者对这种商品的需求关系,称为商品数量越多,格就越低,所以f 是单调递减函数.因此在图1-3中用一条下降曲线f 表示它,称为需求曲线.又假设下一个时段的产量1+t x 是生产者根据上一时期的价格决定的,即设()1.t t x g y +=该函数反映生产者的供应关系,品的价格越高,供给量就越大,g 是单调增加函数. 在图1-3中用一条上升曲线g 表示它,g 称为供给曲线.为了表现出t x 和t y 的变化过程,我们可以借助已有的函数f 和g ,当供需相等时,如图1-3所示求函数f 与供给函数g 相交于()000,y x P ,点0P 即是市场出清的均衡状态.在进行市场经济分析时,f 取决于消费者对某种商品的需求程度和消费水平等因素,g 取决于生产者的生产、经营等能力,当知道具体的需求函数与消费函数时,可以根据f 、g 曲线的具体性质来判定在平衡点()000,y x P 的稳定性.一旦需求曲线和供应曲线确定下来, 商品数量和价格是否趋向稳定状态, 就完全有这两条曲线在平衡点()000,y x P 附近的形状决定.建立差分方程:()t t x f y = ()15()t t y g x =+1 ()16设()000,y x P 点满足:()00x f y =,()00y g x =,设()'0f x α= ,()'01.g y β=在()000,y x P 点附近取f 、g 的一阶泰勒展式,线性近似为()00x x y y t t --=α ()17()001y y x x t t -+=+β ()18 合并()17、()18两式,并消去()0t y y -可得()1010.t t x x x αβαβ++-+= ()19上式是关于t x 的一阶线性差分方程,它是原来方程的近似模型,这是客观实际问题的近似模拟,解这个一阶线性差分方程得:()()()()()()()()()()()()()()()10210010211010100-1-1111111.t t t t t t t t tx x x x x x x x x x x x x x x αβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβ+---=++⎡⎤⎡⎤=-++++=-++-+⎣⎦⎣⎦=⎡⎤=-++-+-++-+⎣⎦⎡⎤=-+--⎣⎦=--+由此可得,当∞→t 时,0x x t →,即()000,y x P 点稳定条件是1<αβ,即βα1<,需求曲线f 在点()000,y x P 的切线斜率绝对值小于供给曲线g 在该点的切线斜率绝对值;反之,()000,y x P 点不稳定的条件是1>αβ,即βα1>,需求曲线f 在点()000,P y x 的切线斜率绝对值大于供给曲线g 在该点的切线斜率绝对值.这个非线性分析使传统的线性蛛网模型的分析有了进一步的推广.西方经济学家认为,蛛网模型解释了某些生产周期较长的商品的产量和价格的波动的情况,是一个有意义的动态分析模型,对理解某些行业产品的价格和产量的波动提供了一种思路.但是,这个模型还是一个很简单的和有缺陷的模型.实际上在大多数情况下, 商品生产数量并不只是根据前一时期的价格决定的,具有相当管理经验的生产经营者在决定产品数量1+t Q 时不会仅仅只参考前一期的价格t P ,可能还会对更前几期的价格做一定的比较和分析,尤其像生产者始终只是简单地把上一期价格作为本期价格预期并以此作为决定产量的依据,这种非理性假设与现实是极不相符的.四、结束语在一般的经济学原理分析中,对蛛网模型理论都给予了动态分析,但分析过程大都仅仅从经济学供求关系角度对产品产量与价格的波动过程进行解释.这种说明性的分析与论证,尽管具有形象、直观的特点.但从数学角度来看,这类分析可以说是不很严密的.本文分别在时间连续的条件下从微分方程的角度与时间离散的条件下从差分方程的角度入手,对蛛网模型进行了数学上的分析与论证,为这一理论的量化分析提供了新的思路.参考文献[1]高鸿业.西方经济学(微观部分)[M].中国人民大学出版社,2007.[2]姜启源,谢金星.数学模型(第三版)[M].高等教育出版社,2003.[3]梁小民.微观经济学[M].中国社会科学出版社,1996.[4]王树禾.微分方程模型与混沌[M].中国科学技术出版社,1999.[5]蒋中一.数理经济学的基本方法[M].商务印书馆,2004.[6]萨缪尔森.经济学[M].华夏出版社,2000.。
差分方程

第八讲 差分方程模型一、差分方程介绍规定t 只取非负整数。
记为变量在t 点的取值,则称t y y t t t y y y −=Δ+1为的一阶向前差分,简称差分,称Δ为的二阶差分。
类似地,可以定义的阶差分。
t y t t t t t y t t y y y y y y +−=Δ−Δ=ΔΔ=+++12122)(t y t y n t ny Δ由及的差分给出的方程称为的差分方程,其中含的最高阶差分的阶数称为该差分方程的阶。
差分方程也可以写成不显含差分的形式。
例如,二阶差分方程也可改写成t y t 、t y t y t y 02=+Δ+Δt t t y y y 012=+−++t t t y y y 。
满足一差分方程的序列称为差分方程的解。
类似于微分方程情况,若解中含有的独立常数的个数等于差分方程的阶数时,称此解为该差分方程的通解。
若解中不含任意常数,则称此解为满足某些初值条件的特解。
t y 称如下形式的差分方程)(110t b y a y a y a t n t n t n =+++−++L (1) 为阶常系数线性差分方程,其中是常数,n n a a a ,,,10L 00≠a 。
其对应的齐次方程为0110=+++−++t n t n t n y a y a y a L (2)容易证明,若序列与均为(2)的解,则也是方程(2)的解,其中为任意常数。
若是方程(2)的解,是方程(1)的解,则也是方程(1)的解。
)1(t y )2(t y )2(2)1(1t tt y c y c y +=21,c c )1(t y )2(t y )2()1(t t t y y y +=方程(1)可用如下的代数方法求其通解: (I )先求解对应的特征方程(3)00110=+++−a a a n nL λλ(II )根据特征根的不同情况,求齐次方程(2)的通解。
(i )若特征方程(3)有n 个互不相同的实根n λλ,,1L ,则齐次方程(2)的通解为t n n t c c λλ++L 11 (为任意常数)n c c ,,1L (ii )若λ是特征方程(3)的重根,通解中对应于k λ的项为t k k tc c λ)(11−++L ,),,1(k i c i L =为任意常数。
2.6市场经济中的蛛网模型
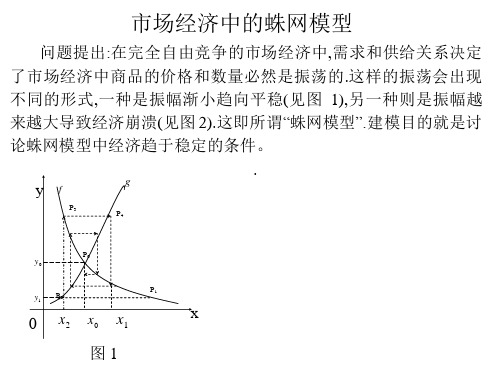
问题提出:在完全自由竞争的市场经济中,需求和供给关系决定 了市场经济中商品的价格和数量必然是振荡的.这样的振荡会出现 不同的形式,一种是振幅渐小趋向平稳(见图 1),另一种则是振幅越 来越大导致经济崩溃(见图 2).这即所谓“蛛网模型”.建模目的就是讨 论蛛网模型中经济趋于稳定的条件。 . g y f
n
∑(yk =1源自y k ) = ( y 2 y1 )∑ (αβ ) k 1 k +1
k =1
n
即
y n +1 = y1 + ( y 2 y1 )∑ (αβ ) k 1
k =1
n
lim y n +1
n →∞
1 = y1 + ( y 2 y1 ) 1 + αβ
,
αβ < 1
说明经济趋于稳定的条件是 αβ < 1. 问题:试证 lim xn+1 = x0 , lim y n+1 = y0 . n→∞ n→∞ 注意到:
x k +1 x 0 = β ( y k y 0 ), β > 0 ( β = g ′( x 0 ))
分析
x k , y k 的极限情况: xk +1 = x0 β y0 + β yk
= x0 βy 0 + β [ y 0 α ( x k x0 )]
= x0 (1 + αβ ) αβxk
由此
xk +1 x k = αβ ( x k x k 1 ) = … = (αβ ) k 1 ( x2 x1 )
n
∑(x
k =1
k +1
xk ) = ( x2 x1 )∑ (αβ ) k 1
蛛网模型的数学推导

假定供给和需求函数都是线性的,蛛网模型可由以下差分方程组表示:Q st =-a+bPt-1(1)Q dt =c-dPt(2)Q s t=Qdt(3)(1)式表示,第t年供给量取决于第t-1年的成交价格,(2)表示需求量取决于当年市场价格,(3)式表示市场必须是出清的,因此每年供给量均等于需求量。
a、b、c、d为常数(参数),且都为正数。
将(1)式和(2)式代入(3)式可得:c-dPt =-a+bPt-1(4)从(4)式中解出Pt:P t =(-bd)Pt-1+a+cd(5)在(5)式中假定t=1可得第1年价格为:P 1=(-bd)P+a+cd(6)以此类推:P 2=(-bd)P1+a+cd(7)将(6)式代入(7)式中:P 2=(-bd)2P+(-bd)a+cd+a+cd重复这一过程,可得到以初始价格P0来表示的第3年、第4年、……第n 年的价格:P n =(-bd)n P+[∑(-bd)k]a+cd=(-bd)n P+a+cb+d[1-(-bd)n] (8)又因为达到均衡点后,价格不再变化,假定第t年达到均衡,则P t =Pt+1=……=PE(9)将(9)式代入(5)式可得均衡价格PE:P E =a+cb+d(10)将(10)式代入(8)式并整理:P n =(-bd)n P+PE[1-(-bd)n]=(P0-PE)(-bd)n+PE(11)从(11)式可得出下列结论:(ⅰ)如果|-bd|<1,则:limPn=PE,即Pn趋近于PE,市场价格将无限趋近均衡价格,蛛网周期是收敛的。
而|-bd|<1,说明d<b,或供给曲线斜率大于需求曲线,供给弹性较小而需求弹性较大。
(ⅱ)如果|-bd|>1,则:limPn=∞,市场价格将振荡至无穷大,蛛网周期是发散的。
此时,d<b,即供给曲线斜率小于需求曲线,供给弹性较大而需求弹性较小。
(ⅲ)如果|-bd|=1,则P2n=P,P2n+1=2PE-P,价格在这两个值之间来回振荡,蛛网周期是循环的,此时d=b,即供给曲线斜率与需求曲线斜率相等。
蛛网模型2

时,即p0点稳定的条件是αβ<1或α<1/β 时,即0p点不稳定的条件是αβ>1或α>1/β
蛛网模型的实际应用
有关数据
建立数学模型
在数学模型中,被解释变量设定为各专业的人才供求,解释变量为各专业 的报酬。
各专业人才供给( 需求) 受报酬的影响,当市场报酬增加时,各专业人才供 给( 需求) 也随之产生变化,它们之间具有某种函数关系。人才供给( 需求) 除了
ห้องสมุดไป่ตู้
改进优化模型
根据原蛛网模型的缺陷进行修改。市场需求取决于市场预期报酬的,
而市场预期报酬不仅要考虑前一期大学生心理上的报酬,又要考虑上一
期市场上的实际报酬,即市场预期报酬。学校的供给量与实际就业人数 是不相等的,其中存在就业率这一因素,供应量乘以就业率才是市场上
较准确的需求量,从而引出改进后的蛛网模型如下:
蛛网模型 记第k时段商品的数量为xk,价格yk,k=1,2,3.....把时间离散化 为时段,1个时段相当于商品的一个生产周期、种植周期或饲养周期同一 时段,商品的价格 yk=f(xk) 下一段商品的数量xk+1由上一时段价格y决定,设 xk+1=h(yk)或yk=g(xk+1) 这里g是h的反函数。 (2) (1)
受市场报酬的影响外,还受一些其他的随机因素影响,将其他随机因素归结到
随机变量 σ 与 α 中。将 09 年视为本期,将 05 年视为上一期( 由于学校根据本 届毕业生所得报酬来确定本届新生的计划招生人数,因此选取 4 年为一个周期 ) 。根据原蛛网模型给出人才供求与市场报酬之间的关系模型:
由表 3 中的样本数据,用 Eviews 软件估计得到以下样本回归方程:
改进后的模型中各专业人才供求与市场报酬之间的关系模型为:
蛛网理论

附录:蛛网理论之推导 一、一阶常系数差分方程差分:1t t y y −−,令其等于t y Δ(差分符号)含有差分符号t y Δ的方程可称为差分方程,亦即含有1t t y y −−的方程 例如,1t t y ay c −+= ∵1t t t y y y −−=Δ∴1t t t y y y −=Δ+则,1(1)t t y a y c −Δ++=(一阶差分方程)又例如,11121()()2t t t t t t t t t 2t y y y y y y y y y y −−−−−ΔΔ=Δ−Δ=−−−=−+−(二阶差分方程) 所谓一阶常系数差分方程的一般式:1()t t y ay f t −+=,其中()f t 为已知函数,当()f t 为常数时,称为常系数差分方程..e g 当时()0f t = ,即10t t y ay −+=1t t y ay −=− 当时,1t =10y ay =−当时, 2t =221()y ay a =−=−0y y y ……当时, t n =0()n n y a =− ∴,令0()t t y a =−0y A = 则,()t t y A a =− 一般来说,一阶常系数差分方程的通解为:()()t t y G t A a =+− c (常数)时,1t t y ay c −+=当()f t =讨论:(i )1a ≠− 当时,1t =10y c ay =−当时,2t =21()0y c ay c a c ay =−=−−222201()(1)()[()1()a y a c a y c a a −−=−+−=+−−−i 0y 0 当时,3t =23320[(1)()][1(1)]()y c ay c a a c a y c a a a y =−=−−+−=−−+− 323201()[1()()]()[()1()a y c a a a y c a y a −−=+−+−+−=+−−−i 30) 附录: 22()(a b a b a b −=+− 3322()(a b a b a ab b −=−++)……则,001()[]()()()1()11t t t t a c y c a y y a a −−=+−=+−−−++i ca a− 令01c y A a−=+,()1t t c y A a =+−+a(ii ) ∴1a =−1t t y y c −−= ∵10y c y =+2120y c y c y =+=+10n n y c y n c y −=+=+i∴0t y t c y =+i 令0y A =, 则t y A t c =+i 二、蛛网条件根据蛛网假设,有1(,(,)t t tt q S P q D P )βα−=⎧⎨=⎩ (α、β分别为需求参数和供给参数) 设为供求均衡价格,为均衡条件下的供需量*P *q **11(,)(,)(,t t t t q S P q q S P S P )βββ−−=⇒−=−根据拉格朗日中值定理**1*(,)(,)(t t Pt q q S P S P S P P ββ−′−=−=−i *1)−* (1) 同理, (2) ***(,)(,)(,)()t t t t Pt q D P q q D P D P D P P ααα′=⇒−=−=−i(1)(2),得:***1**1***1(t P P t t P t PP P S S P P P P D P P D −−′′−=⇒−=′′−i )− 整理,得:***1**(1P Pt t P PS S P P D D −′′−=−′′P显然,此为一阶常系数差分方程,其中**P P S a D ′=−′,***(1P PS c P D ′=−′ 若**PP S D ′≠′,则,*********00******(1(1)[)()()11P P t t P P P t P P P P P PS S P P D D S P P P P P S S D D D D ′′−−′′′=+−=+−′′*P S ′′′−−′′ 令*0P P A −=,则***()t Pt PS P P A D ′=+′ ①当**1PPS D ′<′时,, t →∞*t P P → 价格会趋向均衡价格,收敛的蛛网 ②当**1PPS D ′>′时,, t →∞t P →∞ 价格越来越远离均衡价格,发散型蛛网 ③当**1PPS D ′=′时,, t →∞*t P P A =± 价格围绕均衡价格作等幅摆动,振幅为A ,封闭型蛛网 所以,蛛网模型的稳定条件为**1PP S D ′<′。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n
x1 (k 1) bi xi (k ) (设至少1个bi>0) i 1
x i
1
(k
1)
s i
x i
(k),
i
1,2,,
n
1
b1
s 1
b2 0
bn1 0
bn
0
x(k) [x1(k), x2 (k),xn (k)]T
~按年龄组的分布向量
L
s2
0
x(k 1) Lx(k)
x(k) Lk x(0)
设x1偏离x0
x1 y1 x2 y2 x3
xk x0 , yk y0
xk x0 , yk y0
P1 P2
P3 P0
P P P P
1
2
3
0
P0是稳定平衡点
P0是不稳定平衡点
y
f
y2 P3
yy30 y1
P2
g
y
P4 曲线斜率
P0 | K f || K g | y0
P1
0 x2 x0 x3 x1 x
~ 商品数量减少1单位, 价格上涨幅度 xk1 x0 ( yk y0 )
~ 价格上涨1单位, (下时段)供应的增量
~ 消费者对需求的敏感程度 小, 有利于经济稳定
~ 生产者对价格的敏感程度 小, 有利于经济稳定
1 经济稳定
结果解释
经济不稳定时政府的干预办法
1. 使 尽量小,如 =0
y
g
需求曲线变为水平 y0 以行政手段控制价格不变
0
2. 使 尽量小,如 =0 y
供应曲线变为竖直
靠经济实力控制数量不变
0
f
x g
f
x0
x
模型的推广 生产者管理水平提高 xk1 h( yk )
• 生产者根据当前时段和前一时 段的价格决定下一时段的产量。
xk 1
h
y k
y k 1
2
设供应函数为
生产者的供应关系 供应函数 xk 1 h( yk ) 增函数
y
f
g
y0
P0
0
x0
yk g (xk 1)
f与g的交点P0(x0,y0) ~ 平衡点 一旦xk=x0,则yk=y0,
xk+1,xk+2,…=x0, yk+1,yk+2, …=y0
x
蛛 网 模 型 yk f (xk ) xk1 h( yk ) yk g(xk1)
4) x(k) ck x*, x* [1, s1, s1s2 ,, sn1 ]T
xi1(k ) si xi (k ), i 1,2,, n 1
0
sn1 0
预测任意时段种群
~Leslie矩阵(L矩阵)
按年龄组的分布
稳定状态分析的数学知识
• L矩阵存在正单特征根1,
k
1
,
k
2,3,n
特征向量
x*
1,
s1
1
,
s1s2
2 1
, ,
s s s
T
12
n1
n1 1
• 若L矩阵存在bi, bi+1>0, 则 k 1, k 2,3,, n
x* 1, s1, s1s2 ,s1s2 sn1 T
~ 各年龄组种群 数量不变
稳态分析
3)=1时 Lx* x* x* 1, s1, s1s2,s1s2 sn1 T
b1 b2 bn1 bn
s 1
0
0
0
L
s2
0
0
sn1 0
b1 b2s1 bns1s2 sn1 1
~ 1个个体在整个存活 期内的繁殖数量为1
1, 2~特征根,即方程 22 0 的根
平衡点稳定,即k, xkx0的条件:
1, 2
1
1,2
( )2 8
4
平衡点稳定条件 2
1, 2
2
比原来的条件 1 放宽了
2 按年龄分组的种群增长
• 不同年龄组的繁殖率和死亡率不同 • 以雌性个体数量为对象 • 建立差分方程模型,讨论稳定状况下种群的增长规律
lim x(k ) cx*
k
k
1
1) x(k) ck x* ~ 种群按年龄组的分布趋向稳定,
x*称稳定分布, 与初始分布无关。
2) x(k 1) x(k) ~ 各年龄组种群数量按同一
xi (k 1) xi (k) 倍数增减, 称固有增长率
与基本模型 x(k 1) Lx(k) 比较
3)=1时 x(k 1) x(k) cx*
xk 1
x 0
[( y k
y k
1)/2源自y] 0需求函数不变 y y (x x )
k
0
k
0
2xk2 xk1 xk 2(1)x0 , k 1,2,
二阶线性常系数差分方程
x0为平衡点 研究平衡点稳定,即k, xkx0的条件
模型的推广
2x x x 2(1)x
k2
k 1
k
0
方程通解 xk c11k c2k2 x0 (c1, c2由初始条件确定)
假设与建模
• 种群按年龄大小等分为n个年龄组,记i=1,2,… , n • 时间离散为时段,长度与年龄组区间相等,记k=1,2,… • 第i 年龄组1雌性个体在1时段内的繁殖率为bi • 第i 年龄组在1时段内的死亡率为di, 存活率为si=1- di
假设 与
建模
xi(k)~时段k第i 年龄组的种群数量
1 市场经济中的蛛网模型
供大于求
价格下降
现 象
数量与价格在振荡
增加产量
价格上涨
减少产量 供不应求
描述商品数量与价格的变化规律
问 题 商品数量与价格的振荡在什么条件下趋向稳定
当不稳定时政府能采取什么干预手段使之稳定
蛛网模型
xk~第k时段商品数量;yk~第k时段商品价格
消费者的需求关系 需求函数 yk f (xk ) 减函数
0
P3 f
g P4
P2
P0 | K f || K g
P1
x0
x
方程模型 yk f (xk )
在P0点附近用直线近似曲线
yk y0 (xk x0 ) ( 0)
xk 1 h( yk )
xk1 x0 ( yk y0 ) ( 0)
x x (x x )
k 1
0
k
0
x x ( )k (x x )
k 1
0
1
0
1 ( 1/ )
1 ( 1/ )
xk x0 xk
P0稳定 | K f || K g | P0不稳定| K f || K g |
方程模型与蛛网模型的一致 K f 1/ Kg
结结果果解解释释
考察 , 的含义
xk~第k时段商品数量;yk~第k时段商品价格
yk y0 (xk x0 )
且
lim
k
x(k )
1k
cx* , c是由bi, si, x(0)决定的常数
解 释
x(k) Lk x(0) L对角化 L P[diag(1,n )]P1
Lk P[diag(1k ,kn )]P1 P的第1列是x*
lim
k
x(k)
1k
Pdiag(1,0,0)P1x(0)
cx*
稳态分析——k充分大 种群按年龄组的分布
